Prediction of Thrust Force and Cutting Torque in Drilling Based on the Response Surface Methodology
Abstract
1. Introduction
2. Materials and Methods
2.1. Selection of Materials
2.2. Response Surface Methodology
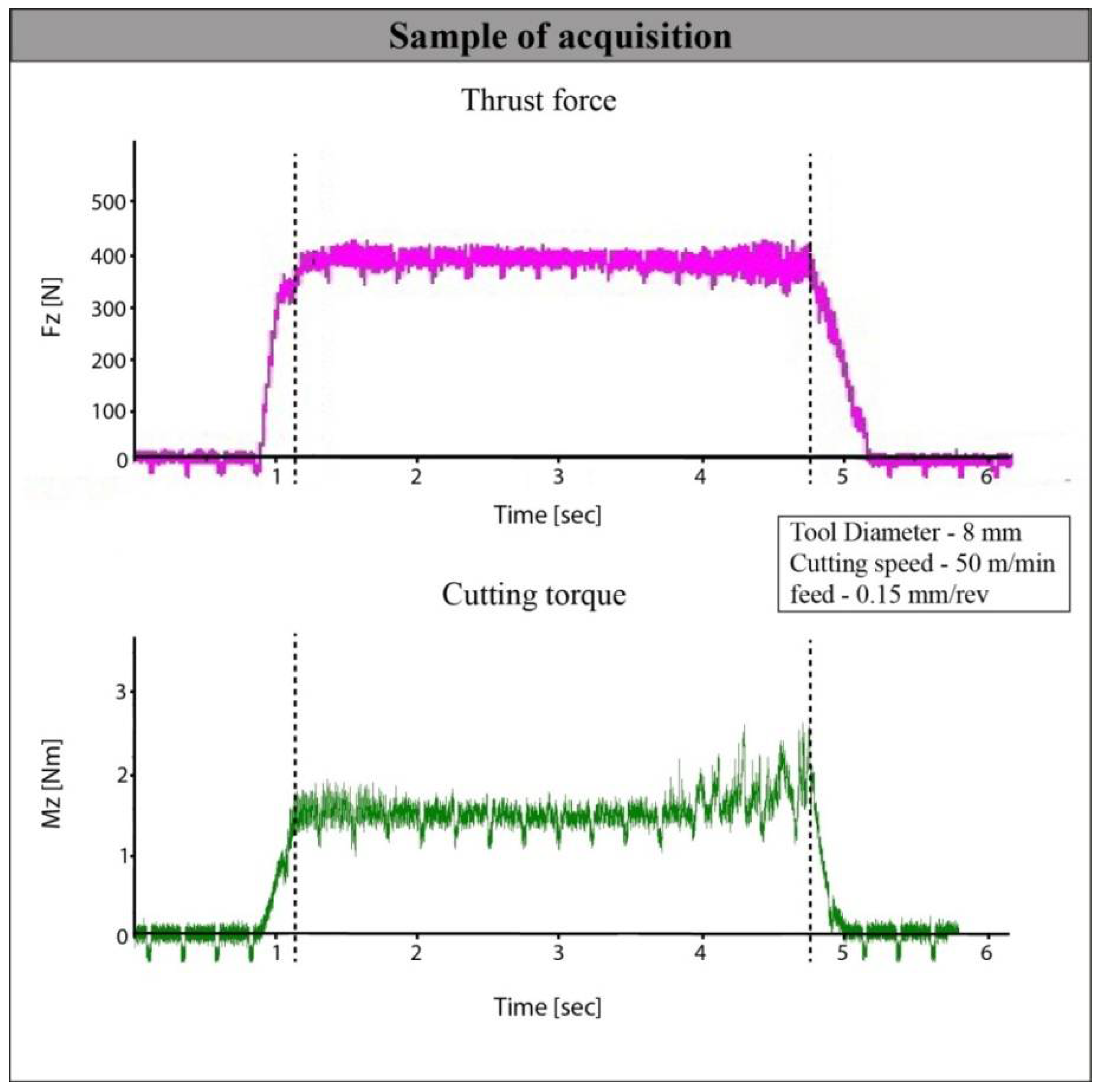
2.3. Experimental Details
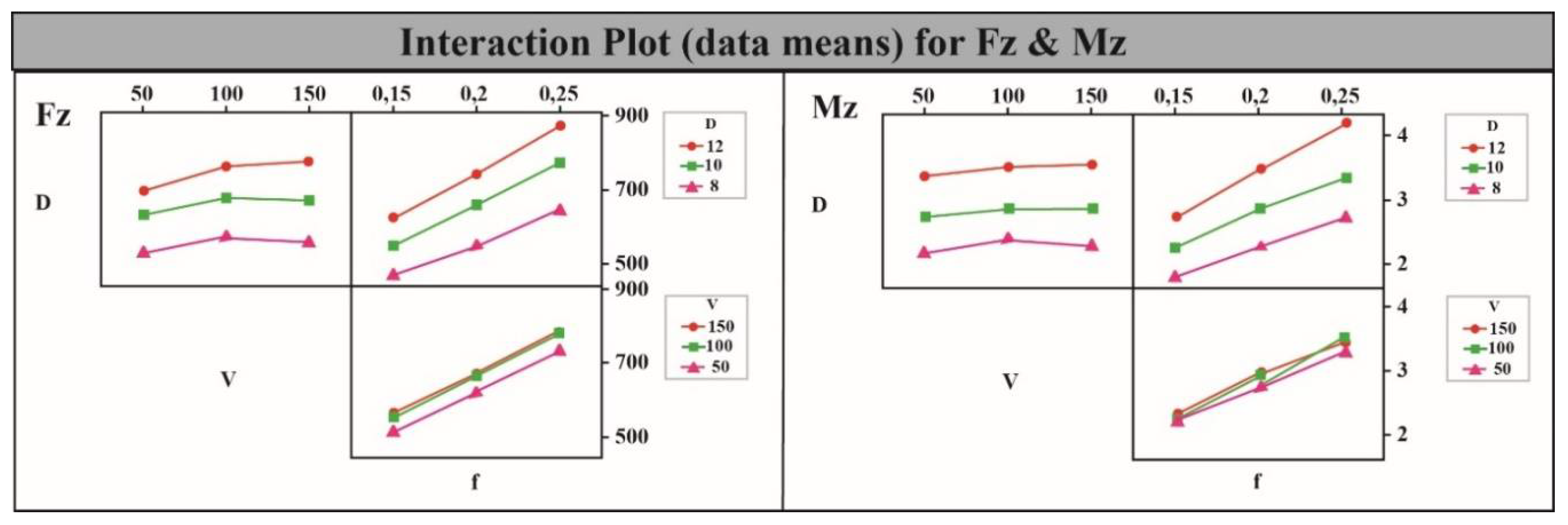
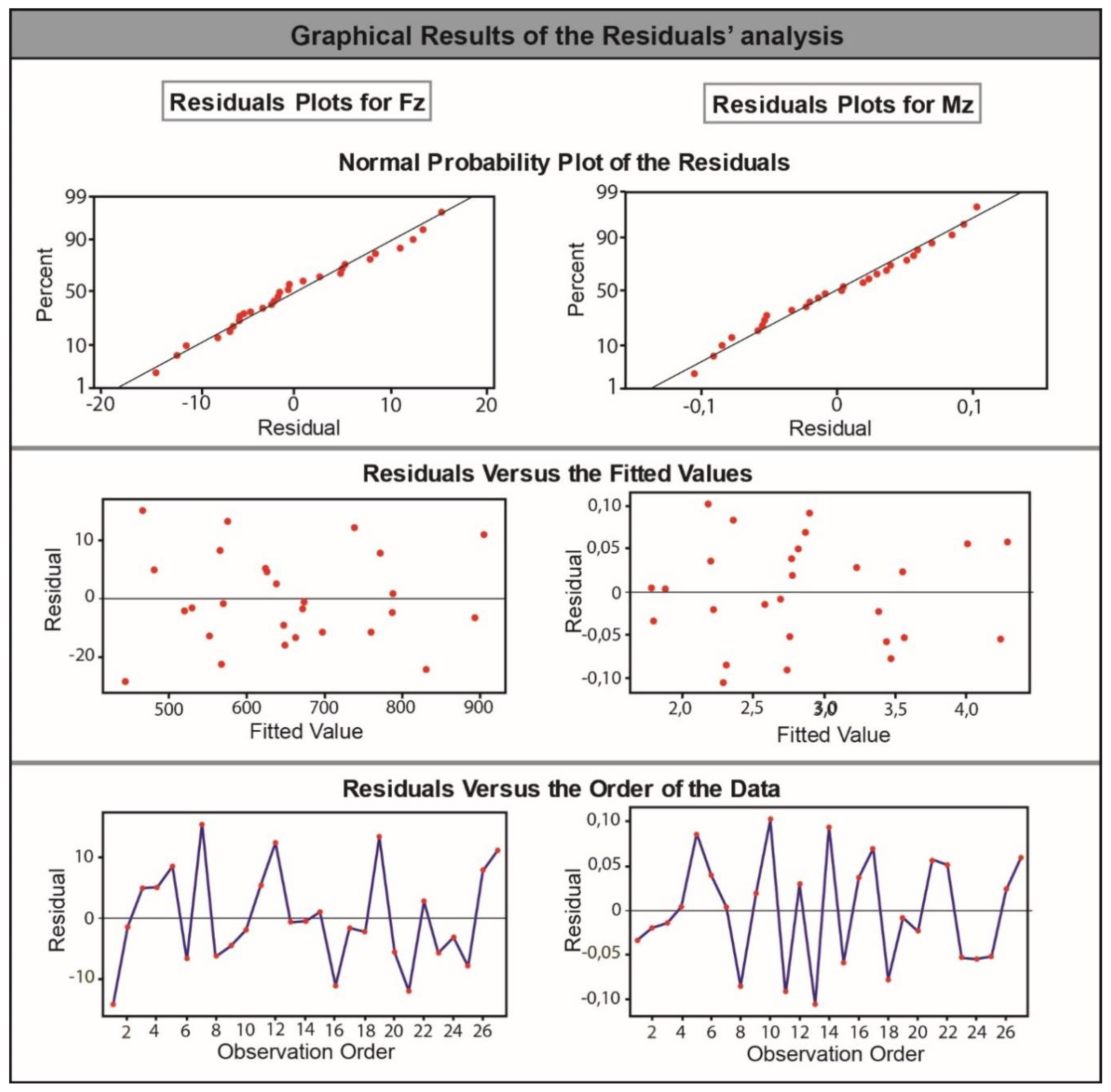
3. Results
RSM-Based Predictive Models
- Y is the response,
- Xi stands for the coded values, and
- bi stands for the model regression coefficients.
- D is the diameter of the tool in mm,
- f is the feed rate in mm/rev, and
- V is the cutting speed in m/min.
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Kumar, V.; Singh, H. Machining optimization in rotary ultrasonic drilling of BK-7 through response surface methodology using desirability approach. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 83. [Google Scholar] [CrossRef]
- Balaji, M.; Venkata, K.; Mohan Rao, N.; Murthyd, B.S.N. Optimization of drilling parameters for drilling of TI-6Al-4V based on surface roughness, flank wear and drill vibration. Measurement 2018, 114, 332–339. [Google Scholar] [CrossRef]
- Balaji, M.; Murthy, B.S.N.; Rao, N.M. Multi response optimization of cutting parameters in drilling of AISI 304 stainless steels using response surface methodology. Proc. Inst. Mech. Eng. Part B J Eng. Manuf. 2018, 232, 151–161. [Google Scholar] [CrossRef]
- Nanda, B.K.; Mishra, A.; Dhupal, D.; Swain, S. Experimentation and optimization of process parameters of abrasive jet drilling by surface response method with desirability based PSO. Mater. Today Proc. 2017, 4, 7426–7437. [Google Scholar] [CrossRef]
- Boyacı, A.I.; Hatipoglu, T.; Balci, E. Drilling process optimization by using fuzzy-based multi-response surface methodology. Adv. Ind. Eng. Manag. 2017, 12, 163–172. [Google Scholar] [CrossRef]
- Ramesh, M.; Gopinath, A. Measurement and analysis of thrust force in drilling sisal-glass fiber reinforced polymer composites. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2017; Volume 197. [Google Scholar]
- Jenarthanan, M.P.; Karthikeyan, M.; Naresh, N. Mathematical modeling of delamination factor on drilling of ARALL composites through RSM. Multidscip. Model. Mater. Struct. 2017, 13, 578–589. [Google Scholar] [CrossRef]
- Rajamurugan, T.V.; Shanmugam, K.; Palanikumar, K. Mathematical Model for Predicting Thrust Force in Drilling of GFRP Composites by Multifaceted Drill. Indian J. Sci. Technol. 2013, 6, 5316–5324. [Google Scholar] [CrossRef]
- Rajkumar, D.; Ranjithkumar, P.; Jenarthanan, M.P.; Sathiya Narayanan, C. Experimental investigation and analysis of factors influencing delamination and thrust force during drilling of carbon-fibre reinforced polymer composites. Pigment Resin Technol. 2017, 46, 507–524. [Google Scholar] [CrossRef]
- Ankalagi, S.; Gaitonde, V.N.; Petkar, P. Experimental Studies on Hole Quality in Drilling of SA182 Steel. Mater. Today Proc. 2017, 4, 11201–11209. [Google Scholar] [CrossRef]
- Natarajan, U.; Suganthi, X.H.; Periyanan, P.R. Modeling and Multiresponse Optimization of Quality Characteristics for the Micro-EDM Drilling Process. Trans. Indian Inst. Met. 2016, 69, 1675. [Google Scholar] [CrossRef]
- Kyratsis, P.; Garcia-Hernandez, C.; Vakondios, D.; Antoniadis, A. Thrust force and torque mathematical models in drilling of Al7075 using the responce surface methodology. In Book Design of Experiments in Production Engineering; Davim, J.P., Ed.; Springer International Publishing: Berlin, Germany, 2016; pp. 151–164. ISBN 978-3-319-23837-1. [Google Scholar]
- Pereira, R.B.D.; Leite, R.R.; Alvim, A.C.; Alvim, A.C.; Paiva, A.P.; Balestrassi, P.P.; Ferreira, J.R.; Davim, J.P. Multivariate robust modeling and optimization of cutting forces of the helical milling process of the aluminum alloy Al 7075. Int. J. Adv. Manuf. Technol. 2018, 95, 2691. [Google Scholar] [CrossRef]
- Zou, X.L.; Yan, H.; Chen, X.H. Evolution of second phases and mechanical properties of 7075 Al alloy processed by solution heat treatment. Trans. Nonferrous Met. Soc. Chin. 2017, 27, 2146–2155. [Google Scholar] [CrossRef]
- John, P.; Davis, R. Performance Study of Electrical Discharge Machining Process in Burn Removal of Drilled Holes in Al 7075. Cogent Eng. 2016, 3, 1–7. [Google Scholar] [CrossRef]

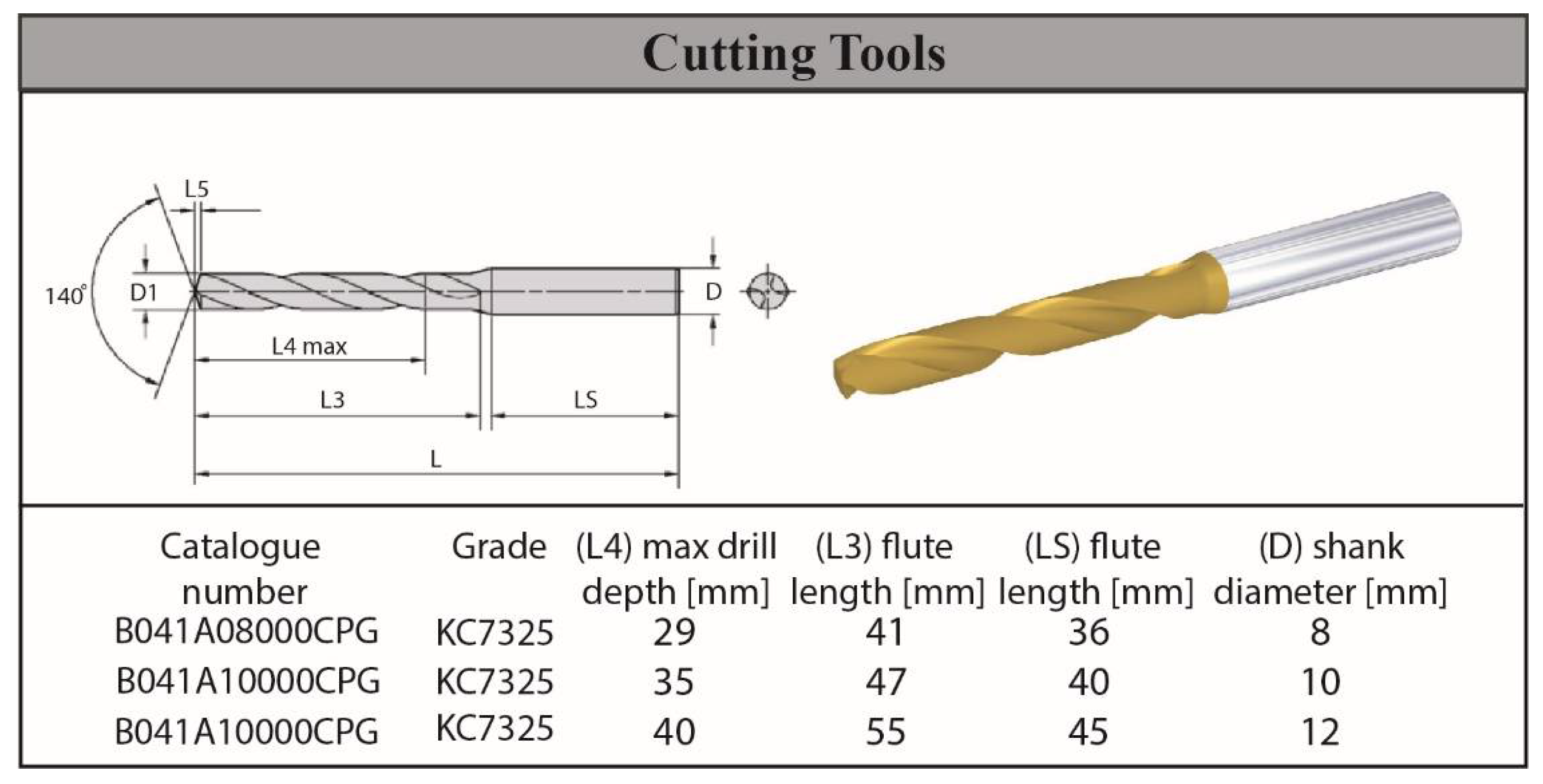


| Mechanical Properties | ||||||||||||
| Young’s Modulus | Density | Hardness, HV | Yield Strength | Tensile Strength | Thermal Conductivity | |||||||
| 72 GPa | 2800 kg/m3 | 173 | 503 MPa | 572 MPa | 130 W/m-K | |||||||
| Chemical Composition | ||||||||||||
| Elements | Zn | Mg | Cu | Cr | Fe | Si | Mn | Ti | Al | |||
| Percentage | 6 | 3 | 2 | 0.3 | 0.6 | 0.5 | 0.4 | 0.3 | Balance | |||
| Factors | Notation | Levels | ||
|---|---|---|---|---|
| I | II | III | ||
| Cutting speed (m/min) | V | 50 | 100 | 150 |
| Feed rate (mm/rev) | f | 0.15 | 0.2 | 0.25 |
| Tool diameters (mm) | D | 8 | 10 | 12 |
| Source | Degree of Freedom | Sum of Squares | Mean Square | f-Value | p-Value |
| Regression | 9 | 405,574 | 45,064 | 467.15 | 0.000 |
| Residual Error | 17 | 1640 | 96 | ||
| Total | 26 | 407,214 | |||
| R-Sq(adj) = 99.4% | |||||
| Predictor | Parameter Estimate Coefficient | Standard Error Coefficient | t-Value | p-Value | |
| Constant | −78.9 | 135.1 | 0.58 | 0.567 | |
| D | 51.36 | 21.06 | 2.44 | 0.026 | |
| V | 1.2224 | 0.4867 | 2.51 | 0.022 | |
| f | −503.7 | 712.0 | −0.71 | 0.489 | |
| D*D | −2.651 | 1.002 | −2.64 | 0.017 | |
| V*V | −0.010202 | 0. | −6.36 | 0.000 | |
| f*f | 2038 | 1604 | 1.27 | 0.221 | |
| D*V | 0.12850 | 0.02835 | 4.53 | 0.000 | |
| D*f | 186.67 | 28.35 | 6.58 | 0.000 | |
| V*f | 0.067 | 1.134 | 0.06 | 0.954 | |
| Source | Degree of Freedom | Sum of Squares | Mean Square | f-Value | p-Value | |
| Regression | 9 | 12.7870 | 1.4208 | 261.36 | 0.000 | |
| Residual Error | 17 | 0.0924 | 0.0054 | |||
| Total | 26 | 12.8794 | ||||
| R-Sq(adj) = 98.9% | ||||||
| Predictor | Parameter Estimate Coefficient | Standard Error Coefficient | t-Value | p-Value | ||
| Constant | 1.505 | 1.014 | 1.48 | 0.156 | ||
| D | −0.3086 | 0.1581 | −1.95 | 0.068 | ||
| V | 0.002357 | 0.003654 | 0.65 | 0.527 | ||
| f | 1.057 | 5.345 | 0.20 | 0.846 | ||
| D*D | 0.016014 | 0.007525 | 2.13 | 0.048 | ||
| V*V | −0.00003691 | 0.00001204 | 3.07 | 0.007 | ||
| f*f | −12.51 | 12.04 | −1.04 | 0.313 | ||
| D*V | 0.0002075 | 0.0002128 | 0.97 | 0.343 | ||
| D*f | 1.3317 | 0.2128 | 6.26 | 0.000 | ||
| V*f | 0.021300 | 0.008514 | 2.50 | 0.023 | ||
| Factors | Fz (N) | Mz (Nm) | |
|---|---|---|---|
| D: 8 mm, V: 70 m/min f: 0.2 mm/rev | Predicted | 707 | 1.899 |
| Exp. Result | 692 | 1.855 | |
| Variation % | 2.1% | 2.4% | |
| D: 10 mm, V: 70 m/min f: 0.2 mm/rev | Predicted | 875 | 2795 |
| Exp. Result | 875 | 2955 | |
| Variation % | 0% | −5.4% | |
| D: 12 mm, V: 70 m/min f: 0.2 mm/rev | Predicted | 1060 | 4.129 |
| Exp. Result | 1057 | 4.041 | |
| Variation % | 0.3% | 2.2% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kyratsis, P.; Markopoulos, A.P.; Efkolidis, N.; Maliagkas, V.; Kakoulis, K. Prediction of Thrust Force and Cutting Torque in Drilling Based on the Response Surface Methodology. Machines 2018, 6, 24. https://doi.org/10.3390/machines6020024
Kyratsis P, Markopoulos AP, Efkolidis N, Maliagkas V, Kakoulis K. Prediction of Thrust Force and Cutting Torque in Drilling Based on the Response Surface Methodology. Machines. 2018; 6(2):24. https://doi.org/10.3390/machines6020024
Chicago/Turabian StyleKyratsis, Panagiotis, Angelos P. Markopoulos, Nikolaos Efkolidis, Vasileios Maliagkas, and Konstantinos Kakoulis. 2018. "Prediction of Thrust Force and Cutting Torque in Drilling Based on the Response Surface Methodology" Machines 6, no. 2: 24. https://doi.org/10.3390/machines6020024
APA StyleKyratsis, P., Markopoulos, A. P., Efkolidis, N., Maliagkas, V., & Kakoulis, K. (2018). Prediction of Thrust Force and Cutting Torque in Drilling Based on the Response Surface Methodology. Machines, 6(2), 24. https://doi.org/10.3390/machines6020024







