Abstract
Annular polishing technology is an important optical machining method for achieving a high-precision mirror surface on silicon carbide. However, the inevitable over-polishing of the specimen edge in annular polishing deteriorates achieved surface quality. In the present work, we first analytically investigate the kinematic coupling of multiple relative motions in the annular polishing process and subsequently derive an analytical model that addresses the principle of material removal at specimen edge based on the Preston equation and the rigid body contact model. We then perform finite element simulations and experiments involving annular polishing of silicon carbide (SiC), which jointly exhibit agreement with the derived analytical model of material removal.
1. Introduction
Silicon carbide (SiC) is one of the preferred materials for manufacturing optical mirrors due to its unique characteristics of low density, high strength, low thermal expansion, high thermal conductivity and high chemical inertness [1,2]. According to the theory of total integrated scattering (TIS), the total surface scattering of a mirror is closely related to its surface roughness. Specifically, with the increase of surface roughness, the TIS rises sharply in conjunction with the decrease of reflectivity, which accordingly results in the degradation of the imaging quality of the optical system [3]. Therefore, achieving an ultra-smooth surface by optical machining methods is critical for the performance of SiC mirrors. At present, annular polishing technology is one of the main methods that has been widely used to obtain high-precision SiC mirrors [4,5,6,7].
The inevitable over-polishing of specimen edge that occurs during annular polishing significantly deteriorates machined surface qualities, such as flatness. Additionally, a fundamental understanding of material removal is required to minimize over-polishing. Material removal during the annular polishing process is complex due to the kinematic coupling of multiple relative motions between the specimen and polishing disc. At present, the Preston equation is widely used to describe the material removal process in annular polishing. For instance, Ji et al. [8] investigated the relationship between surface quality and polishing condition and consequently established the trajectory equation for a point on the single-side polishing part relative to the polishing pad by the coordinate transformation method. Wenski et al. [9] obtained improved non-uniformity for material removal at specimen edge by optimizing the trajectory of the polishing machine. However, the Preston equation still needed to be refined. Nanz et al. [10,11] found, through polishing experiments, that although the product of surface pressure of the specimen and its rotate speed is zero, the polishing removal rate is not zero due to chemistry action. Consequently, a compensation parameter must be introduced to correct underestimation by the Preston equation and which fits well with specific values in the experiments. Luo et al. [12] modified the Preston equation according to the results of both experiments and theoretical calculations.
Although previous analytical and experimental studies have qualitatively analyzed average material removal in the annular polishing process, there is limited work focusing on the over-polishing of specimen edge. In particular, there is no model of a material removal equation that takes into account the phenomenon of edge over-polishing, as the Preston equation only considers the average pressure of the polishing process. Therefore, in the present work, we first analyze the kinematic coupling of multiple relative motions between the specimen and polishing disc in the annular polishing process. Subsequently, based on the Preston equation and the rigid body contact model, we derive an analytical model that addresses the principle of material removal at specimen edge. Finally, finite element (FE) simulations and experiments of annular polishing of SiC are performed to evaluate the accuracy and efficiency of the derived analytical model.
2. Analytical Investigation of Annular Polishing
2.1. Kinematic Coupling of Motions
Figure 1a illustrates a typical annular polisher, which consists of a polishing disc, a carrier disc and a swinging bracket. The specimen is pasted on the carrier disc with paraffin, which means that the specimen has a synchronous speed with the carrier disc. The applied pressure is provided by the weight of the carrier disc. Accordingly, Figure 1b illustrates the simplified motion diagram of the annular polishing, which indicates that the kinematic coupling of relative motions includes the rotation of the polishing disc and the rotation of the carrier disc. We note that the swinging of the carrier disc leads to back and forth movements by the specimen, which consequently reduce the propensity of over-polishing of specimen edge. Therefore, to magnify the over-polishing phenomenon, in the present work the back and forth swinging motions are not considered in the kinematic coupling. As indicated in Figure 1b, the speed of the carrier disc is ω and the speed of the polishing disc is δ. The distance from the center of specimen O2 to point A on the carrier disc is r and the distance from the center of the polishing disc O1 to the center of carrier disc O2 is R. The angle between the line segments AO2 and O1O2 is θ. The speed at point A on the polishing disc relative to O1 is V1 and the speed at point A on the specimen relative to O2 is V2, so the relative speed of the specimen and the polishing disc at point A is V, which can be derived from Equation (1) [13]:
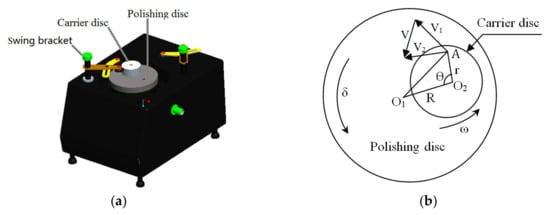
Figure 1.
Illustration of annular polishing. (a) Model of annular polisher; (b) motion analysis of annular polishing.
2.2. Preston Equation
Both material removal rate and surface quality of the specimen in the annular polishing process are strongly affected by processing parameters, which have complex interactions. Preston et al. simplified the Preston equation to characterize the relationship between material removal and polishing speed V, applied pressure P, and other external factors, as shown in Equation (2) [14]:
where h is the amount of material removal and is a proportional constant that is related to various environmental factors. Therefore, the amount of material removal at one specific point can be derived according to Equation (2) [15,16]. However, contact between the specimen and polishing disc changes dynamically with polishing time, which induces uncertainties in analytical investigation of the annular polishing process. Therefore, three main assumptions are made to simplify the operation: (1) The specimen and polishing disc are completely in contact without separation; (2) the applied pressure does not change over polishing time; and (3) the proportional constant does not change over polishing time.
According to the Preston equation, the amount of material removal within a specific polishing time can be derived by integrating time , as shown in Equation (3):
It can be seen from Equation (3) that material removal is only dependent on the resultant speed V, given that k and P are constant. By substituting the relative velocity derived from Equation (1) into Equation (3), material removal at point A can be derived, as shown in Equation (4):
2.3. Rigid Body Contact Model
It can be seen in Equation (4) that the pressure of each point on the specimen must be accounted for precisely when deriving material removal. Contact between the specimen and polishing disc in annular polishing can be analyzed by using the rigid body contact model, as illustrated in Figure 2 [17].
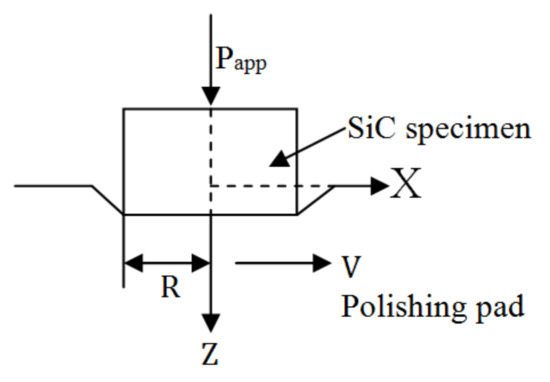
Figure 2.
Illustration of the rigid body contact model.
The rigid body contact model, as a two-dimensional plane strain model, can be used to analyze the distribution of contact pressure on the contact surface between the specimen and polishing disc. Considering the much higher stiffness (Mohs hardness of 9.5 and elastic modulus of 360 GPa) of SiC compared to that of a polishing disc made of cast iron (Mohs hardness of 4.5 and elastic modulus of 170 GPa), the SiC specimen is treated as a rigid body and the polishing disc is treated as an elastic material with small elastic modulus (elastic modulus of 3 MPa). Therefore, the shape of the SiC specimen does not change after being pressed into the polishing disc. Furthermore, it is assumed that the deformation of the polishing disc does not affect the result. The distribution of contact pressure on the specimen surface is expressed in Equations (5) or (6):
where Papp is the pressure applied to the upper surface of specimen and R is the radius of specimen. can be expressed by:
where is the friction coefficient between the specimen and the polishing pad and is the Poisson’s ratio of the polishing pad. While Equation (5) does not consider the friction between contacting surfaces, Equation (6) provides a more accurate description of the contact by considering the frictional force between the two surfaces. By substituting Equation (6) into Equation (4), the removal equation for the specimen in annular polishing can be derived, as seen in Equation (8):
It can be seen from Equations (5) and (6) that contact pressure near specimen edge (i.e., r approaching R) increases sharply. Therefore, Equation (8) also applies to the qualitative description of material removal when considering over-polishing of specimen edge.
3. FE Simulation of Annular Polishing
3.1. FE Modeling
To verify the accuracy of the derived model of material removal presented in Equation (8), FE simulations of annular polishing of SiC were performed by using ABAQUS software, with an emphasis on the distribution of contact pressure on specimen surface. Similarly to the analytical investigation, in the FE simulations the motion of carrier swing was not considered. Accordingly, the swing bracket was omitted in the FE model. Figure 3 shows that the FE model of annular polishing consisted of a SiC specimen colored in blue, a polishing pad in red and a polishing disc in gray, which were treated as deformable parts. The upper surface of the polishing disc and the lower surface of the polishing pad were bound entirely. The polishing disc had a synchronous speed with the polishing pad. Table 1 lists material properties of the three parts. Furthermore, it was assumed that the properties of the SiC specimen were isotropic.
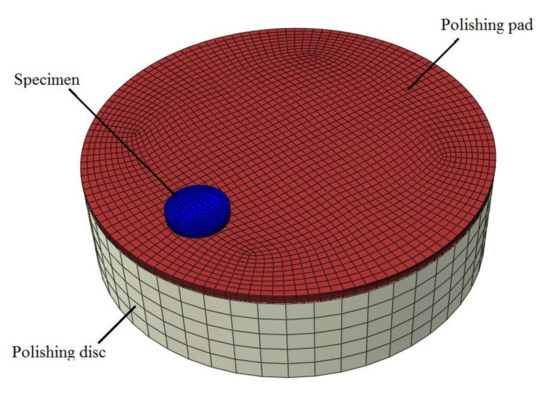
Figure 3.
Finite element model of annular polishing of silicon carbide (SiC).

Table 1.
Material parameters of parts.
It is known that grid configuration greatly affects the accuracy of prediction results in FE simulations. The three aspects of cell type, cell shape and grid density need to be considered when configuring grids. In the present work, a structured mesh was used to divide meshes by using a linear hexahedral C3D8I element with eight nodes. Grid density increased with increasing distance from the center of specimen. Furthermore, the mesh of the polishing pad was denser than that of the polishing disc, as shown in Figure 3.
In the FE simulation, an explicit dynamical analysis step with a total time of 3 s was used. The selection of 3 s was to ensure that the specimen rotated more than two revolutions, which enabled us to obtain more accurate polishing results. It should also be noted that the time cannot be too long due to high computational costs and minimal change in results. The contact between the specimen and polishing pad was set as a general contact with a friction coefficient of 0.1. A uniform pressure of 0.068 MPa was imposed on the specimen.
3.2. Simulation Results and Discussion
Figure 4 presents the distribution of contact pressure and deformation of the SiC specimen surface after FE simulation of annular polishing, in which the polishing disc and specimen have the same speed of 100 r/min. In Figure 4a, distributions of contact pressure in three random radial directions highlighted by the three randomly selected red dash lines are analyzed. For each direction, 30 uniformly-spaced points along the red lines are selected. Accordingly, Figure 4c plots variations of contact pressure along the three directions as a function of off-center distance, which shows that the contact pressure in the vicinity of the center of the specimen is distributed uniformly. However, when the off-center distance is higher than 10 mm, the contact pressure gradually increases with increasing off-center distance, and finally reaches the maximum value at the specimen edge. Figure 4b shows the contour of normal strain after polishing, which is related to the material removal of specimen surface. It can be seen in Figure 4b that the material removal at specimen edge is significantly higher than in the middle of the specimen.
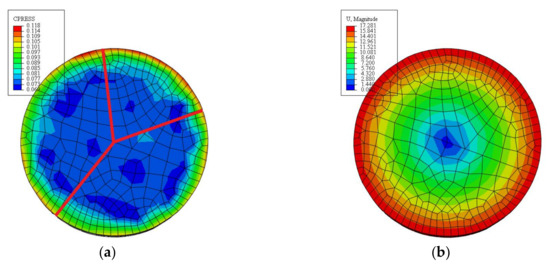
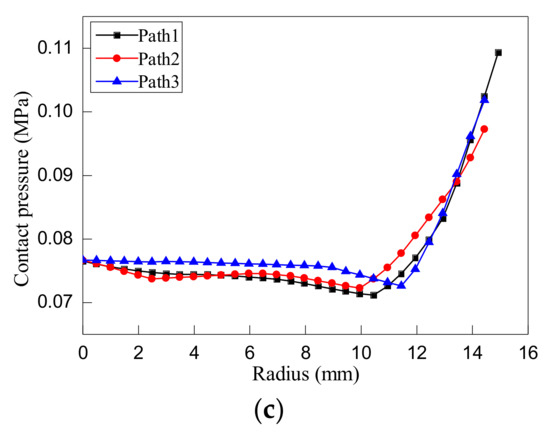
Figure 4.
Distributions of contact pressure and normal strain in finite element (FE) simulations of annular polishing of SiC. (a) Contour of contact pressure; (b) contour of normal strain; and (c) variations of contact pressures.
We further evaluated the influence of the typical parameters (speed, Poisson’s ratio and elastic modulus of polishing pad) on the distribution of contact pressure. Figure 5 plots variations of contact pressure along three directions as a function of off-center distance under different parameters. It was found, as shown in Figure 5, that for each parameter, the contact pressure of the specimen showed similar trends, first remaining stable and then increasing sharply when near the edge. The above results verify the pressure distribution equation obtained by the rigid body contact model presented in Equations (5), (6) and (8).
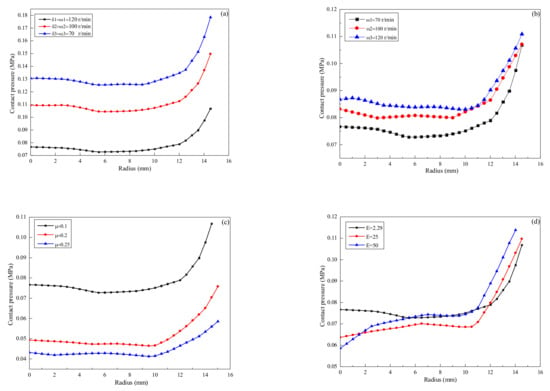
Figure 5.
Distribution of contact pressure on the SiC specimen surface at different parameters. (a) Speed (specimen and polishing plate rotate at equal speed); (b) speed (keeping the speed of the polishing disc as 100 r/min, changing the speed of the specimen); (c) Poisson’s ratio of polishing pad; and (d) elastic modulus of polishing pad.
4. Experimental Study of Annular Polishing of SiC
In addition to the FE simulations that verified the occurrence of over-polishing of specimen edge, annular polishing experiments of SiC were also carried out to further verify the derived model of material removal presented in Equation (8). All the annular polishing experiments were performed by using the UNIPOL-802 precision auto lapping and polishing machine, as shown in Figure 6. The specific parameters used in the annular polishing experiments were: That the velocities of the polyurethane polishing pad and specimen were the same at 100 r/min, the polishing time was 60 min, and a diamond suspension solution was used. After polishing, the obtained surface was measured by using a surface profiler.

Figure 6.
Precision auto lapping and polishing machine.
Figure 7 plots the variation of measured relative surface height with off-center distance. The relative surface height is defined as the change in measured surface height after polishing with respect to surface height before polishing. In order to show the mutual verification of the experimental results and the FE simulation results, Figure 7 further plots the variations of contact pressure shown in Figure 4. It can be seen in Figure 7 that within the off-center distance ranging from 0 to 13 mm, the relative surface height of the specimen remains relatively unchanged. Upon a further increase of off-center distance from 13 to 15 mm, which approaches to the specimen edge, however, the relative surface height of the specimen dropped sharply. This indicates that the amount of material removal also increased sharply. Figure 7 also demonstrates that the experimental results are in agreement with the FE simulation results, as material removal during polishing is proportional to contact pressure. Specifically, there is sharp increase in both pressure and material removal at specimen edge, indicating the occurrence of an over-polishing phenomenon. Therefore, it is indicated by both the simulation and experimental results that the derived analytical model of material removal presented in Equation (8) is indeed capable of describing material removal particularly related to the over-polishing of specimen edge during annular polishing of SiC.
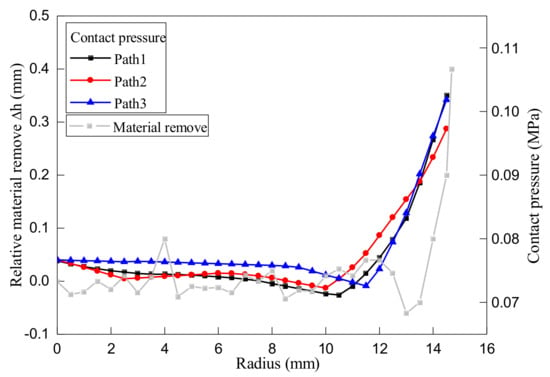
Figure 7.
Distributions of material removal by experiment and contact pressure by FE simulation.
5. Conclusions
In the present work, we performed an analytical investigation, FE simulation and an experimental study to investigate the fundamentals of material removal during annular polishing of SiC, with an emphasis on the underlying mechanisms of over-polishing of specimen edge. According to the analytical investigations of the kinematic coupling of multiple relative motions between the specimen and polishing disc, an analytical model of material removal during the annular polishing process that further accounts for the over-polishing of specimen edge was derived based on the Preston equation and the rigid body contact model. Subsequent FE modeling and simulation showed the non-uniform distribution of contact pressure and the normal strain of the specimen in the annular polishing, i.e., the occurrence of over-polishing at specimen edge, which was further verified by the polishing experiments.
Acknowledgments
The authors acknowledge financial support from the National Natural Science Foundation of China (NSFC) and the German Research Foundation (DFG) International Joint Research Program (51761135106).
Author Contributions
J.Z., L.H. and T.S. conceived and designed the experiments; L.H. performed the analytical investigation and FE simulations, Y.S. performed the experiments; J.Z., L.H. and Y.Y. analyzed the data; J.Z. and L.H. wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Robichaud, J.L.; Schwartz, J.; Landry, D.; Glenn, W.; Rider, B.; Chung, M. Recent advances in reaction bonded silicon carbide optics and optical systems. SPIE 2005, 5868, 586802. [Google Scholar]
- Wang, X.C.; Wang, C.C.; Shen, X.T.; Sun, F.H. Potential material for fabricating optical mirrors: Polished diamond coated silicon carbide. Appl. Opt. 2017, 56, 4113–4122. [Google Scholar] [CrossRef] [PubMed]
- Cook, F.; Brown, N.; Prochnow, E. Annular lapping of precision optical flatware. Opt. Eng. 1976, 15, 450–458. [Google Scholar] [CrossRef]
- Gritti, F.; Guiochon, G. Gradient chromatography under constant frictional heat: Realization and application. J. Chromatogr. A 2013, 1289, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Hutchings, I.M.; Xu, Y.; Sanchez, E.; Ibanez, M.J.; Quereda, M.F. Development of surface finish during the polishing of porcelain ceramic tiles. J. Mater. Sci. 2005, 40, 37–42. [Google Scholar] [CrossRef]
- Fan, Q.T.; Zhu, J.Q.; Zhang, B.A. Effect of the geometry of workpiece on polishing velocity in free annular polishing. Chin. Opt. Lett. 2007, 5, 298–300. [Google Scholar]
- Hashimoto, Y.; Oshika, S.; Suzuki, N.; Shamoto, E. A new contact model of pad surface asperities utilizing measured geometrical features. In Proceedings of the International Conference on Planarization/CMP Technology (ICPT), Chandler, AZ, USA, 30 September–2 October 2015; pp. 1–4. [Google Scholar]
- Yongji, J.I.N. Study on Mechanism of CMP Polishing Motion. Equip. Electron. Prod. Manuf. 2005, 34, 37–41. [Google Scholar]
- Wenski, G.; Altmann, T.; Winkler, W.; Heier, G.; Hölker, G. Doubleside polishing—A technology mandatory for 300 mm wafer manufacturing. Mater. Sci. Semicond. Process. 2003, 5, 375–380. [Google Scholar] [CrossRef]
- Nanz, G.; Lawrence, E.C. Modeling of chemical mechanical polishing: A review. IEEE Trans. Semicond. Manuf. 1995, 8, 382–389. [Google Scholar] [CrossRef]
- Qin, K.D.; Moudgil, B.; Park, C.W. A chemical mechanical polishing model incorporating both the chemical and mechanical effects. Thin Solid Film 2004, 446, 227–286. [Google Scholar] [CrossRef]
- Luo, Q.; Ramarajan, S.; Babuu, S.V. Modification of the Preston equation for the chemical mechanical polishing of copper. Thin Solid Film 1998, 335, 160–167. [Google Scholar] [CrossRef]
- Goedecke, A.; Jackson, R.L.; Mock, R. A fractal expansion of a three dimensional elastic-plastic multi-scale rough surface contact model. Tribol. Int. 2013, 59, 230–239. [Google Scholar] [CrossRef]
- Preston, F. The theory and design of plate glass polishing machines. J. Soc. Glass Technol. 1927, 11, 214–256. [Google Scholar]
- Li, S.X.; Gang, Y.; Zhang, J.C. Single-row laser beam with energy strengthened ends for annular scanning laser surface hardening of largemetal components. Sci. Chin. Phys. Mech. Astron. 2013, 56, 1074–1078. [Google Scholar] [CrossRef][Green Version]
- Zhao, D.L.; Ma, X.; Liu, B.; Xie, L. Rainfall effect on wind waves and the turbulence beneath air-sea interface. Acta Oceanol. Sin. 2013, 32, 10–20. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985; pp. 44–48. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).