One-Dimensional Haptic Rendering Using Audio Speaker with Displacement Determined by Inductance

Abstract

We report overall design considerations and preliminary results for a new haptic rendering device based on an audio loudspeaker. Our application models tissue properties during microsurgery. For example, the device could respond to the tip of a tool by simulating a particular tissue, displaying a desired compressibility and viscosity, giving way as the tissue is disrupted, or exhibiting independent motion, such as that caused by pulsations in blood pressure. Although limited to one degree of freedom and with a relatively small range of displacement compared to other available haptic rendering devices, our design exhibits high bandwidth, low friction, low hysteresis, and low mass. These features are consistent with modeling interactions with delicate tissues during microsurgery. In addition, our haptic rendering device is designed to be simple and inexpensive to manufacture, in part through an innovative method of measuring displacement by existing variations in the speaker’s inductance as the voice coil moves over the permanent magnet. Low latency and jitter are achieved by running the real-time simulation models on a dedicated microprocessor, while maintaining bidirectional communication with a standard laptop computer for user controls and data logging.

1. Introduction

Comparison to Existing Haptic Rendering Devices

Researchers in haptics make extensive use of rendering devices capable of producing the sensation of touch as would occur during interactions with objects in the environment. A broad class of such devices consists of a stationary base supporting a movable component upon which forces are generated relative to the base, in response to translation and/or rotation by an external agent. Most systems presently available to consumers and researchers depend on mechanical linkages to generate these forces and provide mobility. Of those, some, such as the Novint Falcon or the Force Dimension Omega, use parallel linkage mechanisms to generate forces—typically in the three translational degrees of freedom (DOF)—on a control ball or stylus, which is held by the user at the front of the device. The Novint Falcon can generate up to 8.9 N force over a 10 × 10 × 10 cm workspace. The Force Dimension Omega (model 7) can generate up to 12 N force over a cylindrical workspace 16 cm in diameter ×13 cm in length. Another popular device in research is the Geomagic Touch (formerly Sensable Phantom Omni), in which a set of single linkages enables a stylus to move in all six DOF, with force feedback restricted to the 3 translational DOF. The Geomagic Touch can generate up to 3.3 N force over a 16 × 12 × 7 cm workspace.

Since haptic renderers combine mechanical and electrical characteristics in an application accessible to a wide audience, simple 1-DOF haptic interfaces have been developed as educational tools for engineering curricula. For example, Okamura and colleagues developed a “haptic paddle”, a single-axis force feedback joystick, for use in dynamic systems courses at Stanford University [1]. Users can move the paddle, which is shaped like an inverted pendulum, side-to-side over a ±35° range of motion. Feedback forces change with paddle position and velocity, and are generated by a DC motor, producing up to 7.5 N on the handle. Gassert and colleagues have adapted the haptic paddle design for use at ETH Zurich, adding a number of sensors and USB data collection for ease of use in an educational laboratory setting [2]. At the University of Michigan, Gillespie and colleagues have designed two haptic interfaces, the iTouch motor and the Box, for use in undergraduate mechanical engineering and electrical engineering courses. These two renderers are single-axis haptic interfaces that make use of voice coil actuators and brushed motors respectively for force generation [3]. Similarly to the haptic paddles just discussed, the iTouch can move side to side over a 30° range of motion, generating up to 0.2 Nm torque on the handle. The Box is a larger haptic device, driven by a motor, sprocket, and chain mechanism, which can generate up to 5.4 Nm torque on a wheel that is held by the user.

To avoid problems associated with mechanical linkage mechanisms, Hollis developed a magnetically levitated haptic renderer [4], recently commercialized as the Maglev 200 from Butterfly Haptics. This desk-mounted haptic renderer utilizes Lorenz forces to actuate forces and torques in six DOF on a flotor levitated between permanent magnets, while location and angle are determined in six DOF by high-resolution optical tracking. Because there are no mechanical linkages, forces and torques on the flotor are rendered without significant frictional losses or mechanical backlash. The Maglev can generate up to 40 N of force and 3.6 Nm of torque over a 2.4-cm-diameter spherical workspace. It also operates at higher frequencies than the above-mentioned mechanically linked systems, changing position at 140 Hz and generating forces at greater than 2 KHz. We have used the Maglev in experiments involving a new surgical tool that augments the surgeon’s sense of touch in delicate tissues [5], to understand the control of a needle while puncturing a membrane to minimize damage to the underlying tissues [6], and to differentiate between such punctures performed by dominant and non-dominant hands [7].

While it has been a valuable testbed for the experiments just described, the relatively large mass of the flotor (~500 g) in the Maglev makes it less than ideal for modeling delicate tissue. Furthermore, the Maglev does not directly measure the force and torque applied to the flotor by the user, but rather must infer these through their effect on linear and angular acceleration of the flotor, putting limits on the bandwidth of such measurements.

We describe here development of a simpler, less massive platform that exhibits many of the advantageous features of the Maglev, albeit with only one DOF rather than six. We take advantage of an existing commercial device with high bandwidth, low mass, low mechanical resistance, and significant force: the audio loudspeaker. In particular, we use low-frequency speakers (woofers). Even a fairly small woofer can have a relatively high displacement (1 cm), and sufficient bandwidth and force for our purposes. The moving portion of the woofer is generally a light but rigid paper cone, suspended in 1-DOF by a ring of elastic material, driven by a voice coil that surrounds but does not touch a permanent magnet. Thus velocity dependent forces (mechanical resistance) are minimal, because of low air resistance at the velocities we expect the paper cone to be moving.

In the following section, we review our progress, thus far, in developing our speaker-based haptic renderer. In particular, we describe (1) the overall design incorporating a scaffold to provide a mechanical interface for the user with an independent force sensor; (2) a method of determining displacement from the inductance of the speaker itself, and (3) a separate method of determining displacement using an optical reflectance sensor; and (4) a computational architecture that provides high bandwidth, low jitter, and low latency, while preserving flexibility in the user interface and data logging capabilities.

2. Experimental Section

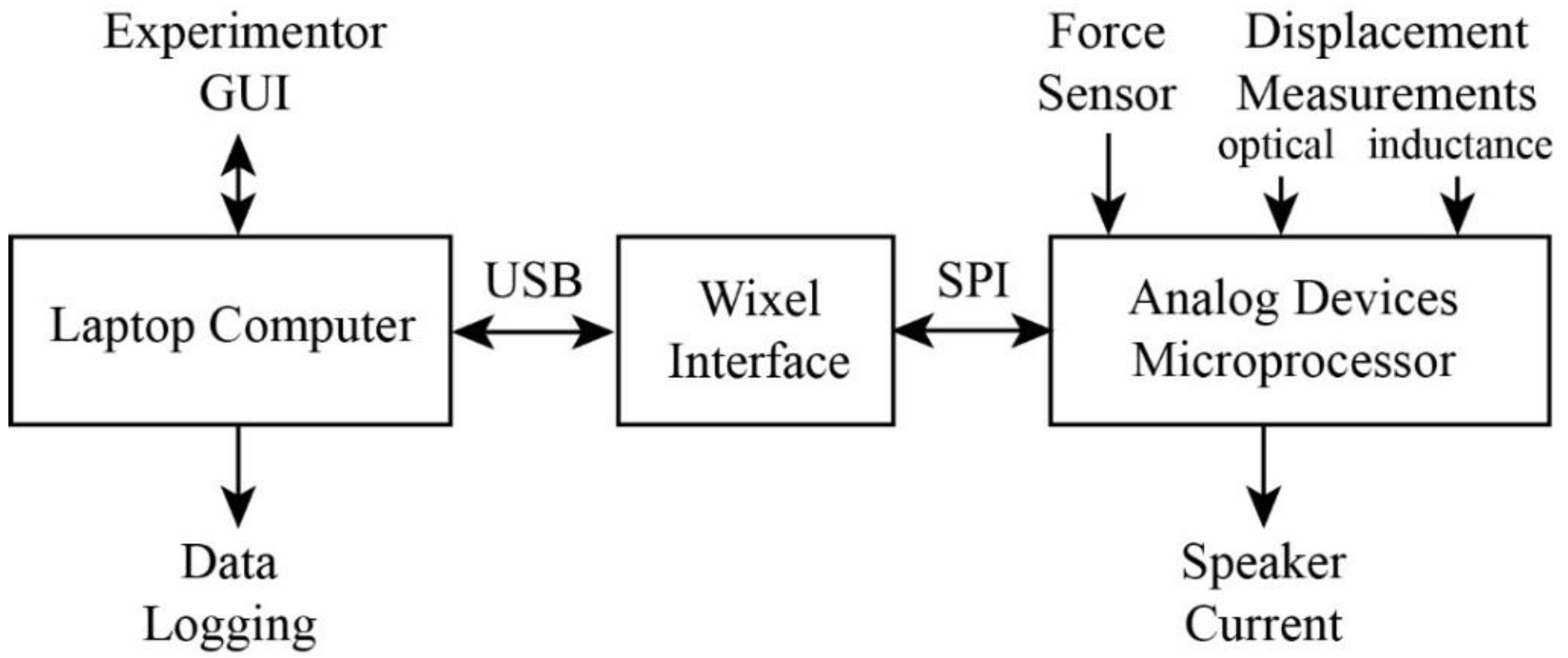
2.1. Overall Design of Speaker-Based Haptic Rendering Device

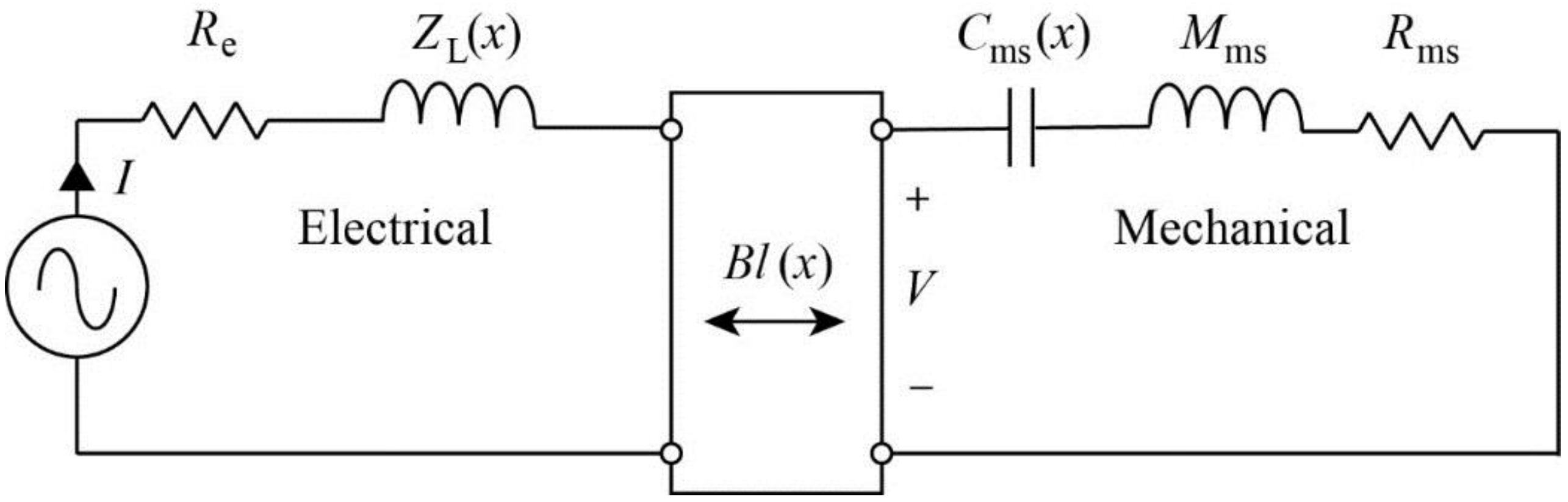
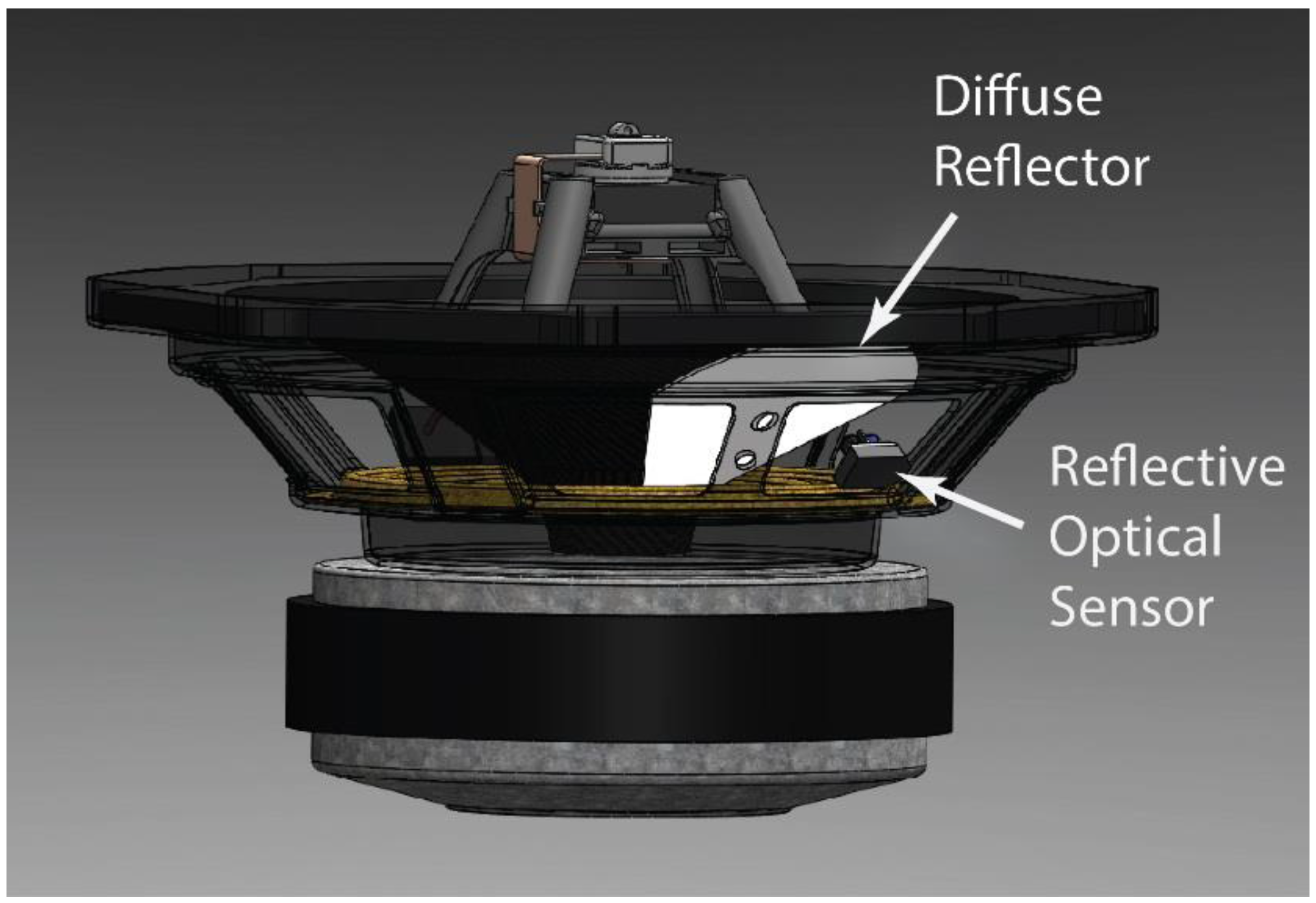
Our haptic rendering system uses a loudspeaker to effect displacement of the mobile component of a 1-DOF haptic renderer, taking advantage of the low friction and inertia exhibited by this inexpensive commercial device. Figure 1 shows the design (SolidWorks) of our initial prototype as well as a photograph of the actual device. A custom plastic scaffold, produced using stereolithography, is attached to the central ring of the speaker cone to move up and down as a unit. The scaffold is made stiff and lightweight by use of hollow beams, supporting an attachment point for user interaction. Here, users will attach mock needles, scalpels, etc., enabling interaction with simulated tissues during psychophysics experiments.

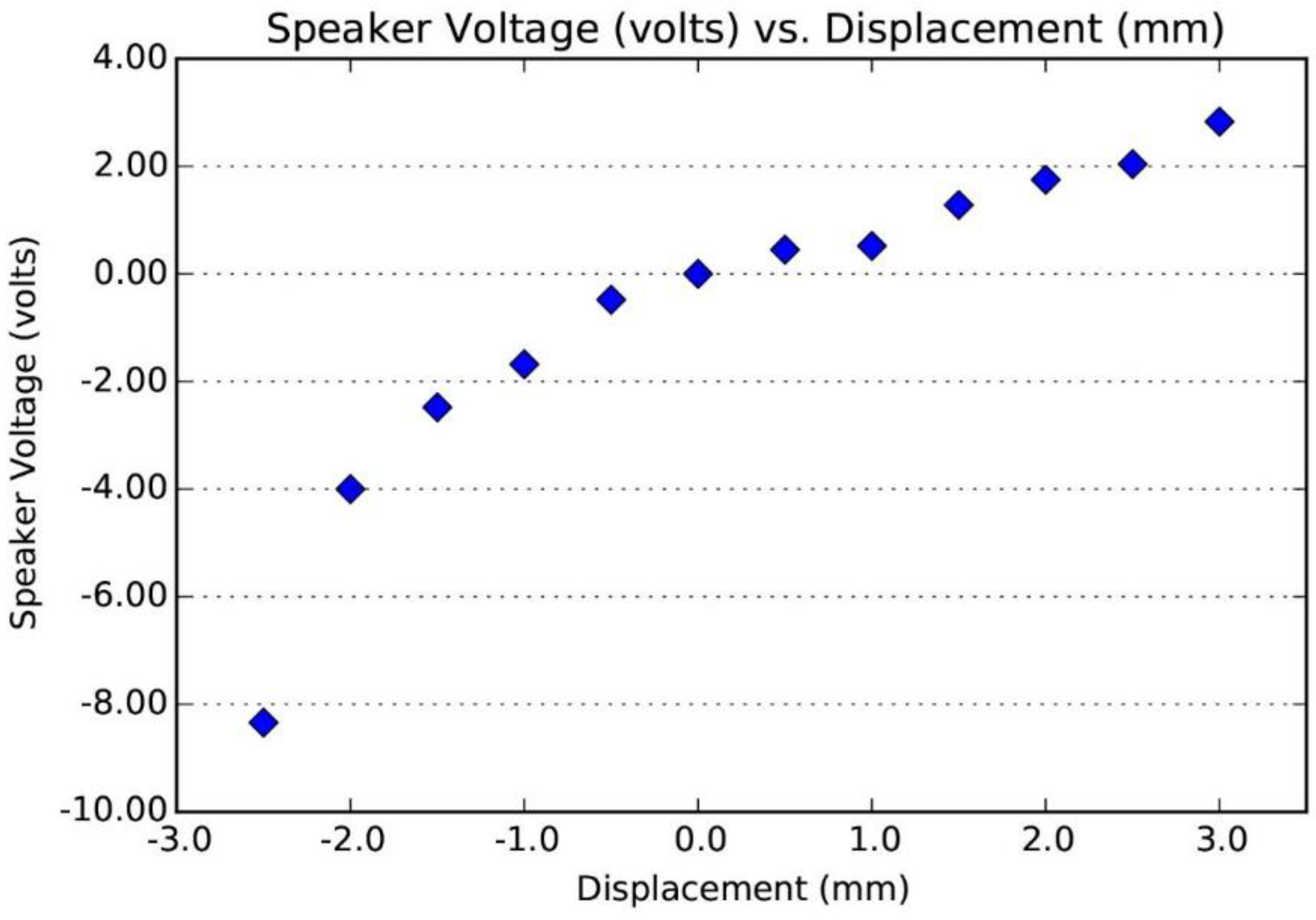
The paper cone of the speaker can be made to move up or down with its attached scaffold by introducing a directional current in the speaker’s voice coil, which is mounted over a permanent magnet mounted to the metal frame of the speaker. The suspension of the cone is stabilized by a spider, a centering spring and damper whose compliance returns the cone to the middle of its displacement range at rest. We have chosen an 80-Watt 5-inch loudspeaker (Faital Pro 5FE120) designed for midrange to bass frequencies, and capable of delivering 10 N of sustained force (as determined below). Its maximum displacement range is approximately 1 cm in each direction from the rest point. During normal operation in the audio range of 20 Hz to 20 KHz, the displacement is far less, allowing the compliance of the spider to be assumed linear. This linearity is important in audio systems to avoid distortion. Our application, however, while benefiting from the ability of the speaker to react at such frequencies, also employs frequencies all the way down to direct current (DC), permitting us to move the cone to any desired displacement and hold it there. Our unorthodox application thus results in greater displacements than normally used for a speaker, requiring consideration of the non-linearity of its compliance. This, and other considerations, require us to know the actual displacement of the speaker at any given time, as will be discussed below.

In determining the useful range of displacements generated by DC currents in the coil, it is important to consider the maximum power rating of the speaker. For our speaker, this is reported by the manufacturer to be 80 W, which, given 5.4 Ω electrical resistance at DC, would seem to imply a maximum DC voltage of 21 V, since DC power equals V²/R. We have found, however, that the safe maximum DC voltage is signficantly less, approximately 10 V. This discrepancy is due to the fact that the manufacturer’s reported maximum power is for audio frequencies, at which much of the energy put into the coil is dissipated as sound instead of heat in the coil. At DC, all of the energy is dissipated as heat, and so the voltage must be less to avoid melting the coil.

We have included a force sensor (Honeywell FS-01) mounted between the attachment point and the scaffold, with a preload spring allowing measurement of push and pull forces exerted by the user at the attachment point (see Figure 1). The sensor has a total range of 6.7 N with precision of approximately ±0.03 N and accuracy of approximately ±0.07 N. We could theoretically compute the externally applied force without a sensor, based on the displacement of the speaker and the force delivered by the voice coil, as is done with the Maglev system described above. However, we choose to include the sensor because it provides an independent measurement with greater accuracy and speed than could be provided by such calculations.

2.2. Measuring Displacement with Inductance

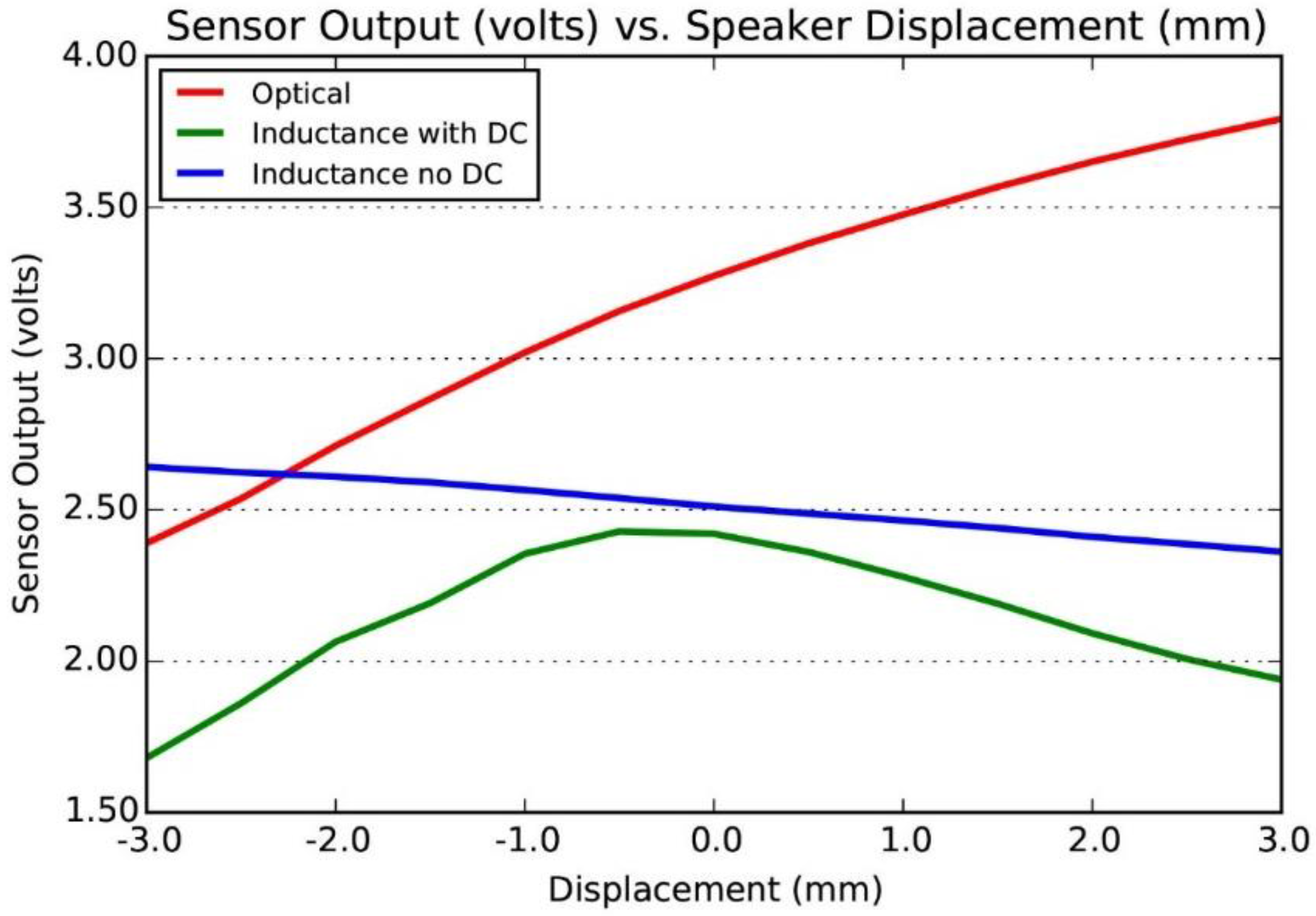
As a first approximation, the displacement of a speaker at steady state is proportional to the current in its voice-coil, and thus displacement might be predictable from that current. However, for a number of reasons, we require independent measurement of speaker displacement. As noted, we are moving the cone further than in normal audio applications, operating it in the range of non-linear compliance. A further nonlinearity is introduced as the voice-coil moves relative to the permanent magnet, because the force produced by a given current changes as more or less of the voice coil is positioned over the permanent magnet. Both of these nonlinearities could be compensated for by calibration. However, in our application the user will apply additional forces to the attachment point, so displacement can no longer be predicted from coil current alone. Thus we need an independent measurement of displacement.

Various technologies are available to measure displacement, including those based on resistance, capacitance, inductance, reluctance, optical encoding, reflected and transmitted light intensity, and coherent light. Some of these require physical contact, which would increase the mass of the moving component, while others do not. Each has advantages and disadvantages in terms of accuracy, range, complexity, expense, etc.

We choose instead to make use of information provided by the speaker itself, namely, changes in the electrical inductance of the voice coil as it moves over the permanent magnet. Electrical inductance is a component of electrical impedance, whose magnitude can be measured by injecting a sinusoidal voltage and monitoring the resulting sinusoidal current at the same frequency. The impedance of a speaker, as a function of frequency, is due to a number of sources, both electrical and mechanical. If we understand these sources, we can isolate the coil’s electrical inductance from its total electrical and mechanical impedance.

Electromechanical systems are often understood in terms of lumped parameter models. Figure 2 shows a simplified lumped parameter model for a speaker adapted from [8], with terms defined in

Table 1. Parameters in Lumped Model (see Figure 2).

Parameter	Description	Value in Specified Speaker
Re	Electrical resistance at DC	5.4 Ω
ZL(x)	Electrical impedance due to inductance, varies with voice-coil displacement x over magnet.	see Figure 3
Bl(x)	Electro-dynamical force factor, varies with voice-coil displacement x over magnet.	6.9 N/amp (at rest)
Cms(x)	Compliance of mechanical suspension, varies with voice-coil displacement x over magnet.	0.55 mm/N at rest (x = 0 mm)
Mms	Mechanical mass of loudspeaker diaphragm assembly, including air load and voice coil (plus added masses).	11 g (23 g with scaffold and force sensor included)
Rms	Mechanical friction and drag of total loudspeaker.	Negligible at low velocity

. The left and right halves of the diagram depict, respectively, the electrical and mechanical properties of the speaker. Notice that electrical symbols are used on both sides, representing, on the right side, their analogous mechanical properties, i.e., inductance represents mass, resistance represents friction or damping, and capacitance represents compliance. The mass of the moving portion (cone + voice-coil + scaffold, etc.) is represented by “inductance” M_ms. The air resistance of the cone and damping in the spider is shown as R_ms. The mechanical compliance is represented by “capacitance” C_ms(x), and is a function of displacement x because, as noted above, it is nonlinear at the extremes of displacement. On the electrical side of the model, we have the DC resistance R_e and the electrical impedance due to inductance Z_L(x), which changes with displacement and thus should allow us to make a measurement of displacement, if we can isolate it from the other elements in the model.

The transduction between the electrical and mechanical halves of the lumped parameter model is represented by the electro-dynamical force factor Bl(x), accounting for energy transfer in both directions. Electrical current in the voice coil I causes the mechanical force that moves the speaker, represented on the mechanical side by “voltage” V. Energy is also transferred in the other direction, with mechanical motion of the coil resulting in an opposing electrical voltage in the voice coil. Thus mechanical properties of the speaker (such as its mechanical resonance) show up as part of its electrical impedance.

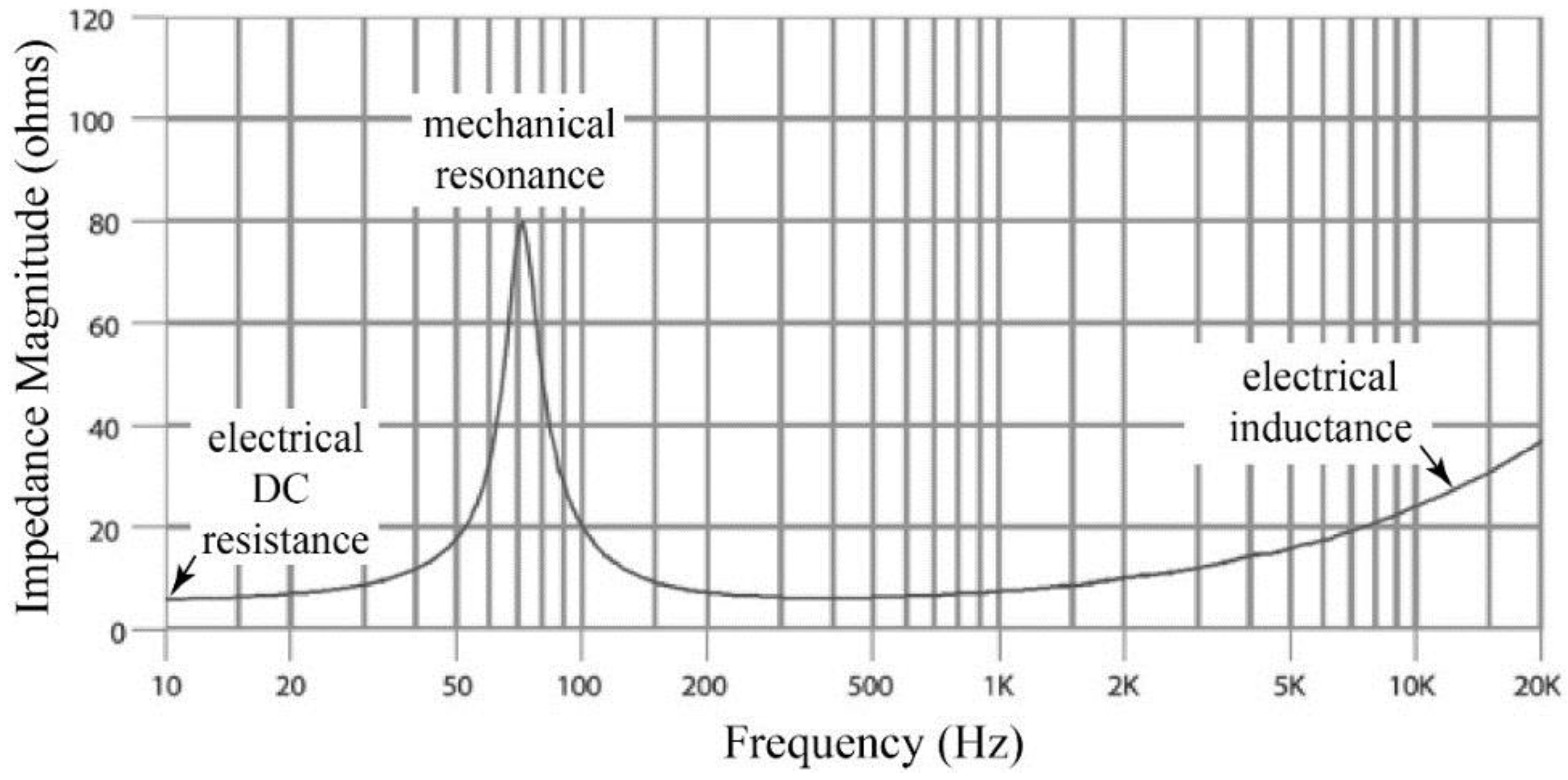
The electrical impedance as a function of frequency for our particular speaker is shown in Figure 3. Impedance is a complex quantity, and the graph displays only its magnitude. The impedance extends from the electrical DC resistance R_e (not shown at 0 Hz due to logarithmic scale), up through mechanical resonance at approximately 60 Hz. The mechanical resonance is due to a minimum in the mechanical impedance at that frequency, with the mass and compliance establishing a resonant system. This minimum mechanical impedance is translated into a maximum electrical impedance by Bl(x), which, as may be recalled, converts electrical current into mechanical “voltage,” thus replacing the definition of impedance with its reciprocal.

At higher frequencies, Figure 3 shows a slowly increasing value due primarily to inductance of the voice coil. As already noted, Z_L(x) changes as the voice coil moves over the ferromagnetic material in the permanent magnet, and it is this value we will use for computing displacement. It also changes as a function of frequency, increasing because of the fundamental nature of inductance:

$$Z_L=j\omega L$$

(1)

where $\omega$ is frequency in radians per second and L is the inductance.

To measure Z_L(x), we introduce a sinusoidal voltage at a frequency well above mechanical resonance, and in fact, above the audio range entirely, so as not to create an audible signal. For reasons discussed below, we have chosen that frequency to be 30 KHz.

Figure 4 shows the configuration of our system to measure the impedance Z_L(x) due to inductance. A high-power linear push-pull amplifier (PA74A, Apex Microtechnology) was used to move the speaker with low-frequency (including DC) current, as well as to introduce the 30 KHz signal, with the two signals being added before the amplifier. Since the amplifier is essentially a voltage source, changes in Z_L(x) result in changes in the 30 KHz voltage across the transformer primary in series with the speaker. An air-core transformer was used to avoid non-linearity due to saturation in a ferromagnetic core. The transformer was constructed from two coils (Jantzen Audio 0.50 mH Crossover Coil) mounted adjacent and coaxially. The 30 KHz voltage in the secondary was processed by a peak detector to yield voltage V_out. The peak detector produced a greater voltage when the inductance of the speaker was reduced, because the speaker coil and the transformer primary formed a voltage divider across the linear amplifier output.

To achieve a maximum change in V_out with Z_L(x), we matched the impedance of the transformer primary Z_T with that of the voice coil at rest, Z_L(0), approximately 0.50 mH. Let us denote the amplitude of the 30 KHz sinusoid at the amplifier output as V_S. Assuming that R_e is much less than |Z_L(x)| at 30 KHz (which is supported by Figure 3), and assuming that the DC resistance of the transformer primary is negligible (its wire gage is much thicker than the voice coil), and that the transformer and peak detector are both 100% efficient, then a reasonable approximation for V_out is:

$$V_{\mathrm{out}}=V_{\mathrm{S}}\frac{\left|Z_{\mathrm{T}}\right|}{\left|Z_{\mathrm{T}}\right|+\left|Z_{\mathrm{L}}\left(x\right)\right|}$$

(2)

which changes monotonically with impedance Z_L(x), and thus with displacement x. Proper calibration of V_out against an independent measurement of displacement should therefore permit determination of x by inductance.

We have chosen 30 KHz, because at higher frequencies the circuit shown in Figure 4 encounters an additional resistance R_eddy (not shown in Figure 2) resulting from eddy currents in the ferromagnetic magnet of the speaker. At a high enough frequency, R_eddy dominates the coil inductance, and as shown in Equation (3), this reduces the sensitivity of V_out to changes in Z_L(x) and thus to changes in x.

$$V_{\mathrm{out}}=V_{\mathrm{S}}\frac{\left|Z_{\mathrm{T}}\right|}{\left|Z_{\mathrm{T}}+Z_{\mathrm{L}}\left(x\right)+R_{\mathrm{eddy}}\right|}$$

(3)

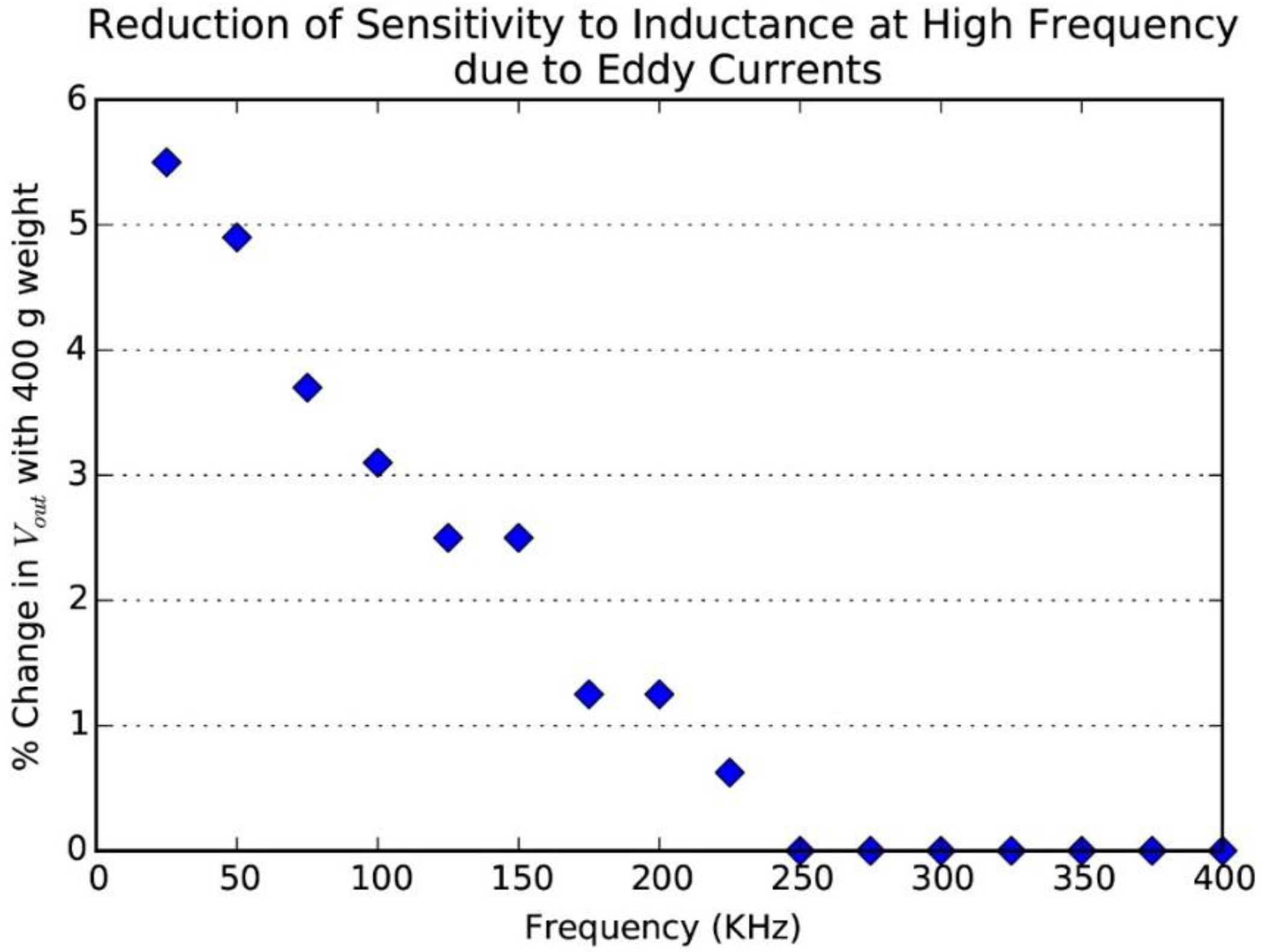
We explored the effect of R_eddy by recording V_out before and after placing a 400 g weight on the scaffold to cause a consistent displacement. This displacement changed V_out by a percentage that depended on the frequency of the sinusoidal voltage. Figure 5 shows the resulting data. Above the upper limit of the audio frequencies (20 KHz), the percentage decreases monotonically to zero because of increasing R_eddy.

These results led us to choose a frequency just above the audio range at 30 KHz to measure the coil inductance.

2.3. Optical Displacement Measurement

To provide a means of evaluating the inductance-based displacement measurement, we implemented an independent high-speed system to measure speaker displacement based on a reflective optical sensor (Vishay TCRT5000L). This device consists of an infrared emitter operating at 940 nm and phototransistor in a leaded package that blocks visible light. As shown in Figure 6, a lightweight diffuse reflector (made of stiff paper) was glued to the outside of the speaker cone. The reflector is wedge-shaped and positioned relative to the stationary optical sensor, such that as the speaker moves down the reflector moves closer to the sensor and also presents a wider area to the sensor. The apparatus, thus, provides a voltage that varies monotonically with displacement, whether generated by current through the speaker coil or force independently applied to the speaker. The optical system was calibrated to a mechanical gage, as discussed below, and will be used in evaluating the inductance-based measure. Assuming the new inductance-based measure proves accurate enough, we will no longer require the optical system in subsequent devices. Until such time, however, the optical system will serve to provide a displacement measurement for haptic rendering.

2.4. Real-Time Computation and Control

Our application for the haptic rendering device involves simulating tissues for microsurgical intervention. The inputs to these models include force applied by the user as measured by the sensor in Figure 1, and displacement as measured by voice-coil inductance or optical reflectance as just described. The output from these models consists of the voltage applied to the voice coil to control the speaker displacement. Given these inputs and outputs, we want to simulate tool-tissue interactions by generating forces and displacements with various relationships to each other and to time, using feedback from the force sensor and displacement measurements to guarantee accurate rendering of these parameters. For this purpose, we have constructed a real-time computation platform (see Figure 7) that includes a dedicated microprocessor (Analog Devices ADuC7026, 16 × 12-bit analog-to-digital, 4 × 12-bit digital-to-analog) capable of operating at a consistent rate of 5 KHz while providing real-time updates to reasonably complex models of tool-tissue interaction. The microprocessor communicates to a standard laptop computer, with the microprocessor acting as the master in a master-slave communications protocol via Serial Peripheral Interface (SPI), through an intervening programmable interface (Wixel, from Pololu). The Wixel converts SPI to the universal serial bus (USB) protocol. This permits the computer to log data synchronously and provide a graphical user interface (GUI) through which the researcher can issue low-bandwidth commands without interrupting real-time operation of the model.

The computer is currently logging 5 bytes of data during each cycle of the microprocessor’s operation (5 KHz) without significant data loss, each byte requiring 2.5 μs from a total 200 μs available in each cycle. Given our current relatively simple algorithm on the microprocessor for real-time control of the haptic renderer, this leaves 140 μs of idle time in each cycle for us to tap, as our control algorithms become more complex and as we log additional values.

3. Results and Discussion

The optical displacement sensor was calibrated using a mechanical gage with a digital readout (iGaging 35-128 DigiIndi), shown in Figure 8. The gage has a nominal resolution of 0.01 mm and is mounted such that its contact point rides up and down with the scaffold attached to the speaker cone. The gage was zeroed at the displacement resulting from no current in its coil. This zero point was affected by the weight of the moving element of the gage, making it lower than the resting point would have been without the gage by approximately 1 mm.

Using the mechanical gage apparatus, we gathered readings from the optical and inductance systems at specific displacements over a −3 mm to +3 mm displacement range, using a precision 5-turn potentiometer to control the DC voltage to the speaker. The results are shown in Figure 9 (red and green curves, respectively).

As can be seen, while the optical system is monotonic with displacement, the inductance system is not. The inductance system appears to show an increase in inductance (decrease in voltage) with displacement in either direction from 0 displacement, which would make displacement measurements in the positive and negative directions difficult to differentiate. We needed to determine whether this non-monotonic behavior is due to the position of the coil relative to the magnet, or to the DC current in the magnet saturating the magnetic core of the speaker.

To determine the effect of the DC current on the inductance measurement, a separate experiment was conducted in which the speaker was moved through the same range of displacements using an externally applied force, with no DC current present in the speaker coil. These results are shown in Figure 9 (blue curve). As can be seen, the resulting function is now monotonic, although demonstrating a lower total dynamic range over the −3 mm to +3 mm displacement range. Thus, if we can separate the effects on inductance of current and displacement when using a DC (or more generally low frequency) current, we can still achieve a monotonic measure of displacement based on inductance. This will be discussed further in the Conclusions section.

The inherent noise in the optical and inductance systems was determined by recording root-mean-squared AC voltages in each (optical: 1.2 mV; inductance: 3.1 mV). Using the maximum range of voltages observed over the −3 mm to +3 mm displacement range (optical: 1.4 V; inductance 0.28 V) yielded a signal-to-noise (S/N) of 61 dB for the optical system and 39 dB for the inductance system.

We then determined displacement vs. speaker voltage over the −3 mm to +3 mm displacement range, shown in Figure 10. The non-linearity in the compliance of mechanical suspension is evident. The non-linearity is asymmetrical in part due to the offset in displacement introduced by the mechanical gage (~1 mm, as discussed above). The data also probably reflect changes in the efficiency of the voice-coil due to coil location relative to the magnet.

Finally, we measured the voltage required to produce 0.98 N (100 g) at zero displacement, the result being 0.95 V. Since force is approximately a linear function of voltage at a given displacement, and we can safely deliver 10 V DC to the speaker coil, this means the system can deliver approximately 10 N of force in either direction at zero displacement. The deliverable force will be less as displacement increases, since the mechanical compliance of the speaker must be overcome.

4. Conclusions

We have developed a novel 1-DOF haptic renderer based on a readily available inexpensive electronic device, the loudspeaker. The design and construction of an initial prototype has been completed. The renderer exhibits high bandwidth, low friction, and low hysteresis, which are advantages it shares with the Maglev haptic rendering device from Butterfly Haptics. As opposed to the Maglev, however, whose flotor weighs 500 g, the entire moving apparatus of our devices weighs 23 g (11 g from the speaker itself and 12 g from our scaffold, sensor, preload spring, and attachment point). The total cost of parts, including microprocessor and custom 3D printing in our rapid prototyping center of the scaffold, is approximately $600.

Our design incorporates a novel method of measuring displacement from inductance. Initial analysis of this displacement measurement shows a precision of approximately 1% (39 dB) of full displacement, which given our test range of −3 mm to +3 mm, translates to ~0.06 mm. Full calibration of displacement will need to account for the observed interaction between the low frequency current used to displace the speaker and the 30 KHz sinusoid used to measure inductance, due to non-linearity in the ferrite core of the speaker. We have shown this interaction to be significant when those low-frequency currents are at DC, and further study will be conducted to establish if additional interactions occur at non-DC low frequencies. Given that we control, and therefore know, the magnitude of the low frequency current, a calibration of the inductance measurement that takes those currents into account should be possible.

With the new haptic rendering device, we expect to develop various models of tissue behavior for use in experiments to explore the psychophysics of tool-tissue interactions. In particular, we expect the device to be central to testing new surgical tools we are developing that augment force perception [5,9]. The haptic rendering device lends itself to simulating 1-DOF procedures such as needle insertion, fluid injection and withdrawal, membrane pealing, etc. Others in the haptics research community may find the device useful for their own experiments, or may even wish to participate in its development. To that end, we are developing the new platform in an open-source format, providing complete specifications for use by others. It is our hope that other researchers will agree about the need for such a low-cost, flexible, and high-performance platform for haptics research, and possibly contribute their own haptic models to the platform.