Dynamic Contact between a Wire Rope and a Pulley Using Absolute Nodal Coordinate Formulation
Abstract
:1. Introduction
2. Modeling of Rope and Pulley
2.1. Formulation of Wire Rope
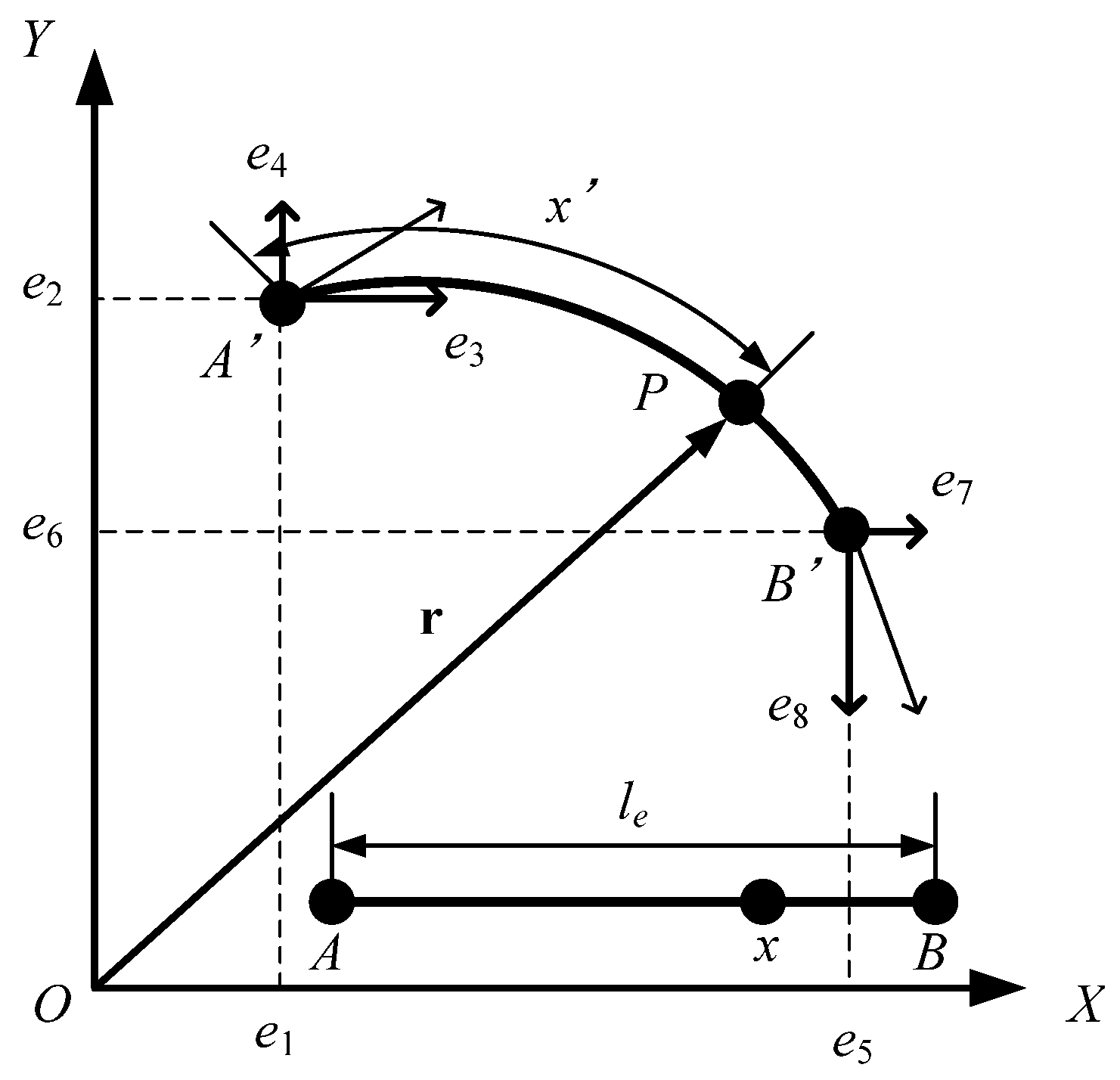
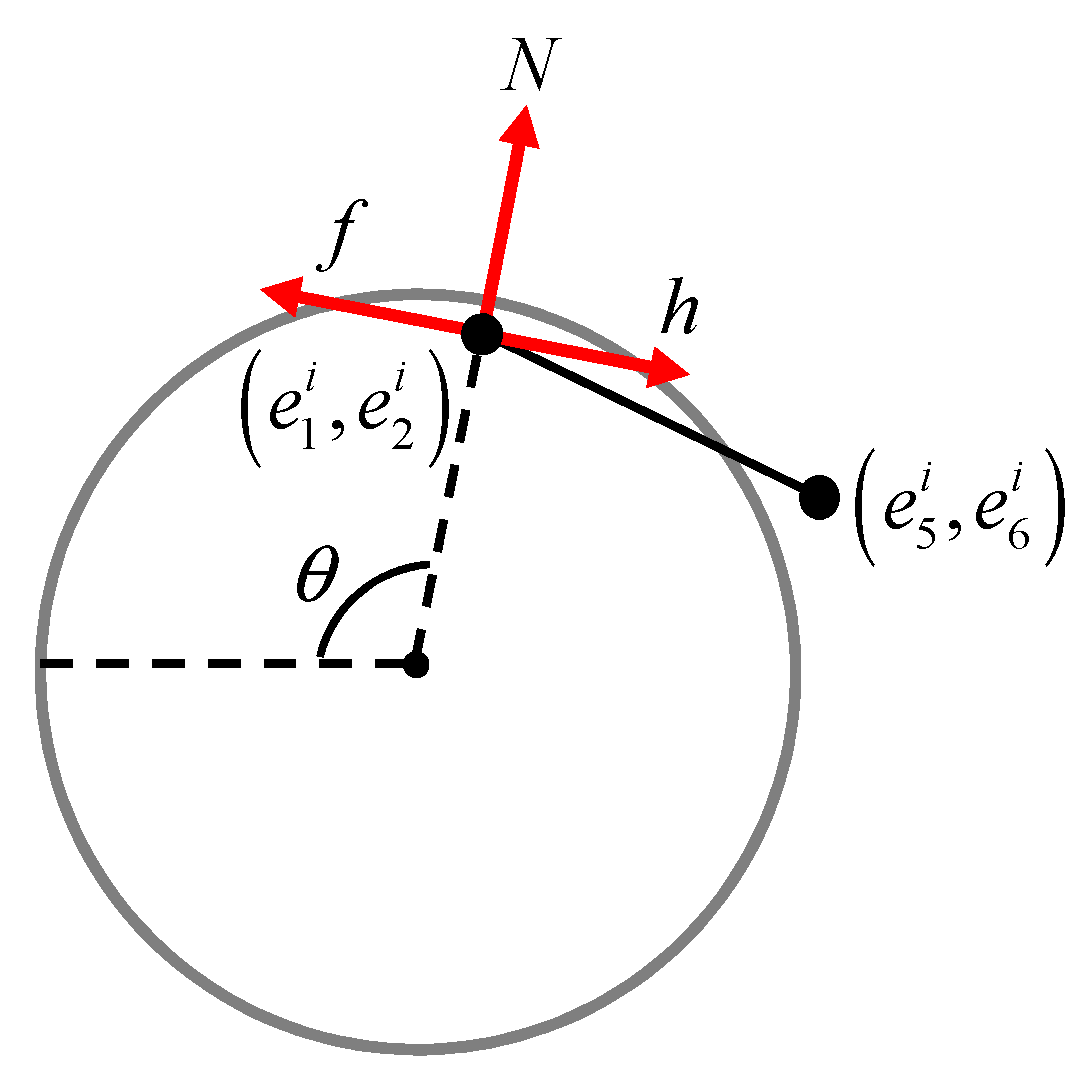
2.2. Formulation of Normal Contact Force, Frictional Force, and Constraint Force
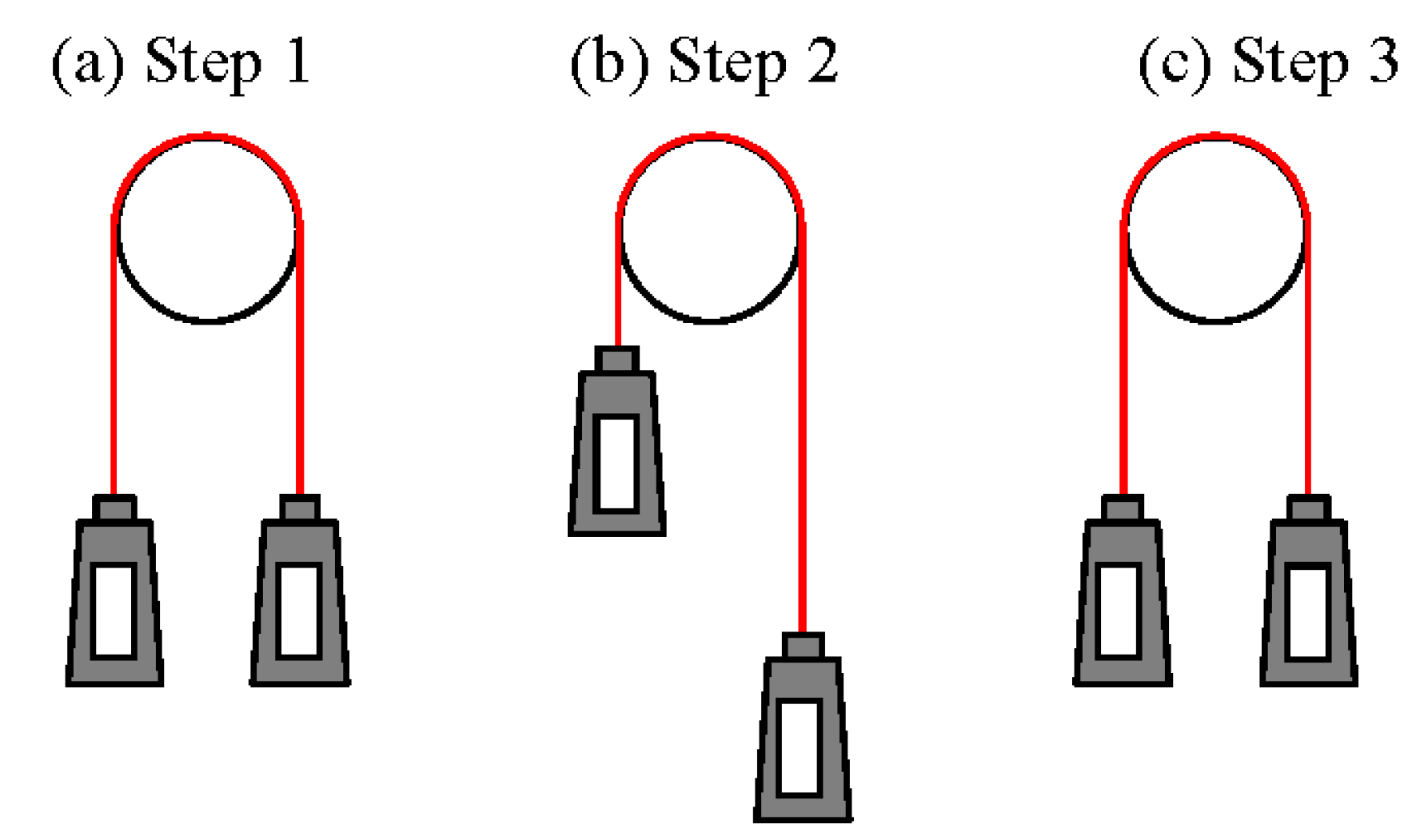
3. Validation of Numerical Model

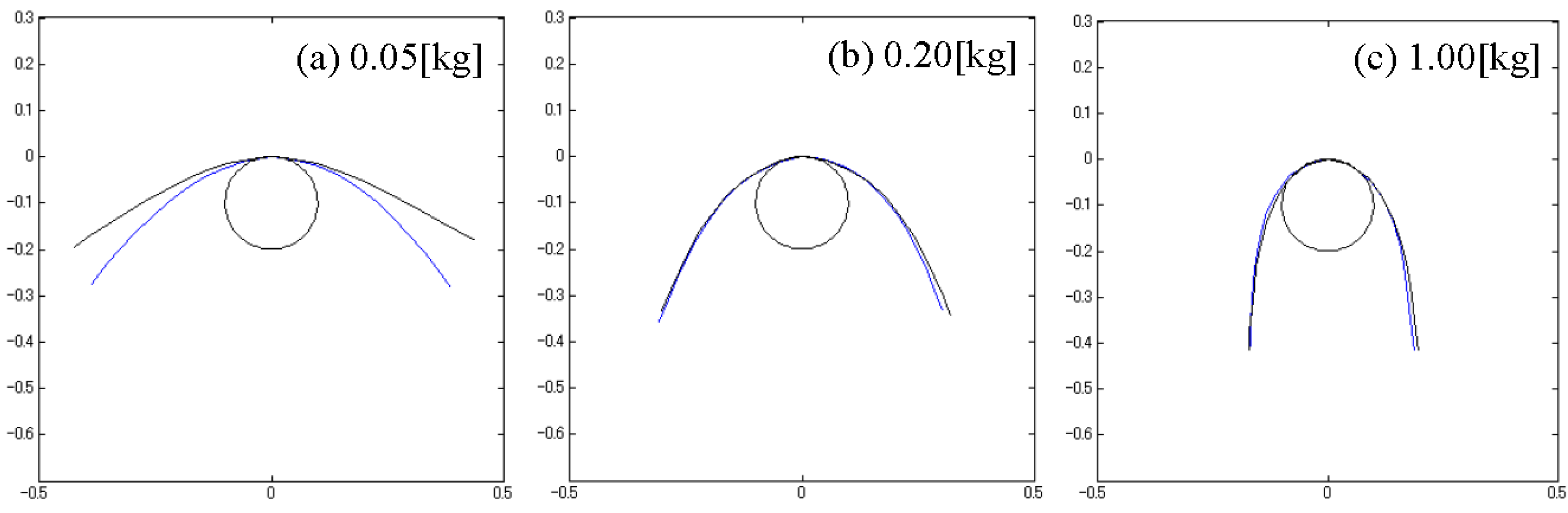
| Symbol | Unit | Value | |
|---|---|---|---|
| l | Length of wire rope | m | 1.00 |
| R | Radius of pulley | m | 0.10 |
| mr, ml | Magnitude of added masses | kg | 1.00 |
| Ee | Longitudinal elastic modulus | N/m2 | 2.91 × 1010 |
| n | Number of elements | - | 20 |
| Symbol | Unit | Value | |
|---|---|---|---|
| l | Length of Lope | m | 2.40 |
| ml, mr | Mass | kg | 294.70 |
| Ee | Coefficient of longitudinal elasticity | N/m2 | 2.91 × 1010 |
| Eb | Coefficient of bending elasticity | N/m2 | 6.00 × 108 |
| ρ | Density of rope | kg/m3 | 1091 |
| R | Diameter of pulley | m | 0.10 |
| kp | Penalty parameter of pulley | N/m | 2.00 × 106 |
| kp2 | Penalty parameter of pulley at edge | N/m | 2.00 × 105 |
| cp | Damping constant of pulley | N/(m/s) | 5.00 × 103 |
| μ | Frictional coefficient | - | 0.10 |
| ε | Fixed regularization parameter | m/s | 0.05 |
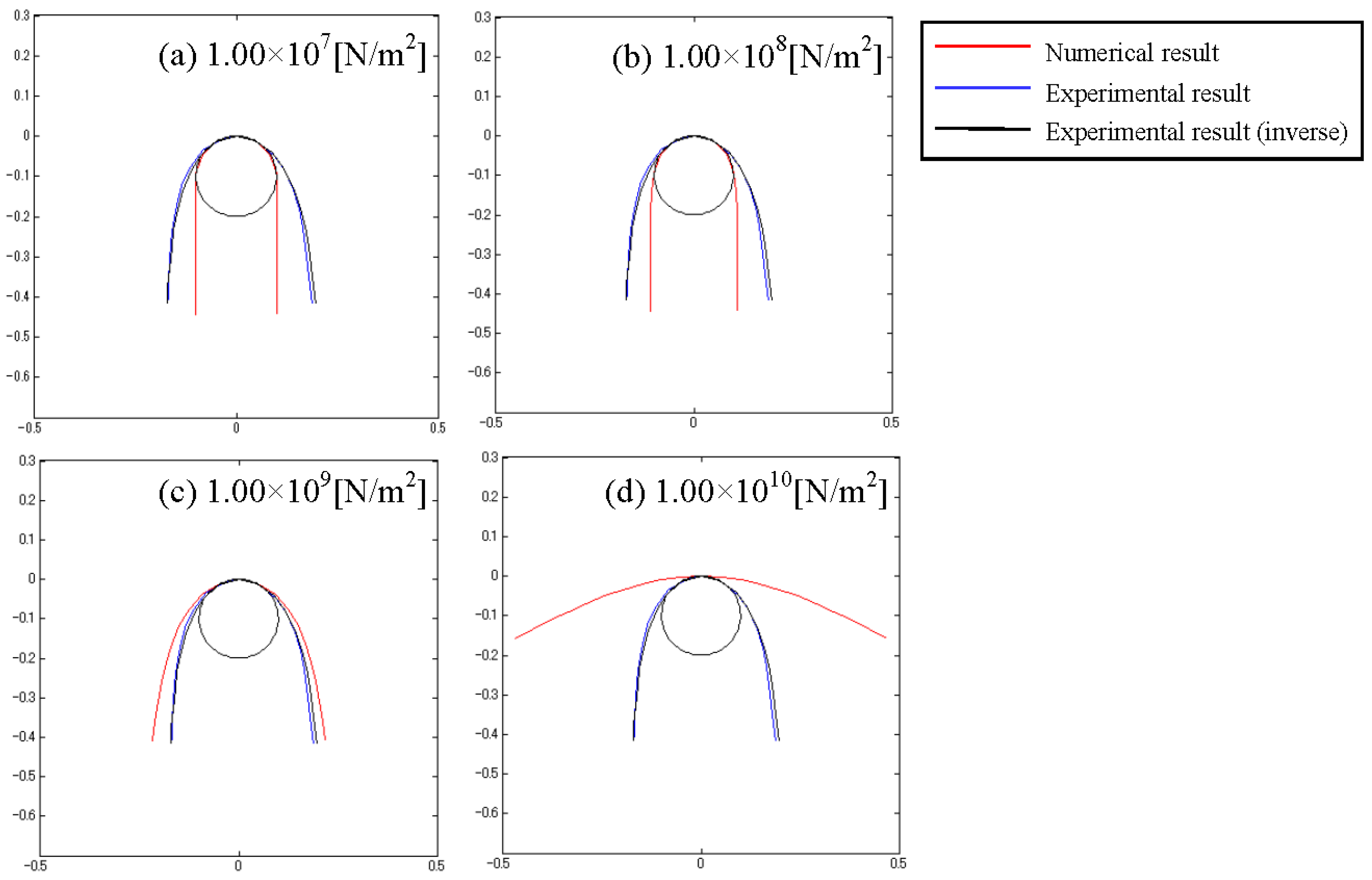
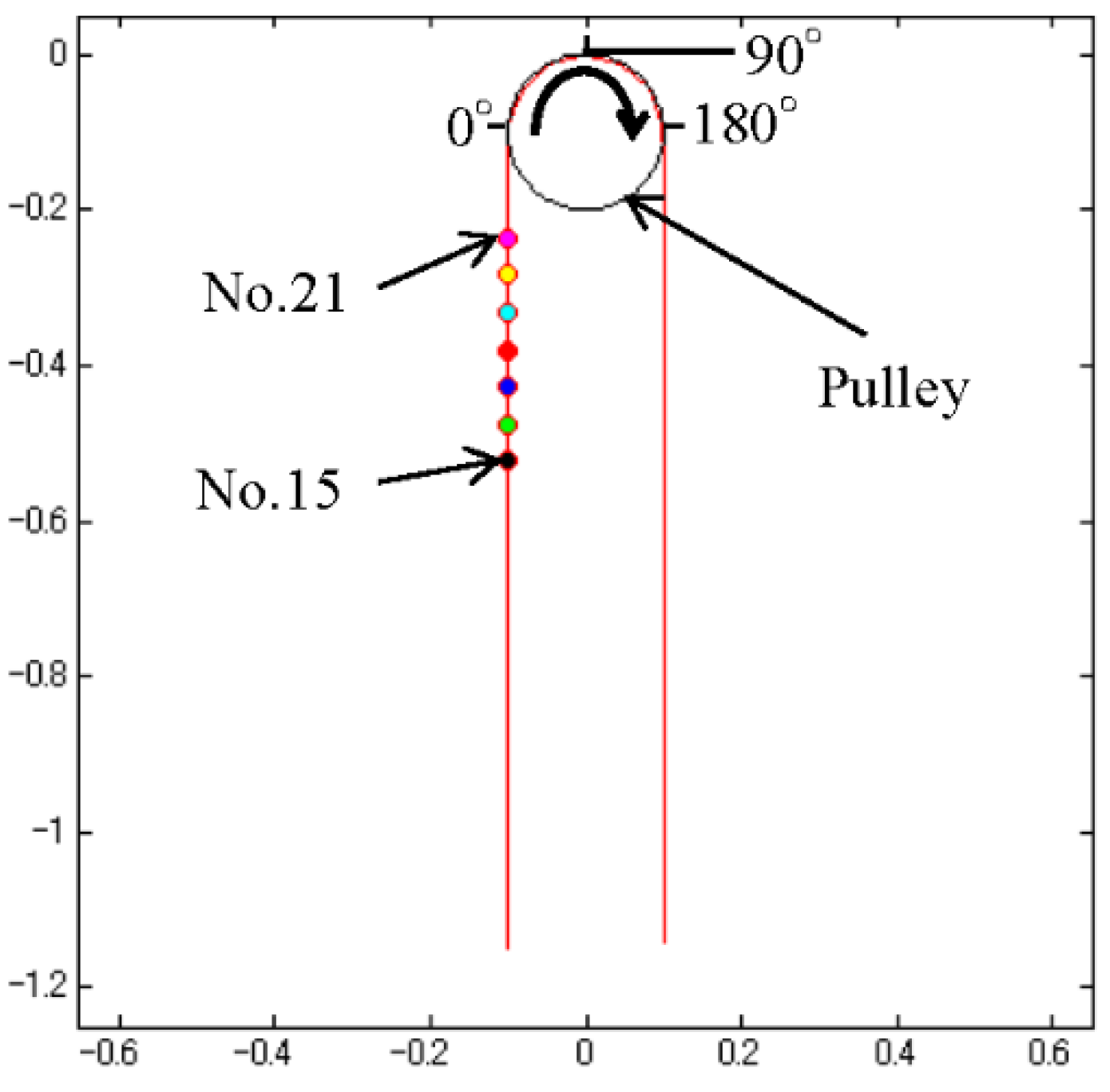
4. Numerical Results and Discussion
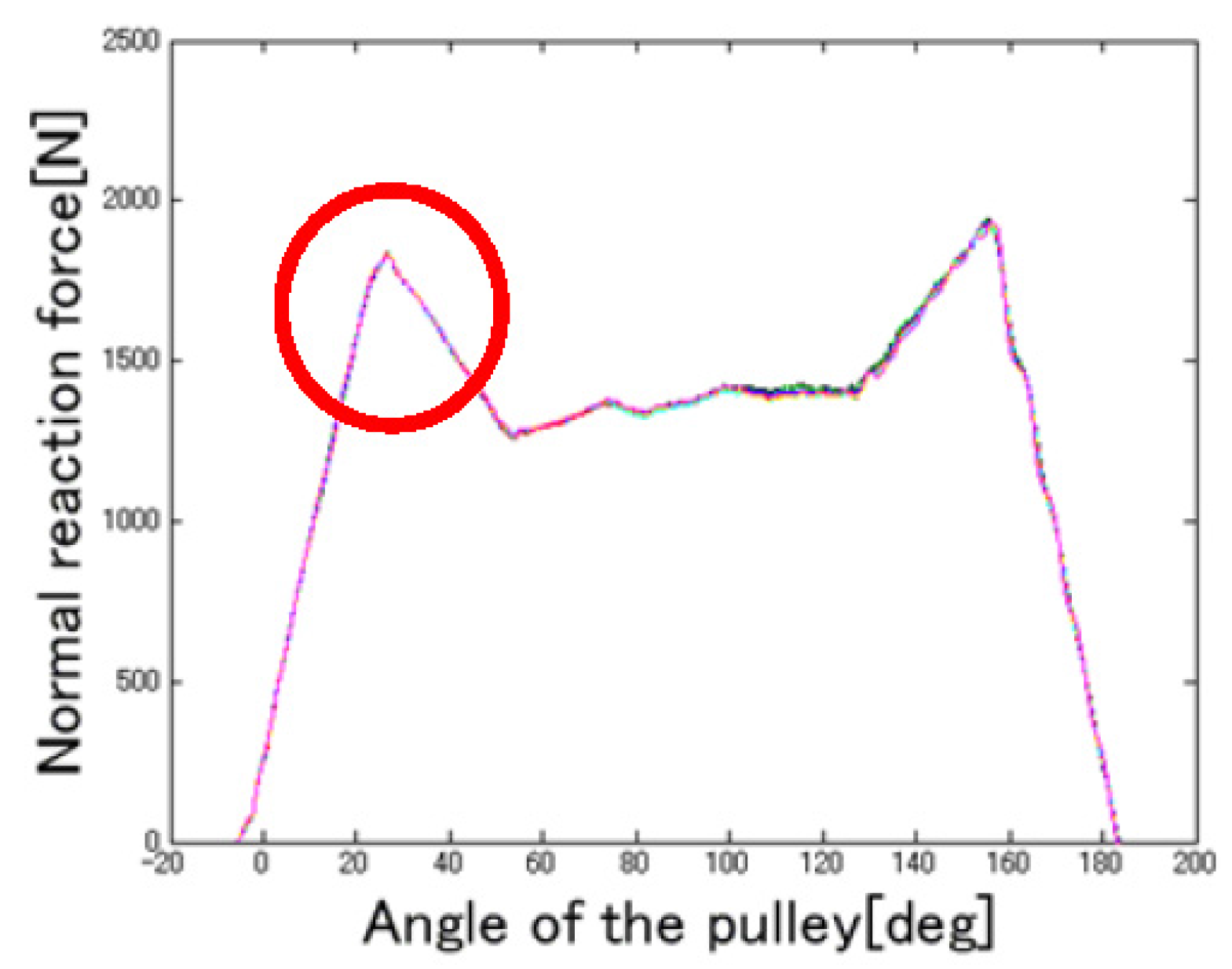
4.1. Force Acting on Rope

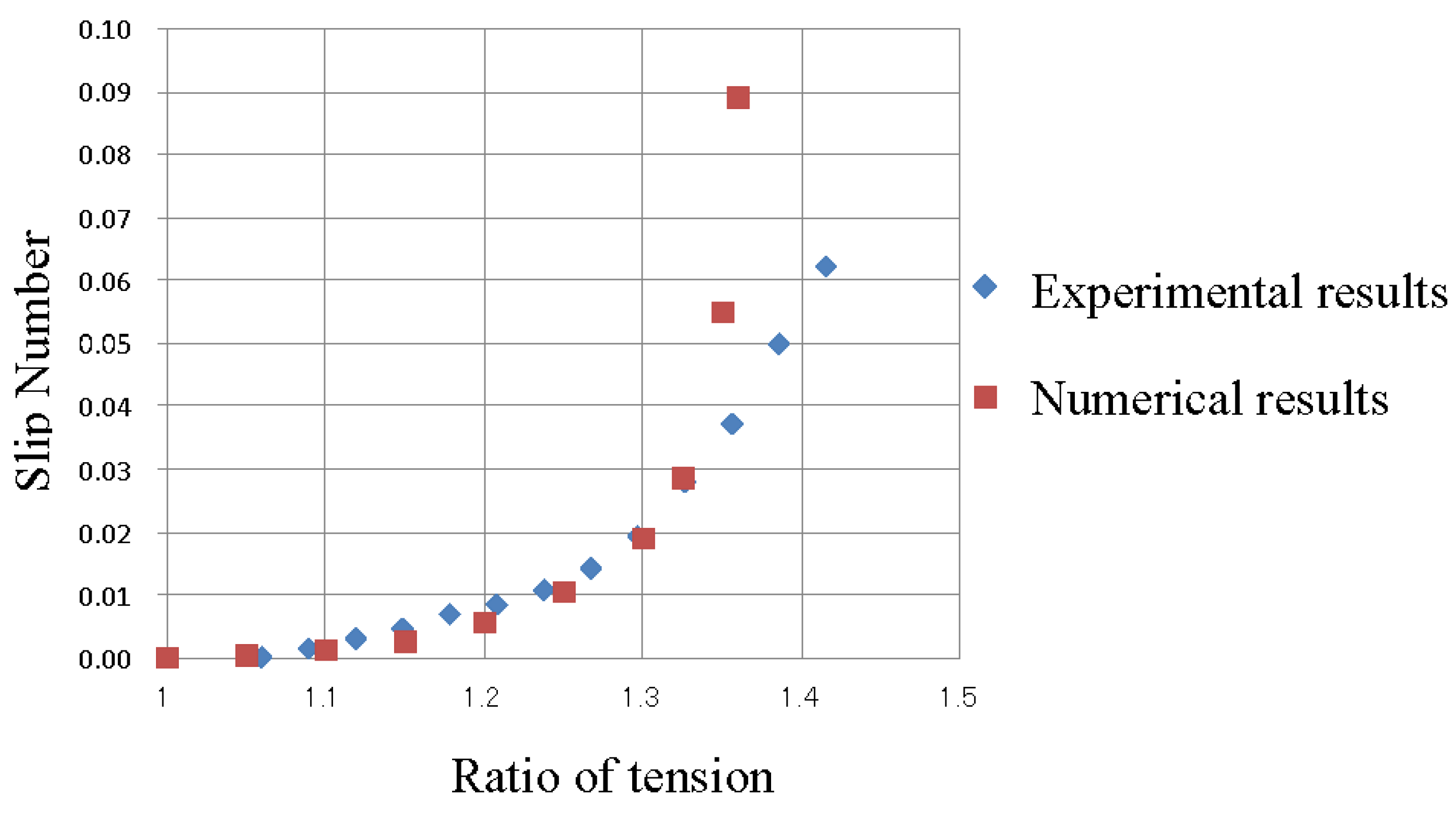
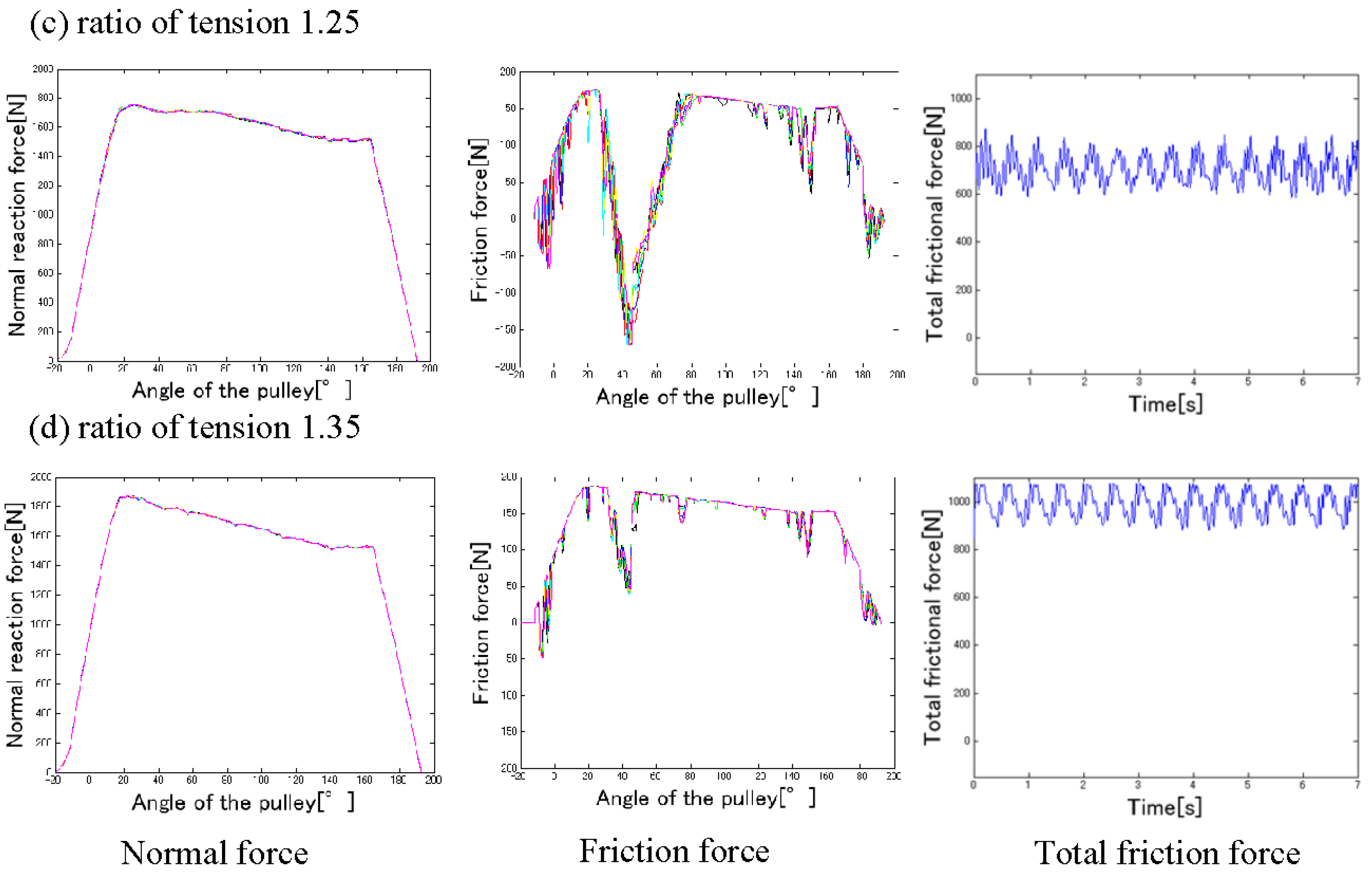
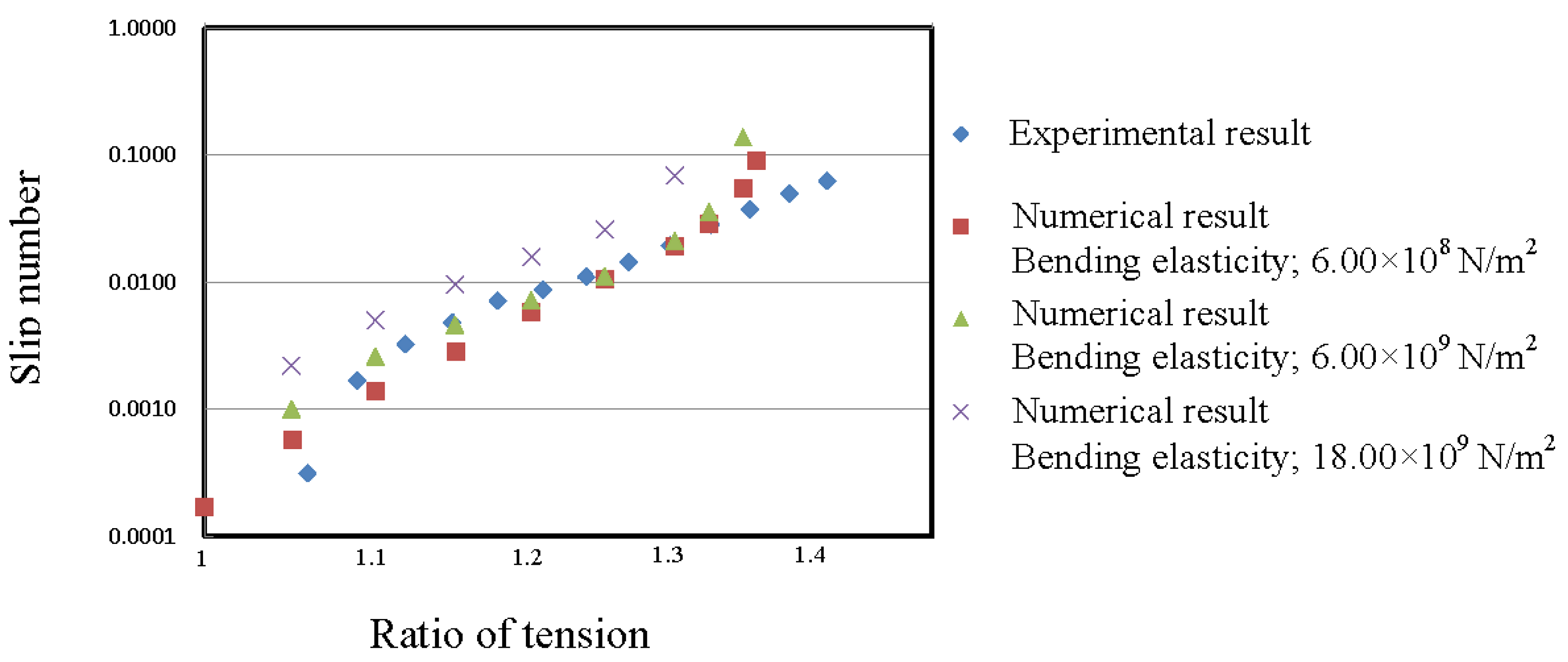
4.2. Influence of Ratio of Tension

4.3. Influence of Bending Elastic Modulus
5. Conclusions
- We proposed a numerical model that can describe in detail the behavior of the contact between a wire rope and a pulley.
- The validity of the developed numerical model was confirmed by comparing the distance of slip predicted by numerical simulations to that measured in experiments, when the wire rope had reciprocal motion.
- From the results of the numerical simulations, we showed that the force acting on a wire rope on a pulley is not uniform, due to the action of partial forces.
- From the results of the numerical simulations, it was determined that the rope slips when the ratio of tension is low, and the bending elastic modulus of the rope is large.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Terumichi, Y.; Yoshizawa, M.; Fukawa, Y.; Tsujioka, Y. Lateral oscillation of a moving elevator rope a cab in high-rise building. Trans. Jpn. Soc. Mech. Eng. 1993, 59, 686–693. [Google Scholar] [CrossRef]
- Nohmi, M.; Yoshida, S.; Terumichi, Y.; Takehara, S.; Uchiyama, M.; Nencherv, D. Space environmental test for a tethered space robot. Space Utiliz. Res. 2008, 24, 115–116. [Google Scholar]
- Nohmi, M.; Yoshida, S. Experimental analysis for attitude control of a tethered space robot under microgravity. Space Technol. 2004, 24, 119–128. [Google Scholar]
- Kimura, H.; Min, Z.; Ishii, T.; Yamamoto, A.; Shiba, H. Vibration analysis of elevator rope(simplified calculation method for detecting rope deflection of moving cage during earthquake). Trans. Jpn. Soc. Mech. Eng. 2009, 75, 2483–2488. [Google Scholar] [CrossRef]
- Kaczmarczyk, S.; Ostachowicz, W. Non-stationary responses of cables with slowly varying length. J. Acoust. Vib. 2000, 5, 117–126. [Google Scholar]
- Imanishi, E.; Nanjo, T.; Hirooka, E.; Kobayashi, T. Dynamic simulation of a wire rope with contact. Trans. Jpn. Soc. Mech. Eng. 2004, 70, 1023–1028. [Google Scholar] [CrossRef]
- Klaus, F. Wire Ropes; Springer: Berlin, Germany, 2007; pp. 194–195. [Google Scholar]
- Shabana, A.A. Finite element incremental approach and exact rigid body inertia. J. Mech. Des. 1996, 118, 171–178. [Google Scholar] [CrossRef]
- Shabana, A.A.; Hussien, H.A.; Escalona, J.L. Application of the absolute nodal coordinate formulation to large rotation and large deformation problems. J. Mech. Des. 1998, 120, 188–195. [Google Scholar] [CrossRef]
- Takahashi, Y.; Shimizu, N.; Suzuki, K. Study on the damping matrix of the beam element formulated by absolute nodal coordinate approach. Trans. Jpn. Soc. Mech. Eng. 2003, 69, 2225–2232. [Google Scholar] [CrossRef]
- Takahashi, Y.; Shimizu, N. Study on the elastic force for the deformed beam by means of the absolute nodal coordinate multibody dynamics formulation (Derivation of the elastic force using finite displacement and infinitesimal strain). Trans. Jpn. Soc. Mech. Eng. 2001, 67, 626–632. [Google Scholar] [CrossRef]
- Abdullah, A.M.; Michitsuji, Y.; Takehara, S.; Nagai, M.; Miyajima, N. Swing-up control of mass body interlinked flexible tether. Arch. Mech. Eng. 2010, 57, 115–131. [Google Scholar] [CrossRef]
- Quinn, D.D. A new regularization of coulomb friction. J. Vib. Acoust. 2004, 126, 391–397. [Google Scholar] [CrossRef]
- Karnopp, D. Computer simulation of stick-slip friction in mechanical dynamic systems. J. Dyn. Syst. Meas. Control 1985, 107, 100–103. [Google Scholar] [CrossRef]
- Salcudean, E.S.; Vlaar, T. On the emulation of stiff walls and static friction with a magnetically levitated input-output device. J. Dyn. Syst. Meas. Control 1997, 119, 127–132. [Google Scholar] [CrossRef]
- Yagawa, G.; Hirayama, H.; Ando, Y. Analysis of two-dimensional bodies and beams in contact using penalty function method. Trans. Jpn. Soc. Mech. Eng. 1980, 46, 1220–1229. [Google Scholar] [CrossRef]
- ImageJ. Available online: http://rsbweb.nih.gov/ij/ (accessed on 19 January 2016).
- Laboratory of Plant Cell Biology in Totipotency Homepage. Available online: http://hasezawa.ib.k.u-tokyo.ac.jp/zp/Kbi/ImageJ/) (accessed on 19 January 2016).
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takehara, S.; Kawarada, M.; Hase, K. Dynamic Contact between a Wire Rope and a Pulley Using Absolute Nodal Coordinate Formulation. Machines 2016, 4, 4. https://doi.org/10.3390/machines4010004
Takehara S, Kawarada M, Hase K. Dynamic Contact between a Wire Rope and a Pulley Using Absolute Nodal Coordinate Formulation. Machines. 2016; 4(1):4. https://doi.org/10.3390/machines4010004
Chicago/Turabian StyleTakehara, Shoichiro, Masaya Kawarada, and Kazunori Hase. 2016. "Dynamic Contact between a Wire Rope and a Pulley Using Absolute Nodal Coordinate Formulation" Machines 4, no. 1: 4. https://doi.org/10.3390/machines4010004






