Mechanical Insertion Force and Electrical Contact Resistance of By-Pass Switches with Axially Canted Coil Springs
Abstract
1. Introduction
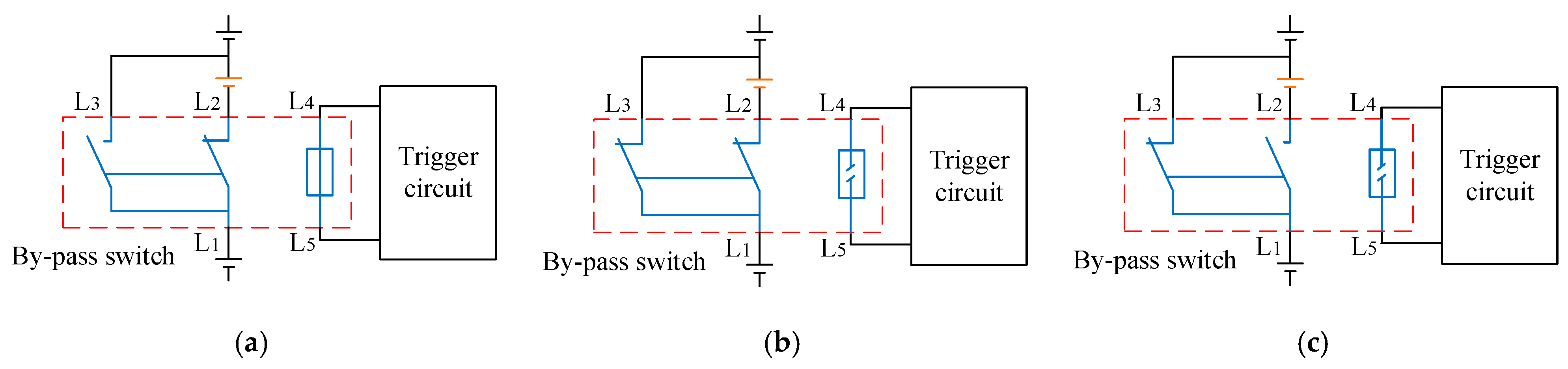
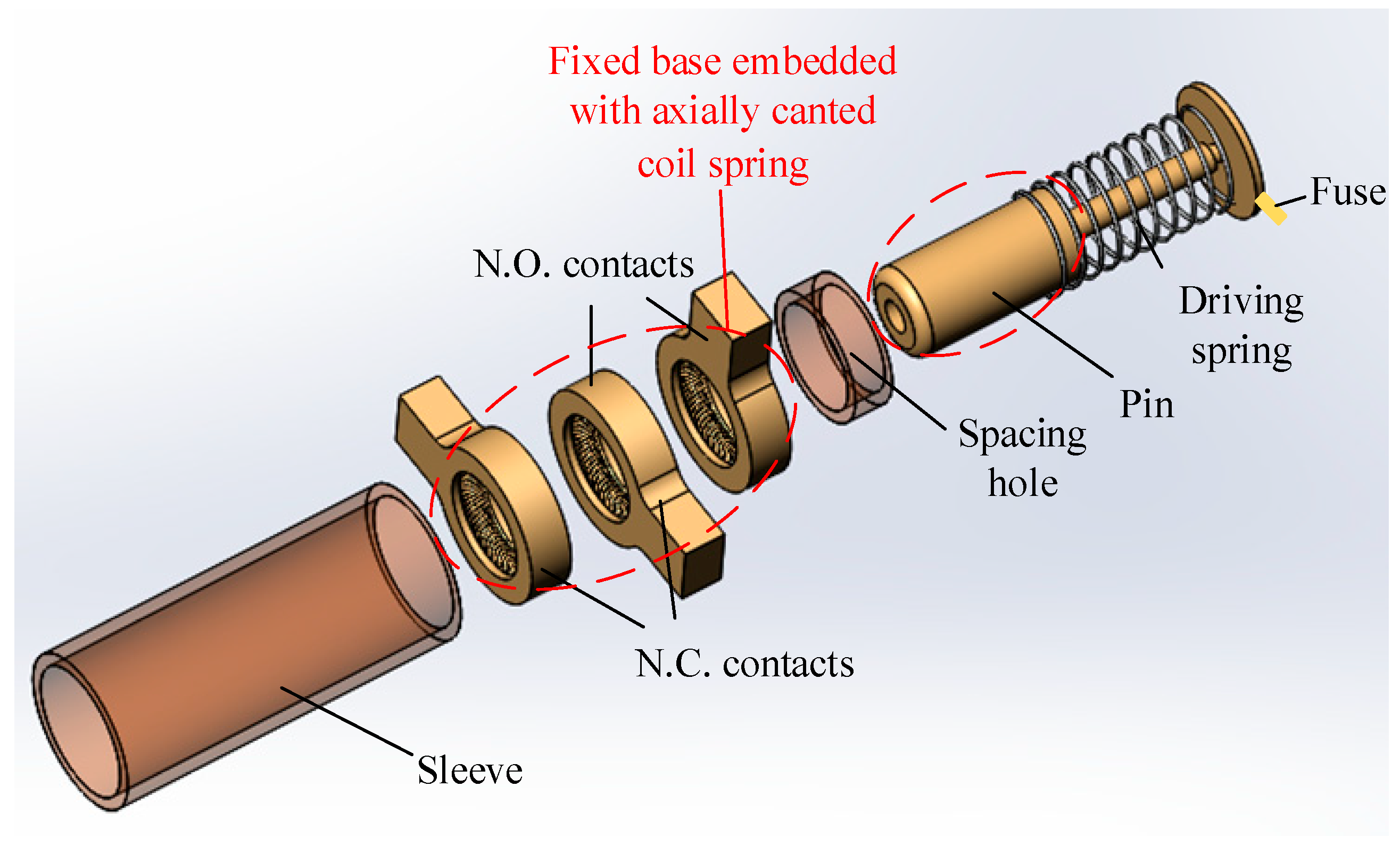
2. Description of By-Pass Switches with Axially Canted Coil Spring
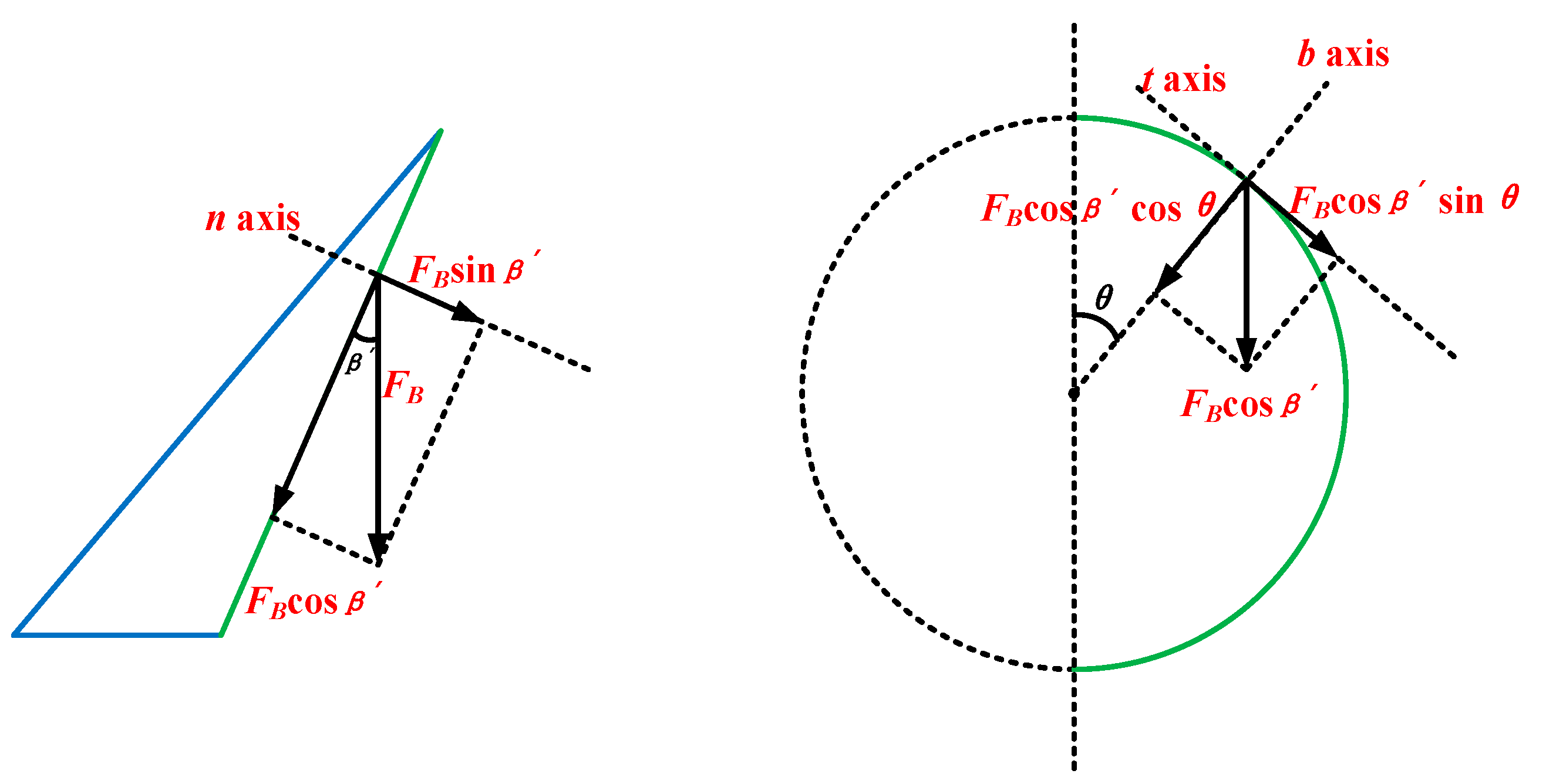
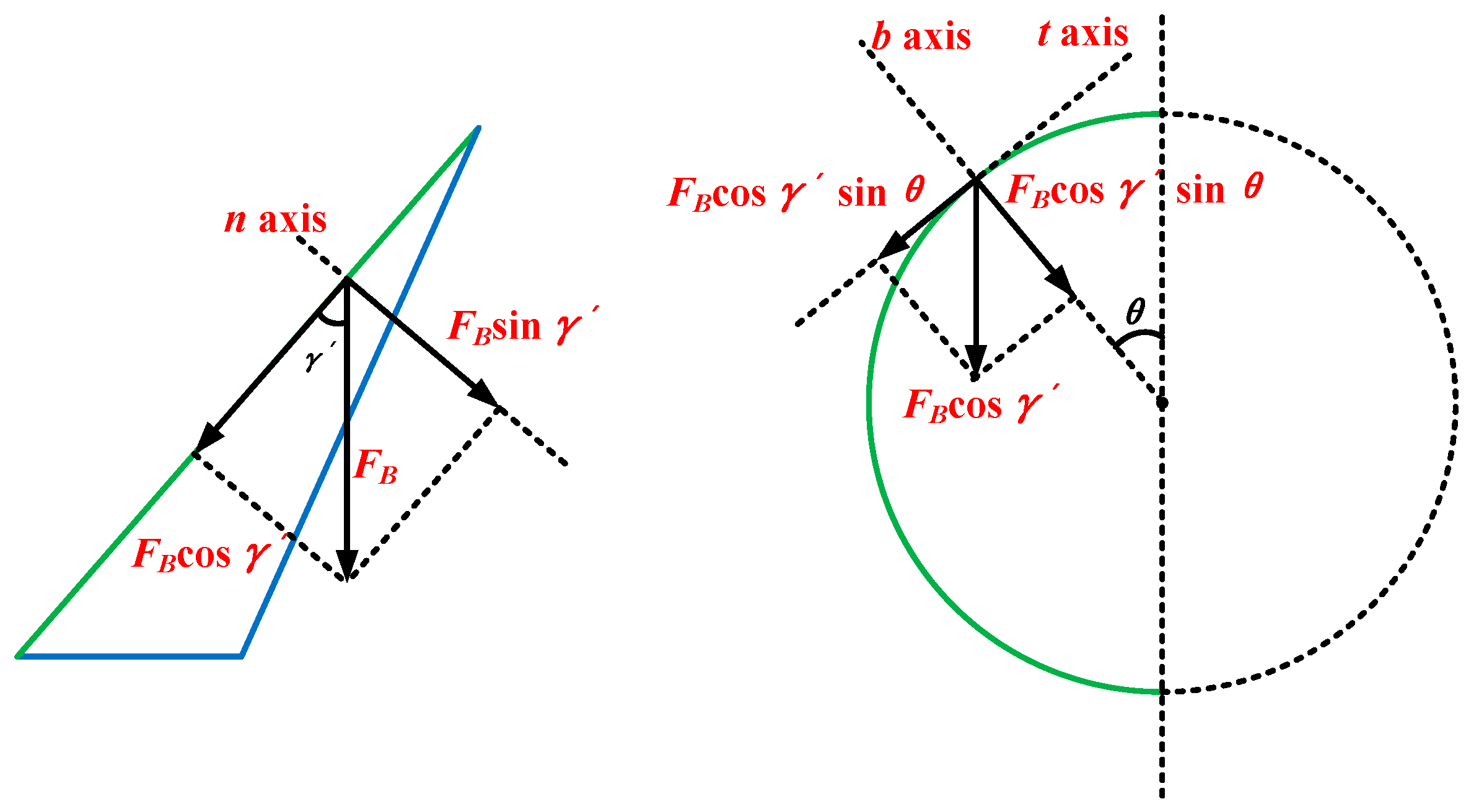
3. Analytical Calculation of Insertion Force and Electrical Contact Resistance
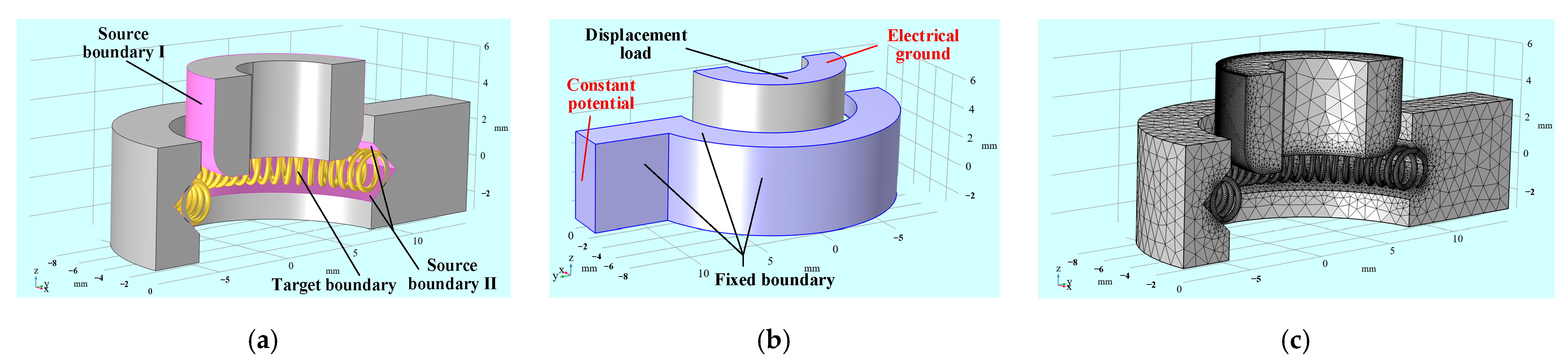
4. FEM Modeling for Mechanical and Electrical Field Analysis
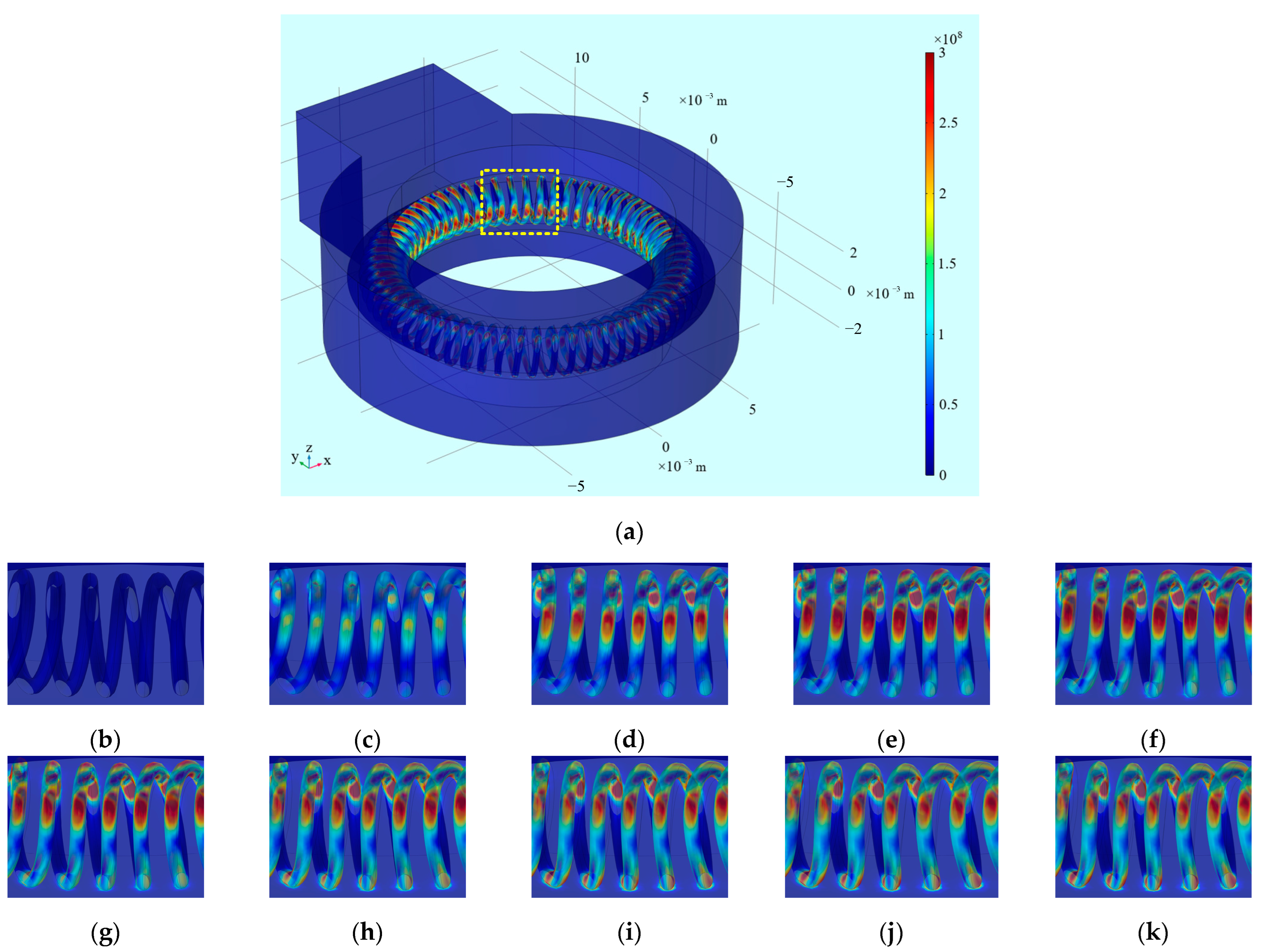
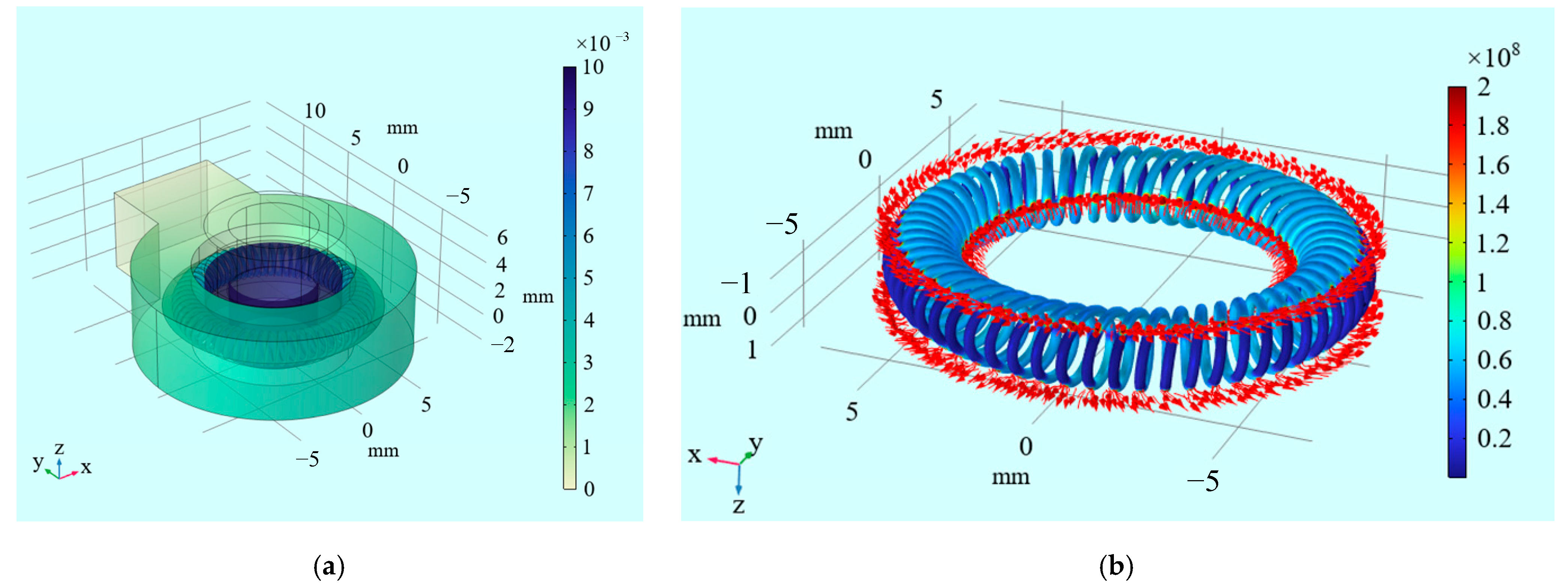
5. Results and Discussion
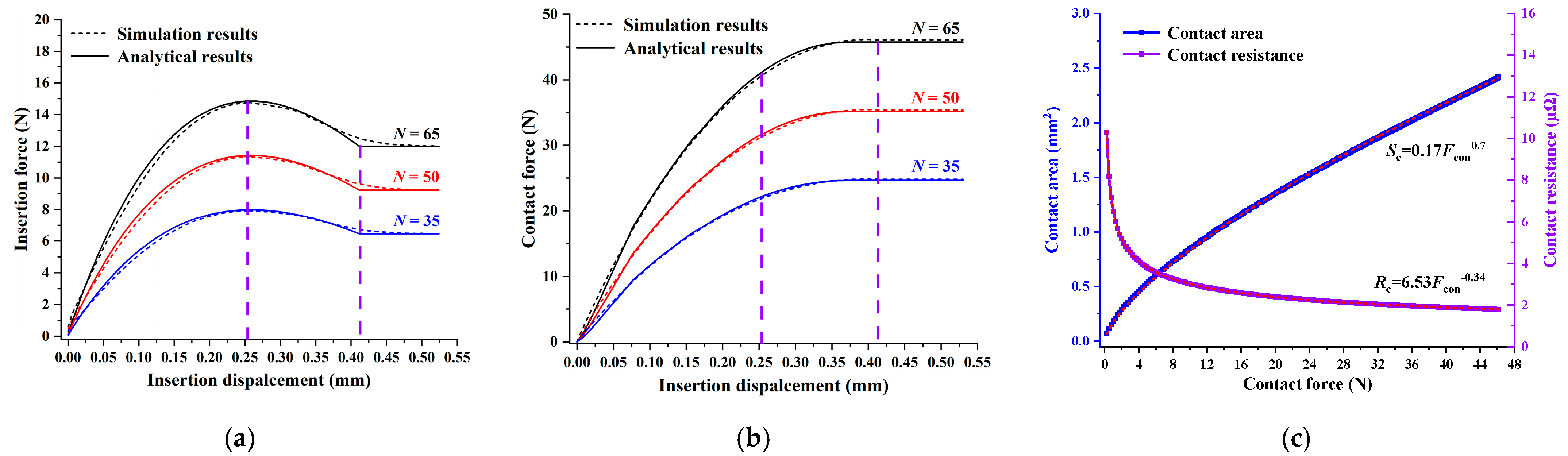
5.1. Validity of Analytical Model
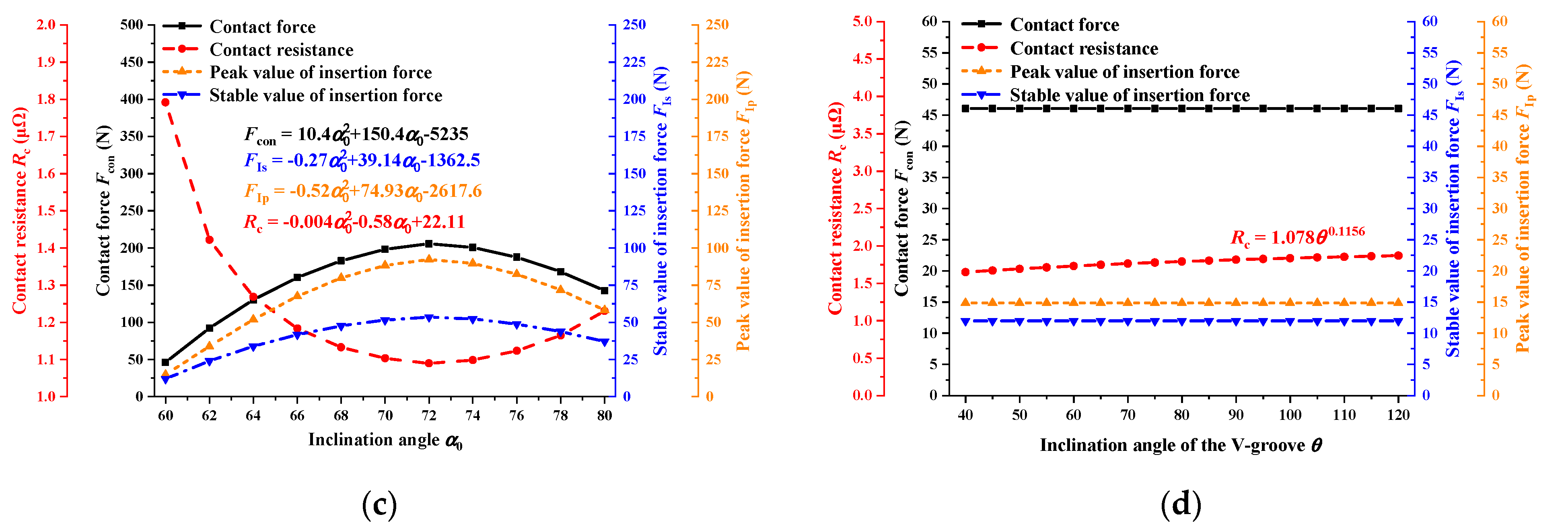
5.2. Influencing Factors
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Kabir, M.N.; Mishra, Y.; Ledwich, G.; Dong, Z.Y.; Wong, K.P. Coordinated Control of Grid-Connected Photovoltaic Reactive Power and Battery Energy Storage Systems to Improve the Voltage Profile of a Residential Distribution Feeder. IEEE Trans. Ind. Inform. 2014, 10, 967–977. [Google Scholar] [CrossRef]
- Strasser, T.; Andren, F.; Kathan, J.; Kathan, J.; Cecati, C.; Buccella, C.; Siano, P.; Leitao, P.; Zhabelova, G.; Vyatkin, V.; et al. A Review of Architectures and Concepts for Intelligence in Future Electric Energy Systems. IEEE Trans. Ind. Electron. 2015, 62, 2424–2438. [Google Scholar] [CrossRef]
- Zubi, G.; Dufo-Lopez, R.; Carvalho, M.; Pasaoglu, G. The lithium-ion battery: State of the art and future perspectives. Renew. Sustain. Energy Rev. 2018, 89, 292–308. [Google Scholar] [CrossRef]
- Rudoy, E.; Semerie, J.P.; Pasquier, E.; Dohan, Y. High capacity battery cell by-pass switches surge/short-circuit current testing results. In Proceedings of the 6th European Space Power Conference (ESPC), Porto, Portugal, 6–10 May 2002; pp. 561–564. [Google Scholar]
- Novak, B.; Szabo, L. Temperature Rise of Canted Spring Contacts During Fault Current. In Proceedings of the 63rd IEEE Holm Conference on Electrical Contacts, Denver, CO, USA, 10–13 September 2017. [Google Scholar]
- Hannan, M.A.; Hoque, M.M.; Mohamed, A.; Ayob, A. Review of energy storage systems for electric vehicle applications: Issues and challenges. Renew. Sustain. Energy Rev. 2017, 69, 771–789. [Google Scholar] [CrossRef]
- Emadi, A.; Rajashekara, K.; Williamson, S.S.; Lukic, S.M. Topological overview of hybrid electric and fuel cell vehicular power system architectures and configurations. IEEE Trans. Veh. Technol. 2005, 54, 763–770. [Google Scholar] [CrossRef]
- Shi, Z.Q.; Li, S.; Wang, Q.S.; Gao, Z.P.; Jia, S.L.; Wang, L.J. Numerical investigation on the steady temperature rise of a by-pass switch. Fusion Eng. Des. 2017, 124, 54–58. [Google Scholar] [CrossRef]
- Holm, R. Electric Contacts: Theory and Application; Springer: New York, NY, USA, 1967; pp. 14–16. [Google Scholar]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. A 1966, 295, 300–319. [Google Scholar]
- Blanc, J.; Grime, D.; Blateyron, F. Surface characterization based upon significant topographic features. In Proceedings of the 13th International Conference on Metrology and Properties of Engineering Surfaces, Twickenham, UK, 12–15 April 2011. [Google Scholar]
- Ning, Y.; Polycarpou, A.A. Extracting summit roughness parameters from random Gaussian surfaces accounting for asymmetry of the summit heights. J. Tribol.-Trans. ASME. 2004, 126, 761–766. [Google Scholar]
- Liu, H.; McBride, J.W. A Finite-Element-Based Contact Resistance Model for Rough surfaces: Applied to a Bilayered Au/MWCNT Composite. IEEE Trans. Compon. Pack. Manuf. Technol. 2018, 8, 919–926. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: New York, NY, USA, 1985; pp. 109–112. [Google Scholar]
- Sano, Y. Effect of space angle on constriction resistance and contact resistance for the case of line contact. IEEE Trans. Compon. Hybrids Manuf. Technol. 1985, 8, 228–234. [Google Scholar] [CrossRef]
- Sharma, A.; Jackson, R.L. A Finite Element Study of an Elasto-Plastic Disk or Cylindrical Contact Against a Rigid Flat in Plane Stress with Bilinear Hardening. Tribol. Lett. 2017, 65, 112. [Google Scholar] [CrossRef]
- Kogut, L.; Komvopoulos, K. Electrical contact resistance theory for conductive rough surfaces. J. Appl. Phys. 2003, 94, 3153–3162. [Google Scholar] [CrossRef]
- Kogut, L.; Komvopoulos, K. Electrical contact resistance theory for conductive rough surfaces separated by a thin insulating film. J. Appl. Phys. 2004, 95, 576–585. [Google Scholar] [CrossRef]
- Riba, J.R.; Mancini, A.G.; Abomailek, C.; Capelli, F. A 3D-FEM-Based Model to Predict the Electrical Constriction Resistance of Compressed Contacts. Measurement 2018, 114, 44–50. [Google Scholar] [CrossRef]
- Soler, J.M.; Rangel, R.H. Geometrical characterization of canted coil springs. Proc. Inst. Mech. Eng. C J. Eng. Mech. Eng. Sci. 2006, 220, 1831–1841. [Google Scholar] [CrossRef]
- Schriefer, T.; Hofmann, M.; Rauh, H.; Eckardt, B.; Maerz, M. Parameter Study on the Electrical Contact Resistance of Axially Canted Coil Springs for High-current Systems. In Proceedings of the 29th International Conference on Electrical Contacts (ICEC)/64th IEEE Holm Conference on Electrical Contacts, Albuquerque, NM, USA, 14–18 October 2018. [Google Scholar]
- Huang, L. Wear and leakage assessments of canted coil spring-energized polytetrafluoroethylene seals under ultra-high cycle operations. Wear 2022, 488–489, 204122. [Google Scholar] [CrossRef]
- Liu, D.; Zhao, J.; Li, S.; Zhao, X.; Huang, L. Experimental study on tribological and leakage characteristics of a rotating spring-energized seal under high and low temperature. Machines 2023, 11, 221. [Google Scholar] [CrossRef]
- Zhao, X.; Li, S.; Liu, D.; Huang, L. Material optimization method for a spring-energized seal based on wear analysis. Lubricants 2024, 12, 288. [Google Scholar] [CrossRef]
- Zhang, F.; Xiang, C.; Guo, F.; Jia, X. An equivalent axisymmetric modeling approach for circumferential springs under large deformation based on mechanical anisotropy. Proc. Inst. Mech. Eng. C J. Mech. Eng. Sci. 2024, 238, 8376–8389. [Google Scholar] [CrossRef]
- Zhang, W.; Schriefer, J.; Liu, J.; Sun, Y.; Zhu, J.; Song, J. Effects of design parameters on the contact force and electrical resistance of axially canted coil springs. J. Mech. Sci. Technol. 2023, 37, 1234–1242. [Google Scholar]
- Chen, S.; Yang, X.; Guo, F.; Zhang, B.; Wang, W.; Wang, Y. Sealing Performance Evaluation and Structural Optimization for Reducing Leakage Failures of Lip Seal Considering High-Speed Rotation Frictional Heat. Tribol. Trans. 2024, 67, 962–979. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, W.; Sun, Y.; Cong, M.; Zhu, J.; Song, J. Simulation analysis of deformation behavior and resilience of Ni-based alloy canted coil spring for dynamic seal. Acta Aeronaut. Astronaut. Sin. 2022, 43, 425527. [Google Scholar]
- Liu, J.; Zhang, W.; Sun, Y.; Cong, M.; Zhu, J.; Song, J. Research on design optimization and simulation analysis of deformation behavior of Ni-based alloy canted coil spring for dynamic seal. J. Appl. Mech. Mater. 2025, 24, 486. [Google Scholar]
- Amenta, F.; Ceretti, E.; Rizzuti, S.; Umbrello, D.; Micari, F. Tribological behaviour of PTFE composites for spring-energized seals under rotary conditions. Wear 2022, 482–483, 203989. [Google Scholar]
- Yan, L.; Guan, L.; Wang, D.; Xiang, D. Application and prospect of wear simulation based on ABAQUS: A review. Lubricants 2024, 12, 57. [Google Scholar] [CrossRef]
- Guan, X.Y.; Wu, L.; Shu, N.Q.; Peng, H.; Li, Q.Q.; Shen, Q.Y. Finite Element Analysis on Forces, Currents, and Magnetic Fluxes of Misaligned GIS Disconnector. IEEE Trans. Power Deliv. 2018, 33, 2484–2491. [Google Scholar] [CrossRef]
- Popov, E.P. Mechanics of Materials, 2nd ed.; Prentice-Hall Inc.: Saddle River, NJ, USA, 1976. [Google Scholar]
- Hertz, H. Über Die Berührung Fester Elastischer Körper. J. Reine Angew. Math. 1882, 92, 156. [Google Scholar] [CrossRef]
- Qin, B.; Zhang, Y. Comprehensive analysis of electro-mechanical characteristics and new regression models of a novel slanted groove electrical connector. Int. J. Non-Linear Mech. 2024, 166, 104863. [Google Scholar] [CrossRef]
- Meng, Y.; Ren, W.B.; Zhang, C. Investigation on Intermittent Failure Phenomenon of Electrical Connectors Under Repetitive Mechanical Insertion and Withdrawal Operations. IEEE Trans. Compon. Pack. Manuf. Technol. 2022, 12, 1533–1541. [Google Scholar] [CrossRef]
- Wu, B.H.; Lee, C.Y.; Chiang, Y.C.; Cao, S.Z.; Cao, X.; Zhang, G.D.; Zhou, S.P.; Wang, B.Q. Study on the contact performance of electronic EON connectors under axial vibration. IEEE Trans. Compon. Pack. Manuf. Technol. 2018, 8, 2090–2097. [Google Scholar] [CrossRef]

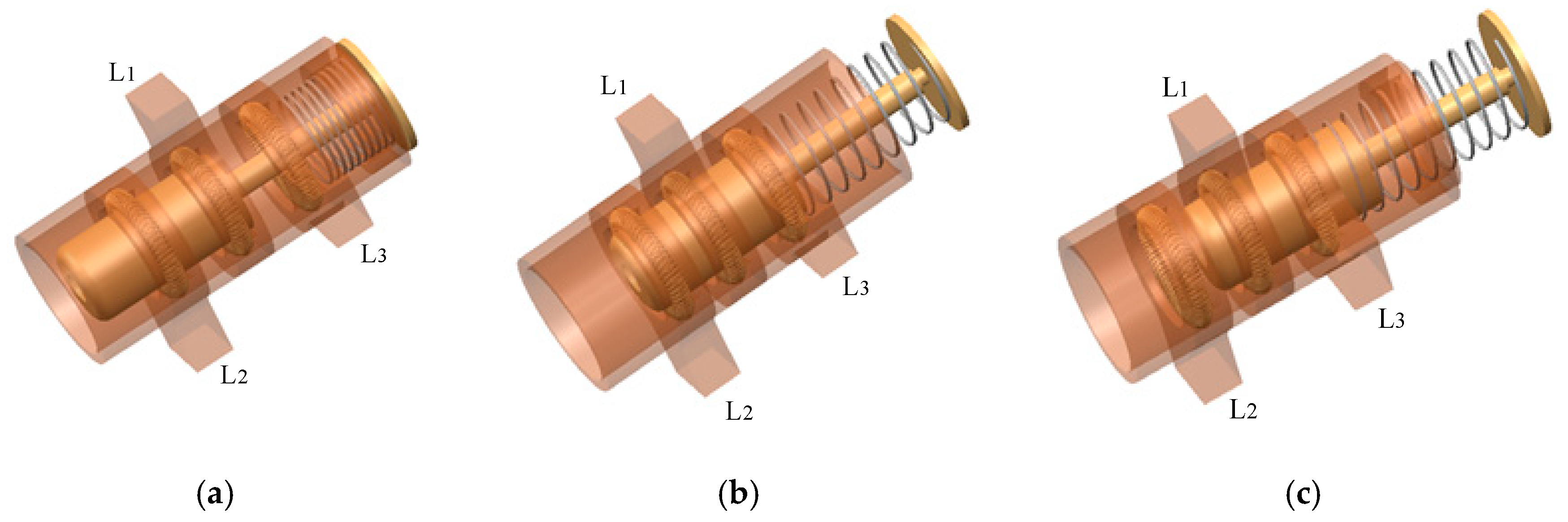
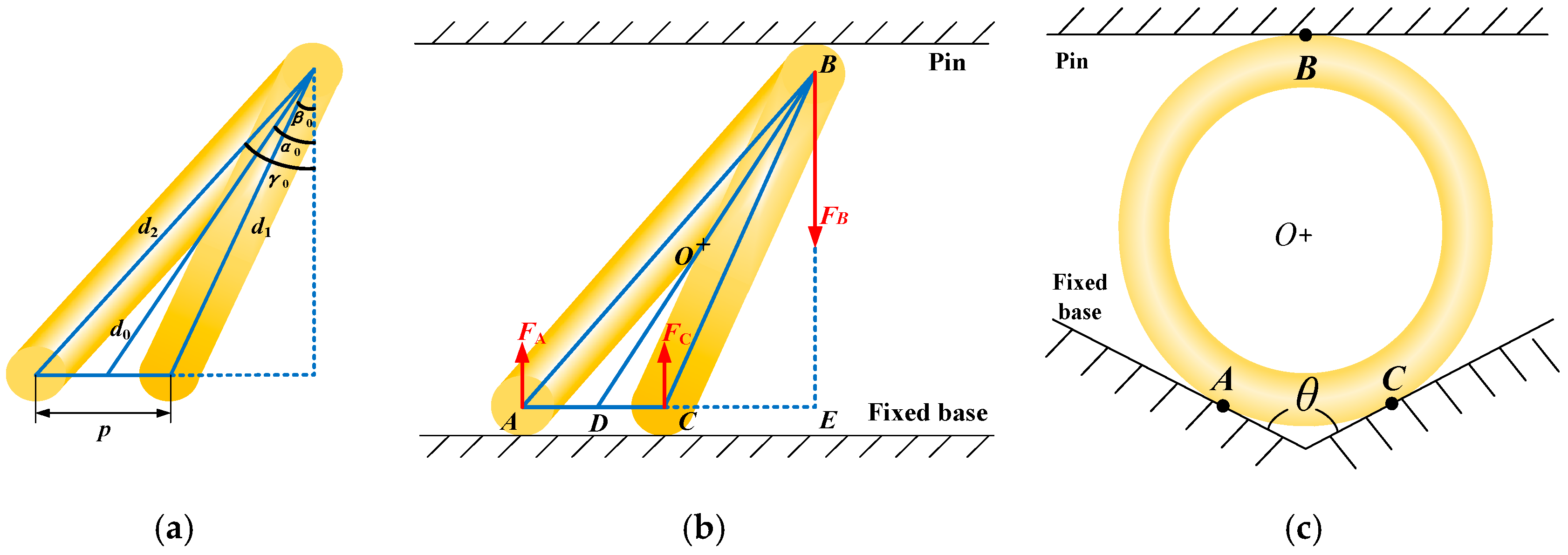


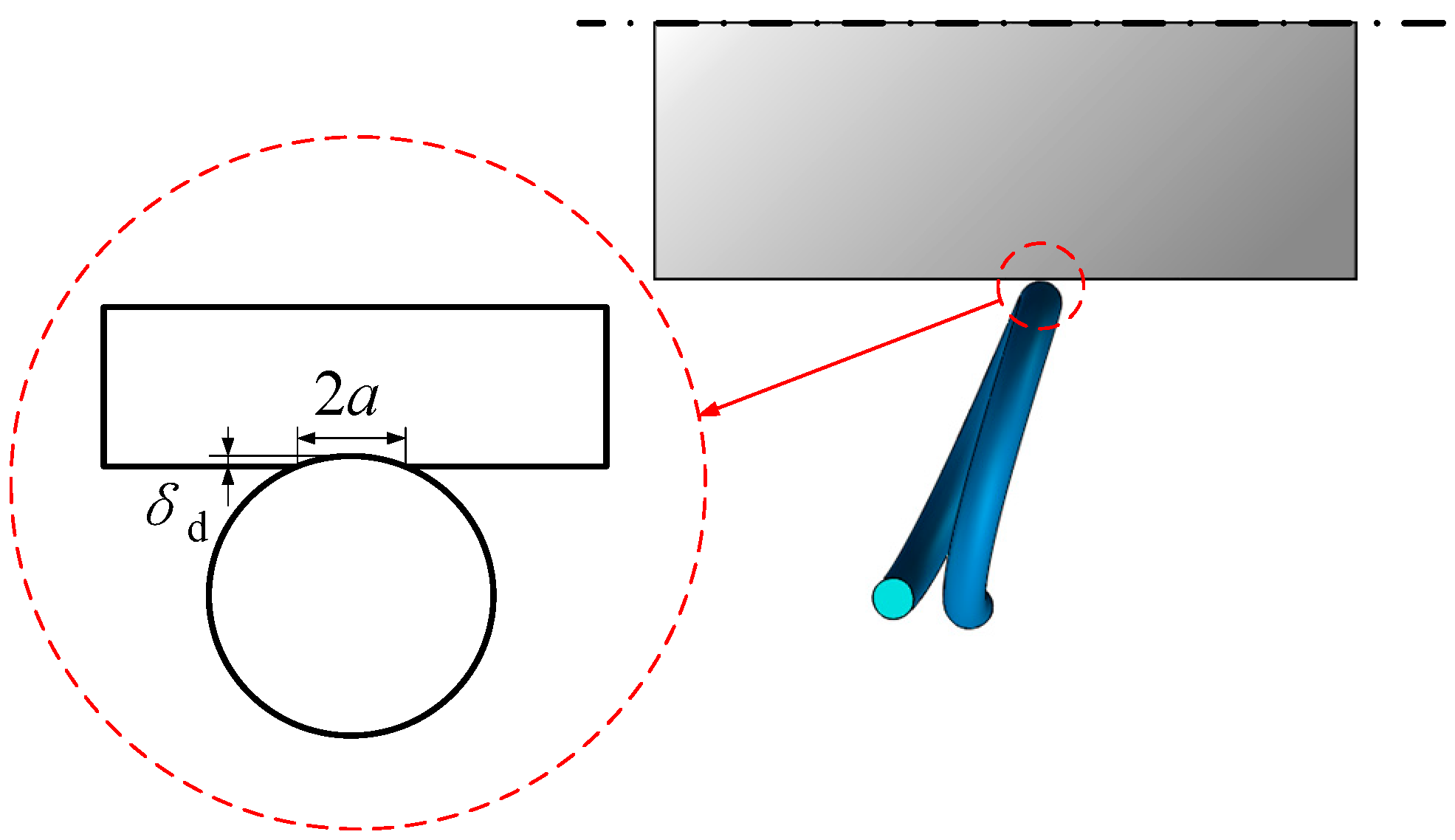
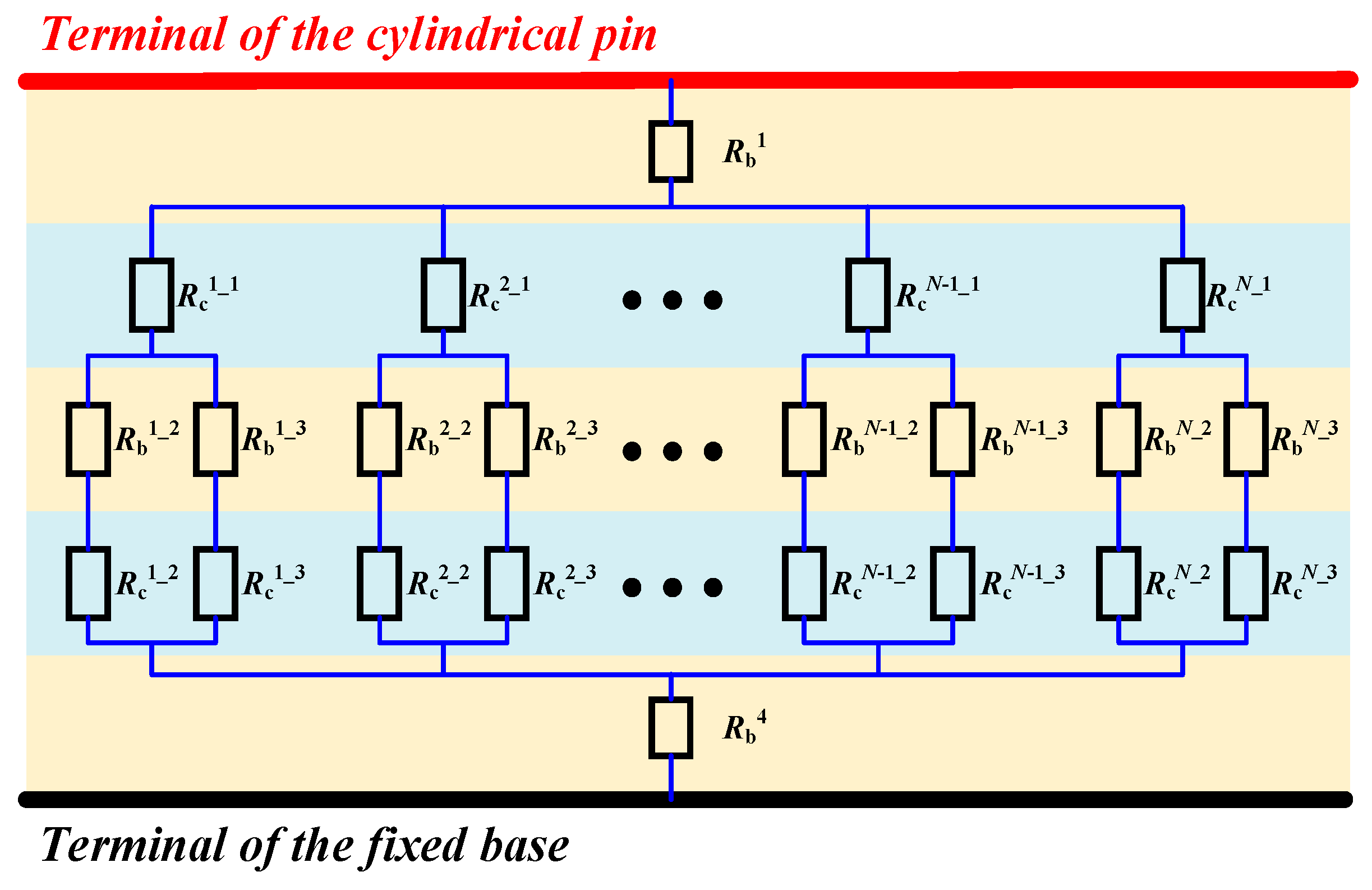


| Components | Parameters | Value |
|---|---|---|
| Axially canted coil spring | Diameter d0 | 2.15 [mm] |
| Inclination angle α0 | 60° | |
| Wire diameter ds | 0.3 [mm] | |
| Turn n | 65 | |
| Pitch p | 0.35 [mm] | |
| Cylindrical pin | Center height hps | 7.0 [mm] |
| Cylinder radius rp | 5.45 [mm] | |
| Chamfer radius rpc | 1.5 [mm] | |
| Fixed base | V-shape groove angle θ | 80° |
| Components | Material | Young’s Modulus (GPa) | Tangent Modulus (GPa) | Density (kg/m3) | Poisson’s Ratio | Electrical Resistivity (Ω·m) |
|---|---|---|---|---|---|---|
| Canted coil spring | Beryllium bronze (CuBe2) | 128 | 50 | 8250 | 0.3 | 9.5 × 10−8 |
| Cylindrical pin | Red copper | 116 | 46 | 8940 | 0.33 | 1.68 × 10−8 |
| Fixed base |
| Parameters | Wire Diameter ds | Chamfer Radius rpc | Inclination Angle of Reference Circle α0 | V-Shape Groove Angle θ |
|---|---|---|---|---|
| Contact force Fcon | 4661.2 × ds3.867 | — | 10.4α02 + 150.4α0 − 5235 | — |
| Peak value of insertion force FIp | 1214.8 × ds3.868 | — | −0.27α02 + 39.14α0 − 1362.5 | — |
| Stable value of insertion force FIs | 1382.1 × ds3.807 | 15.885 × rpc−0.162 | −0.52α02 + 74.93α0 − 2617.6 | — |
| Contact resistance Rc | 0.348 × ds−1.37 | 1.828 × rpc−0.048 | −0.004α02 − 0.58α0 + 22.11 (46,720α0−2.511, 60° ≤ α0 ≤ 72°; 0.0082α0−2.511, 72° < α0 ≤ 80) | 1.078 × θ0.1156 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Li, M.; Ren, W.; Liu, J. Mechanical Insertion Force and Electrical Contact Resistance of By-Pass Switches with Axially Canted Coil Springs. Machines 2025, 13, 878. https://doi.org/10.3390/machines13090878
Zhang C, Li M, Ren W, Liu J. Mechanical Insertion Force and Electrical Contact Resistance of By-Pass Switches with Axially Canted Coil Springs. Machines. 2025; 13(9):878. https://doi.org/10.3390/machines13090878
Chicago/Turabian StyleZhang, Chao, Ming Li, Wanbin Ren, and Jian Liu. 2025. "Mechanical Insertion Force and Electrical Contact Resistance of By-Pass Switches with Axially Canted Coil Springs" Machines 13, no. 9: 878. https://doi.org/10.3390/machines13090878
APA StyleZhang, C., Li, M., Ren, W., & Liu, J. (2025). Mechanical Insertion Force and Electrical Contact Resistance of By-Pass Switches with Axially Canted Coil Springs. Machines, 13(9), 878. https://doi.org/10.3390/machines13090878







