A Cloud-Edge Communication Resource Slicing Allocation Method for Data Monitoring in Integrated Energy Systems
Abstract
1. Introduction
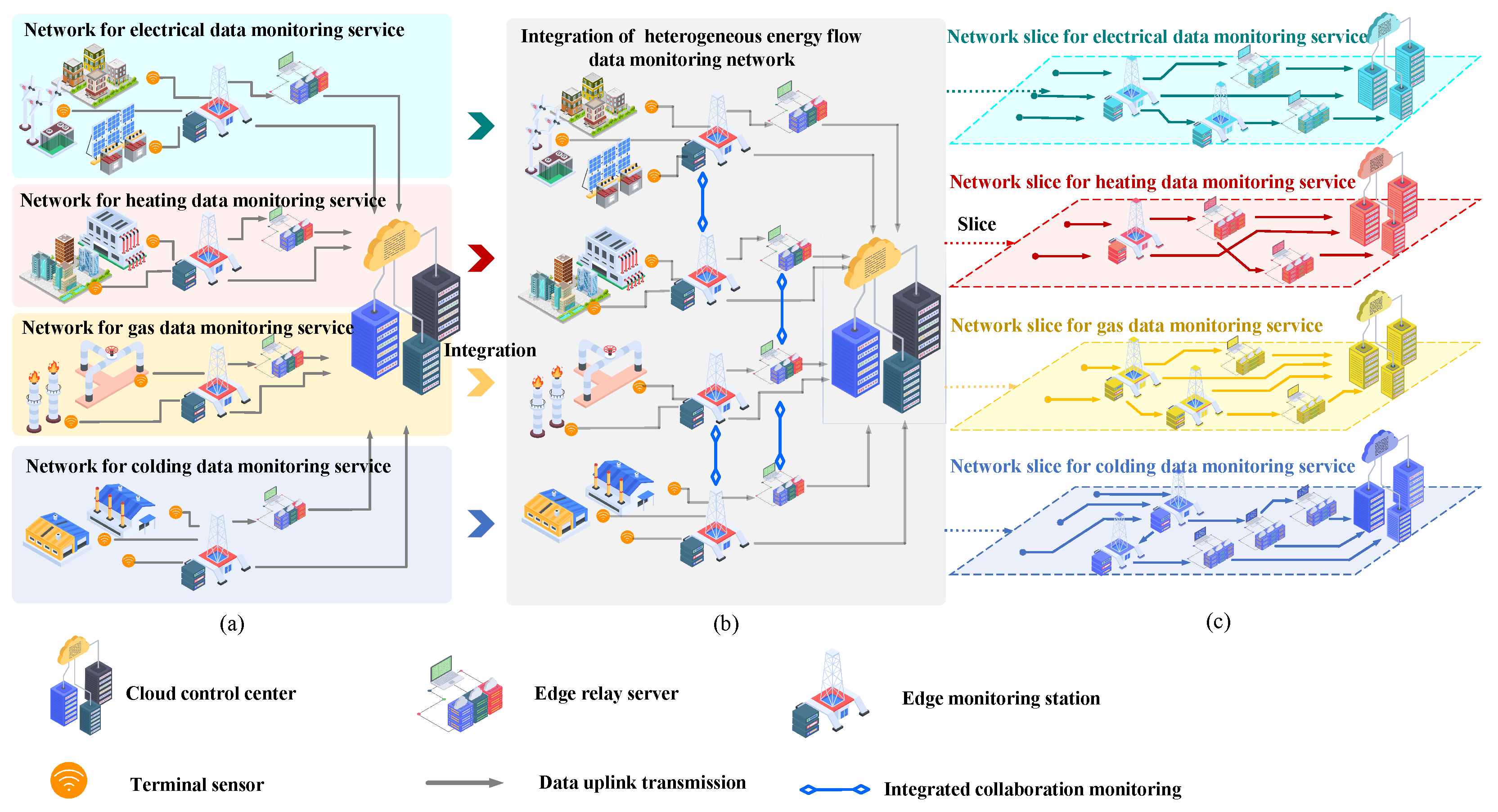
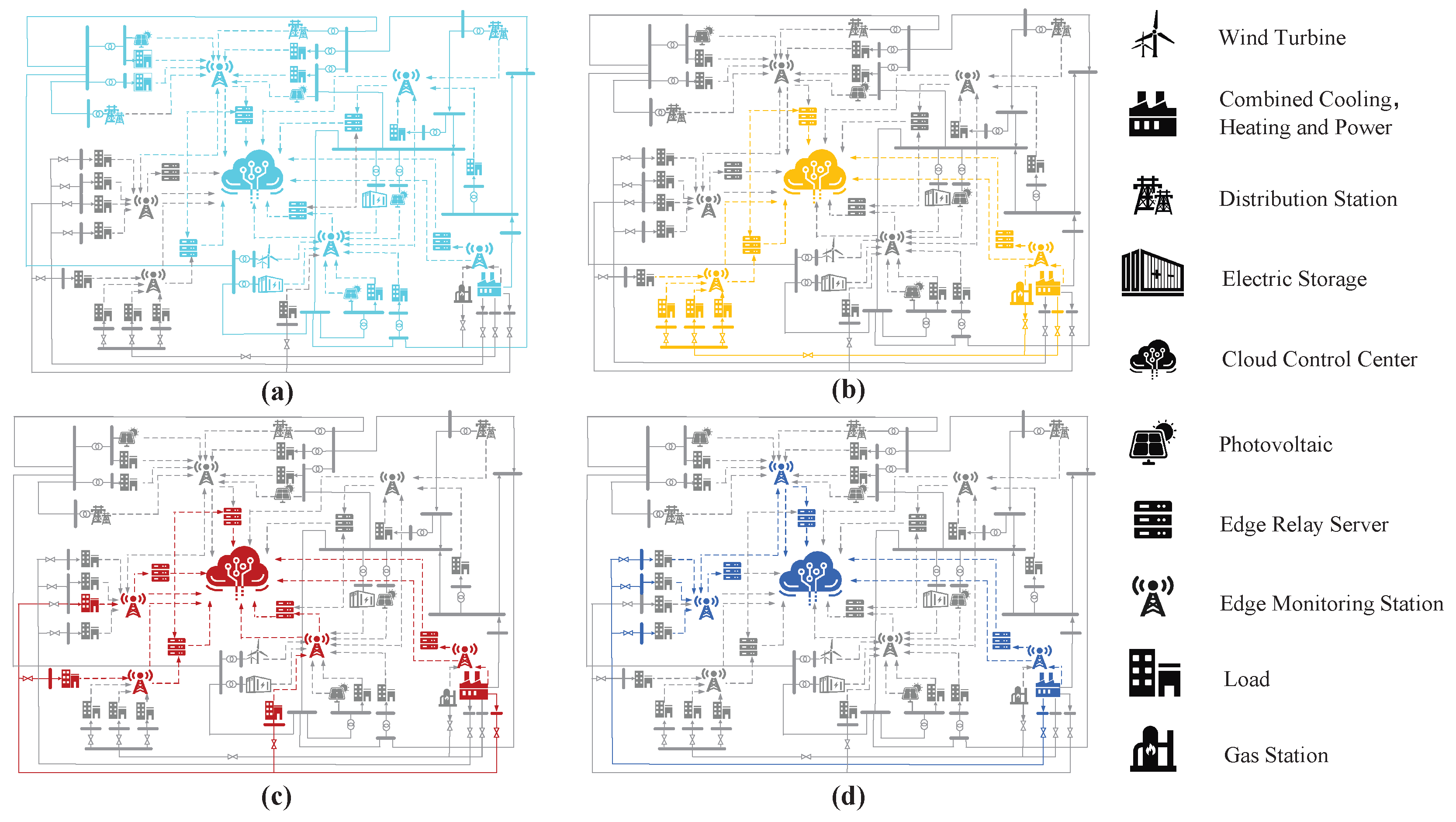
2. Monitoring Resource Slice Allocation Framework
2.1. Monitoring Resource Slice Allocation Strategy
2.2. Monitoring Resource Slice Allocation Model
2.3. Optimal Slice Resource Allocation Problem Formulation
3. Proposed Method
| Algorithm 1: Monitoring resource slicing allocation algorithm |
| Input: Integrated network topology information: , , , , , , |
| Monitoring equipment parameters: , , , , , , , , |
| Transmission channel parameters: , , , , , , |
| Energy flow monitoring parameters: , . |
| Output: Energy flow slicing topology information: , , |
| Intra-slice resource allocation information: P, I, , |
| Sliced data monitoring cost: . |
| If detects changes in terminal energy device information: |
| sends terminal information to CC; |
| CC optimizes energy flow slicing according to Equation (12); |
| Repeat: |
| Initialize , , , , , , , |
| Initialize , , , , , , ; |
| CC broadcasts to ; |
| If receives iteration factors Then: |
| Perform local optimization according to Equations (18)–(26); |
| If P, L, t changed: |
| Update P, L, t; |
| End; |
| If CC receives updated P, L, t Then: |
| Update Equation (27); |
| Until: energy consumption cost change |
| End; |
4. Case Study
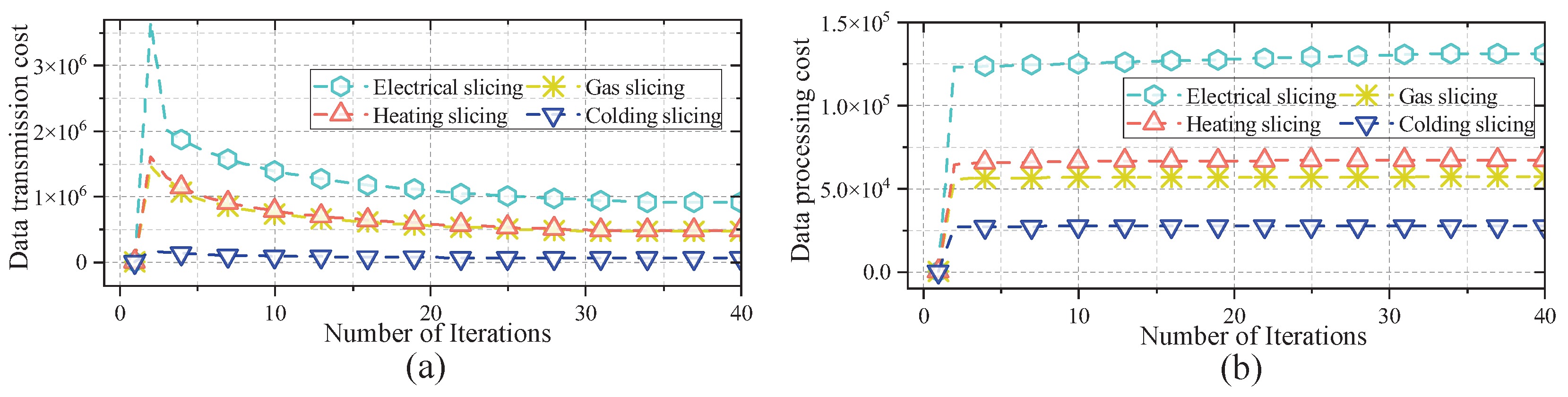
4.1. Effectiveness Analysis
4.2. The Impact of Communication Parameters
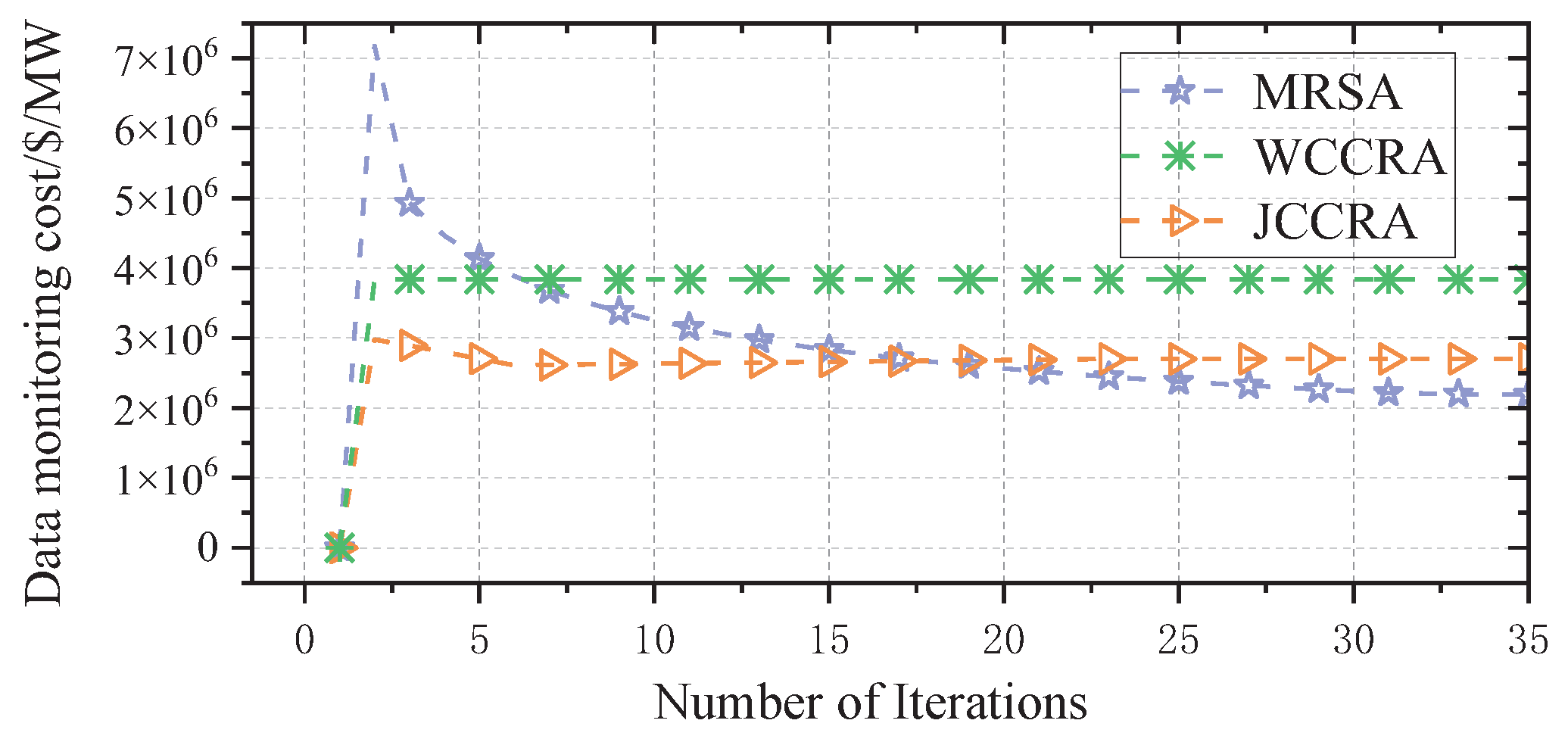
4.3. Algorithm Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, X.; Zhang, J.; Ma, D.; Wang, Q.; Sun, Q. Dual-Stage Agglomeration Strategy: An Approach of Flexible Partitioning for Energy Internet. IEEE Syst. J. 2024, 18, 1560–1569. [Google Scholar] [CrossRef]
- Hussain, M.; Zhang, T.; Chaudhry, M.; Jamil, I.; Kausar, S.; Hussain, I. Review of Prediction of Stress Corrosion Cracking in Gas Pipelines Using Machine Learning. Machines 2024, 12, 42. [Google Scholar] [CrossRef]
- Esposito, D.; Centracchio, J.; Andreozzi, E.; Bifulco, P.; Gargiulo, G.D. Design and Evaluation of a Low-Cost Electromechanical System to Test Dynamic Performance of Force Sensors at Low Frequencies. Machines 2022, 10, 1017. [Google Scholar] [CrossRef]
- Zhang, N.; Sun, Q.; Yang, L.; Li, Y. Event-Triggered Distributed Hybrid Control Scheme for the Integrated Energy System. IEEE Trans. Ind. Inform. 2022, 18, 835–846. [Google Scholar] [CrossRef]
- Ma, D.; Hu, X.; Zhang, H.; Sun, Q.; Xie, X. A Hierarchical Event Detection Method Based on Spectral Theory of Multidimensional Matrix for Power System. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2173–2186. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, H.; Ma, D.; Wang, R. A tnGAN-Based Leak Detection Method for Pipeline Network Considering Incomplete Sensor Data. IEEE Trans. Instrum. Meas. 2021, 70, 3510610. [Google Scholar] [CrossRef]
- Huang, Y.; Sun, Q.; Li, Y.; Gao, W.; Gao, D.W. A Multi-Rate Dynamic Energy Flow Analysis Method for Integrated Electricity-Gas-Heat System with Different Time-Scale. IEEE Trans. Power Deliv. 2023, 38, 231–243. [Google Scholar] [CrossRef]
- de la Puente-Gil, Á.; González-Martínez, A.; Rosales-Asensio, E.; Diez-Suárez, A.-M.; Blanes Peiró, J.-J. Efficient Heating System Management Through IoT Smart Devices. Machines 2025, 13, 643. [Google Scholar] [CrossRef]
- Li, B.; Qin, L.; Zhao, F.; Liu, H.; Yu, J.; He, M.; Wang, J.; Liu, K. Research on Edge Detection Model of Insulators and Defects Based on Improved YOLOv4-tiny. Machines 2023, 11, 122. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, D.; Zhu, H.; Zhou, S.; Zhao, Z. An Efficient IIoT Gateway for Cloud–Edge Collaboration in Cloud Manufacturing. Machines 2022, 10, 850. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, X. Fairness-Aware Task Offloading and Resource Allocation in Cooperative Mobile-Edge Computing. IEEE Internet Things J. 2022, 9, 3812–3824. [Google Scholar] [CrossRef]
- Liu, P.; Wang, J.; Ma, K.; Guo, Q. Joint Cooperative Computation and Communication for Demand-Side NOMA-MEC Systems with Relay Assistance in Smart Grid Communications. IEEE Internet Things J. 2024, 11, 30594–30606. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, Y.; Song, J.; Qiu, C.; Chen, X.; Wang, X. Learn to Coordinate for Computation Offloading and Resource Allocation in Edge Computing: A Rational-Based Distributed Approach. IEEE Trans. Netw. Sci. Eng. 2022, 9, 3136–3151. [Google Scholar] [CrossRef]
- Liu, C.; Chen, L.; Gao, W.; Zhang, X.; Peng, W.; Shu, F. DRL-Based Online Task Offloading and Energy Resource Aggregation for Edge-Computing-Empowered Smart Grid Networks. IEEE Internet Things J. 2024, 11, 41008–41020. [Google Scholar] [CrossRef]
- Wang, J.; Cao, C.; Wang, J.; Lu, K.; Jukan, A.; Zhao, W. Optimal Task Allocation and Coding Design for Secure Edge Computing with Heterogeneous Edge Devices. IEEE Trans. Cloud Comput. 2022, 10, 2817–2833. [Google Scholar] [CrossRef]
- Sun, Y.; Cai, Z.; Guo, C.; Ma, G.; Zhang, Z.; Wang, H.; Liu, J.; Kang, Y.; Yang, J. Collaborative Dynamic Task Allocation with Demand Response in Cloud-Assisted Multiedge System for Smart Grids. IEEE Internet Things J. 2022, 9, 3112–3124. [Google Scholar] [CrossRef]
- Chung, H.-M.; Maharjan, S.; Zhang, Y.; Eliassen, F.; Strunz, K. Optimal Energy Trading with Demand Responses in Cloud Computing Enabled Virtual Power Plant in Smart Grids. IEEE Trans. Cloud Comput. 2022, 10, 17–30. [Google Scholar] [CrossRef]
- Tang, C.; Yan, G.; Wu, H.; Zhu, C. Computation Offloading and Resource Allocation in Failure-Aware Vehicular Edge Computing. IEEE Trans. Consum. Electron. 2024, 70, 1877–1888. [Google Scholar] [CrossRef]
- Mekki, M.; Arora, S.; Ksentini, A. A Scalable Monitoring Framework for Network Slicing in 5G and Beyond Mobile Networks. IEEE Trans. Netw. Serv. Manag. 2022, 19, 413–423. [Google Scholar] [CrossRef]
- Shah, S.D.A.; Gregory, M.A.; Li, S. Toward Network-Slicing-Enabled Edge Computing: A Cloud-Native Approach for Slice Mobility. IEEE Internet Things J. 2024, 11, 2684–2700. [Google Scholar] [CrossRef]
- Liu, W.; Hossain, M.A.; Ansari, N.; Kiani, A.; Saboorian, T. Reinforcement Learning-Based Network Slicing Scheme for Optimized UE-QoS in Future Networks. IEEE Trans. Netw. Serv. Manag. 2024, 21, 3454–3464. [Google Scholar] [CrossRef]
- Luo, X.; Xue, K.; Li, J.; Li, R.; Wei, D.S.L. Make Rental Reliable: Blockchain-Based Network Slice Management Framework with SLA Guarantee. IEEE Commun. Mag. 2023, 61, 142–148. [Google Scholar] [CrossRef]
- Tang, L.; Pu, Z.; Li, Z.; Fang, D.; Li, L.; Chen, Q. Intelligent Dual Time Scale Network Slicing for Sensory Information Synchronization in Industrial IoT Networks. IEEE Internet Things J. 2024, 11, 38615–38630. [Google Scholar] [CrossRef]
- Wu, Y.; Liang, L.; Jia, Y.; Wen, W. HFL-TranWGAN: Knowledge-Driven Cross-Domain Collaborative Anomaly Detection for End-to-End Network Slicing. IEEE Trans. Netw. Serv. Manag. 2025, 22, 760–776. [Google Scholar] [CrossRef]
- Wei, F.; Wang, Y.; Feng, G.; Qin, S. Network-Slicing-Enabled Computation Offloading in Satellite-Terrestrial Edge Computing Networks: A Bi-Level Game Approach. IEEE Internet Things J. 2025, 12, 16282–16297. [Google Scholar] [CrossRef]
- Ayepah-Mensah, D.; Sun, G.; Owusu Boateng, G.; Liu, G. Federated Policy Distillation for Digital Twin-Enabled Intelligent Resource Trading in 5G Network Slicing. IEEE Trans. Netw. Serv. Manag. 2025, 22, 361–379. [Google Scholar] [CrossRef]
- Xu, Z.; Zhuang, L.; Zhuang, W.; Hu, Y.; Mo, W.; Wang, Z. Meta Relational Learning-Based Service-Tailored VNF Deployment for B5G Network Slice. IEEE Internet Things J. 2023, 10, 22542–22554. [Google Scholar] [CrossRef]
- Kwantwi, T.; Sun, G.; Kuadey, N.A.E.; Maale, G.T.; Liu, G. Blockchain-Based Computing Resource Trading in Autonomous Multi-Access Edge Network Slicing: A Dueling Double Deep Q-Learning Approach. IEEE Trans. Netw. Serv. Manag. 2023, 20, 2912–2928. [Google Scholar] [CrossRef]




| Parameter | Device 1 | Device 2 | Device 3 | Device 4 | Device 5 | Device 6 |
|---|---|---|---|---|---|---|
| (MW) | 2 | 8 | 5 | 6 | 3 | 4 |
| (MW) | 5 | 6 | 1 | 5 | 4 | 6 |
| (MW) | 6 | 7 | 2 | 5 | 1 | 5 |
| (cycles/bit) | ||||||
| (cycles/bit) | ||||||
| (MHz) | 16 | 18 | 20 | 25 | 19 | 17 |
| (cycles/bit) |
| Parameter | Electrical | Gas | Heating | Cooling |
|---|---|---|---|---|
| (s) | 60 | 900 | 1000 | 500 |
| (MB) | 0 | 0 | 8 | 5 |
| (MB) | 0 | 10 | 5 | 0 |
| (MB) | 5 | 0 | 0 | 0 |
| (MB) | 10 | 8 | 9 | 3 |
| (MB) | 6 | 0 | 5 | 0 |
| (MB) | 15 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Hu, X.; Wang, J.; Pan, H.; Ren, C. A Cloud-Edge Communication Resource Slicing Allocation Method for Data Monitoring in Integrated Energy Systems. Machines 2025, 13, 857. https://doi.org/10.3390/machines13090857
Zhang M, Hu X, Wang J, Pan H, Ren C. A Cloud-Edge Communication Resource Slicing Allocation Method for Data Monitoring in Integrated Energy Systems. Machines. 2025; 13(9):857. https://doi.org/10.3390/machines13090857
Chicago/Turabian StyleZhang, Mingrui, Xuguang Hu, Jingyu Wang, Huilin Pan, and Chengze Ren. 2025. "A Cloud-Edge Communication Resource Slicing Allocation Method for Data Monitoring in Integrated Energy Systems" Machines 13, no. 9: 857. https://doi.org/10.3390/machines13090857
APA StyleZhang, M., Hu, X., Wang, J., Pan, H., & Ren, C. (2025). A Cloud-Edge Communication Resource Slicing Allocation Method for Data Monitoring in Integrated Energy Systems. Machines, 13(9), 857. https://doi.org/10.3390/machines13090857