Optimal Scaling Parameter Analysis for Optical Mirror Processing Robots via Adaptive Differential Evolution Algorithm
Abstract
1. Introduction
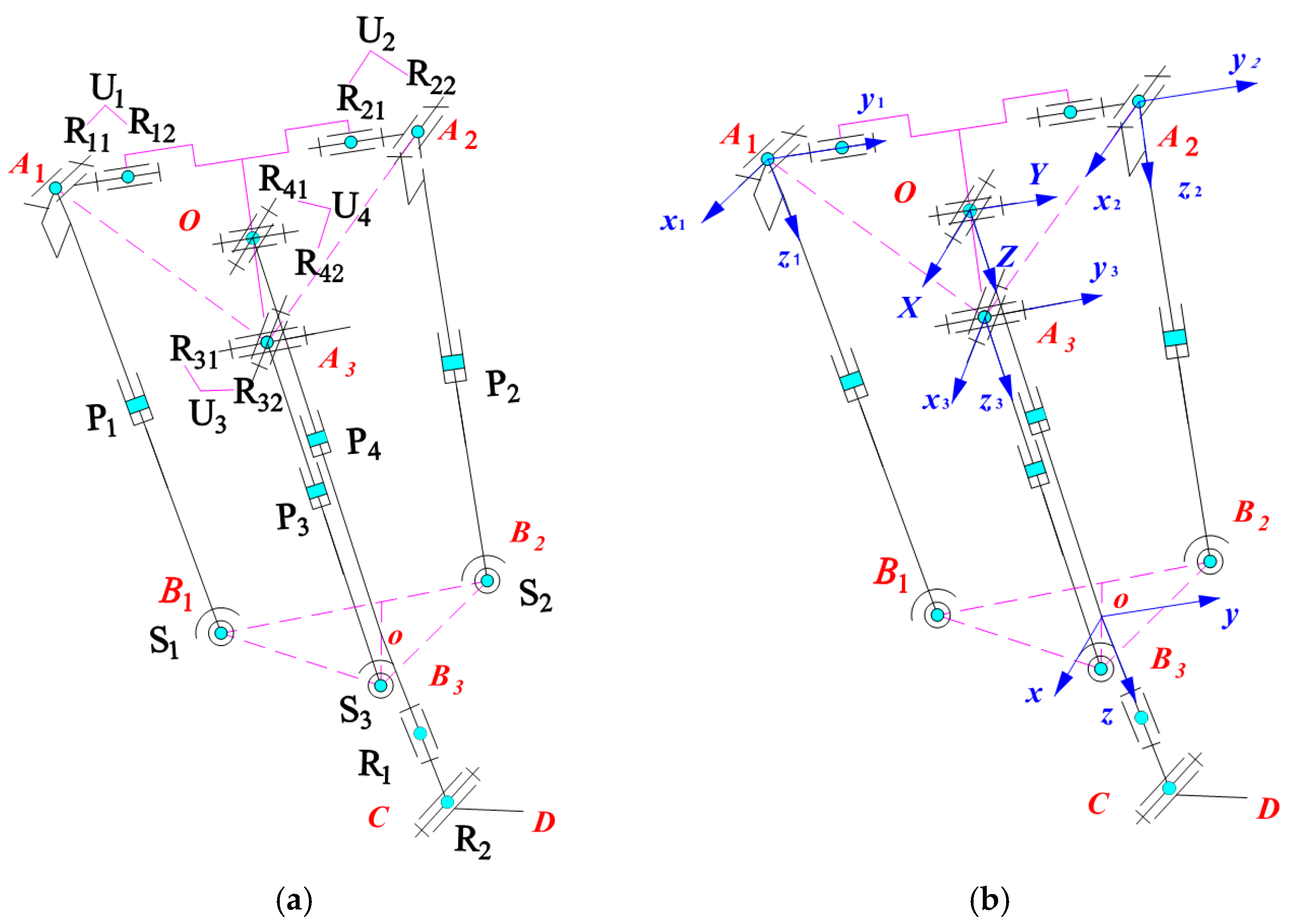
2. LOMP Robot
3. Analysis of Effective Workspace and Actuation Torque
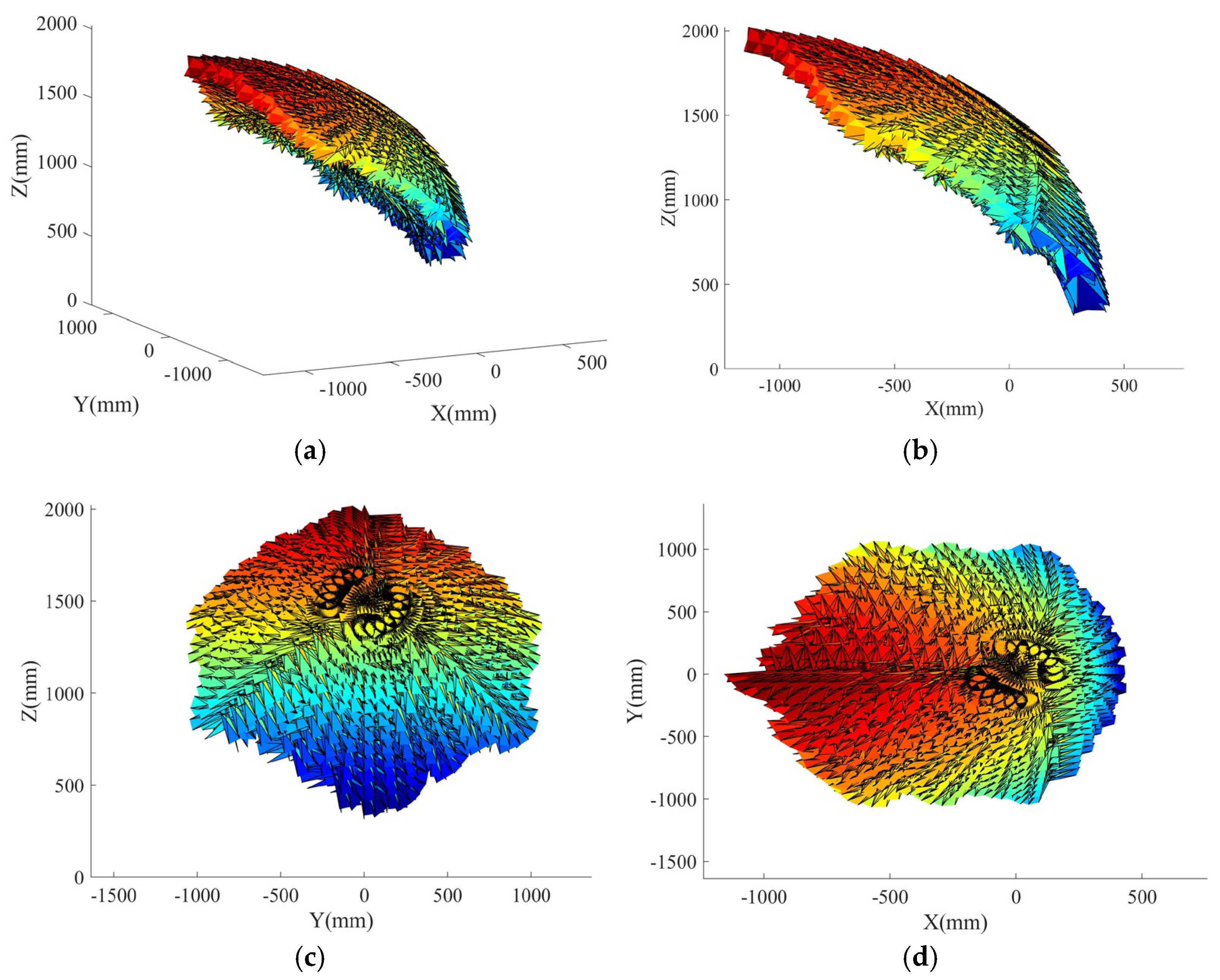
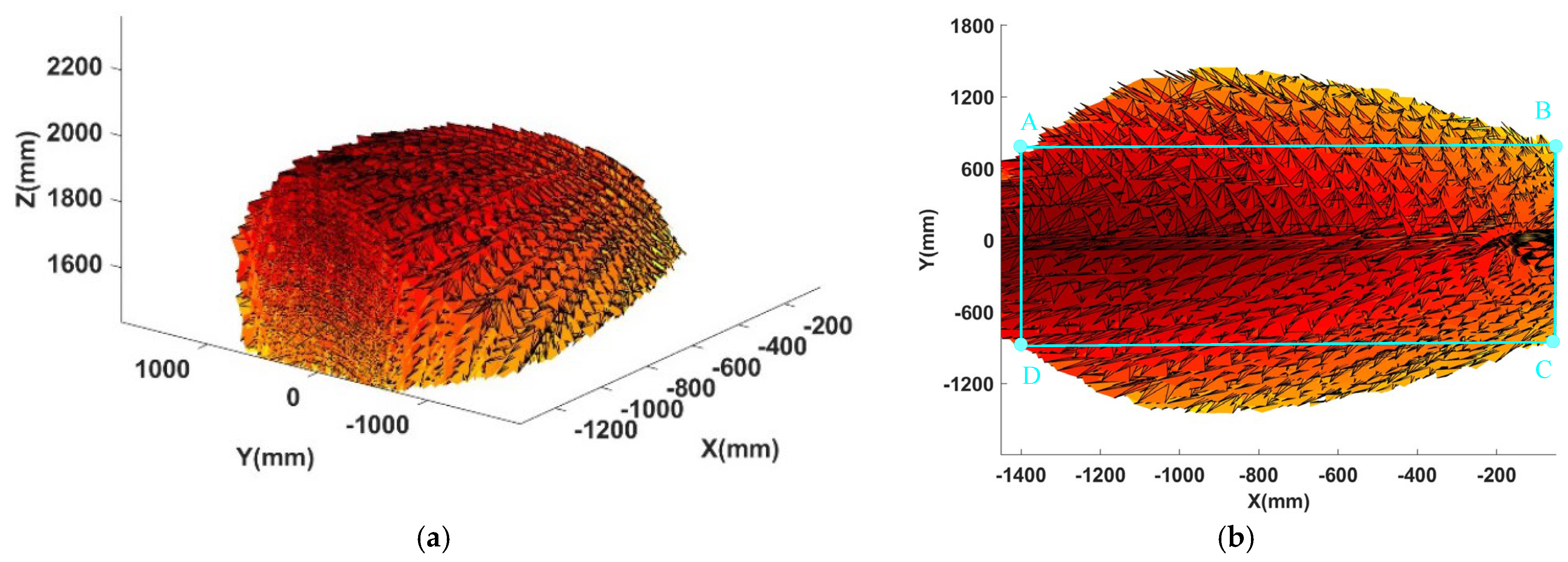
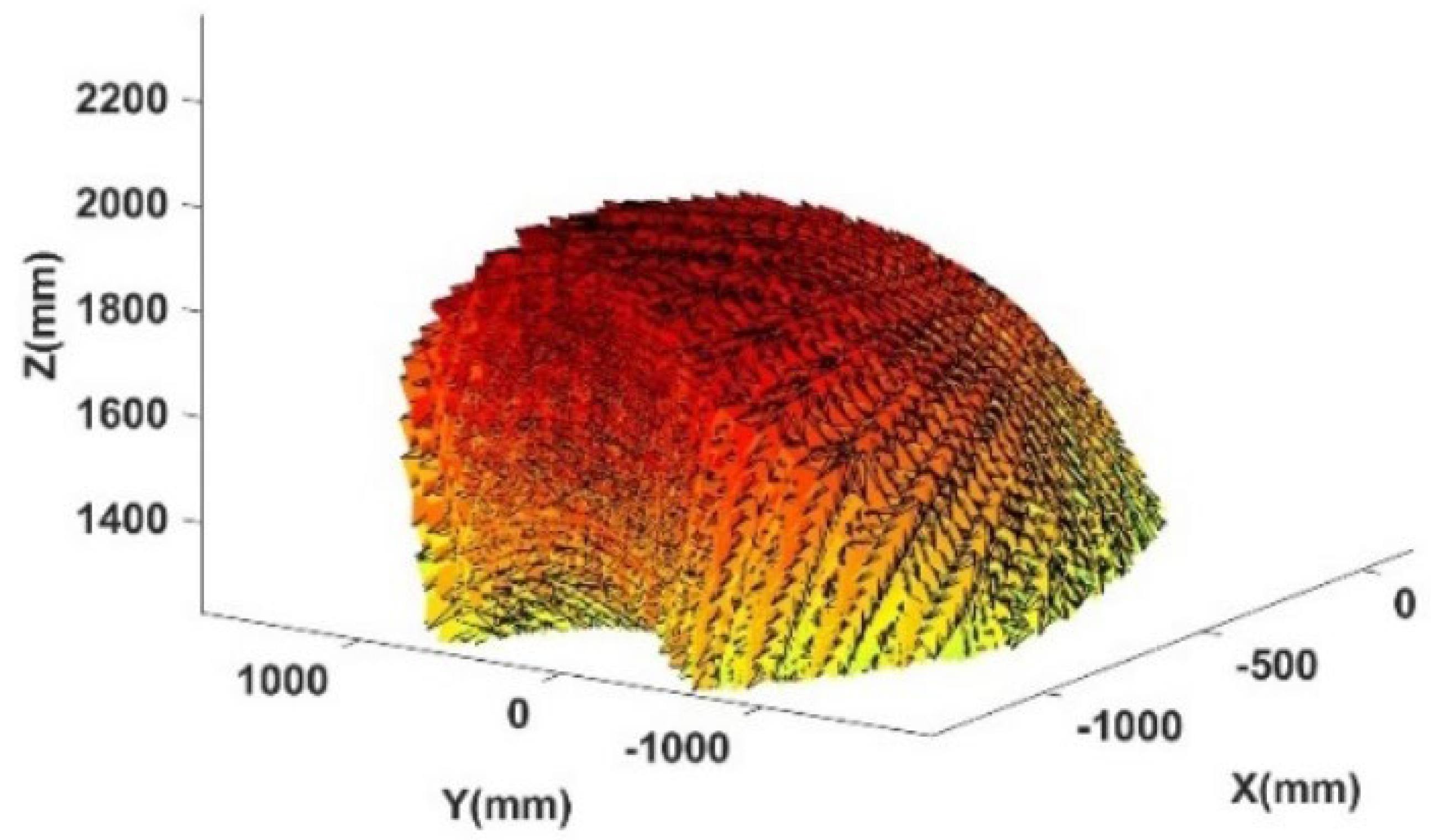
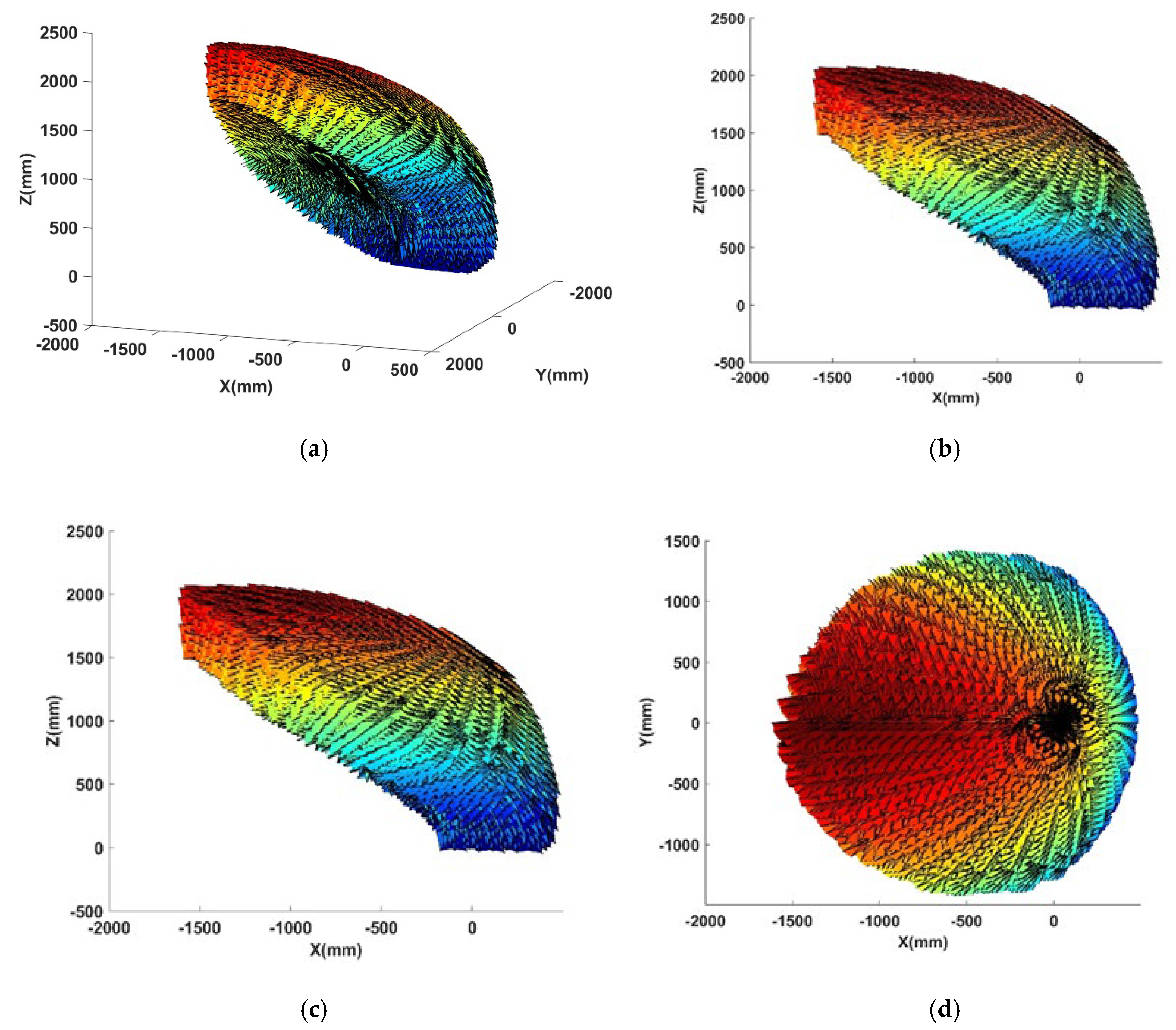
3.1. Analysis of Effective Workspace
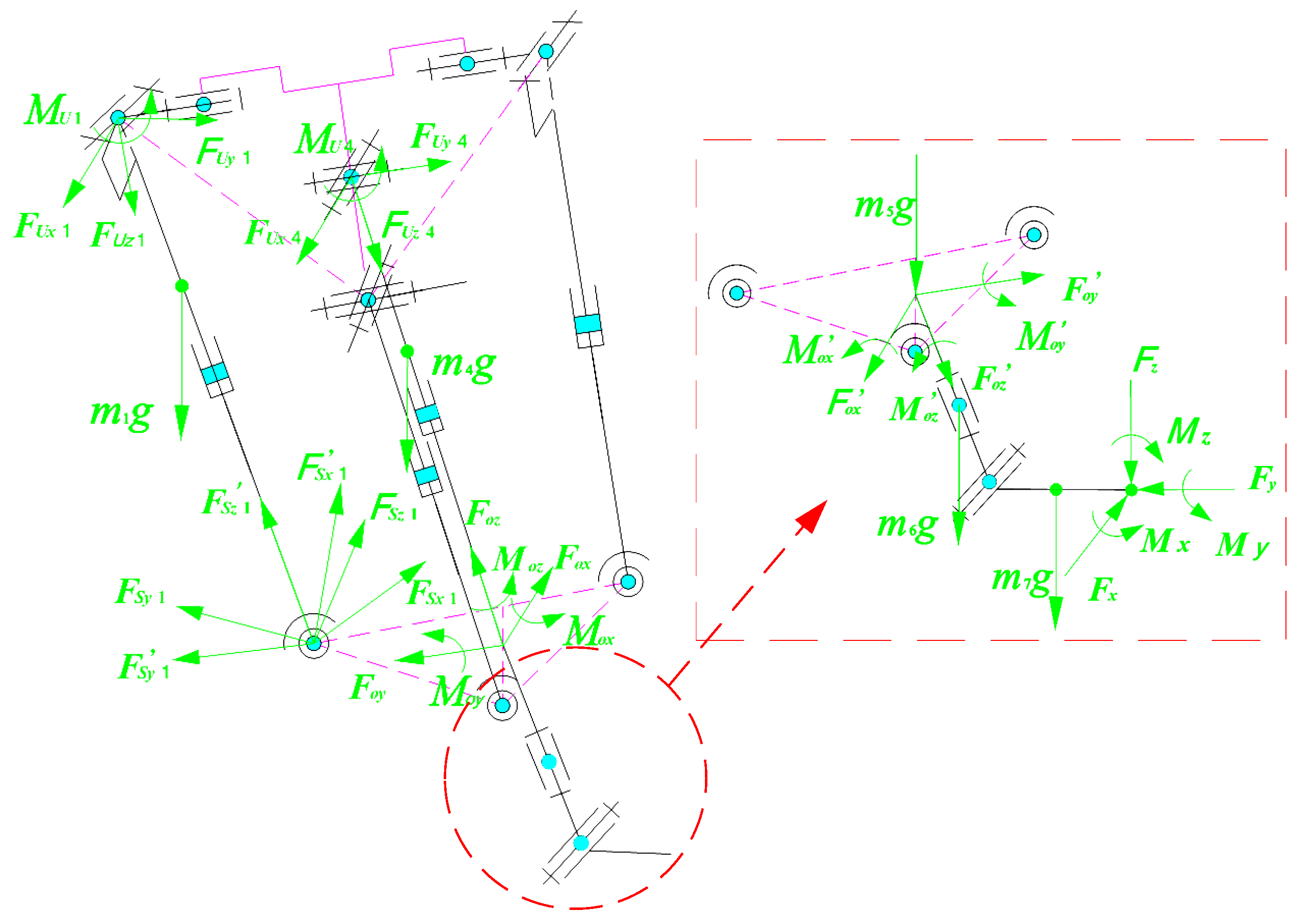
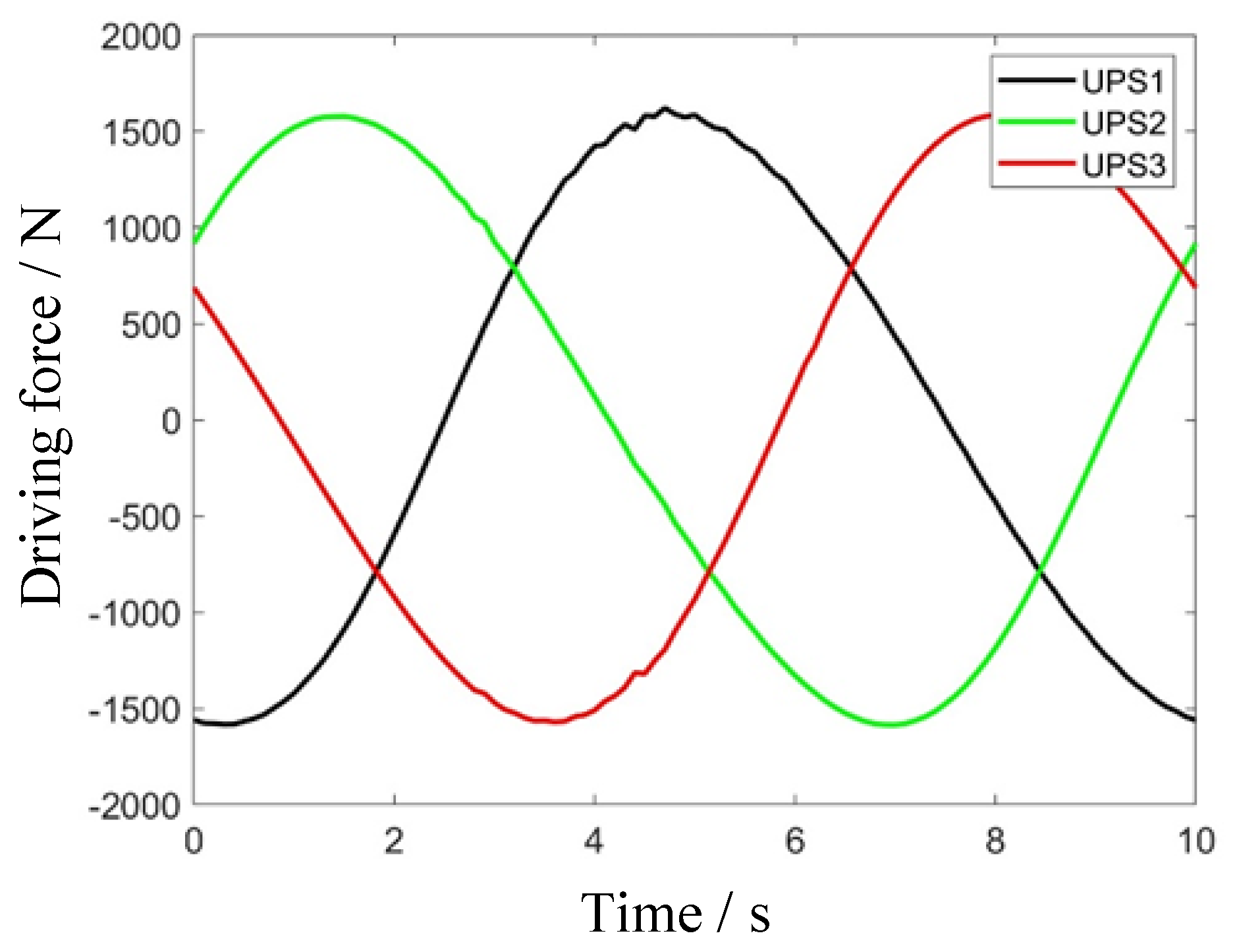
3.2. Analysis of Actuation Torque
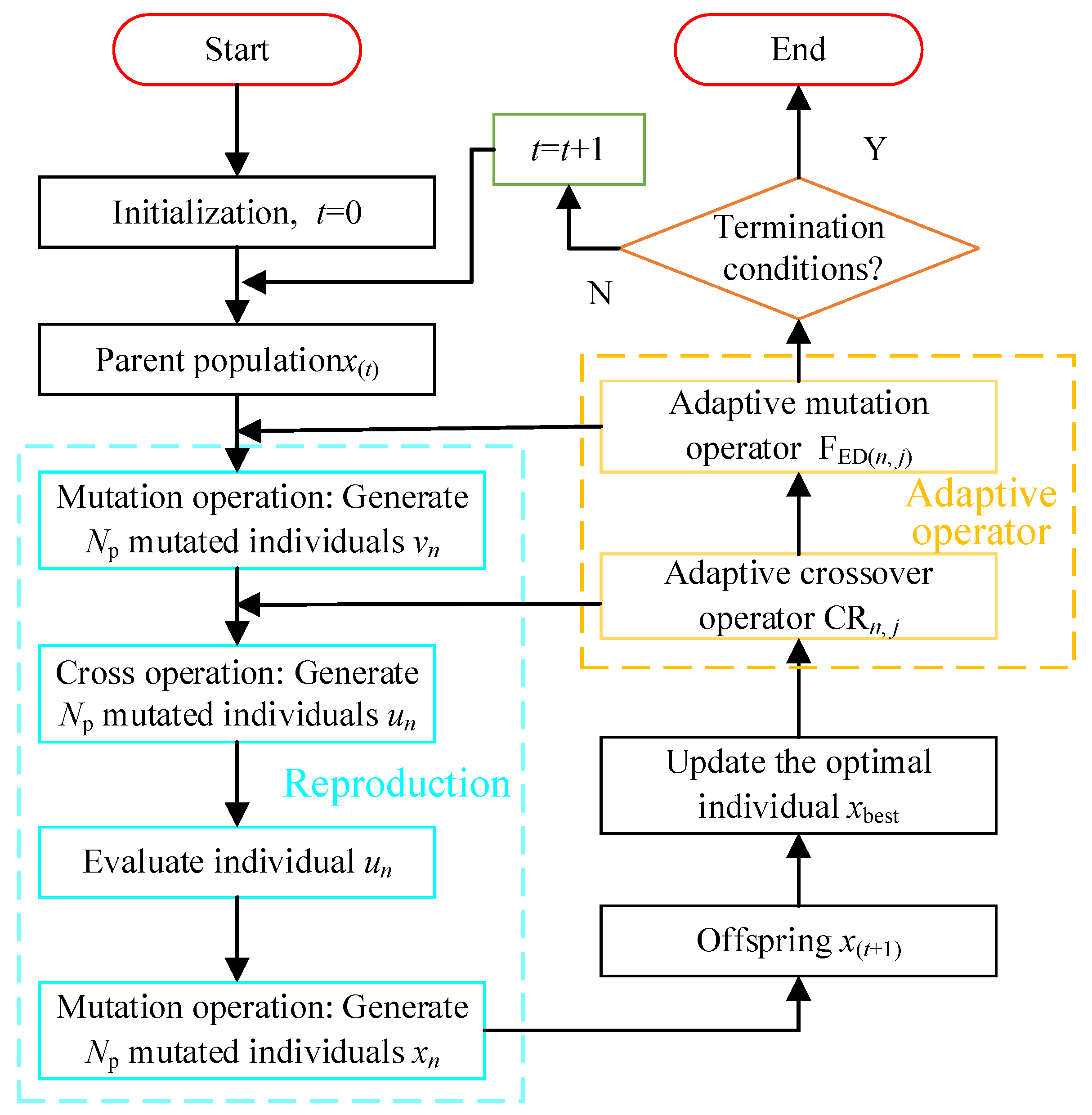
4. Adaptive Differential Evolution Algorithm
- (1)
- Initial population generation
- (2)
- Individual evaluation
- (3)
- Variation
- (4)
- Crossover
- (5)
- Choose
- (6)
- Adaptive factor
5. Scale Parameter Optimization
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jin, Z.J.; Cheng, G.; Guo, F.; Chen, S.B. Human-machine-environment information fusion and control compensation strategy for large optical mirror processing system. Proc. Inst. Mech. Eng. Part C J. Eng. Mech. Eng. Sci. 2020, 35, 2507–2523. [Google Scholar]
- Jin, Z.; Yin, Z.; Liu, H.; Liu, F. Dynamic characteristics, analysis, and measurement of a large optical mirror processing system. Machines 2024, 12, 788. [Google Scholar] [CrossRef]
- Li, L.X.; Li, X.C.; Cheng, Q.; Li, R.G.; Deng, W.J.; Luo, X.; Zhang, F.; Xue, D.L.; Zhang, X.J. Optimized strategy to restrain the mid-spatial-frequency surface error in computer-controlled optical surfacing. Results Phys. 2021, 19, 103356. [Google Scholar]
- Pullen, W.C.; Wang, T.Y.; Choi, H.; Ke, X.L.; Negi, V.S.; Huang, L.; Idir, M.; Kim, D. Statistical tool size study for computer-controlled optical surfacing. Photonics 2023, 10, 286. [Google Scholar] [CrossRef]
- Anvari, Z.; Ataei, P.; Masouleh, M.T. Collision-free workspace and kinetostatic performances of a 4-DOF delta parallel robot. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 99. [Google Scholar] [CrossRef]
- Dastjerdi, A.H.; Sheikhi, M.M.; Masouleh, M.T. A complete analytical solution for the dimensional synthesis of 3-DOF delta parallel robot for a prescribed workspace. Mech. Mach. Theory 2020, 153, 103991. [Google Scholar] [CrossRef]
- Xiao, Y.G.; Yin, K.; Chen, X.B.; Chen, Z.J.; Gao, F. Multi-objective optimization design method for the dimensions and control parameters of curling hexapod robot based on application performance. Mech. Mach. Theory 2024, 204, 105831. [Google Scholar] [CrossRef]
- Panagant, N.; Pholdee, N.; Bureerat, S.; Yildiz, A.R.; Mirjalili, S. A comparative study of recent multi-objective metaheuristics for solving constrained truss optimisation problems. Arch. Comput. Method Eng. 2021, 28, 4031–4047. [Google Scholar] [CrossRef]
- Su, C.X.; Li, B.; Zhang, W.; Tian, W.; Liao, W.H. An analysis and reliability-based optimization design method of trajectory accuracy for industrial robots considering parametric uncertainties. Reliab. Eng. Syst. Saf. 2024, 254, 110626. [Google Scholar] [CrossRef]
- Cui, Q.Y.; Liu, P.F.; Du, H.L.; Wang, H.; Ma, X. Improved multi-objective artificial bee colony algorithm-based path planning for mobile robots. Front. Neurorobotics 2023, 17, 1196683. [Google Scholar]
- Nelson, C.A.; Laribi, M.A.; Zeghloul, S. Multi-robot system optimization based on redundant serial spherical mechanism for robotic minimally invasive surgery. Robotica 2019, 37, 1202–1213. [Google Scholar]
- Fang, Y.L.; Li, Z.Y.; Wang, S.W.; Lu, X.W. Multi-objective multi-fidelity optimisation for position-constrained human-robot collaborative disassembly planning. Int. J. Prod. Res. 2023, 62, 3872–3889. [Google Scholar]
- Li, C.Y.; Wu, H.P.; Eskelinen, H. Design and multi-objective optimization of a dexterous mobile parallel mechanism for fusion reactor vacuum vessel assembly. IEEE Access 2021, 9, 153796–153810. [Google Scholar] [CrossRef]
- Leng, X.K.; Piao, S.H.; Chang, L.; He, Z.C.; Zhu, Z. Parameter design of biped robot motion system based on multi-objective optimization. J. Intell. Fuzzy Syst. 2021, 41, 4307–4318. [Google Scholar] [CrossRef]
- Wu, J.; Wang, X.J.; Zhang, B.B.; Huang, T. Multi-objective optimal design of a novel 6-DOF spray-painting robot. Robotica 2021, 39, 2268–2282. [Google Scholar]
- Yan, L.; Xu, W.F.; Hu, Z.H.; Liang, B. Multi-objective configuration optimization for coordinated capture of dual-arm space robot. Acta Astronaut. 2020, 167, 189–200. [Google Scholar]
- Liang, X.; Zeng, X.; Li, G.T.; Chen, W.T.; Su, T.T.; He, G.P. Design, analysis, and optimization of a kinematically redundant parallel robot. Actuators 2023, 12, 120. [Google Scholar] [CrossRef]
- Wang, H.; Du, Z.J.; Yan, Z.Y.; Gao, Y.Z. Genetic algorithm-based optimal design strategy of a continuum surgical manipulator. Int. J. Control Autom. Syst. 2022, 20, 3312–3320. [Google Scholar]
- Lan, J.Y.; Xie, Y.G.; Liu, G.J.; Cao, M.X. A multi-objective trajectory planning method for collaborative robot. Electronics 2020, 9, 859. [Google Scholar] [CrossRef]
- Zhou, B.; Li, S.P.; Zi, B.; Chen, B.; Zhu, W.D. Multi-objective optimal design of a cable-driven parallel robot based on an adaptive adjustment inertia weight particle swarm optimization algorithm. J. Mech. Des. 2023, 145, 083301. [Google Scholar]
- Gul, F.; Rahiman, W.; Alhady, S.S.N.; Ahmad, A.; Mir, I.; Jalil, A. Meta-heuristic approach for solving multi-objective path planning for autonomous guided robot using PSO-GWO optimization algorithm with evolutionary programming. J. Ambient Intell. Humaniz. Comput. 2021, 12, 7873–7890. [Google Scholar] [CrossRef]
- Maafi, R.A.; Haghighi, S.E.; Mahmoodabadi, M.J. Pareto optimal design of a fuzzy adaptive sliding mode controller for a three-link model of a biped robot via the multi-objective improved team game algorithm. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 428. [Google Scholar] [CrossRef]
- Wu, D.; Hou, G.W.; Qiu, W.J.; Xie, B. T-IK: An efficient multi-objective evolutionary algorithm for analytical inverse kinematics of redundant manipulator. IEEE Robot. Autom. Lett. 2021, 6, 8474–8481. [Google Scholar] [CrossRef]
- Wu, M.L.; Zhang, Y.; Yue, X.Q.; Lv, D.Y.; Chen, M.; Wang, X.H.; Zhang, J. Optimal design of an asymmetrical parallel mechanism. Proc. Inst. Mech. Eng. Part C J. Eng. Mech. Eng. Sci. 2021, 235, 6922–6939. [Google Scholar] [CrossRef]
- Benamor, A.; Boukadida, W.; Messaoud, H. Genetic algorithm-based multi-objective design of optimal discrete sliding mode approach for trajectory tracking of nonlinear systems. Proc. Inst. Mech. Eng. Part C J. Eng. Mech. Eng. Sci. 2019, 233, 5237–5252. [Google Scholar] [CrossRef]
- Hou, R.L.; Niu, J.W.; Guo, Y.L.; Ren, T.; Yu, X.L.; Han, B.; Ma, Q. A novel resolution scheme of time-energy optimal trajectory for precise acceleration controlled industrial robot using neural networks. Actuators 2022, 11, 130. [Google Scholar] [CrossRef]
- Wiedmeyer, W.; Altoé, P.; Auberle, J.; Ledermann, C.; Kröger, T. A real-time-capable closed-form multi-objective redundancy resolution scheme for seven-DOF serial manipulators. IEEE Robot. Autom. Lett. 2021, 6, 431–438. [Google Scholar] [CrossRef]
- Huo, X.M.; Lian, B.B.; Wang, P.F.; Song, Y.M.; Sun, T. Topology and dimension synchronous optimization of 1T2R parallel robots. Mech. Mach. Theory 2023, 178, 105385. [Google Scholar] [CrossRef]


| Parameters | li/mm | r/mm | r/R | Rk/mm | Zmin/mm | Zmax/mm |
|---|---|---|---|---|---|---|
| Values | 950~1750 | 150 | 0.375 | 685 | 200 | 616.82 |
| Parameters | li/mm | r/mm | r/R | Rk/mm | Zmin/mm | Zmax/mm |
|---|---|---|---|---|---|---|
| Values | 950.25~1748.51 | 150.02 | 0.376 | 684.38 | 198.57 | 615.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Z.; Yin, Z.; Liu, H.; Guo, H. Optimal Scaling Parameter Analysis for Optical Mirror Processing Robots via Adaptive Differential Evolution Algorithm. Machines 2025, 13, 853. https://doi.org/10.3390/machines13090853
Jin Z, Yin Z, Liu H, Guo H. Optimal Scaling Parameter Analysis for Optical Mirror Processing Robots via Adaptive Differential Evolution Algorithm. Machines. 2025; 13(9):853. https://doi.org/10.3390/machines13090853
Chicago/Turabian StyleJin, Zujin, Zixin Yin, Hao Liu, and Huanyin Guo. 2025. "Optimal Scaling Parameter Analysis for Optical Mirror Processing Robots via Adaptive Differential Evolution Algorithm" Machines 13, no. 9: 853. https://doi.org/10.3390/machines13090853
APA StyleJin, Z., Yin, Z., Liu, H., & Guo, H. (2025). Optimal Scaling Parameter Analysis for Optical Mirror Processing Robots via Adaptive Differential Evolution Algorithm. Machines, 13(9), 853. https://doi.org/10.3390/machines13090853




