A Mechatronic Design Procedure for Self-Balancing Vehicles According to the MBSE Approach
Abstract
1. Introduction
- A synthetic and effective description, formalized and expressed in the ARCADIA language, not only of the interconnected components and functional sub-groups that constitute the self-balancing vehicle, but also of the relationships between them.
- A general, complete and actionable design procedure applicable to the development of different classes of self-balancing vehicles, represented equivalently as a flow chart or as a nested V-model.
- The identification of a minimal set of variables that must be considered for the successful design of the vehicle.
- A comprehensive example that applies the procedure and results in the overall design of a CTWSBV.
2. Methods
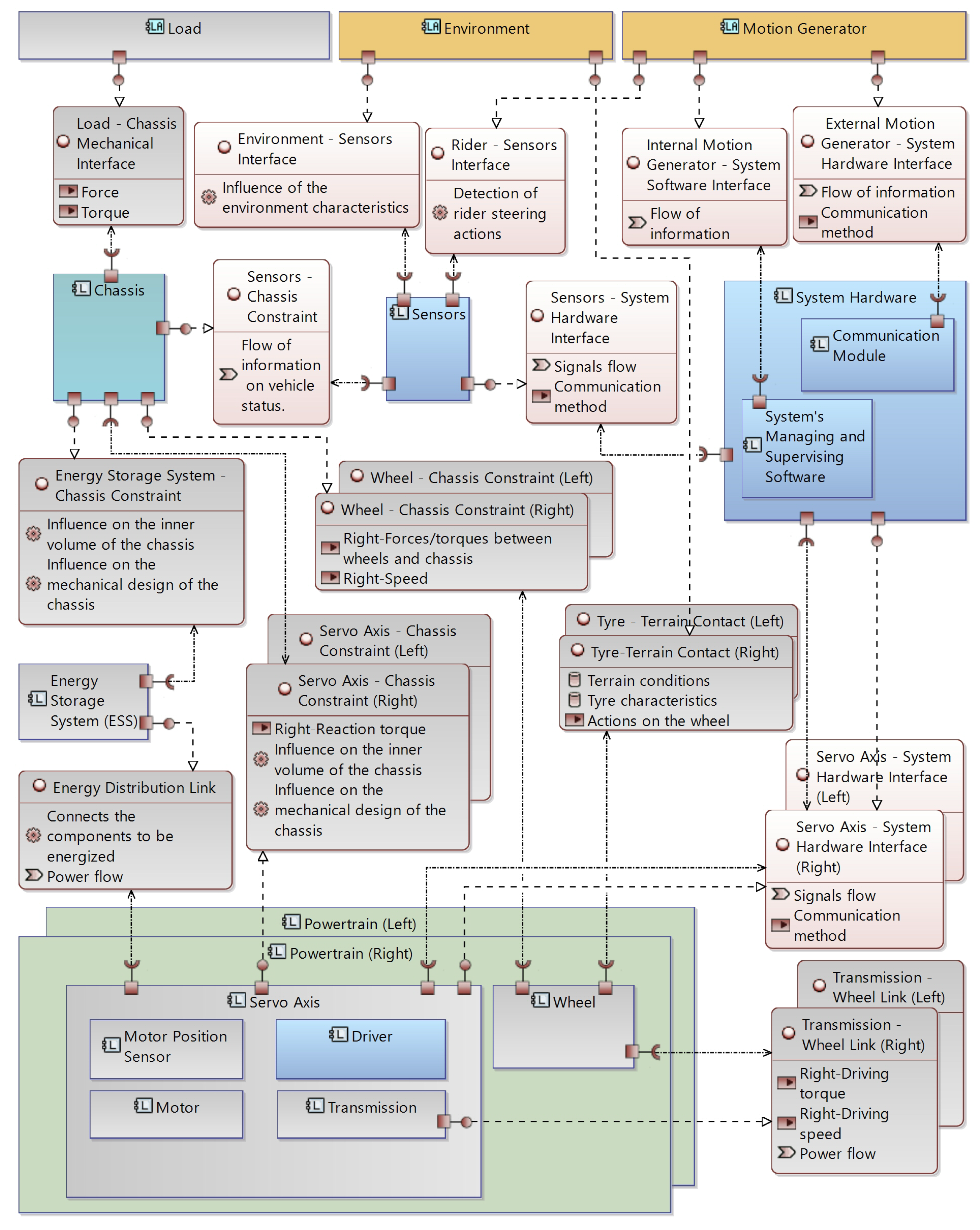
2.1. Mechatronic Description of the Vehicle
2.2. Actors
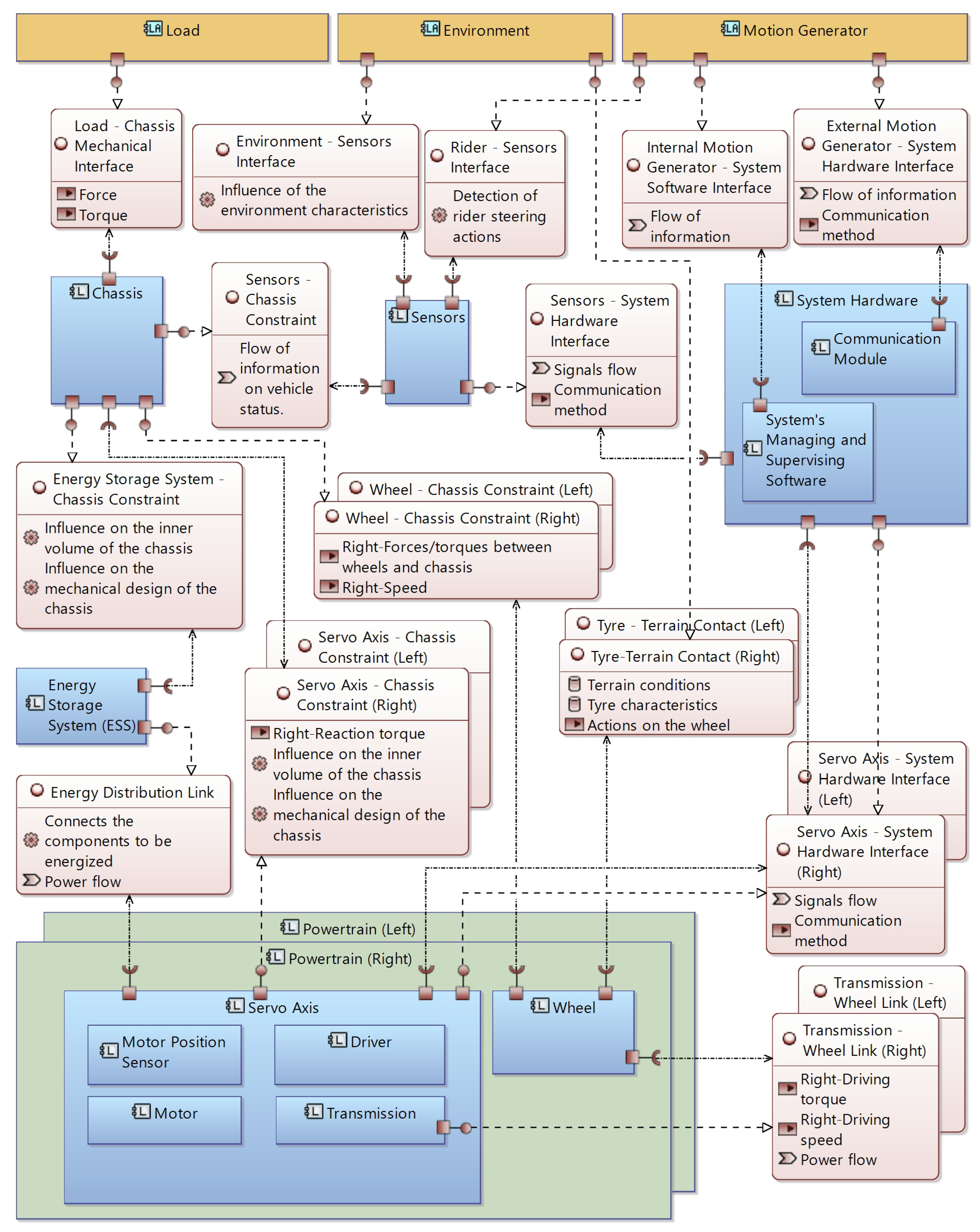
2.3. Components
2.4. Interfaces
2.4.1. Actor–Component Interfaces
2.4.2. Component–Component Interfaces
- Servo Axis–Chassis Constraint. Through this kind of interface, which coincides with the mechanical constraint between the two elements, the reaction torque of the motor-transmission unit is applied to the chassis; beyond this aspect, it may be anticipated that this interface will significantly influence the design of the inner chassis volume at the geometrical level.
- Transmission–Wheel Link. This kind of interface represented by the mechanical connection between the wheel and transmission (for right and left powertrains), and describes the mechanical power flow between these components. As shown in greater detail in the following discussion, the powertrains will be sized according to this quantity.
- Energy Distribution Link. This represents the interface through which the ESS provides and reabsorbs energy to/from the two servo axes in order to allow the motion of the vehicle. During the design process, the two factors of electric power flowing through this interface should be highlighted in relation to the mechanical power required by the vehicle and to the technical characteristics of the other components, as this enables the sizing of the ESS according to the overall needs of the system.
- Energy Storage System–Chassis Constraint. Similarly to the servo axis–chassis interface, it is the mechanical constraint between the ESS and chassis components: it influences the inner chassis volume and its mechanical design.
- Wheel–Chassis Constraint. It represents the mechanical constraints between the wheel (left or right) and chassis, and allows the transmission of non-motive forces and torques from terrain to the chassis. These quantities should be highlighted as a requisite for the proper structural design of the latter component.
- Sensor–Chassis Constraint. It describes the mechanical interface between sensors and chassis. In general, it supports the sensor group; for some specific sensors, it transmits the motion of the chassis to the relevant transducers, allowing it to be measured.
- Sensor–System Hardware Interface. The interface is represented by the signals, and the relevant flow of information exchanged between the components. Notably, the adoption of specific communication technologies will mutually condition the selection and design of the sensors and of the system hardware, as they should be capable of communicating with each other.
- Servo Axis–System Hardware Interface. This bi-directional interface is represented by the signals exchanged between the two components; these are, mainly, commands to the motor drivers and feedback concerning the rotors’ angular position. Again, the selection of specific communication interfaces at the design stage turns into a well-defined specification of some communication capabilities that the driver and the system hardware should possess.
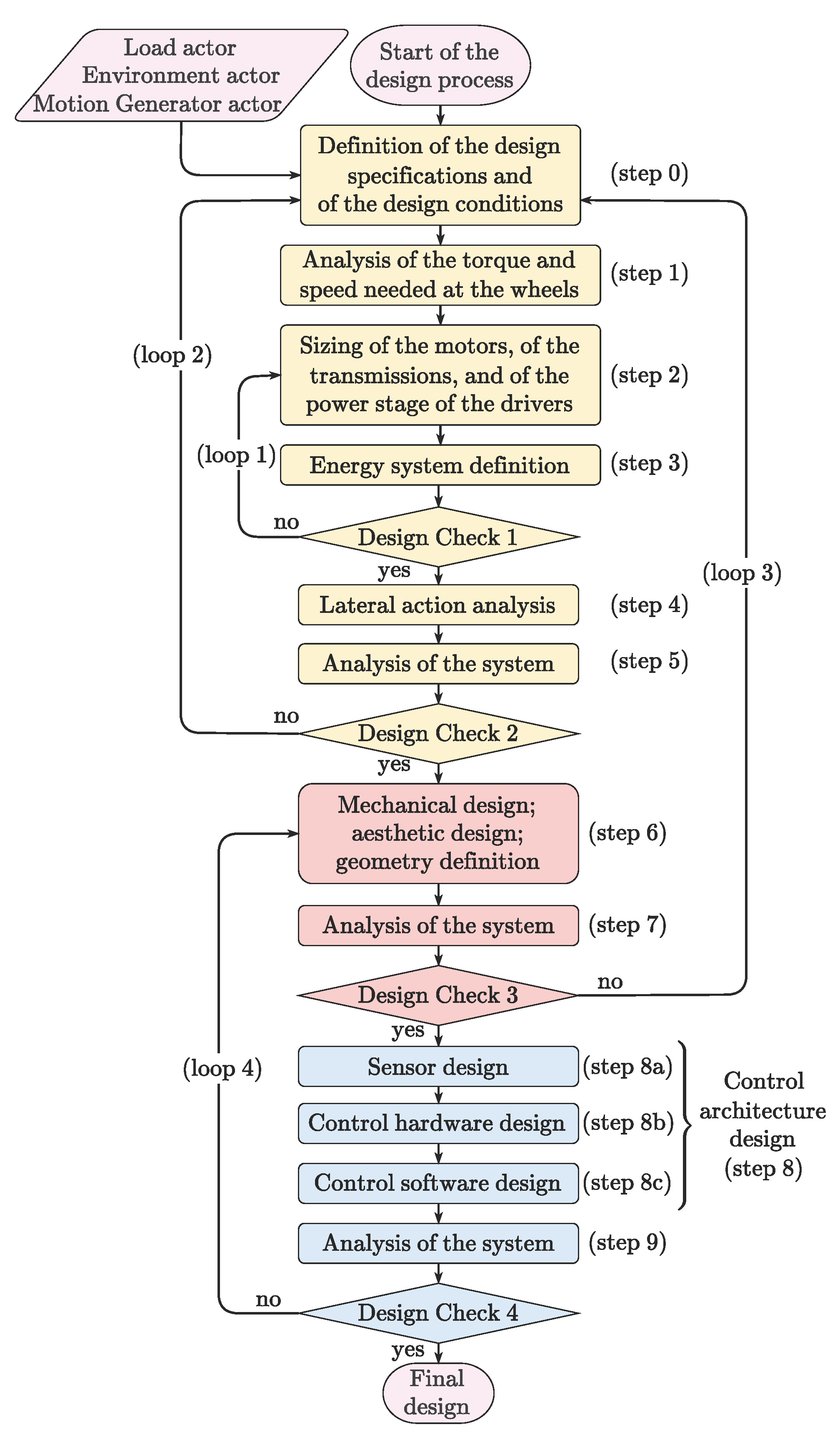
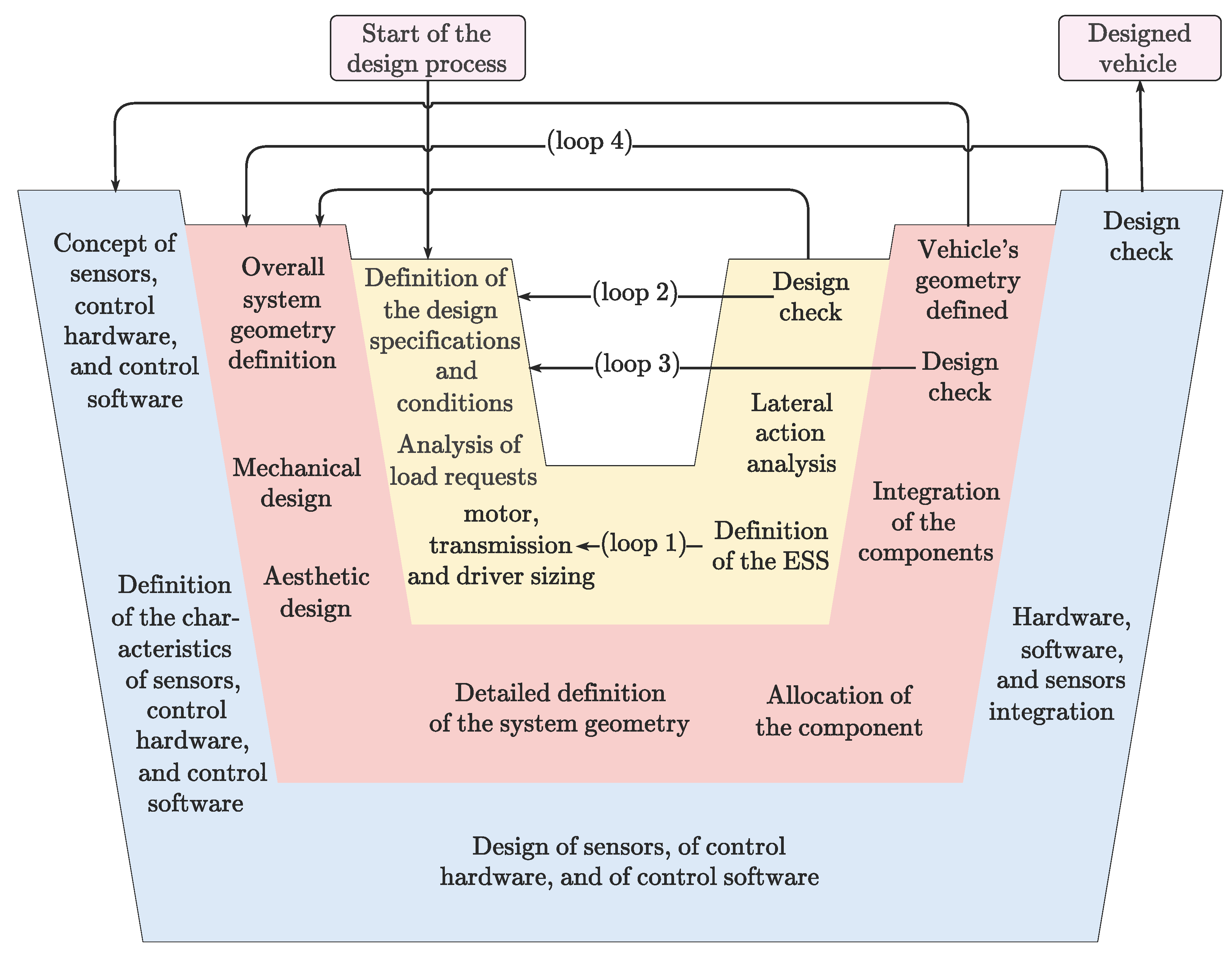
2.5. Design Procedure
2.5.1. Step 0
- The main load characteristics;
- The desired cruise speed;
- The desired driving range;
- The maximum bulk of the vehicle;
- The target maximum slope traversable with the vehicle;
- The general terrain characteristics.
2.5.2. Step 1
- The mass, inertia and center of gravity of the load;
- The maximum longitudinal speed;
- The maximum traversable slope;
- The tire–terrain friction conditions.
- The radius of the wheels;
- The torque and angular velocity at the wheel hubs;
- The power required to run the vehicle;
- The radial forces on the wheels.
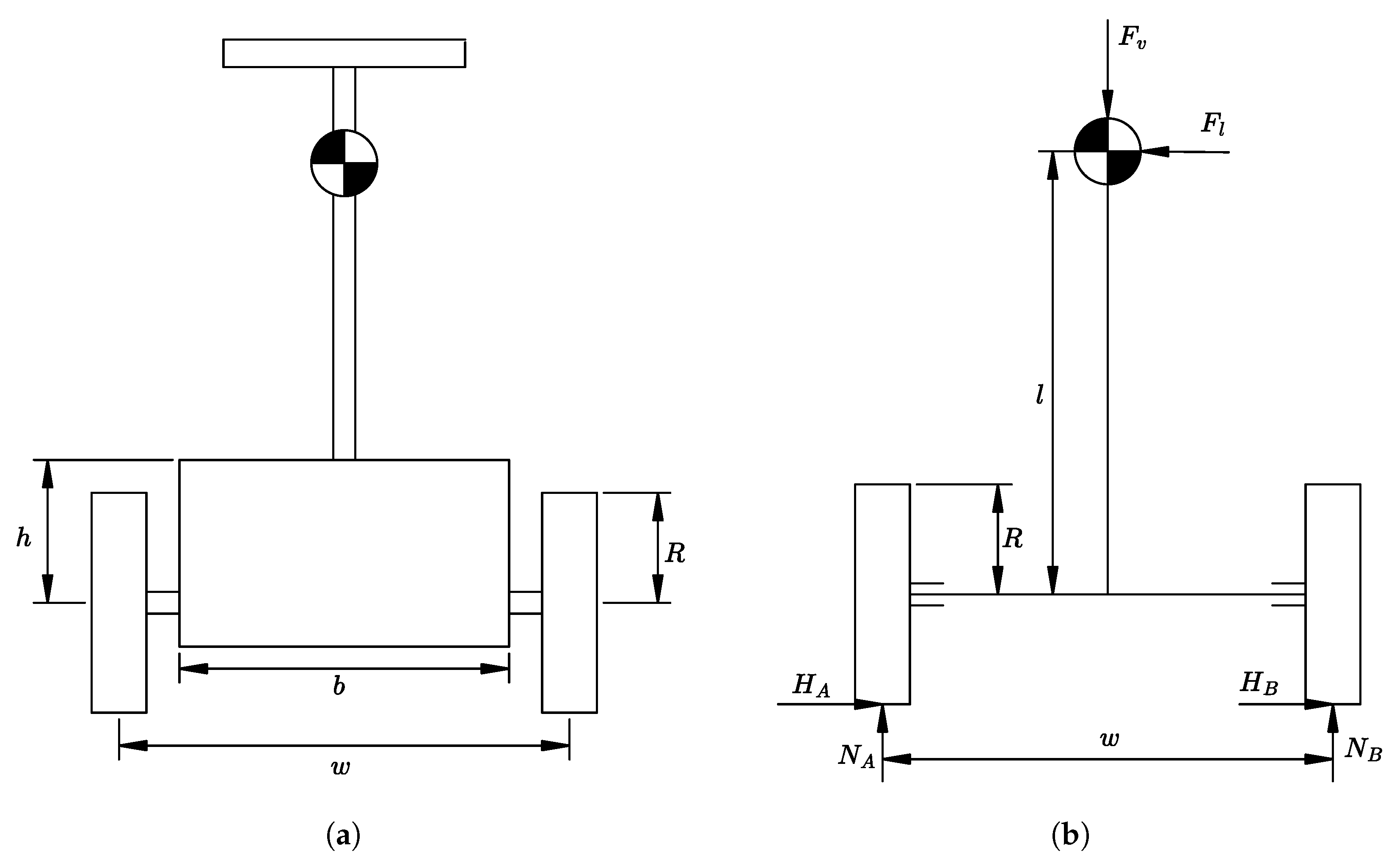
2.5.3. Step 2
- The operating voltage;
- The required currents;
- The motor–transmission units, with their characterizing parameters (geometry, mass, type);
- The power stage of the motor drivers.
2.5.4. Step 3
- The energy storage system’s deliverable and absorbable currents;
- Its capacity;
- Its mass and geometry.
2.5.5. Design Check 1
2.5.6. Step 4
2.5.7. Step 5
2.5.8. Design Check 2
2.5.9. Step 6
- The forces acting on the wheel axles and on the chassis (from step 4);
- The geometry of the main components that should be housed in it (from steps 2 and 3).
2.5.10. Step 7
2.5.11. Design Check 3
2.5.12. Step 8
- 8a—Sensor Design: This sub-step involves the selection of sensors. In this phase, the choices related to the sensors concern, among others, the quantities to be measured, the accuracy, the input range, and the signal communication methods. Such choices are performed by the design team according to the analysis of the actors and the resulting design specifications.
- 8b—Control Hardware Design: This sub-step focuses on the selection and configuration of the control hardware, which must be capable of acquiring sensor data, executing control algorithms in real time, and interfacing with actuators and other components. Both computational performance and I/O capabilities are evaluated according to system needs.
- 8c—Control Software Design: This sub-step addresses the development of the control software. In the case of self-balancing vehicles, it includes the implementation of algorithms that ensure vehicle stability and respond to motion commands. More advanced control strategies may replace simpler regulators introduced in earlier design phases for the initial sizing of the actuation systems and of the mechanical elements; to this end the extensive body of research dedicated specifically to the control issue should be consulted to extract the maximal performances of the system. Depending on the sensor configuration and on the intended driving strategy, the control software may also include functionalities related to fault detection, motion planning, safety enhancement or user interface management.
2.5.13. Step 9
2.5.14. Design Check 4
2.5.15. V-Model Representation
3. Results
3.1. Step 0
- Motion Generator: a single rider, responsible for the motion commands;
- Load: again constituted by the rider only;
- Environment: characterized by unpaved roads with a moderate maximum slope.
- The vehicle should be able to easily accommodate a rider of average height () and weight ();
- The maximum slope is ;
- The cruise speed is .
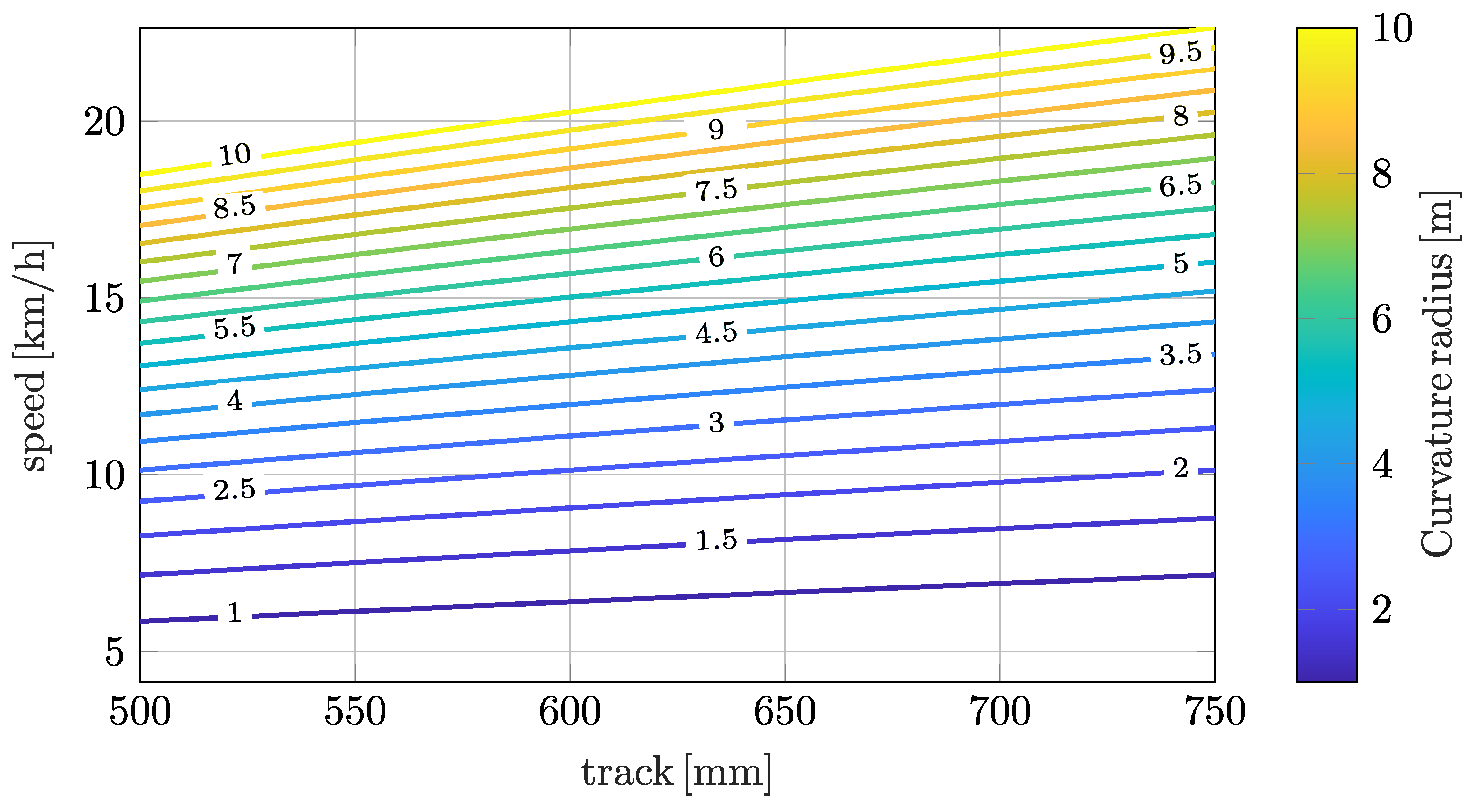
3.2. Step 1
3.3. Step 2
3.4. Step 3 and Design Check 1
3.5. Step 4
3.6. Step 5 and Design Check 2
3.7. Step 6
3.8. Step 7 and Design Check 3
3.9. Step 8
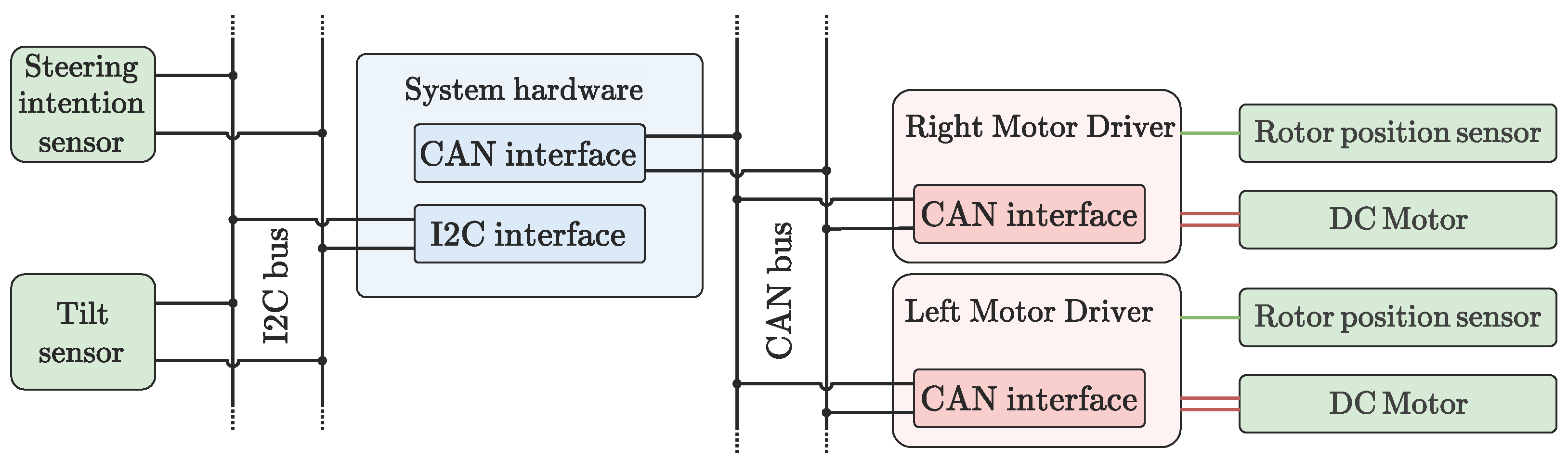
- 8a—Sensor Design: This step focuses on the selection and integration of the sensing devices. The measurement of the vehicle’s attitude and angular velocity is achieved using a triaxial gyroscope and a triaxial accelerometer, both integrated in the MPU-6050 MEMS inertial platform, which exposes an I2C interface. To detect the driver’s intention to steer, the handlebar of the vehicle is instrumented with strain gauges that measure deformation caused by applied forces. The selected transducer is the HBM 1-LY13-6/120 strain gauge. The sensors defined here are in addition to those that belong to the power drive systems. Since the output signal is low in amplitude, it is first amplified and then acquired by an analog-to-digital converter possessing an I2C interface.
- 8b—Control Hardware Design: The system hardware is based on a Raspberry Pi platform, which natively includes the I2C interface needed to acquire the measurements provided by the inertial unit and by the amplification and acquisition hardware associated with the strain gauges; the Raspberry Pi has been furthermore equipped with a CAN add-on board to communicate with the drivers. The work group tackling control hardware design will evaluate in detail fundamental aspects such as bus latency and utilization. A preliminary evaluation may be performed considering a single bus working at a Baud rate of 1 and used to control the two drivers. A standard CAN frame with a payload of 64 bit (used to encode either the setpoint or the feedback signals) is composed of 111 bit. Considering two frames for the setpoints and two frames for the feedback, the total transmission time is 444 , which is compatible with a control loop operating at 500 . Taking as a reference the pole placement controller configured according to step 1 of the design example and the masses defined so far, the frequencies of the closed-loop system are and , i.e., at least two orders of magnitude lower than the hypothesized 500 control frequency.
- 8c—Control Software Design: As each driver is capable of closing the local current control loop, the Raspberry Pi handles the execution of the higher-level control loops and the system logic. The Raspberry Pi acquires all the sensor data and implements the control algorithms to ensure the dynamic stability of the vehicle. Based on the attitude measurements and the steering intention estimated from the strain gauges, the central unit computes the desired current setpoints and transmits them via CAN to the respective drivers. The team working on software development will need to take into account the requirements and technical issues associated with latencies and real-time constraints.
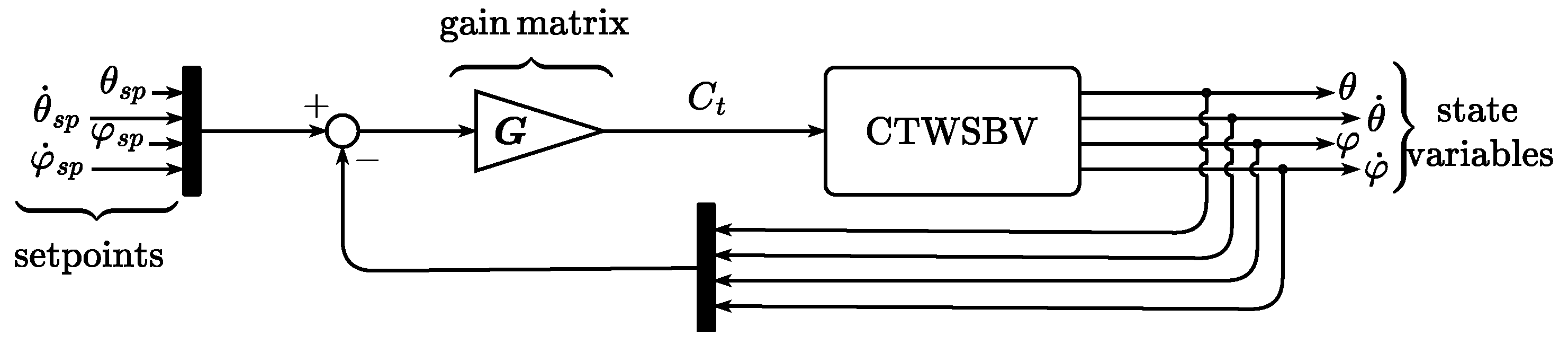
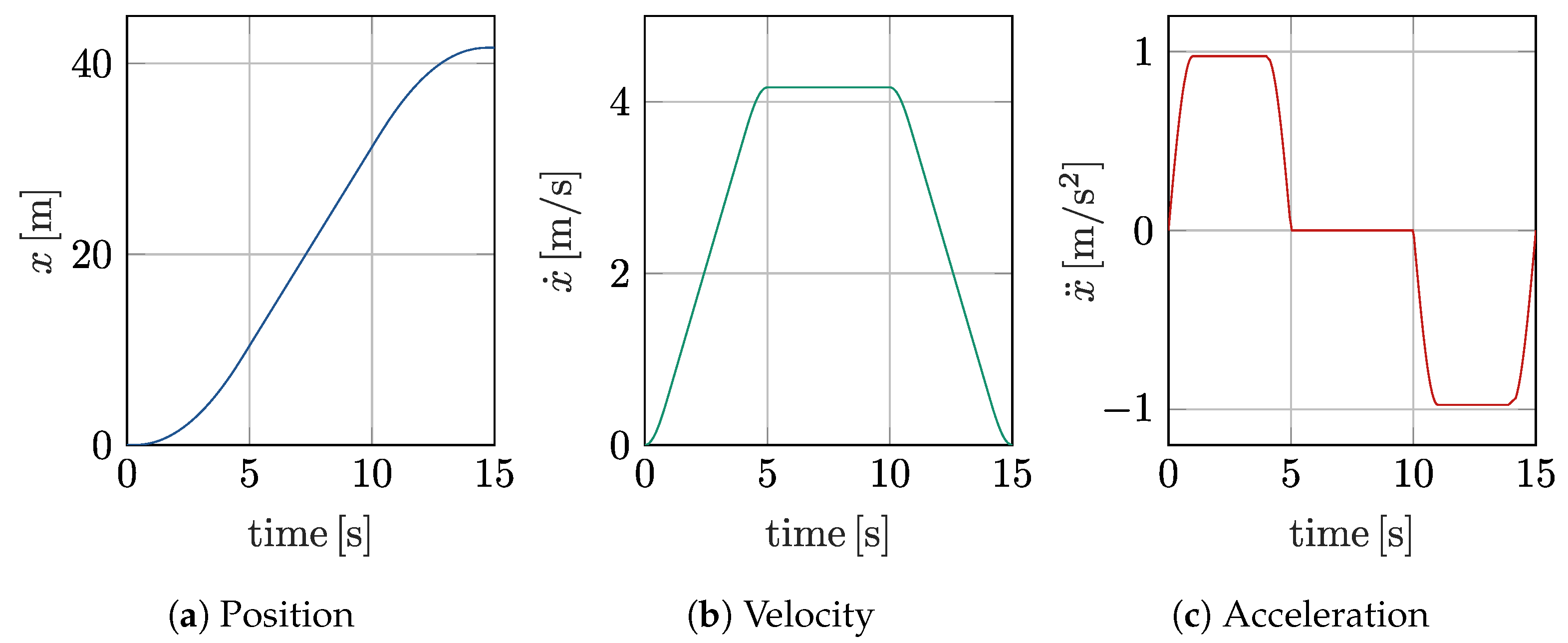
3.10. Step 9 and Design Check 4
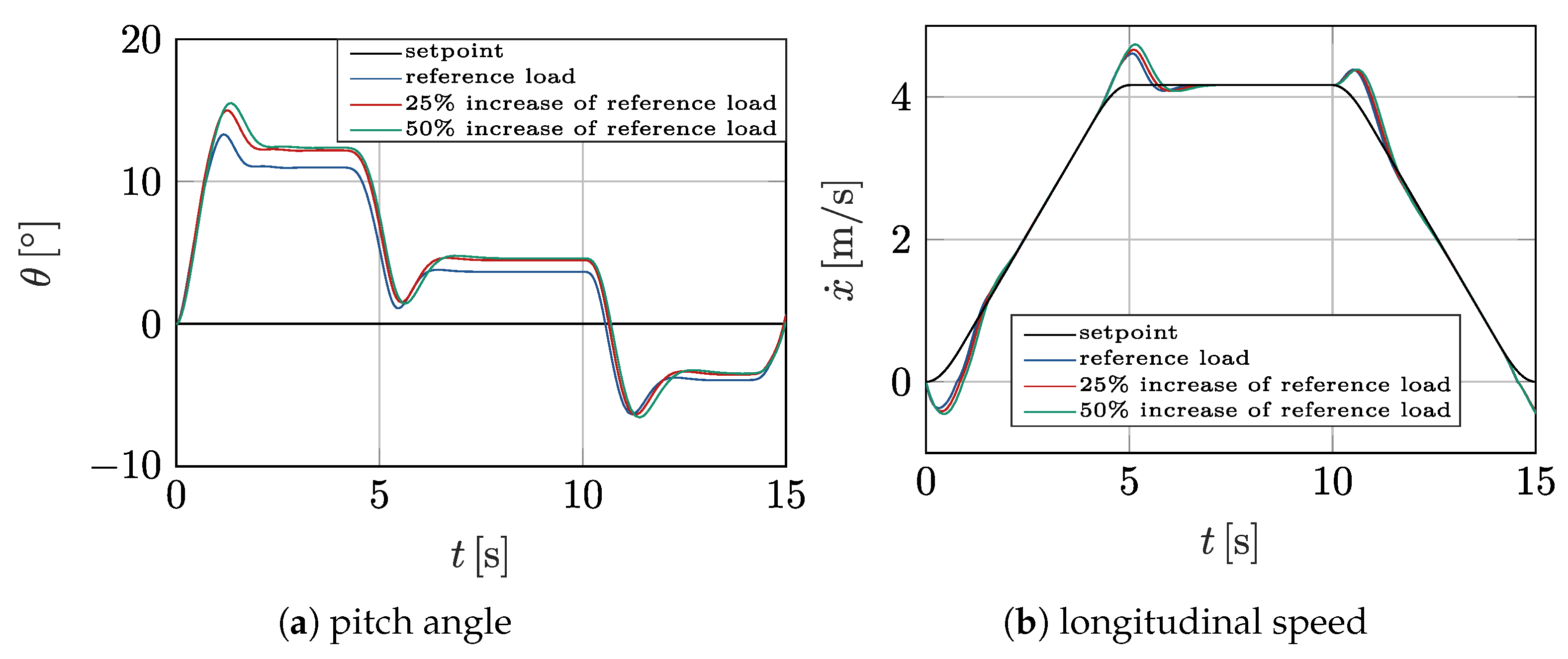
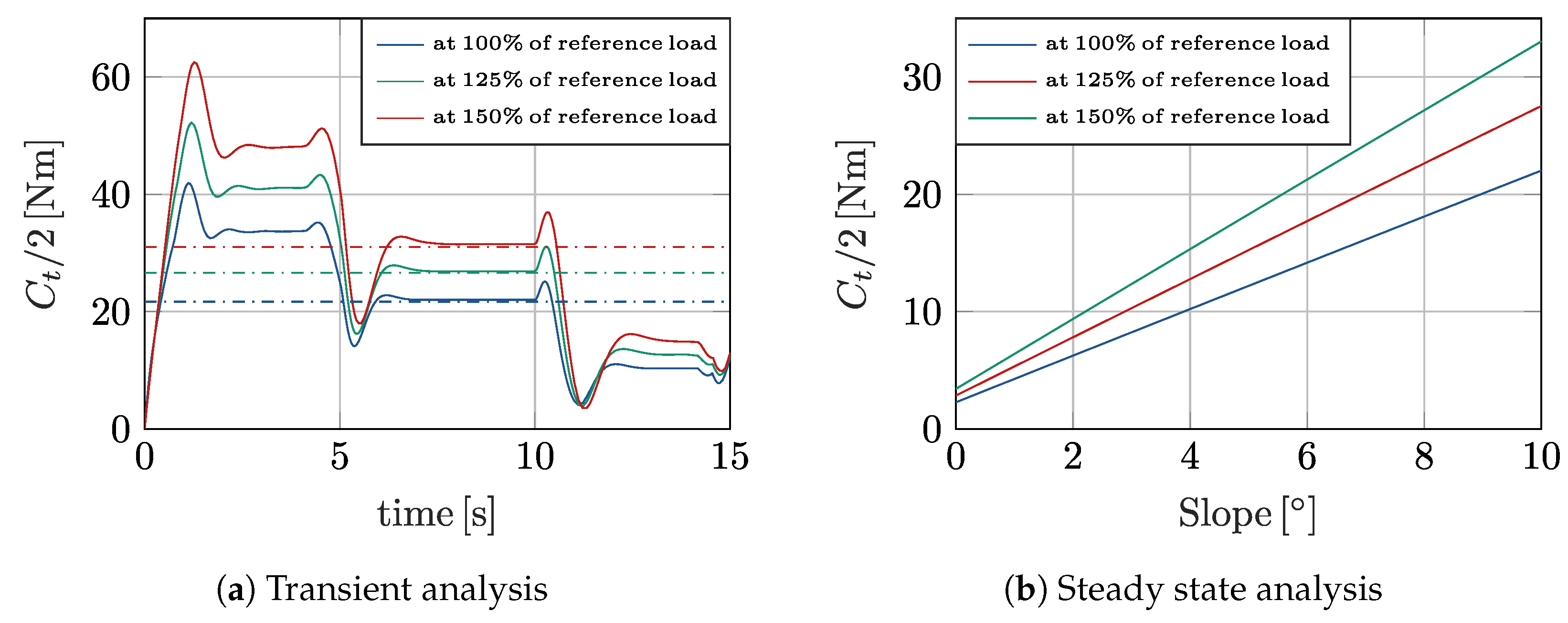
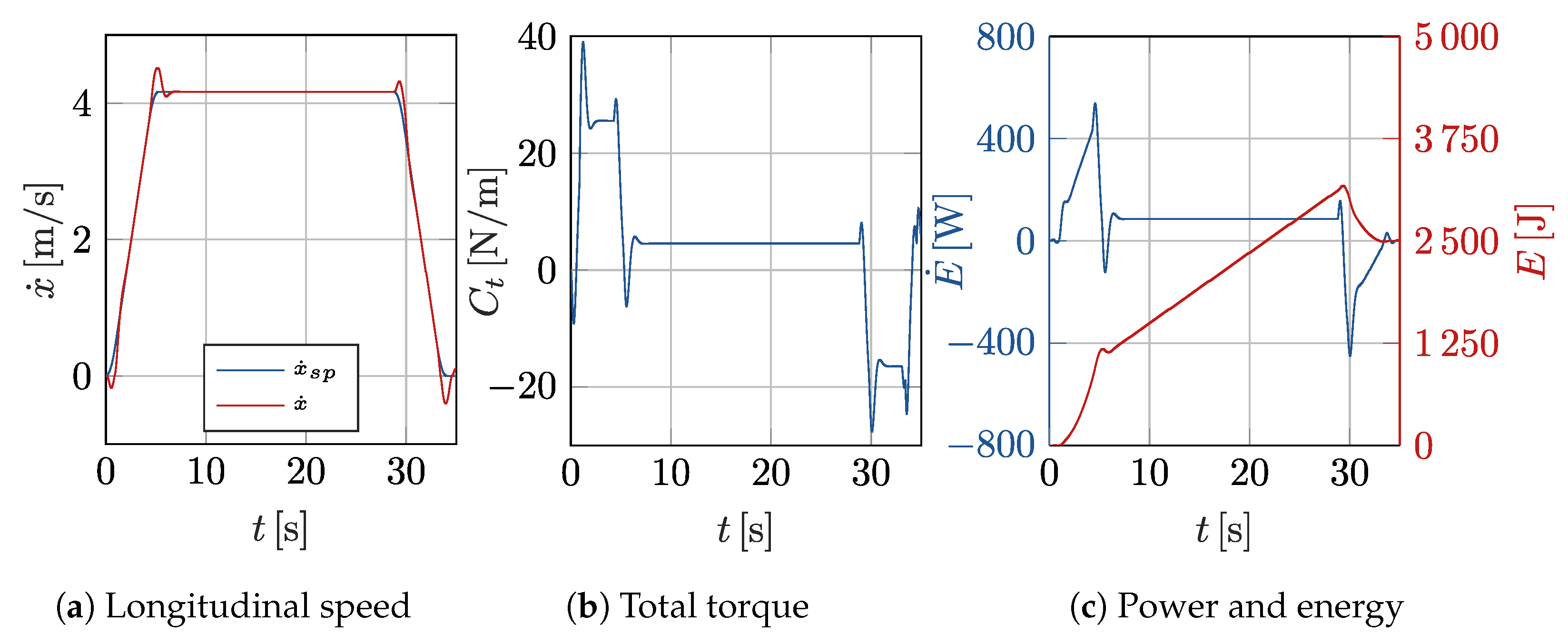
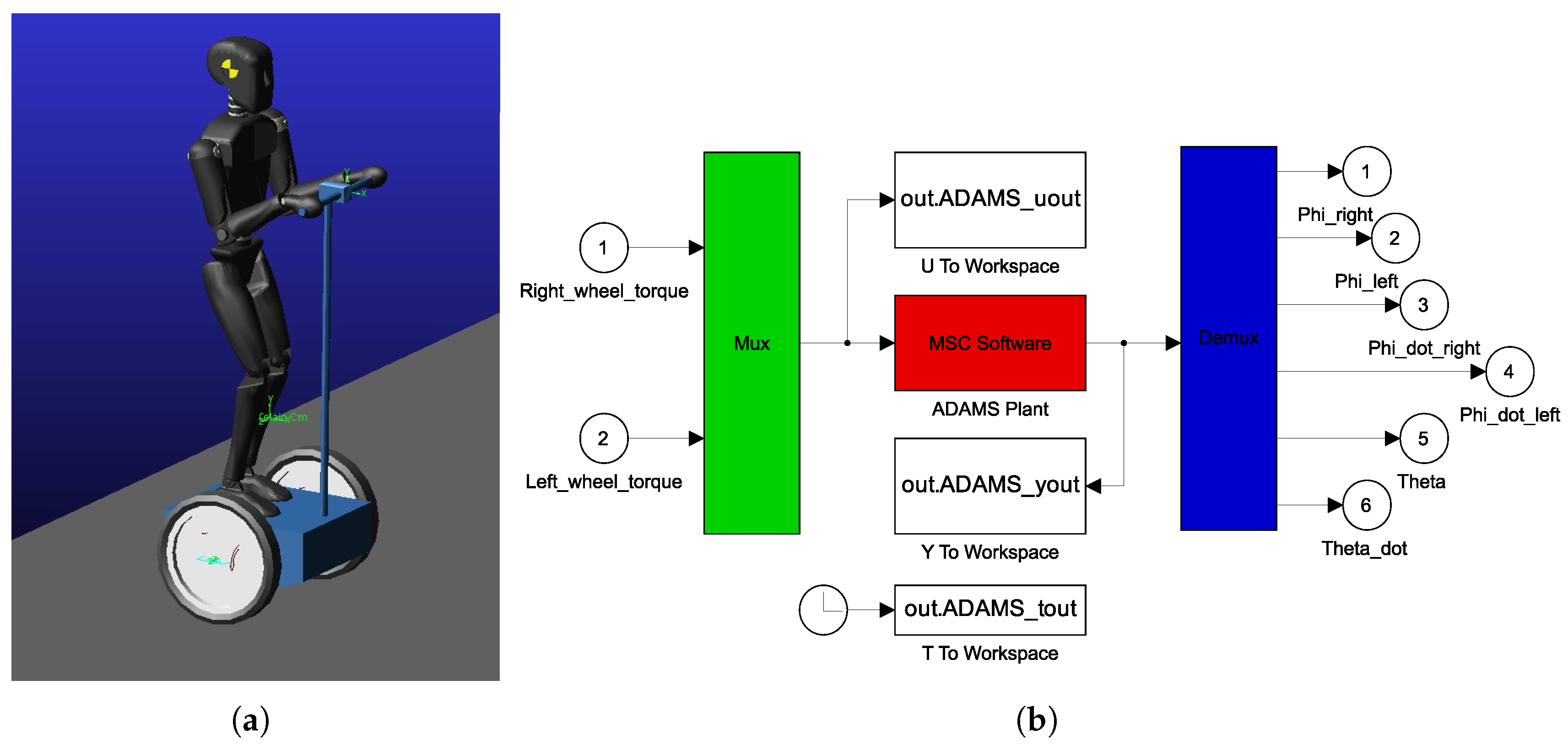
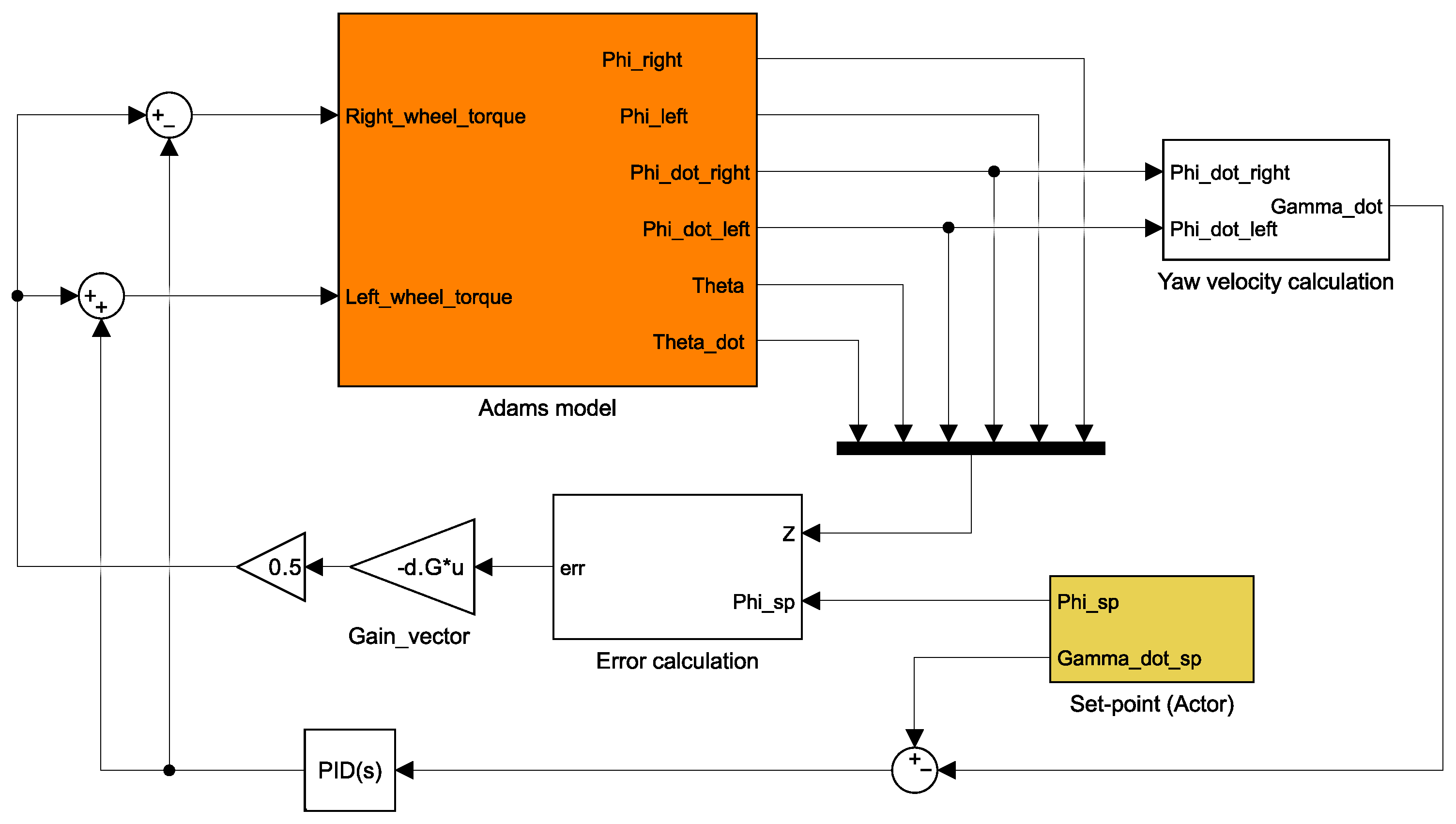
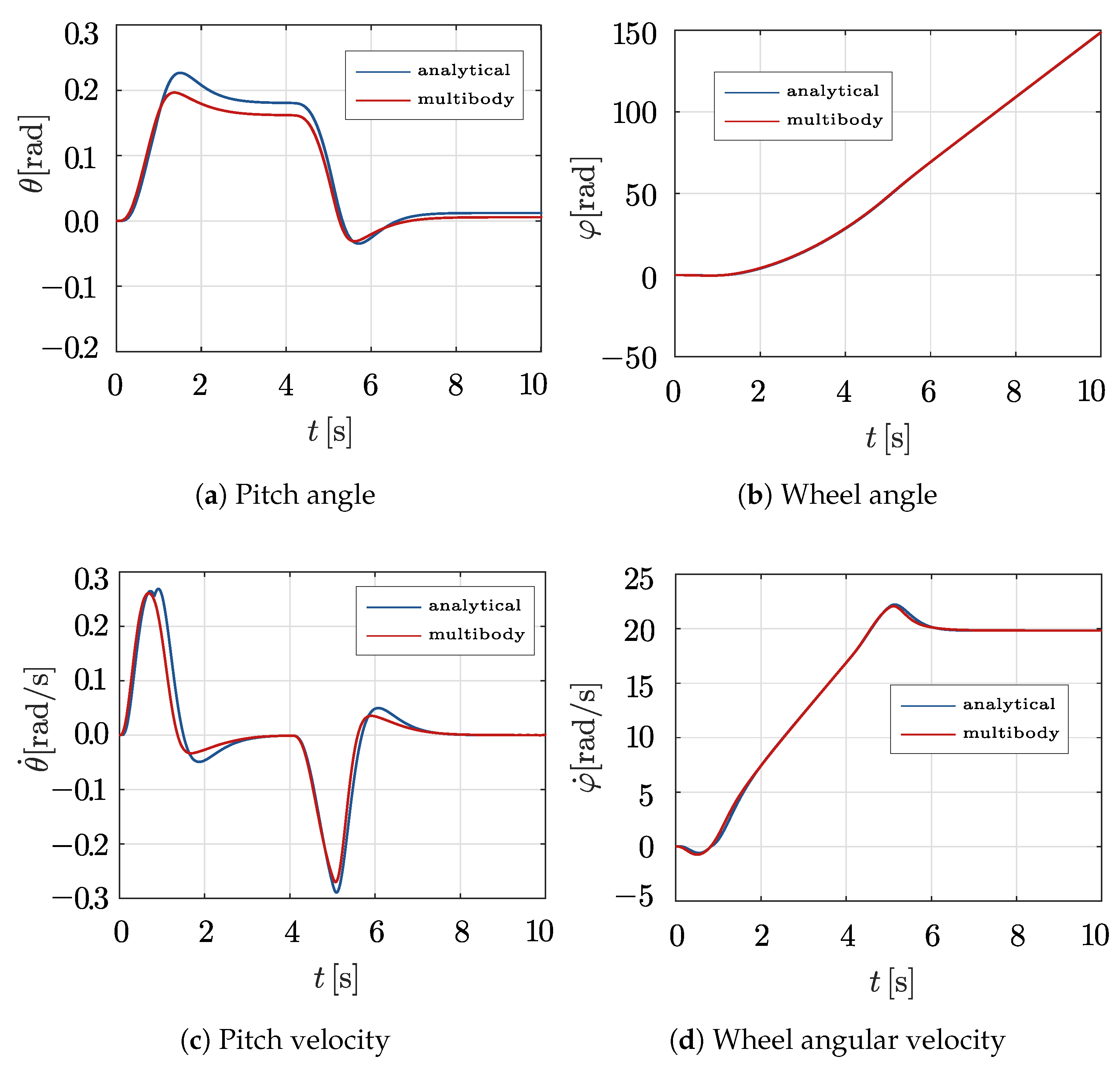
3.11. Validation of the Designed Virtual Prototype
4. Discussion
- “Sport” configuration. The vehicle, steered by a single rider, has high performance that allows it to reach high speed and accelerations, and to move on uneven terrain and along steep slopes.
- “Twin” configuration. The vehicle can accommodate not only the rider, but also a passenger. It is supposed to move on paved roads with modest slopes, and with speed and acceleration values typically suited to personal transportation in an urban environment.
- “Autonomous” configuration. The vehicle is used for the transportation of passive loads, and the motion commands are received from an external automated drive system. It is able to transport higher loads with respect to the previous configurations, moving however on flat terrain at limited speed and acceleration, as appropriate, e.g., in a warehouse.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, J.; Ding, F.; Fukuda, T.; Matsuno, T. Modeling and velocity control for a novel narrow vehicle based on mobile wheeled inverted pendulum. IEEE Trans. Control Syst. Technol. 2013, 21, 1607–1617. [Google Scholar] [CrossRef]
- Larimi, S.; Zarafshan, P.; Moosavian, S. A new stabilization algorithm for a two-wheeled mobile robot aided by reaction wheel. J. Dyn. Syst. Meas. Control. Trans. ASME 2015, 137, 011009. [Google Scholar] [CrossRef]
- D’Arrigo, A. Veicolo Elettrico Sperimentale a Due Ruote Parallele Coassiali Indipendenti. Master’s Thesis, EPFL/Politecnico di Milano, Lausanne, Switzerland; Milan, Italy, 1997. [Google Scholar]
- Grasser, F.; D’Arrigo, A.; Colombi, S.; Rufer, A. JOE: A mobile, inverted pendulum. IEEE Trans. Ind. Electron. 2002, 49, 107–114. [Google Scholar] [CrossRef]
- Mohamed Gad, O.; Saleh, S.; Bulbul, M.; Khadraoui, S. Design and Control of Two Wheeled Self Balancing Robot (TWSBR). In Proceedings of the 2022 Advances in Science and Engineering Technology International Conferences, ASET 2022, Dubai, United Arab Emirates, 21–24 February 2022. [Google Scholar] [CrossRef]
- Navinkumar, T.; Amala Praveen, A.; Sasirekha, P.; Gokila, P.; Kalaivani, C.; Prabhu, V. Design of DC-DC Converter based Self Balancing Segway Transporter for Indoor Applications. In Proceedings of the 6th International Conference on Computing Methodologies and Communication, ICCMC 2022, Erode, India, 29–31 March 2022; pp. 23–26. [Google Scholar] [CrossRef]
- Patel, C.; Putta, N.; Sri Manikanta, A.; Reddy, E.; Babu, K. Design, Analysis and Development of Virtual Working Model of Self Balancing Robot. In Lecture Notes in Mechanical Engineering; Springer Nature: Singapore, 2023; pp. 339–350. [Google Scholar] [CrossRef]
- Velagic, J.; Kovac, I.; Panjevic, A.; Osmanovic, A. Design and Control of Two-Wheeled and Self-Balancing Mobile Robot. In Proceedings of the Elmar—International Symposium Electronics in Marine, Zadar, Croatia, 13–15 September 2021; pp. 77–82. [Google Scholar] [CrossRef]
- Putov, A.; Ilatovskaya, E.; Kopichev, M. Self-balancing Robot Autonomous Control System. In Proceedings of the 2021 10th Mediterranean Conference on Embedded Computing, MECO 2021, Budva, Montenegro, 7–10 June 2021. [Google Scholar] [CrossRef]
- Shekhawat, A.; Rohilla, Y. Design and Control of Two-wheeled Self-Balancing Robot using Arduino. In Proceedings of the International Conference on Smart Electronics and Communication, ICOSEC 2020, Trichy, India, 10–12 September 2020; pp. 1025–1030. [Google Scholar] [CrossRef]
- Chien, S.Y.; Wang, A.S.; Wong, C.C. Design and Implementation of Two-Wheeled Self-Balancing Vehicle Based on Load Sensors. In Proceedings of the 2020 International Conference on System Science and Engineering, ICSSE 2020, Kagawa, Japan, 31 August–3 September 2020. [Google Scholar] [CrossRef]
- Komor, D.; Roman, R.C.; Precup, R.E.; David, R.C.; Pamfilii, I. Models of Two-Wheeled Mobile Robots with Experimental Validation. In Proceedings of the SACI 2020–IEEE 14th International Symposium on Applied Computational Intelligence and Informatics, Timisoara, Romania, 21–23 May 2020; pp. 211–216. [Google Scholar] [CrossRef]
- Pawananont, K.; Charoensuk, K. Design of a Two-Wheeled Auto-Balancing Robot under Impulse Interruption. ECTI Trans. Electr. Eng. Electron. Commun. 2022, 20, 438–449. [Google Scholar] [CrossRef]
- Nghia, V.; Van Thien, T.; Son, N.; Long, M. Adaptive neural sliding mode control for two wheel self balancing robot. Int. J. Dyn. Control 2022, 10, 771–784. [Google Scholar] [CrossRef]
- Olmez, Y.; Koca, G.; Akpolat, Z. Clonal selection algorithm based control for two-wheeled self-balancing mobile robot. Simul. Model. Pract. Theory 2022, 118, 102552. [Google Scholar] [CrossRef]
- Akhavan, M.; Parvahan, H.; Manzar, M. Design and Implementation of a Data-Driven Controller for a Two-Wheeled Self-Balancing Robot. In Proceedings of the 2022 30th International Conference on Electrical Engineering, ICEE 2022, Tehran, Iran, 17–19 May 2022; pp. 55–59. [Google Scholar] [CrossRef]
- Fikri, M.; Djamari, D.; Levy, S. H-Infinity Controller Design of Two-Wheeled Mobile Robot under Disturbance. In Proceedings of the 2021 International Seminar on Intelligent Technology and Its Application: Intelligent Systems for the New Normal Era, ISITIA 2021, Virtual, 21–22 July 2021; pp. 147–152. [Google Scholar] [CrossRef]
- Razmjooy, N.; Ramezani, M. Robust optimal control of two-wheeled self-balancing robot using Chebyshev inclusion method. Majlesi J. Electr. Eng. 2018, 12, 13–21. [Google Scholar]
- Martins, R.; Nunes, F. Control system for a self-balancing robot. In Proceedings of the 2017 4th Experiment at International Conference: Online Experimentation, exp. at 2017, Faro, Portugal, 6–8 June 2017; pp. 297–302. [Google Scholar] [CrossRef]
- Yuan, S.; Lei, G.; Bin, X. Dynamic modeling and sliding mode controller design of a two-wheeled self-balancing robot. In Proceedings of the 2016 IEEE International Conference on Mechatronics and Automation, IEEE ICMA 2016, Harbin, China, 7–10 August 2016; pp. 2437–2442. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, H.; Qin, L. Design of self-balancing vehicle based on cascade PID control system. In Proceedings of the 2022 4th International Conference on Advances in Computer Technology, Information Science and Communications (CTISC), Suzhou, China, 22–24 April 2022; pp. 1–4. [Google Scholar]
- Ramadhan, B.; Binugroho, E.H.; Dewanto, R.S.; Pramadihanto, D. PENS-wheel (self balancing one-wheel vehicle) mechanical design and sensor system. In Proceedings of the 2016 International Electronics Symposium (IES), Denpasar, Indonesia, 29–30 September 2016; pp. 438–443. [Google Scholar]
- Monesh, M.S.; Kumar, A.H.; Durairaj, R. Comprehensive Review of Design and Development of a Self-Balancing Robot with Stability Control for Uneven Surfaces. Int. J. Mech. Eng. Technol. (IJMET) 2025, 16, 140–172. [Google Scholar] [CrossRef]
- Walden, D.D.; Shortell, T.M.; Roedler, G.J.; Delicado, B.A.; Mornas, O.; Yip, Y.S.; Endler, D.; International Council on Systems Engineering (INCOSE) (Eds.) Systems Engineering Handbook: A Guide for System Life Cycle Processes and Activities, 5th ed.; Wiley: Hoboken, NJ, USA, 2023. [Google Scholar]
- Stetter, R. Methodical and model-based design of automated vehicles. Stud. Syst. Decis. Control 2020, 201, 59–91. [Google Scholar] [CrossRef]
- Zheng, C.; Hehenberger, P.; Le Duigou, J.; Bricogne, M.; Eynard, B. Multidisciplinary design methodology for mechatronic systems based on interface model. Res. Eng. Des. 2017, 28, 333–356. [Google Scholar] [CrossRef]
- Hirz, M. An approach supporting integrated modeling and design of complex mechatronics products by the example of automotive applications. In Proceedings of the WMSCI 2018—22nd World Multi-Conference on Systemics, Cybernetics and Informatics, Orlando, FL, USA, 8–11 July 2018; Volume 3, pp. 161–166. [Google Scholar]
- Zheng, C.; Qin, X.; Eynard, B.; Li, J.; Bai, J.; Zhang, Y.; Gomes, S. Interface model-based configuration design of mechatronic systems for industrial manufacturing applications. Robot. Comput.-Integr. Manuf. 2019, 59, 373–384. [Google Scholar] [CrossRef]
- Khandoker, A.; Sint, S.; Gessl, G.; Zeman, K.; Jungreitmayr, F.; Wahl, H.; Wenigwieser, A.; Kretschmer, R. Towards a logical framework for ideal MBSE tool selection based on discipline specific requirements. J. Syst. Softw. 2022, 189, 111306. [Google Scholar] [CrossRef]
- Schmidt, M.M.; Stark, R. Model-Based Systems Engineering (MBSE) as computer-supported approach for cooperative systems development. In Proceedings of the ECSCW, Siegen, Germany, 13–17 June 2020. [Google Scholar] [CrossRef]
- Bajzek, M.; Fritz, J.; Hick, H.; Maletz, M.; Faustmann, C.; Stieglbauer, G. Model Based Systems Engineering Concepts. In Systems Engineering for Automotive Powertrain Development; Hick, H., Küpper, K., Sorger, H., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 1–40. [Google Scholar] [CrossRef]
- Caliò, E.; Di Giorgio, F.; Pasquinelli, M. Deploying Model-Based Systems Engineering in Thales Alenia Space Italia. In Proceedings of the CIISE, Turin, Italy, 14–16 November 2016; pp. 112–118. [Google Scholar]
- Badache, N.; Roques, P. Capella to SysML Bridge: A Tooled-up Methodology for MBSE Interoperability. In Proceedings of the 9th European Congress on Embedded Real Time Software and Systems (ERTS 2018), Toulouse, France, 31 January–2 February 2018. [Google Scholar]
- Roques, P. MBSE with the ARCADIA Method and the Capella Tool. In Proceedings of the 8th European Congress on Embedded Real Time Software and Systems (ERTS 2016), Toulouse, France, 27–29 January 2016. [Google Scholar]
- Righettini, P.; Strada, R.; Santinelli, J. Design of a self balancing vehicle as a test rig for safety control strategies investigations. In Proceedings of the ASME Design Engineering Technical Conference, Virtual, 17–19 August 2021; Volume 7. [Google Scholar] [CrossRef]
- Righettini, P.; Strada, R.; Cortinovis, F. Experimental Evaluation of Centralized Control Strategies on a 5R Robot. Mech. Mach. Sci. 2024, 163, 334–342. [Google Scholar] [CrossRef]
- Righettini, P.; Legnani, G.; Cortinovis, F.; Tabaldi, F.; Santinelli, J. Real Time MEMS-Based Joint Friction Identification for Enhanced Dynamic Performance in Robotic Applications. Robotics 2025, 14, 36. [Google Scholar] [CrossRef]
- Zhou, L.; Gao, J.; Li, Q.; Hu, C. Simulation study on tractive performance of off-road tire based on discrete element method. Math. Biosci. Eng. 2020, 17, 3869–3893. [Google Scholar] [CrossRef] [PubMed]
- Bekakos, C.A.; Papazafeiropoulos, G.; O’Boy, D.; Prins, J.; Mavros, G. Off-road tire-terrain interaction: An analytical solution. SAE Int. J. Commer. Veh. 2016, 10, 244–251. [Google Scholar] [CrossRef]
- Righettini, P.; Strada, R.; Cortinovis, F. General Procedure for Servo-Axis Design in Multi-Degree-of-Freedom Machinery Subject to Mixed Loads. Machines 2022, 10, 454. [Google Scholar] [CrossRef]
- Graessler, I.; Hentze, J. The new V-Model of VDI 2206 and its validation das Neue V-Modell der VDI 2206 und seine Validierung. At-Autom. 2020, 68, 312–324. [Google Scholar] [CrossRef]
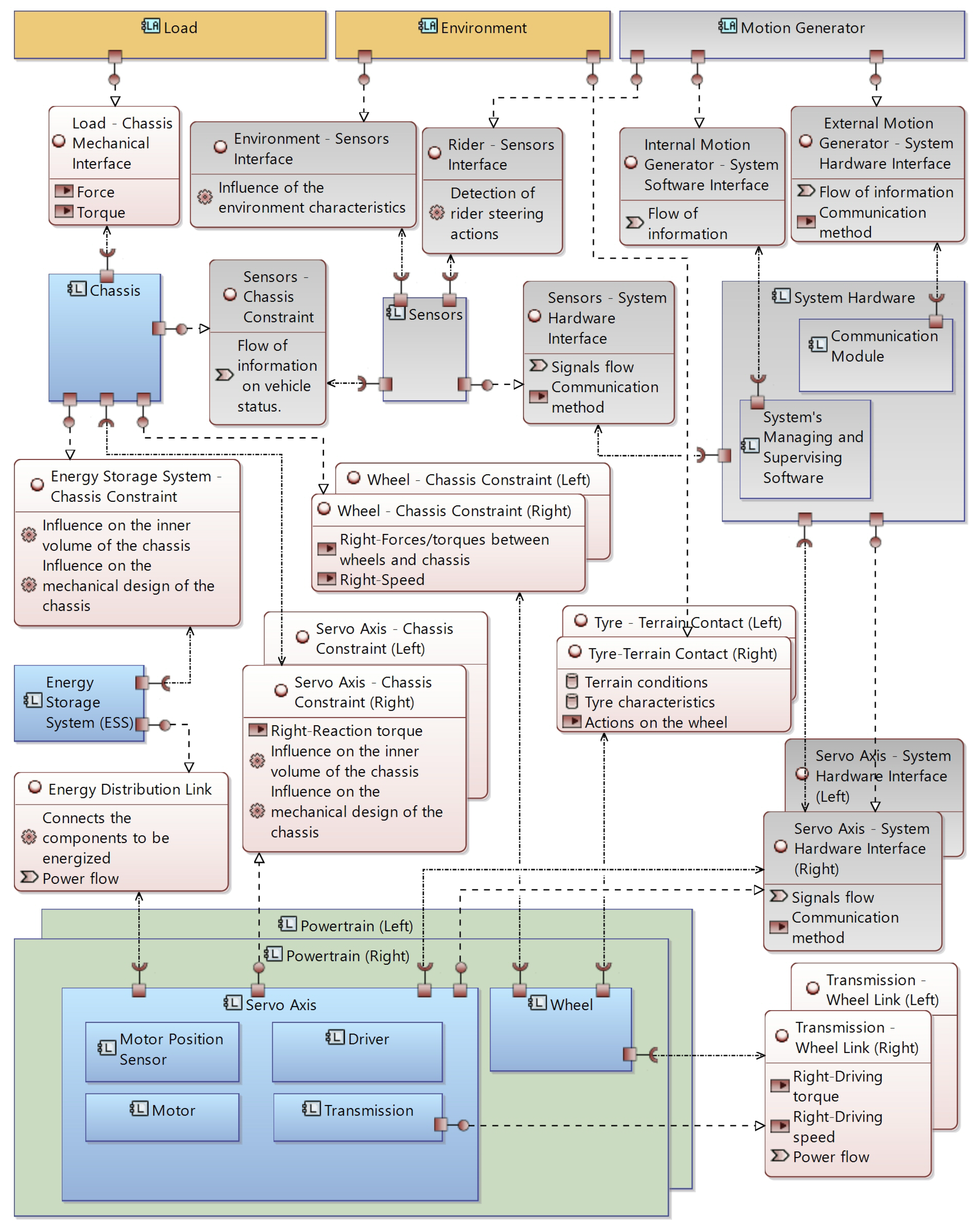
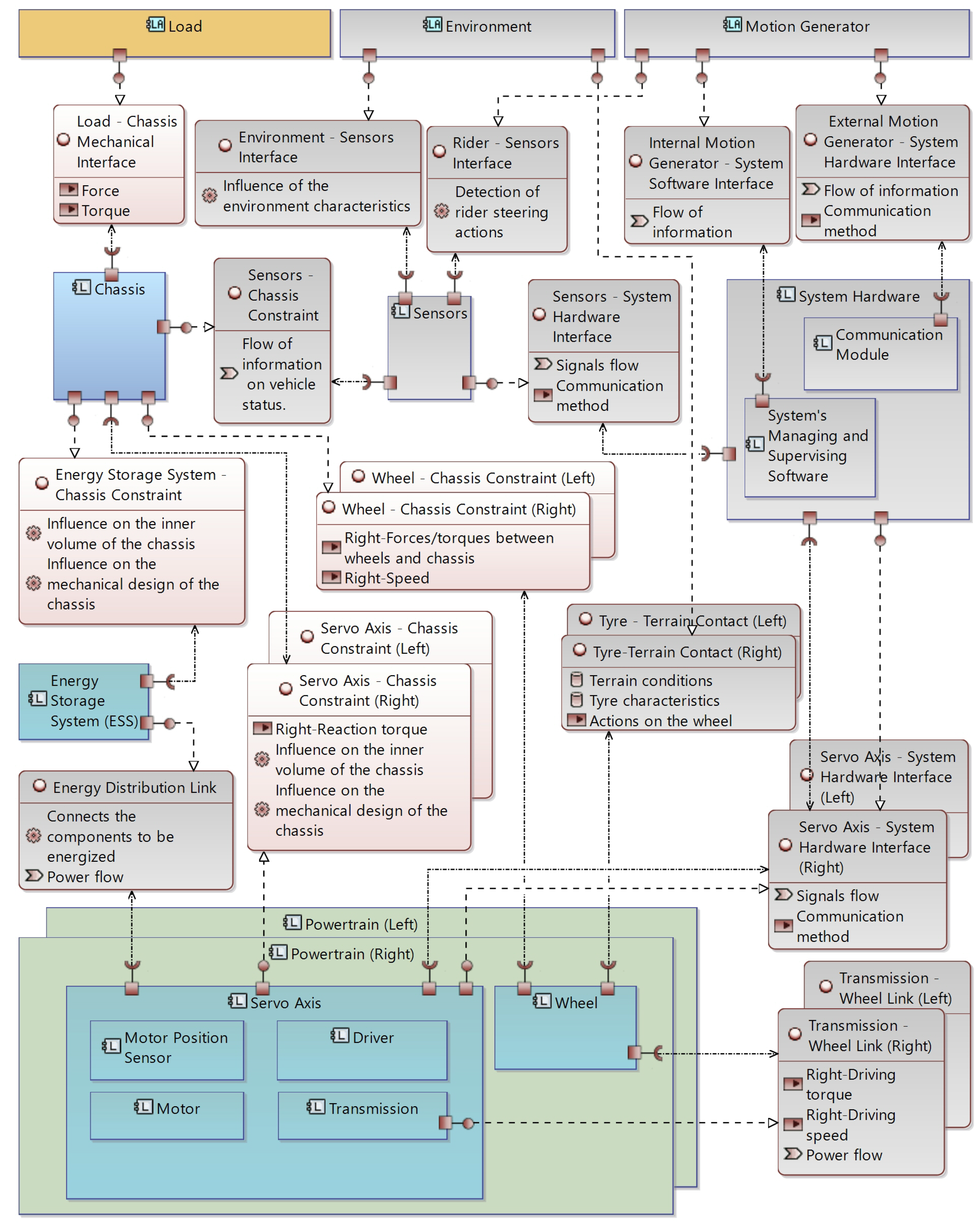





| Interfaces | Steps | ||
|---|---|---|---|
| 1–5 | 6–7 | 8–9 | |
| Load—Chassis Mechanical Interface | x | x | |
| Energy Storage System—Chassis Constraint | x | x | |
| Wheel—Chassis Constraint (Left–Right) | x | x | |
| Servo Axis—Chassis Constraint (Left–Right) | x | x | |
| Energy Distribution Link | x | ||
| Tire—Terrain Contact (Left–Right) | x | ||
| Transmission—Wheel Link (Left–Right) | x | ||
| Environment—Sensor Interface | x | ||
| Rider—Sensor Interface | x | ||
| Internal Motion Generator—System Software Interface | x | ||
| External Motion Generator—System Hardware Interface | x | ||
| Sensors—Chassis Constraint | x | ||
| Sensors—System Hardware Interface | x | ||
| Servo Axis—System Hardware Interface (Left–Right) | x | ||
| Parameter | Symbol | Value |
|---|---|---|
| wheel radius | R | |
| mass of the wheels | m | 3 |
| moment of inertia of the wheels | ||
| mass of chassis–rider assembly | M | 89 |
| moment of inertia of chassis–rider assembly | J | |
| distance between the wheel axis and the center of gravity | l | |
| center of gravity angular position | 0 deg |
| Rated Voltage | Rated Power | Rated Torque | Rated Speed | Nominal Current | Peak Current | Torque Constant | Reduction Ratio |
|---|---|---|---|---|---|---|---|
| 24 | 780 | 2050 | 37 | 111 | 10 | 10 |
| Length | Width | Height | Track | Base Height | |
|---|---|---|---|---|---|
| Symbol | a | b | c | w | h |
| Value | 500 mm | 420 mm | 227 mm | 670 mm | 97 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Righettini, P.; Strada, R.; Cortinovis, F.; Santinelli, J. A Mechatronic Design Procedure for Self-Balancing Vehicles According to the MBSE Approach. Machines 2025, 13, 826. https://doi.org/10.3390/machines13090826
Righettini P, Strada R, Cortinovis F, Santinelli J. A Mechatronic Design Procedure for Self-Balancing Vehicles According to the MBSE Approach. Machines. 2025; 13(9):826. https://doi.org/10.3390/machines13090826
Chicago/Turabian StyleRighettini, Paolo, Roberto Strada, Filippo Cortinovis, and Jasmine Santinelli. 2025. "A Mechatronic Design Procedure for Self-Balancing Vehicles According to the MBSE Approach" Machines 13, no. 9: 826. https://doi.org/10.3390/machines13090826
APA StyleRighettini, P., Strada, R., Cortinovis, F., & Santinelli, J. (2025). A Mechatronic Design Procedure for Self-Balancing Vehicles According to the MBSE Approach. Machines, 13(9), 826. https://doi.org/10.3390/machines13090826






