Development and Experimental Verification of Multi-Parameter Test Bench for Linear Rolling Guide
Abstract
1. Introduction
2. Measurement Principles
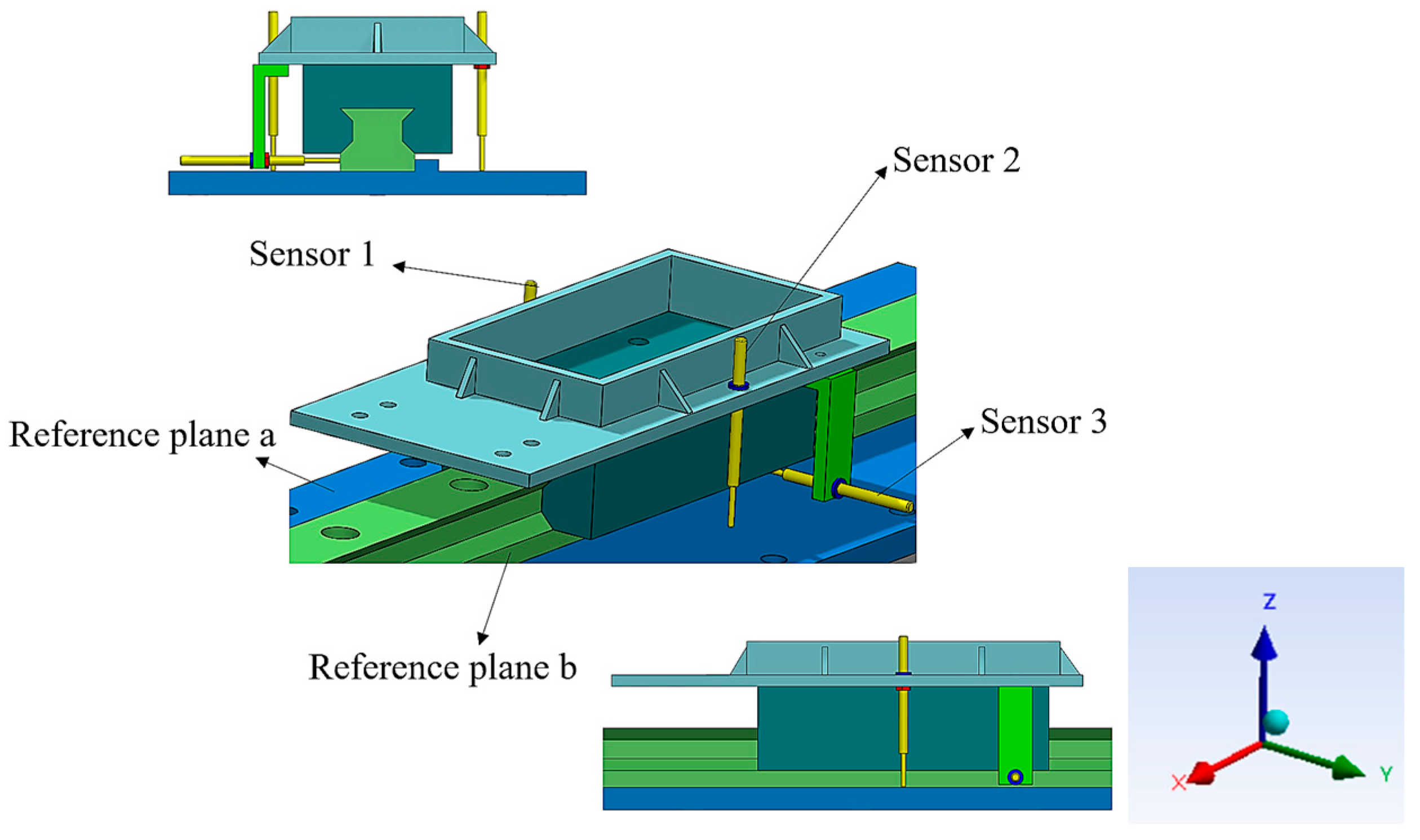
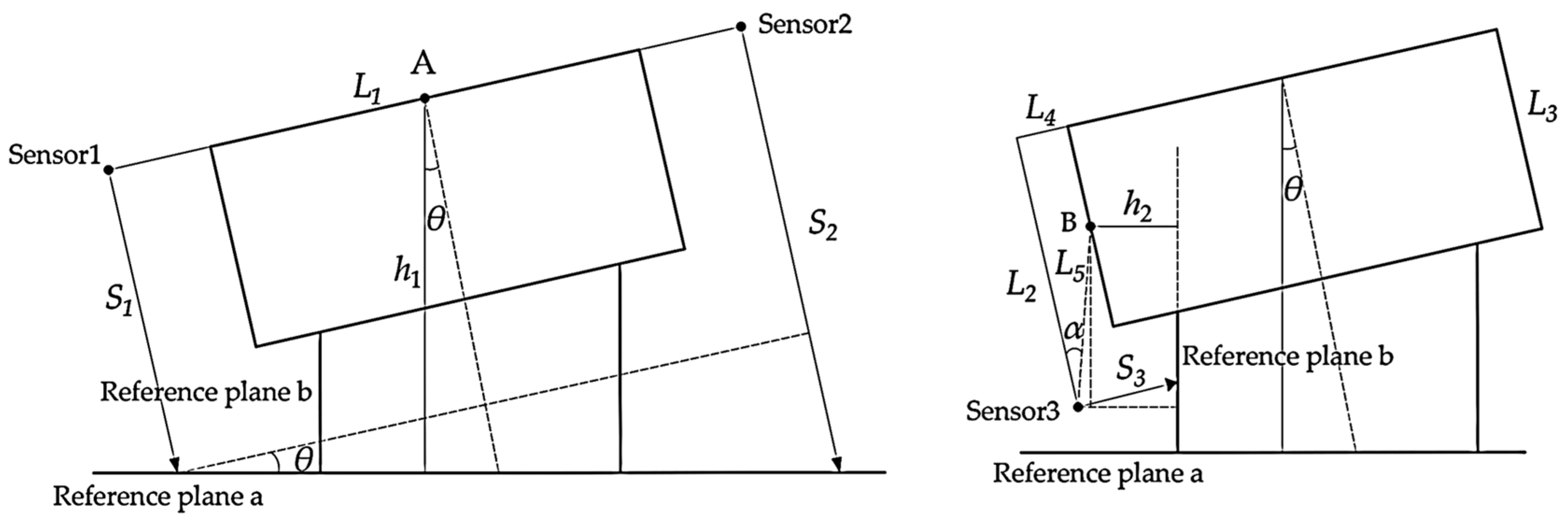
2.1. Measurement Principle of Motion Accuracy
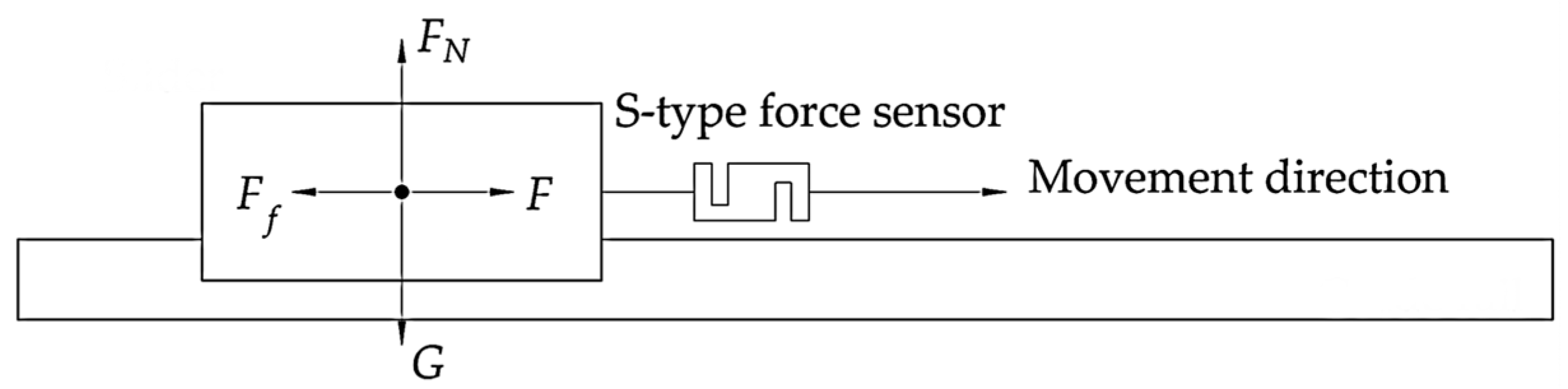
2.2. Measurement Principle of PDF
2.3. Test Principle of Fatigue Life
3. Composition of the Test Bench
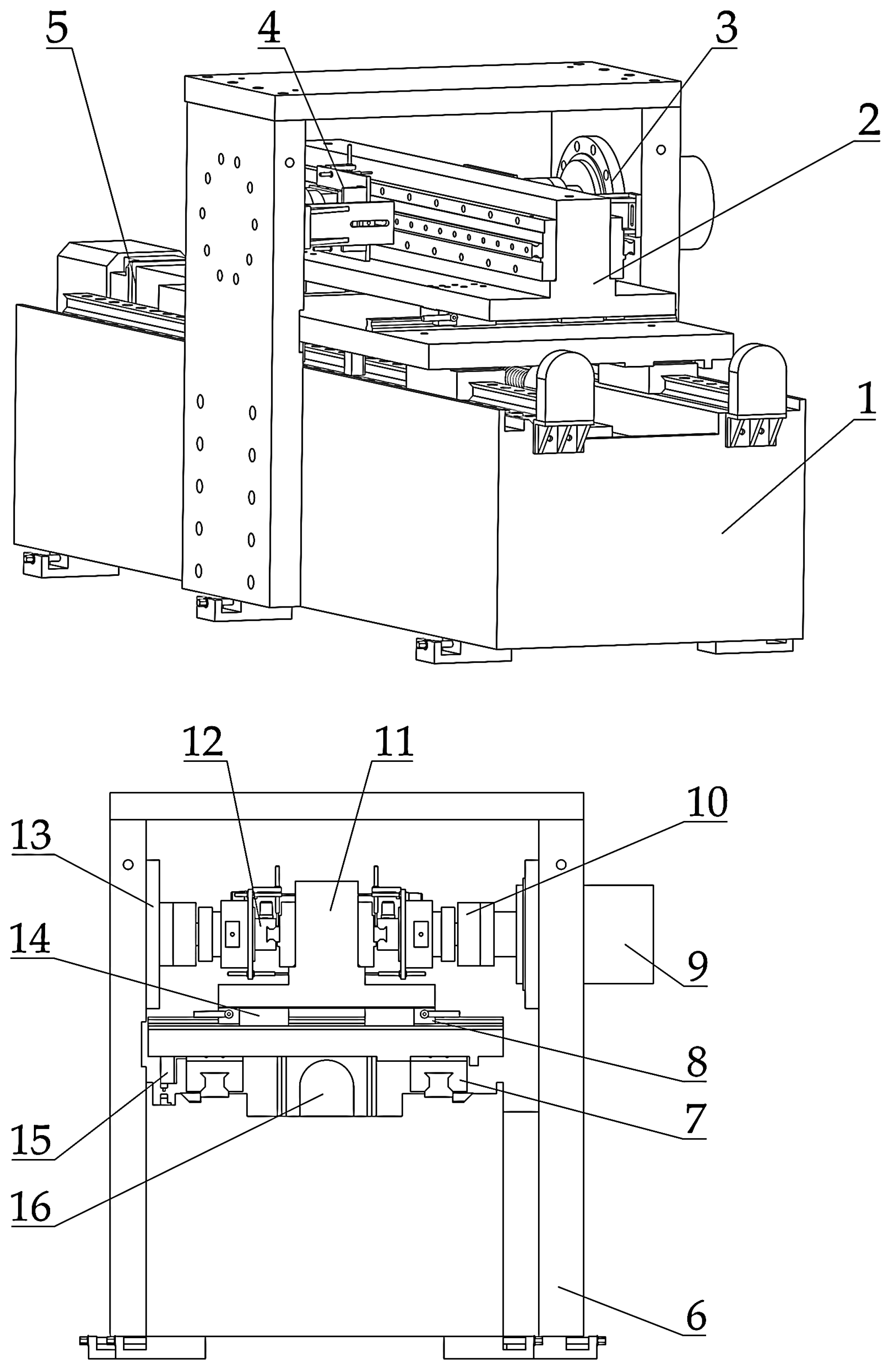
3.1. Mechanical Structure Design
3.1.1. Composition of Overall Structure
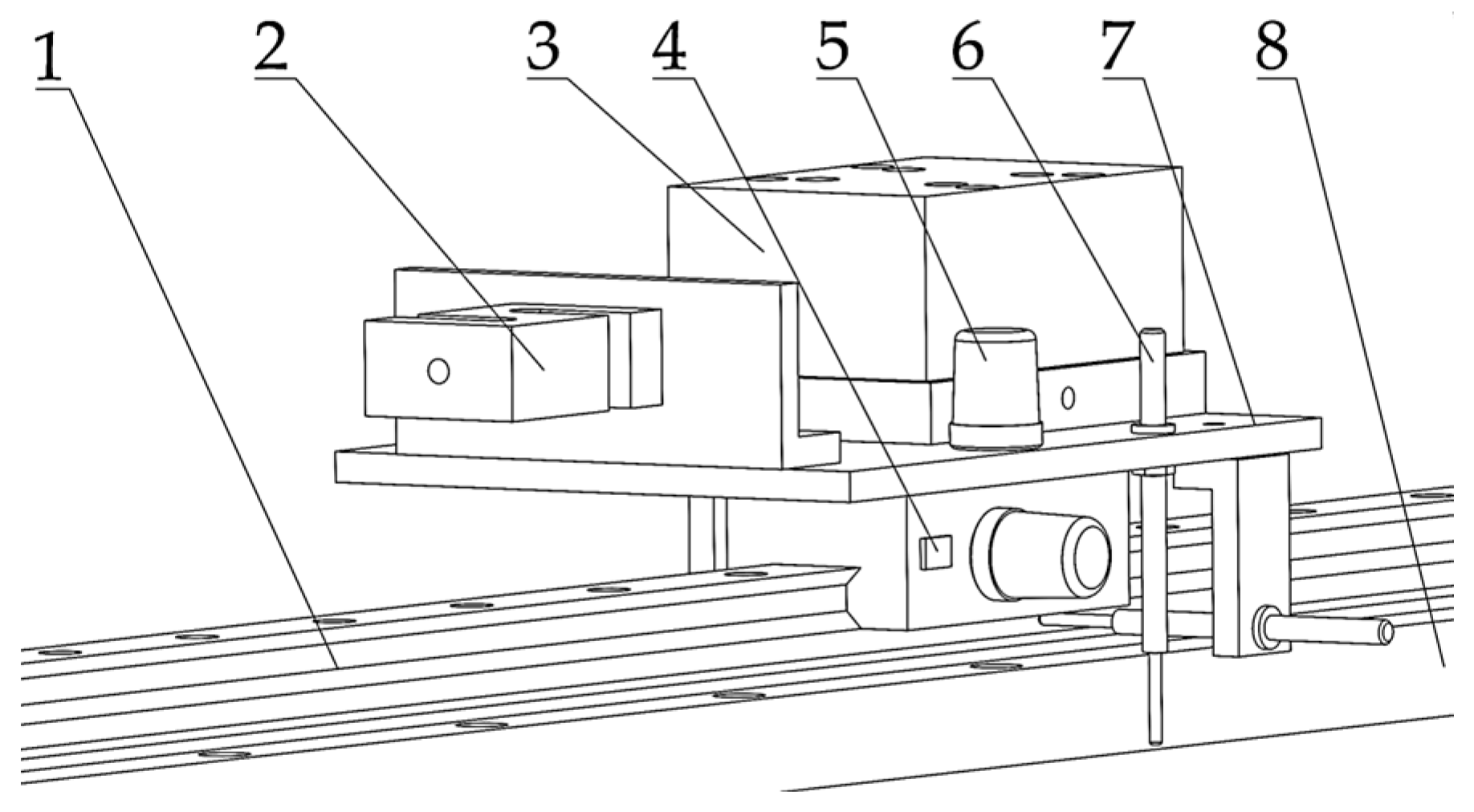
3.1.2. Measurement Setup Structural Design
3.2. Measurement and Control System Design
4. Finite Element Analysis of the Test Bench
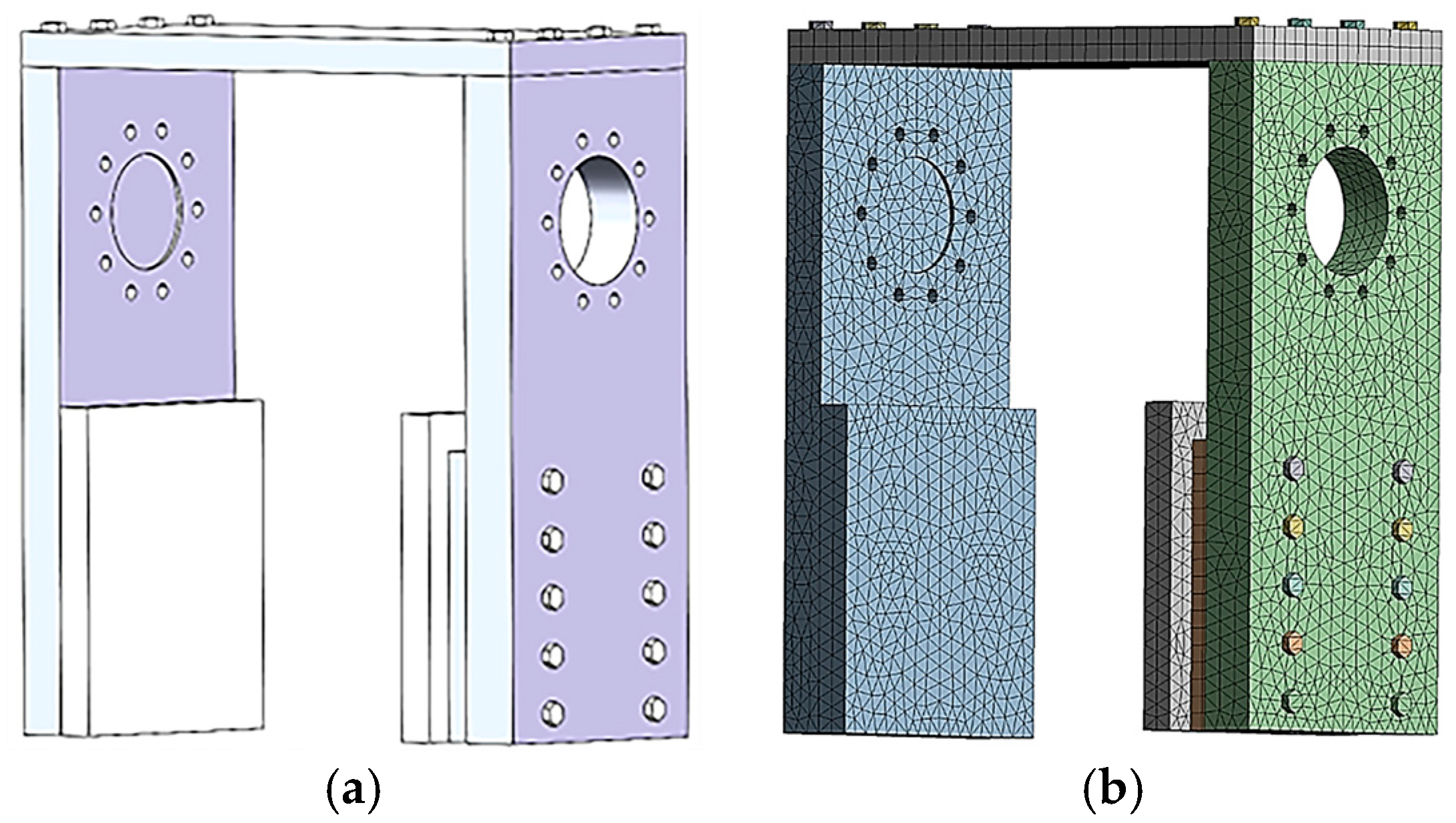
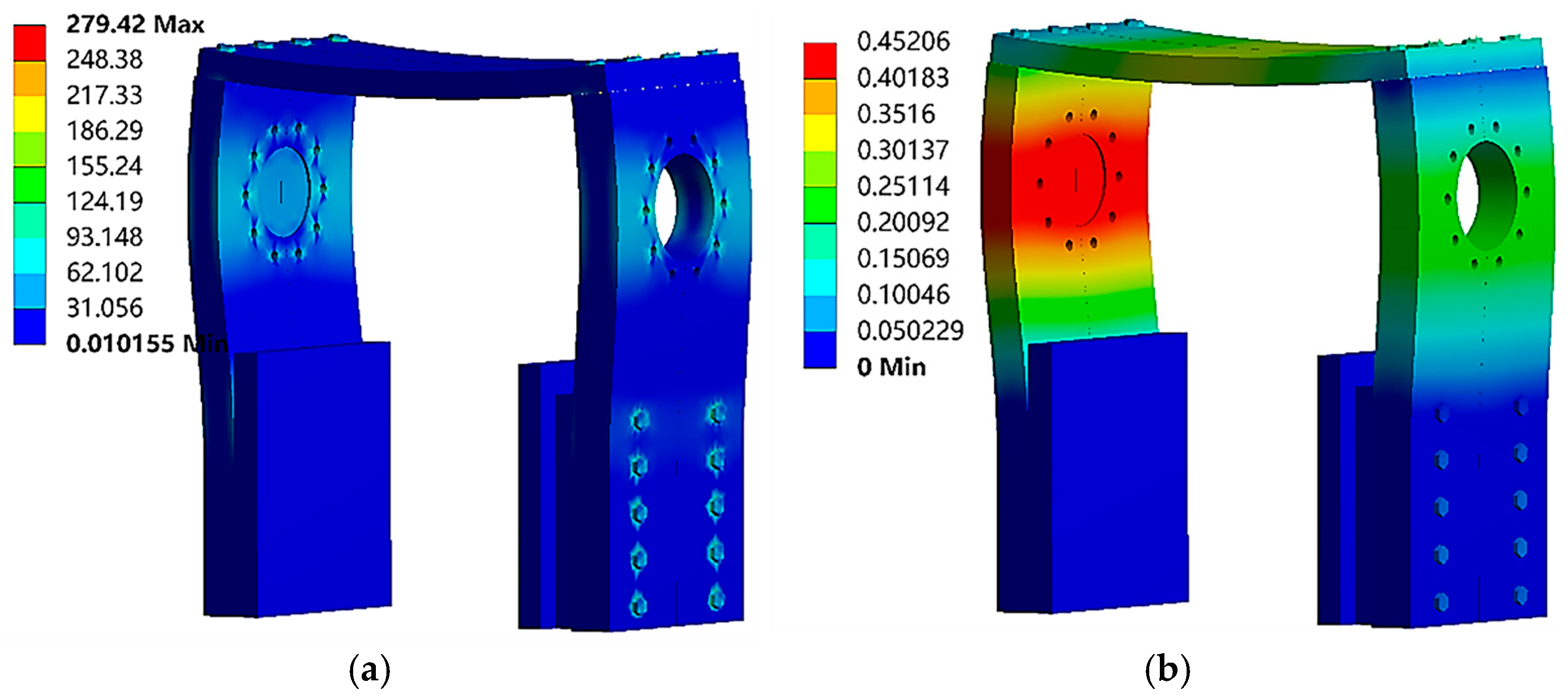
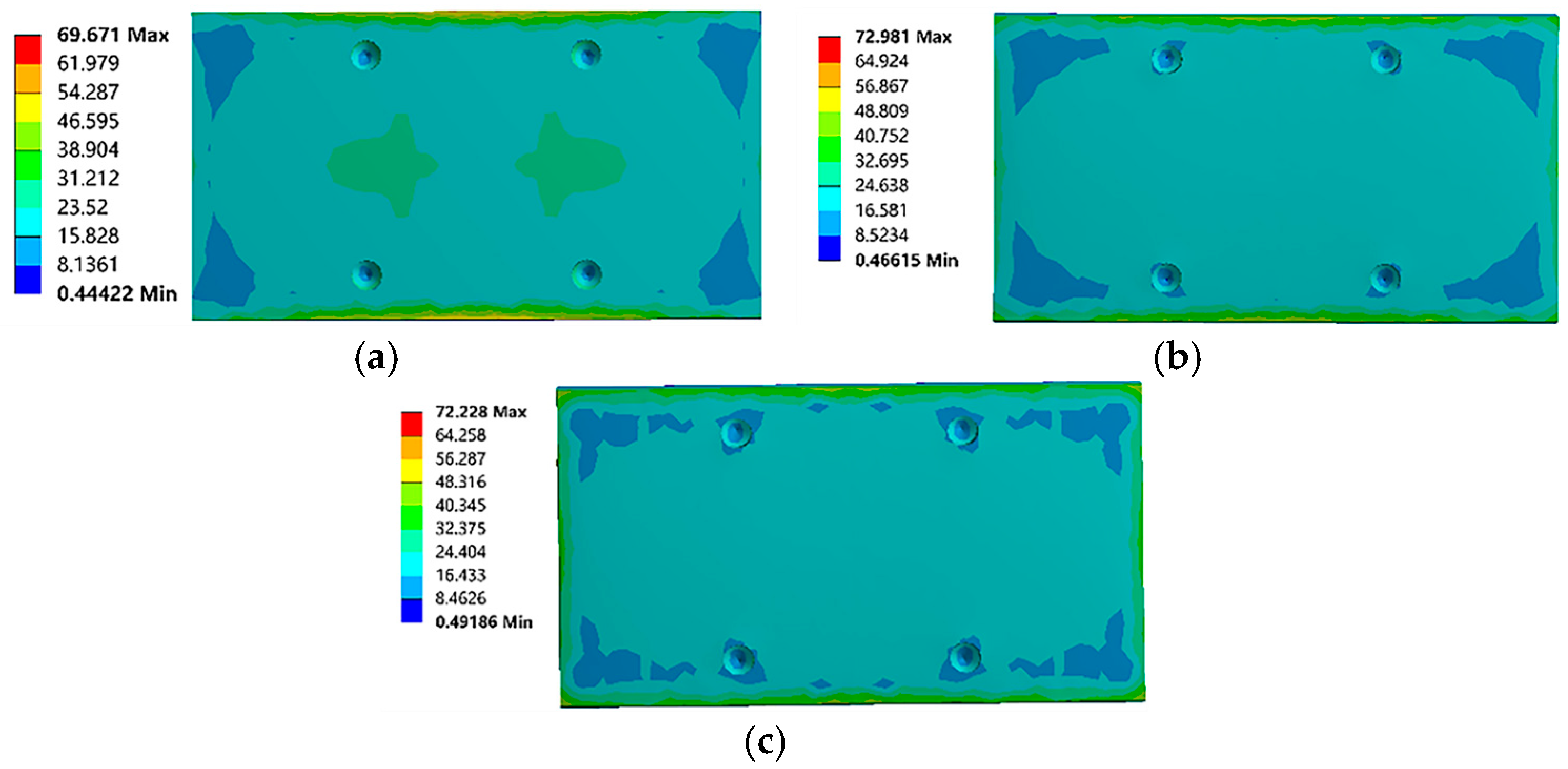
4.1. Static Analysis of the Gantry
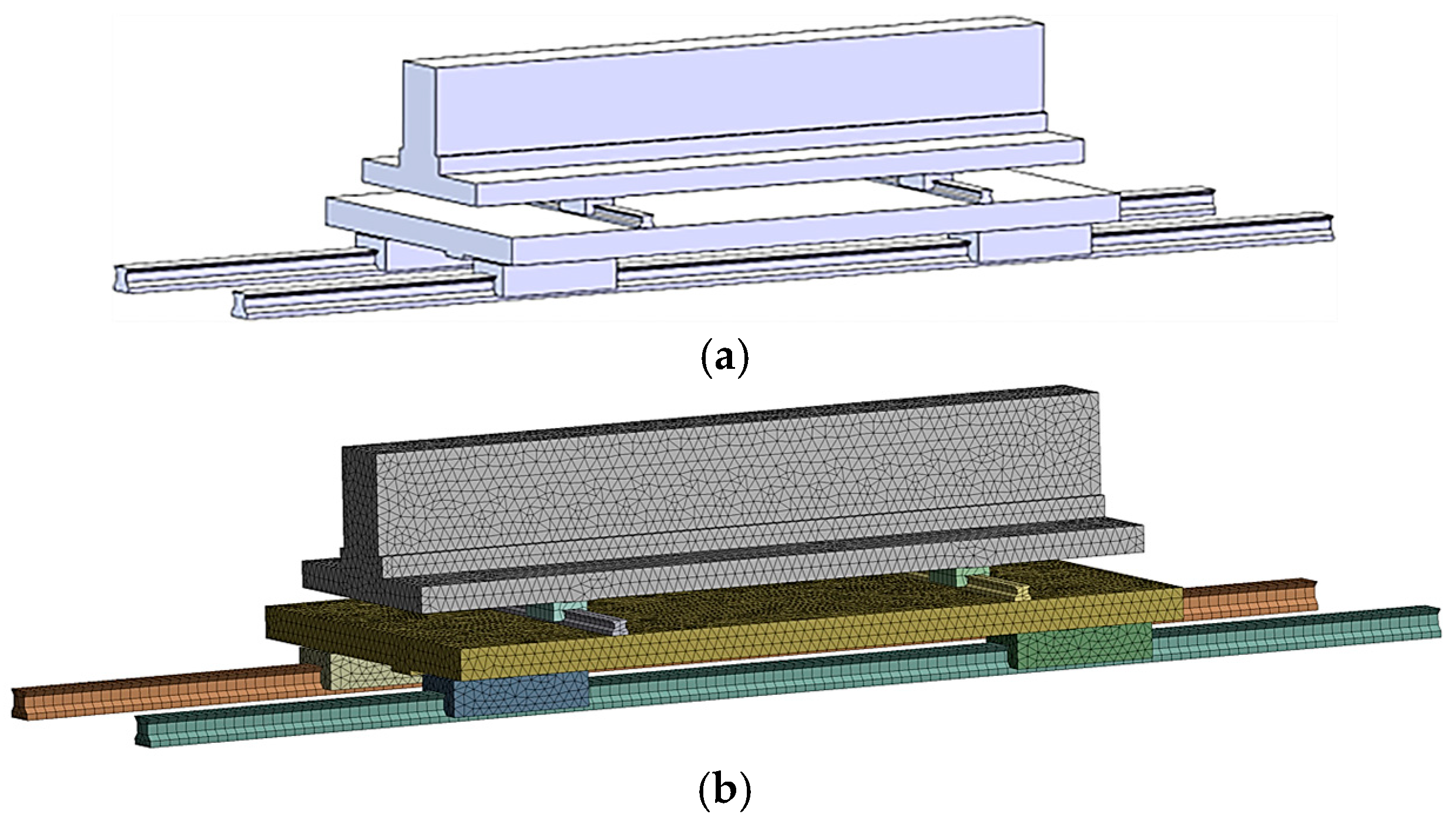
4.2. Modal Analysis of the Upper Bed
4.2.1. The Upper Bed Modal Finite Element Simulation
4.2.2. The Upper Bed Hammer Impact Modal Test
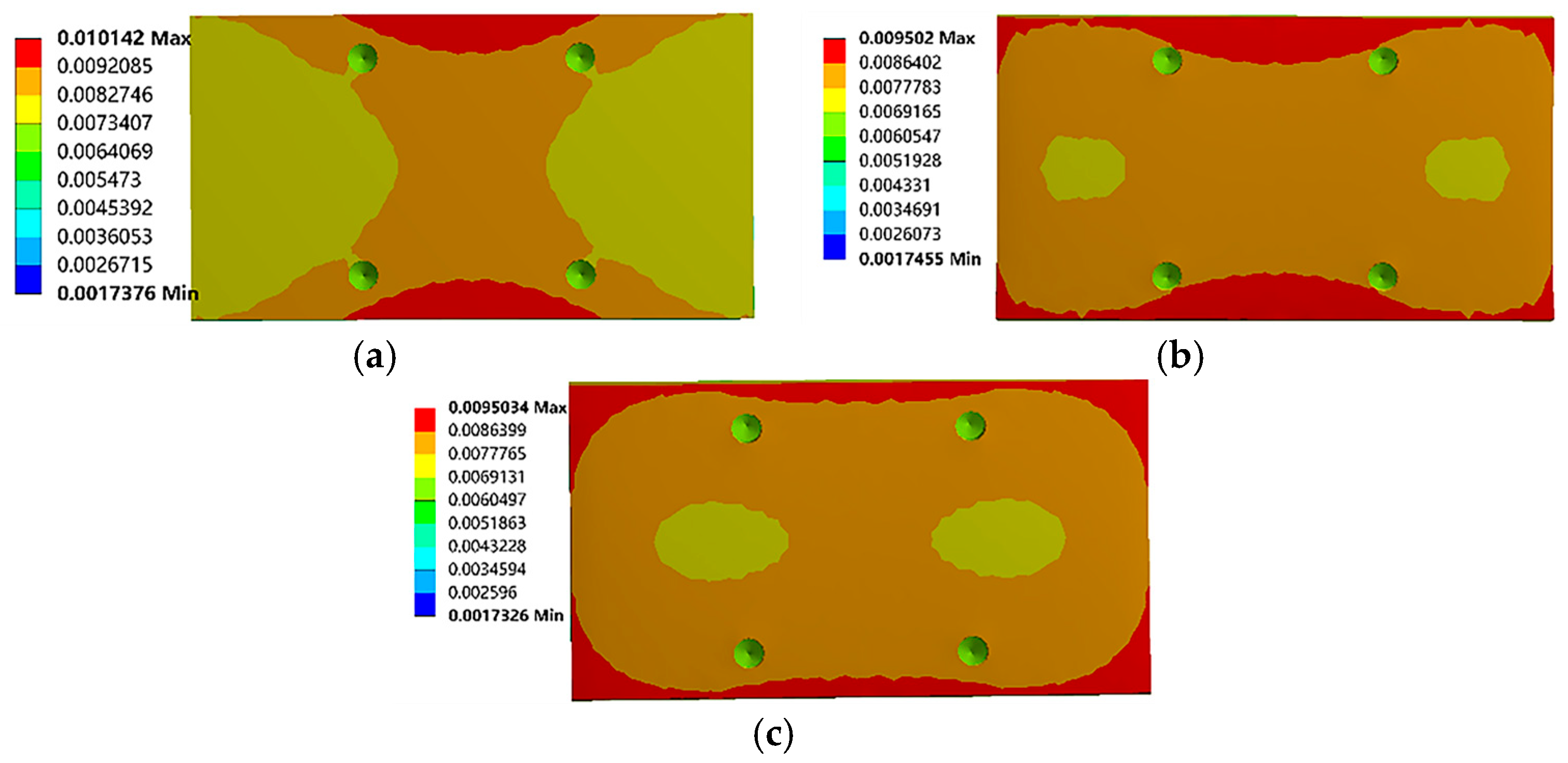
4.3. Comparative Analysis of the Load Uniformity of the Tested LRG
5. Experimental Verification
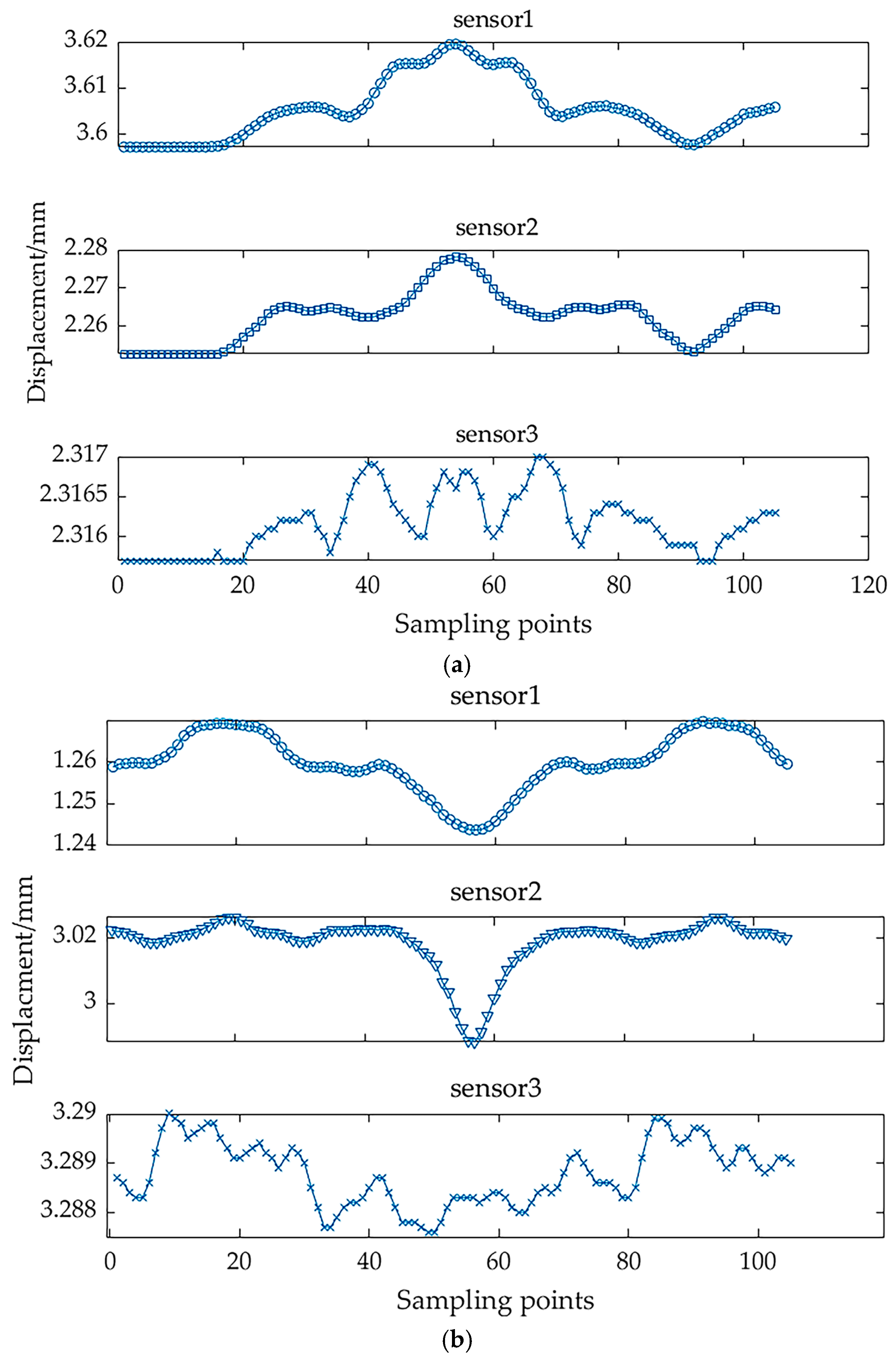
5.1. Verification of Motion Accuracy
5.2. Verification of PDF
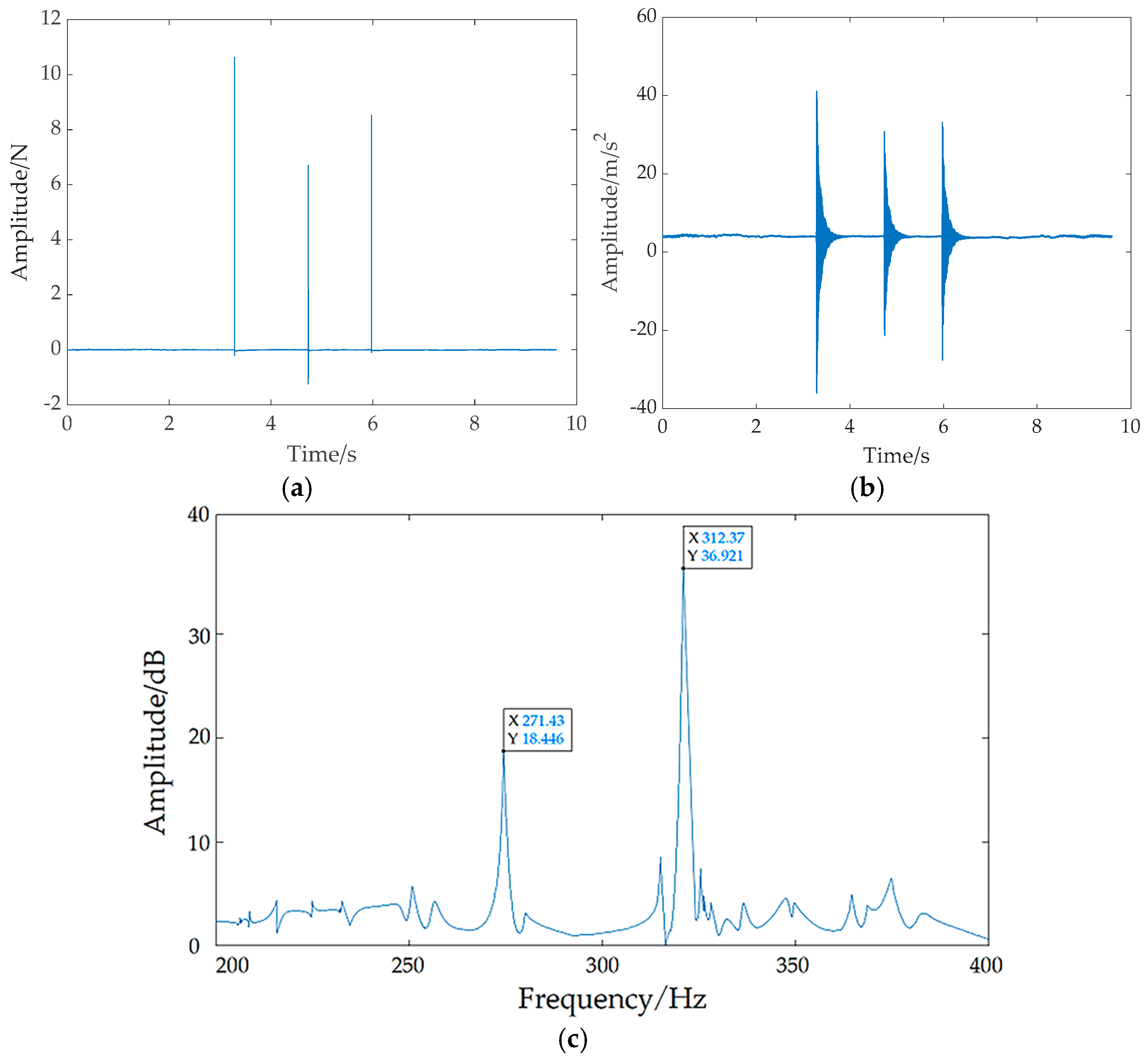
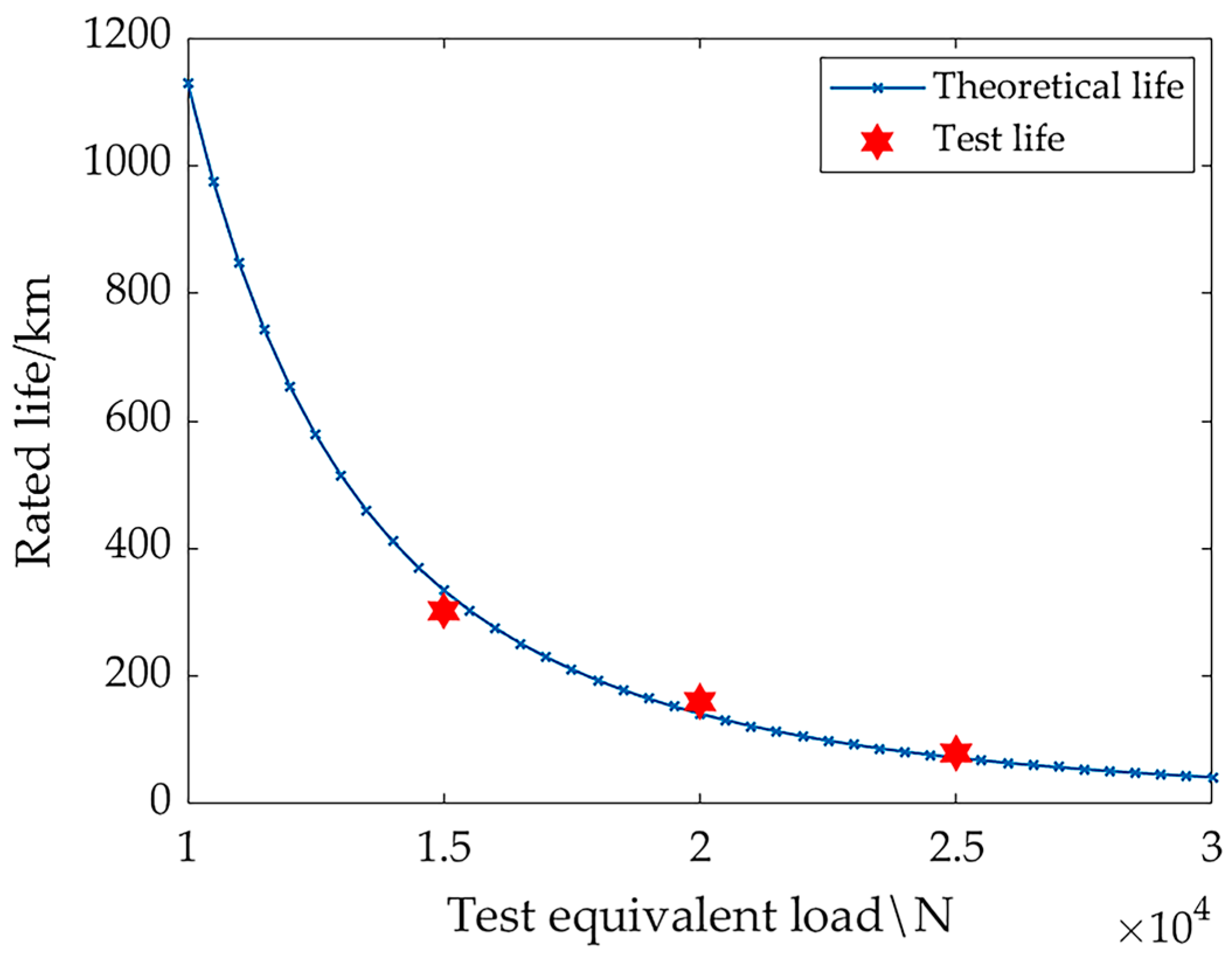
5.3. Verification of Fatigue Life
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, W.J.; Zhang, S.; Lin, J.H.; Jiang, S.N.; Wang, C.F. Stochastic Vibration Analysis for Linear Rolling Guide with Considering Geometric Errors. Nonlinear Dyn. 2024, 112, 19711–19733. [Google Scholar] [CrossRef]
- Liu, W.J.; Zhang, S.; Lin, J.H.; Jiang, S.N.; Chen, Z.Q.; Zhu, H.; Wang, C.F.; Liu, W.Y.; Cong, X.F. Investigation of static characteristics for linear rolling guide with considering geometric errors. Tribol. Int. 2023, 187. [Google Scholar] [CrossRef]
- Su, L.Y.; Zhang, C.H.; Yang, Z.J. Combined Thermal and Wear Analysis of Linear Rolling Guide Subjected to Rigid-Flexible Coupling Motion Stage. Machines 2023, 11, 358. [Google Scholar] [CrossRef]
- Lv, W. The Development and Prospect of by-products of Rolling Linear Guides. Metal Working (Metal Cutting) 2017, 06, 10–14. [Google Scholar]
- Yu, H.; Ran, Y.; Zhang, G.; Ying, G. A dynamic time-varying reliability model for linear guides considering wear degradation. Nonlinear Dynam. 2021, 103, 699–714. [Google Scholar] [CrossRef]
- Xu, D.; Liang, Y.; Feng, H. Design of Test and Control System for Comprehensive Performance Test bed of Rolling Linear Guide. Mach. Build. Autom. 2016, 45, 202–205. [Google Scholar]
- Wang, X.; Liang, Y.; Pei, J.; Wang, K.; Feng, H. Design of Test Bech for Motion Accuracy of Rolling Linear Guide Pair. Mod. Mach. Tool Autom. Manuf. Tech. 2021, 08, 62–65. [Google Scholar]
- Xu, H. Research on the Design and Test Method of the Life Test Bench for Rolling Linear Guide Pairs. Master’s Thesis, Nanjing University of Science and Technology, Nanjing, China, 2014. [Google Scholar]
- Li, C.; Feng, H.; Zhao, J. The Design of Dynamic Friction Measure System of Rolling Linear Guides. Manuf. Technol. Mach. Tool 2009, 9, 25–28. [Google Scholar]
- Li, D.L.; Yang, X.; Zhang, Y.; Zhang, Y.; Wang, Z.Y.; Shao, Y.Q. Development and Experimental Research on Resistance Force Measurement Equipment for Space Rolling Linear Guide. J. Nanjing Univ. Aeronaut. Astronaut. 2022, 54, 34–40. [Google Scholar]
- Zhou, Y. Comprehensive Performance Evaluation Method and Experimental Research of Rolling Linear Guide Pairs. Master’s Thesis, Nanjing University of Science and Technology, Nanjing, China, 2018. [Google Scholar]
- Qiu, Y.; Yan, R.J.; Lei, J.J.; Li, G.R.; Shen, W.; Hu, Y.Y. Ultimate Bearing Capacity and Fatigue Life Analysis of Marine Sandwich Composite Bolted Connection Structure: Fatigue Test and Numerical Simulation. Mar. Struct. 2025, 101, 103770. [Google Scholar] [CrossRef]
- Shi, C.; Wang, Z.; Peng, Y. Influence of Relative Difference Between Paired Guide Rails on Motion Accuracy in Closed Hydrostatic Guideways. J. Mech. Sci. Technol. 2020, 34, 631–648. [Google Scholar] [CrossRef]
- Zhou, C.G.; Wang, X.Y.; Feng, H.T.; Ou, Y.; Zhou, H.X. Research on An Explicit Preload Calculation Method of Linear Rolling Guide THK-SHS35V. Chin. J. Mech. Eng. 2023, 59, 208–217. [Google Scholar]
- Pan, K.; Liang, Y.; Feng, H.T.; Zhou, C.G.; Wang, K. Life Evaluation of Rolling Linear Guide Based on Fatigue Accelerated Life Test. Mod. Mach. Tool Autom. Manuf. Tech. 2021, 05, 38–42. [Google Scholar]
- Palit, P.; Sri, P.; Gokarn, P.; Kumar, A.; Das, S. Rolling Contact Fatigue Failure Analysis of Ball Bearing in Gear Box. J. Fail. Anal. Prev. 2025, 25, 62–69. [Google Scholar] [CrossRef]
- Cheng, H.C.; Li, X.H.; Ma, G.H.; Shi, X.F.; Yang, Z. Fatigue Life and Fatigue Reliability Mechanism of Ball Bearings. J. Mech. 2024, 40, 79–94. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Wei, Y.; Kong, W.Y.; Zhang, W.P.; Guo, Z.; Sun, L.H.; Chen, Y. Failure Analyzes of High-strength Bolted Connection with Over-preload Tightening Torque under Double Shear Test. Structures 2025, 72, 108249. [Google Scholar] [CrossRef]
- Xie, K.; Cheng, L. A Novel Two-dimensional Hilbert Transform Method for Structural Vibration Measurement and Modal Analysis. Mech. Syst. Signal Process. 2025, 225, 112324. [Google Scholar] [CrossRef]
- Üngör, M.; Sen, O.T.; Yavuz, A.; Baykara, C. Feasibility Assessment of Novel Multi-Mode Camshaft Design Through Modal Analysis. Machines 2025, 13, 407. [Google Scholar] [CrossRef]
- Uttachee, C.; Punyakaew, S.; Mai, N.T.; Kamal, M.A.S.; Murakami, I.; Yamada, K. Dynamic Analysis and Resonance Control of a Tunable Pendulum Energy Harvester Using Cone-Based Continuously Variable Transmission. Machines 2025, 13, 365. [Google Scholar] [CrossRef]
- Lee, E.T.; Hong, Y.S.; Eun, H.C. Prediction of the Physical Properties of a Structural Member by the Impact Hammer Test. Sensors 2022, 22, 6762. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, G.; Wang, J. Modeling and Experimental Verification of Static and Dynamic Characteristics of The Linear Rolling Guideway. Proc. Inst. Mech. Eng. C-J. Mech. 2024, 238, 8012–8036. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhang, J.; Xie, F. Design and Experiment Research of RV Reducer Main Bearing Test Benches. Chin. Mech. Eng. 2025, 1–7. Available online: https://kns.cnki.net/kcms2/article/abstract?v=7qDgw1F_0HV98ulQfdC1TIrU849xaxmQ8pLa-fJOi-85zkhI6Wwq6CWr___zVpNogMb6YuCeyB-3j0a6bOcUz5F_7UfOMopHdQu7l45am6r5wI81PB34zF2hCIVeIg32DtvDLf-NpN-Ve9GAQxLwzzSE229HZbLuSs83IT6z3G-kKttXrrxsmw==&uniplatform=NZKPT&language=CHS (accessed on 7 July 2025).
- Wang, Z.Y.; Zhou, Y.; Liu, J.; Xu, Z.; Chen, M.M.; Gao, R.; He, S.J.; Li, F.Z. Fatigue Life Investigation of Rubber Bearing for Heavy Trucks: Optimal Design by Using Finite Element Method with Experimental Verification. Int. J. Fatigue 2024, 180, 108080. [Google Scholar] [CrossRef]
- ISO 14728-1; Rolling Bearings—Linear Motion Rolling Bearings—Part 1: Dynamic Load Ratings and Rating Life. International Organization for Standardization (ISO): Geneva, Switzerland, 2017.







| Test Type | Test Parameters | Yes/No Loading | Yes/No Dragging |
|---|---|---|---|
| Comprehensive performance test | Motion accuracy | No | Yes |
| Vibration | |||
| Temperature rise | |||
| Fatigue life test | Pitting/spalling size | Yes | Yes |
| Vibration | |||
| Temperature rise |
| Design Parameters | Value |
|---|---|
| Overall dimension (m) | 3.14 × 1.42 × 1.22 |
| Weight (kg) | 5113 |
| Maximum test speed (m/s) | 0.83 |
| Maximum acceleration (m/s2) | 8 |
| Maximum stroke (m) | 0.6 |
| Maximum force (kN) | 300 |
| Motion accuracy (mm/m) | 0.01/1000 |
| Speed/force accuracy (%) | 2% |
| Accuracy Level | Manual Measurement (mm) | Test Bench Measurement (mm) | Repeatability | Yes/No Conform to the Standard | ||
|---|---|---|---|---|---|---|
| P3 | Vertical parallelism | 0.012 | Vertical parallelism | 0.01362 | 86.5% | Yes |
| Horizontal parallelism | 0.01 | Horizontal parallelism | 0.01165 | 83.8% | Yes | |
| Tilt angle | — | Tilt angle | 4.68″ | — | Yes | |
| P4 | Vertical parallelism | 0.021 | Vertical parallelism | 0.01834 | 87.3% | Yes |
| Horizontal parallelism | 0.018 | Horizontal parallelism | 0.01588 | 88.2% | Yes | |
| Tilt angle | — | Tilt angle | 12.24″ | — | Yes | |
| Model | Standard Requirements (N) | Manual Measurement (N) | Test Bench Measurement (N) | Repeatability | ||
|---|---|---|---|---|---|---|
| LGD35 | 9.4 ± 1.5 | Light preload level | 10 | Light preload level | 9.8 | 98% |
| 13.9 ± 1.8 | Medium preload level | 15 | Medium preload level | 14.9 | 99.3% | |
| 21.3 ± 1.9 | Heavy preload level | 20 | Heavy preload level | 19.6 | 98% | |
| Model | Loading Force (N) | Theoretical Life (km) | Test Life (km) | Repeatability |
|---|---|---|---|---|
| LGD35 | 15,000 | 334.46 | 302.41 | 90.4% |
| 20,000 | 141.19 | 150.19 | 93.5% | |
| 25,000 | 72.19 | 79.66 | 89.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Wang, G.; Wang, P.; Han, J.; Lu, B.; Xue, M.; Hao, Z. Development and Experimental Verification of Multi-Parameter Test Bench for Linear Rolling Guide. Machines 2025, 13, 811. https://doi.org/10.3390/machines13090811
Zhao Y, Wang G, Wang P, Han J, Lu B, Xue M, Hao Z. Development and Experimental Verification of Multi-Parameter Test Bench for Linear Rolling Guide. Machines. 2025; 13(9):811. https://doi.org/10.3390/machines13090811
Chicago/Turabian StyleZhao, Yunbo, Guobiao Wang, Peng Wang, Junjun Han, Bingxian Lu, Mingming Xue, and Zhongji Hao. 2025. "Development and Experimental Verification of Multi-Parameter Test Bench for Linear Rolling Guide" Machines 13, no. 9: 811. https://doi.org/10.3390/machines13090811
APA StyleZhao, Y., Wang, G., Wang, P., Han, J., Lu, B., Xue, M., & Hao, Z. (2025). Development and Experimental Verification of Multi-Parameter Test Bench for Linear Rolling Guide. Machines, 13(9), 811. https://doi.org/10.3390/machines13090811







