High Disturbance-Resistant Speed Control for Permanent Magnet Synchronous Motors: A BPNN Self-Tuning Improved Sliding Mode Strategy Without Load Observer
Abstract
1. Introduction
- 1.
- Robust sliding surface design:The essence of SMC is designing a sliding surface such that the system state trajectory slides along this surface, thereby achieving system control. In the absence of disturbance observers, robust sliding surface design is critical, primarily involving integral sliding surfaces or higher-order sliding surfaces [23]. Sliding surfaces incorporating integral terms can effectively eliminate steady-state errors. Since integrators have a cumulative effect on persistent disturbances, they can indirectly compensate for the effects of load changes, thereby enhancing the system’s disturbance rejection capability [24,25]. Furthermore, due to the cumulative effect of the integral term on continuous interference, the system’s ability to resist interference from uncertainties and load changes is enhanced. Reference [26] proposes that the sliding surface of the double integral sliding mode controller (DISMC) uses a double integral of the tracking voltage error term, which effectively eliminates steady-state errors. High-order sliding mode control (HOSMC) can limit the impact of disturbances to the higher-order derivatives of the sliding surface, thereby forcing the system state onto the sliding surface in a shorter time and effectively reducing oscillations, while exhibiting stronger robustness against unmodeled dynamics and external disturbances [27]. Reference [28] proposes a fast high-order terminal sliding mode current controller, which improves the convergence speed of the system under interference, suppresses steady-state chatter, reduces oscillation, and enhances the system’s interference resistance robustness by designing the corresponding sliding surface and introducing nonlinear gain.
- 2.
- Improved SMC law:The SMC law determines how the system approaches and maintains the sliding surface, and its design directly affects the system’s disturbance rejection performance. For example, when using non-singular fast terminal sliding mode control (NFTSMC)/fast terminal sliding mode control (FTSMC), these methods aim to provide finite-time convergence, even ultra-fast convergence, thereby eliminating tracking errors in a shorter time. Due to the fast convergence speed, the system responds very quickly to transient disturbances (such as load shocks), able to quickly pull the speed back to the target value [29]. Reference [30] proposes a sliding surface that can completely eliminate singularities in controller inputs. Its key characteristics include rapid error convergence, high tracking accuracy, and robustness to disturbances. Additionally, incorporating an adaptive law into the SMC law allows the control gain to be dynamically adjusted based on system state or error, thereby addressing unknown disturbances and parameter uncertainties [31]. To improve the speed control performance of PMSM under internal and external disturbances, Reference [32] proposes a new adaptive terminal sliding mode tracking law (ATSMRL) and combines it with continuous fast terminal sliding mode control (CFTSMC). ATSMRL aims to reduce control input effort and dynamically provides advantages such as finite time convergence, high tracking accuracy, and reduced control input jitter. Reference [33] investigates an adaptive sliding mode (ASM) control scheme that constrains the displacement and pitch angle of the suspension system through a predefined performance function (PPF), combined with a highly robust integral terminal SMC method and neural networks to handle unknown terms.
- 3.
- Neural network estimation compensation method:Estimating disturbances using neural networks can also effectively suppress disturbances [34,35]. Integrating neural networks into sliding mode controllers can leverage their powerful nonlinear approximation capabilities to estimate and compensate for unknown disturbances [36,37]. Neural networks learn the patterns of disturbances and generate corresponding compensation signals, thereby indirectly suppressing their effects without explicitly observing the disturbances. Reference [38] proposes a radial basis function neural network adaptive sliding mode controller (RBF-NN ASMC). The controller uses a radial basis function neural network (RBF-NN) control algorithm to compensate for friction disturbance torque in electromechanical actuator systems. By adjusting the neural network weights through an adaptive law, real-time compensation for friction is achieved.
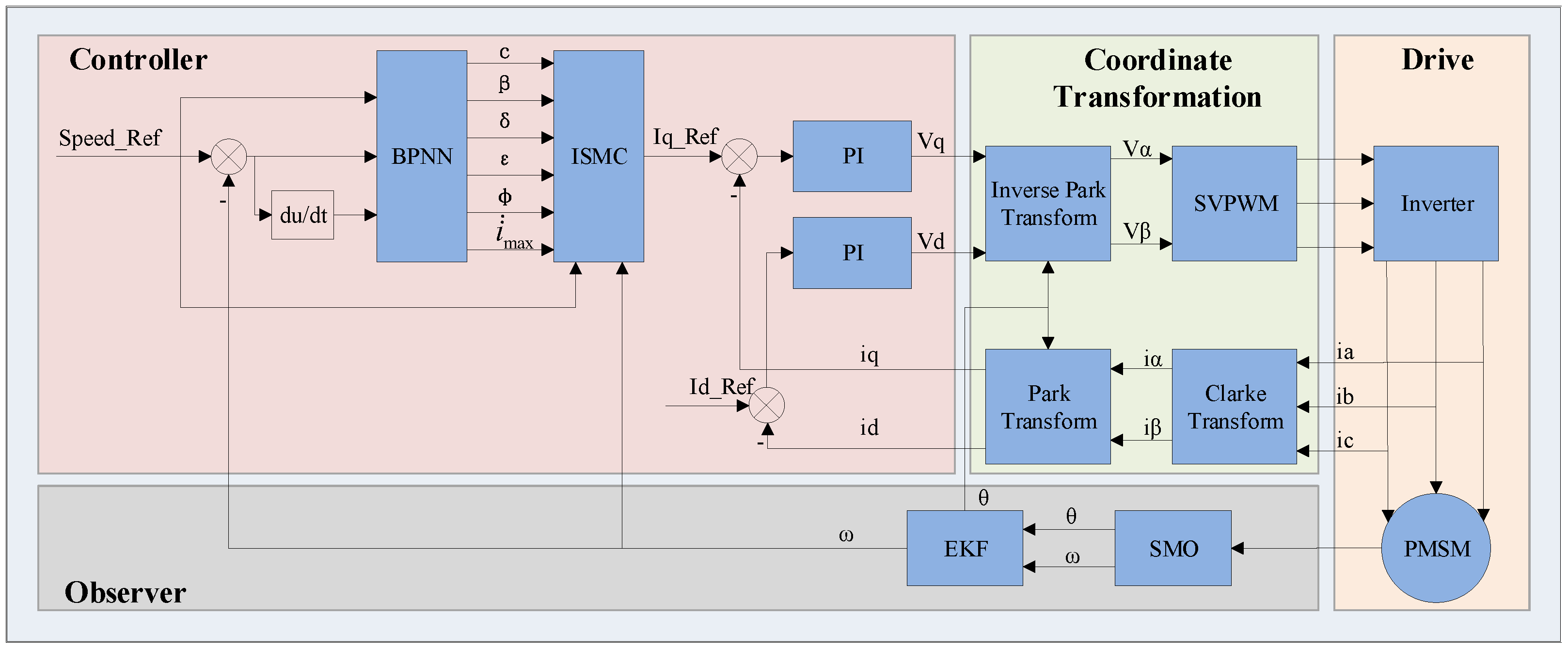
2. PMSM Vector Control
2.1. PMSM Mathematical Model
2.2. Vector Control Principle
3. Improved Sliding Mode Controller Design
3.1. Sliding Mode Controller
3.2. Current Overshoot Suppression
3.3. S-Curve Speed Smoothing Method
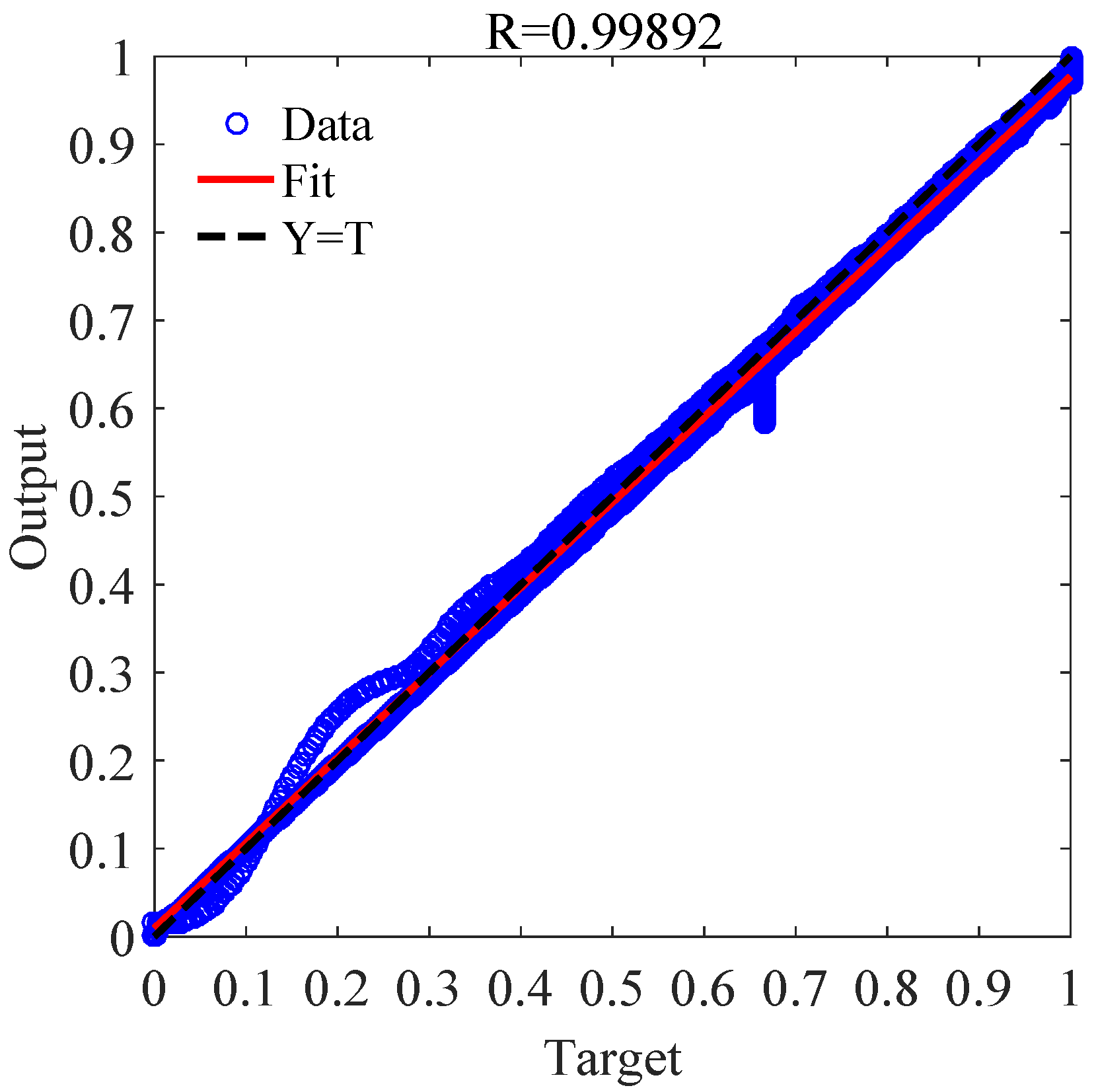
4. BPNN Design
5. Sliding Mode Observer
5.1. Back EMF Estimation
5.2. Rotor Position Estimation
6. Simulation Experiments and Analysis
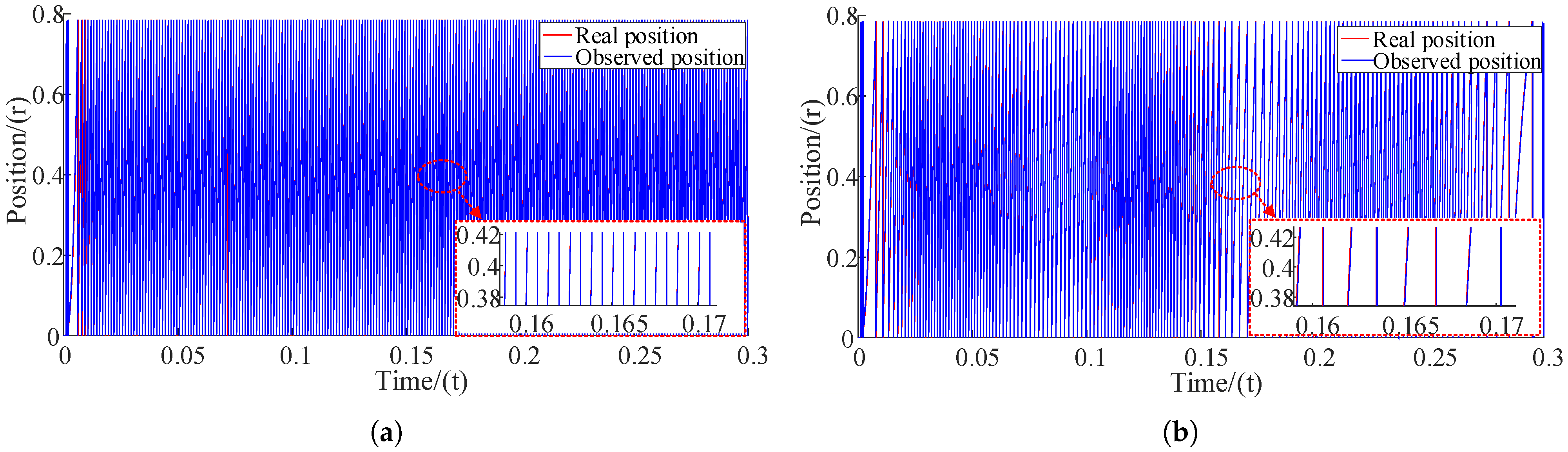
6.1. Rotor Position Observation
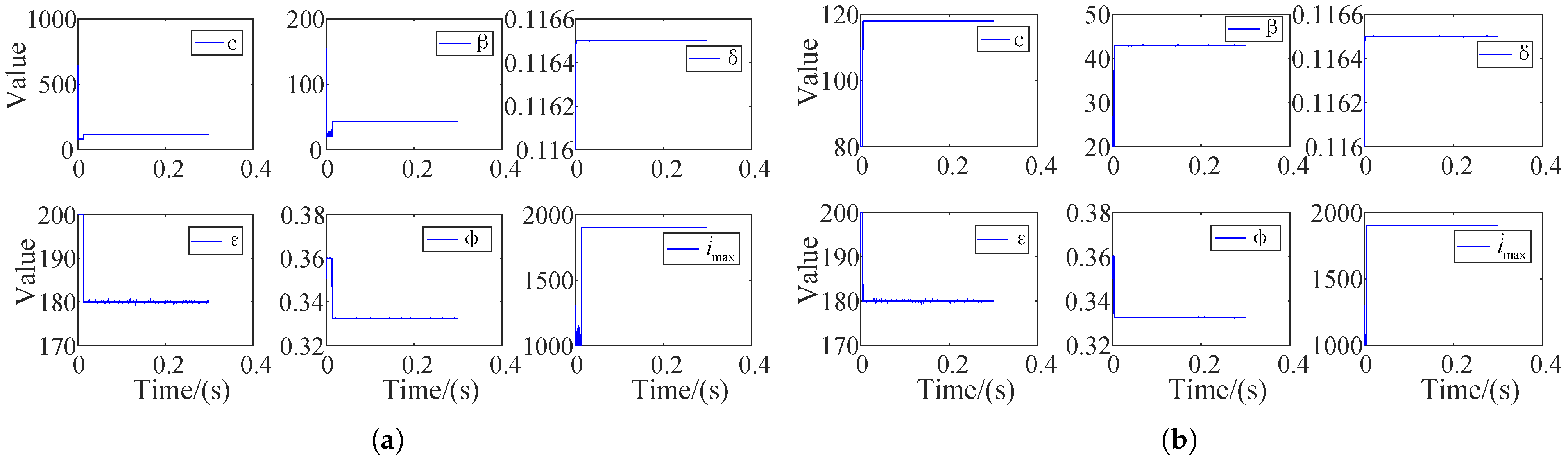
6.2. Controller Parameter Adjustment
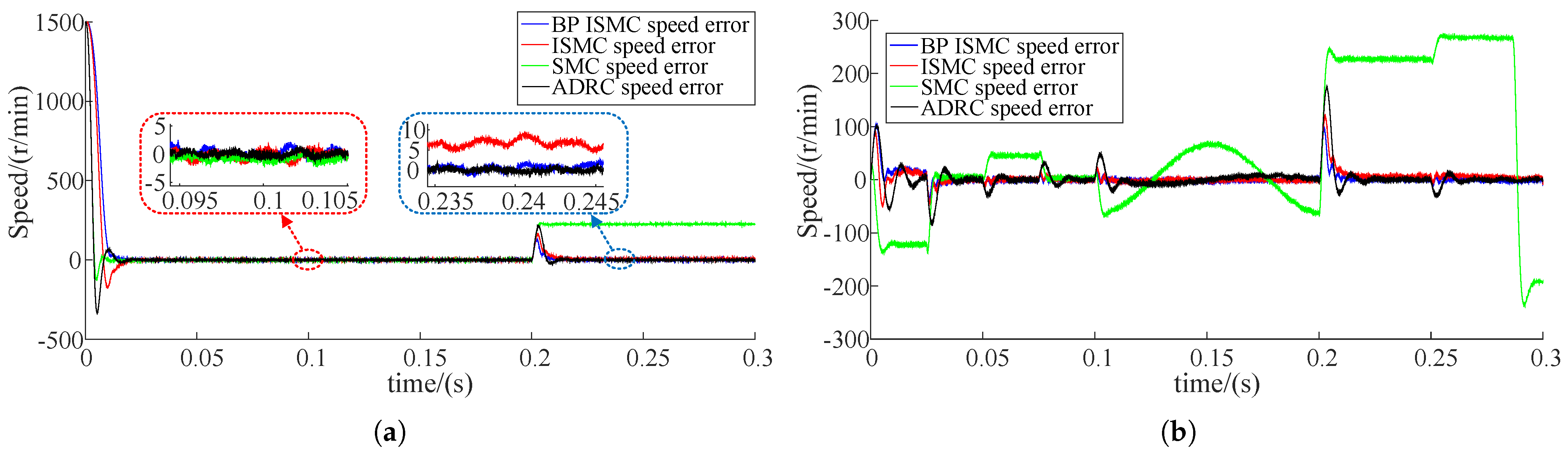
6.3. Motor Output Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, G.; Valla, M.; Solsona, J. Position sensorless permanent magnet synchronous machine drives—A review. IEEE Trans. Ind. Electron. 2019, 67, 5830–5842. [Google Scholar] [CrossRef]
- König, P.; Sharma, D.; Konda, K.R.; Xie, T.; Höschler, K. Comprehensive review on cooling of permanent magnet synchronous motors and their qualitative assessment for aerospace applications. Energies 2023, 16, 7524. [Google Scholar] [CrossRef]
- Geng, H.; Zhang, X.; Yan, S.; Zhang, Y.; Wang, L.; Han, Y.; Wang, W. Magnetic Field Analysis of an Inner-Mounted Permanent Magnet Synchronous Motor for New Energy Vehicles. Energies 2022, 15, 4074. [Google Scholar] [CrossRef]
- Xia, X.; Zhang, B.; Li, X. High precision low-speed control for permanent magnet synchronous motor. Sensors 2020, 20, 1526. [Google Scholar] [CrossRef]
- He, Q.; Yang, Y.; Luo, C.; Zhai, J.; Luo, R.; Fu, C. Energy recovery strategy optimization of dual-motor drive electric vehicle based on braking safety and efficient recovery. Energy 2022, 248, 123543. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Sun, Z.Y.; Chen, C.C. A New Adaptive Control Design of Permanent Magnet Synchronous Motor Systems with Uncertainties. Symmetry 2025, 17, 2. [Google Scholar] [CrossRef]
- Guo, H.; Xiang, T.; Liu, Y.; Zhang, Q.; Liu, S.; Guan, B. Active Disturbance Rejection Control Method for Marine Permanent-Magnet Propulsion Motor Based on Improved ESO and Nonlinear Switching Function. J. Mar. Sci. Eng. 2023, 11, 1751. [Google Scholar] [CrossRef]
- Wang, S.; Doki, S.; Suzuki, T.; Fujii, K.; Hayashi, Y. Decoupled current vector control of dual three phase PMSM drives with two independent micro control units utilizing current observer. IEEJ J. Ind. Appl. 2022, 11, 779–789. [Google Scholar] [CrossRef]
- Valencia, D.F.; Tarvirdilu-Asl, R.; Garcia, C.; Rodriguez, J.; Emadi, A. A review of predictive control techniques for switched reluctance machine drives. Part I: Fundamentals and current control. IEEE Trans. Energy Convers. 2020, 36, 1313–1322. [Google Scholar] [CrossRef]
- Ye, L.; Lu, P.; Zhao, Y.; Dai, B.; Tang, Y. Review of model predictive control for power system with large-scale wind power grid-connected. Proc. CSEE 2021, 41, 6181–6198. [Google Scholar]
- Li, T.; Sun, X.; Lei, G.; Guo, Y.; Yang, Z.; Zhu, J. Finite-control-set model predictive control of permanent magnet synchronous motor drive systems—An overview. IEEE/CAA J. Autom. Sin. 2022, 9, 2087–2105. [Google Scholar] [CrossRef]
- Concari, L.; Toscani, A.; Barater, D.; Concari, C.; Degano, M.; Pellegrino, G. Comparison of flux observers for sensorless control of permanent magnet assisted SynRel motors. In Proceedings of the IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016. [Google Scholar]
- Lakhe, R.K.; Chaoui, H.; Alzayed, M.; Liu, S. Universal control of permanent magnet synchronous motors with uncertain dynamics. Actuators 2021, 10, 49. [Google Scholar] [CrossRef]
- Kolano, K. New method of vector control in PMSM motors. IEEE Access 2023, 11, 43882–43890. [Google Scholar] [CrossRef]
- Xu, X.Y.; Li, Y.Z. Vector Control of Permanent Magnet Synchronous Motor Based on MRAS Method. Int. J. Multiphysics 2022, 16, 119. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, H.; Chien, Y.R.; Tang, J. Vector control of permanent magnet synchronous motor drive system based on new sliding mode control. IEICE Electron. Express 2023, 20, 20230263. [Google Scholar] [CrossRef]
- Achour, H.B.; Ziani, S.; Chaou, Y.; El Hassouani, Y.; Daoudia, A. Permanent magnet synchronous motor PMSM control by combining vector and PI controller. WSEAS Trans. Syst. Control 2022, 17, 244–249. [Google Scholar] [CrossRef]
- Sakunthala, S.; Kiranmayi, R.; Mandadi, P.N. A review on speed control of permanent magnet synchronous motor drive using different control techniques. In Proceedings of the 2018 International Conference on Power, Energy, Control and Transmission Systems (ICPECTS), Chennai, India, 22–23 February 2018. [Google Scholar]
- Shu, S.; Zhang, Y.; Wang, X.; Pan, Q.; Tao, X. Space vector control of a permanent magnet linear synchronous motor based on the improved single neuron PID algorithm. J. Control Eng. Appl. Inform. 2020, 22, 74–84. [Google Scholar]
- Ishwarya, U.; Srimathi, R.; Nithishkumar, K.; Chandrakala, K.R.M.V.; Saravanan, S.; Shankar, V.K.A. Optimum Speed Control of Permanent Magnet Synchronous Motor using Artificial Neural Network-Based Field-Oriented Controller. In Proceedings of the 2024 3rd International Conference on Artificial Intelligence For Internet of Things (AIIoT), Vellore, India, 3–4 May 2024. [Google Scholar]
- Fatemimoghadam, A.; Yan, Y.; Iyer, L.V.; Kar, N.C. Permanent magnet synchronous motor drive using deep-neural-network-based vector control for electric vehicle applications. In Proceedings of the 2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 5–8 September 2022. [Google Scholar]
- Luo, Y.C.; Huang, H.Y.; Chen, B.W.; Kuo, Y.P. Vector-controlled Permanent Magnet Synchronous Motor Drive Speed Identification Using General Regression Neural Network. Sens. Mater. 2023, 35, 1587–1598. [Google Scholar] [CrossRef]
- Jadhav, I.S.; Malwatkar, G.M. Optimal and higher order sliding mode control for systems with disturbance rejection. In Applied Information Processing Systems: Proceedings of ICCET 2021; Springer: Singapore, 2021; pp. 563–574. [Google Scholar]
- Hua, T.; Zhang, H.; Xie, K. Robust sliding mode control of offshore parallel platform. In Proceedings of the 2019 4th International Conference on Automation, Control and Robotics Engineering, Shenzhen, China, 19–21 July 2019. [Google Scholar]
- Niu, S.; Chen, W.H.; Lu, X. Sliding mode control with integral sliding surface for linear uncertain impulsive systems with time delays. Appl. Math. Model. 2023, 113, 439–455. [Google Scholar] [CrossRef]
- Pradhan, R.; Subudhi, B. Double integral sliding mode MPPT control of a photovoltaic system. IEEE Trans. Control Syst. Technol. 2015, 24, 285–292. [Google Scholar] [CrossRef]
- Ren, H.; Zhang, L.; Su, C. Adaptive super twisting sliding mode control with fractional order sliding surface for trajectory tracking of a mobile robot. J. Control Sci. Eng. 2020, 2020, 1–13. [Google Scholar]
- Wang, T.; Wang, B.; Yu, Y.; Xu, D. Fast high-order terminal sliding-mode current controller for disturbance compensation and rapid convergence in induction motor drives. IEEE Trans. Power Electron. 2023, 38, 9593–9605. [Google Scholar] [CrossRef]
- Kong, X.; Zhang, T. Non-singular fast terminal sliding mode control of high-speed train network system based on improved particle swarm optimization algorithm. Symmetry 2020, 12, 205. [Google Scholar] [CrossRef]
- Kim, Y.; Ahn, H.; Hu, M.; You, K. Improved non-singular fast terminal sliding mode control for SPMSM speed regulation. IEEE Access 2023, 11, 65924–65933. [Google Scholar] [CrossRef]
- Roy, S.; Baldi, S.; Fridman, L.M. On adaptive sliding mode control without a priori bounded uncertainty. Automatica 2020, 111, 108650. [Google Scholar] [CrossRef]
- Junejo, A.K.; Xu, W.; Mu, C.; Ismail, M.M.; Liu, Y. Adaptive speed control of PMSM drive system based a new sliding-mode reaching law. IEEE Trans. Power Electron. 2020, 35, 12110–12121. [Google Scholar] [CrossRef]
- Liu, Y.J.; Chen, H. Adaptive sliding mode control for uncertain active suspension systems with prescribed performance. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 6414–6422. [Google Scholar] [CrossRef]
- Yi, Y.; Zheng, W.X.; Liu, B. Adaptive anti-disturbance control for systems with saturating input via dynamic neural network disturbance modeling. IEEE Trans. Cybern. 2020, 52, 5290–5300. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, X.; Wu, Y.; Cai, H.; Yokoi, H. Adaptive neural network control of a flexible spacecraft subject to input nonlinearity and asymmetric output constraint. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6226–6234. [Google Scholar] [CrossRef]
- Wen, Q.; Yang, X.; Huang, C.; Zeng, J.; Yuan, Z.; Liu, P.X. Disturbance observer-based neural network integral sliding mode control for a constrained flexible joint robotic manipulator. Int. J. Control. Autom. Syst. 2023, 21, 1243–1257. [Google Scholar] [CrossRef]
- Song, P.; Yang, Q.; Li, D.; Wen, G.; Zhang, Z.; Peng, J. Disturbance-compensation-based predictive sliding mode control for aero-engine networked systems with multiple uncertainties. IEEE Trans. Autom. Sci. Eng. 2024, 22, 276–292. [Google Scholar] [CrossRef]
- Ruan, W.; Dong, Q.; Zhang, X.; Li, Z. Friction compensation control of electromechanical actuator based on neural network adaptive sliding mode. Sensors 2021, 21, 1508. [Google Scholar] [CrossRef] [PubMed]
- Aziz, A.G.M.A.; Abdelaziz, A.Y.; Ali, Z.M.; Diab, A.A.Z. A comprehensive examination of vector-controlled induction motor drive techniques. Energies 2023, 16, 2854. [Google Scholar] [CrossRef]
- Mohanraj, D.; Gopalakrishnan, J.; Chokkalingam, B.; Mihet-Popa, L. Critical aspects of electric motor drive controllers and mitigation of torque ripple. IEEE Access 2022, 10, 73635–73674. [Google Scholar] [CrossRef]
- Ho, C.H.; Hwang, J.C. Design of Small Permanent-Magnet Linear Motors and Drivers for Automation Applications with S-Curve Motion Trajectory Control and Solutions for End Effects and Cogging Force. Energies 2024, 17, 5719. [Google Scholar] [CrossRef]
- Malgaca, L.; Lök, Ş.İ. Measurement and modeling of a flexible manipulator for vibration control using five-segment S-curve motion. Trans. Inst. Meas. Control 2022, 44, 1545–1556. [Google Scholar] [CrossRef]


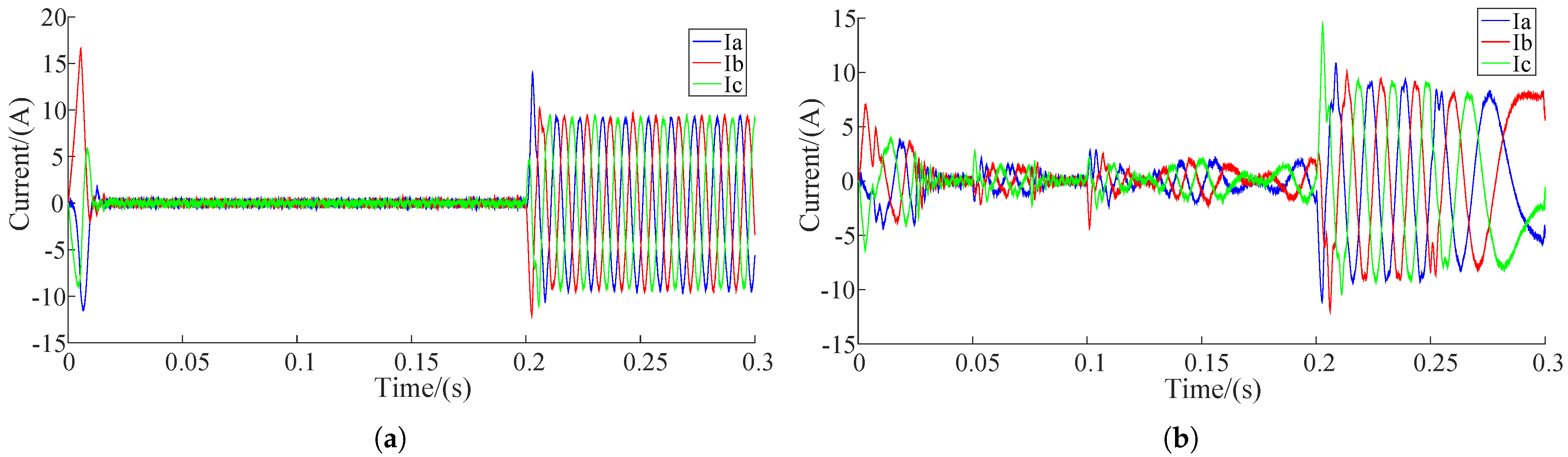
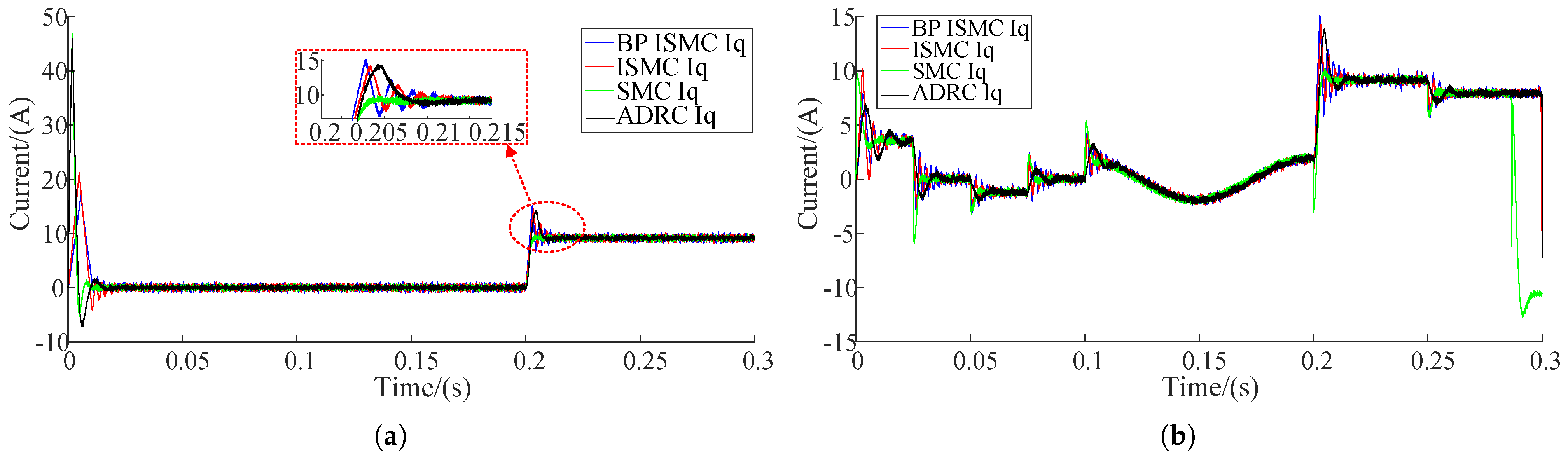
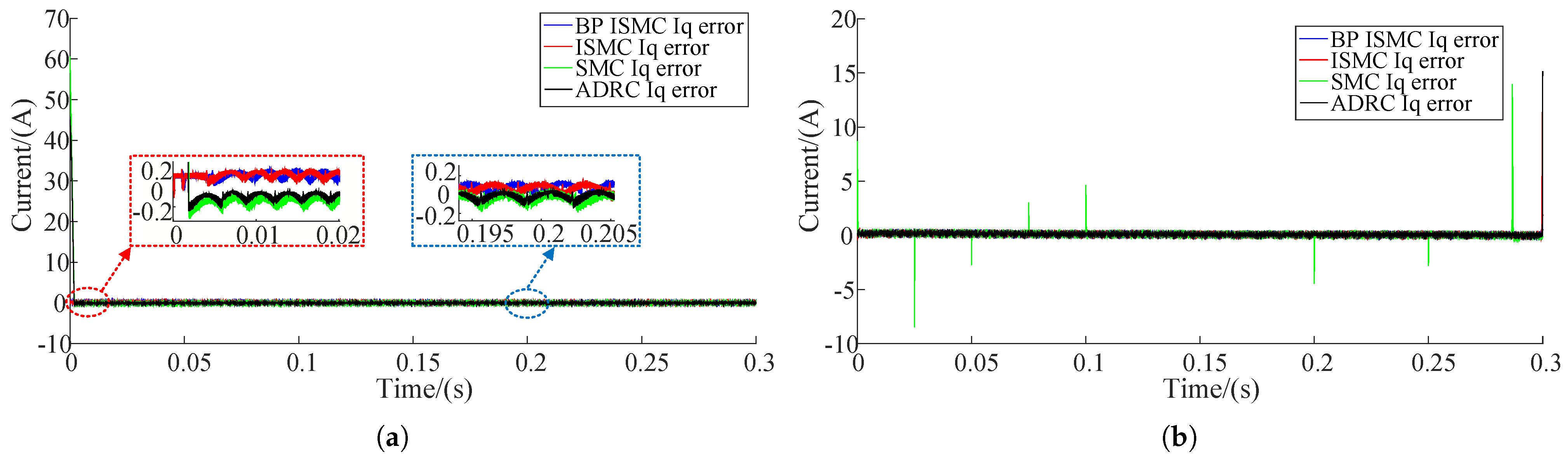
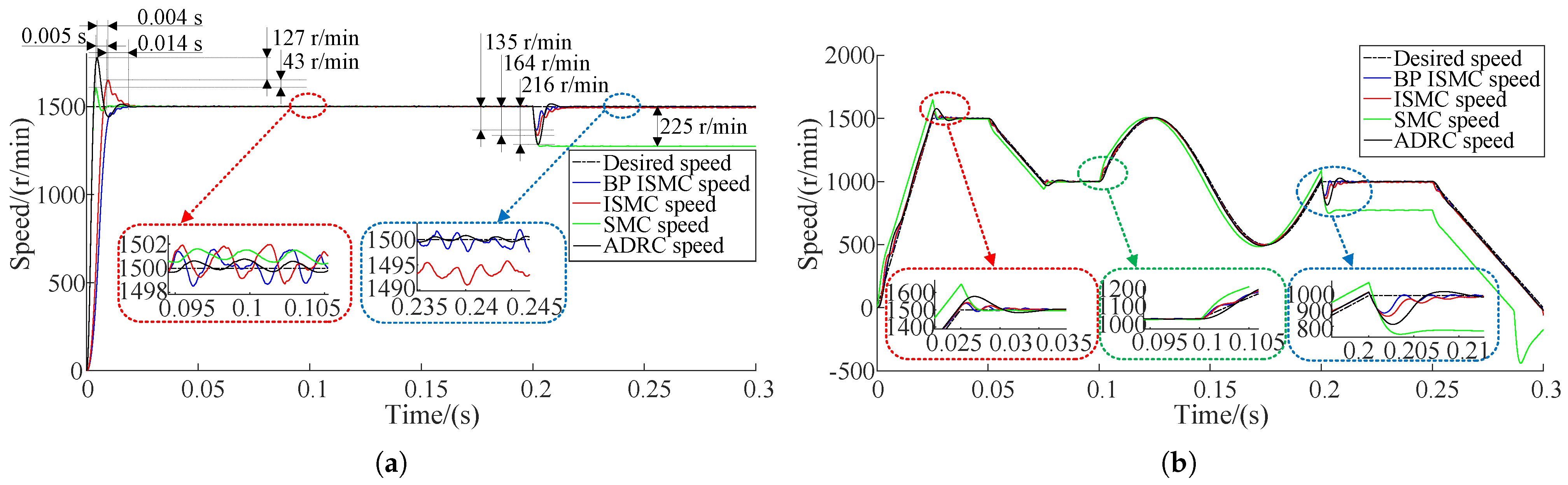
| Parameter Type | Value |
|---|---|
| Rated Voltage | 300 Vdc |
| Rated Torque | 8 N · m |
| Rated Speed | 2000 rpm |
| Operating Frequency | 100 Hz |
| Number of Phases | 3 |
| Pole Pairs | 4 |
| Stator Resistance | 0.9585 |
| Stator Inductance | 0.00525 H |
| Permanent Magnet Flux Linkage | 0.1827 Wb |
| Moment of Inertia | 0.0006329 kg · m2 |
| Parameter Type | Value |
|---|---|
| S-curve Velocity Smoothing Time | 0.01 s |
| d-Axis Proportional Coefficient | 5 |
| d-Axis Integral Coefficient | 3 |
| q-Axis Proportional Coefficient | 5 |
| q-Axis Integral Coefficient | 30 |
| ISMC Initial Parameters c | 110 |
| ISMC Initial Parameters | 27 |
| ISMC Initial Parameters | 0.116 |
| ISMC Initial Parameters | 190 |
| ISMC Initial Parameters | 0.35 |
| Maximum Rate of Change of Current | 1300 |
| Base Learning Rate | 0.0005 |
| Momentum Coefficient | 0.95 |
| Amplification Factor | 300 |
| Cutoff Frequency of Low-Pass Filter | 1000 |
| Load Torque | 10 N · m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huo, Y.; Zhang, C.; Gao, Q.; Yang, T.; Ren, L. High Disturbance-Resistant Speed Control for Permanent Magnet Synchronous Motors: A BPNN Self-Tuning Improved Sliding Mode Strategy Without Load Observer. Machines 2025, 13, 810. https://doi.org/10.3390/machines13090810
Huo Y, Zhang C, Gao Q, Yang T, Ren L. High Disturbance-Resistant Speed Control for Permanent Magnet Synchronous Motors: A BPNN Self-Tuning Improved Sliding Mode Strategy Without Load Observer. Machines. 2025; 13(9):810. https://doi.org/10.3390/machines13090810
Chicago/Turabian StyleHuo, Yuansheng, Chengwei Zhang, Qing Gao, Tao Yang, and Lirong Ren. 2025. "High Disturbance-Resistant Speed Control for Permanent Magnet Synchronous Motors: A BPNN Self-Tuning Improved Sliding Mode Strategy Without Load Observer" Machines 13, no. 9: 810. https://doi.org/10.3390/machines13090810
APA StyleHuo, Y., Zhang, C., Gao, Q., Yang, T., & Ren, L. (2025). High Disturbance-Resistant Speed Control for Permanent Magnet Synchronous Motors: A BPNN Self-Tuning Improved Sliding Mode Strategy Without Load Observer. Machines, 13(9), 810. https://doi.org/10.3390/machines13090810






