A Hybrid Approach Based on a Windowed-EMD Temporal Convolution–Reallocation Network and Physical Kalman Filtering for Bearing Remaining Useful Life Estimation
Abstract
1. Introduction
- Data-driven methods: These approaches utilize statistical techniques or machine learning algorithms, e.g., the Markov process, Kalman filter, Wiener process, or particle filter, to model degradation processes [15]. While effective, large amounts of monitoring information render it difficult to capture complex mapping using statistical distributions [16].
- Direct approach: In this approach, the model employs an end-to-end prediction strategy by integrating the feature extraction step directly into the model framework. For instance, Xia et al. [20] propose a Long Short-Term Memory (LSTM) neural network to provide prognostics. This method segments time sequence data through sliding windows and applies the LSTM model to extract features and predict the RUL for each window. Similarly, Wang et al. [21] introduced a Deep Separable Convolutional Neural Network (DSCN) approach to process overlapping sampling windows for RUL prediction directly. The above methods use a model to segment the raw signal data and obtain a large number of windows mapped to RUL, solving specific nonlinear problems. The model must be capable of dynamically adjusting to large volumes of windowed data, which increases the computation complexity of training.
- Hybrid approach: This approach can flexibly process physically meaningful features based on the characteristics of the signal, and then evaluate HI, in a total of two steps. For example, Chen et al. [22] propose a hybrid method to provide prognostics that combine five bandpass energy values from the frequency spectrum with an attention-based recurrent neural network (RNN) for further prediction. Similarly, Guo et al. [23] propose a health indicator (RNN-HI), which includes correlation similarity features and classical time-domain features based on recurrent neural networks. Moreover, Zhou et al. [24] also introduce a hybrid approach, transformer (TRM), to perform RUL tasks based on 14 time-domain features. Furthermore, Cao et al. [25] propose TCN-RSA, which employs causal dilated convolutions to capture long-term dependencies and extract high-level features from the time-frequency domain, incorporating residual self-attention mechanisms to obtain feature contributions at different time steps during bearing degradation. Additionally, Liu et al. [26] propose a hybrid framework that combines temporal convolutional networks (TCNs) and LSTM networks with a Convolutional Block Attention Module (CBAM) for multi-dimensional feature weighting. In short, the above methods have been proven to be effective in prognostics. This can reduce the parameters and increase calculation speed, but it may face challenges when it comes to dealing with high interference noise and complicated mapping over long distances [27].
- Physics-informed hybrid approach: This emerging paradigm integrates physical degradation laws and domain knowledge into data-driven models to enhance prediction reliability and interpretability. Specifically, Lu et al. [28] integrate physical consistency constraints into the LSTM loss function to ensure predictions comply with monotonic degradation laws. Similarly, Yang et al. [29] utilize dynamic adaptive IDFT frequency domain blocks with multi-state memory units for physics-constrained time–frequency fusion prediction. Furthermore, Hu et al. [30] combine separable convolutional feature extraction with physics-informed neural networks, learning implicit physical degradation patterns while incorporating physics constraint losses. Collectively, these methods address the black-box nature of data-driven approaches by incorporating physical principles, thereby enhancing model interpretability and prediction reliability. Nevertheless, they may face challenges in modeling complex real-world physical relationships and require domain expertise for proper constraint formulation.
- Vibration signals are monitored and analyzed, providing comprehensive degradation information. The feature engineering method is an adjustable windowed EMD time-domain feature extraction method, and its purpose is to convert the denoised vibration signals into TIR-sequences as the input. Moreover, experimental validation demonstrates that this method is feasible for characteristic degradation.
- A one-dimensional temporal convolution model (TFCR) is combined to extract hidden features from TIR-sequences and construct RUL. Specifically, the proposed model employs a causal convolution architecture in the time dimension to preserve temporal information. In parallel, a bottleneck top–down design is used in the channel dimension, with channel weight reallocation at the final stage. It can ensure that channel compression does not lead to a significant loss of critical features. Experimental results also demonstrate that it can address bearing life prediction tasks with high accuracy and efficiency.
- The TFCR model combines flexible configuration to select the most appropriate model, thereby adapting to complex working conditions with different data distributions. Then, TFCR is combined with physics-based Kalman filtering to improve estimation stability.
2. The TIR Sequences for the Temporal Degradation Model
2.1. The Temporal Degradation Model
2.2. The TIR Sequences Extraction Method Based on Windowed EMD
- Step 1: Divide the vibration signal at each time node into adjustable, non-overlapping time windows, and apply EMD to decompose the denoised signal into intrinsic mode functions (IMFs) and residual function (RES).
- Step 2: Extract time-domain features from the IMFs and RES within each window, and concatenate them to form a feature vector representing that time node.
- Step 3: Arrange these feature vectors chronologically to construct a complete TIR-sequence with temporal and feature dimensions.
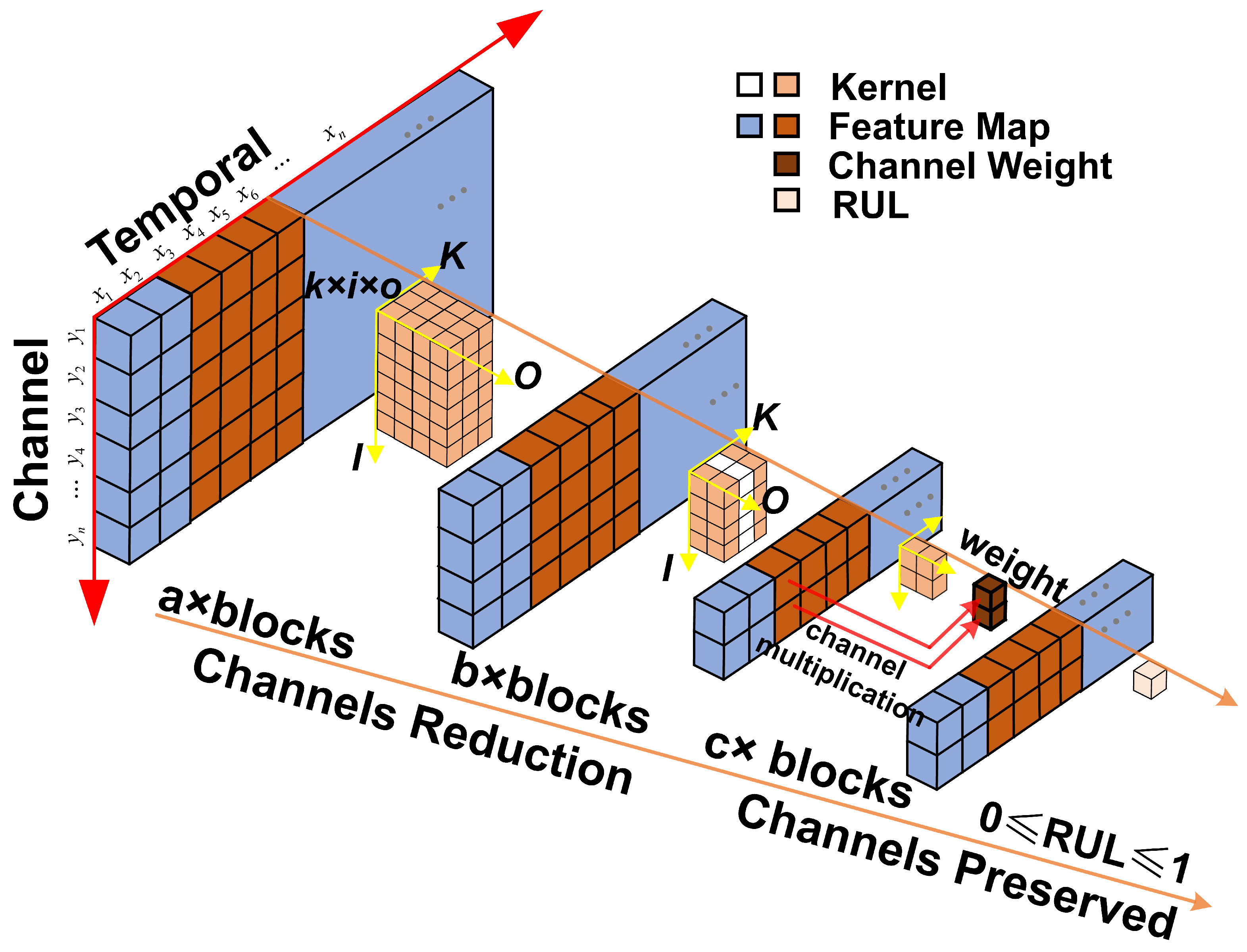
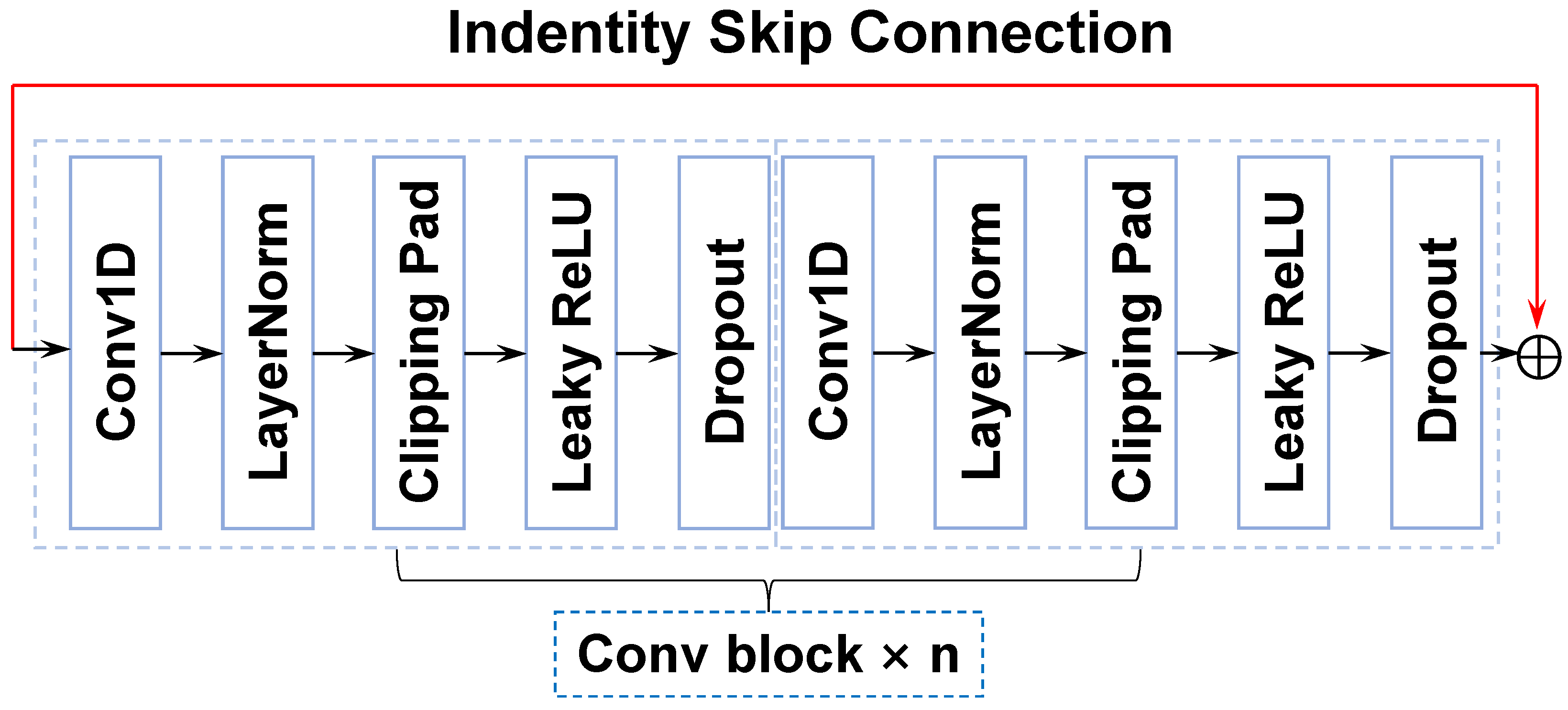
3. The TFCR Model Architecture
3.1. Temporal Feature Compression Layer
3.2. Channel Weight Redistribution Layer
4. The Implementation of RUL Estimation
4.1. Data Preparation and Flexible TFCR Scheme
4.2. Physics-Based Kalman Filtering for RUL Refinement
5. Experimental Evaluation of the Proposed RUL Estimation Approach
5.1. Introduction to the XJTU-SY Dataset
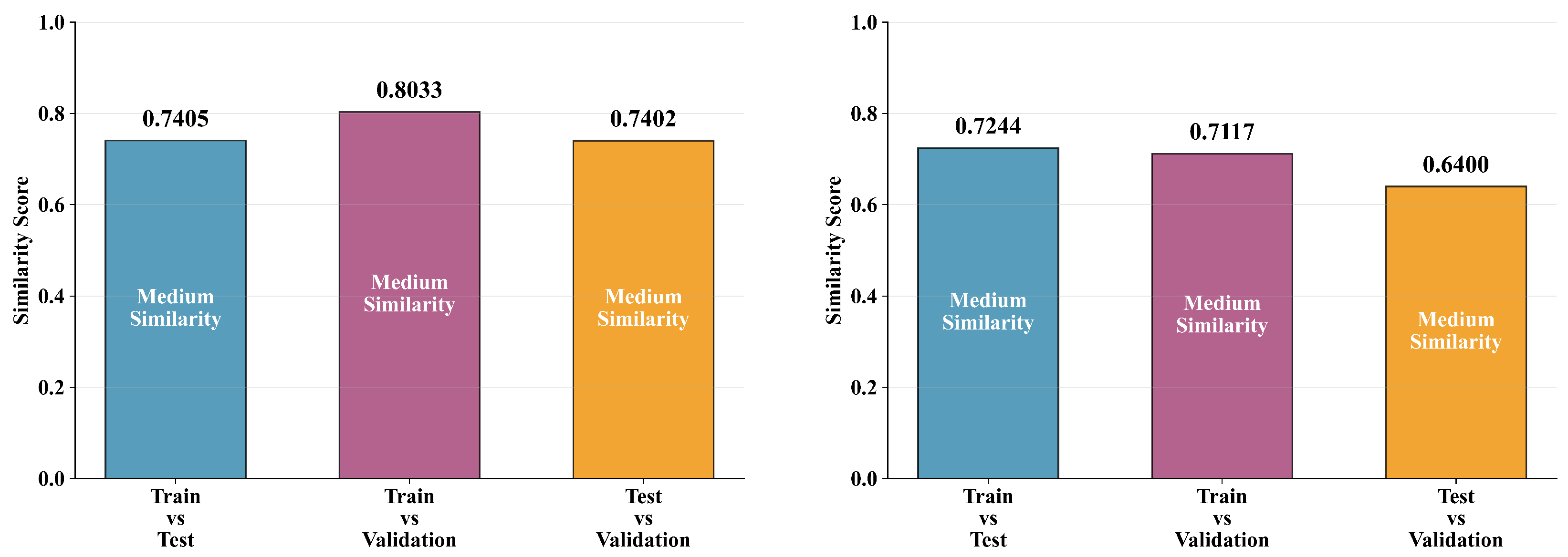
5.2. Training Strategy in Experiment
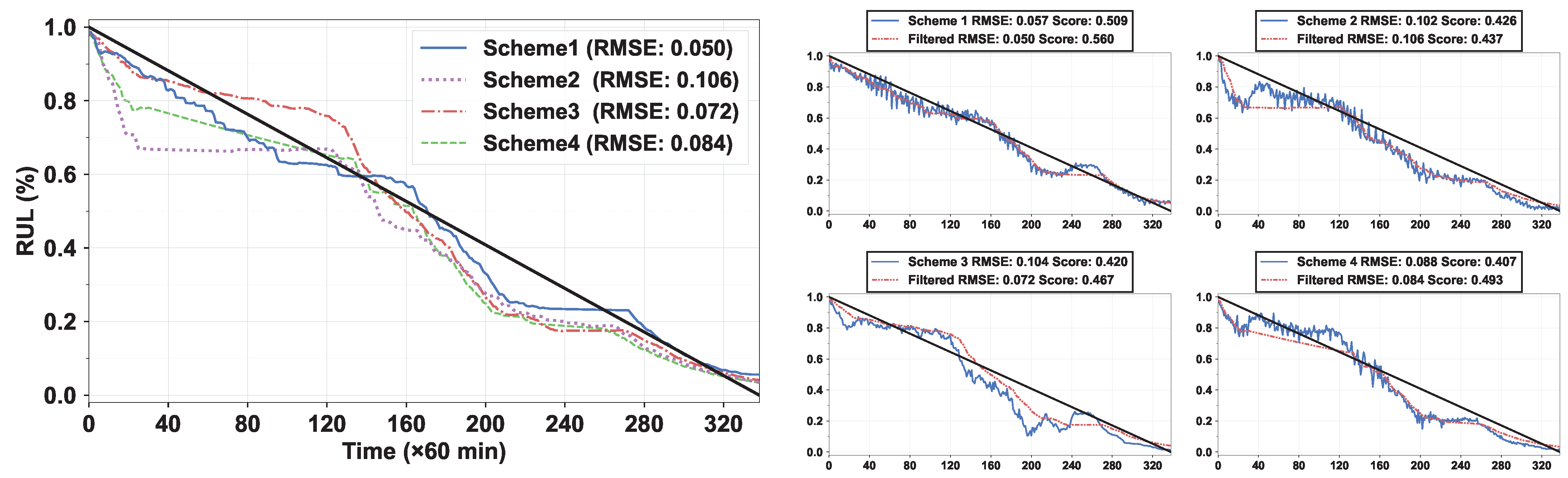
5.3. TFCR–Kalman Filter for RUL Estimation of TIR Sequences
5.4. Result
6. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, X.; Yang, L.T.; Xie, X.; Jin, J.; Deen, M.J. A Cloud-Edge Computing Framework for Cyber-Physical-Social Services. IEEE Commun. Mag. 2017, 55, 80–85. [Google Scholar] [CrossRef]
- Wang, X.; Yang, L.T.; Song, L.; Wang, H.; Ren, L.; Deen, M.J. A Tensor-Based Multiattributes Visual Feature Recognition Method for Industrial Intelligence. IEEE Trans. Ind. Inform. 2021, 17, 2231–2241. [Google Scholar] [CrossRef]
- Ren, L.; Meng, Z.; Wang, X.; Zhang, L.; Yang, L.T. A data-driven approach of product quality prediction for complex production systems. IEEE Trans. Ind. Inform. 2020, 17, 6457–6465. [Google Scholar] [CrossRef]
- Hamdan, S.; Ayyash, M.; Almajali, S. Edge-computing architectures for internet of things applications: A survey. Sensors 2020, 20, 6441. [Google Scholar] [CrossRef]
- Deng, S.; Zhao, H.; Fang, W.; Yin, J.; Dustdar, S.; Zomaya, A.Y. Edge intelligence: The confluence of edge computing and artificial intelligence. IEEE Internet Things J. 2020, 7, 7457–7469. [Google Scholar] [CrossRef]
- Compare, M.; Baraldi, P.; Zio, E. Challenges to IoT-enabled predictive maintenance for industry 4.0. IEEE Internet Things J. 2019, 7, 4585–4597. [Google Scholar] [CrossRef]
- Hamadache, M.; Jung, J.H.; Park, J.; Youn, B.D. A comprehensive review of artificial intelligence-based approaches for rolling element bearing PHM: Shallow and deep learning. JMST Adv. 2019, 1, 125–151. [Google Scholar] [CrossRef]
- Yin, Y.; Tian, J.; Liu, X. Remaining useful life prediction based on parallel multi-scale feature fusion network. J. Intell. Manuf. 2025, 36, 3111–3127. [Google Scholar] [CrossRef]
- Rai, A.; Upadhyay, S.H. A review on signal processing techniques utilized in the fault diagnosis of rolling element bearings. Tribol. Int. 2016, 96, 289–306. [Google Scholar] [CrossRef]
- Li, P.; Liu, X.; Yang, Y. Remaining useful life prognostics of bearings based on a novel spatial graph-temporal convolution network. Sensors 2021, 21, 4217. [Google Scholar] [CrossRef]
- Yang, W.; Wang, Z.; Ma, H.; Qiao, H.; Diao, N. Gear Fault Diagnosis Based on Parameter Optimization VMD and Kurtosis Criterion. Modul. Mach. Tool Autom. Manuf. Tech. 2023, 0, 13–16+21. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, H.; Jin, Y.; Dang, X.; Deng, W. Feature extraction for data-driven remaining useful life prediction of rolling bearings. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Tinga, T.; Loendersloot, R. Physical Model-Based Prognostics and Health Monitoring to Enable Predictive Maintenance. In Predictive Maintenance in Dynamic Systems: Advanced Methods, Decision Support Tools and Real-World Applications; Lughofer, E., Sayed-Mouchaweh, M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 313–353. [Google Scholar] [CrossRef]
- Ramezani, S.; Moini, A.; Riahi, M. Prognostics and Health Management in Machinery: A Review of Methodologies for RUL prediction and Roadmap. Int. J. Ind. Eng. Manag. Sci. 2019, 6, 38–61. [Google Scholar]
- Wang, X.; Wang, T.; Ming, A.; Han, Q.; Chu, F.; Zhang, W.; Li, A. Deep spatiotemporal convolutional-neural-network-based remaining useful life estimation of bearings. Chin. J. Mech. Eng. 2021, 34, 62. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Bai, J.; Al-Sabaawi, A.; Santamaría, J.; Albahri, A.S.; Al-dabbagh, B.S.N.; Fadhel, M.A.; Manoufali, M.; Zhang, J.; Al-Timemy, A.H.; et al. A survey on deep learning tools dealing with data scarcity: Definitions, challenges, solutions, tips, and applications. J. Big Data 2023, 10, 46. [Google Scholar] [CrossRef]
- Ye, Y.; Yong, Z.; Han, D. Research on key technology of industrial artificial intelligence and its application in predictive maintenance. Acta Autom. Sin. 2020, 46, 2013–2030. [Google Scholar]
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Li, W.; Zhang, L.C.; Wu, C.H.; Wang, Y.; Cui, Z.X.; Niu, C. A data-driven approach to RUL prediction of tools. Adv. Manuf. 2024, 12, 6–18. [Google Scholar] [CrossRef]
- Xia, M.; Zheng, X.; Imran, M.; Shoaib, M. Data-driven prognosis method using hybrid deep recurrent neural network. Appl. Soft Comput. 2020, 93, 106351. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.; Li, N.; Yan, T. Deep separable convolutional network for remaining useful life prediction of machinery. Mech. Syst. Signal Process. 2019, 134, 106330. [Google Scholar] [CrossRef]
- Chen, Y.; Peng, G.; Zhu, Z.; Li, S. A novel deep learning method based on attention mechanism for bearing remaining useful life prediction. Appl. Soft Comput. 2020, 86, 105919. [Google Scholar] [CrossRef]
- Guo, L.; Li, N.; Jia, F.; Lei, Y.; Lin, J. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, L.; Song, X.; Chen, K. Remaining useful life prediction method of rolling bearing based on Transformer model. J. Beijing Univ. Aeronaut. Astronaut. 2021, 49, 430–443. [Google Scholar] [CrossRef]
- Cao, Y.; Ding, Y.; Jia, M.; Tian, R. A novel temporal convolutional network with residual self-attention mechanism for remaining useful life prediction of rolling bearings. Reliab. Eng. Syst. Saf. 2021, 215, 107813. [Google Scholar] [CrossRef]
- Liu, Q.; Dai, Z.; Chen, P.; Lai, H.; Liang, Y.; Chen, M.; Xu, X.; Hou, M.; Wang, G. Remaining useful life prediction of rolling bearings based on TCN-LSTM. In Proceedings of the 14th International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (QR2MSE 2024), Harbin, China, 24–27 July 2024; Volume 2024, pp. 1016–1020. [Google Scholar] [CrossRef]
- Zhao, D.; Li, J.; Cheng, W.; He, Z. Generalized demodulation transform for bearing fault diagnosis under nonstationary conditions and gear noise interferences. Chin. J. Mech. Eng. 2019, 32, 7. [Google Scholar] [CrossRef]
- Lu, W.; Wang, Y.; Zhang, M.; Gu, J. Physics guided neural network: Remaining useful life prediction of rolling bearings using long short-term memory network through dynamic weighting of degradation process. Eng. Appl. Artif. Intell. 2024, 127, 107350. [Google Scholar] [CrossRef]
- Yang, S.; Tang, B.; Wang, W.; Yang, Q.; Hu, C. Physics-informed multi-state temporal frequency network for RUL prediction of rolling bearings. Reliab. Eng. Syst. Saf. 2024, 242, 109716. [Google Scholar] [CrossRef]
- Hu, Y.; Chao, Q.; Xia, P.; Liu, C. Remaining useful life prediction using physics-informed neural network with self-attention mechanism and deep separable convolutional network. J. Adv. Manuf. Sci. Technol. 2024, 4, 2024018. [Google Scholar] [CrossRef]
- Merenda, M.; Porcaro, C.; Iero, D. Edge machine learning for ai-enabled iot devices: A review. Sensors 2020, 20, 2533. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Su, B.; Sun, Y. Intelligent Prediction of Bearing Remaining Useful Life Based on Data Enhancement and Adaptive Temporal Convolutional Networks. J. Fail. Anal. Prev. 2023, 23, 2709–2720. [Google Scholar] [CrossRef]
- Meng, Z.; Xie, Y.; Sun, J. Short-term load forecasting using neural attention model based on EMD. Electr. Eng. 2022, 104, 1857–1866. [Google Scholar] [CrossRef]
- Li, G.; Tian, T.; Hao, F.; Yuan, Z.; Tang, R.; Liu, X. Day-Ahead Photovoltaic Power Forecasting Using Empirical Mode Decomposition Based on Similarity-Day Extension Without Information Leakage. Arab. J. Sci. Eng. 2024, 49, 6941–6957. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar] [CrossRef]
- Li, X.; Ding, Q.; Sun, J.Q. Remaining useful life estimation in prognostics using deep convolution neural networks. Reliab. Eng. Syst. Saf. 2018, 172, 1–11. [Google Scholar] [CrossRef]
- Ren, L.; Liu, Y.; Wang, X.; Lü, J.; Deen, M.J. Cloud–edge-based lightweight temporal convolutional networks for remaining useful life prediction in iiot. IEEE Internet Things J. 2021, 8, 12578–12587. [Google Scholar] [CrossRef]
- Eknath, K.G.; Diwakar, G. Prediction of Remaining Useful Life of Rolling Bearing using Hybrid DCNN-BiGRU Model. J. Vib. Eng. Technol. 2023, 11, 997–1010. [Google Scholar] [CrossRef]
- Du, X.; Jia, W.; Yu, P.; Shi, Y.; Gong, B. RUL prediction based on GAM–CNN for rotating machinery. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 142. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-Excitation Networks. arXiv 2017, arXiv:1709.01507. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations Using RNN Encoder-Decoder for Statistical Machine Translation. arXiv 2014, arXiv:1406.1078. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]



| Scheme | Channel | Layer | Dilation | Blocks | |||
|---|---|---|---|---|---|---|---|
| Large 1 | 6 | 8 | 2 | 1056 → 512 | a | 1 | 2 |
| b | 2 | 2 | |||||
| c | 1 | 1 | |||||
| Large 2 | 5 | 8 | 2 | 880 → 220 | a | 1 | 2 |
| b | 2 | 2 | |||||
| c | 1 | 1 | |||||
| Light 3 | 5 | 4 | 2 | 440 → 160 | a | 1 | 1 |
| b | 2 | 2 | |||||
| 4 | 1 | ||||||
| c | 1 | 1 | |||||
| Light 4 | 5 | 2 | 2 | 220 → 60 | a | 1 | 1 |
| b | 2 | 2 | |||||
| 4 | 1 | ||||||
| c | 1 | 1 |
| Condition | Train | Validation | Test | ||
|---|---|---|---|---|---|
| No. | Load (kN) | Speed (rpm) | |||
| 1 | 12 | 2250 | , , , | Synthetic | |
| 2 | 11 | 2500 | , , , | ||
| 3 | 10 | 2400 | , , | ||
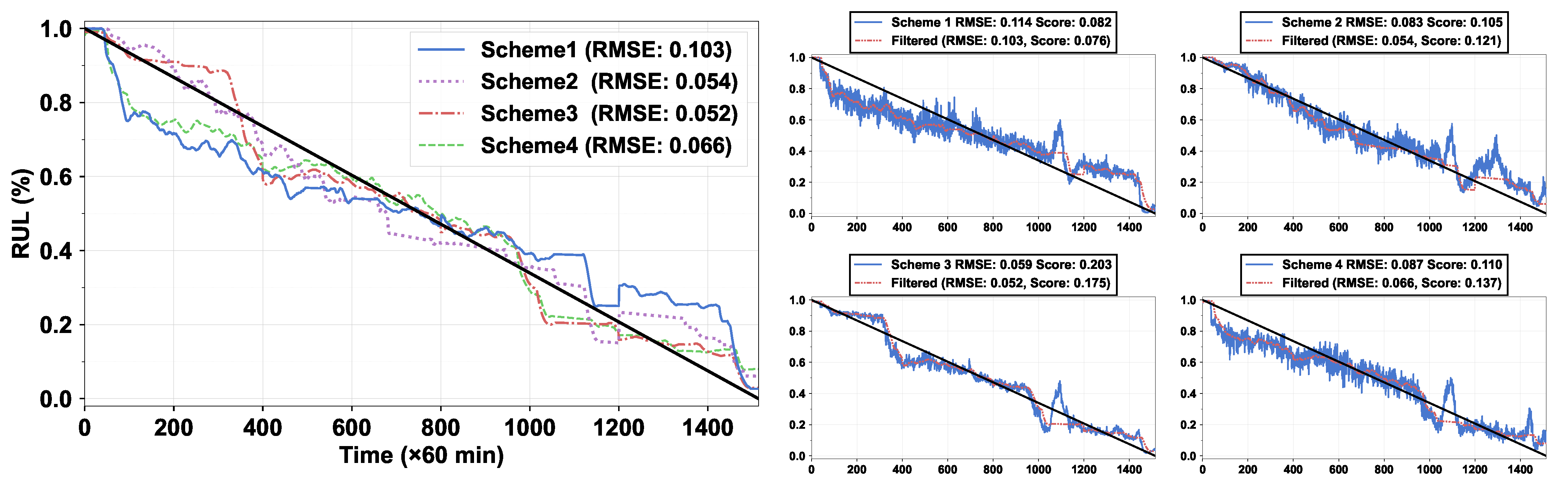
| Scheme | Rmse | Avg. | Score | Avg. | Time | Size | Best Length | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C1 | C2 | C3 | C1 | C2 | C3 | C1 | C2 | C3 | ||||
| 1 | 0.073 | 0.081 | 0.112 | 0.088 | 0.81 | 0.53 | 0.12 | 0.49 | 0.105 | 0.076 | 0.056 | 24.89 | 18 | 40 | 40 |
| 2 | 0.084 | 0.107 | 0.095 | 0.095 | 0.82 | 0.40 | 0.14 | 0.45 | 0.121 | 0.104 | 0.054 | 10.77 | 20 | 56 | 48 |
| 3 | 0.091 | 0.102 | 0.114 | 0.102 | 0.73 | 0.38 | 0.15 | 0.42 | 0.092 | 0.065 | 0.041 | 3.80 | 20 | 40 | 40 |
| 4 | 0.101 | 0.105 | 0.132 | 0.113 | 0.70 | 0.42 | 0.11 | 0.40 | 0.065 | 0.058 | 0.029 | 0.98 | 16 | 48 | 40 |
| Parameter | Scheme 1 | Scheme 2 | Scheme 3 | Scheme 4 |
|---|---|---|---|---|
| Core Parameters (C1, C2, C3) | ||||
| Process Variance () | 0.05, 0.05, 0.001 | 0.05, 0.0005, 0.0005 | 0.02, 0.001, 0.005 | 0.05, 0.02, 0.0005 |
| Meas. Variance () | 0.0001, 0.0001, 0.005 | 0.0001, 0.0001, 0.02 | 0.0001, 0.05, 0.02 | 0.0001, 0.0005, 0.05 |
| Trust Factor () | 0.95, 0.6, 0.85 | 0.9, 0.6, 0.9 | 0.8, 0.6, 0.95 | 0.6, 0.6, 0.98 |
| Outlier Sensitivity () | 5.0, 5.0, 4.0 | 5.5, 2.5, 3.0 | 2.0, 3.0, 3.5 | 2.5, 3.0, 2.5 |
| Filter Parameters (C1, C2, C3) | ||||
| Smoothing Window () | 15, 3, 19 | 15, 3, 19 | 3, 2, 13 | 9, 2, 19 |
| Decay Factor () | 0.998, 0.9995, 0.9999 | 0.998, 0.9998, 0.9995 | 0.995, 0.9998, 0.9995 | 0.999, 0.998, 0.9995 |
| Trend Window () | 0, 4, 5 | 0, 3, 11 | 0, 2, 11 | 0, 3, 11 |
| Performance Changes (C1, C2, C3) | ||||
| RMSE (↓) | 5.9, 12.6, 14.3 | 4.3, 8.2, 30.3 | 15.4, 19.5, 29.2 | 24.3, 6.5, 13.5 |
| Score (↑) | 2.5, 14.0, 9.9 | 0.8, 7.9, 13.4 | 7.2, 9.3, 3.7 | 7.5, 15.4, 14.6 |
| MAE (↓) | 5.6, 11.9, 10.4 | 5.1, 3.2, 29.5 | 15.1, 29.4, 19.9 | 25.3, 9.2, 8.2 |
| Model | Time Per Sample/Length (ms) |
|---|---|
| GRU | 0.0101 |
| LSTM | 0.0120 |
| Transformer | 0.0153 |
| TFCR | 0.0067 |
| Model | RMSE |
|---|---|
| DSCN | 0.0739 |
| RCNN | 0.0803 |
| RVM | 0.1082 |
| MTCN | 0.0732 |
| Transformer | 0.0701 |
| PGLSTM | 0.0866 |
| TCN-RSA | 0.0699 |
| Proposed TFCR 1 | 0.0884 |
| Proposed TFCR 2 | 0.0953 |
| Proposed TFCR 3 | 0.1023 |
| Proposed TFCR 4 | 0.1135 |
| Proposed TFCR-KF 1 | 0.0767 |
| Proposed TFCR-KF 2 | 0.0827 |
| Proposed TFCR-KF 3 | 0.0894 |
| Proposed TFCR-KF 4 | 0.0946 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Z.; Lang, L.; Chen, M.; Ge, C.; Tong, E.; Chen, L. A Hybrid Approach Based on a Windowed-EMD Temporal Convolution–Reallocation Network and Physical Kalman Filtering for Bearing Remaining Useful Life Estimation. Machines 2025, 13, 802. https://doi.org/10.3390/machines13090802
Wei Z, Lang L, Chen M, Ge C, Tong E, Chen L. A Hybrid Approach Based on a Windowed-EMD Temporal Convolution–Reallocation Network and Physical Kalman Filtering for Bearing Remaining Useful Life Estimation. Machines. 2025; 13(9):802. https://doi.org/10.3390/machines13090802
Chicago/Turabian StyleWei, Zhe, Lang Lang, Mo Chen, Chao Ge, Enguo Tong, and Liang Chen. 2025. "A Hybrid Approach Based on a Windowed-EMD Temporal Convolution–Reallocation Network and Physical Kalman Filtering for Bearing Remaining Useful Life Estimation" Machines 13, no. 9: 802. https://doi.org/10.3390/machines13090802
APA StyleWei, Z., Lang, L., Chen, M., Ge, C., Tong, E., & Chen, L. (2025). A Hybrid Approach Based on a Windowed-EMD Temporal Convolution–Reallocation Network and Physical Kalman Filtering for Bearing Remaining Useful Life Estimation. Machines, 13(9), 802. https://doi.org/10.3390/machines13090802







