Remaining Useful Life Prediction of Turbine Engines Using Multimodal Transfer Learning
Abstract
1. Introduction
- (1)
- An innovative model combining transfer learning and multimodal analysis has been proposed, enabling cross-domain multimodal RUL prediction even with limited data.
- (2)
- To better capture the degraded features of the source domain in the target domain, this study employs a supervised two-stage feature transfer method. Additionally, by integrating multidimensional and multimodal features, the model provides a more comprehensive assessment of the overall trend.
- (3)
- Extensive experiments were conducted, and through comparisons between multimodal and transfer learning approaches, the proposed model demonstrated the best performance.
2. Related Work
2.1. Transfer Learning in RUL
2.2. Multimodal Method
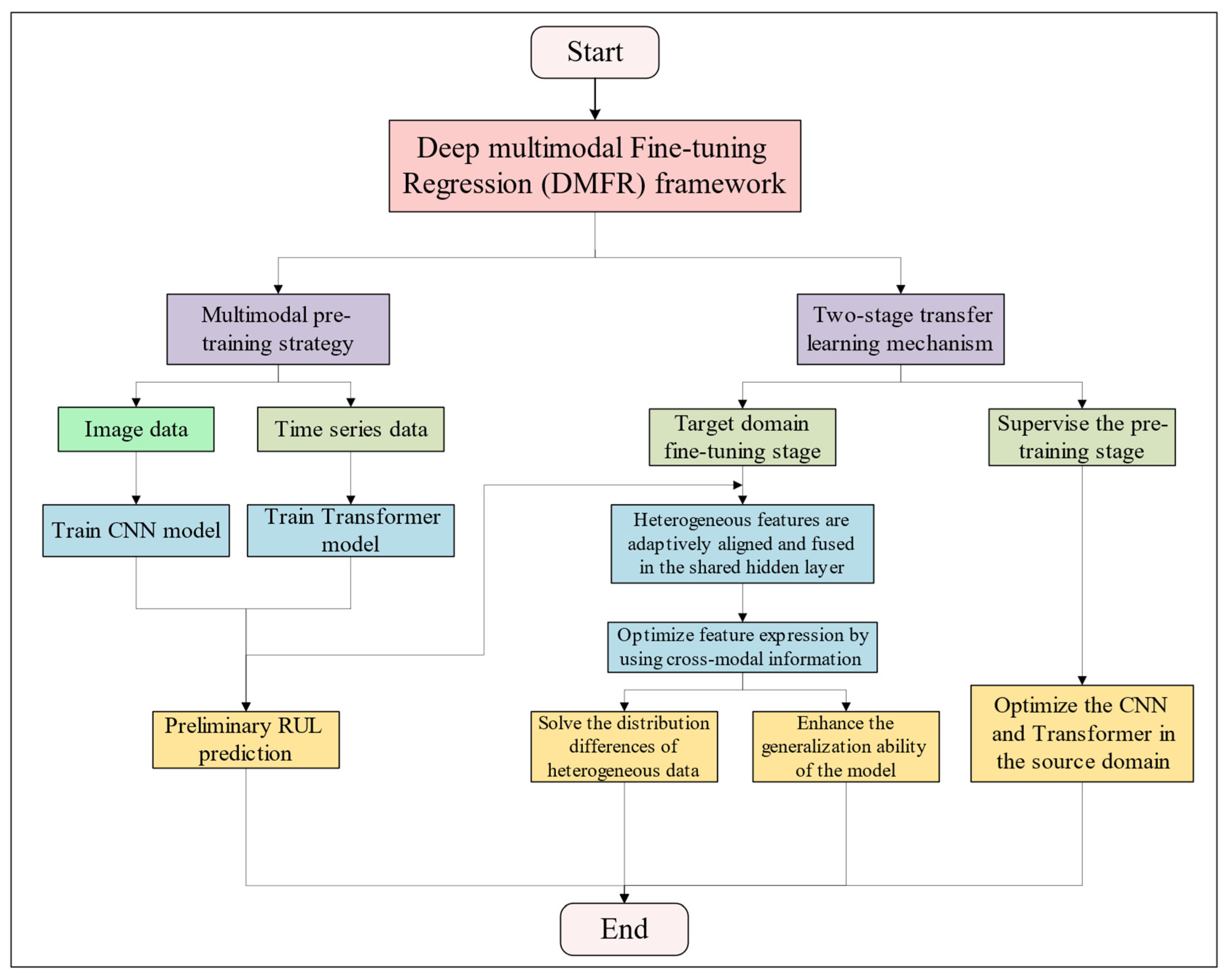
3. Method
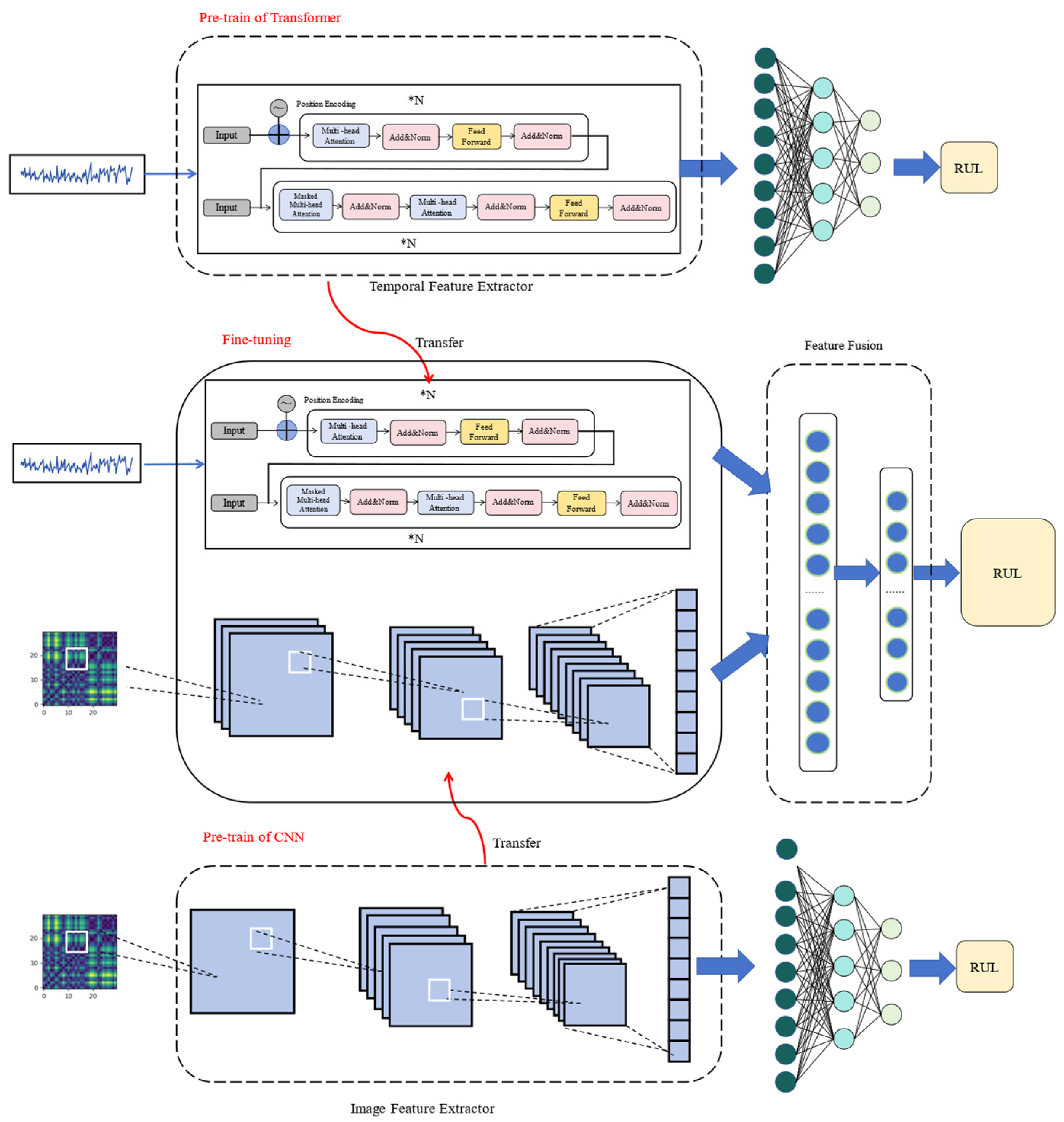
3.1. Overview
3.2. Multimodal Data Input
3.3. RUL Prediction Model
3.3.1. Image Feature Extractor
3.3.2. Time-Series Feature Extractor
3.3.3. Fusion Prediction
3.4. Two-Stage Transfer Strategy
4. Experiment
4.1. Dataset Description
4.2. Dataset Preprocessing
4.3. Evaluation Criteria
4.4. Task Classification
4.5. Experimental Results and Analysis
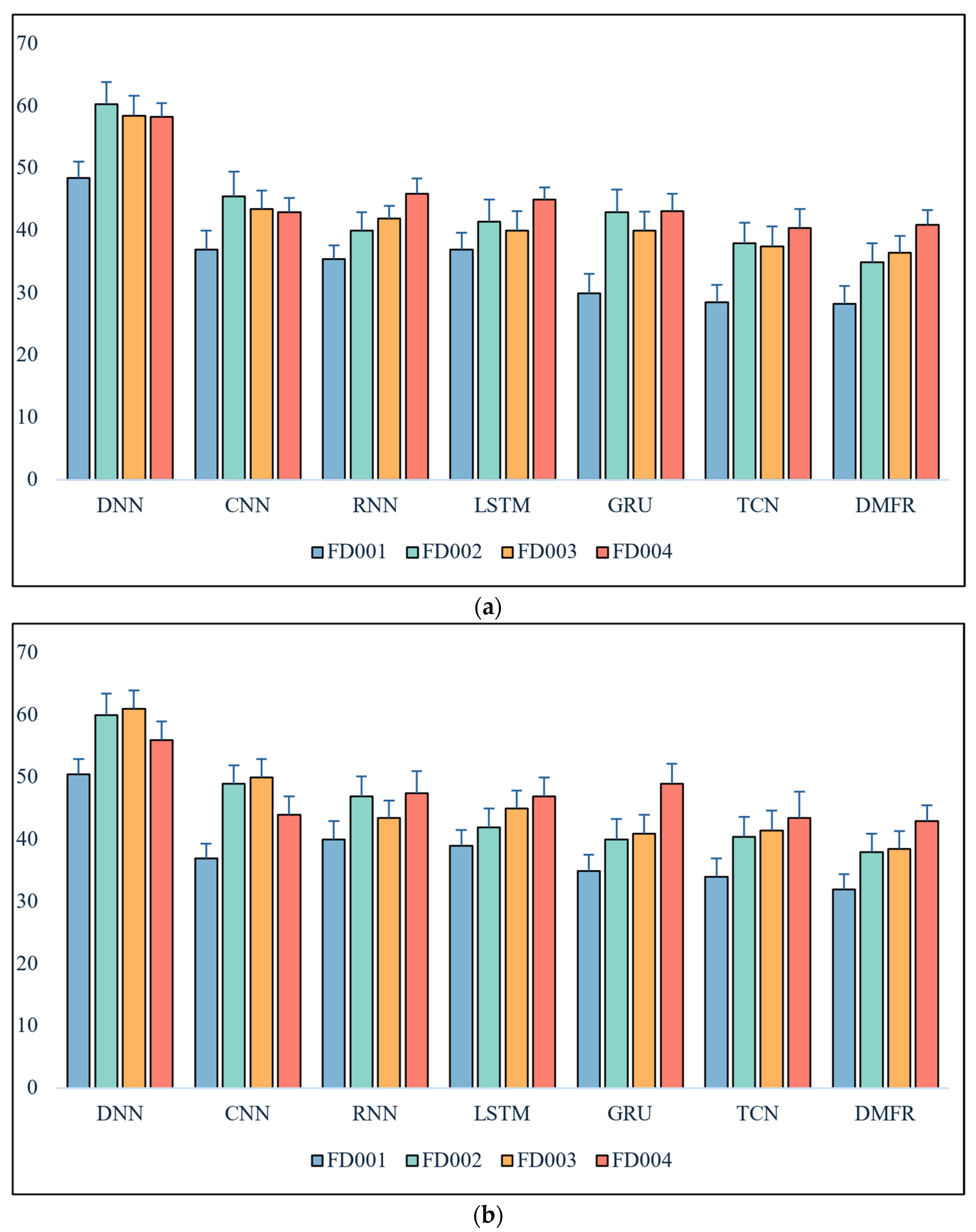
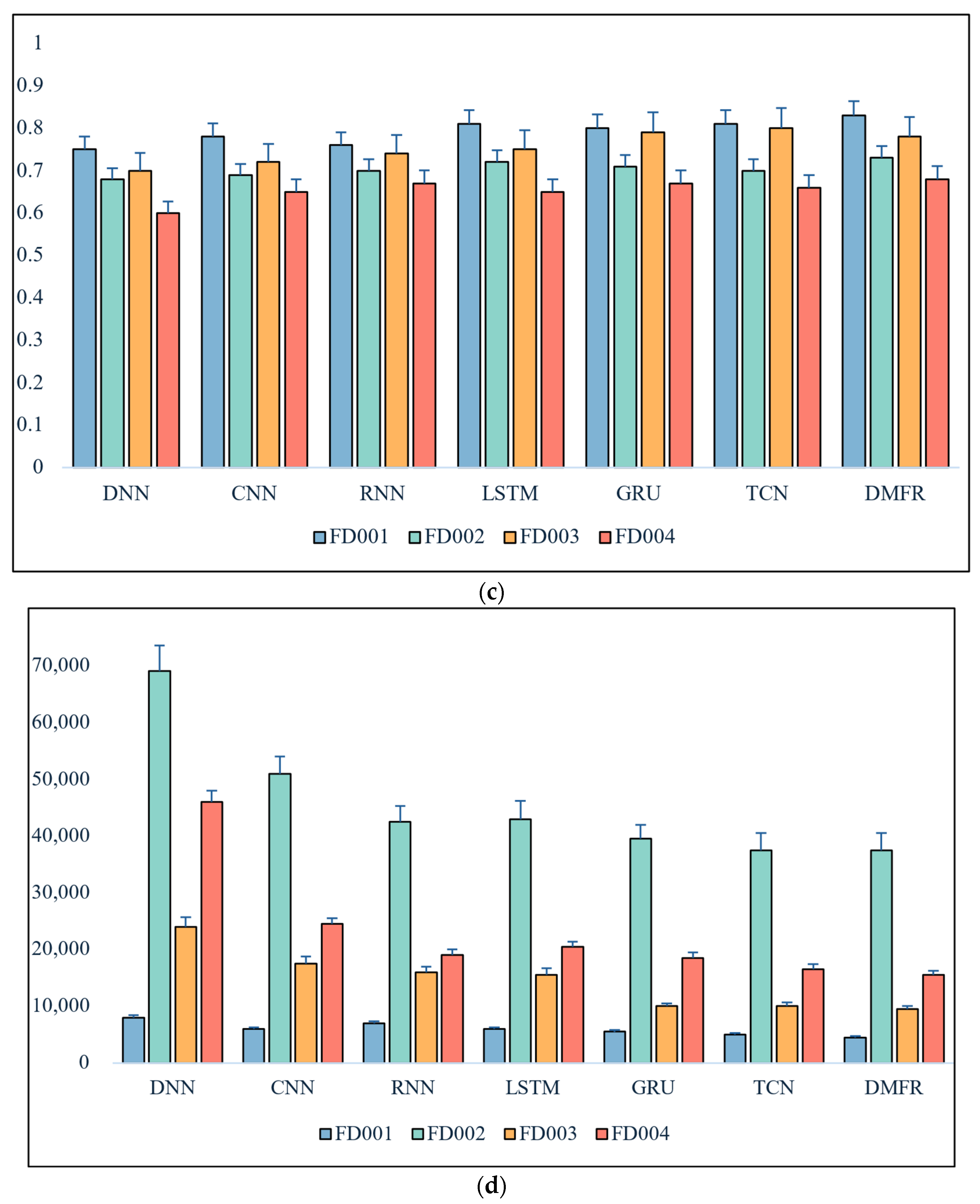
4.5.1. RUL Prediction Results
4.5.2. Comparative Analysis with Benchmark Models
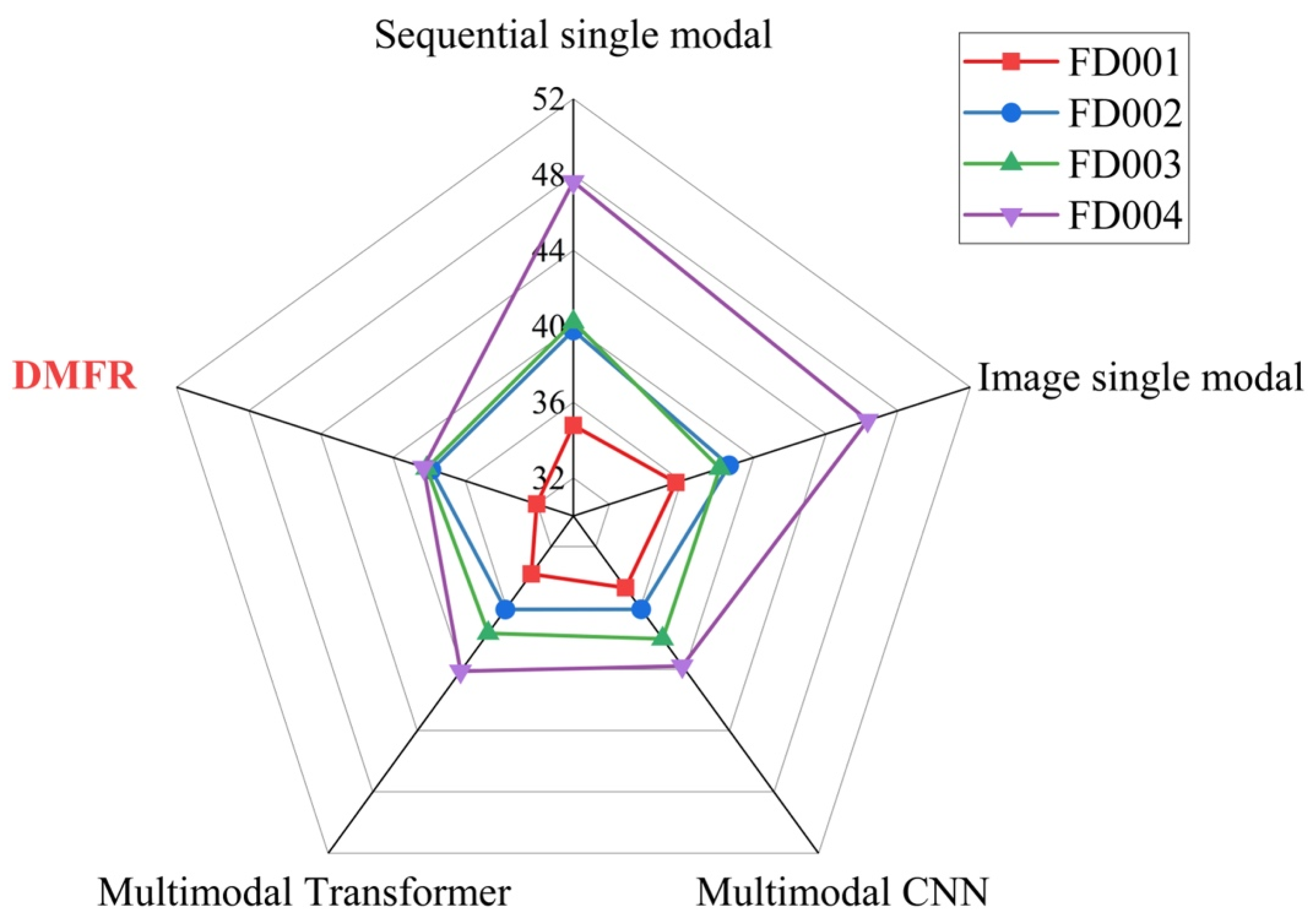
4.5.3. Comparison of Different Modal Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tsui, K.L.; Chen, N.; Zhou, Q.; Hai, Y.; Wang, W. Prognostics and health management: A review on data driven approaches. Math. Probl. Eng. 2015, 2015, 793161. [Google Scholar] [CrossRef]
- Hamadache, M.; Jung, J.H.; Park, J.; Youn, B.D. A comprehensive review of artificial intelligence-based approaches for rolling element bearing PHM: Shallow and deep learning. JMST Adv. 2019, 1, 125–151. [Google Scholar] [CrossRef]
- Liao, L.; Köttig, F. Review of hybrid prognostics approaches for remaining useful life prediction of engineered systems, and an application to battery life prediction. IEEE Trans. Reliab. 2014, 63, 191–207. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Mathew, V.; Toby, T.; Singh, V.; Rao, B.M.; Kumar, M.G. Prediction of Remaining Useful Lifetime (RUL) of turbofan engine using machine learning. In Proceedings of the 2017 IEEE International Conference on Circuits and Systems (ICCS), Thiruvananthapuram, India, 20–21 December 2017. [Google Scholar]
- Berghout, T.; Benbouzid, M. A systematic guide for predicting remaining useful life with machine learning. Electronics 2022, 11, 1125. [Google Scholar] [CrossRef]
- Esfahani, Z.; Salahshoor, K.; Farsi, B.; Eicker, U. A new hybrid model for RUL prediction through machine learning. J. Fail. Anal. Prev. 2021, 21, 1596–1604. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, Y.; Addepalli, S. Remaining useful life prediction using deep learning approaches: A review. Procedia Manuf. 2020, 49, 81–88. [Google Scholar] [CrossRef]
- Ma, M.; Mao, Z. Deep-convolution-based LSTM network for remaining useful life prediction. IEEE Trans. Ind. Inform. 2020, 17, 1658–1667. [Google Scholar] [CrossRef]
- Ren, L.; Cui, J.; Sun, Y.; Cheng, X. Multi-bearing remaining useful life collaborative prediction: A deep learning approach. J. Manuf. Syst. 2017, 43, 248–256. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, Y.; Wu, S.; Li, X.; Luo, H.; Yin, S. Prediction of remaining useful life based on bidirectional gated recurrent unit with temporal self-attention mechanism. Reliab. Eng. Syst. Saf. 2022, 221, 108297. [Google Scholar] [CrossRef]
- Fan, Y.; Nowaczyk, S.; Rögnvaldsson, T. Transfer learning for remaining useful life prediction based on consensus self-organizing models. Reliab. Eng. Syst. Saf. 2020, 203, 107098. [Google Scholar] [CrossRef]
- Wang, P.; Li, J.; Wang, S.; Zhang, F.; Shi, J.; Shen, C. A new meta-transfer learning method with freezing operation for few-shot bearing fault diagnosis. Meas. Sci. Technol. 2023, 34, 074005. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, Q.; Ye, Q. An attention-based temporal convolutional network method for predicting remaining useful life of aero-engine. Eng. Appl. Artif. Intell. 2024, 127, 107241. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Z.; Zhang, H.; Liu, L.; Huang, R.; Cheng, X.; Zhao, H.; Zhao, Z. Omnibind: Large-scale omni multimodal representation via binding spaces. arXiv 2024, arXiv:2407.11895. [Google Scholar]
- Peng, C.; Sheng, Y.; Gui, W.; Tang, Z.; Li, C. A rolling bearing fault diagnosis method based on multimodal knowledge graph. IEEE Trans. Ind. Inform. 2024, 20, 13047–13057. [Google Scholar] [CrossRef]
- Li, H.; Huang, J.; Huang, J.; Chai, S.; Zhao, L.; Xia, Y. Deep multimodal learning and fusion based intelligent fault diagnosis approach. J. Beijing Inst. Technol. 2021, 30, 172–185. [Google Scholar]
- Wang, S.; Wang, B.; Zhang, Z.; Heidari, A.A.; Chen, H. Class-aware sample reweighting optimal transport for multi-source domain adaptation. Neurocomputing 2023, 523, 213–223. [Google Scholar] [CrossRef]
- Zhang, A.; Wang, H.; Li, S.; Cui, Y.; Liu, Z.; Yang, G.; Hu, J. Transfer learning with deep recurrent neural networks for remaining useful life estimation. Appl. Sci. 2018, 8, 2416. [Google Scholar] [CrossRef]
- Ding, Y.; Ding, P.; Zhao, X.; Cao, Y.; Jia, M. Transfer learning for remaining useful life prediction across operating conditions based on multisource domain adaptation. IEEE/ASME Trans. Mechatron. 2022, 27, 4143–4152. [Google Scholar] [CrossRef]
- Sun, C.; Ma, M.; Zhao, Z.; Tian, S.; Yan, R.; Chen, X. Deep transfer learning based on sparse autoencoder for remaining useful life prediction of tool in manufacturing. IEEE Trans. Ind. Inform. 2018, 15, 2416–2425. [Google Scholar] [CrossRef]
- Li, Z.-J.; Cheng, D.-J.; Zhang, H.-B.; Zhou, K.-L.; Wang, Y.-F. Multi-feature spaces cross adaption transfer learning-based bearings piece-wise remaining useful life prediction under unseen degradation data. Adv. Eng. Inform. 2024, 60, 102413. [Google Scholar] [CrossRef]
- Cao, Y.; Jia, M.; Ding, P.; Ding, Y. Transfer learning for remaining useful life prediction of multi-conditions bearings based on bidirectional-GRU network. Measurement 2021, 178, 109287. [Google Scholar] [CrossRef]
- Razzaghi, P.; Abbasi, K.; Shirazi, M.; Rashidi, S. Multimodal brain tumor detection using multimodal deep transfer learning. Appl. Soft Comput. 2022, 129, 109631. [Google Scholar] [CrossRef]
- Rahman, W.; Hasan, M.K.; Lee, S.; Zadeh, A.; Mao, C.; Morency, L.-P.; Hoque, E. Integrating multimodal information in large pretrained transformers. Proc. Conf. Assoc. Comput. Linguist. Meet. 2020, 2020, 2359–2369. [Google Scholar]
- Ji, T.; Vuppala, S.T.; Chowdhary, G.; Driggs-Campbell, K. Multi-modal anomaly detection for unstructured and uncertain environments. arXiv 2020, arXiv:2012.08637. [Google Scholar] [CrossRef]
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- da Costa, P.R.D.O.; Akçay, A.; Zhang, Y.; Kaymak, U. Remaining useful lifetime prediction via deep domain adaptation. Reliab. Eng. Syst. Saf. 2020, 195, 106682. [Google Scholar] [CrossRef]
- Ramasso, E.; Saxena, A. Review and analysis of algorithmic approaches developed for prognostics on CMAPSS dataset. In Proceedings of the Annual Conference of the Prognostics and Health Management Society 2014, Cheney, WA, USA, 22–25 June 2014. [Google Scholar]
- Vollert, S.; Theissler, A. Challenges of machine learning-based RUL prognosis: A review on NASA’s C-MAPSS data set. In Proceedings of the 2021 26th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Västerås, Sweden, 7–10 September 2021. [Google Scholar]


| Data | FD001 | FD002 | FD003 | FD004 |
|---|---|---|---|---|
| Train | 100 | 260 | 100 | 249 |
| Test | 100 | 259 | 100 | 248 |
| OC | 1 | 6 | 1 | 6 |
| FM | 1 | 1 | 2 | 2 |
| Task | Condition | OC | FM |
|---|---|---|---|
| 1 | FD001—FD002 | 1 → 6 | 1 → 1 |
| 2 | FD001—FD003 | 1 → 1 | 1 → 2 |
| 3 | FD001—FD004 | 1 → 6 | 1 → 2 |
| 4 | FD002—FD001 | 6 → 1 | 1 → 1 |
| 5 | FD002—FD003 | 6 → 1 | 1 → 2 |
| 6 | FD002—FD004 | 6 → 6 | 1 → 2 |
| 7 | FD003—FD001 | 1 → 1 | 2 → 1 |
| 8 | FD003—FD002 | 1 → 6 | 2 → 1 |
| 9 | FD003—FD004 | 1 → 6 | 2 → 2 |
| 10 | FD004—FD001 | 6 → 1 | 2 → 1 |
| 11 | FD004—FD002 | 6 → 6 | 2 → 1 |
| 12 | FD004—FD003 | 6 → 1 | 2 → 2 |
| Criteria | RMSE | MAE | R2 | Score |
|---|---|---|---|---|
| Task1 | 31.4 ± 3.1 | 28.6 ± 1.8 | 0.88 ± 0.1 | 3398 ± 2896 |
| Task2 | 25.4 ± 42 | 26.3 ± 3.1 | 0.79 ± 0.2 | 3485 ± 2536 |
| Task3 | 39.3 ± 2.3 | 29.6 ± 2.1 | 0.81 ± 0.1 | 6490 ± 3442 |
| Task4 | 46.6 ± 6.2 | 39.5 ± 4.5 | 0.69 ± 0.3 | 58,782 ± 50,289 |
| Task5 | 43.9 ± 1.3 | 38.7 ± 2.3 | 0.71 ± 0.1 | 51,831 ± 48,971 |
| Task6 | 23.1 ± 3.0 | 26.9 ± 2.2 | 0.80 ± 0.1 | 3025 ± 2054 |
| Task7 | 36.3 ± 2.5 | 33.9 ± 1.0 | 0.76 ± 0.2 | 10,598 ± 15,321 |
| Task8 | 39.1 ± 4.1 | 38.7 ± 1.3 | 0.78 ± 0.3 | 9712 ± 5891 |
| Task9 | 39.0 ± 0.7 | 36.9 ± 1.4 | 0.80 ± 0.1 | 8639 ± 5412 |
| Task10 | 46.1 ± 2.1 | 42.3 ± 1.9 | 0.68 ± 1.0 | 25,909 ± 12,489 |
| Task11 | 34.0 ± 2.2 | 33.7 ± 2.1 | 0.75 ± 0.3 | 19,578 ± 13,247 |
| Task12 | 47.9 ± 1.0 | 46.3 ± 5.0 | 0.62 ± 0.2 | 2851 ± 17,845 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Yang, Z. Remaining Useful Life Prediction of Turbine Engines Using Multimodal Transfer Learning. Machines 2025, 13, 789. https://doi.org/10.3390/machines13090789
Li J, Yang Z. Remaining Useful Life Prediction of Turbine Engines Using Multimodal Transfer Learning. Machines. 2025; 13(9):789. https://doi.org/10.3390/machines13090789
Chicago/Turabian StyleLi, Jiaze, and Zeliang Yang. 2025. "Remaining Useful Life Prediction of Turbine Engines Using Multimodal Transfer Learning" Machines 13, no. 9: 789. https://doi.org/10.3390/machines13090789
APA StyleLi, J., & Yang, Z. (2025). Remaining Useful Life Prediction of Turbine Engines Using Multimodal Transfer Learning. Machines, 13(9), 789. https://doi.org/10.3390/machines13090789





