Data-Driven Method for Robotic Trajectory Error Prediction and Compensation Based on Digital Twin

Abstract

In addressing the limited absolute positioning accuracy of industrial robots, which stems from the discrepancy between the nominal kinematic model and the physical entity, this paper proposes a novel paradigm for online compensation based on data-driven error prediction. The present study utilized a KUKA KR4 R600 robot as the experimental platform to construct a high-fidelity digital twin system capable of real-time synchronization. Within this framework, a new machine learning model, termed the Global Configuration-Error Forest (GCE-Forest), was developed and validated. The fundamental principle of GCE-Forest, based on the Random Forest algorithm, is its offline learning of the complex, highly non-linear mapping from the robot’s six-dimensional joint space configuration to its three-dimensional end-effector Cartesian error space. This facilitates online, feedforward, and predictive compensation for the nominal trajectory during robot operation. Through rigorous comparative experiments, the superiority of the proposed GCE-Forest was established. The final outcomes of dynamic trajectory tracking validation demonstrate that the system, by accurately predicting a mean nominal error of 0.1977 mm, successfully reduced the average spatial positioning error of the end-effector to 0.0845 mm, achieving an accuracy improvement of 57.25%. This research provides comprehensive validation of the method’s robust performance, offering a low-cost, non-invasive, and highly effective solution for significantly enhancing robotic accuracy.

1. Introduction

The advance of Industry 4.0 and smart manufacturing has rapidly expanded the role of industrial robots, now critical components in automated production lines [1]. However, their widespread adoption in high-value applications, such as precision aerospace assembly and robotic milling, is hindered by a persistent technical bottleneck: limited absolute positioning accuracy [2]. The root of this inaccuracy is highly complex. As demonstrated by Li et al. [3], positioning errors in serial robots arise from the intricate coupling of multiple factors. These include both geometric errors and non-geometric sources that are difficult to model, such as joint compliance, gear backlash, thermal deformation, and dynamic load effects. Given these complex error characteristics, improving robot accuracy has become a key challenge for both academic researchers and industrial practitioners.

To tackle this challenge, digital twin technology can be adopted [4,5]. This approach, which creates a dynamic virtual copy of a physical system, offers a powerful way to monitor robot performance in real time [6], predict future behavior, and continuously fine-tune operations. The strategy has already proven its worth in several demanding engineering fields. For example, in the world of CNC machine tools, Liu et al. [7] built a digital twin based on heat transfer theory to anticipate and correct for errors caused by thermal changes. In a similar vein, Zhang et al. [8] designed a digital twin system for parallel robots that uses complex intelligent algorithms to track the robot’s state and adjust its positioning. Even in the tricky domain of automated welding, Shang et al. [9] used a digital twin to preemptively fix seam tracking errors during the process. Given these successes, applying a digital twin framework to address the accuracy issues of serial robots is a logical and promising path forward.

When it comes to digital twins and robotics, a few different schools of thought have emerged for modeling and compensating for errors [10]. The first major camp relies on physics-based models [11]. The goal here is to pinpoint error parameters by carefully analyzing a robot’s kinematics and dynamics. For example, Li et al. [12] took this route by combining finite element analysis with thermodynamics to create a detailed model of a robot’s heat-related errors. The big advantage of these models is that their logic is physically clear and they tend to generalize well. But there is a catch: building them is often incredibly complex. They also struggle to account for hard-to-measure factors like joint compliance or friction. Such inherent limitations ultimately restrict the achievable accuracy of compensation. While physics-based models aim to characterize and compensate for errors, their inherent complexity and limitations in accounting for all unmodeled non-geometric error sources often restrict the achievable precision. Addressing this, a complementary strategy for enhancing robotic accuracy involves optimizing the robot’s intrinsic mechanical characteristics. A prominent approach within this domain is stiffness-oriented posture optimization, which systematically leverages the redundant degrees of freedom often present in industrial manipulators. By strategically selecting optimal joint configurations for a given task, particularly in multi-axis machining operations where certain degrees of freedom may remain unconstrained, the robot’s overall structural stiffness can be significantly maximized. This pre-emptive measure improves accuracy by enabling the robot to inherently resist external forces and dynamic deflections more effectively. Research by Guo et al. [13], Cvitanic et al. [14], and Kratˇena et al. [15] exemplifies this line of inquiry, demonstrating the efficacy of optimizing robot pose for enhanced stiffness to mitigate force-induced errors and improve machining quality. Another camp uses closed-loop feedback [16] from external sensors. Here, the idea is to use instruments like laser trackers or vision systems to spot errors at the robot’s end-effector in real time and correct them on the fly [17,18,19]. A clever take on this comes from Wu et al. [20,21], who introduced a concept called “Information Mutuality.” It uses the mismatch between cheap physical sensors and virtual ones to make corrections, which handily cuts down on system cost. This approach is not without its own headaches, though. It depends on external measurement gear, which makes the system more complex and costly to set up. It can also be thrown off by real-world disturbances, like changing light conditions or something blocking a sensor’s view. On top of that, the system’s performance is always limited by the built-in delay of the feedback loop [22].

Recently, data-driven methods for error compensation [23,24] have caught the eye of many researchers. The core idea is simple: instead of wrestling with complex physics, you treat the problem as a function approximation task and use machine learning [25] to figure out the error patterns directly from the data. This approach has already produced some solid results. For example, Xu et al. [26] used a TCN-BiLSTM deep learning model to predict time-series errors in ultra-precision machining. In another case, Chen et al. [27] applied an optimized Support Vector Regression (SVR) model to correct non-linear positioning errors in robots. While the existing research shows that data-driven methods have a lot of promise, a key problem remains. Most researchers agree that a robot’s joint angles are the root source of its positioning errors, but obtaining clean, high-precision joint angle [28] data is notoriously difficult. Ni et al. [29] tried to get around this with a “joint error equivalence strategy.” Their technique maps the final error measured at the robot’s end-effector back to the joint space with inverse kinematics, allowing them to build a model there. However, they used a hybrid approach that still leans on a physical model [30], meaning its performance is tied to that model’s accuracy. Beyond that, there is another major gap: most of this work is stuck in offline validation. Very few of these algorithms have been fully integrated with digital twin platforms for real-time visualization, monitoring [31], and interaction [32,33].

To address these challenges, a system has been developed that predicts and compensates for a robot’s dynamic trajectory errors [34,35] in real time. These errors specifically refer to the time-varying deviations between the commanded and actual end-effector poses throughout the robot’s continuous motion, encompassing the complex interplay of geometric, non-geometric, and dynamic factors. The approach in this study combined machine learning with a high-fidelity digital twin. At the heart of this system is a purely data-driven predictive model. Therefore, the present study is aimed at developing a data-driven framework for robotic trajectory error prediction and compensation by leveraging a high-fidelity digital twin. Specifically, the objectives of this work are threefold: (i) to construct a digital twin platform that enables real-time synchronization between the physical robot and its virtual counterpart; (ii) to design and train a novel machine learning model, termed the Global Configuration-Error Forest (GCE-Forest), capable of capturing the non-linear mapping between joint-angle vectors and Cartesian errors; and (iii) to integrate the predictive model into the digital twin for forward-looking, online error compensation during trajectory execution.

By pursuing these goals, the study seeks to provide a systematic and generalizable approach to enhancing robotic positioning accuracy without relying on additional external sensors or purely physics-based modeling.

The remainder of this paper is organized as follows. Section 2 details the proposed system framework and its layered architecture. Section 3 presents the kinematic modeling and the development of the 3D visual digital twin. Section 4 introduces the core algorithm, including data collection and the GCE-Forest model. Section 5 presents the experimental results and analysis. Finally, Section 6 provides the conclusions and outlines future work.

2. Overall System Framework

The objective of this paper is to achieve real-time, online, and predictive error compensation for the positioning errors of industrial robots. In order to accomplish this, a comprehensive system has been designed and implemented that integrates a physical entity, a digital twin, and a data-driven intelligent core. The system under discussion here is characterized by a layered and decoupled design philosophy. As illustrated in Figure 1, the overall framework is composed of three primary components: the Physical Layer, the Digital Twin Layer, and the Intelligent Core Layer. These layers interact with one another through well-defined data flows and control flows.

The following section will elaborate on the functions of each layer and their interrelationships.

2.1. Physical Layer

The Physical Layer functions as the operational basis and data source for the entire system. The system under consideration is composed of a KUKA KR4 R600 six-degree-of-freedom industrial robot and its KR C4 controller. The robot controller is responsible for low-level servo control and kinematic solving. In order to facilitate data interaction with the upper layers, a bespoke TCP/IP server application was implemented on the robot’s teach pendant. The program in question disseminates the robot’s internal state, including the real-time joint-angle vector (Hereafter, this parameter is consistently referred to as the joint-angle vector ${\mathit{\theta }}_{realtime}$) and the Cartesian pose of the manipulator, as determined by the controller, to a designated port in accordance with a predetermined protocol format.

2.2. Digital Twin Layer

The Digital Twin Layer constitutes a high-fidelity representation of the physical robot in the information space, thereby serving as the central hub for human–machine interaction and state monitoring. When deployed on a host computer (PC), this layer primarily includes the following modules: Human–Machine Interface (HMI): The application has been developed using the PySide2 framework, providing the user with an operational interface for system connection, parameter setting, data display, and function calls (e.g., data export).

• 3D Visualization Engine: This module utilizes a 3D rendering and simulation engine to construct a 3D model within a virtual environment by parsing the robot’s kinematic description file. The model possesses geometric and kinematic characteristics identical to the physical robot. It receives real-time joint angle data from the Physical Layer, achieving action synchronization between the virtual model and the physical robot.
• Real-time Communication and Control Module: The function of the module under discussion is to act as a TCP/IP client, thereby establishing and maintaining a communication link with the server on the physical layer. A high-frequency polling mechanism, driven by a QTimer, periodically acquires data from the physical layer and disseminates it to other system modules.
• Data Logging and Analysis Module: The function of this module is to record all critical data streams in real time during online operation (for example, timestamps, joint angles, nominal poses, predicted errors, compensated poses). Upon command, the system invokes the analysis module to perform offline visual analysis.

2.3. Intelligence Core Layer

The Intelligent Core Layer is pivotal in achieving the system’s “intelligence.” The system functions independently of the real-time environment, operating in an offline-training, online-inference mode.

• Offline Training Module: In this stage, the proposed Global Configuration-Error Forest (GCE-Forest) model, which is based on the Random Forest algorithm, is trained using data training scripts and a dataset containing high-precision ground-truth measurements from external sensors. The model’s objective is to learn and approximate the complex non-linear mapping from the robot’s joint space to its Cartesian space positioning error. The training produces two key products: a trained GCE-Forest model and scalers, which are used for the input and output of data, respectively.
• Online Real-time Inference Engine: During system operation, this module is initialized and the pre-trained model and scalers are loaded. The Digital Twin Layer provides the joint-angle vector ${\mathit{\theta }}_{realtime}$, which are then processed by a standard inference pipeline, comprising preprocessing, model prediction and inverse transformation. This process ultimately results in the computation of the predicted error vector $∆P$ for the current pose. This vector is then returned to the Digital Twin Layer to calculate the error-compensated pose.
• Data and Control Flow: The system’s operational data flow is characterized by clarity and well-defined parameters: The Physical Layer is responsible for generating raw state data, which is then transmitted to the Digital Twin Layer via the communication link. The Digital Twin Layer employs this data to facilitate the operation of the virtual model and to update the monitoring interface. Conversely, it transmits the core joint-angle vector (${\mathit{\theta }}_{realtime}$) to the Intelligent Core Layer. Subsequent to the execution of the requisite computations, the Intelligent Core Layer disseminates the predicted error data to the Digital Twin Layer. The Digital Twin Layer then integrates the nominal pose with the predicted error ($∆P$) to calculate the final, high-precision compensated pose ($P_{nominal}$) and completes the logging of all data.

3. Method

3.1. Kinematic Modeling and Development of the 3D Visual Digital Twin Environment

In order to facilitate the simulation of the motion of the actual manipulator by the static geometric model, it is imperative to establish an accurate kinematic model. The present study employs the standard Denavit–Hartenberg (D-H) parameter method to describe the relative spatial relationship between the robot’s consecutive links. In accordance with the official dimensions and technical specifications of the KR4 R600 (Robotics Guangdong Co., Ltd., No. 3, Liaoxin Road, Beijiao Tow, Shunde District, Foshan City, Guangdong Province, China) manipulator, a standard D-H parameter model was established for the KUKA KR4 R600 robot.

The D-H model is predicated on the transformation from one joint coordinate frame to the next, which is achieved by utilizing four key parameters: link length $a$, link twist $\alpha$, link offset $d$, and joint angle $\theta$. In the case of a six-degree-of-freedom serial robot, the total transformation matrix T from the base frame to the end-effector frame can be obtained by the serial product of individual homogeneous transformation matrices.

The homogeneous transformation matrix A from link $i-1$ to link $i$ can be expressed as follows:

$$A_i={\mathrm{Rot}}_z({\theta }_i)\cdot {\mathrm{Trans}}_z(d_i)\cdot {\mathrm{Trans}}_x(a_i)\cdot {\mathrm{Rot}}_x({\alpha }_i)$$

(1)

Its specific expression is shown in Formula (2).

$$A_i=\left[\begin{array}{cccc}\cos {\theta }_i& -\sin {\theta }_i\cos {\alpha }_i& \sin {\theta }_i\sin {\alpha }_i& a_i\cos {\theta }_i\\ \sin {\theta }_i& \cos {\theta }_i\cos {\alpha }_i& -\cos {\theta }_i\sin {\alpha }_i& a_i\sin {\theta }_i\\ 0& \sin {\alpha }_i& \cos {\alpha }_i& d_i\\ 0& 0& 0& 1\end{array}\right]$$

(2)

where $\theta$ is the variable joint angle, while $a_i, {\alpha }_i, d_i$ are the fixed link parameters.

The standard D-H parameters for the KUKA KR4 R600 robot in this study are presented in

Table 1. D-H Parameters for the KUKA KR 4 R600 Robot.

$\mathit{i}$	${\mathit{a}}_{\mathit{i}}$	${\mathit{\alpha }}_{\mathit{i}}$ (mm)	${\mathit{d}}_{\mathit{i}}$ (mm)	$\mathit{\theta }$
1	180	0	−330	${\theta }_1$
2	90	0	0	${\theta }_2$
3	0	290	0	${\theta }_3-90$
4	90	20	−310	0
5	−90	0	0	${\theta }_5$
6	90	0	−75	${\theta }_6$

:

The robot’s Forward Kinematics model is the total homogeneous transformation matrix $T_6^0\left(\theta \right)$ from the base to the end-effector, as shown below:

$$T_6^0(\mathit{\theta })=A_1({\theta }_1)A_2({\theta }_2)A_3({\theta }_3)A_4({\theta }_4)A_5({\theta }_5)A_6({\theta }_6)=\left[\begin{array}{cc}R& P\\ 0& 1\end{array}\right]$$

(3)

where $\theta ={[{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5,{\theta }_6]}^T$ is the robot’s joint angle vector, R is the $3\times 3$ rotation matrix representing the orientation of the end-effector, and P is the $3\times 1$ position vector representing its Cartesian coordinates.

3.2. Three-Dimensional Manipulator Model Integration and Visualization

The 3D visual twin environment [1,36] under scrutiny in this study is conceptualized not as a static geometric representation but as a dynamic, functional virtual platform that integrates a precise kinematic model, realistic rendering, and behavior simulation. This environment is instantiated within a custom-developed Human–Machine Interface (HMI), which is illustrated in Figure 2. The HMI serves as the principal medium for real-time state monitoring, kinematic behavior validation, and the visualization of error compensation effects. Crucially, this interface paradigm obviates the need for static annotations on a standalone 3D model by presenting salient state variables—such as the robot’s real-time joint angles, end-effector coordinates, and predicted errors—as dynamic, contextual data overlays. The construction of this environment is characterized by a layered progression, with the ‘geometry-kinematics-behavior’ principle serving as the underlying tenet.

In order to accurately integrate the manipulator model into the 3D visualization framework, it is necessary to establish a rigorous correspondence between the physical joint axes of the robot and the generalized coordinates defined in the kinematic formulation. As illustrated in Figure 3, the KUKA KR4 R600 manipulator possesses six rotational axes (A1–A6), which are denoted as the joint variables ${\mathit{\theta }}_1–{\mathit{\theta }}_6$ in the mathematical model. Each joint axis (J1–J6) is explicitly identified in the figure, and the associated directions of rotation are indicated to preserve consistency between the physical configuration and the analytical description. This joint–parameter mapping provides an unambiguous basis for the subsequent construction of the kinematic chain, the formulation of the scene graph, and the real-time rendering of the manipulator’s motion within the virtual environment.

3.2.1. Geometric Morphology Reconstruction

The foundation of the twin environment’s high visual fidelity is the precise geometric morphology reconstruction of the physical robot. The present study employed advanced 3D reverse engineering techniques, including detailed geometric surveying and specialized 3D modeling software, to perform meticulous reconstruction of each individual link of the KUKA KR4 R600 robot, encompassing its base, arm segments, and wrist components. These highly detailed digital models were then processed and exported as a series of industry-standard mesh files in the .obj (Wavefront OBJ) format. Each .obj file represents an independent rigid body within the robot’s structure, meticulously documenting its three-dimensional appearance through comprehensive vertex, normal, and texture coordinate information. This compendium of digital assets collectively constitutes the static “digital skeleton” that underpins the dynamic digital twin.

3.2.2. Assignment of Kinematic Behavior

The objective of this stage is to imbue the static “digital skeleton” with the capability to simulate the complex, articulated movements of the real robot. To this end, the robot’s inherent kinematic constraints and hierarchical structure are explicitly linked to its geometric models using a declarative scene description methodology. The implementation utilizes a structured YAML (YAML Ain’t Markup Language) data file, which functions as the “kinematic blueprint” governing the digital twin’s dynamic behavior. The primary content defined within this configuration file includes:

• Scene Graph Topology: A tree-like hierarchical structure is meticulously constructed, extending from the robot’s fixed base to its movable end-effector. This is achieved by defining explicit parent–child relationships for each robot link, which dictate the chain of homogeneous transformations and enable forward kinematics computation.
• Joint Kinematic Parameters: The kinematic attributes of each joint are precisely defined within the YAML file. These include the joint’s positional offset relative to its parent node’s coordinate frame (directly corresponding to the link length $a$ and link offset $d$ parameters from the D-H model), and the axis of rotation vector that defines its mode of motion. These parameters rigorously govern the allowable degrees of freedom and spatial relationships between connected links.
• Binding of geometry and joints: It is essential that each .obj format geometric model file is accurately associated with its corresponding link node within the established scene graph topology. The model’s local pose is defined with respect to the origin of the link’s coordinate frame, ensuring precise alignment between the visual appearance and the underlying mathematical kinematic model.

3.3. Virtual Twin Environment Integration and Real-Time Dynamic Rendering

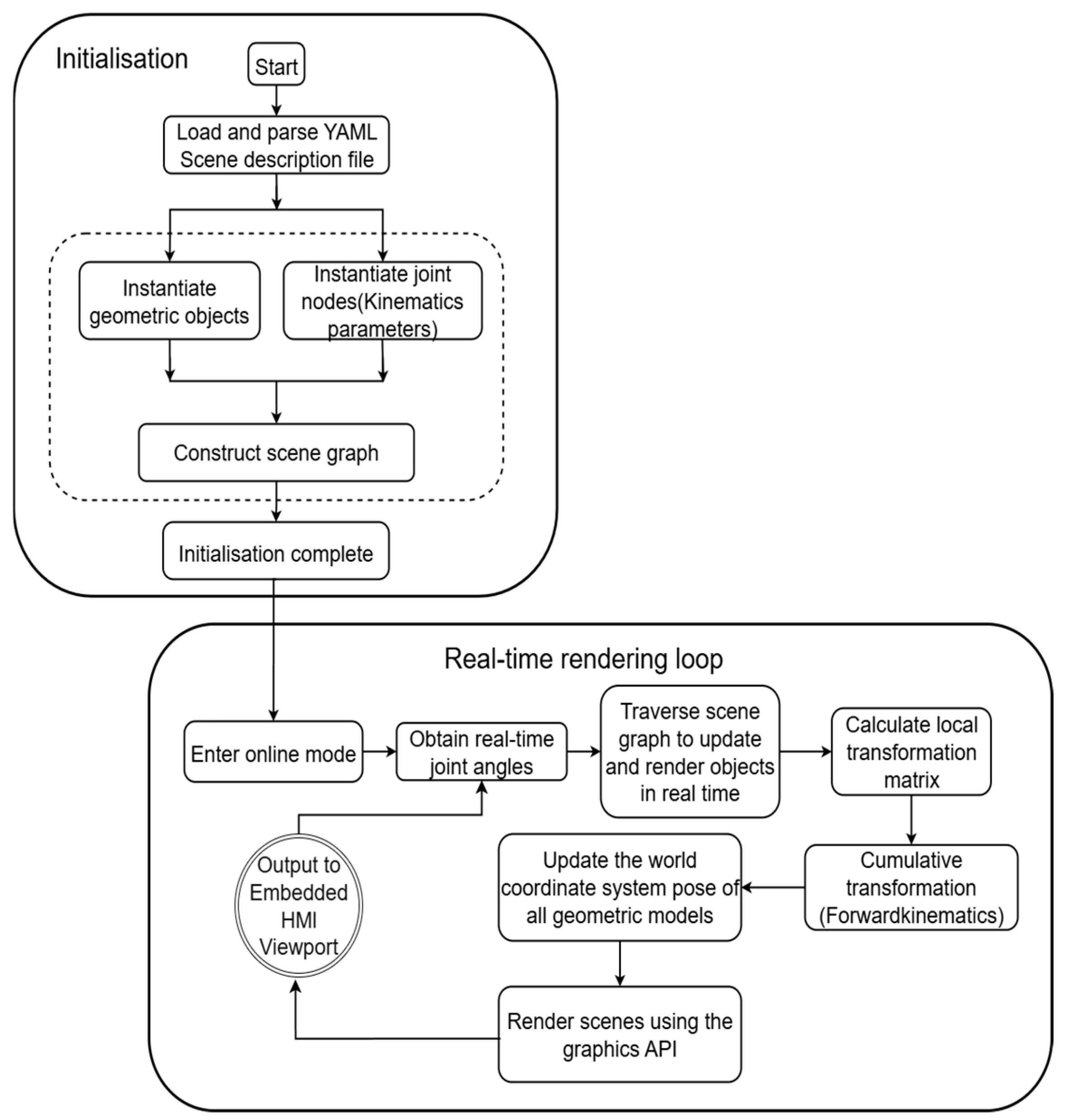
The final integration and operation of the virtual twin environment are orchestrated by a dedicated 3D rendering and simulation engine. The entire construction and operational workflow of this 3D visual twin environment follows a two-stage process, as schematically detailed in Figure 4.

During the initialization stage, the system first loads and parses the predefined YAML scene description file. This foundational process instantiates both the geometric objects representing the robot’s appearance and creates the kinematic joint nodes that define its articulated properties. Subsequently, the engine seamlessly integrates these components to construct a comprehensive Scene Graph, encapsulating the complete kinematic and hierarchical topology of the robot.

Upon entering online mode, the system initiates a continuous real-time rendering loop. In the context of this work, “real-time” operation is defined by a consistent update frequency of 10 Hz, corresponding to a 100 ms cycle time for data acquisition, processing, and visualization. In each frame of this loop, the engine acquires the latest joint-angle vector (${\theta }_{realtime}$) from the Physical Layer. It then traverses the Scene Graph to recursively perform Forward Kinematics (FK) calculations. This iterative process entails the precise computation of local homogeneous transformation matrices for each joint and their subsequent accumulation to accurately determine the global pose of every geometric object within the world coordinate system. Following the completion of this dynamic state update, the engine finally invokes the underlying graphics API to render the entire dynamically updated 3D scene into the embedded viewport of the HMI, thereby completing a full mapping from real-time physical data to high-fidelity virtual visuals.

3.4. Digital Twin Platform Construction

Based on the achieved high-fidelity, real-time synchronization between the digital model and the physical robot, this paper developed a comprehensive industrial robot digital twin platform. The overarching architecture of this platform, illustrating the interplay between its primary layers, is schematically depicted in Figure 5.

Within this architecture, the Personal Computer (PC) serves as the core computational and display carrier, hosting and executing the main digital twin application. This application seamlessly integrates the rendering of the virtual model, real-time kinematic simulation, data processing pipelines, and the Human–Machine Interaction (HMI) interface. The physical model, constituting the experimental equipment in the real industrial scenario, is primarily composed of the KUKA KR4 R600 industrial robot, its KR C4 controller, and the teach pendant for manual operation, which enables direct control of the physical robot by users.

The cornerstone for establishing the robust, bidirectional connection between the physical model and the digital model lies in a customized, high-frequency communication mechanism based on the Transmission Control Protocol/Internet Protocol (TCP/IP). The workflow initiates with an independent TCP server application deployed and running on the robot controller, specifically responsible for securely accessing the robot’s real-time internal status data. Concurrently, a TCP client module, integrated within the digital twin application on the PC, periodically sends data-reading requests to the controller server in a high-frequency polling manner. This establishes a continuous, real-time data stream from the physical world to the information space.

After that, an abstract real-time data stream is established between the physical world and the information space. This data stream contains all the real-time status information of the physical robot Error Prediction Calculation: Inputting the joint angles into the pre-trained machine learn primarily comprising the joint-angle vector (${\mathit{\theta }}_{realtime}$, as previously defined) and the nominal Cartesian pose. This nominal pose, which is computed by the controller’s internal kinematic model without accounting for real-world physical errors, will hereafter be denoted as $P_{nominal}$. The digital twin system on the PC obtains the required information from this data stream, and then completes a series of complex logical and arithmetic operations within its software architecture, including:

• Error Prediction Calculation: Inputting the joint-angle vector (${\mathit{\theta }}_{realtime}$) into the pre-trained machine learning model (GCE-Forest) to calculate the instantaneous positioning error.
• Multimodal Information Fusion and Display: Integrating and dynamically visualizing the original data, the predicted error data, and the error-compensated pose data on the Human–Machine Interaction interface, providing comprehensive operational insights.

Through this meticulously designed platform architecture, a robust, one-way, high-fidelity state mapping from the physical entity to the digital twin is achieved, forming the indispensable foundation for online error compensation.

4. Algorithm

4.1. Robot Point Data Collection

To construct a high-dimensional dataset that can accurately represent the error characteristics of the robot, this study designed a rigorous data collection scheme. The experimental platform (as shown in Figure 6) consists of a KUKA KR4 R600 robot, a laser tracker, and supporting analysis software. The laser tracker provides a true-value reference for measuring the end-pose of the robot. The collection process begins with planning a series of discrete test points in the robot’s workspace that can fully stimulate the movement of each joint. Subsequently, a 0.5-inch Spherically Mounted Retroreflector (SMR) is installed on the end-flange of the robot. In the measurement software, a theoretical kinematic model of the robot is constructed based on the standard D-H parameters of the robot, and then the precise registration of the measurement coordinate system and the robot base coordinate system is completed. During the data collection phase, the robot moves and stops at each preset point in turn. The laser tracker conducts high-precision static measurements of the SMR at each point to obtain its actual position $P_{actual}$. At the same time, the corresponding joint-angle vector $\mathit{\theta }$ (Here, $\mathit{\theta }$ denotes the static joint-angle vector recorded at each sampled pose, distinct from the real-time stream ${\mathit{\theta }}_{realtime}$.) and nominal theoretical position $P_{nominal}$ are synchronously recorded from the robot controller. After completing the measurements of all points, data calculation and export are performed through software, ultimately forming a comprehensive dataset containing hundreds of samples. Each sample contains $P_{nominal}$, $P_{actual}$ two sets of associated data, providing a solid foundation for subsequent data-driven error modeling.

4.2. Construction of Error Prediction Model

Traditional robot error compensation methods, such as kinematic calibration based on parameter identification, can correct geometric errors to a certain extent. However, due to their fixed model structures, they struggle to capture complex, non-linear error components caused by non-geometric factors such as joint flexibility, backlash, and thermal effects. These non-geometric errors are often closely related to the specific joint configurations of the robot. To break through this bottleneck, data-driven modeling approaches offer a promising path. An initial approach, termed the Global Configuration-Error Mapping Network (GCEM-Net), utilizes a Multi-Layer Perceptron (MLP) and has demonstrated the feasibility of learning the error mapping. However, For comparative purposes experiments revealed that neural network models like MLP can be prone to overfitting on smaller datasets, potentially limiting their generalization capability on unseen trajectory data. To address this limitation and enhance the model’s robustness, this study proposes a more advanced data-driven modeling approach: the Global Configuration-Error Forest (GCE-Forest).

The core idea of GCE-Forest is to leverage the power of ensemble learning, specifically the Random Forest algorithm, to construct the end-to-end non-linear mapping function. Instead of relying on a single, complex model, GCE-Forest builds a multitude of individual decision trees during training and outputs the mean prediction of the individual trees. This “wisdom of the crowd” approach makes the model inherently more robust and less susceptible to overfitting. The innovation of this model lies in abstracting the error compensation problem into a high-dimensional function approximation problem. By leveraging the strong predictive power and generalization capability of the Random Forest ensemble, it directly learns the inherent laws of robot errors from a large amount of measured data, thus enabling comprehensive and more reliable prediction and compensation for the coupling effects of multiple error sources.

4.2.1. Mathematical Representation of the Error Mapping Model

The Proposed GCE-Forest Model

The GCE-Forest model is built upon the Random Forest algorithm, a powerful ensemble learning method known for its high accuracy and robustness against overfitting. The fundamental principle of a random forest is to construct a multitude of decision trees at training time and output the mean of the predictions from the individual trees for regression tasks. The construction of GCE-Forest involves two key stages: the training of individual regression trees and the ensemble prediction.

Individual Regression Tree Construction: Each decision tree $T_k$ in the forest is trained on a random bootstrap sample of the original training data. Furthermore, at each node of the tree, a random subset of features is selected to determine the best split, a technique that decorrelates the trees and is crucial for the algorithm’s performance.

The construction process for each individual regression tree in the forest is recursive. Starting from the root, the algorithm iteratively splits each node into two child nodes. For a given node m, the subset of the training data reaching this node is denoted as $Q_m$. The algorithm seeks to find an split, defined by a feature $j$ and a threshold $t_j$, that partitions the data $Q_m$ into two subsets, $Q_m^{left}(\theta )$ and $Q_m^{right}(\theta )$, where $\theta =(j,t_j)$.

$$\begin{array}{c}{Q}_m^{left}(\theta )=\{(X_i,y_i)\in Q_m\left|X_{i,j}\le t_j\right.\}\\ Q_m^{right}(\theta )=\{(X_i,y_i)\in Q_m\left|X_{i,j}>t_j\right.\}\end{array}$$

(4)

The quality of a split is measured by an impurity function. For regression tasks, the standard impurity measure is the Mean Squared Error (MSE). The goal is to find the parameters ${\theta }^{*}$ that minimize this impurity:

$$G(Q_m,\theta )={\displaystyle \frac{n_m^{left}}{n_m}}MSE(Q_m^{left})+{\displaystyle \frac{n_m^{right}}{n_m}}MSE(Q_m^{right})$$

(5)

where $MSE(Q)={\displaystyle \frac{1}{\left|Q\right|}}{{\displaystyle {\sum }_{(X_i,y_i)\in Q}‖y_i-{\overline{y}}_Q‖}}^2$, and ${\overline{y}}_Q$ is the mean of the target values in set $Q$. The optimal split ${\theta }^{*}$ is found by:

$${\theta }^{*}=\arg \underset{\theta }{\min }G(Q_m,\theta )$$

(6)

This process is applied recursively to all new nodes until a stopping criterion is met, such as reaching a maximum depth or a minimum number of samples per leaf.

Ensemble Prediction: Once the forest, a collection of $N_T$ decorrelated trees $\{T_1,T_2,\dots ,T_{N_T}\}$, is trained, it can be used for prediction. For a new input joint vector $\theta$, each tree $T_k$ traverses down to a leaf node and provides an error prediction $\Delta P_k=T_k(\theta )$, which is typically the mean of the target values of the training samples in that leaf. The final prediction of the GCE-Forest is the average of all these individual tree predictions, which reduces the variance of the final model:

$$\Delta P=f_{GCE-Forest}(\theta )={\displaystyle \frac{1}{N_T}}{\displaystyle \sum _{k=1}^{N_T}{T}_k(\theta )}$$

(7)

This ensemble strategy is the key to the model’s high performance. In this implementation, the GCE-Forest is configured with 100 decision trees, a value found to provide a strong balance between predictive accuracy and computational cost.

The Baseline MLP Model (GCEM-Net)

For comparative purposes, a Multi-Layer Perceptron (MLP) model is also implemented, termed GCEM-Net. As a universal function approximator, the MLP’s multi-layer structure and non-linear activation units enable it to model complex relationships. The specific topology of our baseline MLP is as follows:

• Input layer: Contains 6 neurons, corresponding to the 6-degree-of-freedom joints of the robot.
• Hidden layers: Consists of two hidden layers with 150 and 75 neurons, respectively. These layers adopt the Rectified Linear Unit (ReLU) as the activation function.
• Output layer: Contains 3 neurons, corresponding to the predicted Cartesian errors in three dimensions $({\delta }_x,{\delta }_y,{\delta }_z)$. This layer uses a linear activation function.

The final output of the MLP model can be represented as:

$$\Delta P=f_{MLP}(\theta ;W,b)$$

(8)

where $W$ and $b$ represent the sets of all weight matrices and bias vectors in the network, learned through training. By comparing the performance of GCE-Forest against this well-defined MLP baseline, a rigorous evaluation of the advantages of the proposed approach was enabled.

4.3. Model Training and Data Preprocessing

In order to enable the constructed GCEM-Net to effectively learn the error mapping rules from the original data, this study adopted the Python-based Scikit-learn machine learning framework and designed a rigorous process for data preprocessing, model training, and validation (as shown in Figure 7).

4.3.1. Data Preprocessing and Feature Engineering

In this study, after integrating 418 sets of valid [joint angle-theoretical pose-actual pose] sample data from the collected data, the preprocessing steps were initiated (Figure 7):

Target Vector Generation: According to formula $\Delta P_{actual}=P_{actual}-P_{nominal}$, the three-dimensional Cartesian error vector $\Delta \mathit{P}$ corresponding to each sample was calculated as the learning target of the model.

Feature Normalization: Given the significant differences in dimensions and scales between the input features (joint angles) and the output targets (positioning errors), this paper adopted the Z-Score normalization method to process them independently. This transformation adjusts the distribution of features to a standard normal distribution with a mean of 0 and a variance of 1. The formula is as follows:

$$x^{\prime }={\displaystyle \frac{x-{\mu }_{train}}{{\sigma }_{train}}}$$

(9)

where $x$ is the original data point, is the standardized data point, ${\mu }_{train}$ and ${\sigma }_{train}$ are the mean and standard deviation learned from $x^{\prime }$ the training set for this feature, respectively.

4.3.2. Training, Validation and Performance Evaluation

To objectively evaluate and compare the predictive capabilities of the proposed GCE-Forest and the baseline MLP model, a rigorous training and validation protocol was established. The preprocessed dataset, containing 451 samples, was partitioned into a training set (80%) and a test set (20%) using a fixed random seed to ensure the consistency and fairness of the comparison.

Both models were trained on the same training set. The MLP network parameters were iteratively optimized via the back-propagation algorithm using the Adam optimizer, aiming to minimize the Mean Squared Error (MSE) loss function. Concurrently, the GCE-Forest model was trained by constructing its ensemble of 100 decision trees.

Upon completion of training, the performance of each model was comprehensively evaluated on both the training and test sets. Three core metrics were adopted for this evaluation: the coefficient of determination ($R^2$ Score), which measures the proportion of variance in the dependent variable that is predictable from the independent variables; the Root Mean Squared Error (RMSE), which provides a measure of the average magnitude of the prediction errors in physical units (mm); and the Mean Absolute Error (MAE), which represents the average of the absolute differences between predicted and actual values. The comparative results are presented in

Table 2. Comparative performance evaluation of predictive models.

Model	Dataset	${\mathit{R}}^2$	RMSE (mm)	MAE (mm)
MLP	Training Set	0.8248	0.0543	0.0270
	Test Set	0.6899	0.0805	0.0449
GCE-Forest	Training Set	0.9414	0.0324	0.0129
	Test Set	0.7469	0.0726	0.0361

.

4.3.3. Result Analysis and Model Persistence

The quantitative results detailed in Table 2 provide a clear and compelling basis for analyzing the performance of the two models. The baseline MLP model demonstrated a respectable fitting capability, achieving an $R^2$ score of 0.8248 on the training data. This indicates that the neural network architecture is indeed capable of learning the complex, non-linear relationship between the robot’s joint configuration and its positioning error. However, a noticeable performance degradation was observed on the test set, where the $R^2$ score dropped to 0.6899. This gap suggests that the MLP model, while powerful, exhibits a tendency towards overfitting on the available dataset, thus limiting its ability to generalize to new, unseen data.

In stark contrast, the proposed GCE-Forest model delivered a markedly superior performance on the crucial test set. It achieved an $R^2$ score of 0.7469, explaining nearly 75% of the error variance, and reduced the RMSE to 0.0726 mm. These figures represent a significant improvement over the MLP baseline, confirming the GCE-Forest’s enhanced generalization capability. While the GCE-Forest model shows a near-perfect fit on the training data ($R^2$ = 0.9414), a characteristic of the Random Forest algorithm, its superior performance on the test set is the decisive factor. It demonstrates that the ensemble approach effectively mitigates the risk of overfitting and produces a more reliable predictive model.

Based on this comprehensive evaluation, the GCE-Forest model was unequivocally identified as the superior approach for this application. Consequently, the final products of the training process—the serialized GCE-Forest model and its corresponding input and output data scalers—are the components selected for persistence. This trained inference engine is then deployed as the intelligent core of the online real-time compensation system, ensuring that the digital twin is endowed with the most accurate and robust error prediction capability developed in this study.

5. Experimental Results and Analysis

5.1. Random Trajectory Accuracy Verification Experiment

To comprehensively evaluate the actual performance of the GCEM-Net error compensation system proposed in this paper under dynamic conditions, a verification experiment of random trajectory tracking accuracy based on the methodology of online synchronous comparison was designed and implemented. This method utilizes the data-processing sequence executed by the digital twin system within each sampling period (100 ms). That is, from the real-time acquisition of joint angles ${\theta }_{realtime}$ and nominal poses $P_{no\min al}$, to the real-time invocation of the GCEM-Net inference engine to calculate the predicted error $P_{predicted}(t)$ and then to the generation of the pose $P_{actual\_compensated}(t)$ after error compensation. As a result, during the random motion trajectory of the robot, two trajectory data sequences before and after compensation can be synchronously collected.

In the experiment, the user operates the teach pendant to make the robot continuously move along a free-form space curve with multiple segments of different curvatures, so as to fully stimulate the non-linear coupling dynamics of each joint. During this process, the system records the complete nominal pose sequence $P_{nominal}(t)$ and the pose sequence $P_{actual\_compensated}(t)$ after compensation in real-time at a frequency of 10 Hz. This experimental design of online synchronous comparison not only significantly improves the experimental efficiency but also fundamentally eliminates the operational inconsistencies that may be introduced by repeated experiments, ensuring high temporal alignment accuracy and inherent comparability of the data used for subsequent error analysis and performance validation.

5.2. Qualitative Analysis: 3D Spatial Trajectory Comparison

First, the end-effector trajectories of the robot before and after compensation were visualized in three-dimensional space to more conveniently and intuitively evaluate the macroscopic effect of the compensation algorithm. Figure 8 presents a comparative analysis, where the nominal trajectory output by the robot controller is compared against the compensated trajectories generated by the baseline MLP model and the proposed GCE-Forest model, respectively.

As illustrated in Figure 8a, the trajectory compensated by the MLP model exhibits a clear spatial deviation from the nominal trajectory. While the algorithm attempts to correct errors, the resulting trajectory (red line) does not consistently track the intended nominal trajectory (blue line), showing noticeable and non-uniform separation throughout the motion. This indicates that although the MLP model captures some error patterns, its compensation may be suboptimal or affected by overfitting tendencies, resulting in an inaccurate trajectory. The starting point is defined as the first sampled point after compensation, which, due to the random nature of the robot’s spatial motion, does not necessarily coincide with one of the trajectory endpoints.

In contrast, Figure 8b demonstrates the superior performance of the proposed GCE-Forest model. The compensated trajectory (red line) is almost fully aligned with the nominal trajectory (blue line) across the entire workspace. This high degree of overlap, from the starting point through to the distinct theoretical and compensated end points, confirms that the GCE-Forest model provides a more accurate and reliable correction than the MLP baseline.

It is worth noting that only one end point, explicitly labeled in the figures, represents the actual termination of the trajectory. The other two extremities shown correspond to the robot’s motion limits in the respective directions, rather than to true start or end points of the trajectory. This clarification, together with the explicit labeling of the starting point, theoretical end point, and compensated end point in Figure 8, eliminates potential ambiguity. Moreover, the figures serve two primary purposes: (i) to provide an intuitive comparison of the robot’s motion with and without compensation, and (ii) to enable a direct comparison between the MLP and GCE-Forest compensation models. These enhancements highlight the superior accuracy and robustness of the Random Forest–based GCE-Forest approach compared to the MLP method in dynamic trajectory correction.

5.3. Time-Domain Error Characteristic Analysis

To further investigate the dynamic characteristics of the predicted errors from each model, the spatial correction quantity and its constituent axial components were plotted against the time step. This side-by-side comparison, presented in Figure 9 and Figure 10, reveals profound differences in the error patterns learned by the two models.

Figure 9 provides a direct comparison of the total spatial correction magnitude predicted by each model. The prediction from the MLP model, shown in Figure 9a, is notably large, with values fluctuating between 1.35 mm and 1.7 mm. The curve exhibits a relatively smooth profile, suggesting that the MLP has learned a generalized, large-scale error trend. In sharp contrast, the prediction from the proposed GCE-Forest model, seen in Figure 9b, is significantly smaller in magnitude, primarily ranging from 0.185 mm to 0.22 mm. This more conservative and realistically scaled prediction aligns better with the expected error range of a well-maintained industrial robot. Furthermore, the GCE-Forest’s prediction curve is not smooth; instead, it is characterized by distinct steps and sharp transitions, indicating that it has captured more detailed, configuration-dependent error dynamics.

A decomposition of the error into its axial components, as shown in Figure 10, reinforces these findings. The MLP model in Figure 10a attributes the majority of the error to the X-axis (approx. 1.2 mm) and Z-axis (approx. −0.9 mm), with relatively smooth variation over time. Conversely, the GCE-Forest model in Figure 10b predicts much smaller error components on all axes (all under 0.15 mm) and again displays the step-like, dynamic behavior that corresponds to changes in the robot’s kinematic state. This ability of GCE-Forest to decouple and independently predict such fine-grained, anisotropic errors is key to its superior compensation effect.

In summary, the time-domain analysis highlights the fundamental difference between the two models. While the MLP learns a smooth, large-scale approximation of the error, potentially influenced by overfitting, the GCE-Forest captures a more detailed, configuration-sensitive, and realistically scaled error profile. This superior learning capability is the primary reason for the GCE-Forest’s more effective and reliable performance in dynamic trajectory compensation.

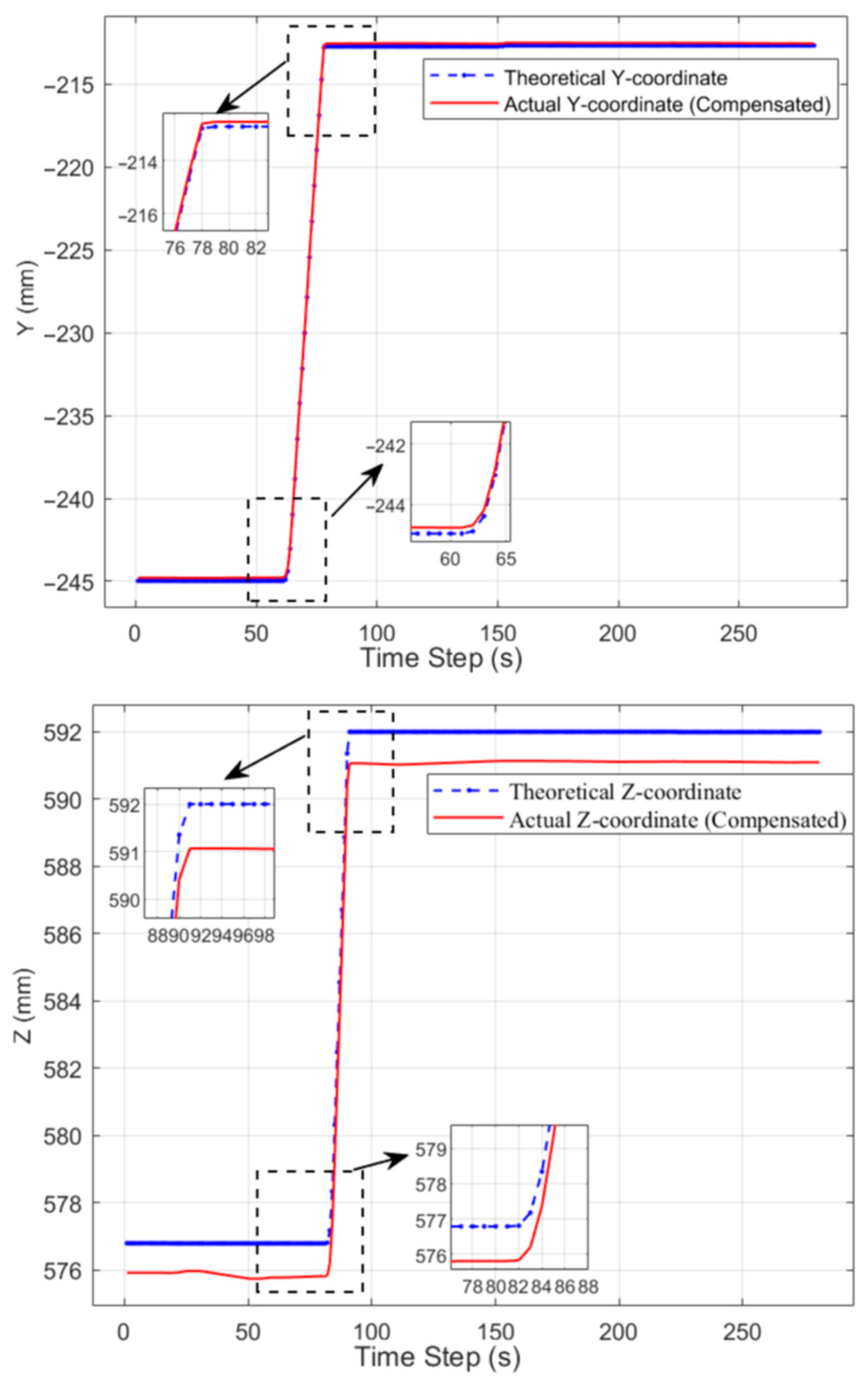
5.4. Micro-Analysis of Axis Tracking Accuracy

To deconstruct the compensation mechanism of each model at a microscopic level, a per-axis comparison was conducted between the nominal trajectory and the compensated trajectories. Results for the baseline Multi-Layer Perceptron (MLP) model and the proposed Global Configuration-Error Forest (GCE-Forest) are presented in Figure 11 and Figure 12, respectively.

An analysis of the MLP model’s performance, as depicted in Figure 11, reveals a critical characteristic of its compensation behavior. Although the compensated trajectory (red dashed line) generally follows the profile of the nominal trajectory (blue solid line), a distinct and quasi-constant DC offset is observable across all three axes. This systematic deviation is particularly pronounced in the Z-axis, where the compensated trajectory maintains a consistent upward shift. This phenomenon suggests that the MLP model primarily learns a large-scale, averaged correction from the training data. This behavior is likely a consequence of the model’s overfitting tendency, causing it to apply a generalized but imprecise correction vector across the entire workspace, thereby failing to adapt to configuration-specific error variations.

In striking contrast, the results for the GCE-Forest model, illustrated in Figure 12, demonstrate a significantly higher degree of tracking accuracy. The compensated trajectory (blue solid line) and the nominal trajectory (red dashed line) are in remarkably close agreement. The large systematic offsets observed with the MLP model are almost entirely eliminated. The zoomed-in insets further confirm that the GCE-Forest’s compensation is highly precise, with the compensated trajectory tracking the nominal trajectory with exceptional fidelity, even during periods of high dynamics and at geometric corners.

This micro-level analysis confirms that the GCE-Forest model excels not only in predicting the correct error magnitude but also in accurately capturing its complex, state-dependent nature. It effectively mitigates both systematic steady-state errors—manifested as the DC offset—and tracks dynamic error components. This refined compensation capability, clearly visualized at the per-axis level, is the key determinant of the superior performance of the proposed GCE-Forest system.

5.5. Comprehensive Quantitative Evaluation

To provide a conclusive quantitative assessment of the overall compensation effect, a statistical evaluation was performed on the trajectory data. The core performance metrics for the nominal trajectory error, as predicted by each model, and the compensated residual error are summarized in

Table 3. Quantitative comparison of trajectory errors for the random curve.

Error Metric (mm)	Model	Nominal Trajectory Error	Compensated Residual Error
Max Error	MLP	1.7121	1.2443
	GCE-Forest	0.2177	1.2486
Mean Error	MLP	1.4889	0.0843
	GCE-Forest	0.1977	0.0845
Std. Dev.	MLP	0.1109	0.2188
	GCE-Forest	0.0084	0.2194

.

The quantitative data in Table 3 offers decisive evidence of the proposed GCE-Forest model’s superior diagnostic accuracy. A critical comparison is found in the “Nominal Trajectory Error” columns, which represent each model’s estimate of the robot’s inherent error. The GCE-Forest model predicts a mean error of only 0.1977 mm, substantially smaller and significantly more plausible than the 1.4889 mm predicted by the MLP. This finding corroborates the preceding qualitative analysis, confirming that GCE-Forest provides a more veracious diagnosis of the robot’s error profile. An examination of the “Compensated Residual Error,” which reflects the final tracking precision, reveals that both models achieve a nearly identical and highly effective mean residual error of approximately 0.084 mm. This demonstrates that both methods are capable of producing a smooth final trajectory. However, the GCE-Forest accomplishes this outcome by applying a much smaller and more precise correction, as evidenced by its lower nominal error prediction, highlighting the efficiency and targeted nature of its compensation mechanism. Furthermore, it is noteworthy that the standard deviation of the nominal error predicted by GCE-Forest (0.0084 mm) is substantially lower than that of the MLP (0.1109 mm). This implies that the GCE-Forest’s error predictions are not only smaller in magnitude but also significantly more stable throughout the trajectory.

In conclusion, based on the mean residual error of the final compensated trajectory, the GCE-Forest system successfully reduced the robot’s positioning error to 0.0845 mm. Relative to its own more realistic error estimate of 0.1977 mm, this represents an accuracy improvement of 57.25%. This achievement, combined with its superior diagnostic capabilities, firmly establishes the GCE-Forest as a more effective and reliable solution for dynamic robot error compensation.

6. Conclusions

This paper addresses the persistent challenge of positioning inaccuracy in industrial robots, a problem rooted in the discrepancy between their nominal kinematic models and physical realities. A novel online error compensation system integrating machine learning with digital twin technology was proposed and implemented to overcome this limitation. By constructing a high-fidelity digital twin of a KUKA KR4 R600 robot, this system provides a robust platform for the real-time, synchronous monitoring and intelligent correction of robot motion.

The primary contribution of this research is the development and validation of the Global Configuration-Error Forest (GCE-Forest), a purely data-driven model for predicting and compensating for dynamic trajectory errors. This work introduces a non-invasive and model-agnostic paradigm for accuracy enhancement by successfully reframing the complex error compensation problem as an end-to-end function approximation task. The GCE-Forest model, based on the Random Forest algorithm, circumvents the need for intricate physical parameter identification and demonstrates a potent capability to learn the non-linear mapping from the robot’s joint space to its Cartesian error space.

Through rigorous comparative experiments against a baseline Multi-Layer Perceptron (MLP), the superiority of the GCE-Forest was unequivocally established. The key findings are twofold:

• Superior Diagnostic Accuracy: The GCE-Forest yielded a significantly more plausible and stable diagnosis of the robot’s inherent positioning error, estimating a mean error of 0.1977 mm compared to the 1.4889 mm estimated by the MLP. This demonstrates an enhanced ability to capture true error characteristics while mitigating overfitting.
• Effective Compensation Performance: The system successfully reduced the average spatial positioning error of the end-effector to 0.0845 mm. This remarkable result, achieved via a more precise and targeted correction mechanism, confirms the model’s efficacy in dynamic operational scenarios.

Building upon these validated capabilities, several critical avenues for future research are identified to enhance the proposed method’s generalizability and robustness in diverse industrial settings.

Firstly, to address data density challenges inherent in high-dimensional mapping, future efforts will explore strategies to augment the training dataset. Secondly, for more comprehensive experimental validation, subsequent investigations will rigorously evaluate the method’s performance under varying dynamic conditions. This will entail accounting for different robot speeds and external payloads, and assessing efficacy across diverse trajectories. Ultimately, these future work are committed to addressing identified limitations, ensuring continuous advancement and practical utility of data-driven robotic trajectory error prediction and compensation. This research provides a solid foundation for the practical implementation of high-precision, data-driven error compensation, presenting significant potential for advancing the capabilities of industrial robots in demanding applications.