Hierarchical Reinforcement Learning-Based Energy Management for Hybrid Electric Vehicles with Gear-Shifting Strategy
Abstract
1. Introduction
- The gear-shifting strategy is incorporated into the EMS, enabling more efficient coordination between the engine and motor across different gear ratios, thereby enhancing overall fuel economy and vehicle performance.
- A hierarchical reinforcement learning (HRL) framework with a hybrid action space is introduced, combining the strengths of SAC and DQN to achieve simultaneous optimization of continuous (engine torque) and discrete (gear selection) control actions.
- Through offline training and online testing, the proposed HRL approach is validated for its practicality and superiority in managing hybrid action spaces. Its adaptability is further demonstrated under long-duration and complex urban bus driving conditions.
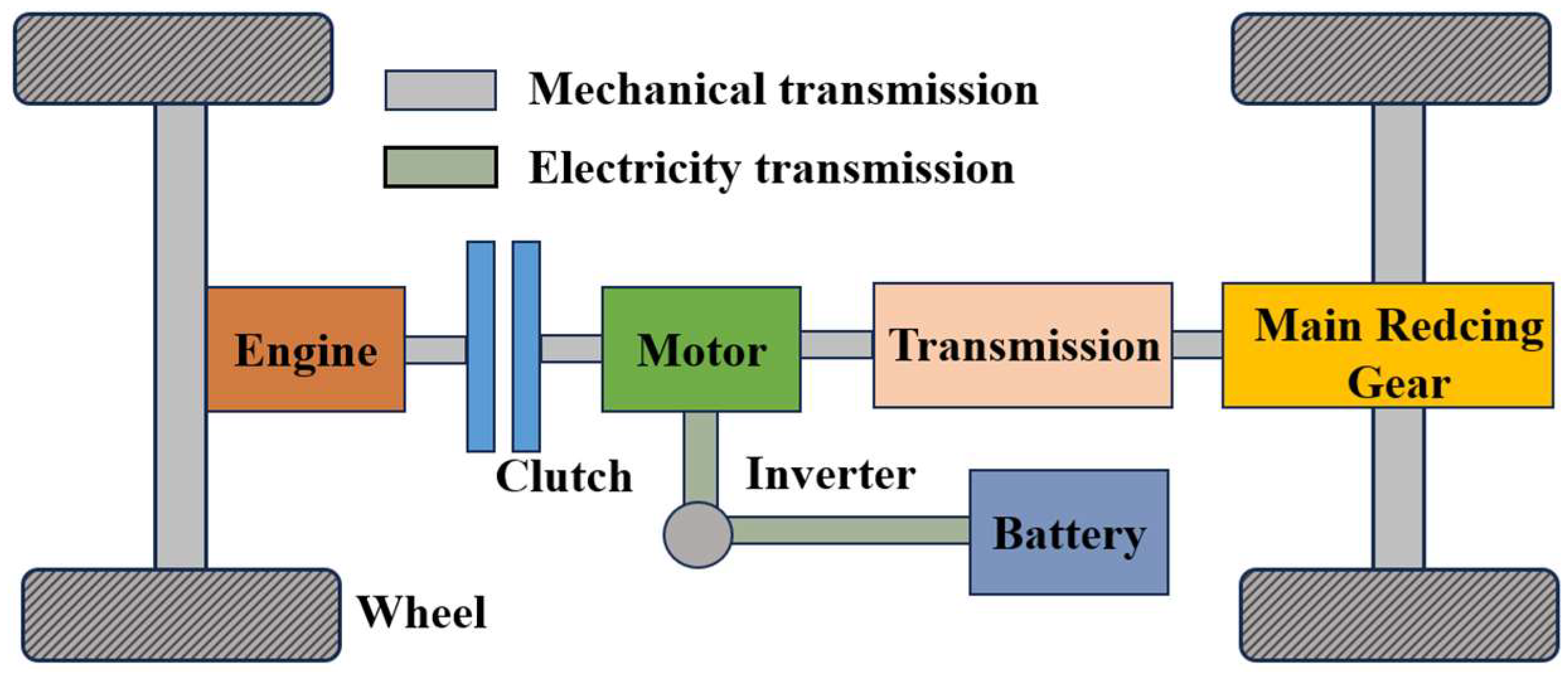
2. Powertrain Modeling and Problem Formulation
2.1. Power Demand Model
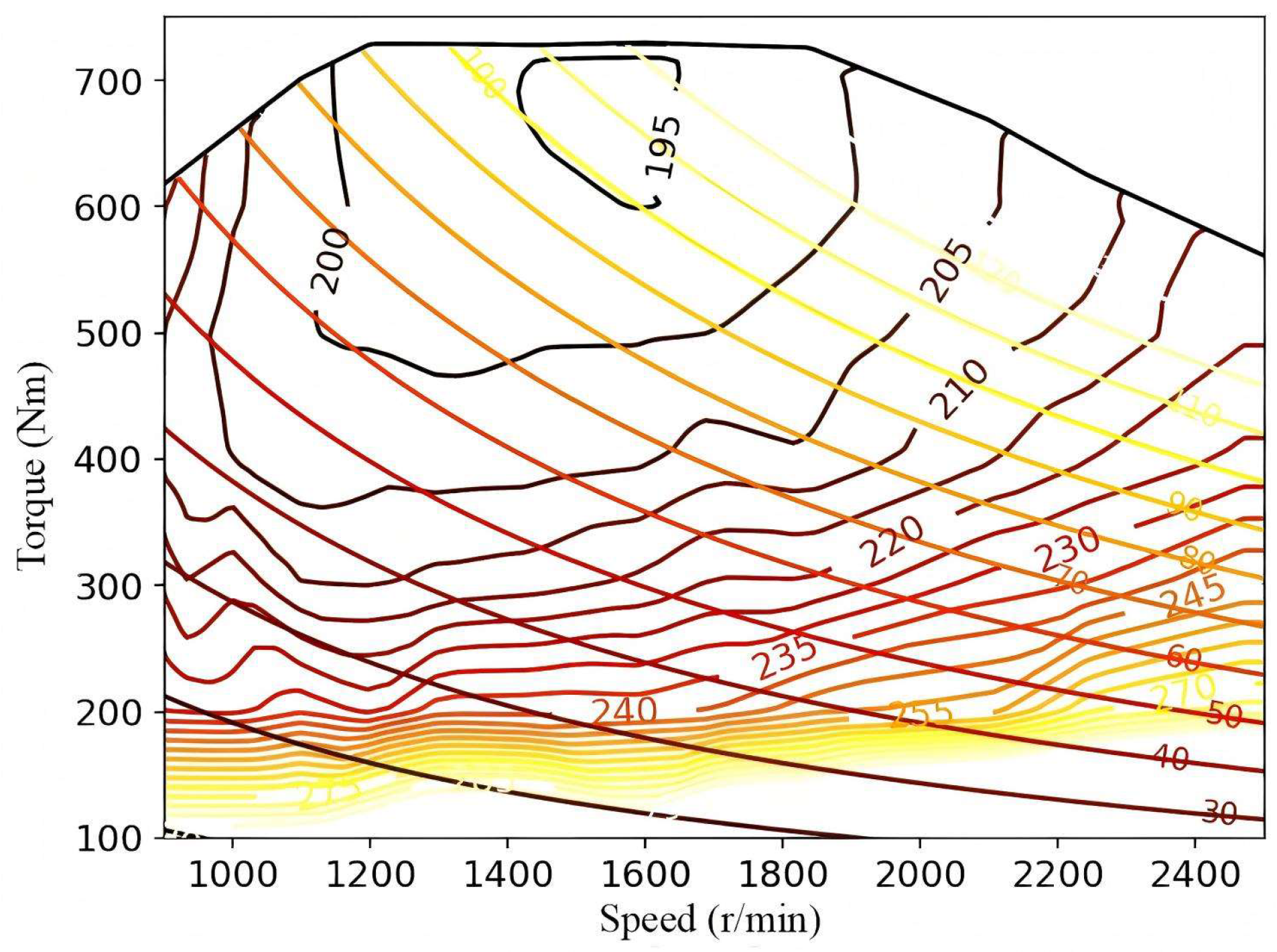
2.2. Engine Model
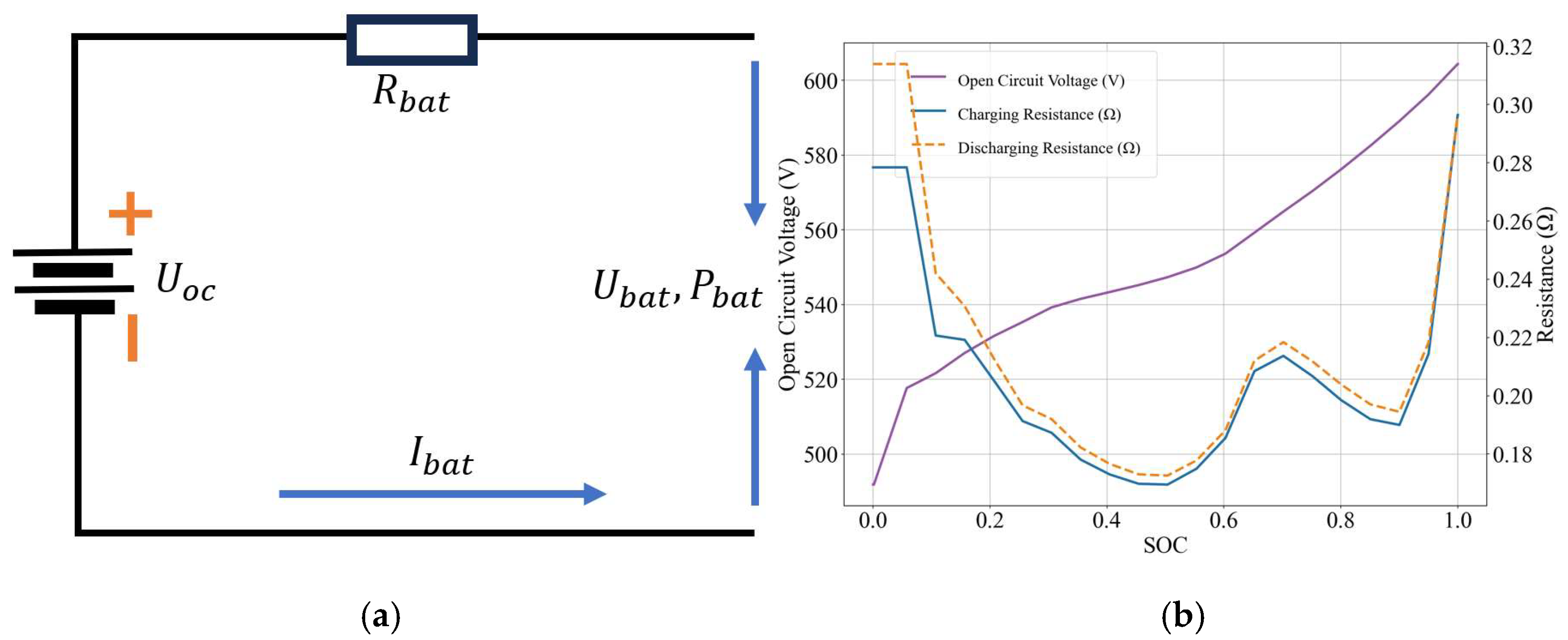
2.3. Battery Model
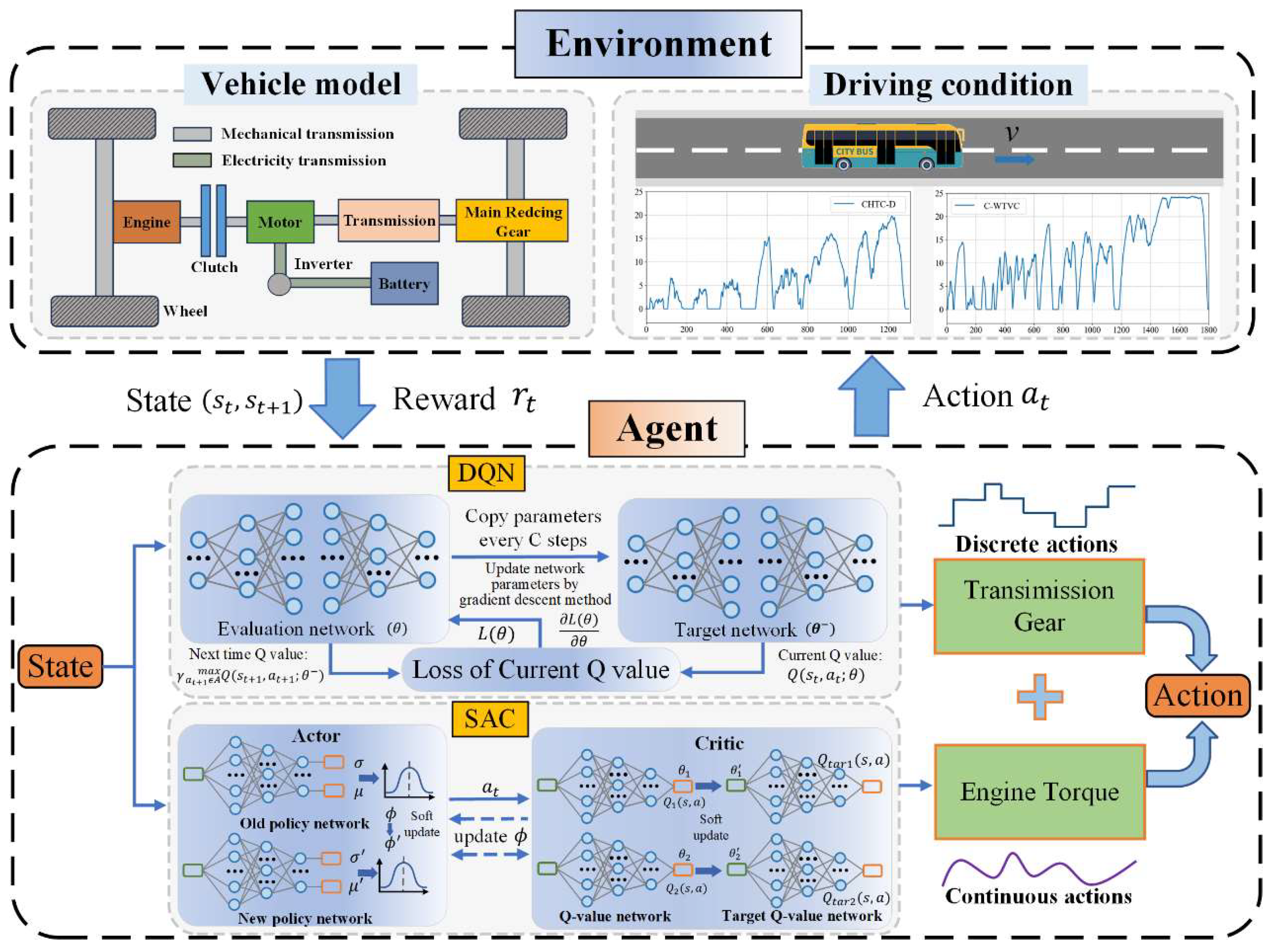
3. Energy Management Strategy with Gear-Shifting
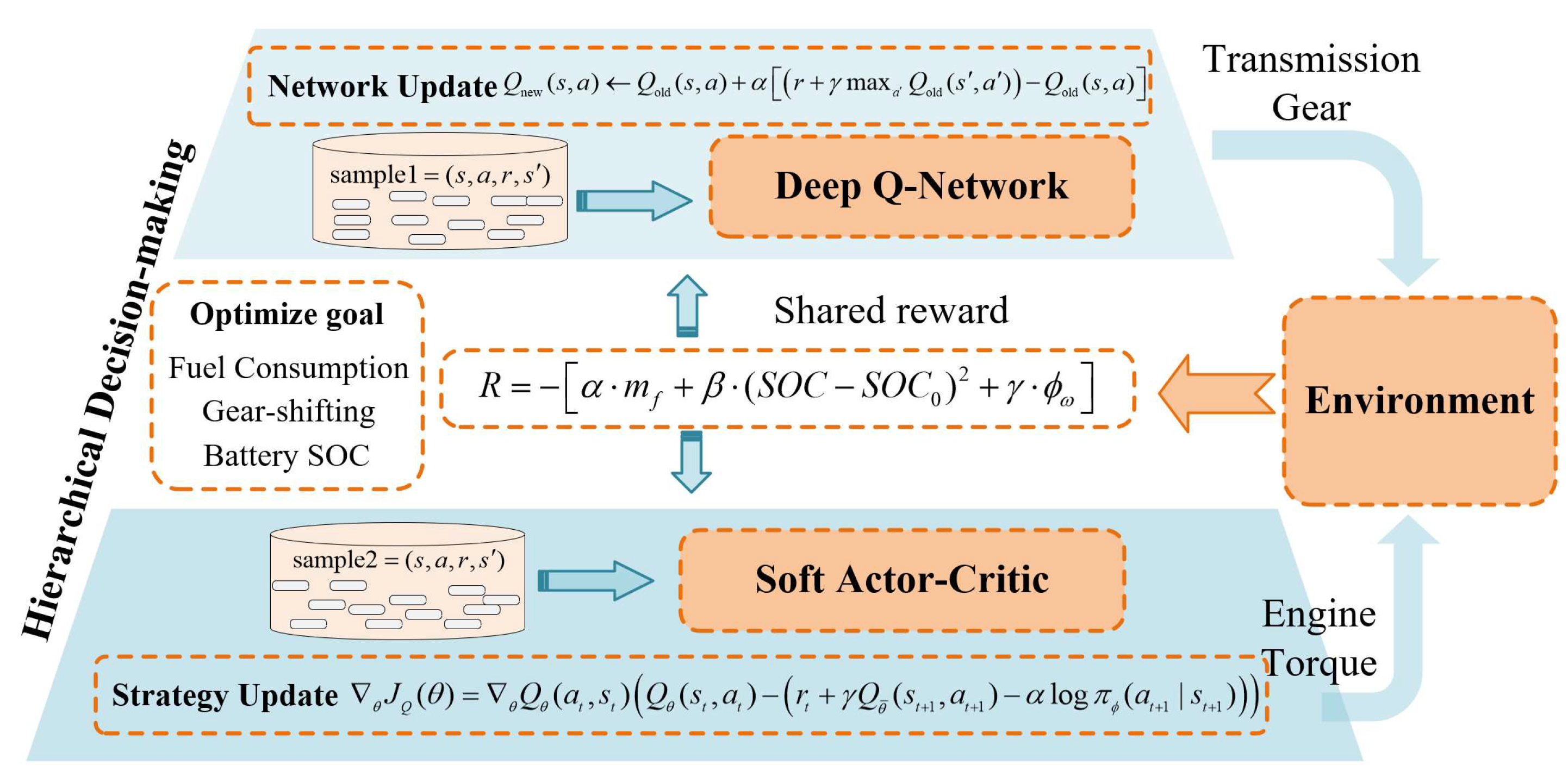
3.1. Deep Q-Network
3.2. Soft Actor–Critic
3.3. Energy Management Strategy Based on Hierarchical Reinforcement Learning
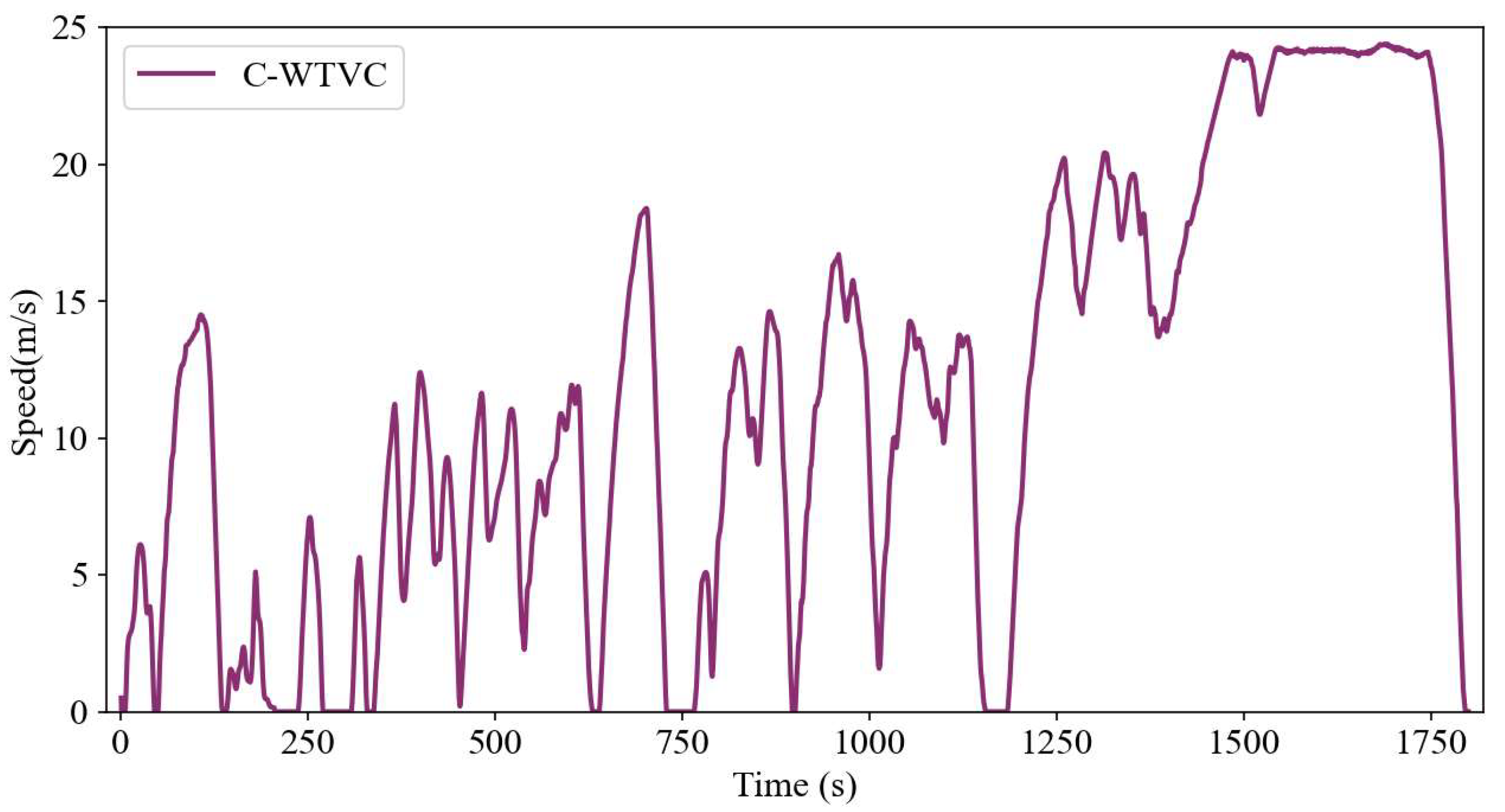
4. Simulation and Evaluation
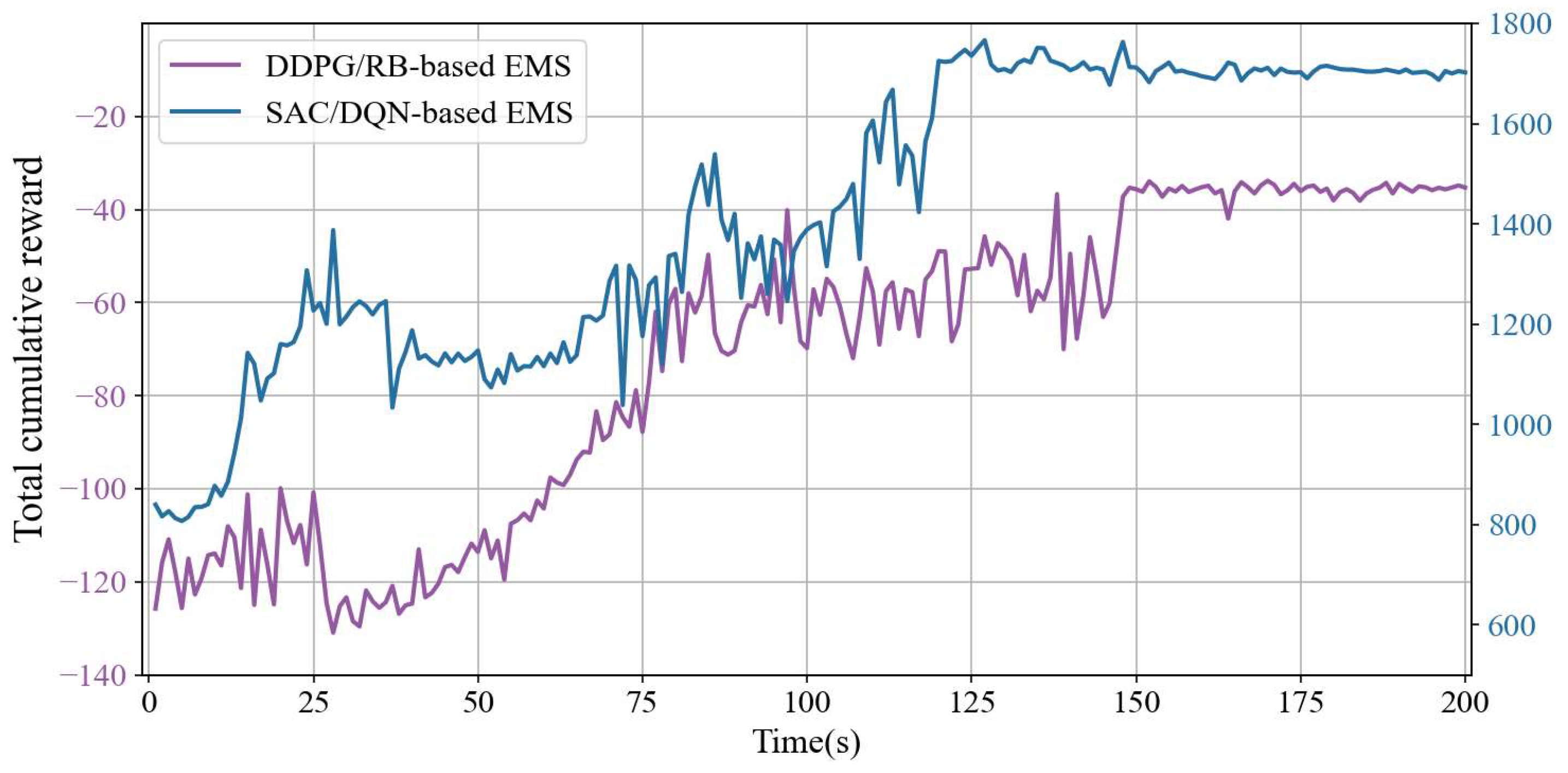
4.1. Offline Training Results and Analysis
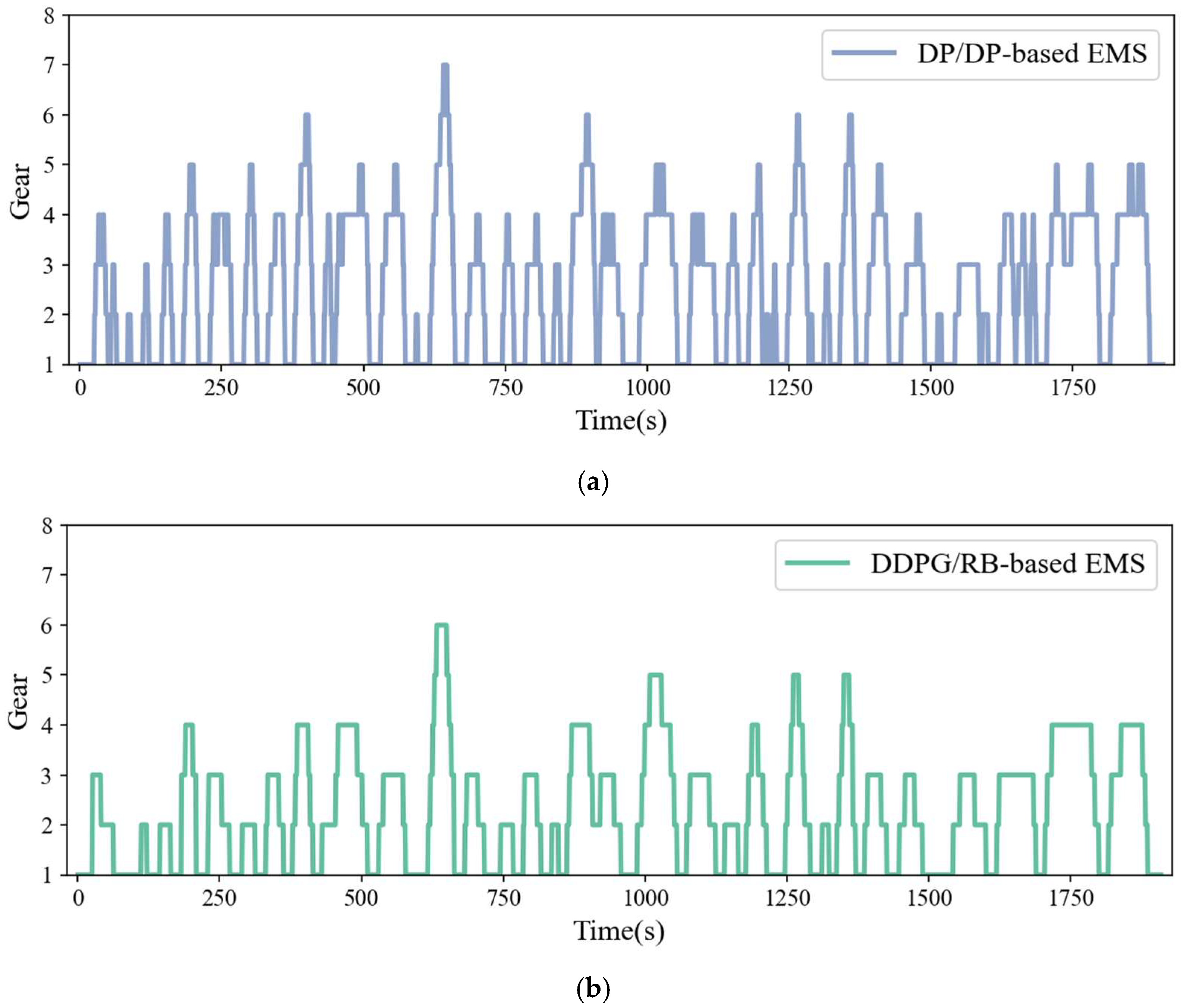
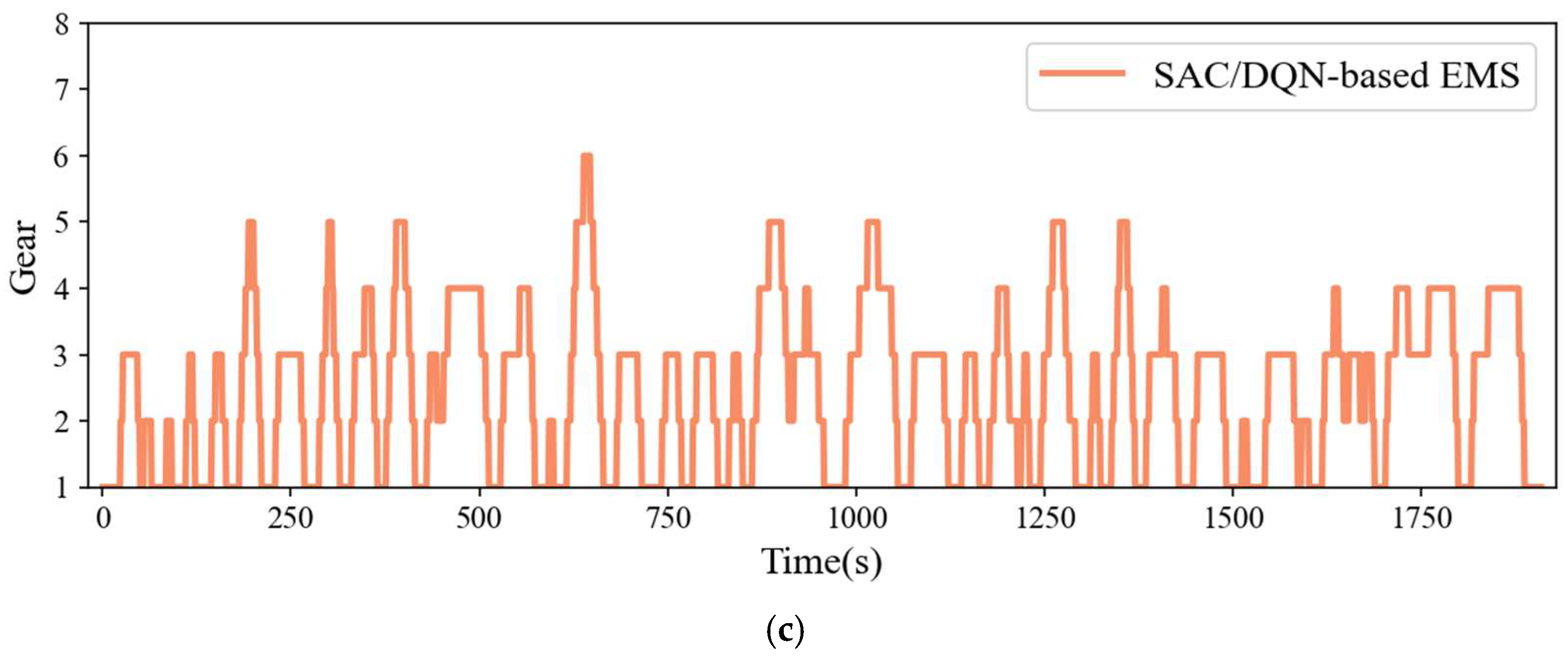
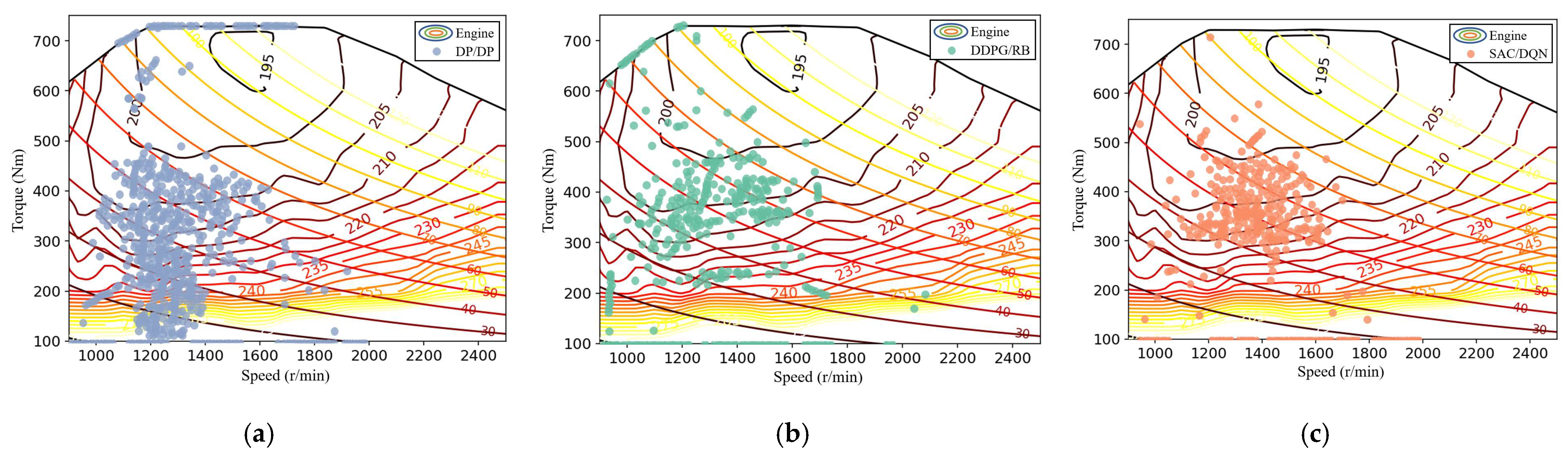
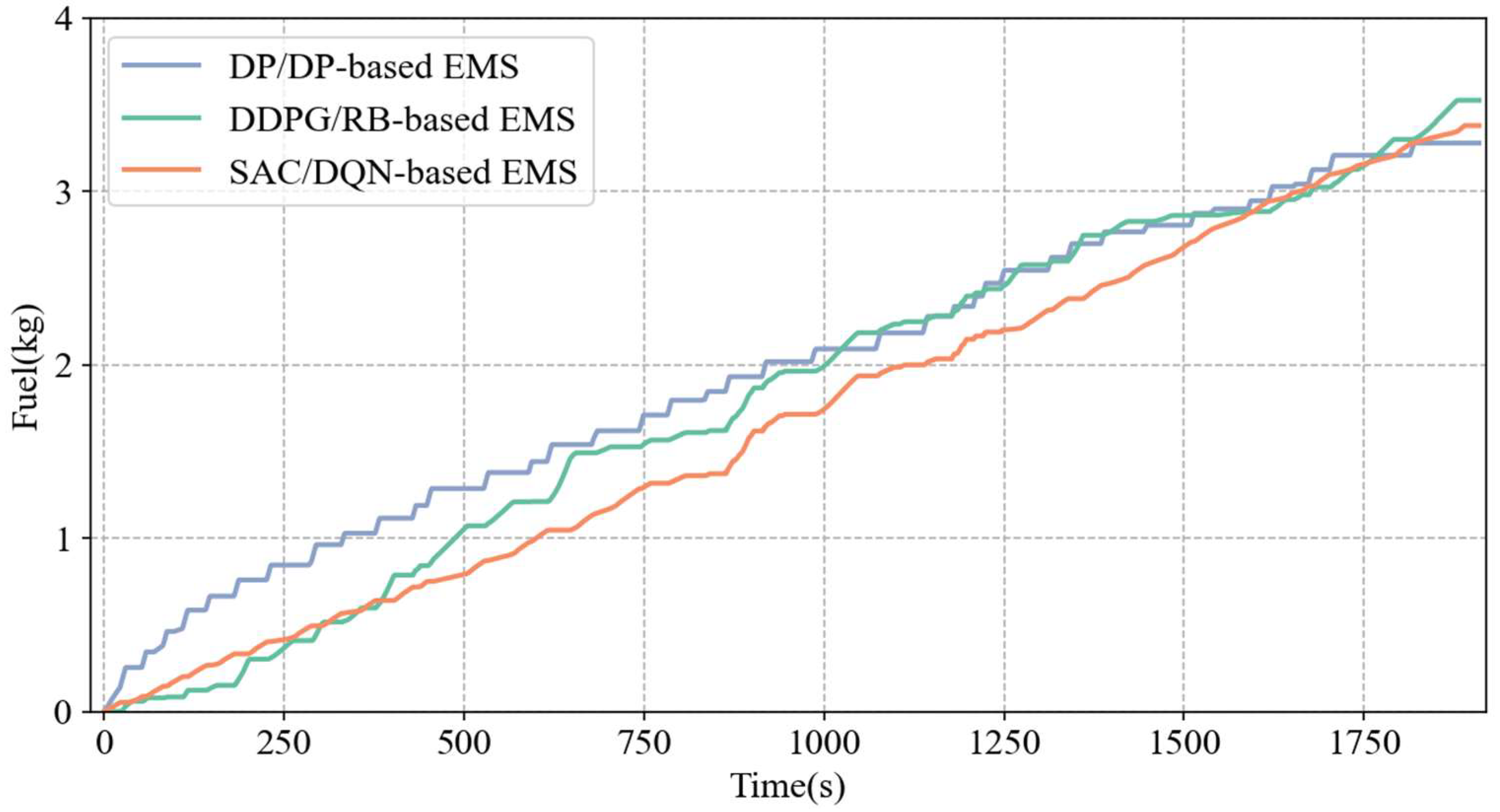
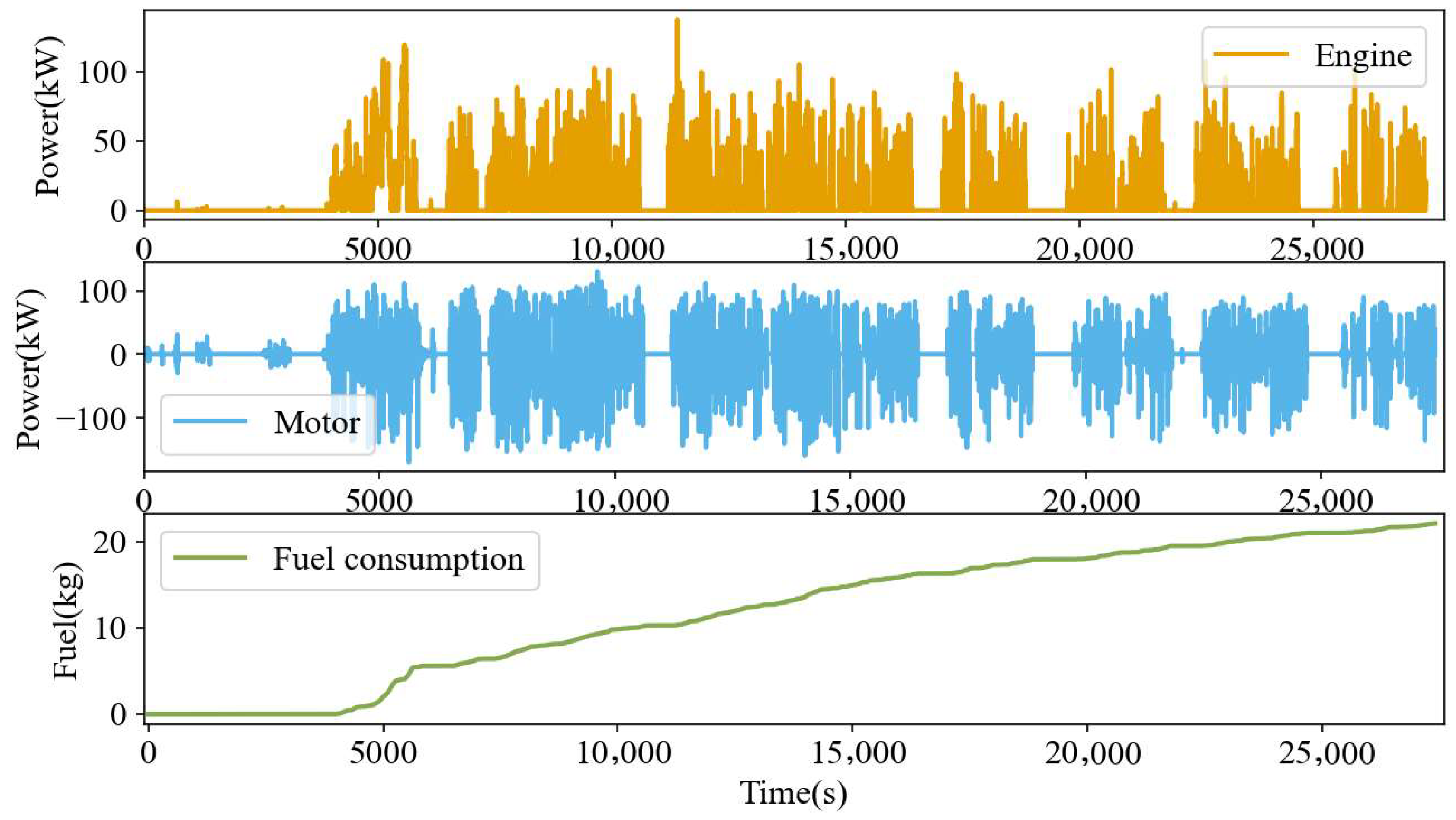
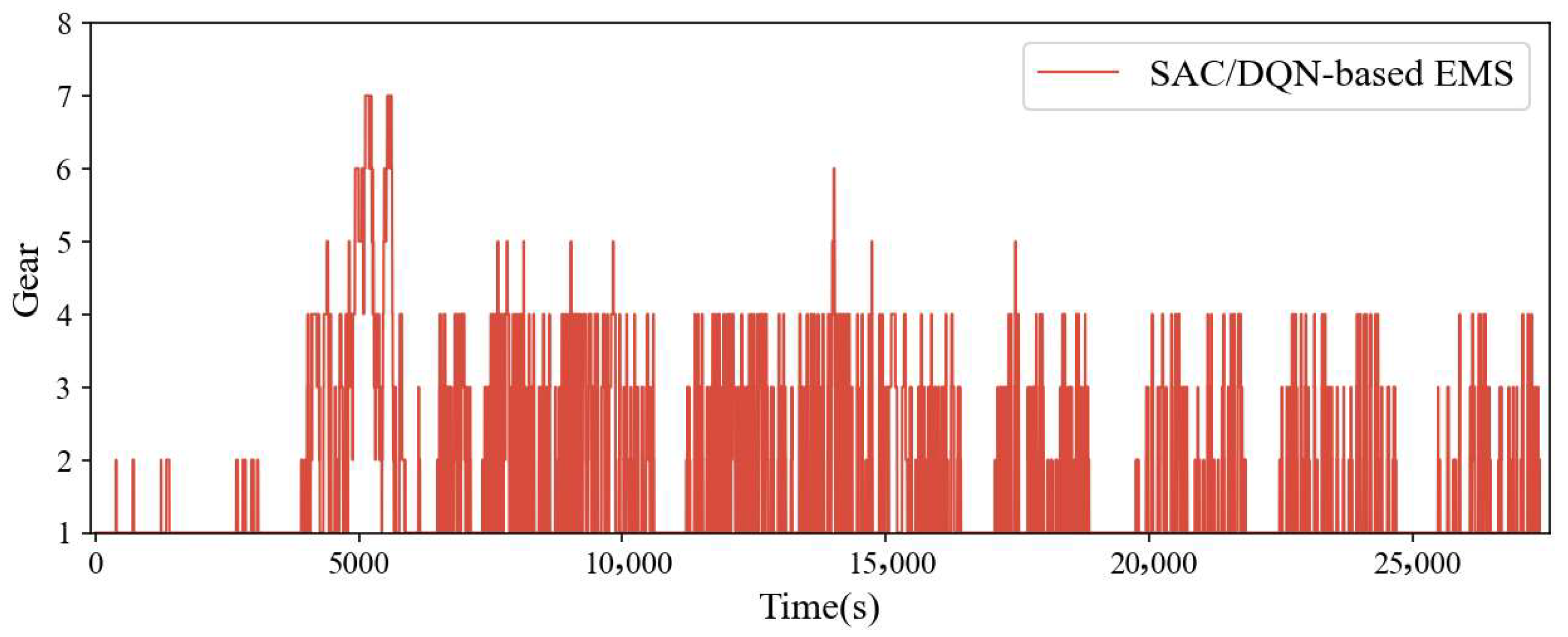
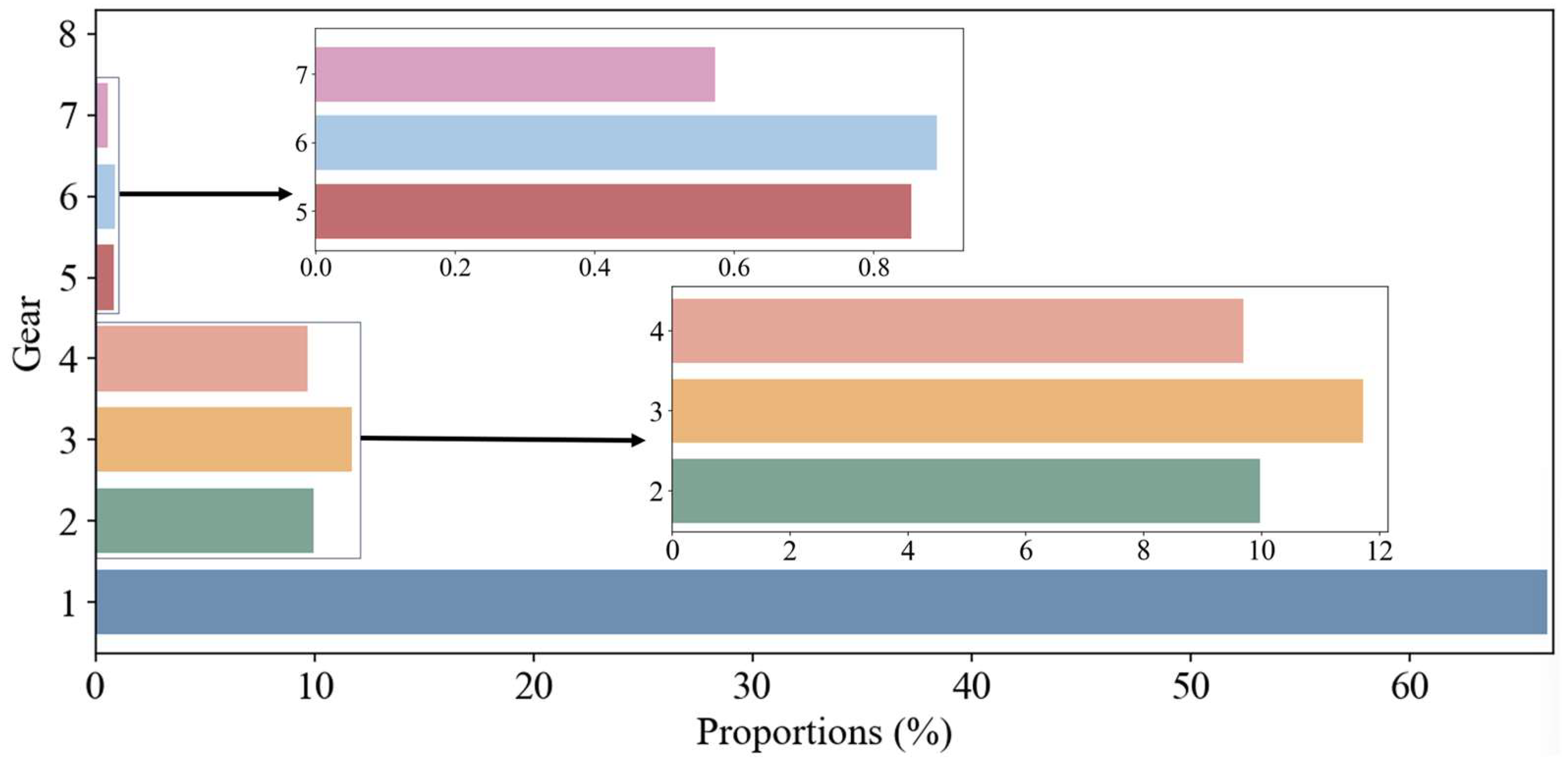
4.2. Online Test Results
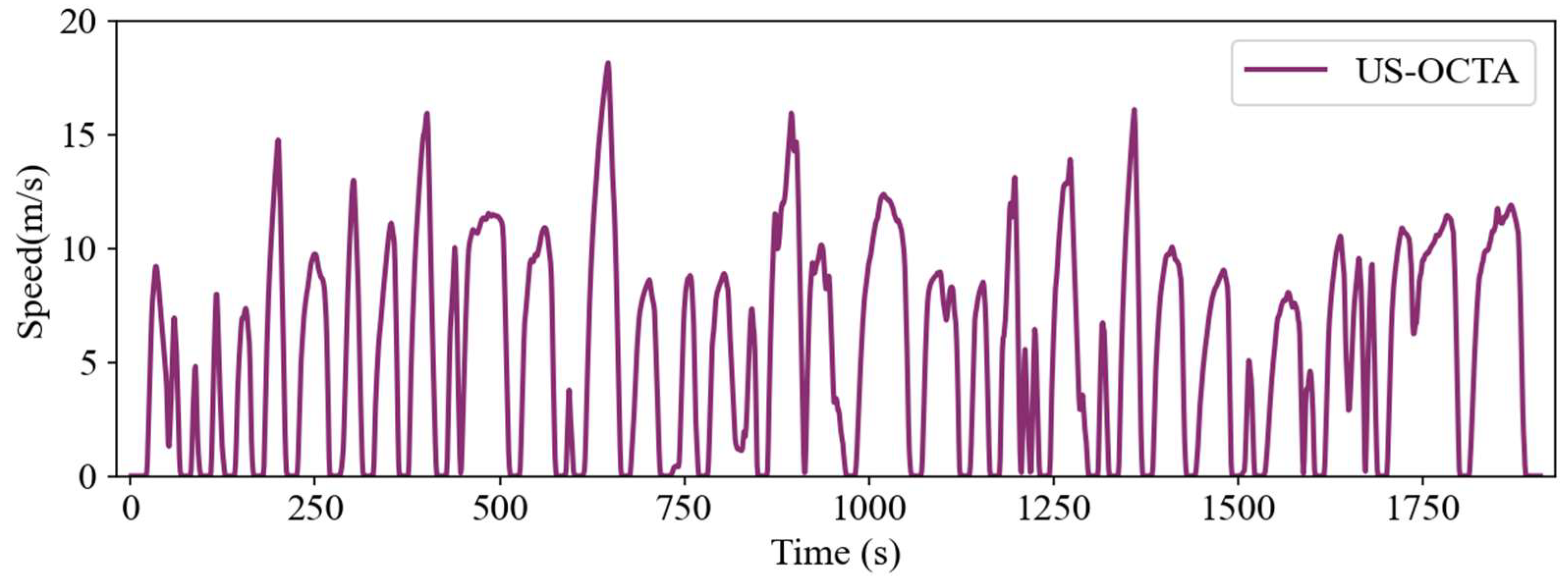
4.3. Analysis of Adaptability
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, X.; Han, J.; Tang, X.; Lin, X. Powertrain Design and Control in Electrified Vehicles: A Critical Review. IEEE Trans. Transp. Electrif. 2021, 7, 1990–2009. [Google Scholar] [CrossRef]
- Cao, Y.; Yao, M.; Sun, X. An Overview of Modelling and Energy Management Strategies for Hybrid Electric Vehicles. Appl. Sci. 2023, 13, 5947. [Google Scholar] [CrossRef]
- Ganesh, A.H.; Xu, B. A Review of Reinforcement Learning Based Energy Management Systems for Electrified Powertrains: Progress, Challenge, and Potential Solution. Renew. Sustain. Energy Rev. 2022, 154, 111833. [Google Scholar] [CrossRef]
- Zhang, K.; Ruan, J.; Li, T.; Cui, H.; Wu, C. The Effects Investigation of Data-Driven Fitting Cycle and Deep Deterministic Policy Gradient Algorithm on Energy Management Strategy of Dual-Motor Electric Bus. Energy 2023, 269, 126760. [Google Scholar] [CrossRef]
- Sun, X.; Fu, J.; Yang, H.; Xie, M.; Liu, J. An Energy Management Strategy for Plug-in Hybrid Electric Vehicles Based on Deep Learning and Improved Model Predictive Control. Energy 2023, 269, 126772. [Google Scholar] [CrossRef]
- Benhammou, A.; Hartani, M.A.; Tedjini, H.; Guettaf, Y.; Soumeur, M.A. Breaking New Ground in HEV Energy Management: Kinetic Energy Utilization and Systematic EMS Approaches Based on Robust Drive Control. ISA Trans. 2024, 147, 288–303. [Google Scholar] [CrossRef]
- Bagwe, R.M.; Byerly, A.; Dos Santos, E.C.; Ben-Miled, Z. Adaptive Rule-Based Energy Management Strategy for a Parallel HEV. Energies 2019, 12, 4472. [Google Scholar] [CrossRef]
- Piras, M.; De Bellis, V.; Malfi, E.; Novella, R.; Lopez-Juarez, M. Adaptive ECMS Based on Speed Forecasting for the Control of a Heavy-Duty Fuel Cell Vehicle for Real-World Driving. Energy Convers. Manag. 2023, 289, 117178. [Google Scholar] [CrossRef]
- Nugroho, S.A.; Chellapandi, V.P.; Borhan, H. Vehicle Speed Profile Optimization for Fuel Efficient Eco-Driving via Koopman Linear Predictor and Model Predictive Control. In Proceedings of the 2024 American Control Conference (ACC), Toronto, ON, Canada, 10 July 2024; pp. 4254–4261. [Google Scholar]
- Chen, B.; Wang, M.; Hu, L.; He, G.; Yan, H.; Wen, X.; Du, R. Data-Driven Koopman Model Predictive Control for Hybrid Energy Storage System of Electric Vehicles under Vehicle-Following Scenarios. Appl. Energy 2024, 365, 123218. [Google Scholar] [CrossRef]
- Wenhao, F.; Bolan, L.; Jingxian, T.; Dawei, Z. Study on Energy Management Strategy for a P2 Diesel HEV Considering Low Temperature Environment. Energy 2025, 318, 134771. [Google Scholar] [CrossRef]
- Wang, Y.; Jiao, X. Dual Heuristic Dynamic Programming Based Energy Management Control for Hybrid Electric Vehicles. Energies 2022, 15, 3235. [Google Scholar] [CrossRef]
- Wang, Z.; Dridi, M.; El Moudni, A. Co-Optimization of Eco-Driving and Energy Management for Connected HEV/PHEVs near Signalized Intersections: A Review. Appl. Sci. 2023, 13, 5035. [Google Scholar] [CrossRef]
- Lü, X.; Qu, Y.; Wang, Y.; Qin, C.; Liu, G. A Comprehensive Review on Hybrid Power System for PEMFC-HEV: Issues and Strategies. Energy Convers. Manag. 2018, 171, 1273–1291. [Google Scholar] [CrossRef]
- Liu, T.; Hu, X.; Li, S.E.; Cao, D. Reinforcement Learning Optimized Look-Ahead Energy Management of a Parallel Hybrid Electric Vehicle. IEEE/ASME Trans. Mechatron. 2017, 22, 1497–1507. [Google Scholar] [CrossRef]
- Saiteja, P.; Ashok, B. Critical Review on Structural Architecture, Energy Control Strategies and Development Process towards Optimal Energy Management in Hybrid Vehicles. Renew. Sustain. Energy Rev. 2022, 157, 112038. [Google Scholar] [CrossRef]
- Wang, H.; Ye, Y.; Zhang, J.; Xu, B. A Comparative Study of 13 Deep Reinforcement Learning Based Energy Management Methods for a Hybrid Electric Vehicle. Energy 2023, 266, 126497. [Google Scholar] [CrossRef]
- Li, Y.; He, H.; Peng, J.; Wang, H. Deep Reinforcement Learning-Based Energy Management for a Series Hybrid Electric Vehicle Enabled by History Cumulative Trip Information. IEEE Trans. Veh. Technol. 2019, 68, 7416–7430. [Google Scholar] [CrossRef]
- Hu, Y.; Li, W.; Xu, K.; Zahid, T.; Qin, F.; Li, C. Energy Management Strategy for a Hybrid Electric Vehicle Based on Deep Reinforcement Learning. Appl. Sci. 2018, 8, 187. [Google Scholar] [CrossRef]
- Lian, R.; Peng, J.; Wu, Y.; Tan, H.; Zhang, H. Rule-Interposing Deep Reinforcement Learning Based Energy Management Strategy for Power-Split Hybrid Electric Vehicle. Energy 2020, 197, 117297. [Google Scholar] [CrossRef]
- Zhang, J.; Tao, J.; Hu, Y.; Ma, L. An Energy Management Strategy Based on DDPG with Improved Exploration for Battery/Supercapacitor Hybrid Electric Vehicle. IEEE Trans. Intell. Transport. Syst. 2024, 25, 3999–4008. [Google Scholar] [CrossRef]
- Han, R.; Lian, R.; He, H.; Han, X. Continuous Reinforcement Learning-Based Energy Management Strategy for Hybrid Electric-Tracked Vehicles. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 19–31. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, Y.; Chang, N.; Zhu, Q.; Lin, X. A Deep Reinforcement Learning Framework for Optimizing Fuel Economy of Hybrid Electric Vehicles. In Proceedings of the 2018 23rd Asia and South Pacific Design Automation Conference (ASP-DAC), Jeju, Republic of Korea, 22–25 January 2018; pp. 196–202. [Google Scholar]
- Wang, Z.; Xie, J.; Kang, M.; Zhang, Y. Energy Management for a Series-Parallel Plug-In Hybrid Electric Truck Based on Reinforcement Learning. In Proceedings of the 2022 13th Asian Control Conference (ASCC), Jeju, Republic of Korea, 4 May 2022; pp. 590–596. [Google Scholar]
- Qi, C.; Zhu, Y.; Song, C.; Yan, G.; Xiao, F.; Wang, D.; Zhang, X.; Cao, J.; Song, S. Hierarchical Reinforcement Learning Based Energy Management Strategy for Hybrid Electric Vehicle. Energy 2022, 238, 121703. [Google Scholar] [CrossRef]
- Xiong, J.; Wang, Q.; Yang, Z.; Sun, P.; Han, L.; Zheng, Y.; Fu, H.; Zhang, T.; Liu, J.; Liu, H. Parametrized Deep Q-Networks Learning: Reinforcement Learning with Discrete-Continuous Hybrid Action Space. arXiv 2018, arXiv:1810.06394. [Google Scholar]
- Tang, X.; Chen, J.; Pu, H.; Liu, T.; Khajepour, A. Double Deep Reinforcement Learning-Based Energy Management for a Parallel Hybrid Electric Vehicle with Engine Start–Stop Strategy. IEEE Trans. Transp. Electrif. 2022, 8, 1376–1388. [Google Scholar] [CrossRef]
- Zhang, D. An Improved Soft Actor-Critic-Based Energy Management Strategy of Heavy-Duty Hybrid Electric Vehicles with Dual-Engine System. Energy 2024, 308, 132938. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-Level Control through Deep Reinforcement Learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Wu, C.; Peng, J.; Chen, J.; He, H.; Pi, D.; Wang, Z.; Ma, C. Battery Health-Considered Energy Management Strategy for a Dual-Motor Two-Speed Battery Electric Vehicle Based on a Hybrid Soft Actor-Critic Algorithm with Memory Function. Appl. Energy 2024, 376, 124306. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Vehicle mass | 18,000 kg |
| Air resistance coefficient | 0.52 |
| Cross section | 7.28 m2 |
| Rolling resistance coefficient | 0.0085 |
| Battery capacity | 48 Ah |
| Driving motor maximum power | 182 kW |
| Engine maximum power | 150 kW |
| Transmission type | 8AMT |
| Total gear ratio | 9.164/5.271/5.305/3.409/3.015/2.168/1.436/1.000 |
| Algorithm parameters: learning rates , entropy coefficient , discount factor , target update rates |
| Initialize SAC actor and critic networks with parameters , DQN evaluation and target networks with parameters , replay buffer Repeat for each episode: For do With ϵ-greedy strategy: Select gear command Select engine torque Execute action , observe reward , next state Store transition Sample mini-batch from Compute soft Q targets and update via Bellman loss Update actor network ϕ using policy gradient and entropy regularization Update target Q-networks with rate if mode then Sample mini-batch from Compute TD target: Update via Equation (7) Update target network: End If End For End Repeat |
| Hyperparameter | Value |
|---|---|
| Learning rate of actor-network | 0.003 |
| Learning rate of critic-network | 0.005 |
| Neurons distribution of actor and critic (target) network | 25,612,864 |
| Experience pool size | 10,000 |
| Mini-batch size | 64 |
| Discount factor | 0.95 |
| Number of training episodes | 200 |
| Activation function | ReLU |
| Initial entropy temperature | 0.2 |
| Optimizer | Adam |
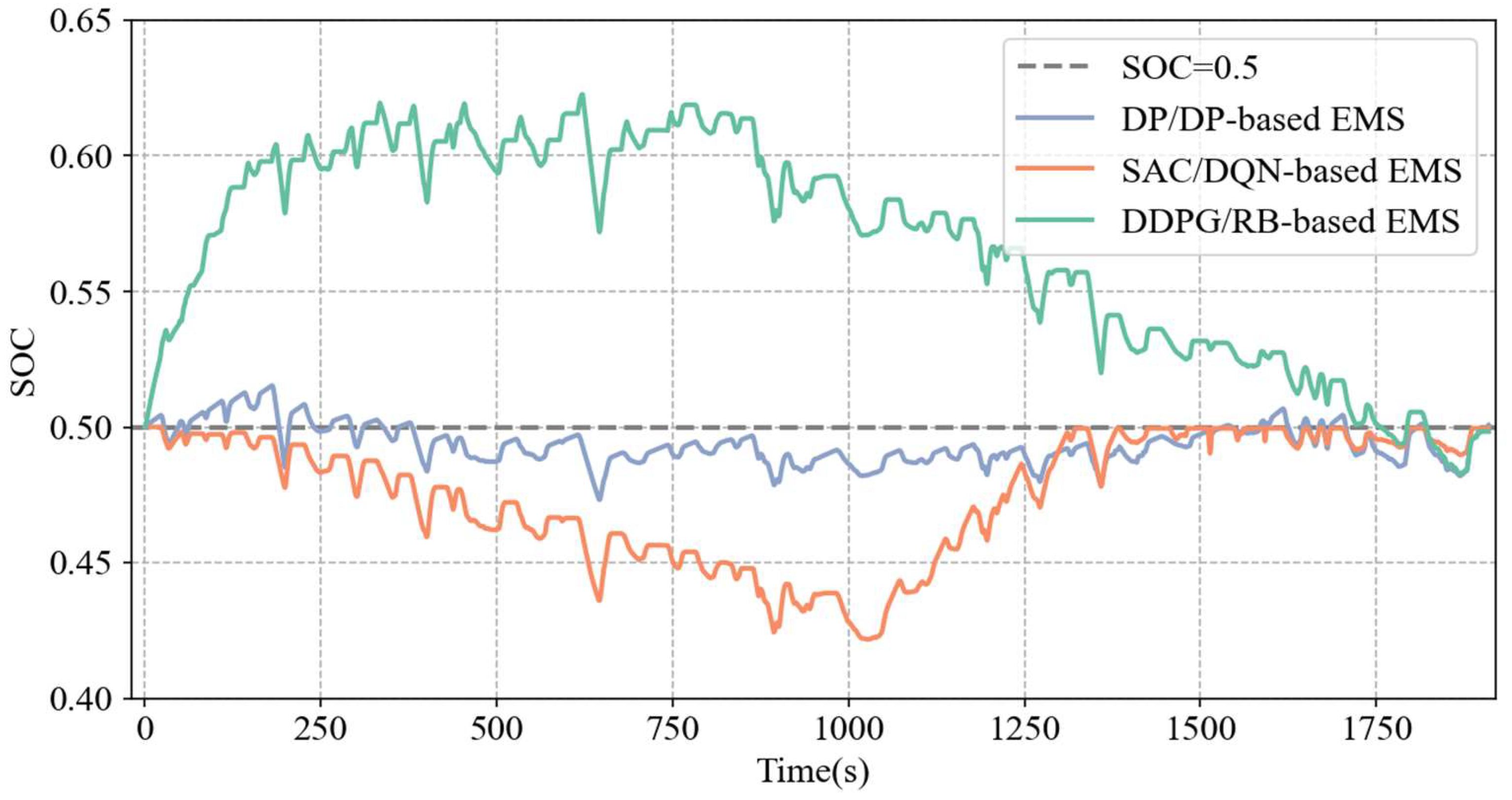
| Method | Initial SOC | Final SOC | Fuel Consumption/kg | Gap | Computing Time/s |
|---|---|---|---|---|---|
| DP/DP-based EMS | 0.5 | 0.4995 | 3.2800 | - | 4724 |
| DDPG/RB-based EMS | 0.5 | 0.5063 | 3.5265 | +7.51% | 1026 |
| SAC/DQN-based EMS | 0.5 | 0.4983 | 3.3804 | +3.06% | 1583 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, C.; Zhang, H.; Zhao, Y.; Du, H.; Ren, J.; Luo, J. Hierarchical Reinforcement Learning-Based Energy Management for Hybrid Electric Vehicles with Gear-Shifting Strategy. Machines 2025, 13, 754. https://doi.org/10.3390/machines13090754
Lan C, Zhang H, Zhao Y, Du H, Ren J, Luo J. Hierarchical Reinforcement Learning-Based Energy Management for Hybrid Electric Vehicles with Gear-Shifting Strategy. Machines. 2025; 13(9):754. https://doi.org/10.3390/machines13090754
Chicago/Turabian StyleLan, Cong, Hailong Zhang, Yongjuan Zhao, Huipeng Du, Jinglei Ren, and Jiangyu Luo. 2025. "Hierarchical Reinforcement Learning-Based Energy Management for Hybrid Electric Vehicles with Gear-Shifting Strategy" Machines 13, no. 9: 754. https://doi.org/10.3390/machines13090754
APA StyleLan, C., Zhang, H., Zhao, Y., Du, H., Ren, J., & Luo, J. (2025). Hierarchical Reinforcement Learning-Based Energy Management for Hybrid Electric Vehicles with Gear-Shifting Strategy. Machines, 13(9), 754. https://doi.org/10.3390/machines13090754






