Multi-Source Error Coupling and Tolerance Optimization for Improving the Precision of Automated Assembly of Aircraft Components
Abstract
1. Introduction
2. Error Propagation and Coordination Modeling in Automated Assembly
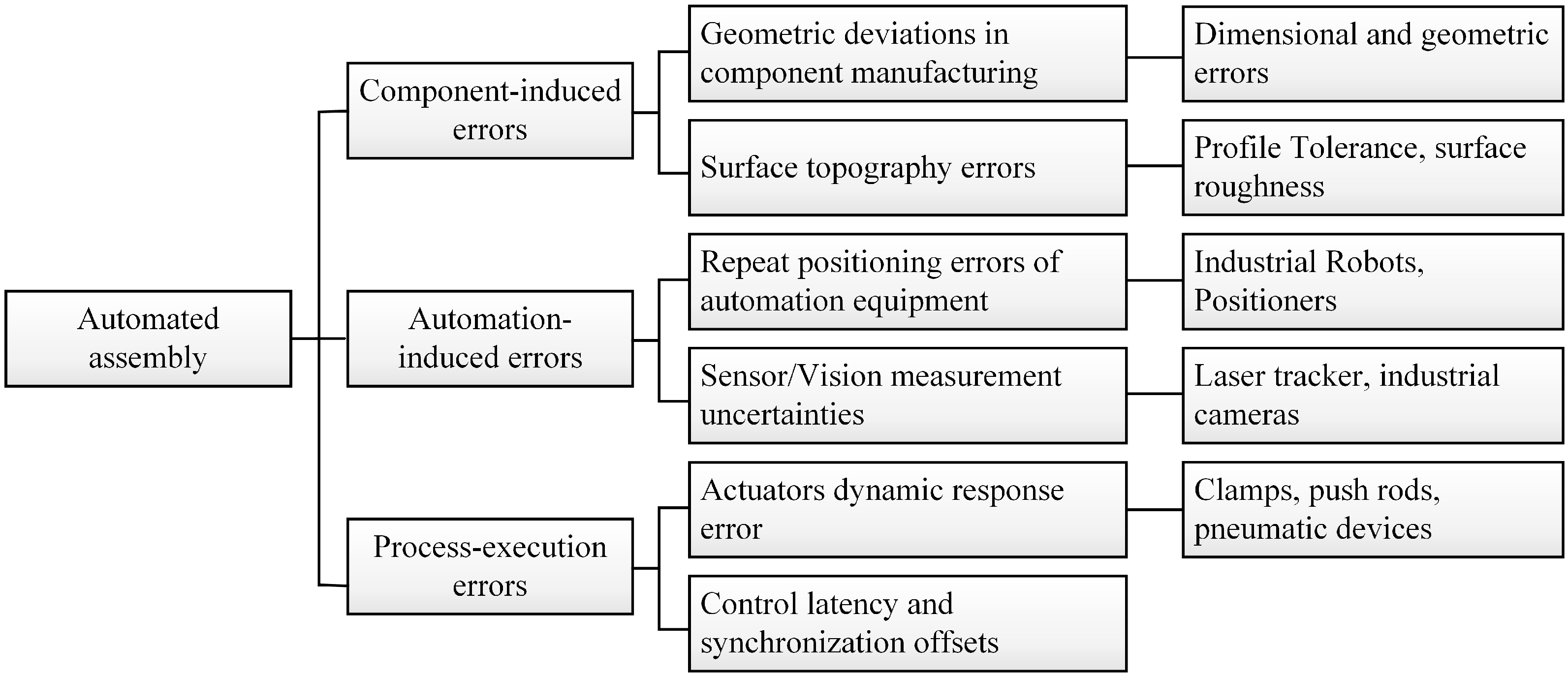
2.1. Multi-Source Error Classification in Automated Assembly
2.1.1. Component-Induced Errors
- Manufacturing geometric deviation
- 2.
- Surface topography errors
2.1.2. Automation-System Errors
- Repeat positioning error
- 2.
- Sensor/vision measurement uncertainties
2.1.3. Process-Execution Errors
- Actuator dynamic response error
- 2.
- Control latency and synchronization offsets
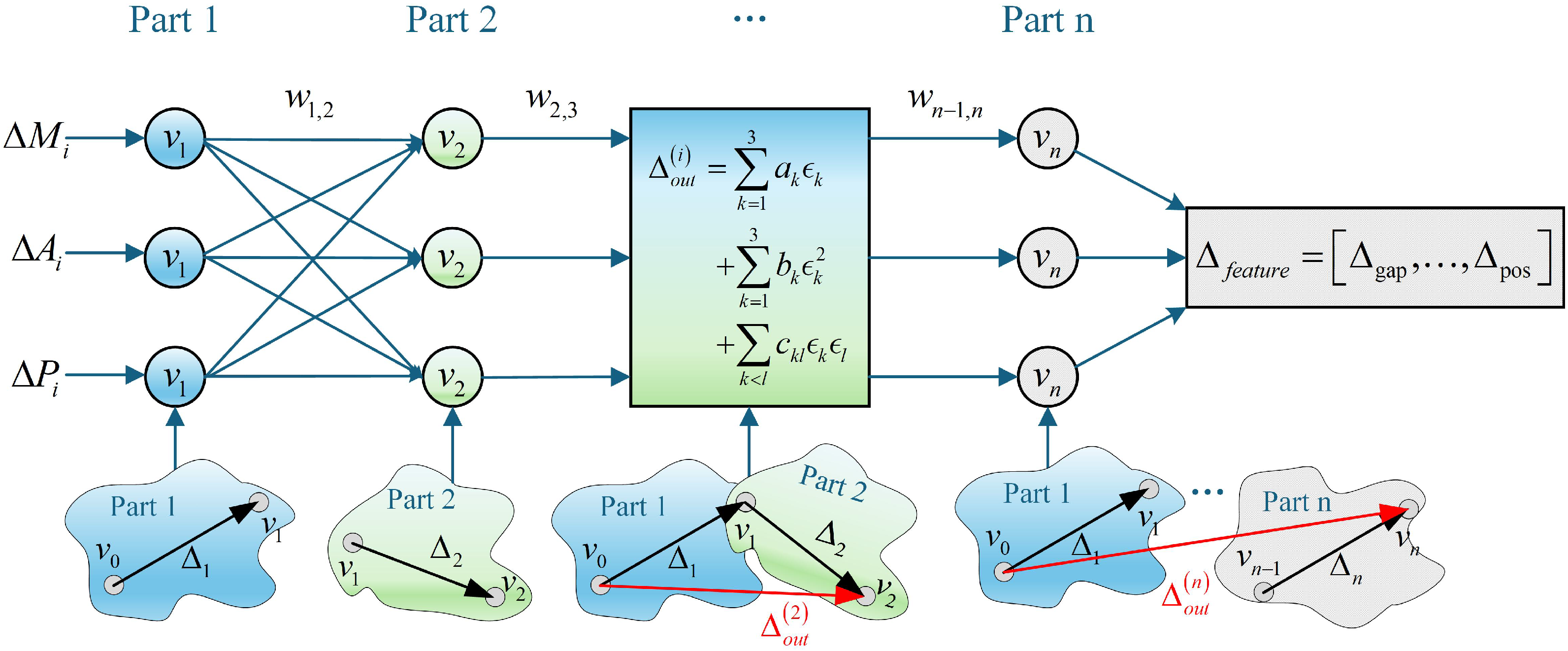
2.2. Multi-Source Error Coupling Modeling
2.2.1. Multi-Source Error Modeling
- Component-induced error modeling
- 2.
- Automation-system error modeling
- 3.
- Process-execution error modeling
2.2.2. Multi-Source Error Coupling Network
- : Component-induced errors;
- : Automation-related pose errors (including robot and sensing);
- : Process-execution errors from operations.
3. Multi-Objective Tolerance Optimization
3.1. Uncertainty Analysis and Optimization Model Construction
- Sample generation: Randomly generate sets of part dimensions according to their tolerance distributions;
- Assembly evaluation: For each sample, apply the multi-source coupling model to compute the assembly feature deviations such as gap, coaxiality, etc.;
- Statistical estimation: Compute performance metrics such as the mean and standard deviation of each error from the ensemble of simulated samples.
3.2. Sensitivity-Guided Multi-Objective Optimization via NSGA-II
- Initialization: An initial population is generated by assigning random values to each retained tolerance parameter within their allowable ranges;
- Evaluation: For each candidate solution, the corresponding geometric deviations are computed using the Monte Carlo-based coupling model;
- Non-dominated sorting: All solutions are ranked into Pareto fronts based on dominance relations;
- Selection and genetic operations: Tournament selection, crossover, and mutation operators are applied to create offspring;
- Iteration: The evaluation and sorting process is repeated over multiple generations until convergence is achieved.
3.3. Optimization Procedure Flowchart
- In the first step, a Monte Carlo simulation is conducted. This stage repeatedly samples tolerance values based on the defined uncertainty ranges and propagates them through the coupling model. By computing the resulting deviation distributions (e.g., for position and coaxiality), this step provides a statistical foundation for evaluating how tolerances impact assembly quality.
- In the second step, a Sobol sensitivity analysis is applied to the simulation results. This variance-based method quantifies the contribution of each tolerance variable to the variation in key performance indicators. By identifying the most influential tolerances, this step effectively reduces the dimensionality of the optimization problem, focusing efforts on parameters that matter most.
- In the third step, the NSGA-II multi-objective evolutionary algorithm is employed to optimize the influential tolerance parameters. NSGA-II searches for a Pareto front of solutions that balance competing objectives (e.g., minimizing positional and coaxiality deviations) while ensuring feasibility and process robustness. The algorithm iteratively evolves candidate solutions by simulating selection, crossover, and mutation across generations, guided by dominance ranking and crowding distance.
3.4. Optimization Scenarios
- Component-only optimization: Only the tolerances related to the manufactured parts () are included as decision variables in the optimization. All process and automation-related parameters (, ) are kept constant at their nominal values.
- Process-only optimization: Only the process-related factors, such as robotic positioning accuracy and process-execution errors ( and ), are optimized. Component tolerances remain fixed at their initial values.
- Full optimization: All tolerance and error-related parameters (, , and ) are optimized simultaneously to achieve the best overall assembly quality.
4. Case Study: Automatic Assembly of Helicopter Rings
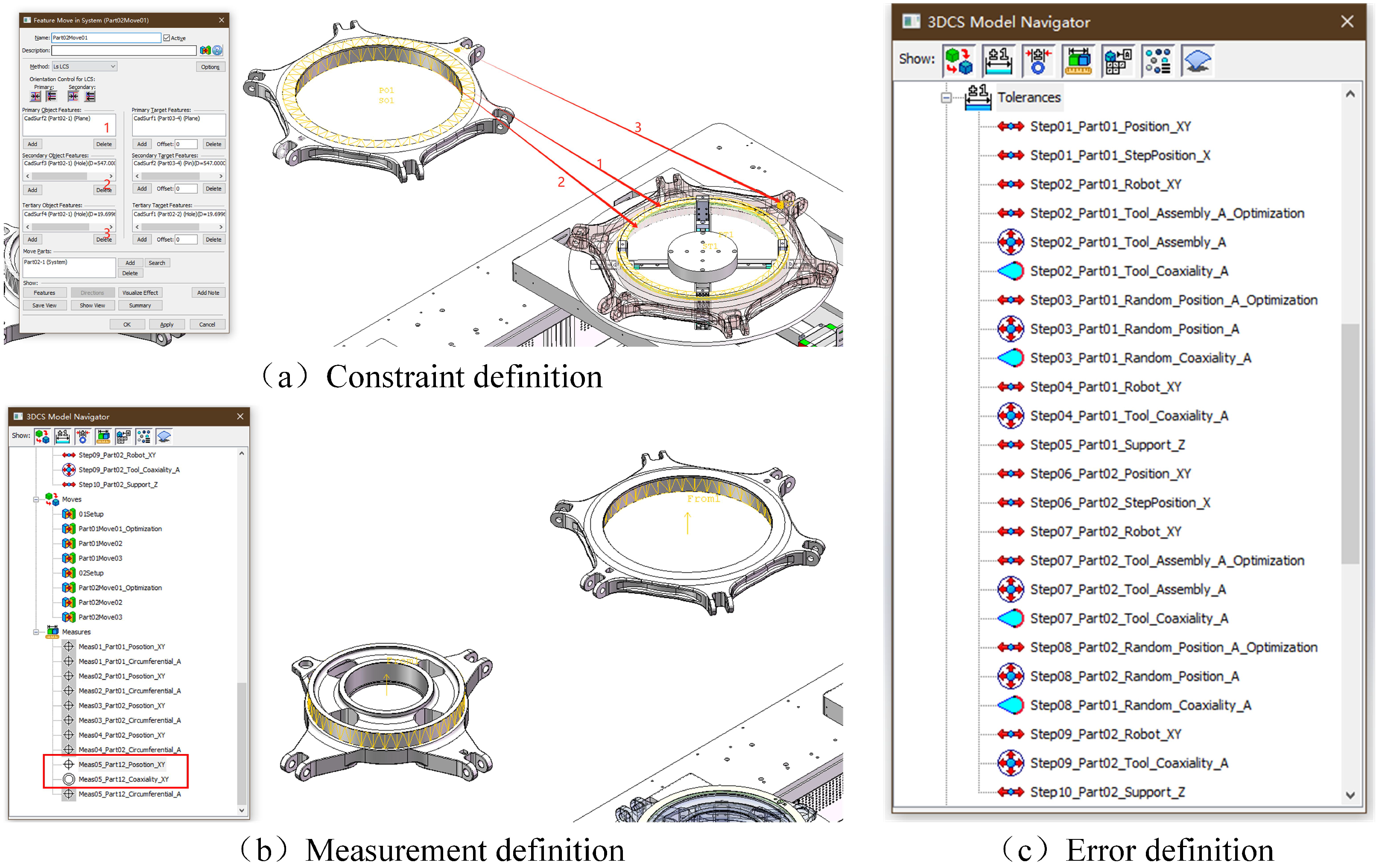
4.1. Case Overview and Setup
- for the geometric error caused by the two rings and the end fixture, initially defined as ±0.2 mm;
- for the positioning error of the industrial robot, defined as ±0.12 mm, ±0.01°, which can be found in Appendix A;
- for the jitter error caused by the gripper during the pick-and-place process, initially defined as ±0.3 mm.
- for the positional deviation between the centers of the rings;
- for the angular deviation between the center axes of the rings.
- CPK : The process capability is considered good, meaning it can stably and consistently produce products within specifications.
- CPK : The process capability is moderate, indicating that while products generally meet specifications, continuous monitoring and improvement are required to maintain quality.
- CPK : The process capability is insufficient, suggesting that the process is unable to reliably produce within specifications and corrective actions are necessary.
- Step 1:
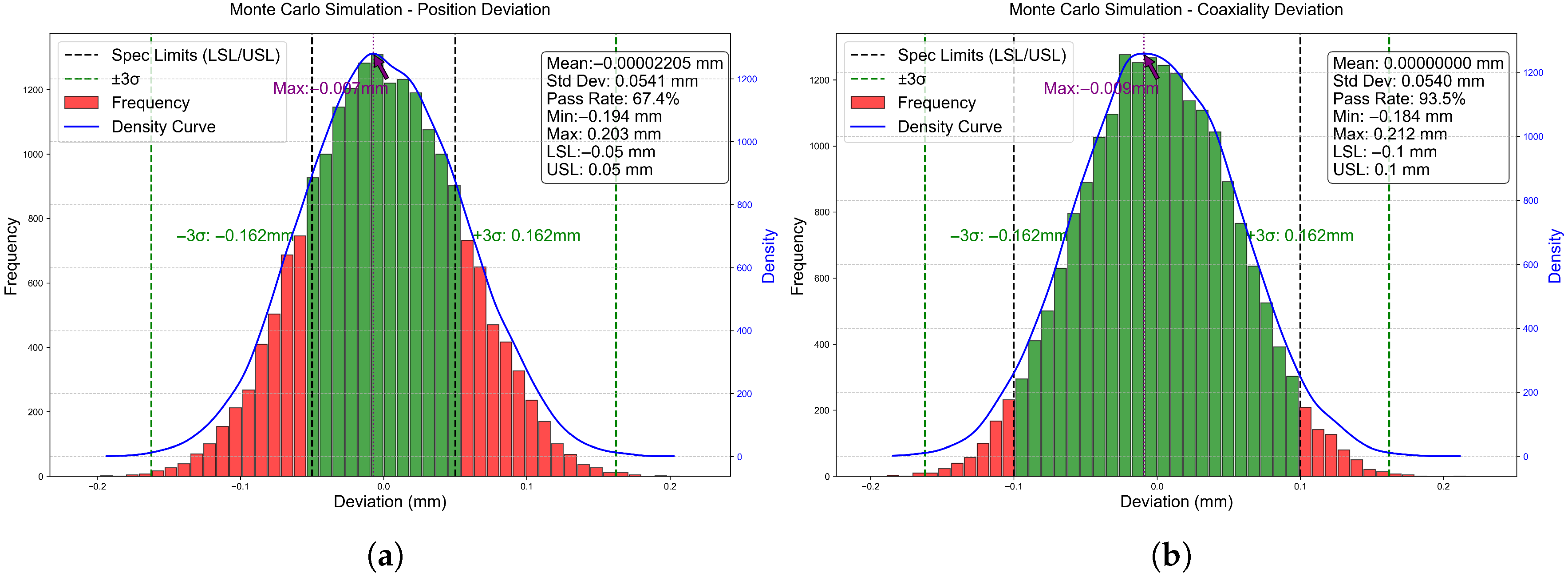
- Monte Carlo Uncertainty Propagation: The initial simulation quantified the combined effect of all error sources on the assembly deviations, as shown in Figure 8.
- Step 2:
- Global Sensitivity Analysis: The total Sobol index of each error source is calculated to distribute the output variance. The results show that contributes ~86.4% of the variance, ~12.8%, and only ~0.8%. This confirms that geometric variation is the dominant source, gripper jitter is secondary, and robot error is negligible. Consequently, is fixed at its nominal tolerance in the optimization to reduce complexity.
- Step 3:
- Multi-Objective Tolerance Optimization: The remaining tolerances and are optimized using NSGA-II. The goal was to minimize the combined standard deviation of and while improving CPK. Each candidate tolerance set was evaluated through 20,000 Monte Carlo runs to assess its performance. The algorithm identified the Pareto frontier of solutions that traded off between tight tolerances and achievable variability.
- : Tightened from the initial ±0.20 mm to ±0.15 mm;
- : Retained at ±0.12 mm and ±0.01°, due to its negligible influence (Sobol contribution < 1%);
- : Tightened from ±0.30 mm to ±0.12 mm.
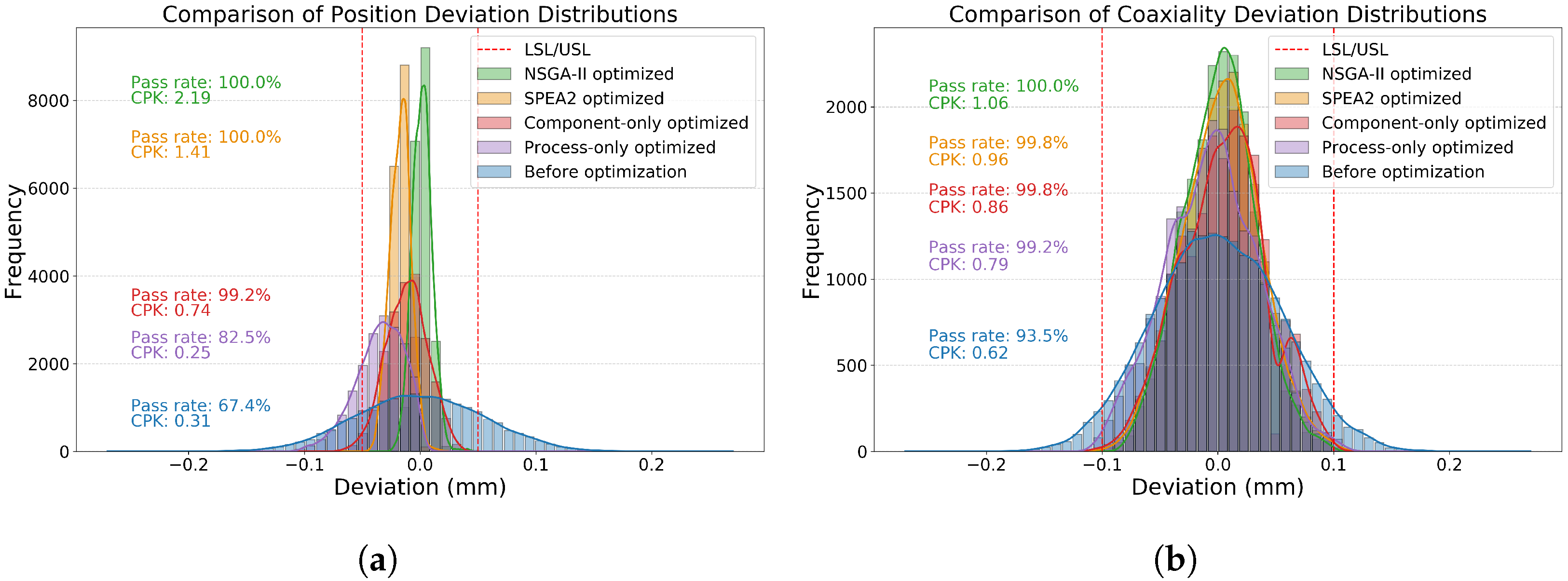
4.2. Comparison of Optimization Strategies
- In the component-only strategy, only component-related tolerances () are adjusted, such as machining or manufacturing precision of parts.
- The process-only strategy focuses on reducing automation and execution errors (, ), such as robotic positioning deviations and gripper jitter, while holding part tolerances constant.
- The full optimization strategy jointly considers all types of errors for a comprehensive improvement.
4.3. Optimization Results and Discussion
5. Discussion: Generalizability and Limitations
6. Conclusions
- A three-level uncertainty classification model that systematically captures geometric manufacturing deviations, robotic system positioning errors, and execution-induced process fluctuations;
- A directed graph-based semi-parametric coupling network that models the dynamic propagation of deviations across sequential assembly operations, enabling accurate quality estimation via Monte Carlo simulation;
- A tolerance optimization strategy that integrates Sobol-based global sensitivity analysis to identify dominant parameters with NSGA-II to explore Pareto-optimal tolerance configurations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NSGA-II | Non-dominated sorting genetic algorithm II |
| CPK | Process capability index |
| CAD | Computer-aided design |
| SPEA2 | Strength pareto evolutionary algorithm 2 |
| RMSE | Root mean square error |
Appendix A. Experiment on the Repeatability of KUKA KR90 Robot
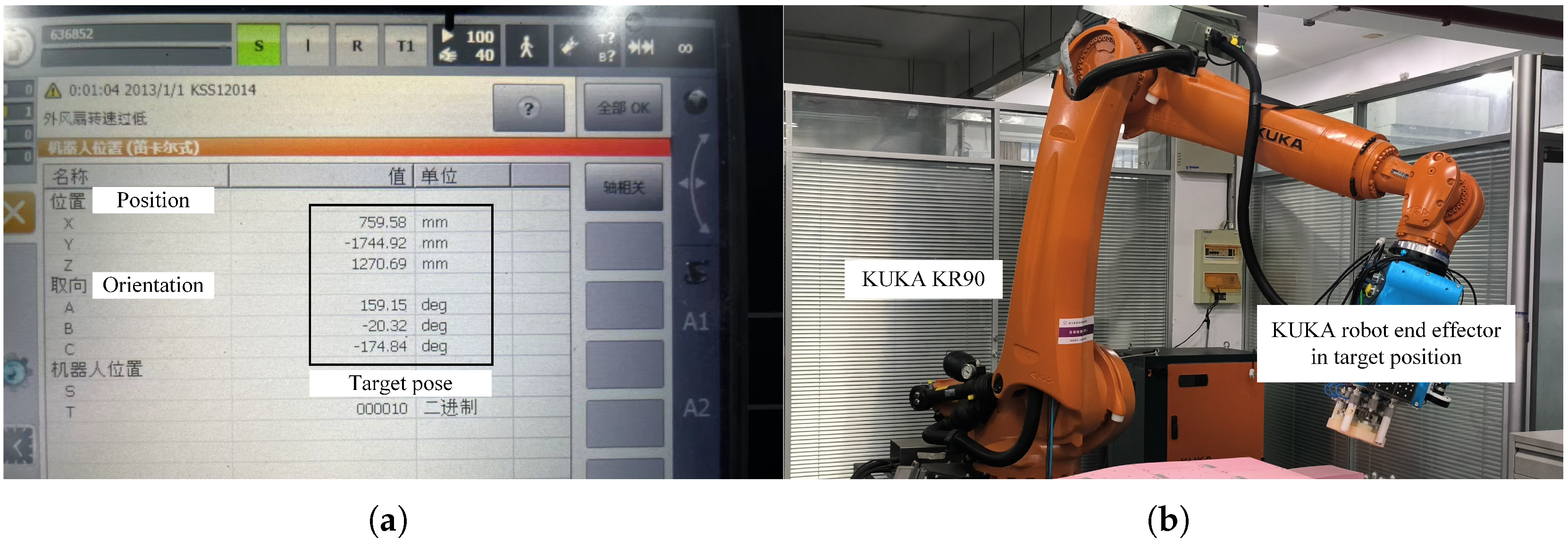
| Num | x (mm) | y (mm) | z (mm) | (°) | (°) | (°) | Linear (mm) | Angular (°) |
|---|---|---|---|---|---|---|---|---|
| Target | 759.58 | −1744.92 | 1270.69 | 159.15 | −20.32 | −174.84 | ||
| 1 | 759.70 | −1744.91 | 1270.66 | 159.16 | −20.31 | −174.84 | 0.1283 | 0.0085 |
| 2 | 759.70 | −1744.93 | 1270.68 | 159.16 | −20.31 | −174.83 | 0.1192 | 0.0119 |
| 3 | 759.71 | −1744.93 | 1270.68 | 159.15 | −20.31 | −174.83 | 0.1274 | 0.0144 |
| 4 | 759.72 | −1744.91 | 1270.67 | 159.16 | −20.31 | −174.83 | 0.1367 | 0.0128 |
| 5 | 759.70 | −1744.90 | 1270.69 | 159.16 | −20.32 | −174.84 | 0.1195 | 0.0060 |
| 6 | 759.70 | −1744.90 | 1270.70 | 159.15 | −20.32 | −174.84 | 0.1194 | 0.0051 |
| 7 | 759.72 | −1744.94 | 1270.73 | 159.16 | −20.31 | −174.83 | 0.1419 | 0.0153 |
| 8 | 759.71 | −1744.93 | 1270.69 | 159.16 | −20.31 | −174.84 | 0.1279 | 0.0096 |
| 9 | 759.70 | −1744.91 | 1270.70 | 159.15 | −20.31 | −174.83 | 0.1156 | 0.0092 |
| 10 | 759.71 | −1744.90 | 1270.69 | 159.16 | −20.30 | −174.83 | 0.1269 | 0.0194 |
| 11 | 759.70 | −1744.93 | 1270.65 | 159.15 | −20.31 | −174.84 | 0.1220 | 0.0074 |
| 12 | 759.70 | −1744.92 | 1270.69 | 159.16 | −20.31 | −174.84 | 0.1154 | 0.0122 |
| 13 | 759.70 | −1744.94 | 1270.69 | 159.16 | −20.31 | −174.84 | 0.1244 | 0.0125 |
| 14 | 759.68 | −1744.94 | 1270.74 | 159.15 | −20.31 | −174.84 | 0.1148 | 0.0076 |
| 15 | 759.68 | −1744.90 | 1270.69 | 159.16 | −20.32 | −174.84 | 0.1041 | 0.0098 |
| 16 | 759.69 | −1744.92 | 1270.70 | 159.16 | −20.31 | −174.84 | 0.1177 | 0.0097 |
| 17 | 759.69 | −1744.92 | 1270.69 | 159.16 | −20.32 | −174.83 | 0.1099 | 0.0127 |
| 18 | 759.70 | −1744.90 | 1270.67 | 159.16 | −20.32 | −174.84 | 0.1269 | 0.0115 |
| 19 | 759.69 | −1744.91 | 1270.71 | 159.15 | −20.32 | −174.84 | 0.1135 | 0.0067 |
| 20 | 759.69 | −1744.93 | 1270.71 | 159.15 | −20.31 | −174.83 | 0.1077 | 0.0080 |
| 21 | 759.71 | −1744.91 | 1270.71 | 159.15 | −20.31 | −174.83 | 0.1358 | 0.0153 |
| 22 | 759.70 | −1744.89 | 1270.67 | 159.15 | −20.32 | −174.84 | 0.1230 | 0.0027 |
| 23 | 759.70 | −1744.92 | 1270.72 | 159.15 | −20.31 | −174.83 | 0.1239 | 0.0120 |
| 24 | 759.69 | −1744.89 | 1270.66 | 159.16 | −20.32 | −174.83 | 0.1138 | 0.0078 |
| 25 | 759.69 | −1744.97 | 1270.70 | 159.16 | −20.32 | −174.84 | 0.1265 | 0.0071 |
| 26 | 759.70 | −1744.90 | 1270.73 | 159.16 | −20.31 | −174.83 | 0.1298 | 0.0128 |
| 27 | 759.69 | −1744.92 | 1270.67 | 159.16 | −20.31 | −174.83 | 0.1103 | 0.0091 |
| 28 | 759.70 | −1744.93 | 1270.68 | 159.16 | −20.32 | −174.84 | 0.1244 | 0.0100 |
| 29 | 759.69 | −1744.92 | 1270.69 | 159.15 | −20.32 | −174.83 | 0.1140 | 0.0073 |
| 30 | 759.70 | −1744.96 | 1270.68 | 159.16 | −20.31 | −174.84 | 0.1241 | 0.0154 |
| 31 | 759.69 | −1744.92 | 1270.66 | 159.16 | −20.32 | −174.83 | 0.1182 | 0.0091 |
| 32 | 759.72 | −1744.91 | 1270.69 | 159.15 | −20.31 | −174.83 | 0.1387 | 0.0093 |
| 33 | 759.70 | −1744.89 | 1270.67 | 159.15 | −20.31 | −174.83 | 0.1253 | 0.0112 |
| 34 | 759.69 | −1744.93 | 1270.70 | 159.16 | −20.32 | −174.84 | 0.1103 | 0.0072 |
| 35 | 759.71 | −1744.94 | 1270.67 | 159.15 | −20.31 | −174.83 | 0.1305 | 0.0167 |
| 36 | 759.69 | −1744.93 | 1270.72 | 159.16 | −20.31 | −174.84 | 0.1126 | 0.0100 |
| 37 | 759.70 | −1744.90 | 1270.67 | 159.16 | −20.32 | −174.84 | 0.1244 | 0.0079 |
| 38 | 759.68 | −1744.91 | 1270.68 | 159.15 | −20.31 | −174.83 | 0.1008 | 0.0100 |
| 39 | 759.69 | −1744.93 | 1270.71 | 159.15 | −20.32 | −174.83 | 0.1085 | 0.0070 |
| 40 | 759.70 | −1744.91 | 1270.67 | 159.15 | −20.31 | −174.84 | 0.1249 | 0.0082 |
| 41 | 759.71 | −1744.92 | 1270.69 | 159.15 | −20.32 | −174.84 | 0.1275 | 0.0063 |
| 42 | 759.70 | −1744.90 | 1270.72 | 159.16 | −20.32 | −174.84 | 0.1260 | 0.0096 |
| 43 | 759.70 | −1744.93 | 1270.66 | 159.16 | −20.31 | −174.84 | 0.1239 | 0.0092 |
| 44 | 759.70 | −1744.93 | 1270.69 | 159.15 | −20.31 | −174.83 | 0.1172 | 0.0108 |
| 45 | 759.69 | −1744.93 | 1270.70 | 159.16 | −20.32 | −174.83 | 0.1056 | 0.0083 |
| 46 | 759.69 | −1744.95 | 1270.71 | 159.16 | −20.32 | −174.84 | 0.1176 | 0.0079 |
| 47 | 759.70 | −1744.91 | 1270.67 | 159.15 | −20.32 | −174.83 | 0.1182 | 0.0088 |
| 48 | 759.71 | −1744.91 | 1270.66 | 159.16 | −20.32 | −174.83 | 0.1333 | 0.0086 |
| 49 | 759.70 | −1744.92 | 1270.70 | 159.16 | −20.31 | −174.83 | 0.1239 | 0.0137 |
| 50 | 759.68 | −1744.92 | 1270.70 | 159.15 | −20.31 | −174.83 | 0.1026 | 0.0094 |
| RMSE | 0.121054 | 0.010466 |
References
- Webb, P.; Eastwood, S.; Jayweera, N.; Ye, C.; Keown, C.M. An Automated Fuselage Panel Assembly and Riveting Cell-Validation and Testing; Technical report, SAE Technical Paper; SAE: Warrendale, PA, USA, 2006. [Google Scholar]
- Bhatia, V.; Kumar, A.; Sidharth, S.; Khare, S.K.; Ghorpade, S.C.; Kumar, P.; AlZohbi, G. Industry 4.0 in Aircraft Manufacturing: Innovative Use Cases and Patent Landscape. In Industry 4.0 Driven Manufacturing Technologies; Springer: Berlin/Heidelberg, Germany, 2024; pp. 103–137. [Google Scholar]
- Buergin, J.; Helming, S.; Andreas, J.; Blaettchen, P.; Schweizer, Y.; Bitte, F.; Haefner, B.; Lanza, G. Local order scheduling for mixed-model assembly lines in the aircraft manufacturing industry. Prod. Eng. 2018, 12, 759–767. [Google Scholar] [CrossRef]
- Larsen, L.; Endrass, M.; Jarka, S.; Bauer, S.; Janek, M. Exploring ultrasonic and resistance welding for thermoplastic composite structures: Process development and application potential. Compos. Part B Eng. 2025, 289, 111927. [Google Scholar] [CrossRef]
- Mei, B.; Zhu, W. Accurate positioning of a drilling and riveting cell for aircraft assembly. Robot. Comput.-Integr. Manuf. 2021, 69, 102112. [Google Scholar] [CrossRef]
- Muelaner, J.; Martin, O.; Maropoulos, P. Achieving low cost and high quality aero structure assembly through integrated digital metrology systems. Procedia CIRP 2013, 7, 688–693. [Google Scholar] [CrossRef]
- Chen, C.; Sun, J.; Wang, L.; Chen, G.; Xu, M.; Ni, J.; Ramli, R.; Su, S.; Chu, C. Pneumatic bionic hand with rigid-flexible coupling structure. Materials 2022, 15, 1358. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wei, Y.; Qiu, Y. Advanced flexible skin-like pressure and strain sensors for human health monitoring. Micromachines 2021, 12, 695. [Google Scholar] [CrossRef]
- Dong, Y.; Hussain, I.; He, S. Structural topology optimization of aircraft wing leading edge fabricated of multilayer composites. Aerosp. Sci. Technol. 2025, 159, 109993. [Google Scholar] [CrossRef]
- Torres, Y.; Nadeau, S.; Landau, K. Classification and quantification of human error in manufacturing: A case study in complex manual assembly. Appl. Sci. 2021, 11, 749. [Google Scholar] [CrossRef]
- Jamshidi, J.; Kayani, A.; Iravani, P.; Maropoulos, P.G.; Summers, M. Manufacturing and assembly automation by integrated metrology systems for aircraft wing fabrication. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2010, 224, 25–36. [Google Scholar] [CrossRef]
- Klagesa, B.; Grafa, J.; Zaeha, M. Human errors in manual assembly—A survey on current and future relevance. Procedia CIRP 2024, 130, 1556–1561. [Google Scholar] [CrossRef]
- Slamani, M.; Nubiola, A.; Bonev, I. Assessment of the positioning performance of an industrial robot. Ind. Robot. Int. J. 2012, 39, 57–68. [Google Scholar] [CrossRef]
- Grohmann, P.; Walter, M.S. Speeding up Statistical Tolerance Analysis to Real Time. Appl. Sci. 2021, 11, 4207. [Google Scholar] [CrossRef]
- Sigron, P.; Aschwanden, I.; Bambach, M. Compensation of geometric, backlash, and thermal drift errors using a universal industrial robot model. IEEE Trans. Autom. Sci. Eng. 2023, 21, 6615–6627. [Google Scholar] [CrossRef]
- Bell, J.; Redmond, L.; Carpenter, K.; de la Croix, J.P. Numerical Simulation and Influence of Non-Gaussian Vibrations on Flexible Robotic Systems. J. Spacecr. Rocket. 2024, 61, 1084–1098. [Google Scholar] [CrossRef]
- Liu, X.; Zheng, L.; Wang, Y.; Yang, W.; Wang, B.; Liu, B. Assembly error modeling and tolerance dynamic allocation of large-scale space deployable mechanism toward service performance. Appl. Sci. 2023, 13, 4999. [Google Scholar] [CrossRef]
- Makulavičius, M.; Petkevičius, S.; Rožėnė, J.; Dzedzickis, A.; Bučinskas, V. Industrial robots in mechanical machining: Perspectives and limitations. Robotics 2023, 12, 160. [Google Scholar] [CrossRef]
- Nagarajan, L.; Mahalingam, S.K.; Salunkhe, S.; Nasr, E.A.; Davim, J.P.; Hussein, H.M. A novel methodology for simultaneous minimization of manufacturing objectives in tolerance allocation of complex assembly. Appl. Sci. 2021, 11, 9164. [Google Scholar] [CrossRef]
- Zhang, B.; Lu, H.; Liu, S.; Yang, Y.; Sang, D. Aero-engine rotor assembly process optimization based on improved harris hawk algorithm. Aerospace 2022, 10, 28. [Google Scholar] [CrossRef]
- Lauri, M.; Hsu, D.; Pajarinen, J. Partially observable markov decision processes in robotics: A survey. IEEE Trans. Robot. 2022, 39, 21–40. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Guo, F.; Zhang, Y.; Song, C.; Sha, X. Identification and precise optimization of key assembly error links for complex aviation components driven by mechanism and data fusion model. Adv. Eng. Informat. 2025, 64, 103059. [Google Scholar] [CrossRef]
- Chen, T.; Li, C.; Xiao, H.; Zhu, Z.; Wang, G. A review of digital twin intelligent assembly technology and application for complex mechanical products. Int. J. Adv. Manuf. Technol. 2023, 127, 4013–4033. [Google Scholar] [CrossRef]
- Liu, L.; Jin, X.; Guo, H.; Li, C. Six-Dimensional Spatial Dimension Chain Modeling via Transfer Matrix Method with Coupled Form Error Distributions. Machines 2025, 13, 545. [Google Scholar] [CrossRef]
- Yi, Y.; Zhang, A.; Liu, X.; Jiang, D.; Lu, Y.; Wu, B. Digital twin-driven assembly accuracy prediction method for high performance precision assembly of complex products. Adv. Eng. Informat. 2024, 61, 102495. [Google Scholar] [CrossRef]
- Guo, F.; Zou, F.; Liu, J.; Xiao, Q.; Wang, Z. Assembly error propagation modeling and coordination error chain construction for aircraft. Assem. Autom. 2019, 39, 308–322. [Google Scholar] [CrossRef]
- Huang, X.; Mei, G.; Zhang, J.; Abbas, R. A comprehensive survey on point cloud registration. arXiv 2021, arXiv:2103.02690. [Google Scholar] [CrossRef]
- Zhang, H.; Jin, L.; Ye, C. An RGB-D camera based visual positioning system for assistive navigation by a robotic navigation aid. IEEE/CAA J. Autom. Sin. 2021, 8, 1389–1400. [Google Scholar] [CrossRef]
- Glira, P.; Weidinger, C.; Otepka-Schremmer, J.; Ressl, C.; Pfeifer, N.; Haberler-Weber, M. Nonrigid point cloud registration using piecewise tricubic polynomials as transformation model. Remote Sens. 2023, 15, 5348. [Google Scholar] [CrossRef]
- Hartmann, C.; Lechner, P.; Himmel, B.; Krieger, Y.; Lueth, T.C.; Volk, W. Compensation for geometrical deviations in additive manufacturing. Technologies 2019, 7, 83. [Google Scholar] [CrossRef]
- Abellán-Nebot, J.V.; Vila Pastor, C.; Siller, H.R. A review of the factors influencing surface roughness in machining and their impact on sustainability. Sustainability 2024, 16, 1917. [Google Scholar] [CrossRef]
- La Fé-Perdomo, I.; Ramos-Grez, J.A.; Jeria, I.; Guerra, C.; Barrionuevo, G.O. Comparative analysis and experimental validation of statistical and machine learning-based regressors for modeling the surface roughness and mechanical properties of 316L stainless steel specimens produced by selective laser melting. J. Manuf. Process. 2022, 80, 666–682. [Google Scholar] [CrossRef]
- Królczyk, G.; Kacalak, W.; Wieczorowski, M. 3D Parametric and Nonparametric Description of Surface Topography in Manufacturing Processes. Materials 2021, 14, 1987. [Google Scholar] [CrossRef] [PubMed]
- Scimone, R.; Taormina, T.; Colosimo, B.M.; Grasso, M.; Menafoglio, A.; Secchi, P. Statistical modeling and monitoring of geometrical deviations in complex shapes with application to additive manufacturing. Technometrics 2022, 64, 437–456. [Google Scholar] [CrossRef]
- Robbe-Valloire, F. Statistical analysis of asperities on a rough surface. Wear 2001, 249, 401–408. [Google Scholar] [CrossRef]
- Khanesar, M.A.; Karaca, A.; Yan, M.; Isa, M.; Piano, S.; Branson, D. Enhancing Positional Accuracy of Mechanically Modified Industrial Robots Using Laser Trackers. Robotics 2025, 14, 42. [Google Scholar] [CrossRef]
- Isheil, A.; Gonnet, J.P.; Joannic, D.; Fontaine, J.F. Systematic error correction of a 3D laser scanning measurement device. Opt. Lasers Eng. 2011, 49, 16–24. [Google Scholar] [CrossRef]
- Pu, W.; Liu, Y.; Yan, J.; Liu, H.; Luo, Z. Optimal estimation of sensor biases for asynchronous multi-sensor data fusion. Math. Program. 2018, 170, 357–386. [Google Scholar] [CrossRef]
- Adel, M.; Ahmed, S.M.; Fanni, M. End-effector position estimation and control of a flexible interconnected industrial manipulator using machine learning. IEEE Access 2022, 10, 30465–30483. [Google Scholar] [CrossRef]
- Bodie, K.; Tognon, M.; Siegwart, R. Dynamic end effector tracking with an omnidirectional parallel aerial manipulator. IEEE Robot. Autom. Lett. 2021, 6, 8165–8172. [Google Scholar] [CrossRef]
- Salman, M.; Niu, Z.; Singh, R.; Kshetrimayum, L.; Hussain, I. Robust control of a compliant manipulator with reduced dynamics and sliding perturbation observer. Sci. Rep. 2025, 15, 8934. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhu, K.; Liaw, H.C. Generalized synchronization control of multi-axis motion systems. Control Eng. Pract. 2005, 13, 809–819. [Google Scholar] [CrossRef]
- Şirinterlikçi, A.; Tiryakioğlu, M.; Bird, A.; Harris, A.; Kweder, K. Repeatability and accuracy of an industrial robot: Laboratory experience for a design of experiments course. Technol. Interface J. 2009, 9, 1–10. [Google Scholar]
- Kluz, R.; Trzepieciński, T. The repeatability positioning analysis of the industrial robot arm. Assem. Autom. 2014, 34, 285–295. [Google Scholar] [CrossRef]
- Gon, Y.; Kogiso, N. Effect of Member Length Uncertainty and Backlash on Deformation Accuracy for a High-Precision Space Truss Structure. Trans. Jpn. Soc. Aeronaut. Space Sci. 2021, 64, 31–39. [Google Scholar] [CrossRef]
- Beasley, R.A.; Howe, R.D. Model-based error correction for flexible robotic surgical instruments. In Proceedings of the Robotics: Science and Systems; Massachusetts Institute of Technology: Cambridge, MA, USA, 2005; Volume 2005, pp. 359–364. [Google Scholar]
- Pham, L.; DeSimone, A. Vibration Rectification in MEMS Accelerometers; Analog Devices, Inc.: Wilmington, MA, USA, 2017. [Google Scholar]
- Ballester-Ripoll, R.; Leonelli, M. Computing Sobol indices in probabilistic graphical models. Reliab. Eng. Syst. Saf. 2022, 225, 108573. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, Y.; Sun, S.; Liu, T.; Shan, Y. A comprehensive survey on NSGA-II for multi-objective optimization and applications. Artif. Intell. Rev. 2023, 56, 15217–15270. [Google Scholar] [CrossRef]
- Pallasdies, F.; Norton, P.; Schleimer, J.H.; Schreiber, S. Neural optimization: Understanding trade-offs with Pareto theory. Curr. Opin. Neurobiol. 2021, 71, 84–91. [Google Scholar] [CrossRef]
- Gao, Y. Tolerance analysis and optimization based on 3DCS. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2021; Volume 2137, p. 012070. [Google Scholar]
- Andrén, H. Towards Zero Defects in the Aerospace Industry Through Statistical Process Control: A Case Study at GKN Aerospace Engine Systems. Master’s Thesis, Luleå University of Technology, Luleå, Sweden, 2020. [Google Scholar]
- Lin, T.H.; Huang, L.C.; Chen, Y.Y.; Lee, L.C.; Lin, D.Y. Implementing Process Capability Index (Cpk) for Effective Product Quality Stabilization: The Case of a Lock Manufacturing Company. Sens. Mater. 2025, 37, 1211–1227. [Google Scholar] [CrossRef]
- Pearn, W.; Chen, K. A practical implementation of the process capability index Cpk. Qual. Eng. 1997, 9, 721–737. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, W.; Yang, M.; Han, D. A multi-objective evolutionary algorithm model for product form design based on improved SPEA2. Appl. Sci. 2019, 9, 2944. [Google Scholar] [CrossRef]
- Kaucic, M.; Moradi, M.; Mirzazadeh, M. Portfolio optimization by improved NSGA-II and SPEA 2 based on different risk measures. Financ. Innov. 2019, 5, 26. [Google Scholar] [CrossRef]
- ISO 9283; Manipulating Industrial Robots–Performance Criteria and Related Test Methods. ISO (International Organization for Standardization): Geneva, Switzerland, 1998.



| Error Sources | Mathematical Expressions | Distribution Type |
|---|---|---|
| Manufacturing geometric deviation | ||
| Surface topography errors | ||
| Repeat positioning error | ||
| Sensor/vision measure uncertainties | ||
| Actuator dynamic response error | — | |
| Control latency and synchronization offsets |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, T.; Huang, X.; Li, S.; Hou, G. Multi-Source Error Coupling and Tolerance Optimization for Improving the Precision of Automated Assembly of Aircraft Components. Machines 2025, 13, 736. https://doi.org/10.3390/machines13080736
Cao T, Huang X, Li S, Hou G. Multi-Source Error Coupling and Tolerance Optimization for Improving the Precision of Automated Assembly of Aircraft Components. Machines. 2025; 13(8):736. https://doi.org/10.3390/machines13080736
Chicago/Turabian StyleCao, Tailong, Xiang Huang, Shuanggao Li, and Guoyi Hou. 2025. "Multi-Source Error Coupling and Tolerance Optimization for Improving the Precision of Automated Assembly of Aircraft Components" Machines 13, no. 8: 736. https://doi.org/10.3390/machines13080736
APA StyleCao, T., Huang, X., Li, S., & Hou, G. (2025). Multi-Source Error Coupling and Tolerance Optimization for Improving the Precision of Automated Assembly of Aircraft Components. Machines, 13(8), 736. https://doi.org/10.3390/machines13080736






