Vibration Characteristic Analysis and Dynamic Reliability Modeling of Multi-Rotor UAVs

Abstract

To address the unclear vibration failure mechanism and the lack of system-level reliability evaluation methods for multirotor transport UAVs under complex operating conditions, this paper proposes a comprehensive analysis method that combines fluid–structure interaction dynamics with dynamic reliability theory. First, the study analyzes rotor dynamics and vibration characteristics under bidirectional fluid–structure coupling and obtains vibration displacement data. Then, it builds a dynamic reliability model using the Second-Order Reliability Method (SORM) and the Laplace method. The model explores reliability evolution in a dynamic airflow coupling environment. Finally, it establishes a multi-rotor UAV system reliability evaluation method and analyzes the impact of rotor number and layout on system reliability. The results provide a theoretical basis for structural optimization, reliability assurance, and fault tolerance improvement of multi-rotor UAVs under complex conditions.

1. Introduction

UAV technology is an important sign of a country’s overall strength. Its development deeply affects military and economic patterns. It also has great significance in reshaping the future international order [1]. With the expansion of application fields, improving UAV reliability becomes a key to overcoming technical bottlenecks and promoting industrial upgrades [2,3,4]. During missions, UAVs face many controllable and uncontrollable factors. Vibration faults are one of the key factors that affect UAV flight safety [5,6]. Vibration sources include airflow disturbances, rotor interference, structural installation errors, and load changes. Vibration faults seriously affect flight safety and system stability. Strong wind and rain cause complex vibration features and transmission patterns. Ignoring elastic vibration will accelerate structural fatigue damage and reduce mission success. Therefore, analyzing vibration features and modeling dynamic reliability for multirotor UAVs is very important.

Currently, multidisciplinary research on vibration characteristics and structural optimization plays an important role in improving UAV reliability, stability, and engineering applications [7]. Wu et al. [8] summarized the common fault types and diagnosis methods in UAV systems. They systematically reviewed detection mechanisms for sensor and actuator faults. These studies provided theoretical support and practical guidance for highly autonomous UAV flight missions. Liu et al. [9] used the state-space method to analyze the dynamics of the frame. They emphasized the importance of understanding vibration characteristics for flight stability and structural reliability. Dai et al. [10] studied the dynamic behavior of UAV components by analyzing fluid–structure coupled base structures. They reduced the vibration transmitted inside the UAV. Yang et al. [11] proposed a new quadcopter blade fault diagnosis method called sPSDAE-CNN. It combines a stacked pruning sparse denoising autoencoder and a convolutional neural network. It uses one-dimensional sliding window slicing and converts time-domain signals into two-dimensional images. This achieves effective feature extraction and model pruning to reduce complexity. Li et al. [12] built a negative Poisson’s ratio metamaterial (NPRM) structure. This structure reduces vibrations broadly in the 0–2000 Hz range. Y. Jiang et al. [13] combined adaptive disturbance rejection control (ADR) with nonlinear dynamic modeling. Their method effectively suppresses resonance vibrations in flexible wings and improves flight stability. Tian et al. [14] used Gaussian Process Regression (GPR) to build a model between PWM and the main vibration frequency. They designed an adaptive notch filter based on GPR. This filter can effectively remove vibration noise with a main frequency. Wang et al. [15] developed a magnetic spring AV-TENG vibration sensor. It monitors motor vibration frequency and acceleration in real time, reducing interference from the source. These studies improve vibration suppression and flight stability at multiple levels, including structural design, control modeling, and sensor monitoring.

Mechanical structure reliability research includes factors such as material properties, uncertain loads, and manufacturing errors. Numerical simulation methods combine computational fluid dynamics (CFD) and finite element method (FEM). These methods build a system process from modeling, simulation, and analysis. They predict the flow field distribution and structural response of UAVs under complex conditions. This prediction can improve flight stability and structural life [16]. Meng et al. [17] proposed a time-varying reliability analysis framework based on a performance degradation model. This framework dynamically evaluates material degradation and operational wear over time. It is used for maintenance planning and lifecycle management. To handle cognitive and modeling uncertainties, Zhang et al. [18] proposed a cubic spline probabilistic transformation method. It improves the accuracy of uncertain information processing in evidence theory. Shen et al. [19] built a mixed distribution model to verify its probabilistic representation ability. For surrogate models, Yuan et al. [20] designed a new Kriging update strategy. It improves model iteration efficiency. Li [21] proposed an anisotropic radial basis function (RBF) with a fast cross-validation strategy. It enhances model generalization and adaptability. Liu et al. [22] proposed a non-intrusive analysis framework based on probabilistic integration for nonlinear thin-shell structures. It considers large deflections and nonlinear dynamic responses. This expands the method’s applicability to complex structural scenarios. Gan et al. [23] adopted a topology optimization framework based on the response surface method. This framework includes manufacturing errors, material properties, and loading conditions in the reliability analysis to improve the robustness of structural design. Therefore, structural reliability methods continue to advance in handling model uncertainty, improving surrogate modeling efficiency, and adapting to complex multiphysics conditions. They show wide applicability and great potential in UAV structural design and reliability improvement.

Some studies focus on UAV reliability problems at the mission environment and component levels. Zhang [24] combined transfer learning with the Kriging model. He proposed the RBDO-TL method. This method adapts to different UAV models and mission conditions for reliability design. Chen [25] proposed the FOTRE method. It calculates the MPP only once over the entire life cycle, greatly reducing computing cost. Yang [26] used generalized fiducial inference. This improved the confidence interval estimation accuracy for fatigue life with small samples. Wang [27] combined multi-level statistical theory with neural networks. He evaluated fatigue crack growth in lifting lug structures, suitable for reliability prediction of UAV load-bearing parts. Li [28] started from stress field scale similarity. He proposed an equivalent initial crack modeling method. This method assesses durability for structures with blunt notches or manufacturing defects. Alastair et al. [29] proposed a hierarchical and thermally enhanced reliability modeling framework for electric propulsion systems. This framework helps to fully understand the impact of component failures on overall system reliability at different mission phases. Zhao [30] proposed an improved active learning Kriging method (Improved AK-IS). It uses multi-level sample screening to improve efficiency in solving small failure probability problems. Yang [31] combined Gauss-Hermite nodes with marginal integration strategies. He developed a global adaptive Kriging method for multi-objective design. Liang et al. [32] proposed a formation algorithm that uses a distributed control strategy to enable UAV swarms to deploy quickly in three-dimensional space. This algorithm improves robustness against communication failures and increases the probability of collective task success. Although systematic research on UAV reliability is still limited, existing studies provide multiple paths for reliability modeling, optimization, and fatigue assessment. They show great development potential.

In summary, current research has made some progress in flight control, structural optimization, and local reliability analysis. However, it still lacks in system-level vibration modeling and reliability assessment under complex conditions. First, most vibration studies focus on simplified structures and ideal environments. They do not systematically reveal the structural response under aerodynamic loads. Second, reliability assessment usually stays at the component level. It does not cover the full process from vibration mechanism analysis to system redundancy optimization. Therefore, this paper builds a multi-level research framework. It is based on bidirectional fluid–structure interaction simulation, single-rotor modeling, and system redundancy analysis. The framework systematically explores how rotor vibration affects flight safety. It proposes reliability optimization methods suitable for engineering practice. In our study, fluid dynamics simulations based on bidirectional fluid–structure interaction reveal that the vibration response of the rotor under aerodynamic loads shows significant spatial and temporal distribution characteristics. The displacement peak at the blade tip reaches 0.02553 mm, and the maximum stress at the root is 11.598 MPa. The system enters a stable periodic state after 0.12 s. A single-rotor reliability model is constructed using the second-order reliability method (SORM) and the Laplace approximation method. The failure-free operation probability under the given condition is 93.10%, which confirms the consistency between this method and the Monte Carlo simulation. Through system reliability evaluation, we find that increasing the number of rotors causes the reliability index of the series system to decrease and that of the voting system to increase. In the “3-out-of-6” voting model of the hexarotor system, a higher redundancy value leads to higher reliability. This highlights the positive effect of redundancy design on improving fault tolerance. These results provide useful references for structural optimization, reliability assurance, and fault-tolerant design of multirotor UAVs under complex working conditions.

2. Modeling Theory of UAV Rotor Structures

To investigate the vibration characteristics of UAV rotor and propeller components, this section introduces relevant fluid dynamics theories into rotor structural design. The main theories include the ideal actuator (propulsor) theory and the ideal propeller theory, which can be further divided into momentum theory, blade element theory, and strip theory.

2.1. The Actuator Disk Theory

The Actuator Disk Theory (ADT) was proposed by Rankine and R. E. Froude. It treats the propeller as an actuator disk with an infinite number of blades. The theory assumes that the airflow passing through the disk does not rotate and that the axial velocities before and after the disk are equal. A uniformly distributed thrust is generated on the disk. The airflow through the actuator disk is considered to be incompressible and ideal.

The kinetic energy change of the airflow passing through the actuator disk is the main source of thrust. The specific value depends on the disk loading, rotational speed, and flow field distribution. As shown in Figure 1, assume the inflow air has a density of $\rho$, with an undisturbed axial velocity and pressure of $V_0$ and $p$, respectively. As the airflow approaches the propeller, its velocity increases and pressure decreases. The pressure just before the actuator disk becomes $p^{\prime }$, and after passing through the disk, the pressure increases by $\mathsf{\Delta }p$, while the axial velocity becomes $V_0=(1+a)$. In the slipstream zone, the axial velocity further increases to $V_0=(1+b)$, but the pressure drops back to the original value $p$.

Assuming the flow is an incompressible and ideal potential flow, the Bernoulli equation can be applied before and after the disk. The energy equation upstream of the disk is given by:

$$p^{*}=p+{\displaystyle \frac{1}{2}}\rho {V_0}^2=p^{\prime }+{\displaystyle \frac{1}{2}}\rho {V_0}^2{\left(1+a\right)}^2$$

(1)

The energy equation downstream of the disk is given by:

$$p_1^{*}=p^{\prime }+\mathsf{\Delta }p+{\displaystyle \frac{1}{2}}\rho {V_0}^2{(1+a)}^2=p+{\displaystyle \frac{1}{2}}\rho {V_0}^2{(1+b)}^2$$

(2)

The pressure difference across the actuator disk is:

$$\mathsf{\Delta }p=p_1^{*}-p^{*}=\left[p+{\displaystyle \frac{1}{2}}\rho {V_0}^2{(1+b)}^2\right]-\left(p+{\displaystyle \frac{1}{2}}\rho {V_0}^2\right)=\rho {V_0}^{2}b\left(1+{\displaystyle \frac{b}{2}}\right)$$

(3)

Let the actuator disk area be $\mathrm{A}$. The aerodynamic force generated by blade rotation in the flight direction is the thrust:

$$T=\mathrm{A}\mathsf{\Delta }p=\mathrm{A}\rho {V_0}^{2}b\left(1+{\displaystyle \frac{b}{2}}\right)$$

(4)

The force exerted by the propeller on the airflow is equal to the momentum change of the flow through the disk per unit time:

$$T=\rho \mathrm{A}{V}_0\left(1+a\right)\left[V_0\left(1+b\right)-V_0\right]$$

(5)

By combining Equations (4) and (5), it can be shown that the velocity increment at the actuator disk is half of the slipstream velocity increment. The total work done by the actuator disk on the airflow per unit time is:

$$\mathsf{\Delta }E={\displaystyle \frac{1}{2}}\rho \mathrm{A}{V}_0\left(1+a\right)\left[{V_0}^2{\left(1+b\right)}^2-{V^2}_0\right]=\rho \mathrm{A}{V_0}^{3}b{\left(1+a\right)}^2$$

(6)

The useful work done by the thrust $T$ is:

$$\mathsf{\Delta }{E}_1=T{V}_0=\rho \mathrm{A}{V_0}^{3}b\left(1+a\right)$$

(7)

According to momentum theory, the ideal propeller efficiency is given by:

$$\eta ={\displaystyle \frac{T{V}_0}{\mathsf{\Delta }E}}={\displaystyle \frac{\mathsf{\Delta }{E}_1}{\mathsf{\Delta }E}}={\displaystyle \frac{1}{1+a}}$$

(8)

The kinetic energy carried away by the airflow per unit time is the slipstream loss, which reduces the ideal efficiency:

$$\begin{array}{cc}\mathsf{\Delta }{E}_f& =\mathsf{\Delta }E-\mathsf{\Delta }{E}_1=\rho A{V_0}^{3}b{(1+a)}^2-T{V}_0\hfill \\ & =\rho A{V_0}^{3}b{(1+a)}^2-\rho A{V_0}^{3}b(1+a)\hfill \\ & ={\displaystyle \frac{1}{2}}\rho A{V}_0(1+a){(b{V}_0)}^2={\displaystyle \frac{1}{2}}\rho A{V_0}^2(1+a)b(b{V}_0)\hfill \\ & ={\displaystyle \frac{1}{2}}T{V}_{0}b=T{V}_{0}a\hfill \end{array}$$

(9)

Therefore, the efficiency of the propeller is:

$$\eta ={\displaystyle \frac{\mathsf{\Delta }E}{\mathsf{\Delta }{E}_1+\mathsf{\Delta }{E}_f}}={\displaystyle \frac{T{V}_0}{T{V}_0+T{V}_{0}a}}={\displaystyle \frac{1}{1+a}}$$

(10)

The thrust coefficient is defined as:

$$C_T={\displaystyle \frac{T}{\frac{1}{2}\rho {V_0}^{2}A}}$$

(11)

Thus, we have:

$$\eta ={\displaystyle \frac{2}{C_T}}\left(\sqrt{1+C_T}-1\right)$$

(12)

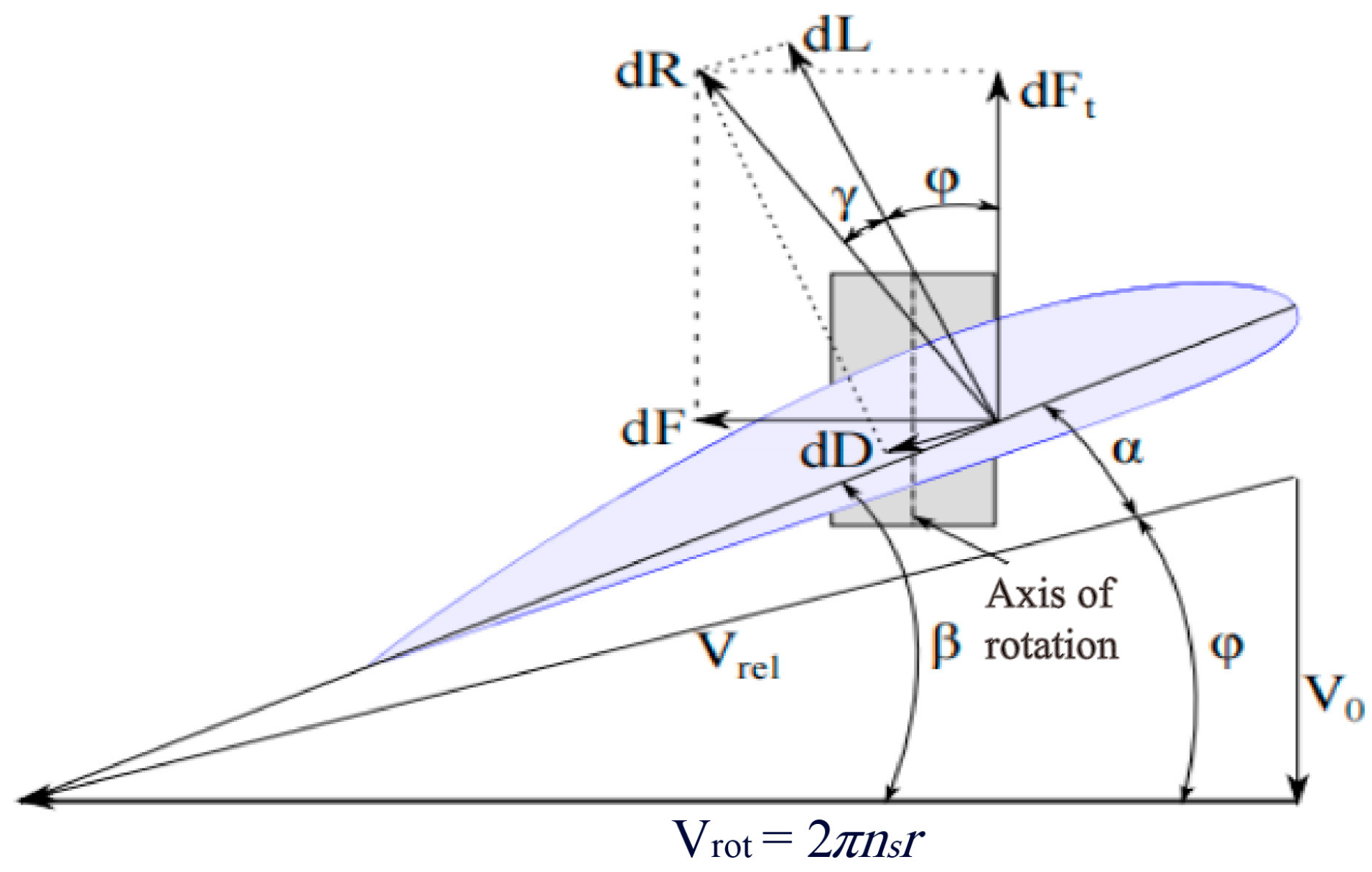
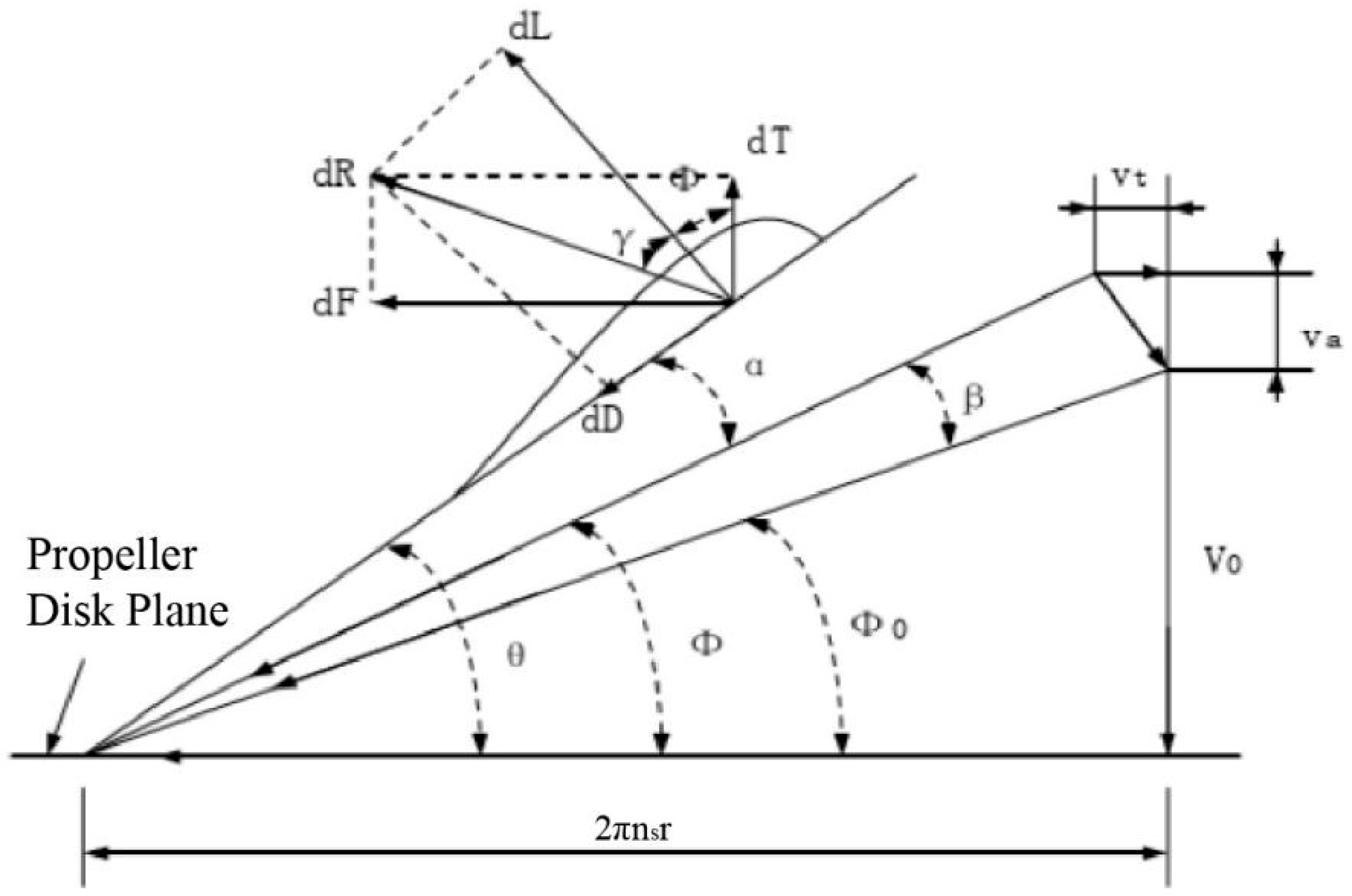
2.2. The Blade Element Theory

Blade Element Theory (BET) focuses on aerodynamic forces acting on the blade. The blade is divided into small segments called elements, each contributing to the total aerodynamic force through summation. Unlike momentum theory, BET directly analyzes forces on the blade itself. BET relies on three assumptions: independence, two-dimensional flow, and steady flow. Independence assumes no spanwise interference between elements. Two-dimensional flow ignores 3D effects like vortex diffusion. Steady flow assumes stable conditions; unsteady states require dynamic correction.

As shown in Figure 2, at radial position $r$, a small element of length $\mathrm{d}r$ and chord length $b$ is considered. During flight, the element follows a helical path. The forward speed is $V_0$, and the tangential velocity in the disk plane is $2\pi n_{s}r$, where $n_s$ is the rotation speed per second. Let $n$ be the rotation speed in rpm, then $n_s=n/60$.

The geometric relative velocity of the airflow to the element is:

$$W_0=\sqrt{{V_0}^2+{\left(2\pi n_{s}r\right)}^2}$$

(13)

The angle between the geometric relative velocity and the plane of rotation is:

$$\tan {\phi }_0={\displaystyle \frac{V_0}{2\pi n_{s}r}}$$

(14)

With installation angle $\beta$ defined between the chord line and the rotation plane, the angle of attack becomes $\alpha =\beta -{\phi }_0$. Given lift and drag coefficients $C_L$ and $C_D$:

$$C_L={\displaystyle \frac{L}{\frac{1}{2}\rho {V_0}^{2}A}};C_D={\displaystyle \frac{D}{\frac{1}{2}\rho {V_0}^{2}A}}$$

(15)

When airflow passes through the cross-section of a blade element, it produces an aerodynamic force. This force is perpendicular to the incoming airflow. It is called lift:

$$\mathrm{d}L={\displaystyle \frac{1}{2}}\rho {W_0}^2{C}_{L}b\mathrm{d}r$$

(16)

The aerodynamic force parallel to the relative airflow direction is the drag on the blade element:

$$\mathrm{d}D={\displaystyle \frac{1}{2}}\rho {W_0}^2{C}_{D}b\mathrm{d}r$$

(17)

The angle between lift and drag vectors:

$$\gamma =\arctan {\displaystyle \frac{\mathrm{d}D}{\mathrm{d}L}}$$

(18)

Total aerodynamic force (vector sum of lift and drag):

$$\mathrm{d}R=\sqrt{\mathrm{d}{L}^2+\mathrm{d}{D}^2}={\displaystyle \frac{\mathrm{d}L}{\cos \gamma }}$$

(19)

Axial projection of aerodynamic force provides rotor thrust:

$$\mathrm{d}T=\mathrm{d}R\cos ({\phi }_0+\gamma )$$

(20)

Substituting from (19) and $W_0=V_0/\sin {\phi }_0$:

$$\begin{array}{cc}\mathrm{d}T& ={\displaystyle \frac{1}{2}}\rho {V_0}^2{\displaystyle \frac{C_{L}b}{{\sin }^2{\phi }_0\cos \gamma }}\cos ({\phi }_0+\gamma )\mathrm{d}r\hfill \\ & ={\displaystyle \frac{1}{2}}\rho {V_0}^2{T}_{c}dr\hfill \end{array}$$

(21)

In the function, $T_c=K\cos ({\phi }_0+\gamma )$, $K=C_{L}b/{\sin }^2{\phi }_0\cos \gamma$. Tangential component of aerodynamic force in the rotation plane:

$$\mathrm{dF}={\displaystyle \frac{1}{2}}\rho {V_0}^{2}K\sin ({\phi }_0+\gamma )\mathrm{d}r$$

(22)

The moment of this force about the rotation axis is the torque of the blade element:

$$\mathrm{d}M={\displaystyle \frac{1}{2}}\rho {V_0}^2{Q}_c\mathrm{d}r$$

(23)

In the function, $Q_c=Kr\sin ({\phi }_0+\gamma )$. Effective power of the blade element:

$$\mathrm{d}{P}_e=\mathrm{d}T{V}_0$$

(24)

Power absorbed (torque power):

$$\mathrm{d}{P}_w=2\pi n_s\mathrm{d}M$$

(25)

Blade efficiency is the ratio of aerodynamic power to available wind energy, affected by lift-drag ratio, inflow angle, and induced losses:

$$\eta ={\displaystyle \frac{\mathrm{d}{P}_e}{\mathrm{d}{P}_w}}={\displaystyle \frac{\mathrm{d}T{V}_0}{2\pi n_s\mathrm{d}M}}={\displaystyle \frac{V_0}{2\pi n_{s}r}}{\displaystyle \frac{\mathrm{d}T}{\mathrm{d}F}}={\displaystyle \frac{\tan {\phi }_0}{\tan ({\phi }_0+\gamma )}}$$

(26)

Let hub radius of blades be $r_0$. The overall propeller efficiency is:

$$\eta ={\displaystyle \frac{P_e}{P_w}}={\displaystyle \frac{T{V}_0}{2\pi n_{s}M}}={\displaystyle \frac{V_0}{2\pi n_s}}{\displaystyle \frac{{\displaystyle {\int }_{r_0}^R{T}_c\mathrm{d}r}}{{\displaystyle {\int }_{r_0}^R{Q}_c\mathrm{d}r}}}$$

(27)

2.3. The Standard Strip Analysis

Standard Strip Analysis (SSA) is based on Joukowski’s vortex theorem and Prandtl’s finite wing theory. It introduces the bound vortex–free vortex model to correct for tip vortex and spanwise flow interference. According to the finite wing theory, a finite-span wing that generates lift will change the airflow direction when air passes over it. This causes downwash of the airflow. The downwash angle depends on the lift and the wingspan. In the case of infinite wingspan, there is no downwash. The airflow around the wing only depends on the airfoil shape.

As shown in Figure 3, at the radial position $r$, take a small segment of length $\mathrm{d}r$, with a corresponding chord length $b$. During flight, the motion path of the blade element is a spiral. The forward flight speed is $V_0$, and the tangential speed in the rotor disk plane is $2\pi n_{s}r$. The geometric relative velocity of the airflow to the blade element is:

$$W_0=\sqrt{{V_0}^2+{(2\pi n_{s}r)}^2}$$

(28)

The angle between the geometric relative velocity and the plane of rotation is:

$$\tan {\varphi }_0={\displaystyle \frac{V_0}{2\pi n_{s}r}}$$

(29)

Let $\theta$ be the installation angle between the blade element chord and the rotational plane, $\beta$ the interference angle from the trailing vortex, and $\alpha =\theta -\beta -{\phi }_0$ the angle of attack relative to the blade element. The angle between the inflow velocity and the plane of rotation is defined as:

$$\tan \phi ={\displaystyle \frac{V_0+v_a}{2\pi n_{s}r-v_t}}$$

(30)

In the formula, $v_a$ represents the induced axial velocity at the rotor disk, and $v_t$ represents the induced tangential velocity at the rotor disk. The instantaneous velocity of the fluid at a specific position and direction is the actual airflow velocity:

$$W=\sqrt{{\left(V_0+v_a\right)}^2+{(2\pi n_{s}r-v_t)}^2}$$

(31)

The torque on the annular elemental area is:

$$\mathrm{d}M=4\pi r^2\mathrm{d}r\rho v_t(V_0+v_a)=4\pi \rho V_0(1+a)(2\pi n_{s}r)a^{\prime }{r}^2\mathrm{d}r$$

(32)

In the formula, $a=v_a/V_0$ is the axial induction factor, and $a^{\prime }=v_t/\left(2\pi n_{s}r\right)$ is the tangential induction factor. By combining blade element theory and momentum theory, the efficiency of the blade element can be obtained as follows:

$$\eta ={\displaystyle \frac{\mathrm{d}{P}_{\mathrm{e}}}{\mathrm{d}{P}_{\mathrm{w}}}}={\displaystyle \frac{(1-a^{\prime })\tan \phi }{(1+a)\tan (\phi +\gamma )}}$$

(33)

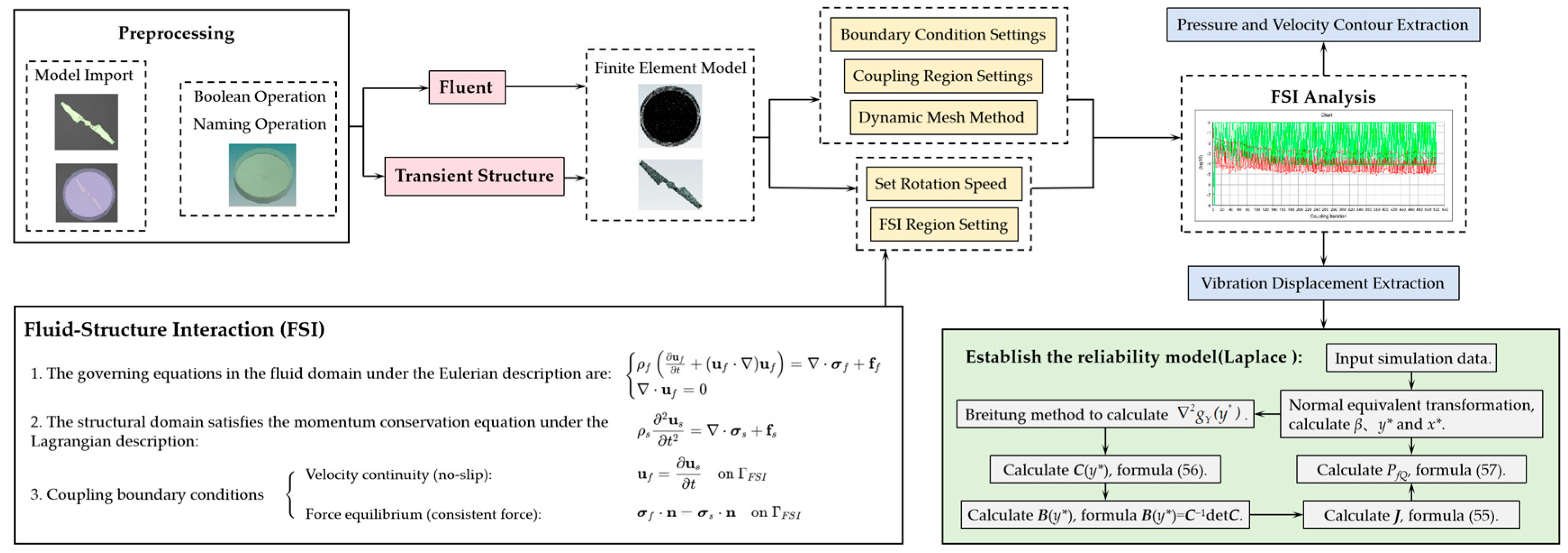
3. Vibrational Model Based on Bidirectional Fluid–Structure Interaction

To accurately simulate the aerodynamic response of rotors under complex conditions, this study introduces actuator disk theory (ADT), blade element theory (BET), and strip theory (SSA) in Section 2 as the theoretical basis. These models are used to qualitatively analyze the velocity and pressure distribution around the rotors. Their predicted trends are compared with numerical simulation results. Although these theories are not directly involved in the numerical solution process, their predictions are reflected in the simulation outcomes. This confirms the physical consistency and reliability of the simulation results. This section takes a small quadrotor UAV with dual-blade rotors as an example. In the Fluent environment of Ansys Workbench, a vibration response dataset of the UAV structure under aerodynamic loads is obtained through the combined computation of flow field analysis, modal analysis, transient analysis, and fluid–structure interaction modules. The geometric and material properties of the rotor and blades are shown in

Table 1. Geometric and material properties of the rotor and blade.

Parameter	Value	Description
Rotor diameter	20 mm	Tip-to-tip diameter of the rotor
Number of blades	2	Dual-blade configuration
Blade material	PA612 nylon	Polyamide 612 (engineering thermoplastic)
Density (ρ)	1.07 g/cm3	Material density
Young’s modulus (E)	1.4~1.7 GPa	Depends on moisture and processing
Tensile strength	60~80 MPa	Typical range for PA612
Poisson’s ratio	0.3~0.4	Assumed value for nylon materials

below.

3.1. Rotor Dynamic Modeling

To study the interaction mechanism between flexible rotor vibration and the flow field, its vibration displacement can significantly change the flow separation point in the boundary layer. The bidirectional fluid–structure coupling effect forms a closed-loop system through dynamic feedback; that is, rotor vibration changes the flow pressure distribution in real time, which then affects the aerodynamic damping characteristics. The mathematical expression of the bidirectional fluid–structure coupling is as follows:

$$\begin{array}{l}{F}_{fluid}=f(u_{flow},d_{structure})\hfill \\ d_{structure}=g(F_{fluid})\hfill \end{array}$$

(34)

In the formula, the fluid load $F_{fluid}$ depends on both the flow velocity $u_{flow}$ and the structure displacement $d_{structure}$. The structure displacement is driven by the fluid load as a reaction. This effectively captures aeroelastic effects such as blade flutter. Therefore, bidirectional fluid–structure coupling calculation can significantly improve the accuracy of UAV rotor vibration prediction and enhance the engineering applicability of rotor design. As shown in Figure 4, the rotor vibration dynamic analysis based on bidirectional fluid–structure coupling can be divided into five parts: preprocessing, flow field analysis, transient structure analysis, system coupling, and postprocessing.

As shown in Figure 4, the simulation process includes the following key steps: In preprocessing, the rotor model of the UAV is created. A cylindrical rotating domain and flow field domain are generated around the rotor axis. Boolean operations are performed to ensure the fluid–solid interface matches correctly. The blade surface is defined as the fluid–structure coupling interface. The mesh uses tetrahedral elements with a global size of 5 mm. The rotor rotation domain is locally refined to 2 mm. In the Fluent setup, the SST k-omega turbulence model is selected. This model is suitable for complex flow phenomena. It can accurately predict the development and variation of turbulent structures. The inlet is set as a velocity inlet with a flow speed of 3 m/s to simulate low-speed flight of the UAV. The outlet is set as a pressure outlet. Dynamic mesh calculation is activated, and the blade surface is assigned as the coupling region. The time step is 0.001 s, with 250 steps and 5000 iterations. In the transient solid analysis, the rotor is assumed to be made of PA612 nylon. The physical properties, such as density, elastic modulus, and Poisson’s ratio, are defined. Boundary conditions and the fluid–structure coupling region are set. A rotational speed of 1200 rpm is applied to capture dynamic behavior. In system coupling, the convergence of coupling variables is monitored through ANSYS 2024 R2 system coupling convergence plots. In the post-processing stage, extract the pressure contour cloud and velocity volume cloud. Also, obtain the vibration displacement cloud. Extract the vibration magnitude and frequency curves at key points, and use them for the reliability calculation in Section 4.2.

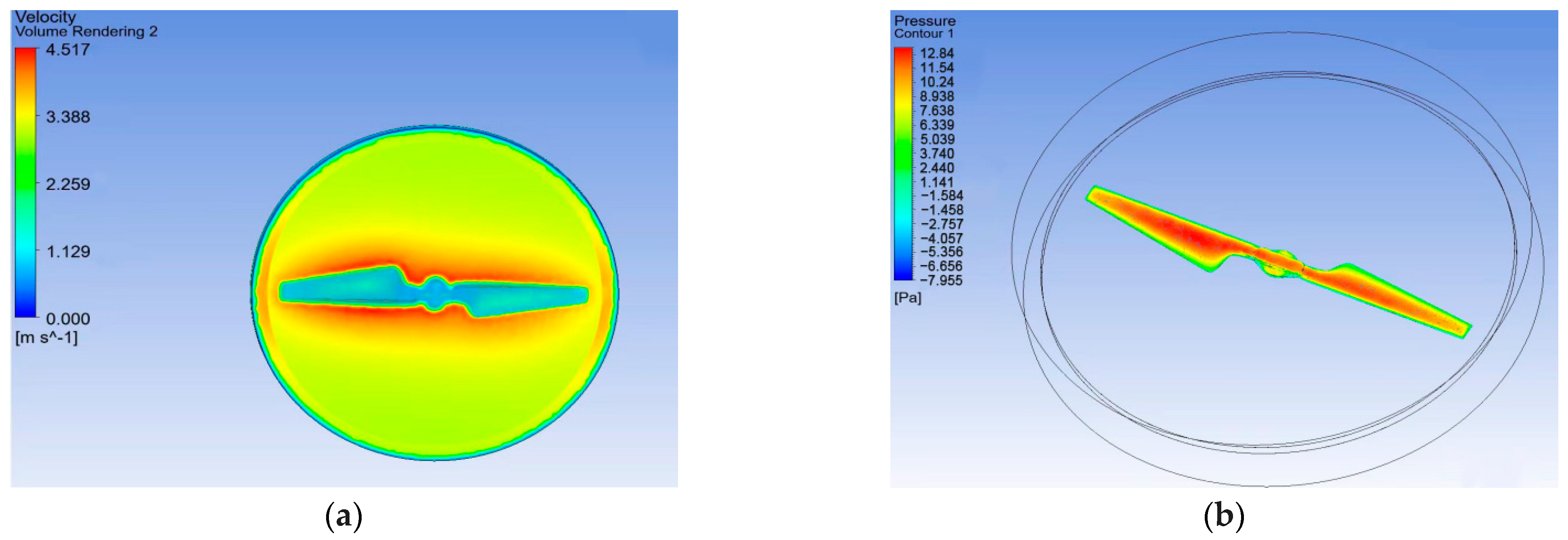
3.2. Rotor Vibration Analysis

Figure 5 shows the convergence curves of rotor vibration based on bidirectional fluid–structure coupling. It reflects the error convergence trend during the iteration process of the coupling simulation. In the figure, the horizontal axis represents the number of coupling iterations, from 0 to 540. The vertical axis shows the logarithm of the error magnitude. The green and red curves represent the residual changes of the structural subsystem and the fluid subsystem, respectively. Figure 5 shows that during the first 60 initial iterations, the error magnitude is large and fluctuates obviously. This mainly results from the large inconsistency between the initial fields at the fluid–structure coupling interface. The system quickly adjusts variables in each coupling domain to achieve coordination. From iteration 60 to 250, the curve enters the mid-stage convergence. The residual shows a clear downward trend. This indicates that the coupled fields gradually become stable. However, the error curves of the structural subsystem and the fluid subsystem still have some fluctuations. Especially, the residual of the fluid domain, shown in red, exhibits periodic oscillations. After 250 iterations, the curve gradually becomes stable. This means the system is close to convergence. Finally, the error converges. This shows that the coupling solution setup is numerically reasonable.

Figure 6 shows the velocity and pressure contours of the rotor. According to the ADT, the rotor induces a noticeable increase in axial flow speed after the rotor disk. This is reflected by the high-speed ring structure observed at the rotor edge in the simulation. The maximum velocity reaches 4.517 m/s. The middle region shows clear velocity layering, and the minimum velocity approaches zero, which agrees with ADT’s prediction of lower flow speed near the center. The pressure field shows that the positive pressure zone concentrates at the rotor leading-edge stall point. It has a clear impact pressure peak. The maximum pressure is about 12.84 Pa. This agrees with the BET, which predicts a local pressure rise near the blade center due to aerodynamic loading. The low-pressure zone mainly appears near the rotor trailing edge and the fluid separation areas on both sides. The minimum pressure is about −7.96 Pa. This also matches BET, which predicts a pressure drop behind the rotor due to increased flow speed. The overall pressure field is stable and shows a continuous transition from high to low along the blade chord and span directions. This trend is consistent with SSA, which takes into account chord-wise and span-wise variations. These consistencies with classical aerodynamic theories confirm that the simulation results are physically reasonable.

Figure 7a,b shows the rotor deformation and pressure distribution at 0.25 s. The maximum rotor displacement is about 0.02553 mm. It concentrates at the blade tip. The minimum displacement is about 5.55 × 10⁻¹⁴ mm. It is located near the blade root constraint area. At this time, the deformation at both blade ends is clearly larger than in the middle. The largest warping occurs along the Z-axis. This shows typical edge warping and rigid middle response. The deformation increases from root to tip along the blade span. This reflects bending caused by lift. The deformation changes smoothly from the smallest blue area to the largest red area. No local jumps or discontinuities appear. This matches the typical rotor response under aerodynamic loads. It confirms the structural response is continuous and reasonable. The maximum stress is 11.598 MPa. It appears at the blade root region. The minimum stress is about 0.0021 MPa. It distributes at the free edge away from the connection. High-stress zones mainly focus on the transition between the blade and hub. This area usually has stress concentration and complex forces. Most of the blade surface has a fairly uniform stress distribution between 0 and 7 MPa. It shows as a smooth color transition from blue to green to yellow. The stress cloud is continuous with no local jumps. This further proves that the model’s boundary conditions, load cases, and mesh are reasonable. The current maximum Von Mises stress is about 500 MPa. It is far below the aluminum alloy yield strength. This indicates the structure works safely.

Figure 8 shows the time-domain response curve of rotor vibration displacement from 0 to 0.25 s. The curve has three typical stages: In the initial vibration stage (0 to 0.03 s), the amplitude changes sharply with peaks close to 2.3 mm. This shows a clear transient high-frequency response. This matches the energy disturbance effect in the early stage of fluid–structure coupling. In the transition stage (0.03 to 0.12 s), the response has several local fluctuations. The amplitude gradually decreases to below about 1 mm. The system’s energy dissipation, such as structural and aerodynamic damping, becomes more obvious. In the steady modal stage (0.12 to 0.25 s), the vibration response enters a stable periodic state. The frequency is lower, and the amplitude stays between 0.5 and 1 mm. This shows the structure reaches a dynamic balance dominated by modal behavior.

The overall response curve has no sudden jumps and shows a reasonable trend. It agrees with the dynamic evolution law of fluid–structure coupling systems. This verifies the reliability of the rotor vibration dynamic model based on bidirectional fluid–structure coupling established in this study.

4. UAV Dynamic Reliability Model

Vibration faults severely affect flight safety and system stability. Environmental factors such as strong wind and rainfall further induce complex vibration characteristics and transmission patterns. The magnitude of vibration directly affects the reliability, safety, and stability of the UAV during flight missions, which in turn leads to reliability degradation. This section establishes a dynamic reliability model for multirotor UAVs, focusing on the impact of vibrations—caused by dynamic factors such as flight attitude changes, airflow disturbances, and the coordination between motors and rotors—on system reliability during dynamic operation under complex conditions and uncertainties.

4.1. Second-Order Reliability Method (SORM)

SORM transforms non-normal random variables into standard normal space. It applies a second-order Taylor expansion at the Most Probable Point (MPP) and incorporates principal curvatures for accurate failure probability estimation [33].

A limit state function is constructed using vibration displacement responses from Section 3.2. The function evaluates the probability of the UAV remaining functional under displacement thresholds. Let the function be:

$$\mathit{Z}=\mathsf{\theta }-\mathit{H}\{z_1,z_2,z_3,\dots ,z_n\}$$

(35)

$\mathit{Z}$ is the limit function, $\mathit{H}$ is the simulation response, and $\mathsf{\theta }$ is the threshold. If $\mathit{Z}>0$ ($\mathsf{\theta }>\mathit{H}\{z_1,z_2,z_3,\dots ,z_n\}$), the UAV is reliable; otherwise, failure occurs.

To ensure that the threshold used in system reliability assessment is statistically justified and appropriate, this paper adopts the three-sigma rule to determine the vibration threshold. This rule is widely used in engineering tolerance analysis and quality control. Based on the assumption of a normal distribution, it holds that most natural fluctuations in system response fall within the range of the mean ± three standard deviations, covering approximately 99.73% of all data. Therefore, this range is considered the statistical stability region of the system, and values beyond it are regarded as abnormal fluctuations. In Equation (35), if condition $\mathit{Z}>0$ or $\mathsf{\theta }>\mathit{H}\{z_1,z_2,z_3,\dots ,z_n\}$ is met, which means the rotor vibration response does not exceed the threshold $\mathsf{\theta }$, the UAV system is considered to be in a reliable state. Otherwise, if condition $\mathsf{\theta }<\mathit{H}\{z_1,z_2,z_3,\dots ,z_n\}$ is met, the system deviates from the simulation prediction beyond the allowable range and is considered to be in a failure state.

The core of structural reliability analysis lies in obtaining the failure probability by processing random information [34]. Considering that the limit state function $\mathit{Z}$ of the UAV system is a continuous random variable, let $f_Z(Z)$ be its probability density function and $F_Z(Z)$ be its cumulative distribution function. According to the definitions of reliability $P_r$ and failure probability $P_f$, the following relationship can be further derived:

$$P_r=P(Z>0)={\displaystyle {\int }_0^{\infty }{f}_Z}(Z)\mathrm{d}Z=1-F_Z(0)$$

(36)

$$P_f=P(\mathit{Z}<0)={\displaystyle {\int }_{-\infty }^0{f}_{\mathit{Z}}}(\mathit{Z})\mathrm{d}z=F_{\mathit{Z}}(0)$$

(37)

Let the basic random variables of the UAV rotor structure be $\mathit{X}={\left(X_1,X_2,\dots ,X_n\right)}^T$. Their joint probability density function is $f_X\left(x\right)=f_X\left(x_1,x_2,\dots ,x_n\right)$, and the joint cumulative distribution function is $F_X\left(x\right)=F_X\left(x_1,x_2,\dots ,x_n\right)$. Then, the structural failure probability is:

$$\begin{array}{cc}{P}_f& ={{\displaystyle {\int }_{\mathit{Z}\le 0}\mathrm{d}F}}_{\mathit{X}}(x)={{\displaystyle {\int }_{\mathit{Z}\le 0}f}}_{\mathit{X}}(x)\mathrm{d}x\hfill \\ & ={\displaystyle \int }\cdots {{\displaystyle {\int }_{\mathit{Z}\le 0}f}}_{\mathit{X}}(x_1,x_2,\dots ,x_n)\mathrm{d}{x}_1\mathrm{d}{x}_2\dots \mathrm{d}{x}_n\hfill \end{array}$$

(38)

If the variables $X_i$ are mutually independent, and the probability density function of each $X_i$ is $f_{Xi}(x_i)$, then:

$$P_f={\displaystyle \int }\cdots \underset{\mathbf{Z}\le 0}{{\displaystyle \int }}{f}_{X_1}(x_1)f_{X_2}(x_2)\cdots f_{X_n}(x_n)\mathrm{d}{x}_1\mathrm{d}{x}_2\cdots \mathrm{d}{x}_n$$

(39)

The most basic function of two random variables $R$ and $S$ is $Z=g\left(R,S\right)=R-S$. Let their joint probability density function be $f_{RS}\left(r,s\right)$, and the joint cumulative distribution function be $F_{RS}\left(r,s\right)$. The failure domain ${\mathsf{\Omega }}_f$ can be simply defined as $R\le S$. Then, we have:

$$P_f=\mathrm{P}(R\le S)={{\displaystyle {\iint }_{R\le S}\mathrm{d}F}}_{RS}(r,s)={\displaystyle {\iint }_{R\le S}{f}_{RS}}(r,s)\mathrm{d}r\mathrm{d}s$$

(40)

If $R$ and $S$ are independent random variables, $f_R\left(r\right)$ and $f_S\left(s\right)$ are their probability density functions, while $F_R\left(r\right)$ and $F_S\left(s\right)$ are their cumulative distribution functions, then:

$$P_f=\mathrm{P}(R\le S)={\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\mathrm{s}}{f}_R}}(r)f_S(s)\mathrm{d}r\mathrm{d}s={\displaystyle {\int }_{-\infty }^{\infty }{F}_R}(r)f_S(s)\mathrm{d}s$$

(41)

$$P_f={\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_r^{\infty }{f}_R}}(r)f_S(s)\mathrm{d}r\mathrm{d}s={\displaystyle {\int }_{-\infty }^{\infty }[1}-F_S(s)]f_R(r)\mathrm{d}r$$

(42)

By introducing geometric corrections, SORM applies a second-order Taylor expansion at the design point to construct a quadratic hypersurface that approximates the actual limit state surface. The Hessian matrix is used to calculate the principal curvature parameters, which quantify the effect of surface curvature on the failure probability. Based on the curvature correction factors, Breitung’s asymptotic formula is adopted to improve the linear approximation results of FORM [33]:

$$P_f\approx \mathsf{\Phi }(-\beta ){\displaystyle \prod _{i=1}^{n-1}{(1+\beta {\kappa }_i)}^{-1/2}}$$

(43)

In the formula, $\beta$ is the reliability index. ${\kappa }_i$ is the main curvatures of the limit state surface. SORM calculation still uses the basic reliability results from FORM. But SORM adds curvature correction. This makes failure probability estimates more accurate. It also improves calculation accuracy for strongly nonlinear reliability problems.

4.2. Reliability Calculation Based on Laplace Method

The Laplace Method is a reliability modeling approach based on the Laplace transform. It is mainly used to calculate time-varying reliability indices, such as instantaneous availability and failure frequency. This method converts time-domain differential or integral equations into frequency-domain algebraic equations. It avoids complex time-domain integration and accurately describes the full transition from transient to steady-state behavior. It provides theoretical support for the reliability design of repairable systems. In this paper, the vibration displacement of the UAV rotor is mapped to the standard normal space using an equal-probability transformation. The Laplace method is then used to calculate structural reliability in the standard normal space. This approach is essentially a type of second-moment, second-order method.

The integral value is approximated using the asymptotic property of integrals with large parameters. The Laplace-type integral has the following form:

$$I(\lambda )={\displaystyle {\int }_{g(x)\le 0}p}(x)\exp \left[{\lambda }^{2}h(x)\right]dx$$

(44)

The behavior of the integral is determined by the properties of the integrand near its maximum point. If $h\left(x\right)$ and $g\left(x\right)$ are twice continuously differentiable, and $p\left(x\right)$ is continuous, and if $h\left(x\right)$ reaches its maximum only at a point $x^{*}$ on the boundary $\left\{x\left|g\left(x\right)\right.=0\right\}$, then the integral can be asymptotically written as:

$$I(\lambda )\approx {\displaystyle \frac{{(2\pi )}^{(n-1)/2}}{{\lambda }^{n+1}}}{\displaystyle \frac{p(x^{*})\exp [{\lambda }^{2}h(x^{*})]}{\sqrt{\left|\mathit{J}\right|}}}$$

(45)

In the equation:

$$\mathit{J}={[\nabla h(x^{*})]}^{\mathrm{T}}\mathit{B}(x^{*})\nabla h(x^{*})$$

(46)

In the equation, the matrix $\mathit{B}(x^{*})$ is the adjugate matrix of the following matrix:

$$\mathit{C}(x^{*})={\nabla }^{2}h(x^{*})-{\displaystyle \frac{\Vert \nabla h(x^{*})\Vert }{\Vert \nabla g(x^{*})\Vert }}{\nabla }^{2}g(x^{*})$$

(47)

The Laplace method using asymptotic expressions can also be used to calculate structural failure probability. Let $\mathit{Y}={\left(Y_1,Y_2,\dots ,Y_n\right)}^T$ be independent standard normal random variables. The limit state function is $Z=g_Y\left(\mathit{Y}\right)$. Then, the structural failure probability $P_f$ is:

$$P_f={\displaystyle {\int }_{g_Y(y)\le 0}{\phi }_n}(y)dy={\displaystyle {\int }_{g_Y(y)\le 0}\frac{1}{{(2\mathsf{\pi })}^{n/2}}}\exp \left(-{\displaystyle \frac{y^{T}y}{2}}\right)\mathrm{d}y$$

(48)

${\phi }_n$ is the probability density function of an n-dimensional standard normal distribution. Considering a linear transformation, we obtain:

$$\mathit{Y}=\lambda \mathit{V}$$

(49)

The Jacobian determinant of this transformation is $\det {\mathit{J}}_{YV}={\lambda }^n$. Substituting this into Equation (48) provides:

$$P_f={\displaystyle {\int }_{g_Y(\lambda v)\le 0}\frac{{\lambda }^n}{{(2\mathsf{\pi })}^{n/2}}}\exp \left(-{\displaystyle \frac{{\lambda }^2{v}^{T}v}{2}}\right)\mathrm{d}v$$

(50)

Since $p\left(\mathit{V}\right)={\lambda }^n/{\left(2\pi \right)}^{n/2}$ and $h\left(\mathit{V}\right)=-{\mathit{V}}^T\mathit{V}/2$, the function $h\left(\mathit{V}\right)$ reaches its maximum at the origin $v=0$ in the $\mathit{V}$ space. For typical structural reliability problems, if the point $v=0$ lies inside the safe domain, it means that $h\left(\mathit{V}\right)$ has a maximum at a point $v^{*}=y^{*}/\lambda$ on the failure surface. Therefore, the integral value of $P_f$ is mainly determined by the point $v^{*}$ on the failure surface $g_Y\left(\lambda \mathit{V}\right)$ where $h\left(\mathit{V}\right)$ is maximized, and the geometric characteristics of the failure surface near $v^{*}$. According to the geometric meaning of the reliability index $\beta$, the critical point $v^{*}$ is the design point of the structure in the $\mathit{V}$ space. If the limit state function is twice differentiable, then based on Equations (45) and (50), it can be written as:

$$P_{fQ}={\displaystyle \frac{1}{\sqrt{2\mathsf{\pi }}\lambda \sqrt{\left|{\mathit{J}}_1\right|}}}\exp \left(-{\displaystyle \frac{{\lambda }^2{v}^{*\mathrm{T}}{v}^{*}}{2}}\right)$$

(51)

In the above equation, ${\mathit{J}}_1$ can be expressed as:

$${\mathit{J}}_1={[\nabla h(v^{*})]}^{\mathrm{T}}{\mathit{B}}_1(v^{*})\nabla h(v^{*})=v^{*\mathrm{T}}{\mathit{B}}_1(v^{*})v^{*}={\displaystyle \frac{1}{{\lambda }^2}}{y}^{*\mathrm{T}}{\mathit{B}}_1(v^{*})y^{*}$$

(52)

In the equation, $\mathit{B}\left(v^{*}\right)$ is the adjugate matrix of the following matrix $\mathit{C}\left(v^{*}\right)$:

$${\mathit{C}}_1(v^{*})={\nabla }^{2}h(v^{*})-{\displaystyle \frac{\Vert \nabla h(v^{*})\Vert }{\Vert \nabla g_Y(\lambda v^{*})\Vert }}{\nabla }^2{g}_Y(\lambda v^{*})$$

(53)

Substituting Equation (52) into Equation (51), the geometric meaning of $\beta$ is ${\beta }^2=y^{*T}{y}^{*}$. Equation (51) can be written in the $\mathit{Y}$ space as:

$$P_{fQ}={\displaystyle \frac{1}{\sqrt{2\mathsf{\pi }}\sqrt{\left|\mathit{J}\right|}}}\exp \left(-{\displaystyle \frac{y^{*\mathrm{T}}{y}^{*}}{2}}\right)={\displaystyle \frac{\phi (\beta )}{\sqrt{\left|\mathit{J}\right|}}}$$

(54)

In the equation:

$$\mathit{J}=y^{*\mathrm{T}}\mathit{B}(y^{*})y^{*}$$

(55)

And $\mathit{B}(y^{*})={\mathit{B}}_1(v^{*})$ is the adjugate matrix of the following matrix $\mathit{C}(y^{*})={\mathit{C}}_1(v^{*})$:

$$\begin{array}{cc}\mathit{C}(y^{*})& =-{\mathit{I}}_n-{\displaystyle \frac{\Vert y^{*}\Vert /\lambda }{\lambda \Vert \nabla g_Y(y^{*})\Vert }}{\lambda }^2{\nabla }^2{g}_Y(y^{*})\hfill \\ & =-{\mathit{I}}_n-{\displaystyle \frac{\beta }{\Vert \nabla g_Y(y^{*})\Vert }}{\nabla }^2{g}_Y(y^{*})\hfill \end{array}$$

(56)

Usually, $\beta$ is a relatively large positive value. Then, $\phi \left(\beta \right)\approx \left(-\beta \right)$. Equation (54) can be rewritten as:

$$P_{fQ}\approx \Phi (-\beta ){\displaystyle \frac{\beta }{\sqrt{\left|\mathit{J}\right|}}}$$

(57)

The SORM based on the Laplace method was used to calculate the vibration response reliability of a multi-rotor UAV. The main computational procedure is summarized in

Table A1. Computation of Single-Rotor Reliability Based on Laplace Method.

Step	Description
Input	$\mathrm{Mean} \mathrm{vector} \mu \mathrm{X}$$, \mathrm{standard} \mathrm{deviation} \mathrm{vector} \sigma \mathrm{X}$$, \mathrm{transformation} \mathrm{gradient} xY$
1	Initialize $x$←small positive values (e.g., machine epsilon)
2	Repeat
3	Compute cumulative distribution function (CDF) of $x$$:cdfX$$\leftarrow \varphi ((x-\mu X)/\sigma X)$
4	Transform to standard normal space: $y$$\leftarrow {\varphi }^{-1}(cdfX)$
5	$\mathrm{Define} \mathrm{limit} \mathrm{state} \mathrm{function}: g(x)=x_2-x_1$
6	$\mathrm{Compute} \mathrm{gradient} \mathrm{in} \mathrm{physical} \mathrm{space}: gX$$\leftarrow [1;-1]$
7	$\mathrm{Compute} \mathrm{probability} \mathrm{density} \mathrm{function}\left(\mathrm{PDF}\right) \mathrm{adjustment}: pdfX$$\leftarrow \phi (y)/\phi X$
8	$\mathrm{Compute} \mathrm{gradient} \mathrm{in} \mathrm{standard} \mathrm{normal} \mathrm{space}: gY$$\leftarrow gX\odot xY$
9	$\mathrm{Compute} \mathrm{search} \mathrm{direction}: \alpha Y$$\leftarrow -gY/‖gY‖$
10	Compute reliability index $\beta$$\leftarrow (g-g{Y}^T\cdot y)/‖gY‖$
11	Update $y$:$y$$\leftarrow \beta \cdot \alpha Y$
12	Transform back: $x$$\leftarrow \mu X+\sigma X\odot {\varphi }^{-1}(\varphi (y))$
13	$\mathrm{Until} \mathrm{convergence} (\mathrm{e}.\mathrm{g}., ‖x-x_0‖/‖x_0‖<tolerance$)
14	$\mathrm{Compute} \mathrm{first}-\mathrm{order} \mathrm{failure} \mathrm{probability}: P_{fL}$$\leftarrow \varphi (-\beta )$
15	$\mathrm{Define} \mathrm{Hessian} \mathrm{of} \mathrm{limit} \mathrm{state} (\mathrm{if} \mathrm{available}): gXX$$\leftarrow zeros(n,n)$
16	$\mathrm{Compute} \mathrm{second}-\mathrm{order} \mathrm{terms}: fX$$\leftarrow (\mu X-x)/\sigma X^2\odot pdfX$ $gYY$$\leftarrow xY\cdot x{Y}^T\odot gXX-diag(gX\odot (y\odot xY+x{Y}^2\odot fX/pdfX))$
17	Construct correction matrix: $C$$\leftarrow -I-\beta /‖gY‖\cdot gYY$
18	$\mathrm{Compute} \mathrm{adjugate} (\mathrm{or} \mathrm{pseudo}-\mathrm{inverse}): CS$$\leftarrow \det {(C)}^{-1}\cdot C$
19	$\mathrm{Compute} \mathrm{corrected} \mathrm{failure} \mathrm{probability} (\mathrm{Laplace}-\mathrm{based}): P_{fQ}$$\leftarrow \varphi (-\beta )\cdot \beta /\sqrt{\left|y^T\cdot CS\cdot y\right|}$
20	Compute reliability: $R$$\leftarrow 1-P_{fQ}$
Output	Reliability $R$ of the rotor

in Appendix A for clarity. This pseudocode outlines the transformation of input variables into the standard normal space, the iterative search for the design point, and the Laplace-based approximation of failure probability.

Based on this method, the reliability of a single rotor was found to be R = 0.9310. This means that under the particular simulation conditions and input data, the single rotor system has a 93.10% probability of fault-free operation. This indicates that the designed single rotor of the UAV is relatively reliable. Assuming this single rotor is a component of the redundancy design in a multi-rotor UAV, its 93.10% reliability shows that the probability of failure during system operation (6.90%) is low. This feature is useful in redundancy design. When other rotors fail or degrade, this rotor can maintain system functionality by redistributing loads. This helps avoid total system failure and ensures flight stability and mission continuity.

From a practical application perspective, the reliability results have not only theoretical value but also directly affect the availability and mission success rate of multirotor UAVs in critical tasks. For high-risk or high-value scenarios such as medical emergencies and military reconnaissance, UAVs must operate stably for long periods under extreme conditions, often requiring ultra-high reliability, such as 99.9%. Therefore, the reliability results obtained in this section can be used as a basis for evaluating UAV mission adaptability. They also provide theoretical support for redundancy design and structural optimization to ensure sufficient safety margin and operational assurance in critical missions.

The dynamic reliability method based on Laplace transform is applicable to any system that satisfies the assumptions of differentiability and normal perturbations. Similar methods can be used to analyze low-probability failure events in wind turbines under extreme wind speeds and structural fatigue. However, wind turbines usually include more complex subsystems, such as pitch control mechanisms, electrical responses of generators, and coupled vibrations between blades and the tower. These factors introduce interactions and nonlinear behaviors. These features exceed the scope of the current UAV model. Therefore, although the proposed method provides a general theoretical basis, it still requires further structural adaptation. It also needs the integration of domain-specific observers or diagnostic frameworks before being effectively applied to wind turbine systems. Recent research in wind turbine fault diagnosis has explored the combination of fuzzy inference system-based modeling and zonotopic observers to handle such complexity. For instance, Pérez-Pérez et al. [35] developed a robust fault diagnosis methodology using a Multiple Output Adaptive Neuro-fuzzy Inference System (MANFIS) and Takagi–Sugeno (TS) models, while Pérez-Pérez et al. [36] proposed a hybrid approach to fault detection and isolation (FDI) based on an adaptive network-based fuzzy inference system (ANFIS) and quasi-Linear Parameter Varying (qLPV) zonotopic observers. Compared to these approaches, our method currently emphasizes physical-model-based structural reliability modeling rather than real-time residual generation or observer-based fault detection.

5. Reliability Assessment of UAV System

5.1. Reliability Calculation of Single Rotor System

Monte Carlo Simulation, also called the Direct Sampling Method or General Sampling Method, is a numerical method that solves complex problems by random sampling and statistical simulation. It is widely used in engineering, physics, finance, and other fields. In this section, the Monte Carlo method is used to perform extensive sampling of random variables that affect UAV rotor performance. By simulating the stability and fault tolerance of the multi-rotor system under environmental disturbances and vibration-induced uncertainties, the reliability level and failure probability are evaluated.

Let the limit state function of the multi-rotor UAV system be $Z=g_X\left(\mathit{X}\right)$, where $\mathit{X}$ includes basic random variables such as rotor performance parameters and factors causing UAV vibration. Its joint probability density function is $f_X\left(\mathit{x}\right)$. Based on this probability distribution, sample points $\mathit{x}$ are generated by random sampling. These points are substituted into the limit state function to calculate the corresponding response values $Z=g_X\left(\mathit{x}\right)$. When $Z<0$, the system fails to meet design requirements, which is considered a structural failure event. If a total of $N$ simulations are performed and the number of failures is $n_f$, then according to the Bernoulli theorem under the law of large numbers, the failure probability $p_f$ can be estimated by the frequency ratio $n_f/N$. This approximates the structural failure risk of the multi-rotor UAV system under uncertain parameters. The mathematical expression is:

$${\widehat{P}}_f={\displaystyle \frac{n_f}{N}}$$

(58)

Or expressed as:

$$P_f={\displaystyle {\int }_{g_X(x)\le 0}{f}_X}(x)dx={\displaystyle {\int }_{{ℝ}^n}I}[g_X(x)]f_X(x)dx=E\left\{I[g_X(x)]\right\}$$

(59)

In the equation, $I\left(x\right)$ is the indicator function of the variable $x$. It is defined as $I\left(x\right)=1$ when $x<0$, and $I\left(x\right)=0$ when $x\ge 0$. In the reliability assessment of multi-rotor UAV structures, the indicator function $I\left[g_X\left(x\right)\right]$ is introduced. It extends the failure domain defined by $g_X\left(x\right)\le 0$ to the entire ${\mathit{R}}^n$ space. This transforms the failure probability calculation into a full-space integral, which facilitates numerical processing and simulation analysis. The estimated value of $P_f$ is:

$$P_f={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^{N}I}[g_X(x_i)]$$

(60)

In the structural reliability analysis of multi-rotor UAVs, let $I\left[g_X\left(x_i\right)\right](i=1,2,\dots ,N)$ be the indicator function sample values corresponding to the limit state function. According to the estimation Formulas (58)–(60), the mean of these sample values is the estimator ${\widehat{P}}_f$ of the failure probability. Based on probability theory, regardless of the distribution of $I\left[g_X\left(x_i\right)\right]$, the expectation and variance are ${\mu }_{{\widehat{P}}_f}={\mu }_{I[g_X(x)]}$ and ${\sigma }_{{\widehat{p}}_f}^2={\sigma }_{I[g_X(x)]}^2/N$, respectively. Thus, ${\widehat{P}}_f$ is an unbiased estimator of the true failure probability $P_f$. When the sample size is large, the Monte Carlo simulation generally meets the conditions of the Central Limit Theorem. The sample mean ${\widehat{P}}_f$ then asymptotically follows a normal distribution. Therefore, based on the variance estimate of the indicator function samples, a confidence interval for the failure probability $P_f$ can be constructed. Half of this interval length can be regarded as the absolute error estimate of the simulation results:

$$\mathsf{\Delta }=|{\widehat{P}}_f-P_f|\le {\displaystyle \frac{u_{\alpha /2}}{\sqrt{N}}}{\sigma }_{I[g_X(x)]}={\displaystyle \frac{u_{\alpha /2}}{2}}{\sigma }_{{\widehat{p}}_f}$$

(61)

According to Equation (61), to reduce the error in estimating the structural failure probability of the multi-rotor UAV system by Monte Carlo simulation, one can increase the number of simulation samples $N$ to improve estimation accuracy. On the other hand, variance reduction techniques can be introduced to lower the variance ${\sigma }_{{\widehat{p}}_f}^2$ or the coefficient of variation ${\sigma }_{{\widehat{p}}_f}$ of the failure probability estimate.

In a Monte Carlo simulation, the indicator function $I\left[g_X\left(x_i\right)\right]$ takes values of either 0 or 1, corresponding to the binary outcomes of “no failure” or “failure”. This forms a Bernoulli trial. Let the true failure probability of the structure be $P_f$. Then the probability of no failure is $P_r=1-P_f$. After $N$ independent simulations, the number of failures $n_f$ follows a binomial distribution with parameters $(N,P_f)$. Its mean and variance are ${\mu }_{n_f}=N_{P_f}$ and ${\sigma }_{n_f}^2=N_{P_f}(1-P_f)$, respectively. Based on the relationship between the number of failures and the probability estimate, the variance of the failure probability estimator ${\widehat{P}}_f$ can be further derived as:

$${\sigma }_{{\widehat{p}}_f}^2={\displaystyle \frac{{\sigma }_{n_f}^2}{N^2}}={\displaystyle \frac{1}{N}}{P}_f(1-P_f)$$

(62)

According to Equations (61) and (62), given a significance level $\alpha$ (for example, $\alpha =5\%$), the estimated failure probability ${\widehat{P}}_f$ can be substituted into the theoretical model. This allows calculation of the required number of Monte Carlo simulations to meet a specific error tolerance or simulation accuracy. For a single rotor system, if the structural failure probability is between 10⁻³ and 10⁻⁵, and the estimation error must not exceed 20%, the required number of simulations is approximately between N = 10⁵ and 10⁷. Therefore, direct sampling methods have high computational costs for high-accuracy or very low failure probability evaluations. They are usually suitable for cases with low accuracy requirements or high failure probabilities.

Figure 9 shows the dynamic reliability curves of the single rotor system under different vibration threshold means. It analyzes how reliability changes with vibration response variations. The results are compared and verified against the Monte Carlo method. In the figure, the horizontal axis is the mean vibration threshold, which represents the set level of the vibration threshold for the single rotor system. A larger value means the system can tolerate higher vibration response limits, allowing more faults. A smaller value means stricter conditions, requiring more normal rotors. The vertical axis is the dynamic reliability index, which is the probability that the rotor operates normally under the corresponding vibration threshold. Its value ranges from 0 to 1. A value closer to 1 means higher reliability at that threshold. The blue curve represents the reliability function of the single rotor system calculated by the Laplace method. The red stars are actual reliability data points obtained by Monte Carlo simulation, based on a large number of random samples. Figure 9 shows that as the mean vibration threshold increases, the rotor system’s reliability rises nonlinearly. The theoretical reliability calculations closely match the Monte Carlo simulation results. The red star samples lie tightly around the blue fitted curve. This verifies the accuracy and reliability of the rotor reliability mathematical model developed in this study. It also shows that the Laplace method can effectively replace the costly Monte Carlo simulation. This makes it suitable for fast engineering reliability prediction and design optimization. At the same time, it can provide quantitative references for system redundancy margin design.

5.2. Reliability Assessment of Multi-Rotor System

The dynamic reliability of a multi-rotor UAV means a greater probability that the system keeps stable flight within a specific time. It considers possible failures of key components such as rotors and batteries during flight. This concept highlights the time-varying nature of performance. It matches the actual operating conditions of multi-rotor UAVs in complex environments. The multi-rotor UAV system can be divided into several key subsystems [37] and one integrated system, as shown in Figure 10.

As shown in Figure 10, the multi-rotor UAV consists of several subsystems with different functions. These modules work together to achieve flight control and mission execution. The flight control subsystem is the core control unit. It collects flight status data in real time through inertial sensors such as gyroscopes and accelerometers. After processing by the microcontroller, it outputs control commands to adjust the attitude dynamically and ensure flight stability. The rotor subsystem is the actuator that enables flight. It consists of brushless motors, electronic speed controllers, and propellers. The rotor speed changes according to flight control commands. This converts electrical energy into lift and thrust. The UAV can then take off vertically, hover, and track trajectories. The power supply subsystem uses high-energy-density lithium batteries. These batteries power all subsystems and ensure continuous operation during frequent missions. The communication subsystem connects the ground control station and the flight control system. It transmits remote control commands, flight parameters, and mission data in real time. This ensures reliable human–machine interaction with low latency. The mission subsystem carries functional modules such as cameras or sensors. These modules vary according to different application scenarios to complete specific tasks. The airframe structure acts as the installation base for all subsystems. It often has vibration reduction designs. These designs reduce rotor vibrations that affect electronic devices. They also ensure the structural strength and reliable operation of the UAV.

As the core actuators of a multi-rotor UAV system, the number and configuration of rotors directly affect reliability. Different numbers and layouts of rotors show different characteristics in the system’s reliability structure.

5.2.1. Series System Reliability

A series system is a system in which the failure of any single component causes the entire system to fail. In other words, a series system can maintain full functionality only when all components are working properly. Suppose the lifetime of the iii-th component in the series system is ${\xi }_i$. Then, the system lifetime is $\xi =\min ({\xi }_1,{\xi }_2,\dots ,{\xi }_n)$. The system reliability $R_s(t)$ is:

$$\begin{array}{cc}{R}_s(t)& =P\left\{min({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)>t\right\}\hfill \\ & =P\{{\xi }_1>t,{\xi }_2>t,\cdots ,{\xi }_n>t\}\hfill \\ & ={\displaystyle \prod _{i=1}^{n}P}\{{\xi }_i>t\}\hfill \\ & ={\displaystyle \prod _{i=1}^n{R}_i}(t)\hfill \end{array}$$

(63)

The system failure distribution $F_s(t)$ and the failure distributions of individual components $F_i(t)$ can be derived from Equation (63) as follows:

$$F_s(t)=1-{\displaystyle \prod _{i=1}^n\left[1-F_i(t)\right]}$$

(64)

Its probability density function is:

$$f_s(t)=F_s^{\prime }(t)={\displaystyle \sum _{i=1}^n\{f_i(t){\displaystyle \prod _{j\ne i,j=1}^n[}1-F_j(t)]\}}$$

(65)

As shown in Figure 11, the reliability of the multi-rotor UAV rotor system consists of n independent rotor units connected in series. When the system uses a non-redundant design and strong functional dependencies exist between rotors, the system reliability is calculated using a series model based on the reliability of all rotor units. In this case, the failure of any rotor unit will cause flight instability or even crash, leading to complete system failure. Therefore, the series system model can be used to evaluate the rotor system reliability. Assume that the UAV needs at least three working rotors to maintain flight. The series system reliability of the UAV rotor system is shown in Figure 12. A low threshold mean indicates harsh conditions and requires more functioning rotors. A high threshold mean indicates relaxed conditions and allows more failures.

Figure 12 shows that the reliability of the tri-rotor UAV increases rapidly as the threshold mean rises. It reaches about 0.9 when the threshold mean is around 1.75. The reliability of the quad-, penta-, and hexa-rotor UAVs also increases with the threshold mean. However, the growth becomes slower as the number of rotors increases. When the threshold mean is less than 1.0, the difference in reliability between the tri-rotor and quad-rotor UAVs is less than or equal to 0.15. The effect of system redundancy on reliability is not obvious. When the threshold mean is greater than 1.0, the reliability of the tri-rotor UAV grows faster. The gap with the hexa-rotor UAV becomes larger than 0.2. This indicates that redundant rotors may introduce extra risks under high threshold conditions.

In a series model, increasing the number of components actually reduces reliability. This relates to the series system principle in reliability engineering, which states that failure of any component causes the whole system to fail. Therefore, although the quad-rotor has one more rotor as redundancy, if each rotor has the same reliability, the overall system reliability decreases because of the increased number of components. This explains why the tri-rotor performs better in Figure 12. From the formula $R_s=R^m$, when the single rotor reliability $R<1$, increasing m causes the system reliability $R_s$ to decrease exponentially. Thus, the series system reliability for rotors shows the effect of rotor number on overall reliability under a no-redundancy design. If each rotor’s reliability is fixed, adding more rotors decreases the overall system reliability.

5.2.2. Voting System Reliability

The rotor voting system in multi-rotor UAVs is a redundancy design strategy achieved by increasing the number of rotors. This allows the UAV to maintain basic flight control even if some rotors fail. The system uses a “k-out-of-n” logic, meaning that as long as at least k rotors out of n work normally, the UAV can keep functioning. For example, in a hexarotor UAV, if any five rotors work properly, the UAV can maintain flight stability. This is called a “5-out-of-6: G” voting system. Similarly, in an octocopter system using a “6-out-of-8: G” strategy, the UAV can still fly even if two rotors fail at the same time. This method quantifies the reliability improvement brought by redundancy. It is suitable for analyzing fault tolerance in different configurations, especially for mission-critical industrial UAVs.

The voting system, also called a k-out-of-n system or $k/n(G)$ system, is a fault-tolerant system structure. In this structure, the system consists of n parallel units. The system can continue to work normally only if at least k units are functioning properly. Specifically, when k = n, the system is equivalent to a series system where all units must work to ensure functionality. When k = 1, the system is a parallel system that works as long as any one unit functions.

Taking the “k-out-of-n: G” system with $(k<n)$ as the multi-rotor UAV system model, suppose the lifetimes of the n UAV rotors are ${\xi }_i(i=1,2,\dots ,n)$ and are mutually independent. Their reliabilities are $R_i(t)=P\{{\xi }_i>t\}$. The system can work normally if all n rotors work or if at least k rotors work. Therefore, the system reliability is the sum of the probabilities of these situations:

$$R_s(t)={\displaystyle \sum _{i=k}^n{C}_n^i}\cdot {[R(t)]}^i\cdot {[1-R(t)]}^{n-i}$$

(66)

The reliability results of the rotor voting system for multi-rotor UAVs are shown in Figure 13.

Figure 13 uses Equation (65), where n is the total number of rotors, R is the reliability of a single rotor, and $R_s$ is the system reliability of the UAV. The UAV is assumed to need at least three functioning rotors to keep flying. As shown in Figure 13, the six-rotor system has higher initial reliability due to greater redundancy. It reaches about 0.8 when the threshold mean is around 0.8. After the threshold mean exceeds 1.0, its reliability increases more slowly. UAVs with fewer rotors have lower initial system reliability and slower growth in reliability. The six-rotor system gains a reliability advantage because it allows more rotor failures due to its higher redundancy.

In the “3-out-of-6: G” voting system, changing the number of rotors required to function creates a curve similar to a normal distribution, as shown in Figure 14. This happens because the system reaches its highest combination probability when the reliability of a single rotor is at a medium level. This resembles the peak of a binomial distribution and forms a bell-shaped curve. Figure 14 shows that the three-rotor mode reaches a peak reliability of about 0.3 when the threshold mean is around 0.7, then drops quickly due to a lack of redundancy. The four-rotor mode peaks at about 0.33 when the threshold mean is around 1.0 but performs worse overall than the five- and six-rotor modes. The five-rotor mode reaches a peak of about 0.4 when the threshold mean is around 1.25, then declines slowly because of reduced redundancy efficiency. The reliability of the six-rotor mode increases steadily with the threshold mean and reaches 0.9 when the threshold mean is about 2.

The study of voting system reliability for the number of rotors in multi-rotor UAV systems has significant engineering and practical value. On one hand, it helps improve the fault tolerance of the UAV when some rotors fail, enhancing flight stability and safety. On the other hand, by building reliability models and conducting system analysis, it provides theoretical support for optimizing rotor redundancy design. This achieves a reasonable balance among system reliability, structural weight, and cost. In addition, voting system reliability analysis can be applied to risk assessment and mission assurance in high-reliability scenarios such as inspection and emergency response for mission-critical UAVs. It also provides a modeling basis for system fault prediction and health management, helping to build more efficient intelligent operation and maintenance mechanisms.

6. Conclusions

This paper focuses on the vibration characteristics and reliability assessment of multi-rotor transport UAVs under complex conditions. It builds a complete technical chain from mechanism analysis to engineering application through bidirectional fluid–structure interaction simulation, single-rotor reliability modeling, and system-level redundancy analysis. The study focuses on how rotor vibration affects flight safety. By combining CAD modeling and flow field simulation, it achieves dynamic coupling of flow and structural fields, providing data support to reveal vibration transmission laws of rotors under complex conditions. At the same time, reliability assessment models are built based on the Laplace method and Monte Carlo simulation. The single-rotor reliability study is extended to system-level redundancy design analysis, forming a reliability optimization method suitable for multi-rotor UAVs. The conclusions of this paper are as follows:

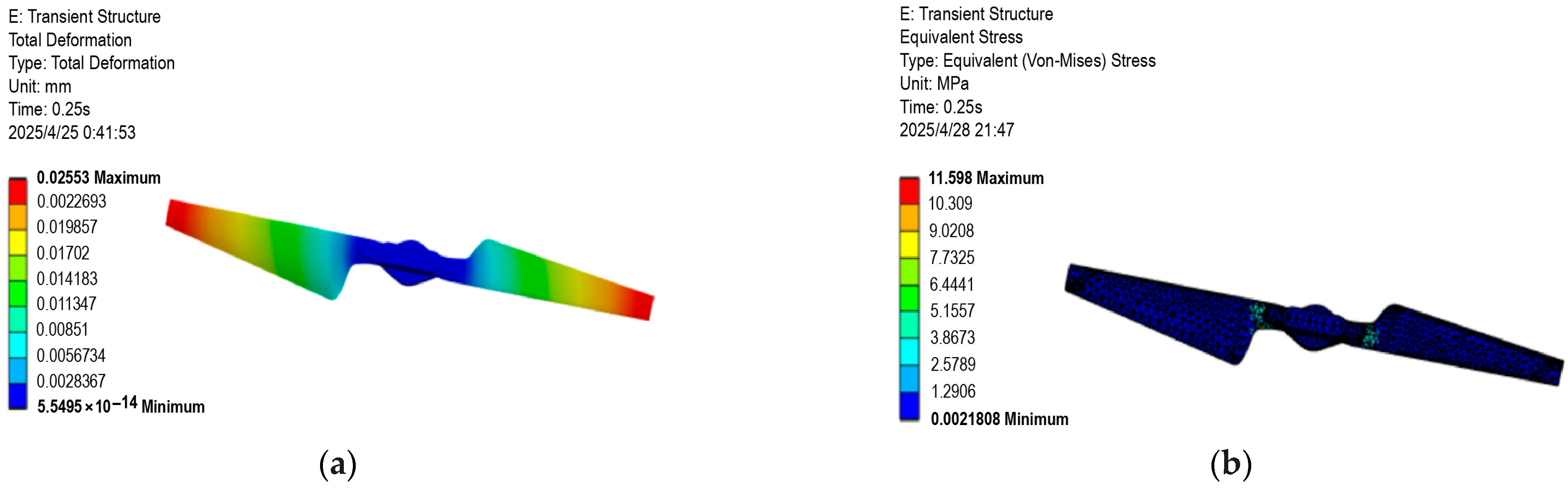
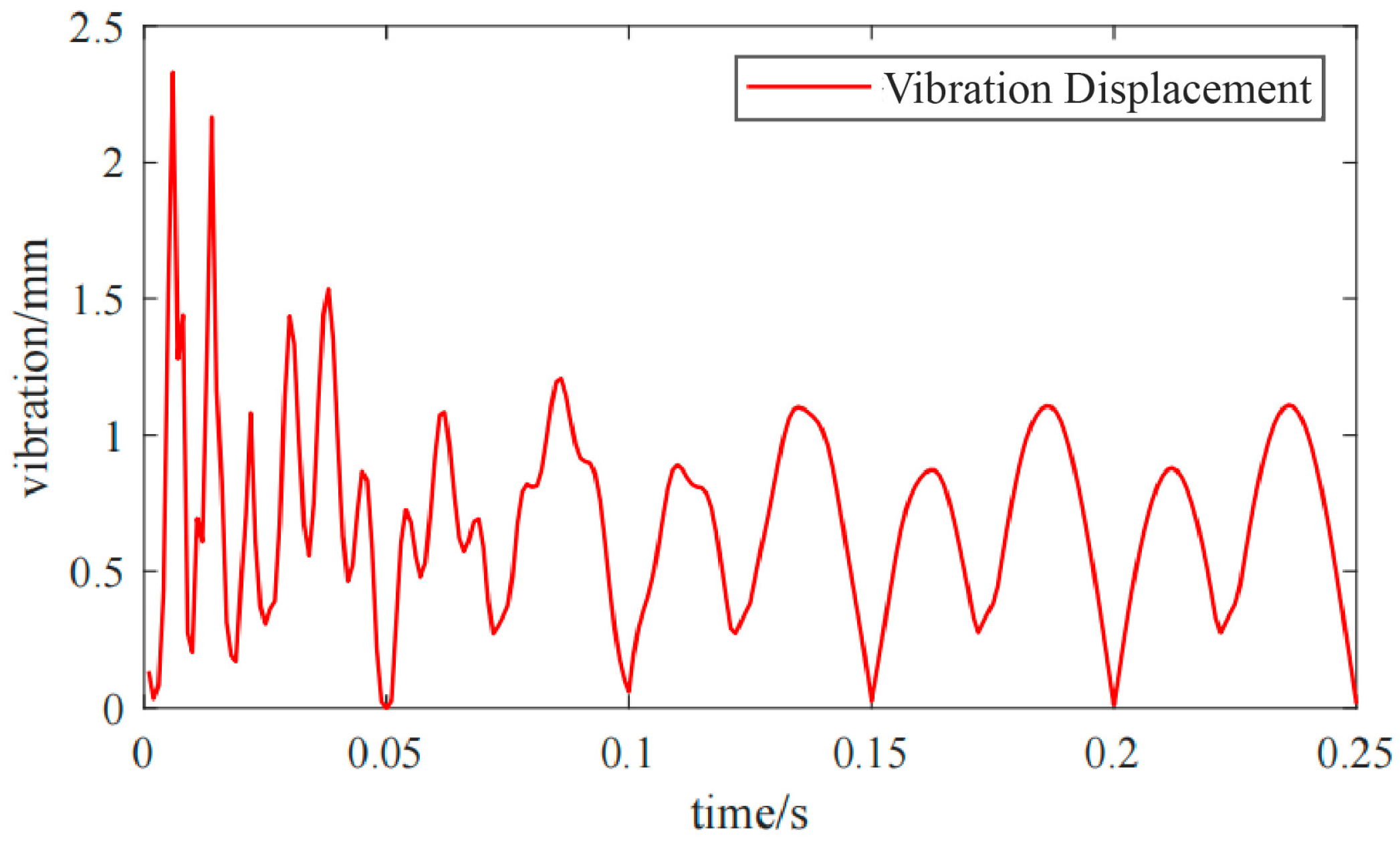
• A rotor CAD model was built based on momentum theory, blade element theory, and strip theory. A single-rotor vibration dynamic model considering bidirectional fluid-structure interaction was established. The results show that the rotor’s vibration response under aerodynamic load has significant spatiotemporal distribution characteristics. The blade tip displacement peak reaches 0.02553 mm, and the maximum stress in the root stress concentration area is 11.598 MPa. The vibration response enters a stable periodic state after 0.12 s;
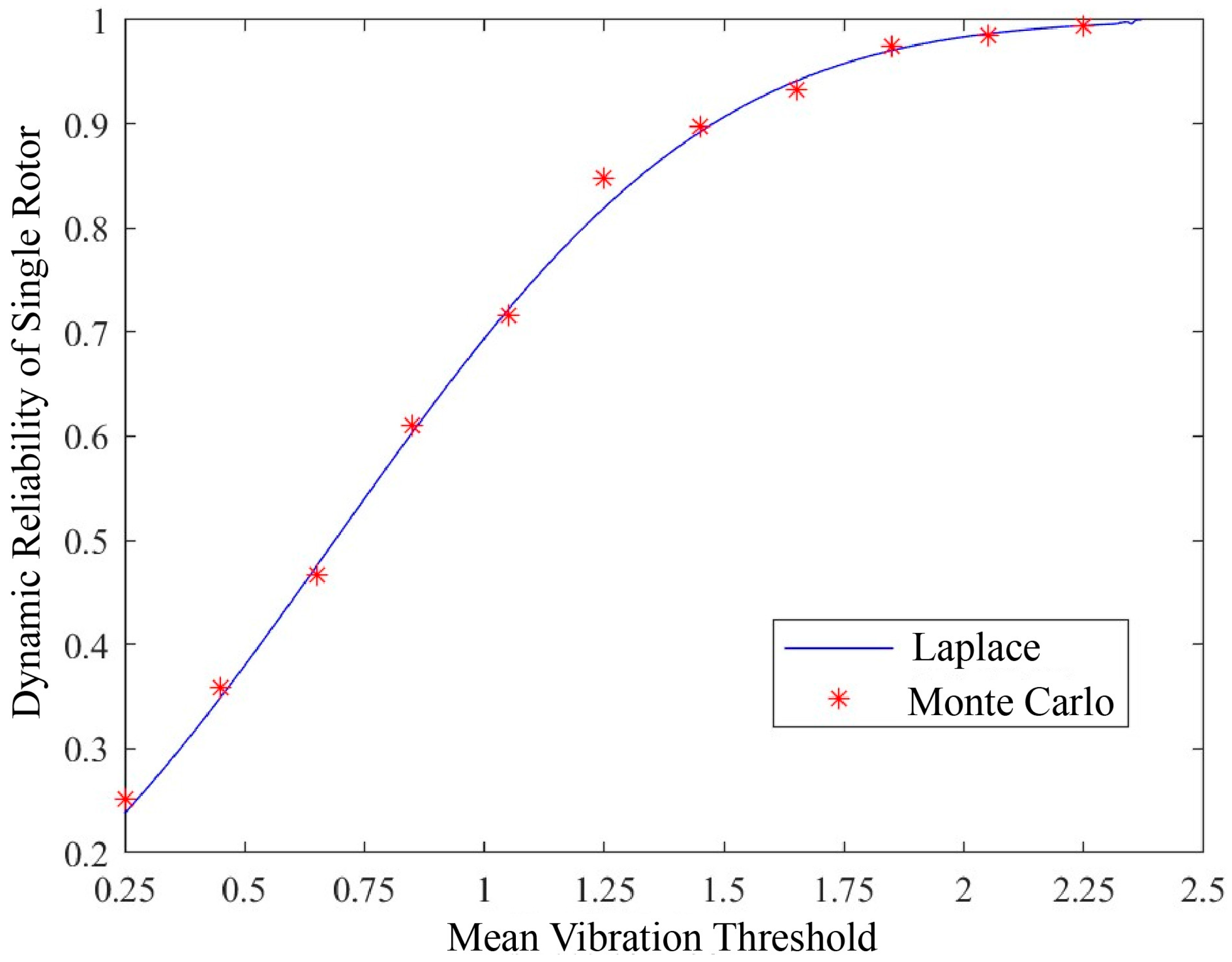
• The single rotor reliability model based on vibration data shows that, under the given condition, the failure-free probability of the single rotor system is 93.10%. If this rotor is part of a multi-rotor redundant system, it shows that the failure probability during operation is low. This result confirms the high consistency between the Laplace method and Monte Carlo simulation.
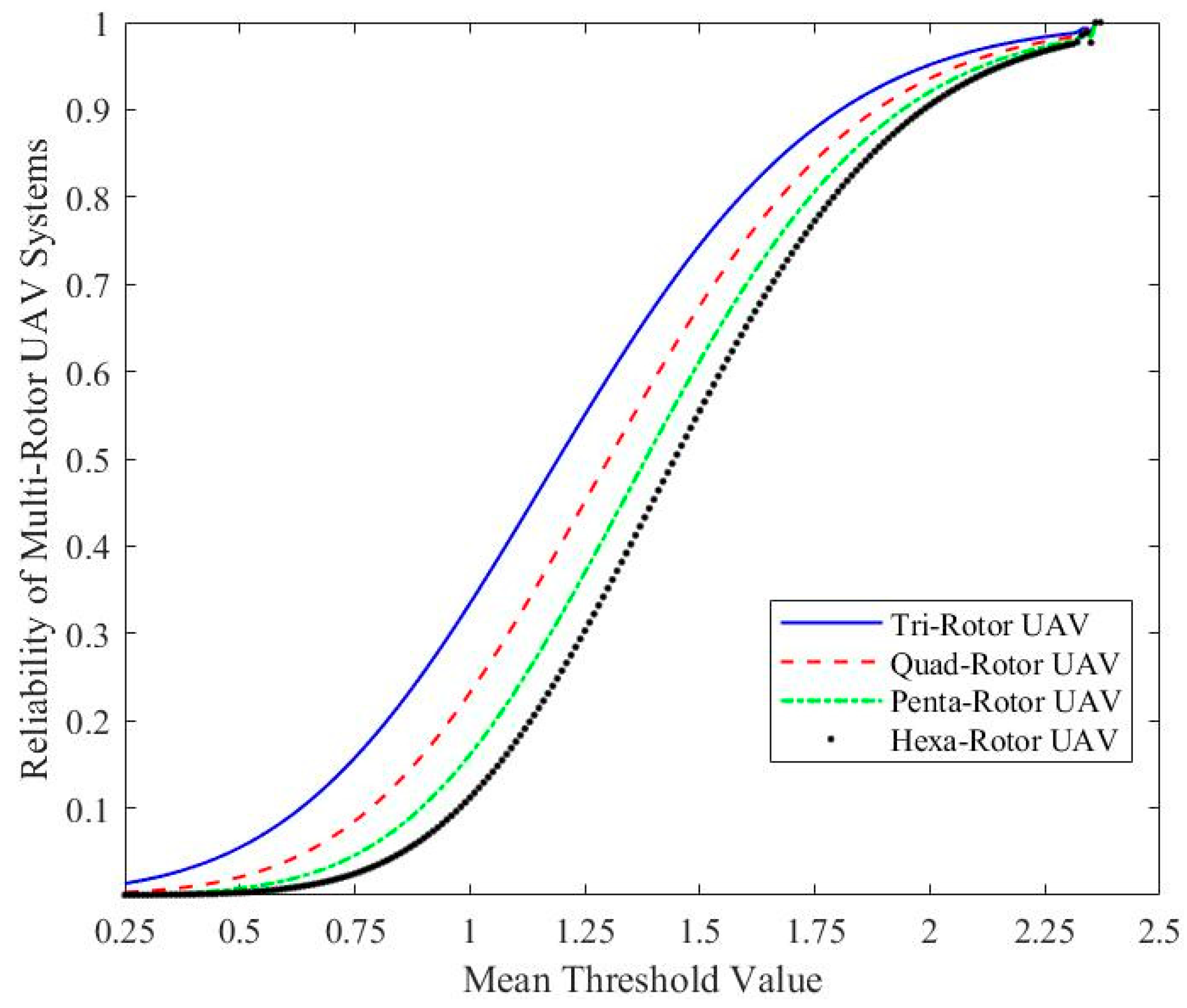
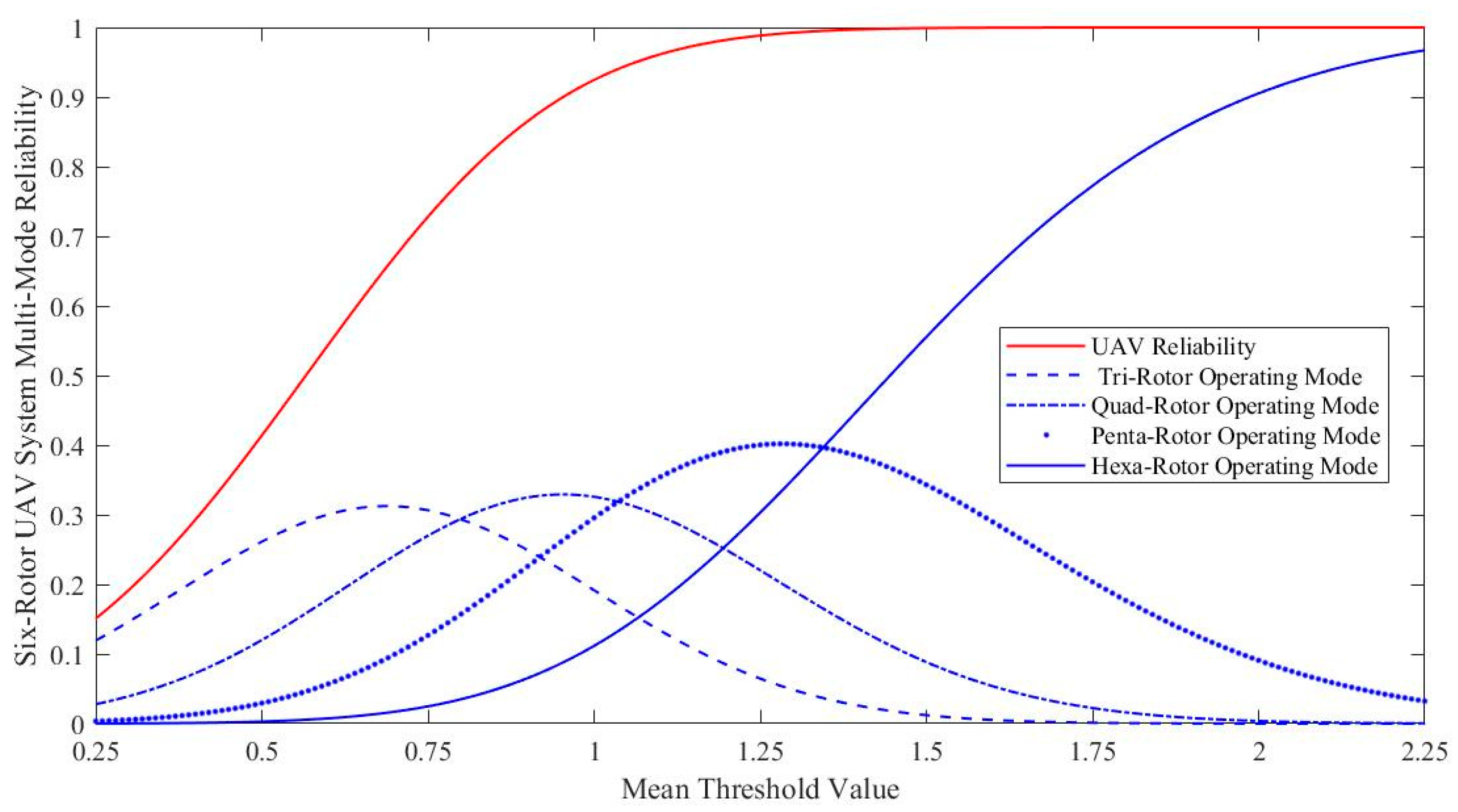
• System reliability evaluation shows that more rotors reduce the reliability index in the multi-rotor series system. More rotors increase the reliability index in the voting system. In the voting model, the hexacopter system under the “3-out-of-6” redundancy configuration reaches higher reliability with greater redundancy. This result shows that redundancy design improves fault tolerance.

This study establishes, for the first time, a quantitative mapping between rotor vibration response and system reliability. It reveals the evolution law of “vibration amplitude–failure probability” under dynamic loads. The results provide dual value for structural optimization and reliability assurance of multi-rotor UAVs. They also offer a theoretical reference for setting airworthiness standards in the large-scale application of UAVs in the low-altitude economy.