Modeling and Adaptive Neural Control of a Wheeled Climbing Robot for Obstacle-Crossing
Abstract
1. Introduction
2. Materials and Methods
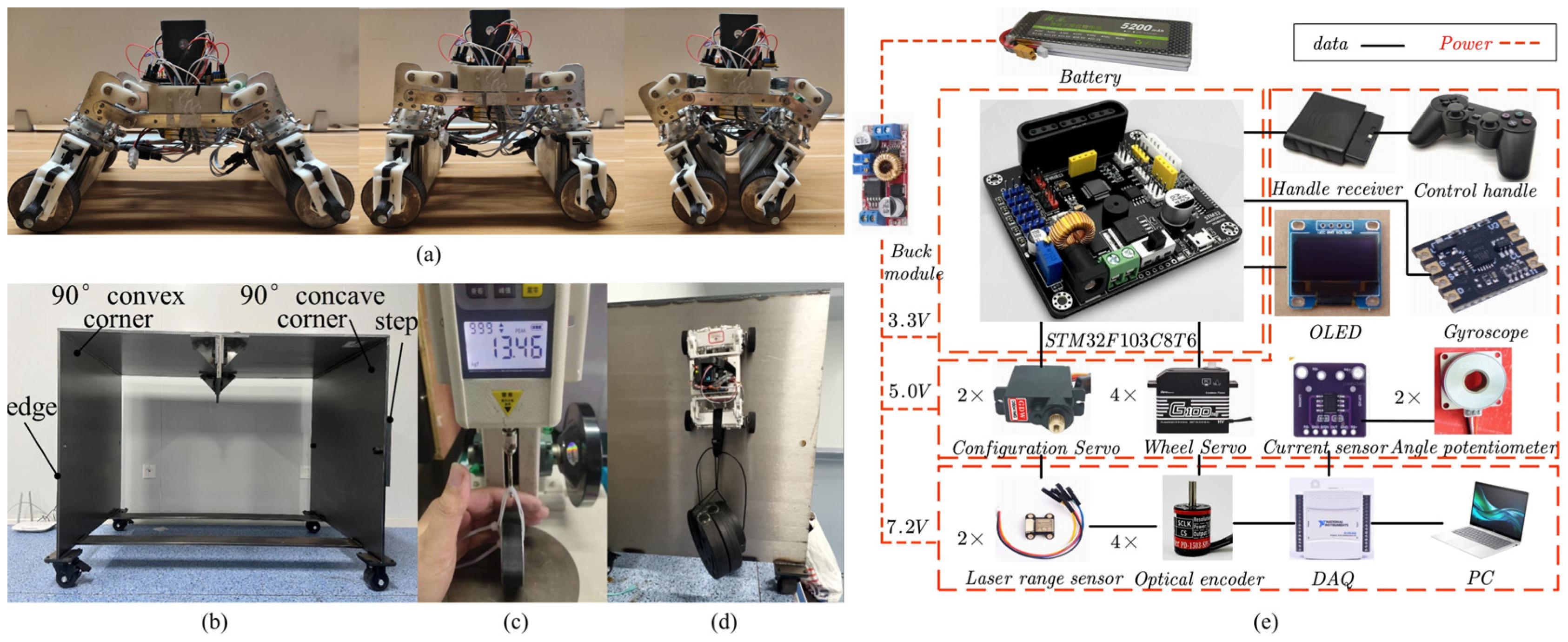
2.1. Mechanical Structure and the Obstacle-Crossing Principle
2.2. Kinematic Modeling for Obstacle-Crossing
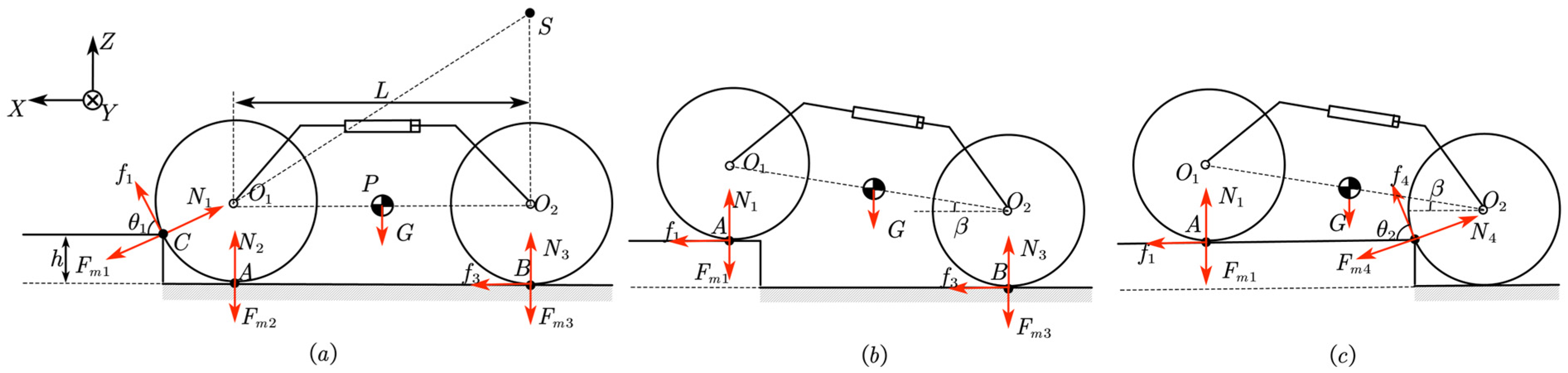
2.3. Phase-Based Obstacle-Crossing Dynamics Modeling
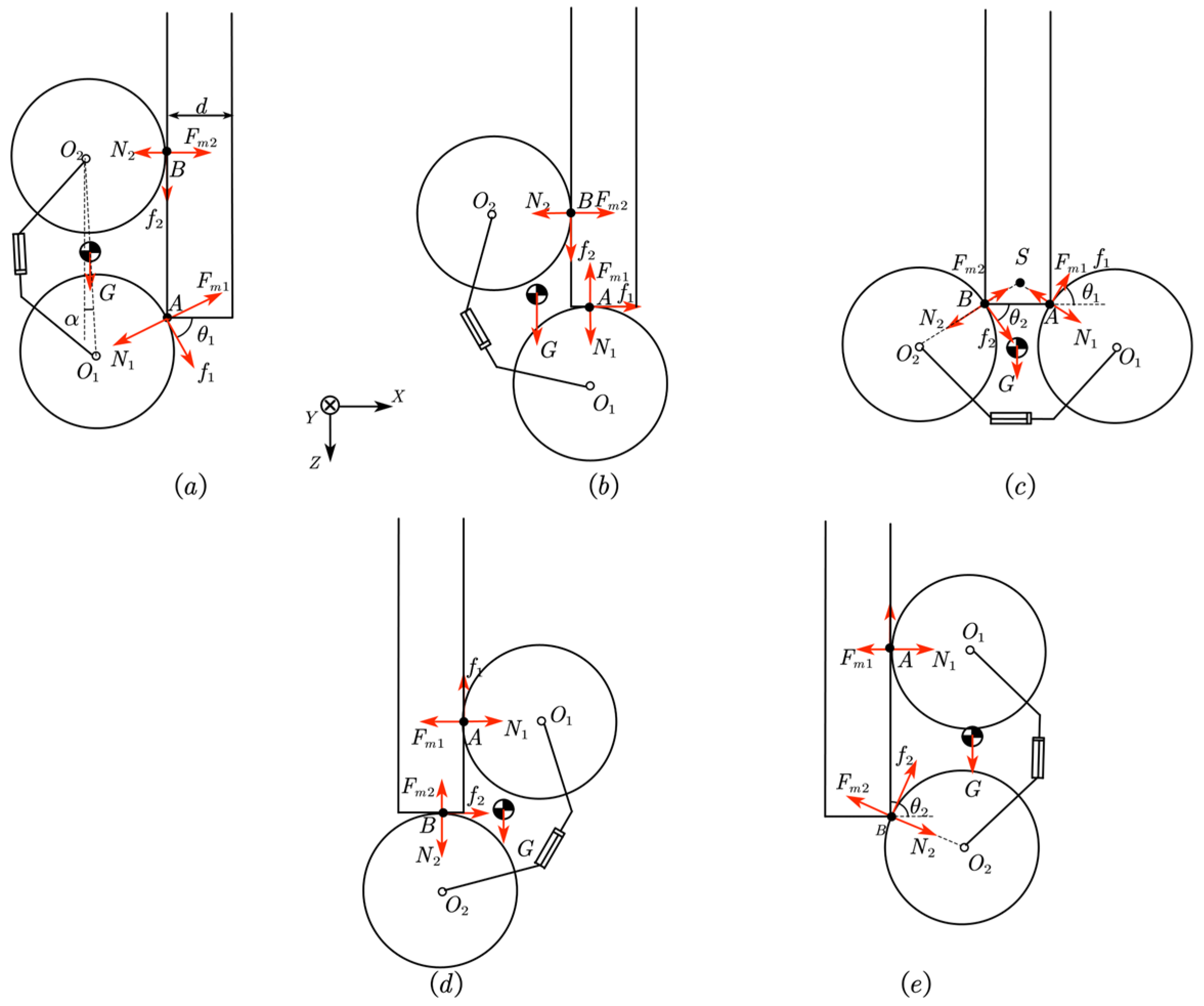
2.3.1. Step
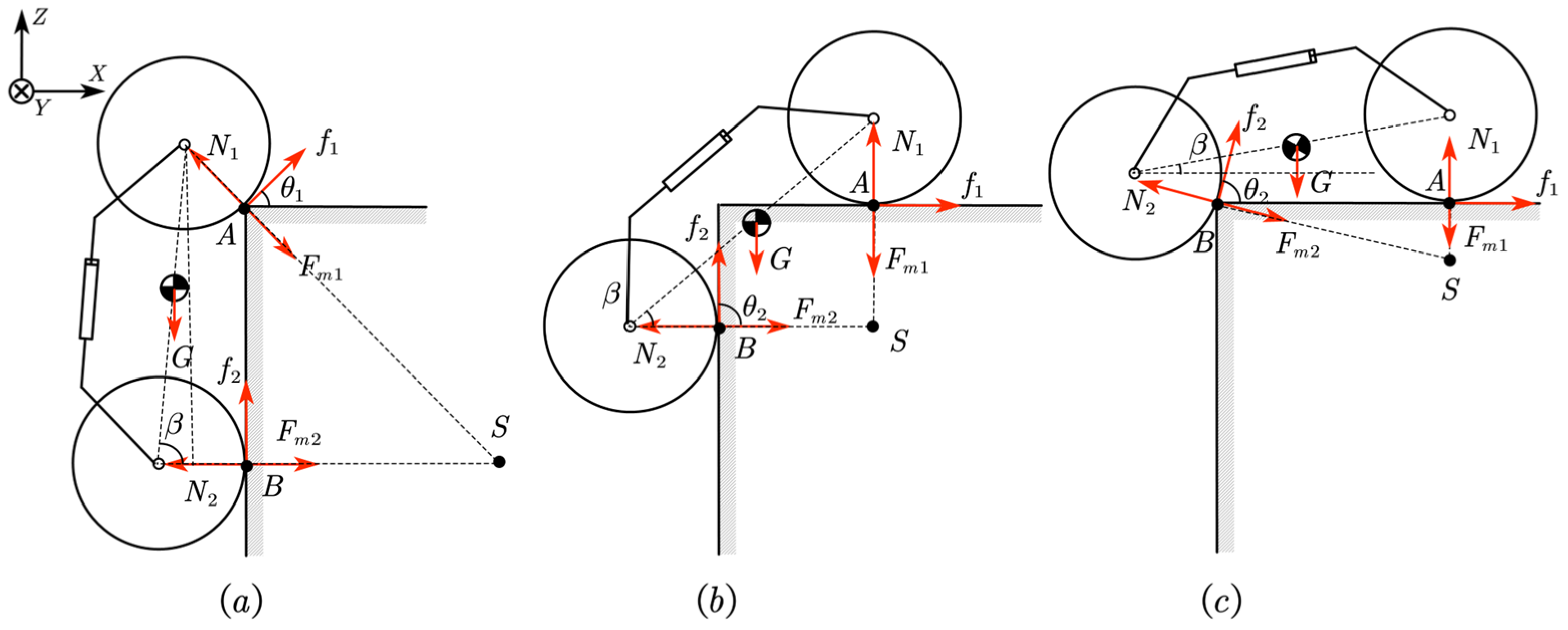
2.3.2. 90° Concave Corner
2.3.3. 90° Convex Corner
2.3.4. Thin Plate
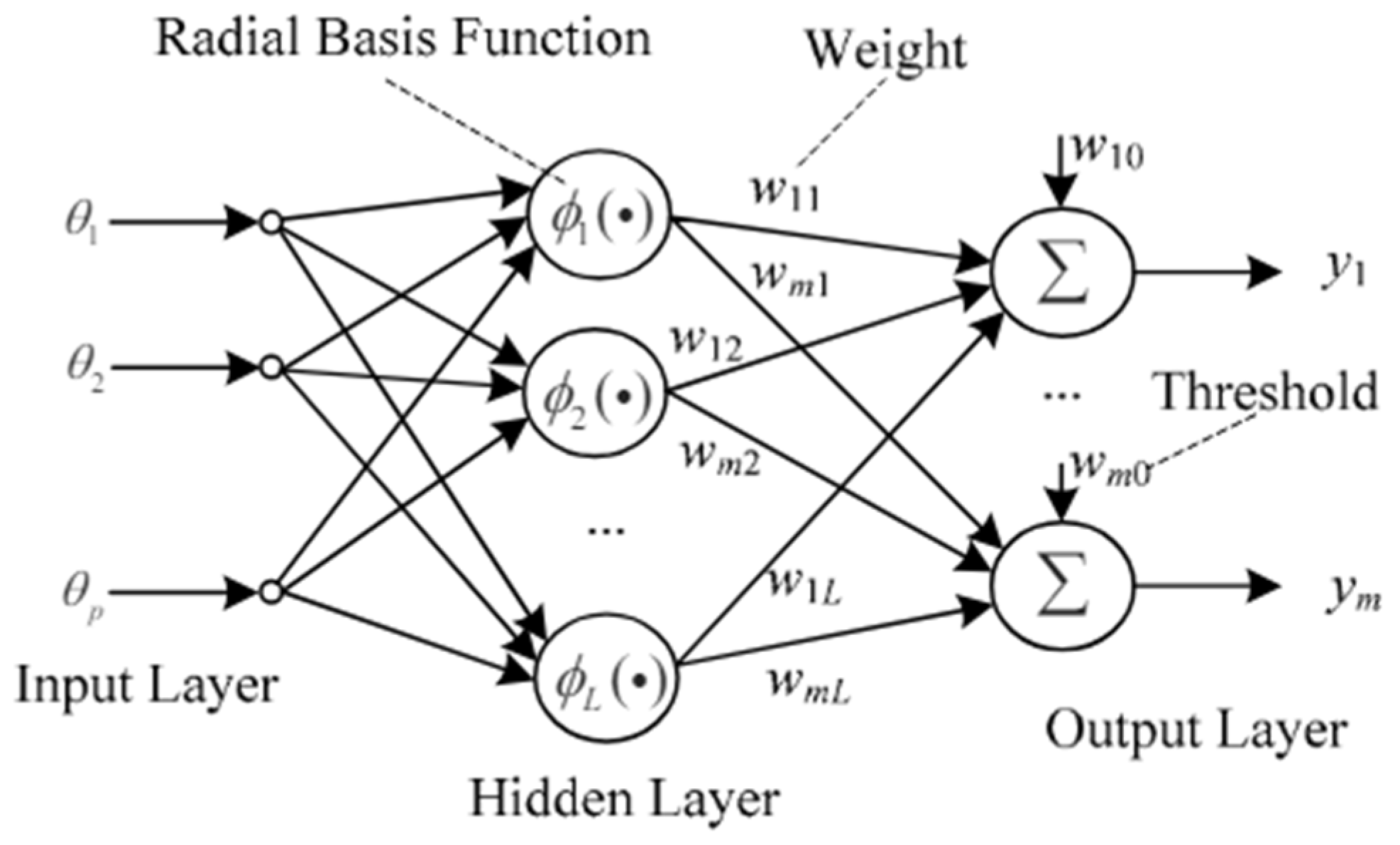
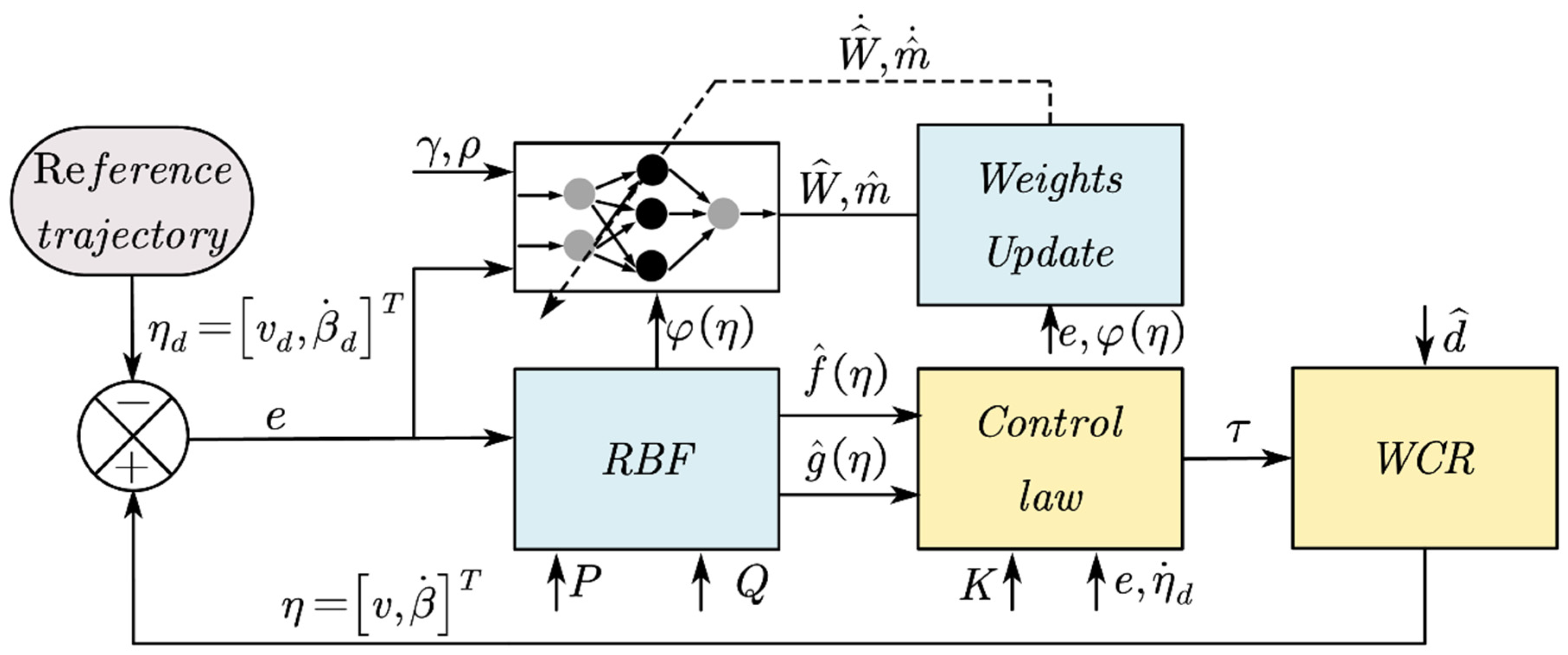
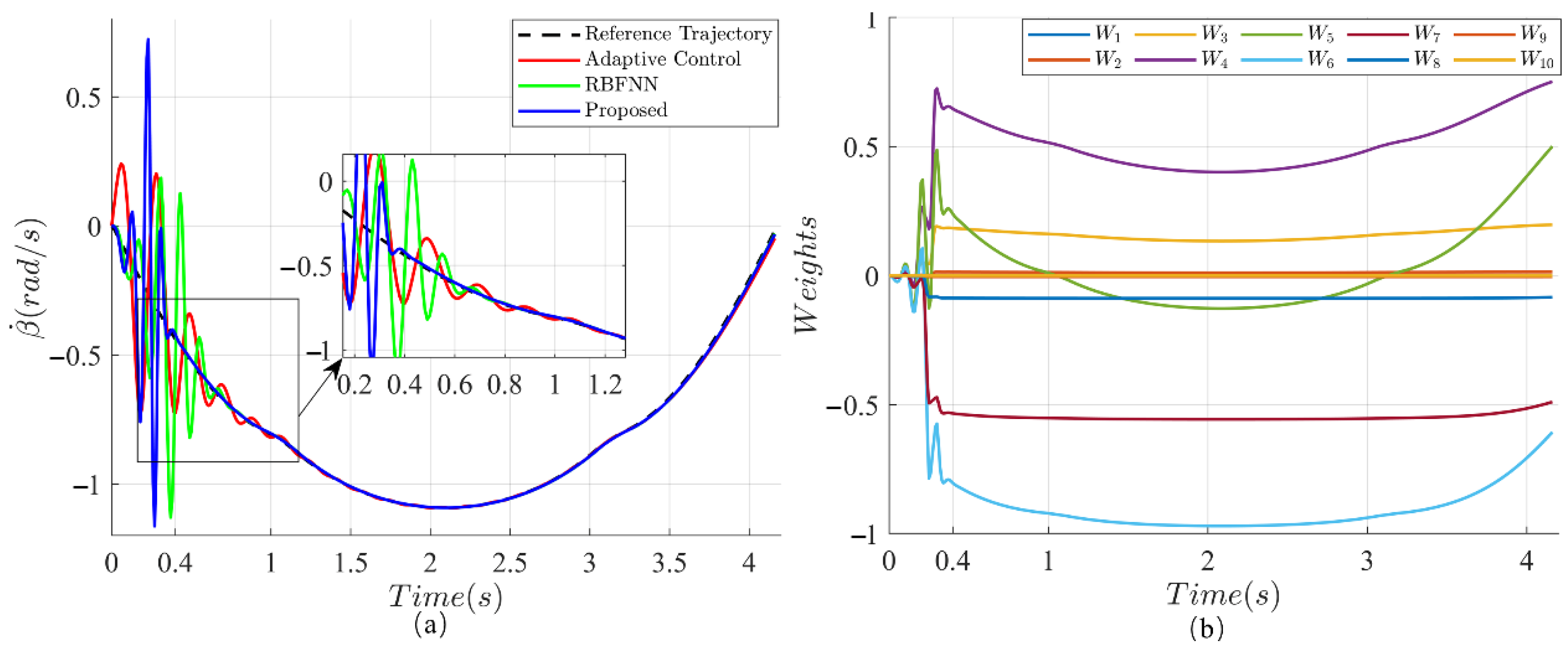
2.4. Obstacle Climbing Motion Control Based on Radial Basis Function Neural Network Compensation
3. Results
3.1. The Simulation Experiment
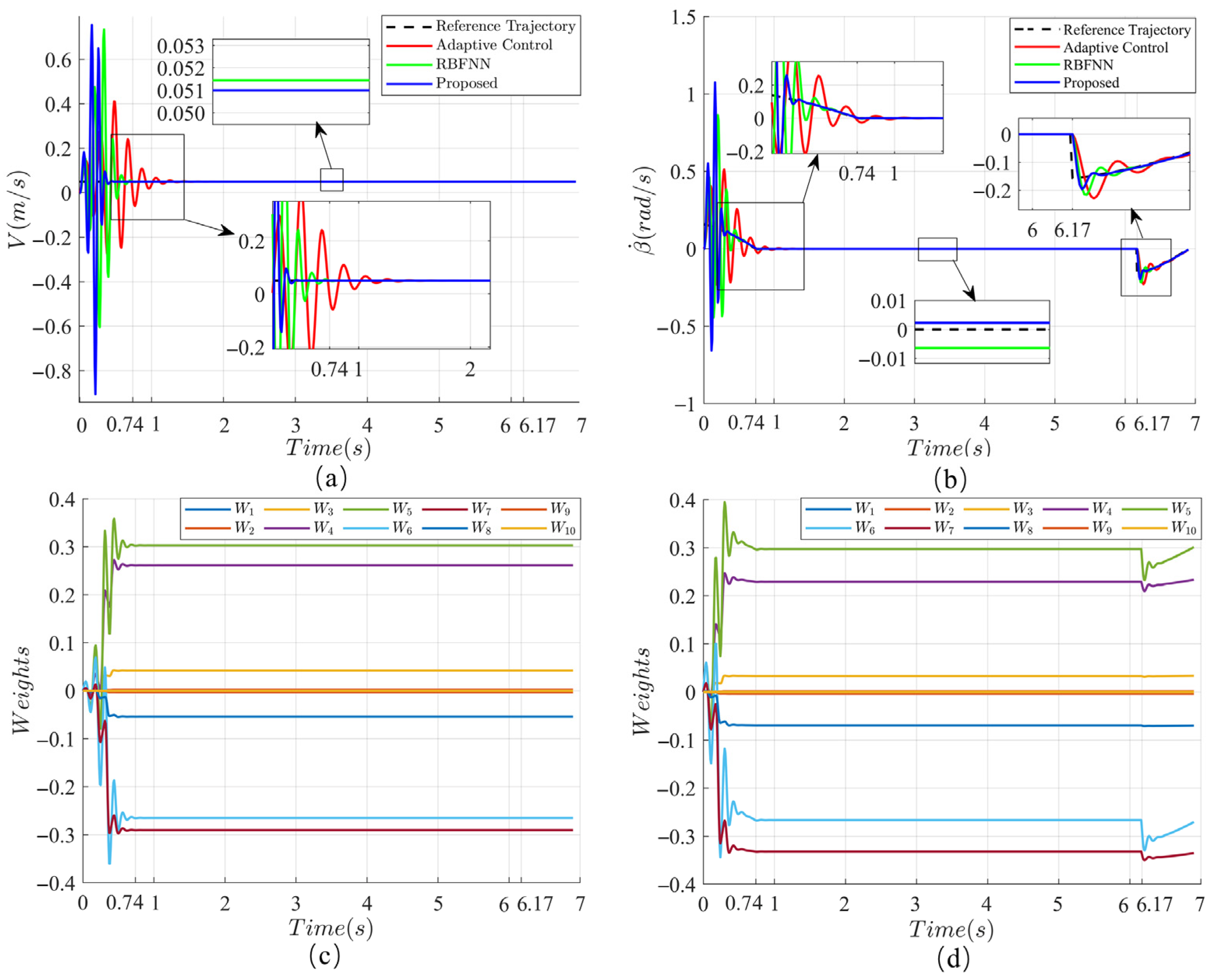
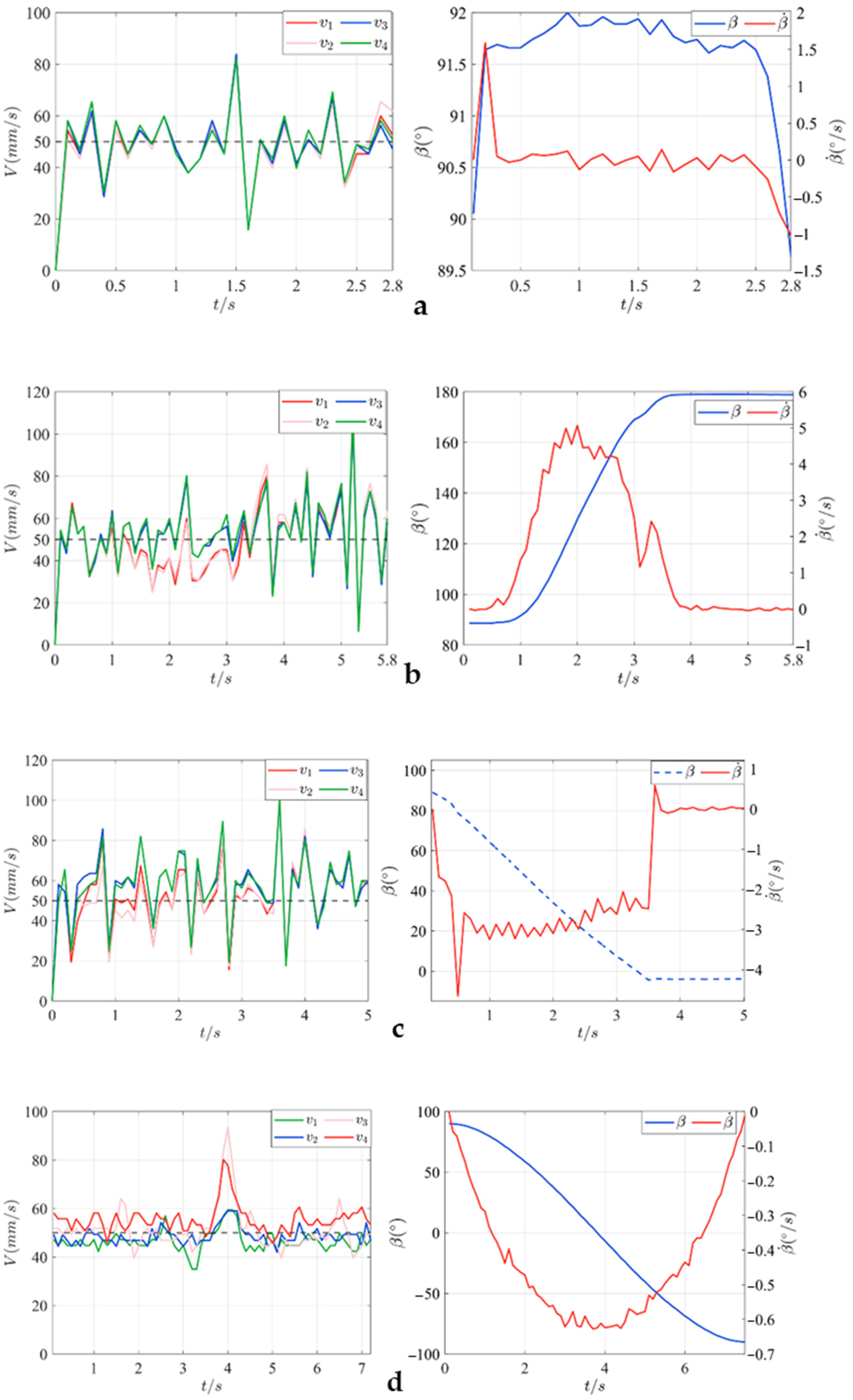
3.1.1. The Step Climbing Control Experiment
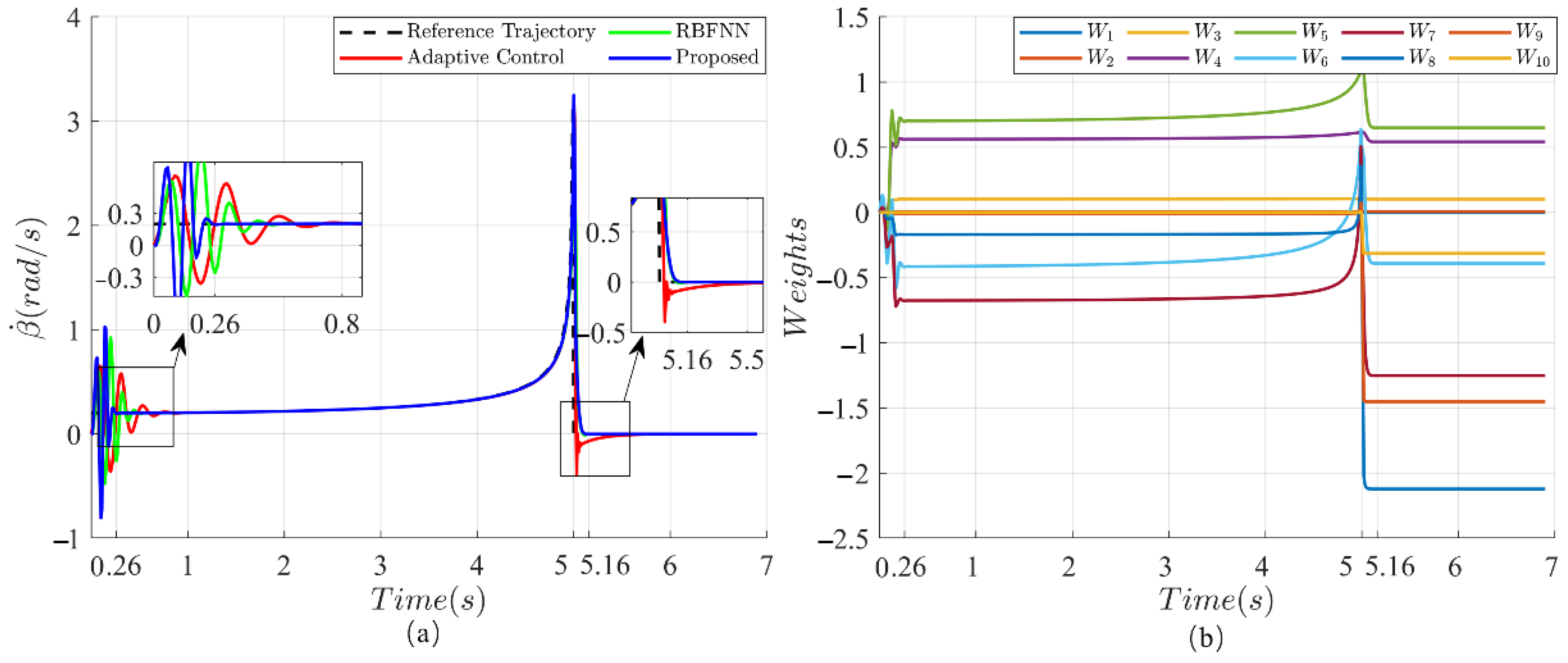
3.1.2. The 90° Concave Corner Climbing Control Experiment
3.1.3. The 90° Convex Corner Climbing Control Experiment
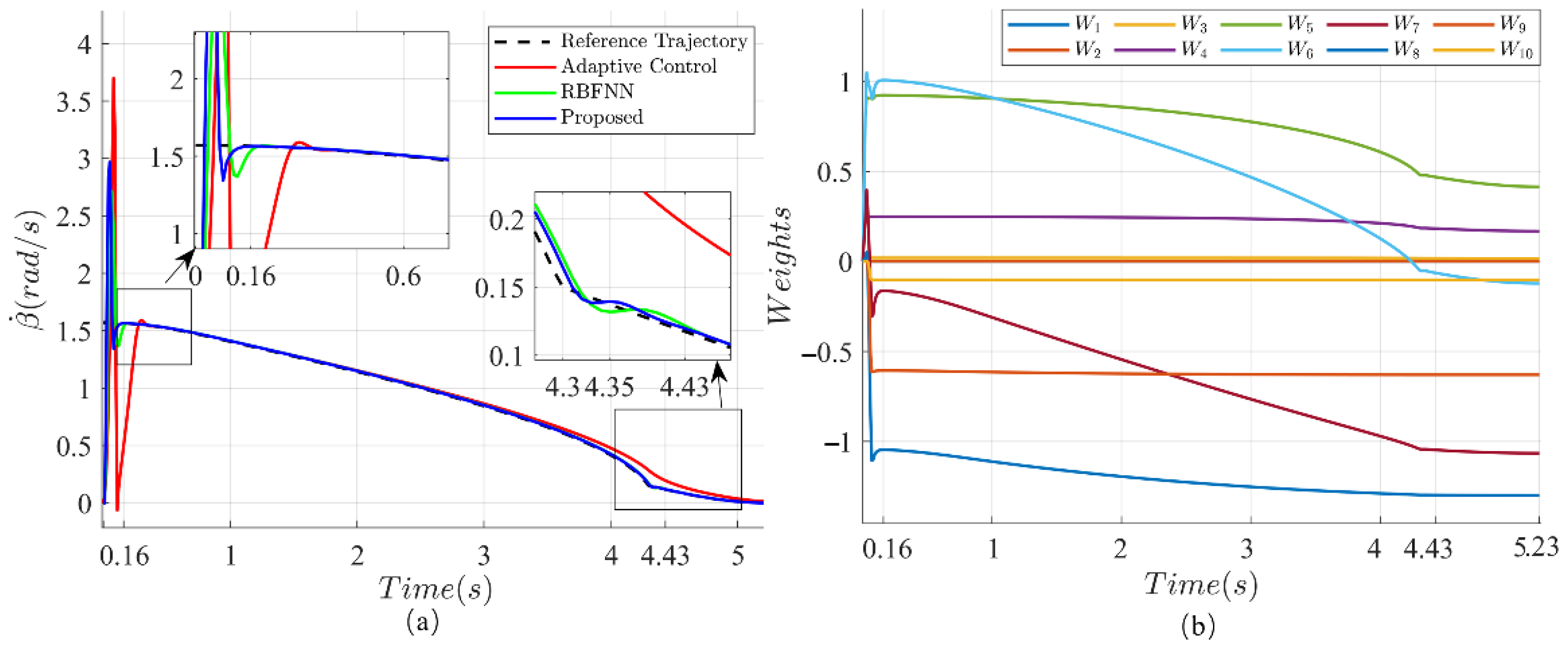
3.1.4. The Thin Plate Climbing Control Experiment
3.2. The Field Test
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, R.; Kawamura, Y. Development of Climbing Robot for Steel Bridge Inspection. Ind. Robot. 2016, 43, 429–447. [Google Scholar] [CrossRef]
- Nguyen, S.T.; Nguyen, H.; Bui, S.T. An Agile Bicycle-like Robot for Complex Steel Structure Inspection. In Proceedings of the International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022. [Google Scholar] [CrossRef]
- Motley, C.; Nguyen, S.T.; La, H.M. Design of A High Strength Multi-Steering Climbing Robot for Steel Bridge Inspection. In Proceedings of the IEEE/SICE International Symposium on System Integration (SII), Narvik, Norway, 8–12 January 2022. [Google Scholar] [CrossRef]
- Wang, R.; Kawamura, Y. A Magnetic Climbing Robot for Steel Bridge Inspection. In Proceedings of the World Congress on Intelligent Control and Automation (WCICA), Shenyang, China, 29 June–4 July 2014. [Google Scholar] [CrossRef]
- Nguyen, S.T.; La, K.T. Agile Robotic Inspection of Steel Structures: A Bicycle-like Approach with Multisensor Integration. J. Field Robot. 2023, 41, 396–419. [Google Scholar] [CrossRef]
- Wang, B.; Li, P. Development of a Wheeled Wall-Climbing Robot with an Internal Corner Wall Adaptive Magnetic Adhesion Mechanism. J. Field Robot. 2024, 42, 97–114. [Google Scholar] [CrossRef]
- Yodai, M.; Takehiro, S. Development of Magnetic Bridge Inspection Robot Aimed at Carrying Heavy Loads. Int. J. Robot. Eng. 2018, 3, 010. [Google Scholar] [CrossRef] [PubMed]
- Pham, A.Q.; La, H.M.; La, K.T. A Magnetic Wheeled Robot for Steel Bridge Inspection. In Proceedings of the International Conference on Engineering Research and Applications (ICERA), Thai Nguyen, Vietnam, 1–2 December 2019. [Google Scholar] [CrossRef]
- Sirken, A.; Knizhnik, G.; McWilliams, J. Bridge Risk Investigation Diagnostic Grouped Exploratory (BRIDGE) Bot. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017. [Google Scholar] [CrossRef]
- Eich, M.; Vogele, T. Design and Control of a Lightweight Magnetic Climbing Robot for Vessel Inspection. In Proceedings of the 19th Mediterranean Conference on Control & Automation (MED), Corfu, Greece, 1–4 July 2011. [Google Scholar] [CrossRef]
- Eto, H.; Asada, H.H. Development of a Wheeled Wall-Climbing Robot with a Shape-Adaptive Magnetic Adhesion Mechanism. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–15 June 2020. [Google Scholar] [CrossRef]
- Zhang, Q.; Gao, X. DP-Climb: A Hybrid Adhesion Climbing Robot Design and Analysis for Internal Transition. Machines 2022, 10, 678. [Google Scholar] [CrossRef]
- Morales, R.; Chocoteco, J. Obstacle Surpassing and Posture Control of a Stair-Climbing Robotic Mechanism. Control Eng. Pract. 2013, 21, 604–621. [Google Scholar] [CrossRef]
- Song, Z.; Luo, Z. A Portable Six-Wheeled Mobile Robot with Reconfigurable Body and Self-Adaptable Obstacle-Climbing Mechanisms. J. Mech. Robot. 2022, 14, 51–72. [Google Scholar] [CrossRef]
- Kim, G.; Chung, H. MOBINN: Stair-Climbing Mobile Robot with Novel Flexible Wheels. IEEE Trans. Ind. Electron. 2023, 71, 9182–9191. [Google Scholar] [CrossRef]
- Wardana, A.A.; Takaki, T. Dynamic Modeling and Step-Climbing Analysis of a Two-Wheeled Stair-Climbing Inverted Pendulum Robot. Adv. Robot. 2019, 34, 313–327. [Google Scholar] [CrossRef]
- Nguyen, T.; Le, L. Neural Network-Based Adaptive Tracking Control for a Nonholonomic Wheeled Mobile Robot with Unknown Wheel Slips, Model Uncertainties, and Unknown Bounded Disturbances. Turk. J. Electr. Eng. Comput. Sci. 2018, 26, 378–392. [Google Scholar] [CrossRef]
- Annaswamy, A.M. Adaptive control and intersections with reinforcement learning. Annu. Rev. Control Robot. Auton. Syst. 2023, 6, 65–93. [Google Scholar] [CrossRef]
- Liu, J. Radial Basis Function (RBF) Neural Network Control for Mechanical Systems: Design, Analysis and Matlab Simulation, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 70–83. [Google Scholar] [CrossRef]
- Shojaei, K.; Shahri, A.M. Adaptive trajectory tracking control of a differential drive wheeled mobile robot. Robotica 2010, 29, 391–402. [Google Scholar] [CrossRef]



| Variables | Symbol | Units | Value |
|---|---|---|---|
| moment of inertia | J | kg·cm | 12.6 |
| magnetic wheel radius | r | mm | 30 |
| step height | h | mm | 20 |
| mass | m | kg | 3.8 |
| mass of wheel | mw | kg | 0.4 |
| plate thickness | D | mm | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, H.; Zhu, S.; Wang, C.; Song, W. Modeling and Adaptive Neural Control of a Wheeled Climbing Robot for Obstacle-Crossing. Machines 2025, 13, 674. https://doi.org/10.3390/machines13080674
Fan H, Zhu S, Wang C, Song W. Modeling and Adaptive Neural Control of a Wheeled Climbing Robot for Obstacle-Crossing. Machines. 2025; 13(8):674. https://doi.org/10.3390/machines13080674
Chicago/Turabian StyleFan, Hongbo, Shiqiang Zhu, Cheng Wang, and Wei Song. 2025. "Modeling and Adaptive Neural Control of a Wheeled Climbing Robot for Obstacle-Crossing" Machines 13, no. 8: 674. https://doi.org/10.3390/machines13080674
APA StyleFan, H., Zhu, S., Wang, C., & Song, W. (2025). Modeling and Adaptive Neural Control of a Wheeled Climbing Robot for Obstacle-Crossing. Machines, 13(8), 674. https://doi.org/10.3390/machines13080674





