This section presents the proposed fault-detection approach based on GAT with uncertainty estimation. This approach comprises four main steps: data preprocessing, fault-detection model development, fault-detection performance measurement, and uncertainty estimation. Each step is crucial for ensuring the robustness and accuracy of the anomaly-detection process and for facilitating further analysis of the fault-detection results.
3.1. Data Preprocessing
The initial step in developing the fault-detection model involves comprehensive data preprocessing to ensure that the time-series data are suitable for analysis and model training. To standardize the range of features and ensure that each feature contributes equally to the model, min–max normalization is applied to the time-series data. This technique scales the data values to a range between 0 and 1 using the following formula:
where
x represents the original data and
and
are the minimum and maximum values of the data, respectively. To capture the temporal dependencies within the multivariate time-series data, a sliding-window approach is employed. This step promotes numerical stability by ensuring that each sensor’s amplitude is scaled comparably—particularly important when dealing with multichannel vibration data derived from heterogeneous sensor hardware.
Next, to account for the strong temporal dependencies in rotating-machinery dynamics, we employ a sliding-window segmentation strategy. Each window, of length L, captures a short sequence of vibration samples, thereby preserving local time correlations relevant to faults (e.g., impulses from bearing damage, cyclic patterns from misalignment). In this study, we chose L based on typical shaft speeds and fault characteristic frequencies, ensuring that each window spans at least one complete rotation under normal operating speeds. Adjacent windows are shifted by a small stride to retain continuity in the dataset. After segmentation, we separate normal-operation windows for training and validation, while additional windows containing known faults are reserved for testing.
3.2. Fault Detection Model
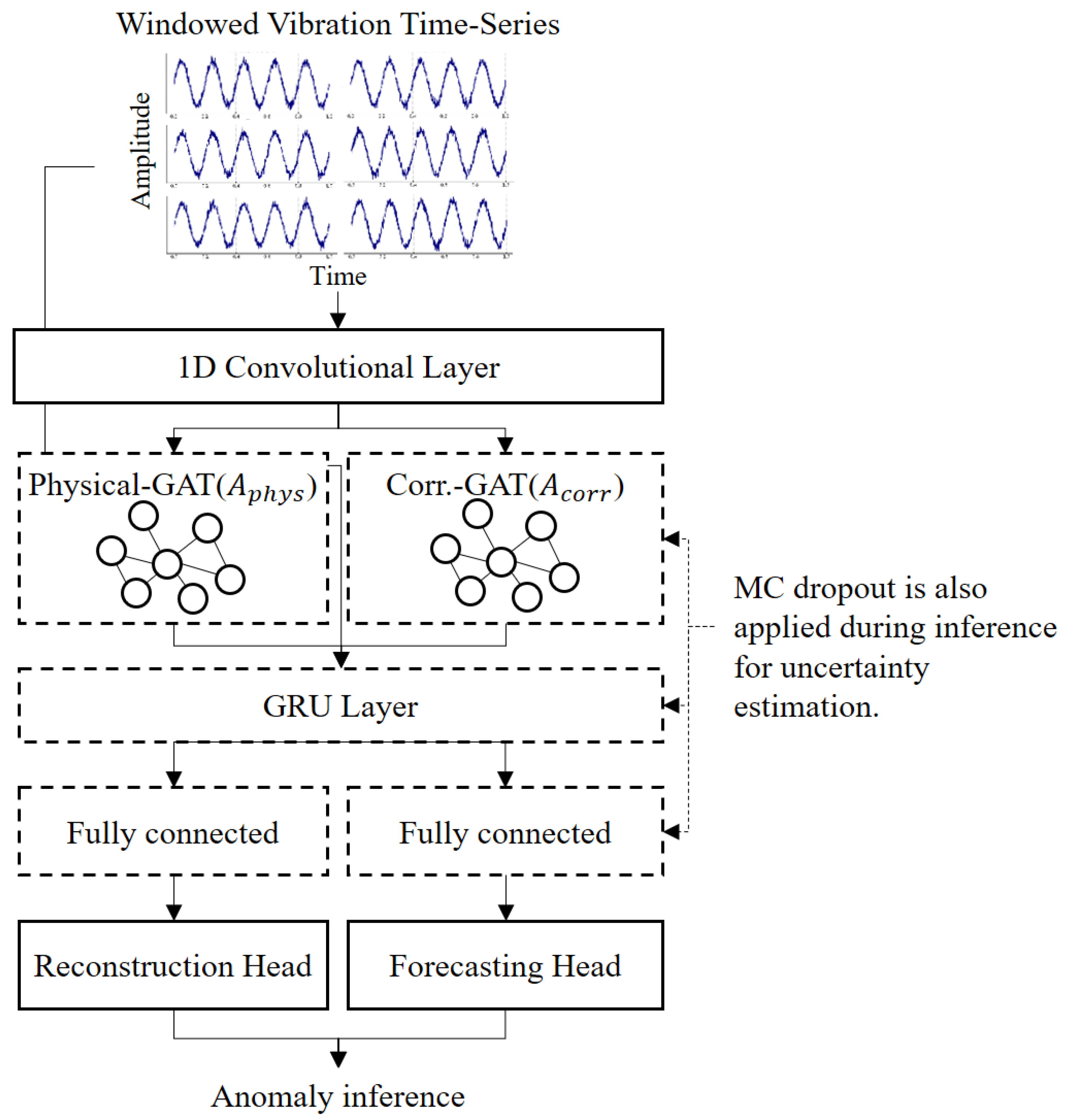
Building on standard deep-learning components for time-series processing, this approach introduces two complementary graph representations (one domain-based and the other data-driven) and a dynamic weighting mechanism for forecasting and reconstruction losses. As illustrated in
Figure 1, the revised architecture includes a one-dimensional convolutional feature extractor, dual GAT layers for each graph type, a gated recurrent unit (GRU) for longer-term temporal modeling, and two task-specific output heads (forecasting and reconstruction) connected by an adaptive loss-balancing module. Monte Carlo (MC) dropout is incorporated at multiple layers to capture uncertainty in both tasks. This novel combination provides richer spatiotemporal embeddings, dynamic objective prioritization, and enhanced robustness under uncertain or varying operational conditions.
3.2.1. Dual Graph Construction
Rotating compressor vibrations often exhibit both physically localized correlations (for example, sensors on the same bearing pedestal) and empirically discovered interdependencies (such as correlated frequency components across distant measurement points). To capture these nuances, the proposed framework maintains two distinct adjacency matrices.
Domain-Informed Adjacency (A
phys): This binary matrix is derived from machine geometry and known couplings (for instance, shared housings or rotor segments). If two sensors
and
lie on physically adjacent components, or on the same rigid body or whose centroidal distance does not exceed 1.5D (shaft diameter), then A
phys (i, j) = 1; otherwise, A
phys (i, j) = 0.
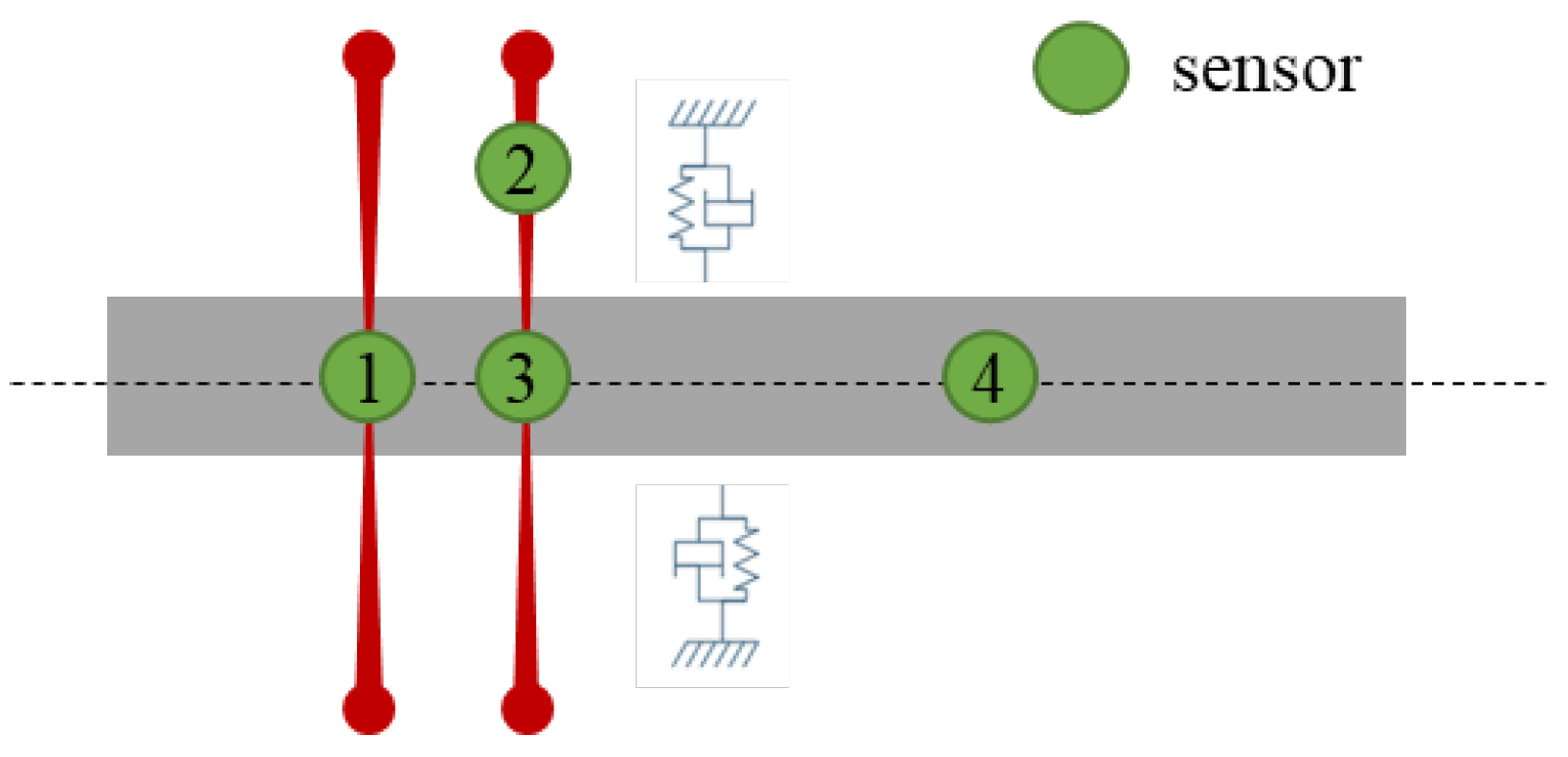
Figure 1 illustrates the rule on a four-sensor rotor train. The left bearing block links
and
(
). The axial proximity of the over-hung sensor
and
activates
. And the shared shaft segment between
and
gives
. All other pairs remain zero, producing the sparse, block-diagonal pattern in the accompanying adjacency matrix. This design encodes real-world proximity, so the subsequent GAT layer can respect the ways faults propagate through mechanical linkages or shared structural paths.
Data-Correlation Adjacency (Acorr): This matrix is learned from historical or real-time data by computing cross-correlation or mutual information among sensor channels and retaining only those edges that exceed a predefined threshold. It thereby captures relationships that may not be strictly physical, such as resonance-induced couplings or synchronous vibrations that arise under specific load conditions. By maintaining both adjacency matrices, the model exploits first-principle knowledge of machine layout while also incorporating emergent data-driven patterns.
3.2.2. Parallel Dual-Gat Embeddings
Once local vibration features are extracted by one-dimensional convolutions, those features are fed into two parallel GAT layers. One layer operates on A
phys, while the other operates on A
corr. Each GAT layer transforms node features according to
where
αij denotes attention coefficients derived from the respective adjacency matrix A,
W is a trainable weight matrix, and
σ is a nonlinear activation. The attention mechanism redistributes importance among connected nodes, possibly amplifying channels or time steps that are strongly indicative of emerging faults.
The physical graph attention network (Physical-GAT) uses Aphys to emphasize direct mechanical pathways, such as misaligned couplings. The correlation graph attention network (Correlation-GAT) uses Acorr to highlight data-driven relationships, for instance those involving sensor pairs that consistently co-vary under certain operational loads. The outputs of these two GAT layers are then fused, either by concatenation or by an additive scheme, before they are fed into the temporal model. This fusion ensures that the final embedding captures both physically interpretable pathways and latent data associations.
3.2.3. Temporal Modeling with GRU
Although GAT layers can incorporate short-range temporal connections (either through time-oriented edges or within a sliding window), rotating machinery faults may develop gradually or exhibit multi-rotation persistence. Therefore, the fused embeddings are passed to a GRU that processes consecutive windows. The GRU’s hidden state evolves according to
where
zt is the fused GAT representation at time
t. This recurrent mechanism retains a “memory” of how anomalies progress through multiple cycles and changing loads, thereby capturing both near-instantaneous anomalies and longer-term degradations.
3.2.4. Dual-Task Heads with Adaptive Loss Balancing
From the GRU’s final state, the network branches into two heads (
Figure 2). The forecasting head predicts near-future vibration samples (for example, one step ahead) and is penalized using the root-mean-square error (RMSE). Sudden deviations in these short-term predictions often indicate emerging faults. The reconstruction head is formulated as an autoencoder-like decoder that reconstructs the entire input window from a latent representation. Large reconstruction errors, measured by the mean squared error (MSE), typically suggest that the observed waveform deviates from normal behavior.
To adaptively prioritize these two objectives, a learnable weighting parameter
λ governs the balance between forecasting and reconstruction losses. The overall training loss is
where
λ ∈ [0, 1] can be tuned or learned via gradient-based methods. This approach allows the model to shift emphasis depending on whether short-term anomalies (forecasting) or overall waveform fidelity (reconstruction) offers more informative fault indicators. Additionally, skip connections from the fused GAT embeddings to the reconstruction decoder can preserve high-frequency features relevant to sudden events, thereby improving the fidelity of reconstructed signals. The decoder is used only during training. It is dropped at deployment, so the dual-task design does not increase online computational cost. Also, reconstruction of the head provides complementary effects. First, slow or quasi-stationary defects may leave one-step forecasts largely unchanged while progressively distorting a full window; reconstruction error therefore catches faults that the predictor alone can miss. Second, optimizing both heads force the latent representation to preserve short- and long-term information, stabilizing training and sharpening uncertainty estimates.
The Dual-GAT encoder uses four heads for the physical graph and four heads for the correlation graph, each producing 64-dimensional node embeddings. A single-layer GRU with 128 hidden units aggregates the temporal context. Dropout is applied after both the GAT and GRU blocks with a probability of 0.20; during inference, the same rate is kept active for Monte-Carlo sampling. The dual-task loss weight is initialized at λ = 0.50 and learned jointly with the network. Optimization employs Adam optimizer (learning rate , weight decay
3.3. Uncertainty Estimation
Uncertainty estimation is a crucial component of the proposed fault-detection model because it enhances the robustness and reliability of the predictions.
A posterior distribution with two distinct peaks, as shown in
Figure 3, highlights this problem; the highest peak, which would be the maximum a posteriori (MAP) estimate, is not representative of the entire distribution—a common problem with MAP estimation; it focuses on the single most likely parameter value, potentially overlooking other significant modes that reflect the underlying uncertainty. By contrast, a Bayesian approach that considers the full posterior distribution provides a more comprehensive picture. By accounting for all possible parameter values and their associated probabilities, the Bayesian approach captures the overall uncertainty and variability within the data, particularly important in cases where the distribution is broad or multimodal because it ensures that the inference is robust and reflective of the true complexity of the parameter space. Therefore, although MAP estimation can be useful for unimodal and narrow distributions, its application to more complex scenarios is limited. The Bayesian approach, which incorporates the entire posterior distribution, offers a richer and more accurate representation of uncertainty, leading to better-informed decision-making.
Bayesian inference enables the measurement of prediction uncertainty. In Bayesian inference, we aim to compute the posterior distribution of the model parameters given the observed data. The posterior distribution provides a probabilistic framework for making predictions, accounting for uncertainty in the model parameters. Mathematically, the posterior distribution is given by Bayes’ theorem:
where
p(θ∣D) is the posterior distribution of the parameters θ given the data D.
p(D∣θ) is the likelihood of the data given the parameters.
p(θ) is the prior distribution of the parameters.
p(D) is the marginal likelihood or evidence, computed as shown below.
The integral in the denominator, p(D), is practically intractable for complex models because it requires integrating over all possible values of the parameters p(θ). This intractability arises from the high dimensionality of the parameter space and the complexity of the likelihood function, making the exact computation of the posterior distribution computationally infeasible.
The MC dropout, introduced by Gal and Ghahramani [
63], provides a method to approximate Bayesian inference in deep neural networks. By incorporating dropouts during both training and inference, we can obtain a distribution of the model predictions. During inference, dropout is applied multiple times to the same input, generating a range of outputs. These outputs are then used to estimate the mean and variance of the predictions, thereby effectively approximating the posterior distribution.
The key idea is to perform multiple stochastic forward passes with dropouts enabled during inference, effectively sampling from the approximate posterior distribution. During training, a dropout is applied to the neurons with a certain probability, p, randomly setting a fraction of the neurons to zero, thus forcing the network to learn redundant representations and preventing overfitting. Mathematically, if h is the hidden layer activation, the dropout modifies it as follows:
where r is a binary mask sampled from a Bernoulli distribution with probability p, and ⊙ denotes element-wise multiplication.
During inference, the dropout remains active, allowing multiple forward passes through the network with different dropout masks. Each forward pass can be viewed as sampling from a different subnetwork, providing a diverse set of predictions. Let be the prediction from the t-th forward pass. By performing T such forward passes, we obtain a distribution of predictions.
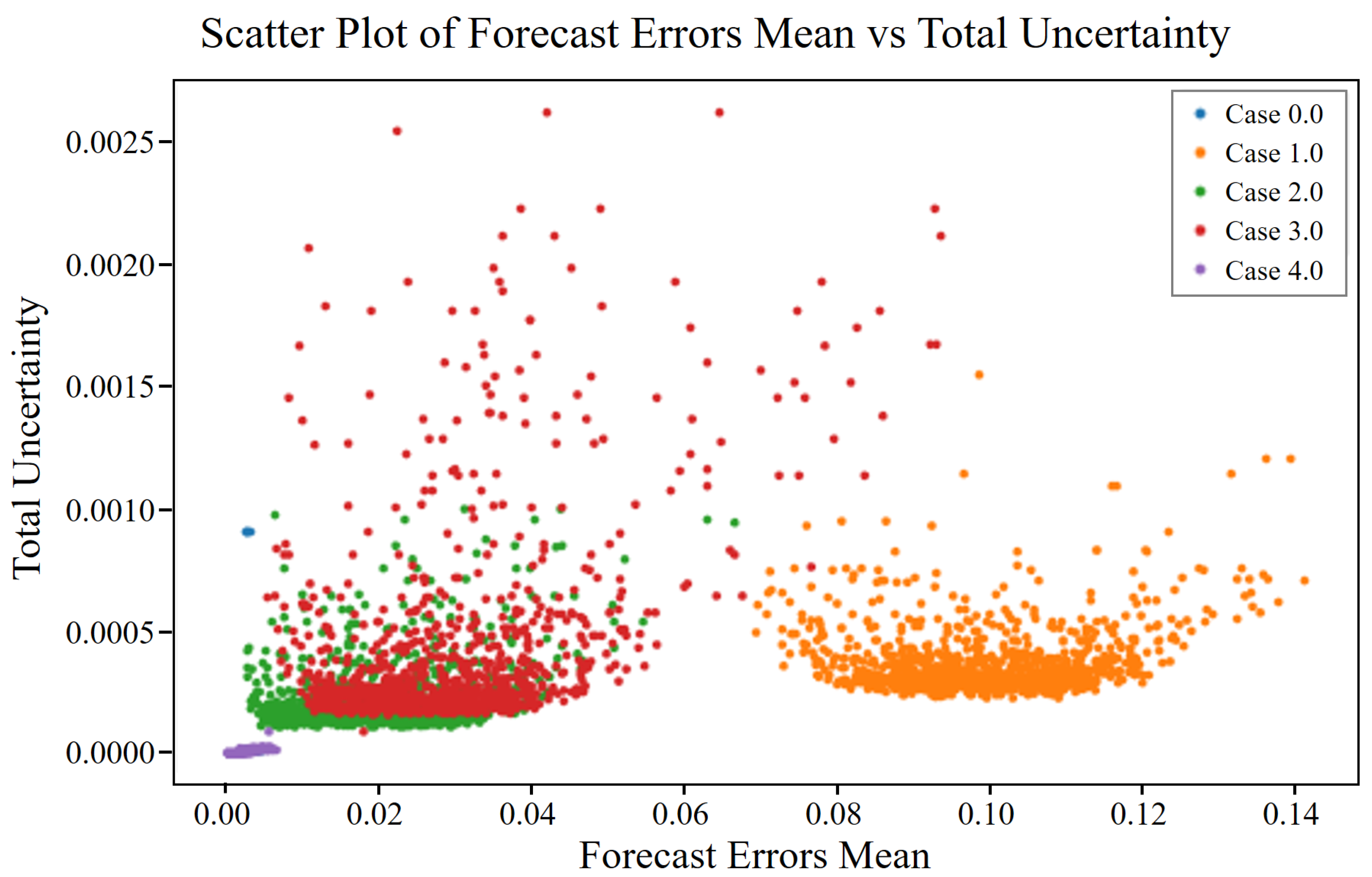
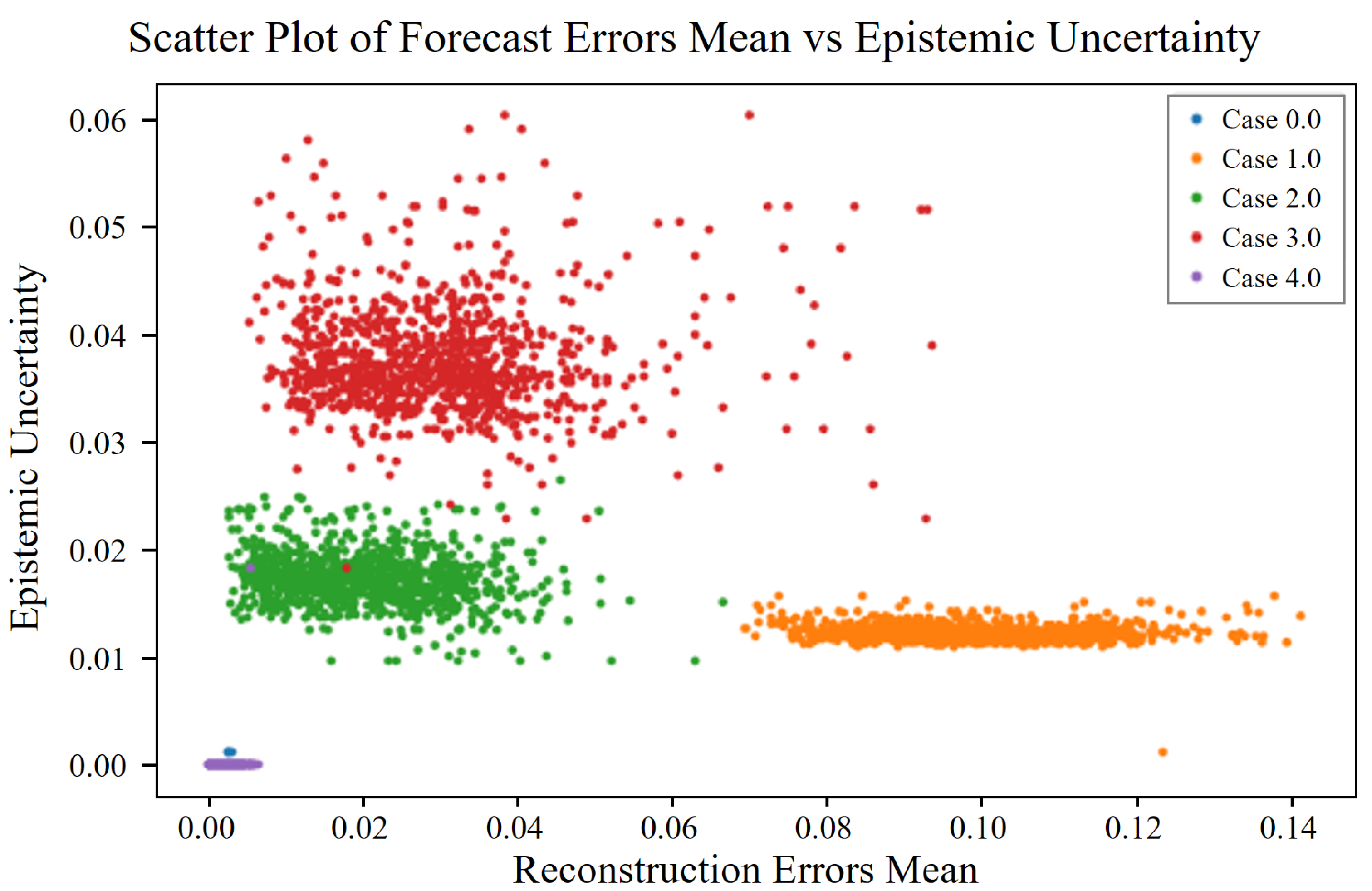
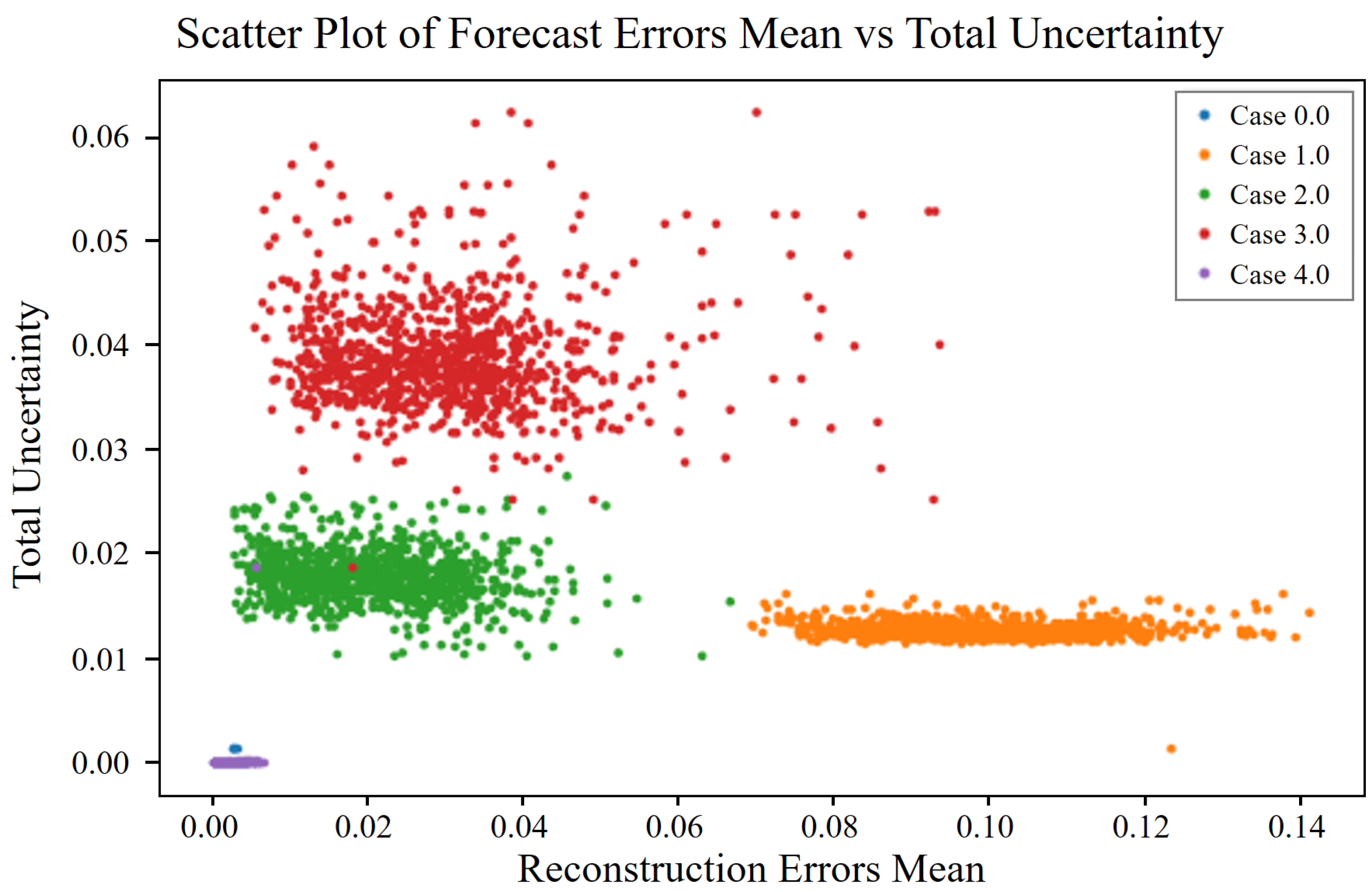
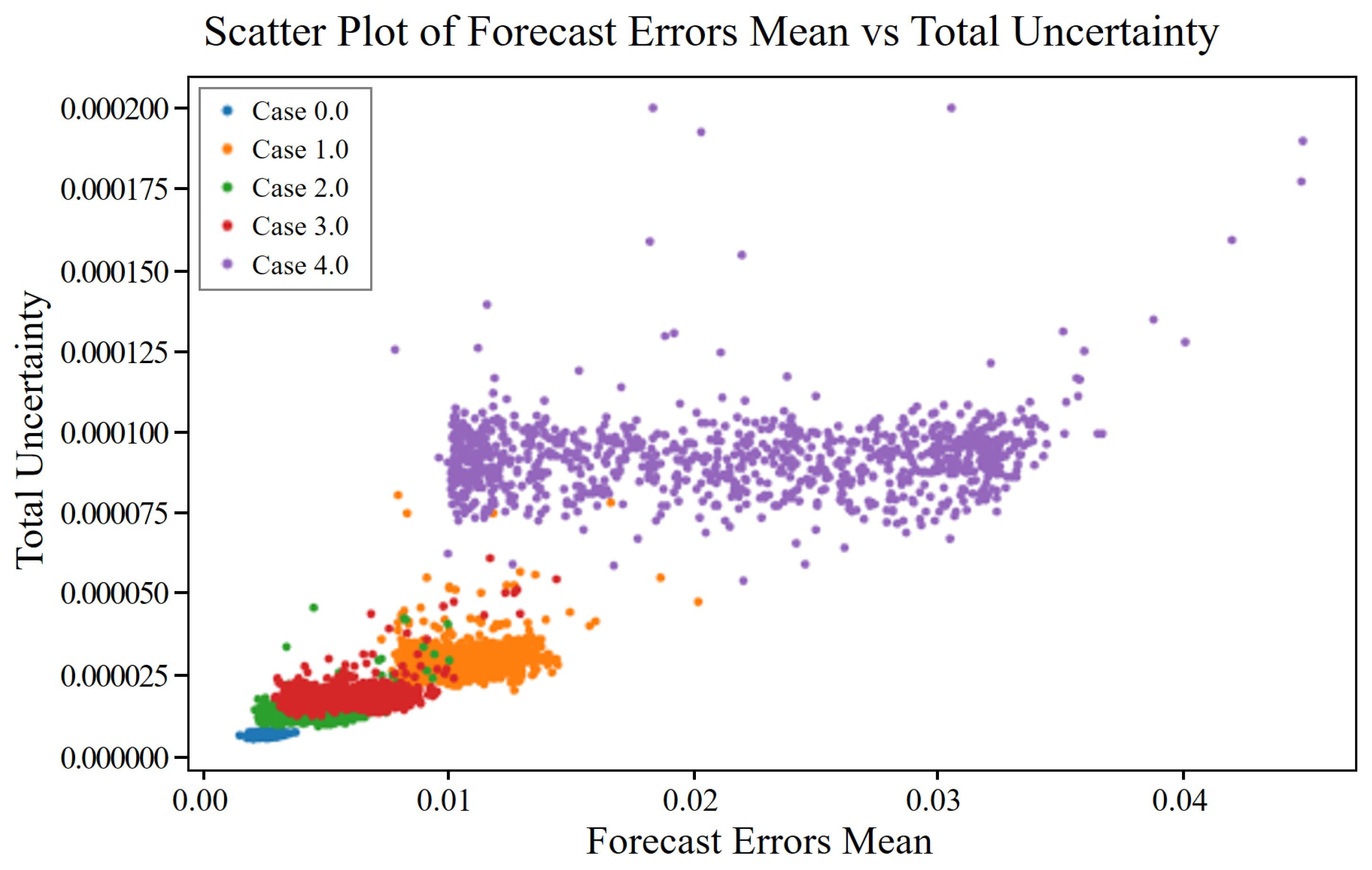
These approximations allow us to estimate the uncertainty in the predictions of the model without explicitly computing the intractable posterior distribution. Afterward, the types of uncertainty in the model can be determined. Uncertainties in machine learning models can be broadly categorized into aleatoric and epistemic uncertainties. Understanding and quantifying these uncertainties are essential for developing reliable predictive models, particularly for safety-critical applications such as industrial maintenance.
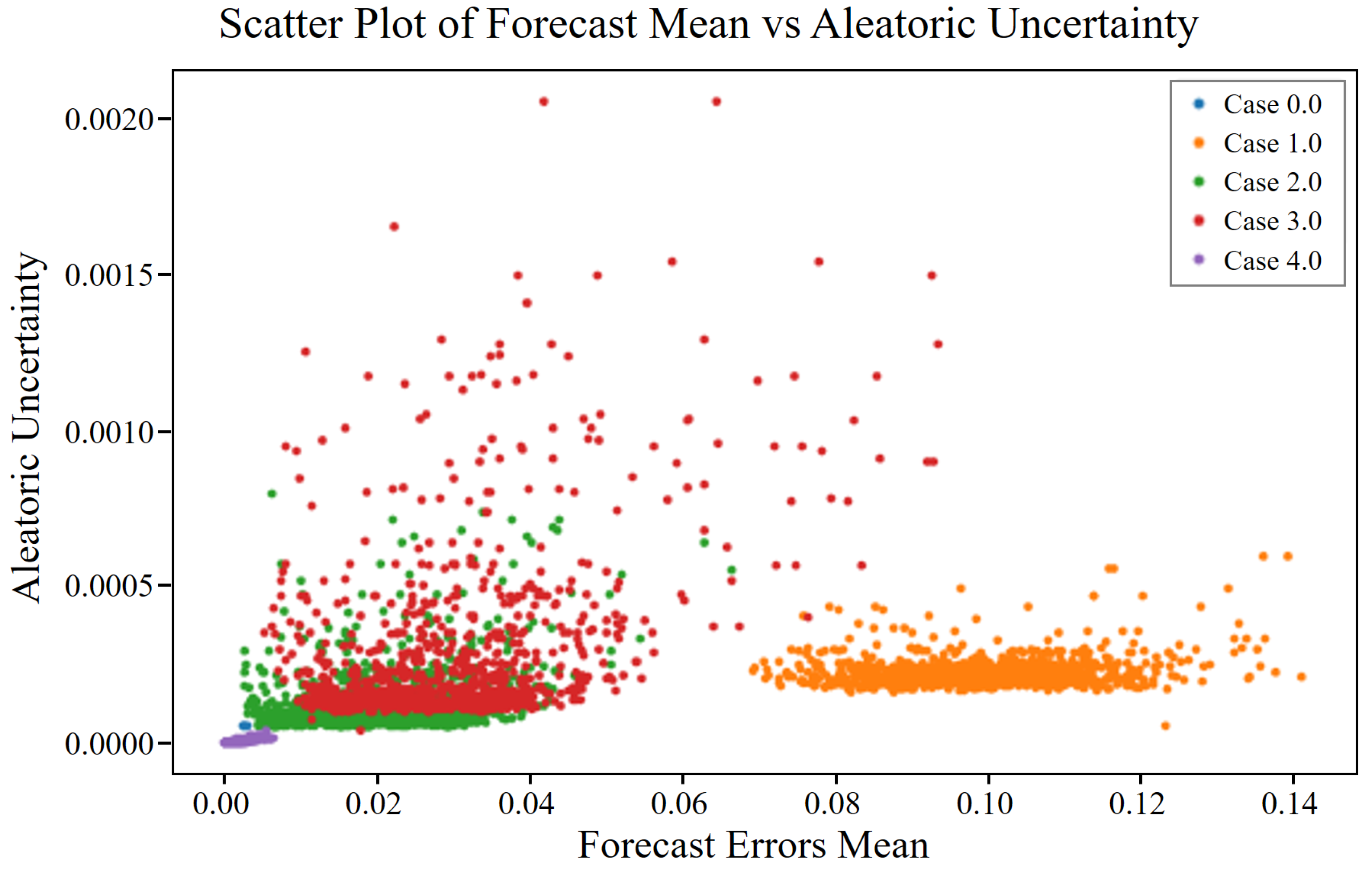
Aleatoric uncertainty, derived from the Latin word “alea”, meaning “dice”, refers to the inherent variability in the data themselves. This type of uncertainty is irreducible and originates from noise inherent in the observations. For example, in compressor vibration data, aleatoric uncertainty may arise from measurement errors owing to sensor precision limits or environmental variations affecting the readings.
Aleatoric uncertainty, often represented as a probabilistic distribution over the output variables, given the input data, can be visualized by plotting confidence intervals around the predictions, indicating regions with high variability due to noise. Notably, increasing the amount of data does not reduce the aleatoric uncertainty because it is intrinsic to the observations.
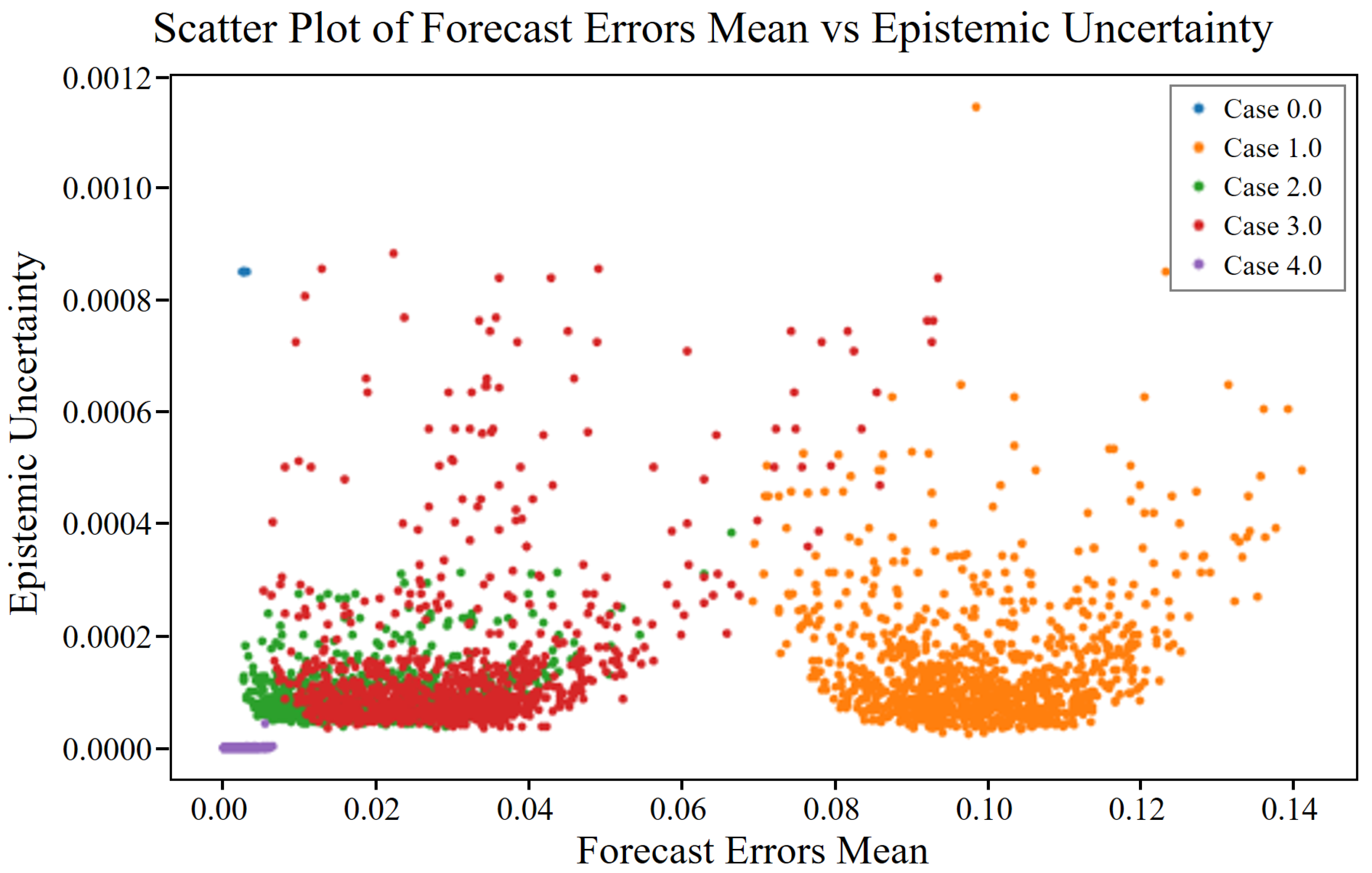
By comparison, epistemic uncertainty, from the Greek word “episteme”, meaning “knowledge”, pertains to uncertainty in the model parameters and structure. This uncertainty is reducible and arises from insufficient training data or a lack of knowledge about the model itself. In the context of compressor vibration data, epistemic uncertainty may be caused by limited data representing certain operational conditions, leading to uncertain predictions in those regions.
Epistemic uncertainty can be mitigated by acquiring additional data or improving the model, reflecting the confidence of the model in its predictions, based on the knowledge it has gained during training. High epistemic uncertainty often indicates regions where the model has not encountered sufficient similar examples during training, suggesting that further data collection in those areas could improve its performance.
Under a Gaussian weight prior and a Lipschitz feature extractor, the epistemic term scales with the squared Mahalanobis distance from the normal data manifold . Because fault severity monotonically increases this distance, epistemic uncertainty also grows monotonically whereas aleatoric uncertainty remains bounded by the intrinsic sensor noise.