EMG-Driven Shared Control Architecture for Human–Robot Co-Manipulation Tasks †
Abstract
1. Introduction
2. Materials and Methods
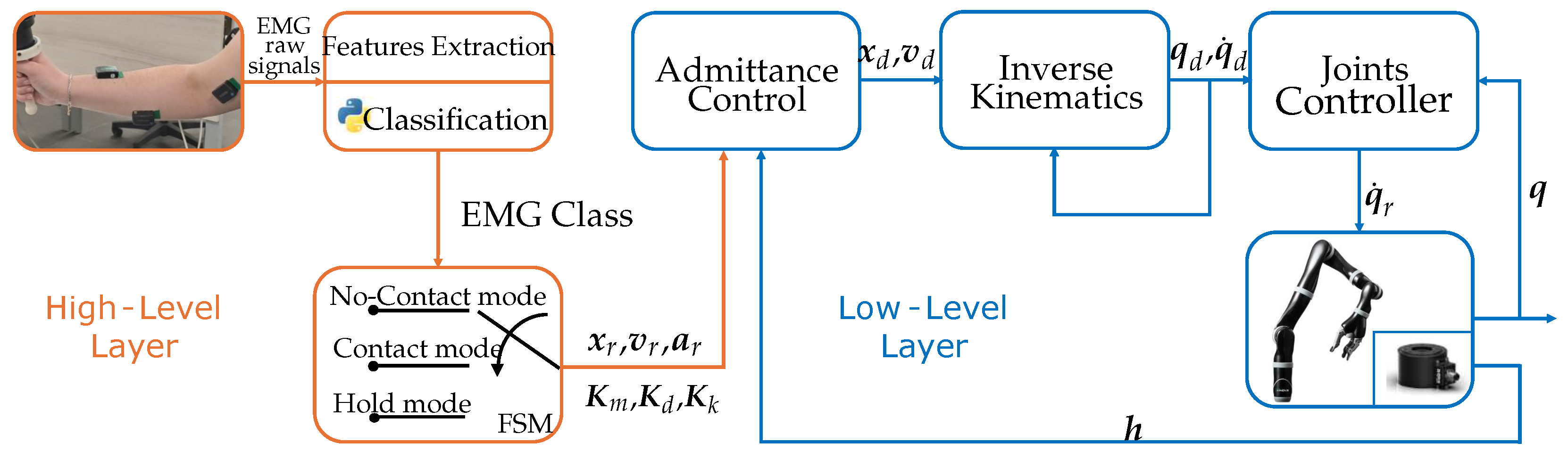
2.1. Shared Control Architecture
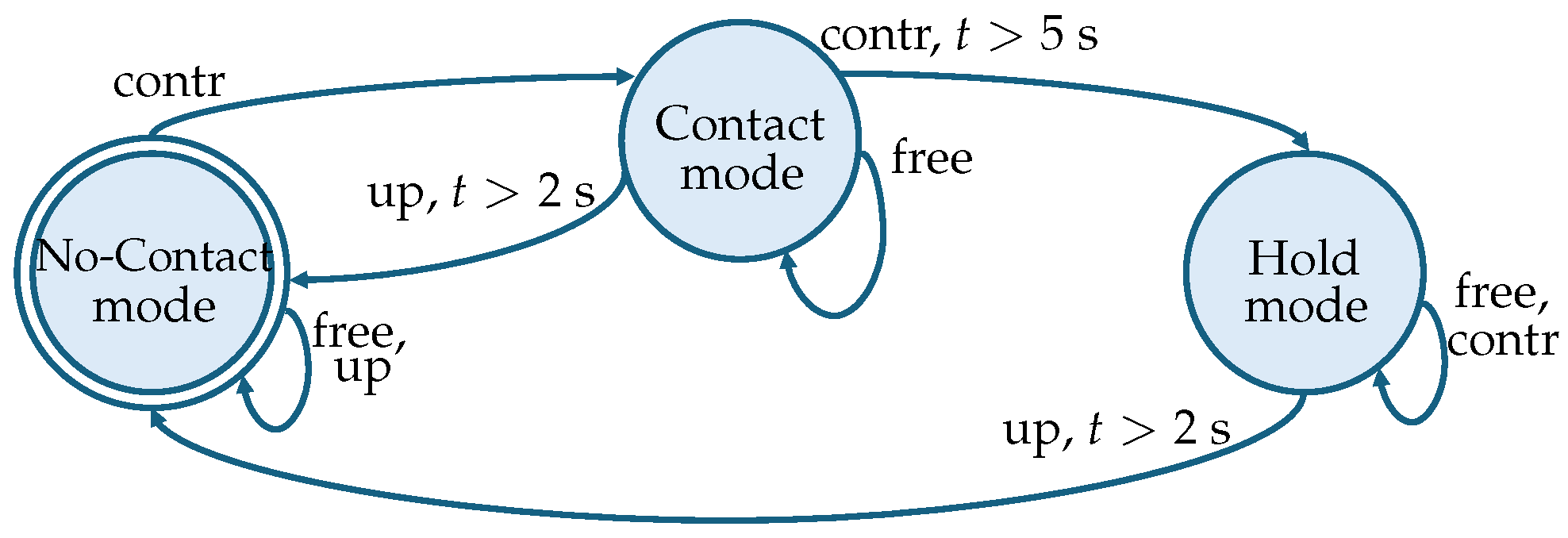
- no-contact mode: hand-guidance of the end-effector in the free space to allow the operator to move the end-effector towards, e.g., a workpiece;
- contact mode: hand-guidance of the end-effector while in contact with a stiff surface to allow performing operations like, e.g., carving, welding or drawing;
- hold mode: in case of external disturbances, the manipulator is designed to elastically return the end-effector to a fixed position; this position is the same at which the switch to the hold mode occurs. This allows for the temporary relocation of the robot away from the point of interest, facilitating the placement of a workpiece that the robot is then responsible for maintaining in that position.
2.2. Low-Level Layer
2.2.1. Inverse Kinematics and Joints Controller
2.2.2. Admittance Control
2.3. High-Level Layer
2.3.1. EMG Signal Processing and Classification
- The Root Mean Square (RMS) can be used to evaluate muscle activity and fatigue; it is defined as:
- The Mean Absolute Value (MAV) can be used to assess the intensity of muscle contraction. It’s definition is:
- The Average Amplitude Change (AAC) provides information about fluctuations in muscle activity over a period of time and about the level of muscle activation during that period. It is useful for assessing muscle fatigue, tracking changes in muscle activity, and comparing muscle involvement during different activities or conditions. It can be computed as:
2.3.2. Finite State Machine
3. Results
3.1. Experimental Setup
3.2. Training and Test of the Classifier
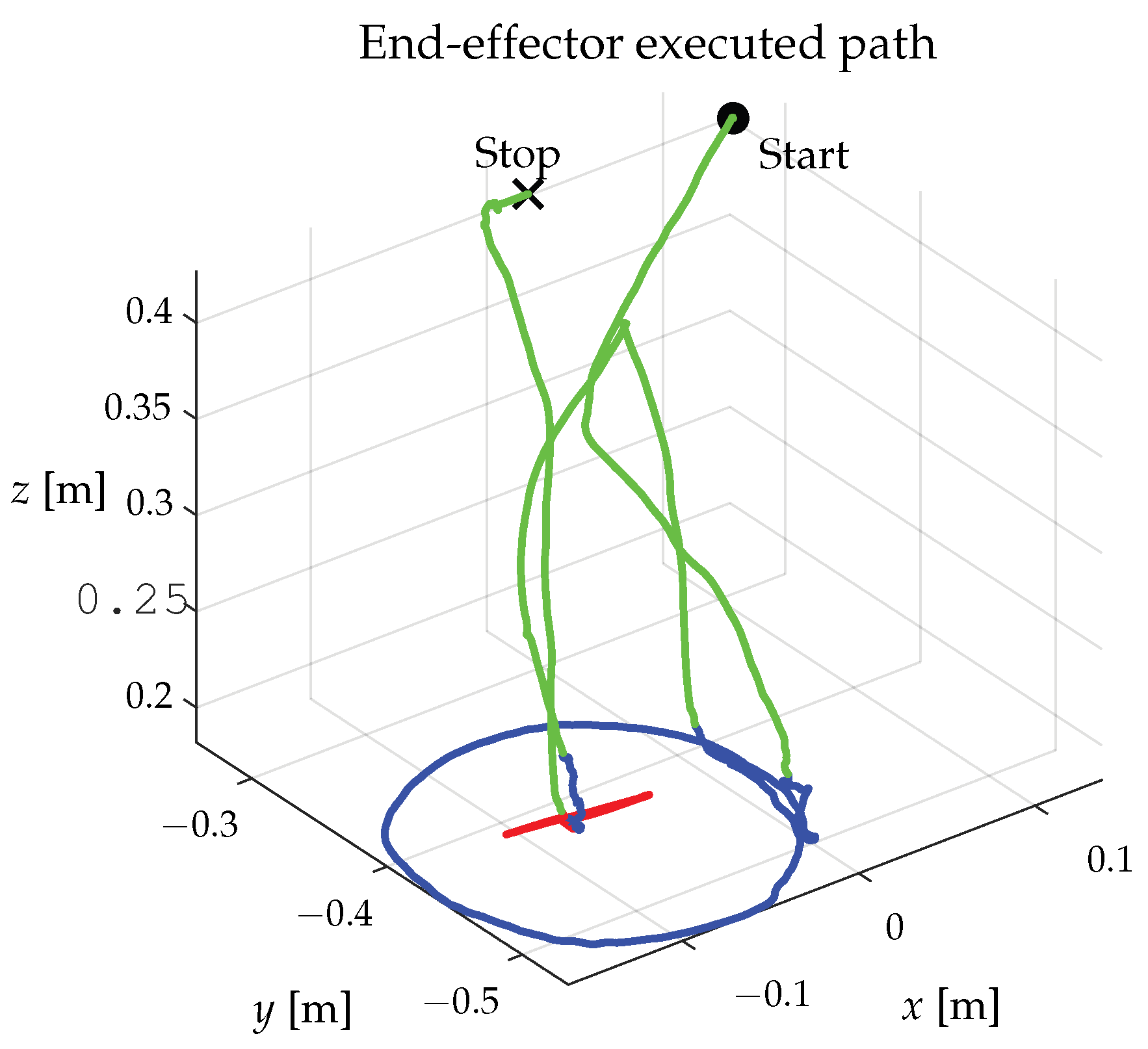
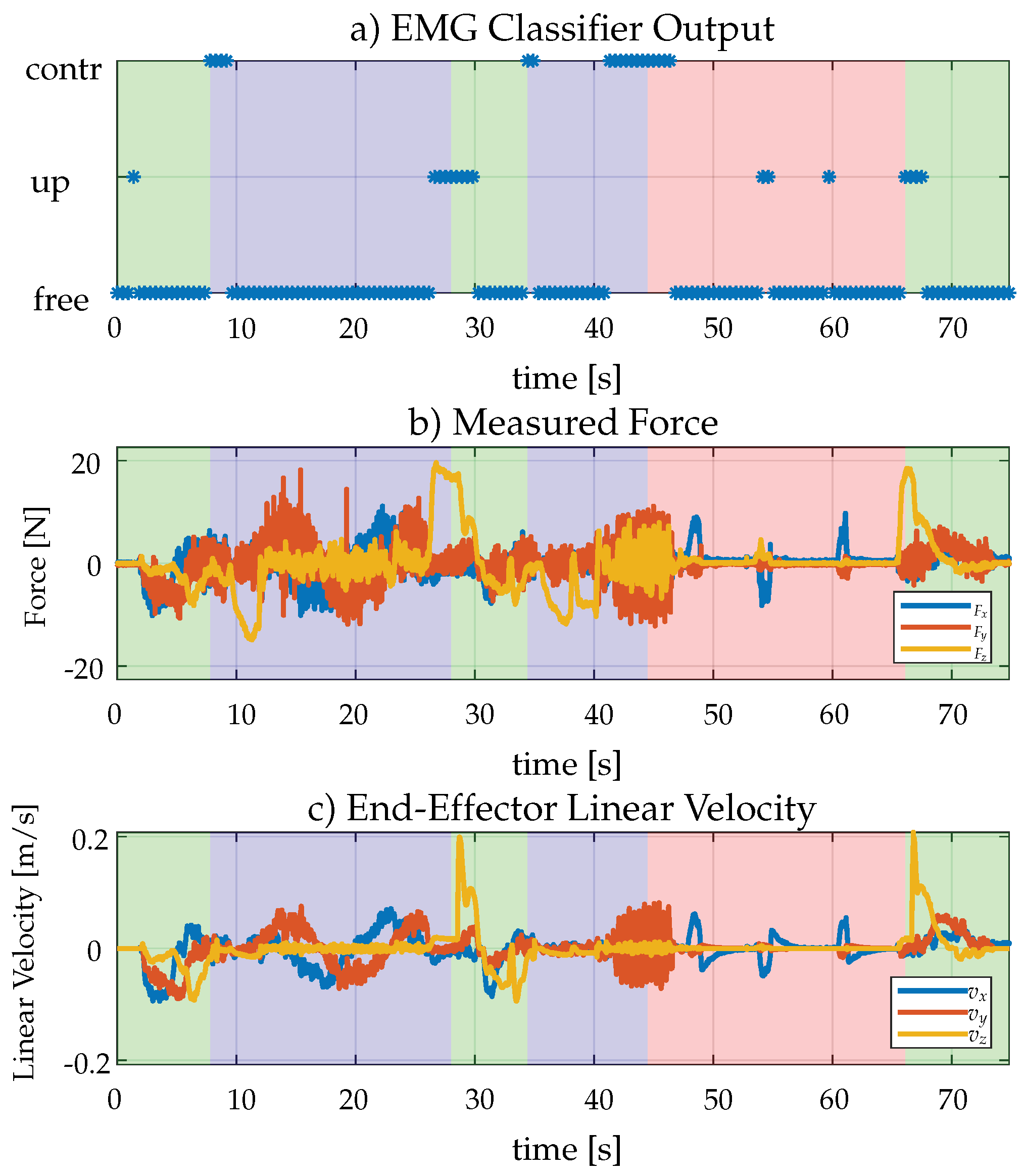
3.3. Experimental Results
4. Discussion and Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Villani, V.; Pini, F.; Leali, F.; Secchi, C. Survey on human–robot collaboration in industrial settings: Safety, intuitive interfaces and applications. Mechatronics 2018, 55, 248–266. [Google Scholar] [CrossRef]
- Matheson, E.; Minto, R.; Zampieri, E.G.G.; Faccio, M.; Rosati, G. Human–Robot Collaboration in Manufacturing Applications: A Review. Robotics 2019, 8, 100. [Google Scholar] [CrossRef]
- Cherubini, A.; Passama, R.; Crosnier, A.; Lasnier, A.; Fraisse, P. Collaborative manufacturing with physical human–robot interaction. Robot.-Comput.-Integr. Manuf. 2016, 40, 1–13. [Google Scholar] [CrossRef]
- Sladić, S.; Lisjak, R.; Runko Luttenberger, L.; Musa, M. Trends and Progress in Collaborative Robot Applications. Politehnika 2021, 5, 32–37. [Google Scholar] [CrossRef]
- Sharifi, M.; Zakerimanesh, A.; Mehr, J.K.; Torabi, A.; Mushahwar, V.K.; Tavakoli, M. Impedance Variation and Learning Strategies in Human–Robot Interaction. IEEE Trans. Cybern. 2022, 52, 6462–6475. [Google Scholar] [CrossRef]
- Abu-Dakka, F.J.; Saveriano, M. Variable Impedance Control and Learning—A Review. Front. Robot. AI 2020, 7, 590681. [Google Scholar] [CrossRef] [PubMed]
- Abbink, D.A.; Carlson, T.; Mulder, M.; de Winter, J.C.F.; Aminravan, F.; Gibo, T.L.; Boer, E.R. A Topology of Shared Control Systems—Finding Common Ground in Diversity. IEEE Trans.-Hum.-Mach. Syst. 2018, 48, 509–525. [Google Scholar] [CrossRef]
- Kong, H.; Yang, C.; Li, G.; Dai, S.L. A sEMG-Based Shared Control System with No-Target Obstacle Avoidance for Omnidirectional Mobile Robots. IEEE Access 2020, 8, 26030–26040. [Google Scholar] [CrossRef]
- Selvaggio, M.; Cognetti, M.; Nikolaidis, S.; Ivaldi, S.; Siciliano, B. Autonomy in Physical Human-Robot Interaction: A Brief Survey. IEEE Robot. Autom. Lett. 2021, 6, 7989–7996. [Google Scholar] [CrossRef]
- Cacace, J.; Caccavale, R.; Finzi, A.; Lippiello, V. Variable Admittance Control based on Virtual Fixtures for Human-Robot Co-Manipulation. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 1569–1574. [Google Scholar] [CrossRef]
- Zahedi, F.; Arnold, J.; Phillips, C.; Lee, H. Variable Damping Control for pHRI: Considering Stability, Agility, and Human Effort in Controlling Human Interactive Robots. IEEE Trans.-Hum.-Mach. Syst. 2021, 51, 504–513. [Google Scholar] [CrossRef]
- Ficuciello, F.; Villani, L.; Siciliano, B. Variable Impedance Control of Redundant Manipulators for Intuitive Human–Robot Physical Interaction. IEEE Trans. Robot. 2015, 31, 850–863. [Google Scholar] [CrossRef]
- Ferraguti, F.; Talignani Landi, C.; Sabattini, L.; Bonfe, M.; Fantuzzi, C.; Secchi, C. A variable admittance control strategy for stable physical human–robot interaction. Int. J. Robot. Res. 2019, 38, 747–765. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, J. Based on human-like variable admittance control for human–robot collaborative motion. Robotica 2023, 41, 2155–2176. [Google Scholar] [CrossRef]
- Losey, D.P.; O’Malley, M.K. Trajectory Deformations From Physical Human–Robot Interaction. IEEE Trans. Robot. 2018, 34, 126–138. [Google Scholar] [CrossRef]
- Dimeas, F.; Aspragathos, N. Fuzzy learning variable admittance control for human-robot cooperation. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 4770–4775. [Google Scholar] [CrossRef]
- Grafakos, S.; Dimeas, F.; Aspragathos, N. Variable admittance control in pHRI using EMG-based arm muscles co-activation. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 1900–1905. [Google Scholar] [CrossRef]
- Adeola-Bello, Z.A.; Azlan, N.Z. Power Assist Rehabilitation Robot and Motion Intention Estimation. Int. J. Robot. Control Syst. 2022, 2, 297–316. [Google Scholar] [CrossRef]
- Gonzalez-Mendoza, A.; Quinones-Uriostegui, I.; Salazar-Cruz, S.; Perez Sanpablo, A.I.; López, R.; Lozano, R. Design and Implementation of a Rehabilitation Upper-limb Exoskeleton Robot Controlled by Cognitive and Physical Interfaces. J. Bionic Eng. 2022, 19, 1374–1391. [Google Scholar] [CrossRef] [PubMed]
- Aydin, Y.; Sirintuna, D.; Basdogan, C. Towards collaborative drilling with a cobot using admittance controller. Trans. Inst. Meas. Control 2021, 43, 1760–1773. [Google Scholar] [CrossRef]
- Bae, J.; Kim, K.; Huh, J.; Hong, D. Variable Admittance Control with Virtual Stiffness Guidance for Human–Robot Collaboration. IEEE Access 2020, 8, 117335–117346. [Google Scholar] [CrossRef]
- Li, J.; Li, G.; Chen, Z.; Li, J. A Novel EMG-Based Variable Impedance Control Method for a Tele-Operation System Under an Unstructured Environment. IEEE Access 2022, 10, 89509–89518. [Google Scholar] [CrossRef]
- Zeng, C.; Yang, C.; Cheng, H.; Li, Y.; Dai, S.L. Simultaneously Encoding Movement and sEMG-Based Stiffness for Robotic Skill Learning. IEEE Trans. Ind. Inform. 2021, 17, 1244–1252. [Google Scholar] [CrossRef]
- Tian, J.; Wang, H.; Zheng, S.; Ning, Y.; Zhang, X.; Niu, J.; Vladareanu, L. sEMG-Based Gain-Tuned Compliance Control for the Lower Limb Rehabilitation Robot during Passive Training. Sensors 2022, 22, 7890. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Wang, N.; Cheng, H.; Yang, C. Neural Learning Enhanced Variable Admittance Control for Human–Robot Collaboration. IEEE Access 2020, 8, 25727–25737. [Google Scholar] [CrossRef]
- Zhuang, Y.; Yao, S.; Ma, C.; Song, R. Admittance Control Based on EMG-Driven Musculoskeletal Model Improves the Human–Robot Synchronization. IEEE Trans. Ind. Inform. 2019, 15, 1211–1218. [Google Scholar] [CrossRef]
- Wu, Q.; Chen, B.; Wu, H. Adaptive Admittance Control of an Upper Extremity Rehabilitation Robot with Neural-Network-Based Disturbance Observer. IEEE Access 2019, 7, 123807–123819. [Google Scholar] [CrossRef]
- Zhuang, Y.; Leng, Y.; Zhou, J.; Song, R.; Li, L.; Su, S.W. Voluntary Control of an Ankle Joint Exoskeleton by Able-Bodied Individuals and Stroke Survivors Using EMG-Based Admittance Control Scheme. IEEE Trans. Biomed. Eng. 2021, 68, 695–705. [Google Scholar] [CrossRef] [PubMed]
- Villa-Parra, A.; Delisle Rodriguez, D.; Botelho, T.; Villarejo Mayor, J.; Delis, A.; Carelli, R.; Frizera, A.; Freire, T. Control of a robotic knee exoskeleton for assistance and rehabilitation based on motion intention from sEMG. Res. Biomed. Eng. 2018, 34, 198–210. [Google Scholar] [CrossRef]
- Han, L.; Zhao, L.; Huang, Y.; Xu, W. Variable admittance control for safe physical human–robot interaction considering intuitive human intention. Mechatronics 2024, 97, 103098. [Google Scholar] [CrossRef]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Gašpar, T.; Bevec, R.; Ridge, B.; Ude, A. Base Frame Calibration of a Reconfigurable Multi-robot System with Kinesthetic Guidance. In Advances in Service and Industrial Robotics; Aspragathos, N.A., Koustoumpardis, P.N., Moulianitis, V.C., Eds.; Springer: Cham, Switzerland, 2019; pp. 651–659. [Google Scholar] [CrossRef]
- Mielke, E.; Townsend, E.; Wingate, D.; Salmon, J.L.; Killpack, M.D. Human-robot planar co-manipulation of extended objects: Data-driven models and control from human-human dyads. Front. Neurorobotics 2024, 18, 1291694. [Google Scholar] [CrossRef]
- Musić, S.; Prattichizzo, D.; Hirche, S. Human-Robot Interaction Through Fingertip Haptic Devices for Cooperative Manipulation Tasks. In Proceedings of the 2019 28th IEEE International Conference on Robot and Human Interactive Communication (RO-MAN), New Delhi, India, 14–18 October 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Du, G.; Zhang, P. A Markerless Human–Robot Interface Using Particle Filter and Kalman Filter for Dual Robots. IEEE Trans. Ind. Electron. 2015, 62, 2257–2264. [Google Scholar] [CrossRef]
- Maimon-Dror, R.O.; Fernandez-Quesada, J.; Zito, G.A.; Konnaris, C.; Dziemian, S.; Faisal, A.A. Towards free 3D end-point control for robotic-assisted human reaching using binocular eye tracking. In Proceedings of the 2017 International Conference on Rehabilitation Robotics (ICORR), London, UK, 17–20 July 2017; pp. 1049–1054. [Google Scholar] [CrossRef]
- Yacoub, A.; Flanagan, M.; Buerkle, A.; Bamber, T.; Ferreira, P.; Hubbard, E.M.; Lohse, N. Data-Driven Modelling of Human-Human Co-Manipulation Using Force and Muscle Surface Electromyogram Activities. Electronics 2021, 10, 1509. [Google Scholar] [CrossRef]
- Patriarca, F.; Di Lillo, P.; Arrichiello, F. EMG-based shared control framework for human-robot co-manipulation tasks. In Proceedings of the International Conference on Informatics in Control, Automation and Robotics, Porto, Portugal, 18–20 November 2024. [Google Scholar]
- Di Lillo, P.; Simetti, E.; Wanderlingh, F.; Casalino, G.; Antonelli, G. Underwater Intervention with Remote Supervision via Satellite Communication: Developed Control Architecture and Experimental Results Within the Dexrov Project. IEEE Trans. Control Syst. Technol. 2021, 29, 108–123. [Google Scholar] [CrossRef]
- Di Lillo, P.; Vito, D.D.; Antonelli, G. Merging Global and Local Planners: Real-Time Replanning Algorithm of Redundant Robots Within a Task-Priority Framework. IEEE Trans. Autom. Sci. Eng. 2023, 20, 1180–1193. [Google Scholar] [CrossRef]
- Manjunatha, H.; Jujjavarapu, S.S.; Esfahani, E.T. Classification of Motor Control Difficulty using EMG in Physical Human-Robot Interaction. In Proceedings of the 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Toronto, ON, Canada, 11–14 October 2020; pp. 2708–2713. [Google Scholar] [CrossRef]
- Kramer, O. Scikit-learn. In Machine Learning for Evolution Strategies; Springer: Cham, Switzerland, 2016; pp. 45–53. [Google Scholar]
- Campbell, E.; Phinyomark, A.; Scheme, E. Deep Cross-User Models Reduce the Training Burden in Myoelectric Control. Front. Neurosci. 2021, 15, 657958. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Chen, X.; Ruan, Y.; Zhang, X. Cross-User Electromyography Pattern Recognition Based on a Novel Spatial-Temporal Graph Convolutional Network. IEEE Trans. Neural Syst. Rehabil. Eng. 2024, 32, 72–82. [Google Scholar] [CrossRef] [PubMed]



| Parameter | Value | Description |
|---|---|---|
| Control parameters | ||
| Inverse kinematics gain | ||
| Joints controller gain | ||
| 80 | Low-damping gain | |
| 1000 | High-damping gain | |
| 100 | Stiffness gain in hold mode | |
| Classifier parameters | ||
| C | 1 | Regularization parameter |
| γ | ‘scale’ 1 | Parameter of a Gaussian Kernel |
| Kernel | ’RBF’ | Kernel used in the SVM Classifier |
| Subject | Accuracy (%) | Precision (%) | Recall (%) | F1 Score (%) |
|---|---|---|---|---|
| S1 | 91.40 | 95.18 | 87.59 | 90.59 |
| S2 | 81.69 | 82.16 | 78.97 | 78.11 |
| S3 | 90.84 | 89.22 | 89.28 | 88.81 |
| S4 | 84.13 | 88.41 | 76.61 | 80.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patriarca, F.; Di Lillo, P.; Arrichiello, F. EMG-Driven Shared Control Architecture for Human–Robot Co-Manipulation Tasks. Machines 2025, 13, 669. https://doi.org/10.3390/machines13080669
Patriarca F, Di Lillo P, Arrichiello F. EMG-Driven Shared Control Architecture for Human–Robot Co-Manipulation Tasks. Machines. 2025; 13(8):669. https://doi.org/10.3390/machines13080669
Chicago/Turabian StylePatriarca, Francesca, Paolo Di Lillo, and Filippo Arrichiello. 2025. "EMG-Driven Shared Control Architecture for Human–Robot Co-Manipulation Tasks" Machines 13, no. 8: 669. https://doi.org/10.3390/machines13080669
APA StylePatriarca, F., Di Lillo, P., & Arrichiello, F. (2025). EMG-Driven Shared Control Architecture for Human–Robot Co-Manipulation Tasks. Machines, 13(8), 669. https://doi.org/10.3390/machines13080669






