1. Introduction
The parallel mechanism offers advantages such as a large carrying capacity, high precision, and ease of control [
1,
2]. Wheel-legged robots with parallel mechanisms as legs have become a research hotspot in the field of mobile robots. This type of robot has advantages of adaptability to multiple terrains, such as flat and rugged terrains, good stability, and strong load-bearing capacity. It has broad application prospects in complex and variable unknown underground spaces, earth’s surface disaster rescue, planetary exploration, and other fields [
3].
The configuration and layout of parallel leg mechanisms are the core foundation of the design of wheeled-legged robots, directly determining the robot’s motion performance, load-bearing capacity, and terrain adaptability in complex environments [
4]. Feller [
5] proposed a serial-parallel three-legged robot and solved its positive and inverse kinematics problems by means of the spherical trigonometry and spatial vector geometry methods. Li et al. [
6] studied a mobile heavy-duty pouring robot based on the 4-UPU parallel mechanism to analyze its kinematics and model the pouring process. Jia et al. [
7], Marínez et al. [
8], and Niu et al. [
9] focused on parallel/hybrid mechanisms: Jia et al. used a dual Stewart platform to optimize dynamics and stability, Martínez et al. used a 3-CUP geometry vector method to solve forward kinematics, and Niu et al.used a 3-DOF series-parallel hybrid mechanism to fully analyze the position, velocity, and stiffness. All three verified the advantages of parallel mechanisms in the design of robots with high stiffness and stability.
Li et al. [
10] synthesized a family of modular 3-DOF parallel leg mechanisms, which consisted of a 3-DOF drive system and a 2-DOF walking mechanism. A larger and more regular workspace endowed the walking robot with strong obstacle-surmounting capacity. Zhang et al. [
11] proposed a 3-DOF leg mechanism for a hexapod firefighting robot, which is composed of a 2RUS + RU parallel mechanism as a driving mechanism and a spatial parallelogram mechanism as walking mechanism, and the two are connected by a spherical pair. A dynamics model was developed, and the leg mechanism was improved to reduce the torque requirement of the drive joints. Efrain et al. [
12] presented a design, kinematic analysis, and dimensional optimization methodology for a linear triangular parallel robot aimed at improving performance and efficiency in additive manufacturing (3D printing). Sang et al. [
13] presented a human-carried quadruped walking robot based on the 2-UPS + UP parallel leg mechanism and investigated its kinematic analysis, gait planning, and control strategy. Wu et al. [
14] presented a 5-DOF hybrid leg mechanism and its application to a quadruped Earth exploration vehicle, BJTUBOT.
Parallel leg mechanisms with reconfigurable or deformable features can better adapt to complex environments and various tasks through mode switching. Xu et al. [
15] proposed a metamorphic parallel leg mechanism with a reconfigurable moving platform, which evolves from a full configuration state to a specific configuration state by increasing constraints or decreasing DOFs. Zhang et al. [
16] designed a 4-DOF parallel bipedal robot mechanism that adopts an improved virtual chain method for type synthesis, optimizes the hip joint design, and designs the lower limb mechanism based on the humanoid principle. Zhao et al. [
17] proposed a 3-DOF serial-parallel hybrid leg design. It optimizes the leg structure of a quadruped robot by combining the advantages of the large workspace of the serial mechanism and the high stiffness and load-carrying capacity of the parallel mechanism. These studies have mainly focused on basic theoretical issues, such as structure design, kinematic modeling, and dynamic analyses of parallel or hybrid robots. However, there are issues with complex mechanisms and redundant drivers, resulting in heavy system weight, high costs, and complex controls.
An et al. [
18] studied the dynamic behavior of an integrated crawler mobile parallel robot under obstacle-crossing conditions, such as climbing steps, spanning gaps, and climbing slopes, analyzing its kinematic stability, contact force variations, and slippage rate fluctuations. Li et al. [
19] designed a multi-modal mobile robot based on a quadrupedal parallel mechanism, with branching variations. The robot has three locomotion modes: leg mode, wheel mode, and tracked mode, and seven gaits: tracked rolling, stair and slope climbing, gap crossing, trot walking, fast moving, and direction-switching gait. Zhao et al. [
20] proposed a self-reconfigurable dobby robot mechanism design method based on deployable kinematic chains (DKCs). Niu et al. [
21] proposed a wheel-legged rescue robot with a (2-UPS + U)&R series-parallel structure. The structure modeling and kinematic characteristics of the robot were presented. The leg mechanism can meet the requirement of walking in the unstructured environment. Ping et al. [
22] designed a multi-mode mobile parallel mechanism with a deployable platform for patrolling and monitoring industrial substation areas. Ushimi [
23] developed a four-wheeled reconfigurable mobile robot for sloping terrain that adjusts its body attitude and center of gravity by means of a parallel linkage mechanism and four active legs to avoid wheel slipping and overturning. Zhao et al. [
24] proposed an inverted modeling method to support motion planning for footed robots. Pan et al. [
25] investigated the computational complexity of the kinematic model of a hexapod robot with two 1UP-2UPS parallel mechanism topologies. Although these studies have provided useful solutions for obstacle-crossing modes, mechanism reconstruction, and environmental adaptability, there are also general problems, such as complex mode-switching mechanisms, low reliability, and difficulty of maintenance.
Wheel-legged robots have made significant progress in lightweighting, biomimetic gait, and stability assessment. Hao et al. [
26] designed a single-leg walking mechanism for a quadruped robot, which is composed of a crank rocker mechanism and scaling mechanism in series. The advantages of the single-leg walking mechanism are fewer driving elements, more simple design, and high gait stability. Chamas et al. [
27] proposed a stabilization scheme for unmanned aerial vehicle platforms based on a 3-SRR parallel mechanism. They introduced an artificial neural network control strategy, significantly improving the stability and accuracy of the system under complex disturbances. Liu et al. [
28] and Tazaki et al. [
29] both pursued lightweight, multi-modal locomotion: the former presented a two-segment series-parallel worm robot that combines straight-line, lateral, and peristaltic gaits, while the latter embedded all six actuators in the torso to minimize the leg inertia of a 6-DOF parallel-link bipedal leg. Xu et al. [
30] proposed a gait analysis method for a radially symmetric hexapod robot based on a parallel mechanism. Liu et al. [
31] presented a hexapod walking machine tool for kinematic calibration, which is composed of a six-legged robot integrated with a parallel manipulator on the body. Through the inverse kinematics bias-based objective function optimization method, the hexapod robot and its parallel manipulator showed improved kinematic accuracy. Fu et al. [
32] introduced a dynamic stability assessment method called moment ratio stability margin (MRSM). Pan et al. [
33] analyzed the fault tolerance and walking capability of a parallel hexapod walking robot, defined the leg fault tolerance criterion, and demonstrated the robot’s capability to walk in the case of fault tolerance failures of a single leg or both legs.
Despite extensive theoretical research on wheel-legged robots based on parallel mechanisms, there are still some technical challenges. Existing robots often struggle to balance their adaptability to complex terrains with structure compactness, especially in terms of multi-mode motion switching.
Unlike existing research, this study proposes a novel 2-UPS&PRPU parallel mechanism used for mechanical legs and constructs a six-wheel and four-leg robot, abbreviated as 6W4L robot. The auxiliary devices added to the mechanical legs enable it to freely switch between wheels and legs, greatly improving its ability to navigate in changing terrain environments.
The remainder of this article is organized as follows. In
Section 2, a novel 2-UPS&PRPU parallel mechanism is proposed to improve the mobility of mobile robots in complex terrain environments.
Section 3 details the kinematic analysis of the parallel mechanism.
Section 4 presents the performance analysis, including a dexterity analysis, carrying capacity analysis, and dimension optimization. An application example is provided in
Section 5. The conclusions are drawn in
Section 6.
2. Configuration Analysis
2.1. Configuration of 2-UPS&PRPU Parallel Mechanism
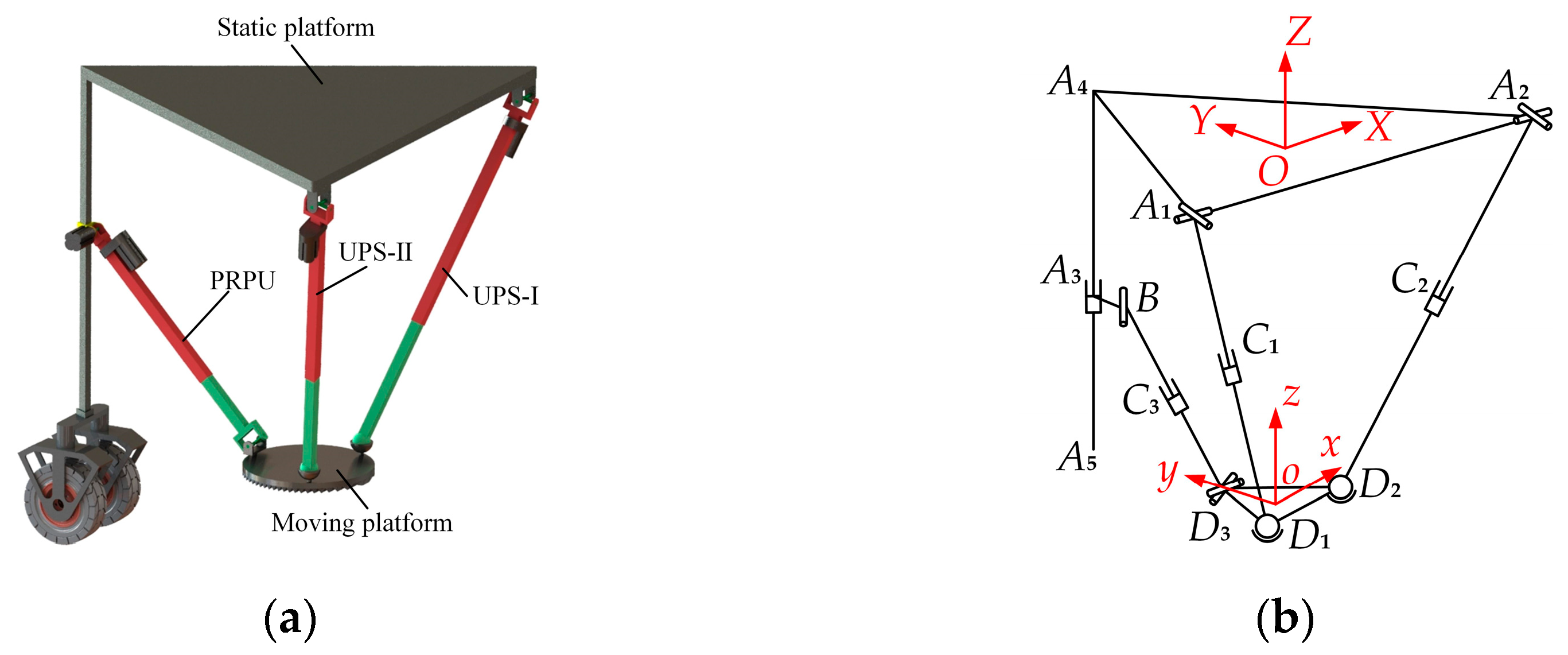
The designed 2-UPS&PRPU parallel mechanism with variable DOFs is shown in
Figure 1a. The parallel mechanism consists of a static platform, a moving platform, two UPS branched chains, and one PRPU branched chain. A kinematic diagram of the 2-UPS&PRPU parallel mechanism is shown in
Figure 1b.
The static platform, A1A2A4, is an equilateral triangular structure, and the rod, A4A5, is fixed to vertex A4 of the triangle. The moving platform, D1D2D3, is a circular structure, but the kinematic pairs of the three branched chains connected to the moving platform also form an equilateral triangle.
Hooke joints A1 and A2 of the two UPS branched chains are connected to the static platform, and the spherical pairs D1 and D2 are connected to the moving platform. In the PRPU branched chain, the first prismatic pair, A3, moves along A4A5, the Hooke joint D3 is connected to the moving platform, and revolute pair B is fixed to A3.
The coordinate system (O-XYZ) of the static platform is fixed. The coordinate origin, O, is fixed at the geometric center of the static platform with an equilateral triangle, the X-axis is parallel to A1A2, pointing from A1 to A2, the Y-axis passes through vertex A4 of the triangle, and the Z-axis is upwardly perpendicular to the static platform.
The coordinate system (o-xyz) of the moving platform is also fixed. The coordinate origin, o, is fixed at the geometric center of the moving platform, the x-axis is parallel to D1D2, pointing from D1 to D2, the y-axis passes through vertex D3, and the z-axis is upwardly perpendicular to the moving platform.
2.2. DOFs Calculation of 2-UPS&PRPU Parallel Mechanism
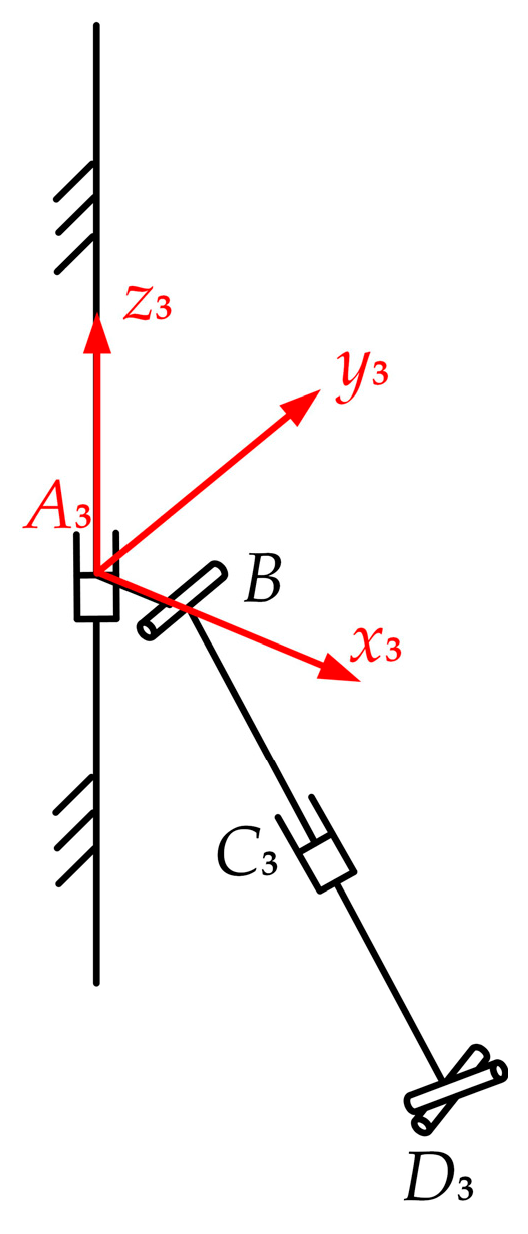
Screw theory is used to determine the DOFs of the 2-UPS&PRPU parallel mechanism. For the PRPU branched chain, the branched-chain coordinate system
A3-
x3y3z3 is established, and the origin of the coordinate system is located at the
A3,
x3 prismatic pair axis, which is perpendicular and points in the direction of the branched chain. The
z3 axis is upward along the guide of prismatic pair
A3, and the direction of the
y3 axis is determined using the right-hand rule, as shown in
Figure 2.
The PRPU branched chain’s helical system of motion in this coordinate system can be expressed as:
where
f12 represents the torque of the spherical pair
B in the
z3 axis direction in
Figure 3,
d13 and
f13 represent the torques of the prismatic pair
C3 in the
x3 and
z3 directions,
d14 and
f14 represent the torques in the
x3 and
z3 directions of the spherical pair parallel to
y13 in Hooke joint
D3,
a15 and
c15 represent the direction cosine of the spherical pair in the
x3 and
z3 directions, which is not parallel to
y3 in Hooke joint
D3, and
e15 represents its torque in the
y3 direction.
According to the reciprocal product relationship of the twist between the motion and constraint, the constraint twist of Equation (1) can be determined as follows:
The PRPU branched chain is subject to two constraint twists in this state, which constrain the movement of the Hooke joint U end of the PRPU branched chain along the
X-axis direction and the rotation axis perpendicular to the rotation axis of the Hooke joint U end. Similarly, we can establish the coordinate system of the 2-UPS branched chain to analyze the motion helix, determining its motion helix as follows:
The expression of the parameters in Equation (3) is similar to that of the parameters in Equation (1).
Analyzing the helix in Equation (3) shows that its rank is 6, and there is no constraint helix, meaning that the branched-chain UPS has a spatial 6-DOF kinematic performance. In summary, the analysis of the three branched chains connecting the moving platform shows that the 2-UPS&PRPU parallel mechanism has four DOFs in this mode in one case. However, it cannot achieve movement along the X-axis and, at the same time, it cannot rotate around the axis perpendicular to the end face of the Hooke joint U end at point D3.
The DOFs of the parallel mechanism can be calculated based on the modified Grübler–Kutzbach equation:
where the order of the parallel mechanism is
d = 6, the number of all the rods in the mechanism (including the frame) is
n = 9, the number of kinematic pairs in the mechanism is
g = 10, all the kinematic pairs form 17 DOFs, and there are no redundant constraints in the mechanism (
v = 0). Since the revolute pair R in the PRPU branched chain and one of the Hooke joints in the rotating axes of the mechanism are parallel during the motion process, the local DOF is
δ = 1.
Thus, our analysis and validation show that the 2-UPS&PRPU parallel mechanism has a total of 4 DOFs.
3. Kinematic Analysis
3.1. Inverse Solution Calculation
As shown in
Figure 1b, since the 2-UPS&PRPU parallel mechanism has four DOFs, we need to provide at least four drives for the mechanism to achieve the motion function of the mechanism. Therefore, we set the variations of four prismatic pairs as the mechanism drives, including the length
li (
i = 1, 2, 3) of the rod
AiDi (i = 1, 2) and
BD3, and the length
l4, which represents the displacement
A3A4 of the driving pair
A3 in the rod
A4A5.
The inverse solution problem of the 2-UPS&PRPU parallel mechanism is to solve the length li (i = 1, 2, 3) of the equivalent driving rod for given position parameters and orientation parameters (x, y, z and α, β, γ) of the moving platform.
The rotation angle of the revolute pair
B around the
X-axis is denoted by
θ. The side length of the static platform is 2
R, and the side length of the moving platform is 2
r. The prismatic pair
A3 and the revolute pair
B in the branched-chain PRPU are solidly connected, and the distance
k between the two is fixed. The parameters of the static platform can be expressed in the static coordinate system as:
The coordinates of the moving platform in the moving coordinate system are expressed as:
Based on the fixed coordinates, the coordinate transformation of the moving coordinates is based on the
X-Y-Z-type mode with the transformation matrix
where c represents cos, and s represents sin.
The transformation of the coordinates of the moving platform in the fixed system can be expressed as:
where
P represents the relative position of the coordinate origin of the moving platform relative to the fixed coordinate system of the static platform.
To facilitate calculations, the transformation matrix
T is abbreviated as:
The parameters in Equation (9) correspond to the parameters in Equation (7). Substituting these parameters into Equation (8) yields:
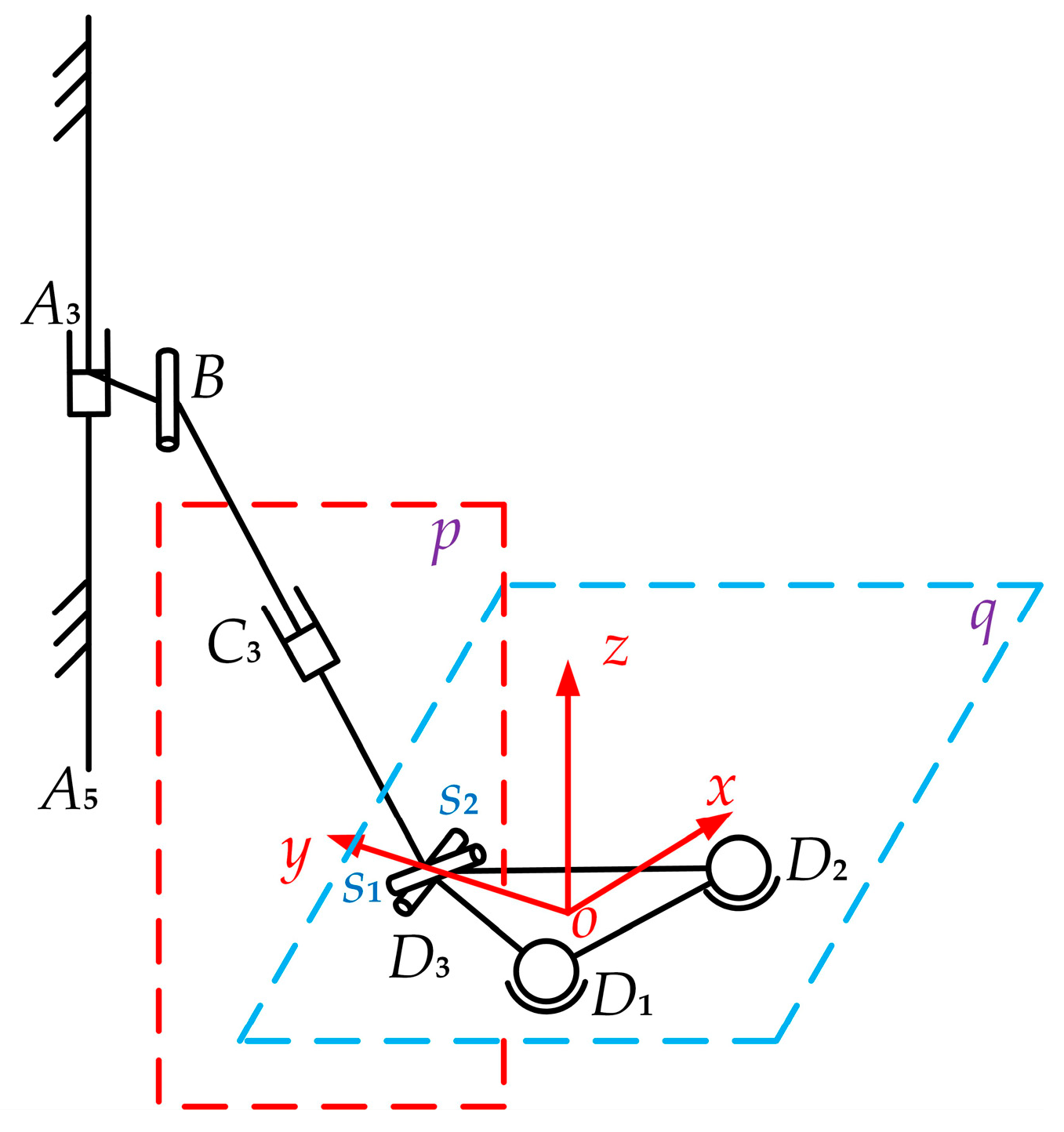
According to the closed-loop vector method, the length of each rod can be determined as the modulus of its endpoint vector. Due to structural constraints, the transverse coordinate of OD3 should be 0. After the above analysis, the lengths l1 and l2 can be obtained by calculating the position of the end piece, but the θ angles of l3 and l4, as well as revolute pair B, are still undeterminable. However, only two of the three unknowns need to be determined to determine the third.
According to the structural properties of Hooke joint
D3, its two rotating axes are perpendicular to each other. In
Figure 3,
D3 connects the PRPU branched chain and the moving platform. Since the PRPU branched chain moves up and down along vertical guide
A4A5 in the static platform, its motion plane is plotted as the
p-plane in
Figure 3. One rotation axis,
s2, in
D3 moves in the
p-plane, and the direction of the
s1 rotation axis is related to the angle of rotation (
θ) of the R pair in the PRPU branched chain. After the center of
D3 is parallel to the moving platform, determining a plane
q, combined with the mechanism model in
Figure 1a, another rotation axis (
s2) of
D3 is parallel to the
x-axis of the coordinate system of the moving platform. This changes with the motion of the moving platform, but the relative position remains unchanged. The rotation axes
s1 and
s2 are always perpendicular to each other, and do not change with the movement of the mechanism.
The initial direction of vector
s2 is
s2 = (1, 0, 0), and its coordinates in the fixed coordinate system will change with the motion of the moving platform:
For the PRPU branched chain, the prismatic pair
A3 and the revolute pair
B are always in the same horizontal position, and it is assumed that the change in revolute pair
B is expressed through the angle between the connecting rod of the PRPU and the vertical rod of the fixed platform. Thus,
where
θ is the angle between
BD3 and
A4A5.
The mutual perpendicularity of the two rotation axes of the Hooke joint can be obtained as:
Equation (11) shows that the rotational drive of the PRPU branched chain is only related to the angles of the end pieces around the Y- and Z-axes. In this example, we assume that the angles of the end pieces around the X- and Y-axes are independent, and the angle around the Z-axis is non-independent.
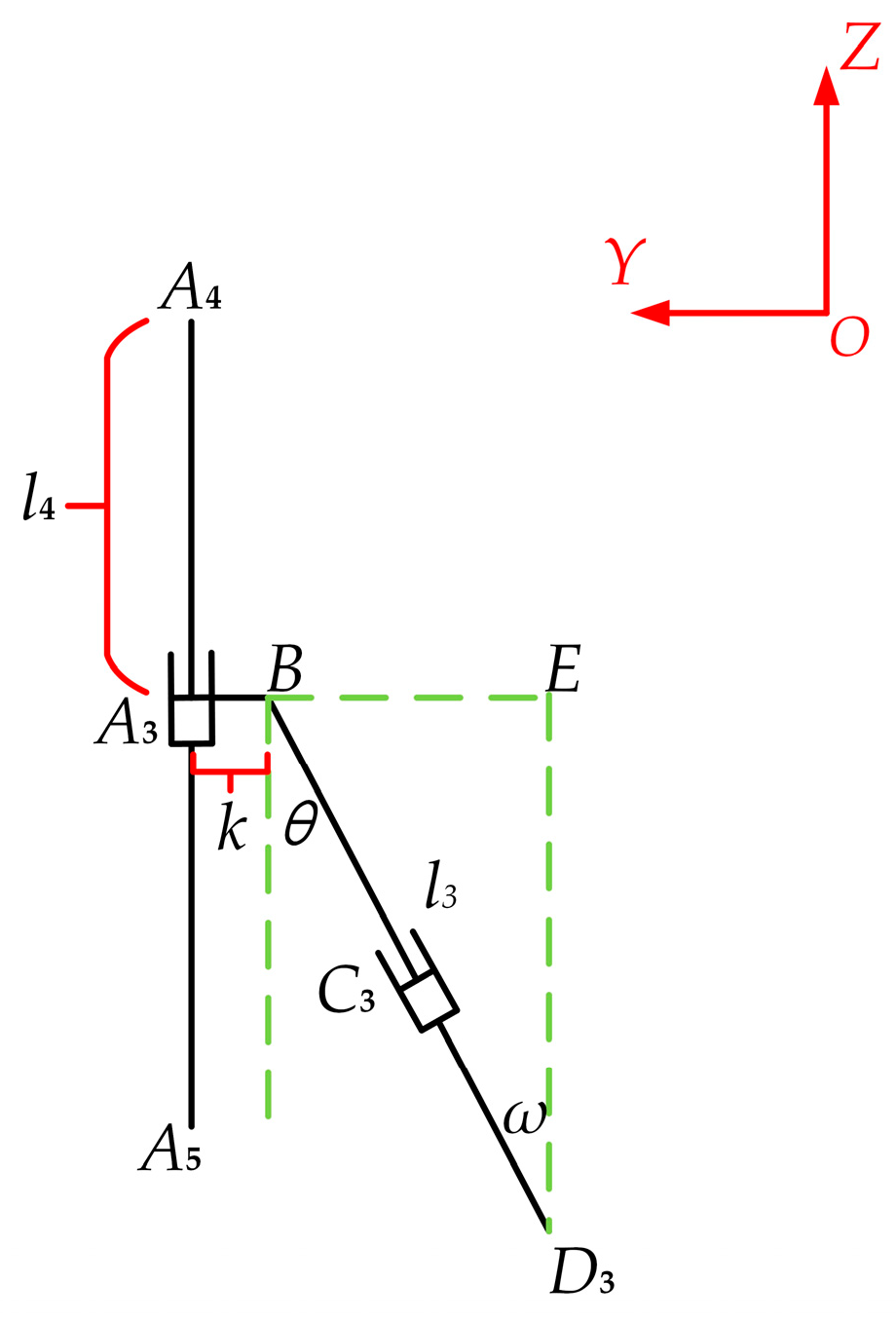
The lengths of
l3 and
l4 and the known coordinate parameters of point
D3 can be determined with the positional display in
Figure 4, as follows:
In the mechanism end piece around the fixed coordinate system of the three rotation axes for (
α β γ)—where two are independent and one non-independent—we can determine that
α and
β are independent; now, we can analyze the relationship between the three angles of rotation.
α is the tangent value angle of the origin of the dynamic coordinate system and the difference in point
D3 in the
Z-axis. It is also the projected difference in the value ratio of the
Y-axis. It is determined through simplification:
In summary, the inverse solution drive solution equation for the 2-UPS&PRPU parallel mechanism can be obtained as follows:
where
t11 = c
βc
γ,
t12 = s
αs
βc
γ−c
αs
γ,
t21 = c
βs
γ,
t22 = s
αs
βs
γ + c
αc
γ,
t31 =
−s
β, and
t32 = s
αc
β:
In addition, l4 can be determined according to Equation (15). Therefore, the mechanism has four drive inputs, three prismatic actuations, and one revolute actuation, and the four outputs are the YZ coordinates of the moving platform and rotations around XY.
3.2. Singularity Analysis
In the process of movement, the parallel mechanism may appear to be a singular configuration. However, a singular configuration will change the DOFs, such that motion coherence is reduced. Therefore, singularity analysis of parallel mechanisms is particularly important. In the following, we use the properties of the Jacobian matrix of the mechanism to analyze its singularities:
where
denotes the input drive velocity of the mechanism,
v represents the output velocity of the moving platform,
Jq represents the input Jacobian matrix of the mechanism, and
Jp represents the output Jacobian matrix:
According to Equation (17), the mechanism undergoes positional singularity when θ is equal to 0° and 90°. Below, we detail the two singular configurations that have appeared.
The Hooke joint will have different kinematic properties in different postures owing to its special characteristics. In the PRPU branched chain of the 2-UPS&PRPU parallel mechanism, one of the Hooke joints changes with the branched chain’s postures, and the moving rod, BD3, passes through the center of this Hooke joint at point D3. It perpendicularly lies in the plane formed by two rotating pivots in the Hooke joint. Since the UPS branched chain does not provide constraints on the moving platform, the variation in the DOFs of the moving platform mainly relies on the PRPU branched chain.
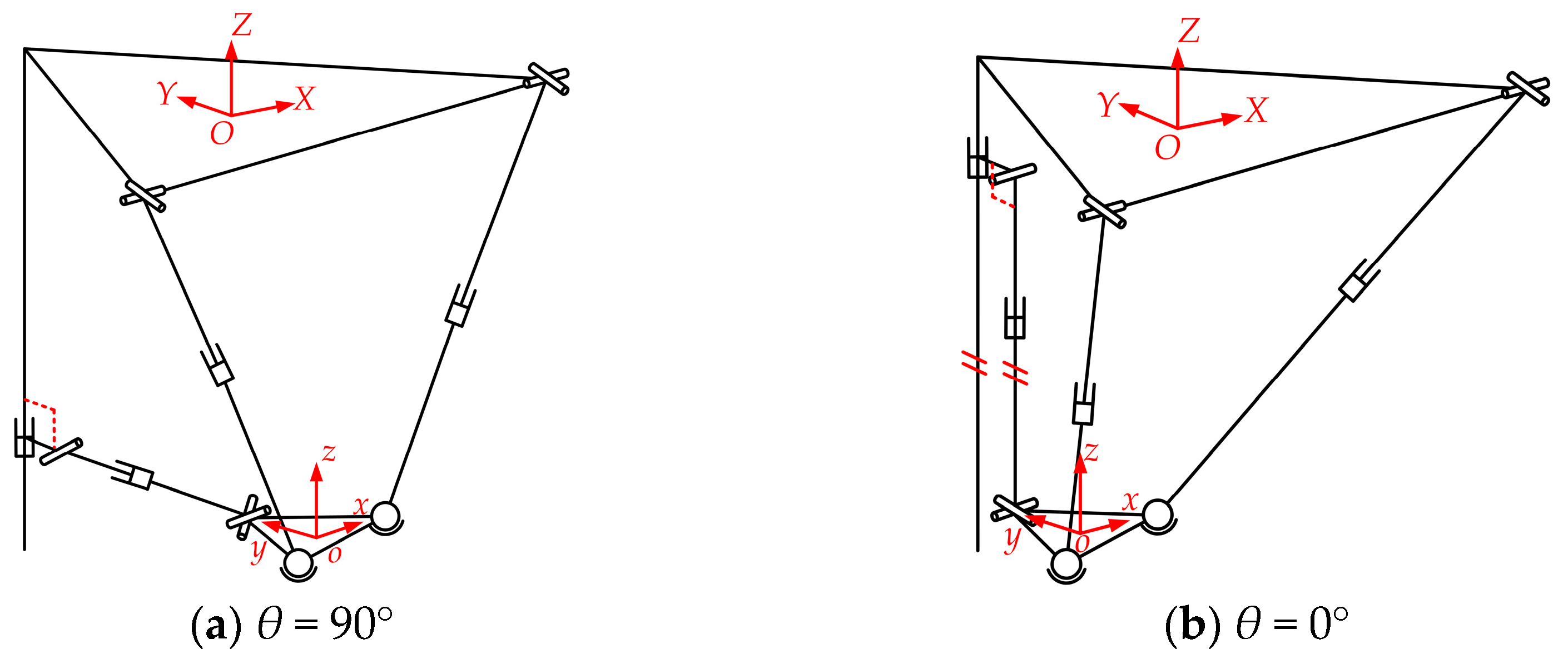
According to the different positions of the PRPU branched chain—i.e., the axis where BD3 is located is at a different angle to the static platform in the branched chains—the structural modes of the mechanism are divided into three cases. When the angle between BD3 and the static platform is anything other than 0° and 90°, it is the normal mode, when BD3 is parallel to the static platform, it is in mode II, and when BD3 is perpendicular to the static platform at 90°, it is in mode III. Modes II and III are the singular pattern cases when θ is equal to 0° and 90°.
Mode I is the normal mode.
Figure 5 shows two singularity position patterns of the 2-UPS&PRPU parallel mechanism during the motion process. These two singular patterns also have four DOFs, but their modes are different.
Figure 5a shows the state of mode II, and
Figure 5b shows the state of mode III.
When the mechanism is in mode II, the singularity position type, the moving rod of the PRPU branched chains is parallel to the static platform. At this time, the parallel mechanism still has four DOFs, the Hooke joint of branched chain 3 is in a vertical state, and the moving platform cannot move along the X-axis or rotate around the Y-axis because of the constraints caused by branched chain 3. When applying this mechanism to the branch legs of a mobile robot, this situation arises due to its inability to rotate around the Y-axis. In uneven lateral road conditions, the moving platform may only have partial contact with the ground while the other part is suspended, which can cause uneven force on the left and right support chains of the parallel mechanism, affecting the stability of the robot’s movement. However, this state is conducive to turning under smooth road conditions.
When the mechanism is in the singularity position of mode III, the moving rod in the PRPU branched chain is perpendicular to the static platform. At this time, the parallel mechanism still has four DOFs, the Hooke joint of branched chain 3 is in a horizontal state, and the movable platform is constrained by the branched chain 3, unable to move along the X-axis or rotate around the Z-axis. When applying this mechanism to the branch leg of a mobile robot, this situation arises due to its inability to rotate around the Z-axis. In this state, the robot cannot turn. Owing to the vertical force concentration of the PRPU branch, the service life of the rod will be reduced. Moreover, the PRPU branched chain will be too close to the A4A5 branch, and improper control can also cause collisions between the rods, increasing the requirement for control accuracy. Therefore, in practical processes, this position should be avoided as much as possible.
3.3. Workspace Analysis
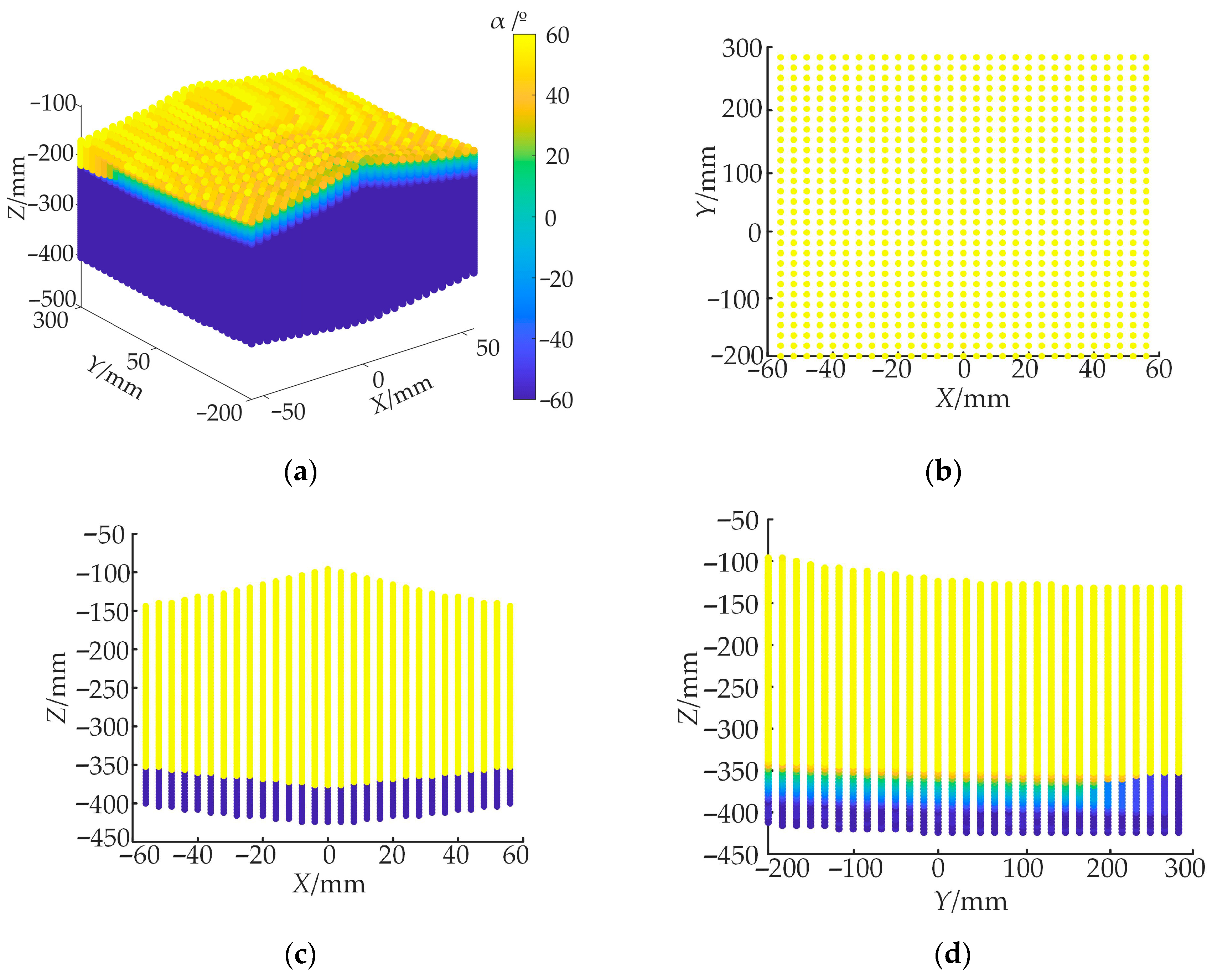
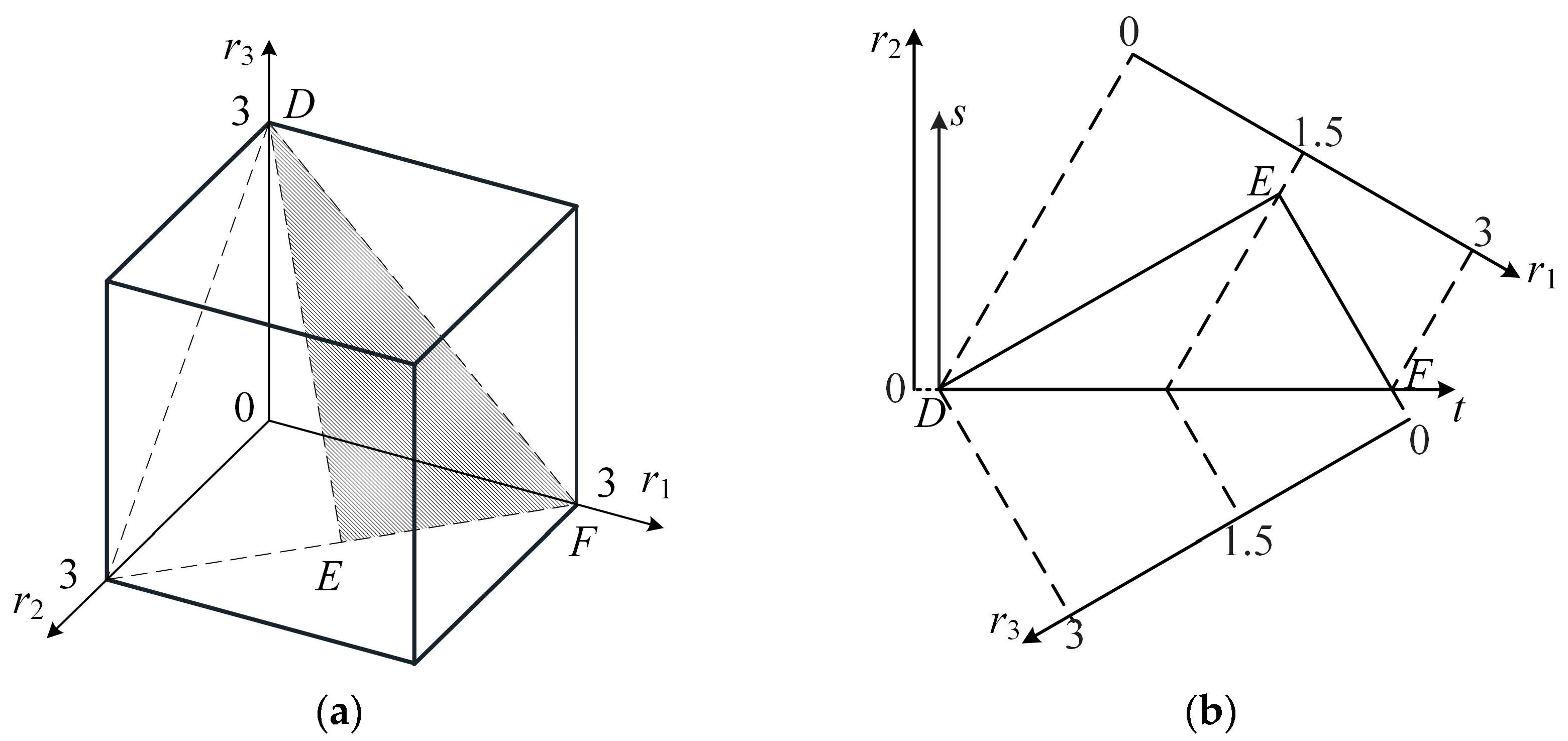
Below, we carry out a workspace analysis for the case of non-singular positions. The workspace of the mechanism can directly illustrate the spatial range that can be reached by the end-effector of the mechanism. Assuming the initial parameters of the parallel mechanism (R = 200 mm, r = 50 mm, and k = 10 mm), since the contact end of the PRPU branched chain and the static platform can achieve different structures in several positions, we first analyze its specific position, i.e., when l4 = 250 mm.
The maximum angle between the thigh and vertical direction during human and animal stepping is representative of the stepping ability of parallel mechanisms, such as moving legs; thus, the rotational angle
θ of the PRPU branched chain was considered as 60°. Due to the application of parallel mechanisms in the branched legs of mobile robots, we aim to achieve forward and backward movement, whereas a set of human leg movements requires lifting, extending, and landing. To complete these movements in this design, the parallel mechanism aims to achieve rotation around the
X-axis and movement in the
Y-
Z plane. Therefore, certain rotations were overlooked in the simulation design, and we can assume that the rotation angles of the end effector around the
Y- and
Z-axes are both 0. Given these mechanism parameter settings, the workspace of the mechanism can be obtained, which is shown in
Figure 6.
The workspace under specific conditions is shown in
Figure 6a, demonstrating the position of the end actuator of the mechanism in the
X-Y-Z axis direction and its rotation around the
X-axis. Its working range meets the working requirements when installed on both sides of the 6W4L robot, and the movement along the
X-axis direction can realize the robot’s forward torsion.
Figure 6 shows that the parallel mechanism has a large moving space in different directions, which can meet the walking space range of the mobile robot; furthermore, the overall space change area is smooth, verifying the feasibility of the parallel mechanism.
5. Application Example
Four sets of 2-UPS&PRPU parallel mechanisms were installed at the four corners of a square loading platform as four supporting legs. Four sets of parallel double wheels were installed at the lower end of the vertical rod of each parallel mechanism. A rubber protective layer was laid at the lower end of the moving platform.
Due to the instability in the robot’s overall center of gravity caused by it having only four sets of wheels, two auxiliary foldable supporting legs were installed at the middle position of the front and rear ends of the loading platform, and a set of parallel dual wheels was also installed at the end of the auxiliary supporting legs. The auxiliary supporting leg structure is shown in
Figure 13. The six-wheeled–four-legged hybrid mobile robot is shown in
Figure 14, abbreviated as 6W4L.
As shown in
Figure 14a, when the 6W4L robot moves on flat terrain, the moving platform of the parallel mechanism is lifted, and only six sets of wheels touch the ground. The robot is in wheel mode, with the auxiliary supporting legs in an extended state and in contact with the ground. The robot can move rapidly, and auxiliary steering devices that control left and right rotation can be installed on the wheels to achieve steering of the mobile robot.
In this state, the mobile robot mainly relies on six wheels for movement. The driving state relies on the support of the end wheels of the auxiliary foldable legs. These two wheels can control the forward and backward steering of the mobile robot, and the folding changes of the auxiliary foldable legs can be controlled by hydraulic pressure. The four moving wheels integrated with the parallel mechanism do not have power devices installed and only play a supporting role. When moving in this state, the square platform above can carry goods, and the load distribution is uniform. Two of the six wheels are located at the front and back, and four are located on the left and right, which also play a role in preventing tipping.
As shown in
Figure 14b, when the robot needs to navigate rough terrain or turn, the parallel mechanism feature is utilized. Four sets of 2-UPS&PRPU parallel mechanism moving platforms serve as supporting legs to lift the robot and shift it into leg mode, with the auxiliary supporting legs in a retracted state. In this state, the robot can navigate through complex road conditions. The movement of the parallel mechanism rotates the end platform around the
Z-axis to achieve turning of the 6W4L robot.
Due to the retraction of the auxiliary supporting legs, the 6W4L robot relies on four parallel mechanisms to move. Each parallel mechanism is driven by four motors, as shown in
Figure 1a, which control the position of the moving platform in space to move the robot. This state requires adjusting the postures of the four parallel mechanisms based on the quality of the transported goods and their position on the square platform. When the robot moves, one of the four parallel mechanisms needs to be lifted, while the other three serve as support. At this time, these three parallel mechanisms must be adjusted to control the robot’s center of gravity such that it is within the range of the triangle formed by the three parallel mechanisms on the moving platform. This characteristic should also be ensured during the movement process, in order to ensure the smoothness of the robot’s movement in this state.
At present, the design of parallel mechanisms applied to wheel-legged robots mostly bundles the moving wheel with the parallel mechanism; that is, the moving wheel is fixed to the moving platform, and the moving wheel changes with the position of the parallel mechanism’s moving platform. This design means that the moving wheels cannot independently support the mobile robot in walking if the parallel mechanism fails. If the moving wheel malfunctions, it will also seriously affect the pose changes in the parallel mechanism. This design integrates the wheel mode and leg mode. When both mobile modes have no faults, switching between them can be achieved. When one mobile mode fails, it does not affect the operation of the other, making the two modes a backup solution for each other and avoiding system failure caused by single-mode failure.
The 6W4L robot was simulated using the parameters set in
Section 3.3. The initial distance between the wheel contact surface and the robot’s cargo platform was set to 260 mm. Since
θ was set to 60°, this caused a change in the angle
α, as shown in
Figure 6. At this point, we do not consider the rotation of the parallel mechanism’s end around the
X-axis; instead, we only consider the spatial positions that its end center can reach. As shown in
Figure 14, the 2-UPS&PRPU parallel mechanism serves as one of the 6W4L robot’s supporting legs, primarily enabling the robot’s forward and backward movements. Therefore, we analyzed the movement of a set of parallel mechanisms within the
Y-Z plane.
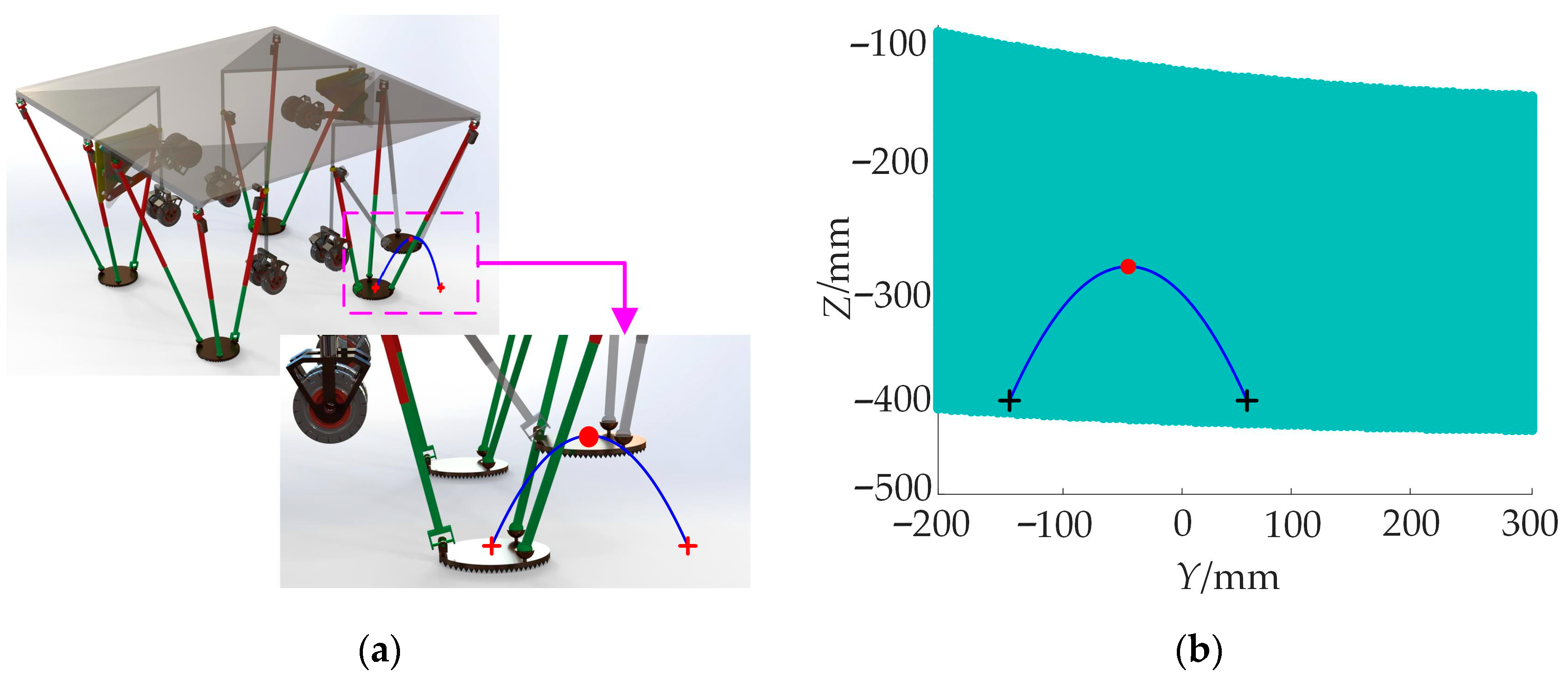
For the step-path-planning analysis of the robot’s front leg, due to the constraints of the wheeled linkages, the step length along the
Y-axis was set to 200 mm, and the step height along the
Z-axis was set to 100 mm. The initial position in the
Y-Z plane was set to (60, −400). The results were obtained through software simulation and modeling, as shown in
Figure 15, which shows the stride path plan. The right front leg of the 6W4L robot performs a stride action along the blue trajectory.
Figure 15b moves the proposed stride trajectory into the mechanism’s workspace, indicating that the parallel mechanism can complete the robot’s stride action.
6. Conclusions
We proposed a novel 2-UPS&PRPU parallel mechanism with multi-DOF motion capabilities, which is suitable for movement in complex environments. Firstly, the DOFs of the parallel mechanism were systematically analyzed and verified. After establishing a three-dimensional model and coordinate systems for the parallel mechanism, the closed-loop vector method was used to model and analyze its kinematics. By introducing the motion characteristics of a Hooke joint, the kinematic equations of the mechanism were further derived and, based on this, the Jacobian matrix of the mechanism was solved. Through analysis of the Jacobian matrix, two singular configurations of the mechanism were identified within its workspace. These singular configurations can cause the mechanism to lose its ability to move; thus, they should be avoided as much as possible in practical applications to ensure the stability and safety of the mechanism. Based on the kinematic analysis, combined with the 6W4L robot application scenario, reasonable initial structural parameters were set.
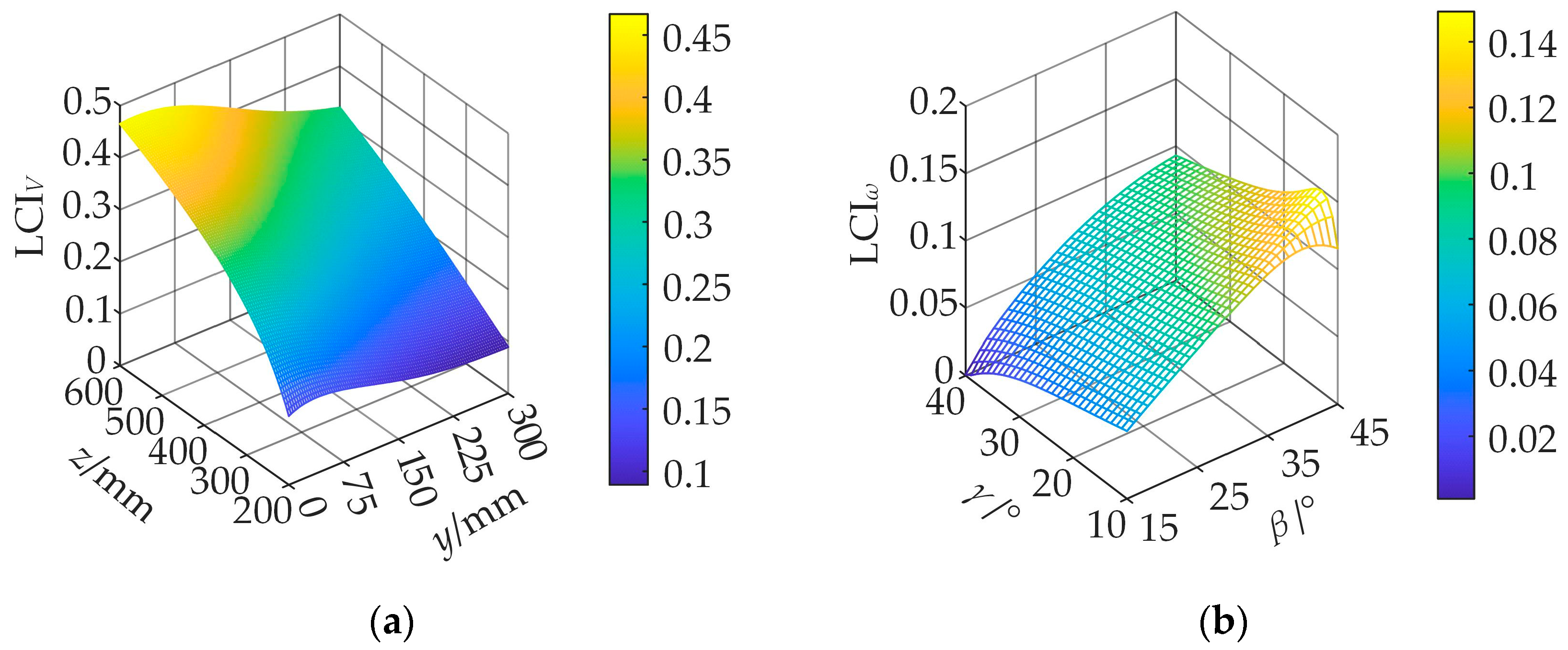
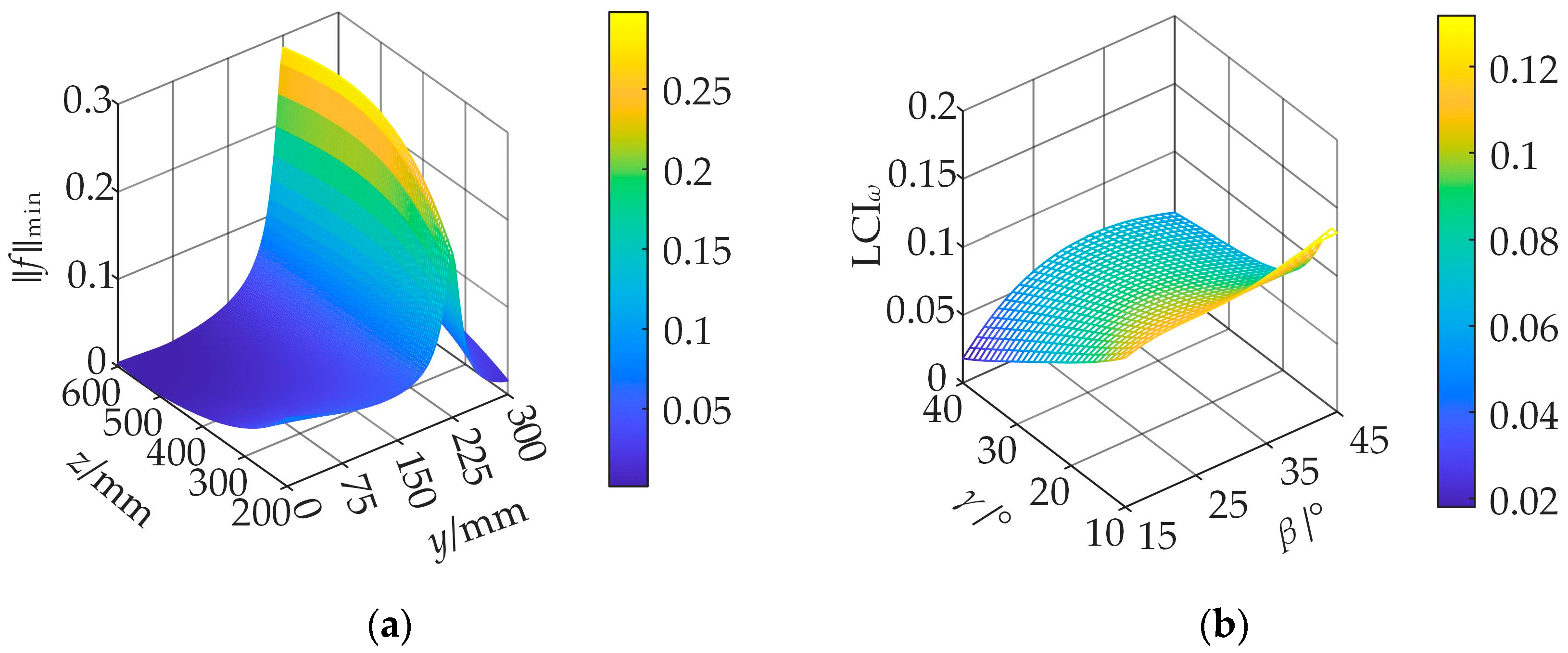
Further analysis was conducted on the workspace of the mechanism under specific postures, evaluating its accessibility and clarifying its applicability and performance boundaries in practical applications. To enhance the overall performance of the mechanism, this study also conducted a systematic analysis of the robot’s agility and load-bearing capacity. Its motion transmission performance was evaluated and optimized by introducing evaluation indicators, such as linear velocity agility and minimum output carrying capacity. The optimization results showed that, through reasonable design, the mechanism presented significantly improved dynamic response capability and load adaptability while maintaining a compact structure.
Finally, the potential application of the 2-UPS&PRPU parallel mechanism in practical engineering was discussed. This mechanism can serve as a mobile robot leg, effectively enhancing the obstacle-crossing capability and motion stability of such robots under rugged terrain conditions, thus presenting good engineering application prospects.