Dynamic Characteristics of a Digital Hydraulic Drive System for an Emergency Drainage Pump Under Alternating Loads
Abstract
1. Introduction
- (1)
- A DHDS suitable for EDPs is introduced. This system adopts the energy transmission mode of hydraulic power source–hydraulic valve group–hydraulic motor–drainage pump. The HSV serves as the pilot control module for the proportional directional control valve, and a composite PWM signal is employed to drive and control its output flow, thereby enabling stepless speed adjustments for the hydraulic motor and enhancing the robustness and dynamic efficiency of drive system.
- (2)
- The mechanical–hydraulic multi-field coupling drive mechanism of a DHDS for EDPs is revealed. A multi-field coupling simulation platform and test platform are constructed, and the output characteristics and dynamic response characteristics of the system under alternating loads are clarified.
2. DHDS Modeling
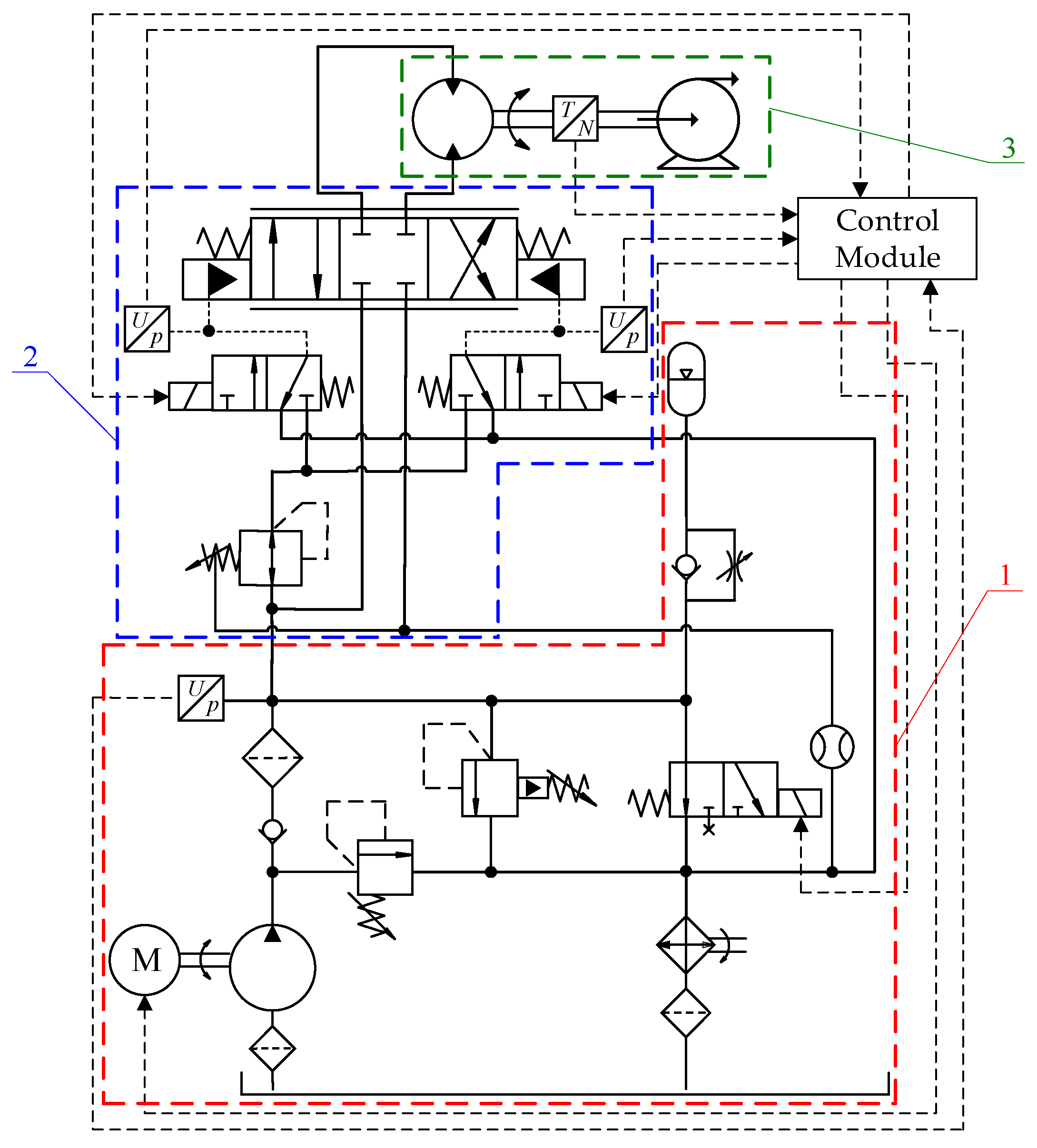
2.1. System Composition and Working Principle
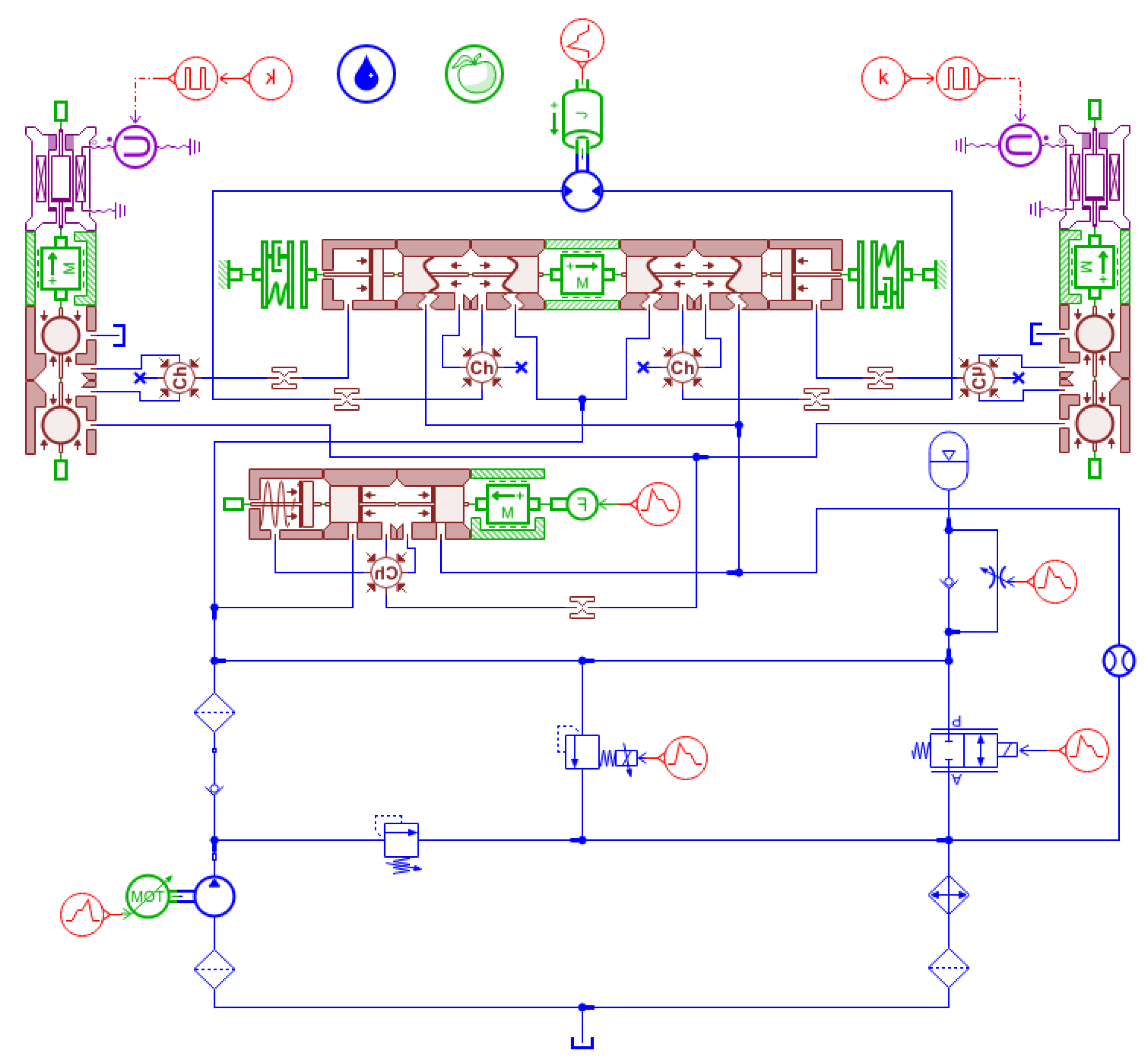
2.2. Modeling of the Hydraulic System
2.2.1. Model of the Power Unit
2.2.2. Model of the Hydraulic Valve Control Unit
2.2.3. Model of the Execution Unit
2.3. DHDS Model Verification
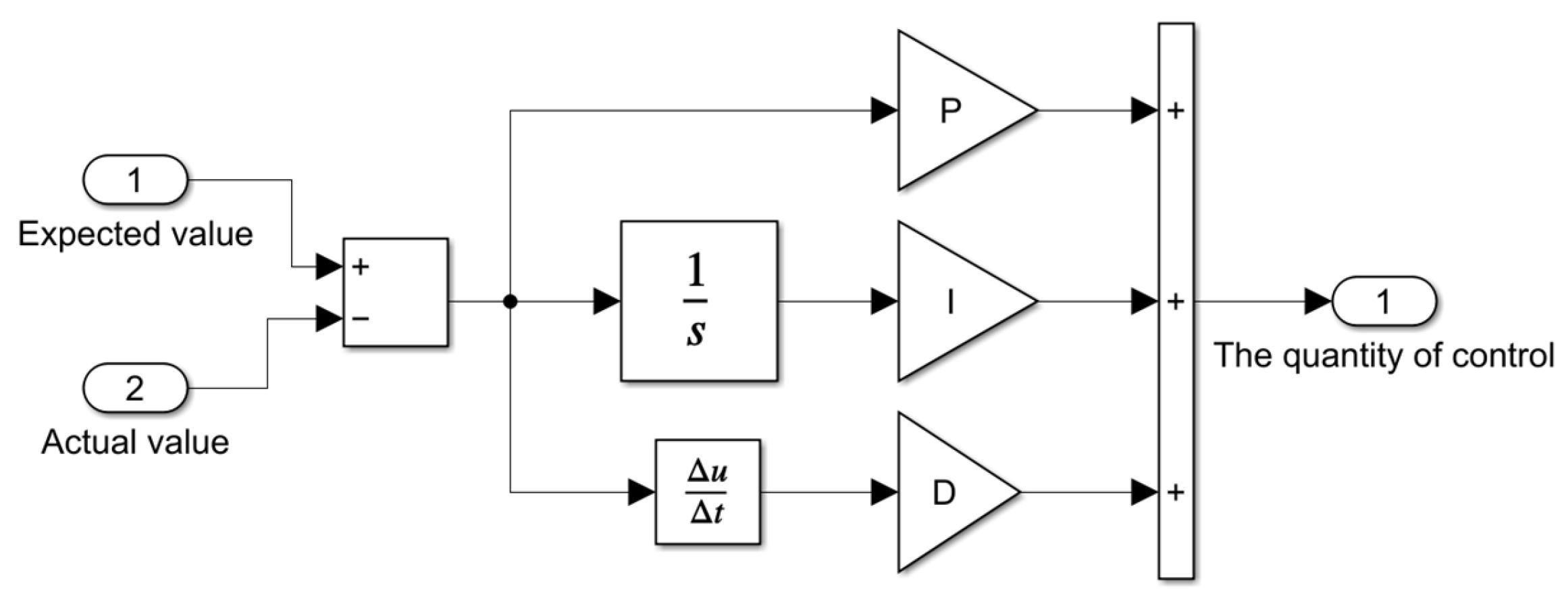
3. Closed-Loop Control Performance Analysis for the DHDS
4. Simulation Analysis of the DHDS Under Alternating Loads
5. Experimental Study
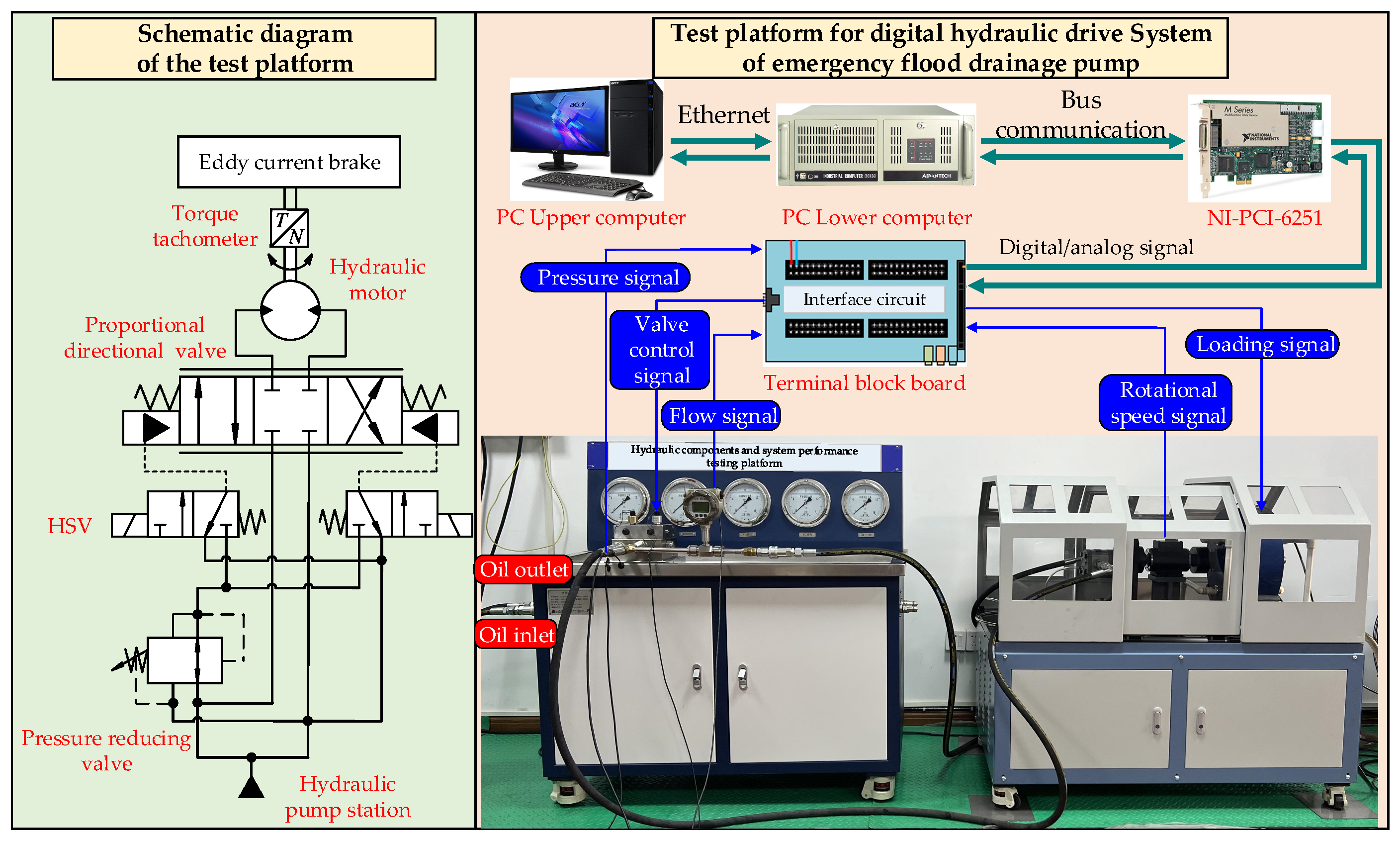
5.1. Test System
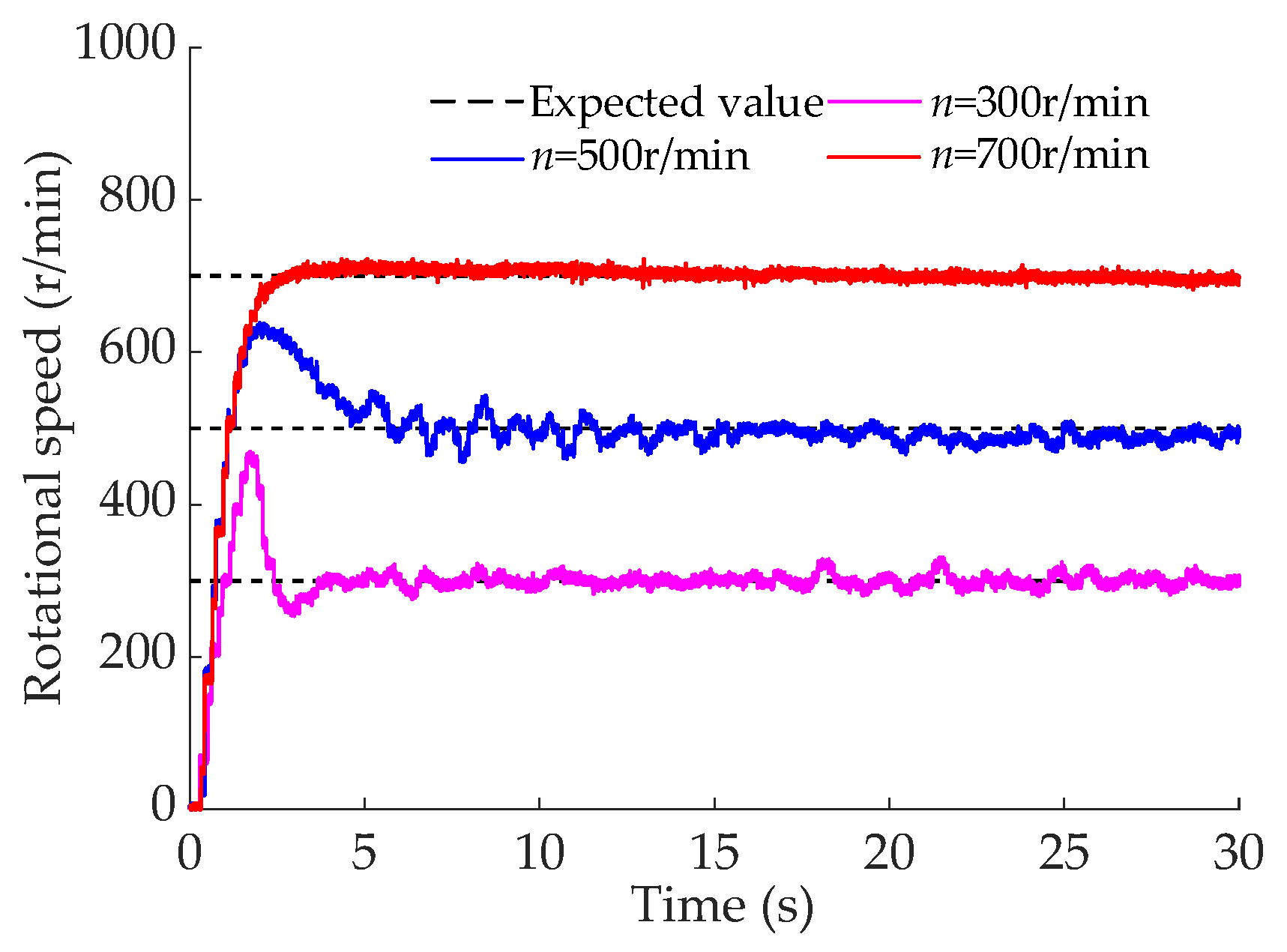
5.2. Closed-Loop Control Performance Test
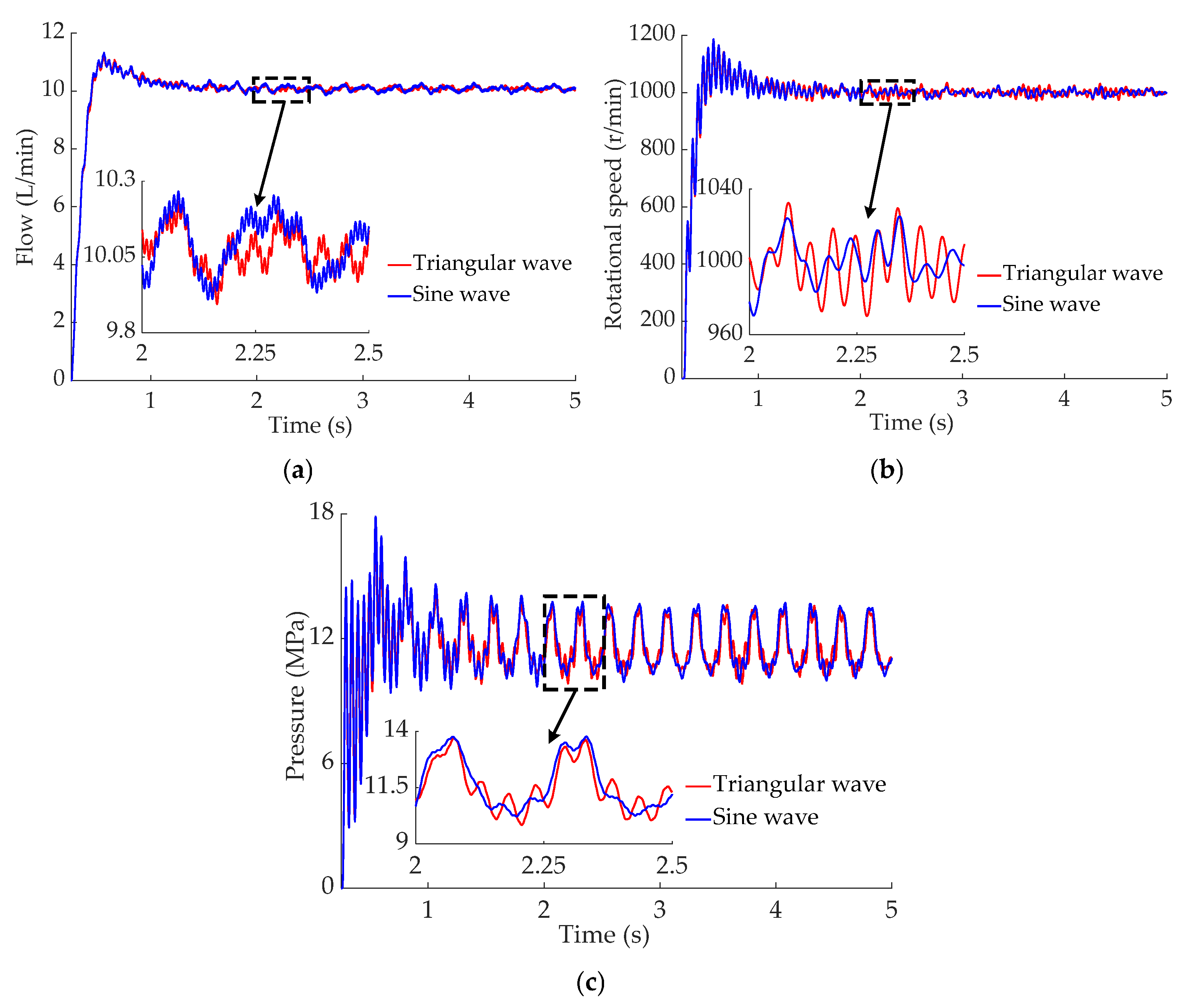
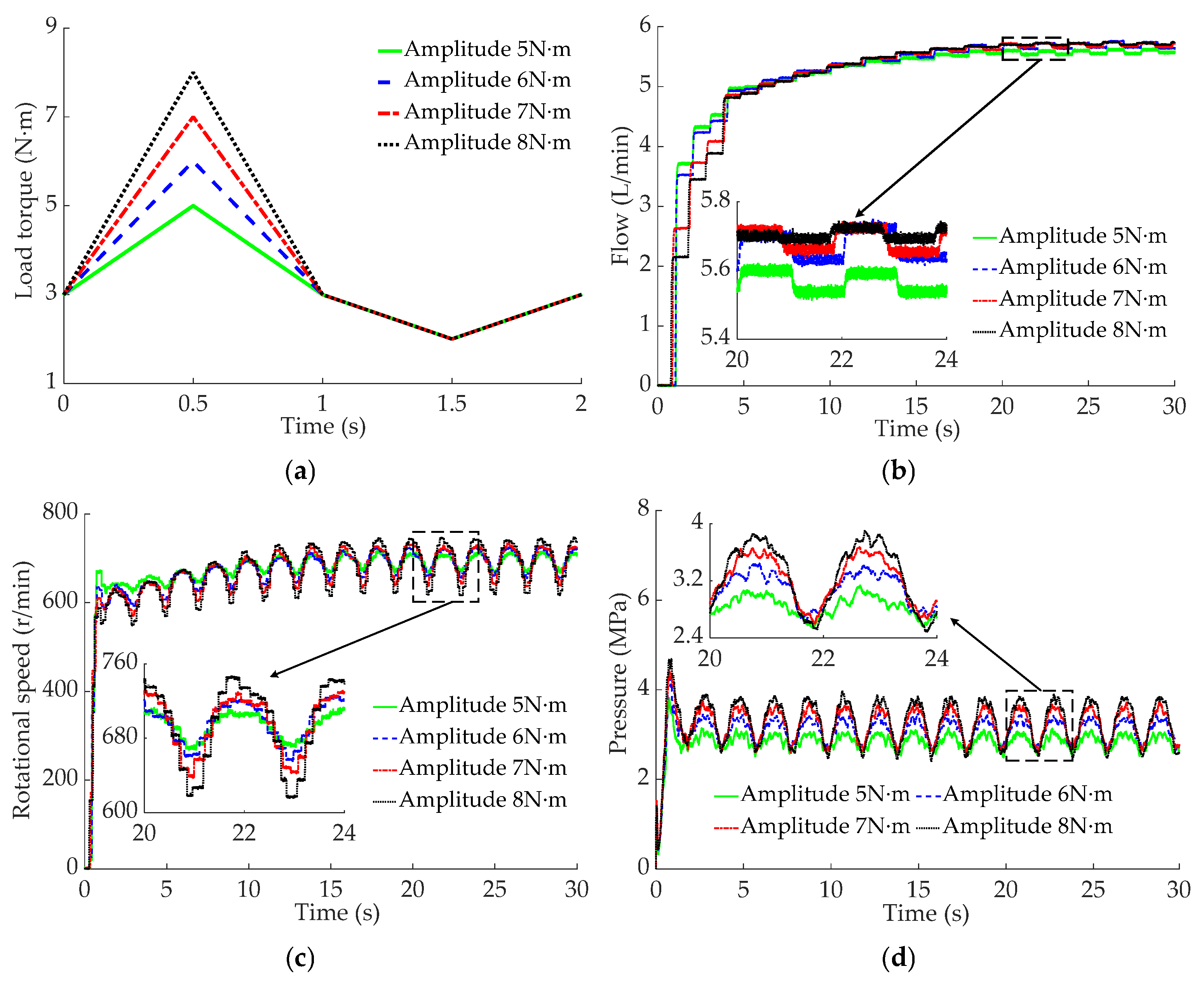
5.3. Alternating-Load Test
6. Conclusions
- (1)
- A hydraulic drive system suitable for use in EDPs has been developed, and the working principle of this DHDS has been expounded. The electromechanical hydraulic multi-field coupling dynamic simulation platform of the DHDS for EDPs was further constructed using AMESim and Simulink, and the dynamic response characteristics of the lumped simulation model have been proven.
- (2)
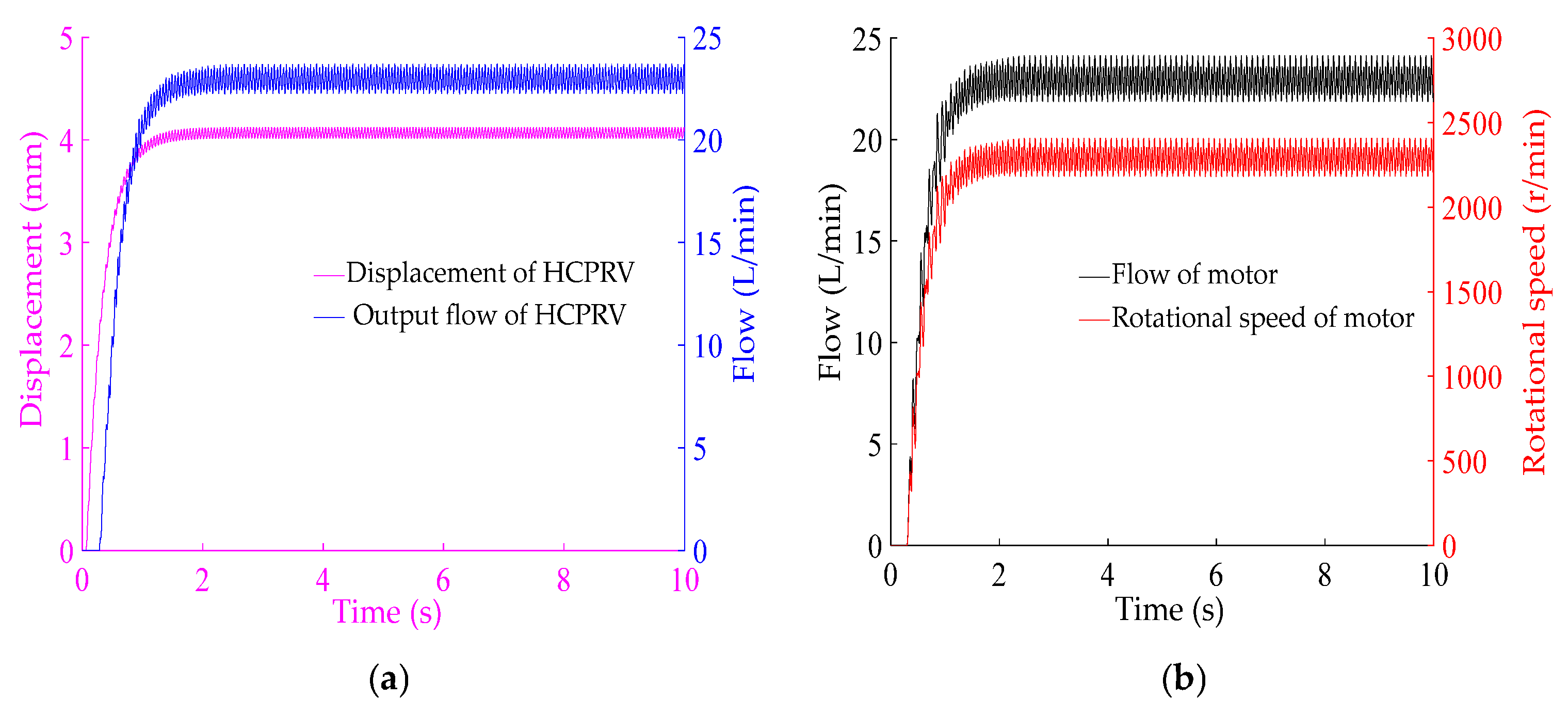
- Based on the custom functions of the MATLAB software, the parameters of multi-condition loads were set. Variable parameters of amplitude, frequency, and waveform of the alternating loads were also set. The dynamic response characteristics and load action law of the DHDS for EDPs under multi-condition loads was explored. The research and analysis showed that the system can respond quickly to changes in the load under variable working conditions and recover to a stable state in a short time, verifying that the system has good anti-interference ability and output stability.
- (3)
- The results of the closed-loop control test showed that when the expected rotational speed is 700 r/min, the overshoot is 2.7%, the stabilization time is 7.1 s, and the stability and followability are good. When tracking square wave signals with amplitudes of 200 r/min and 400 r/min, the overtones are 31.5% and 45.7%, respectively, and the adjustment times are 2.43 s and 2.65 s, respectively. The response characteristics of the square wave signal with an amplitude of 200 r/min are slightly better. When tracking sinusoidal signals with amplitudes of 100 r/min and 200 r/min, the maximum errors are 69 r/min and 87 r/min, respectively, the average errors are 31 r/min and 43 r/min, respectively, and the standard errors are 3.54 r/min and 4.16 r/min, respectively. Thus, the tracking accuracy and stability for the sinusoidal signal with an amplitude of 100 r/min are superior to those for the signal with an amplitude of 200 r/min.
- (4)
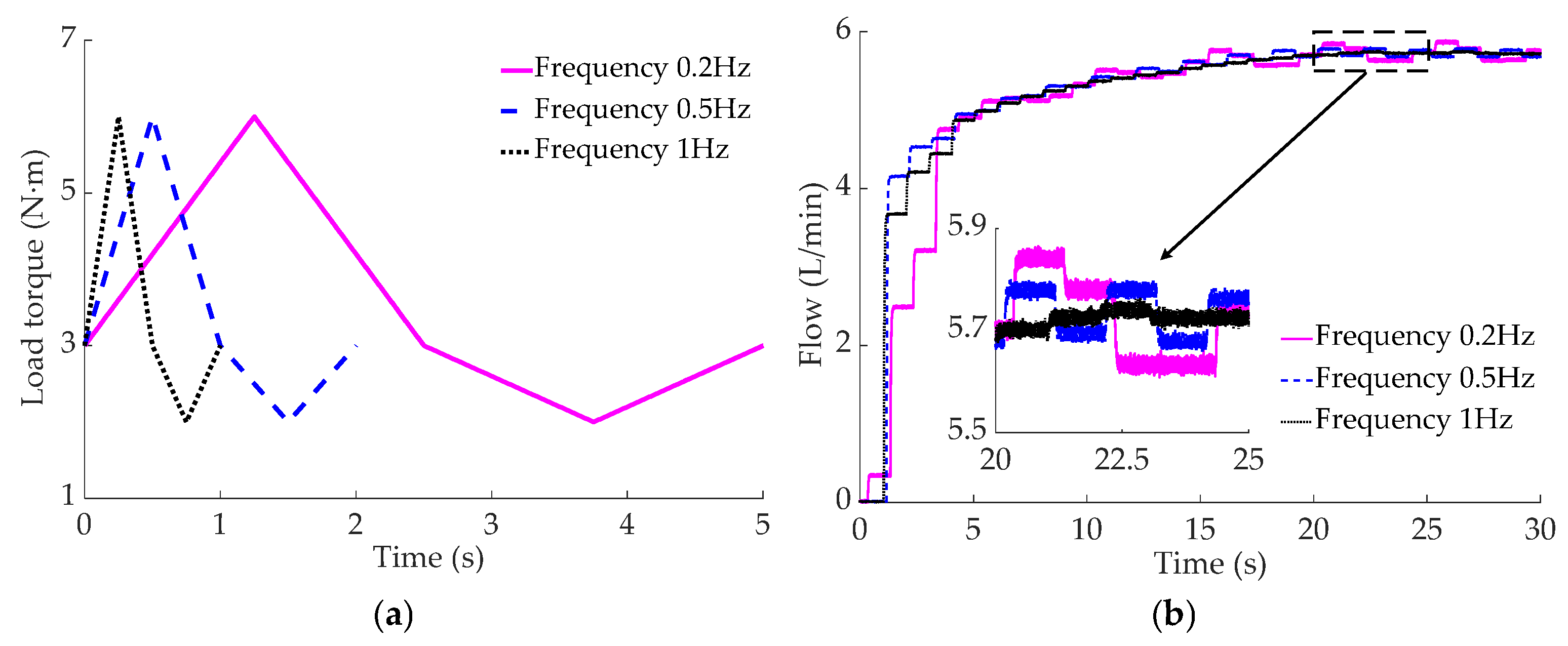
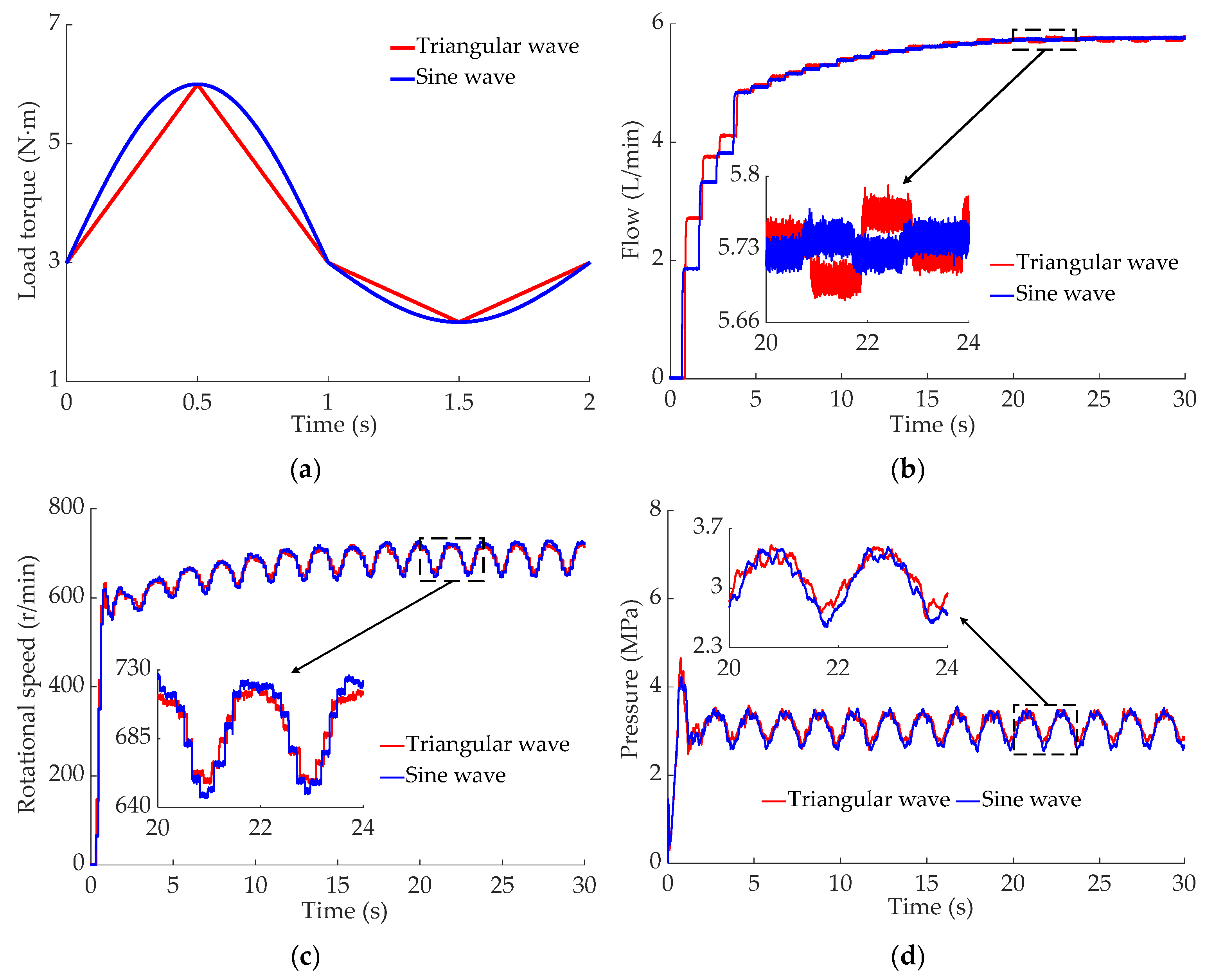
- The alternating-load test results indicate that as the load torque enhances from 5 to 8 N·m, the peak pressure of the motor rises from 3.12 to 3.97 MPa, the output flow of the HCPRV fluctuates between 5.61 and 5.72 L/min, and the maximum fluctuation range of the rotational speed of motor extends from 617 to 746 r/min. When the load frequency increases from 0.2 to 1 Hz, the peak value of the pressure of the motor increases from 2.55 to 3.52 MPa, the fluctuation range of the output flow of the HCPRV gradually decreases, and the peak value of the rotational speed of the motor is, at most, 722 r/min. The fluctuation ranges of the pressure and the rotational speed of the motor are basically unaffected by the alternating-load waveforms, which are 2.58~3.51 MPa and 651~721 r/min, respectively. However, the pressure curve of the motor with a sine wave is smoother and has better continuity. The fluctuation range of the output flow of the HCPRV under the influence of the sine wave is slightly smaller. They are 5.72~5.74 L/min and 5.69~5.76 L/min, respectively. The principles derived from the test results are generally in agreement with those from the simulation outcomes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Variable | Unit | Variable | Unit | Variable | Unit |
| Vp | m3/rad | Us | V | Qpi | L/min |
| ωp | rad/s | I | A | Qpj | L/min |
| ppi | Pa | Rs | Ω | Tp | N·m |
| ppj | Pa | RL | Ω | Qd | m3/min |
| Cv | No unit | e | V | Dd | m |
| α | ° | N | No unit | pd | Pa |
| ρ | kg/m3 | μ0 | H/m | md | kg |
| xd | m | S | m2 | B | T |
| F01 | N | ωm | rad/s | F02 | N |
| ld | m | xz | m | Qc | m3/min |
| Dc | m | Fd | N | φ | ° |
| xc | m | Fz | N | pc | Pa |
| kqc | No unit | Cv | No unit | Qz | m3/min |
| Dz | m | Dz1 | m | αz | ° |
| y | m | θ | ° | pz | Pa |
| k1 | N/m | pi | Pa | y0 | m |
| pf1 | Pa | po | Pa | pf2 | Pa |
| Af1 | m2 | Be | N·s/m | Af2 | m2 |
| pe1 | Pa | pe2 | Pa | le1 | m |
| le2 | m | me | kg | Bf | T |
| ks | N/m | x0 | m | Qpc | L/min |
| Qct | L/min | Cd | No unit | Apc | m2 |
| Act | m2 | ps | Pa | pc | Pa |
| pt | Pa | θv | ° | Dv | m |
| xvm | m | mf | kg | xf | m |
| Fs | N | Ft | N | k | No unit |
| As | mm2 | W | m | pms | Pa |
| pmt | Pa | x0 | m | Mm | kg |
| Fm | N | Bm | T | xk0 | m |
| kd | No unit | Bd | T | E | Pa |
| V0 | m3 | Jm | kg·m2 | Vm | m3/rad |
| ωm | rad/s | Qmi | L/min | Qmj | L/min |
| pmi | Pa | pmj | Pa | Tload | N·m |
| ξ | kg·m2/s | Tm | N·m | Tp | N·m |
| Tξ | N·m | Δpp | Pa | ηm | No unit |
| Qv | m3/min | Qp | m3/min | kξ | N·m·s/rad |
| A1 | No unit | A2 | No unit | A3 | No unit |
| pp | Pa | pp1 | Pa | ppc | Pa |
| kω | No unit | hgv | m | kv | No unit |
| kc | No unit | g | m/s2 | Av | m2 |
References
- Tian, D.; Si, Q.R.; Liang, K.; Zhang, Y.; Ju, Y.Z.; Yuan, J.P. Study on the Internal Flow Characteristics of High Flowrate Emergency Drainage Series-Parallel Pump. J. Phys. Conf. Ser. 2024, 2854, 012062. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.L.; Liu, H.L.; Xie, L. Optimization and Analysis of Mine Drainage Pump with High Efficiency and Large Flow. J. Low Freq. Noise Vib. Act. 2022, 41, 1091–1107. [Google Scholar] [CrossRef]
- Rakibuzzaman, M.; Suh, S.H.; Kim, H.H.; Didarul Islam, M.; Zhou, L.; El-Emam, M. Cavitation and Erosion Effects on Hydraulic Performances of a Submersible Drainage Pump. Alexandria Eng. J. 2025, 113, 431–450. [Google Scholar] [CrossRef]
- Cao, W.D.; Yang, X.Y.; Wang, H.; Leng, X.Y. Numerical Simulation of Gas-Liquid Two-Phase Flow in Emergency Rescue Drainage Pump Based on MUSIG Model. J. Appl. Fluid Mech. 2024, 17, 1730–1745. [Google Scholar]
- Gong, Y.; Zou, W.H. Optimal Operation of Urban Tidal Drainage Pumping Station Based on Genetic Algorithm Coupled with Head-Water Level Successive Approximation. Front. Energy Res. 2023, 10, 1074529. [Google Scholar] [CrossRef]
- Huang, X.K.; Wu, X.F.; Tian, Z.Z.; Lin, S.K.; Ji, J.J.; Guo, Y.Y.; Xie, F.W. Fault Diagnosis Study of Mine Drainage Pump Based on MED-WPD and RBFNN. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 347. [Google Scholar] [CrossRef]
- Ye, J.; Qin, P.; Xing, Z.R.; Fan, Y.W.; Gao, J.Y.; Deng, Z.S.; Liu, J. Liquid Metal Hydraulic Actuation and Thermal Management Based on Rotating Permanent Magnets Driven Centrifugal Pump. Int. Commun. Heat Mass Transfer 2022, 139, 106472. [Google Scholar] [CrossRef]
- Kushwaha, P.; Dasgupta, K.; Ghoshal, S.K. A Comparative Analysis of The Pump Controlled, Valve Controlled and Prime Mover Controlled Hydromotor Drive to Attain Constant Speed for Varying Load. ISA Trans. 2022, 120, 305–317. [Google Scholar] [CrossRef]
- Zhu, Y.; Tang, S.N.; Yuan, S.Q. Multiple-Signal Defect Identification of Hydraulic Pump Using an Adaptive Normalized Model and S Transform. Eng. Appl. Artif. Intell. 2023, 124, 106548. [Google Scholar] [CrossRef]
- Tang, S.N.; Jiang, Y.X.; Zhou, T.; Zhu, Y.; Lim, K.M. Bayesian Algorithm Optimized Deep Model for Multi-Signal Fault Identification of Hydraulic Pumps. Alexandria Eng. J. 2025, 121, 465–483. [Google Scholar] [CrossRef]
- Chang, H.; Yang, J.H.; Wang, Z.Q.; Peng, G.J.; Lin, R.Y.; Lou, Y.; Shi, W.D.; Zhou, L. Efficiency Optimization of Energy Storage Centrifugal Pump by Using Energy Balance Equation and Non-dominated Sorting Genetic Algorithms-II. J. Energy Storage 2025, 114, 115817. [Google Scholar] [CrossRef]
- Tang, S.N.; Jiang, Y.X.; Su, H.; Zhu, Y. A Fault Identification Method of Hydraulic Pump Fusing Long Short-Term Memory and Synchronous Compression Wavelet Transform. Appl. Acoust. 2025, 232, 110553. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, Y.J.; Rakibuzzaman, M.; Agarwal, R.; Zhou, L. Numerical and Experimental Investigations of a Double-Suction Pump with a Middle Spacer and a Staggered Impeller. Irrig. Drain. 2025, 74, 944–956. [Google Scholar] [CrossRef]
- Zhao, Z.J.; Jiang, L.; Bai, L.; Pan, B.; Zhou, L. Numerical Simulation and Entropy Production Analysis of Centrifugal Pump with Various Viscosity. Comput. Model. Eng. Sci. 2024, 141, 1730–1745. [Google Scholar] [CrossRef]
- Pang, Y.Y.; Tang, P.; Li, H.; Marinello, F.; Chen, C. Optimization of Sprinkler Irrigation Scheduling Scenarios for Reducing Irrigation Energy Consumption. Irrig. Drain. 2024, 73, 1329–1343. [Google Scholar] [CrossRef]
- Wang, W.T.; Chao, Q.; Shi, J.J.; Liu, C.L. Condition Monitoring of Axial Piston Pumps Based on Machine Learning-Driven Real-Time CFD Simulation. Eng. Appl. Comput. Fluid Mech. 2025, 19, 2474676. [Google Scholar] [CrossRef]
- Sciatti, F.; Tamburrano, P.; Distaso, E.; Amirante, R. Digital Hydraulic Technology: Applications, Challenges, and Future Direction. J. Phys. Conf. Ser. 2023, 2648, 012053. [Google Scholar] [CrossRef]
- Gao, Q.; Wang, J.; Zhu, Y.; Wang, J.; Wang, J.C. Research Status and Prospects of Control Strategies for High Speed On/Off Valves. Processes 2023, 11, 160. [Google Scholar] [CrossRef]
- Yang, S.; Yao, J.; Wang, P.; Zhang, P.Y.; Wei, T.F.; Li, D.M. A Novel Dual-Magnetic Circuit Actuated Fast-Switching Valve with Multi-Stage Excitation Control Algorithm. Measurement 2024, 230, 114483. [Google Scholar] [CrossRef]
- Xu, E.G.; Zhong, Q.; He, X.J.; Mao, Y.X.; Huang, Y.; Yang, H.Y. A Novel Current-Based Identification Method for Dynamic Performance of High-Speed On/Off Valve. Measurement 2024, 232, 114719. [Google Scholar] [CrossRef]
- Gao, Q.; Liu, H.Y.; Lan, B.; Zhu, Y. A Model-based Sliding Mode Control with Intelligent Distribution for a Proportional Valve Driven by Digital Valve Arrays. ISA Trans. 2024, 151, 312–323. [Google Scholar] [CrossRef]
- Huang, S.; Zhou, H. Optimizing Multi-Coil Integrated High-Speed On/Off Valves for Enhanced Dynamic Performance with Voltage Control Strategies. Appl. Comput. Electrom. 2024, 39, 1019–1034. [Google Scholar] [CrossRef]
- Kogler, H. High Dynamic Digital Control for a Hydraulic Cylinder Drive. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2022, 236, 382–394. [Google Scholar] [CrossRef]
- Gao, Q. Nonlinear Adaptive Control with Asymmetric Pressure Difference Compensation of a Hydraulic Pressure Servo System Using Two High Speed On/Off Valves. Machines. 2022, 10, 66. [Google Scholar] [CrossRef]
- Yang, X.; Wu, D.F.; Wang, C.L.; Gao, C.Q.; Gao, H.; Liu, Y.S. Adaptive Fuzzy PID Control of High-Speed On-Off Valve for Position Control System Used in Water Hydraulic Manipulators. Fusion Eng. Des. 2024, 203, 114437. [Google Scholar] [CrossRef]
- Li, Q.Z.; Hao, P.; Wang, J.; Deng, H. Pulse-Width-Modulation-Based Ttime-Delay Compensation Control for High-Speed On/Off Valves. Electronics. 2023, 12, 3627. [Google Scholar] [CrossRef]
- Zhong, Q.; Mao, Y.X.; Xu, E.G.; Wang, X.L.; Li, Y.B.; Yang, H.Y. Fast Dynamics and Low Power Losses of High-Speed Solenoid Valve Based on Optimized Pre-Excitation Control Algorithm. Therm. Sci. Eng. Prog. 2024, 47, 102363. [Google Scholar] [CrossRef]
- Zhong, Q.; Wang, J.X.; Xu, E.G.; Yu, C.; Li, Y.B. Multi-Objective Optimization of a High Speed On/Off Valve for Dynamic Performance Improvement and Volume Minimization. Chin. J. Aeronaut. 2024, 37, 435–444. [Google Scholar] [CrossRef]
- Stosiak, M.; Karpenko, M. The Influence of the Hydropneumatic Accumulator on the Dynamic and Noise of the Hydrostatic Drive Operation. Eksploat. Niezawodn. 2024, 26, 2. [Google Scholar] [CrossRef]
- Stosiak, M.; Karpenko, M.; Ivannikova, V.; Maskeliunaite, L. The Impact of Mechanical Vibrations on Pressure Pulsation, Considering the Nonlinearity of the Hydraulic Valve. J. Low Freq. Noise Vib. Act. Control 2024, 44, 706–719. [Google Scholar] [CrossRef]
- Guo, D.D.; Wang, M.; Jiang, N.; Zeng, Y.Y.; Cao, H.Q.; Wang, D.Y.; Lu, J.; Wu, D.Y. Operation Characteristics of Soil Blasting Vibration Test Device under Vibration Load. Rev. Sci. Instrum. 2023, 94, 045007. [Google Scholar] [CrossRef]


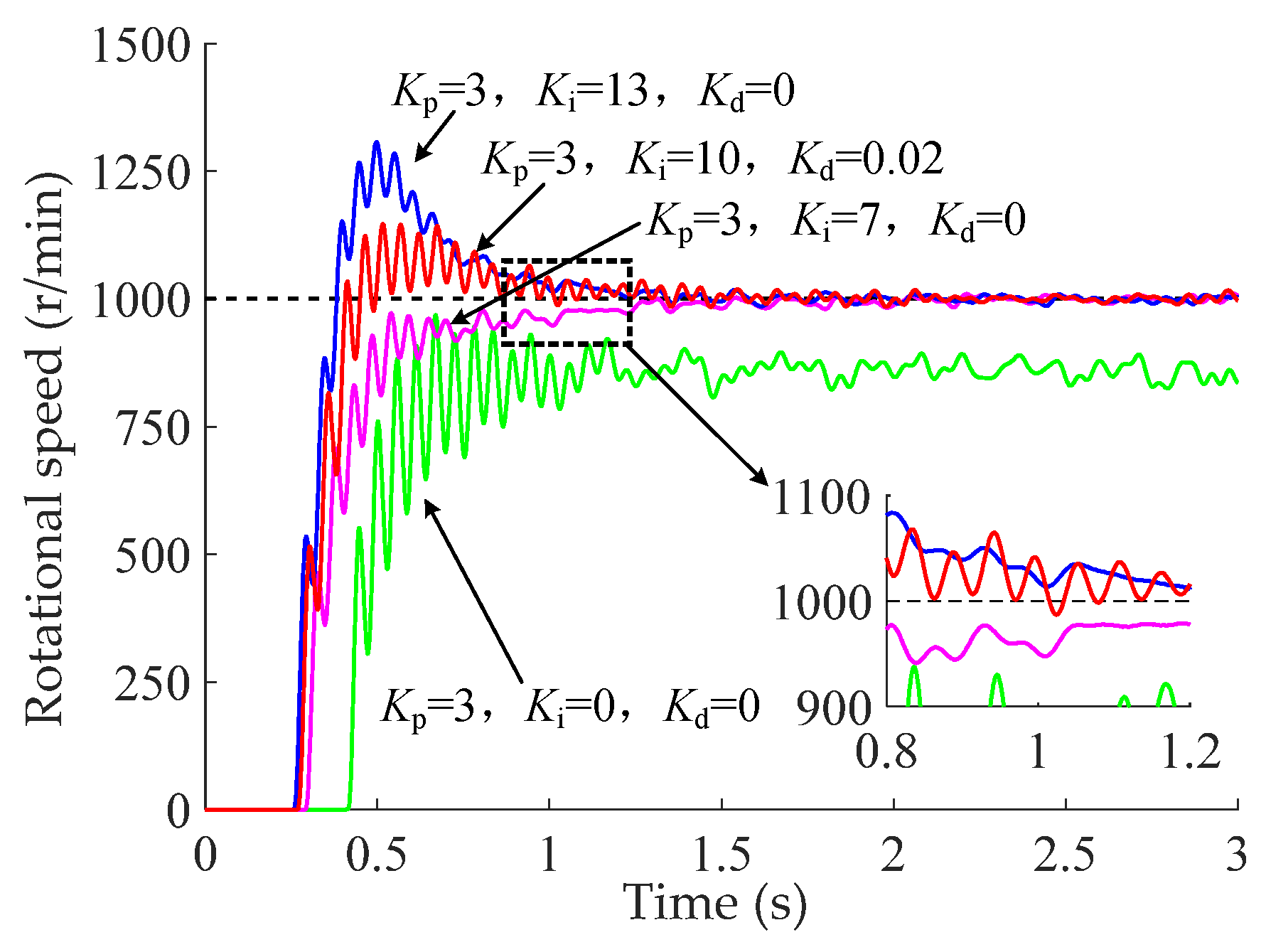
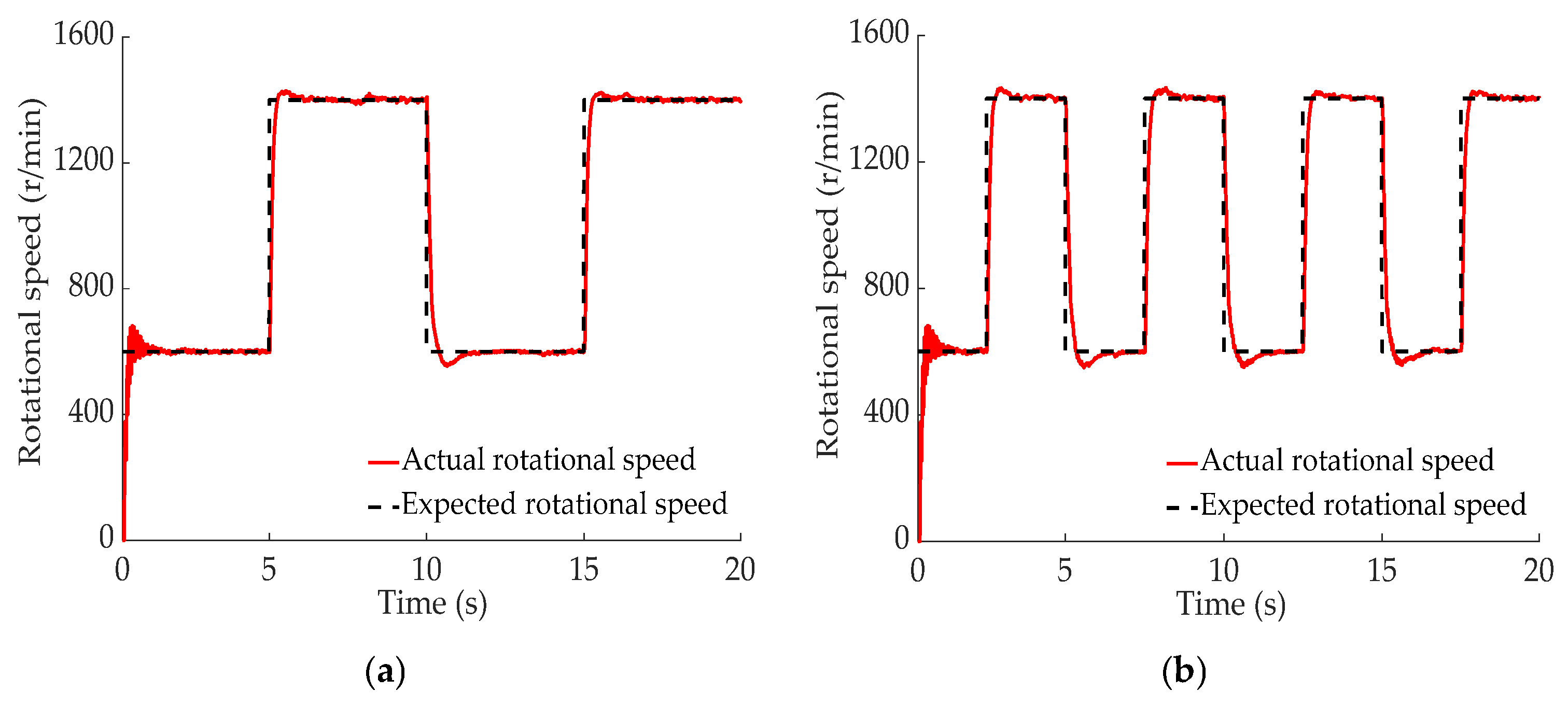


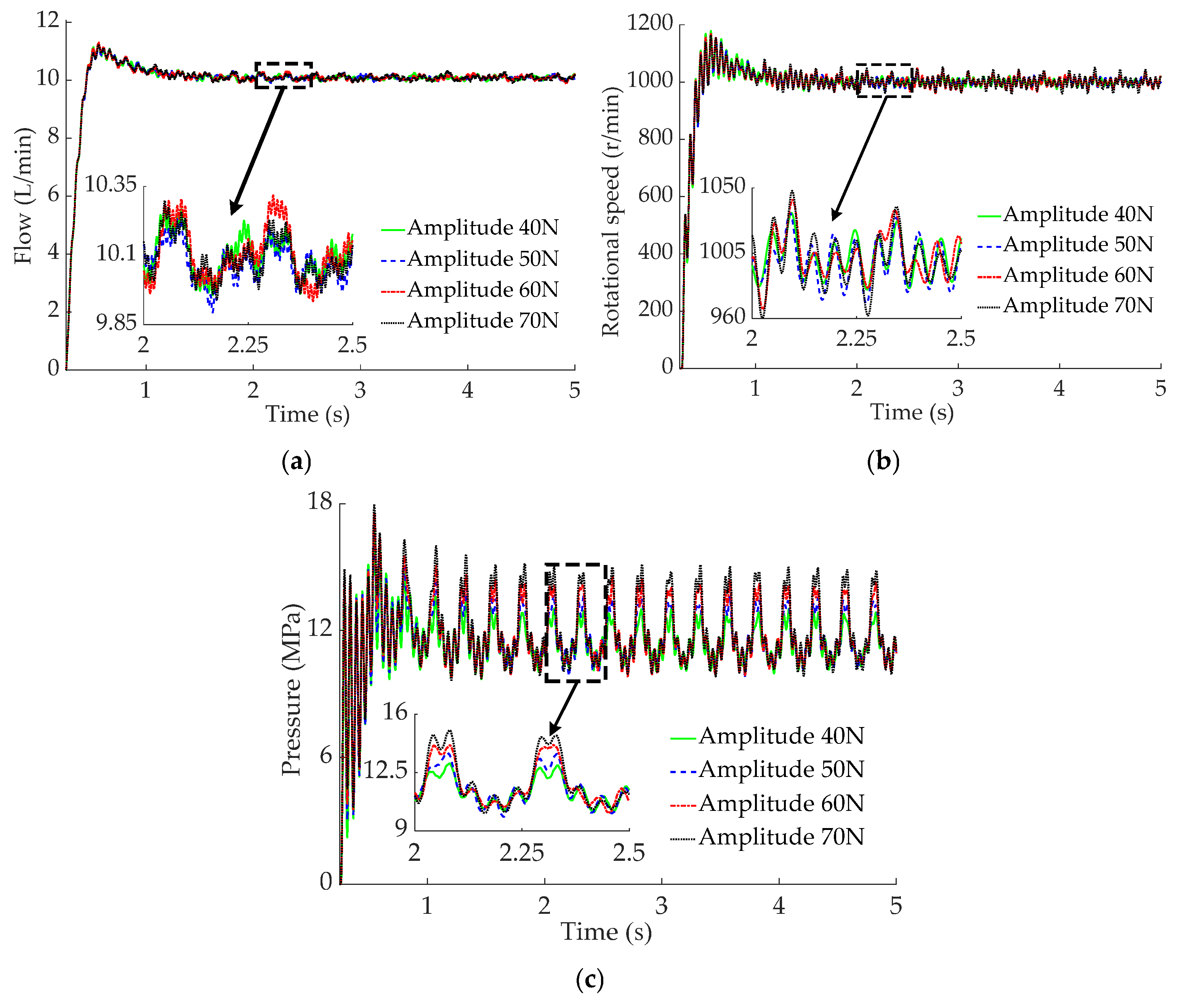
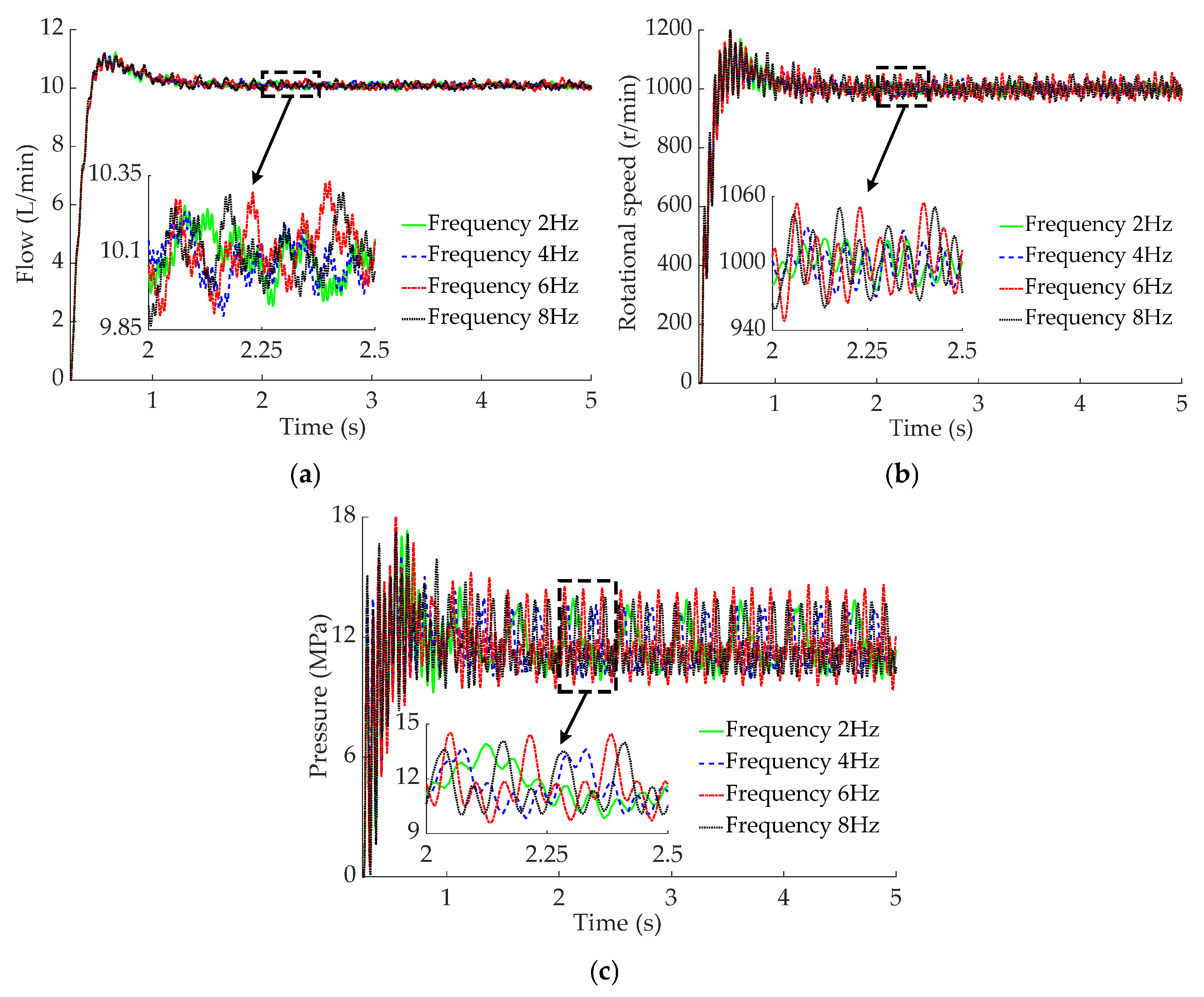



| Performance Index | Square Wave Signal Amplitude | Performance Index | Sine Wave Signal Amplitude | ||
|---|---|---|---|---|---|
| 200 r/min | 400 r/min | 200 r/min | 400 r/min | ||
| Overshoot (%) | 31.5 | 45.7 | Maximum error (r/min) | 69 | 87 |
| Adjustment time (s) | 2.43 | 2.65 | Average error (r/min) | 31 | 43 |
| Rising time (s) | 0.77 | 0.75 | Standard error (r/min) | 3.54 | 4.16 |
| Steady-state error (r/min) | 34 | 23 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Liu, Y.; Wu, Q.; Gao, Q. Dynamic Characteristics of a Digital Hydraulic Drive System for an Emergency Drainage Pump Under Alternating Loads. Machines 2025, 13, 636. https://doi.org/10.3390/machines13080636
Zhu Y, Liu Y, Wu Q, Gao Q. Dynamic Characteristics of a Digital Hydraulic Drive System for an Emergency Drainage Pump Under Alternating Loads. Machines. 2025; 13(8):636. https://doi.org/10.3390/machines13080636
Chicago/Turabian StyleZhu, Yong, Yinghao Liu, Qingyi Wu, and Qiang Gao. 2025. "Dynamic Characteristics of a Digital Hydraulic Drive System for an Emergency Drainage Pump Under Alternating Loads" Machines 13, no. 8: 636. https://doi.org/10.3390/machines13080636
APA StyleZhu, Y., Liu, Y., Wu, Q., & Gao, Q. (2025). Dynamic Characteristics of a Digital Hydraulic Drive System for an Emergency Drainage Pump Under Alternating Loads. Machines, 13(8), 636. https://doi.org/10.3390/machines13080636








