GA-Synthesized Training Framework for Adaptive Neuro-Fuzzy PID Control in High-Precision SPAD Thermal Management

Abstract

This study presents a hybrid adaptive control strategy that integrates genetic algorithm (GA) optimization with an adaptive neuro-fuzzy inference system (ANFIS) for precise thermal regulation of single-photon avalanche diodes (SPADs). To address the nonlinear and disturbance-sensitive dynamics of SPAD systems, a performance-oriented dataset is constructed through multi-scenario simulations using settling time, overshoot, and steady-state error as fitness metrics. The genetic algorithm (GA) facilitates broad exploration of the proportional–integral–derivative (PID) controller parameter space while ensuring control stability by discarding low-performing gain combinations. The resulting high-quality dataset is used to train the ANFIS model, enabling real-time, adaptive tuning of PID gains. Simulation results demonstrate that the proposed GA-ANFIS-PID controller significantly enhances dynamic response, robustness, and adaptability over both the conventional Ziegler–Nichols PID and GA-only PID schemes. The controller maintains stability under structural perturbations and abrupt thermal disturbances without the need for offline retuning, owing to the real-time inference capabilities of the ANFIS model. By combining global evolutionary optimization with intelligent online adaptation, this approach improves both accuracy and generalization, offering a practical and scalable solution for SPAD thermal management in demanding environments such as quantum communication, sensing, and single-photon detection platforms.

1. Introduction

Single-photon detectors (SPDs) are highly sensitive optoelectronic devices engineered to detect individual photons, serving as critical components in emerging quantum technologies such as quantum communication, quantum computing, and quantum metrology [1]. In these applications, where photons act as the fundamental carriers of quantum information, the performance of SPDs directly dictates the efficacy and practical viability of quantum systems [2]. To meet the rigorous demands of high-fidelity detection under ultra-low photon flux conditions, SPDs must exhibit a low dark count rate (DCR), high detection efficiency, and stable, reliable registration of incident photons [3].

In this work, we focus on single-photon avalanche diodes (SPADs), a specialized subclass of APD-based SPDs, due to their high gain, fast response, and suitability for low-flux quantum detection applications. However, Na et al. [4] demonstrated that the performance of SPADs is critically limited by their strong temperature dependence, particularly in terms of the DCR, which directly affects system stability and noise performance. The primary contributors to the DCR in SPADs include thermally generated electron–hole pairs, tunneling currents induced by material imperfections [5], and localized avalanche events caused by electric field non-uniformities within the depletion region [6]. Mitigating these effects requires targeted innovations in both device design (such as material purification and field homogenization) and system-level strategies, notably precise and adaptive thermal regulation [7].

In recent years, substantial progress in the performance of SPADs has been driven by innovations in device structure and system-level enhancements. For example, Gramuglia et al. introduced a P-I-N-configured SPAD with an expanded avalanche region to improve carrier multiplication [8], while Kleinow et al. utilized molecular beam epitaxy to enhance electric field uniformity and suppress tunneling currents [9]. Wu et al. further reduced the DCR by combining high-speed gating with thermoelectric cooling [10], and Krynski et al. demonstrated that laser-annealing effectively mitigates radiation-induced defects [11].

Despite substantial advances in SPAD design, such as improved structural configurations and material engineering, DCR remains fundamentally limited by thermally activated carrier generation processes intrinsic to semiconductor materials [12,13]. These inherent thermal sensitivities cannot be fully mitigated through physical enhancements alone. Consequently, research attention has shifted toward developing precise and adaptive thermal management strategies that are capable of maintaining real-time temperature stability, thereby ensuring consistent low-noise performance under the dynamic and often harsh conditions encountered in quantum applications [14,15].

As the limitations of structural optimization became evident, researchers began exploring system-level thermal control techniques to ensure stable SPAD performance. Early efforts in thermal management, such as integrating thermoelectric coolers (TECs) with PI control algorithms or employing multi-parameter coordinated regulation schemes [16], achieved high temperature-control precision but faced notable drawbacks, such as slow dynamic response, system complexity, and sensitivity to environmental variations, all of which hindered their practical deployment in real-world applications [17]. For instance, Guo et al. proposed a method that simultaneously regulated operating current, coolant flow, and temperature to improve control accuracy, but its strong reliance on environmental stability and intricate coordination severely limited applicability across diverse settings [18].

Current research on APD temperature control primarily follows two technical trajectories. The dominant approach integrates SPAD structural optimization with conventional proportional–integral–derivative (PID)-based feedback control. While this method is straightforward and widely adopted, it faces significant challenges in modeling the system’s nonlinear thermal–electrical dynamics, and its control accuracy is inherently limited by the constraints of classical feedback mechanisms [19,20].

In parallel, a growing body of work has begun to explore intelligent control algorithms as a means to overcome these limitations. Techniques such as fuzzy logic control, neural networks, and adaptive neuro-fuzzy inference systems (ANFISs) offer enhanced capabilities for handling system nonlinearities and dynamic uncertainties, often yielding better transient response and steady-state performance than traditional controllers [21]. However, these methods also bring their own drawbacks, including heavy reliance on high-quality training data, increased computational complexity, and reduced robustness in noisy or time-varying environments. Although ANFIS combines the interpretability of fuzzy logic with the learning ability of neural networks, it still inherits key limitations from the latter, such as susceptibility to local minima and constrained generalization in complex scenarios [22].

To overcome the limitations of standalone intelligent controllers, researchers have proposed hybrid optimization frameworks (such as GA-ANFIS and PSO-ANFIS) that integrate global search algorithms with ANFIS to enhance adaptability, autonomously optimize control parameters, and improve robustness under environmental variations [23]. In these approaches, the genetic algorithm (GA) and particle swarm optimization (PSO) serve as effective global optimizers for tuning ANFIS parameters, resulting in improved predictive accuracy and dynamic response [24].

Although experimental results show that GA/PSO-ANFIS hybrid models outperform standalone ANFIS and classical PID controllers in terms of fitting accuracy under stationary conditions [25], several critical limitations remain. First, these models typically lack performance-driven optimization; control parameters are not explicitly linked to key dynamic metrics such as overshoot, settling time, and steady-state error. Second, the nested optimization of fuzzy membership functions and neural network weights imposes high computational demands, making real-time implementation challenging [26]. Third, in high-dimensional parameter spaces, these algorithms may converge to near-optimal rather than truly optimal solutions, reducing robustness under perturbations. Finally, their heavy reliance on static or empirical training data limits generalization, particularly under non-stationary or unforeseen operating conditions.

To overcome the aforementioned limitations, recent studies have explored performance-driven approaches that link controller parameters directly to dynamic performance goals. For instance, Rodríguez-Abreo et al. employed a genetic algorithm to generate training data aligned with performance specifications, using a backpropagation neural network to adaptively predict controller gains, thereby enhancing disturbance rejection and adaptability [27]. Similarly, Liu et al. combined system simulation and ANFIS modeling to optimize PID parameters, demonstrating improved transient and steady-state performance under nonlinear conditions [28].

Building on these insights, this study proposes a performance-driven GA-ANFIS framework for adaptive PID control. Unlike prior approaches based on empirical data or single-scenario training, the proposed method systematically simulates diverse dynamic conditions using the system’s transfer function. Genetic algorithms are used to optimize PID gains with respect to key performance metrics—overshoot, settling time, and steady-state error—while excluding unstable or oscillatory combinations. The resulting high-quality dataset is used to train an ANFIS model capable of real-time gain adjustment. By combining offline global optimization with intelligent online adaptation, the controller achieves high precision, strong robustness, and fast response in nonlinear, time-varying environments. Applied to SPAD thermal regulation, the framework enables reliable temperature stabilization under dynamic workloads, effectively reducing dark count rate and improving system reliability in quantum sensing and communication applications.

2. Methodology and System Modeling

2.1. Thermal System Modeling of SPAD-TEC

To realize the proposed control strategy, an accurate model of the SPAD-TEC thermal system is first established, laying the foundation for controller design and simulation. In order to design an effective temperature control system for the SPAD, it is first essential to analyze and model its temperature response dynamics. Accurate characterization of how the SPAD’s temperature evolves under varying thermal conditions is critical for achieving stable operation, given the device’s high sensitivity to temperature fluctuations.

However, the SPAD itself does not actively regulate its temperature; instead, it passively follows the cold-side temperature of the thermoelectric cooler (TEC) to which it is thermally coupled. As such, precise modeling of the TEC’s thermal dynamics is essential to implementing effective temperature regulation in SPAD systems.

In this study, the mathematical model of the TEC system is adopted from the work of Samsuddin et al. [29], in which a linearized dynamic model of the TEC was derived through analytical thermal and electrical energy balance. The cold-side temperature of the TEC is modeled as a function of input current, cooling load, and ambient temperature. After model reduction and simplification, the final transfer function relating the input current to the cold-side temperature is expressed as follows:

$$G\left(s\right)=6.4061·{\displaystyle \frac{0.0646s+0.00854}{s^2+0.5964s+0.00855}}$$

(1)

This second-order transfer function captures the key dynamics of the TEC when the cooling load and ambient temperature are assumed constant. The model reflects the highly nonlinear characteristics of TECs due to the Peltier and Seebeck effects, yet provides sufficient accuracy and simplicity for control system design. Therefore, it is deemed appropriate for the control-oriented simulation and algorithm development in this study.

2.2. Performance-Oriented PID Dataset Generation via GA

Genetic algorithms, inspired by the principles of Darwinian natural selection and genetic evolution, have demonstrated strong robustness and adaptability across a wide range of optimization problems [30]. Leveraging these capabilities, this study adopts a GA-based approach as a metaheuristic for the offline optimization of PID controller gains.

The primary objective of the GA framework is to generate a performance-oriented database that maps specific PID parameter combinations to their corresponding dynamic responses. This database serves as the foundation for training the subsequent ANFIS-PID model, enabling adaptive gain tuning aligned with various performance criteria such as overshoot, settling time, and steady-state error [31].

In this implementation, a fixed-structure GA is utilized, in which each individual encodes a candidate PID controller as a real-valued vector consisting of proportional ($K_p$), integral ($K_i$), and derivative ($K_d$) gains. The optimization process follows the standard continuous-time PID control law:

$$u\left(t\right)=K_{p}e\left(t\right)+K_i{\int }_0^{t}e\left(\tau \right)d\tau +K_d{\displaystyle \frac{de\left(t\right)}{dt}}$$

(2)

where $e\left(t\right)$ denotes the control error at time t, defined as the difference between the reference input and the actual system output.

As illustrated in Figure 1, the GA iteratively adjusts the controller parameters based on closed-loop performance. This enables the generation of high-quality control responses and establishes a solid foundation for the subsequent adaptive controller design.

To promote genetic diversity and ensure sufficient exploration of the solution space, an initial population P of size N is randomly generated. Each individual within the population encodes a candidate PID controller in the form of a real-valued vector:

$$P=\left(K_{p1},K_{i1},K_{d1}\right),\cdots ,\left(K_{pN},K_{iN},K_{dN}\right)$$

(3)

For each individual, the step response of the closed-loop system is simulated using the previously described SPAD-TEC model. To evaluate the control performance of each candidate solution, a weighted composite cost function is employed:

$$J={\omega }_1{T}_s+{\omega }_2{M}_p+{\omega }_3{e}_{ss}$$

(4)

In this formulation, $T_s$ represents the settling time, $M_p$ denotes the maximum overshoot, and $e_{ss}$ is the steady-state error. The weighting coefficients ${\omega }_1$, ${\omega }_2$, and ${\omega }_3$ are tunable parameters that allow the cost function to prioritize different aspects of dynamic performance depending on specific control objectives. In the context of SPAD thermal regulation, where steady-state temperature precision critically affects the dark count rate (DCR) and overall detection reliability, the weight assigned to the steady-state error was set to the highest value (${\omega }_3=10$) to ensure minimal long-term deviation. The overshoot weight (${\omega }_2=5$) was given intermediate priority to suppress abrupt temperature transients that could lead to thermal stress or noise degradation. Conversely, the settling time weight (${\omega }_1=2$) was deliberately set lower, reflecting a preference for stability and precision over aggressive response speed. This weighting scheme was selected based on domain-specific requirements and was empirically validated to yield a well-balanced trade-off between responsiveness, robustness, and steady-state accuracy.

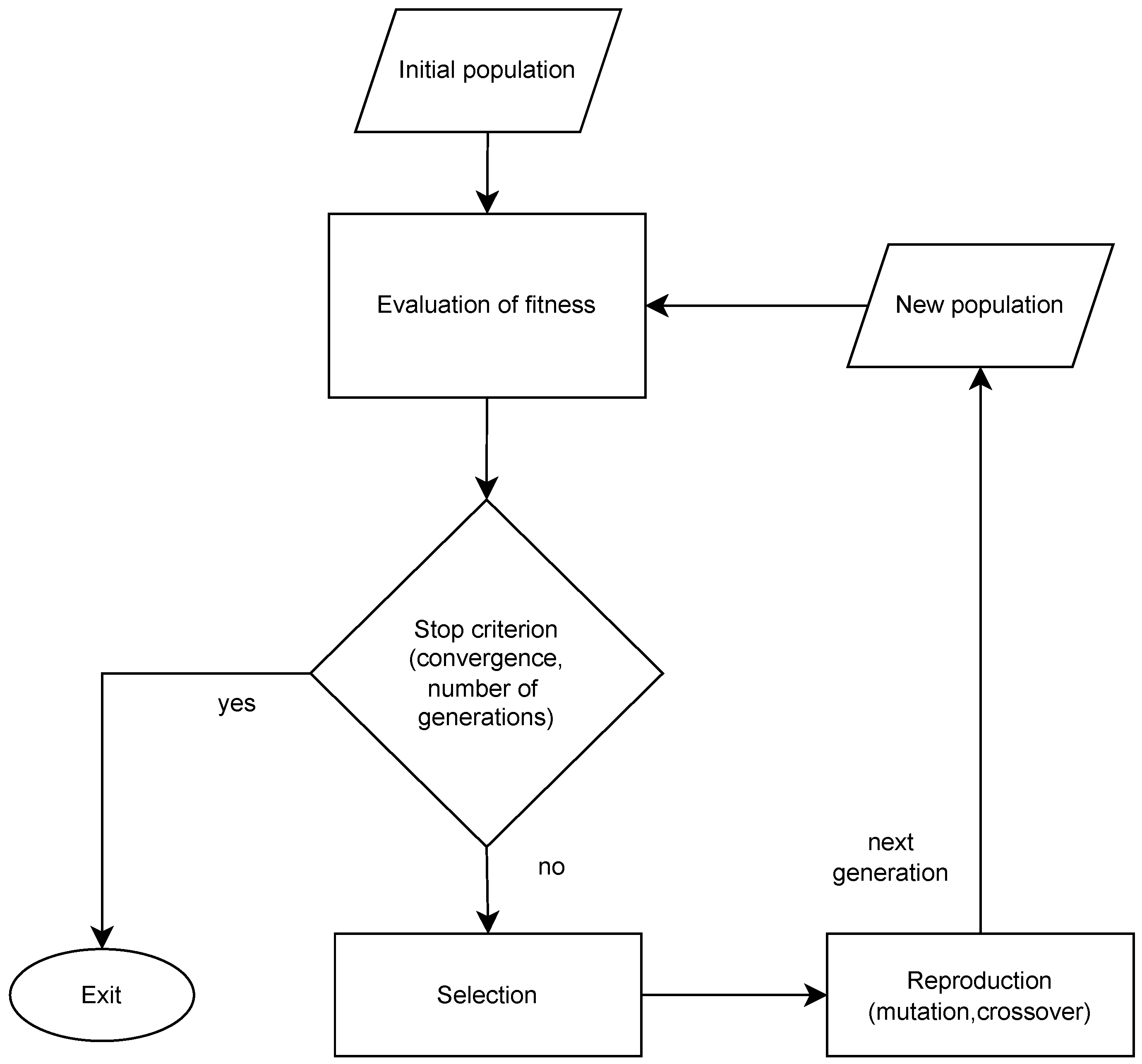
2.3. Genetic Algorithm Optimization Procedure

To guide the population toward optimal solutions, a roulette wheel selection mechanism is employed. This method assigns selection probabilities to individuals in proportion to their fitness values, thereby increasing the likelihood of selecting higher-performing candidates for reproduction.

For the i-th individual, the selection probability in the roulette wheel method is computed as follows:

$$P_i={\displaystyle \frac{F_i}{{\sum }_{j=1}^N{F}_j}}$$

(5)

where $F_i=1/J_i$ denotes the fitness value, which is defined as the reciprocal of the performance index $J_i$. Here, N is the total number of individuals in the population.

Based on these probabilities, the cumulative probability distribution is constructed as:

$$C_1=P_1,C_2=C_1+P_2,\cdots ,C_N=1$$

(6)

A uniformly distributed random number $r\in [0,1]$ is drawn, and the i-th individual is selected if the following condition holds:

$$C_{i-1}<r\le C_i$$

(7)

Here, $P_i$ is the normalized selection probability, $C_i$ represents the cumulative probability, and r is the selection threshold drawn from a uniform distribution.

2.3.1. Genetic Crossover Strategy

To introduce genetic diversity and explore new regions of the solution space, an arithmetic crossover operator is applied. Given two parent solutions, $(K_{p1},K_{i1},K_{d1})$ and $(K_{p2},K_{i2},K_{d2})$, two offspring vectors, $C_1$ and $C_2$, are generated using weighted linear combinations as follows:

$$\begin{array}{cc}\hfill C_1& =\left(w_1{K}_{p1}+(1-w_1)K_{p2},w_2{K}_{i1}+(1-w_2)K_{i2},w_3{K}_{d1}+(1-w_3)K_{d2}\right)\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill C_2& =\left(w_1{K}_{p2}+(1-w_1)K_{p1},w_2{K}_{i2}+(1-w_2)K_{i1},w_3{K}_{d2}+(1-w_3)K_{d1}\right)\hfill \end{array}$$

(9)

Here, $K_{p1},K_{i1},K_{d1}$ and $K_{p2},K_{i2},K_{d2}$ are the proportional, integral, and derivative gains of the first and second parent individuals, respectively. Weights $w_1,w_2,w_3\in [0,1]$ are sampled independently from a uniform distribution.

The crossover is conditionally executed if a random number $r<P_c$, where $P_c$ is the predefined crossover probability.

2.3.2. Adaptive Mutation Mechanism

To prevent premature convergence and maintain population diversity, a mutation operator introduces small perturbations into selected individuals. If a random number, $r<P_m$, where $P_m$ is the predefined mutation probability, the mutation is applied as follows:

$$K_p^{\mathrm{new}}=K_p+{\delta }_p,K_i^{\mathrm{new}}=K_i+{\delta }_i,K_d^{\mathrm{new}}=K_d+{\delta }_d$$

(10)

Here, ${\delta }_p$, ${\delta }_i$, and ${\delta }_d$ are perturbation terms sampled from zero-mean Gaussian distributions. This stochastic modification helps the algorithm escape local optima and promotes global exploration.

2.3.3. Convergence and Stopping Conditions

The genetic optimization process iteratively performs selection, crossover, and mutation until one of the following stopping conditions is satisfied:

• The maximum number of generations, $k_{max}$, is reached.
• The convergence criterion is met:

  $$\left|J_{k+1}-J_k\right|<ϵ$$

  (11)

  where $ϵ$ is a small positive threshold indicating negligible improvement.

The overall workflow of the genetic algorithm is illustrated in Figure 2.

The performance of the GA is influenced by its parameter settings. The initial values for population size, crossover rate, mutation rate, and selection method were chosen based on prior studies [30], and further tuned according to empirical performance. Importantly, the algorithm accepts any solution that meets the criteria, even if it is not globally optimal, allowing for parameter configurations within a reasonable tolerance. A complete list of the algorithmic parameters and their definitions is provided in

Table 1. Genetic Algorithm configuration.

Parameter	Value	Description
Population size	50	Individuals per generation
Generations	50	Max number of iterations
Search range	[$K_p$: 0–20, $K_i$: 0–20, $K_d$: $-20$–20]	PID gain bounds
Initial population	Preset + LHS	One fixed + LHS sampling
Mutation strategy	Adaptive	Strength varies with diversity
Crossover fraction	80%	Offspring from crossover
Selection method	Roulette Wheel	Fitness-proportional selection
Crossover type	Single Point	One-point gene exchange
Fitness function	$5M_p+10e_{ss}+2T_s$	Weighted dynamic index
Termination	$\Delta J<{10}^{-6}$ or max gen	Convergence or max limit
Input variables	$[e,\dot{e}]$	Error and error rate
Output variables	$[K_p,K_i,K_d]$	PID gain outputs

.

Figure 3 presents the unit step responses of three PID controllers optimized using a genetic algorithm, namely, GA-PID1, GA-PID2, and GA-PID3. In comparison, a conventional controller tuned via the internal model control-based PID (IMC-PID) method exhibits a noticeably slower response, with a typical settling time of approximately 65 s. By contrast, the GA-optimized controllers significantly improve dynamic performance, reducing the settling time to around 10 s. This substantial enhancement highlights the ability of GA to efficiently search the parameter space and generate high-performance PID configurations tailored to the system’s dynamic characteristics.

As illustrated in Figure 3, GA-PID1 exhibits a noticeably higher overshoot of approximately 10%, along with a slower rise time compared to the other two configurations. This suboptimal performance can likely be attributed to an overly narrow parameter search range during the GA optimization process, which may have constrained the algorithm from exploring more effective PID gain combinations. In contrast, GA-PID2 and GA-PID3 not only achieve faster response times but also maintain lower overshoot levels of around 5%, indicating more favorable dynamic behavior. Among the two, GA-PID2 presents a slightly more balanced trade-off between speed and stability, making it the most effective configuration overall.

Table 2. Comparison of GA-PID parameter settings and optimal values.

Model	PID Search Range	Optimal PID Parameters	Fitness
GA-PID1	[10, 10, 10]	$K_p=5.2969$, $K_i=10.00$, $K_d=3.7019$	11.1086
GA-PID2	[20, 20, 20]	$K_p=10.9865$, $K_i=20.00$, $K_d=9.4643$	10.3713
GA-PID3	[20, 30, 20]	$K_p=12.4018$, $K_i=30.00$, $K_d=14.5523$	10.1133

summarizes the parameter search ranges and the corresponding optimal PID values obtained through optimization of the genetic algorithm (GA). The selection of search boundaries plays a crucial role in shaping control performance. If the range is too wide, it may produce outlier parameter sets that lead to unstable system responses and introduce noise into the training data, ultimately degrading the generalization capability of the ANFIS model.

Although GA is well-suited for global exploration, it may yield extreme parameter combinations that cause undesirable behaviors such as excessive overshoot or long settling times. These effects negatively impact the quality and consistency of the training dataset. Therefore, adopting a conservative and well-defined parameter range is essential for generating high-quality and stable training data.

Given these considerations, the parameter range used in GA-PID2 was selected as the basis for ANFIS dataset generation. This configuration achieves a favorable balance between dynamic diversity and parameter stability, effectively avoiding overfitting and ensuring that the data is both representative and consistent. As a result, it supports improved accuracy, robustness, and generalization in the trained ANFIS model.

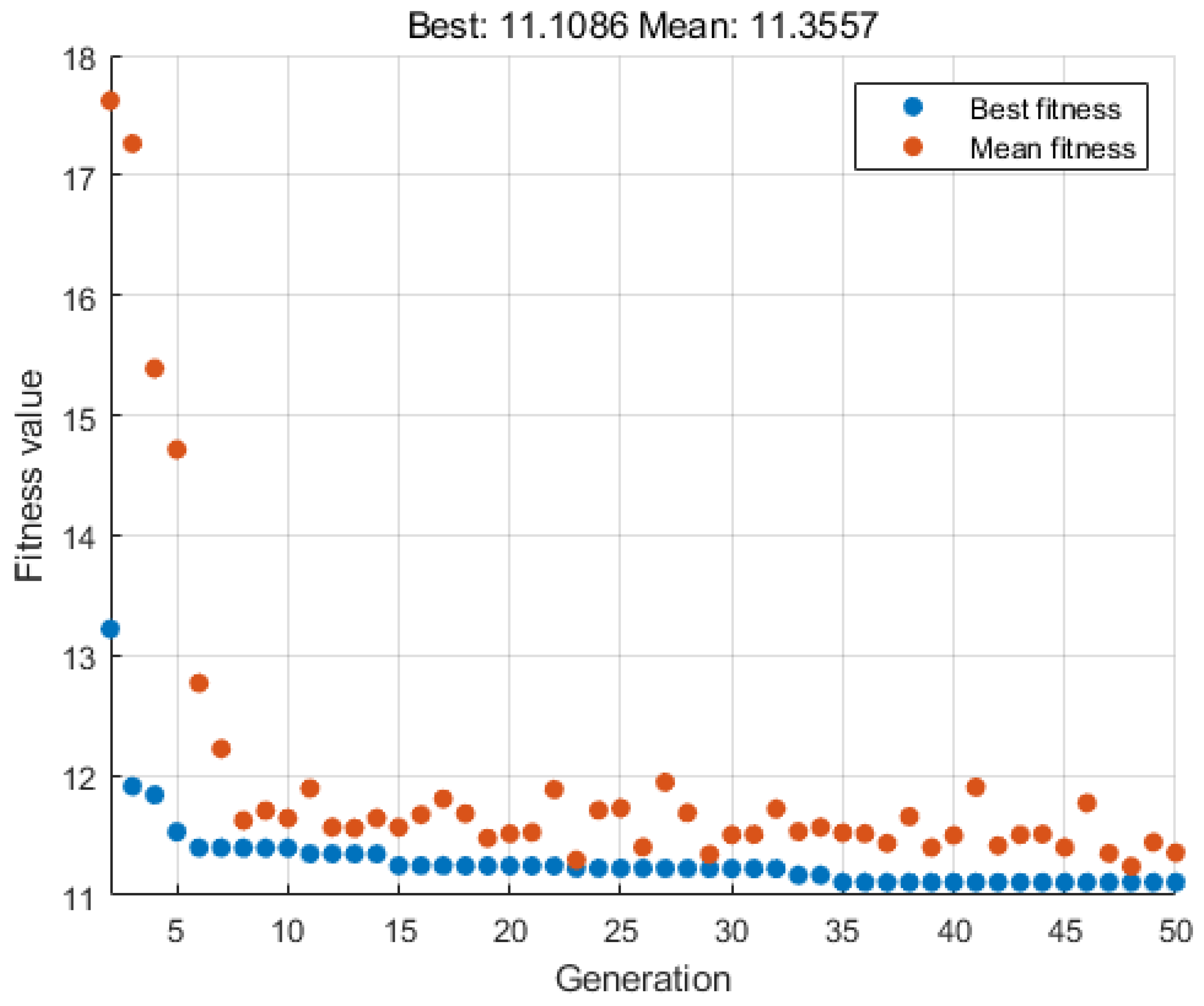
Based on the data presented in Figure 4, utilizing the parameter search range established by GA-PID2, a total of 862 distinct PID parameter sets were successfully generated across 50 iterations of the genetic algorithm. It is noteworthy that the optimal fitness value was identified as early as the 35th generation. Subsequently, the average fitness of the population progressively converged toward this optimal value, eventually stabilizing at 11.1087. This stabilization signifies robust convergence behavior, highlighting the effectiveness of the genetic algorithm in identifying high-quality PID parameter sets for subsequent ANFIS training.

To ensure the reliability and consistency of the training data, only individuals from populations with an average fitness value below 15 were retained in the dataset. Each PID configuration was simulated to obtain the corresponding unit step response, from which key performance features were extracted. The training inputs consisted of the error signal e and its derivative $ec$, while the outputs were the associated PID parameters ($Kp$, $Ki$, and $Kd$). This filtering strategy effectively eliminated unstable or suboptimal parameter sets, ensuring that even suboptimal samples were close to the global optimum, thereby enhancing the overall quality of the training dataset.

By leveraging the global search capability of the genetic algorithm, the resulting dataset covered a broad solution space while avoiding entrapment in local minima. This comprehensive and carefully curated sampling process establishes a strong foundation for training the subsequent ANFIS–PID controller and enhances its generalization and robustness.

Although GA performs well in global optimization under static conditions, its offline nature restricts adaptability. To overcome this limitation, we embed knowledge derived from GA into a real-time adaptive control framework using ANFIS.

3. ANFIS-Based Adaptive PID Tuning

3.1. Model Structure of ANFIS-PID Controller

The proposed ANFIS model, as shown in Figure 5, is based on a Sugeno-type fuzzy inference system. It takes two inputs—the error (e) and its rate of change ($ec$)—and produces three outputs corresponding to the PID controller gains—$K_p$, $K_i$, and $K_d$.

The inference mechanism is constructed using a total of 49 fuzzy rules, where each rule maps the same input pair $(e,ec)$ to a set of linear output functions for the three PID parameters. For example,

Rule i: If e is $A_i$ and $ec$ is $B_i$, then

$$\left\{\begin{array}{c}{K}_p^{\left(i\right)}=p_{i}e+q_{i}ec+r_i\hfill \\ K_i^{\left(i\right)}=p_i^{\prime }e+q_i^{\prime }ec+r_i^{\prime }\hfill \\ K_d^{\left(i\right)}=p_i^{\prime \prime }e+q_i^{\prime \prime }ec+r_i^{\prime \prime }\hfill \end{array}\right.$$

(12)

Here, $A_i$ and $B_i$ represent the fuzzy membership functions for the inputs e and $ec$, while $p_i,q_i,r_i$ (and their respective counterparts) are the consequent parameters associated with each output.

Given 49 rules and 3 outputs per rule, the network effectively consists of 147 distinct linear models, providing rich representational capacity to capture nonlinear control behaviors.

3.2. Layered Inference Mechanism

The ANFIS model is composed of five sequential layers, each responsible for a specific operation in the fuzzy inference process:

Layer 1: Fuzzification Each input variable, e and $ec$, is transformed into a fuzzy value using a membership function:

$$O_{1,i}={\mu }_{A_i}\left(x\right)$$

(13)

The generalized bell-shaped membership function is adopted:

$${\mu }_{A_i}\left(x\right)={\left[1+{\left|{\displaystyle \frac{x-c_i}{a_i}}\right|}^{2b_i}\right]}^{-1}$$

(14)

where $a_i$, $b_i$, and $c_i$ denote the shape, slope, and center parameters, respectively.

Layer 2: Rule evaluation Each node in this layer corresponds to a fuzzy rule. The firing strength ${\omega }_k$ of the k-th rule is calculated as the product of the membership grades of all inputs:

$$O_{2,k}={\omega }_k=\prod _{j=1}^n{\mu }_{A_{j,k}}\left(x_j\right)$$

(15)

Layer 3: Normalization The firing strengths are normalized to ensure they sum to unity:

$$O_{3,k}={\overline{\omega }}_k={\displaystyle \frac{{\omega }_k}{{\sum }_{l=1}^R{\omega }_l}}$$

(16)

Layer 4: Defuzzification Each node computes a weighted linear output based on the normalized firing strength:

$$O_{4,k}={\overline{\omega }}_k·f_k={\overline{\omega }}_k(p_{k}e+q_{k}ec+r_k)$$

(17)

Layer 5: Output Aggregation The overall system output is obtained by summing all the weighted rule outputs:

$$O_5=\sum _{k=1}^R{\overline{\omega }}_k{f}_k$$

(18)

The complete structure of the network implementing this five-layer inference process is illustrated in Figure 6.

3.3. Hybrid Learning and Parameter Training

With the network structure defined, we now turn to the training methodology that ensures accurate approximation of the PID gain functions.

The parameters of the membership functions, namely, $a_i$, $b_i$, and $c_i$, are iteratively optimized through an error-driven learning process across multiple epochs. The training phase employs a hybrid learning algorithm that combines gradient descent with least squares estimation to refine both the premise and consequent parameters.

The overall workflow is illustrated in Figure 7 and includes dataset partitioning, parameter initialization, model training, and evaluation criteria.

This process ensures that the Extreme-ANFIS model can accurately learn the nonlinear mapping from the inputs e and $ec$ to the PID control gains $K_p$, $K_i$, and $K_d$, while minimizing the output error.

3.4. Implementation Overview

This layered approach enables ANFIS to accurately approximate the nonlinear relationships between the inputs and the PID parameters. The performance of the model is improved through a combination of fuzzy inference rules and optimized parameters of the membership function.

4. Simulation Results and Discussion

Based on the visualization in Figure 8 and the quantitative results summarized in

Table 3. Optimization parameters and error evaluation of ANFIS under different NC values.

NC	3	5	7	9
Parameters	9	25	49	81
RMSE	0.6451	0.5893	0.5542	0.5670

, the root mean square error (RMSE) of ANFIS models trained on datasets generated via the genetic algorithm exhibits significant variation across different numbers of clusters (NCs). Four configurations were evaluated, with NC values of 3, 5, 7, and 9.

As the number of clusters increases, a general downward trend in RMSE is observed, suggesting that finer clustering resolution improves the model’s capacity to capture the underlying nonlinear relationships. However, the benefit of increased complexity diminishes beyond a certain point. Specifically, the model with NC = 3 exhibits the highest error (RMSE = 0.6451), indicating insufficient capacity to represent the system dynamics. As NC increases to 5, the RMSE drops to 0.5893, reflecting improved fitting accuracy. The best performance is achieved at NC = 7, where the RMSE reaches its lowest value of 0.5542, with fast convergence and minimal fluctuation. However, further increasing NC to 9 results in a slight rise in error (RMSE = 0.5670), along with visible oscillations in the training curve, indicating a tendency toward overfitting and parameter redundancy. While increasing the number of fuzzy rules (e.g., NC = 9) theoretically enhances the model’s expressiveness, it also introduces more parameters, which may degrade generalization, particularly in the presence of limited training diversity or numerical noise, as evidenced by the slightly increased RMSE and training instability.

Given these findings, the NC = 7 configuration was adopted as the baseline for subsequent modeling and control experiments. Under this setting, the ANFIS model trained using a hybrid learning algorithm demonstrated the best overall performance, achieving the lowest training RMSE (0.5542) and exhibiting minimal fluctuations. The predicted outputs closely matched the actual values, and the error distribution approximated a Gaussian profile, indicating strong generalization and predictive accuracy. 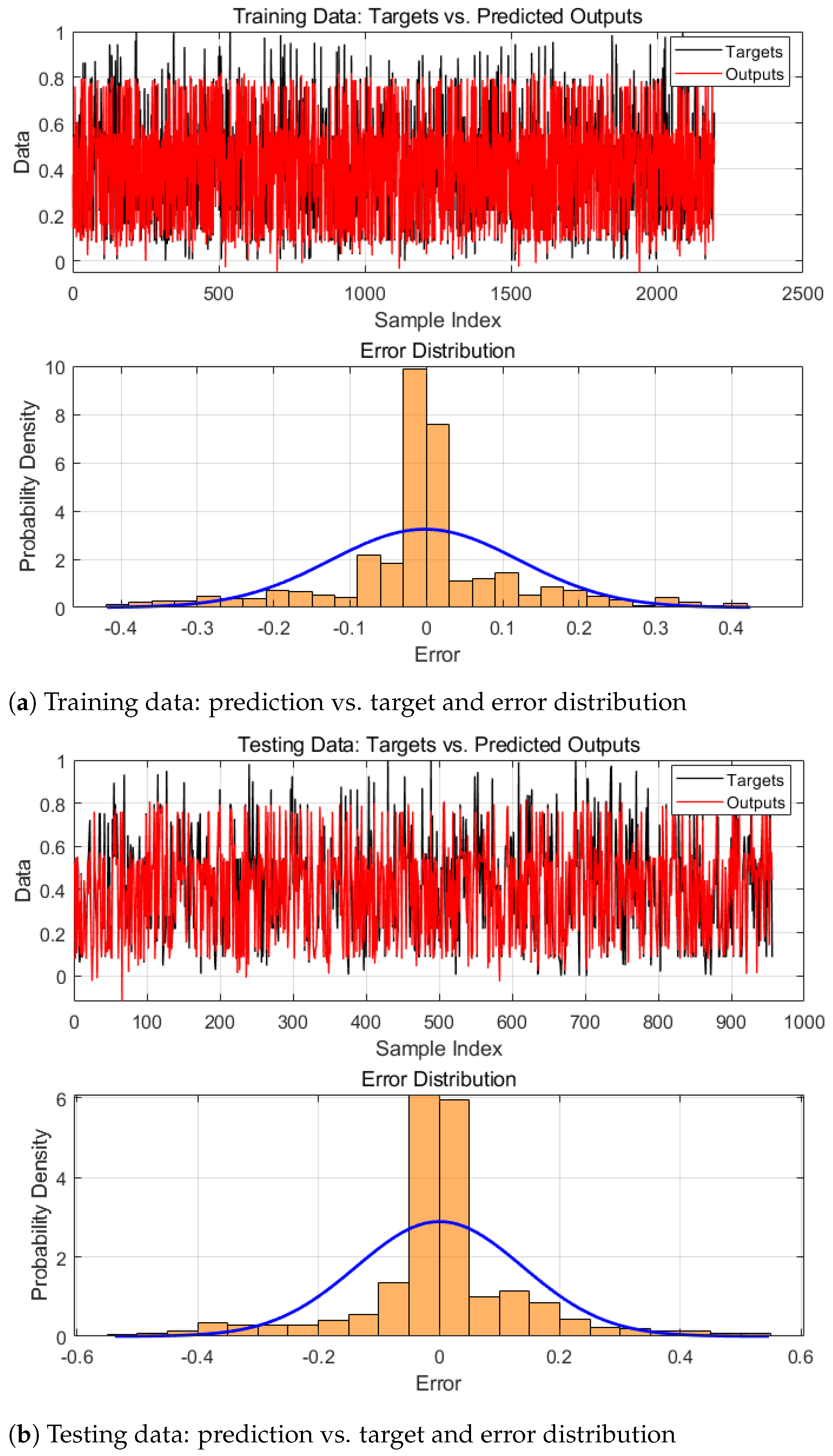Figure 9 illustrates the predictive performance of the ANFIS model trained using the GA-based dataset on both the training and testing sets. As shown in Figure 9a,b, the predicted outputs closely match the actual targets, indicating strong fitting capability and generalization performance. The corresponding error distribution plots demonstrate that most prediction errors are concentrated around zero and approximately follow a normal distribution, further validating the effectiveness of the model structure and parameter configuration. Overall, the proposed ANFIS model exhibits stable and accurate prediction performance across both datasets, fulfilling the accuracy and robustness requirements for controller design.

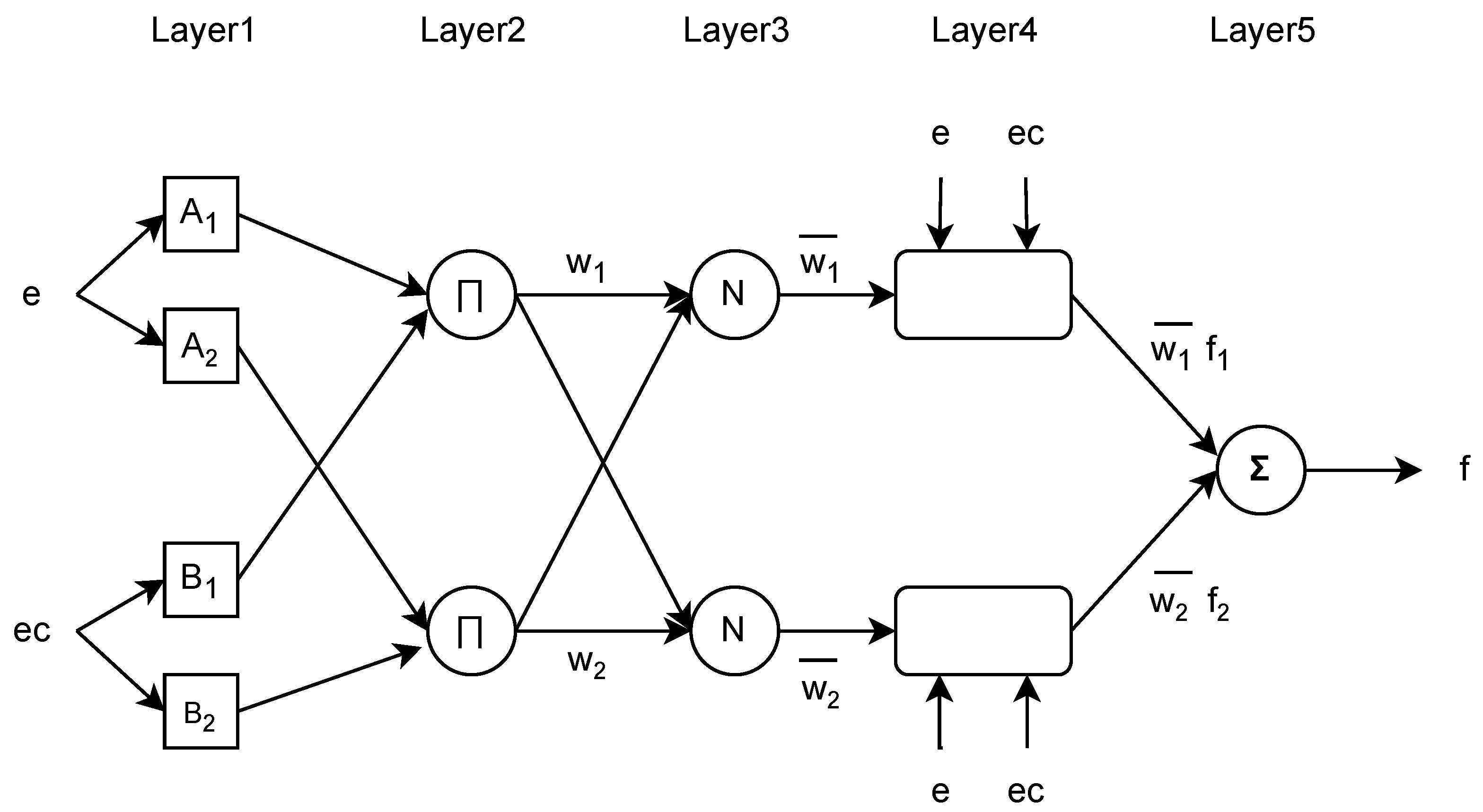
Structurally, the ANFIS model developed using the Fuzzy C-Means (FCM) clustering algorithm consists of 49 parameters. Among them, 28 are premise parameters that define the membership functions of the input variables e and $ec$, while the remaining 21 are consequent parameters that determine the linear outputs of the fuzzy rules. This configuration provides a well-balanced compromise between model complexity and representational capacity, making it well suited for nonlinear control applications.

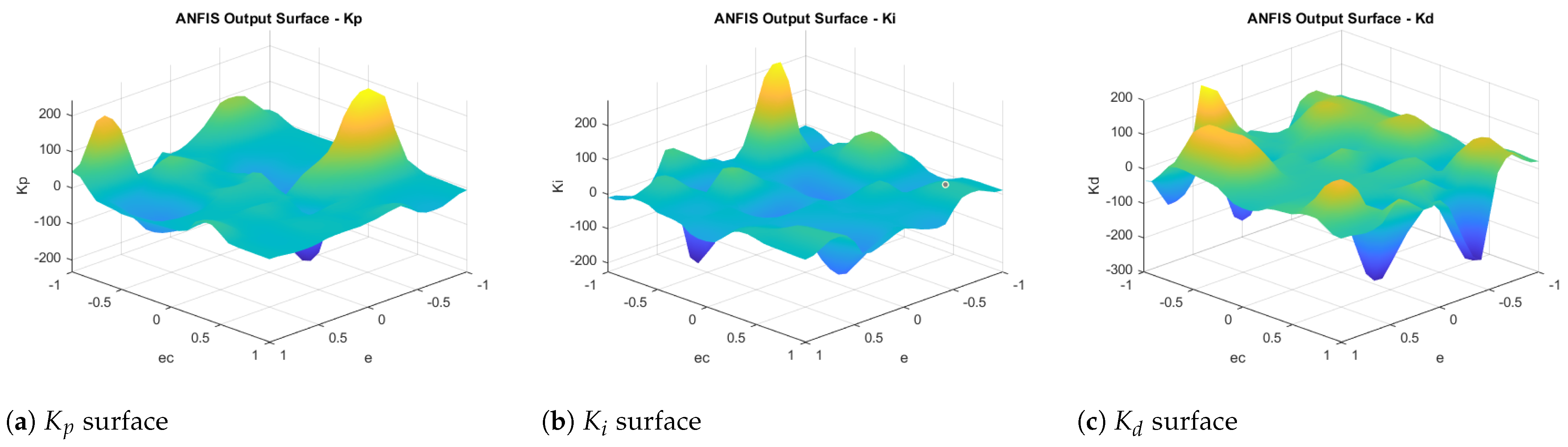
While the preceding analysis validates the external performance of the ANFIS model using RMSE, it is also instructive to examine the internal control logic learned by the model. To visualize the internal control strategy learned by the ANFIS model, Figure 10 presents the three-dimensional output surfaces of the PID gains ($K_p$, $K_i$, and $K_d$) as functions of the input variables e and $ec$. These surfaces demonstrate how the model dynamically adjusts each gain in response to the current error and its rate of change, thereby capturing the system’s nonlinear characteristics.

The generalized bell-shaped membership function was employed for input fuzzification, with the fuzzy domain defined over the interval $(-1,1)$. During training, the parameters of these membership functions were optimized to satisfy both transient and steady-state performance objectives, which are key criteria in fuzzy control design. The resulting surfaces represent the underlying control strategy learned through the data-driven training process.

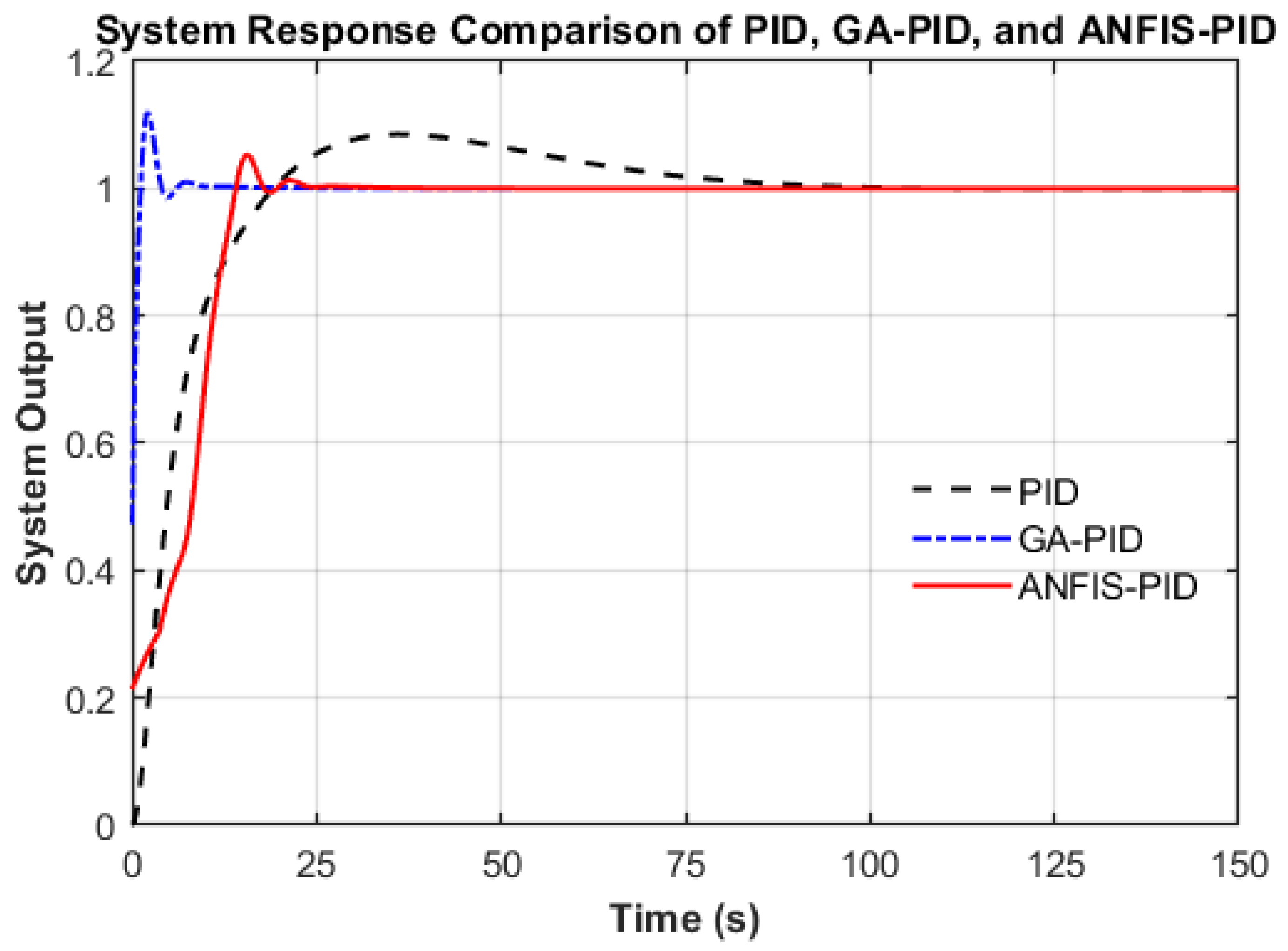
Figure 11 illustrates the system step response under three different control strategies—the conventional PID controller (black dashed line), the genetic algorithm–optimized PID controller (GA-PID, blue dash-dot line), and the adaptive neuro-fuzzy inference system PID controller (ANFIS-PID, red solid line).

To evaluate the dynamic performance of each controller, two primary time-domain metrics were analyzed—overshoot and settling time. The conventional Ziegler–Nichols (ZN)-tuned PID controller exhibited an overshoot of approximately 8% and a settling time of around 90 s, indicating limited adaptability to dynamic changes and insufficient accuracy for rapid thermal regulation. These shortcomings are mainly due to the use of fixed PID gains, which cannot accommodate nonlinear effects such as the coupling between damping and temperature in SPAD thermal control systems.

The GA-PID controller significantly reduces the settling time to 10 s by leveraging globally optimized parameters obtained through evolutionary search. However, this improvement comes with a trade-off—the overshoot increases to approximately 10%, and the transient phase exhibits noticeable oscillations. This behavior results from the optimization process prioritizing fast response, leading to an elevated proportional gain ($K_p$) that accelerates system reaction but amplifies overshoot. At the same time, the integral gain ($K_i$) receives relatively low optimization weight, which, while sufficient to ensure steady-state convergence, is inadequate to suppress the accumulation of overshoot during the transient stage.

In contrast, the ANFIS-PID controller achieves a more balanced and superior performance, with an overshoot of just 4% and a settling time of 25 s—providing fast, stable, and accurate control without oscillation. Unlike GA-PID, which relies on offline tuning for fixed scenarios, ANFIS-PID leverages GA-optimized data as a foundation and further improves upon it by adapting PID gains in real time through fuzzy inference. This dynamic adjustment enables the controller to maintain optimal performance under varying conditions. Therefore, ANFIS-PID not only retains the global optimization advantages of GA-PID but also surpasses it by enhancing robustness and adaptability, effectively resolving the typical “speed–overshoot” trade-off encountered in static control schemes.

In summary, ANFIS-PID integrates the global optimization capabilities of GA with adaptive fuzzy inference, forming a hybrid intelligent control strategy. Its measured performance—4% overshoot and 25-s settling time—clearly outperforms Z-N PID (8%, 90 s) and GA-PID (10%, 10 s), validating its value as a robust and precise solution for nonlinear and high-precision thermal control systems.

4.1. Disturbance Communication

Beyond nominal step responses, controller performance under external disturbances and structural perturbations is critical. The following sections evaluate robustness under such scenarios.

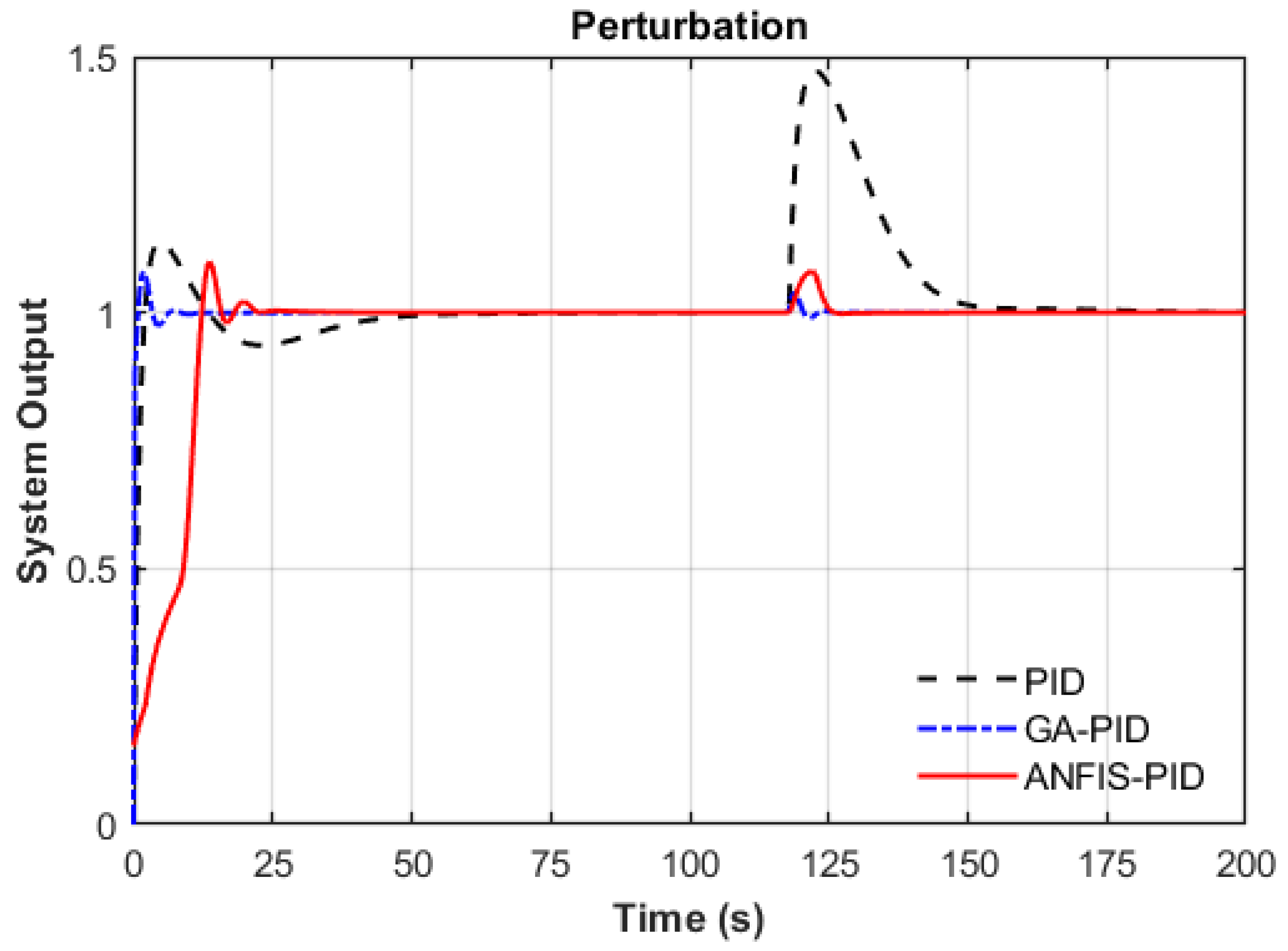
As illustrated in Figure 12, a step disturbance of magnitude 0.4 is introduced at 120 s to evaluate the disturbance rejection capabilities of the three controllers. The conventional PID controller exhibits a pronounced overshoot, peaking near 1.5, and requires considerable time to return to steady state, highlighting its limited robustness.

The GA-PID controller, optimized through a global search algorithm, significantly improves performance with a reduced overshoot of approximately 6% and a post-disturbance peak of 1.04. However, its static parameter structure limits its adaptability to dynamic system variations.

In contrast, the ANFIS-PID controller—built upon the GA-PID framework and augmented with adaptive fuzzy inference—achieves comparable steady-state performance while offering enhanced robustness under disturbances. Although it presents a slightly higher nominal overshoot of around 9%, its post-disturbance peak remains well-controlled at 1.07. This result demonstrates that ANFIS-PID not only inherits the globally optimized baseline of GA-PID but also enhances disturbance rejection through real-time gain adjustment, making it more suitable for complex and time-varying environments.

4.2. Zero-Damping Response Evaluation

Figure 13 compares the control performance of three strategies under a zero-damping condition, where the damping term is removed from the system model to simulate abrupt dynamic changes. The Ziegler–Nichols PID controller, tuned for the original system, fails to adapt and exhibits persistent high-amplitude oscillations without convergence, revealing its sensitivity to model variations. The GA-PID controller, re-optimized offline for the updated model, reduces oscillation amplitude but is still limited by its static parameter configuration, requiring repeated retuning for different conditions. In contrast, the ANFIS-PID controller delivers a smooth response with minimal overshoot and no need for offline reconfiguration, leveraging fuzzy inference trained on GA-optimized data to dynamically adjust gains, such as increasing the derivative component to compensate for the lack of physical damping. These results highlight that while GA-PID enhances performance through global optimization, ANFIS-PID extends adaptability by combining offline learning with real-time parameter adjustment, offering a robust and generalizable solution for control tasks under unmodeled dynamics.

4.3. Negative-Damping Robustness Test

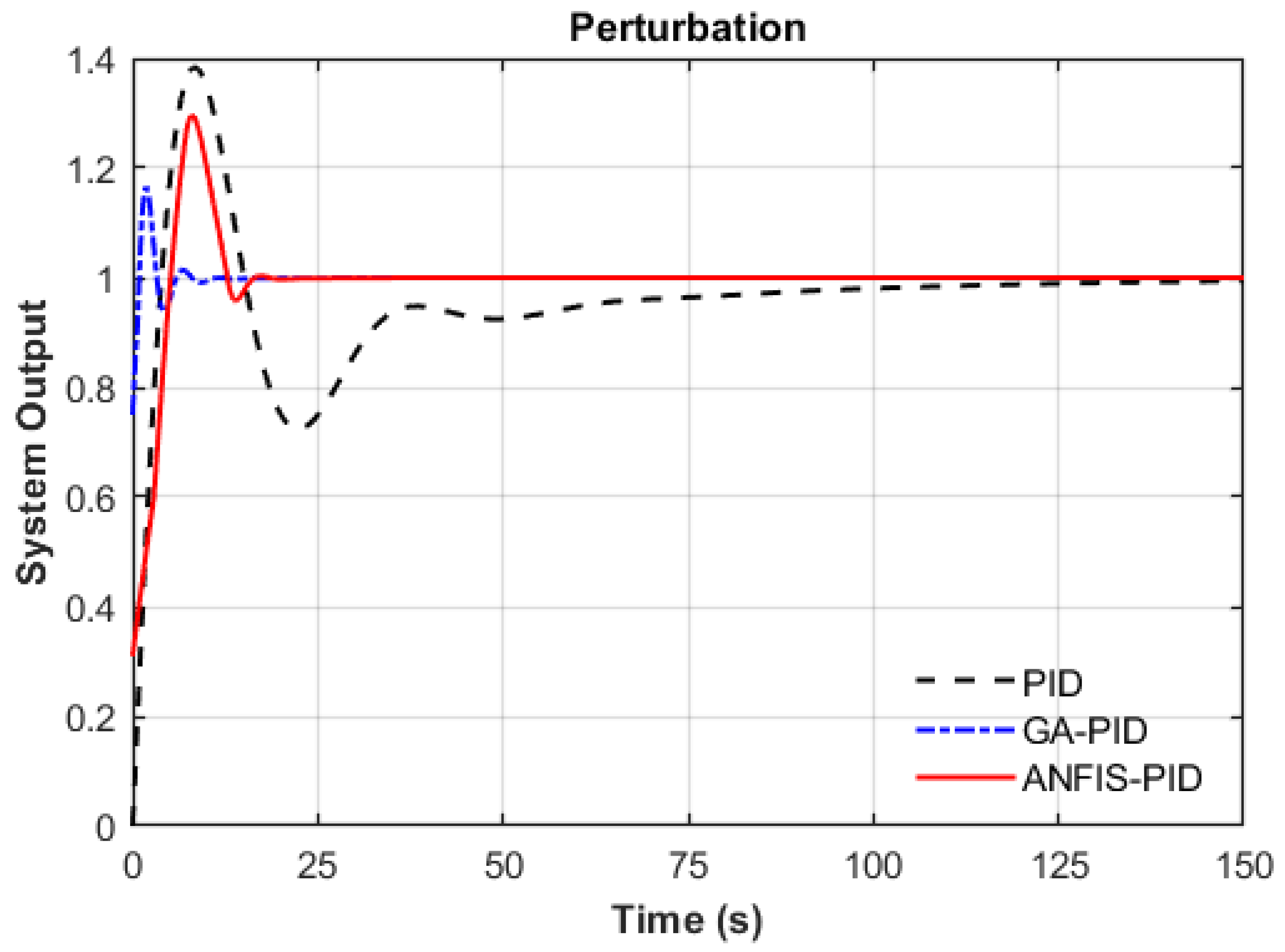
Figure 14 and Figure 15 compare the disturbance rejection performance of PID, GA-PID, and ANFIS-PID controllers under an unstable system with negative damping ($d=-0.1$), simulating a divergent dynamic environment. In Figure 14, the original PID controller (without retuning) becomes unstable, exhibiting increasing oscillation amplitudes and complete failure to suppress the disturbance. In contrast, both GA-PID and ANFIS-PID maintain system stability, with ANFIS-PID showing better damping characteristics.

In Figure 15, the PID controller is retuned using the Ziegler–Nichols method, which improves stability but still results in notable overshooting and oscillation. The recalculated GA-PID achieves the best overall suppression performance due to its scenario-specific re-optimization. Nevertheless, ANFIS-PID continues to maintain a stable, accurate response without offline retuning, demonstrating strong disturbance attenuation and general robustness. A closer quantitative comparison of Figure 14 and Figure 15 highlights these differences. In Figure 14, ANFIS-PID stabilizes around 10 s despite strong external perturbations, while the re-optimized GA-PID stabilizes more quickly at approximately 6 s. In Figure 15, the GA-PID controller achieves a lower overshoot (about 1.18) and settles within 13 s, whereas ANFIS-PID settles more slowly (approximately 18 s) with a slightly higher overshoot (about 1.30). Despite this, ANFIS-PID’s ability to retain robust performance across varying conditions without the need for scenario-specific adjustment confirms its generalization advantage. Across all scenarios from Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15, ANFIS-PID consistently delivers superior control performance—balancing low overshoot, fast settling, and adaptive resilience—particularly in the presence of modeling uncertainty, structural changes, or external disturbances. These results confirm ANFIS-PID as a reliable and versatile solution for complex, nonlinear, and time-varying systems.

In addition to controlling performance, computational efficiency and deployment feasibility are also critical for real-world applications. Compared with GA-BPNN and traditional multi-scenario ANFIS-PID controllers, the proposed GA-ANFIS-PID achieves lower inference complexity and better deployability. GA-BPNN involves multi-layer neural networks, leading to high computational costs, while conventional ANFIS-PID requires large training datasets and exhibits heavier inference overhead.

In contrast, our controller uses a compact Sugeno-type ANFIS with 49 rules and 3 outputs, requiring only basic arithmetic operations per control step. The inference complexity is $\mathcal{O}\left(147\right)$, enabling efficient execution on microcontrollers or DSPs. Combined with fully offline GA optimization, the framework supports real-time adaptive control while remaining lightweight and hardware-friendly.

5. Conclusions

This study presents a hybrid adaptive control strategy for temperature regulation in SPAD-based detection systems by combining GA optimization with an ANFIS-based PID controller. The proposed GA-ANFIS-PID framework effectively addresses the nonlinearities and uncertainties of thermoelectric cooling systems, achieving improved control accuracy, robustness, and real-time adaptability compared to conventional and GA-tuned PID methods.

Simulation results demonstrate that the GA module generates high-quality PID datasets across diverse conditions, enabling the ANFIS to generalize effectively. The controller achieves reduced overshoot, faster settling time, and superior disturbance rejection under various test scenarios, including step inputs, zero damping, and unstable dynamics. Compared with existing methods, it exhibits strong adaptability in time-varying environments.

Nevertheless, the current validation is limited to simulations based on a verified TEC-SPAD model. Practical deployment may face challenges such as sensor delay, actuator saturation, and real-time computational constraints. In addition, the offline-trained ANFIS model may require retraining when faced with significant system changes.

Future work will focus on embedded implementation using DSP platforms and hardware-in-the-loop (HIL) testing. Deployment constraints like processing latency and memory usage will be examined to ensure applicability to real-world systems. Physical validation will be conducted in future work using real-time implementation on a microcontroller-based TEC regulation platform. Moreover, combining this approach with reinforcement learning or model predictive control may further improve adaptability in complex and uncertain thermal environments.