Improving the Reliability of Safety Instrumented Systems Under Degradation with an Alternating Testing Strategy

Abstract

This paper presents an alternating testing strategy to improve the reliability of multi-state safety instrumented systems (SISs) under degradation conditions. A dynamic Bayesian network (DBN) model is developed to assess SIS unavailability, integrating proof-testing parameters and capturing multi-state component behavior. Applied initially to the actuator layer of a SIS with a 1oo3 (one-out-of-three) redundancy structure, the study examines the impact of extended test durations, showing that the alternating strategy reduces non-zero test durations compared to the simultaneous test strategy. The approach is then extended to a complete SIS, with a case study demonstrating its potential to enhance system reliability and optimize maintenance management by considering degradation and redundancy factors.

1. Introduction

Industrial facilities can present risks to people and the environment. These risks must be analyzed, assessed, and ultimately reduced to a level acceptable by society [1]. If passive risk reduction measures are insufficient to reach this level, active protection elements such as safety instrumented systems (SISs) may be employed [2].

A SIS is an E/E/PE (Electrical/Electronic/Programmable Electronic) system dedicated to safety, designed to monitor the physicochemical parameters of Equipment Under Control (EUC), determine whether it must be placed in a safe state, and execute the necessary shutdown action [3]. The SIS is intended to reduce the risk of a given Risk Reduction Factor (RRF) to an acceptable residual level [4]. Depending on the extent of reduction required, a specific Safety Integrity Level (SIL) must be met, which imposes both performance expectations and architectural constraints [5]. Ideally, the Safety Instrumented Function (SIF) provided by the SIS would eliminate risk completely [3]. However, because the components of a SIS are not perfectly reliable, failures of the safety function can occur. The probability of such failures depends on the availability of the SIS components and the architecture of the system. This failure probability is measured using appropriate indicators, depending on the demand rate of the SIF [5].

When the SIS is frequently or continuously demanded (e.g., an anti-lock braking system), the performance metric is the Probability of Failure per Hour (PFH) [6]. For low-demand applications (less than once per year, e.g., airbags), the key metric is the Average Probability of Failure on Demand (PFD${}_{avg}$) [7,8]. In both cases, the SIS must execute its SIF when required. If one or more components fail or are temporarily unavailable due to maintenance or testing, the SIF may not be performed. Failures on demand often reveal latent faults or the temporary unavailability of components [5].

To detect latent failures, especially in low-demand SISs, internal checks such as sensor signal comparison, partial testing, or complete proof testing of SIS components can be conducted. However, components under test are not able to perform their safety function during the test, which directly affects their instantaneous performance and, consequently, increases the PFD${}_{avg}$ [4,9]. Thus, the testing strategy significantly affects performance and must be carefully evaluated [3]. This requires a flexible and accurate computational model that accounts for all relevant parameters, including those related to testing. It is equally crucial to characterize the system’s unavailability state during testing [10,11].

Several modeling tools are used to assess SIS performance [12]. Fault tree analysis is unsuitable when partial testing is involved [13,14], and analytic expressions can become too complex when many parameters must be considered [15]. Markov chains are well adapted for assessing unavailability with testing but become impractical when structural changes occur during component testing [16].

To address this, some authors propose switching Markov chains [17,18] or stochastic Petri nets [19,20]. However, Petri nets often require Monte Carlo simulations, which can be computationally expensive to yield accurate probability estimates. Bayesian networks (BNs) have emerged as attractive alternatives to switching Markov models due to their modeling simplicity [21] and their ability to reflect knowledge, such as known component states (e.g., under test or failed). Furthermore, dynamic Bayesian networks (DBNs), particularly those based on Two-Time Bayesian Networks (2TBNs), are well suited for capturing temporal variations in component reliability [21,22].

This article focuses on enhancing the reliability of SISs operating under degradation by proposing an alternating proof-testing strategy. To support this objective, a probabilistic modeling framework based on DBNs is developed to analyze the PFDavg under various testing configurations and system degradation scenarios. The study focuses on redundant architectures and aims to undertake the following:

• Investigate the influence of SIS architecture on the effectiveness of testing strategies.
• Develop a DBN model that accurately considers the behavior and dependencies of SIS components under testing conditions.
• Evaluate the impact of key test parameters (e.g., frequency, duration, and coverage) on system performance through a representative case study.

To address these objectives, the paper is structured as follows: Section 2 discusses the problem statement, examining the limitations in the current approaches for modeling low-demand SISs with proof testing. In Section 3, the system architecture is defined, with emphasis on KooN structures and their implications on availability during testing. Section 4 introduces the proposed DBN modeling approach and the integration of the test-related parameters. In Section 5, the proposed model is applied to a case study, evaluating the testing strategies and quantifying their effects on PFDavg. Finally, Section 6 presents the main conclusions of this work and outlines directions for future research.

2. Problem Statement

In safety instrumented systems (SISs) operating in low-demand mode, performance is predominantly determined by three interrelated factors: the reliability of individual components, the system architecture, and the proof test strategy implemented. The Average Probability of Failure on Demand (PFDavg), which serves as a key performance indicator in accordance with international safety standards such as IEC 61508 [5] and IEC 61511 [23], is directly influenced by these dimensions.

One of the critical challenges lies in the design and implementation of effective proof test strategies, which are inherently dependent on the architecture of the SIS. In simple 1oo1 configurations, which lack redundancy, testing any component renders the entire SIS temporarily unavailable. This creates a significant exposure to risk during the test period and imposes operational constraints, particularly in continuous process industries where shutdowns are costly or infeasible. In such cases, the number of testing strategies that can be effectively implemented is severely limited, as components cannot be tested independently without compromising the safety function.

The situation changes fundamentally when redundancy is introduced within the SIS layers, such as in K-out-of-N (KooN) architectures (e.g., 1oo2 and 2oo3). Redundancy not only improves fault tolerance but also expands the range of applicable proof test strategies. With redundant components, the following become possible:

• Testing components of each layer alternately, ensuring that at least one component remains operational to maintain the safety function.
• Testing success paths within the redundant architecture, targeting specific combinations of components required to fulfill the safety objective.

These architectural choices open the door to alternating testing strategies, which support a more flexible and dynamic approach to maintenance and reliability management. However, optimizing such strategies requires a systematic understanding of the interdependencies among architectural redundancy, test sequencing, and component degradation behavior.

Moreover, many existing reliability models assume perfect and instantaneous testing, ignoring the realities of imperfect proof testing, non-zero test durations, and progressive degradation of components over time. These simplifications limit their applicability in real-world industrial environments, where such factors significantly affect overall system availability.

3. Safety Instrumented System Structure

To ensure safety functions, various structural approaches can be used. One straightforward method is to design a system of three distinct layers. The initial layer is tasked with monitoring the physicochemical characteristics through sensors. The logical layer processes inputs, computes decisions, and performs online diagnostics. Finally, the actuator layer executes the determined responses [17]. These layers typically adopt redundant architectures that consist of one or more components. Among the commonly utilized redundant structures are M-out-of-N (MooN) voting structures [18]. In such structures, MooN indicates that at least M out of the N components must operate correctly for the safety function to be effectively ensured.

In a standard MooN voting structure, if M equals N, it represents a serial system with N components. Conversely, if M equals 1, it signifies a parallel system with N components. This redundancy configuration is referred to as 1 out of N (1ooN) [18].

3.1. Safety Instrumented System Structure

Figure 1 shows the whole structure of a typical safety instrumented system that monitors an Entity Under Control (chemical reactor). When designing safety instrumented systems, various layer structures must be considered, each incorporating redundant channels sensitive to common cause failure. In Figure 1, actuators (FCs) and Logic Solvers (LSs) are arranged in 1oo3 voting structures. The sensor layer is separated into temperature and pressure sections, each employing a 1oo2 voting architecture.

For clarity of the applicability of the proposed methodology, this study focuses on the actuator layer, modeled as a 1oo3 configuration consisting of three identical valves. These valves are designed to isolate flow and reduce excess pressure when safety limits are surpassed, ensuring the protection of the system as long as at least one valve functions as required on demand [18].

The choice of this redundant layer as the focal point allows for a detailed analysis of testing strategies while maintaining the general applicability of the approach. Since this layer predominantly comprises mechanical components, it is particularly susceptible to degradation mechanisms and performance loss over time, making it especially suitable for reliability evaluation.

The mean value of the PDF metric is used to assess a SIS operating in low-demand mode. Its assessment integrates various parameters such as failure rates, diagnostic coverage, and common cause failure. Additionally, the testing strategy must be integrated into the unavailability assessment process. Proof testing can be conducted through various test strategies [17].

3.2. Proof Test Strategies

The primary objective of proof testing is to uncover latent dangerous failures that may not be detected by online diagnostic tests [4]. This aspect is crucial in safety instrumented systems and should be integrated into performance assessments. Therefore, it is imperative to have a comprehensive understanding of the principal parameters related to proof testing. Various proof test strategies have been defined for safety instrumented system verification. The authors of [24] proposed the following classifications of these strategies:

• Simultaneous test: All the components are tested together, necessitating a sufficient number of repair teams to test all components simultaneously. The safety instrumented system becomes unavailable during simultaneous testing [25].
• Sequential test: The components are tested consecutively, one after the other. Once a component is tested and restored to service, the next component is tested, assuming that other components remain operational [21].
• Staggered test: All the safety instrumented system components are tested at different intervals. The most common form is the uniform staggered test, where each component has its own testing period, assuming the other components are functional.
• Random test: In this strategy, the test intervals for the components are not predetermined but are randomly chosen [24] or computed based on the current system state.

The selection of elements or combinations thereof for testing defines the strategy. For a redundant layer’s elements, choosing to test all or only one of them presents contrasting solutions, determining whether the Safety Instrumented Function remains available [18]. Additionally, proof testing effectiveness, harmlessness, and duration significantly impact performance index and modeling efforts [8]. As proof testing may not always detect all failures, its effectiveness is quantified by $\xi$, representing the inability to uncover undetected failures. The parameter $(1-\xi )$ denotes the fraction of all detected but undetected (DU) failures during a proof test, known as the proof test coverage by some researchers [3].

Other parameters related to proof testing, such as $\gamma$ (probability of failure due to the test) and $\pi$ (test duration), are crucial. $\gamma$ corresponds to on-demand failures resulting from proof testing, while $\pi$ represents the test duration during which the safety instrumented system is reconfigured, with the tested component rendered unavailable [21].

Considering a non-null test duration $\pi$ and component redundancy, alternating test strategies may be used. Instead of testing the entire layer at once, a subset of components (not the full set) can be tested individually, making them temporarily unavailable while still ensuring the overall availability of the layer. However, this approach is not applicable to 1-out-of-1 (1oo1) configurations, where no redundancy exists.

Despite their significance, proof-testing parameters are often overlooked in the modeling of unavailability. Therefore, the objective of this paper is to develop a model incorporating proof-testing parameters and analyze their effects on unavailability.

4. Materials and Methods

4.1. DBN Model

Dynamic Bayesian networks (DBNs) are probabilistic graphical models that capture temporal dependencies among variables by extending traditional Bayesian networks to handle sequential and time-series data. They model system dynamics by representing the probabilistic relationships between system states across successive time steps. Fundamental to DBNs are the principles of conditional probability and Bayes’ rule, which together enable the inference of system behavior over time.

In a DBN, the conditional probability $P(X_k\mid X_{k-1})$ denotes the likelihood of the system being in a particular state at time k, given its state at time $k-1$. This conditional distribution is governed by transition probabilities that encode how the system evolves temporally.

The general formulation of the transition model at time k is expressed as follows:

$$P(X_k\mid X_{k-1})=\prod _{i=1}^{n}P(X_k^i\mid \mathrm{pa}\left(X_k^i\right)),$$

(1)

where $X_k^i$ represents the $i\mathrm{th}$ node at time k, and $\mathrm{pa}\left(X_k^i\right)$ denotes the set of parent nodes of $X_k^i$, typically including nodes from time $k-1$. The term $P(X_k^i\mid \mathrm{pa}\left(X_k^i\right))$ corresponds to the conditional probability of node $X_k^i$ given its parents, often encoded via Conditional Probability Tables (CPTs). Equation (1) thus defines the joint distribution on all the variables at time k, conditioned on their respective parents.

4.2. System Unavailability Modeling

To model the performance of a safety instrumented system (SIS) under varying proof-testing conditions, we extend the transition model to incorporate a test state variable $T_k$. Specifically, we determine $P(X_k\mid X_{k-1},T_k)$, which represents the probability distribution of the state system at time k, given its state at the previous time step $X_{k-1}$ and the test condition $T_k$. This extension allows for the representation of context-sensitive transitions, enabling the DBN to account for modifications in system behavior during proof-testing phases.

The DBN model thus explicitly integrates the temporal dimension of the target system behavior [26]. At each discrete time step $k·\Delta T$, the system state is modeled by a random variable $X_k\in \{s_1^X,\dots ,s_M^X\}$, with its distribution determined via a CPT conditioned on $X_{k-1}$. The exogenous variable $T_k$, representing the activity of the proof test, serves as a selector of transition models, capturing changes in the architecture or behavior of the system. The states of the proof test $T_k$ are defined as follows:

• $T_k=0$: test inactive;
• $T_k=1$: test active;
• $T_k=0\to 1$: test initialization phase;
• $T_k=1\to 0$: test completion phase.

This modeling approach enables a structured and dynamic representation of SIS behavior throughout the operational and testing phases, as depicted in Figure 2.

In the proposed model, we consider a DBN defined over discrete time steps $k\in \mathbb{N}$, where the system is characterized by three main variables:

• $X_k$ is the system state at time step k.
• $X_k\in {\mathcal{S}}^X=\{s_1^X,\dots ,s_M^X\}$ is the system’s operational state at time k).
• $s_i^X$ is the $i^{\mathrm{th}}$ possible state of the system at time k, with $i\in \{1,\dots ,M\}$.
• $T_k\in {\mathcal{S}}^T=\{0,0\to 1,1,1\to 0\}$ is the test state variable at time k, where ${\mathcal{S}}^T$ is the set of all possible test states.
• $U_k\in {\mathcal{S}}^U=\{s_1^U,s_2^U\}$ is the unavailability indicator, where $s_r^U$ is the $r^{\mathrm{th}}$ possible unavailability state of layer, with $r\in \{1,2\}$ typically indicating available or unavailable.

The evolution of the system’s state is governed by a time-inhomogeneous Markov process conditioned on the test state $T_k$

$$\underset{\_}{\begin{array}{ccccc}\hfill & & & X_k& \\ \hfill & & s_1^X\hfill & \dots \dots & s_M^X\\ \hfill & s_1^X& q_{11}^l\hfill & \dots \dots & q_{M1}^l\\ \hfill & & & & \\ \hfill X_{k-1}& ⋮& ⋮& & ⋮\\ \hfill & & & & \\ \hfill & s_M^X& q_{1M}^l\hfill & \dots \dots & q_{MM}^l\end{array}}$$

(2)

with $P(X_k=s_j^X\mid X_{k-1}=s_i^X,T_k=l)=q_{ij}^{\left(l\right)},\forall i,j\in \{1,\dots ,M\},l\in {\mathcal{S}}^T$.

The matrix $Q^{\left(l\right)}=\left[q_{ij}^{\left(l\right)}\right]\in {\mathbb{R}}^{M\times M}$ denotes the conditional transition matrix under the test condition $T_k=l$.

The gray node $U_k$ in Figure 2 represents the instantaneous unavailability of the system layer, modeled as a probabilistic function of the current system state $X_k$ and the proof test condition $T_k$. It reflects the likelihood that the layer is unable to perform its safety function at time step k, considering the system’s evolving behavior and the current test phase.

$$\underset{\_}{\begin{array}{ccccc}\hfill & & & U_k& \\ \hfill & & s_1^U\hfill & & s_2^U\\ \hfill & s_1^X& \hfill p_{11}^l& & p_{21}^l\\ \hfill & & & & \\ \hfill X_k& ⋮\hfill & ⋮\hfill & & ⋮\\ \hfill & & & & \\ \hfill & s_M^X& \hfill p_{1M}^l& & p_{2M}^l\end{array}}$$

(3)

with $p_{ir}^{\left(l\right)}=P(U_k=s_r^U\mid X_k=s_i^X,T_k=l),\forall i\in \{1,\dots ,M\},r\in \{1,2\},l\in {\mathcal{S}}^T$.

$p_{ir}^{\left(l\right)}$ is the conditional probability that the system is in unavailability state $s_r^U$, given it is in system state $s_i^X$ and the test condition is $T_k=l$.

The instantaneous unavailability is computed as the sum of the probabilities corresponding to the system states in which the layer fails to perform its safety function. The PFD at time step k is expressed as

$$\mathrm{PFD}\left(k\right)=\sum _{i=1}^M{p}_{ir}^{\left(l\right)}·P(X_k=s_i^X)·P(U_k=s_2^U)$$

(4)

Throughout a proof test cycle of duration $i·T_i$, where $T_i$ denotes the interval between two successive tests, the average unavailabilityis estimated using discrete-time numerical integration as follows:

$${\mathrm{PFD}}_{\mathrm{avg}}={\displaystyle \frac{1}{i·T_i}}\sum _{k=1}^{i·T_i}\mathrm{PFD}\left(k\right)$$

(5)

4.3. Study of a 1oo3 Structure

A 1-out-of-3 (1oo3) architecture comprises three elements configured in parallel, each independently capable of performing the required safety function. This redundant structure ensures that the system remains operational and continues to provide the intended safety function as long as at least one of the three elements remains functional. This configuration enhances system reliability by tolerating up to two individual element failures without compromising overall safety [16].

In this study, an alternating test strategy is used at a fixed frequency. During testing, only one component out of three is tested while the others remain in service. Consequently, the 1oo3 structure temporarily transitions to a 1-out-of-2 (1oo2) configuration during the test and reverts to a 1oo3 structure afterward (see Figure 3). The stochastic process part in the model, represented by the relationship between $X_{k-1}$ and $X_k$, conforms to a Markov model as illustrated in Figure 4a.

In a system composed of three components, each of which can be in one of three states—Functional (OK), Dangerous Detected (DD), or Dangerous Undetected (DU)—a total of 27 distinct global states must initially be considered. To reduce the model’s complexity, a state grouping technique is applied, simplifying the system to 12 representative states (cf. Figure 4b). However, this simplification results in the loss of detailed information about the condition of individual components.

When the proposed alternating test strategy is applied with a non-zero test duration, only one component is tested at a time within the 1oo3 configuration. During testing, the selected component is temporarily removed from service, while the system remains operational if the other two components are available. As a result, the specific condition of the tested component cannot be clearly determined. To address this limitation, the system is represented by three equivalent 1oo2 configurations, each corresponding to one of the components being tested and using the same probability distribution (cf. Figure 4b). Each representative state in the original 1oo3 structure is interpreted differently depending on the active test scenario $T_k$, as presented in

Table 1. States of a 1oo3 structure given test phase.

States	Test Phases
$1oo3\to 1oo2$	($T_k=0$)	($T_k=1$)
	($T_k=1\to 0$)	($T_k=0\to 1$)
$s_1$	{3OK}	{2OK}
$s_2$	{2OK, 1DD}	{1OK, 1DD}
$s_3$	{2OK, 1DU}	{1OK, 1DU}
$s_4$	{1OK, 2DD}	{2DD}
$s_5$	{1OK, 1DD, 1DU}	{1DD, 1DD}
$s_6$	{1OK 2DU}	{2DU}
$s_7$	{3DD}	{2OK}
$s_8$	{2DD, 1DU}	{1OK, 1DD}
$s_9$	{1DD, 2DU}	{1OK, 1DU}
$s_{10}$	{3DU}	{2DD}
$s_{11}$	-	{1DD, 1DD}
$s_{12}$	-	{2DU}
$s_{13}$	-	{2OK}
$s_{14}$	-	{1OK, 1DD}
$s_{15}$	-	{1OK,1DU}
$s_{16}$	-	{2DD}
$s_{17}$	-	{1DD, 1DU}
$s_{18}$	-	{2DU}

.

The detailed mechanism of this transition process is presented in the following, illustrating how each state in the 1oo3 configuration is reinterpreted within the corresponding 1oo2 structures, depending on the active proof test state $T_k$.

• If the test state is ineffective ($T_k=0$), the 1oo3 structure and its associated Conditional Probability Table are determined using the Markov graph in Figure 4a. The relative CPT for the 1oo3 structure, when the ($T_k=0$), is provided in

  Table 2. CPT of 1oo3 system when ($T_k=0$).

  	${\mathit{X}}_{\mathit{k}}$
  ${\mathit{T}}_{\mathit{k}}$	${\mathit{X}}_{\mathit{k}-\mathbf{1}}$	{3OK}	{2OK,1DD}	{2OK,1DU}	{1OK,2DD}	{1OK,1DD,1DU}	{1OK,2DU}	{3DD}	{2DD,1DU}	{1DD,2DU}	{3DU}
  	{3OK}	-	$3(1-{\beta }_D){\lambda }_{DD}$	$3(1-{\beta }_U){\lambda }_{DU}$	0	0	0	${\beta }_D{\lambda }_{DD}$	0	0	${\beta }_U{\lambda }_{DU}$
  	{2OK,1DD}	${\mu }_{DD}$	-	0	$2(1-{\beta }_D){\lambda }_{DD}$	$2(1-{\beta }_U){\lambda }_{DU}$	0	${\beta }_D{\lambda }_{DD}$	0	${\beta }_U{\lambda }_{DU}$	0
  	{2OK,1DU}	0	0	-	0	$2(1-{\beta }_D){\lambda }_{DD}$	$2(1-{\beta }_U){\lambda }_{DU}$	0	${\beta }_D{\lambda }_{DD}$	0	${\beta }_U{\lambda }_{DU}$
  	{1OK,2DD}	0	0	0	-	0	0	${\lambda }_{DD}$	${\lambda }_{DU}$	0	0
  	{1OK,1DD,1DU}	0	0	0	0	-	0	0	${\lambda }_{DD}$	${\lambda }_{DU}$	0
  0	{1OK,2DU}	0	0	0	0	0	-	0	0	${\lambda }_{DD}$	${\lambda }_{DU}$
  	{3DD}	0	0	0	$3{\mu }_{DD}$	0	0	-	0	0	0
  	{2DD,1DU}	0	0	0	0	$2{\mu }_{DD}$	0	0	-	0	0
  	{1DD,2DU}	0	0	0	0	0	${\mu }_{DD}$	0	0	-	0
  	{3DU}	0	0	0	0	0	0	0	0	0	1

  .
• Upon test initiation ($T_k=0\to 1$), state probabilities before testing are redistributed across three anonymous 1oo2 structures, where one component is under test and the others are not. The corresponding CPT is outlined in

  Table 3. CPT of 1oo3 system when ($T_k=0\to 1$).

  ${\mathit{X}}_{\mathit{k}}$
  ${\mathit{X}}_{\mathit{k}-\mathbf{1}}$	{2OK}	{1OK,1DD}	{1OK,1DU}	{2DD}	{1DD,1DU}	{2DU}
  {3OK}	1/3	0	0	0	0	0
  {2OK,1DD}	1/6	1/6	0	0	0	0
  {2OK,1DU}	1/6	0	1/6	0	0	0
  {1OK,2DD}	0	1/6	0	1/6	0	0
  {1OK,1DD,1DU}	0	1/9	1/9	0	1/9	0
  {1OK, 2DU}	0	0	1/6	0	0	1/6
  {3DD}	0	0	0	1/3	0	0
  {2DD,1DU}	0	0	0	1/6	1/6	0
  {1DD,2DU}	0	0	0	0	1/6	1/6
  {3DU}	0	0	0	0	0	1/3

  .
• When the test is effective ($T_k=1$), the 1oo3 structure transitions into three 1oo2 architectures.

  Table 4. CPT of 1oo3 structure when ($T_k=1$).

  		${\mathit{X}}_{\mathit{k}}$
  ${\mathit{X}}_{\mathit{k}-\mathbf{1}}$	${\mathit{s}}_{\mathbf{1}}$	…	${\mathit{s}}_{\mathbf{6}}$	${\mathit{s}}_{\mathbf{7}}$	…	${\mathit{s}}_{\mathbf{12}}$	${\mathit{s}}_{\mathbf{13}}$	…	${\mathit{s}}_{\mathbf{18}}$
  $s_1$	-	–	-	0	…	0	0	…	0
  ⋮	-	1oo2	-	⋮	⋱	⋮	⋮	⋱	⋮
  $s_6$	-	–	-	0	…	0	0	…	0
  $s_7$	0	…	0	-	–	-	0	…	0
  ⋮	⋮	⋱	0	-	1oo2	-	⋮	⋱	⋮
  $s_{12}$	0	…	0	-	-	-	0	…	0
  $s_{13}$	0	…	0	0	…	0	-	–	-
  ⋮	⋮	⋱	⋮	⋮	⋱	⋮	-	1oo2	-
  $s_{18}$	0	…	0	0	…	0	-	–	-

  presents the Conditional Probability Table (CPT) for the 1oo3 structure under testing, derived from the Markov model shown in Figure 4b, where the CPT for the 1oo2 architecture is given in

  Table 5. CPT of 1oo2 structure.

  		${\mathit{X}}_{\mathit{k}}$
  ${\mathit{T}}_{\mathit{k}}$	${\mathit{X}}_{\mathit{k}-\mathbf{1}}$	{2OK}	{1OK,1DD}	{1OK,1DU}	{2DD}	{1DD,1DU}	{2DU}
  	{2OK}	-	$2·(1-{\beta }_D)·{\lambda }_{DD}$	$2·(1-{\beta }_U)·{\lambda }_{DU}$	${\beta }_D·{\lambda }_{DD}$	0	${\beta }_U·{\lambda }_{DU}$
  	{1OK,1DD}	${\mu }_{DD}$	-	0	${\lambda }_{DD}$	${\lambda }_{DU}$	0
  	{1OK,1DU}	0	0	-	0	${\lambda }_{DD}$	${\lambda }_{DU}$
  0	{2DD}	0	$2·{\mu }_{DD}$	0	-	0	0
  	{1DD,1DU}	0	0	${\mu }_{DD}$	0	-	0
  	{2DU}	0	0	0	0	0	1

  .
• At the test’s conclusion ($T_k=1\to 0$), the probabilities are reallocated from three 1oo2 structures to one 1oo3 architecture, guided by the CPT presented in

  Table 6. CPT of 1oo3 structure when $(T_k=1\to 0$).

  		${\mathit{X}}_{\mathit{k}}$
  ${\mathit{X}}_{\mathit{k}-\mathbf{1}}$	${\mathit{s}}_{\mathbf{1}}$	${\mathit{s}}_{\mathbf{2}}$	${\mathit{s}}_{\mathbf{3}}$	${\mathit{s}}_{\mathbf{4}}$	${\mathit{s}}_{\mathbf{5}}$	${\mathit{s}}_{\mathbf{6}}$	${\mathit{s}}_{\mathbf{7}}$	${\mathit{s}}_{\mathbf{8}}$	${\mathit{s}}_{\mathbf{9}}$	${\mathit{s}}_{\mathbf{10}}$
  $s_1$	$(1-\gamma )$	$\gamma ·(1-\xi )$	$\gamma ·\xi$	0	0	0	0	0	0	0
  $s_2$	0	$(1-\gamma )$	0	$\gamma ·(1-\xi )$	$\gamma ·\xi$	0	0	0	0	0
  $s_3$	0	0	$(1-\gamma )$	0	$\gamma ·(1-\xi )$	$\gamma ·\xi$	0	0	0	0
  $s_4$	0	0	0	$(1-\gamma )$	0	0	$\gamma ·(1-\xi )$	$\gamma ·\xi$	0	0
  $s_5$	0	0	0	0	$(1-\gamma )$	0	0	$\gamma ·(1-\xi )$	$\gamma ·\xi$	0
  $s_6$	0	0	0	0	0	$(1-\gamma )$	0	0	$\gamma ·(1-\xi )$	$\gamma ·\xi$

  .

Within the framework of the proposed testing strategy, the behavior of the 1oo3 system configuration is modeled using the dynamic Bayesian network (DBN) depicted in Figure 2. The CPTs associated with this DBN, detailed in Table 2, Table 3, Table 4, Table 5 and Table 6, correspond to four distinct proof test states. These CPTs reflect the different stages of the testing process and define the probabilistic transitions that influence system unavailability under various testing scenarios.

5. Application

This section presents illustrative examples to demonstrate the application of the proposed approach to evaluate the performance of a safety system. The first example focuses on simulating a 1oo3 architecture to calculate its on-demand unavailability. The second example addresses the complete safety instrumented system (SIS) dedicated to a chemical reactor, as initially defined by [13]. The analysis highlights key factors influencing the reliability of the system, including the role of inspection tests and the interaction between different components of the system.

5.1. 1oo3 Structure

This specific architecture, previously introduced and extensively analyzed in the preceding section, led to the formulation of several Conditional Probability Tables (CPTs), as shown in Table 2, Table 3, Table 4, Table 5 and Table 6. These CPTs represent the probabilistic dependencies between component states, conditioned on the status of the proof test, and form the core of the dynamic Bayesian network (DBN) model. Based on this foundation, the next step involves implementing the complete probabilistic model illustrated in Figure 2. This model enables the evaluation of system unavailability by computing the instantaneous PFD at a given time, which subsequently allows for the determination of the average PFD over the mission period (PFD${}_{\mathrm{avg}}$). These two reliability indicators play a crucial role in evaluating the performance of the architecture and gaining insights into its behavior under demand scenarios.

To illustrate the applicability of the proposed model and assess the effectiveness of the testing strategy, a numerical case study is presented, focusing on a 1oo3 system architecture. Although the analysis focuses on this configuration, this choice is made strictly for illustrative purposes and does not limit the applicability of the approach to the entire SIS. Based on the defined testing strategies, two extreme cases are examined for the actuator layer operating under imperfect proof-testing conditions.

• Strategy I: Simultaneous testing, where the three components are tested at the same time during each test cycle of the proof.
• Strategy II: The proposed strategy introduced in this study, where only one component is tested during each proof test interval.

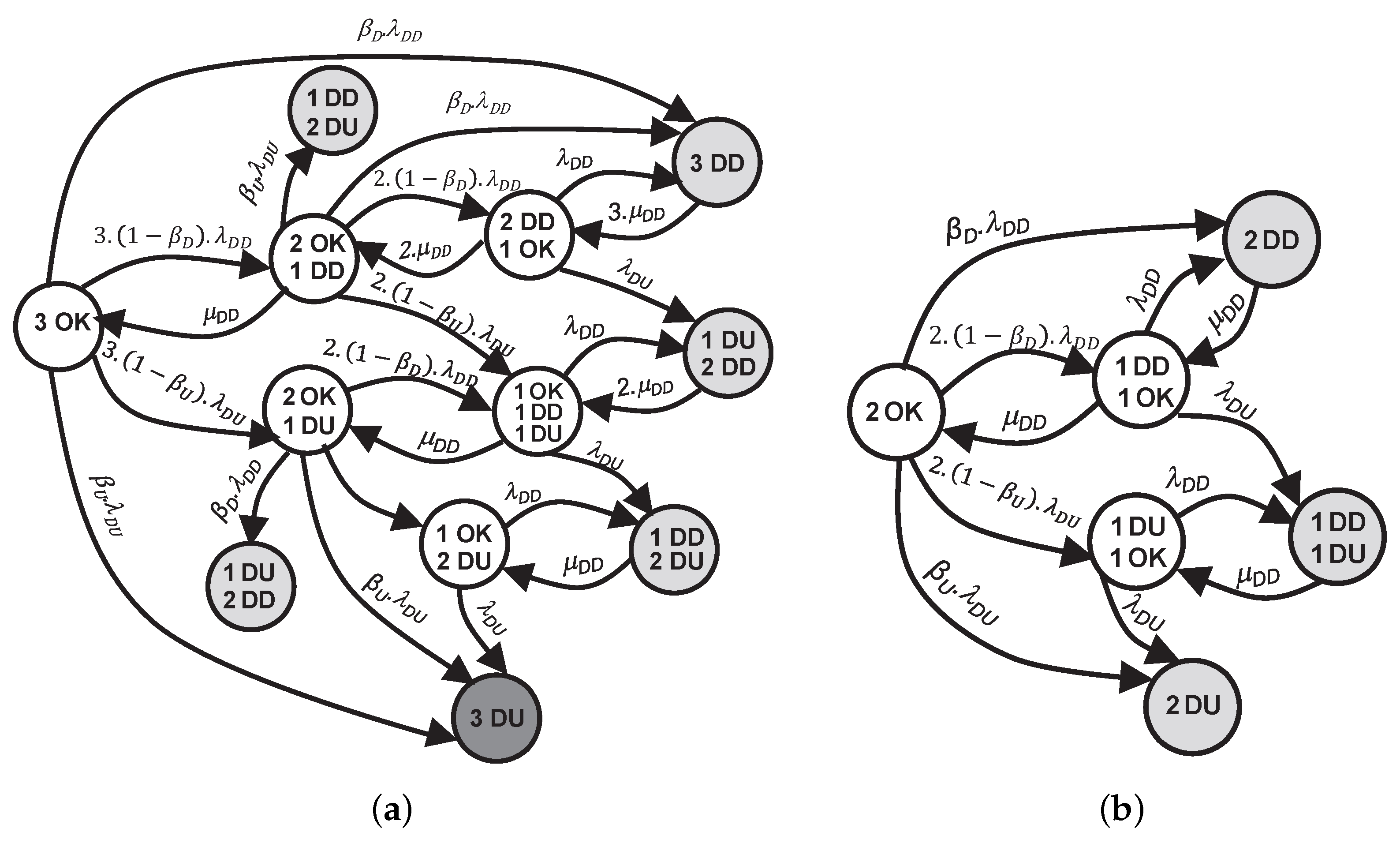
A comparative analysis between the two strategies for the 1oo3 structure is presented based on proof test parameters. In our proposed model, the test nodes for each layer serve as exogenous variables, influencing the stochastic process and layer unavailability computation. By simulating the dynamic model, the instantaneous Probability of Failure on Demand for the actuator layer is computed through successive inferences using the Conditional Probability Table provided in Table 3, Table 4, Table 5 and Table 6.

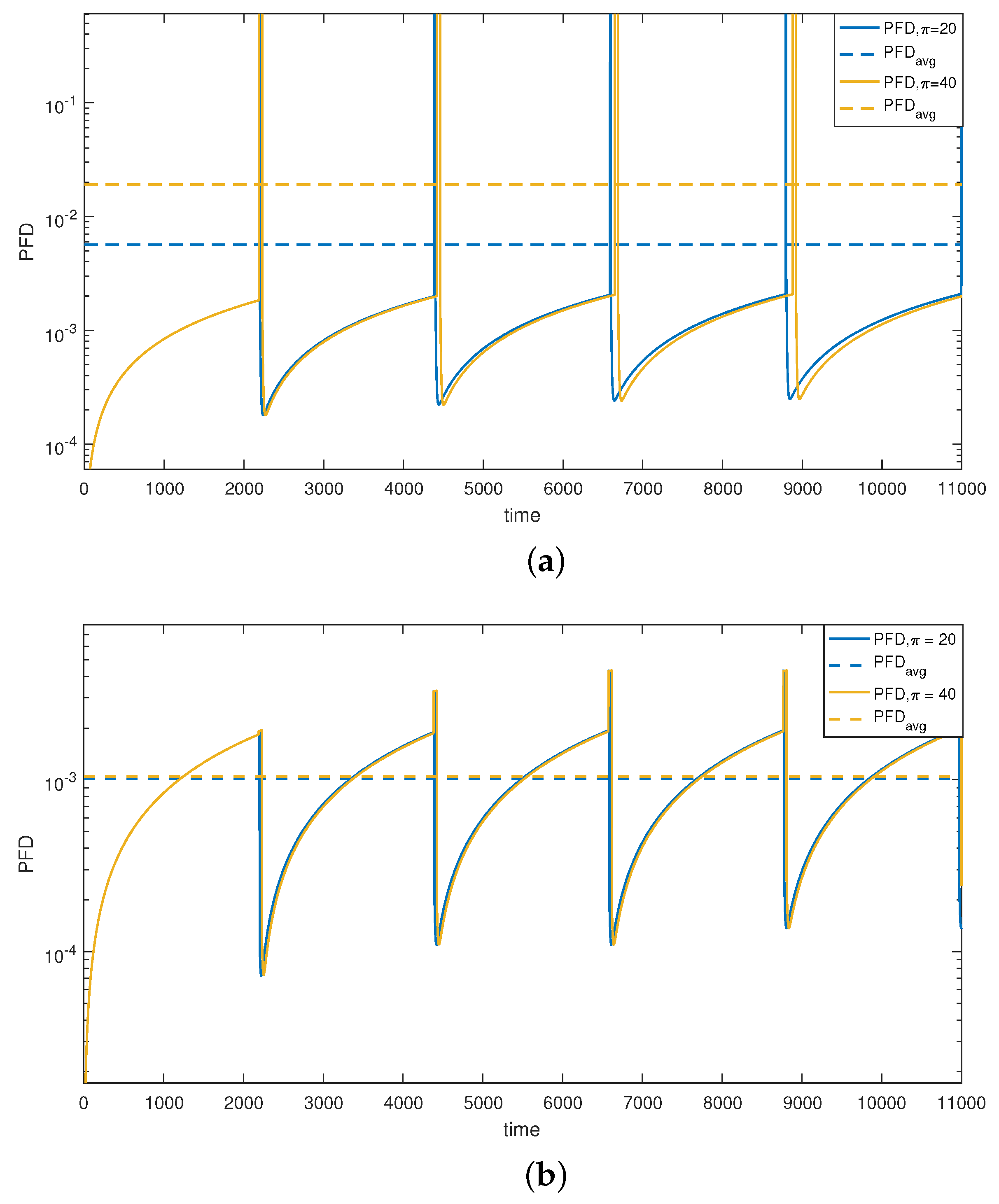
Under Strategy I, Figure 5a illustrates the variation in the 1oo3 structure unavailability and its average value, ${\mathrm{PFD}}_{avg}$, represented semi-logarithmically for two test durations (20 h and 40 h). Comparing the simulation cases reveals the pronounced impact of $\pi$ on ${\mathrm{PFD}}_{avg}$ variation. As depicted in Figure 5a, the PFD of the structure increases to 1 for all the test periods, indicating complete unavailability of the 1oo3 architecture throughout the test duration ($\pi \ne 0$) due to simultaneous testing of all the components.

To address complete unavailability, we propose modifying the test strategy for the actuator layer. Strategy II, our proposed alternating test strategy, is then implemented to mitigate the impact of prolonged test durations ($\pi \ne 0$). Figure 5b demonstrates that Strategy II induces less variation in unavailability compared to the previous case, thanks to non-simultaneous tests. The observed decrease in availability is primarily attributed to the structural change in the actuator layer from a 1oo3 to a 1oo2 configuration. Notably, the variation in the ${\mathrm{PFD}}_{avg}$ due to the alternating test strategy is clearly discernible. With $\pi =20$ h, the ${\mathrm{PFD}}_{avg}$ ranges from 1.0134 × ${10}^{-2}$ (Figure 5a) to 0.10276 × ${10}^{-2}$ (Figure 5b).

Furthermore, to assess the effectiveness of the proposed alternating proof test strategy, a detailed sensitivity analysis was carried out. This analysis explores the influence of critical parameters related to both proof and diagnostic testing on the PFD${}_{\mathrm{avg}}$ for the actuator layer, which is modeled using a dynamic Bayesian network (DBN) approach.

The parameters under consideration include $\xi$, $\gamma$, $\pi$, and the rate $DC$. These variables are known to play a significant role in shaping the unavailability profile of safety instrumented components. In this analysis, four distinct scenarios were investigated. In each case, two of the parameters mentioned above were varied simultaneously, while the remaining two were kept constant. This approach enables a comprehensive evaluation of the joint impact of the variable parameters on the PFD${}_{\mathrm{avg}}$ and thus on the overall reliability of the system. 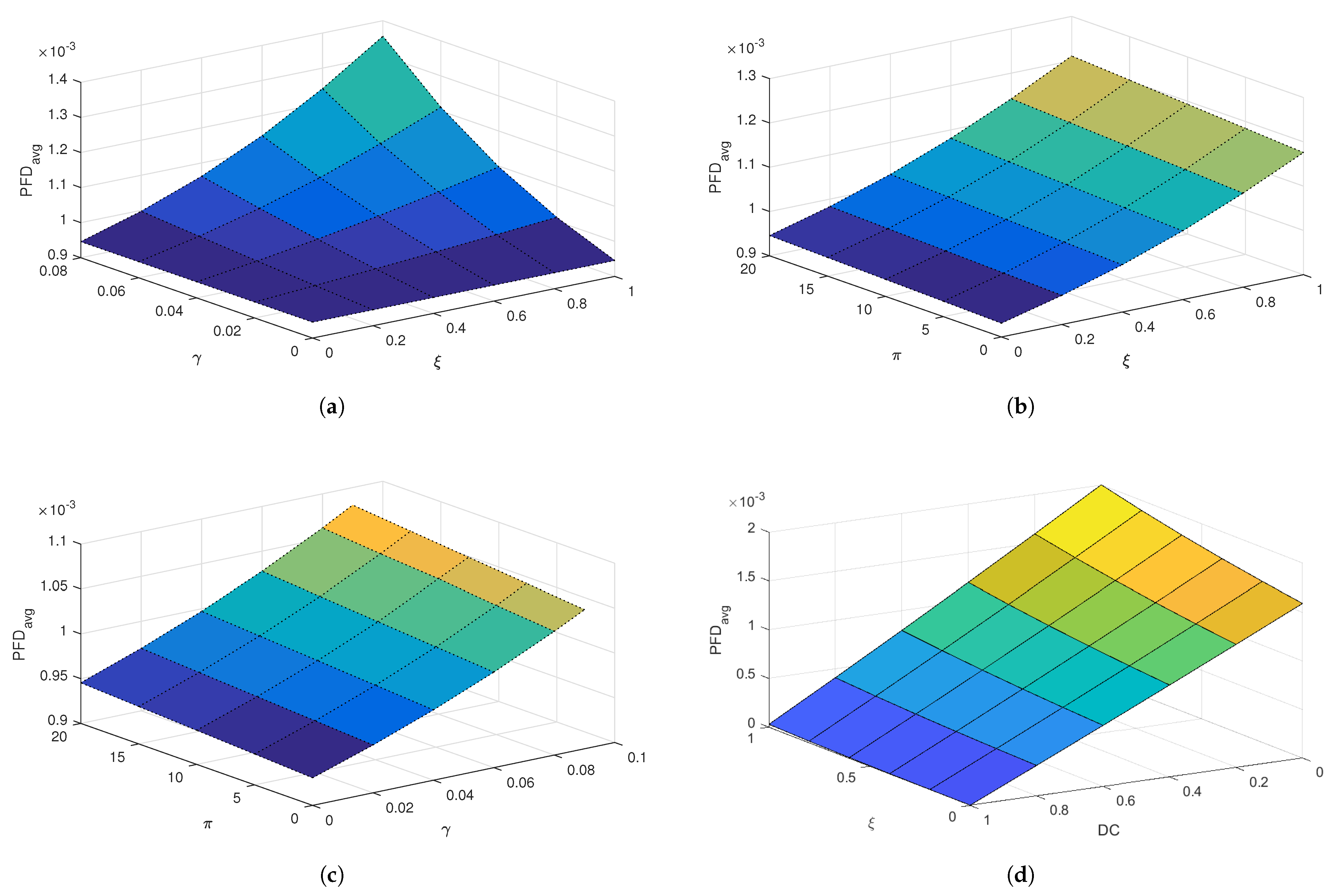The simulation results are illustrated using 3D surface plots, as shown in Figure 6.

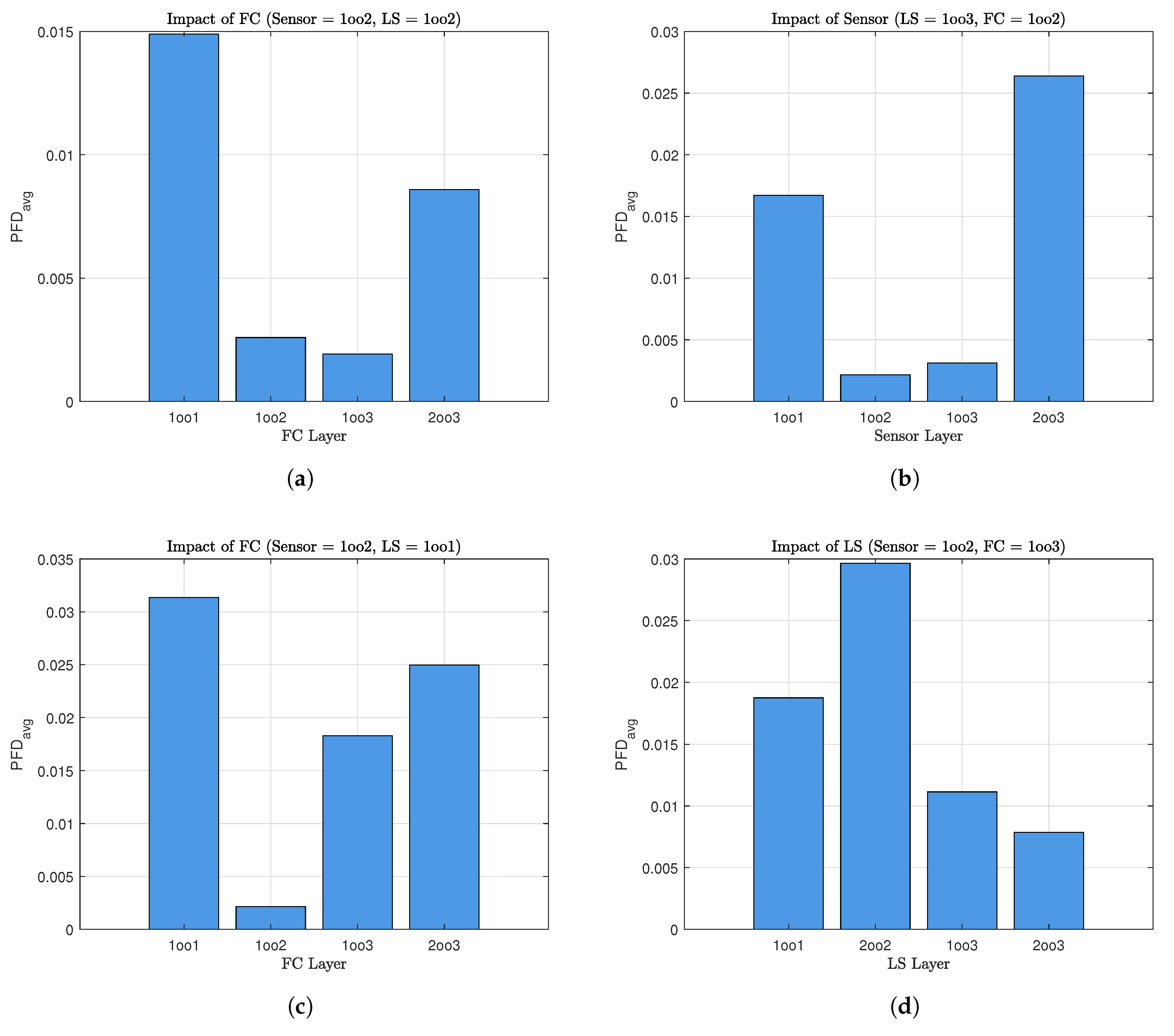
The first case, illustrated in Figure 6a, presents the variation in the PFDavg as a function of $\gamma$ and $\xi$. The results indicate that increasing either $\gamma$ or $\xi$ leads to a noticeable rise in the PFDavg. This shows that proof tests that are both ineffective and prone to causing failures significantly degrade system reliability. Figure 6b illustrates the second case, in which the influence of $\xi$ and $\pi$ on the PFD${}_{\mathrm{avg}}$ is examined. The results demonstrate that ineffective tests allow for latent faults to persist, while longer testing periods increase the exposure to unavailability. The alternating test strategy proposed in this study mitigates these effects by avoiding simultaneous testing of all redundant components, thereby preserving partial functionality during test intervals.

Figure 6c illustrates the third case, which investigates the combined influence of $\gamma$ and $\pi$, with $\xi$ and $DC$ held constant. The results reveal that both parameters contribute to an increase in system unavailability, and their combined impact becomes more significant as $\pi$ increases. The alternating test strategy helps reduce the adverse impact of extended test durations on the PFD${}_{\mathrm{avg}}$. In this final case depicted in Figure 6d, the relationship between $\xi$ and $DC$ is examined. The PFD${}_{\mathrm{avg}}$ increases with higher test ineffectiveness, while it decreases with improved diagnostic coverage. This result illustrates the compensatory role of diagnostics: even if the proof test is suboptimal, a robust diagnostic system can detect failures during normal operation, significantly enhancing reliability.

The results of the sensitivity analysis emphasize the effectiveness of the proposed alternating testing strategy to reduce the negative impact of imperfect and prolonged testing on system availability. This strategy allows for alternating tests, where only one component of a layer is tested at a time rather than testing all the components simultaneously. The integration of this strategy into the maintenance planning of safety instrumented systems is therefore recommended, especially in configurations with extended proof test durations.

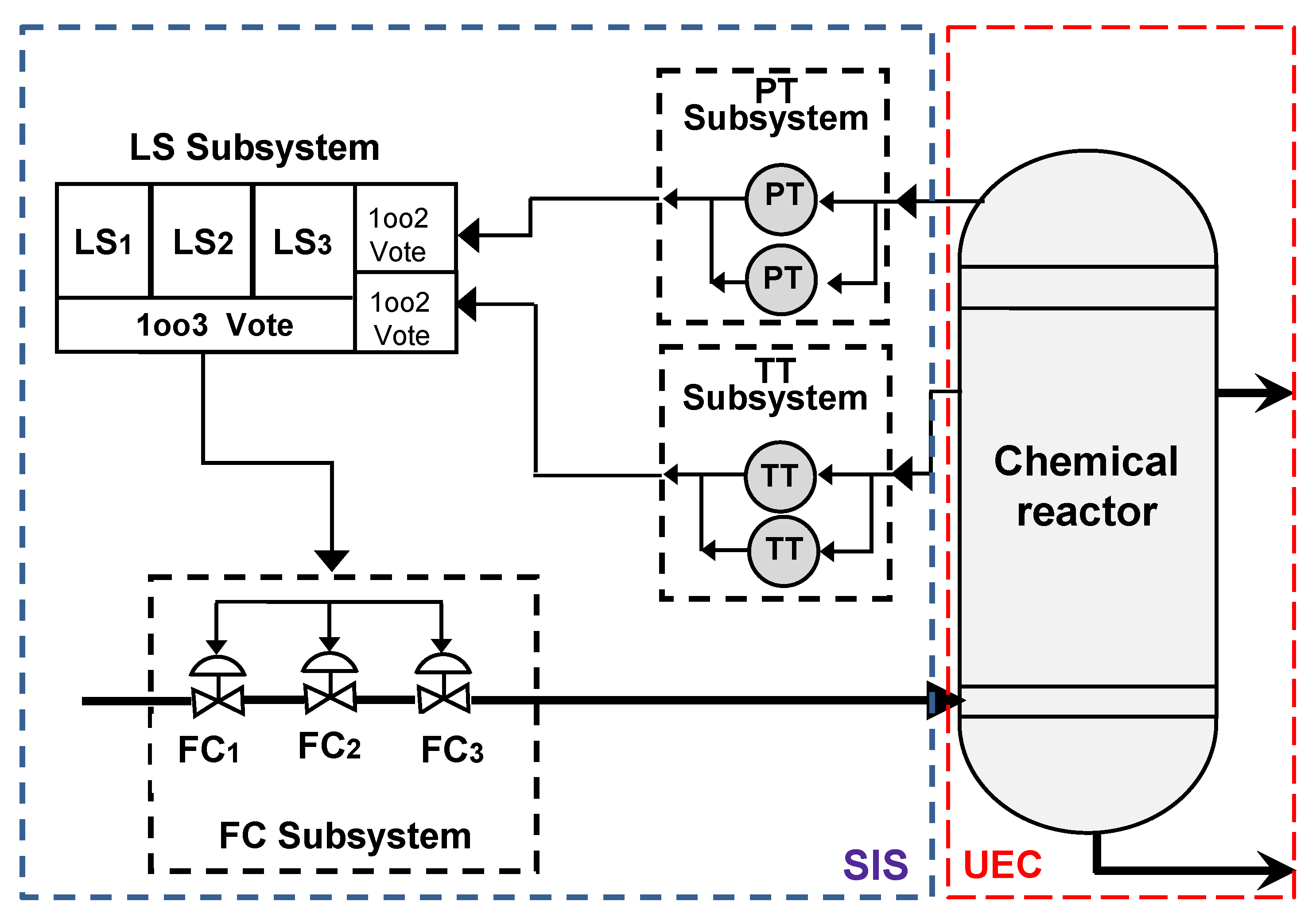
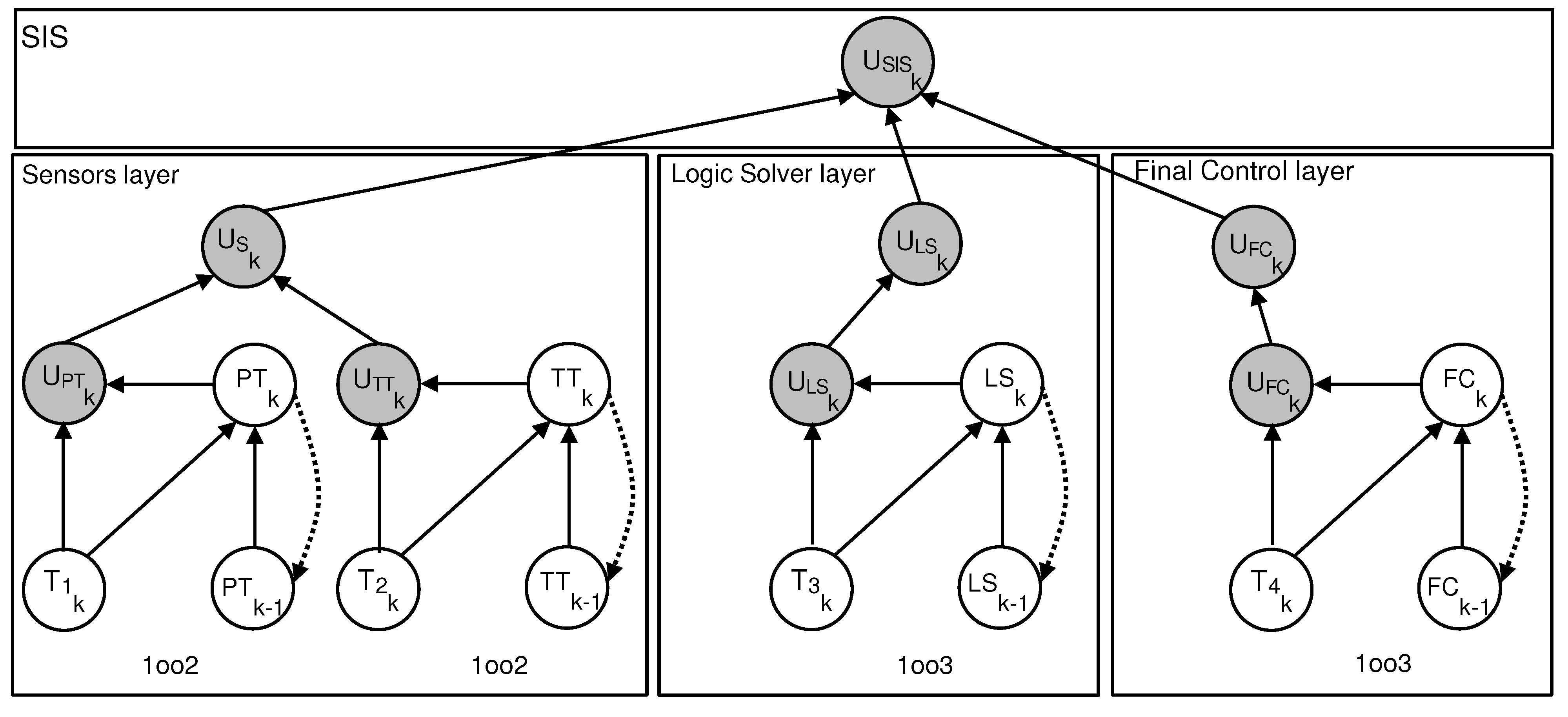
5.2. Overview of the Entire SIS

The considered SIS is organized into three distinct layers. The sensor layer includes two blocks, each composed of two sensors, temperature transmitters (TTs) and pressure transmitters (PTs), arranged in parallel. The Logic Solver (LS) layer operates in a 1oo3 configuration, whose behavior has already been described in the previous section. Finally, the actuator layer, comprising the final control elements, also follows a 1oo3 architecture.

Figure 7 illustrates the functional architecture of the SIS studied, which is organized into three distinct and independent layers. Each layer or subsystem can be individually modeled using a DBN, as depicted in the reference model of Figure 2.

The global functionality of the SIS is captured through a combination of these layer-specific models, arranged in a serial/parallel configuration. This structure enables the estimation of the overall unavailability of the system (that is, PFD), based on the unavailability of each layer, which is modeled using a configuration $1ooN$.

The construction of the equivalent DBN model of the entire SIS involves defining the CPTs that determine the state of each layer based on the states of its components and the status of the proof-testing process. In particular, the adopted alternating test strategy assumes that, during each test cycle, only one component per layer is subjected to verification, which introduces temporal dynamics into the unavailability of the entire SIS.

The structure of each layer is represented by a dedicated node within the DBN, and the corresponding CPT can be derived with relative ease. The DBN model described in Figure 7 constitutes the equivalent probabilistic representation of the entire SIS studied. This structure is systematically derived from the functional graph depicted in Figure 2, which models the logical dependencies and dynamic interactions between the various operational layers.

The numerical data of the key parameters that characterize the components of each functional layer, together with those related to the proof-testing strategies, are summarized in

Table 7. Numerical data parameters of SIS components.

	Components	PT${}_{\mathit{i}}$	TT${}_{\mathit{i}}$	LS${}_{\mathit{i}}$	FC${}_{\mathit{i}}$
Parameters
${\lambda }_D(\times {10}^{-6}/h)$		1.50	1.50	4.60	5.00
$DC$		0.6	0.6	0.4	0.2
${\beta }_U(\%)$		20	20	20	20
$MTTR\left(h\right)$		8	8	10	10
T${}_i\left(h\right)$		730	730	1460	2190
$\pi \left(h\right)$		8	8	20	20
$\xi$		0.4	0.4	0.5	0.6
$\gamma$		0.001	0.001	0.002	0.003

Others’ data: ${\beta }_D={\displaystyle \frac{1}{2}}·{\beta }_U$, ${\mu }_{DD}={\displaystyle \frac{1}{MTTR}}$.

. These values are then used to compute the overall PFD${}_{\mathrm{avg}}$ of the SIS by combining the average PFDs of the individual layers, while accounting for their mutual interactions.

The parameter numerical values presented in Table 7 were selected based on commonly cited sources in the literature on safety instrumented systems (SISs), particularly concerning performance evaluation under proof-testing policies (e.g., [27,28]). These values fall within realistic ranges observed in engineering practice and are frequently employed in numerical studies to support the validation and benchmarking of reliability modeling approaches. The aim is to illustrate the methodological applicability of the proposed strategy rather than to replicate a specific case.

6. Results and Discussion

6.1. Presentation of Results

The complete DBN was simulated over a mission time of 10,000 h to evaluate the dynamic behavior of the SIS. Figure 8 depicts the instantaneous evolution of the PFD for each layer, as well as for the overall SIS to further visualize the behavior of the SIS under the proposed alternating test strategy. The periodic oscillations visible on each curve highlight the influence of the distinct testing intervals assigned to each layer: notably, the sensor layer, which is subject to more frequent proof tests than the LS and FE layers, exhibits a higher density of unavailability reduction cycles.

The PFD results presented in Figure 8 are relatively repeatable. This is directly linked to the operational characteristics of low-demand SISs subject to planned proof testing. In this context, each component is assumed, restored to an “as good as new” condition after the test, in accordance with the requirements of IEC 61508. As a result, the system’s reliability profile is periodically reset, leading to recurring PFD trends over the mission time. While the shape of these curves remains consistent, the magnitude of the PFD values is directly influenced by the components’ failure rates: higher failure rates yield increased PFD values, whereas lower rates reduce them.

The periodic behavior of the PFD trend remains consistent even in complex SIS architectures, provided the system operates in low-demand mode with regular testing. However, increased system complexity significantly raises the modeling effort, especially due to the exponential increase in the size of CPTs within the DBN framework.

The SIS under study is structured into three functionally distinct layers, each contributing differently to the overall reliability and performance of the system. In this context, Figure 9 illustrates the variation in the instantaneous PFD and its corresponding average value PFD${}_{avg}$ over time, as observed in each layer of the SIS, as well as for the overall system.

To begin with, Figure 9a presents the evolution of the PFD in the sensor layer, which consists of two independent sensor blocks. The PFD curve displays a steep sawtooth pattern characterized by frequent and sharp decreases resulting from periodic proof testing. Following this, Figure 9b shows the PFD variation in the LS layer, which operates in a 1oo3 configuration. This arrangement enables the system to tolerate up to two simultaneous failures. The PFD trajectory demonstrates a gradual increase between test intervals, followed by sudden resets, and results in a moderate average unavailability of $6.53\times {10}^{-4}$.

Furthermore, the PFD behavior of the actuator layer, which includes the final control elements (e.g., valves or actuators), is illustrated in Figure 9c. This layer also follows a 1oo3 configuration, but differs from the others by employing an alternating test strategy, where components are tested sequentially. Despite this optimization, the actuator layer exhibits the highest average unavailability among all the layers, with $4.262\times {10}^{-3}$.

Finally, Figure 9d represents the variation in the PFD of the overall SIS, integrating the contributions of the three layers and their respective test policies. The global PFD profile reflects the combined effects of the architecture, test frequency, and scheduling strategy. The resulting average unavailability of the complete system is $0.962\times {10}^{-3}$. Notably, the alternating test strategy proves effective in limiting simultaneous unavailability peaks and supporting a more stable operational profile throughout the mission time. Additionally, the results confirm that the alternating testing strategy significantly contributes to maintaining a lower and more stable unavailability over time, particularly in layers with longer test intervals.

The alternating test strategy proves its effectiveness in significantly lowering the peaks of global unavailability when compared to what would be observed under synchronized or identical testing intervals for all layers. Over time, the PFD of each individual layer, as well as that of the overall SIS, converges toward their respective stationary PFD${}_{avg}$ values. These results clearly demonstrate the ability of the proposed strategy to maintain system safety performance within acceptable thresholds throughout the mission duration.

To provide a more detailed quantitative evaluation of the proposed approach,

Table 8. PFD${}_{avg}$ and relative improvement for overall SIS.

Test Duration	Test Strategy	PFD${}_{\mathit{avg}}$	RI
$\mathit{\pi }\mathbf{\left(}\mathit{h}\mathbf{\right)}$		$\times \mathbf{\left(}{\mathbf{10}}^{\mathbf{-}\mathbf{3}}\mathbf{\right)}$	(%)
5	Simultaneous	$2.029$	–
5	Alternating	$1.289$	36.5%
10	Simultaneous	$2.478$	–
10	Alternating	$1.306$	47.3%
15	Simultaneous	$3.402$	–
15	Alternating	$1.311$	61.7%
20	Simultaneous	$5.510$	–
20	Alternating	$1.317$	76.2%

presents the PFD${}_{avg}$ values computed for the overall SIS under different proof test durations ($\pi$) and two test strategies: simultaneous and alternating. Table 8 also includes the relative improvement obtained by adopting the alternating test strategy, expressed as the percentage reduction in PFD${}_{avg}$.

The simulation results clearly demonstrate that the alternating strategy yields significantly lower PFD${}_{avg}$ values compared to the simultaneous strategy for all considered durations. For example, at $\pi$ = 5 h, the overall SIS PFDavg decreases from $2.029\times {10}^{-3}$ (simultaneous) to $1.289\times {10}^{-3}$ (alternating), corresponding to a relative improvement of 36.5%. The benefit becomes even more marked as the test duration increases at $\pi$= 20 h; the PFD${}_{avg}$ is reduced from $5.510\times {10}^{-3}$ under the simultaneous strategy to just $1.317\times {10}^{-3}$ with the alternating strategy, an improvement of 76.2%. This clear contrast highlights the limitations of the simultaneous testing strategy when test durations become longer, which can significantly affect system performance.

As the test duration $\pi$ increases, the performance gap between the two strategies becomes more significant, showing that alternating testing is especially well suited for systems subject to extended proof tests. This improvement becomes increasingly important as test durations increase, underlining the relevance of test planning as a critical parameter in the maintenance and reliability management of safety instrumented systems.

6.2. Benchmark Study

A comprehensive benchmark study was carried out to demonstrate the applicability and robustness of the proposed method on a wide spectrum of SIS configurations. Each SIS is composed of three layers, sensor, LS, and FC, with each layer capable of adopting one of six commonly used architectures: 1oo1, 1oo2, 1oo3, 2oo2, 2oo3, and 3oo3. This results in a total of $6^3=216$ unique combinations.

The simulations were performed using the numerical parameters detailed in Table 7. A representative subset of 36 combinations is presented in

Table 9. PFD${}_{avg}$ values for 36 SIS combinations.

Case	Sensor	LS	FC	PFD${}_{\mathit{avg}}$
C1	1oo1	1oo1	1oo1	0.04592
C2	1oo2	1oo2	1oo1	0.01498
C3	1oo1	1oo3	1oo2	0.01671
C4	1oo2	1oo1	2oo3	0.02497
C5	1oo3	1oo1	1oo2	0.01982
C6	1oo2	1oo1	1oo3	0.01830
C7	1oo2	1oo1	1oo1	0.03135
C8	1oo2	1oo1	3oo3	0.07620
C9	1oo3	1oo1	1oo3	0.01915
C10	1oo3	1oo1	3oo3	0.07705
C11	1oo3	1oo1	2oo3	0.02582
C12	1oo2	1oo2	1oo2	0.00259
C13	1oo3	1oo2	1oo2	0.00344
C14	1oo2	1oo2	1oo3	0.00192
C15	1oo2	1oo2	2oo3	0.00859
C16	1oo2	1oo2	3oo3	0.05982
C17	1oo3	1oo2	3oo3	0.06067
C18	1oo3	1oo2	1oo3	0.00277
C19	1oo3	1oo2	2oo3	0.00944
C20	1oo3	1oo3	1oo2	0.00301
C21	1oo3	1oo3	1oo3	0.00234
C22	1oo3	1oo3	2oo3	0.00901
C23	1oo3	1oo3	3oo3	0.06024
C24	1oo2	1oo3	1oo2	0.00215
C25	1oo2	1oo3	1oo3	0.00148
C26	1oo2	1oo3	2oo3	0.00815
C27	1oo2	1oo3	3oo3	0.05938
C28	1oo3	1oo3	1oo1	0.01540
C29	1oo2	1oo2	2oo3	0.00853
C30	1oo3	1oo2	1oo1	0.01583
C31	1oo2	2oo3	1oo2	0.00860
C32	1oo2	2oo3	3oo3	0.06576
C33	1oo3	2oo3	1oo2	0.00939
C34	2oo3	1oo3	1oo2	0.02639
C35	2oo3	2oo3	1oo3	0.01602
C36	1oo2	1oo3	1oo3	0.01114

. These configurations reflect various levels of redundancy and illustrate the ability of the proposed approach to evaluate the PFD${}_{avg}$ in diverse SIS architectures.

This benchmark confirms the flexibility and extensibility of the proposed DBN-based modeling framework for analyzing a broad spectrum of real-world SIS designs. The resulting PFD${}_{avg}$ values in Table 9 were used to generate histograms by fixing the redundancy of two layers while varying the third. Figure 10 illustrates the impact of individual layer redundancies on the global SIS PFD${}_{avg}$. Among them, the four most informative cases are highlighted in Figure 10, representing the most informative bar charts to understand the influence of layer redundancies on SIS performance.

Figure 10 presents a comparative analysis of the impact of redundancy in each SIS layer, sensor, LS, and FC, on the global PFD${}_{avg}$. Each sub-figure isolates the effect of a specific layer by fixing the configuration of the two other layers, allowing for a focused sensitivity study.

• Figure 10a shows the impact of varying the FC layer architecture while keeping the sensor and LS layers fixed at 1oo2. The results clearly demonstrate that increasing the redundancy in the FC layer (from 1oo1 to 1oo2 or 1oo3) significantly reduces the PFD${}_{avg}$. This highlights the critical role of the final control layer in improving the overall SIS availability.
• Figure 10b evaluates the sensor layer by fixing the LS in 1oo3 and FC in 1oo2. The chart reveals that moving from 1oo1 to 1oo2 or 1oo3 considerably improves availability. However, the 3oo3 architecture results in performance degradation, which may be attributed to increased complexity and testing inefficiencies.
• Figure 10c presents another FC layer variation, this time with the sensor in 1oo2 and LS in 1oo1. The same decreasing trend in the PFD${}_{avg}$ is observed when using the 1oo2 or 1oo3 architectures, confirming the robustness of redundancy benefits in the configuration.
• Figure 10d analyzes the LS layer with the sensor in 1oo2 and FC in 1oo3. The results show that architectures like 1oo2 and 1oo3 achieve the best performance, while there is over-redundancy (e.g., 3oo3).

6.3. Discussion

The DBN formalism offers significant advantages by effectively modeling multi-state system behaviors, non-instantaneous proof test duration, and complex component dependencies. In this context, to illustrate its added value, we contrast our approach with several representative methods from the literature. In this context, several notable studies have contributed to the modeling of SIS performance, but each presents certain limitations in scope. Innal et al. [16] developed a PFDavg formulation for MooN systems aligned with IEC 61508 standards, incorporating partial and full proof tests through the parameter $\xi$. However, their model does not account for essential aspects such as the proof test duration $pi$, which is critical for realistic performance evaluation. Similarly, Torres-Echeverria et al. [24] proposed a fault tree-based method for SIS assessment but omitted key test parameters such as $\gamma$ and $\xi$, reducing its ability to capture more nuanced testing behaviors. Cai et al. [22] employed a DBN framework to model the effects of common cause failures and imperfect proof testing. However, their approach does not include the impact of non-zero test duration $\pi$, limiting the realism of their assessment. Zhang et al. [18] used a Markov chain-based approach to develop maintenance strategies under imperfect detection assumptions. Nevertheless, their model does not fully integrate critical parameters, such as proof test duration ($\pi$), common cause failures (CCFs), and repair times. Simplifying assumptions, such as negligible repair durations and idealized failure detection, further restrict the generality of their method.

In contrast to many existing studies that assume instantaneous proof testing and tend to offer a simplistic representation of maintenance dynamics, the approach proposed in this work distributes test scheduling among system components. This reduces simultaneous unavailability and enables a more realistic and compact evaluation of SIS reliability. Although the proposed framework is implemented using a DBN model, the same evaluation process can also be carried out using a Markov chain model. Specifically, the CPTs defined in the DBN can be used to construct the Markov chain transition matrices based on the system’s states under test. While the transformation between a DBN model and a Markov chain is relatively simple to implement, the DBN formulation offers a more modular and compact representation, particularly suited to modeling systems with complex temporal and structural dependencies. Notably, the Markov chain method can produce numerical results that are nearly identical to those obtained through the proposed approach. Conversely, fault tree analysis lacks the ability to capture such dynamic behavior and cannot integrate key parameters associated with proof testing, especially test duration and the proposed alternating test strategy. These limitations highlight the superior modeling flexibility and accuracy of the DBN framework for evaluating the performance of SIS architectures under operational conditions.

The SIS architecture used in this study is derived from widely adopted configurations in the reliability and safety literature. It serves as a representative and realistic testbed to evaluate the proposed alternating proof test strategy through a DBN modeling approach. The method was validated at two levels. First, a subsystem with a 1oo3 configuration, frequently used in safety critical applications for redundancy, was assessed. The simulation results demonstrated that the alternating test strategy yields a substantial reduction in the PFD${}_{a}vg$ value compared to the simultaneous test strategy, especially in the presence of non-zero test durations ($\pi$) (cf. Figure 5). Second, a complete SIS architecture comprising three layers, the sensor layer, LS, and FC layer, was modeled. This enabled a comprehensive assessment of how the performance of each layer contributes to the overall system unavailability.

The modeling framework presented in this work is designed to be modular and generic, making it applicable to a wide range of SISs in the real world. The genericity of the approach is based on its ability to decompose any SIS into a layered structure that can be modeled using standard $KooN$ architectures. These configurations are typically represented using Reliability Block Diagrams (RBDs), which serve as the foundation for modeling individual layers or subsystems. The use of generic modeling templates for instance, those representing 1oo1, 1oo2, or 2oo3 structures, allows for the creation of adaptable components that can be easily reused across different SIS architectures.

The DBN model is constructed by capturing the dynamic dependencies between the states of the system components and the availability state of their parent subsystems. These relationships are formally encoded using CPTs, which define the logical rules by which the state of each subsystem depends on the states of its constituent components. This structured representation supports automated model construction and enables simulation of a wide variety of operating conditions and testing strategies. Assuming that the functional architecture of a SIS is known, typically documented through system reliability diagrams or design specifications, the proposed DBN-based modeling strategy can be applied. The approach supports a wide range of system configurations and enables the evaluation of system performance under proof tests with non-zero durations. It also facilitates sensitivity analysis with respect to key parameters, allowing engineers and decision makers to assess the impact of various strategies on overall system safety.

This methodology is therefore not limited to academic or theoretical examples but is fully adaptable to industrial systems. Future work will focus on extending the application of the proposed approach to real SIS case studies in collaboration with industrial partners. This will allow the methodology to be validated with operational data and enhance its practical relevance in safety-critical domains, such as energy production, chemical processing, transportation, and aerospace.

7. Conclusions

This paper presents an approach to assess the performance of redundant actuator layers within SISs under imperfect proof-testing conditions. Specifically, a DBN model was developed to determine the instantaneous unavailability of the operational layer by integrating proof test strategies and associated parameters. Consequently, the developed framework provides a systematic and flexible methodology for constructing detailed models to evaluate SIS performance. Moreover, by explicitly considering proof test parameters, the proposed model effectively offers a dynamic representation of multi-state components during the testing phases, thus providing a better way to understand how proof tests influence system unavailability.

A numerical case study, based on a 1oo3 architecture, demonstrated that the proposed alternating test strategy can significantly improve the performance of the actuator layer, particularly when compared to the conventional simultaneous testing approach. Moreover, the analysis extended and generalized the application of this alternating test strategy to the entire SIS. As the system’s complexity increases, the number of possible states expands exponentially with the number of components, thereby highlighting the critical importance of utilizing adaptable modeling strategies.

The accuracy of simulation results is highly dependent on the reliability of the input parameters, such as component failure rates, repair durations, and proof test intervals, in particular, the proof test duration parameter introduced in our model. These parameters are typically derived from standardized reliability databases or expert judgment. However, in actual industrial contexts, these parameters can be influenced by a wide range of operational factors, including environmental variations, varying maintenance practices, equipment aging, and human-related variability.

To address this inherent uncertainty and assess its influence on system performance, a detailed sensitivity analysis was conducted on a 1oo3 structure. This analysis examines how variations in key parameters affect the PFD${}_{avg}$. The results show that even moderate changes, such as longer test durations, can significantly affect system unavailability. These findings highlight the importance of careful parameter estimation and the need for regular model updates using real-world data related to proof testing. Furthermore, the proposed DBN-based approach offers a flexible framework that can be extended to incorporate uncertainty quantification techniques, such as probabilistic parameter distributions or Bayesian updating. These capabilities will help bridge the gap between simulated outputs and actual system performance and are part of our future research directions.

Based on the simulation results, the proposed alternating test strategy effectively reduces the impact of extended proof test durations, which enhances the overall availability and reliability of the SIS. However, a limitation of the current approach is the assumption that only one component within a layer is tested at a time, without specifying which one. As a result, this assumption introduces potential inefficiencies, as a component may be tested multiple times during the mission, while more degraded components requiring urgent testing receive lower priority. To overcome this limitation, it is possible that a more generic modeling framework could be developed, in which each component within a layer is represented by its own DBN sub-model. In this case, the alternating test strategy could then be individually applied to each component. Furthermore, by integrating maintenance policies that identify the component to be tested based on degradation states, maintenance activities could be dynamically scheduled, with priority given to the most critical components. This priority adjustment will consequently enhance the reliability and performance of complex SIS architectures, particularly under real operational conditions. Therefore, future work will focus on developing and validating such an adaptive testing and maintenance framework.