Dynamic Correction of Preview Weighting in the Driver Model Inspired by Human Brain Memory Mechanisms
Abstract
1. Introduction
2. Theoretical Foundation and Model Construction
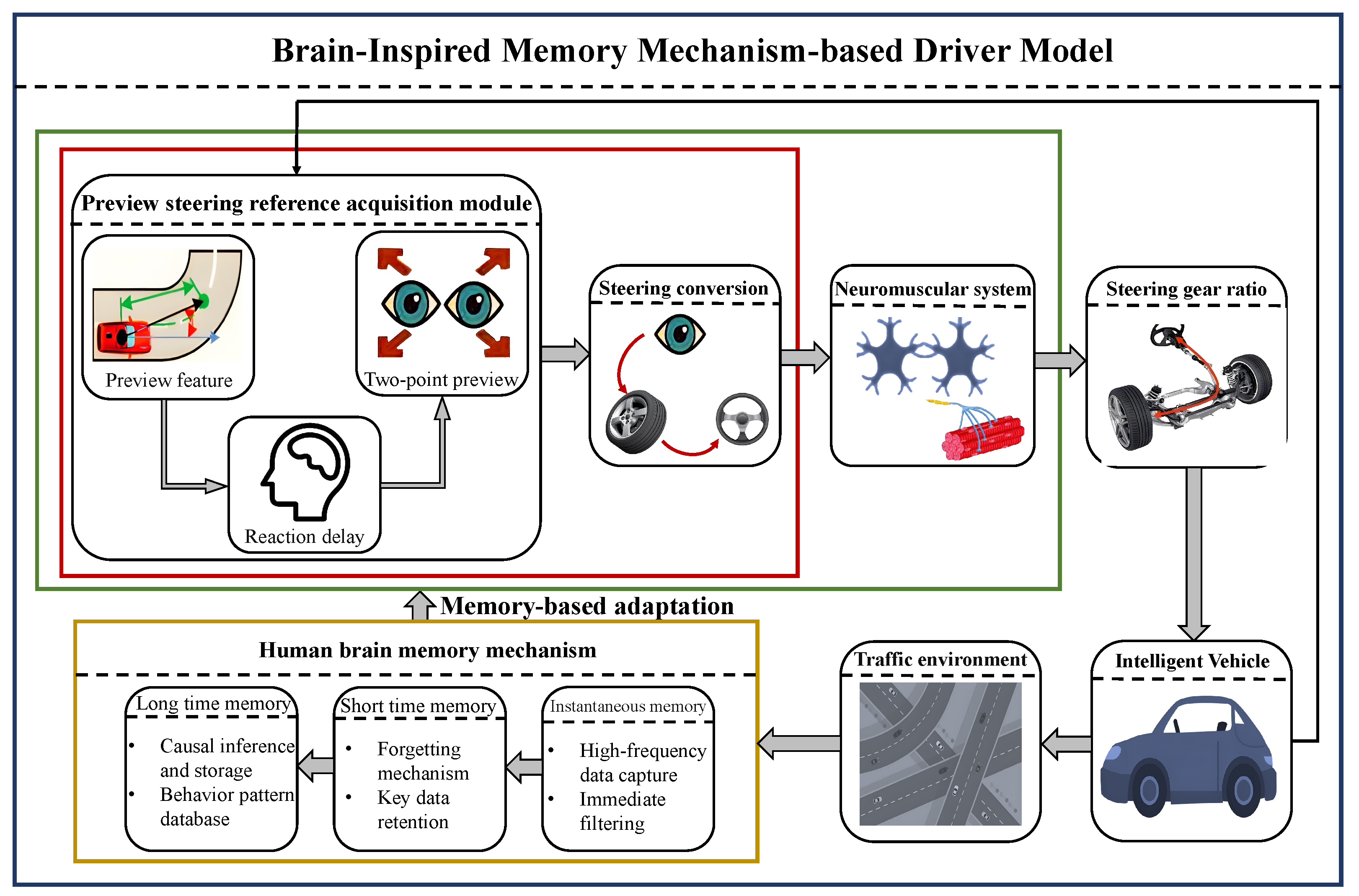
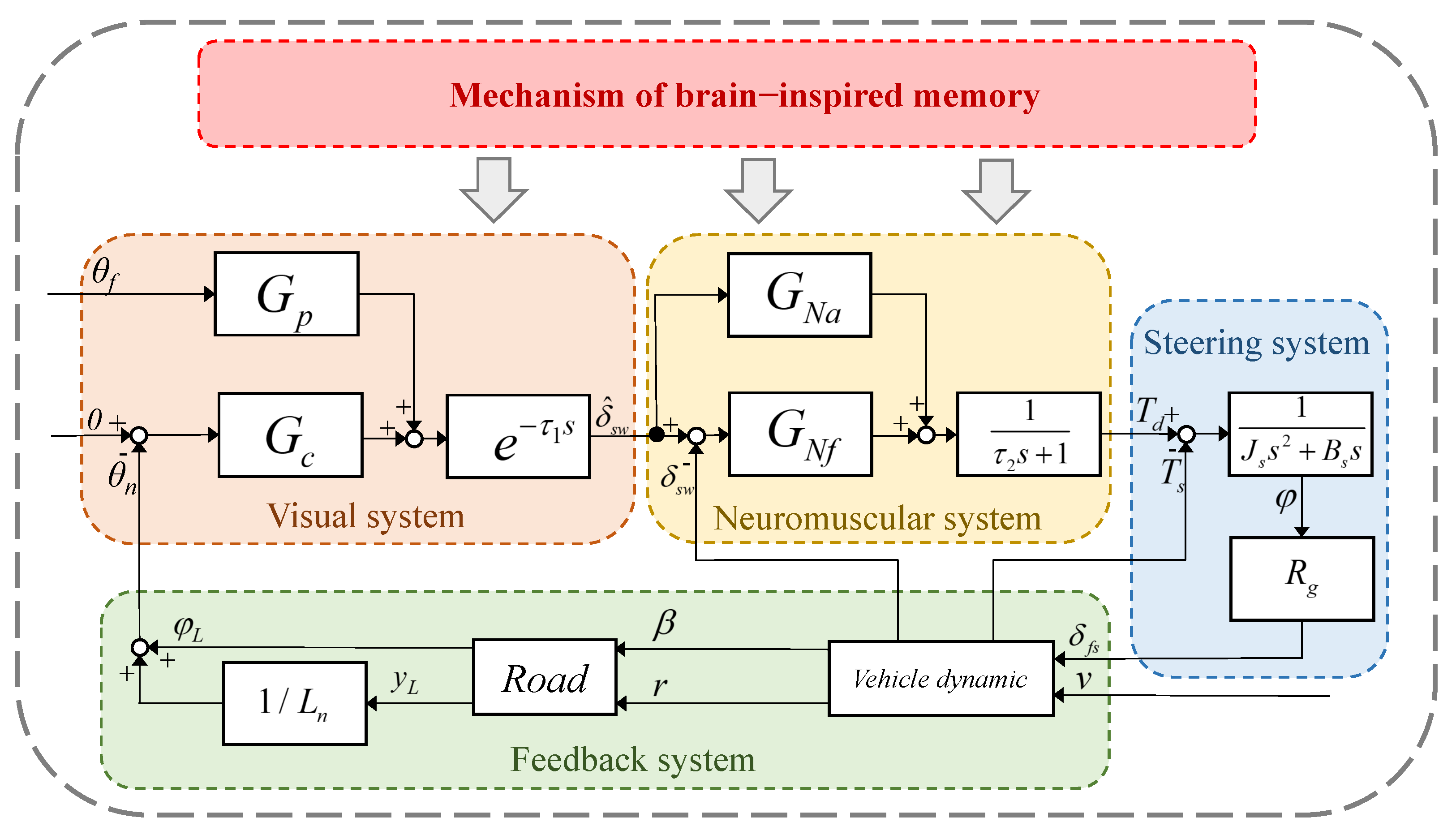
2.1. Overall Model Architecture
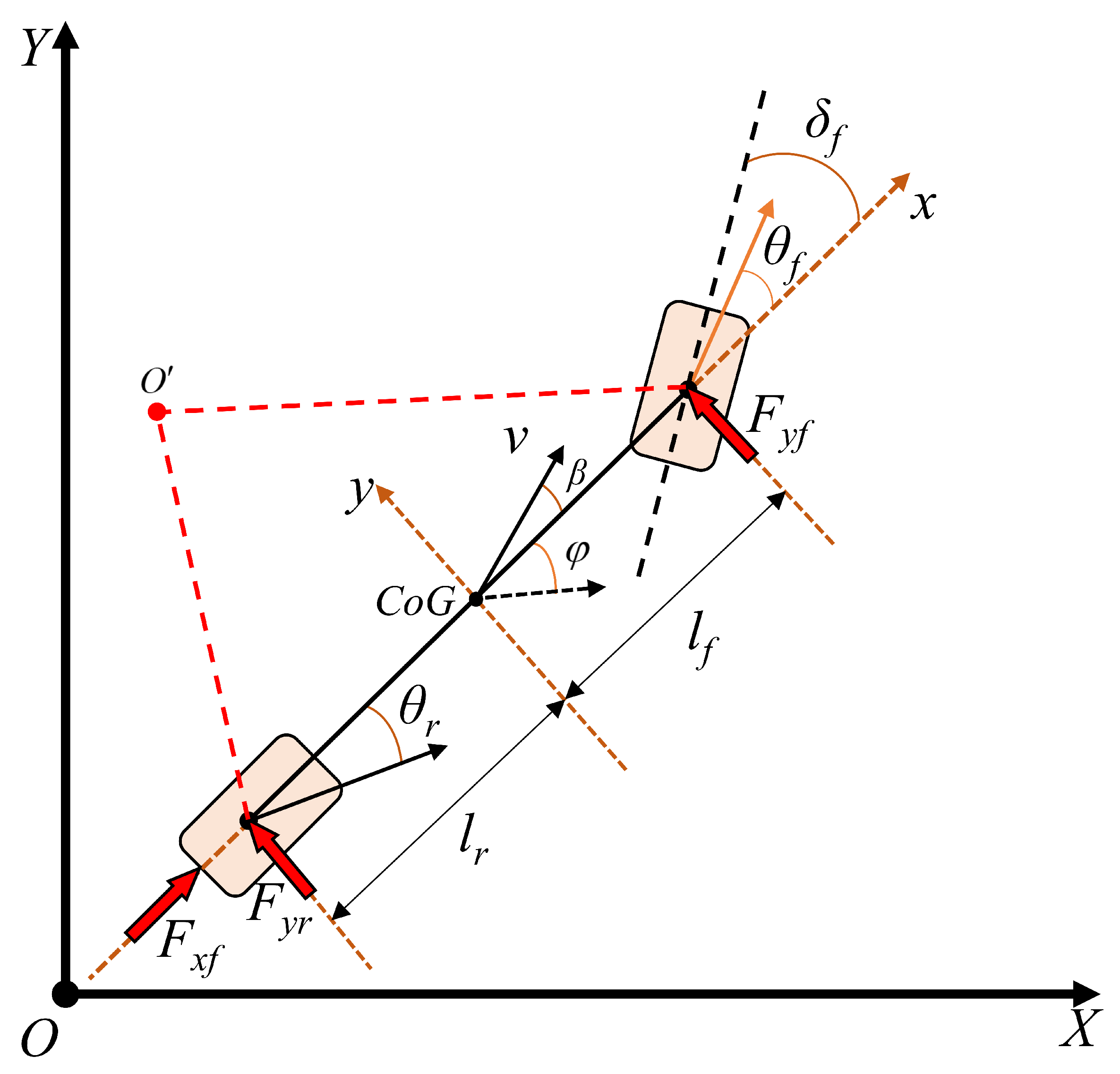
2.2. Vehicle Dynamics Model
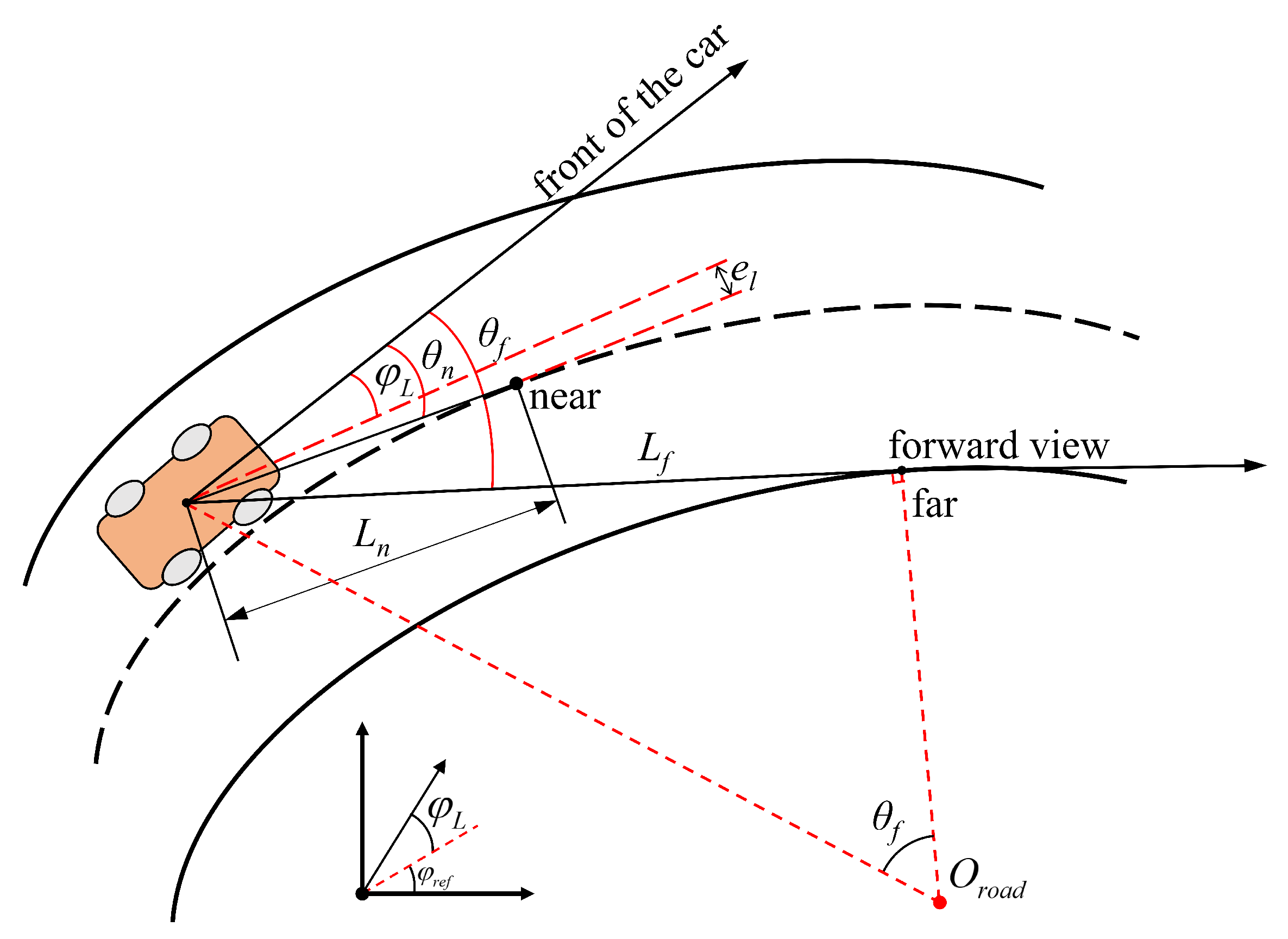
2.3. Driver Model
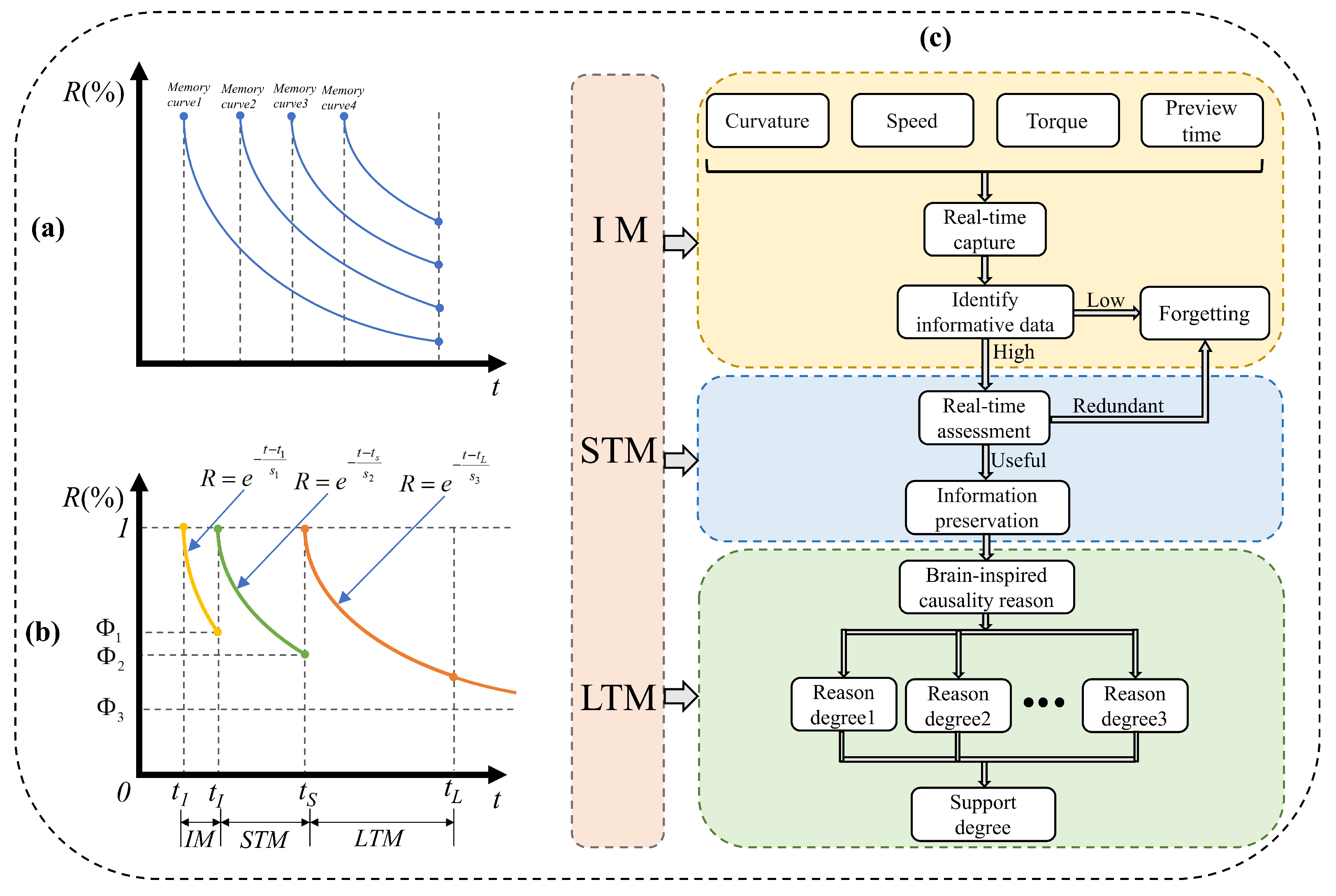
3. Human Brain Memory Mechanism
3.1. Mechanism Overview
3.2. Implementation of Human Brain Memory Mechanism
3.2.1. IM Data Capture
3.2.2. STM Data Filtering
3.2.3. LTM Data Storage
4. Experimental and Discussion
4.1. Experimental Background
4.2. Database Construction and Training
4.3. Data Volume Analysis
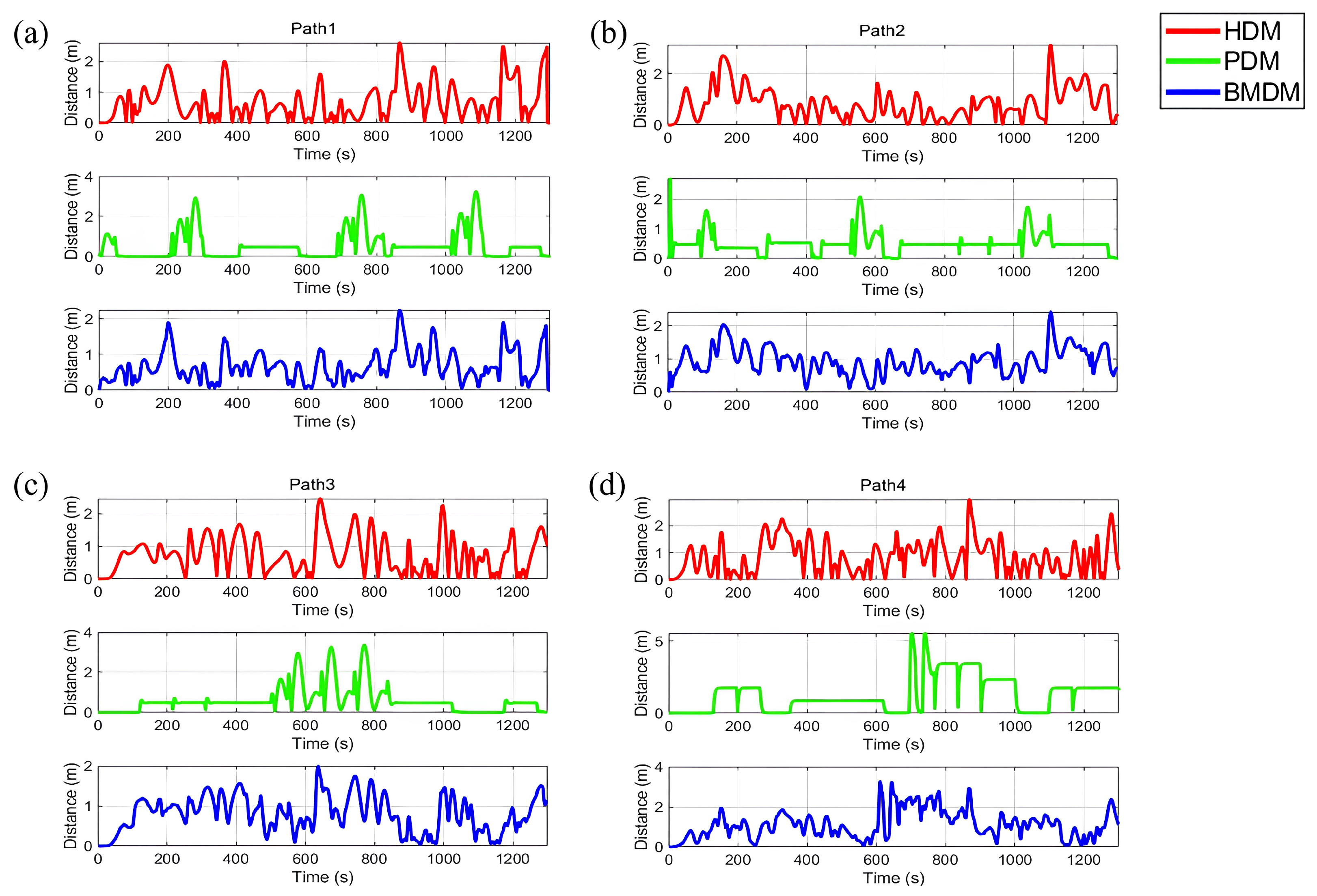
4.4. Comparative Performance Analysis
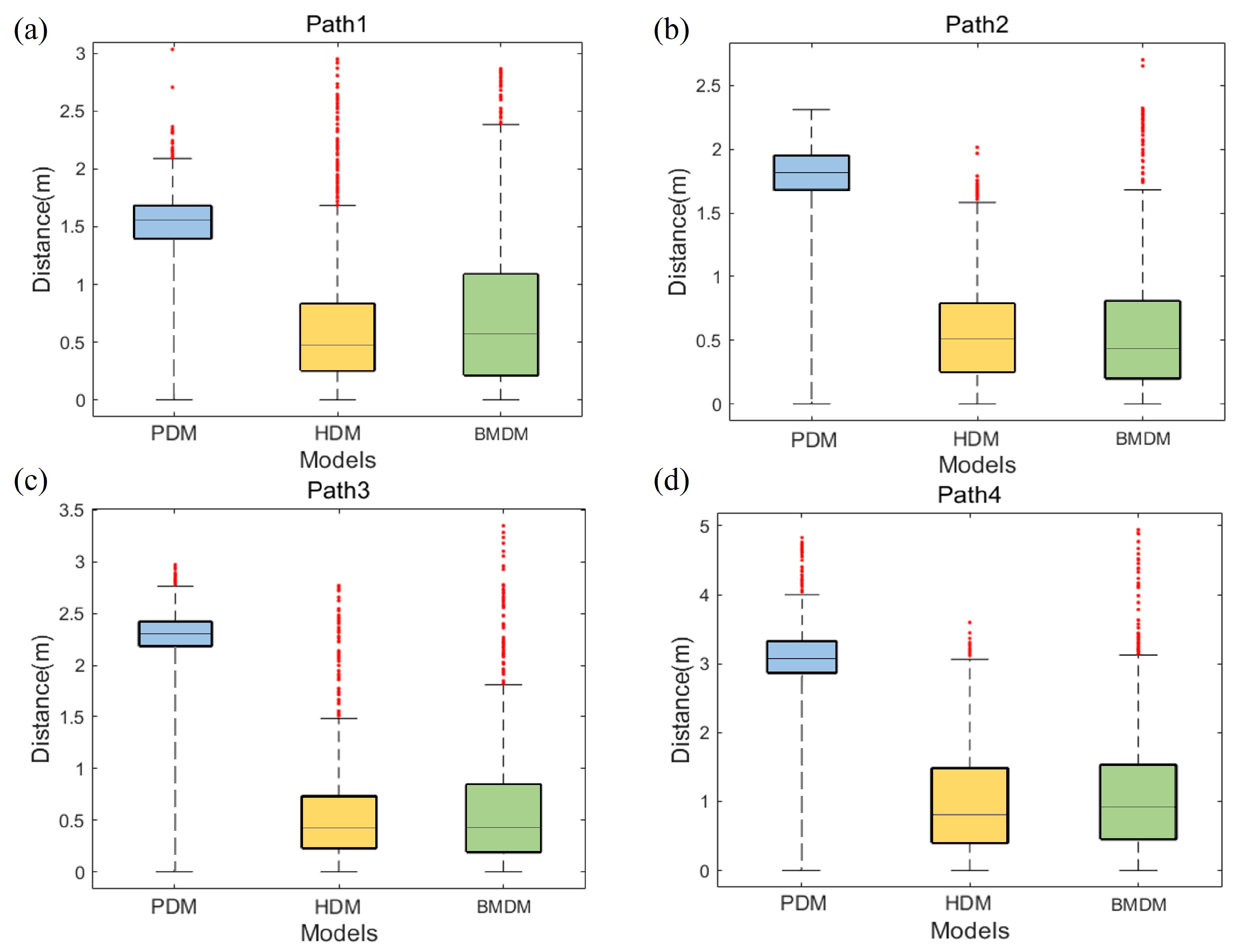
4.5. Statistical Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ungoren, A.; Peng, H. An adaptive lateral preview driver model. Veh. Syst. Dyn. 2005, 43, 245–259. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhou, L.; Luo, Y.; Li, K. Emergency Steering Evasion Assistance Control Based on Driving Behavior Analysis. IEEE Trans. Intell. Transp. Syst. 2019, 20, 457–475. [Google Scholar] [CrossRef]
- Na, X.; Cole, D.J. Experimental Evaluation of a Game-Theoretic Human Driver Steering Control Model. IEEE Trans. Cybern. 2023, 53, 4791–4804. [Google Scholar] [CrossRef] [PubMed]
- Na, X.; Cole, D.J. Linear quadratic game and non-cooperative predictive methods for potential application to modelling driver–AFS interactive steering control. Veh. Syst. Dyn. 2013, 51, 165–198. [Google Scholar] [CrossRef]
- Wang, W.; Na, X.; Cao, D.; Gong, J.; Xi, J.; Xing, Y.; Wang, F.Y. Decision-making in driver-automation shared control: A review and perspectives. IEEE/CAA J. Autom. Sin. 2020, 7, 1289–1307. [Google Scholar] [CrossRef]
- Negash, N.M.; Yang, J. Driver Behavior Modeling Toward Autonomous Vehicles: Comprehensive Review. IEEE Access 2023, 11, 22788–22821. [Google Scholar] [CrossRef]
- Khanum, A.; Lee, C.Y.; Yang, C.S. Involvement of Deep Learning for Vision Sensor-Based Autonomous Driving Control: A Review. IEEE Sens. J. 2023, 23, 15321–15341. [Google Scholar] [CrossRef]
- Wei, S.; Zou, Y.; Zhang, X.; Zhang, T.; Li, X. An Integrated Longitudinal and Lateral Vehicle Following Control System with Radar and Vehicle-to-Vehicle Communication. IEEE Trans. Veh. Technol. 2019, 68, 1116–1127. [Google Scholar] [CrossRef]
- Thombare, S.S. The Future of Car Automation Field with Smart Driverless Technologies. In Computational Intelligence in Machine Learning; Kumar, A., Zurada, J.M., Gunjan, V.K., Balasubramanian, R., Eds.; Springer: Singapore, 2022; pp. 103–121. [Google Scholar] [CrossRef]
- Gao Zhenhai, F.A.; Jiang Liyong, S.B. Optimal preview trajectory decision model of lane-keeping system with driver behavior simulation and Artificial Potential Field. In Proceedings of the 2009 IEEE Intelligent Vehicles Symposium, Xi’an, China, 3–5 June 2009; pp. 797–801. [Google Scholar] [CrossRef]
- Salvucci, D.D.; Gray, R. A Two-Point Visual Control Model of Steering. Perception 2004, 33, 1233–1248. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Wang, Z.; Zhou, X.; Zhou, X.; Shen, H.; Shen, H.; Wang, J.; Wang, J. Algebraic Driver Steering Model Parameter Identification. J. Dyn. Syst. Meas. Control-Trans. ASME 2022, 144, 051006. [Google Scholar] [CrossRef]
- Wang, Z.; Zheng, R.; Nacpil, E.J.C.; Nakano, K. Modeling and Analysis of Driver Behaviour under Shared Control through Weighted Visual and Haptic Guidance. IET Intell. Transp. Syst. 2022, 16, 648–660. [Google Scholar] [CrossRef]
- Gordon, T.J.; Best, M.C.; Dixon, P.J. An Automated Driver Based on Convergent Vector Fields. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2002, 216, 329–347. [Google Scholar] [CrossRef]
- Ekinci, S.; Izci, D.; Abualigah, L.; Zitar, R.A. A Modified Oppositional Chaotic Local Search Strategy Based Aquila Optimizer to Design an Effective Controller for Vehicle Cruise Control System. J. Bionic Eng. 2023, 20, 1828–1851. [Google Scholar] [CrossRef]
- Mouri, H.; Furusho, H. Automatic path tracking using linear quadratic control theory. In Proceedings of the Proceedings of Conference on Intelligent Transportation Systems, Boston, MA, USA, 12 November 1997; pp. 948–953. [Google Scholar] [CrossRef]
- Yu, R.; Guo, H.; Sun, Z.; Chen, H. MPC-Based Regional Path Tracking Controller Design for Autonomous Ground Vehicles. In Proceedings of the 2015 IEEE International Conference on Systems, Man, and Cybernetics, Hong Kong, China, 9–12 October 2015; pp. 2510–2515. [Google Scholar] [CrossRef]
- Vatankhah, R.; Etemadi, S.; Alasty, A.; Vossoughi, G. Adaptive Critic-Based Neuro-Fuzzy Controller in Multi-Agents: Distributed Behavioral Control and Path Tracking. Neurocomputing 2012, 88, 24–35. [Google Scholar] [CrossRef]
- Fernandez, S.; Ito, T. Driver Classification for Intelligent Transportation Systems Using Fuzzy Logic. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 1212–1216. [Google Scholar] [CrossRef]
- Wang, W.; Xi, J.; Hedrick, J.K. A Learning-Based Personalized Driver Model Using Bounded Generalized Gaussian Mixture Models. IEEE Trans. Veh. Technol. 2019, 68, 11679–11690. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, D.; Han, W.; Xi, J. A Learning-Based Approach for Lane Departure Warning Systems with a Personalized Driver Model. IEEE Trans. Veh. Technol. 2018, 67, 9145–9157. [Google Scholar] [CrossRef]
- Okamoto, K.; Tsiotras, P. Data-Driven Human Driver Lateral Control Models for Developing Haptic-Shared Control Advanced Driver Assist Systems. Robot. Auton. Syst. 2019, 114, 155–171. [Google Scholar] [CrossRef]
- Kukkala, V.K.; Kukkala, V.K.; Tunnell, J.A.; Tunnell, J.A.; Pasricha, S.; Pasricha, S.; Bradley, T.H.; Bradley, T.H. Advanced Driver-Assistance Systems: A Path Toward Autonomous Vehicles. IEEE Consum. Electron. Mag. 2018, 7, 18–25. [Google Scholar] [CrossRef]
- Hang, P.; Zhang, Y.; Lv, C. Brain-Inspired Modeling and Decision-Making for Human-Like Autonomous Driving in Mixed Traffic Environment. IEEE Trans. Intell. Transp. Syst. 2023, 24, 10420–10432. [Google Scholar] [CrossRef]
- Han, J.; Zhao, J.; Zhu, B.; Song, D. Adaptive Steering Torque Coupling Framework Considering Conflict Resolution for Human-Machine Shared Driving. IEEE Trans. Intell. Transp. Syst. 2022, 23, 10983–10995. [Google Scholar] [CrossRef]
- Mwaita, K.F.; Bhaumik, R.; Ahmed, A.; Sharma, A.; De Angeli, A.; Haller, M. Emotion-Aware In-Car Feedback: A Comparative Study. Multimodal Technol. Interact. 2024, 8, 54. [Google Scholar] [CrossRef]
- Filippini, C.; Spadolini, E.; Cardone, D.; Bianchi, D.; Preziuso, M.; Sciarretta, C.; del Cimmuto, V.; Lisciani, D.; Merla, A. Facilitating the Child–Robot Interaction by Endowing the Robot with the Capability of Understanding the Child Engagement: The Case of Mio Amico Robot. Int. J. Soc. Robot. 2021, 13, 677–689. [Google Scholar] [CrossRef]
- Tao, K.; Zheng, W. Structural Damage Location and Evaluation Model Inspired by Memory and Causal Reasoning of the Human Brain. Struct. Control Health Monit. 2018, 25, e2249. [Google Scholar] [CrossRef]
- Tao, K.; Zheng, W. An Anthropomorphic Fuzzy Model for the Time-Spatial Assessment of Sandstone Seepage Damage. Autom. Constr. 2020, 109, 102989. [Google Scholar] [CrossRef]
- Liu, J.; Dai, Q.; Guo, H.; Guo, J.; Chen, H. Human-Oriented Online Driving Authority Optimization for Driver-Automation Shared Steering Control. IEEE Trans. Intell. Veh. 2022, 7, 863–872. [Google Scholar] [CrossRef]
- Marcano, M.; Díaz, S.; Pérez, J.; Irigoyen, E. A Review of Shared Control for Automated Vehicles: Theory and Applications. IEEE Trans. Hum.-Mach. Syst. 2020, 50, 475–491. [Google Scholar] [CrossRef]
- El Hajjami, L.; Mellouli, E.M.; Berrada, M. Autonomous Vehicle Lateral Control for the Lane-change Maneuver. In Proceedings of the 6th International Conference on Wireless Technologies, Embedded, and Intelligent Systems (WITS 2020), Fez, Morocco, 14–16 October 2020; Bennani, S., Lakhrissi, Y., Khaissidi, G., Mansouri, A., Khamlichi, Y., Eds.; Springer: Singapore, 2022; pp. 285–295. [Google Scholar] [CrossRef]
- Zha, Y.; Deng, J.; Qiu, Y.; Zhang, K.; Wang, Y. A Survey of Intelligent Driving Vehicle Trajectory Tracking Based on Vehicle Dynamics. SAE Int. J. Veh. Dyn. Stab. NVH 2023, 7, 221–248. [Google Scholar] [CrossRef]
- Ataei, M.; Ataei, M.; Khajepour, A.; Khajepour, A.; Jeon, S.; Jeon, S. Development of a novel general reconfigurable vehicle dynamics model. Mech. Mach. Theory 2021, 156, 104147. [Google Scholar] [CrossRef]
- Dahmani, H.; Chadli, M.; Rabhi, A.; El Hajjaji, A. Road curvature estimation for vehicle lane departure detection using a robust Takagi–Sugeno fuzzy observer. Veh. Syst. Dyn. 2013, 51, 581–599. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Su, C.; Gong, X.; Huang, J.; Yang, D. Adaptive Authority Allocation Approach for Shared Steering Control System. IEEE Trans. Intell. Transp. Syst. 2022, 23, 19428–19439. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, G.; Wang, R.; Schnelle, S.C.; Wang, J. A Gain-Scheduling Driver Assistance Trajectory-Following Algorithm Considering Different Driver Steering Characteristics. IEEE Trans. Intell. Transp. Syst. 2017, 18, 1097–1108. [Google Scholar] [CrossRef]
- Saleh, L.; Chevrel, P.; Claveau, F.; Lafay, J.F.; Mars, F. Shared Steering Control Between a Driver and an Automation: Stability in the Presence of Driver Behavior Uncertainty. IEEE Trans. Intell. Transp. Syst. 2013, 14, 974–983. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, J.; Yang, S.; Li, Z. Study on improvement of LuGre dynamical model and its application in vehicle handling dynamics. J. Mech. Sci. Technol. 2019, 33, 545–558. [Google Scholar] [CrossRef]
- Sentouh, C.; Chevrel, P.; Mars, F.; Claveau, F. A Sensorimotor Driver Model for Steering Control. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 2462–2467. [Google Scholar] [CrossRef]
- Jiang, J.; Astolfi, A. Lateral Control of an Autonomous Vehicle. IEEE Trans. Intell. Veh. 2018, 3, 228–237. [Google Scholar] [CrossRef]
- Murre, J.M.J.; Murre, J.M.J.; Dros, J.; Dros, J. Replication and Analysis of Ebbinghaus’ Forgetting Curve. PLoS ONE 2015, 10, e0120644. [Google Scholar] [CrossRef] [PubMed]
- Raaijmakers, J.G.; Shiffrin, R.M. Search of Associative Memory. Psychol. Rev. 1981, 88, 93–134. [Google Scholar] [CrossRef]


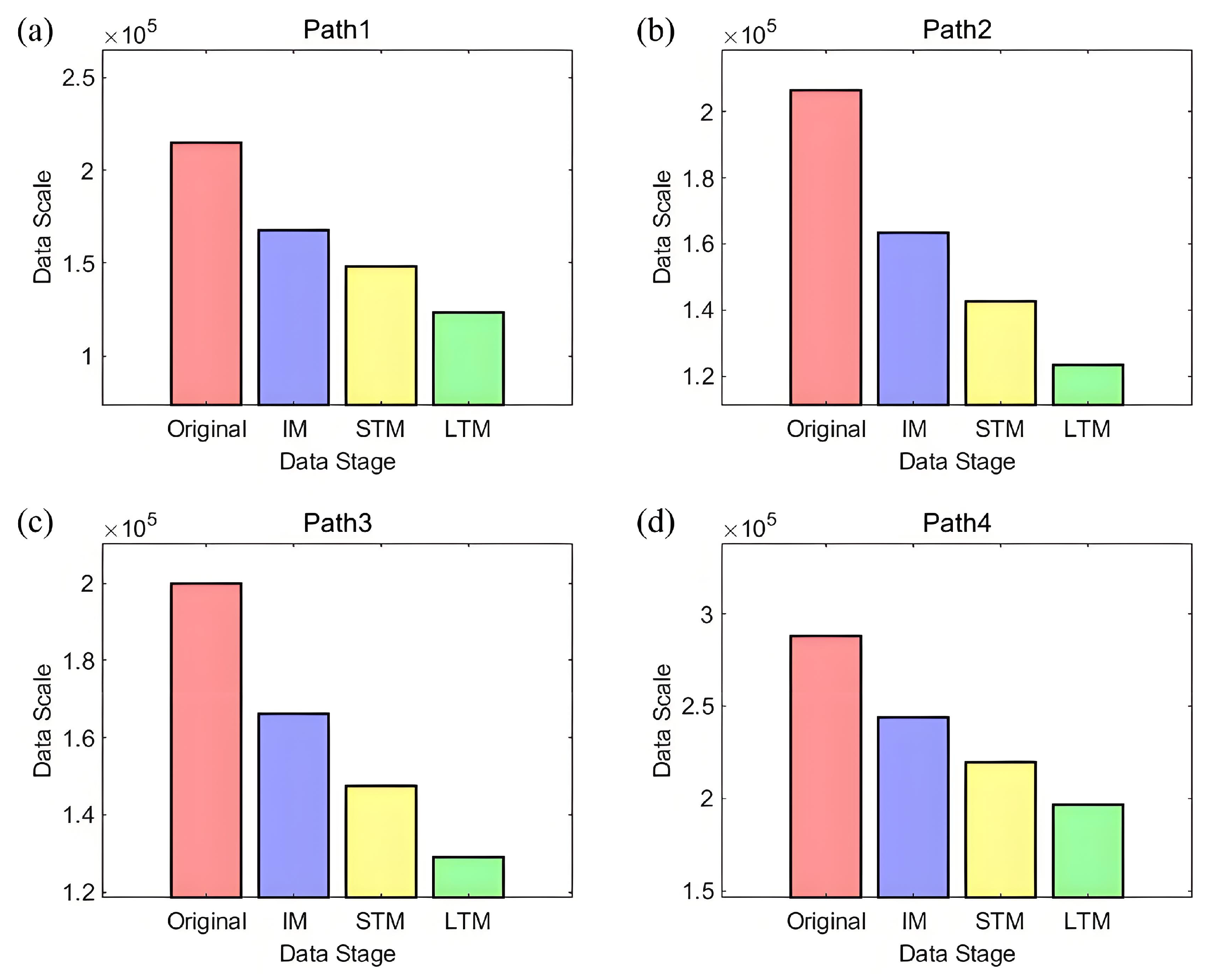
| Path | IM | STM | LTM | Total |
|---|---|---|---|---|
| 1 | 21.86% | 9.09% | 11.60% | 42.55% |
| 2 | 20.79% | 10.11% | 9.27% | 40.17% |
| 3 | 16.83% | 9.42% | 9.15% | 35.40% |
| 4 | 15.39% | 8.46% | 7.96% | 31.81% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Wang, H.; Yang, B.; Luo, H.; Liu, J.; Zheng, W. Dynamic Correction of Preview Weighting in the Driver Model Inspired by Human Brain Memory Mechanisms. Machines 2025, 13, 617. https://doi.org/10.3390/machines13070617
Li C, Wang H, Yang B, Luo H, Liu J, Zheng W. Dynamic Correction of Preview Weighting in the Driver Model Inspired by Human Brain Memory Mechanisms. Machines. 2025; 13(7):617. https://doi.org/10.3390/machines13070617
Chicago/Turabian StyleLi, Chang, Hengyu Wang, Bo Yang, Haotian Luo, Jianjin Liu, and Wei Zheng. 2025. "Dynamic Correction of Preview Weighting in the Driver Model Inspired by Human Brain Memory Mechanisms" Machines 13, no. 7: 617. https://doi.org/10.3390/machines13070617
APA StyleLi, C., Wang, H., Yang, B., Luo, H., Liu, J., & Zheng, W. (2025). Dynamic Correction of Preview Weighting in the Driver Model Inspired by Human Brain Memory Mechanisms. Machines, 13(7), 617. https://doi.org/10.3390/machines13070617








