A Biochemistry-Inspired Algorithm for Path Planning in Unmanned Ground Vehicles

Abstract

Unmanned ground vehicles (UGVs) have gained significant attention due to their extensive applications in both military and civilian sectors. For effective UGV deployment, path planning algorithms must prioritize computational efficiency, solution reliability, and runtime performance while maintaining path quality. Autonomous path planning remains a critical challenge in UGV navigation, as conventional methods, while effective, often suffer from considerable computational overhead. To address this issue, we propose a novel biochemistry-inspired path planning algorithm designed specifically for static grid-based scenarios. MetaPath demonstrates remarkable computational efficiency while maintaining solution quality across different obstacle densities in benchmark environments. Specifically, the algorithm achieves path lengths within ±5% of all benchmark algorithms while dramatically reducing the exploration space, visiting up to 10% of the cells explored by conventional approaches such as A*. This superior efficiency translates into exceptional runtime performance, executing up to 3000 times faster than bio-inspired algorithms like Ant Colony Optimization (ACO) and the Genetic Algorithm (GA), performing nearly three times faster than the widely used A* algorithm, and maintaining competitive performance with efficient algorithms like Breadth-First Search (BFS) and Particle Swarm Optimization (PSO), thereby establishing the algorithm as a highly efficient pathfinding solution. Most notably, MetaPath introduces a novel approach as the first chemistry-inspired pathfinding algorithm, guaranteeing path discovery when one exists within reasonable computational time, a crucial advantage over some benchmark algorithms that may fail to converge or require excessive computational resources in complex scenarios.

1. Introduction

Autonomous unmanned ground vehicles (UGVs) are capable of operating independently without human intervention [1]. Initially driven by military applications, the use of UGVs has expanded dramatically over recent years to encompass a wide array of civilian applications. These include power line inspection, surveillance, mine detection, data collection, imaging, security, agriculture, deep-ocean exploration, and scientific exploration in space [2]. UGVs are particularly valuable for tasks that are dangerous, remote, costly, or difficult for humans to perform [3].

UGV navigation presents a significant challenge as it must be effective on both smooth roads and off-road environments [4]. Efficient navigation minimizes energy consumption [5], which can be achieved by reducing path length and runtime. Path planning is essential for enabling UGVs to move from a start position to a goal position while avoiding obstacles and achieving predefined objectives [6]. Therefore, path planning remains a crucial issue in UGV research [7,8].

This paper addresses the global path planning problem for a single UGV in static 2D grid environments. To tackle this problem, we developed “MetaPath”, a novel heuristic algorithm inspired by metabolic pathways in biochemistry. While most nature-inspired algorithms derive inspiration from biology or physics, the potential of chemistry-inspired algorithms remains underexplored [9], particularly in path planning. This represents a missed opportunity to leverage potentially valuable optimization principles from chemical processes. Additionally, existing algorithms face significant challenges with computational overhead in larger, more complex environments. Traditional algorithms like A* struggle with scalability in expansive environments, while nature-inspired approaches such as Ant Colony Optimization (ACO) and the Genetic Algorithm (GA) often require substantial computational resources. Furthermore, current path planning approaches typically expand one cell at a time during path search, leading to inefficient exploration of the search space and increased computational overhead. These gaps highlight the need for novel approaches that can improve both the efficiency and scalability of path planning algorithms.

This paper seeks to fill these gaps by introducing the MetaPath algorithm, leveraging concepts from metabolic pathways to enhance path planning efficiency. The MetaPath algorithm simulates the generation of a metabolic pathway in biochemistry. Here, the start position of the UGV corresponds to the initial substrate, and the goal position is analogous to the final product. The waypoints connecting the start and goal positions represent metabolic reactions converting the initial substrate to the final product. MetaPath addresses current path planning challenges through three integrated techniques: First, metabolic-reaction-based generation where each planning step mirrors a metabolic reaction, considering three cells simultaneously (substrate, enzyme, intermediate product) to enable more informed path decisions while reducing computational overhead. Second, enzyme-inspired search pruning that applies enzyme specificity principles to selectively evaluate neighboring cells, efficiently reducing the search space while maintaining path optimality. Third, pathway optimization, which uses a dual-objective heuristic function that evaluates both immediate moves and future positions, balancing path optimality with computational efficiency. This innovative approach allows MetaPath to generate efficient paths with fewer visited cells, near-optimal path lengths, and reduced runtimes.

To evaluate MetaPath, two types of experiments were conducted: a random map experiment for testing scalability across various map sizes (8 × 8 to 256 × 256) and obstacle densities (0–60%), and a benchmark map experiment to evaluate performance on standardized complex environments. We have considered three performance metrics: path length, runtime, and number of visited cells. We used Statistical Validation, using factor analysis and parametric methods to provide robust statistical evidence, and we conducted comparative analysis against rival path planning algorithms including A*, Breadth-First Search (BFS), Particle Swarm Optimization (PSO), ACO, the GA, and Tabu Search. The results indicated that MetaPath improved overall path generation performance by visiting fewer cells and achieving near-optimal path lengths and runtimes compared to benchmark algorithms.

This research addresses fundamental challenges in autonomous navigation with significant implications for both theory and practice. The development of chemistry-inspired algorithms represents a paradigm shift in path planning, offering new perspectives beyond traditional biological and physical models. This approach is particularly significant as UGVs increasingly operate in complex, resource-constrained environments where computational efficiency is crucial. The successful adaptation of metabolic pathway principles to path planning demonstrates the untapped potential of chemical process models in solving computational challenges. Furthermore, this work’s significance extends to practical applications in urban exploration, disaster response, and industrial automation, where efficient path planning directly impacts operational effectiveness. The methodology developed in this study also provides a foundation for evaluating future path planning algorithms in realistic scenarios, contributing to the broader advancement of autonomous navigation systems.

The main contributions of this paper include the following:

• Introduction of the MetaPath algorithm: a novel path planning algorithm inspired by biochemistry, tailored for grid-based scenarios.
• Comprehensive performance evaluation: rigorous assessment of Meta-Path against established algorithms (A*, BFS, PSO, ACO, GA, Tabu Search) using benchmark and randomly generated maps of diverse sizes and complexities.
• Statistical analysis: application of factor analysis and parametric methods to provide robust statistical inferences supporting Meta-Path’s performance.
• Scalability and efficiency: demonstration of MetaPath’s ability to generate competitive path lengths, reduced runtimes, and fewer visited cells, particularly excelling in specific obstacle ratios and map sizes.

The remainder of this paper is structured as follows. Section 2 presents an overview of related work in the literature. Section 3 describes the MetaPath algorithm in detail, including its biochemical inspiration and implementation. Section 4 outlines the evaluation framework, and Section 5 presents and discusses the results. Finally, Section 6 concludes this paper, summarizing the findings and suggesting directions for future research.

2. Related Work

The exploration of path planning algorithms for UGVs spans a diverse range of methodologies, bridging classical approaches and nature-inspired innovations. Foundational to this domain are classical algorithms, including prominent examples such as Dijkstra’s algorithm and the A* algorithm. Despite its initial inefficiency, Dijkstra’s algorithm has undergone substantial enhancements to improve both its performance and storage efficiency [10,11,12,13,14,15]. Similarly, the A* algorithm, while optimal for many scenarios, faces scalability issues in expansive environments, leading to the development of variants such as Partial and Global A* for specialized applications [8,16,17,18,19,20,21]. Other traditional methods, such as Breadth-First Search and Tabu Search, have also been adapted to optimize performance in dynamic environments and to integrate with contemporary techniques, thereby reducing travel distances in complex terrains [22,23,24,25,26,27,28,29,30,31].

In recent years, the field has witnessed a surge in algorithms inspired by natural phenomena, mirroring the intricate behaviors and processes observed in biological, physical, and chemical systems. Among these, biology-inspired algorithms such as the Genetic Algorithm, Ant Colony Optimization, and Particle Swarm Optimization are notable for their innovative applications. These algorithms draw inspiration from natural selection, the collective behavior of ants, and the social dynamics of bird flocks and fish schools, respectively. They have been refined through various adaptations to address the complex problem of path planning with enhanced efficiency and adaptability [7,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47].

Similarly, algorithms based on physical principles, such as Artificial Potential Fields, the Gravitational Search Algorithm, and Simulated Annealing, apply fundamental laws of physics to the challenges of UGV path planning. These methods exploit concepts of potential fields, gravitational forces, and the process of annealing to determine optimal paths through challenging environments [48,49,50,51,52,53,54,55,56,57,58,59].

While less frequently employed, chemistry-inspired algorithms introduce a unique dimension to path planning strategies. For instance, the Chemical Reaction Optimization algorithm emulates the dynamics of chemical reactions, presenting a novel approach to optimization problems within path planning. This methodology underscores the potential of harnessing diverse scientific principles to enhance the efficiency and adaptability of UGV navigation in unexplored territories [60,61,62].

The analysis of the existing literature reveals several important research gaps. Classical algorithms like Dijkstra and A*, while optimal for many scenarios, face significant scalability challenges in large environments [8,16]. Nature-inspired algorithms such as the GA, ACO, and PSO have attempted to address these limitations but often introduce their own computational overhead. Furthermore, most existing approaches share a common limitation in their search space exploration strategy—they typically expand one cell at a time, which can lead to inefficient path generation in complex environments. Physics-inspired algorithms have contributed valuable concepts but still struggle with computational efficiency in dense-obstacle scenarios. Notably, while biological and physical principles have been extensively explored, the potential of chemistry-inspired approaches remains largely untapped in path planning applications. The few existing chemistry-inspired algorithms have focused primarily on general optimization problems rather than specifically addressing the unique challenges of path planning. This gap in the literature suggests an opportunity to leverage chemical process principles, particularly those from metabolic pathways, to develop more efficient path planning approaches. This paper addresses this gap by introducing the MetaPath algorithm, which leverages concepts from metabolic pathways in biochemistry to enhance path planning efficiency.

3. Algorithm Design

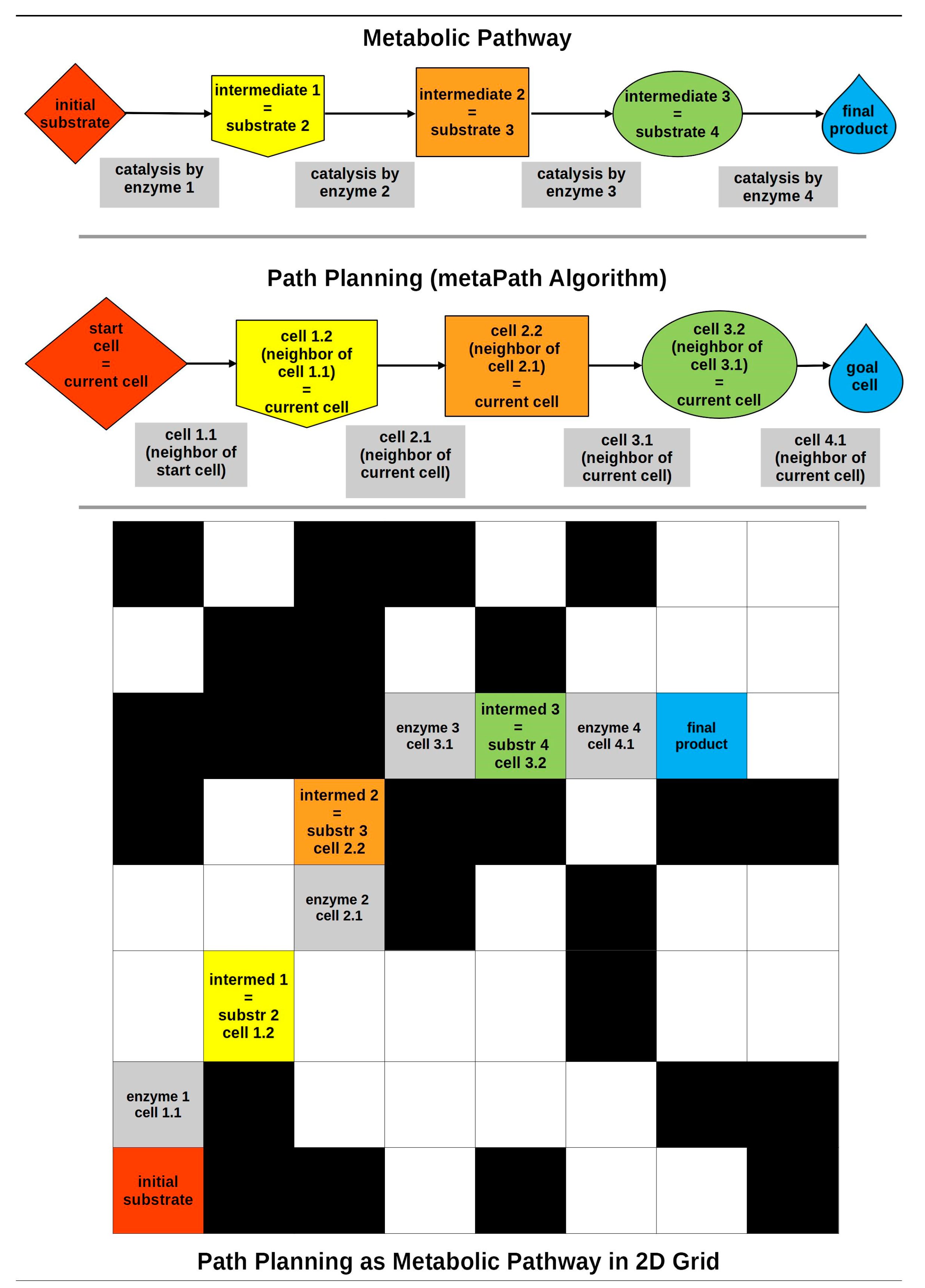
3.1. Biochemistry Inspiration

A metabolic pathway is a series of consecutive enzyme-catalyzed biochemical reactions that occur within a cell [63]. It begins with a specific initial substrate, which is converted through a series of enzymatic reactions into a final product.

Figure 1 illustrates a metabolic pathway that consists of four distinct steps or metabolic reactions. It starts with a specific initial substrate, initiating a series of reactions that ultimately produce the desired final product. The continuity and connectivity of the pathway are maintained, as the intermediate product of one reaction serves as the substrate for the subsequent reaction. This seamless transition between reactions ensures the efficient progression of the metabolic process.

As illustrated in Figure 1 and

Table 1. A metabolic pathway’s detailed steps for the metabolic reactions in Figure 1.

Metabolic Reaction	Substrate	Enzyme	Intermediate Product/ Final Product	Next-Step Substrate
1	initial substrate	enzyme 1	intermediate 1	substrate 2
2	substrate 2	enzyme 2	intermediate 2	substrate 3
3	substrate 3	enzyme 3	intermediate 3	substrate 4
4	substrate 4	enzyme 4	final product	-

, the pathway begins with metabolic reaction 1 (red curly bracket), where the initial substrate interacts with enzyme 1 to produce an intermediate product, termed “intermediate 1”. This intermediate then acts as the substrate for metabolic reaction two, continuing the sequence. Each intermediate product subsequently becomes the substrate for the next reaction, ensuring a linked series of steps. In the last step (green curly bracket), “intermediate 3” transforms into “substrate 4” and, with the aid of enzyme 4, converts into the final product. This mechanism guarantees a consecutive and interconnected flow of reactions.

To further understand the structure and function of metabolic pathways, it is important to consider their key components.

• Substrate: the molecule upon which an enzyme acts, serving as the starting point for enzyme-catalyzed reactions [63].
• Intermediate (or Intermediate Metabolite): the product of one enzymatic reaction that serves as the substrate for the subsequent enzyme in the pathway, highlighting the pathway’s connectivity [63,64].
• Enzymes: catalysts that facilitate biochemical reactions essential for life processes in all living organisms, characterized by several distinct properties [65,66]:

  ○

  Enzymes are integral at every step of a metabolic pathway, with specific enzymes responsible for converting substrates into various products.

  ○

  They channel reactants into useful pathways, directing metabolic activities.

  ○

  Enzymes exhibit specificity, interacting with one or a few substrates and catalyzing only one type of chemical reaction.

Additionally, the efficiency of metabolic pathways is often enhanced through multi-objective optimization. This approach seeks to find a global solution that can minimize or maximize specific parameters, such as reducing the number of steps in the pathway. By applying optimization techniques, the pathway can operate more effectively, ensuring the metabolic process is both efficient and robust. Figure 2 illustrates the process of generating a metabolic pathway.

3.2. From Inspiration to Algorithm

We propose adopting the metabolic pathway generation model to enhance the efficiency of UGV path planning, recognizing a substantial correlation between the two systems. Both systems not only share analogous components but also exhibit key similarities, particularly in the relevance of optimization principles. This suggests that a unified approach could effectively tackle complex optimization challenges in UGV path planning.

It is possible to define the process of path planning for UGVs in a way that simulates the process of generating metabolic pathways. The start position of the UGV corresponds to the initial substrate, and the goal position of the UGV corresponds to the final product. The way points that link start and goal positions correspond to the metabolic reactions that take place to convert the initial substrate to a final product.

Table 2. From similarity facets to inspiration.

Feature	Metabolic Pathway	Path Planning
Environment	Living cell	2D grid
Path generation	A metabolic pathway is generated from an initial substrate to a final product.	A path is generated from a start position to a goal position.
Starts at	Initial substrate	Start position
Connected by	Enzymes and intermediate products	Way points
Ends at	Final product	Goal position
Optimization	Minimize the number of steps in the metabolic pathway, intermediate-product levels, and enzyme levels.	Minimize the path length, runtime, and visited cells.

lists the similar facets between the metabolic pathway system and the path planning process in general. The inspiration from the metabolic pathway topic has been drawn from these similar facets.

The mapping between the metabolic pathway and the path planning in the MetaPath algorithm is depicted in Figure 3. The figure consists of three analogous parts. The top part shows a complete metabolic pathway with its composed metabolic reactions. The middle part of Figure 3 depicts the path planning process in the MetaPath algorithm, while the bottom part illustrates the path planning process inspired by the metabolic pathway in a 2D grid environment.

It is important to note that the intermediate-product cell becomes the substrate (current cell) for next decision-making. Figure 4 shows the terminology borrowed from the metabolic pathways and illustrates how they are applied to MetaPath algorithm path planning.

3.3. MetaPath Search Strategy

The MetaPath algorithm employs informed or heuristic search strategies, utilizing predefined heuristics to evaluate the potential of non-goal states. These heuristics play a crucial role in minimizing the search space, with the effectiveness of the heuristic directly impacting the number of generated and stored states, thereby accelerating the solution discovery process.

In typical search algorithms, identifying a solution involves expanding the current cell to explore all adjacent cells, generating new states in the process [67]. These newly generated states are cataloged in an open list, while already expanded cells are archived in a closed list. The distinctive aspect of various search algorithms lies in their method for incorporating newly generated cells (nodes) into the frontier, generally represented by an open list. While conventional approaches add each new cell individually along with its cost estimate (evaluation function) to the frontier, the MetaPath algorithm innovates by adding groups of three cells as a single entry with a consolidated cost estimate. This method significantly enhances the efficiency of the search process.

Figure 5 illustrates the standard practice among search algorithms of adding single cells to the frontier, showing, for example, the addition of cell 56 with a cost estimate of 8. Conversely, Figure 6 highlights the MetaPath algorithm’s approach of grouping three cells as one entry in the frontier. These triads symbolize a metabolic reaction, comprising a substrate (magenta), an enzyme (blue), and an intermediate product (orange), with each frontier entry representing one such reaction. For instance, the MetaPath algorithm introduces a metabolic reaction, MetabolicReaction (Cell 56, Cell 48, Cell 41), with an associated cost of 12 to the frontier. By aggregating states in this manner, the MetaPath algorithm reduces the number of generated states, leading to a more efficient solution discovery process. It is noteworthy that the MetaPath algorithm’s search extends to all eight directional vectors.

3.4. Heuristic and Objective Functions

As in any path planning algorithm, a decision must be made to decide the next step and reach the final goal. In MetaPath, the decision-making process to generate the path is analogous to metabolic pathways. The metabolic pathway is formed by linked steps composed of enzyme-catalyzed metabolic reactions, and the single metabolic reaction can be formulated as follows:

$$\mathrm{s}\mathrm{u}\mathrm{b}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}+\mathrm{e}\mathrm{n}\mathrm{z}\mathrm{y}\mathrm{m}\mathrm{e}=\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{m}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{e} \mathrm{p}\mathrm{r}\mathrm{o}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t}$$

(1)

The intermediate product is used as a substrate for the next step; consequently, the metabolic reactions are connected and form a metabolic pathway. Therefore, in the MetaPath algorithm, the decision to take the next step is a metabolic reaction that will result in two cells at a time (an enzyme and an intermediate product), which makes it better than other algorithms that produce one cell with each decision made. MetaPath is better because, as discussed in the previous section, its search strategy is more efficient since it adds three cells at a time in its open list, in contrast to other algorithms that add a single cell. Thus, the MetaPath algorithm is designed with two heuristics in its heuristic function. The heuristics are inspired by the metabolic pathways’ mechanism. These two heuristics are the enzyme and the intermediate product.

Let $\mathrm{f}(\mathrm{E},\mathrm{P})$ be the heuristic function of each metabolic reaction in the metabolic pathway so that E is the enzyme cell and P is the intermediate-product cell.

$$\mathrm{f}\left(\mathrm{E},\mathrm{P}\right)=\mathrm{e}\mathrm{u}\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\left(\mathrm{E},\mathrm{g}\mathrm{o}\mathrm{a}\mathrm{l}\right)+\mathrm{e}\mathrm{u}\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\left(\mathrm{P},\mathrm{g}\mathrm{o}\mathrm{a}\mathrm{l}\right)$$

(2)

Let n be the number of metabolic reactions in the open list; then, the optimal metabolic reaction is found according to the following objective function:

$$\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}{\sum }_{\mathrm{i}=1}^{\mathrm{n}}\left\{\mathrm{f}\left(\mathrm{E},\mathrm{P}\right)=\mathrm{e}\mathrm{u}\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\left(\mathrm{E}\mathrm{n}\mathrm{z}\mathrm{y}\mathrm{m}\mathrm{e},\mathrm{g}\mathrm{o}\mathrm{a}\mathrm{l}\right)+\mathrm{e}\mathrm{u}\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\left(\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{m}\mathrm{e}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t},\mathrm{g}\mathrm{o}\mathrm{a}\mathrm{l}\right)\right\}$$

(3)

To this extent, it is important to highlight the differences between the MetaPath algorithm and the A* algorithm as summarized in

Table 3. Difference between MetaPath and A*.

Difference Facets	MetaPath Algorithm	A* Algorithm
Type	Biochemistry-inspired	Classical
Evaluation Function	All the terms are admissible heuristics. $\mathrm{f}\left(\mathrm{E},\mathrm{P}\right)=\mathrm{e}\mathrm{u}\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\left(\mathrm{E},\mathrm{g}\mathrm{o}\mathrm{a}\mathrm{l}\right)+\mathrm{e}\mathrm{u}\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{n}\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\left(\mathrm{P},\mathrm{g}\mathrm{o}\mathrm{a}\mathrm{l}\right)$	One term is an actual cost, and the other is an admissible heuristic. $\mathrm{f}\left(n\right)=\mathrm{g}\left(n\right)+\mathrm{h}\left(n\right)$
Open List	With each decision, MetaPath adds three cells together (one metabolic reaction) as a single entry with its cost estimate to the frontier (open list), as shows.	With each decision, A* adds a single cell (node) with its cost estimate (evaluation function) to the frontier (open list), as Figure 5 depicts.
Deciding Next Step	Produces two cells in the path.	Produces one cell in the path.
Neighboring Cells	Neighboring cells are excluded based on metabolic pathway principles.	Neighboring cells are excluded based on their pre-existence in the closed list.

.

3.5. The MetaPath Algorithm

In MetaPath, the decision to take the next step starts with a specific substrate cell. To form a single enzyme-catalyzed metabolic reaction, the algorithm must decide which neighboring cell of the substrate can serve as the catalyst enzyme. After selecting the enzyme cell, the algorithm must decide which of the enzyme’s neighboring cells qualifies as an intermediate product for that particular metabolic reaction step. This selection process ensures that not all neighboring cells are considered, thus reducing the number of potential neighbors generated. In making these choices, MetaPath takes advantage of the optimization principles applied to the metabolic pathways.

Assume $D$ is a discretized or gridded space on which the map $M$ is constructed. Map $M$ has complete information about the environment; hence, the environment is completely known. Each discrete position $d \in M$ is called a cell, so $M$ is constructed as a 2D grid of cells.

Let MR be a metabolic reaction represented by the tuple $〈S,E,P〉$ so that $S\in M, E\in M, \mathrm{a}\mathrm{n}\mathrm{d}P\in M$. The first value $S$ represents the substrate cell, the second value $E$ represents the enzyme cell, and the last value $P$ represents the intermediate-product cell.

Let $O_{mr}$ be the set of metabolic reactions in the open list so that $MR\in O_{mr}$, and let $C_{mr}$ be the set of metabolic reactions in the closed list so that $MR\in C_{mr}$.

Figure 7 illustrates the flowchart of the MetaPath algorithm and how it works. The algorithm starts by initializing $M$ as a 2D grid of cells and assigning the obstacles to this grid. Also, it initializes the initial substrate $S_{initial}$ cell with the UGV’s start position and initializes the final-product $P_{final}$ cell with the UGV’s goal position. Then, the first metabolic reaction tuple ${MR}_{first}〈S,E,P〉$, which starts with the initial substrate cell, is created so that $S=E=P=S_{initial}$.

The heuristic function for this metabolic reaction is calculated as follows:

$$f\left(E,P\right)=euclideanDistance\left(E,goal\right)+euclideanDistance\left(P,goal\right)$$

(4)

where E is the enzyme cell and P is the intermediate-product cell.

Next, the calculated heuristic function is assigned to ${MR}_{first}$. Then, ${MR}_{first}$ is added to the open list $O_{mr}$, which is a priority queue.

After that, the algorithm starts with its main loop, which continues as long as the open list $O_{mr}$ is not empty. The main loop consists of five main parts, which are listed in

Table 4. MetaPath algorithm main parts as appear in Figure 7.

Part #	Purpose
Part 1	Find the optimal metabolic reaction (substrate cell, enzyme cell, intermediate-product cell) in the open list.
Part 2	Start the next metabolic reaction.
Part 3	Find the catalyst enzyme cells.
Part 4	Find the intermediate-product cells.
Part 5	Create metabolic reactions and add them to the open list.

and illustrated in Figure 7.

Importantly, the second, third, and fourth parts represent the essential contribution of the MetaPath algorithm and represent the heart of the inspiration from metabolic pathways. The following paragraphs describe the five main parts.

In the first part, the algorithm removes the optimal metabolic reaction ${MR}_{optimal}〈S_{optimal},E_{optimal},P_{optimal}〉$, which is the one with the minimum heuristic function, from the open list $O_{mr}$:

$$Minimize {\sum }_{i=1}^n\{f\left(E,P\right)=euclideanDistance\left(Enzyme,goal\right)+euclideanDistance\left(intermediateProduct,goal\right)\}$$

(5)

where n is the number of metabolic reactions in the open list.

Then, the algorithm adds ${MR}_{optimal}〈S_{optimal},E_{optimal},P_{optimal}〉$ to the closed list, which is a list containing expanded cells.

In the second part, the algorithm starts with the next metabolic reaction ${MR}_{next}$. This is achieved by assigning the intermediate product of the optimal metabolic reaction to the substrate cell; that is, $S_{next}=P_{optimal}$ and ${MR}_{next}〈S_{next},E_{catalyst}, P_{intermed}〉$ so that $E_{catalyst}$ and $P_{intermed}$ will be assigned later as the reaction proceeds.

In the third part, the algorithm needs to find the catalyst enzyme cells $E_{catalyst}$ to continue the metabolic reaction ${MR}_{next}$. To do this, the algorithm searches for the free neighboring cells for the substrate cell $S_{next}$. Let $N_s$ be the set of all neighboring cells of $S_{next}$. In MetaPath, not all neighboring cells in $N_s$ are catalyst enzyme cells for $S_{next}$ because, first, based on the optimization principles applied to metabolic pathways, the algorithm must minimize the enzyme levels. Second, based on the enzyme’s properties, the enzymes are highly specific, binding with particular substrates. This means that the MetaPath algorithm should not consider all the neighboring cells in $N_s$ as enzyme cells; instead, MetaPath must exclude some neighbors (minimize enzyme levels). Therefore, the algorithm sets two conditions to specify which free neighbors in $N_s$ can be catalyst enzyme cells. Let $c_{free}$ be a free neighbor cell in $N_s$, then $\forall c_{free}\in N_s$, and ${ c}_{free}$ is a catalyst enzyme if it satisfies the conditions as follows:

(1)

$c_{free}$ $\ne$ previous enzyme or previous intermediate product in closedList $C_{mr}$.

(2)

$c_{free}\ne$ previous enzyme or previous intermediate product in openList $O_{mr}$.

When both conditions are met, then $E_{catalyst}$ = $E_{catalyst}+\left\{c_{free}\right\}$. The set of catalyst enzyme cells $E_{catalyst}$ is created to contain the cells that satisfy the two conditions, which are set based on metabolic pathway principles as described above. If one of the catalyst enzyme cells is the goal, the algorithm terminates, constructs the path using the metabolic reactions in the closed list $C_{mr}$, and returns the path; otherwise, the algorithm proceeds to the fourth part.

In the fourth part, the algorithm continues the metabolic reaction ${MR}_{next}$ that has started previously by trying to find the set of intermediate-product cells $P_{intermed}$ for each $e_{catalyst} \in E_{catalyst}$. That is, for each catalyst enzyme cell found, the algorithm tries to find the intermediate-product cells. For this purpose, the algorithm searches for the free neighboring cells for each $e_{catalyst}\in E_{catalyst}$. Let $N_e$ be the set of all neighboring cells of $e_{catalyst}$. In MetaPath, not all neighboring cells in $N_e$ are considered intermediate-product cells for $e_{catalyst}$ because some of the neighbors could be an enzyme, which cannot be an intermediate product, as they are different substances; also, a neighbor could be a substrate or an intermediate product in previous reactions, which cannot be an intermediate product again in the same pathway. This means that the MetaPath algorithm should not consider all the neighboring cells in $N_e$ as intermediate-product cells; however, MetaPath must exclude some neighbors (minimize the level of intermediate products). Thus, the algorithm identifies a set of conditions to specify which free neighbors in $N_e$ can be intermediate-product cells. Let $c_{free}$ be a free neighbor cell in $N_e$, then $\forall c_{free}\in N_e$, and $c_{free}$ is an intermediate product if it satisfies the conditions as follows:

(1)

$c_{free} \ne$ previous enzyme or intermediate product in closedList $C_{mr}$.

(2)

$c_{free} \ne$ $e_{catalyst}$.

(3)

$c_{free} \ne$ $S_{next}$.

(4)

$c_{free} \ne$ previous enzyme or intermediate product in openList $O_{mr}$.

When all conditions are met, then $P_{intermed}=P_{intermed}+{\{c}_{free}\}$. This set of intermediate-product cells $P_{intermed}$ is created to contain the neighboring cells that satisfy the conditions above.

In the fifth part, the algorithm creates a set of metabolic reactions so that all these metabolic reactions share the same substrate cell $S_{next},$ identified in the second part. The enzymes and intermediate-product cells are assigned to these metabolic reactions using the catalyst enzyme cells $E_{catalyst}$ and the intermediate-product cells $P_{intermed}$ identified in the third and fourth parts, respectively. Also, the heuristic function for all these metabolic reactions is calculated, as noted before. Next, these metabolic reactions are added to the open list. If the goal cell is identified as an intermediate-product cell in the newly created metabolic reactions, the algorithm adds these reactions to another list called the final reaction list in addition to the open list. In this case, the algorithm finds the optimal metabolic reaction in the final reaction list and adds it to the closed list, which is used to construct and return the path. When none of the intermediate-product cells are the goal cell, the algorithm restarts its main loop again. The algorithm continues the execution of these five parts until it finds a path, or the open list is empty, which indicates that there is no path to the goal.

MetaPath introduces several unique characteristics that distinguish it from traditional path planning approaches: First, MetaPath employs a novel metabolic reaction model for path exploration. Unlike conventional algorithms that evaluate single cells sequentially, MetaPath processes three cells simultaneously in each decision step: the substrate cell (current position), enzyme cell (potential next position), and intermediate-product cell (future position). As illustrated in Figure 6, this triad-based expansion approach enables more comprehensive path evaluation while significantly reducing the total number of cell visits required to find an optimal path. Second, MetaPath implements selective search space pruning inspired by enzyme specificity. Traditional algorithms typically evaluate all neighboring cells as potential next steps. In contrast, MetaPath selectively filters neighboring cells based on metabolic pathway principles. As shown in Section 3.5, cells must satisfy specific conditions derived from enzyme–substrate interactions to be considered as either enzyme cells or intermediate products. This selective approach substantially reduces the search space while maintaining path optimality. Third, MetaPath features a unique dual-objective heuristic function that evaluates both immediate and future path segments simultaneously. As defined in Equation (4), the heuristic function f (E, P) considers both the enzyme cell E (immediate move) and intermediate-product cell P (future position). This dual consideration allows MetaPath to make more informed decisions about path progression, often resulting in shorter overall paths while maintaining computational efficiency. The effectiveness of this approach is demonstrated in the experimental results, where MetaPath achieves competitive path lengths while visiting significantly fewer cells than traditional algorithms.

3.6. Computational Complexity Analysis

The computational efficiency of MetaPath has been analyzed in terms of both its per-step computation and the total number of steps required to reach a solution. This analysis clarifies how MetaPath achieves competitive runtime performance despite having more complex individual steps compared to those of traditional algorithms like A*.

In path planning algorithms, the metric “Number of Visited Cells” traditionally represents the count of times an entry is selected from the open list for expansion. For classical algorithms like A*, an entry is a single cell, and the computational cost per step primarily involves evaluating neighboring cells and updating the open/closed lists. In MetaPath, however, an entry is a metabolic reaction tuple (substrate, enzyme, intermediate product), representing a group of three cells processed as a single unit.

The per-step computation in MetaPath involves several components:

• For each substrate cell s, MetaPath evaluates potential enzyme–product cell pairs (e, p) from the neighboring cells
• Each metabolic reaction MR (s, e, p) requires the following:

  ○

  Calculation of Euclidean distances between cells;

  ○

  Evaluation of the objective function incorporating pathway-inspired constraints;

  ○

  Assessment of product cell validity based on metabolic rules.

• Some reaction pairs, such as MR (s, e, p) and MR (s, p, e), yield identical objective values due to the symmetrical nature of Euclidean distance calculations.

While this might suggest higher computational overhead, MetaPath implements several optimization strategies:

• Metabolic-pathway-inspired pruning significantly reduces the number of neighbor combinations evaluated;
• The grouping of cells allows MetaPath to make more informed decisions per step, reducing the total number of steps needed;
• Implementation optimizations handle similar reaction pairs efficiently, avoiding redundant calculations.

The overall computational efficiency of MetaPath emerges from the balance between these factors. While each step requires more computation than that of traditional algorithms, the reduction in total steps often leads to competitive or superior runtime performance, particularly in complex environments. This is evidenced by our empirical results, where MetaPath demonstrates lower overall runtime despite the additional per-step calculations. The relationship between visited cells and runtime can be expressed as follows:

Total Runtime = Number of Visited Cells × Average Time Per Step

While MetaPath’s average time per step (Ts_MetaPath) is higher than that of A* (Ts_A*), its significantly lower number of visited cells (Vc_MetaPath < Vc_A*) often results in better overall runtime performance:

Runtime_MetaPath = Vc_MetaPath × Ts_MetaPath

Runtime_A* = Vc_A* × Ts_A*

This analysis explains how MetaPath can achieve competitive runtime performance despite more complex per-step computations, particularly in scenarios with higher obstacle densities or larger map sizes where the reduction in total steps becomes more significant.

4. Evaluation Framework

To ensure robust performance evaluation, the experiments were conducted using two different hardware configurations:

• DELL PowerEdge T620 Server: equipped with an Intel Xeon processor E5-2667, 32 GB RAM, and Ubuntu 16.04 LTS, the 2D simulator was designed, implemented, and run on this server.
• High-Performance Computing (HPC) Node: Specifically, a node from the SANAM supercomputer [68] was utilized to run both the random map experiment and the benchmark map experiment. This node was equipped with two CPUs (Xeon E5-2650 8 Cores 2.000 GHz, totaling sixteen cores), two dual AMD FirePro S10000 GPUs, and 128 GB RAM.

The performance of the MetaPath algorithm was compared to that of six benchmark algorithms.

• A* [69,70]: A* finds the optimal path by using the evaluation function f(n) so that f(n) = g(n) + h(n). This function is used to determine which node should be selected to expand the search. The function g(n) represents the actual cost of the optimal path from the start node to n, while h(n) represents the actual cost of the optimal path from n to the goal node. Basically, h(n) is an optimistic or admissible heuristic (the Euclidean distance) used to guide the search. Therefore, unlike Dijkstra’s algorithm, A* is computationally efficient.
• BFS [11,22]: The implementation of BFS is very simple and straightforward. To explain, the start node is pushed into a queue. Then, a node is expanded; that is, it is popped out of the queue, and its neighbors are pushed into it. This approach is repeated till the goal is reached or the queue is empty. While the path produced by BFS is optimal, the BFS search is not efficient due to the vast number of visited cells.
• Tabu Search [69,70]: Tabu Search is a local search technique applied to many combinatorial optimization problems. The algorithm begins with a random initial path generated by greedy methods. Next, the algorithm iteratively tries to enhance the current path over a specified neighborhood. Transforming a solution to another in the defined neighborhood is called a move, which could be an inserting move, remove move, and swap move. Before applying for a new move, the algorithm must ensure that it enhances the current path and that it is not a tabu. The algorithm stores the recent moves in a tabu list to avoid local optimum and to avoid visited paths.
• GA [69,70]: Generally, the GA is based on natural biological genetics and the theory of natural selection. The GA can solve optimization problems efficiently. The algorithm begins with generating an initial chromosome population. Each chromosome represents a feasible path from the start cell to the goal cell. Generating the initial population starts with constructing a path using the greedy method and the Euclidean distance as a heuristic. To generate the other paths in the initial population, a random intermediate cell, which does not exist in the initial path, is selected and used to construct a new path from the start to the goal cell. After that, the fitness evaluation starts by using a fitness function (path length) to evaluate each path (each individual) in the population. The fitness value is assigned to each path to indicate its quality. Next, the best paths (individuals) are chosen to form the current generation. In each iteration, the chosen paths are subject to two genetic operators: crossover and mutation. These operators aim to produce a new generation of individuals (paths) from the current individuals. The process is repeated until it reaches a termination condition.
• ACO [71]: ACO imitates the behavior of ants when searching for food by finding the optimal path between the food and their nest. Each ant releases a substance called a pheromone along its food searching path. The pheromone amount will be higher in the repeatedly used path and lower in the less repeatedly used path. Afterward, the pheromone concentration becomes higher for the shortest path. Consequently, an ant colony is led to the optimal path. Using the ACO algorithm, in each iteration, all ants are initialized in the start cell. Then, for each ant, the next cell is calculated based on the pheromone rule probability. When all ants construct their paths, the pheromone trails are updated by the evaporation equation and based on the ants that successfully reached the goal.
• PSO [72]: The PSO algorithm is inspired by the behaviors of swarms of birds or fish. The swarm is composed of particles moving in the search space at a specific velocity. PSO uses few parameters: inertia weight(w), individual cognitive factor (c1), social cognitive factor (c2), and random values (r1 and r2). The inertia weight (w) guides the algorithm toward global exploration when w is large. On the other hand, local exploitation is conducted with a smaller w value. The parameters c1 and c2 are also called the acceleration constants since c1 brings the particle to its personal best position while c2 brings it to its global best position. The parameters r1 and r2 are random values between 0 and 1. The steps of PSO are simple. At first, the positions and velocities of N particles are randomly initialized, and the N particles form a discrete map of the environment composed of cells 0…N. Next, the algorithm’s parameters are set (w, r1, r2, c1, c2). Then, at each iteration, the fitness of all N particles is computed, which is used to find the personal best position X_pbest and the global best position X_gbest. After that, the position and velocity of each particle are updated so that the possible particle velocities are −1, 0, and 1, so the PSO algorithm can achieve the vertical, horizontal, and diagonal cell-by-cell movement to construct the path. However, it is important to note that we encountered challenges in finding a suitable implementation of PSO for grid environments. Consequently, we developed our own discretized version of the algorithm tailored for this study. The parameter sittings for each benchmark algorithm are listed in

  Table 5. Parameter settings of the benchmark algorithms.

  Tabu Search	Parameter		Settings
  	Tenure		7
  	Number of Iterations	Map 8 × 8, 16 × 16	10
  		Map 32 × 32	30
  		Map 46 × 46	60
  		Map 128 × 128	120
  		Map 256 × 256	250
  GA	Crossover Type		one point
  	Crossover Probability		0.9
  	Mutation Probability		0.01
  	Mutation Iteration Number		50
  	Minimum Initial Path Cost		0
  	Radius		2
  	Population Size	Map 8 × 8, 16 × 16	10
  		Map 32 × 32, 46 × 46	40
  		Map128 × 128, 256 × 256	60
  	Number of Iterations	Map 8 × 8, 16 × 16	10
  		Map 32 × 32	30
  		Map 46 × 46	60
  		Map 128 × 128	120
  		Map 256 × 256	250
  ACO algorithm	Alpha		1
  	Beta		9
  	Evaporation Rate		0.5
  	Q		10
  	Number of Ants	Map 8 × 8, 16 × 16	10
  		Map 32 × 32, 46 × 46	40
  		Map128 × 128, 256 × 256	60
  	Number of Iterations	Map 8 × 8, 16 × 16	10
  		Map 32 × 32	30
  		Map 46 × 46	60
  		Map 128 × 128	120
  		Map 256 × 256	250
  PSO algorithm	wMin		0.2
  	wMax		0.7
  	C1		2
  	C2		2
  	Swarm Size	Map 8 × 8, 16 × 16	10
  		Map 32 × 32, 46 × 46	40
  		Map128 × 128, 256 × 256	60
  	Number of Iterations	Map 8 × 8, 16 × 16	10
  		Map 32 × 32	30
  		Map 46 × 46	60
  		Map 128 × 128	120
  		Map 256 × 256	250

  . These parameters have been carefully selected based on the literature’s recommendations and preliminary testing to ensure fair comparison.

Our evaluation framework considered three key measures to ensure a comprehensive assessment of the algorithms.

• Path length: This is the number of cells in the generated path from start to goal. For the Robot Operating System (ROS) environment, the path length is measured in meters.
• Runtime average: This is the time (measured in microseconds) that the algorithm requires to generate a path. For each start–goal scenario, each algorithm was run five times, and the average was calculated.
• Number of visited cells: The number of cells checked while the path is generated. The calculation of this measure differs based on the algorithm’s behavior. The number of visited cells by the algorithm is strongly related to the algorithm’s efficiency. This measure requires careful interpretation as it represents different units in different algorithms.

  Table 6. Definition of the number of visited cells for each algorithm.

  Algorithm	Number of Visited Cells
  MetaPath	The number of times the optimal metabolic reaction (with the minimum heuristic function) is chosen from the open list.
  A*	The number of times the optimal cell (with the minimum heuristic function) is chosen from the open list.
  BFS	The number of times a neighboring cell is marked visited.
  Tabu Search	The number of cells in the initial path, plus the number of cells in the best paths.
  GA	The number of cells in the initial paths, plus the number of cells in the best paths.
  ACO	The number of steps for each ant in each iteration.
  PSO	The number of cells visited by each particle.

  defines the meaning of this measure for each algorithm. In MetaPath, it counts the number of times a metabolic reaction tuple (substrate, enzyme, intermediate product) is selected as optimal from the open list. In contrast, for traditional algorithms like A*, it counts the number of times a single cell is selected. While the absolute numbers are not directly comparable, this metric provides insight into each algorithm’s search efficiency within its own paradigm. A lower number of visited cells indicates more efficient search space exploration, though the computational cost per visit may vary between algorithms.

Then, factor analysis and parametric statistics were applied to gain deeper insights into the algorithms’ performance.

In a similar approach to [73], two experiments were designed to ensure a rigorous and comprehensive evaluation of the MetaPath algorithm, considering different types of maps as shown in

Table 7. Environments of the two experiments.

Experiment	Environment	Number of Maps	Sample Size
Random map experiment	Abstract randomized 2D maps	24	32,000
Benchmark map experiment	Realistic complex benchmark 2D rooms	3	210

. Section 4.1 introduces the random map experiment, while Section 4.2 presents the benchmark map experiment

4.1. Random Map Experiment

Although fixed benchmark maps provide valuable insights into an algorithm’s performance, they might also introduce bias, potentially leading to constrained conclusions. Accordingly, random maps were utilized in this experiment to address potential biases, with map parameterization—altering map size, obstacle ratios, and start–goal positioning—employed as a mitigating strategy.

The objective of the random map experiment was to explore the behavior of the MetaPath algorithm and assess its performance against established benchmark algorithms using randomly generated maps. This investigation focused on two principal factors that significantly influence unmanned ground vehicle (UGV) navigation: the size of the map and the ratio of obstacles. A range of map sizes (88, 1616, 3232, 6464, 128,128, 256,256) was selected to encompass a variety of potential UGV operational environments. Obstacles were randomly placed, with their number represented as a percentage (0%, 20%, 40%, 60%) of the total cells on the map.

A specialized algorithm was developed for generating maps for this experiment. It initiates by setting the map size from predefined options. Subsequently, for each map size, the algorithm generates 200 unique start–goal scenarios, ensuring a balanced distribution among short-, medium-, and long-distance paths. The methodology for classifying the paths into short, medium, and long distances is based on the Euclidean distance between start and goal positions and the map’s dimensions, as illustrated in

Table 8. Path classification conditions.

Path Class	Condition
Short-distance path	$S\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{T}\mathrm{o}\mathrm{G}\mathrm{o}\mathrm{a}\mathrm{l} \mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}>\left(\mathrm{i}\mathrm{n}\mathrm{t}\right){\log }_2\left({\displaystyle \frac{1}{4}} \mathrm{e}\mathrm{n}\mathrm{v}\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t} \mathrm{d}\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}\right)$ $\mathrm{A}\mathrm{N}\mathrm{D} \mathrm{S}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{T}\mathrm{o}\mathrm{G}\mathrm{o}\mathrm{a}\mathrm{l} \mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\le {\displaystyle \frac{1}{4}} \mathrm{e}\mathrm{n}\mathrm{v}\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t} \mathrm{d}\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}$
Medium-distance path	$\mathrm{S}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{T}\mathrm{o}\mathrm{G}\mathrm{o}\mathrm{a}\mathrm{l} \mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}>{\displaystyle \frac{1}{4}} \mathrm{e}\mathrm{n}\mathrm{v}\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t} \mathrm{d}\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}$ $\mathrm{A}\mathrm{N}\mathrm{D} \mathrm{S}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{T}\mathrm{o}\mathrm{G}\mathrm{o}\mathrm{a}\mathrm{l} \mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\le {\displaystyle \frac{3}{4}} \mathrm{e}\mathrm{n}\mathrm{v}\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t} \mathrm{d}\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}$
Long-distance path	$\mathrm{S}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{T}\mathrm{o}\mathrm{G}\mathrm{o}\mathrm{a}\mathrm{l} \mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}>{\displaystyle \frac{3}{4}} \mathrm{e}\mathrm{n}\mathrm{v}\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t} \mathrm{d}\mathrm{i}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}$ $\mathrm{A}\mathrm{N}\mathrm{D} \mathrm{S}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{T}\mathrm{o}\mathrm{G}\mathrm{o}\mathrm{a}\mathrm{l} \mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\le \mathrm{e}\mathrm{n}\mathrm{v}\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t} \mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\mathrm{o}\mathrm{n}\mathrm{a}\mathrm{l}$

.

Once the map size and start–goal scenarios have been established, the algorithm proceeds to create four distinct maps for each scenario, reflecting the various obstacle ratios (0%, 20%, 40%, and 60%), resulting in a total of 24 unique maps. It is noteworthy that the experiment did not control the shape and distribution of obstacles, which could potentially affect the results. The complexity introduced by the obstacle percentage is not universally applicable across all scenarios [73].

The experiment adopted several assumptions regarding the UGV’s navigation within the map: the UGV is represented as a moving cell on the map, the start and goal positions each occupy one cell, and each obstacle is assigned one cell. Diagonal movement is permitted, with each cell having eight neighboring cells for movement options.

For each of the 24 random maps, from Map1 to Map24, the seven algorithms considered in this research (MetaPath, A*, BFS, Tabu Search, GA, ACO, and PSO) were executed across 200 scenarios. Each scenario was executed five times, and the average for each performance metric (path length, runtime, and number of visited cells) was calculated. The total data sample size was calculated as follows:

6 map sizes × 4 obstacle ratios × 7 algorithms × 200 scenarios = 33,600 data samples.

Nevertheless, due to the ACO algorithm’s excessive runtime on maps of sizes 128 × 128 and 256 × 256, which surpassed six hours for a single scenario, these samples were excluded, adjusting the final sample size to 32,000 data samples after deducting 1600 samples associated with the ACO algorithm’s performance on larger maps.

4.2. Benchmark Map Experiment

This experiment aimed to investigate the behavior of the MetaPath algorithm and to determine if it outperforms other benchmark algorithms using specifically chosen benchmark maps. Notably, maps presented in references [74,75,76,77,78,79,80] encompass diverse complexities and applications but fall short of the analytical requirements of this study due to their non-grid structures and instances where obstacles do not fully occupy their allocated cells. Consequently, we embraced the benchmarking strategy outlined in [81], which introduces a complexity index (CI) devised explicitly for grid-based path planning. This CI distinguishes search spaces into four complexity levels, offering a comprehensive framework for assessing algorithmic performance. By leveraging benchmark maps from [82], assessed via the CI, we could execute a thorough analysis of the MetaPath algorithm’s performance. This approach underscores the significance of obstacle distribution across the grid as a pivotal element in determining the CI and, hence, the maps’ appropriateness for detailed algorithmic scrutiny. Figure 8 illustrates the maps in [82] as represented within our Graphical User Interface (GUI) model.

For this experiment, several assumptions regarding the UGV’s path planning were established:

• The UGV is depicted as a movable cell on the map.
• The start and goal positions are designated to single cells.
• Each obstacle is confined to a single cell.
• Diagonal movement is facilitated, allowing access to eight neighboring cells for each cell.

The experimental design involved running the seven algorithms under consideration—MetaPath, A*, BFS, Tabu Search, the GA, ACO, and PSO—across each of the benchmark maps, shown in Figure 8, using ten start–goal scenarios to evaluate the path length, runtime, and number of visited cells. Each scenario was executed five times to ascertain the average for these performance measures. The size of the collected data sample (the single sample consists of path length, runtime, and the number of visited cells) was calculated as follows:

3 maps × 7 algorithms × 10 scenarios = 210 data samples.

5. Results and Discussion

Section 5.1 and Section 5.2 present and analyze the results of two experiments described in Section 4, focusing on three key performance measures: path length, number of visited cells, and runtime. These sections provide an in-depth discussion of how MetaPath’s unique biochemistry-inspired design contributes to its performance in each of these areas. Furthermore, each section concludes with an overall performance and lag factor analysis, offering clear insight into the algorithm’s performance.

5.1. Results of the Random Map Experiment

The random map experiment aimed to rigorously assess the MetaPath algorithm’s performance in comparison to that of established benchmark algorithms. We conducted tests using randomly generated maps of varying sizes and obstacle densities, as described in Section 4.1. This section details and analyzes the results, with a focus on path length, number of visited cells, and run times across different obstacle distributions.

5.1.1. Path Length

Figure 9 illustrates the path lengths generated by each algorithm across different obstacle percentages (0%, 20%, 40%, and 60%). The results demonstrate that MetaPath consistently produces competitive path lengths across all obstacle densities. At 0% obstacle density, MetaPath performs comparably to A* and BFS, which are known for their optimality in unobstructed environments. As the obstacle density increases, MetaPath maintains average efficiency comparable to that of PSO, the GA, and ACO. On the other hand, Tabu Search consistently demonstrates the least favorable performance in terms of path length across all obstacle densities. This can be attributed to its reliance on local search and its tendency to get trapped in local optima making it less effective for global path planning in grid-based environments, especially as obstacle density increases.

The competitive performance of MetaPath, particularly in environments with moderate obstacle densities, can be attributed to several key aspects of its unique design. At the core of MetaPath’s approach is the metabolic reaction analogy, where each step in path planning is analogous to a metabolic reaction. Unlike traditional algorithms that consider only the next immediate cell, MetaPath evaluates a triad of cells: the current cell (substrate), a potential next cell (enzyme), and a future cell (intermediate product). This multi-cell consideration allows MetaPath to make more informed decisions about path progression, often resulting in shorter overall paths. The heuristic function design in MetaPath also plays a crucial role in its path length performance as it considers both the enzyme cell (E) and intermediate-product cell (P). This dual consideration allows for a more nuanced evaluation of potential paths, often leading to better decisions in complex environments. By looking ahead to the intermediate-product cell, MetaPath can often avoid local minima that might trap other algorithms, resulting in more efficient overall paths. Furthermore, MetaPath incorporates optimization principles from metabolic pathways, such as minimizing enzyme levels and intermediate-product levels. In the context of path planning, this translates to efficiently navigating obstacles while maintaining a goal-oriented trajectory. This optimization approach is particularly evident in the 20% and 40% obstacle scenarios, where MetaPath occasionally generates slightly shorter paths than A*, as shown in Figure 10. While these improvements are marginal, typically not exceeding one cell in length, they demonstrate MetaPath’s high competence in finding optimal paths. This slight advantage can be attributed to MetaPath’s preference for diagonal movements in certain scenarios, a characteristic stemming from its unique cell selection process inspired by metabolic pathways. Although the practical impact of these marginally shorter paths may be limited, this observation underscores MetaPath’s potential to match or even surpass traditional algorithms in path optimality in scenarios where even small improvements in path length can yield significant benefits.

In high-density environments (60% obstacles), MetaPath tends to generate relatively longer paths compared to those of its performance in lower densities. This behavior can be attributed to the fact that as the environment becomes more cluttered, the number of viable “metabolic pathways” decreases, limiting the algorithm’s options for optimal path selection. The triad cell consideration, while beneficial in moderate densities, may sometimes lead to slightly longer paths in highly constrained spaces where more direct routes might be preferable. However, this trade-off is balanced by MetaPath’s consistent ability to find feasible paths in complex environments where some other algorithms, such as ACO, struggle or fail and their performance cannot be measured due to excessive computational time requirements.

5.1.2. Number of Visited Cells

Figure 11 presents the number of cells visited by each algorithm during path planning. This metric is crucial as it directly relates to the computational efficiency of the algorithms. It is important to note that the y-axis uses a logarithmic scale due to the wide range of the number of visited cells across different algorithms and scenarios.

MetaPath demonstrates superior performance, consistently visiting fewer cells than all other algorithms across all obstacle densities and map sizes. This efficiency is particularly pronounced in more complex environments (40% and 60% obstacles) and larger map sizes, where MetaPath’s advantage becomes even more significant.

The data reveal that ACO consistently demonstrates the poorest performance in terms of the number of visited cells, followed by the GA. This stark difference highlights the exceptional efficiency of MetaPath. ACO’s poor performance can be attributed to its nature of exploring multiple paths simultaneously through a population of ants. Each ant in the colony explores the environment, leading to a high number of cell visits. As the environment becomes more complex or larger, the number of visited cells increases dramatically. For example, in a 64 × 64 map with 60% obstacles, ACO visits an average of 658,313 cells, which is an order of magnitude higher than that of other algorithms. For map sizes larger than 64 × 64, ACO’s data are not available due to excessive computational requirements, further highlighting its limitations in complex environments. The GA also visits a high number of cells due to its evolutionary approach. It generates and evaluates multiple paths (individuals) in each generation, leading to many cell visits. While it performs better than ACO, it still lags significantly behind MetaPath and other algorithms like A* and BFS.

A* generally performs well in terms of visited cells, often ranking second after MetaPath. However, the difference is still significant. For example, in a 256 × 256 map with 40% obstacles, A* visits an average of 3168 cells, while MetaPath visits only 73 cells. BFS and PSO show moderate performance, generally visiting fewer cells than ACO and the GA but more than MetaPath and A*. Tabu Search, while not the worst performer, still visits significantly more cells than MetaPath across all scenarios. For instance, in a 64 × 64 map with 40% obstacles, Tabu Search visits an average of 2436 cells, placing it between the GA and PSO in terms of efficiency.

The reduced number of visited cells in MetaPath can be attributed to its unique triad cell expansion approach, unlike traditional algorithms that expand one cell at a time. By expanding three cells simultaneously (substrate, enzyme, and intermediate product), MetaPath explores the search space more efficiently. This approach, inspired by the structure of metabolic reactions, enables MetaPath to cover more ground with fewer iterations, resulting in a significantly reduced number of visited cells. Another key factor contributing to MetaPath’s efficiency is its selective neighbor consideration. Instead of evaluating all neighboring cells as potential next steps, MetaPath applies conditions inspired by enzyme specificity and metabolic pathway optimization to select which cells can serve as enzymes or intermediate products. This selective approach effectively prunes the search space, leading to fewer cell visits overall. By focusing only on the most promising paths, MetaPath avoids wasting computational resources on less optimal routes. The open-list structure in MetaPath also plays a crucial role in reducing the number of visited cells. Unlike traditional algorithms that store individual cells in the open list, MetaPath’s open list contains entire metabolic reactions. This design choice allows MetaPath to manage and prioritize potential paths more effectively, reducing redundant cell visits. By considering paths in terms of metabolic reactions rather than individual cells, MetaPath can make more informed decisions about which areas of the map to explore, further contributing to its efficiency.

5.1.3. Algorithm Runtime

Figure 12 illustrates the runtime performance of each algorithm across different obstacle densities and map sizes. The y-axis uses a logarithmic scale to represent the wide range of runtime values, spanning several orders of magnitude.

MetaPath exhibits competitive runtime performance that becomes evident in larger maps and mild obstacle densities (20–40%). For instance, in a 256 × 256 map with 40% obstacles, MetaPath completes its execution in 13.26 s, significantly outperforming A* (1343.47 s), BFS (74.81 s), PSO (24.66 s), and the GA (41,112.06 s). This demonstrates MetaPath’s superior scalability in complex environments.

As map size increases, all algorithms show increased runtime, but at different rates. MetaPath’s runtime growth is gradual, increasing from 1.14 s in 8 × 8 maps to 13.26 s in 256 × 256 maps with 40% obstacles. In contrast, the GA’s runtime escalates from 27.83 s to 41,112.06 s under the same conditions.

PSO consistently ranks among the top performers in runtime, showing efficiency in smaller maps. A* performs well in simpler scenarios but struggles with larger maps. On the contrary, the GA and ACO show the poorest runtime performance. ACO becomes computationally infeasible for larger maps, failing to complete the task for map sizes above 64 × 64, highlighting significant scalability limitations.

These results suggest that MetaPath’s biochemistry-inspired design offers a balanced approach to path planning, with particular advantages in complex environments. The algorithm’s efficiency in scenarios with large, mildly dense obstacles addresses a key challenge in real-time UGV navigation.

5.1.4. Overall Performance and Lag Factor Analysis

The multivariate analysis of the algorithms’ overall performance lag factor scores, as presented in

Table 9. Multivariate Linear Regression Analysis of the experimented algorithms’ overall performance lag factor score. N = 32,000.

	95% C.I Beta Coefficient
Model Term	Beta Coefficient	Lower	Upper	p-Value
Intercept	−1.279	−1.311	−1.247	<0.001
Algorithm = Tabu-search	1.136	1.093	1.179	<0.001
Algorithm = PSO	0.388	0.345	0.43	<0.001
Algorithm = A*	0.213	0.17	0.255	<0.001
Algorithm = GA	1.461	1.418	1.503	<0.001
Algorithm = BFS	0.157	0.115	0.200	<0.001
Algorithm = ACO	1.814	1.77	1.857	<0.001
Algorithm = Meta-Path - reference comparison
Map size	0.009	0.009	0.010	<0.001
Obstacles ratio	−0.001	−0.001	−0.001	<0.001
Interaction: Map size*Obstacles ratio	−0.0001	−0.00012	−0.0001	<0.001

, provides strong statistical evidence for MetaPath’s efficiency. MetaPath consistently achieved the lowest mean overall performance lag factor score among all tested algorithms. This indicates that MetaPath maintains a balance between path optimality and computational efficiency across various map sizes and obstacle ratios.

Notably, the analysis showed that all other algorithms, TabuSearch, PSO, A*, the GA, BFS, and ACO, had significantly higher mean overall performance lag factor scores compared to those of MetaPath. This comprehensive measure, which considers path length, visited cells, and runtime, underscores MetaPath’s superior performance across diverse scenarios. The analysis also revealed interesting trends related to map size and obstacle ratio. Larger map sizes led to higher performance lag scores, while higher obstacle ratios tended to lower the lag scores. However, MetaPath consistently outperformed other algorithms regardless of these environmental factors, demonstrating its robustness and adaptability.

The superior performance of MetaPath can be attributed to the synergistic effect of its various design elements. At its core, MetaPath’s design strikes a balance between exploring promising paths (through its metabolic reaction model) and exploiting known good directions (through its heuristic function). This balance allows it to perform well across various map sizes and obstacle ratios. The algorithm’s scalability is particularly noteworthy, as its performance relative to that of other methods improves as the environment becomes more complex (larger maps, higher obstacle ratios). This scalability is a direct result of its efficient search space pruning and informed decision-making process.

Furthermore, MetaPath’s biochemistry-inspired design allows it to adapt to different environmental conditions. The algorithm’s ability to selectively consider neighbors based on the current “substrate” cell enables it to navigate both open spaces and cluttered areas effectively. This adaptability is crucial in real-world scenarios where environments can vary widely in their characteristics.

5.2. Results of the Benchmark Map Experiment

The benchmark map experiment was designed to evaluate the performance of the MetaPath algorithm against established benchmark algorithms using specifically chosen maps with varying levels of complexity. The experiment, described in Section 4.2, utilized three benchmark maps with low, medium, and high obstacle distributions, as illustrated in Figure 8. This section presents and analyzes the results of this experiment, focusing on the algorithm’s performance in terms of path length, number of visited cells, and run times across different obstacle distributions.

5.2.1. Path Length

Figure 13 presents the path lengths generated by each algorithm across different obstacle densities in the benchmark map experiment. It is important to note the remarkably small scale of the y-axis, which magnifies even fractional differences between algorithms. This minute scale is necessitated by the fact that all tested algorithms are well-established path planning methods, resulting in highly comparable performance in terms of path length.

The figure illustrates a clustering of performance among the algorithms. MetaPath generates an average path length of 23.90 across all obstacle densities, while A* and BFS produce slightly shorter paths at 23.70. PSO and ACO follow closely with average path lengths ranging from 24.00 to 24.20. Tabu Search stands out, producing notably longer paths with an average length of 25.50 in low- and medium-density environments, improving slightly to 24.10 in high-density scenarios.

Interestingly, the consistency of these results across different obstacle densities in the benchmark maps contrasts with the more variable performance observed in the random map experiment. In the latter, algorithms showed more pronounced differences in path length as obstacle density and map size increased. This discrepancy highlights the impact of environmental structure on algorithm performance. The more structured nature of the benchmark maps provides a more stable context for path planning, resulting in more consistent performance across varying obstacle densities.

The performance of MetaPath across both experiments offers intriguing insights. In the benchmark maps, it maintains a consistent average path length regardless of obstacle density. However, in the random maps, MetaPath demonstrated more variability, occasionally outperforming A* in scenarios with 20% and 40% obstacle densities, particularly in larger maps. This suggests that MetaPath’s biochemistry-inspired approach may have advantages in certain types of complex, unstructured environments.

Tabu Search consistently produced longer paths in both experiments, indicating that its local search strategy may be less suited to grid-based path planning compared to that of the other tested algorithms. This consistency across different environmental contexts provides valuable information about the algorithm’s characteristics and limitations.

The performance of ACO presents another point of interest. While it performs competitively in the benchmark maps, it struggled with larger map sizes in the random map experiment. This disparity suggests that ACO’s pheromone-based approach may be more effective in structured environments but may face challenges in highly random or large-scale scenarios.

These observations underscore the importance of testing path planning algorithms across diverse environmental contexts. The differences in performance between structured benchmark maps and random environments reveal nuances in algorithm behavior that might not be apparent from a single type of test.

Given the minimal differences in path length among these algorithms, particularly in the benchmark maps, it becomes evident why additional metrics are crucial for a comprehensive evaluation. The lag factor analysis, which incorporates not only path length but also runtime and number of visited cells, provides a more holistic view of algorithm performance. This multi-dimensional analysis is essential for differentiating between algorithms that produce similar path lengths but may differ significantly in computational efficiency or exploration strategies.

5.2.2. Number of Visited Cells

Figure 14 illustrates the number of cells visited by each algorithm during path planning across the benchmark maps. It is crucial to note that the y-axis in this figure uses a logarithmic scale due to the vast range of values across different algorithms, spanning from just over 10 to nearly 30,000 visited cells.

Based on the figure, MetaPath demonstrates remarkable efficiency, visiting an average of only 12.90 cells in low- and medium-obstacle-density environments, and slightly fewer (12.60) in high-density scenarios. This performance is substantially superior to that of all other tested algorithms. The next most efficient algorithm, A*, visits an average of 124.00 cells in low-density environments, nearly ten times more than MetaPath.

Comparing these results to the random map experiment reveals interesting patterns. In both experiments, MetaPath consistently demonstrates superior performance, visiting the fewest cells across all scenarios. However, the efficiency gap is even more pronounced in the benchmark maps. For instance, in the random maps with a 64 × 64 grid and 40% obstacles, MetaPath visited an average of 19.50 cells, while in the benchmark maps, it visited only 12.90 cells on average.

A* maintains its position as the second-most-efficient algorithm in both experiments. However, the difference between A* and MetaPath is more substantial in the benchmark maps. In the random maps, A* visited 220.06 cells on average in a 64 × 64 grid with 40% obstacles, while in the benchmark maps, it visited 124.00 cells in low-density environments. BFS shows consistent performance across both experiments, visiting more cells than A* but fewer than the GA and the ACO algorithm. In the benchmark maps, BFS visits an average of 832.10 to 834.20 cells across different obstacle densities, which aligns with its performance in similarly sized random maps. PSO, the GA, and ACO consistently visit the highest number of cells in both experiments. However, their relative performance differs between the two scenarios. In the benchmark maps, ACO visits approximately 29,000 cells regardless of obstacle density, while in the random maps, its performance deteriorated with increasing map size and obstacle density, reaching over 658,313 cells in a 64 × 64 map with 60% obstacles. The GA visits around 7900 cells on average in benchmark maps, while in the random maps, it showed more variability, visiting 8695 cells in a 64 × 64 map with 40% obstacles. Tabu Search demonstrates interesting performance variations between the two experiments. In the benchmark maps, it shows moderate performance, visiting between 885.40 and 937.20 cells on average across different obstacle densities. This places it between PSO and BFS in terms of efficiency in the benchmark maps. In the random map experiment, Tabu Search’s performance was more variable and generally less efficient. For instance, in a 64 × 64 map with 40% obstacles, Tabu Search visited an average of 2436 cells, significantly more than in the benchmark maps. This discrepancy suggests that Tabu Search may be more effective in structured environments like benchmark maps but struggles more with the randomness in the other experiment.

The stark contrast in the number of visited cells between MetaPath and other algorithms is evident in both experiments, but it is particularly pronounced in the structured environments of the benchmark maps. This suggests that MetaPath’s biochemistry-inspired approach to pruning the search space is effective in both structured and unstructured environments, with its advantages being even more significant in structured scenarios.

In conclusion, the analysis of visited cells in both benchmark and random map experiments underscores MetaPath’s exceptional efficiency in search space exploration. While all algorithms show consistent trends across both types of experiments, the structured nature of the benchmark maps amplifies the efficiency gains of MetaPath’s approach and benefits some algorithms like Tabu Search more than others. This efficiency highlights the potential of biochemistry-inspired approaches in advancing the field of path planning, particularly in structured environments.

5.2.3. Algorithm Runtime

Figure 15 illustrates the runtime performances of algorithms across different obstacle densities in benchmark maps, using a logarithmic scale to represent the wide range of values. This analysis reveals intriguing patterns in pathfinding efficiency within structured environments.

Based on the figure, MetaPath demonstrates remarkable consistency in benchmark maps, with runtimes ranging from 2.03 to 2.09 s across all obstacle densities. This stability contrasts with its performance in random maps, where runtimes increased with map size and obstacle density. PSO exhibits the lowest computational time in benchmark maps, with runtimes between 1.55 and 1.62 s, showing significant improvement over its performance in random maps.

A* and BFS also show improved efficiency in benchmark maps compared to their struggle with larger, more complex random maps. The GA, ACO, and Tabu Search, while still showing higher runtimes, perform better in benchmark maps than in random scenarios where they often became computationally infeasible for larger sizes.

The performance variability between experiments can be attributed to the fundamental differences in environment complexity. Random maps, representing synthetic scenarios, often present more challenging conditions, particularly in high-obstacle-density situations. This increased complexity poses a more stringent test of algorithm robustness and adaptability.

These performance shifts underscore the critical role of environmental structure and complexity in determining algorithm efficiency. MetaPath’s ability to maintain relatively consistent performance across both types of environments is particularly noteworthy, suggesting a balanced approach to handling structured and chaotic scenarios.

However, runtime alone does not provide a complete picture of algorithm performance. The variability in results across different metrics (path length, visited cells, and runtime) and between the two types of experiments emphasizes the importance of comprehensive evaluation through lag factor analysis.

In conclusion, this analysis provides valuable insights into algorithm performance under varying conditions, highlighting the need for adaptive pathfinding approaches capable of maintaining efficiency across diverse scenarios. Future research could explore leveraging MetaPath’s consistent performance principles to develop even more robust and versatile pathfinding algorithms.

5.2.4. Overall Performance and Lag Factor Analysis

The multivariate analysis of the algorithms’ overall performance lag factor scores (

Table 10. Multivariate Linear Regression Analysis of the experimented algorithms overall performance lag factor score. N = 210.

		95% C.I Beta Coefficient
Model Term	Beta Coefficient	Lower	Upper	p-Value
Intercept	−0.937	−1.166	−0.707	<0.001
Algorithm = Tabu-search	2.466	2.18	2.752	<0.001
Algorithm = PSO	1.808	1.522	2.094	<0.001
Algorithm = A*	1.122	0.836	1.408	<0.001
Algorithm = GA	0.489	0.203	0.775	0.001
Algorithm = BFS	0.425	0.139	0.711	0.004
Algorithm = ACO	0.292	0.006	0.578	0.045
Algorithm = Meta-Path - reference comparison
Obstacle density = High	−0.01	−0.197	0.177	0.915
Obstacle density = Medium	−0.0101	−0.197	0.178	0.919
Obstacle density = Low - Reference comparison

) provides strong statistical evidence for MetaPath’s efficiency across the benchmark maps. MetaPath consistently achieved the lowest mean overall performance lag factor score among all tested algorithms. Notably, the analysis showed that Tabu-search, PSO, and A* had significantly higher mean performance lag factor scores compared to those of MetaPath (p-value < 0.05 for each). The beta coefficients indicate that Tabu-search exceeded MetaPath’s mean score by 2.466 standard points, PSO exceeded it by 1.808 points, and A* exceeded it by 1.122 points. While the GA, BFS, and ACO also showed higher mean performance lag factor scores compared to those of MetaPath, these differences were not statistically significant (p-value > 0.05).

Interestingly, the obstacle density (low, medium, high) did not significantly impact the algorithms’ measured overall performance lag scores (p-value > 0.05). This suggests that MetaPath maintains its performance advantage across varying levels of environmental complexity, demonstrating its robustness and adaptability.

5.3. Discussions

The results from both the random map experiment and the benchmark map experiment provide compelling evidence for the effectiveness and efficiency of the MetaPath algorithm in diverse and complex environments. This section discusses the key findings and their implications for path planning in unmanned ground vehicles (UGVs).

MetaPath’s biochemistry-inspired design has demonstrated significant advantages over traditional and nature-inspired algorithms in several key areas. In terms of path length optimization, MetaPath consistently generated competitive path lengths across various obstacle densities and map complexities. Its ability to occasionally outperform A* in moderately complex environments is particularly noteworthy, as A* is generally considered optimal for path length. This performance can be attributed to MetaPath’s unique approach of considering a triad of cells (substrate, enzyme, and intermediate product) in each decision step, allowing it to make more informed choices and avoid local minima that might trap other algorithms.

The significant reduction in the number of visited cells, especially in complex environments, highlights MetaPath’s superior computational efficiency. This efficiency stems from the algorithm’s selective neighbor consideration, inspired by enzyme specificity in metabolic pathways. By pruning the search space more effectively than traditional algorithms, MetaPath can navigate complex environments with fewer computational resources. This aspect is crucial for real-world UGV applications, where resource management is often a critical concern.

MetaPath’s competitive runtime, particularly in complex environments, indicates its potential for real-time path planning applications. This could enable UGVs to respond more quickly to dynamic environments or changing mission parameters, a vital capability in many practical scenarios. The algorithm’s efficiency in handling larger, obstacle-dense environments addresses a key challenge in autonomous navigation for UGVs.

A crucial aspect of MetaPath’s performance lies in the trade-off between computational complexity per step and total steps required. While each MetaPath step involves more complex calculations due to processing metabolic reaction tuples (substrate, enzyme, intermediate product) rather than single cells, this approach often leads to better overall efficiency. The increased per-step computation includes the evaluation of enzyme–product pairs, calculation of reaction costs, and application of metabolic-pathway-inspired pruning rules. However, this additional computation is often offset by two key factors: (1) the significant reduction in total steps needed to reach the solution, as evidenced by our visited cells metric, and (2) the efficiency gains from processing cell groups. This is particularly evident in complex environments where traditional algorithms must evaluate many individual cells. Our empirical results, shown in Figure 10, demonstrate that despite more intensive per-step calculations, MetaPath achieves competitive and often superior runtime performance, especially in scenarios with higher obstacle densities or larger map sizes. This validates our design decision to trade increased per-step complexity for reduced total steps, resulting in an algorithm that effectively balances computational overhead with search efficiency.

The lag factor analysis provided strong statistical evidence for MetaPath’s overall efficiency. Consistently achieving the lowest mean overall performance lag factor score among all tested algorithms in both random and benchmark map experiments, MetaPath demonstrated its scalability and adaptability across diverse scenarios. This comprehensive measure, considering path length, visited cells, and runtime, underscores MetaPath’s balanced approach to solving the path planning problem.

The consistent superior performance of MetaPath across various map sizes and obstacle densities has important implications for the field of UGV path planning. Its ability to generate efficient paths with fewer visited cells and competitive runtimes, especially in cluttered environments, suggests significant potential for improving UGV navigation in challenging real-world scenarios such as disaster response, urban exploration, or off-road navigation.

Moreover, the reduced computational overhead demonstrated by MetaPath could lead to the more efficient use of onboard resources in UGVs. This efficiency could potentially extend operational times, allow for the use of less powerful (and thus less expensive or energy-intensive) hardware, or free up computational resources for other critical tasks.

Finally, the success of MetaPath demonstrates the potential of drawing inspiration from seemingly unrelated fields, such as biochemistry, to solve complex computational problems. This interdisciplinary approach opens up new avenues for innovation in algorithm design across various domains, potentially leading to novel solutions in other areas of robotics and artificial intelligence.

6. Conclusions

This study introduces MetaPath, a novel biochemistry-inspired algorithm for path planning in unmanned ground vehicles (UGVs). Our primary contribution lies in developing a unique approach that draws inspiration from metabolic pathways for navigating complex environments. We have established a comprehensive evaluation framework that encompasses both random map and benchmark scenarios, enabling thorough comparison with established algorithms including A*, BFS, Tabu Search, PSO, the GA, and ACO.

The evaluation of MetaPath yielded significant results across multiple dimensions. In path length optimization, MetaPath demonstrated competitive performance, successfully generating efficient routes across various obstacle densities and map complexities, with notable advantages in moderately complex environments. A standout achievement was MetaPath’s computational efficiency, evidenced by visiting significantly fewer cells than other algorithms, particularly in complex scenarios. The algorithm showed particular strength in runtime performance for larger maps with mild to moderate obstacle densities, often completing tasks faster than its counterparts in these challenging conditions. Our statistical analysis, employing factor analysis and parametric methods, provided robust evidence for these findings. The multivariate analysis of the overall performance lag factor scores revealed that MetaPath consistently achieved the lowest mean score among all tested algorithms, with other algorithms showing significantly higher scores. This comprehensive measure, considering path length, visited cells, and runtime, demonstrated MetaPath’s superior performance across diverse scenarios. The performance advantage was particularly evident in larger map sizes and higher obstacle ratios, highlighting MetaPath’s scalability and adaptability to complex environments.

Future research directions could focus on enhancing MetaPath’s adaptability and performance in more challenging scenarios. Investigating its behavior in dynamic environments with moving obstacles would be crucial for real-world UGV applications. The algorithm could be enhanced to incorporate critical safety considerations, including minimum clearance from obstacles, risk-weighted path planning, and safety-conscious trajectory generation. Exploring multi-agent coordination using MetaPath could open new possibilities for swarm robotics and collaborative navigation. Another promising avenue is the integration of machine learning techniques to optimize MetaPath’s parameters dynamically based on environmental characteristics. Extending the algorithm to three-dimensional path planning would broaden its applicability to aerial and underwater autonomous vehicles. Additionally, investigating MetaPath’s potential in other domains such as network routing, logistics optimization, or molecular pathway analysis could reveal interesting cross-disciplinary applications. Finally, a comprehensive comparison with emerging quantum-inspired and hybrid algorithms could further establish MetaPath’s position in the evolving landscape of path planning techniques.

MetaPath represents a significant advancement in UGV path planning, offering an efficient and scalable solution for complex environments. Its success, supported by rigorous statistical analysis, demonstrates the value of interdisciplinary approaches in solving computational challenges and opens new avenues for bio-inspired algorithms in robotics and artificial intelligence.