Multi-Objective Optimization Design of Low-Frequency Band Gap for Local Resonance Acoustic Metamaterials Based on Genetic Algorithm
Abstract
1. Introduction
2. The Method
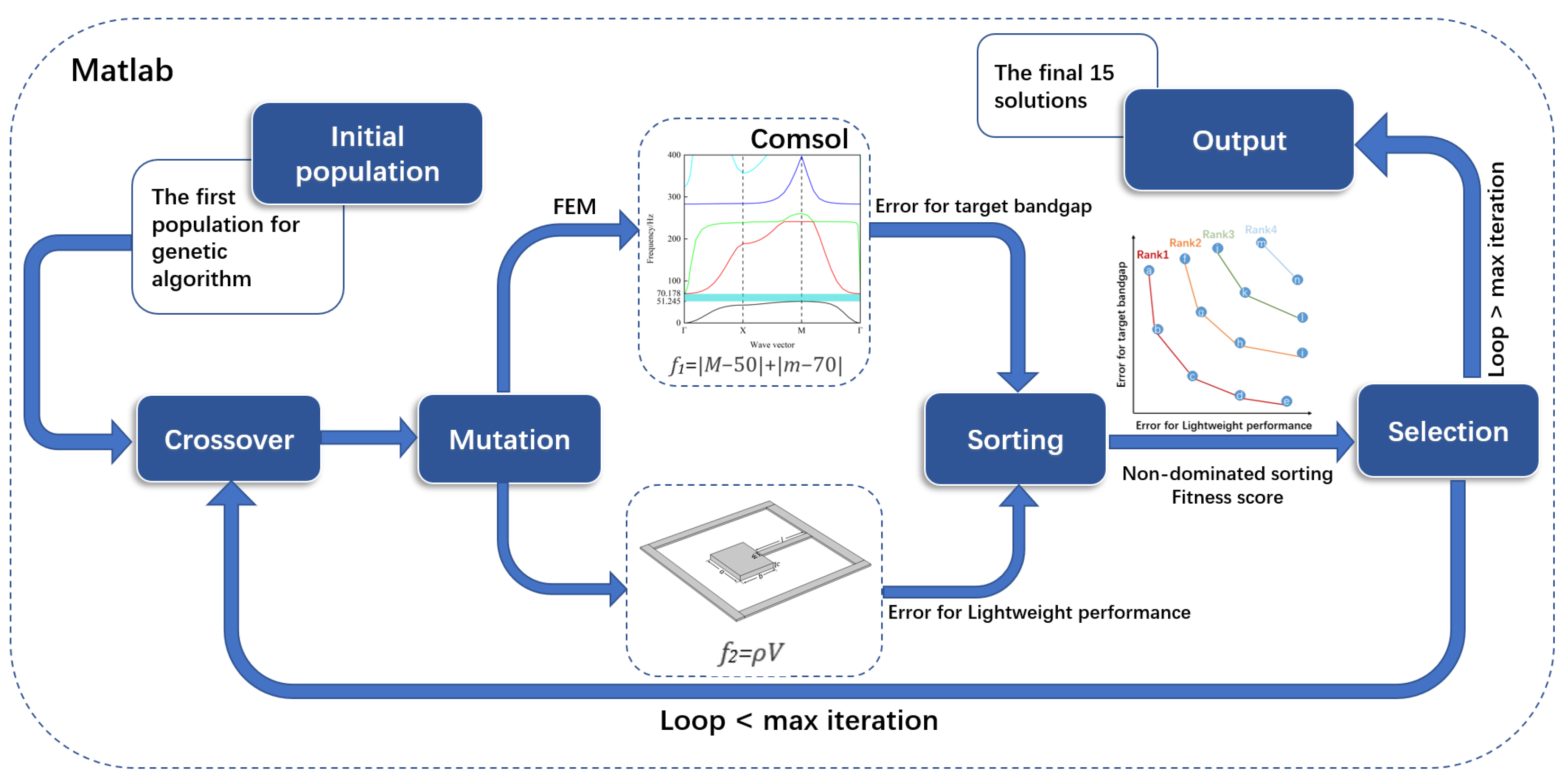
2.1. COMSOL with MATLAB Joint Simulation Optimization Process
2.2. A Multi-Objective Genetic Algorithm and Fitness Function Design
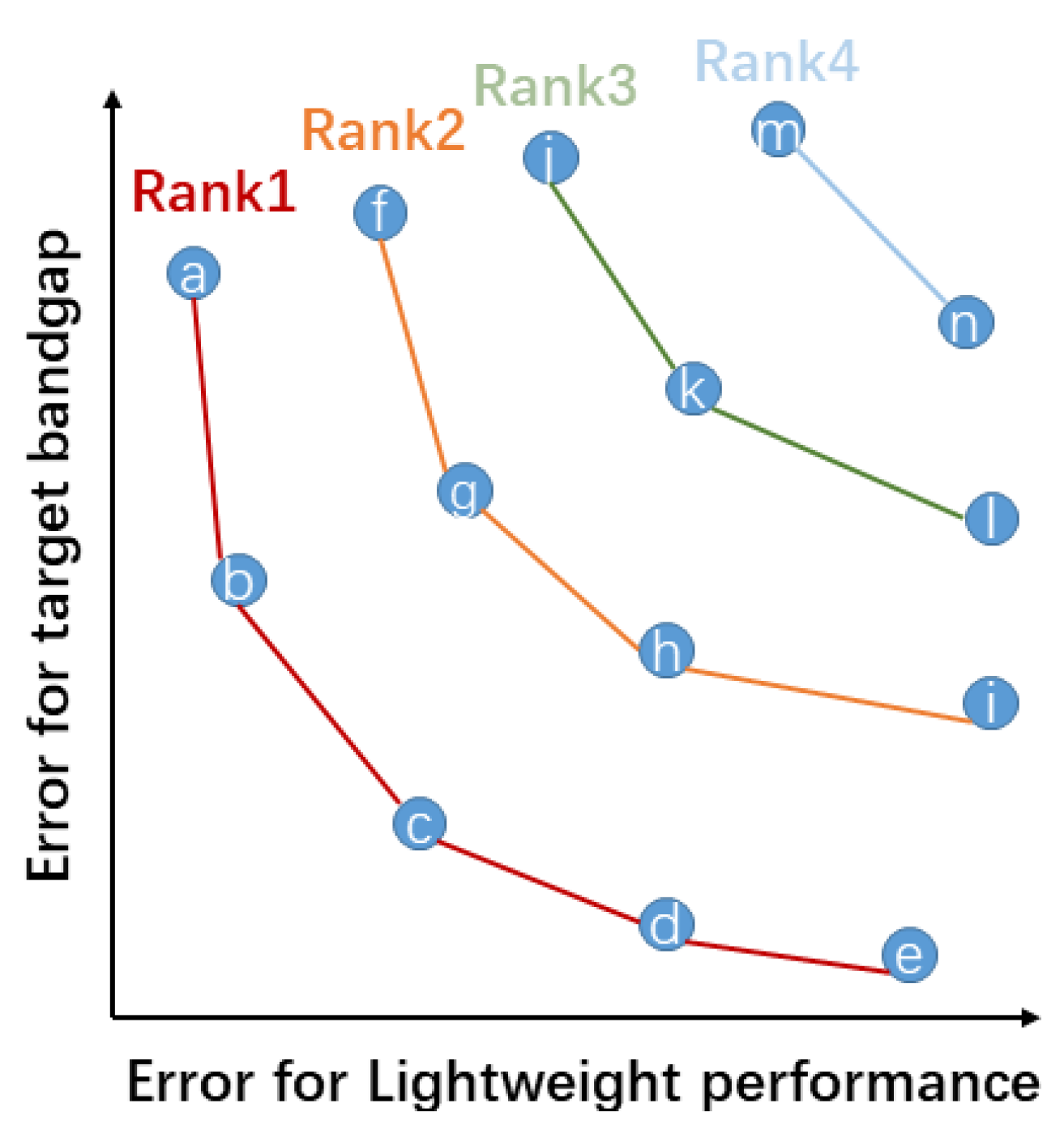
2.3. The Elite Strategy and Sorting Mechanism
3. Optimization of the Design
3.1. Parameterized Modeling of Local Resonance Units
3.2. Dispersion Curve Solution
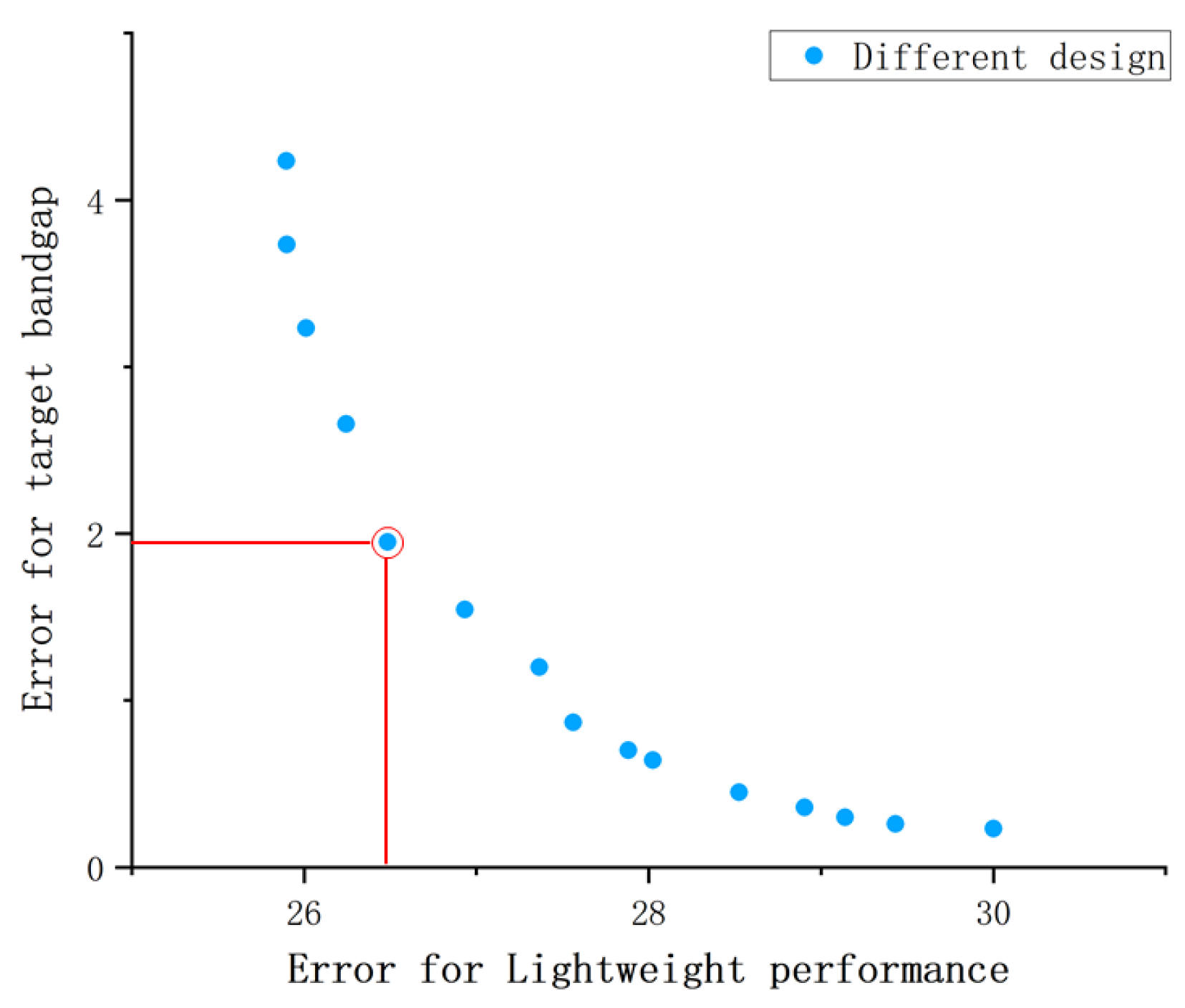
3.3. The Optimization Design Method Based on NSGA-II
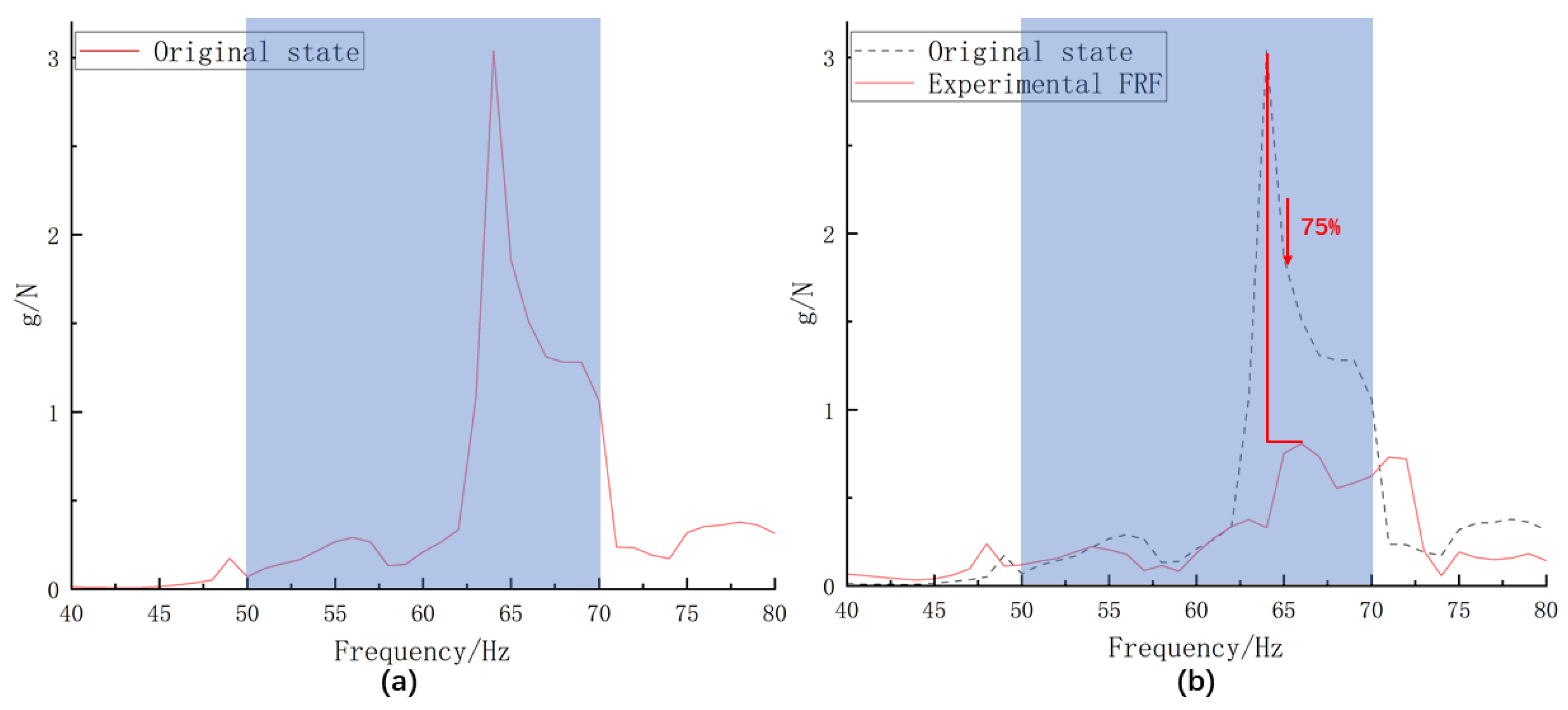
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Masri, J.; Amer, M.; Salman, S.; Ismail, M.; Elsisi, M. A survey of modern vehicle noise, vibration, and harshness: A state-of-the-art. Ain Shams Eng. J. 2024, 15, 102957. [Google Scholar] [CrossRef]
- Mishra, V.N.; Gupta, D.A.; Sarangi, D.S.K. Numerical and Experimental Study of Layered Beams with Vibration-Damping Coatings for Improved Vibration Mitigation. Mech. Res. Commun. 2025, 148, 104476. [Google Scholar] [CrossRef]
- AktaŞ, K.G.; GüvenÇ, M.A. Numerical and Analytical Free Vibration Analysis of Composite Plate with Auxetic Core Layer and Functionally Graded Surface Layers. Aerosp. Res. Lett. (ASREL) 2024, 3, 158. [Google Scholar] [CrossRef]
- Kang, X.; Li, H.; Zhu, X.; Zhang, A.; Tang, J.; Shi, X. Optimization of vibration control of adjacent buildings structures by a new inertial amplified mass-tuned damper. J. Inst. Eng. (India) Ser. A 2025, 106, 241–258. [Google Scholar] [CrossRef]
- Hansen, C.H.; Snyder, S.D.; Qiu, X.; Brooks, L.A.; Moreau, D.J. Active Control of Noise and Vibration; E & Fn Spon London: London, UK, 1997; p. 1267. [Google Scholar]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022. [Google Scholar] [CrossRef]
- Xu, J.; Mao, W.; Yu, X.; Liu, B. Prediction and optimization of acoustic absorption performance of quasi-Helmholtz acoustic metamaterials based on LightGBM algorithm. AIP Adv. 2025, 15, 015125. [Google Scholar] [CrossRef]
- Chen, Z.; Guo, B.; Yang, Y.; Cheng, C. Metamaterials-based enhanced energy harvesting: A review. Phys. B Condens. Matter 2014, 438, 1–8. [Google Scholar] [CrossRef]
- Liu, N.; Sun, Y.; Wang, Y.; Sun, P.; Li, W.; Guo, H. Mechanism of interior noise generation in high-speed vehicle based on anti-noise operational transfer path analysis. Proc. Inst. Mech. Eng. Part J. Automob. Eng. 2021, 235, 273–287. [Google Scholar] [CrossRef]
- Cummer, S.A.; Christensen, J.; Alù, A. Controlling sound with acoustic metamaterials. Nat. Rev. Mater. 2016, 1, 1–13. [Google Scholar] [CrossRef]
- Fahy, F.J. Sound and Structural Vibration: Radiation, Transmission and Response; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Zhang, Y.; Zhu, Z.; Sheng, Z.; He, Y.; Wang, G. Vibro-acoustic suppression of metamaterial plates in multi-bandgaps. Int. J. Mech. Sci. 2025, 286, 109873. [Google Scholar] [CrossRef]
- Wu, Y.; Yan, W.; Wen, G.; He, Y.; Deng, S.; Ding, W. Design and Application of a Lightweight Plate-Type Acoustic Metamaterial for Vehicle Interior Low-Frequency Noise Reduction. Crystals 2024, 14, 957. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, L.; Sun, L.; Li, N. Optimization of graded filleted lattice structures subject to yield and buckling constraints. Mater. Des. 2021, 206, 109746. [Google Scholar] [CrossRef]
- Yang, N.; Qian, Z.; Wei, H.; Zhao, M. Anisotropy and deformation of triply periodic minimal surface based lattices with skew transformation. Mater. Des. 2023, 225, 111595. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, D.Z.; Li, Z.; Zhang, T.; Zhou, H.; Ren, Z. Design, mechanical properties, and optimization of BCC lattice structures with taper struts. Compos. Struct. 2022, 295, 115830. [Google Scholar] [CrossRef]
- Yang, F.; Yang, J.S.; Wang, Y.; Li, S.; Chen, Y.Y. Low frequency bandgap characteristics of a 3D chiral acoustic metamaterial structure. Wave Motion 2024, 128, 103303. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Huang, J.; Chen, J.; Mai, H.; Wan, H.; Chen, R.; He, T. Performance prediction and inverse design of cylindrical plate-type acoustic metamaterials based on deep learning. Appl. Acoust. 2025, 234, 110633. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Maamoun, K.S.A.; Wrona, S.; Pawelczyk, M.; Karimi, H.R. Optimizing design of openings in vibrating plates for enhanced vibro-acoustic performance using a genetic algorithm approach. J. Sound Vib. 2025, 598, 118847. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Wang, Y.; Luo, Y. Ultra-wide low-frequency bandgap design of acoustic metamaterial via multi-material topology optimization. Compos. Struct. 2023, 306, 116584. [Google Scholar] [CrossRef]
- Hu, Z.; Ding, J.; Ding, S.; Ma, W.W.S.; Chua, J.W.; Li, X.; Zhai, W.; Song, X. Machine learning–enabled inverse design of shell-based lattice metamaterials with optimal sound and energy absorption. Virtual Phys. Prototyp. 2024, 19, e2412198. [Google Scholar] [CrossRef]
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Li, P.; Zhang, Z.; Wang, W.; Ji, W.; Yu, T.; Gao, P. Vibration Manipulation Properties of Phononic Crystals and Acoustic Metamaterials for Fluid-Conveying Pipeline Systems: A Review. J. Vib. Eng. Technol. 2025, 13, 114. [Google Scholar] [CrossRef]
- Sun, H.; Hai, H.; Zhou, C.; Wang, W.; Chen, C.; Xu, W. Attenuation effects of seismic metamaterials based on local resonance and Rayleigh wave dispersion phenomena. Mech. Res. Commun. 2025, 143, 104367. [Google Scholar] [CrossRef]
- Zhang, K.; Guo, Y.; Liu, X.; Hong, F.; Hou, X.; Deng, Z. Deep learning-based inverse design of lattice metamaterials for tuning bandgap. Extrem. Mech. Lett. 2024, 69, 102165. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, J.; Qin, Y.; Chen, X.; He, Y.; Song, Y.; Zhang, X.; Ma, W.; Li, S.; Wu, Y. Multi-Objective Optimization Design of Low-Frequency Band Gap for Local Resonance Acoustic Metamaterials Based on Genetic Algorithm. Machines 2025, 13, 610. https://doi.org/10.3390/machines13070610
Deng J, Qin Y, Chen X, He Y, Song Y, Zhang X, Ma W, Li S, Wu Y. Multi-Objective Optimization Design of Low-Frequency Band Gap for Local Resonance Acoustic Metamaterials Based on Genetic Algorithm. Machines. 2025; 13(7):610. https://doi.org/10.3390/machines13070610
Chicago/Turabian StyleDeng, Jianjiao, Yunuo Qin, Xi Chen, Yanyong He, Yu Song, Xinpeng Zhang, Wenting Ma, Shoukui Li, and Yudong Wu. 2025. "Multi-Objective Optimization Design of Low-Frequency Band Gap for Local Resonance Acoustic Metamaterials Based on Genetic Algorithm" Machines 13, no. 7: 610. https://doi.org/10.3390/machines13070610
APA StyleDeng, J., Qin, Y., Chen, X., He, Y., Song, Y., Zhang, X., Ma, W., Li, S., & Wu, Y. (2025). Multi-Objective Optimization Design of Low-Frequency Band Gap for Local Resonance Acoustic Metamaterials Based on Genetic Algorithm. Machines, 13(7), 610. https://doi.org/10.3390/machines13070610





