Optimal Dimensional Synthesis of Ackermann and Watt-I Six-Bar Steering Mechanisms for Two-Axle Four-Wheeled Vehicles
Abstract
1. Introduction
2. Ackermann Principle and Steering Angular Position Analysis of Linkage-Type Steering Mechanisms
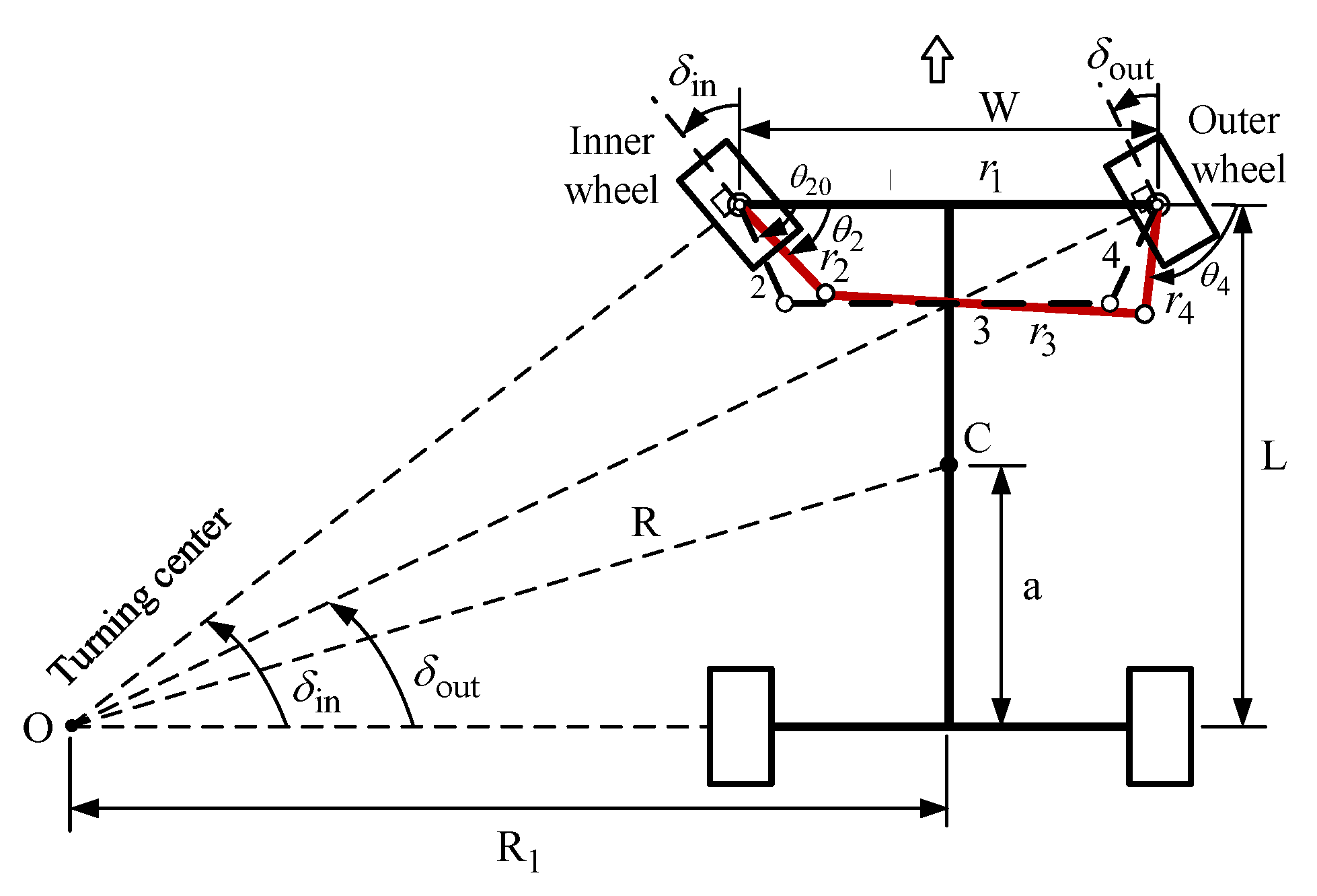
2.1. The Ackermann Steering Mechanism
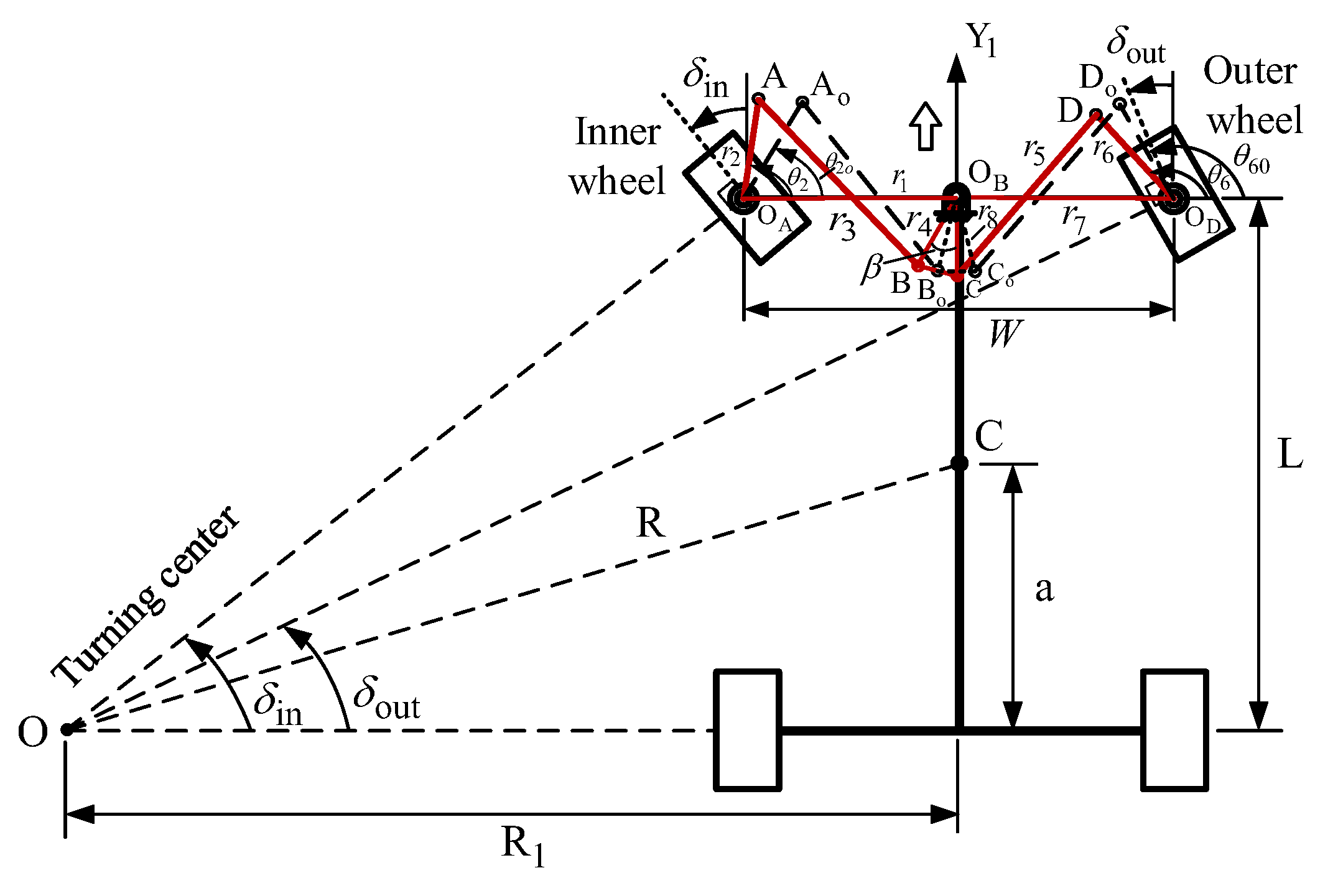
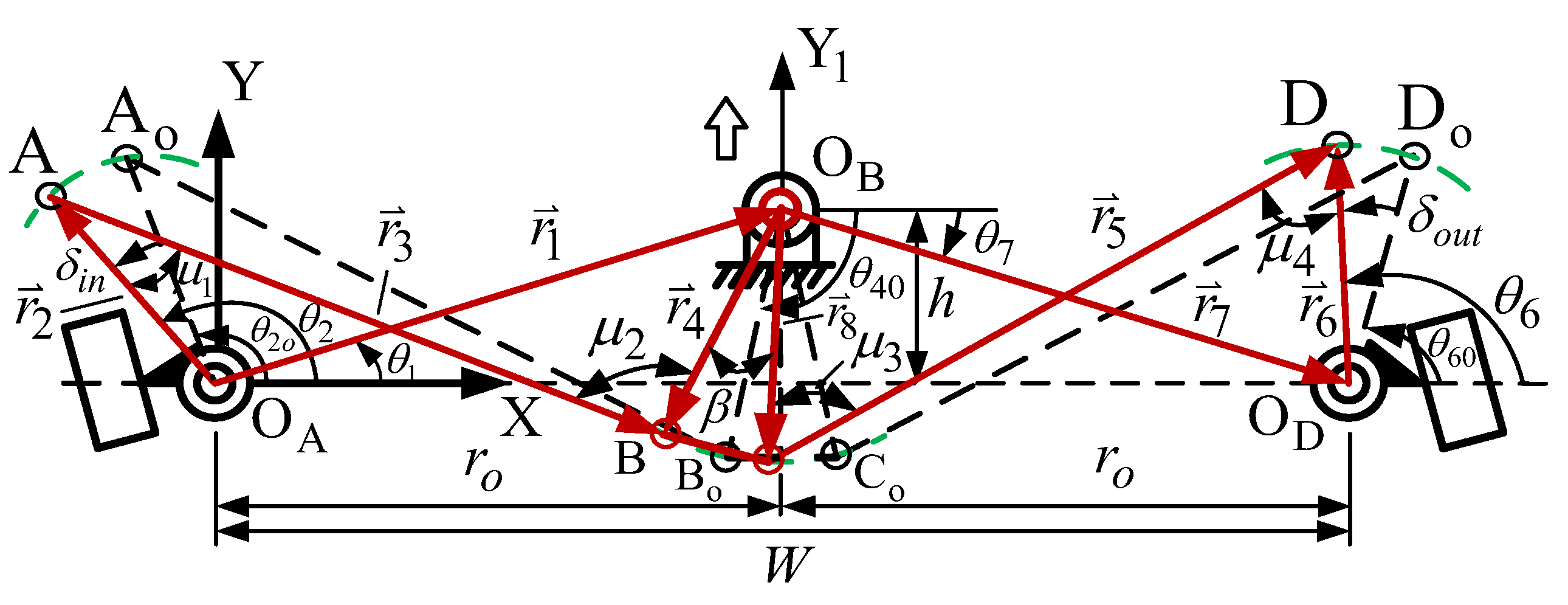
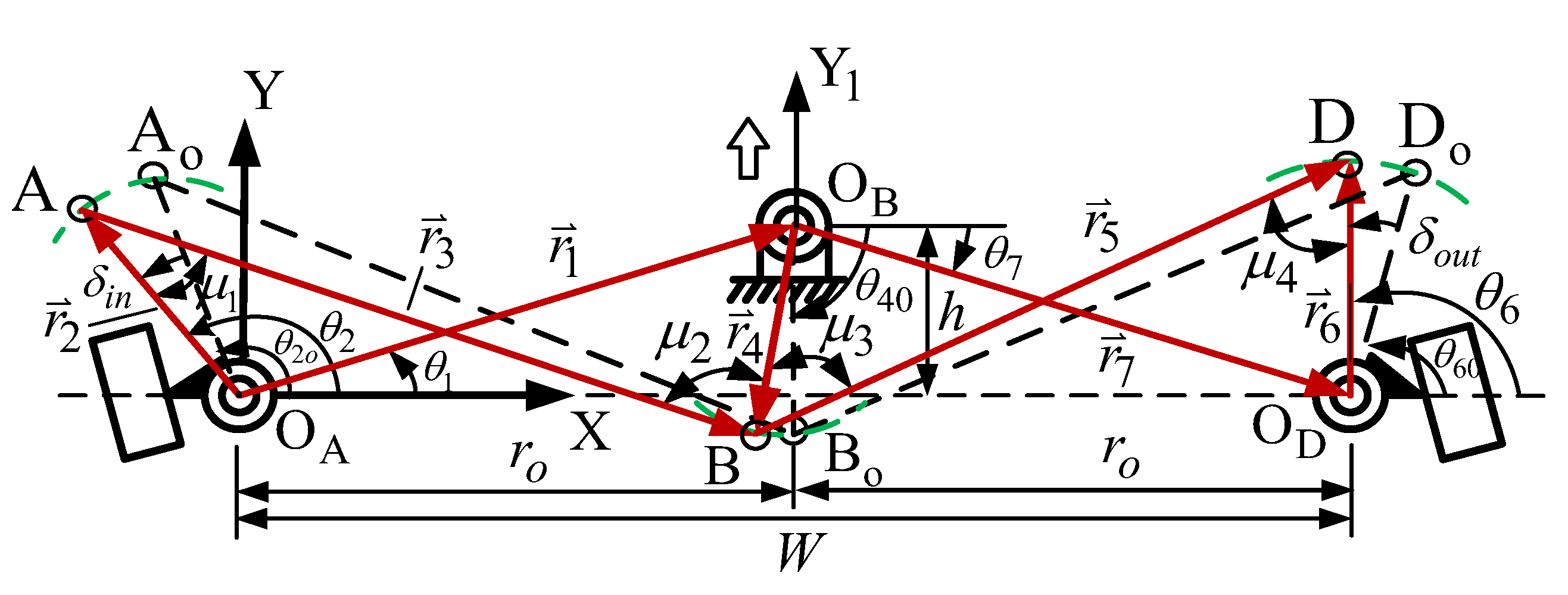
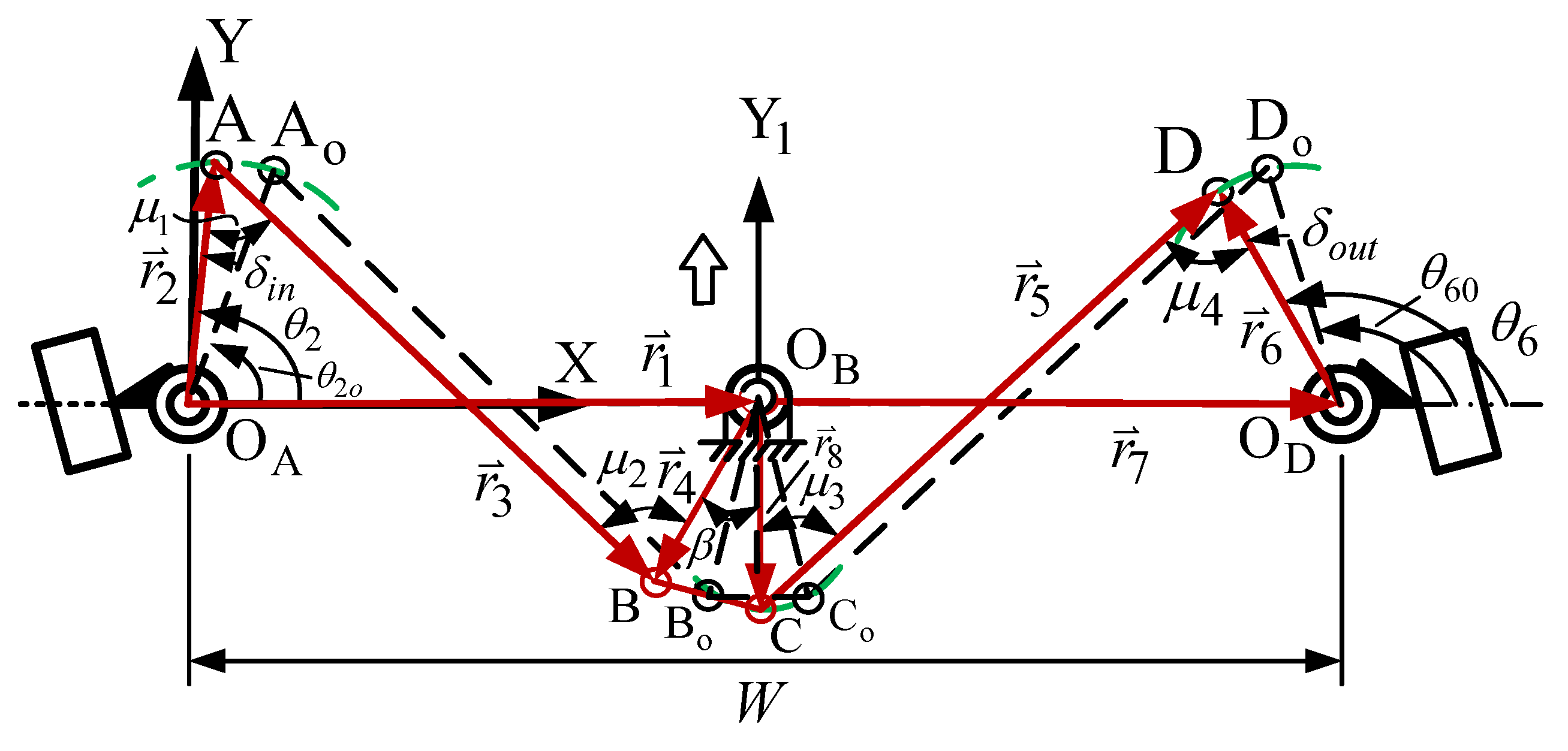
2.2. The Watt-I Six-Bar Steering Mechanism
2.2.1. Type I of the Watt-I Six-Bar Steering Mechanism
2.2.2. Type II of the Watt-I Six-Bar Steering Mechanism
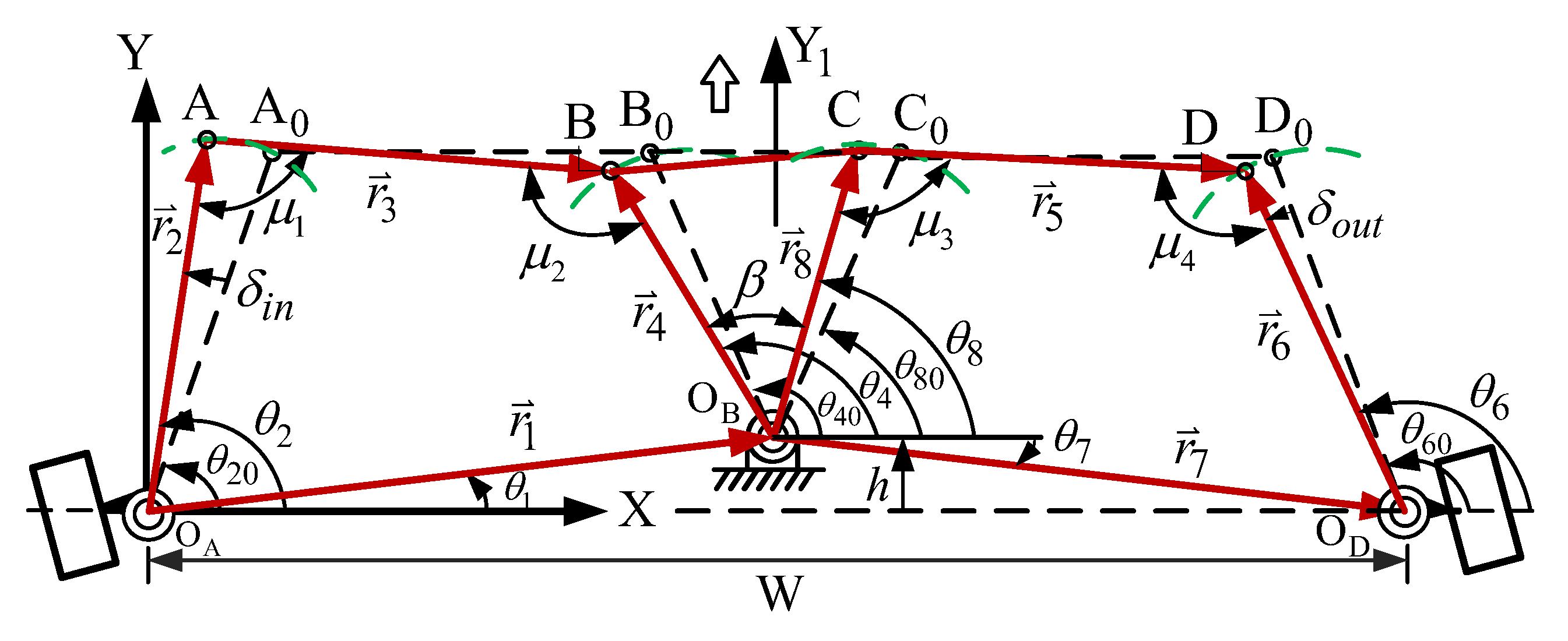
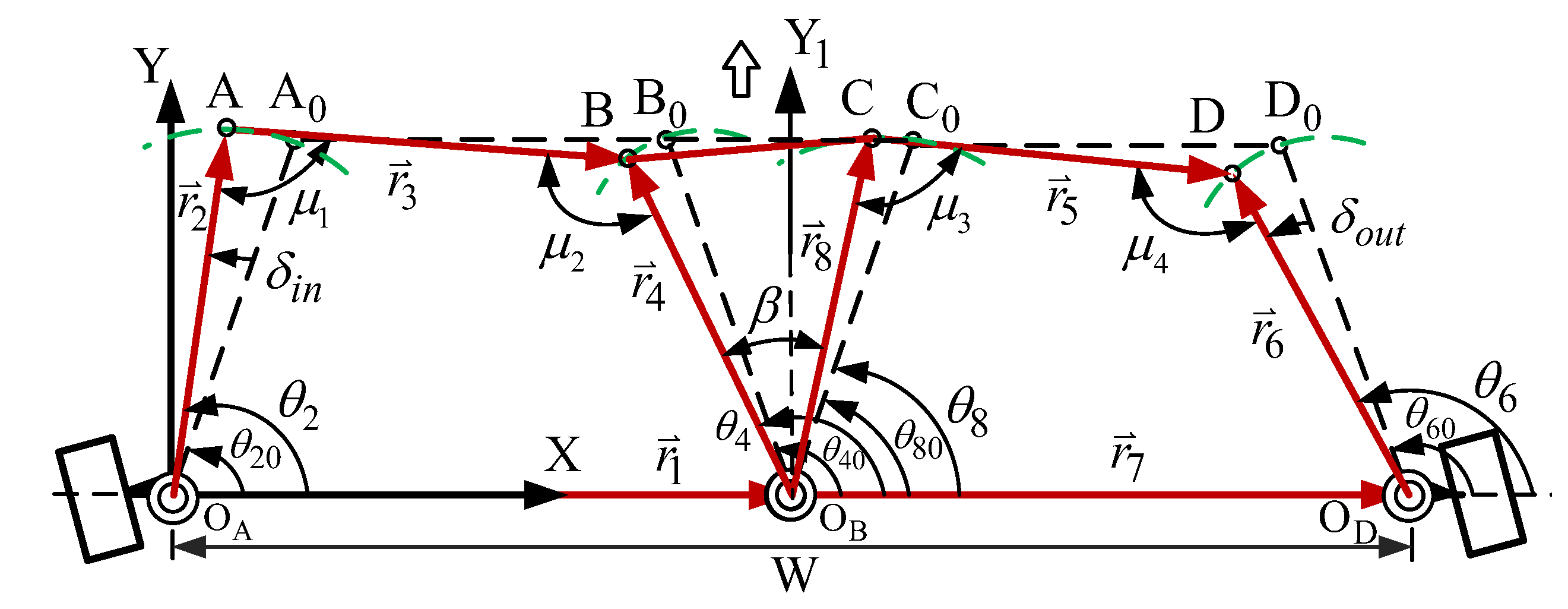
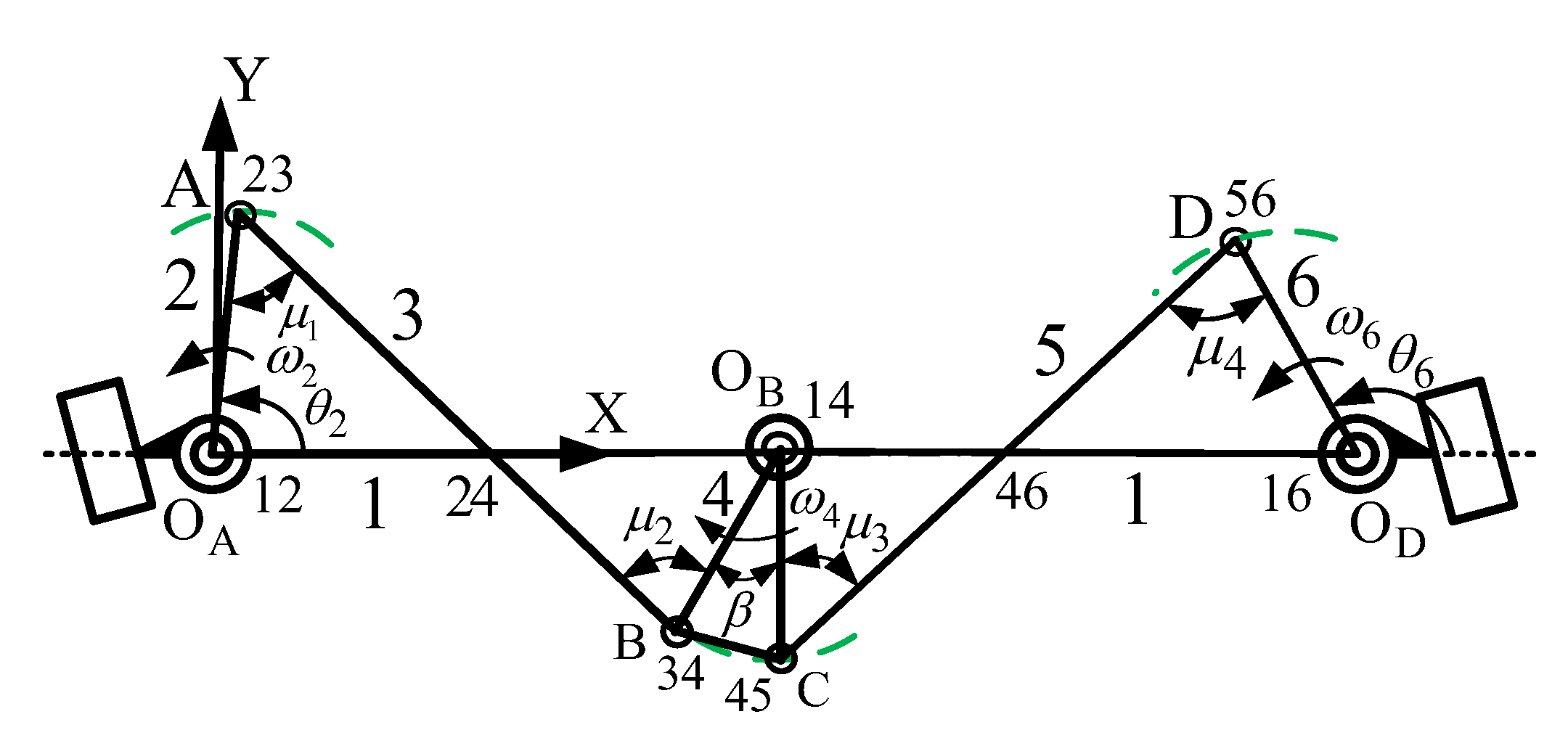
2.3. Position Analysis of the Watt-I Six-Bar Mechanism
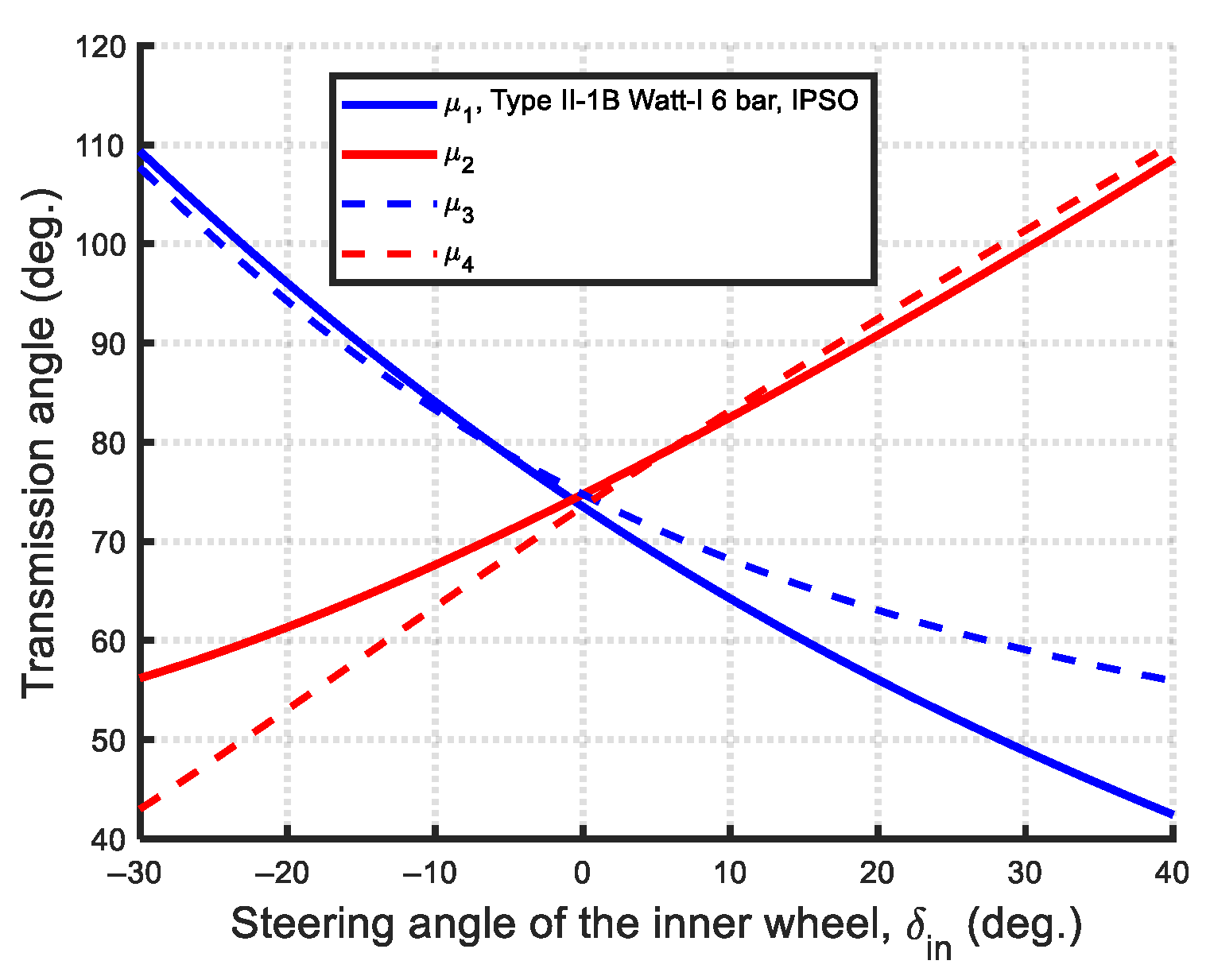
2.4. Mechanical Advantage (MA)
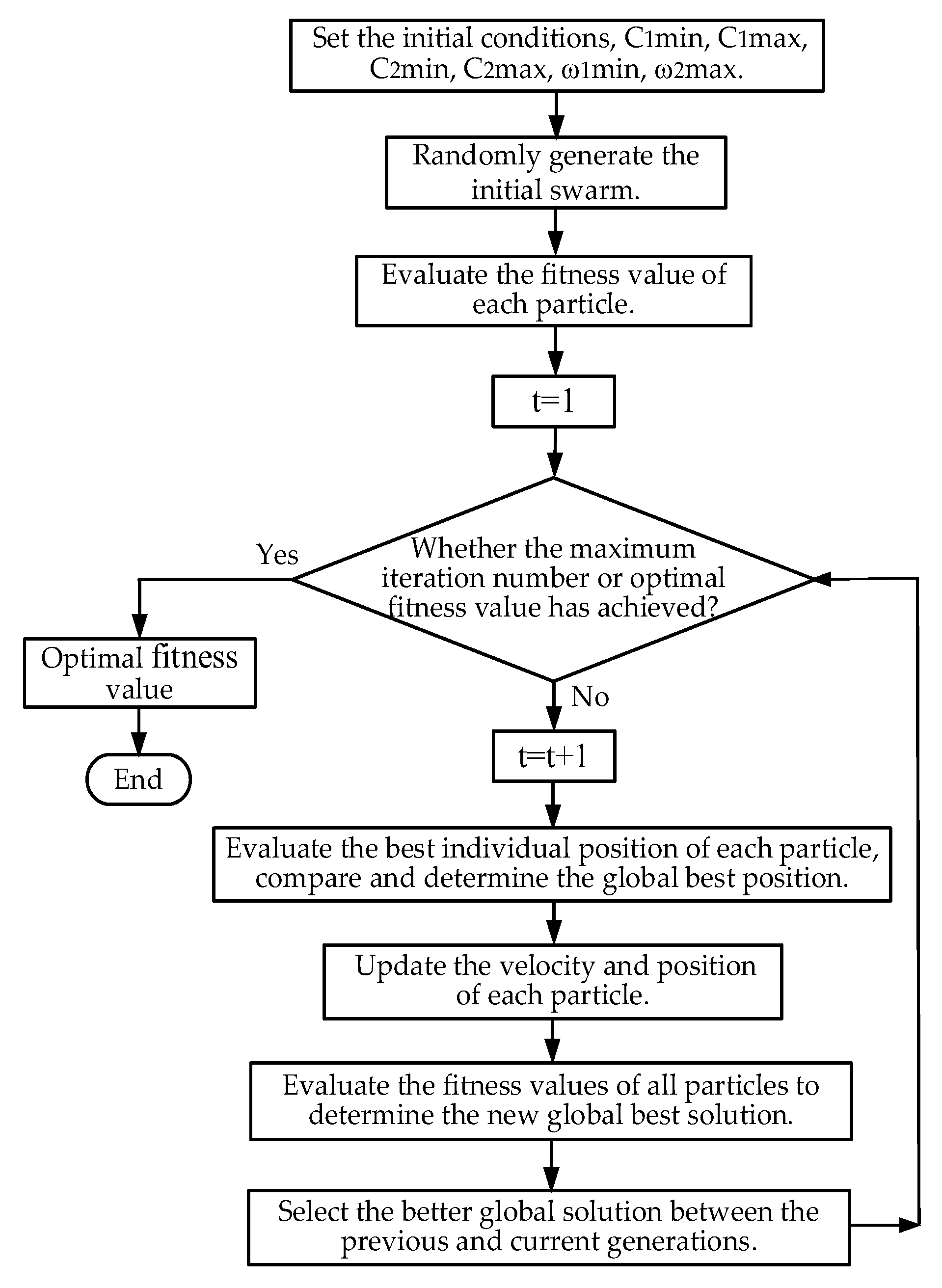
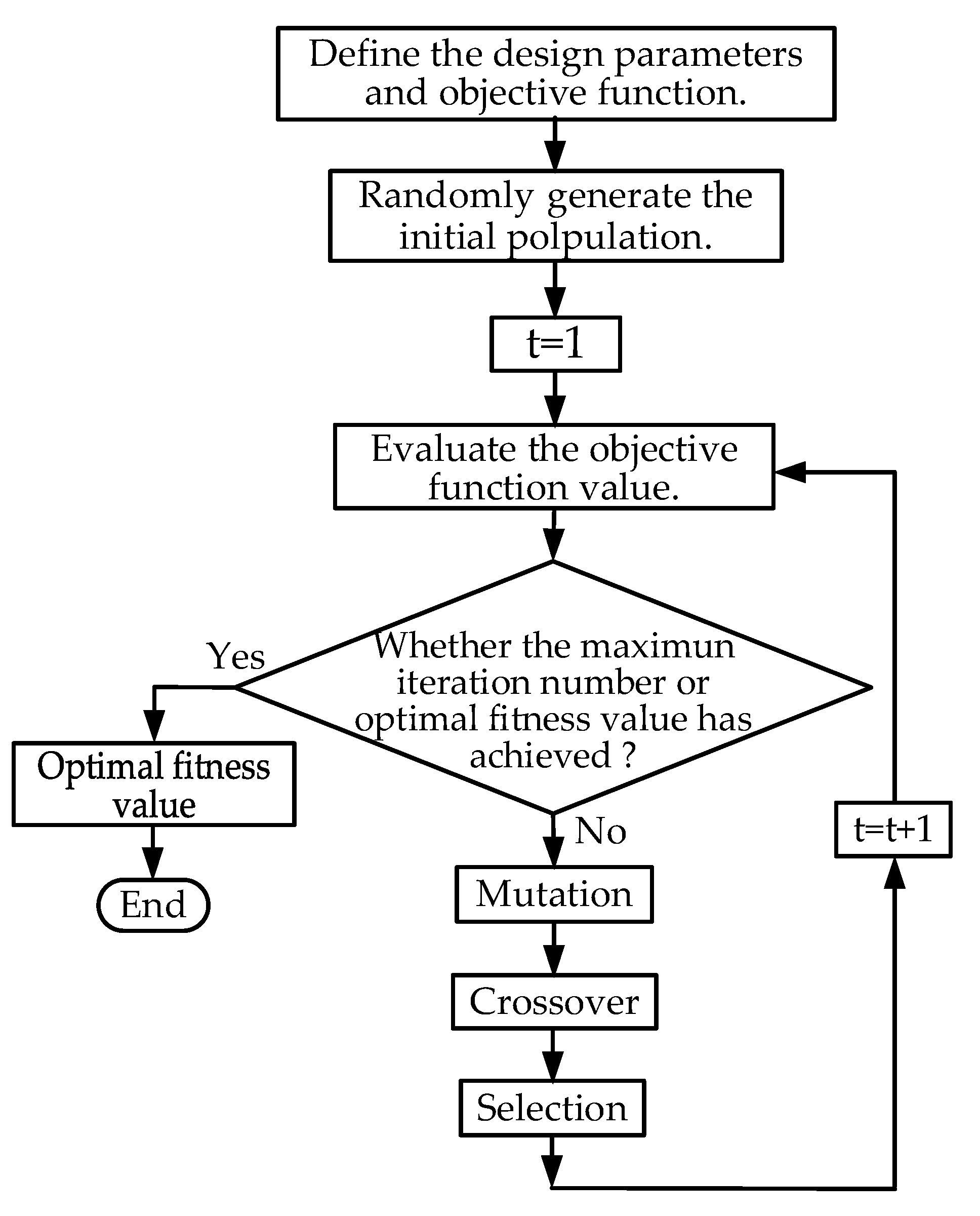
3. IPSO and DE-gr Optimization Methods
3.1. PSO and IPSO Algorithms
3.2. Differential Evolution Algorithm
- (1)
- Initialization
- (2)
- Mutation
- DE/rand/1:
- (3)
- Crossover
- (4)
- Selection
4. Optimization Design of the Ackermann Steering Mechanisms
- (i)
- For the Grashof mechanisms:
- (ii)
- For the Non-Grashof mechanisms:
5. Optimal Design of the Watt-I Six-Bar Steering Mechanisms
5.1. Optimal Synthesis Results of the Type I Watt-I Six-Bar Steering Mechanisms
- (1)
- Optimal synthesis results of the Type I-1
- (A)
- Type I-1A:
- (B)
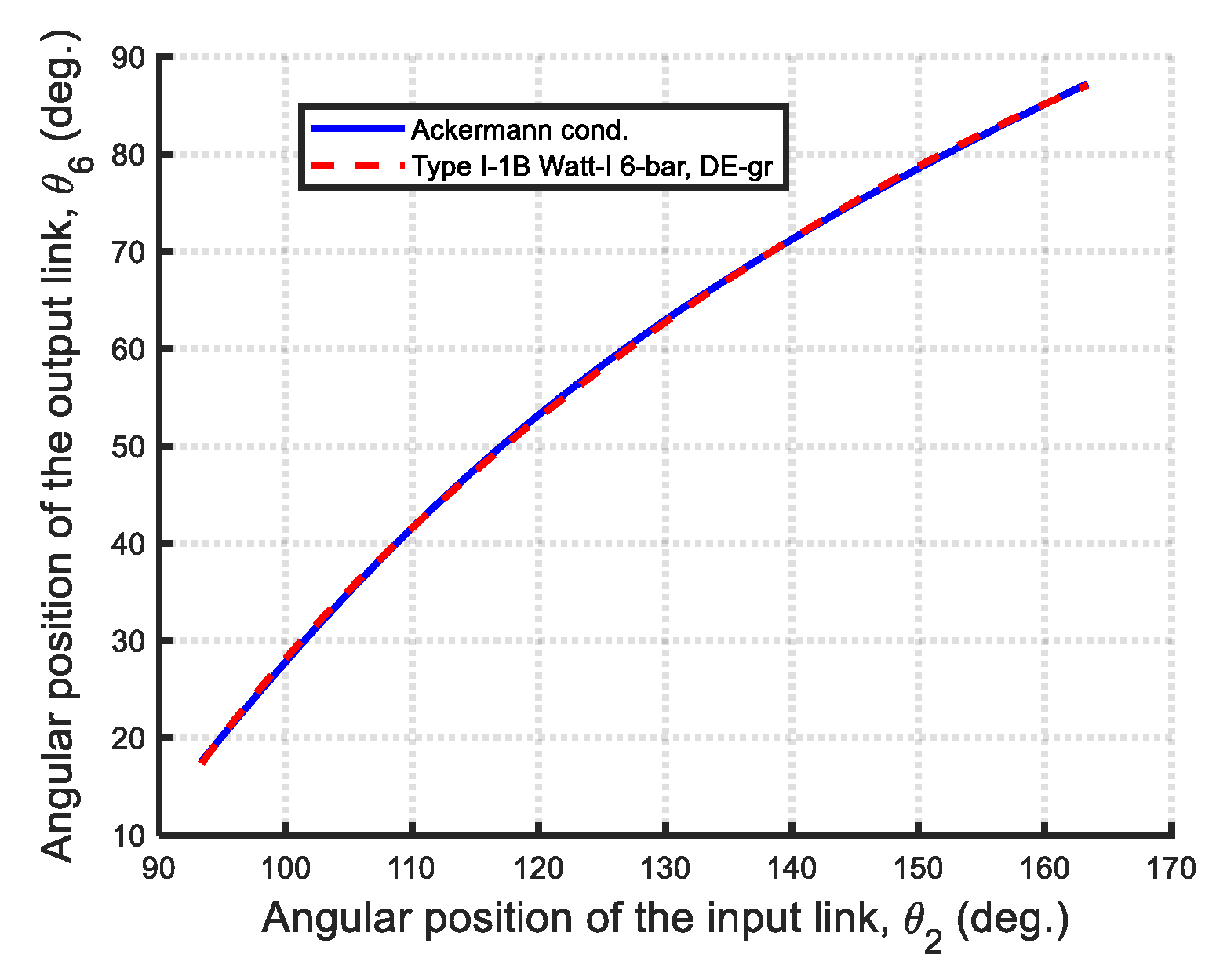
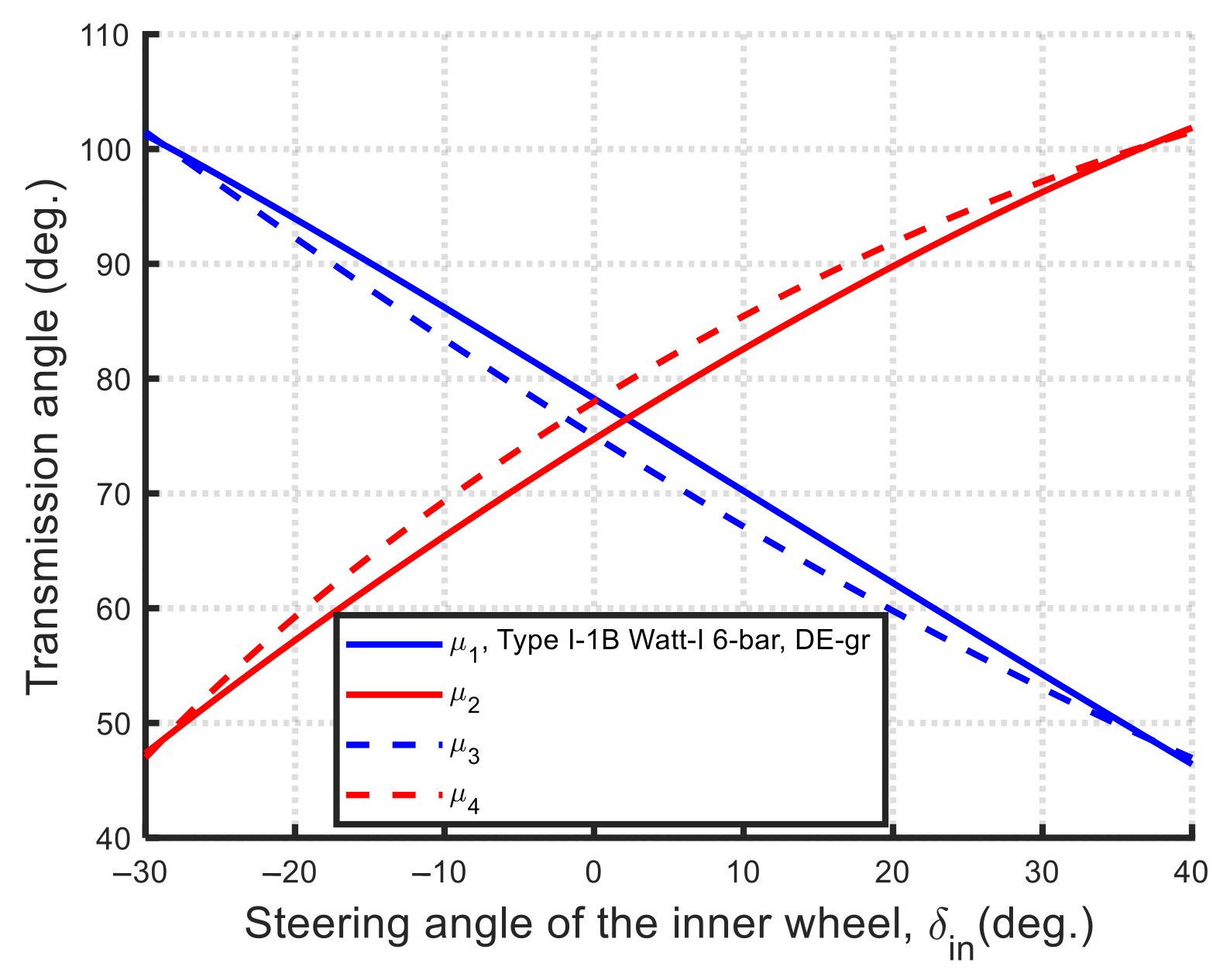
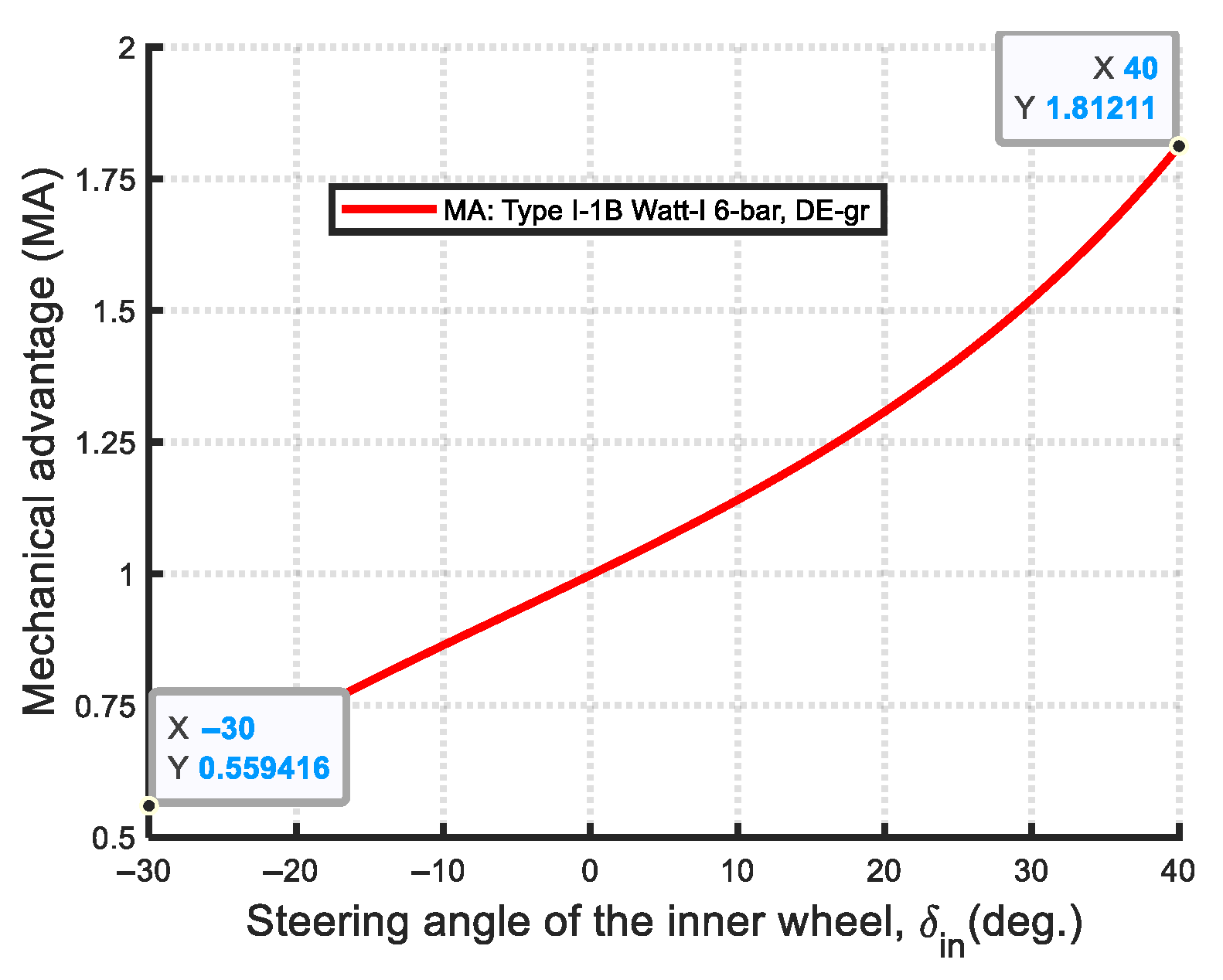
- Type I-1B:
- (2)
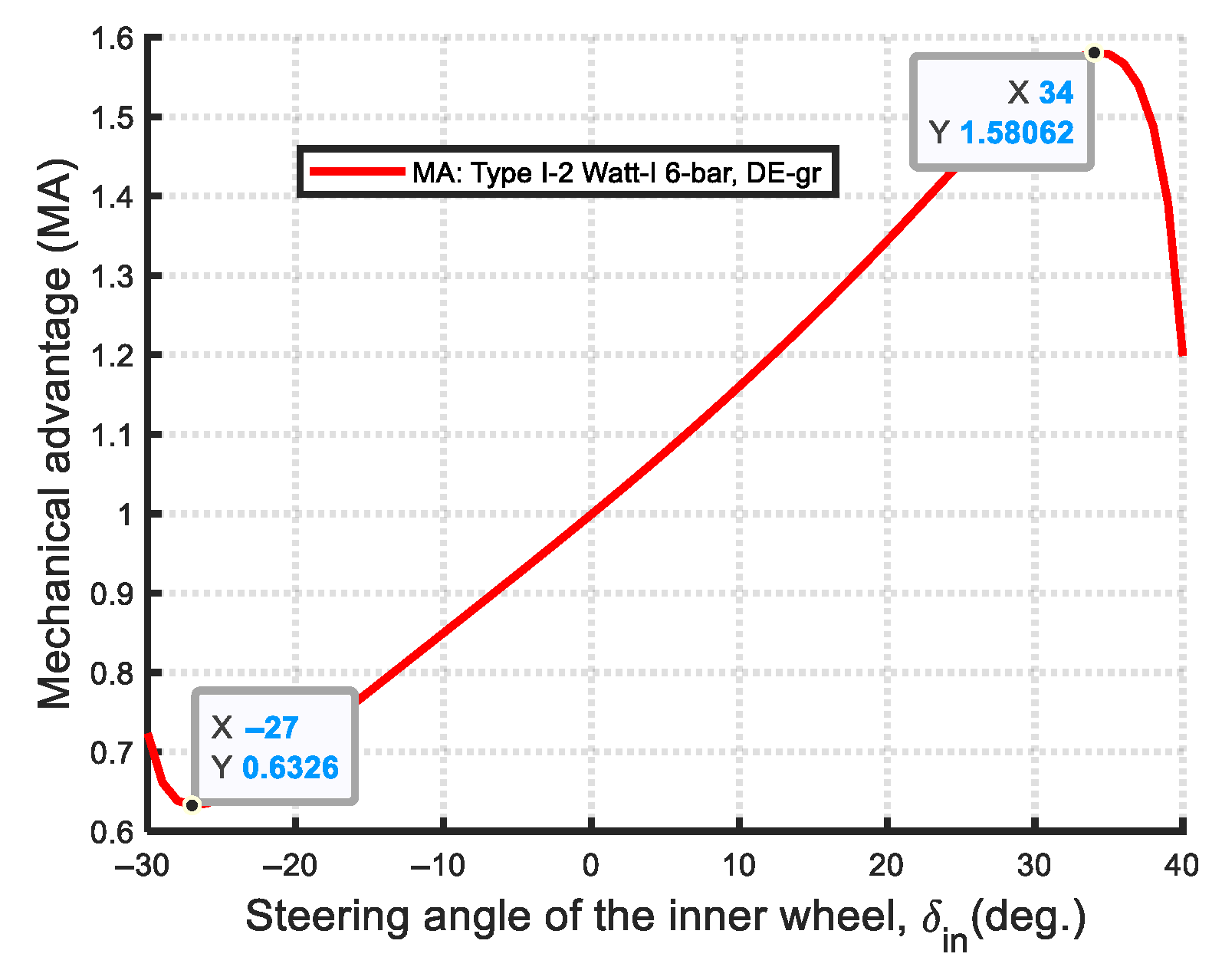
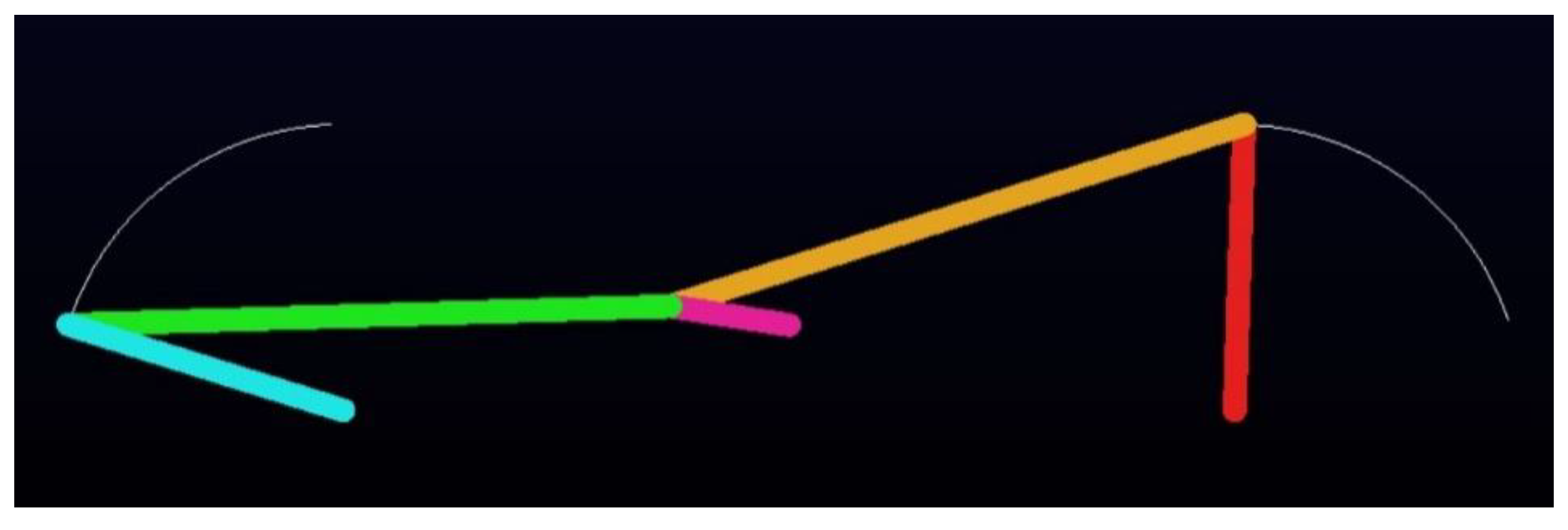
- Optimal synthesis results of Type I-2
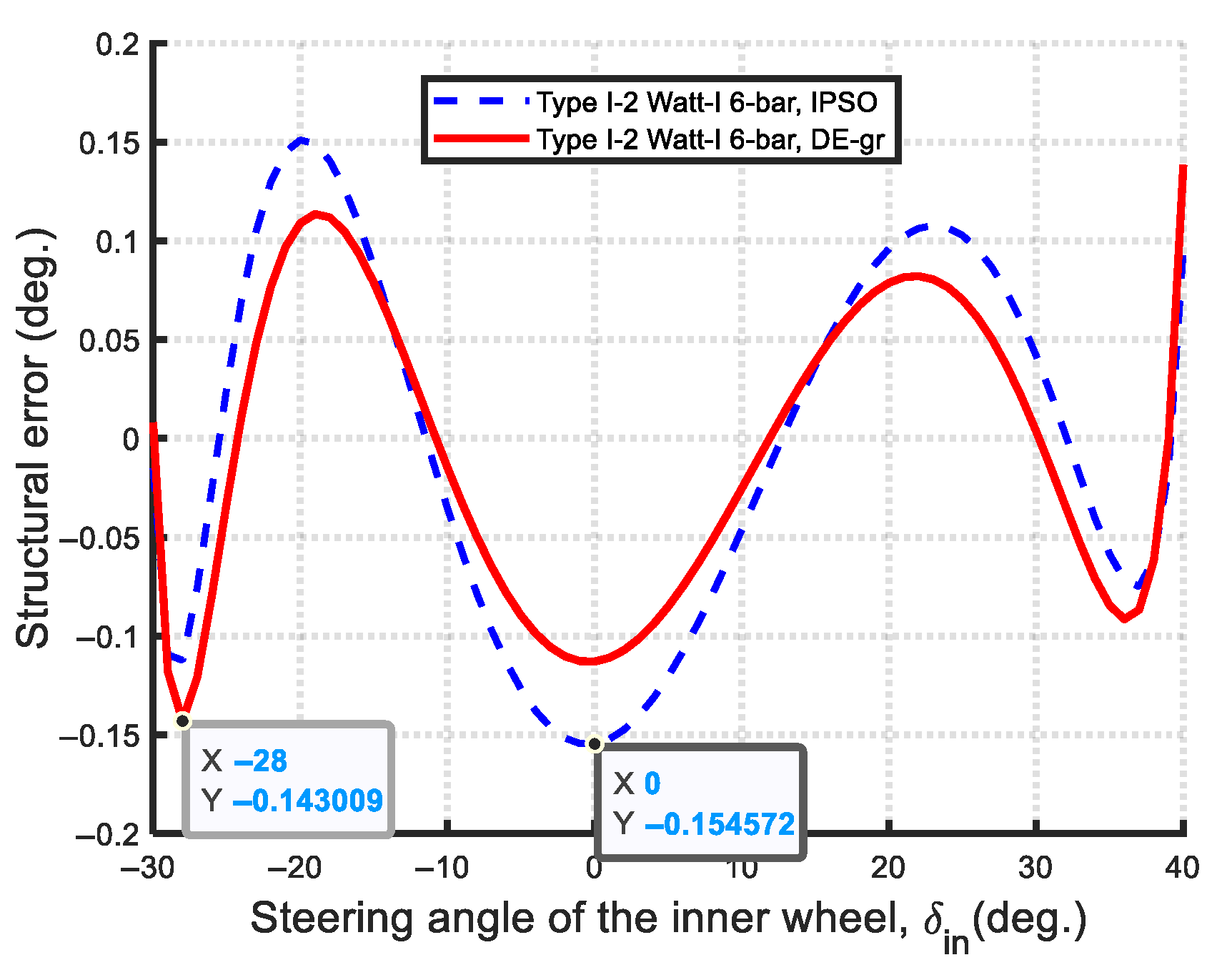
- Type I-2:
- (3)
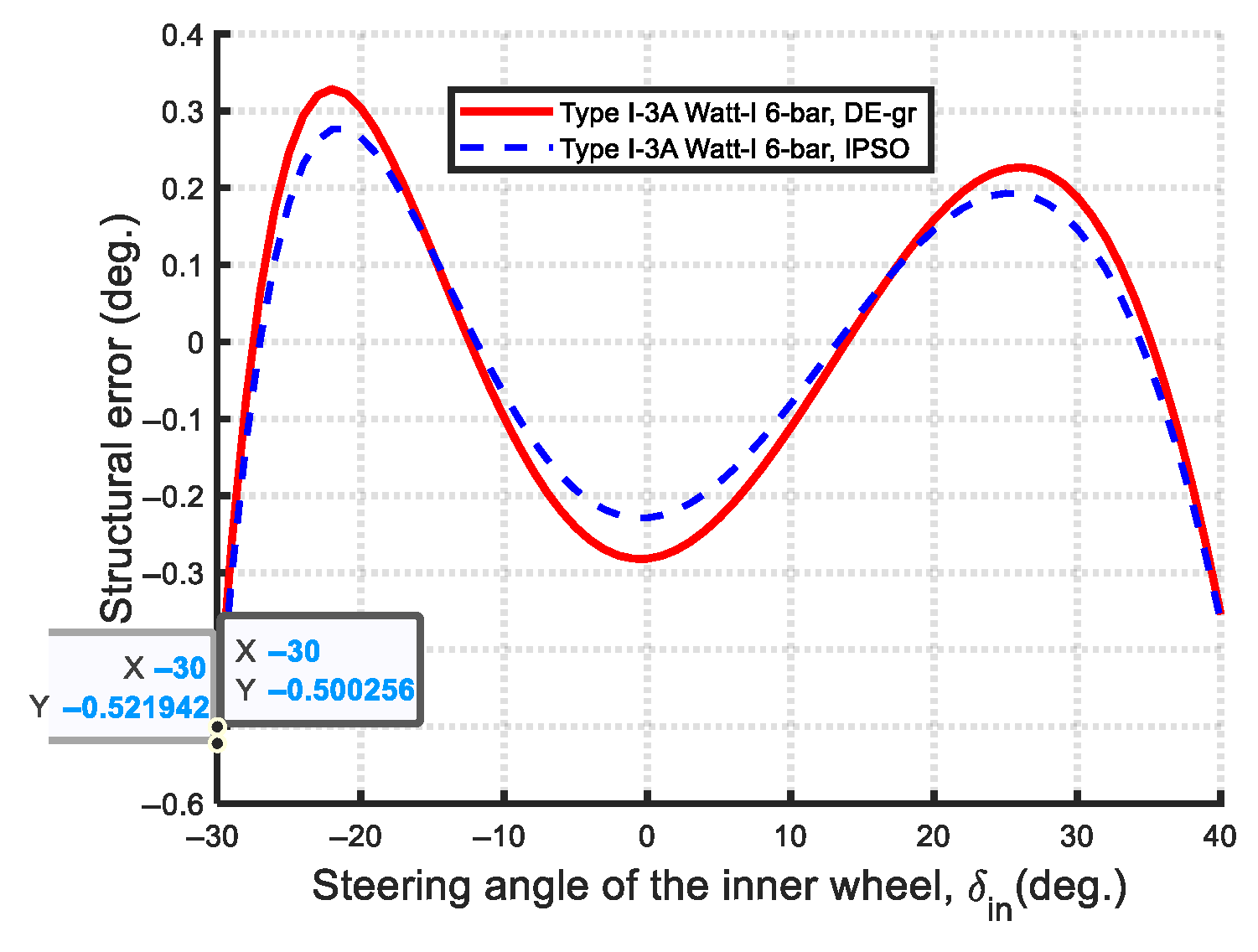
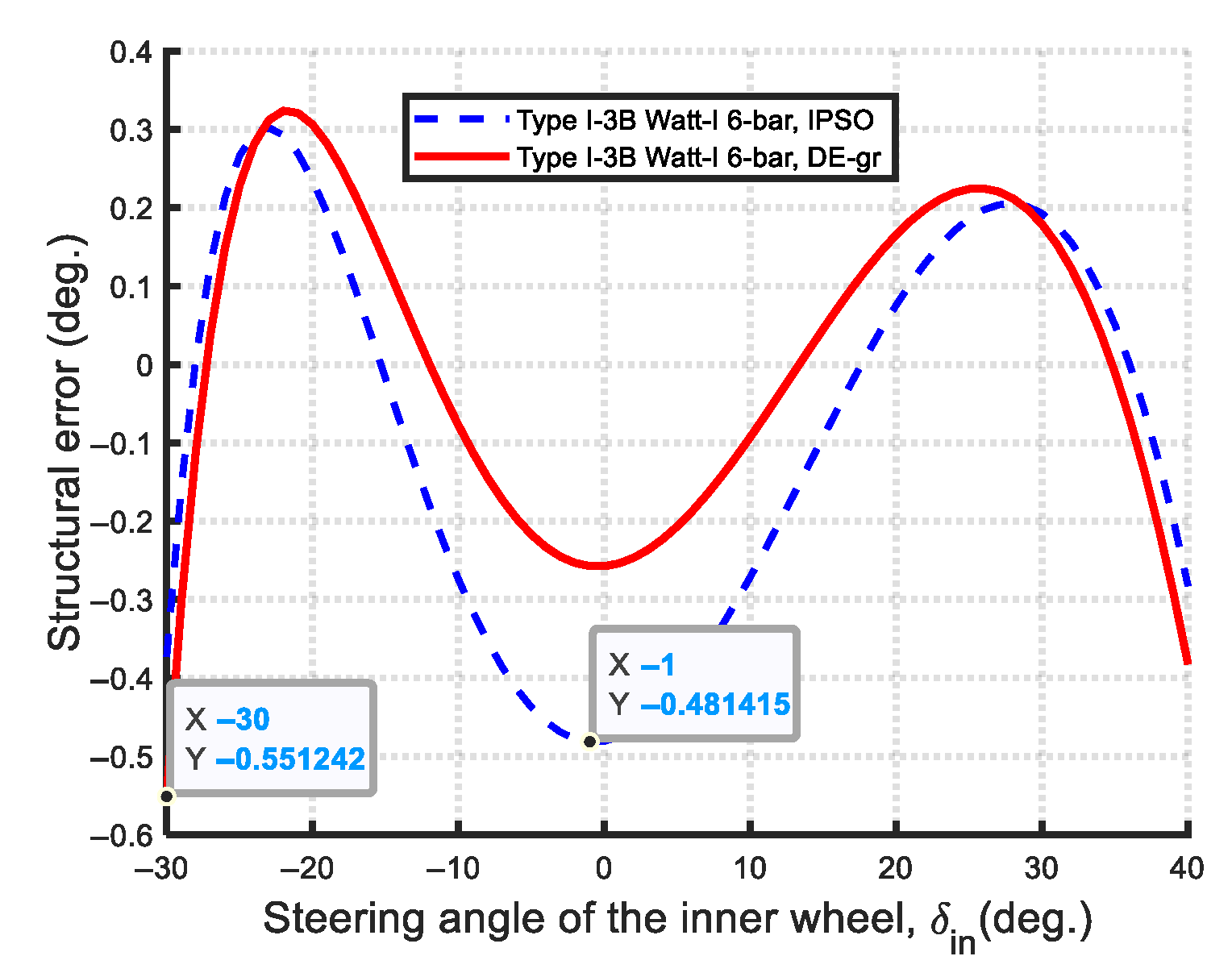
- Optimal synthesis results of Type I-3
- Type I-3: ()
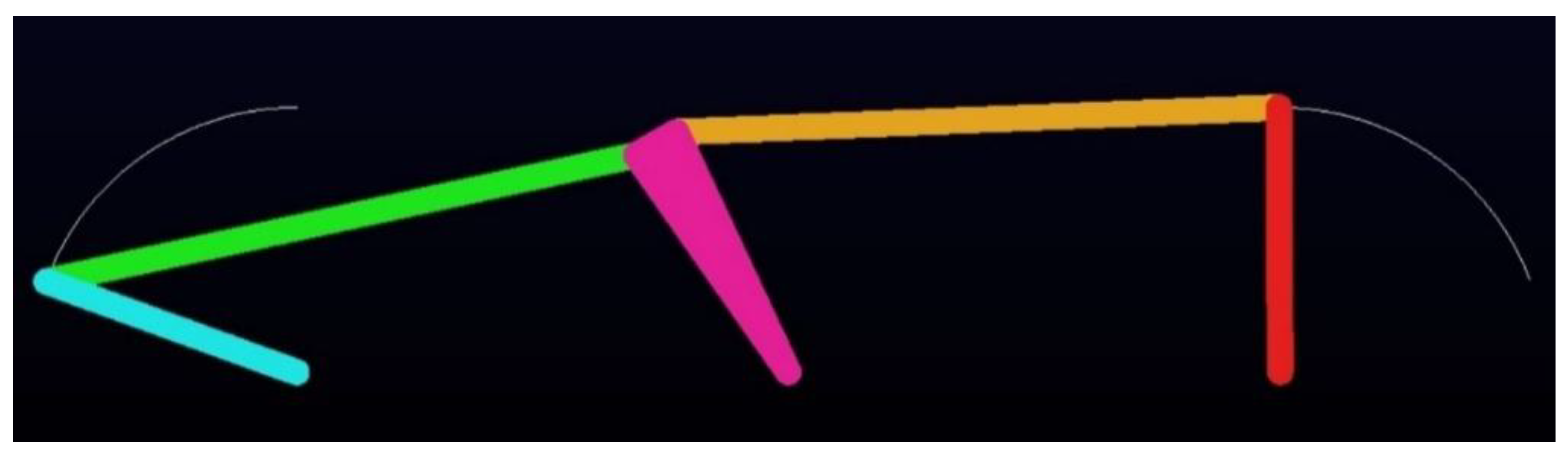
- Type I-3C:
5.2. Optimal Synthesis Results of the Type II Watt-I Six-Bar Steering Mechanism
- (1)
- Optimal synthesis results of Type II-1
- (A)
- Type II-1A:
- (B)
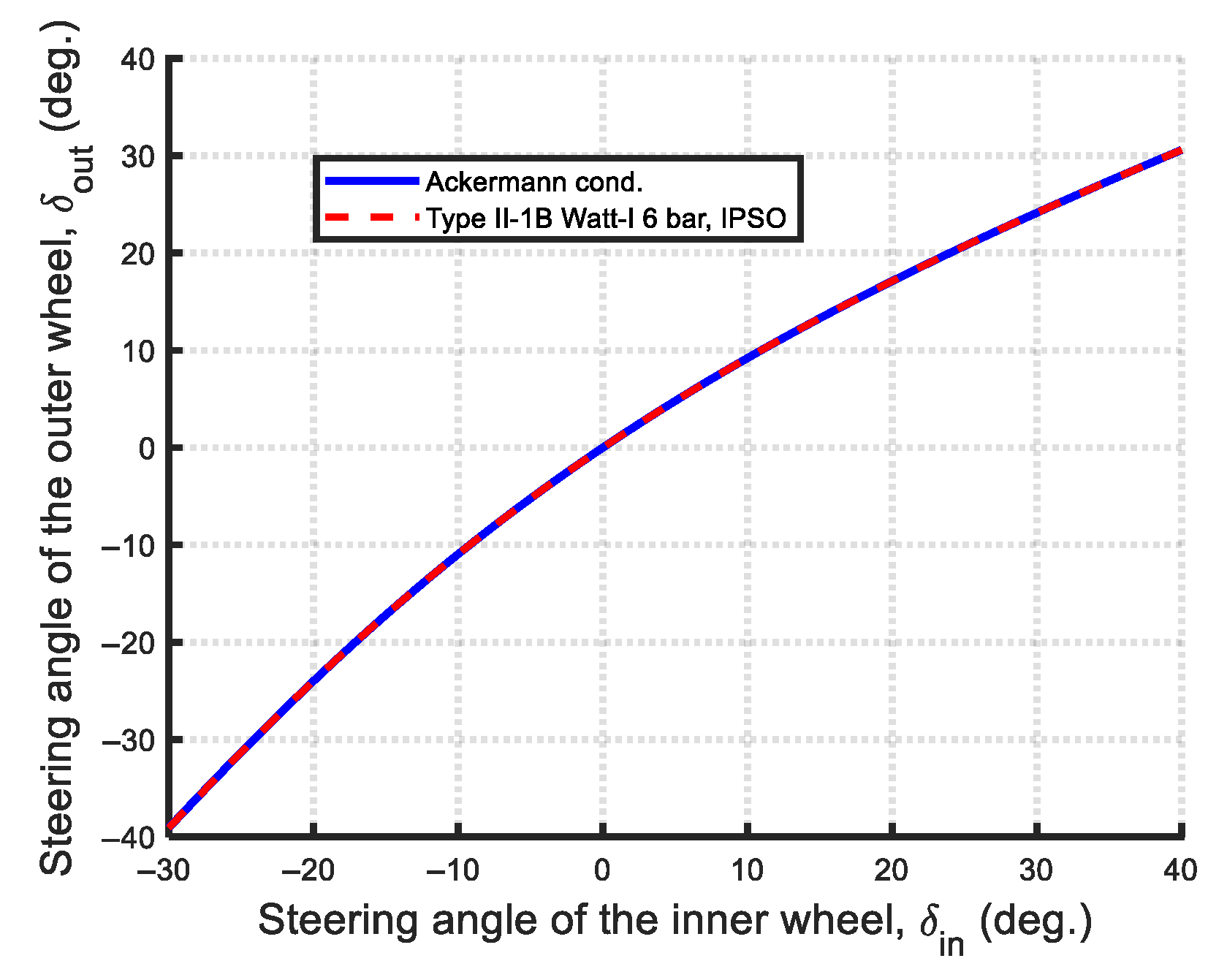
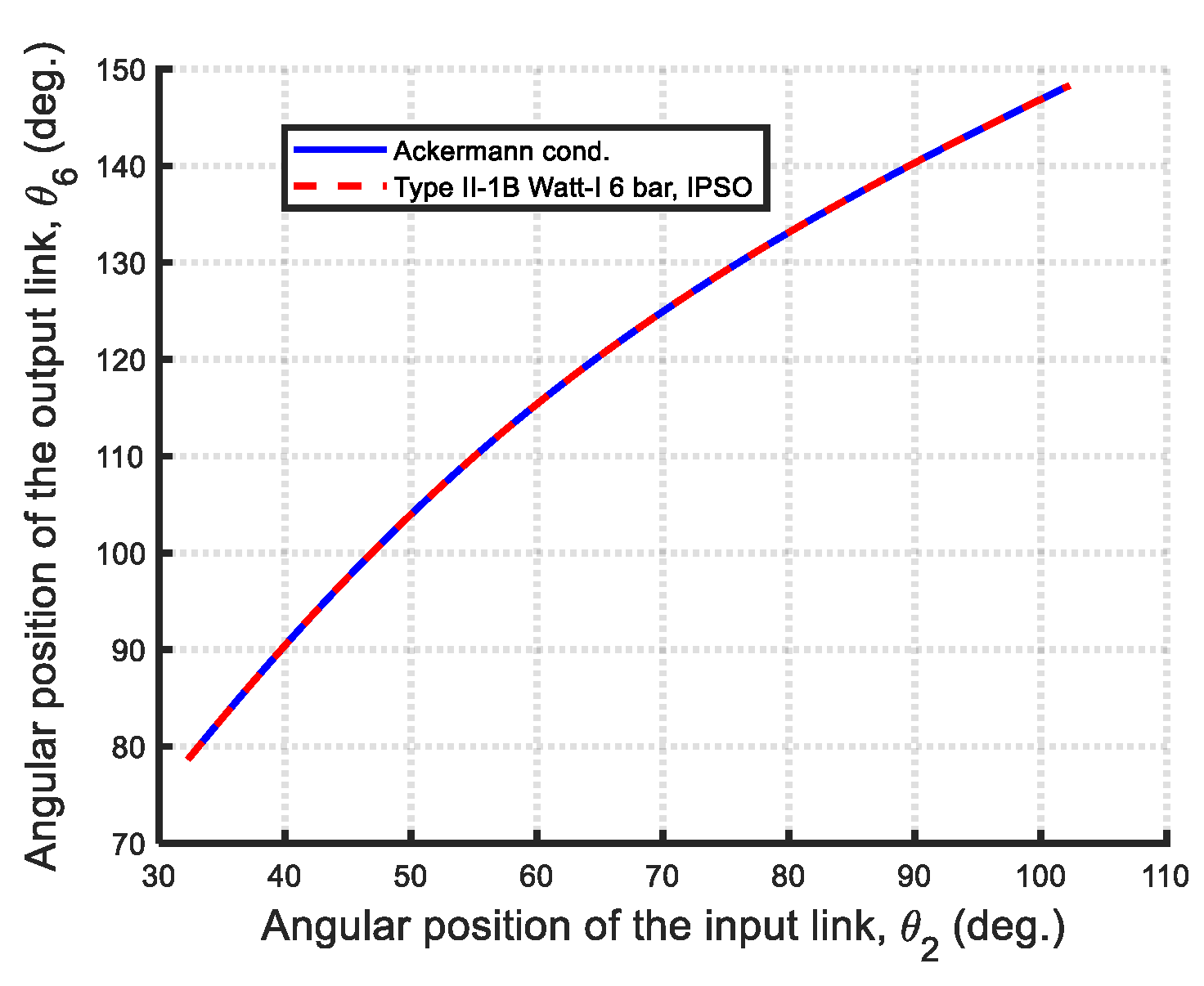
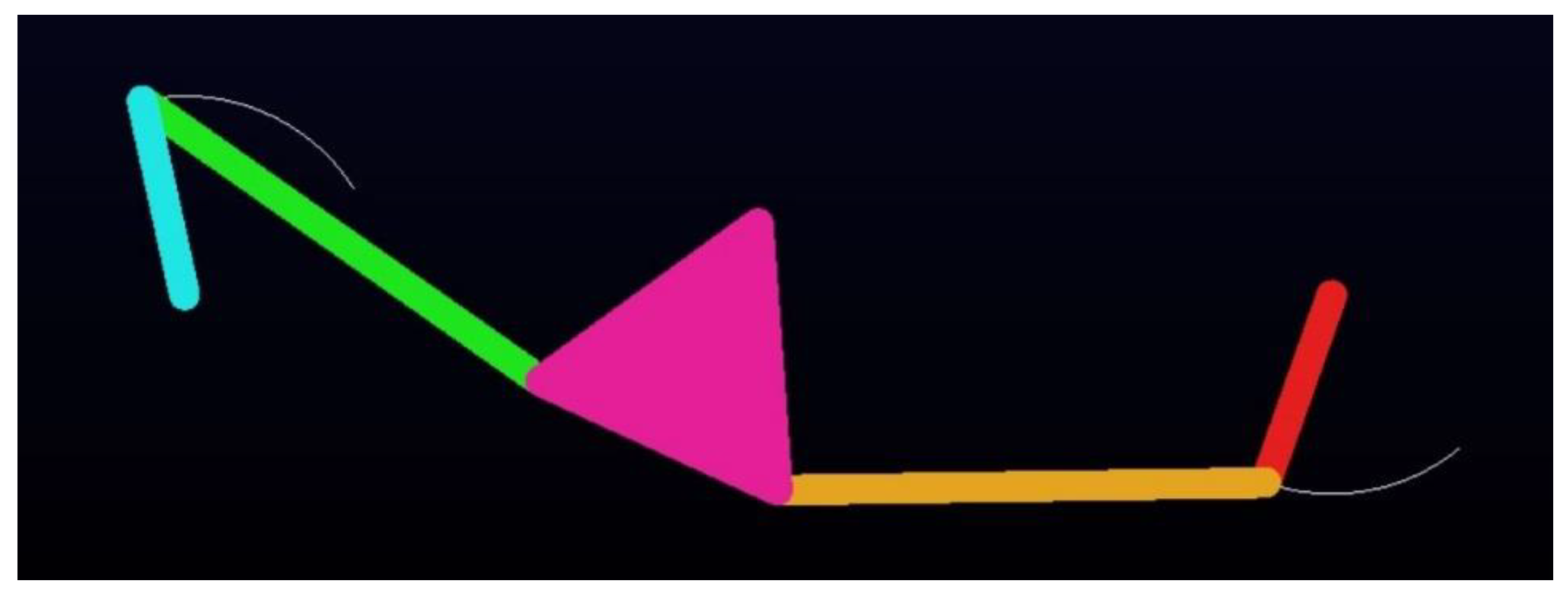
- Type II-1B:
- (2)
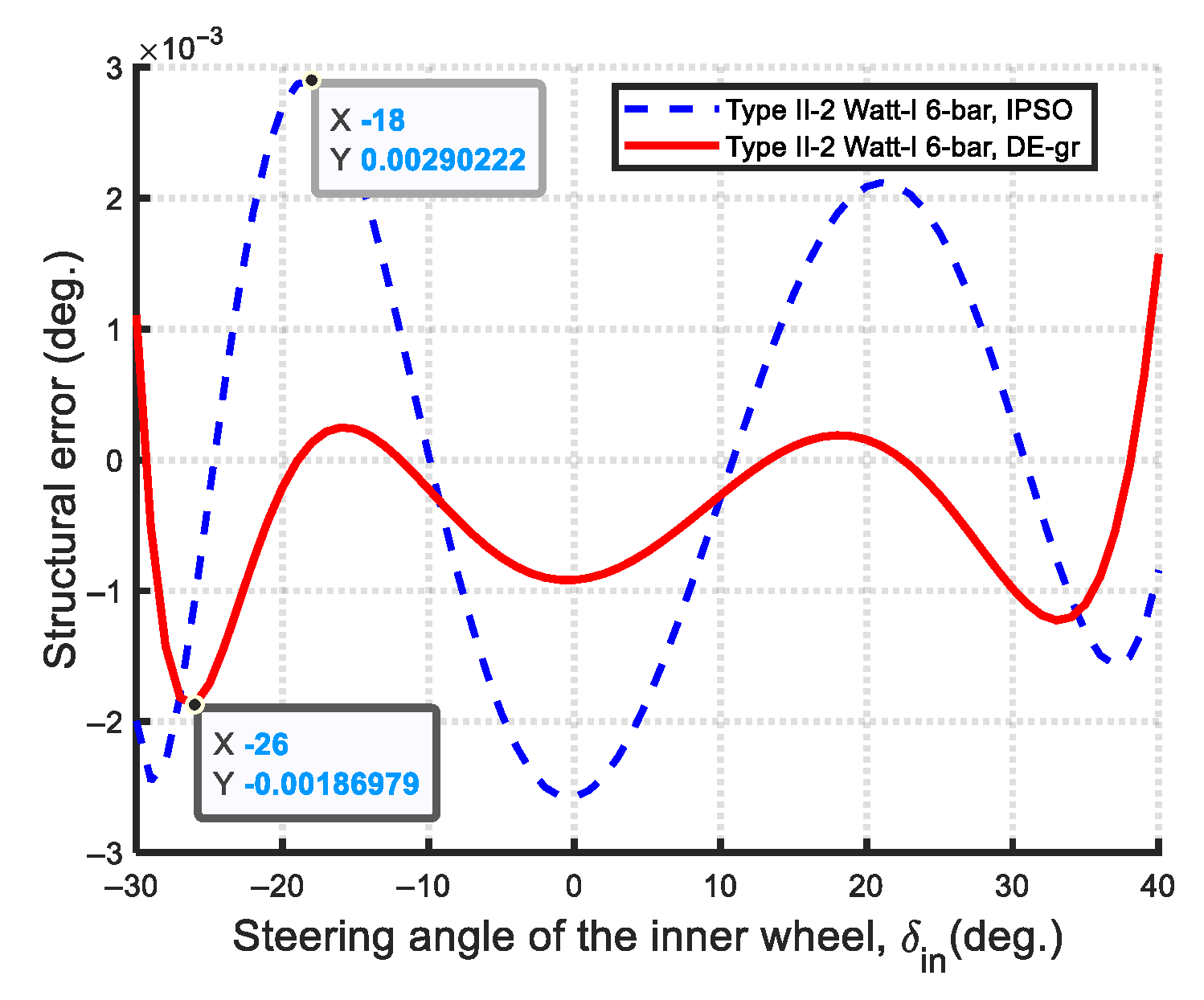
- Optimal synthesis results of the Type II-2
- Type II-2:
- (3)
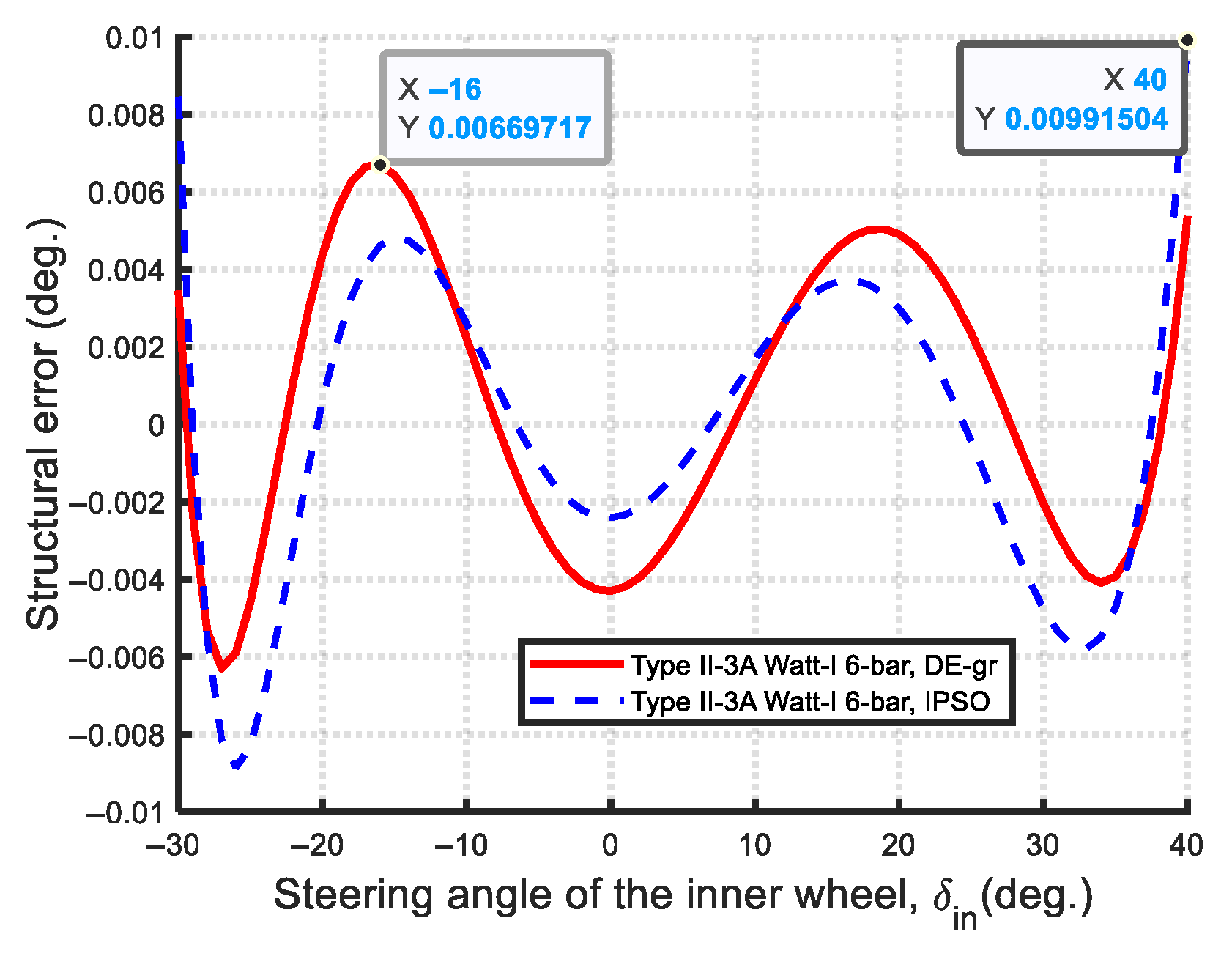
- Optimal synthesis results of the Type II-3
6. Discussion
- (1)
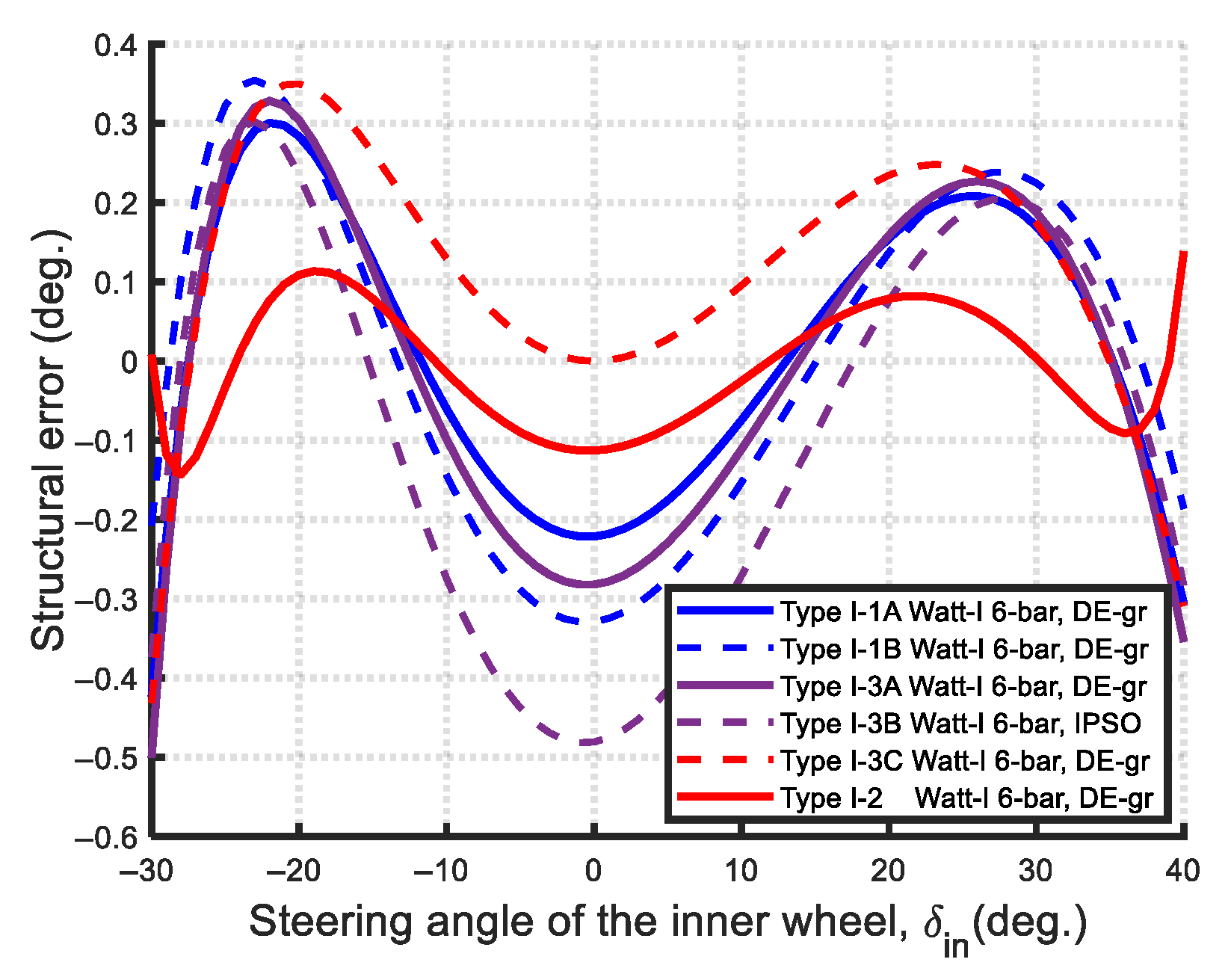
- Ackermann-like Watt-I mechanisms (equal-length steering links, Non-Grashof): The optimal Ackermann-like Watt-I six-bar steering mechanisms—specifically, Type I-1A, Type I-3A, Type I-3C, Type II-1A, and Type II-3A—all consisted of Non-Grashof four-bar linkages with equal-length steering links , a similar characteristic to that of the Ackermann steering mechanism. Notably, all these optimal designs were synthesized using the DE-gr method.
- (2)
- Non-Ackermann-like Watt-I mechanisms (unequal-length steering links, Grashof/Non-Grashof): The Non-Ackermann-like Watt-I six-bar mechanisms—including Type I-1B, Type I-2, Type I-3B, Type II-1B, Type II-2, and Type II-3B—feature unequal-length links . Among these, the constituent four-bar linkages in Type I-1B, I-3B, II-1B, and II-3B exhibit Non-Grashof mechanisms, while in Type I-2 and II-2 are Grashof four-bar linkages. The presence of Grashof mechanisms in Non-Ackermann-like Watt-I mechanisms is reported here for the first time.
- (3)
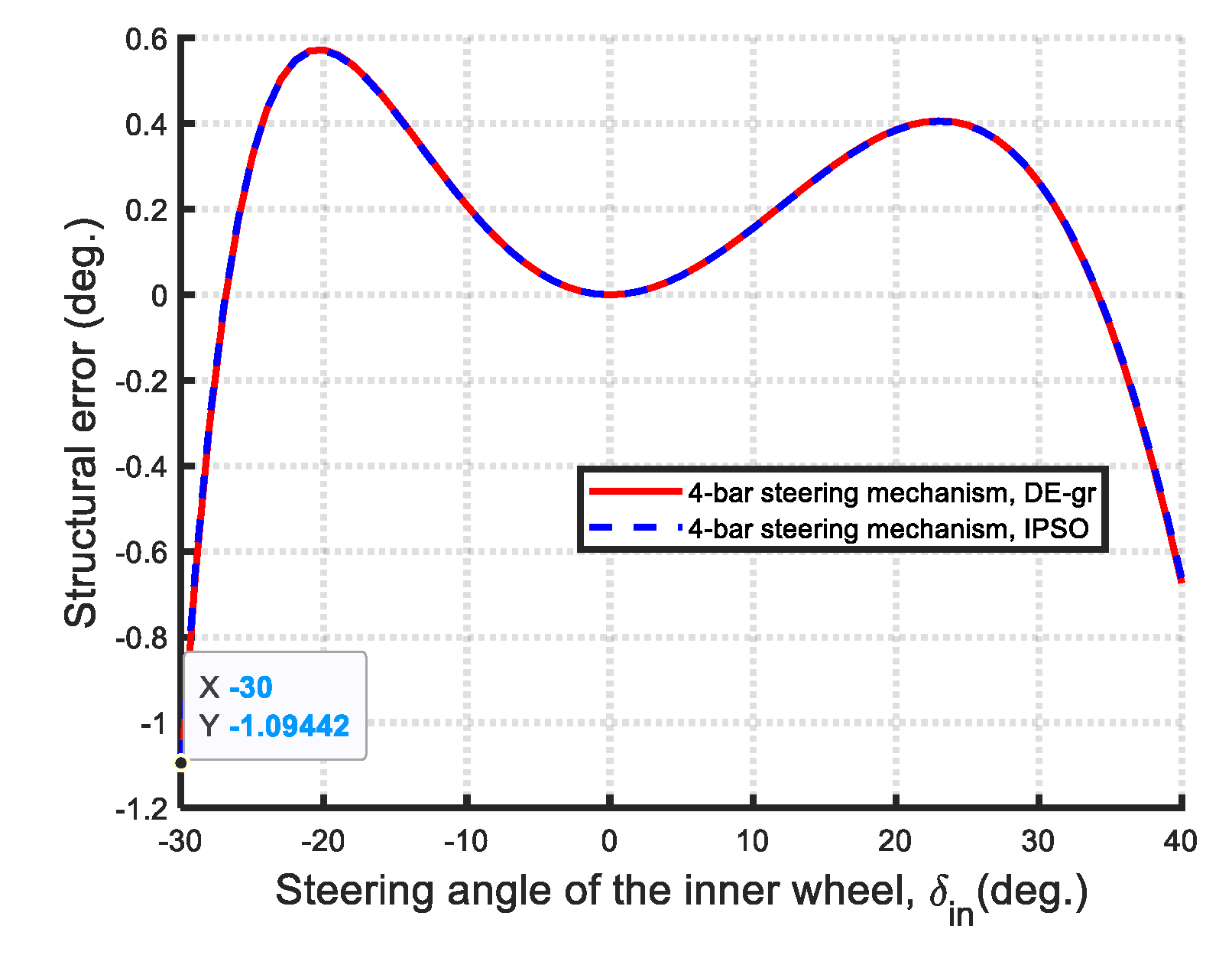
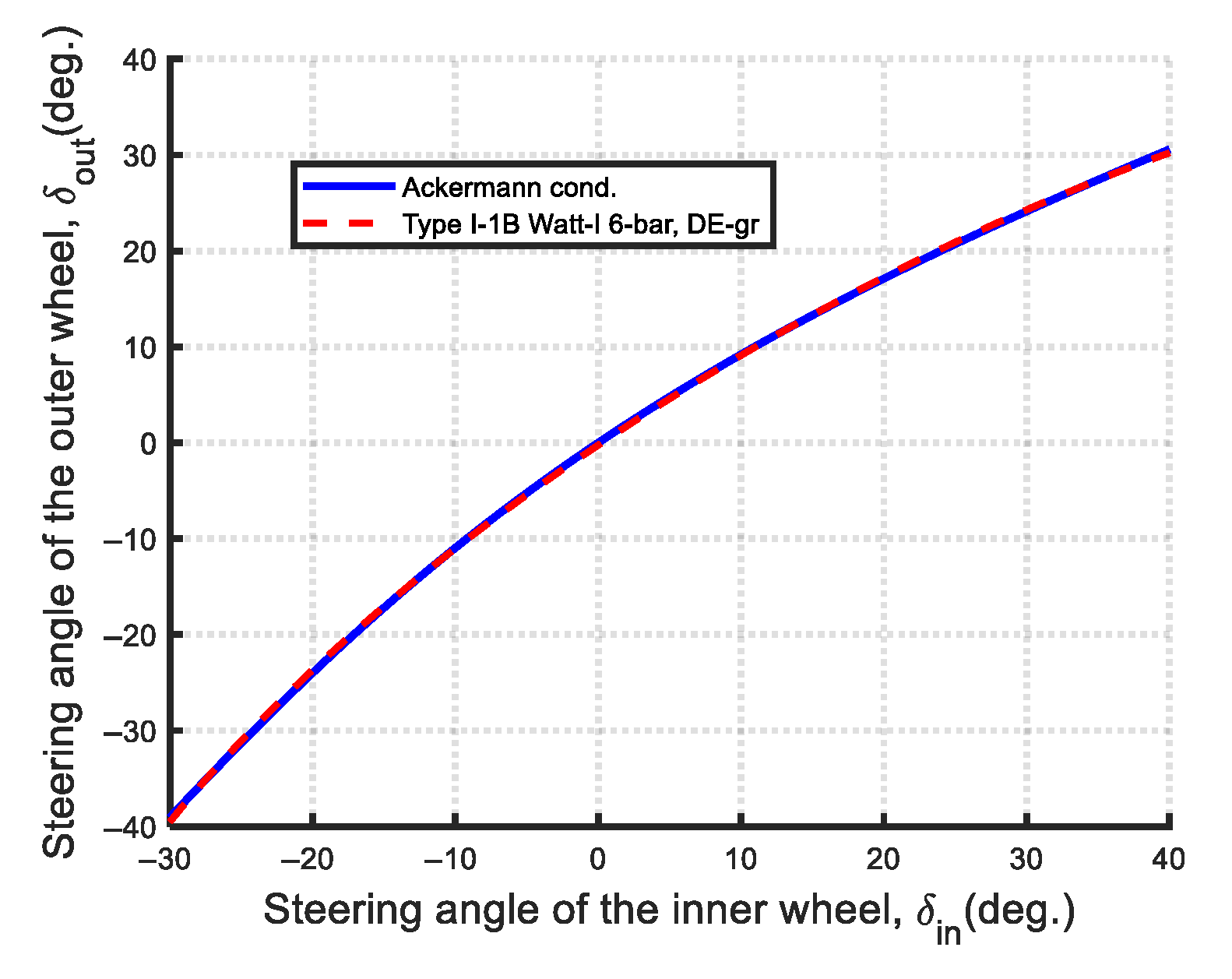
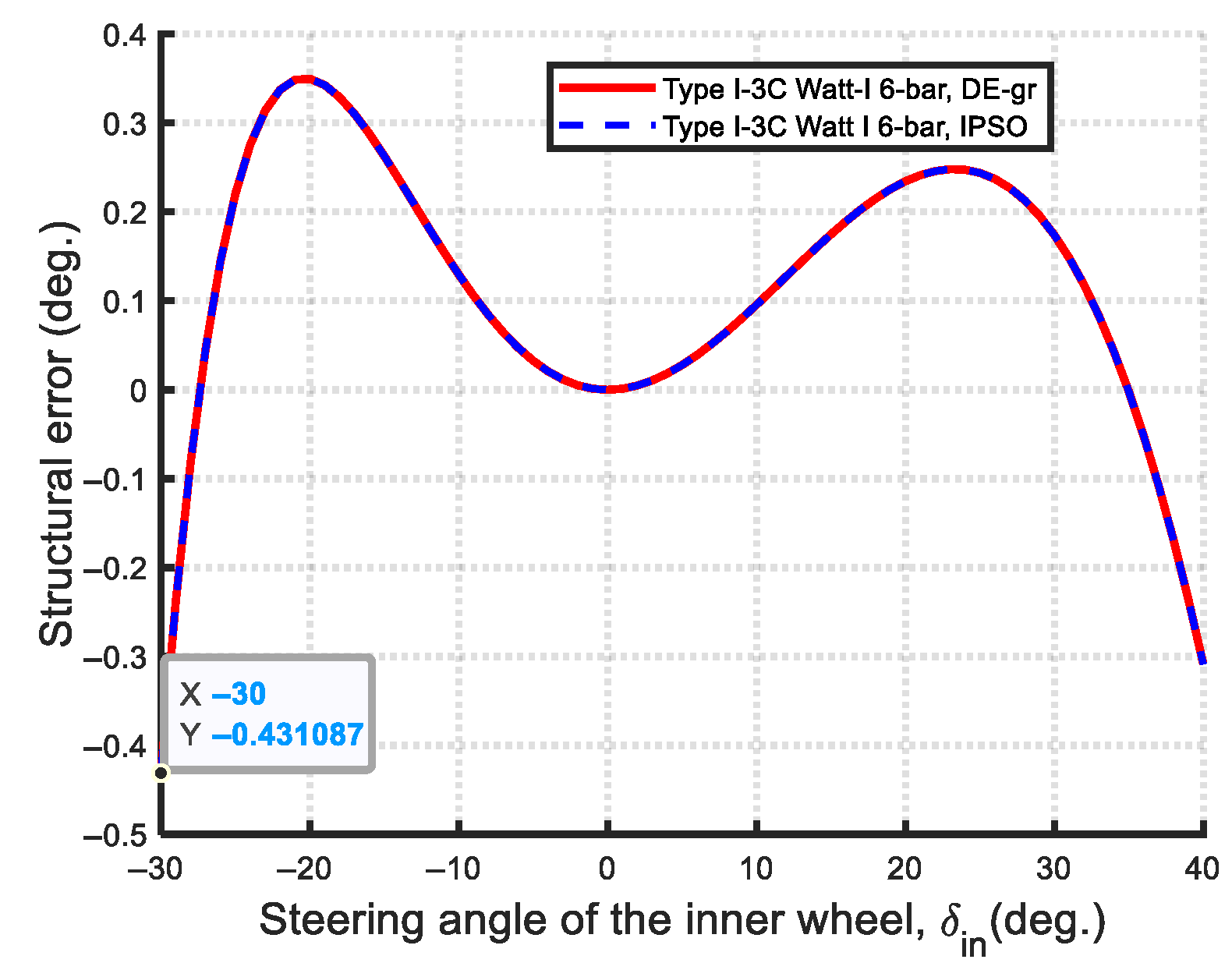
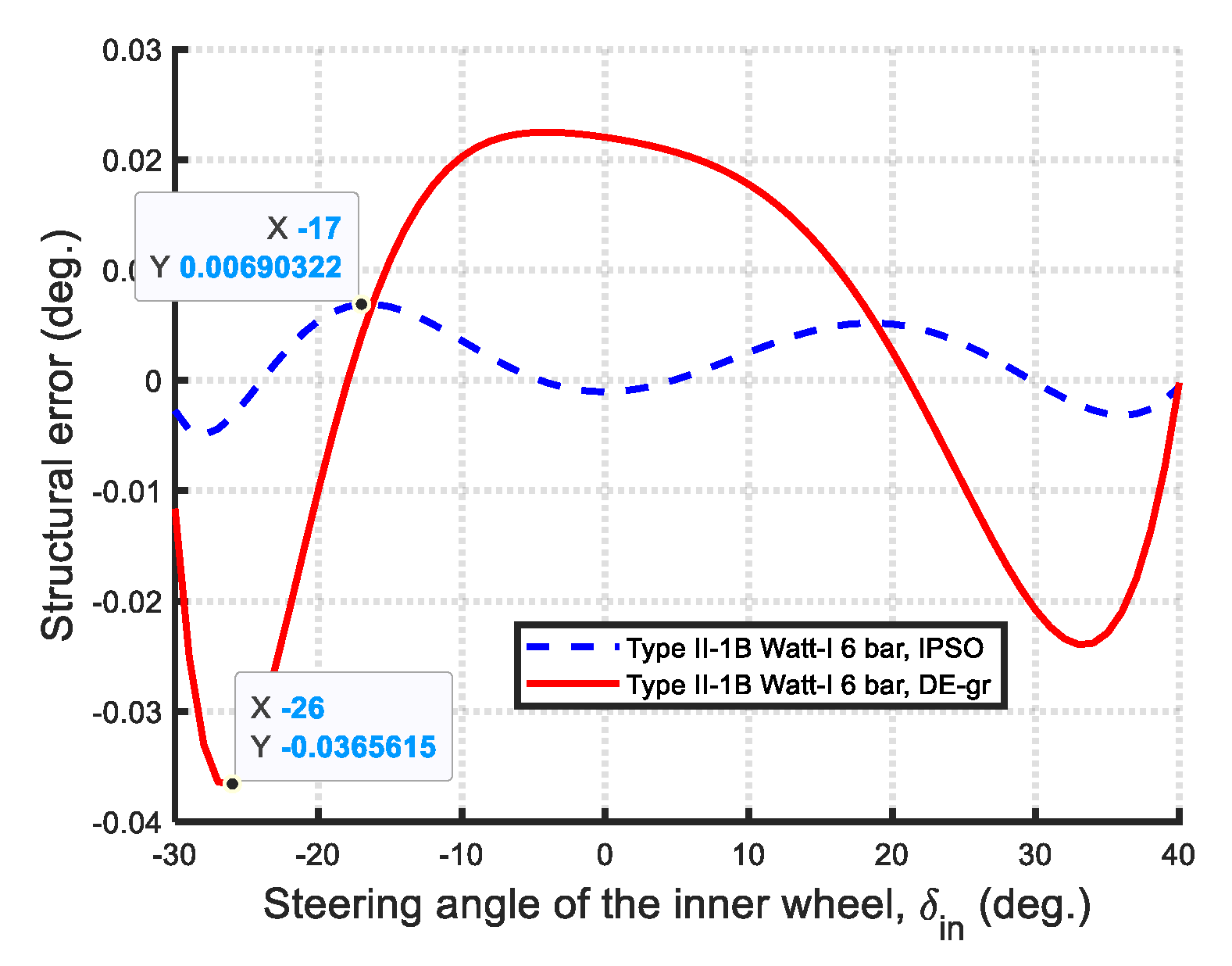
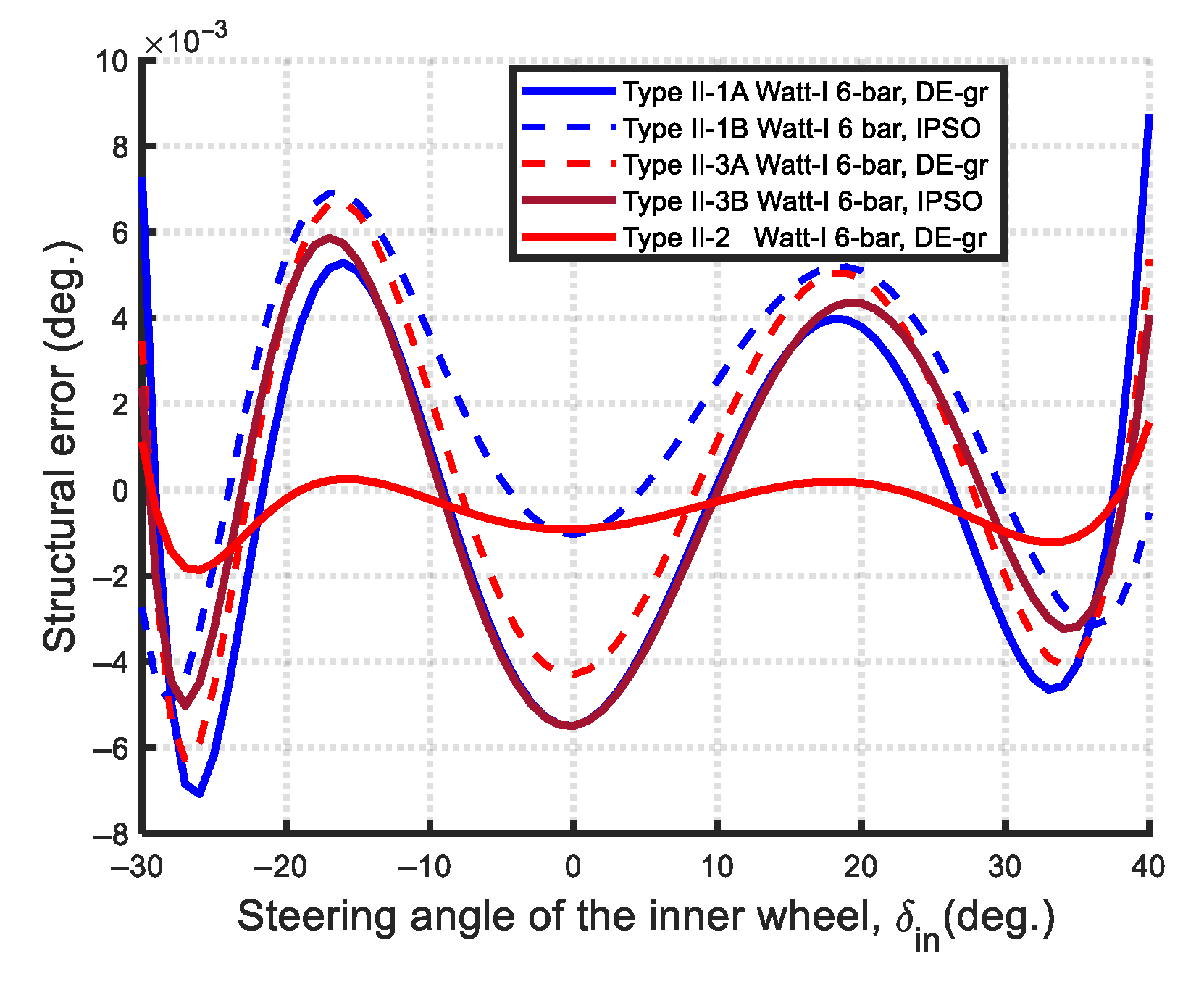
- Steering accuracy (Min-Max structural error): In terms of steering accuracy, all eleven Watt-I six-bar mechanisms outperform the Ackermann mechanism based on the Min-Max structural error metric. As shown in Figure 67, the optimal Type II-2 mechanism achieves a remarkably low steering error of 0.0019, which is two orders of magnitude lower than that of the Type I-2 mechanism (0.1431), and approximately 1% of its value—demonstrating near-perfect satisfaction of the Ackermann condition.
- (4)
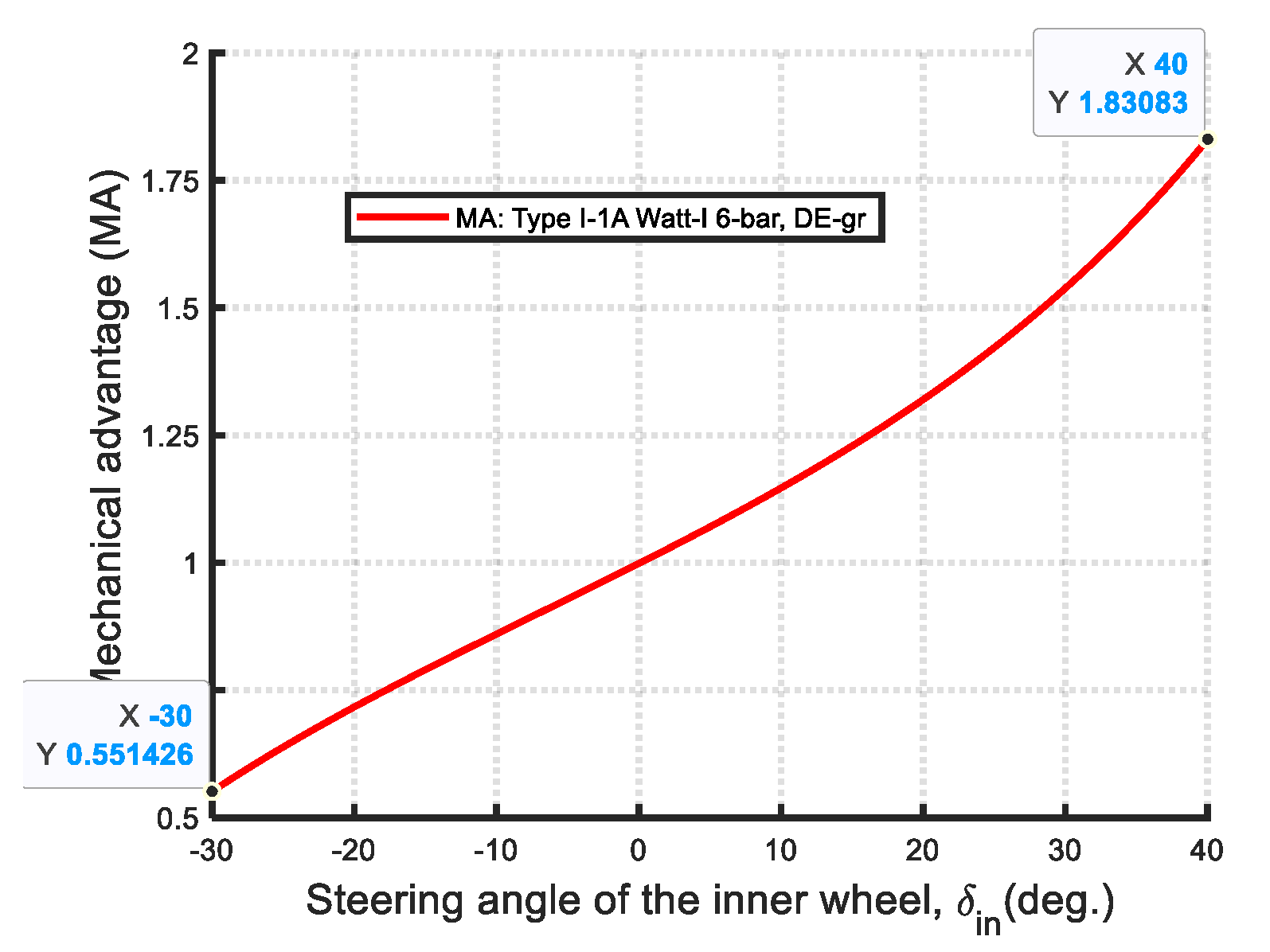
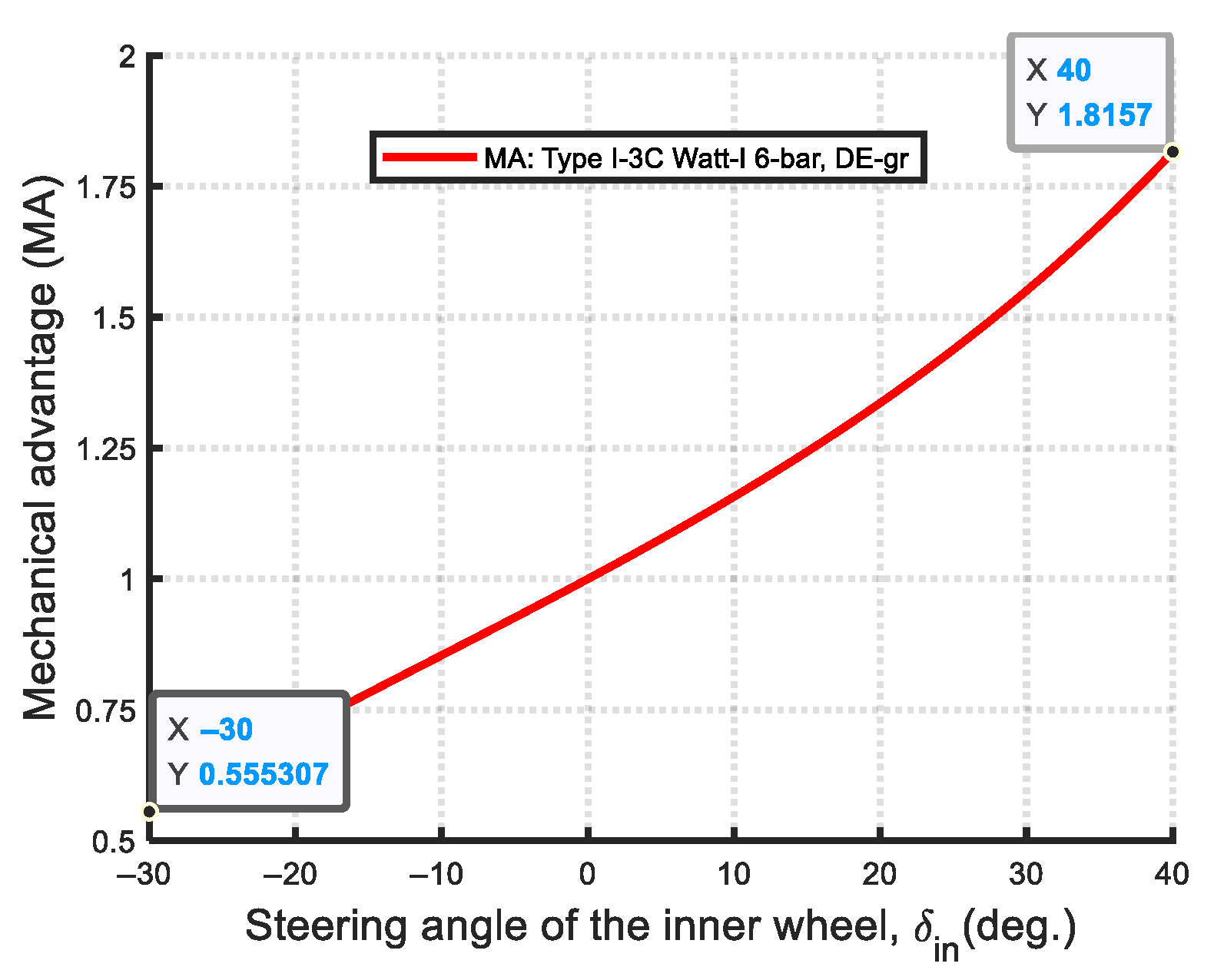
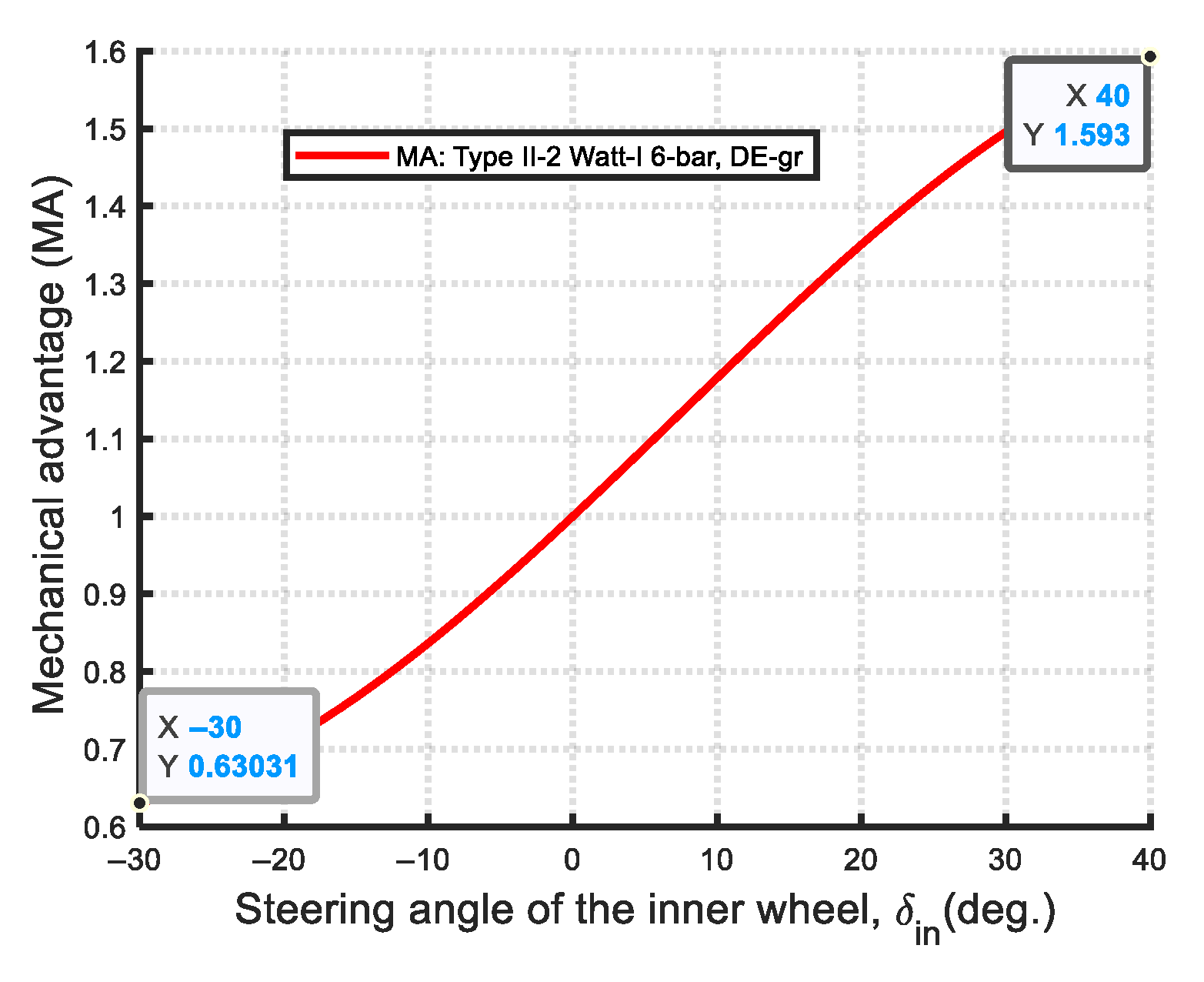
- Transmission efficiency (mechanical advantage): The maximum mechanical advantage (MAmax) serves as an indicator of transmission efficiency. The Ackermann steering mechanism exhibits the highest MAmax among all synthesis cases, but also the lowest MAmin, indicating greater variation and less uniform efficiency. As shown in Figure 68, the MA values across all mechanisms are comparable within the steering range of [−23°, 25°]. However, in the interval of [−30°, −23°], the Watt-I six-bar mechanisms exhibit higher MA values than the Ackermann mechanism. Conversely, in the [25°, 40°] range, the Ackermann mechanism demonstrates notably higher MA values. Notably, within the [35°, 40°] interval, the MA values of Type I-2 decline sharply, reaching a minimum of 1.2.
- (5)
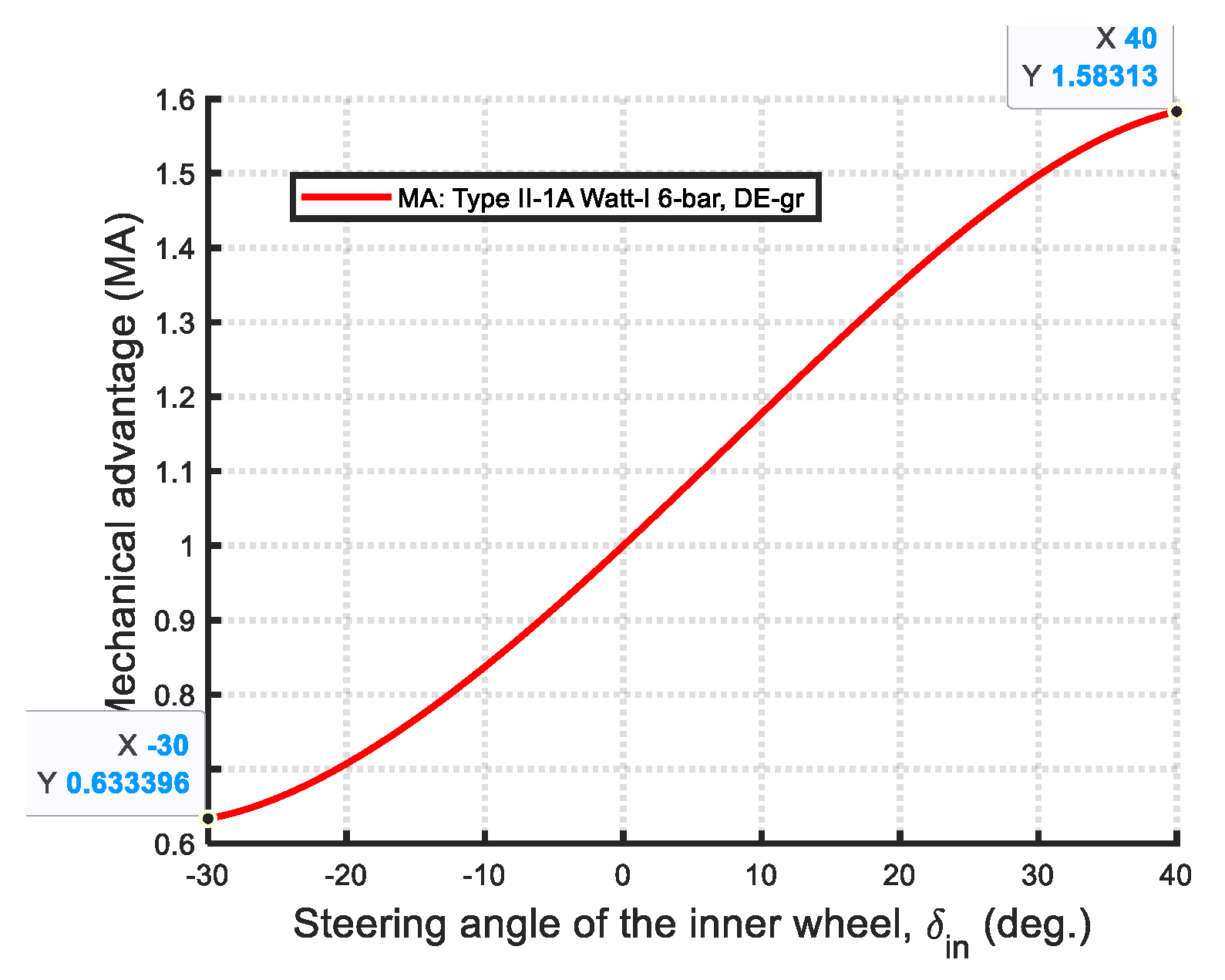
- Comparison between Type I and Type II Watt-I mechanisms: Among the Watt-I six-bar mechanisms, Type I designs generally achieve higher maximum mechanical advantage (MAmax) values but lower minimum mechanical advantage (MAmin) values compared to Type II designs. The Type I-3A mechanism demonstrates the highest MAmax (1.8729), but also the lowest MAmin (0.5389). In contrast, the Type II-1A mechanism exhibits the lowest MAmax (1.5831) while achieving the highest MAmin (0.6334), indicating a more consistent mechanical efficiency. With the exception of the Type I-2 mechanism, all Type I designs exceed Type II designs in terms of MAmax, but fall behind in MAmin.
- (6)
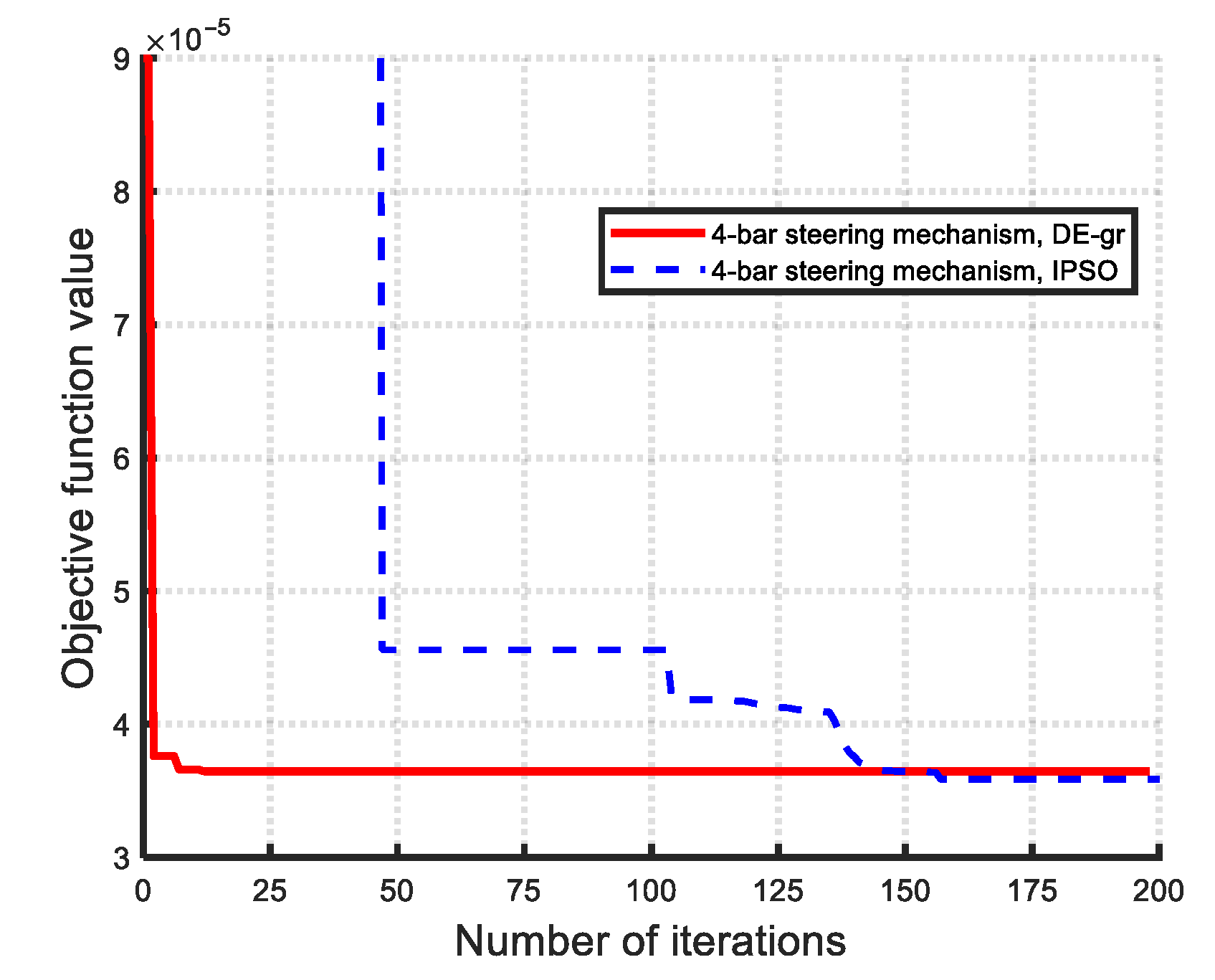
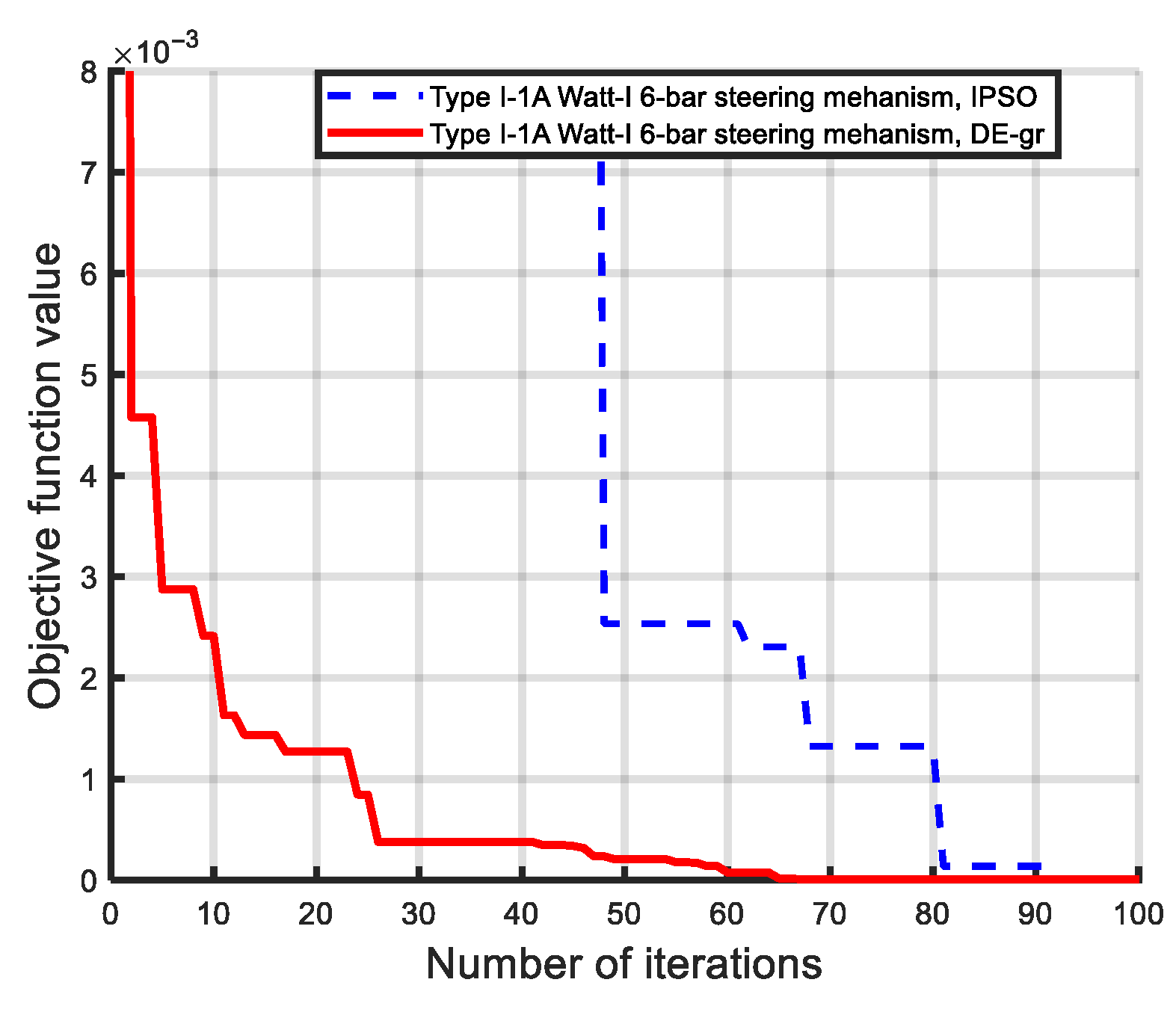
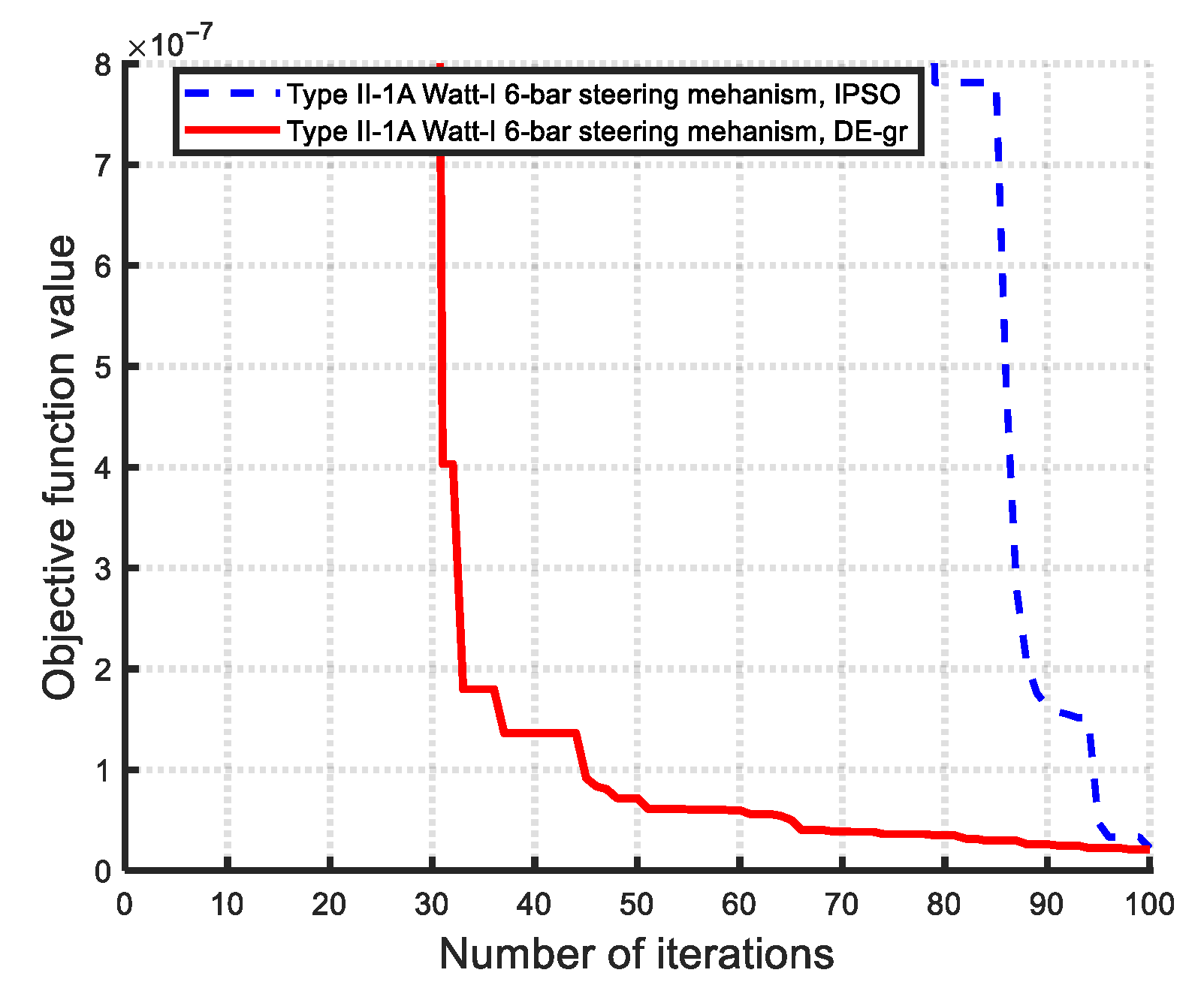
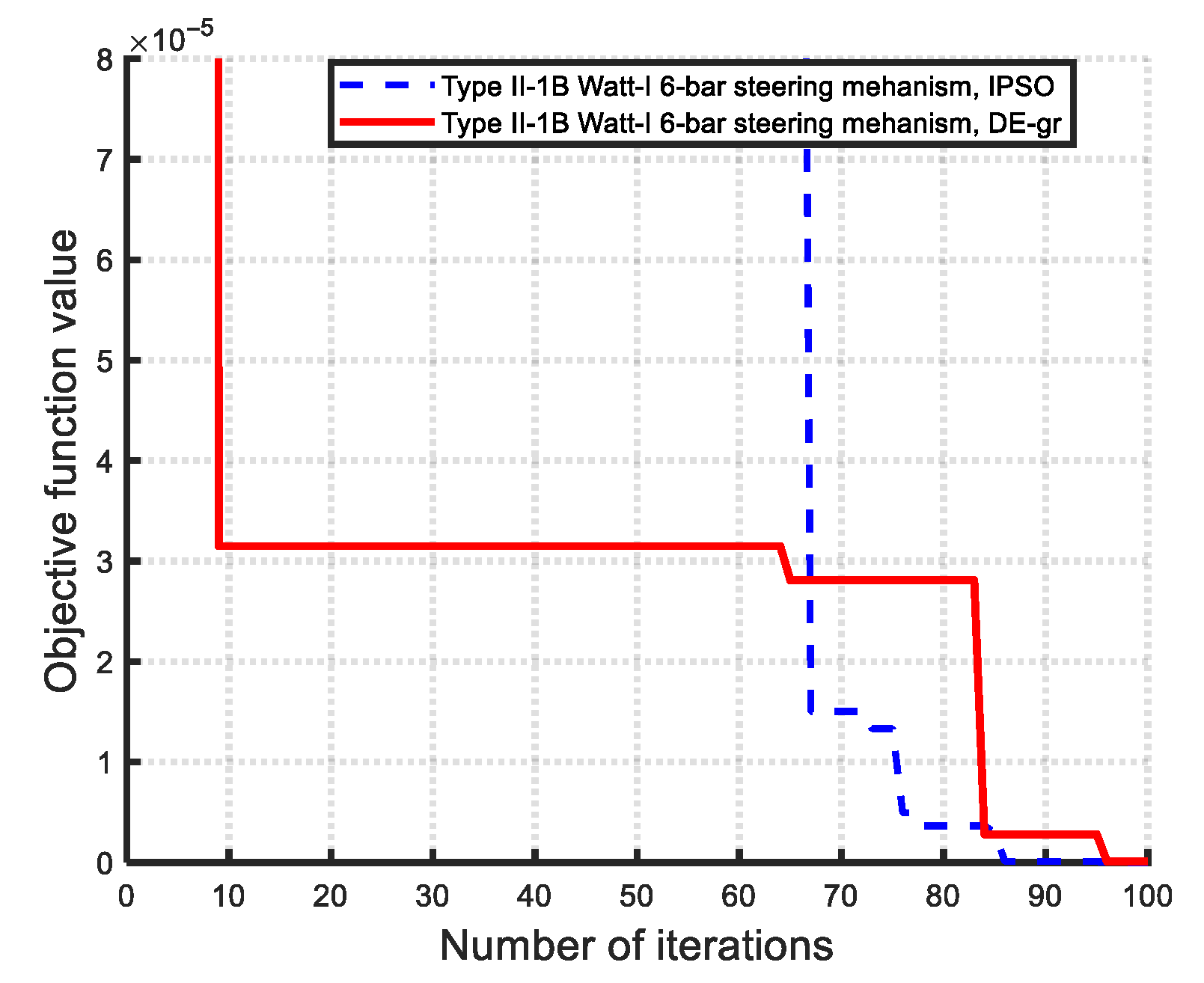
- Comparison of optimization methods (DE-gr vs. IPSO): Both DE-gr and IPSO methods proved effective in achieving optimal solutions. For the Ackermann steering synthesis, which involves two design variables, IPSO performed slightly better. However, for the more complex Watt-I six-bar mechanisms—featuring up to six design variables—DE-gr demonstrated superior efficiency and robustness. For a fair comparison of convergence efficiency and precision between the two employed algorithms, the population size (Np) was initially set to a smaller, consistent value (Np = 10 or 20), such as Np = 10 for Type I-3 and II-3 six-bar mechanisms and Np = 20 for Type I-2 and II-2 six-bar mechanisms. However, in Type I-1 and II-1 six-bar mechanisms, DE-gr successfully converged with Np = 10, while IPSO required Np = 20 to achieve feasible solutions. This demonstrates DE-gr’s greater robustness and convergence efficiency with smaller population sizes. Specifically, DE-gr outperformed IPSO in seven out of eleven Watt-I synthesis cases, while IPSO prevailed in three cases, and one case (Type I-3C, two design variables) resulted in a tie. The enhanced performance of the DE-gr method is primarily due to its efficient search strategy and the application of golden ratio-based crossover (0.618) and mutation (0.382) rates, which improve convergence precision.
7. Conclusions
- (1)
- Transmission Efficiency: The mechanical advantage (MA) is considered an indicator of transmission efficiency. A higher maximum mechanical advantage (MAmax) corresponds to greater transmission efficiency. The optimal Ackermann steering mechanism exhibits the highest MAmax among all cases but the lowest minimum mechanical advantage (MAmin), indicating less consistent efficiency compared to the Watt-I six-bar steering mechanisms. Furthermore, in Watt-I six-bar steering mechanism design, with the exception of the Type I-2 design, all Type I designs exceed Type II designs in terms of MAmax, yet fell behind in MAmin, indicating that Type II designs have a more consistent mechanical efficiency.
- (2)
- Steering Accuracy: The maximum structural error was used to evaluate steering accuracy. All eleven optimized Watt-I six-bar mechanisms outperform the Ackermann mechanism in this regard. Among them, the Type II designs are notably more accurate than the Type I variants. Specifically, the optimal Type II-2 mechanism achieves an exceptionally low maximum steering error of 0.00149, indicating near-perfect adherence to the Ackermann condition—superior even to the results reported in previous studies on central-lever steering mechanisms.
- (3)
- Novel Linkage Characteristics: Both the optimal Type I-2 and Type II-2 Watt-I six-bar steering mechanisms comprise two symmetric Grashof four-bar linkages with inclined angle β = 0 and unequal-length steering links , and the initial positions of intermediate steering link 4 lies along the longitudinal axis of the vehicle: or . These features of Grashof four-bar linkages within Watt-I six-bar steering mechanisms have not been reported in the previous literature and thus represent a key novel finding of this study.
- (4)
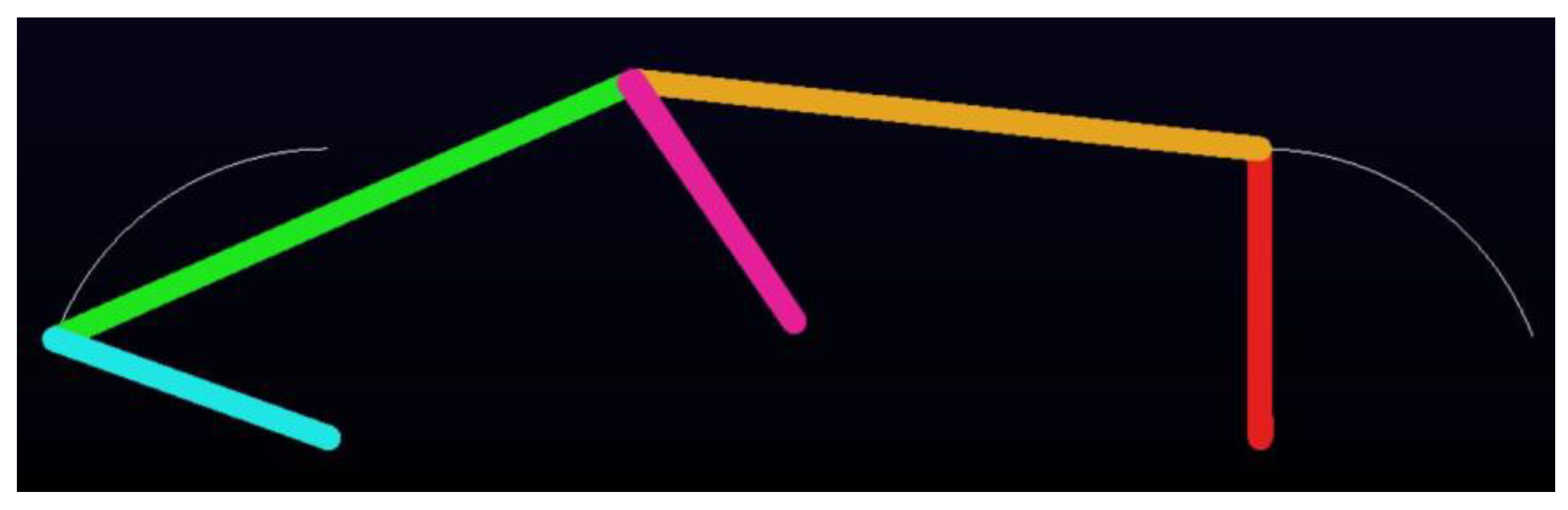
- Practical Trade-Offs: Although Watt-I six-bar steering mechanisms are more complex and costly to manufacture and maintain than the Ackermann mechanism, they offer significantly improved steering accuracy and vehicle maneuverability. When high precision is required and their cost is acceptable, they are recommended for front-wheel-drive vehicles or wheeled mobile robots. Furthermore, considering both steering accuracy and mechanical advantage, the optimal Type I-2 (Figure 5 and Figure 36) and optimal Type II variant designs are preferred for these applications. Among these, Type II-2 designs (Figure 8 and Figure 60) are particularly recommended due to their simple, symmetric, initial configuration with , and superior steering accuracy.
- (5)
- Kinematic Simulation: All optimized steering mechanisms were fully kinematically simulated using the multi-body dynamics analysis software ADAMS v2015 to visualize and eliminate improper configurations, validating the accuracy and feasibility of the steering motion.
- (6)
- Algorithmic Performance: Both the DE-gr and IPSO methods proved to be effective, easily implementable optimization methods with high convergence efficiency for the dimensional synthesis of linkage-type steering mechanisms. Across all twelve optimization cases, both algorithms achieved high-precision solutions within 100 or 200 iterations when using a population size of 10 (for Type I-3 and II-3 designs) or 20 (for Type I-2 and II-2 designs). Notably, in Type I-1 and II-1 designs, DE-gr consistently converged with Np = 10, while IPSO required Np = 20, highlighting DE-gr’s superior robustness with smaller populations. Leveraging golden ratio-based crossover and mutation rates (0.618:0.382), DE-gr also demonstrated faster convergence and higher solution accuracy. Overall, DE-gr outperformed IPSO in seven cases, IPSO prevailed in four, and one case was a tie—indicating a slight overall advantage for DE-gr.
- (7)
- Future Works: The linkage-type steering mechanisms synthesized by incorporating factors such as the limitations of the maximum transmission angle, minimum turning radius, and mechanical advantage into the multi-objective function—using the metaheuristic optimization methods DE-gr and IPSO—will be the focus of future work. Both optimization algorithms are also well-suited to more complex synthesis tasks, including the dimensional synthesis of eight-bar steering mechanisms for road vehicles, complex multi-link prosthetic devices, and multi-link walking robots for path generation.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Paul, B. A reassessment of Grashof’s criterion. J. Mech. Des. 1979, 101, 515–518. [Google Scholar] [CrossRef]
- Simionescu, P.A.; Beale, D. Optimum synthesis of the four-bar function generator in its symmetric embodiment: The Ackermann steering linkage. Mech. Mach. Theory 2002, 37, 1487–1504. [Google Scholar] [CrossRef]
- Emura, T.; Arakawa, A. A new steering mechanism using noncircular gears. JSME Int. J. Ser. 3 Vib. Control Eng. Eng. Ind. 1992, 35, 604–610. [Google Scholar] [CrossRef][Green Version]
- Zhao, S.; Zhao, J.S.; Feng, Z.J. Design of a pair of noncircular gears meeting Ackermann steering principle. In Proceedings of the 2011 International Conference on Consumer Electronics, Communications and Networks (CECNet), Xianning, China, 16–18 April 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 217–221. [Google Scholar]
- Carcaterra, A.; D’Ambrogio, A. Function generating differential mechanism for an exact solution of the steering problem. Mech. Mach. Theory 1998, 33, 535–549. [Google Scholar] [CrossRef]
- Chen, Z.F.; Xie, X.L.; Gao, F.; Liu, Z.Y.; Li, Y.Y. Pure rolling steering system design and research for wheeled mobile robot. J. Phys. Conf. Ser. 2019, 1345, 042071. [Google Scholar] [CrossRef]
- Simionescu, P.A.; Smith, M.R.; Tempea, I. Synthesis and analysis of the two-loop translational input steering mechanism. Mech. Mach. Theory 2000, 35, 927–943. [Google Scholar] [CrossRef]
- De-Juan, A.; Sancibrian, R.; Viadero, F. Optimal synthesis of function generation in steering linkages. Int. J. Automot. Technol. 2012, 13, 1033–1046. [Google Scholar] [CrossRef]
- Sleesongsom, S.; Bureerat, S. Multiobjective optimization of a steering linkage. J. Mech. Sci. Technol. 2016, 30, 3681–3691. [Google Scholar] [CrossRef]
- Wolfe, W.A. Analytical design of an Ackermann steering mechanism. J. Eng. Ind. 1959, 81, 10–13. [Google Scholar]
- Yao, J.; Angeles, J. The kinematic synthesis of steering mechanisms. Trans. Can. Soc. Mech. Eng. 2000, 24, 453–476. [Google Scholar] [CrossRef]
- Shariati, M.; Norouzi, M. Optimal synthesis of function generator of four-bar linkages based on distribution of precision points. Meccanica 2011, 46, 1007–1021. [Google Scholar] [CrossRef]
- Stoicescu, A.P. On the optimization of an Ackermann steering linkage. University POLITEHNICA of Bucharest. Sci. Bull. Ser. D Mech. Eng. 2013, 75, 59–70. [Google Scholar]
- Ettefagh, M.M.; Javash, M.S. Optimal synthesis of four-bar steering mechanism using AIS and genetic algorithms. J. Mech. Sci. Technol. 2014, 28, 2351–2362. [Google Scholar] [CrossRef]
- Zhao, J.S.; Liu, X.; Feng, Z.J.; Dai, J.S. Design of an Ackermann-type steering mechanism. Proc. IMechE Part C J. Mech. Eng. Sci. 2013, 227, 2549–2562. [Google Scholar] [CrossRef]
- Simionescu, P.A.; Smith, M.R. Initial estimates in the design of central-lever steering linkages. J. Mech. Des. 2002, 124, 646–651. [Google Scholar] [CrossRef]
- Pramanik, S. Kinematic synthesis of a six-member mechanism for automotive steering. J. Mech. Des. 2002, 124, 642–645. [Google Scholar] [CrossRef]
- Gautam, N.S.; Awadhiya, P. Kinematic Synthesis of a Modified Ackermann Steering Mechanism for Automotive; SAE Technicial Paper Series 2007-01-3636; SAE International: Warrendale, PA, USA, 2007. [Google Scholar]
- Soh, G.S.; McCarthy, J.M. The synthesis of six-bar linkages as constrained planar 3R chains. Mech. Mach. Theory 2008, 43, 160–170. [Google Scholar] [CrossRef]
- De-Juan, A.; Sancibrian, R. Optimal synthesis of steering mechanisms including transmission angles. In Proceedings of the EUCOMES 08: The Second European Conference on Mechanism Science 2008, Cassino, Italy, 17–20 September 2008; pp. 175–181. [Google Scholar]
- Peñuñuri, F.; Peón-Escalante, R.; Villanueva, C.; Pech-Oy, D. Synthesis of mechanisms for single and hybrid tasks using differential evolution. Mech. Mach. Theory 2011, 46, 1335–1349. [Google Scholar] [CrossRef]
- Pramanik, S.; Ingle, R.B.; Latey, A.A. Comparative study of steering mechanism for large wheelbase vehicles. Int. J. Veh. Struct. Syst. 2012, 4, 64–68. [Google Scholar] [CrossRef]
- Pramanik, S. Kinematic synthesis of a trailing six-member mechanism for automotive steering. Int. J. Automot. Eng. 2013, 3, 577–581. [Google Scholar]
- Wang, H.X.; Dai, E.H. Design on double axial steering mechanism of vehicles and research on its steering error properties. Appl. Mech. Mater. 2014, 528, 297–301. [Google Scholar] [CrossRef]
- Romero-Núñez, N.N.; Tuiran-Villalba, R.E. Optimization method of a six-bar steering mechanism formulated with natural coordinates. DYNA 2018, 85, 168–173. [Google Scholar] [CrossRef]
- Zhou, C.G.; Hua, T.; Wang, H.W.; Wang, X.Y. Design and error analysis of the linkage type steering mechanism for multiple wheel heavy vehicle. Adv. Intell. Syst. Res. 2019, 165, 219–225. [Google Scholar]
- Pramanik, S.; Thipse, S.S. Kinematic synthesis of central-lever steering mechanism for four wheel vehicles. Acta Polytech. 2020, 60, 252–258. [Google Scholar] [CrossRef]
- Romero-Nuñez, N.N.; Cuta, C.H.P.; Vieira, R.S.; Martins, D. Optimal dimensional synthesis of central-lever steering linkage using natural coordinates as design variables. In Proceedings of the 27th ABCM International Congress of Mechanical Engineering, Florianopolis, SC, Brazil, 4–8 December 2023. [Google Scholar]
- Pramanik, S. Minimization of structural error of the steering mechanism of an agricultural harvesting machine. In Advances in Manufacturing Engineering; Lecture Notes in Mechanical Engineering; Springer Nature: Singapore, 2023; pp. 427–435. [Google Scholar]
- Tuleshoy, A.; Tuleshoy, E.; Kuatova, M.; Kamal, A.; Kerimkuloy, D. The synthesis of a two-circuit steering mechanism of the Ackermann transport mobile robot. Preprints 2024. [Google Scholar] [CrossRef]
- Fahey, S.O.F.; Huston, D.R. A novel automotive steering linkage. J. Mech. Des. 1997, 119, 481–484. [Google Scholar] [CrossRef]
- Dooner, D.B. Function generation utilizing an eight-link mechanism and optimized non-circular gear elements with application to automotive steering. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2001, 215, 847–857. [Google Scholar] [CrossRef]
- Romero, N.; Flórez, E.; Mendoza, L. Optimization of a multi-link steering mechanism using a continuous genetic algorithm. J. Mech. Sci. Technol. 2017, 31, 3183–3188. [Google Scholar] [CrossRef]
- Kang, Y.-H.; Pang, D.-C.; Zeng, Y.-C. Optimal dimensional synthesis of Ackermann steering mechanisms for three-axle, six-wheeled vehicles. Appl. Sci. 2025, 15, 800. [Google Scholar] [CrossRef]
- Kang, Y.-H.; Lin, J.-W.; You, W.-C. Comparative study on the synthesis of path-generating four-bar linkages using metaheuristic optimization algorithms. Appl. Sci. 2022, 12, 7368. [Google Scholar] [CrossRef]
- Kang, Y.-H.; Huang, H.-C.; Yang, B.-Y. Optimal design and dynamic analysis of a spring-actuated cam-linkage mechanism in a vacuum circuit breaker. Machines 2023, 11, 150. [Google Scholar] [CrossRef]
- Yan, H.-S. Mechanisms: Theory and Applications; McGraw-Hill Education: New York, NY, USA, 2015. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Shi, Y.H.; Eberhart, R.C. A modified particle swarm optimizer. In Proceedings of the IEEE 1998 International Conference on Evolutionary Computation, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Ratnaweera, A.; Halgamuge, S.K.; Watson, H.C. Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients. IEEE Trans. Evol. Comput. 2004, 8, 240–255. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution- a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]


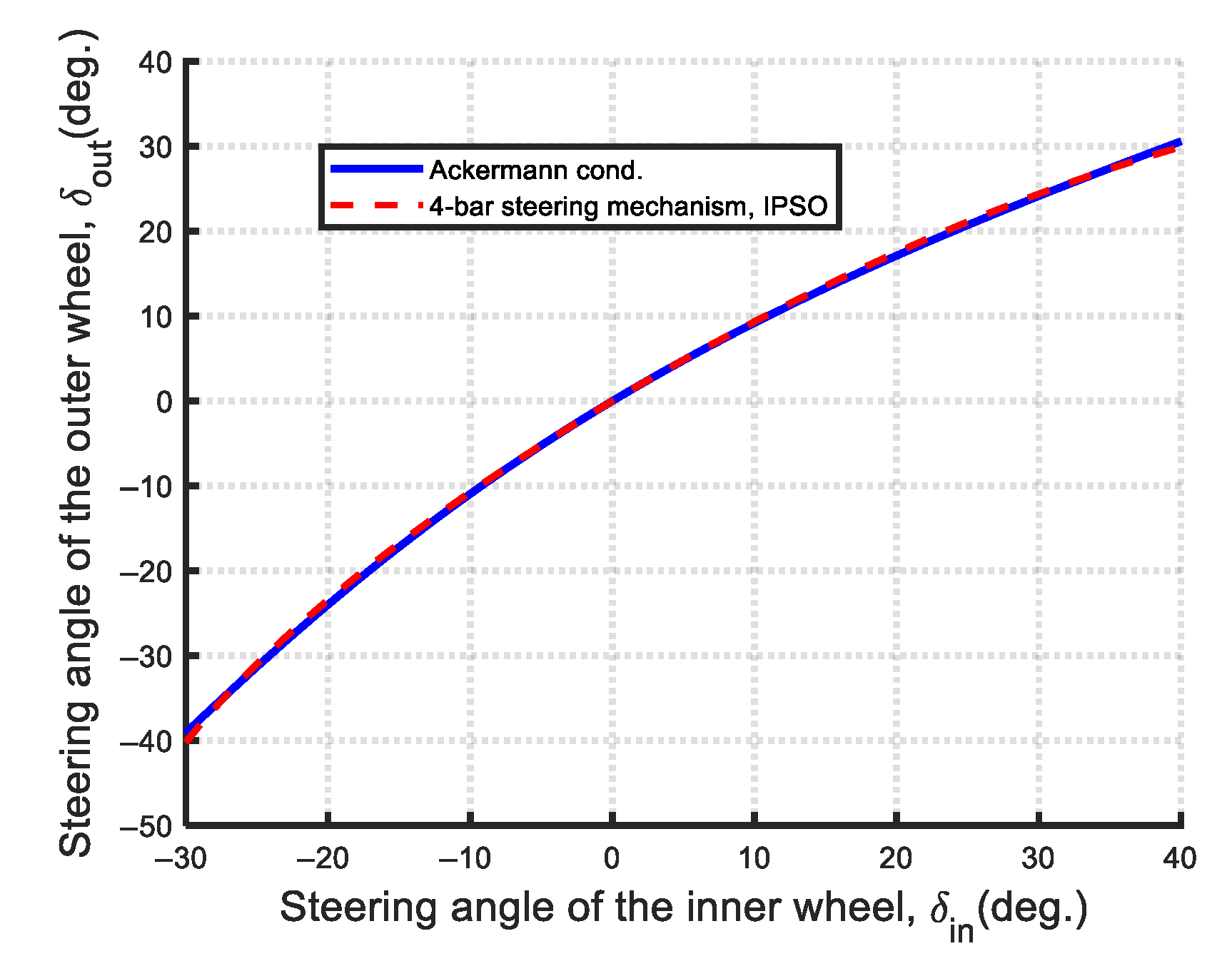
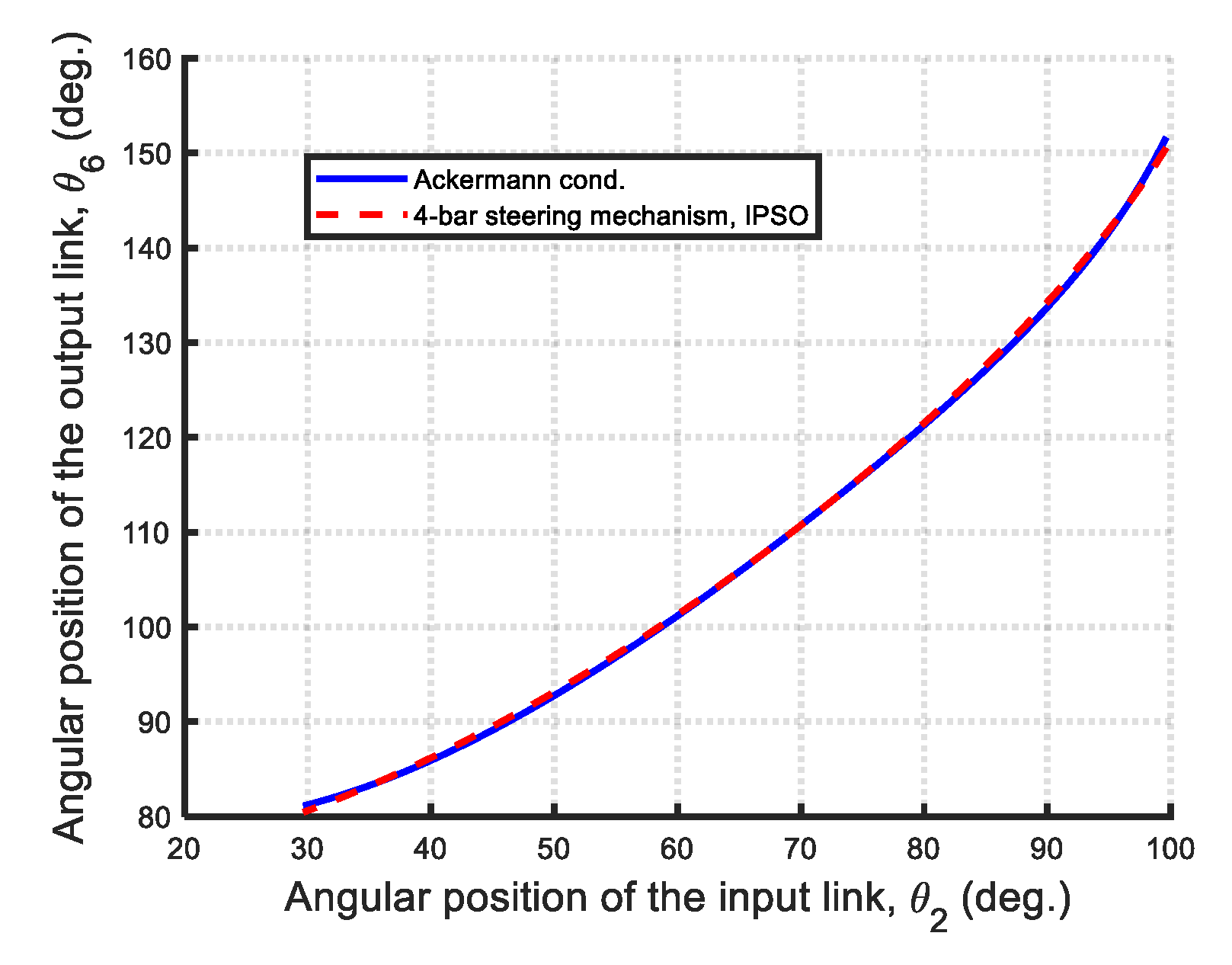
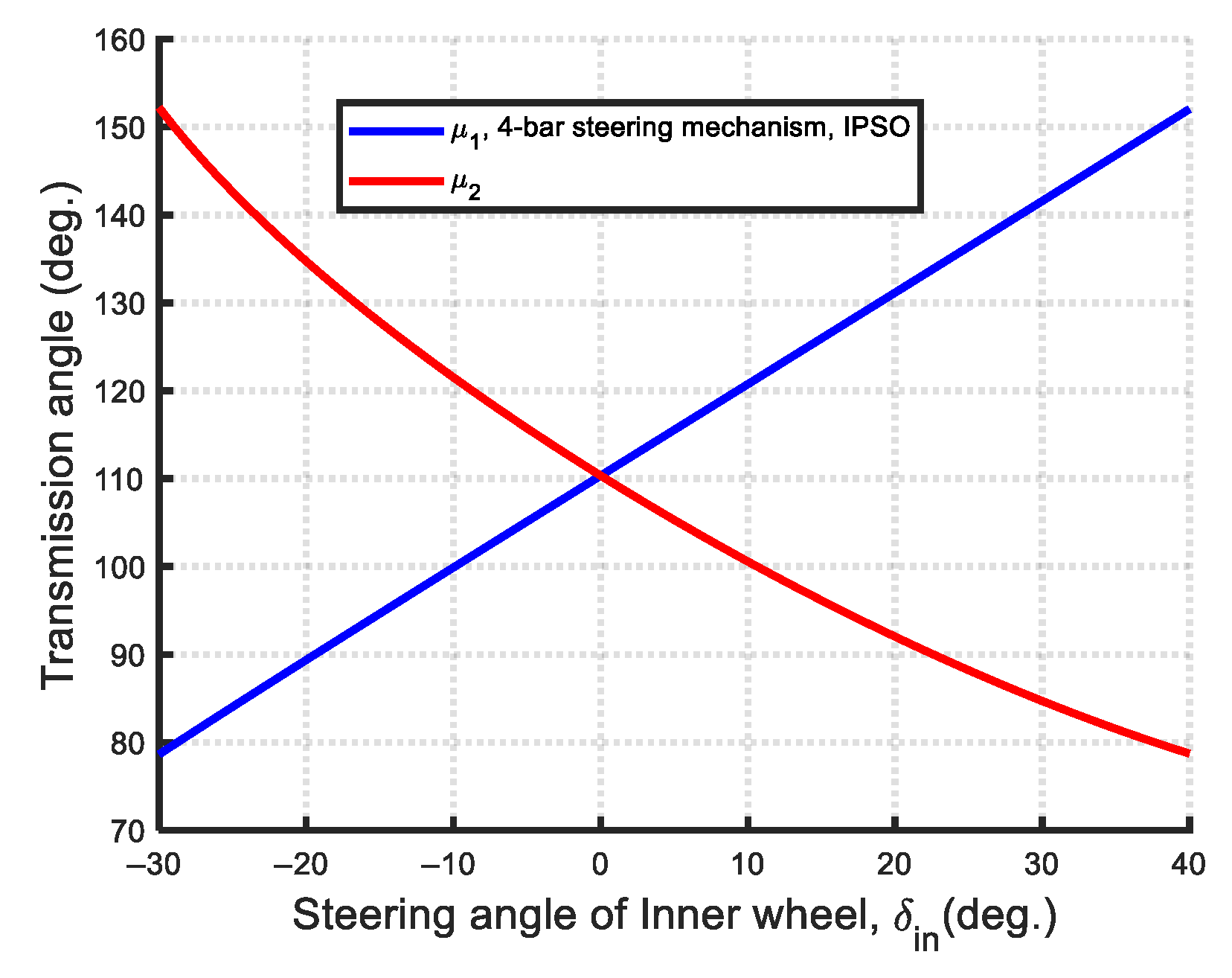

















| Type of the Watt-I Six-Bar Steering Mechanism | Variable Number | Design Vector | Geometry Conditions | |
|---|---|---|---|---|
| Type I-1 | Type I-1A | 5 | ||
| Type I-1B | 6 | |||
| Type I-2 | Type I-2 | 5 | ||
| Type I-3 | Type I-3A | 4 | ||
| Type I-3B | 5 | |||
| Type I-3C | 2 | |||
| Type II-1 | Type II-1A | 5 | ||
| Type II-1B | 6 | |||
| Type II-2 | Type II-2 | 5 | ||
| Type II-3 | Type II-3A | 4 | ||
| Type II-3B | 5 | |||
| Algorithm | DE-gr | IPSO |
|---|---|---|
| Population size (Np) | 10/20 | 10/20 |
| Iteration times | 100/200 | 100/200 |
| Experimental times | 100 | 100 |
| Mutation method | DE/best/1 DE/best/2 | -- |
| Mutation factor | 0.382 | -- |
| Crossover method | Exponential crossover | -- |
| Crossover rate (CR) | 0.618 | -- |
| Selection method | Competitive selection | -- |
| Learning factor ( , ) | -- | 0.5 |
| Inertia weighting (w) | -- | 0.4 |
| Obj. Fun | MAmax/MAmin | Min-Max Error | ||||||
|---|---|---|---|---|---|---|---|---|
| DE-gr | 3.646 × 10−5 | 1480.00 | 100.000 | 1410.9531 | 100.000 | 69.8039 | 2.0982/0.4738 | 1.1160 |
| IPSO | 3.590 × 10−5 | 1480.00 | 85.6320 | 1420.4602 | 85.1017 | 69.6564 | 2.0917/0.4756 | 1.0944 |
| Type I Watt-I Six-Bar Steering Mechanism | Geometric Relations/ Design Vector | Range of the Design Parameters (Angle) | The Constituent Four-Bar Linkage |
|---|---|---|---|
| Type I-1A Ackermann-like | Non-Grashof mechanism | ||
| Type I-1B Non-Ackermann-like | Non-Grashof mechanism | ||
| Type I-2 Non-Ackermann-like | Grashof mechanism | ||
| Type I-3A Ackermann-like | Non-Grashof mechanism | ||
| Type I-3B Non-Ackermann-like | Non-Grashof mechanism | ||
| Type I-3C Ackermann-like | Non-Grashof mechanism |
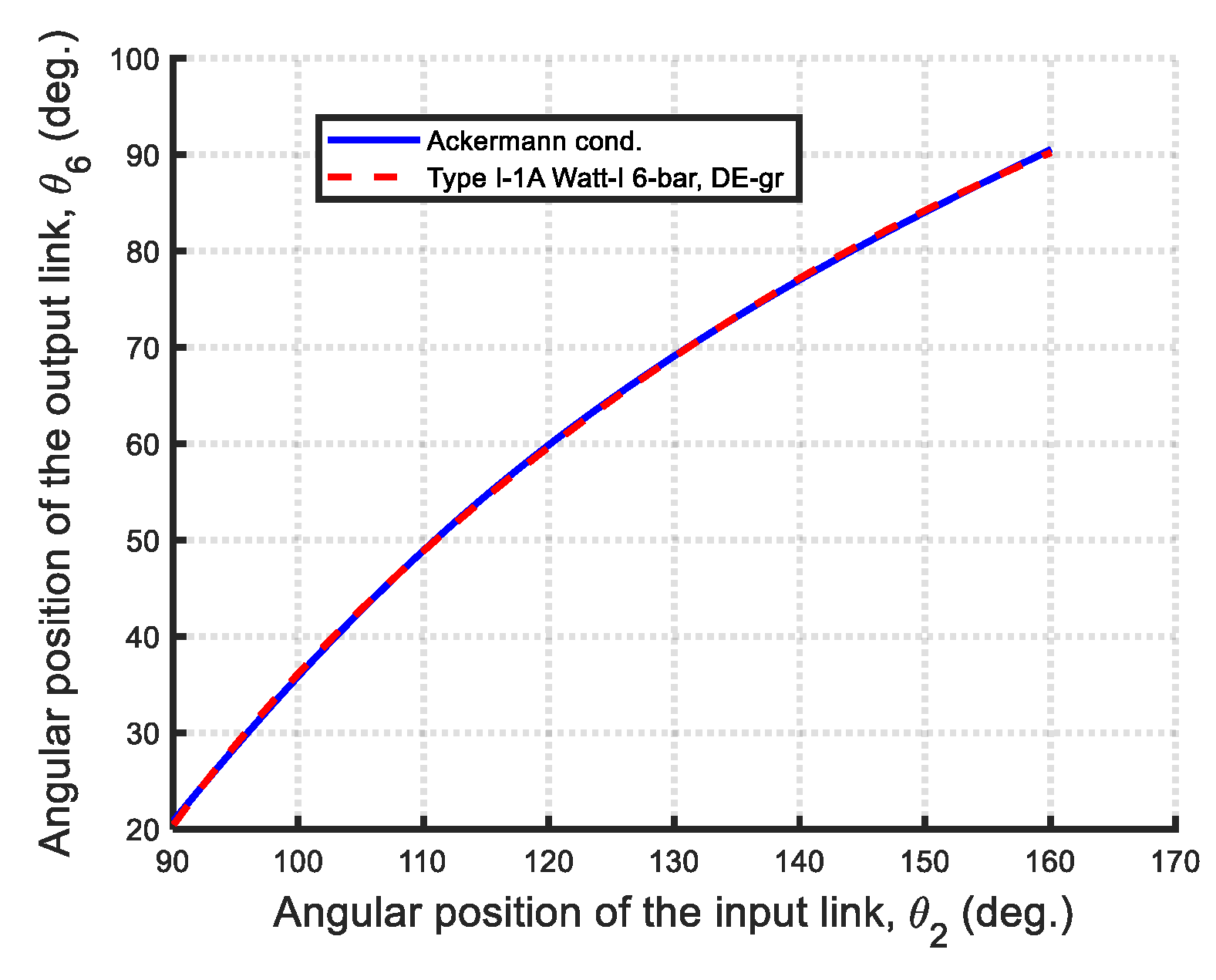
| Type I-1A: | |||||||||
| Obj. fun | Min-Max error | ||||||||
| DE-gr | 9.597 × 10−7 | 762.9638 | 461.8052 | 999.9605 | 461.8052 | 185.7788 | 0.8596 | 120.0609 | 0.4233 |
| IPSO | 1.47 × 10−5 | 771.6305 | 181.0549 | 845.3780 | 181.0549 | 218.6631 | 0.9378 | 113.9334 | 0.4690 |
| Type I-1B: | |||||||||
| Obj. fun | Min-Max error | ||||||||
| DE-gr | 1.400 × 10−5 | 798.3499 | 421.9384 | 995.2772 | 421.9719 | 299.6040 | 13.0402 | 123.3578 | 0.3544 |
| IPSO | 2.732 × 10−5 | 743.0465 | 405.5785 | 835.8964 | 406.3062 | −67.2164 | 38.7673 | 124.3703 | 0.4898 |
| Type I-2: | |||||||||
| Obj. fun | Min-Max error | ||||||||
| DE-gr | 1.749 × 10−6 | 753.6278 | 478.2386 | 999.8593 | 199.4626 | 142.6703 | 0.0000 | 122.5954 | 0.1431 |
| IPSO | 2.686 × 10−6 | 742.1067 | 305.8035 | 894.1713 | 135.7050 | 55.8785 | 0.0000 | 119.5292 | 0.1546 |
| Type I-3A: | |||||||||
| Obj. fun | Min-Max error | ||||||||
| DE-gr | 1.289 × 10−5 | 740.0000 | 400.5041 | 907.5244 | 400.5041 | 0.0000 | 10.0000 | 119.9686 | 0.5002 |
| IPSO | 9.951 × 10−5 | 740.0000 | 482.1574 | 957.7717 | 482.1574 | 0.0000 | 51.5706 | 90.6975 | 0.5219 |
| Type I-3B: | |||||||||
| Obj. fun | Min-Max error | ||||||||
| DE-gr | 1.252 × 10−5 | 740.000 | 298.7328 | 863.9833 | 350.9215 | 0.0000 | 10.0620 | 109.7300 | 0.5512 |
| IPSO | 2.172 × 10−5 | 740.000 | 324.0593 | 856.9544 | 346.4544 | 0.0000 | 16.1074 | 109.7300 | 0.4814 |
| Type I-3C: | |||||||||
| Obj. fun | Min-Max error | ||||||||
| DE-gr | 9.027 × 10−6 | 740.000 | 736.3713 | 1237.181 | 736.3713 | 0.0000 | −39.46 | 109.7300 | 0.4311 |
| IPSO | 9.027 × 10−6 | 740.000 | 736.3713 | 1237.181 | 736.3713 | 0.0000 | −39.46 | 109.7300 | 0.4311 |
| Type II Watt-I Six-Bar Steering Mechanism | Geometric Relations/ Design Vector | Range of the Design Parameters (Angle) | The Constituent Four-Bar Linkage |
|---|---|---|---|
| Type II-1A Ackermann-like | Non-Grashof mechanism | ||
| Type II-1B Non-Ackermann-like | Non-Grashof mechanism | ||
| Type II-2 Non-Ackermann-like | Grashof mechanism | ||
| Type II-3A Ackermann-like | Non-Grashof mechanism | ||
| Type II-3B Non-Ackermann-like | Non-Grashof mechanism |
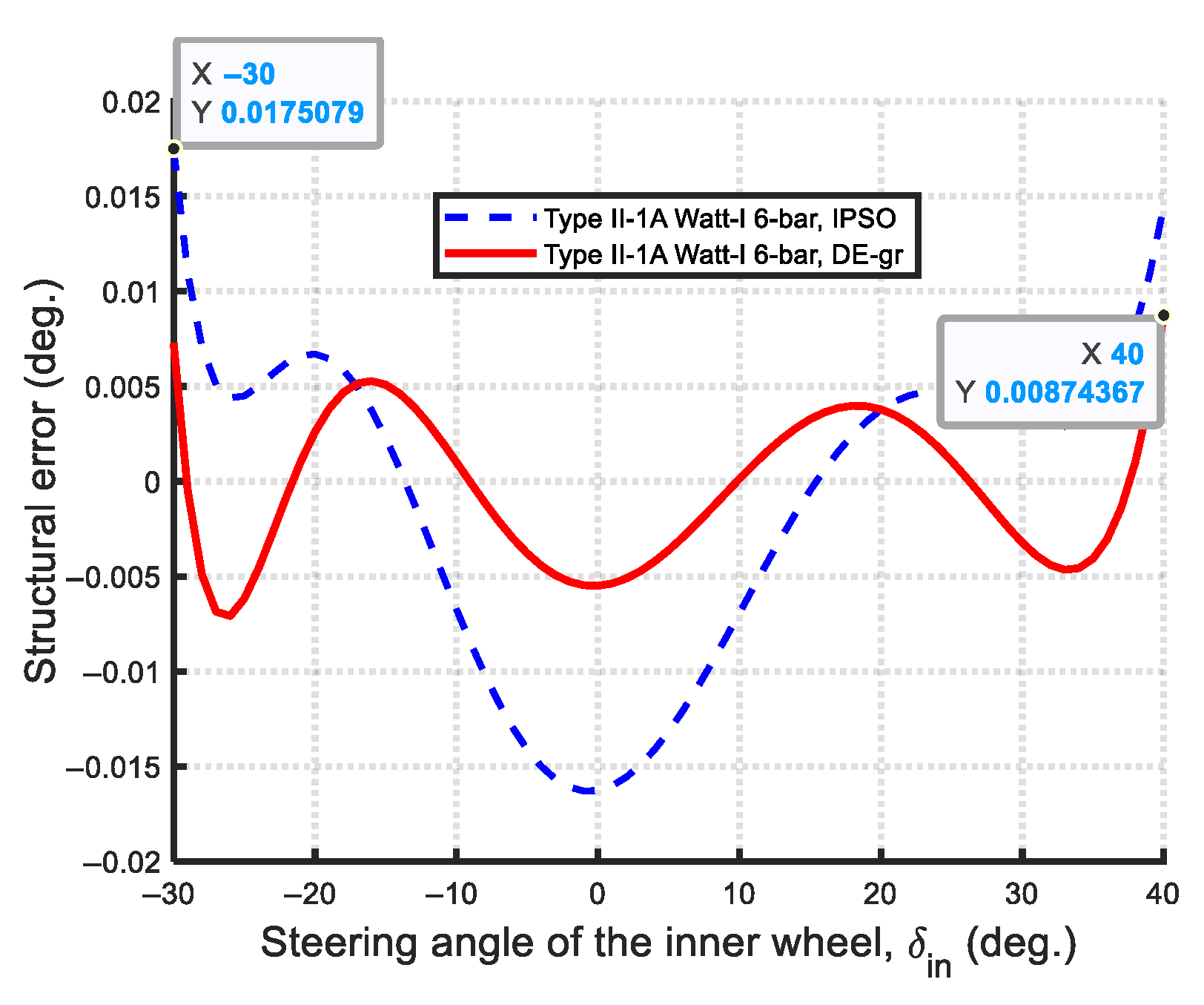
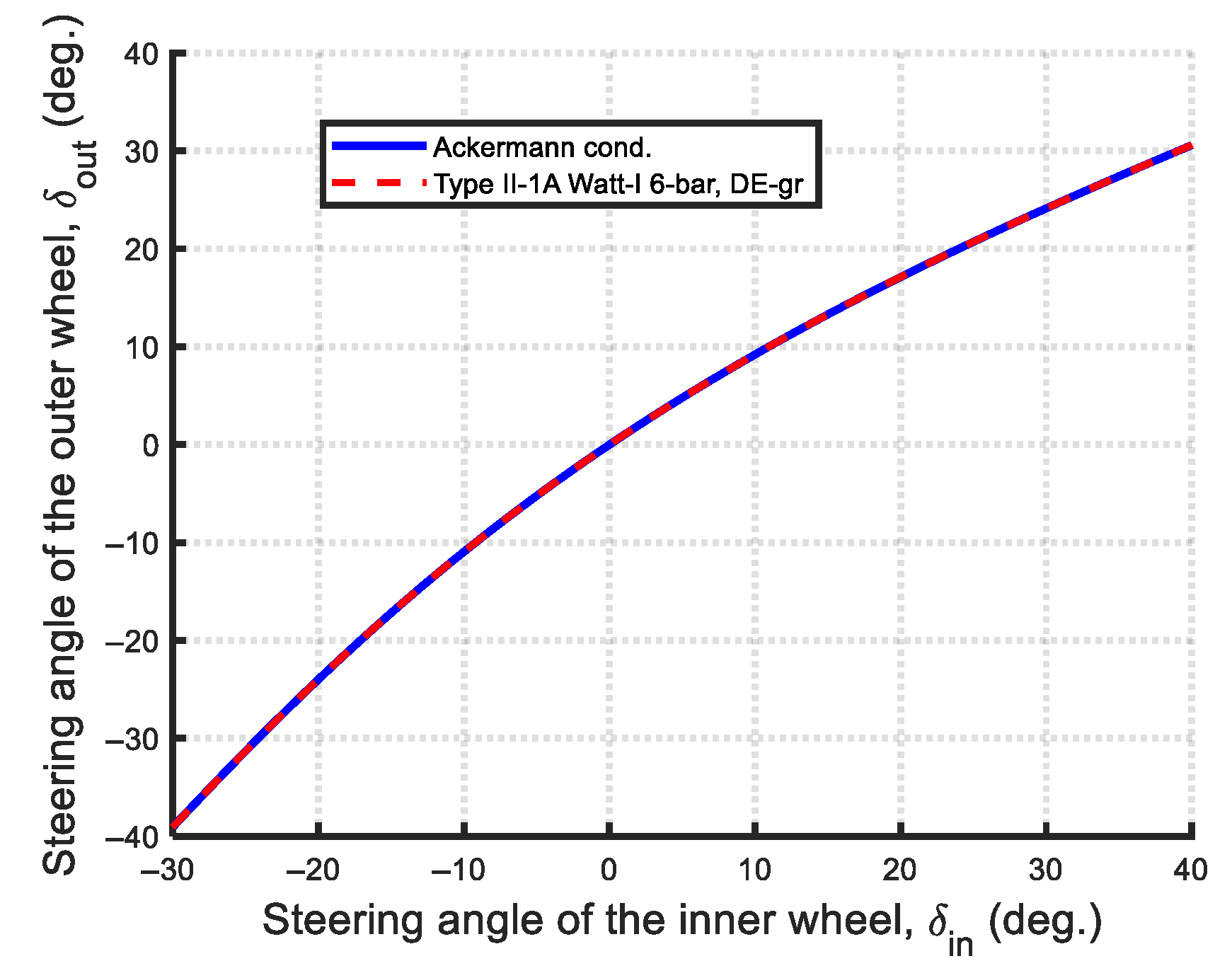
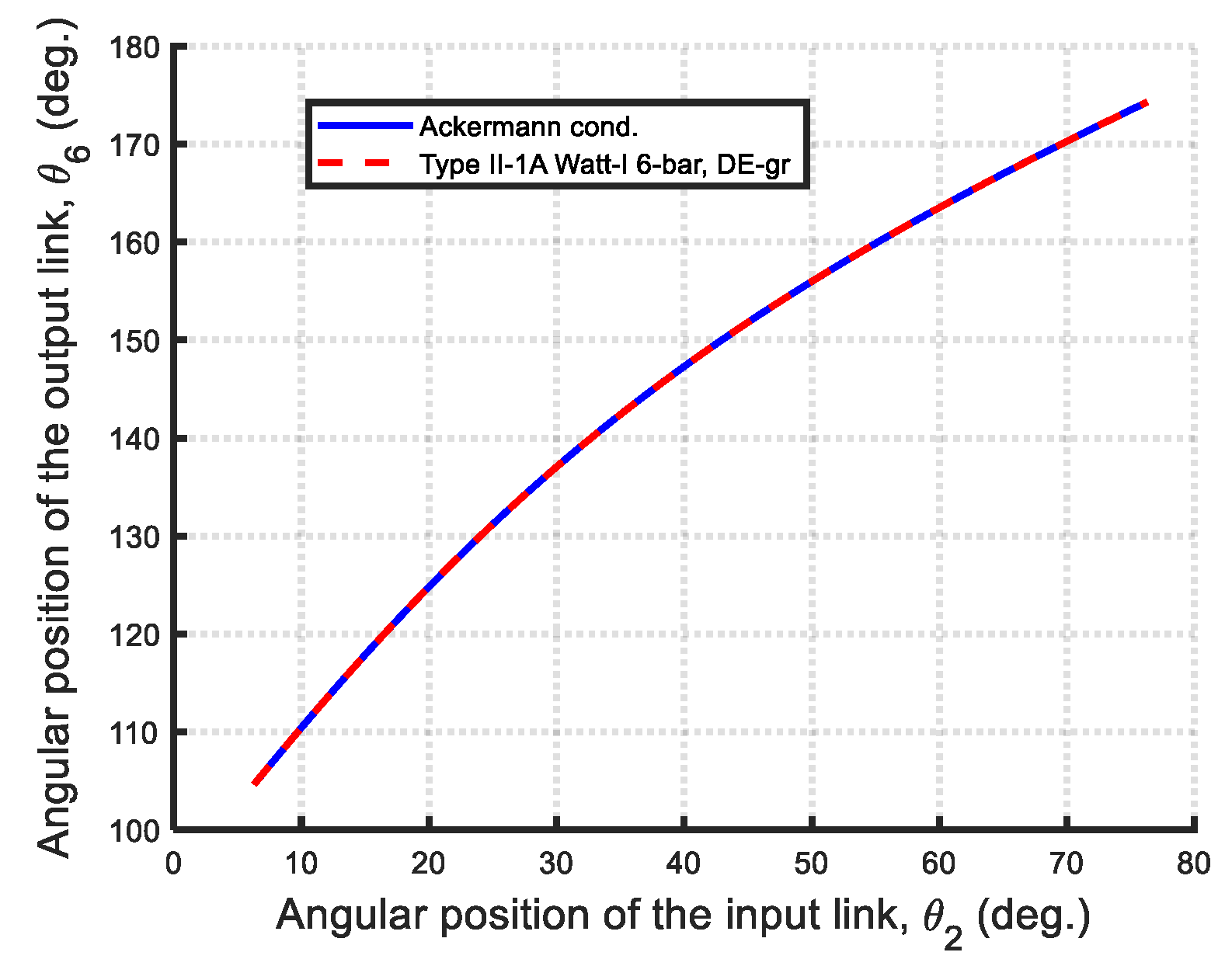
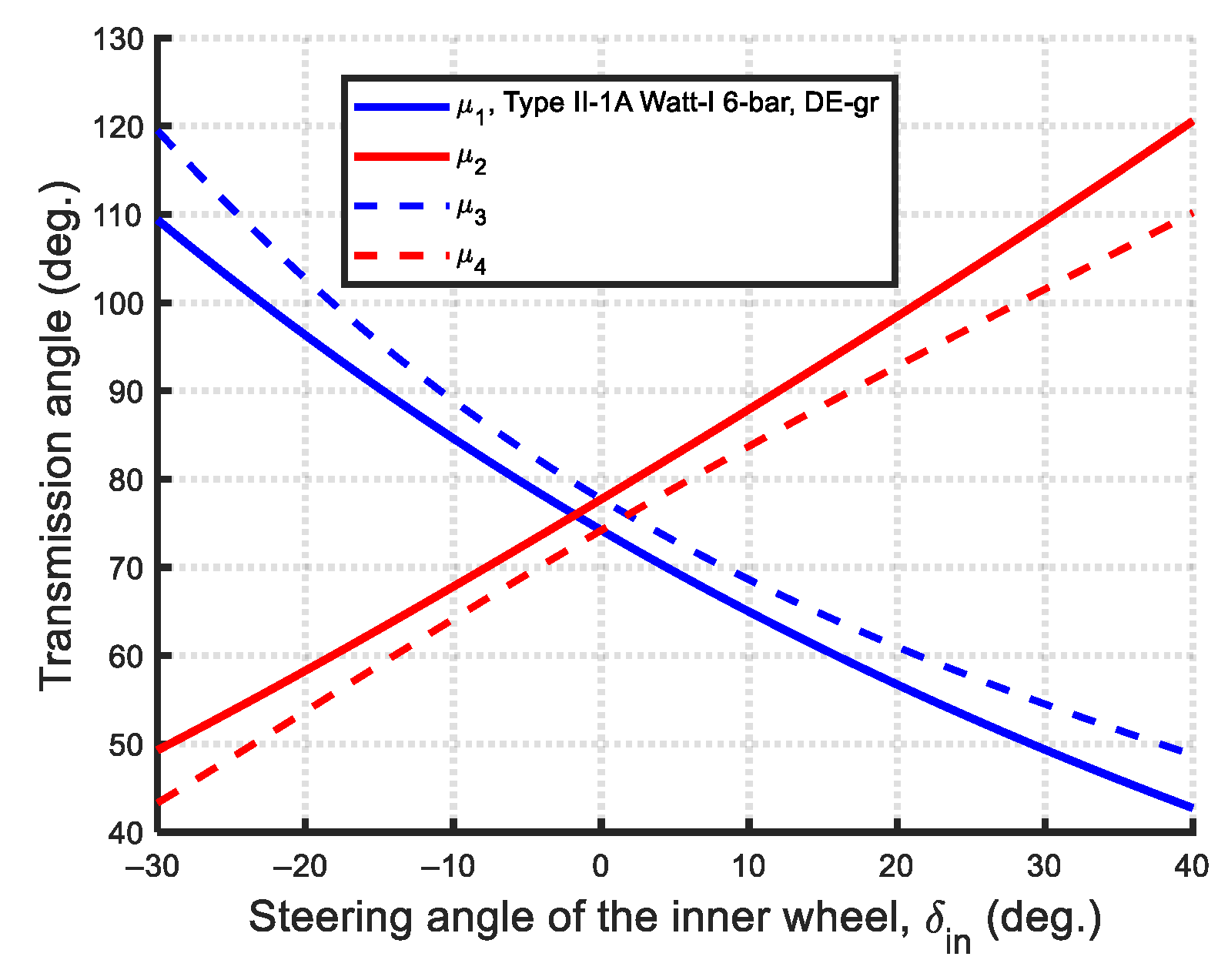
| Type II-1A: | |||||||||
| Obj. fun | Min-Max. error | ||||||||
| DE-gr | 2.082 × 10−8 | 875.7030 | 272.8332 | 829.9922 | 272.8332 | −468.248 | 114.4533 | 36.2884 | 0.0087 |
| IPSO | 2.235 × 10−8 | 740.3005 | 226.9415 | 703.0517 | 226.9415 | 21.0902 | 39.5867 | 67.5769 | 0.0175 |
| Type II-1B: | |||||||||
| Obj. fun | Min-Max. error | ||||||||
| DE-gr | 1.093 × 10−7 | 891.1493 | 293.2764 | 532.3469 | 623.1802 | 496.5351 | 78.8091 | 115.3626 | 0.0366 |
| IPSO | 3.843 × 10−9 | 745.8287 | 258.1550 | 630.1374 | 347.4222 | 93.0615 | 57.9349 | 62.2768 | 0.0069 |
| Type II-2: | |||||||||
| Obj. fun | Min-Max. error | ||||||||
| DE-gr | 1.77 × 10−10 | 835.8608 | 326.5826 | 745.1541 | 619.7032 | 388.6686 | 0.0000 | 55.14699 | 0.0019 |
| IPSO | 8.99 × 10−10 | 809.5860 | 296.6413 | 732.0895 | 488.1507 | 328.3741 | 0.0000 | 61.6331 | 0.0029 |
| Type II-3A: | |||||||||
| Obj. fun | Min-Max. error | ||||||||
| DE-gr | 4.28 × 10−9 | 740.0000 | 218.5374 | 713.2952 | 218.5374 | 0.0000 | 15.0224 | 56.6099 | 0.0067 |
| IPSO | 4.56 × 10−9 | 740.0000 | 231.0028 | 700.2822 | 231.0028 | 0.0000 | 47.5693 | 67.1493 | 0.0099 |
| Type II-3B: | |||||||||
| Obj. fun | Min-Max. error | ||||||||
| DE-gr | 4.28 × 10−9 | 740.0000 | 250.5453 | 658.1444 | 317.3321 | 0.0000 | 56.9750 | 55.1396 | 0.0094 |
| IPSO | 3.72 × 10−9 | 740.0000 | 256.0664 | 601.1974 | 357.0553 | 0.0000 | 94.5935 | 65.0170 | 0.0059 |
| Type of Steering Mechanism | Min-Max Structural ) | MAmax/MAmin | Constituent Four-Bar Linkages | Population Sizes of DE-gr/IPSO | Itmax/Exp | Winner of Optimal Method |
|---|---|---|---|---|---|---|
| Ackermann steering mechanism | 1.1079 | 2.0917/0.4756 | Non-Grashof mechanism | 10/10 | 200/100 | IPSO |
| Watt-I six-bar steering mechanism | ||||||
| Type I-1A (Ackermann-like) | 0.4233 | 1.8308/0.5514 | Non-Grashof mechanism | 10/20 | 100/100 | DE-gr |
| Type I-1B (Non-Ackermann-like) | 0.3544 | 1.8121/0.5594 | Non-Grashof mechanism | 10/20 | 100/100 | DE-gr |
| Type I-2 (Non-Ackermann-like) | 0.1431 | 1.5806/0.6326 | Grashof mechanism | 20/20 | 200/100 | DE-gr |
| Type I-3A (Ackermann-like) | 0.5002 | 1.8729/0.5389 | Non-Grashof mechanism | 10/10 | 200/100 | DE-gr |
| Type I-3B (Non-Ackermann-like) | 0.4814 | 1.8574/0.5452 | Non-Grashof mechanism | 10/10 | 200/100 | IPSO |
| Type I-3C (Ackermann-like) | 0.4311 | 1.8157/0.5553 | Non-Grashof mechanism | 10/10 | 100/100 | DE-gr, IPSO |
| Type II-1A (Ackermann-like) | 0.0087 | 1.5831/0.6334 | Non-Grashof mechanism | 10/20 | 100/100 | DE-gr |
| Type II-1B (Non-Ackermann-like) | 0.0069 | 1.5919/0.6305 | Non-Grashof mechanism | 10/20 | 100/100 | IPSO |
| Type II-2 (Non-Ackermann-like) | 0.0019 | 1.5930/0.6301 | Grashof mechanism | 20/20 | 200/100 | DE-gr |
| Type II-3A (Ackermann-like) | 0.0067 | 1.5859/0.6325 | Non-Grashof mechanism | 10/10 | 200/100 | DE-gr |
| Type II-3B (Non-Ackermann-like) | 0.0059 | 1.5878/0.6319 | Non-Grashof mechanism | 10/10 | 200/100 | IPSO |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, Y.-H.; Pang, D.-C.; Zheng, D.-H. Optimal Dimensional Synthesis of Ackermann and Watt-I Six-Bar Steering Mechanisms for Two-Axle Four-Wheeled Vehicles. Machines 2025, 13, 589. https://doi.org/10.3390/machines13070589
Kang Y-H, Pang D-C, Zheng D-H. Optimal Dimensional Synthesis of Ackermann and Watt-I Six-Bar Steering Mechanisms for Two-Axle Four-Wheeled Vehicles. Machines. 2025; 13(7):589. https://doi.org/10.3390/machines13070589
Chicago/Turabian StyleKang, Yaw-Hong, Da-Chen Pang, and Dong-Han Zheng. 2025. "Optimal Dimensional Synthesis of Ackermann and Watt-I Six-Bar Steering Mechanisms for Two-Axle Four-Wheeled Vehicles" Machines 13, no. 7: 589. https://doi.org/10.3390/machines13070589
APA StyleKang, Y.-H., Pang, D.-C., & Zheng, D.-H. (2025). Optimal Dimensional Synthesis of Ackermann and Watt-I Six-Bar Steering Mechanisms for Two-Axle Four-Wheeled Vehicles. Machines, 13(7), 589. https://doi.org/10.3390/machines13070589







