Research on Wheel Polygonal Wear Based on the Vehicle–Track Coupling Vibration of Metro
Abstract
1. Introduction
2. Field Test of Vehicle System
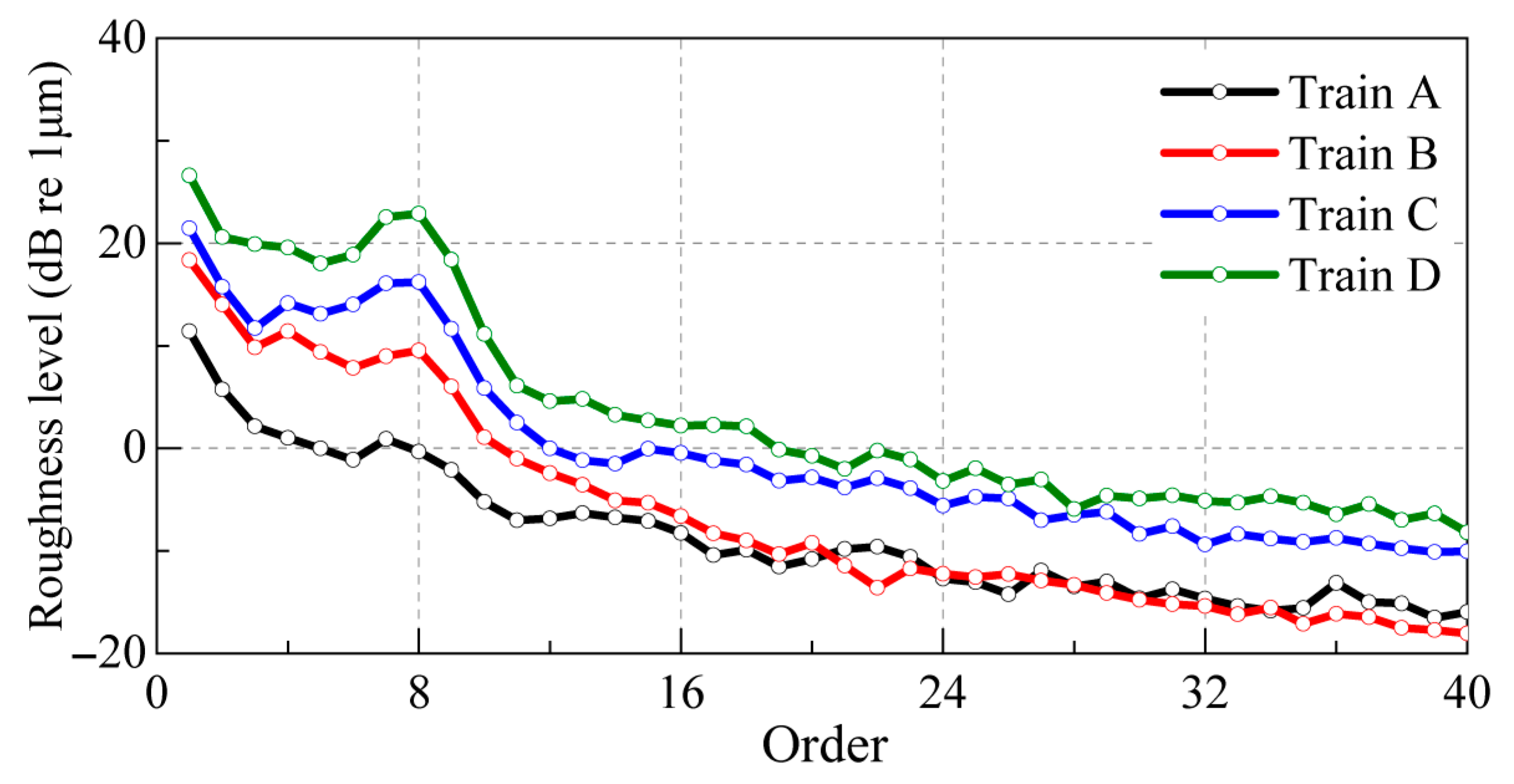
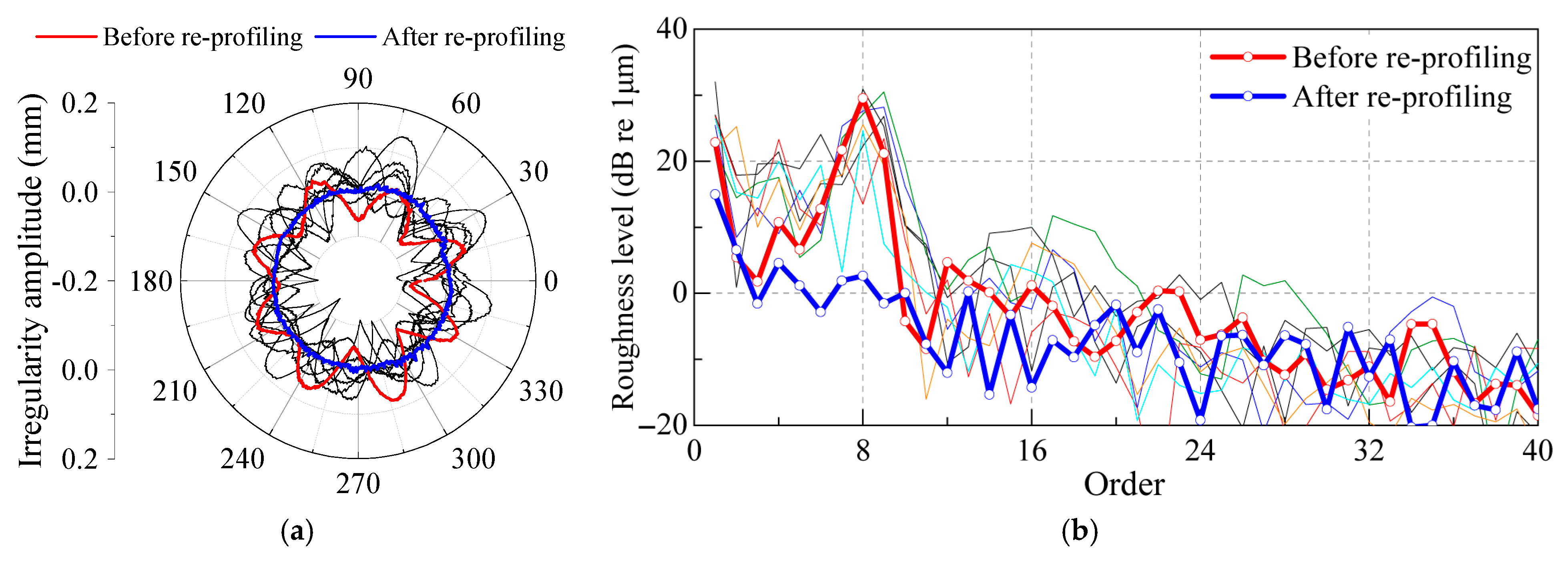
2.1. Polygonal Measurement
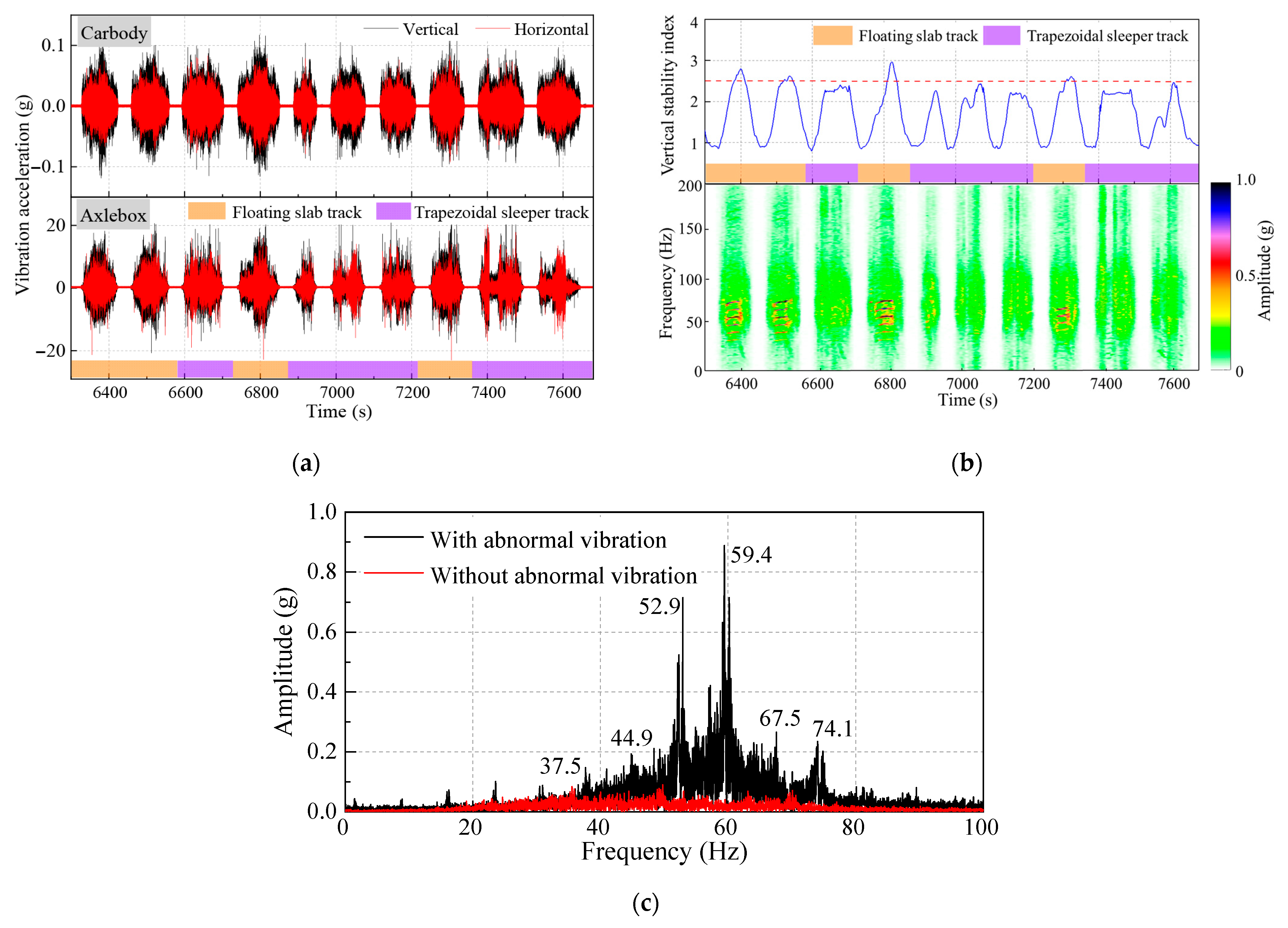
2.2. Dynamics Testing and Analysis
3. Formation Analysis of Wheel Polygonal
3.1. Modal Analysis of Track Structure
3.2. Formation of Wheel Initial Polygonal
4. Conclusions
- (1)
- Distinct seventh-order to ninth-order polygonal wear patterns were observed on the wheel tread, with corresponding abnormal vertical vibration frequencies at the axlebox matching the polygonal excitation frequencies.
- (2)
- The wheel’s polygonal wear characteristics are influenced by the underlying track structure, and their dominant frequency components closely align with the P2 resonance frequency arising from wheel–rail interaction.
- (3)
- A modal analysis of the vehicle–track coupling system revealed multiple peaks in the track frequency response curve within the same range, confirming a strong correlation with the polygonal wear excitation frequencies.
- (4)
- For eighth-order polygonal wear, the irregularity at rail joints acts as a localized excitation source, while the P2 force resonance under coupled vibration conditions plays a key role in amplifying and sustaining the wear process.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FFT | fast Fourier transform |
| STFT | short-time Fourier transform |
| EF | finite element |
| RMS | root mean square |
References
- Diana, G.; Cheli, F.; Collina, A.; Corradi, R.; Melzi, S. The development of a numerical model for railway vehicle comfort assessment through comparison with experimental measurements. Vehicle Syst. Dyn. 2002, 38, 165–183. [Google Scholar] [CrossRef]
- Wang, J.; Ding, X.; Liu, Z.; Teng, W.; Liu, T.; Li, Y. An experimental study on abnormal vibration of metro trains caused by out-of-round wheels. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2022, 237, 224–231. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J.; Yang, J.; Yao, D. A real-time polygonal wheel-rail force identification method based on convolutional neural networks (CNN). Urban Rail Transit 2025, 11, 178–194. [Google Scholar] [CrossRef]
- Johansson, A.; Andersson, C. Out-of-round railway wheels a study of wheel polygonalization through simulation of three-dimensional wheel-rail interaction and wear. Vehicle Syst. Dyn. 2025, 43, 539–559. [Google Scholar] [CrossRef]
- Tao, G.; Wen, Z.; Liang, X.; Ren, D.; Jin, X. An investigation into the mechanism of the out-of-round wheels of metro train and its mitigation measures. Vehicle Syst. Dyn. 2019, 57, 1–16. [Google Scholar] [CrossRef]
- Cai, W.; Chi, M.; Wu, X.; Li, F.; Wen, Z.; Liang, S.; Jin, X. Experimental and numerical analysis of the polygonal wear of high-speed trains. Wear 2019, 440–441, 203079. [Google Scholar] [CrossRef]
- Yang, X.; Tao, G.; Li, W.; Wen, Z. On the formation mechanism of high-order polygonal wear of metro train wheels: Experiment and simulation. Eng. Fail. Anal. 2021, 127, 105572. [Google Scholar] [CrossRef]
- Qu, S.; Zhu, B.; Zeng, J.; Dai, H.; Wu, P. Experimental investigation for wheel polygonisation of high-speed trains. Vehicle Syst. Dyn. 2020, 59, 1573–1586. [Google Scholar] [CrossRef]
- Wei, L.; Zong, L.; Luo, S.; He, X. Research into the problem of wear creating a polygon-shaped wheel on metro trains. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2016, 230, 43–55. [Google Scholar] [CrossRef]
- Wang, Z.; Mei, G.; Zhang, W.; Cheng, Y.; Zou, H.; Huang, G.; Li, F. Effects of polygonal wear of wheels on the dynamic performance of the gearbox housing of a high-speed train. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 1852–1863. [Google Scholar] [CrossRef]
- Shi, Y.; Dai, H.; Mao, Q.; Shi, H.; Wang, Q. Study on formation mechanism of metro wheel polygonal based on vehicle-track coupling. J. Southwest Jiaotong Univ. 2023, 59, 1357–1367. [Google Scholar]
- Jin, X.; Wu, L.; Fang, J.; Zhong, S.; Ling, L. An investigation into the mechanism of the polygonal wear of metro train wheels and its effect on the dynamic behavior of a wheel/rail system. Vehicle Syst. Dyn. 2012, 50, 1817–1834. [Google Scholar] [CrossRef]
- Shi, Y.; Dai, H.; Wang, Q.; Li, D.; Peng, X. Abnormal vibration analysis of metro axlebox based on vehicle-track coupling system. Adv. Mech. Eng. 2023, 15, 16878132221143573. [Google Scholar] [CrossRef]
- GB/T 5599–2019; Specification for Dynamic Performance Assessment and Testing Verification of Rolling Stock. Standardization Administration of China: Beijing, China, 2019.
- Wu, T.; Thompson, D. An investigation into rail corrugation due to micro-slip under multiple wheel/rail interactions. Wear 2005, 258, 1115–1125. [Google Scholar] [CrossRef]
- Koro, K.; Abe, K.; Ishida, M.; Suzuki, T. Timoshenko beam finite element for vehicle-track vibration analysis and its application to jointed railway track. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2004, 218, 159–172. [Google Scholar] [CrossRef]
- Sharmaa, S.; Kumarb, A. Dynamics analysis of wheel rail contact using FEA. Procedia Eng. 2006, 144, 1119–1128. [Google Scholar] [CrossRef]
- Guan, Q.; Zhou, Y.; Li, W.; Wen, Z.; Jin, X. Study on the P2 resonance frequency of vehicle track system. J. Mech. Eng. 2019, 55, 118–127. [Google Scholar] [CrossRef]
- Ma, C.; Gao, L.; Cui, R.; Xin, T. The initiation mechanism and distribution rule of wheel high-order polygonal wear on high-speed railway. Eng. Fail. Anal. 2021, 119, 104937. [Google Scholar] [CrossRef]
- Shi, H.; Wang, J.; Wu, P.; Song, C.; Teng, W. Field measurements of the evolution of wheel wear and vehicle dynamics for high-speed trains. Vehicle Syst. Dyn. 2018, 56, 1187–1206. [Google Scholar] [CrossRef]
- Zhong, S.; Zhou, X.; Sheng, X. Study on metro operation safety based on a specific contact model for resilient wheel. Urban Rail Transit 2025, 11, 123–137. [Google Scholar] [CrossRef]
- Shi, Y.; Mao, Q.; Dai, H.; Wang, Q.; Qi, Y. Research on abnormal vibration of high-speed train based on wheel-rail coupling modal analysis. Vehicle Syst. Dyn. 2024, 63, 457–474. [Google Scholar] [CrossRef]
- Wang, Q.; Li, D.; Zeng, J.; Peng, X.; Wei, L.; Du, W. A diagnostic method of freight wagons hunting performance based on wayside hunting detection system. Measurement 2024, 227, 114274. [Google Scholar] [CrossRef]
- Fu, B.; Bruni, S.; Luo, S. Study on wheel polygonization of a metro vehicle based on polygonal wear simulation. Wear 2019, 438, 203071. [Google Scholar] [CrossRef]
- Zhang, H.; Guan, Q.; Wen, Z. Influence of P2 resonance of metro wheel-rail system on fatigue failure of rail fastening clips. Inter. J. Rail Transp. 2025, 13, 539–556. [Google Scholar] [CrossRef]
- Morais, J.; Morais, P.; Santos, C.; Paixão, A.; Fortunato, E. Railway track support condition assessment—Initial developments on a vehicle-based monitoring solution through modal analysis. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2022, 236, 1058–1069. [Google Scholar] [CrossRef]

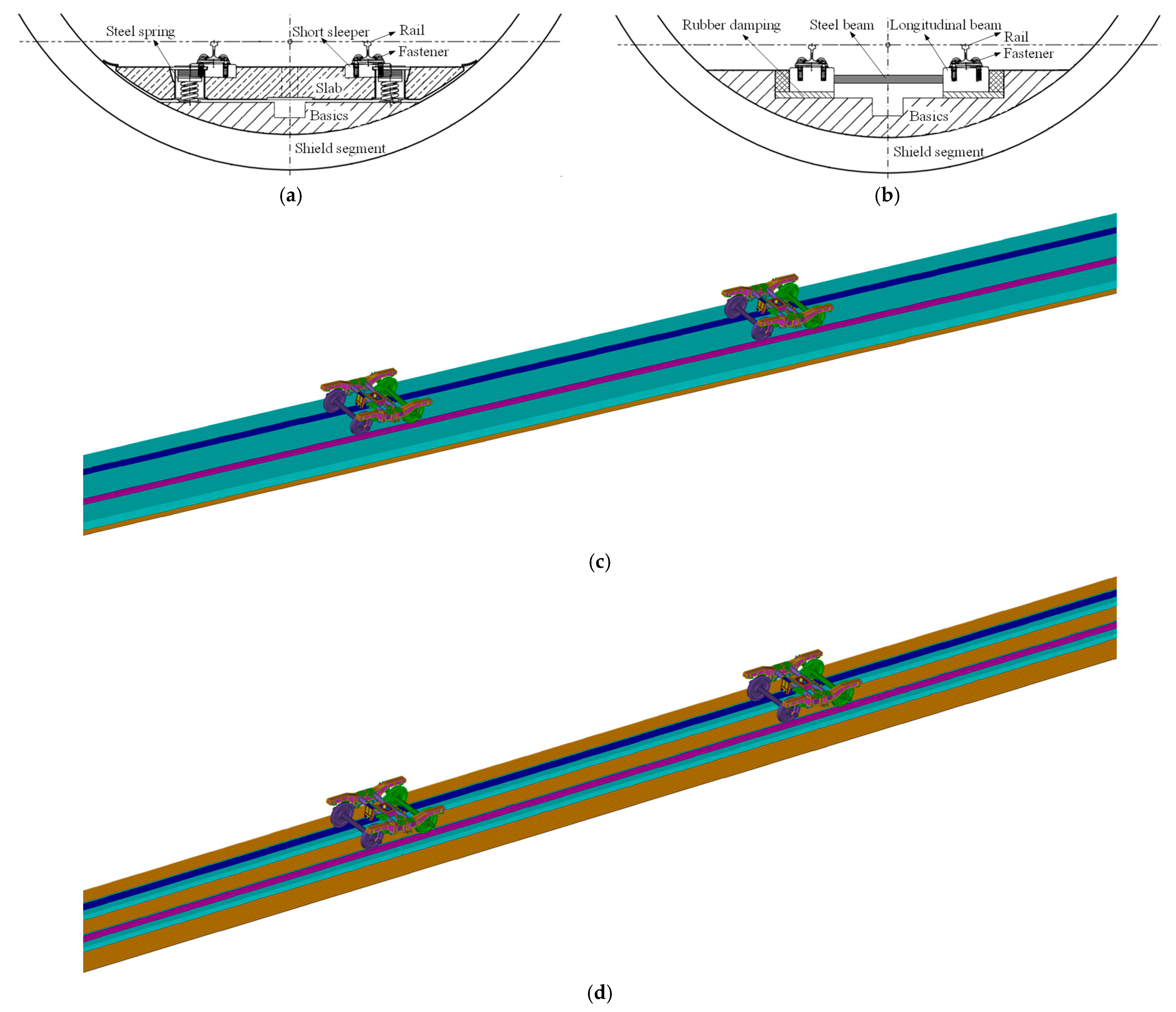
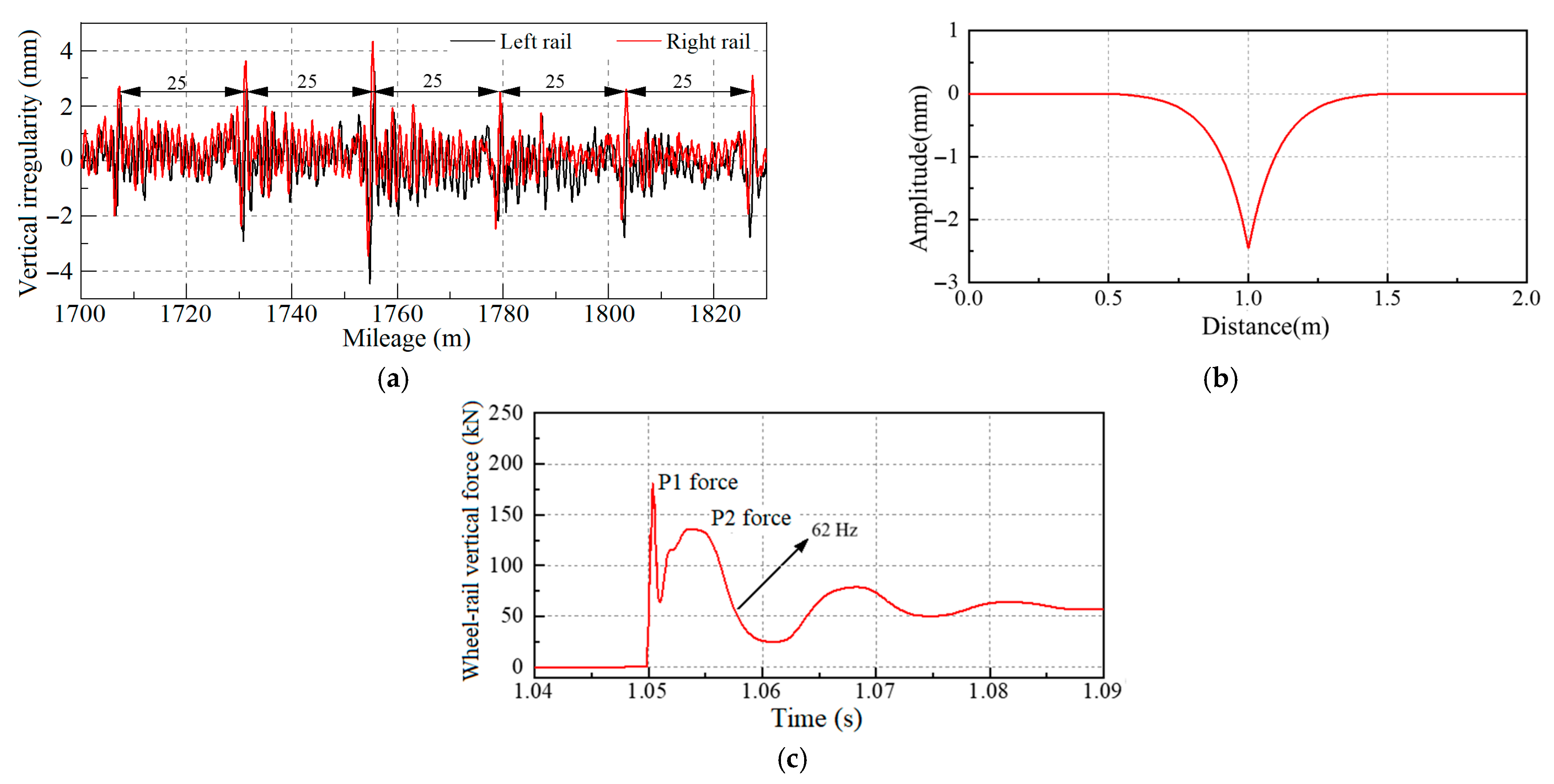
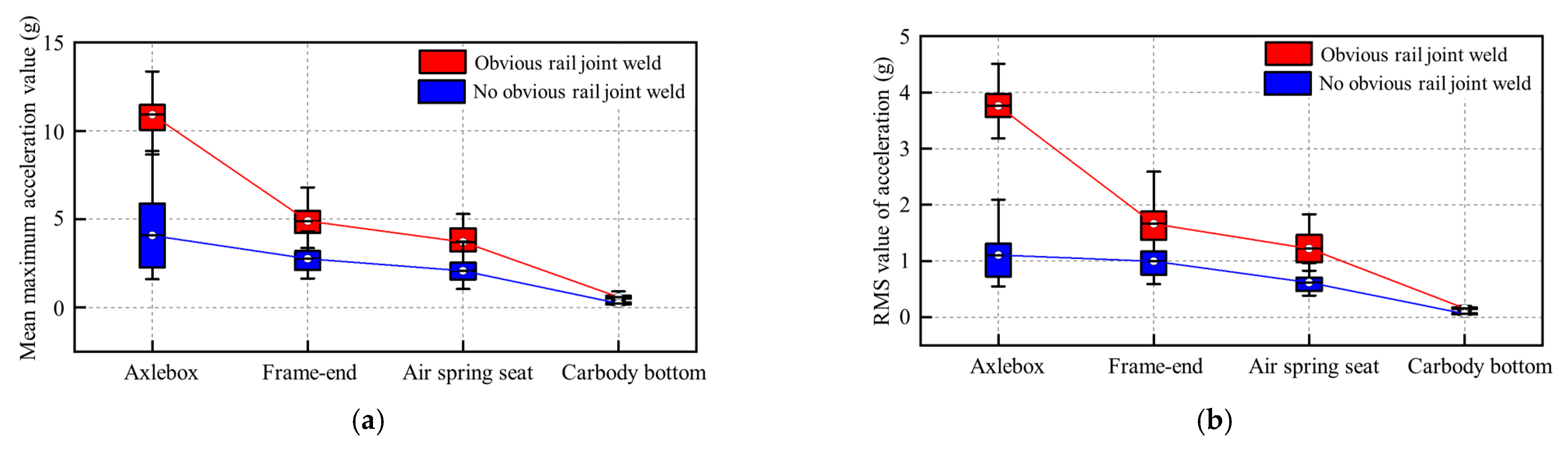
| System | Parameter | Symbol | Value | Unit |
|---|---|---|---|---|
| Vehicle system | Nominal radius of wheel | R0 | 0.42 | m |
| Half distance between two bogie frames | lc | 6.3 | m | |
| Half distance between two axles of wheelset | lw | 1.15 | m | |
| Mass of carbody | Mc | 24,937 | kg | |
| Mass of bogie frame | Mf | 1830 | kg | |
| Mass of wheelset | Mw | 1231 | kg | |
| Vertical stiffness of primary suspension | Kp | 1.5 | MN/m | |
| Vertical stiffness of secondary suspension | Cp | 2 | kN·s/m | |
| Vertical damping of primary suspension | Ks | 0.4 | MN/m | |
| Vertical damping of secondary suspension | Cs | 60 | kN·s/m | |
| Track system | Density of concrete | ρs | 2500 | kg/m3 |
| Young’s modulus of concrete | Es | 0.35 × 1011 | Pa | |
| Poisson’s ratio of concrete | υs | 0.22 | - | |
| Vertical stiffness of DTVI2 fastener | Kf1 | 50 | MN/m | |
| Vertical stiffness of ZX-3 fastener | Kf2 | 60 | MN/m | |
| Vertical stiffness of steel spring | Kd1 | 10 | MN/m | |
| Vertical damping of steel spring | Cd1 | 20 | kN·s/m | |
| Vertical stiffness of rubber damping | Kd2 | 20 | MN/m3 | |
| Vertical damping of rubber damping | Cd2 | 10 | kN·s/m3 | |
| Longitudinal spacing of steel spring | Lx | 1.2 | m | |
| Transverse spacing of steel spring | Ly | 1.8 | m |
| Order | Vibration Mode | Frequency/Hz | Modal Shape |
|---|---|---|---|
| 1 | Wheel–rail P2 force resonance | 59.647 |  |
| 2 | First-order vertical bending | 103.482 |  |
| 3 | Second-order vertical bending | 141.378 |  |
| 4 | Third-order vertical bending | 141.827 |  |
| 5 | Fourth-order vertical bending | 172.866 |  |
| Order | Vibration Mode | Frequency/Hz | Modal Shape |
|---|---|---|---|
| 1 | Wheel–rail P2 force resonance | 108.615 |  |
| 2 | First-order vertical bending | 188.672 |  |
| 3 | Second-order vertical bending | 189.338 |  |
| 4 | Third-order vertical bending | 193.165 |  |
| 5 | Fourth-order vertical bending | 203.816 |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Mao, Q.; Wang, Q.; Dai, H.; Peng, X.; Dong, C. Research on Wheel Polygonal Wear Based on the Vehicle–Track Coupling Vibration of Metro. Machines 2025, 13, 587. https://doi.org/10.3390/machines13070587
Shi Y, Mao Q, Wang Q, Dai H, Peng X, Dong C. Research on Wheel Polygonal Wear Based on the Vehicle–Track Coupling Vibration of Metro. Machines. 2025; 13(7):587. https://doi.org/10.3390/machines13070587
Chicago/Turabian StyleShi, Yixuan, Qingzhou Mao, Qunsheng Wang, Huanyun Dai, Xinyu Peng, and Cuijun Dong. 2025. "Research on Wheel Polygonal Wear Based on the Vehicle–Track Coupling Vibration of Metro" Machines 13, no. 7: 587. https://doi.org/10.3390/machines13070587
APA StyleShi, Y., Mao, Q., Wang, Q., Dai, H., Peng, X., & Dong, C. (2025). Research on Wheel Polygonal Wear Based on the Vehicle–Track Coupling Vibration of Metro. Machines, 13(7), 587. https://doi.org/10.3390/machines13070587






