Design Technique on Speed Control Combined with an Inertial Element for Vibration Suppression
Abstract
1. Introduction
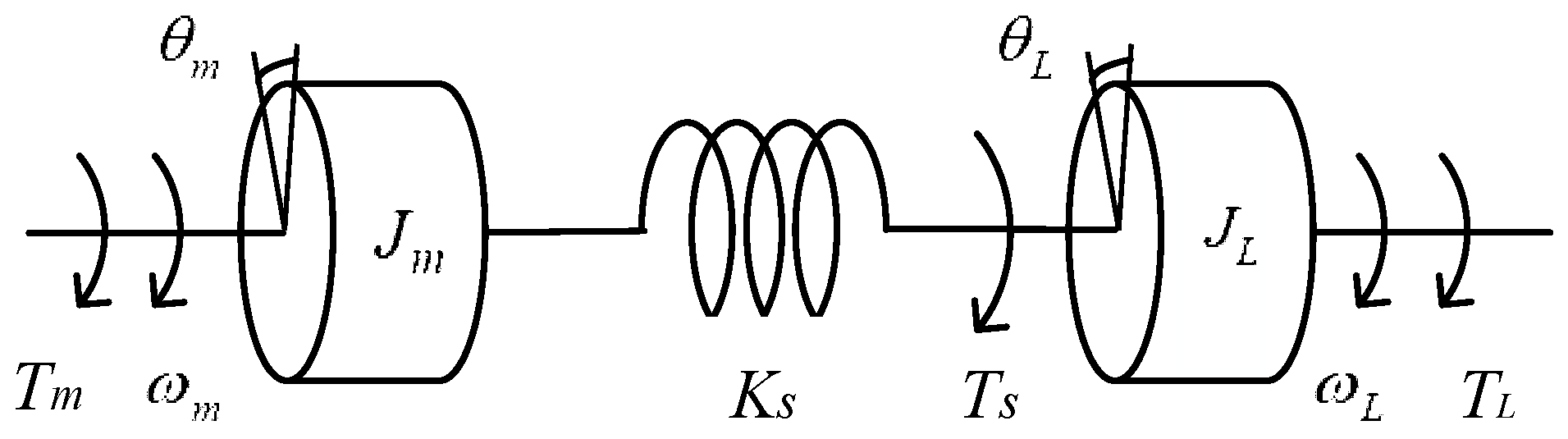
2. Two-Inertia System
2.1. Two-Inertia System
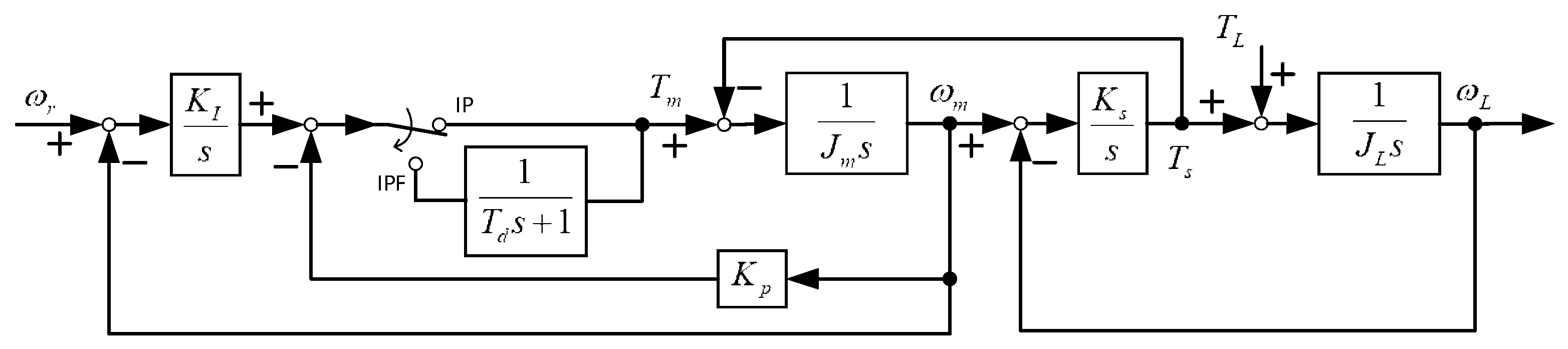
2.2. Speed Control System
3. Speed Control
3.1. IP Speed Control
3.2. Pole Assignment and Parameter Design
4. Speed Control with a First-Order Inertial Element
4.1. Speed Control with a First-Order Inertial Element
4.2. Pole Assignment
5. Mechanism for Performance Improvement
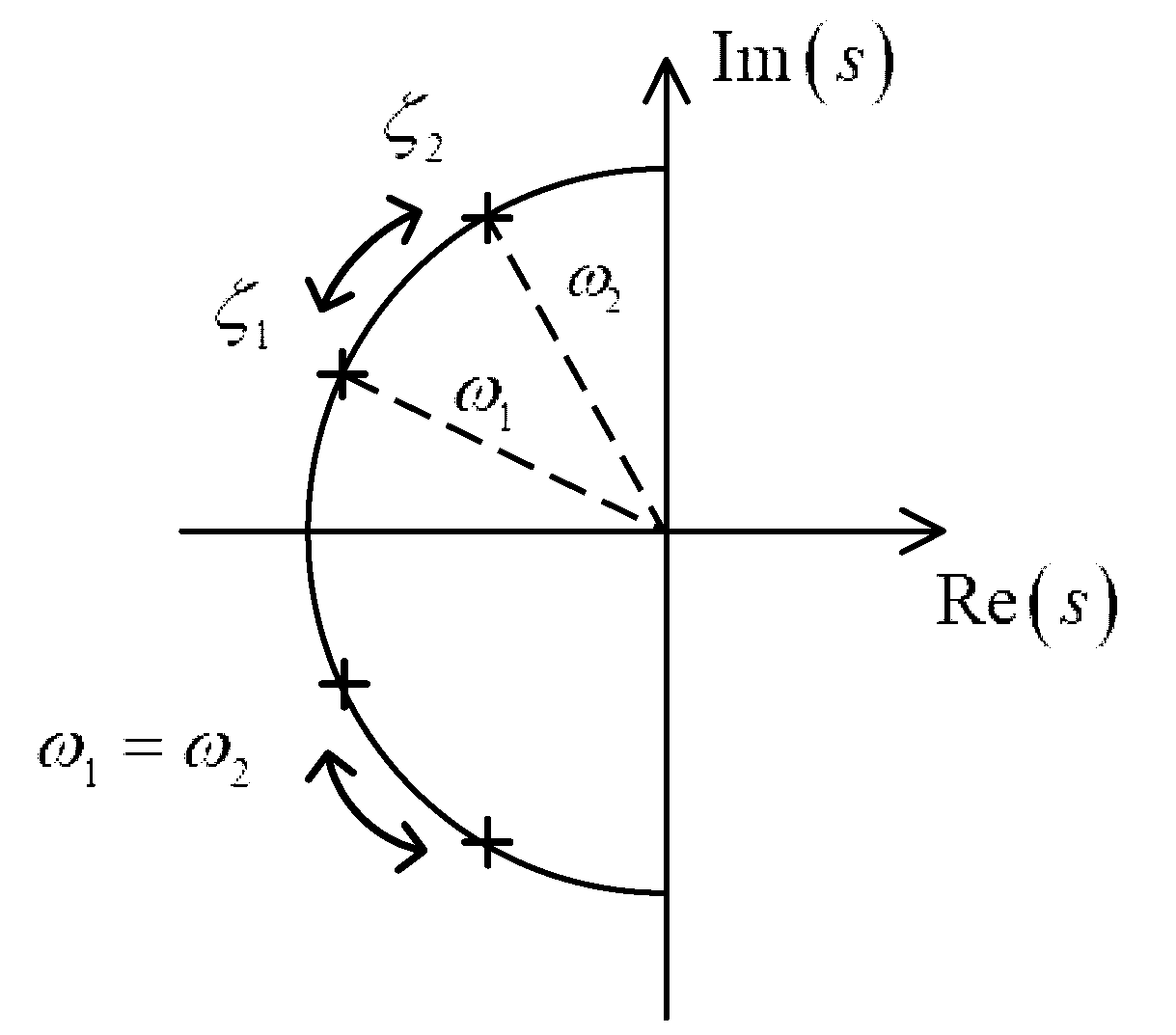
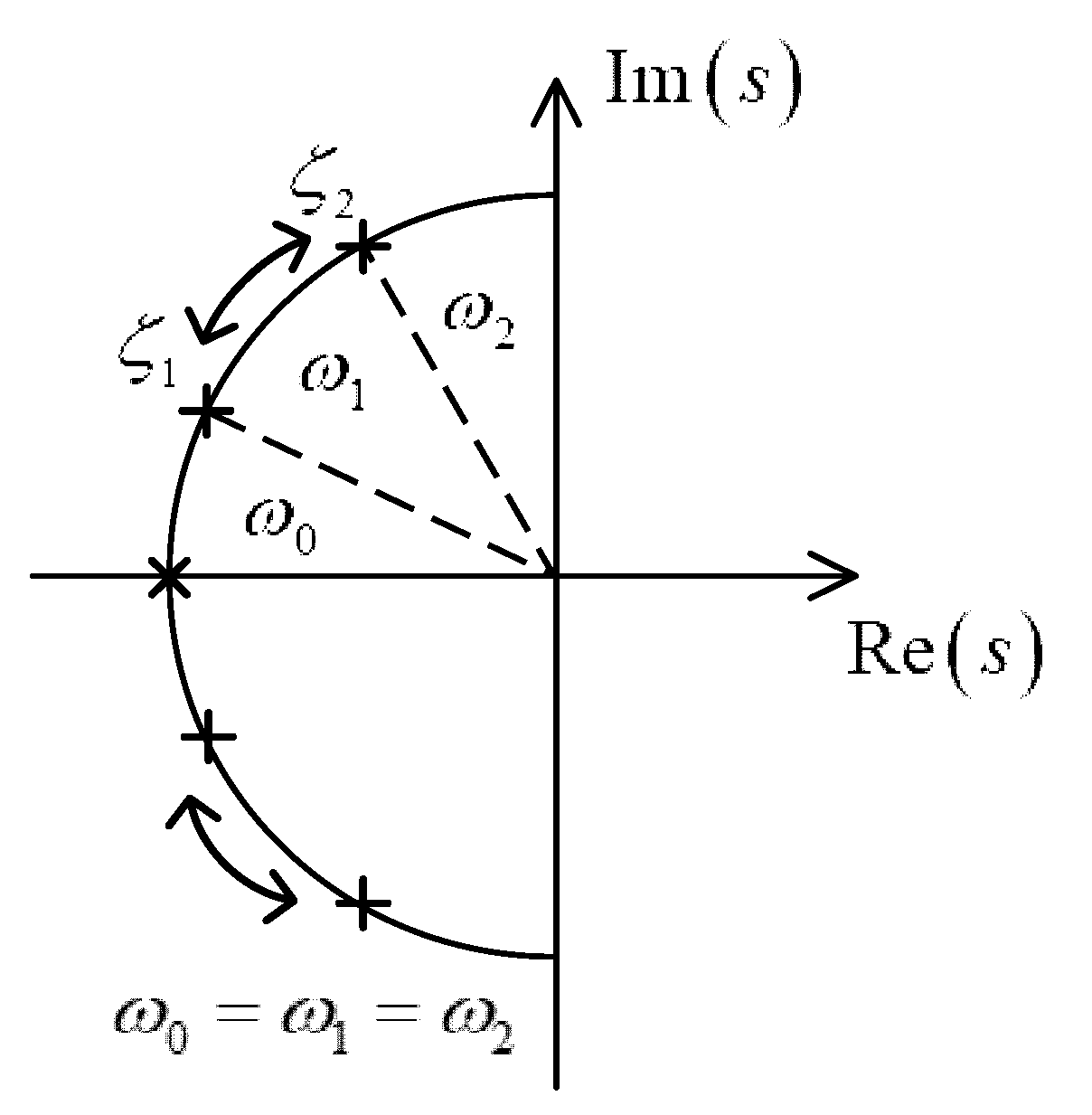
5.1. Comparison of Damping Characteristics
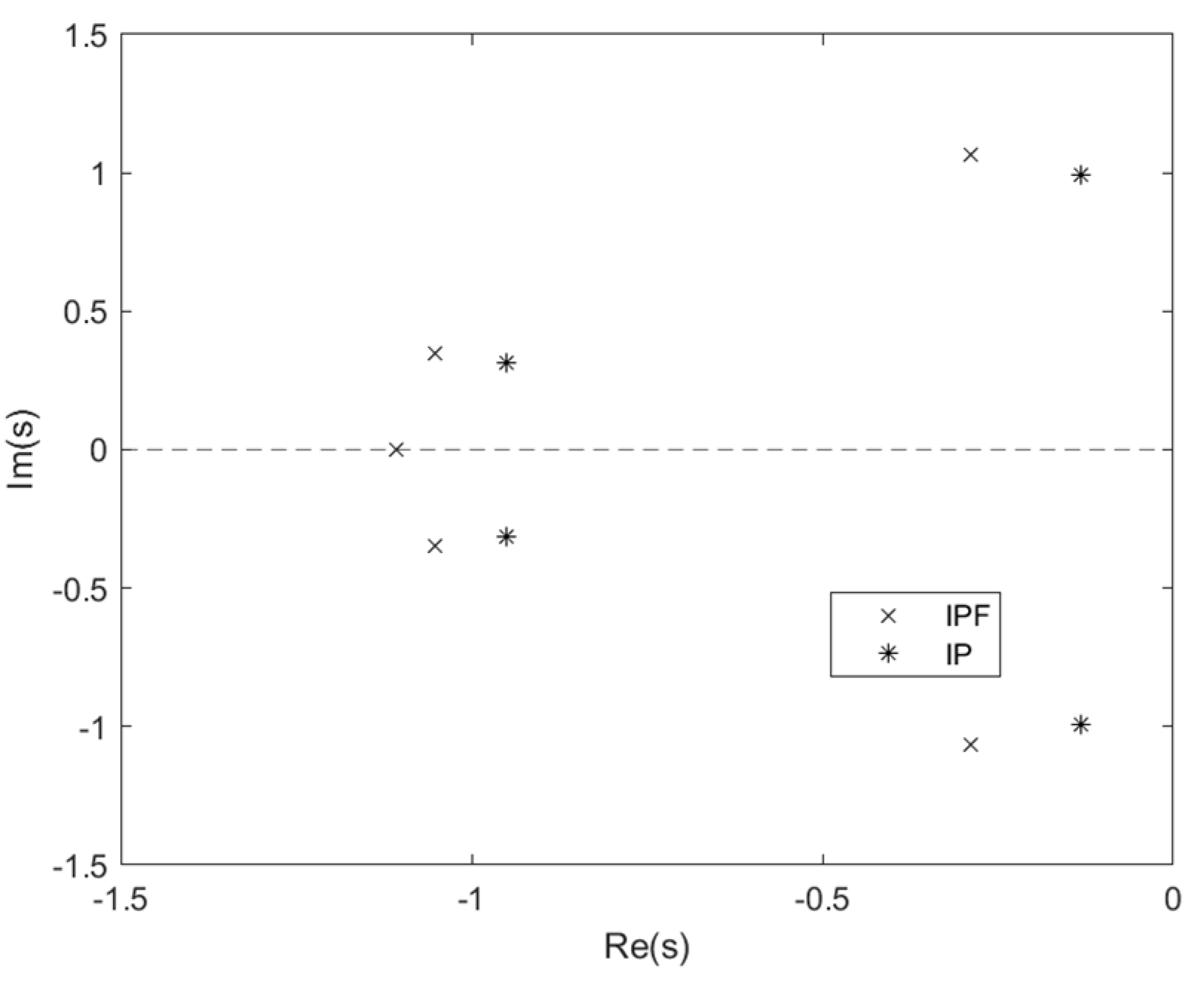
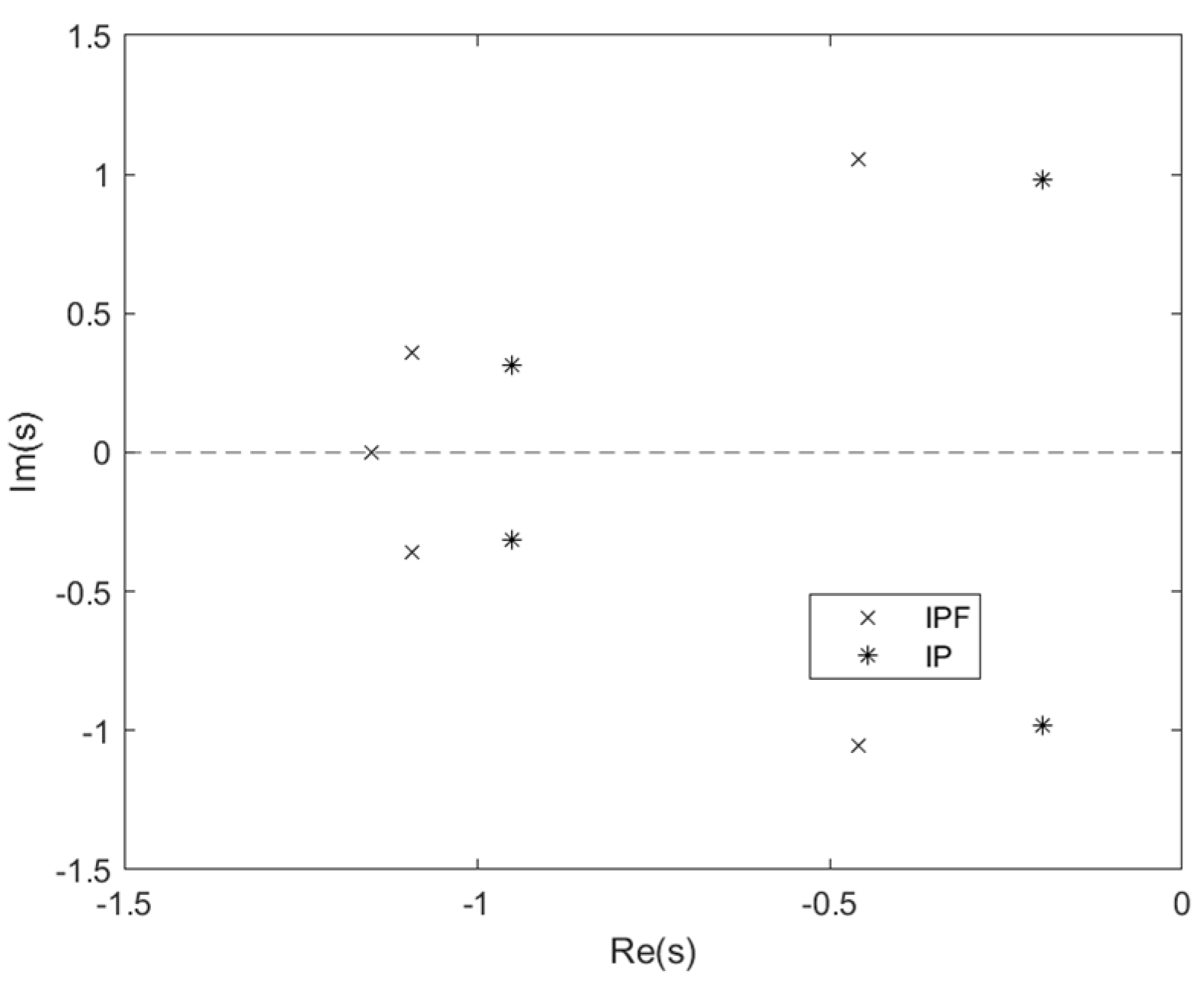
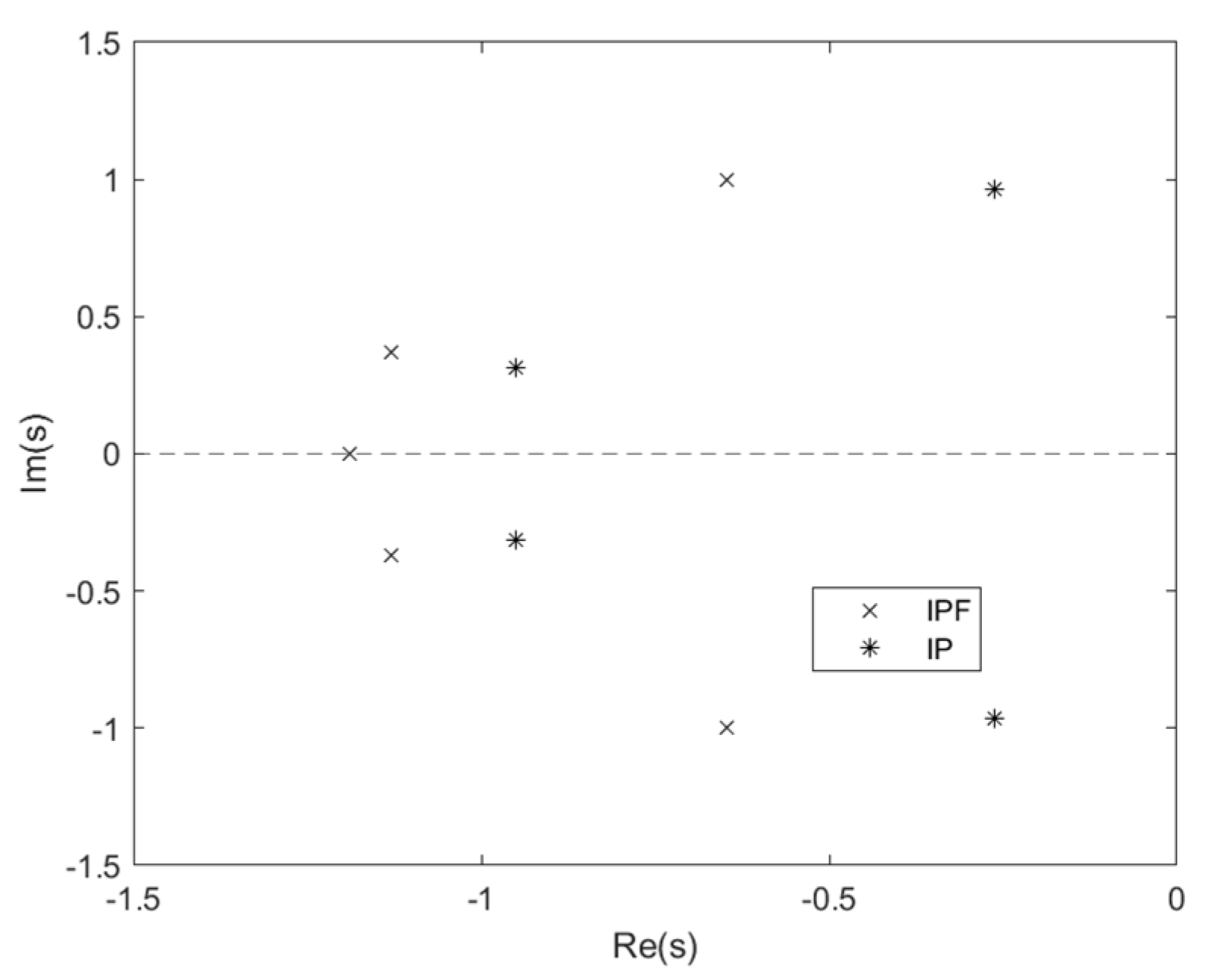
5.2. Comparison of Pole Distributions
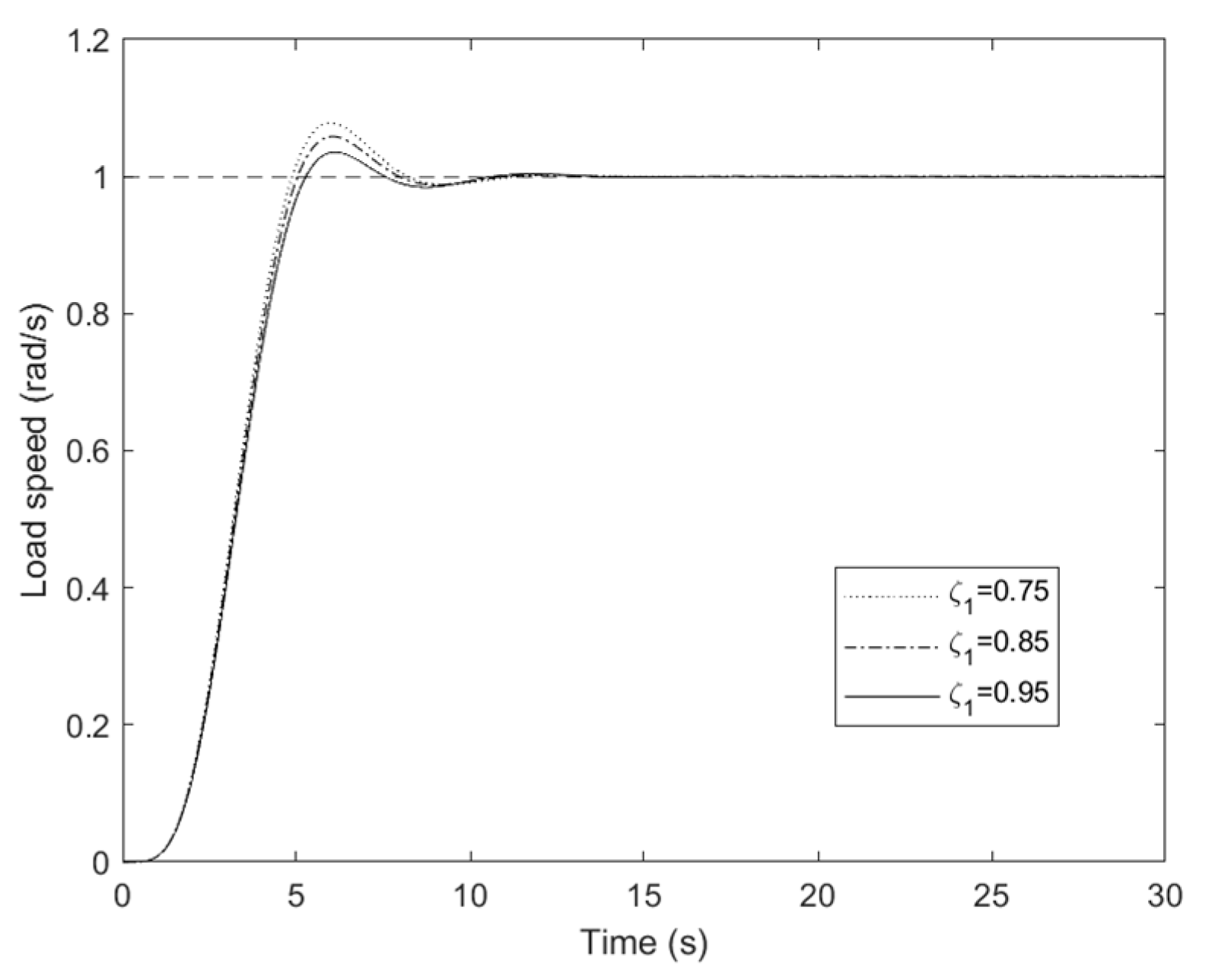
5.3. Simulation Comparison
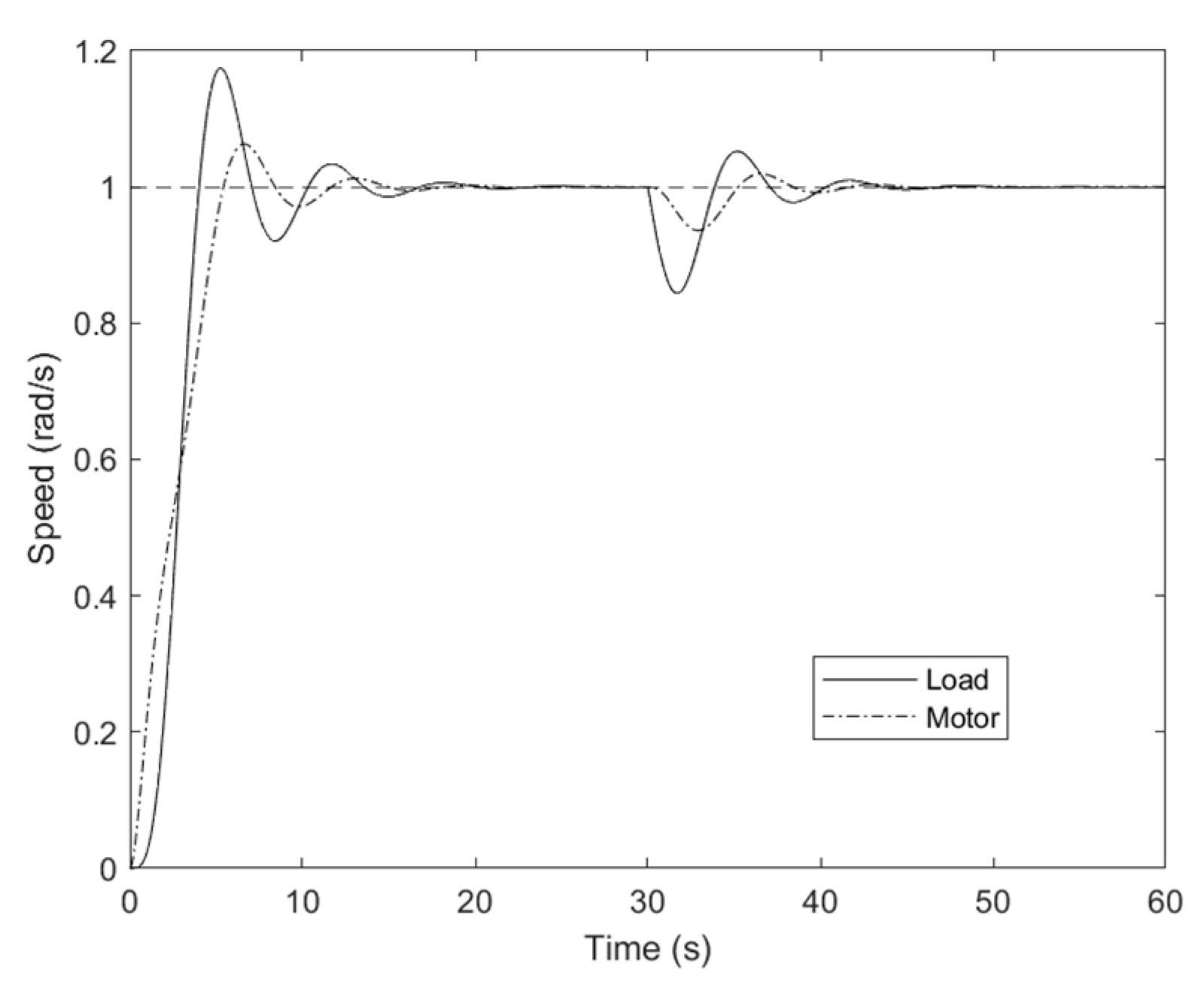
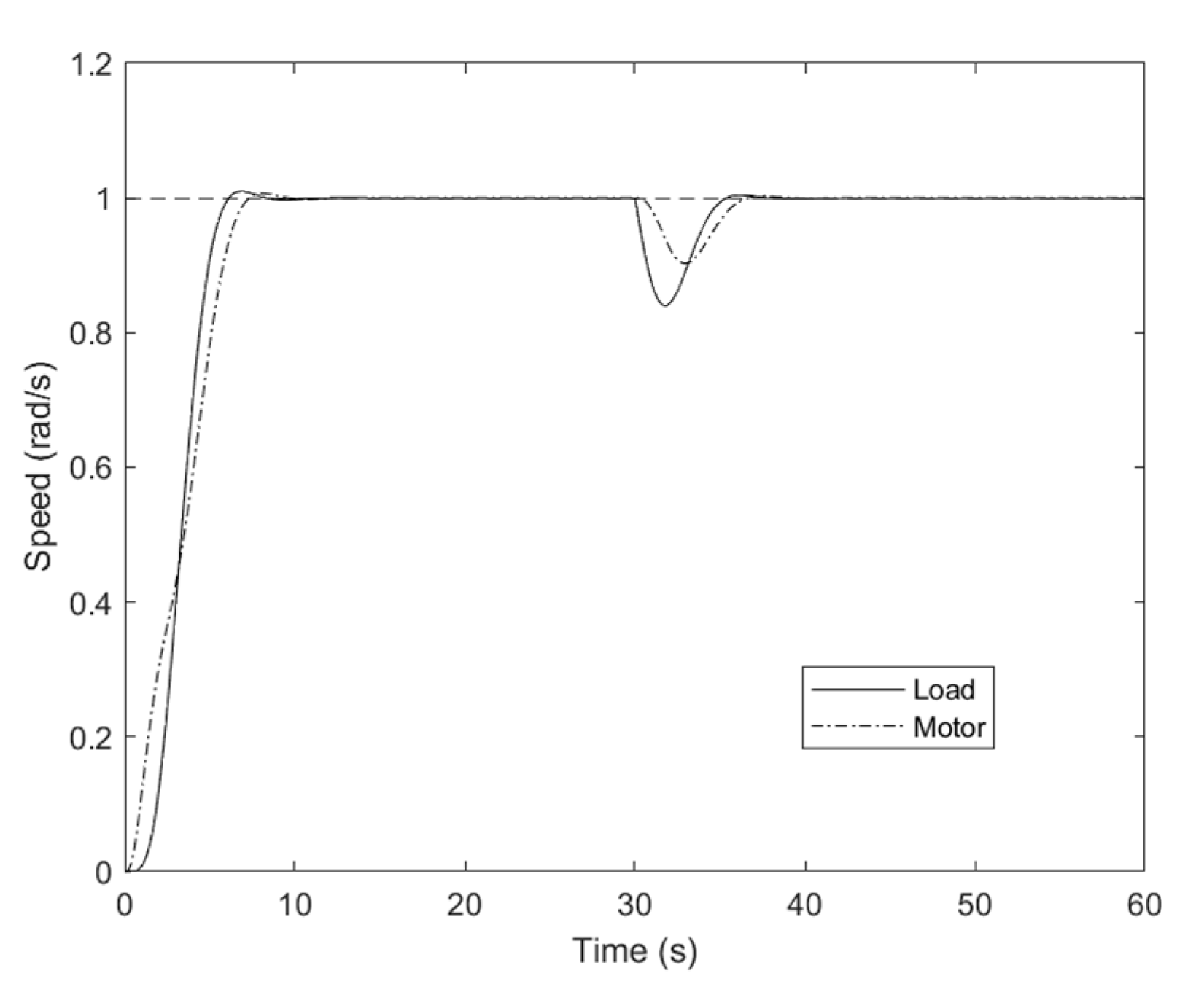
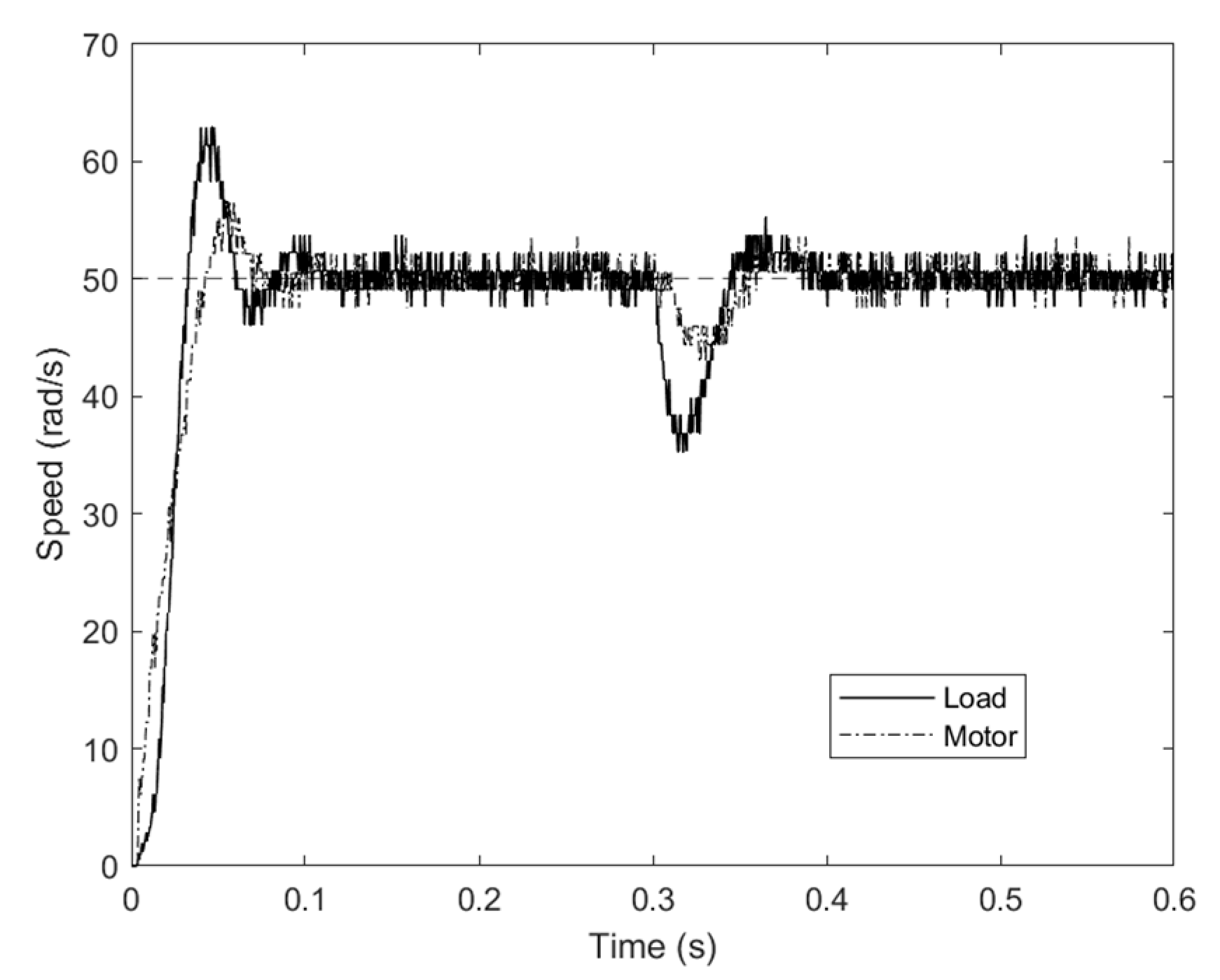
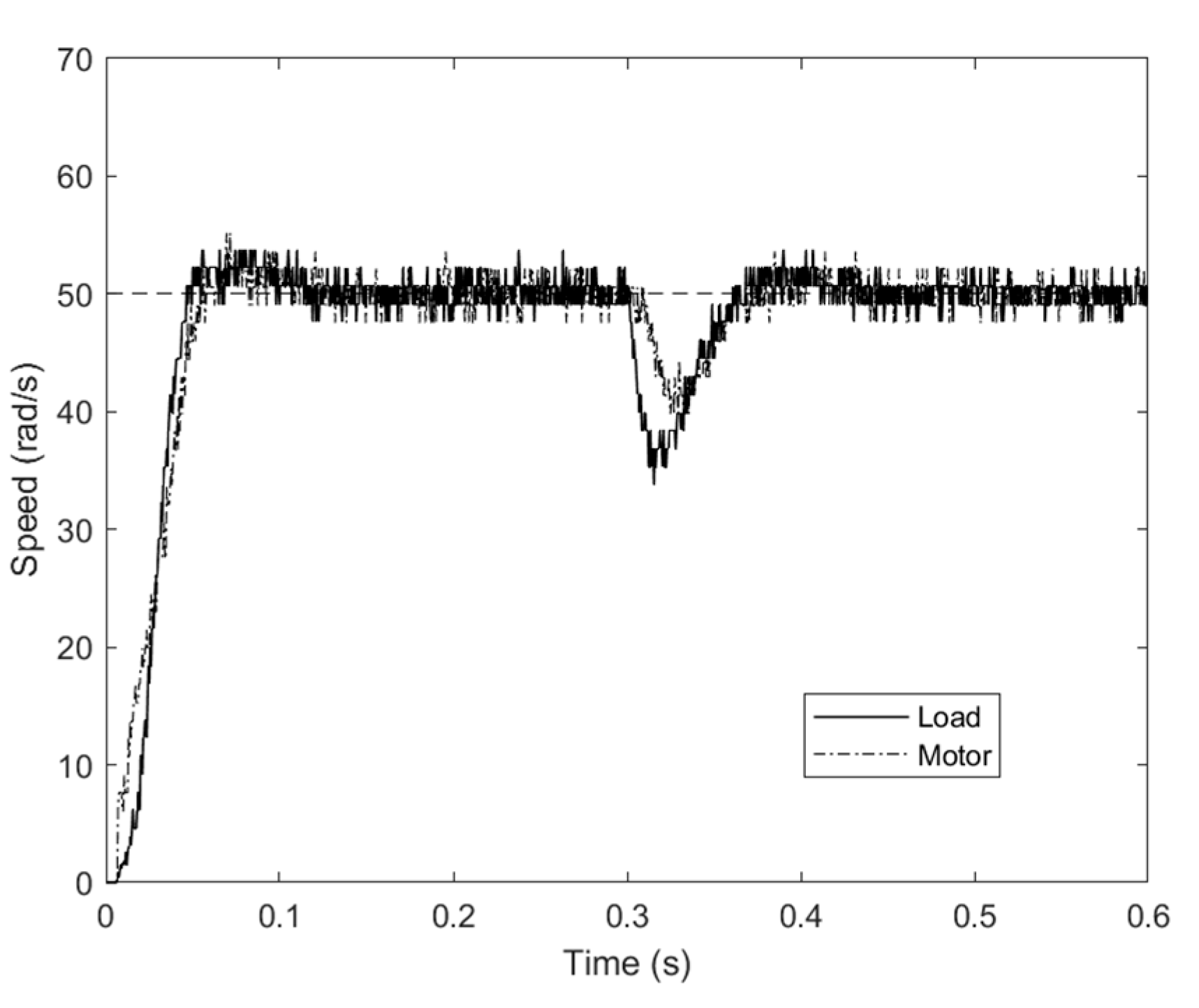
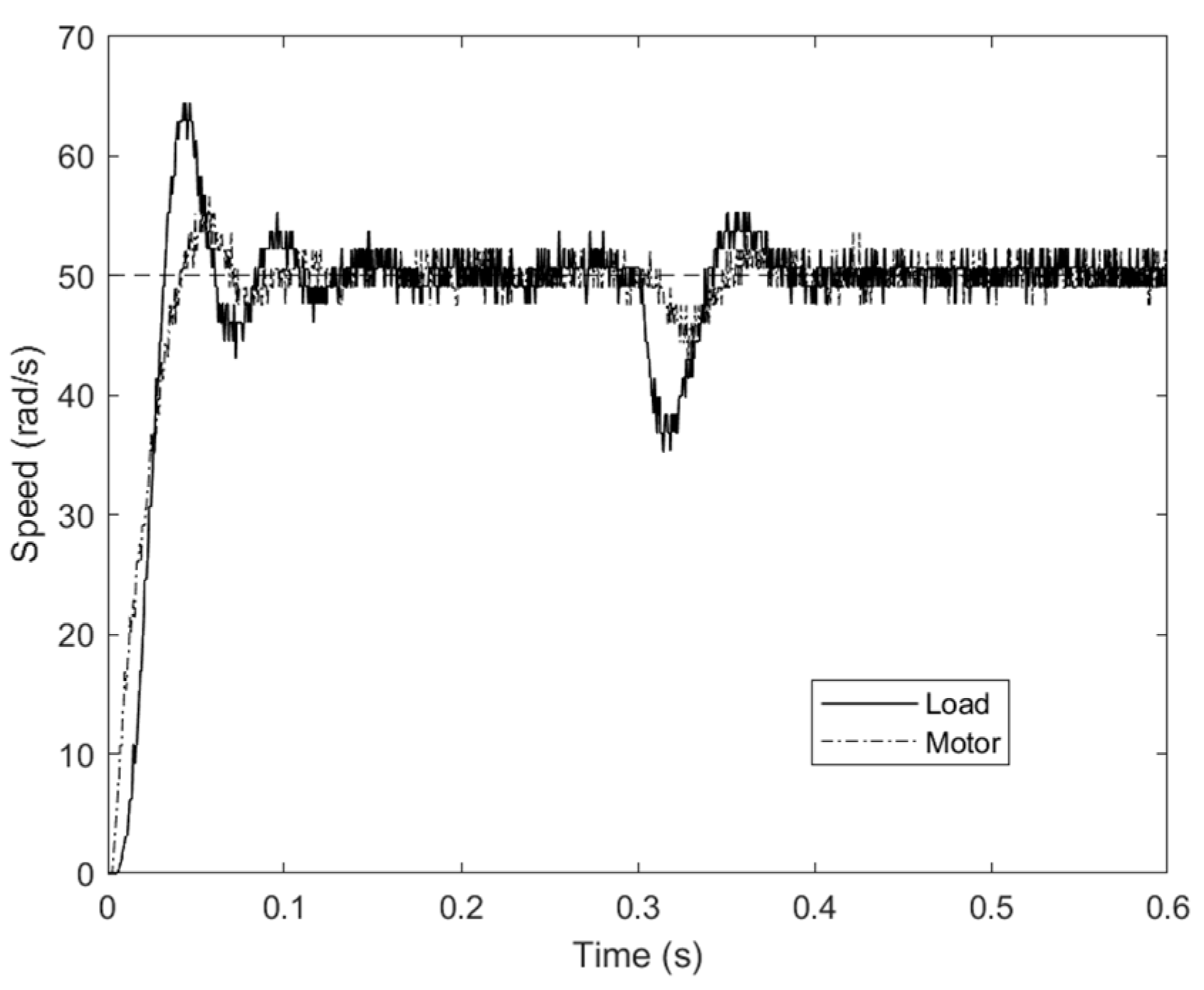
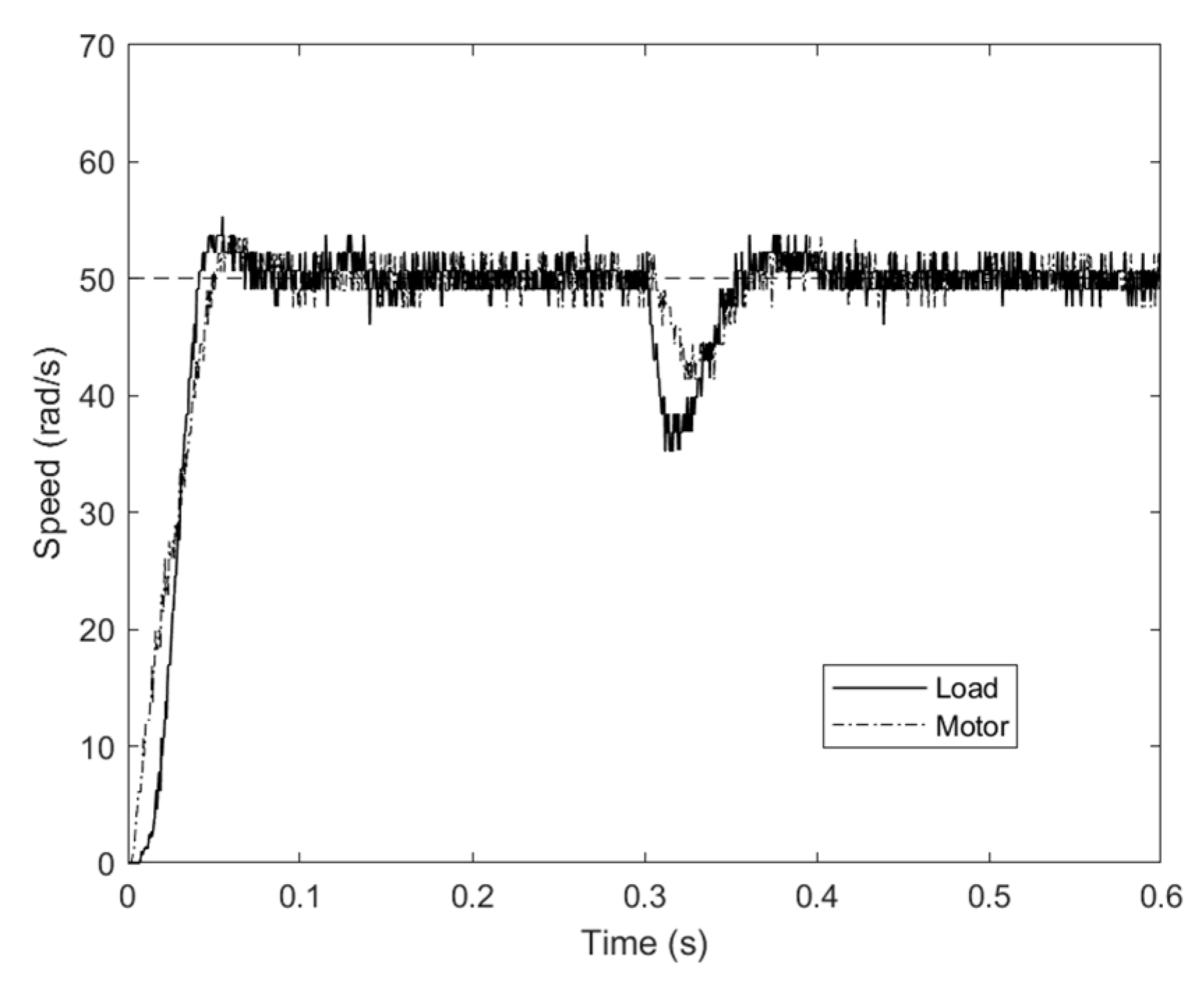
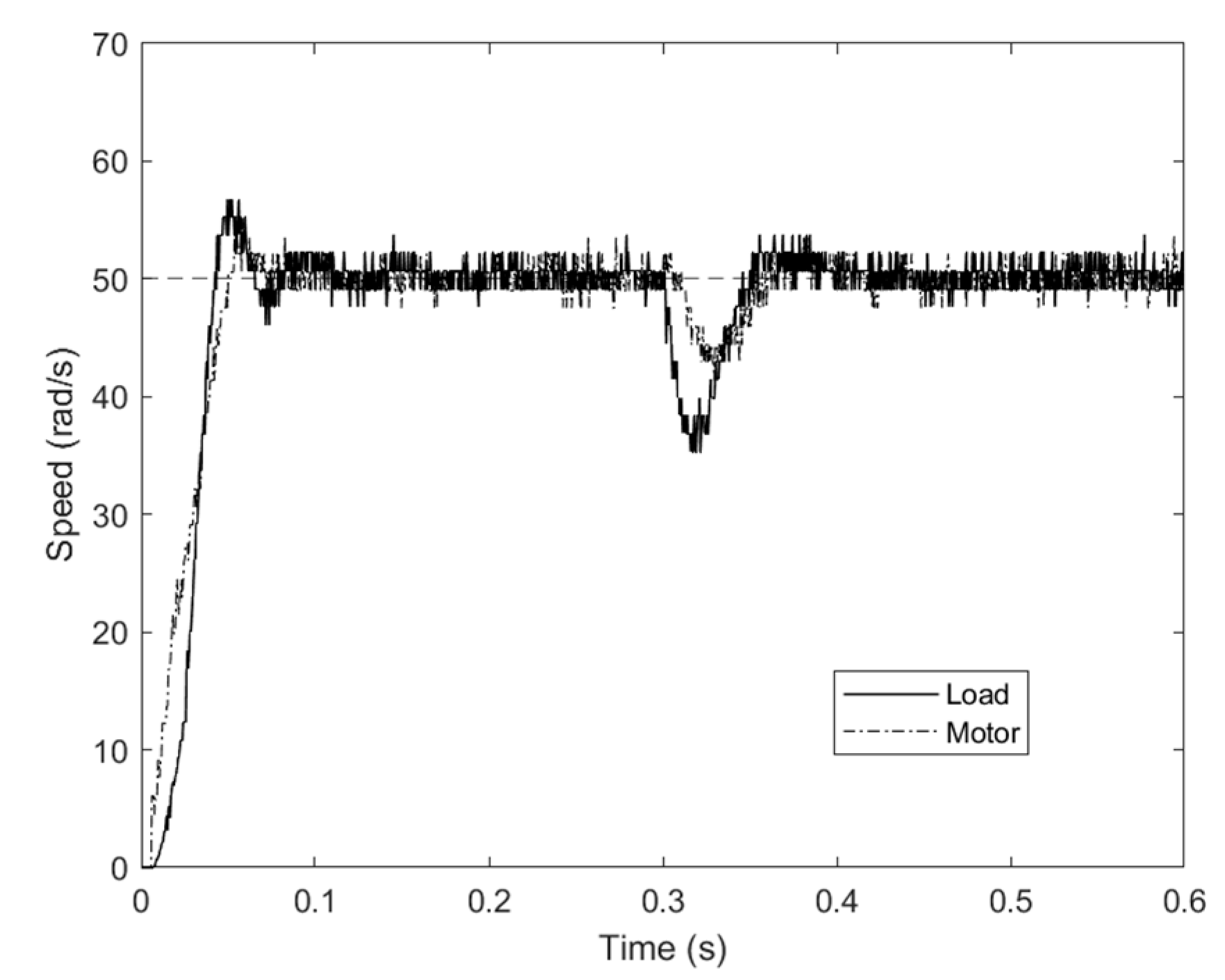
6. Experimental Section
7. A Comprehensive Comparison of Control Strategy
- Regarding the first-order inertial element, there is no need for additional feedback as state feedback or derivative computation as PID control. Moreover, the order of the inertial element is lower than that of a notch filter.
- IP with a first-order inertial element can effectively enhance system damping for IP control. Although there is a boundary for the inertia ratio in Formula (35), the boundary is useful enough since it completely covers the range of the relatively small inertia ratio for application.
| Control Strategy | Feedback Parameters | System Order | Issues or Limitations in Application | |
|---|---|---|---|---|
| PI/IP | two | fourth order | limited performance and underdamping at relatively small ratio | |
| PI/IP “+” | State feedback | three or more | fourth order | sensor cost |
| Notch filter | three or more | fourth order | Non-additional feedback, sensitive to resonance characteristic | |
| Derivative (D) | three | fourth order | sensitive to derivative computation | |
| Inertial element | three | fifth order | Non-additional feedback, no derivative computation as PID, damping improvement but limited-scope inertial ratio in Formula (35) | |
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, G.; Furusho, J. Speed control of two-inertia system by PI/PID control. IEEE Trans. Ind. Electron. 2000, 47, 603–609. [Google Scholar] [CrossRef]
- Zhang, G.; Furusho, J. Control of robot arms using joint torque sensors. IEEE Control Syst. Mag. 1998, 18, 48–55. [Google Scholar]
- Li, X.; Shang, D.; Li, H.; Li, F. Resonant Suppression Method Based on PI control for Serial Manipulator Servo Drive System. Sci. Prog. 2020, 103, 1–29. [Google Scholar] [CrossRef]
- Moberg, S.; Öhr, J.; Gunnarsson, S. A Benchmark Problem for Robust Feedback Control of a Flexible Manipulator. IEEE Trans. Control Syst. Technol. 2009, 17, 1398–1405. [Google Scholar] [CrossRef]
- Franklin, G.F.; Powell, J.D.; Emami-Naeini, A. Feedback Control of Dynamic Systems, 7th ed.; Pearson Higher Education, Inc.: New York, NY, USA, 2015; Chapter 10. [Google Scholar]
- Wang, D.; Zhang, S.; Wang, L.; Liu, Y. Developing A Ball Screw Drive System of High-Speed Machine Tool Considering Dynamics. IEEE Trans. Ind. Electron. 2022, 69, 2966–2976. [Google Scholar] [CrossRef]
- Kambrath, J.K.; Wang, Y.; Yoon, Y.J.; Alexander, A.A.; Liu, X.; Wilson, G.; Gajanayake, C.J.; Gupta, A.K. Modeling and Control of Marine Diesel Generator System with Active Protection. IEEE Trans. Transp. Electrif. 2018, 4, 249–271. [Google Scholar] [CrossRef]
- Kambrath, J.K.; Khan, M.S.U.; Wang, Y.; Maswood, A.I.; Yoon, Y.J. A Novel Control Technique to Reduce the Effects of Torsional Interaction in Wind Turbine System. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 2090–2105. [Google Scholar] [CrossRef]
- O’Sullivan, M.; Bingham, C.M.; Schofield, N. High-Performance Control of Dual-Inertia Servo-Drive Systems Using Low-Cost Integrated SAW Torque Transducers. IEEE Trans. Ind. Electron. 2006, 53, 1226–1237. [Google Scholar] [CrossRef]
- Kai, T.; Sekiguchi, H.; Ikeda, H. Relative Vibration Suppression in a Position Machines with Acceleration Feedback control. IEEJ J. Ind. Appl. 2018, 7, 15–21. [Google Scholar]
- Thomsen, S.; Hoffmann, N.; Fuchs, F.W. PI Control, PI-Based State Space Control, and Model-Based Predictive Control for Drive Systems With Elastically Coupled Loads—A Comparative Study. IEEE Trans. Ind. Electron. 2011, 58, 3647–3657. [Google Scholar] [CrossRef]
- Szabat, K.; Orlowska-Kowalska, T. Vibration suppression in a two-mass drive system using PI speed controller and additional feedbacks—Comparative study. IEEE Trans. Ind. Electron. 2007, 54, 1193–1206. [Google Scholar] [CrossRef]
- Saarakkala, S.E.; Hinkkanen, M. State-Space Speed Control of Two-Mass Mechanical Systems: Analytical Tuning and Experimental Evaluation. IEEE Trans. Ind. Appl. 2014, 50, 3428–3437. [Google Scholar] [CrossRef]
- Szabat, K.; Orlowska-Kowalska, T.; Dybkowski, M. Indirect adaptive control of induction motor drive system with an elastic coupling. IEEE Trans. Ind. Electron. 2009, 56, 4038–4042. [Google Scholar] [CrossRef]
- Szabat, K.; Than-Van, T.; Kaminski, M. A modified fuzzy luenberger observer for a two-mass drive system. IEEE Trans. Ind. Inform. 2015, 11, 531–539. [Google Scholar] [CrossRef]
- Li, P.; Duan, G.R. High-Order Fully Actuated Control Approaches of Flexible Servo Systems Based on Singular Perturbation Theory. IEEE/ASME Trans. Mechatron. 2023, 28, 3386–3399. [Google Scholar] [CrossRef]
- Wang, S.; Na, J.; Chen, Q. Adaptive Predefined Performance Sliding Mode Control of Motor Driving Systems with Disturbances. IEEE Trans. Energy Convers. 2021, 31, 1931–1939. [Google Scholar] [CrossRef]
- Jung, H.; Jeon, K.; Kang, J.; Oh, S. Iterative Feedback Tuning of Cascade Control of Two-Inertia System. IEEE Control Syst. Lett. 2021, 5, 785–790. [Google Scholar] [CrossRef]
- Szabat, K.; Wróbel, K.; Dróżdż, K.; Janiszewski, D.; Pajchrowski, T.; Wójcik, A. A Fuzzy Unscented Kalman Filter in the Adaptive Control System of a Drive System with a Flexible Joint. Energies 2020, 13, 2056. [Google Scholar] [CrossRef]
- Szczepanski, R.; Kaminski, M.; Tarczewski, T. Auto-Tuning Process of State Feedback Speed Controller Applied for Two-Mass System. Energies 2020, 13, 3067. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering, 5th ed.; Pearson Hall Inc.: New York, NY, USA, 2010; Chapter 8. [Google Scholar]
- Chen, Y.; Yang, M.; Long, J.; Hu, K.; Xu, D.; Blaabjerg, F. Analysis of Oscillation Frequency Deviation in Elastic Coupling Digital Drive System and Robust Notch Filter Strategy. IEEE Trans. Ind. Electron. 2019, 66, 90–101. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, M.; Sun, Y.; Long, J.; Xu, D.; Blaabjerg, F. A Modified Bi-Quad Filter Tuning Strategy for Mechanical Resonance Suppression in Industrial Servo Drive Systems. IEEE Trans. Power Electron. 2021, 36, 10395–10408. [Google Scholar] [CrossRef]
- Sonzogni, G.; Mazzoleni, M.; Polver, M.; Ferramosca, A.; Previdi, F. Notch filter design with stability guarantees for mechanical resonance suppression in SISO LTI two-mass drive systems. In Proceedings of the 2023 62nd IEEE Conference on Decision and Control (CDC), Singapore, 13–15 December 2023; pp. 7745–7750. [Google Scholar]
- Ma, C.; Cao, J.; Qiao, Y. Polynomial-method-based design of low-order controllers for two-mass systems. IEEE Trans. Ind. Electron. 2013, 60, 969–978. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, C.; Lai, S.; Chen, Z.; Chen, L. Frequency-dependent equivalent impedance analysis for optimizing vehicle inertial suspensions. Nonlinear Dyn. 2024, 113, 9373–9398. [Google Scholar] [CrossRef]
- Graham, D.; Lathrop, R.C. The Synthesis of “Optimum” Transient Response: Criteria and Standard Forms. Trans. Am. Inst. Electr. Eng. Part II Appl. Ind. 1953, 72, 273–288. [Google Scholar] [CrossRef]
- Zhang, G.; Hou, P. Optimization Design of Cogging Torque for Electric Power Steering Motors. Machines 2024, 12, 517. [Google Scholar] [CrossRef]




| R | ||
|---|---|---|
| 1 | 0.354 | 0.5 |
| 0.75 | 0.265 | 0.375 |
| 0.5 | 0.177 | 0.25 |
| R | |
|---|---|
| 1 | [0.707, 1] |
| 0.75 | [0.595, 1] |
| 0.5 | [0.466, 1] |
| 0.75 | 0.480 | 1.150 | 0.251 | 0.506 | 0.521 |
| 0.85 | 0.434 | 1.150 | 0.244 | 0.491 | 0.521 |
| 0.95 | 0.399 | 1.150 | 0.235 | 0.473 | 0.521 |
| R | = 0.75 | = 0.85 | = 0.95 | |||
|---|---|---|---|---|---|---|
| 1 | 0.667 | 0.333 | 0.596 | 0.294 | 0.544 | 0.263 |
| 0.75 | 0.480 | 0.250 | 0.434 | 0.221 | 0.399 | 0.197 |
| 0.5 | 0.308 | 0.167 | 0.282 | 0.147 | 0.262 | 0.132 |
| R | ||
|---|---|---|
| 0.5 | 1.107 | 1 |
| 0.75 | 1.150 | 1 |
| 1 | 1.189 | 1 |
| Inertia Ratio | ||
|---|---|---|
| 1 | 1.3 × 10−4 | 1.3 × 10−4 |
| 0.73 | 1.78 × 10−4 | 1.3 × 10−4 |
| 0.56 | 2.32 × 10−4 | 1.3 × 10−4 |
| Setting Time (s) for Reference Speed | Setting Time (s) for Disturbance | |||||
|---|---|---|---|---|---|---|
| R = 1 | R = 0.73 | R = 0.56 | R = 1 | R = 0.73 | R = 0.56 | |
| IP | 0.15 | 0.155 | 0.16 | 0.088 | 0.1 | 0.11 |
| IPF | 0.057 | 0.062 | 0.063 | 0.057 | 0.078 | 0.082 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Xie, S.; Hou, P.; Wang, X. Design Technique on Speed Control Combined with an Inertial Element for Vibration Suppression. Machines 2025, 13, 573. https://doi.org/10.3390/machines13070573
Zhang G, Xie S, Hou P, Wang X. Design Technique on Speed Control Combined with an Inertial Element for Vibration Suppression. Machines. 2025; 13(7):573. https://doi.org/10.3390/machines13070573
Chicago/Turabian StyleZhang, Guoguang, Shuntai Xie, Peng Hou, and Xiaoguang Wang. 2025. "Design Technique on Speed Control Combined with an Inertial Element for Vibration Suppression" Machines 13, no. 7: 573. https://doi.org/10.3390/machines13070573
APA StyleZhang, G., Xie, S., Hou, P., & Wang, X. (2025). Design Technique on Speed Control Combined with an Inertial Element for Vibration Suppression. Machines, 13(7), 573. https://doi.org/10.3390/machines13070573





