Machine Learning Applications in Parallel Robots: A Brief Review
Abstract
1. Introduction
2. Machine Learning for Kinematics
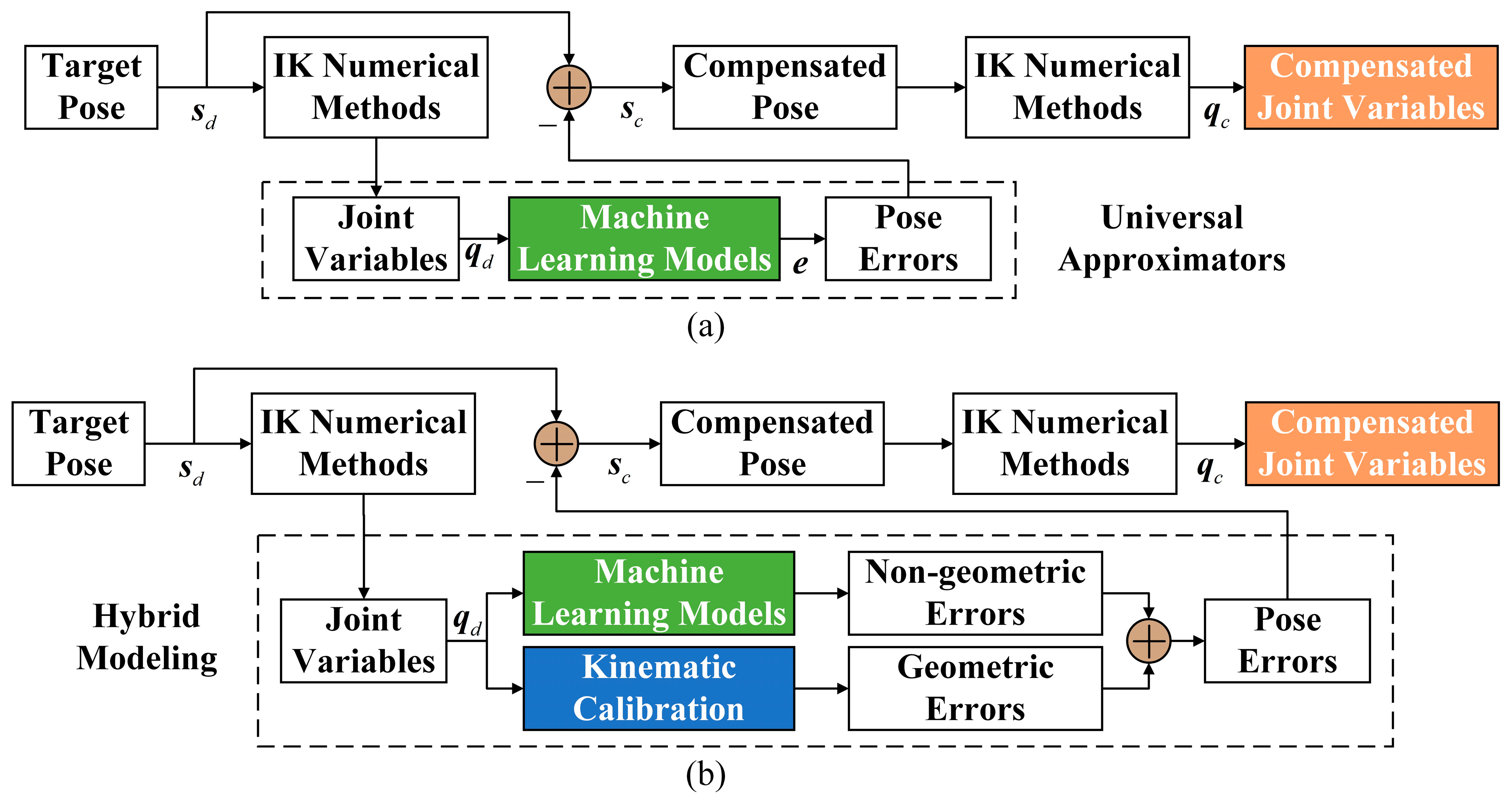
3. Machine Learning for Error Compensation
4. Machine Learning for Trajectory Tracking and Control
4.1. Hybrid Machine Learning-Augmented Control
4.2. Adaptive Neural Network Controllers
4.3. Fuzzy Neural Network Controllers
4.4. Deep Learning and Reinforcement Learning Approaches
5. Machine Learning for Other Applications
6. Conclusions and Outlook
- Kinematic computation: ML has proven effective in improving the efficiency of IK computations and delivering reliable FK solutions. It also shows clear advantages in handling redundancy and singularities—areas traditionally difficult for analytical and numerical methods.
- Error compensation: data-driven models eliminate the need for explicit error modeling, enabling unified handling of both geometric and non-geometric errors.
- Control and trajectory tracking: ML-based controllers—especially hybrid and adaptive neural controllers— improve system adaptability and robustness under dynamic uncertainties through online learning, particularly in CDPR systems that are highly affected by nonlinearity and external disturbances.
- Emerging applications: In addition to the above, ML applications have also expanded into design synthesis, workspace analysis, trajectory generation, and fault diagnosis, accelerating the development of next-generation intelligent parallel robotic systems.
- Developing hybrid modeling frameworks that integrate physics-based models with data-driven techniques to improve generalization and robustness.
- Leveraging transfer learning and domain adaptation to reduce data requirements and enhance model transferability across different robot platforms.
- Advancing lightweight NN architectures and edge computing approaches to support efficient deployment on real-time embedded systems.
- Establishing open datasets and standardized benchmarking platforms, along with deeper interdisciplinary collaboration between the robotics and AI communities, to foster reproducibility and accelerate innovation in the field.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AI | Artificial intelligence |
| ANN | Artificial neural network |
| BP | Backpropagation |
| CDPR | Cable-driven parallel robot |
| CNN | Convolutional neural network |
| DDPG | Deep deterministic policy gradient |
| DL | Deep learning |
| DOF | Degree of freedom |
| DRL | Deep reinforcement learning |
| DRNN | Diagonal recurrent neural network |
| DT | Decision tree |
| FK | Forward kinematics |
| FNN | Fuzzy neural network |
| GA | Genetic algorithm |
| GNN | Graph neural network |
| IDC | Inverse dynamic controller |
| IK | Inverse kinematics |
| LSTM | Long short-term memory |
| ML | Machine learning |
| MLP | Multi-layer perceptron |
| NN | Neural network |
| PID | Proportional-integral-derivative |
| RBF | Radial basis function |
| RF | Random forest |
| RL | Reinforcement learning |
| RNN | Recurrent neural network |
| SGD | Stochastic gradient descent |
| SMC | Sliding mode control |
| SVM | Support vector machine |
References
- Meng, Q.; Kecskeméthy, A.; Liu, X.J. Motion–Force Interaction Performance of Parallel Robotic Mechanisms. SmartBot 2025, 1, e12006. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z.; Shao, Z. Kinematic performance analysis and promotion of a spatial 3-RPaS parallel manipulator with multiple actuation modes. J. Mech. Sci. Technol. 2019, 33, 889–902. [Google Scholar] [CrossRef]
- Stewart, D. A platform with six degrees of freedom. Proc. Inst. Mech. Eng. 1965, 180, 371–386. [Google Scholar] [CrossRef]
- Dasgupta, B.; Mruthyunjaya, T.S. The Stewart Platform Manipulator: A Review. Mech. Mach. Theory 2000, 35, 15–40. [Google Scholar] [CrossRef]
- Cao, W.A.; Yang, D.; Ding, H. A method for stiffness analysis of overconstrained parallel robotic mechanisms with Scara motion. Rob. Comput. Integr. Manuf. 2018, 49, 426–435. [Google Scholar] [CrossRef]
- Zheng, F.; Xin, S.; Han, X.; Hua, L.; Zhuang, W.; Hu, X.; Chai, F. Heavy-load Nonapod: A novel flexible redundant parallel kinematic machine for multi-DoF forming process. Int. J. Mach. Tools Manuf. 2024, 200, 104183. [Google Scholar] [CrossRef]
- Staicu, S.; Shao, Z.; Zhang, Z.; Tang, X.; Wang, L. Kinematic analysis of the X4 translational–rotational parallel robot. Int. J. Adv. Rob. Syst. 2018, 15, 1729881418803849. [Google Scholar] [CrossRef]
- Hesselbach, J.; Wrege, J.; Raatz, A.; Becker, O. Aspects on design of high precision parallel robots. Assem. Autom. 2004, 24, 49–57. [Google Scholar] [CrossRef]
- Dong, W.; Du, Z.; Xiao, Y.; Chen, X. Development of a parallel kinematic motion simulator platform. Mechatronics 2013, 23, 154–161. [Google Scholar] [CrossRef]
- Meng, Q.; Xie, F.; Liu, X.J. Conceptual design and kinematic analysis of a novel parallel robot for high-speed pick-and-place operations. Front. Mech. Eng. 2018, 13, 211–224. [Google Scholar] [CrossRef]
- Russo, M.; Zhang, D.; Liu, X.J.; Xie, Z. A review of parallel kinematic machine tools: Design, modeling, and applications. Int. J. Mach. Tools Manuf. 2024, 196, 104118. [Google Scholar] [CrossRef]
- Liu, G.; Qu, Z.; Han, J.; Liu, X. Systematic optimal design procedures for the Gough-Stewart platform used as motion simulators. Ind. Robot. 2013, 40, 550–558. [Google Scholar] [CrossRef]
- Pierrot, F.; Reynaud, C.; Fournier, A. DELTA: A simple and efficient parallel robot. Robotica 1990, 8, 105–109. [Google Scholar] [CrossRef]
- Chen, X.; Liu, X.J.; Xie, F.; Sun, T. A comparison study on motion/force transmissibility of two typical 3-DOF parallel manipulators: The sprint Z3 and A3 tool heads. Int. J. Adv. Rob. Syst. 2014, 11, 5. [Google Scholar] [CrossRef]
- Zhang, Z.; Shao, Z.; You, Z.; Tang, X.; Zi, B.; Yang, G.; Gosselin, C.; Caro, S. State-of-the-art on theories and applications of cable-driven parallel robots. Front. Mech. Eng. 2022, 17, 37. [Google Scholar] [CrossRef]
- Zarebidoki, M.; Dhupia, J.S.; Xu, W. A review of cable-driven parallel robots: Typical configurations, analysis techniques, and control methods. IEEE Rob. Autom. Mag. 2022, 29, 89–106. [Google Scholar] [CrossRef]
- Duan, J.; Shao, Z.; Zhang, Z.; Peng, F. Performance simulation and energetic analysis of TBot high-speed cable-driven parallel robot. ASME J. Mech. Rob. 2022, 14, 024504. [Google Scholar] [CrossRef]
- Cui, Z.; Tang, X.; Hou, S.; Sun, H. Research on controllable stiffness of redundant cable-driven parallel robots. IEEE/ASME Trans. Mechatron. 2018, 23, 2390–2401. [Google Scholar] [CrossRef]
- Tang, X.; Shao, Z. Trajectory generation and tracking control of a multi-level hybrid support manipulator in FAST. Mechatronics 2013, 23, 1113–1122. [Google Scholar] [CrossRef]
- Shao, Z.; Xie, G.; Zhang, Z.; Wang, L. Design and analysis of the cable-driven parallel robot for cleaning exterior wall of buildings. Int. J. Adv. Rob. Syst. 2021, 18, 1729881421990313. [Google Scholar] [CrossRef]
- Zhang, Z.; Shao, Z.; Wang, L. Optimization and implementation of a high-speed 3-DOFs translational cable-driven parallel robot. Mech. Mach. Theory 2020, 145, 103693. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhang, Z. An efficient numerical method for forward kinematics of parallel robots. IEEE Access 2019, 7, 128758–128766. [Google Scholar] [CrossRef]
- Wen, K.; Gosselin, C. Forward kinematic analysis of kinematically redundant hybrid parallel robots. ASME J. Mech. Rob. 2020, 12, 061008. [Google Scholar] [CrossRef]
- Xie, G.; Zhang, Z.; Shao, Z.; Wang, L. Research on the orientation error of the translational cable-driven parallel robots. ASME J. Mech. Rob. 2022, 14, 031003. [Google Scholar] [CrossRef]
- Huang, C.; Xie, F.; Liu, X.J.; Meng, Q. Error modeling and sensitivity analysis of a parallel robot with R-(SS)2 branches. Int. J. Intell. Rob. Appl. 2020, 4, 416–428. [Google Scholar] [CrossRef]
- Mo, J.; Shao, Z.; Guan, L.; Xie, F.; Tang, X. Dynamic performance analysis of the X4 high-speed pick-and-place parallel robot. Rob. Comput. Integr. Manuf. 2017, 46, 48–57. [Google Scholar] [CrossRef]
- Zhang, Z.; Shao, Z.; Peng, F.; Li, H.; Wang, L. Workspace analysis and optimal design of a translational cable-driven parallel robot with passive springs. ASME J. Mech. Rob. 2020, 12, 051005. [Google Scholar] [CrossRef]
- Shao, Z.; Tang, X.; Wang, L.; Chen, X. Dynamic modeling and wind vibration control of the feed support system in FAST. Nonlinear Dyn. 2012, 67, 965–985. [Google Scholar] [CrossRef]
- Soori, M.; Arezoo, B.; Dastres, R. Artificial intelligence; machine learning and deep learning in advanced robotics, a review. Cognit. Rob. 2023, 3, 54–70. [Google Scholar] [CrossRef]
- Zou, J.; Han, Y.; So, S.S. Overview of artificial neural networks. In Artificial Neural Networks: Methods and Applications; Livingstone, D.J., Ed.; Humana Press: Totowa, NJ, USA, 2009; Volume 458, pp. 14–22. [Google Scholar] [CrossRef]
- Agatonovic-Kustrin, S.; Beresford, R. Basic concepts of artificial neural network (ANN) modeling and its application in pharmaceutical research. J. Pharm. Biomed. Anal. 2000, 22, 717–727. [Google Scholar] [CrossRef]
- Kruse, R.; Mostaghim, S.; Borgelt, C.; Braune, C.; Steinbrecher, M. Multi-layer perceptrons. In Computational Intelligence: A Methodological Introduction; Springer: Cham, Switzerland, 2022; pp. 53–124. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6999–7019. [Google Scholar] [CrossRef] [PubMed]
- Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Phys. D 2020, 404, 132306. [Google Scholar] [CrossRef]
- Mahesh, B. Machine Learning Algorithms-A Review. Int. J. Sci. Res. (IJSR) 2020, 9, 381–386. [Google Scholar] [CrossRef]
- Toquica, J.S.; Oliveira, P.S.; Souza, W.S.; Motta, J.M.; Borges, D.L. An analytical and a Deep Learning model for solving the inverse kinematic problem of an industrial parallel robot. Comput. Ind. Eng. 2021, 151, 106682. [Google Scholar] [CrossRef]
- Chauhan, D.K.; Vundavilli, P.R. Forward kinematics of the Stewart parallel manipulator using machine learning. Int. J. Comput. Methods 2022, 19, 2142009. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, Z.; Cai, C.; Yang, M.; Zhang, H.; Fu, L.; Zhang, J. Deep learning-based predicting and compensating method for the pose deviations of parallel robots. Comput. Ind. Eng. 2024, 191, 110179. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, H.; Liu, Z.; Cai, C.; Fu, L.; Yang, M.; Chen, H. Deep learning-based interpretable prediction and compensation method for improving pose accuracy of parallel robots. Expert Syst. Appl. 2025, 268, 126289. [Google Scholar] [CrossRef]
- Azar, A.T.; Zhu, Q.; Khamis, A.; Zhao, D. Control design approaches for parallel robot manipulators: A review. Int. J. Modell. Identif. Control 2017, 28, 199–211. [Google Scholar] [CrossRef]
- Nomanfar, P.; Notash, L. Brief review of reinforcement learning control for cable-driven parallel robots. In Cable-Driven Parallel Robots. CableCon 2023. Mechanisms and Machine Science; Caro, S., Pott, A., Bruckmann, T., Eds.; Springer: Cham, Switzerland, 2023; Volume 132, pp. 161–172. [Google Scholar] [CrossRef]
- Thomas, M.J.; Sanjeev, M.M.; Sudheer, A.P.; ML, J. Comparative study of various machine learning algorithms and Denavit–Hartenberg approach for the inverse kinematic solutions in a 3-PP SS parallel manipulator. Ind. Robot 2020, 47, 683–695. [Google Scholar] [CrossRef]
- Ghasemi, J.; Moradinezhad, R.; Hosseini, M.A. Kinematic synthesis of parallel manipulator via neural network approach. Int. J. Eng. 2017, 30, 1319–1325. [Google Scholar] [CrossRef]
- Yang, C.; Zheng, S.; Jin, J.; Zhu, S.; Han, J. Forward kinematics analysis of parallel manipulator using modified global Newton-Raphson method. J. Cent. South Univ. Technol. 2010, 17, 1264–1270. [Google Scholar] [CrossRef]
- Parikh, P.J.; Lam, S.S. A hybrid strategy to solve the forward kinematics problem in parallel manipulators. IEEE Trans. Rob. 2005, 21, 18–25. [Google Scholar] [CrossRef]
- Dehghani, M.; Ahmadi, M.; Khayatian, A.; Eghtesad, M.; Farid, M. Neural network solution for forward kinematics problem of HEXA parallel robot. In Proceedings of the 2008 American Control Conference, Seattle, WA, USA, 11–13 June 2008; pp. 4214–4219. [Google Scholar] [CrossRef]
- Morell, A.; Tarokh, M.; Acosta, L. Solving the forward kinematics problem in parallel robots using Support Vector Regression. Eng. Appl. Artif. Intell. 2013, 26, 1698–1706. [Google Scholar] [CrossRef]
- Zubizarreta, A.; Larrea, M.; Irigoyen, E.; Cabanes, I.; Portillo, E. Real time direct kinematic problem computation of the 3PRS robot using neural networks. Neurocomputing 2018, 271, 104–114. [Google Scholar] [CrossRef]
- Prado, A.; Zhang, H.; Agrawal, S.K. Artificial neural networks to solve forward kinematics of a wearable parallel robot with semi-rigid links. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 14524–14530. [Google Scholar] [CrossRef]
- Khalapyan, S.Y.; Glushchenko, A.I.; Rybak, L.A.; Gaponenko, E.V.; Malyshev, D.I. Intelligent computing based on neural network model in problems of kinematics and control of parallel robot. In Proceedings of the 2018 3rd Russian-Pacific Conference on Computer Technology and Applications (RPC), Vladivostok, Russia, 18–25 August 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, D.; Lei, J. Kinematic analysis of a novel 3-DOF actuation redundant parallel manipulator using artificial intelligence approach. Rob. Comput. Integr. Manuf. 2011, 27, 157–163. [Google Scholar] [CrossRef]
- Wu, G.; Shi, G.; Shi, Y. Modeling and analysis of a parallel continuum robot using artificial neural network. In Proceedings of the 2017 IEEE International Conference on Mechatronics (ICM), Churchill, VIC, Australia, 13–15 February 2017; pp. 153–158. [Google Scholar] [CrossRef]
- Khattab, Y.; Zidane, I.F.; El-Habrouk, M.; Rezeka, S. Solving Kinematics of a Parallel Manipulator Using Artificial Neural Networks. In Proceedings of the 2021 31st International Conference on Computer Theory and Applications (ICCTA), Alexandria, Egypt, 11–13 December 2021; pp. 84–89. [Google Scholar] [CrossRef]
- Liu, C.; Cao, G.; Qu, Y. Safety analysis via forward kinematics of delta parallel robot using machine learning. Saf. Sci. 2019, 117, 243–249. [Google Scholar] [CrossRef]
- Makwana, M.A.; Patolia, H.P. Forward Kinematics of Delta Manipulator by Novel Hybrid Neural Network. Int. J. Math. Eng. Manag. Sci. 2021, 6, 1694–1708. [Google Scholar] [CrossRef]
- Chawla, I.; Pathak, P.M.; Notash, L.; Samantaray, A.K.; Li, Q.; Sharma, U.K. Neural network-based inverse kineto-static analysis of cable-driven parallel robot considering cable mass and elasticity. In Cable-Driven Parallel Robots. CableCon 2021. Mechanisms and Machine Science; Gouttefarde, M., Pott, A., Bruckmann, T., Eds.; Springer: Cham, Switzerland, 2021; Volume 104, pp. 50–62. [Google Scholar] [CrossRef]
- Chawla, I.; Pathak, P.M.; Notash, L.; Samantaray, A.K.; Li, Q.; Sharma, U.K. Inverse and forward kineto-static solution of a large-scale cable-driven parallel robot using neural networks. Mech. Mach. Theory 2023, 179, 105107. [Google Scholar] [CrossRef]
- Mishra, U.A.; Caro, S. Forward kinematics for suspended under-actuated cable-driven parallel robots with elastic cables: A neural network approach. ASME J. Mech. Rob. 2022, 14, 041008. [Google Scholar] [CrossRef]
- Chen, H.; Kim, M.C.; Ko, Y.; Kim, C.S. Compensated Motion and Position Estimation of a Cable-driven Parallel Robot Based on Deep Reinforcement Learning. Int. J. Control Autom. Syst. 2023, 21, 3507–3518. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, L.; Sun, C.; Shang, W.; Jiang, L.; Pan, J. CafkNet: GNN-Empowered Forward Kinematic Modeling for Cable-Driven Parallel Robots. In Proceedings of the 2024 IEEE International Conference on Robotics and Biomimetics (ROBIO), Bangkok, Thailand, 10–14 December 2024; pp. 1712–1719. [Google Scholar] [CrossRef]
- Majarena, A.C.; Santolaria, J.; Samper, D.; Aguilar, J.J. An overview of kinematic and calibration models using internal/external sensors or constraints to improve the behavior of spatial parallel mechanisms. Sensors 2010, 10, 10256–10297. [Google Scholar] [CrossRef]
- Zhang, Z.; Xie, G.; Shao, Z.; Gosselin, C. Kinematic calibration of cable-driven parallel robots considering the pulley kinematics. Mech. Mach. Theory 2022, 169, 104648. [Google Scholar] [CrossRef]
- Bilancia, P.; Locatelli, A.; Tutarini, A.; Mucciarini, M.; Iori, M.; Pellicciari, M. Online motion accuracy compensation of industrial servomechanisms using machine learning approaches. Rob. Comput. Integr. Manuf. 2025, 91, 102838. [Google Scholar] [CrossRef]
- Yu, D. Parallel robots pose accuracy compensation using artificial neural networks. In Proceedings of the 2008 IEEE International Conference on Mechatronics and Automation, Takamatsu, Japan, 5–8 August 2008; pp. 750–754. [Google Scholar] [CrossRef]
- Yu, D. A new pose accuracy compensation method for parallel manipulators based on hybrid artificial neural network. Neural Comput. Appl. 2021, 33, 909–923. [Google Scholar] [CrossRef]
- Wang, D.; Bai, Y. Calibration of Stewart platforms using neural networks. In Proceedings of the 2012 IEEE Conference on Evolving and Adaptive Intelligent Systems, Madrid, Spain, 17–18 May 2012; pp. 170–175. [Google Scholar] [CrossRef]
- Fabritius, M.; Kraus, W.; Pott, A. Improving the Accuracy of Cable-Driven Parallel Robots Through Model Optimization and Machine-Learning. In Advances in Mechanism and Machine Science. IFToMM WC 2023. Mechanisms and Machine Science; Okada, M., Ed.; Springer: Cham, Switzerland, 2023; Volume 147, pp. 565–576. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, X.; Yang, M.; Liu, Z.; Cai, C. A deep learning approach for pose error prediction in parallel robots. Measurement 2025, 242, 115815. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, L.; Yang, M.; Fu, L. Deep Learning-Based CNN-LSTM Model Used for Predicting Pose Error of Stewart Platform. In Proceedings of the 16th International Conference on Intelligent Robotics and Applications (ICIRA2023), Hangzhou, China, 5–7 July 2023; pp. 358–370. [Google Scholar] [CrossRef]
- Akhmetzyanov, A.; Rassabin, M.; Maloletov, A.; Fadeev, M.; Klimchik, A. Deep Learning with Transfer Learning Method for Error Compensation of Cable-driven Robot. In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2020), Lieusaint-Paris, France, 7–9 July 2020; pp. 553–559. [Google Scholar] [CrossRef]
- Liao, S.; Zeng, Q.; Ehmann, K.F.; Cao, J. Parameter identification and nonparametric calibration of the tri-pyramid robot. IEEE/ASME Trans. Mechatron. 2020, 25, 2309–2317. [Google Scholar] [CrossRef]
- Song, Y.; Tian, W.; Tian, Y.; Liu, X. Calibration of a Stewart platform by designing a robust joint compensator with artificial neural networks. Precis. Eng. 2022, 77, 375–384. [Google Scholar] [CrossRef]
- Gu, L.; Xie, F.; Liu, X.J.; Chen, J.; Luo, X. Kinematic and Nonparametric Calibration of a Parallel Machining Robot Based on an Artificial Neural Network. In Advances in Mechanism, Machine Science and Engineering in China. CCMMS 2022. Lecture Notes in Mechanical Engineering; Liu, X., Ed.; Springer: Singapore, 2023; pp. 1977–1991. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y. Trajectory tracking control of a redundantly actuated parallel robot using diagonal recurrent neural network. In Proceedings of the 2009 Fifth International Conference on Natural Computation, Tianjian, China, 14–16 August 2009; pp. 292–296. [Google Scholar] [CrossRef]
- Escorcia-Hernández, J.M.; Aguilar-Sierra, H.; Aguilar-Mejía, O.; Chemori, A.; Arroyo-Núnez, J.H. An intelligent compensation through B-spline neural network for a delta parallel robot. In Proceedings of the 2019 6th International Conference on Control, Decision and Information Technologies (CoDIT), Paris, France, 23–26 April 2019; pp. 361–366. [Google Scholar] [CrossRef]
- Rahimi, S.; Jalali, H.; Yazdi, M.R.; Kalhor, A.; Masouleh, M.T. Design and practical implementation of a Neural Network self-tuned Inverse Dynamic Controller for a 3-DoF Delta parallel robot based on Arc Length Function for smooth trajectory tracking. Mechatronics 2022, 84, 102772. [Google Scholar] [CrossRef]
- Piao, J.; Kim, E.S.; Choi, H.; Moon, C.B.; Choi, E.; Park, J.O.; Kim, C.S. Indirect force control of a cable-driven parallel robot: Tension estimation using artificial neural network trained by force sensor measurements. Sensors 2019, 19, 2520. [Google Scholar] [CrossRef]
- Achili, B.; Daachi, B.; Amirat, Y.; Ali-Cherif, A.; Daâchi, M.E. A stable adaptive force/position controller for a C5 parallel robot: A neural network approach. Robotica 2012, 30, 1177–1187. [Google Scholar] [CrossRef]
- Zabihifar, S.; Yuschenko, A. Hybrid force/position control of a collaborative parallel robot using adaptive neural network. In Interactive Collaborative Robotics. ICR 2018. Lecture Notes in Computer Science; Ronzhin, A., Rigoll, G., Meshcheryakov, R., Eds.; Springer: Cham, Switzerland, 2018; Volume 11097, pp. 280–290. [Google Scholar] [CrossRef]
- Asl, H.J.; Janabi-Sharifi, F. Adaptive neural network control of cable-driven parallel robots with input saturation. Eng. Appl. Artif. Intell. 2017, 65, 252–260. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Lin, C.Y.; Su, S.F.; Tran, Q.V. Adaptive chattering free neural network based sliding mode control for trajectory tracking of redundant parallel manipulators. Asian J. Control 2019, 21, 908–923. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, X.; Liu, L.; Dai, T. Adaptive sliding mode neural network control and flexible vibration suppression of a flexible spatial parallel robot. Electronics 2021, 10, 212. [Google Scholar] [CrossRef]
- Achili, B.; Daachi, B.; Ali-Cherif, A.; Amirat, Y. Combined multi-layer perceptron neural network and sliding mode technique for parallel robots control: An adaptive approach. In Proceedings of the 2009 International Joint Conference on Neural Networks, Atlanta, GA, USA, 14–19 June 2009; pp. 28–35. [Google Scholar] [CrossRef]
- Jalaeian, F.M.; Akbarzadeh-T., M.R.; Akbarzadeh, A.; Ghaemi, M. A dynamic-growing fuzzy-neuro controller, application to a 3PSP parallel robot. In Proceedings of the 2012 IEEE International Conference on Fuzzy Systems, Brisbane, QLD, Australia, 10–15 June 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Zhu, D.; Fang, Y. Adaptive control of parallel manipulators via fuzzy-neural network algorithm. J. Control Theory Appl. 2007, 5, 295–300. [Google Scholar] [CrossRef]
- Hung, V.M.; Na, U.J. Adaptive neural fuzzy control for robot manipulator friction and disturbance compensator. In Proceedings of the 2008 International Conference on Control, Automation and Systems, Seoul, South Korea, 14–17 October 2008; pp. 2569–2574. [Google Scholar] [CrossRef]
- Lu, X.; Zhao, Y.; Liu, M. Self-learning interval type-2 fuzzy neural network controllers for trajectory control of a Delta parallel robot. Neurocomputing 2018, 283, 107–119. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Q.; Lin, Q. Parallel robot with fuzzy neural network sliding mode control. Adv. Mech. Eng. 2018, 10, 1687814018801261. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Z.; Li, M.; Gao, P. RP-YOLOX-DL: A deep learning hybrid method for parallel robots target positioning. Meas. Sci. Technol. 2023, 34, 105010. [Google Scholar] [CrossRef]
- Yadavari, H.; Aghaei, V.T.; İkizoğlu, S. Deep reinforcement learning-based control of Stewart platform with parametric simulation in ROS and Gazebo. ASME J. Mech. Rob. 2023, 15, 035001. [Google Scholar] [CrossRef]
- Sabahi, F. Introducing convex BiLSTM-based controller applied to 3-PSP spatial parallel robot manipulator. Trans. Inst. Meas. Control. 2023, 45, 3126–3137. [Google Scholar] [CrossRef]
- Zhang, X.; Diao, S.; Yang, T.; Fang, Y.; Sun, N. LSTM-NN-Enhanced Tracking Control for PAM-Driven Parallel Robot Systems With Guaranteed Performance. IEEE Trans. Circuits Syst. I Reg. Papers 2025, 1–14. [Google Scholar] [CrossRef]
- Zhang, D.; Guo, B. Utilizing Reinforcement Learning to Drive Redundant Constrained Cable-Driven Robots with Unknown Parameters. Machines 2024, 12, 372. [Google Scholar] [CrossRef]
- Lu, Y.; Wu, C.; Yao, W.; Sun, G.; Liu, J.; Wu, L. Deep reinforcement learning control of fully-constrained cable-driven parallel robots. IEEE Trans. Ind. Electron. 2022, 70, 7194–7204. [Google Scholar] [CrossRef]
- Lu, Y.; Yao, W.; Wu, C.; Li, X.; Sun, G. Disturbance observer-based control for cable-driven parallel robots with external disturbance using deep reinforcement learning. Asian J. Control 2024, 26, 2523–2538. [Google Scholar] [CrossRef]
- Grimshaw, A.; Oyekan, J. Applying deep reinforcement learning to cable driven parallel robots for balancing unstable loads: A ball case study. Front. Rob. AI 2021, 7, 611203. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.M.; Choi, S.H.; Park, J.W.; Park, K.S. Position error prediction using hybrid recurrent neural network algorithm for improvement of pose accuracy of cable-driven parallel robots. Microsyst. Technol. 2020, 26, 209–218. [Google Scholar] [CrossRef]
- Sancak, C.; Yamac, F.; Itik, M. Position control of a planar cable-driven parallel robot using reinforcement learning. Robotica 2022, 40, 3378–3395. [Google Scholar] [CrossRef]
- Bouaouda, A.; Pannequin, R.; Charpillet, F.; Martinez, D.; Boutayeb, M. Dynamic modeling and AI-based control of a cable-driven parallel robot. IFAC-Pap. 2023, 56, 10021–10026. [Google Scholar] [CrossRef]
- Ma, T.; Xiong, H.; Zhang, L.; Diao, X. Control of a cable-driven parallel robot via deep reinforcement learning. In Proceedings of the 2019 IEEE International Conference on Advanced Robotics and Its Social Impacts (ARSO), Beijing, China, 31 October–2 November 2019; pp. 275–280. [Google Scholar] [CrossRef]
- Sun, H.; Tang, X.; Wei, J. Vibration suppression for large-scale flexible structures using deep reinforcement learning based on cable-driven parallel robots. In Proceedings of the ASME 2020 International Mechanical Engineering Congress and Exposition, 16–19 November 2020; Volume 84546, p. V07AT07A035. [Google Scholar] [CrossRef]
- Raman, A.; Salvi, A.; Schmid, M.; Krovi, V. Reinforcement Learning Control of a Reconfigurable Planar Cable Driven Parallel Manipulator. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 9644–9650. [Google Scholar] [CrossRef]
- Xiong, H.; Ma, T.; Zhang, L.; Diao, X. Comparison of end-to-end and hybrid deep reinforcement learning strategies for controlling cable-driven parallel robots. Neurocomputing 2020, 377, 73–84. [Google Scholar] [CrossRef]
- Nomanfar, P.; Notash, L. Motion Control of a Cable-Driven Parallel Robot Using Reinforcement Learning Deep Deterministic Policy Gradient Multi-Agent. In Proceedings of the 2024 6th International Conference on Reconfigurable Mechanisms and Robots (ReMAR), Chicago, IL, USA, 23–26 June 2024; pp. 44–49. [Google Scholar] [CrossRef]
- Huo, X.; Song, Z.; Sun, T. A machine learning-based approach for automatic motion/constraint and mobility analysis of parallel robots. Robotica 2024, 42, 2403–2429. [Google Scholar] [CrossRef]
- Elgammal, A.T.; Magdy, M.; Lashin, M. Learning complex nonlinear dynamics of a 3D translational parallel manipulator using neural network. Heliyon 2024, 10, e37669. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, D.; Ge, Y. Design optimization of a spatial six degree-of-freedom parallel manipulator based on artificial intelligence approaches. Rob. Comput. Integr. Manuf. 2010, 26, 180–189. [Google Scholar] [CrossRef]
- Modungwa, D.; Tlale, N.; Twala, B. Application of ensemble learning approach in function approximation for dimensional synthesis of a 6 DOF parallel manipulator. In Proceedings of the 2013 6th Robotics and Mechatronics Conference (RobMech), Durban, South Africa, 30–31 October 2013; pp. 26–33. [Google Scholar] [CrossRef]
- Umakarthikeyan, S.; Ranganathan, B.N. Expanding the wrench feasible workspace of quadrotor-based mobile cable-driven parallel manipulators using multi-objective optimization and machine learning. Comput. Electr. Eng. 2024, 117, 109273. [Google Scholar] [CrossRef]
- Liu, Y.; Cao, Z.; Xiong, H.; Du, J.; Cao, H.; Zhang, L. Dynamic obstacle avoidance for cable-driven parallel robots with mobile bases via sim-to-real reinforcement learning. IEEE Rob. Autom. Lett. 2023, 8, 1683–1690. [Google Scholar] [CrossRef]
- Vu, D.; Alsmadi, A. Trajectory Planning of a CableBased Parallel Robot using Reinforcement Learning and Soft ActorCritic. WSEAS Trans. Appl. Theor. Mech. 2020, 15, 165–172. [Google Scholar] [CrossRef]
- Bettega, J.; Piva, G.; Richiedei, D.; Trevisani, A. Load torque estimation for cable failure detection in cable-driven parallel robots: A machine learning approach. Multibody Sys. Dyn. 2024, 2024, 1–29. [Google Scholar] [CrossRef]

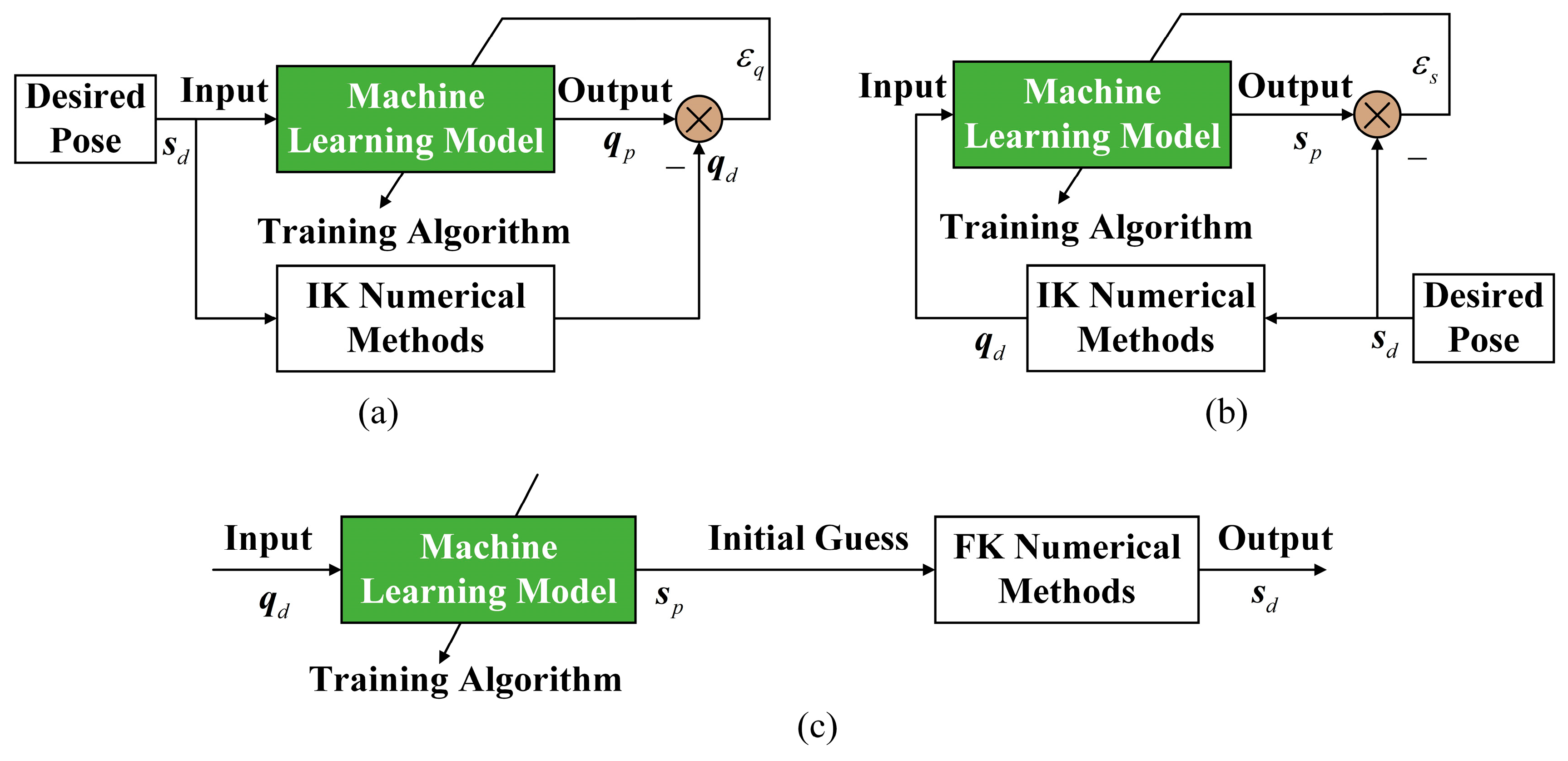
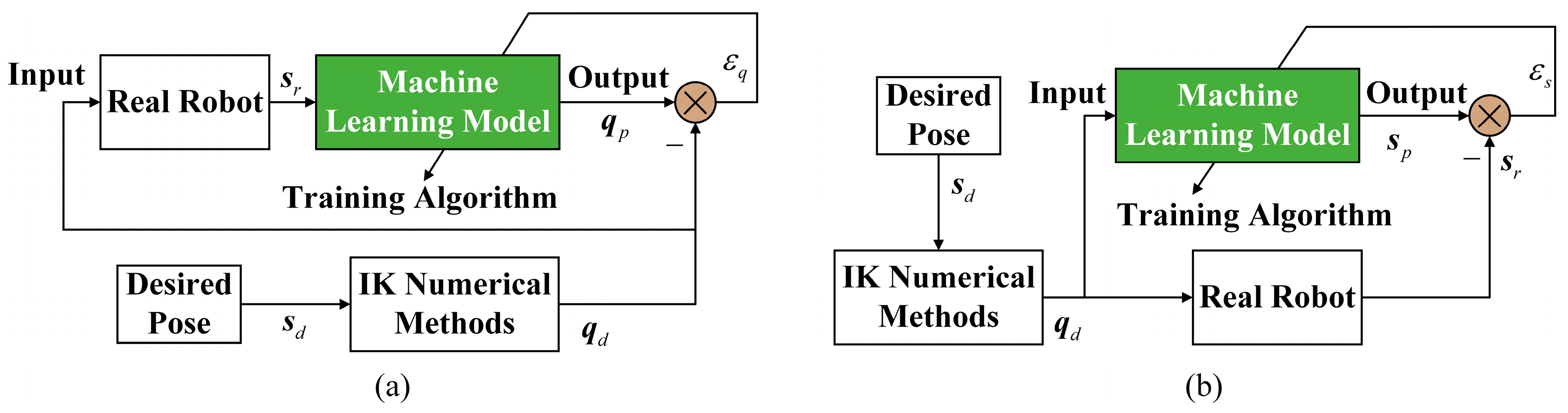

| Application Focus | Methods/Algorithms Used | Achievements | Limitations |
|---|---|---|---|
| IK | DT [42], RF [42], SVM [42] | Overcome the computational difficulties and approximation problems involved in analytical methods. | Inefficient for large-scale data. |
| MLP [42,43], RBF [43] | Faster calculation speed meets the requirements of real-time control. | Training requires a large amount of data and computing resources. | |
| IK for CDPRs | DNN [56,57] | Significant improvement in computational speed compared to numerical methods. | Requires large training time and a large dataset for initial training. |
| FK | SVM [47,51] | Fast online evaluation and better performance in convergence speed and generalization ability. | Model performance depends heavily on parameter selection. |
| MLP [46,48,50,51,52,53,58] | Effectively learning the nonlinear mapping to improve pose accuracy; faster computation than numerical method. | Requires a large training dataset and fine-tuning. | |
| GA-MLP [52,54,55] | GA optimizes NN parameters and improves accuracy. | Accuracy is sensitive to training data distribution and GA optimization increases computation time. | |
| MLP and Newton–Raphson hybrid method [45] | Reducing iterations and improving convergence efficiency. | Still relies partially on numerical methods and the hybrid strategy introduces a slight increase in memory. | |
| FK of CDPR | DL [56,57] | Significant improvement in computational speed. | A large training dataset is required due to complexity. |
| DRL [59] | Improved position estimation accuracy of CDPR in high-load scenarios. | Complex trajectory applications require more training data and high computation GPUs. | |
| GNN [60] | Superior generality, high accuracy, and low time cost. | Graph-based methods are still emerging and complex, only considers straight cables now. |
| Application Focus | Methods/Algorithms Used | Achievements | Limitations |
|---|---|---|---|
| Universal approximators | MLP [64,66] MLP + RBF [65] | Achieved accurate pose error prediction and online compensation. | Limited generalization, sensitive to data quality; training complexity increases with hybrid model. |
| DL with attention module [68] | Captures high-dimensional error features; uncertainty-aware prediction. | More complex networks and require large, labeled datasets and computing power. | |
| RNN (LSTM) [38,69] | Capturing time-dependent and sequential error patterns, beneficial in dynamic environments. | High data demand, computational burden, low interpretability, training instability. | |
| TL [70] | Shortens the data acquisition cost while maintaining compensation accuracy. | Pre-training may bias model, sim-to-real transfer gaps. | |
| Hybrid modeling | Kinematic calibration + MLP [71,72,73] | Higher modeling accuracy by applying MLP to integrate non-geometric errors into the kinematic calibration model. | Calibration effort required, hybrid models harder to tune, require data collecting for both calibration and MLP. |
| Application Focus | Methods/Algorithms Used | Achievements | Limitations |
|---|---|---|---|
| Hybrid ML-Augmented Control | DRNN + PID [74] B-spline NN + PD [75] ANN + IDC [76] ANN + P [77] | NNs compensate the nonlinear terms of the system, reduce the tracking error and vibration, and improve trajectory smoothness. | The lack of modeling accuracy of the NN model can cause the control performance of the hybrid method to be inferior, needs careful design and model tuning. |
| Adaptive Neural Network Controllers | Adaptive MLP-based controller [78,80] Adaptive RBF-based controller [79] | Generalized approximation and adaptive law help to realize stable control of position and force without the need for a complete mathematical model of the system. | Slow training convergence, strong dependence on training data, poor interpretability. |
| Adaptive RBF + SMC controller [81,82] Adaptive MLP + SMC controller [83] | The NNs extend the adaptability of SMC to the system model, enabling adaptive control of system dynamics and external environmental changes. | Difficulty in parameter adjustment, more controller design parameters, high design and debugging costs. | |
| FNN | Adaptive FNN [84,85,86] | Ability to continuously update the fuzzy rules and network parameters according to the input data, adapting to the dynamic changes in the system. | High computational complexity, sensitive to parameters such as the shape of the initial affiliation function and the learning rate. |
| FNN + SMC [87,88] | Enhanced suppression ability for system parameter uncertainty and external perturbation of SMC by combining with FNN. | More complex in design, including fuzzy rules, NN training, and sliding mold surface design, etc., with high debugging cost. | |
| DL | DL [89] | Improves accuracy and response speed. | High data and resource dependency, overfitting and generalization risk. |
| LSTM-based [91,92,97] | Captures time-varying error dynamics and improves robustness under uncertainty. | Training requires sequential labeled data, requires continuous adaptation, high resource use. | |
| DRL | DRL [90,93,94] RL + SMC [95] RL + PID [96] DRL with DDPG [98,99,100,101,102,103] | Automatic feature extraction and dynamic environment adaptation capability. | High computational resource and time cost, sensitive reward function design and uncertain convergence stability. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Meng, Q.; Cui, Z.; Yao, M.; Shao, Z.; Tao, B. Machine Learning Applications in Parallel Robots: A Brief Review. Machines 2025, 13, 565. https://doi.org/10.3390/machines13070565
Zhang Z, Meng Q, Cui Z, Yao M, Shao Z, Tao B. Machine Learning Applications in Parallel Robots: A Brief Review. Machines. 2025; 13(7):565. https://doi.org/10.3390/machines13070565
Chicago/Turabian StyleZhang, Zhaokun, Qizhi Meng, Zhiwei Cui, Ming Yao, Zhufeng Shao, and Bo Tao. 2025. "Machine Learning Applications in Parallel Robots: A Brief Review" Machines 13, no. 7: 565. https://doi.org/10.3390/machines13070565
APA StyleZhang, Z., Meng, Q., Cui, Z., Yao, M., Shao, Z., & Tao, B. (2025). Machine Learning Applications in Parallel Robots: A Brief Review. Machines, 13(7), 565. https://doi.org/10.3390/machines13070565



_Zhang.png)





