Nonblocking Modular Supervisory Control of Discrete Event Systems via Reinforcement Learning and K-Means Clustering
Abstract
1. Introduction
1.1. Traditional Methods for Coordinator Computing
1.2. RL-Based Methods
1.3. Motivation and Contributions
2. Preliminaries
2.1. Deterministic Finite Automata (DFA)
- Q denotes a finite, nonempty set of states;
- is a finite, nonempty alphabet representing the set of event labels;
- is a (partially defined) transition function;
- is the designated initial state;
- represents the set of marker (or accepting) states.
2.2. SCT and Local Modular Supervisors
- is the state set;
- is the set of events;
- is the partial transition function. For and ,
- is the initial state;
- is the set of marker states.
2.3. Optimal Controller for the Markov Decision Process
- S denotes a finite state space containing at least one state;
- represents the finite set of available actions;
- specifies state transition probabilities;
- identifies the initial system state;
- defines the step reward function.
2.4. K-Means Clustering
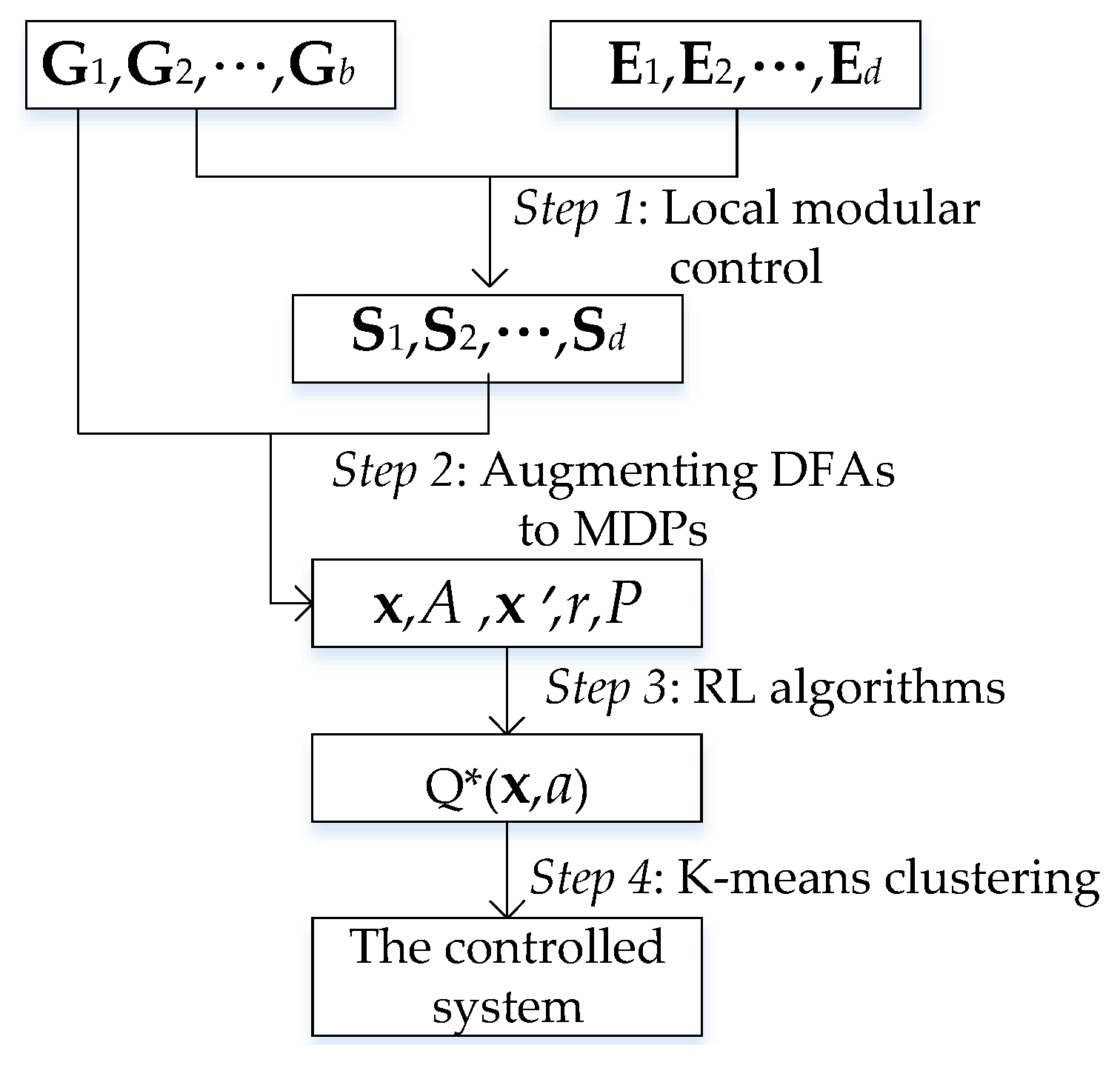
3. Schema of the Overall Approach
4. Combination of SCT, RL, and K-Means Clustering
4.1. Augmenting DFAs to MDPs
4.2. Online Inference by K-Means Clustering
| Algorithm 1: Q-learning for computing state-action values |
| Data: , , , , , e, , and |
| Result: A converged state-action table |
 |
| Algorithm 2: Computing the permitted event subset at based on and K-means clustering |
| Data: The learned Q-function , a reachable state , and the threshold |
| Result: Permitted event subset |
 |
5. Case Studies for Quantitative Evaluations
5.1. Supervisory Control of a Production Transfer Line
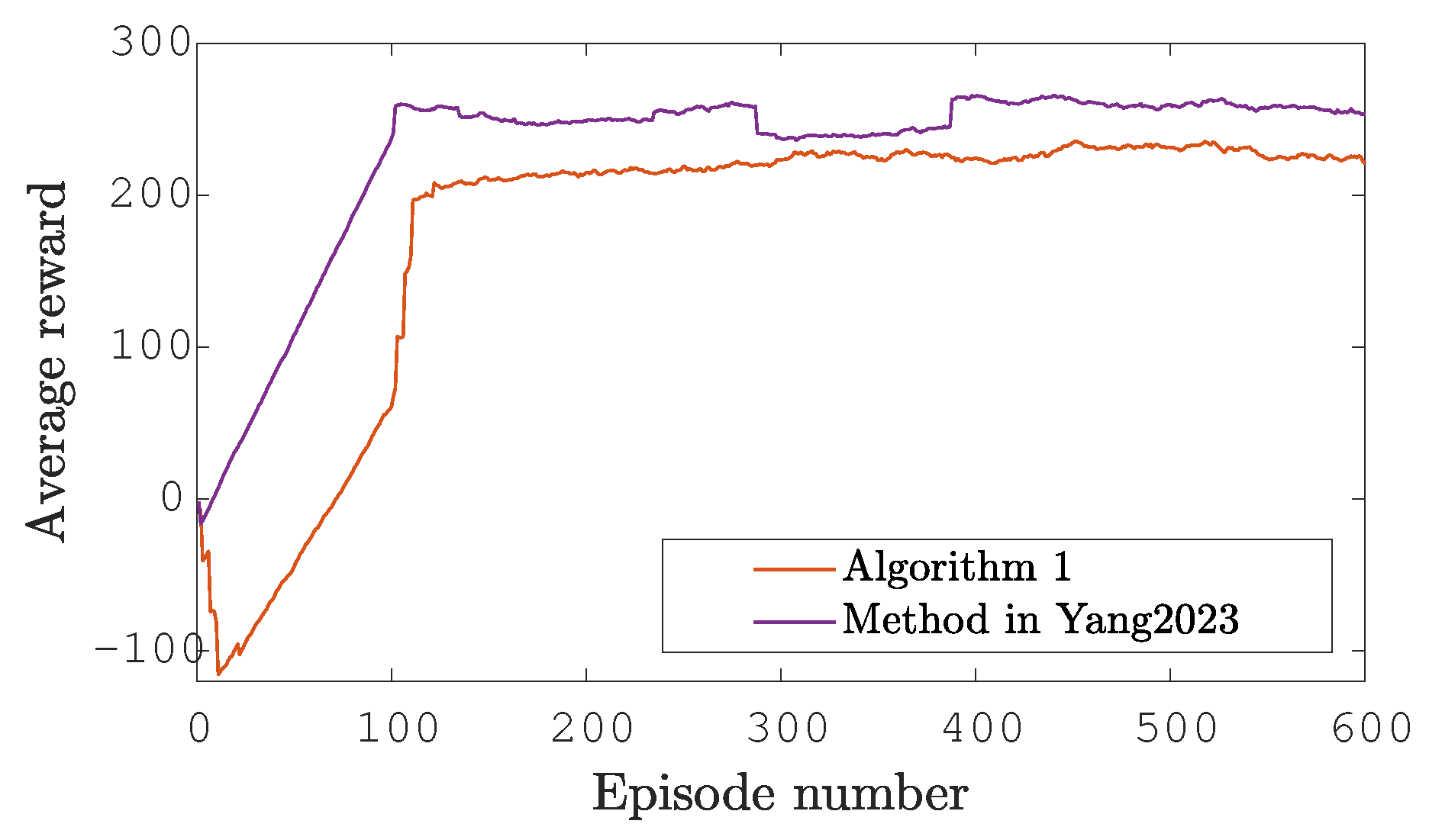
5.1.1. Computation of the Q Function Values
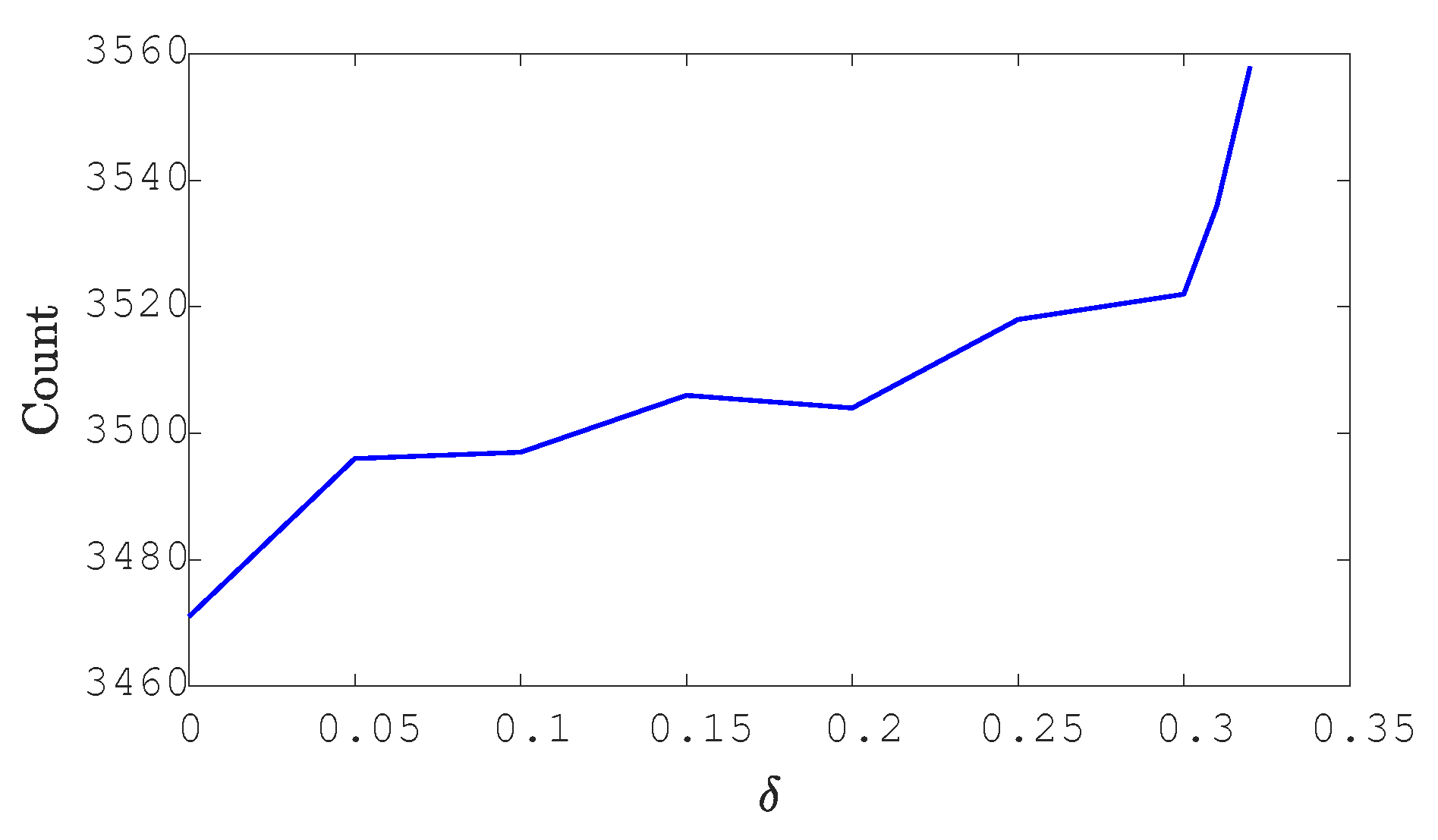
5.1.2. Online Inference for the Final Supervisor
5.2. Control of an Automatically Guided Vehicles System
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wonham, W.M.; Cai, K. Supervisory Control of Discrete-Event Systems; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Patrik, B.; Fabian, M. Calculating Restart States for Systems Modeled by Operations Using Supervisory Control Theory. Machines 2013, 1, 116–141. [Google Scholar] [CrossRef]
- Wonham, W.M.; Ramadge, P.J. Modular supervisory control of discrete-event systems. Math. Control. Signals Syst. 1988, 1, 13–30. [Google Scholar] [CrossRef]
- Queiroz, M.H.d.; Cury, J.E.R. Modular supervisory control of large scale discrete event systems. In Proceedings of the International Conference on Discrete Event Systems, Anchorage, AK, USA, 27 September 2000; pp. 103–110. [Google Scholar]
- Feng, L.; Wonham, W.M. Computationally Efficient Supervisor Design: Control Flow Decomposition. In Proceedings of the IEEE 8th International Workshop on Discrete Event Systems, Ann Arbor, MI, USA, 10–12 July 2006; pp. 9–14. [Google Scholar]
- Goorden, M.; van de Mortel-Fronczak, J.; Reniers, M.; Fabian, M.; Fokkink, W.; Rooda, J. Model properties for efficient synthesis of nonblocking modular supervisors. Control Eng. Pract. 2021, 112, 104830. [Google Scholar] [CrossRef]
- Schmidt, K.; Marchand, H.; Gaudin, B. Modular and decentralized supervisory control of concurrent discrete event systems using reduced system models. In Proceedings of the IEEE 8th International Workshop on Discrete Event Systems, Ann Arbor, MI, USA, 10–12 July 2006; pp. 149–154. [Google Scholar]
- Schmidt, K.; Moor, T.; Perk, S. Nonblocking hierarchical control of decentralized discrete event systems. IEEE Trans. Autom. Control 2008, 53, 2252–2265. [Google Scholar] [CrossRef]
- Leduc, R.J.; Brandin, B.A.; Lawford, M.; Wonham, W.M. Hierarchical interface-based supervisory control-part I: Serial case. IEEE Trans. Autom. Control 2005, 50, 1322–1335. [Google Scholar]
- Liu, Y.; Liu, F. Optimal control of discrete event systems under uncertain environment based on supervisory control theory and reinforcement learning. Sci. Rep. 2024, 14, 25077. [Google Scholar] [CrossRef]
- Dai, J.; Lin, H. A learning-based synthesis approach to decentralized supervisory control of discrete event systems with unknown plants. Control Theory Technol. 2014, 12, 218–233. [Google Scholar] [CrossRef]
- Malik, R.; Åkesson, K.; Flordal, H.; Fabian, M. Supremica–an efficient tool for large-scale discrete event systems. IFAC-PapersOnLine 2017, 50, 5794–5799. [Google Scholar] [CrossRef]
- Farooqui, A.; Hagebring, F.; Fabian, M. MIDES: A tool for supervisor synthesis via active learning. In Proceedings of the IEEE 17th International Conference on Automation Science and Engineering, Lyon, France, 23–27 August 2021; pp. 792–797. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Kajiwara, K.; Yamasaki, T. Adaptive supervisory control based on a preference of agents for decentralized discrete event systems. In Proceedings of the IEEE SICE Annual Conference, Taipei, Taiwan, 18–21 August 2010; pp. 1027–1032. [Google Scholar]
- Zielinski, K.M.C.; Hendges, L.V.; Florindo, J.B.; Lopes, Y.K.; Ribeiro, R.; Teixeira, M.; Casanova, D. Flexible control of Discrete Event Systems using environment simulation and Reinforcement Learning. Appl. Soft Comput. 2021, 111, 107714. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, D.; Yang, M.; He, J. Integrating reinforcement learning and supervisory control theory for optimal directed control of discrete-event systems. Neurocomputing 2024, 613, 128720. [Google Scholar] [CrossRef]
- Konishi, M.; Sasaki, T.; Cai, K. Efficient safe control via deep reinforcement learning and supervisory control-csae study on multi-robot warehouse automation. IFAC-PapersOnLine 2022, 55, 16–21. [Google Scholar] [CrossRef]
- Yang, J.; Tan, K.; Feng, L.; Li, Z. A model-based deep reinforcement learning approach to the nonblocking coordination of modular supervisors of discrete event systems. Inf. Sci. 2023, 630, 305–321. [Google Scholar] [CrossRef]
- Yang, J.; Tan, K.; Feng, L.; El-Sherbeeny, A.M.; Li, Z. Reducing the learning time of reinforcement learning for the supervisory control of discrete event systems. IEEE Access 2023, 11, 59840–59853. [Google Scholar] [CrossRef]
- Ran, X.; Xi, Y.; Lu, Y.; Wang, X.; Lu, Z. Comprehensive survey on hierarchical clustering algorithms and the recent developments. Artif. Intell. Rev. 2023, 56, 8219–8264. [Google Scholar] [CrossRef]
- Kurani, A.; Doshi, P.; Vakharia, A.; Shah, M. A comprehensive comparative study of artificial neural network (ANN) and support vector machines (SVM) on stock forecasting. Ann. Data Sci. 2023, 10, 183–208. [Google Scholar] [CrossRef]
- Kriegel, H.P.; Kröger, P.; Sander, J.; Zimek, A. Density-based clustering. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 231–240. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Ikotun, A.M.; Ezugwu, A.E.; Abualigah, L.; Abuhaija, B.; Heming, J. K-means clustering algorithms: A comprehensive review, variants analysis, and advances in the era of big data. Inf. Sci. 2023, 622, 178–210. [Google Scholar] [CrossRef]
- Feng, L.; Wonham, W.M. TCT: A computation tool for supervisory control synthesis. In Proceedings of the IEEE 8th International Workshop on Discrete Event Systems, Ann Arbor, MI, USA, 10–12 July 2006; pp. 3–8. [Google Scholar]
- Su, R.; Wonham, W.M. What information really matters in supervisor reduction? Automatica 2018, 95, 368–377. [Google Scholar] [CrossRef]
- Malik, R.; Teixeira, M. Optimal modular control of discrete event systems with distinguishers and approximations. Discret. Event Dyn. Syst. 2021, 31, 659–691. [Google Scholar] [CrossRef]
- Lewis, F.L.; Vrabie, D.; Vamvoudakis, K.G. Reinforcement learning and feedback control: Using natural decision methods to design optimal adaptive controller. IEEE Control Syst. Mag. 2012, 32, 76–105. [Google Scholar]
- Feng, L.; Cai, K.; Wonham, W. A structural approach to the non-blocking supervisory control of discrete-event systems. Int. J. Adv. Manuf. Technol. 2009, 41, 1152–1168. [Google Scholar] [CrossRef]
- Wonham, W.M.; Ramadge, P.J. On the supremal controllable sublanguage of a given language. SIAM J. Control Optim. 1987, 25, 637–659. [Google Scholar] [CrossRef]
- Saglam, B.; Mutlu, F.B.; Cicek, D.C.; Kozat, S.S. Actor prioritized experience replay. J. Artif. Intell. Res. 2023, 78, 639–672. [Google Scholar] [CrossRef]







| Parameter | e | dec | MaxSt | MaxEp | Len | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| TL | 0.9 | 0.96 | 0.98 | 30 | −50 | 0.001 | 0.05 | 100 | 1000 | 30 |
| AGV | 0.95 | 0.99 | 0.95 | 30 | −50 | 0.001 | 5 × 10−5 | 100 | 5000 | 100 |
| State | Controllable Events | ||
|---|---|---|---|
| ld1 | ld2 | tst | |
| : (0,0,0,0,0) | 68.77 | −50 | −50 |
| : (0,0,1,5,0) | 89.41 | 51.41 | 83.66 |
| : (0,0,0,4,2) | 82.89 | −50 | 40.83 |
| : (1,1,0,6,1) | −42.88 | −43.08 | −43.29 |
| Methods | SCT + RL | SCT + RL + K-Means | SCT |
|---|---|---|---|
| State space size | 56 | 72 | 72 |
| Nonblocking | Yes | Yes | Yes |
| Methods | SCT + RL | SCT + RL + K-Means | SCT |
|---|---|---|---|
| State space size | 481 | 3558 | 4406 |
| Nonblocking | Yes | Yes | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Tan, K.; Feng, L. Nonblocking Modular Supervisory Control of Discrete Event Systems via Reinforcement Learning and K-Means Clustering. Machines 2025, 13, 559. https://doi.org/10.3390/machines13070559
Yang J, Tan K, Feng L. Nonblocking Modular Supervisory Control of Discrete Event Systems via Reinforcement Learning and K-Means Clustering. Machines. 2025; 13(7):559. https://doi.org/10.3390/machines13070559
Chicago/Turabian StyleYang, Junjun, Kaige Tan, and Lei Feng. 2025. "Nonblocking Modular Supervisory Control of Discrete Event Systems via Reinforcement Learning and K-Means Clustering" Machines 13, no. 7: 559. https://doi.org/10.3390/machines13070559
APA StyleYang, J., Tan, K., & Feng, L. (2025). Nonblocking Modular Supervisory Control of Discrete Event Systems via Reinforcement Learning and K-Means Clustering. Machines, 13(7), 559. https://doi.org/10.3390/machines13070559








