Research on Robot Force Compensation and Collision Detection Based on Six-Dimensional Force Sensor

Abstract

To address the shortcomings of existing robot collision detection algorithms that use six-dimensional force sensors, a force compensation algorithm based on Kane’s dynamics is proposed, along with a collision detection algorithm that uses the six-dimensional force sensor data combined with the robot’s outer surface equations to derive the robot body’s collision point coordinates. Firstly, a collision detection model for a joint-type collaborative robot is presented. Secondly, based on Kane’s dynamics equations, a force compensation model for the joint-type collaborative robot is established and the corresponding force compensation algorithm is derived. Thirdly, a collision detection algorithm is derived, and an example using a cylindrical joint robot with a link’s outer surface equation is used to solve the collision point. The collision is categorized into nine cases, and the coordinates of the collision point are solved for each case. Finally, force compensation and collision detection experiments are conducted on an AUBO-I5 joint-type collaborative robot. The results of the force compensation show that the comparison curves for forces/torques in three directions are consistent, and the relative error is below 5.6%. The collision detection results indicate that the computed collision positions match the actual collision positions, thus verifying the correctness of the theoretical analysis of the force compensation and collision detection algorithms. The research results provide a theoretical basis for ensuring safety in human–robot collaboration.

1. Introduction

In today’s global economic environment, innovation has become a key driver of economic growth and competitiveness. With rapid advancements in technology, countries around the world are seeking new breakthroughs in the field of robotics. Collaborative robots have gained increasing recognition and adoption globally, demonstrating an indispensable role in both industrial and non-industrial sectors [1,2,3,4]. The original design intention of collaborative robots is to interact and collaborate with humans in the workplace, improving both work efficiency and safety. In a work scenario, collaborative robots directly cooperate with humans, making safety concerns of paramount importance [5,6,7]. To ensure the safety of human–robot collaboration, collision point detection in robots has become a crucial issue that needs to be addressed.

Collision point detection is not only an important means to ensure safety but also a critical basis for timely repairs of the robot body after a collision [8,9,10,11]. In the context of robot safety, operators can analyze the cause of a collision based on the specific coordinates of the collision point, preventing secondary collisions. During the later repair process, force/torque analysis can be conducted at the specific collision location, allowing for timely repairs and preventing more severe damage during subsequent operations.

In order to ensure that the robot can interact with the external environment and provide feedback with important information in a timely manner during collision point detection, the use of sensors becomes a crucial component in collision detection [12,13,14,15,16,17]. Sensors assist the robot in perceiving the external environment and help the robot make correct behavioral decisions. Vision sensors analyze and interpret the captured environmental images, converting them into symbols, enabling the robot to identify object positions and various states. However, their stability and reliability in complex environments are questionable, and the maintenance cost is relatively high. Infrared sensors detect the presence of objects by sensing certain forms of thermal radiation emitted by surrounding environmental objects. These sensors are easily interfered with by various heat sources and sunlight, and their sensitivity to detection can be influenced by the ambient temperature.

The six-dimensional force sensor can convert multidimensional force/torque signals into electrical signals, and can be used to monitor the changes in the magnitude and direction of forces/torques in three spatial directions. It represents a new branch of force sensors [18,19,20,21,22,23,24,25,26]. By installing the six-dimensional force sensor on the robot’s base to ensure safety in human–robot interaction, it not only reduces costs but also effectively reduces the system’s computational load, improving the system’s response speed. When the six-dimensional force sensor provides force/torque feedback to the robot’s control system and outputs the data to the upper-level computer, the operator can respond immediately and formulate the next task, achieving better compliance control during the robot’s operations and human–robot interaction [18,27,28].

In safety studies of robots using six-dimensional force sensors, the robot’s own gravity and dynamic forces generated by inertia can cause the six-dimensional force sensor’s detection results to be non-zero even when no external force is applied, which greatly increases the error in collision detection. Therefore, before collision detection, force compensation control should be applied to the robot, ensuring that the six-dimensional force sensor’s detection result is consistently zero under no external force, providing the foundation for the collision detection algorithm. In the area of force compensation using six-dimensional force sensors, reference [29] conducted a force-following algorithm study after compensating for gravity, allowing the robot to adjust its end-effector pose in real-time according to the feedback from the force sensor, achieving compliance with external forces. However, the study did not address dynamic force compensation. Reference [30] divides force compensation into gravity compensation and dynamic force compensation, with dynamic force compensation using the more traditional Newton–Euler method that requires more calculations. This algorithm is relatively complex, and dividing force compensation into two parts will reduce the accuracy of the algorithm.

In terms of collision point detection using six-dimensional force sensors, reference [31] projects the external collision force vector into the optimal plane for solution, obtaining two coordinates. The actual collision point is near these two points, but the exact position cannot be calculated, and the collision point can only be approximated as the midpoint of the two points, leading to a significant error between the algorithm’s collision point and the actual collision point. Further exploration of the optimal solution is needed. Reference [32] used a similar method, but the intersection of the projection lines can only fall near the real contact point’s projection, and a decision factor must be introduced to search for the optimal contact point.

In response to the shortcomings of existing collision point detection algorithms for robots using six-dimensional force sensors, this paper proposes a force compensation algorithm and a collision detection algorithm. The force compensation algorithm is based on Kane’s dynamics, converting dynamic forces into the generalized resultant force to be compensated. It unifies the derivation of force compensation and compensates the sensor’s zero position value in real-time when the robot is not subjected to external forces, addressing the issues of complexity and insufficient accuracy in previous force compensation algorithms. This provides the foundation for improving the robot collision detection algorithm. The collision detection algorithm utilizes the six-dimensional force sensor installed on the base of a joint robot and combines the robot’s outer surface equations to derive the collision point coordinates on the robot body after a collision, enabling the detection of the robot body’s collision point.

The remaining work arrangement is organized as follows: Section 2 presents the derivation process of the force compensation algorithm and collision detection algorithm for articulated collaborative robots, and takes the articulated robot with a cylindrical outer surface as an example to solve the collision point. Section 3 presents the verification of the force compensation algorithm and collision detection algorithm, and conducts error analysis on the experimental results. Section 4 summarizes the work of this article and looks forward to its future development.

2. Theoretical Analysis

2.1. Collision Detection Model

In the detection results of the six-dimensional force sensor, the force vector belongs to the generalized six-dimensional external force, allowing the sensor to detect the force’s magnitude, direction, and line of action. By analyzing the changes in the generalized force vector and torque vector expressions of the six-dimensional force sensor at the base, it can be concluded that

$$\mathcal{F}=\left[\begin{array}{c}\mathit{F}\\ \mathit{M}\end{array}\right]$$

(1)

In the Equation, F is the force vector of ${(\begin{array}{ccc}{F}_x& F_y& F_z\end{array})}^{\mathrm{T}}$; M is the torque vector of ${(\begin{array}{ccc}{M}_x& M_y& M_z\end{array})}^{\mathrm{T}}$. By using the detection results of $\mathcal{F}$, the direction vector and a point in space can be solved to obtain the representation of the spatial force vector in the sensor coordinate system. Therefore, the magnitude, direction vector, and direction cosine of the calculated resultant force are

$$F_{\mathrm{R}}=\sqrt{F_x^2+F_y^2+F_z^2}$$

(2)

$$\mathit{u}=\left(\cos \alpha ,\cos \beta ,\cos \gamma \right)$$

(3)

$$\left\{\begin{array}{c}\cos \alpha =\cos \left(F_{\mathrm{R}},\mathit{i}\right)={\displaystyle \frac{F_x}{F_{\mathrm{R}}}}\hfill \\ \cos \beta =\cos \left(F_{\mathrm{R}},\mathit{j}\right)={\displaystyle \frac{F_y}{F_{\mathrm{R}}}}\hfill \\ \cos \gamma =\cos \left(F_{\mathrm{R}},\mathit{k}\right)={\displaystyle \frac{F_z}{F_{\mathrm{R}}}}\hfill \end{array}\right.$$

(4)

Among them, the point $\mathit{P}\left(x_P,y_P,z_P\right)$ that the spatial force vector passes through can be represented by Equations (5) and (6).

$$\mathit{M}=\mathit{F}\mathit{P}$$

(5)

$$\left\{\begin{array}{c}{x}_P={\displaystyle \frac{M_x}{F_x}}\\ y_P={\displaystyle \frac{M_y}{F_y}}\\ z_P={\displaystyle \frac{M_z}{F_z}}\end{array}\right.$$

(6)

The final expression of the spatial force vector obtained in the sensor coordinate system is

$${\displaystyle \frac{x-x_P}{\cos \alpha }}={\displaystyle \frac{y-y_P}{\cos \beta }}={\displaystyle \frac{z-z_P}{\cos \gamma }}$$

(7)

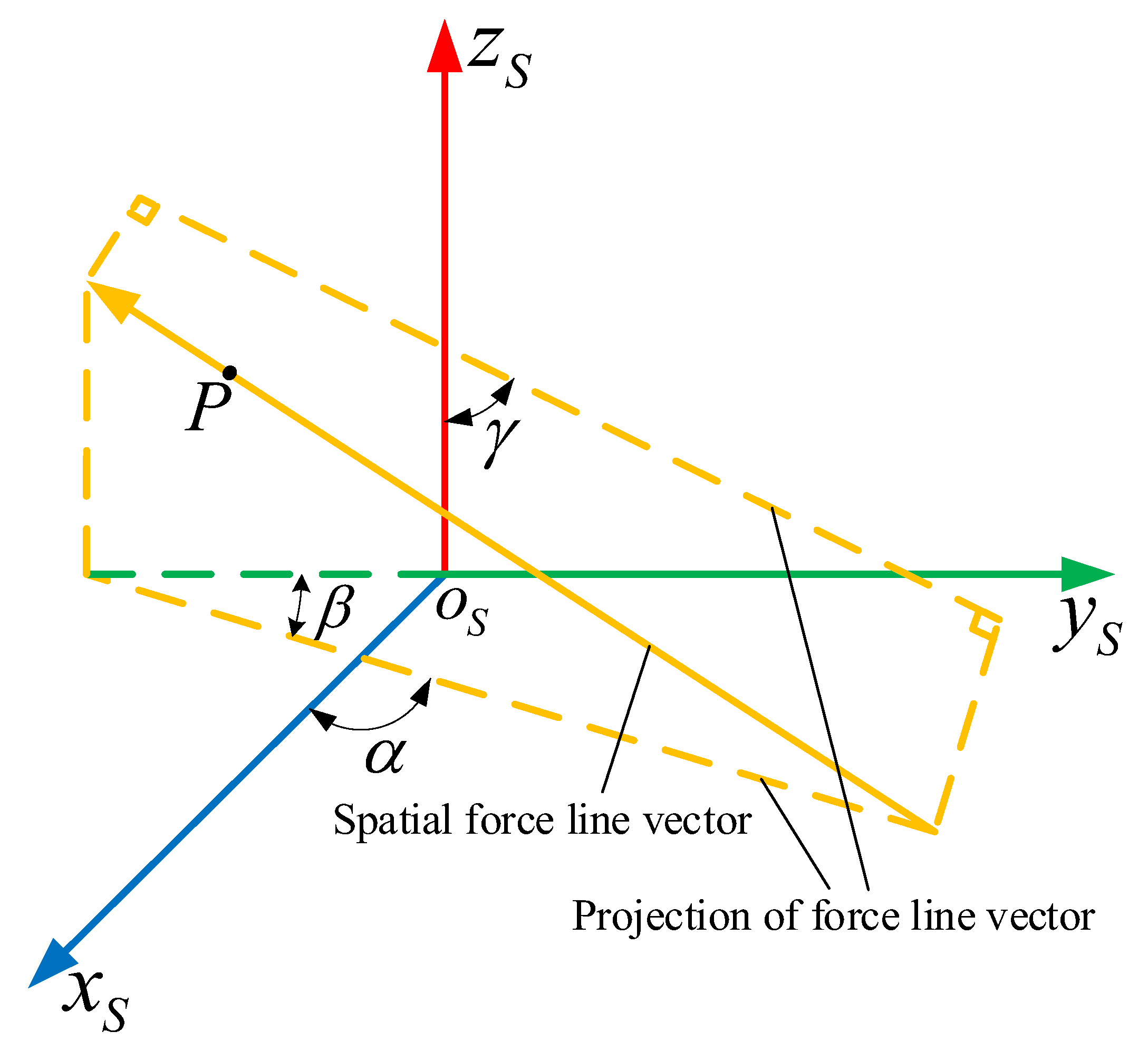
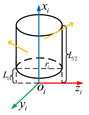
Figure 1 illustrates a schematic diagram of spatial force line vectors.

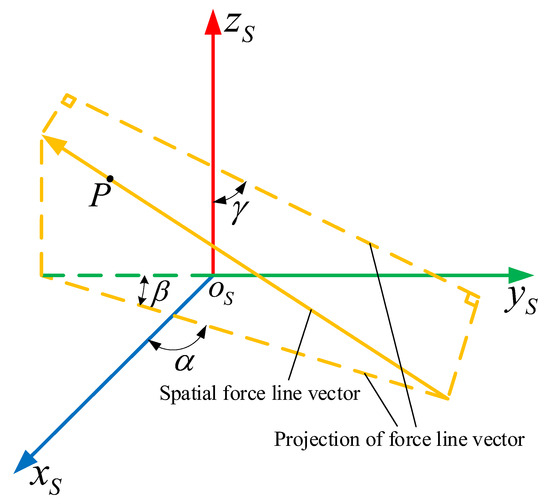
Figure 1. Schematic diagram of the spatial force line vector.

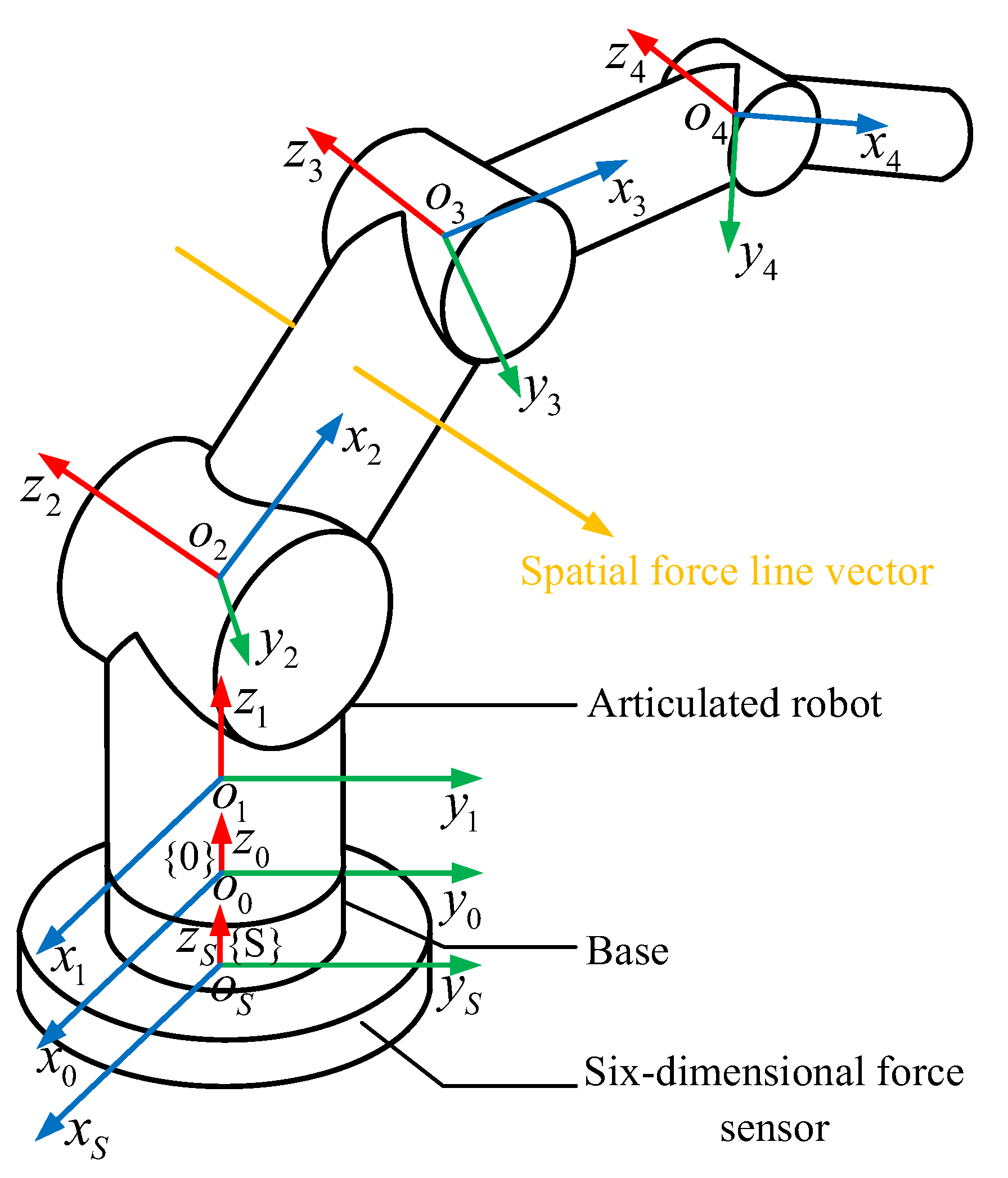
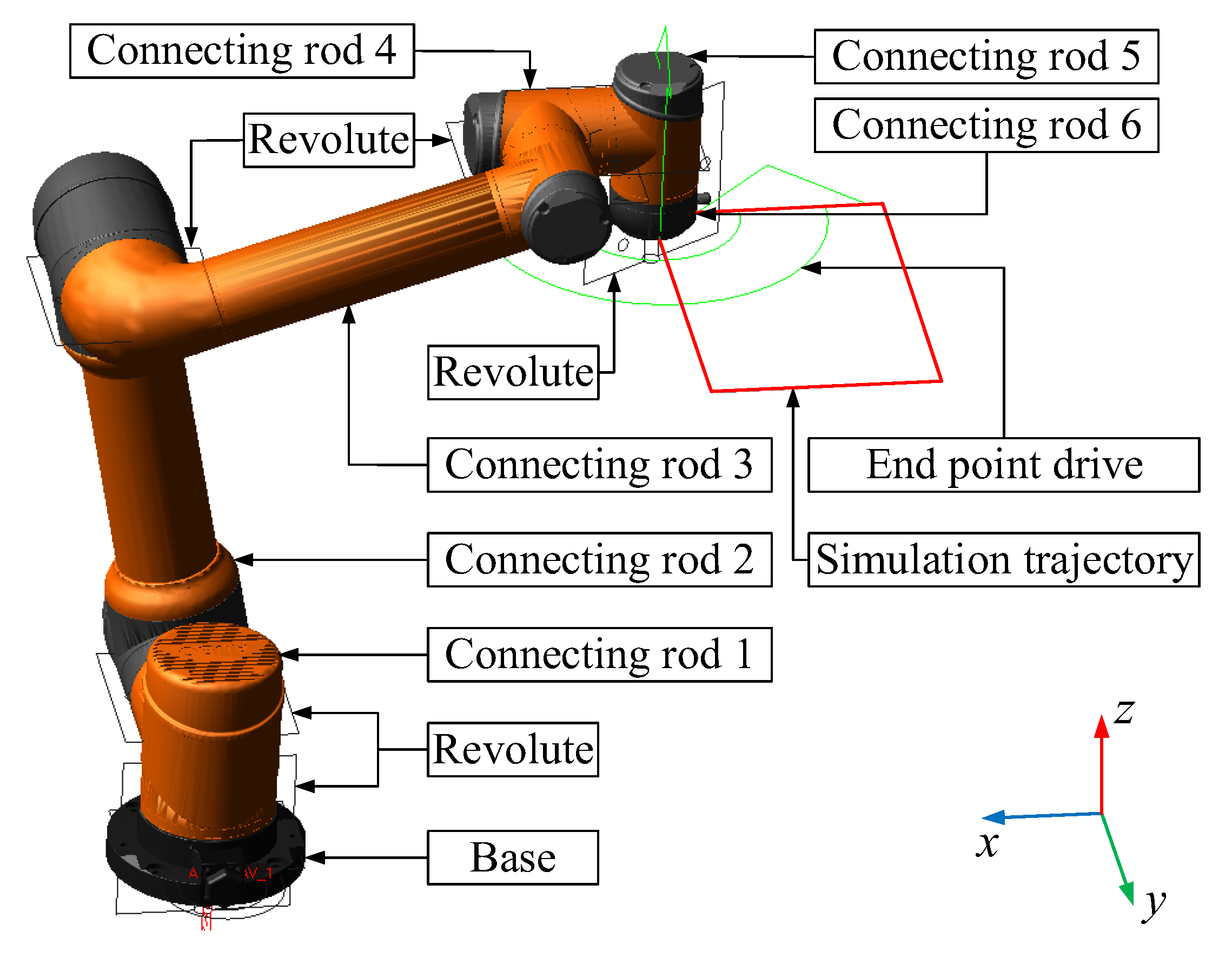
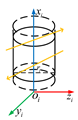
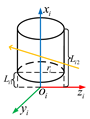
Based on the known model of the robot, the D-H parameter method is applied to establish the coordinate system of each joint of the robot, represented as $\left\{i\right\}$, $\left\{i+1\right\},\left\{i+2\right\}\cdots$. Figure 2 shows the collision detection model of the articulated robot. In this model, the coordinate system of each joint of the robot and the visual rays of the spatial force line vector are displayed. When the force line vector rays pass through the robot body, they represent that the robot has collided.

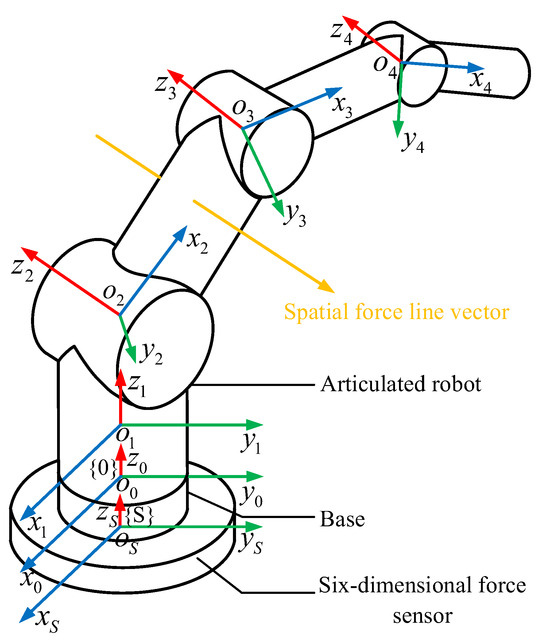
Figure 2. Collision detection model of the articulated robots.

The general expression for the homogeneous transformation matrix ${}_i{}^{i-1}\mathit{T}$ of a connecting rod is

$${}_i{}^{i-1}\mathit{T}=\left[\begin{array}{cccc}\mathrm{c}{\theta }_i& -\mathrm{s}{\theta }_i& 0& a_{i-1}\\ \mathrm{s}{\theta }_i\mathrm{c}{\alpha }_{i-1}& \mathrm{c}{\theta }_i\mathrm{c}{\alpha }_{i-1}& -\mathrm{s}{\alpha }_{i-1}& -\mathrm{s}{\alpha }_{i-1}{d}_i\\ \mathrm{s}{\theta }_i\mathrm{s}{\alpha }_{i-1}& \mathrm{c}{\theta }_i\mathrm{s}{\alpha }_{i-1}& \mathrm{c}{\alpha }_{i-1}& \mathrm{c}{\alpha }_{i-1}{d}_i\\ 0& 0& 0& 1\end{array}\right]$$

(8)

In Equation (8), $\mathrm{s}{\theta }_i$ is the abbreviation for $\sin {\theta }_i$; $\mathrm{c}{\theta }_i$ is the abbreviation for $\cos {\theta }_i$.

2.2. Force Compensation Algorithm

Robot dynamics is the core field of studying the relationship between robot motion and force/torque, providing mathematical models and physical laws for robot design, control, and optimization. The main methods for dynamic modeling include the Newton–Euler method, Lagrange method, and Kane method. The Newton–Euler method uses recursive calculations, which are divided into forward recursion and backward recursion, while the Lagrange method requires constructing the kinetic and potential energy of the system to obtain the equation of motion. The Kane method is suitable for both complete and incomplete systems. For complex systems with multiple degrees of freedom such as robotic mechanisms, applying the Kane method can reduce computational steps and improve computational efficiency [33]. In terms of modeling accuracy, the Kane method also has an advantage [34,35]. From Table 1, it can be seen that the Kane method has greater advantages in terms of computational complexity and efficiency.

Table 1. The computational scale of the robot dynamics modeling method.

Modeling Method	Number of Operations
	Multiplication	Addition
Lagrange method	2195	1719
Newton–Euler method	1541	1196
Kane method	646	394

Joint robots can be seen as a system composed of n rigid bodies, each of which can be viewed as a mass point with a mass of $m_i$ and the centroid of $C_i$, where i = 1, 2, $\cdots$, n. The Kane’s dynamics equation of the rigid-body system is

$${\displaystyle \sum _{i=1}^n\left[\left({\mathit{f}}_i-m_i{\mathit{a}}_i\right)\cdot \delta {\mathit{r}}_i\right]}=\mathbf{0}$$

(9)

In Equation (9),

${\mathit{f}}_i$—active force vector acting on mass point i;

$m_i$—the mass of mass point i;

${\mathit{a}}_i$—the acceleration vector of mass point i;

${\mathit{r}}_i$—the position vector of mass point i in the reference coordinate system;

$\delta {\mathit{r}}_i$—differential displacement of mass point i.

In Kane’s dynamics, the partial velocity ${\mathit{v}}_{C_i,{\dot{p}}_j}$ and the partial angular velocity ${\mathit{\omega }}_{C_i,{\dot{p}}_j}$ of the center of mass point i are defined as

$${\mathit{v}}_{C_i,{\dot{p}}_j}={\displaystyle \frac{\partial {\mathit{v}}_i}{\partial {\dot{\mathit{p}}}_j}}$$

(10)

$${\mathit{\omega }}_{C_i,{\dot{\mathit{p}}}_j}={\displaystyle \frac{\partial {\mathit{\omega }}_i}{\partial {\dot{\mathit{p}}}_j}}$$

(11)

Among them, ${\mathit{v}}_i$ and ${\mathit{\omega }}_i$ are the system velocity and angular velocity of connecting rod i, respectively, and ${\mathit{p}}_j$ is the centroid position coordinate of connecting rod i, where j = 1, 2, $\cdots$, n.

The differential displacement of mass point i can be expressed as

$$\delta {\mathit{r}}_i={\displaystyle \sum _{j=1}^n\frac{\partial {\mathit{r}}_i}{\partial {\mathit{p}}_j}}\delta {\mathit{p}}_j={\displaystyle \sum _{j=1}^n{\mathit{v}}_{C_i,{\dot{\mathit{p}}}_j}}\delta {\mathit{p}}_j$$

(12)

By using Equations (9)–(12), the Kane’s dynamics equation can be rewritten as

$$\left\{\begin{array}{c}{\mathit{F}}_j+{\mathit{F}}_j^{\ast }=\mathbf{0}\\ {\mathit{F}}_j={\displaystyle \sum _{i=1}^n{f}_i{\mathit{v}}_{C_i,{\dot{p}}_j}}\\ {\mathit{F}}_j^{\ast }=-{\displaystyle \sum _{i=1}^n{m}_i{\dot{\mathit{v}}}_{C_i}{\mathit{v}}_{C_i,{\dot{p}}_j}}\end{array}\right.$$

(13)

In Equation (13), ${\mathit{F}}_j$ represents the generalized active force of connecting rod i, while ${\mathit{F}}_j^{\ast }$ denotes the generalized inertial force of connecting rod i. Additionally, ${\dot{\mathit{v}}}_{C_i}$ represents the centroid acceleration of connecting rod i.

The generalized joint torques are defined as ${\mathit{M}}_1,{\mathit{M}}_2,\cdots ,{\mathit{M}}_n$, and they are expressed as

$${\mathit{M}}_i={\displaystyle \sum _{i=j}^n{m}_i}{\dot{\mathit{v}}}_{C_i}g{\mathit{v}}_{C_i,{\dot{p}}_j}+\left[{\mathit{I}}_i{\dot{\mathit{\omega }}}_i+{\mathit{\omega }}_i\times \left({\mathit{I}}_i{\mathit{\omega }}_i\right)\right]{\mathit{\omega }}_{C_i,{\dot{p}}_j}$$

(14)

In Equation (14), ${\dot{\mathit{\omega }}}_i$ represents the angular acceleration of connecting rod i, and ${\mathit{I}}_i$ denotes the inertia tensor of connecting rod i, given by

$${\mathit{I}}_i=\left[\begin{array}{ccc}{I}_{xx}& -I_{xy}& -I_{xz}\\ -I_{xy}& I_{yy}& -I_{yz}\\ -I_{xz}& -I_{yz}& I_{zz}\end{array}\right]$$

(15)

The elements in the matrix are

$$\begin{array}{l}{I}_{xx}={\displaystyle {\iiint }_V(y^2+z^2)}\rho dv\\ I_{yy}={\displaystyle {\iiint }_V(x^2+z^2)}\rho dv\\ I_{zz}={\displaystyle {\iiint }_V(x^2+y^2)}\rho dv\\ I_{xy}={\displaystyle {\iiint }_{V}xy}\rho dv\\ I_{xz}={\displaystyle {\iiint }_{V}xz}\rho dv\\ I_{yz}={\displaystyle {\iiint }_{V}yz}\rho dv\end{array}$$

(16)

In Equation (16), the rigid body consists of unit body dv and the density of the unit body is $\rho$.

The joint torque ${\mathit{M}}_i$ of each connecting rod can be decomposed into three directions of torque components, that is

$${\mathit{M}}_i={\left[\begin{array}{ccc}{M}_{ix}& M_{iy}& M_{iz}\end{array}\right]}^{\mathrm{T}}$$

(17)

The articulated robot has n rotating joints, denoted as $J_1,J_2,\cdots ,J_n$, with a distance of $l_n$ between the joints. The distance from the centroid $C_i$ of connecting rod i to joint $J_i$ is $d_i$. The joint angle ${\theta }_i$ is considered the generalized coordinate, and the rotational speed ${\dot{\theta }}_i$ is taken as the generalized velocity. The recursive algorithm for its velocity, acceleration, and partial velocity is as follows

$$\begin{array}{l}{}^i\mathit{\omega }_i={}_{i-1}{}^i\mathit{R}{}^{i-1}\mathit{\omega }_{i-1}+{\dot{\theta }}_i{}^i\overrightarrow{\mathit{Z}}_i\hfill \\ {}^i\dot{\mathit{\omega }}_i={}_{i-1}{}^i\mathit{R}{}^{i-1}\mathit{\omega }_{i-1}+{}_{i-1}{}^i\mathit{R}{}^{i-1}\mathit{\omega }_{i-1}\times {\dot{\theta }}_i{}^i\overrightarrow{\mathit{Z}}_i+{\dot{\theta }}_i{}^i\dot{\overrightarrow{\mathit{Z}}}_i\hfill \\ {}^i\mathit{v}_i={}_{i-1}{}^i\mathit{R}({}^{i-1}\mathit{\omega }_{i-1}\times {}^{i-1}l_{i-1}+{}^{i-1}\mathit{v}_{i-1})\hfill \\ {}^i\mathit{v}_{C_i}={}^i\mathit{v}_i+{}^i\mathit{\omega }_i\times {}^{i}d_i\hfill \\ {}^i\dot{\mathit{v}}_i={}_{i-1}{}^i\mathit{R}[{}^{i-1}\dot{\mathit{v}}_{i-1}+{}^{i-1}\dot{\mathit{\omega }}_{i-1}\times {}^{i-1}l_{i-1}+{}^{i-1}\dot{\mathit{\omega }}_{i-1}\times ({}^{i-1}\mathit{\omega }_{i-1}\times {}^{i-1}l_{i-1})]\hfill \\ {}^i\dot{\mathit{v}}_{C_i}={}^i\dot{\mathit{v}}_i+{}^i\dot{\mathit{\omega }}_i\times {}^{i}d_i+{}^i\mathit{\omega }_i\times ({}^i\mathit{\omega }_i\times {}^{i}d_i)\hfill \\ {}^i\mathit{\omega }_{i{\dot{\theta }}_j}={}_{i-1}{}^i\mathit{R}{}^{i-1}\mathit{\omega }_{i-1{\dot{\theta }}_j}\hfill \\ {}^i\mathit{v}_{i{\dot{\theta }}_j}={}_{i-1}{}^i\mathit{R}({}^{i-1}\mathit{\omega }_{i-1{\dot{\theta }}_j}\times {}^{i-1}l_{i-1}+{}^{i-1}\mathit{v}_{i-1{\dot{\theta }}_j})\hfill \\ {}^i\mathit{v}_{C_i,{\dot{p}}_j}={}^i\mathit{v}_{i{\dot{\theta }}_j}+{}^i\mathit{\omega }_{i{\dot{\theta }}_j}\times {}^{i}d_i\hfill \end{array}$$

(18)

In Equation (18), ${}_{i-1}{}^i\mathit{R}$ is the rotation matrix from coordinate system $\left\{i-1\right\}$ to coordinate system $\left\{i\right\}$, ${}^i\dot{\mathit{v}}_i$ represents the acceleration of connecting rod i, ${}^i\mathit{\omega }_{i{\dot{\theta }}_j}$ denotes the joint deflection velocity of connecting rod i, and ${}^i\overrightarrow{\mathit{Z}}_i$ is the unit vector of the rotational angular velocity of connecting rod i, which corresponds to the unit vector in the Z direction of coordinate system $\left\{i\right\}$, where ${}^i\overrightarrow{\mathit{Z}}_i={\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^{\mathrm{T}}$.

Subsequently, the relationship between the position, velocity, acceleration, and torque of various joints in multi-rigid-body systems is analyzed using the Kane’s dynamics equation. Based on Equation (18), the center of mass and angular velocity of each connecting rod are derived and then combined with the Kane’s dynamics equation to establish the recursive formulas for the driving force and torque of each joint actuator. Finally, we summarize the dynamic model of the multi-rigid-body system.

The Kane’s dynamics algorithm is divided into two parts: generalized active force and generalized inertial force. Generalized inertial force refers to the force generated by a robot during start stop, variable speed motion, or external force to maintain its own motion state. The joint torque generated by the inertia force of the robot can be derived from Equations (14)–(17).

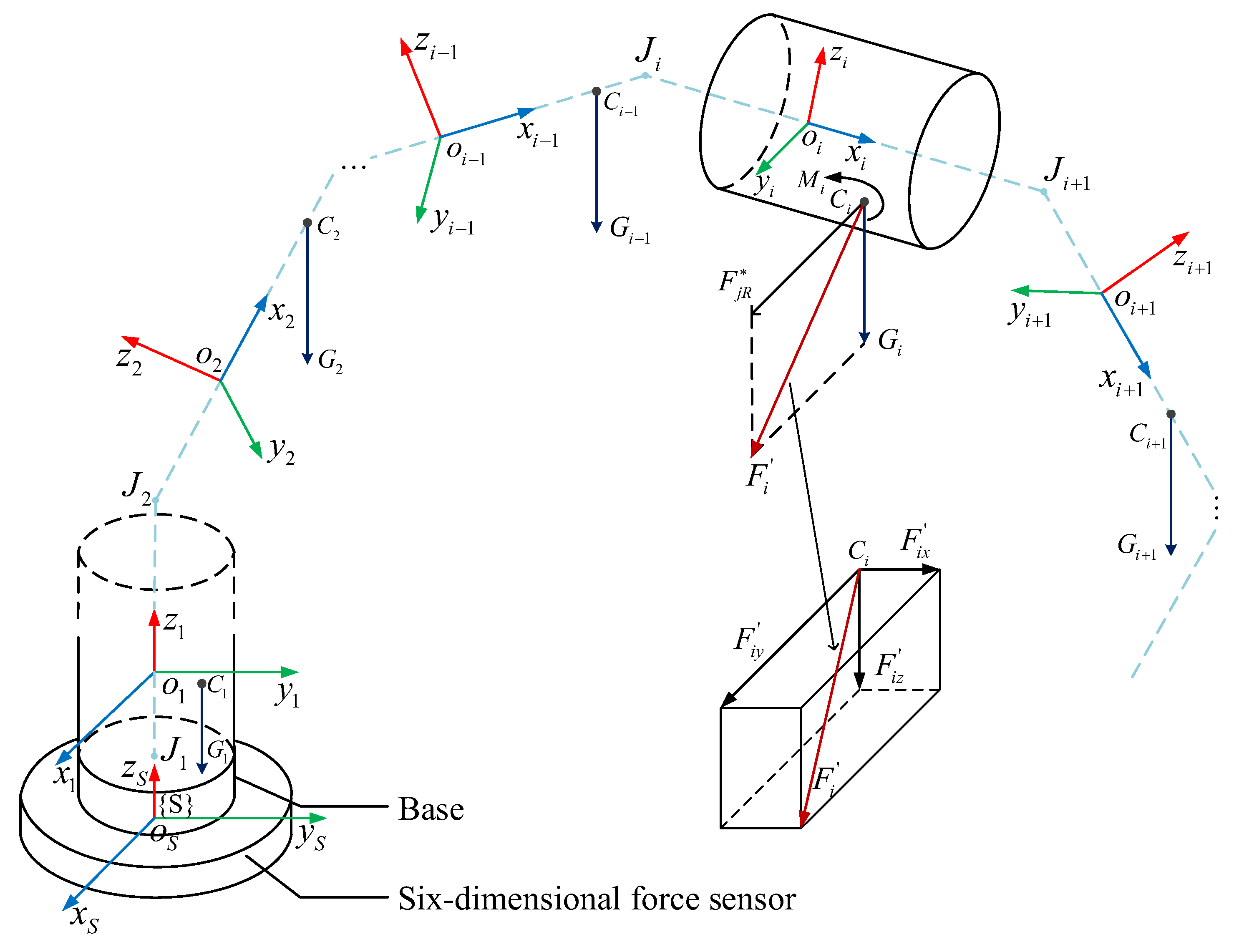
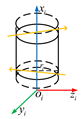
According to the Kane’s dynamics equation, the force compensation model of the joint-type collaborative robot can be established, as shown in Figure 3. Among them, the dashed line represents each link of the robot, and the coordinate system of each connecting rod and its own gravity are also represented. The generalized compensating force of connecting rod i is also shown in the figure.

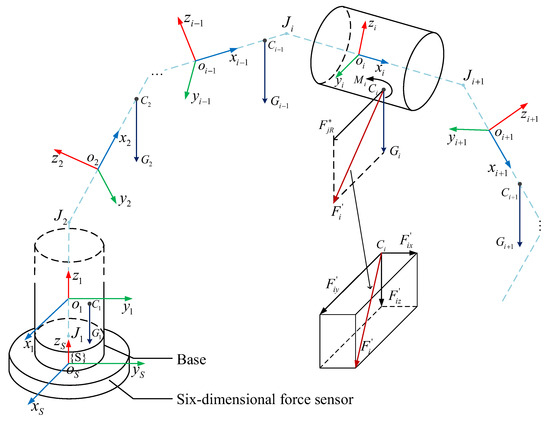
Figure 3. Force compensation model of the joint-type collaborative robot.

According to the force compensation model, the robot needs to represent the generalized compensation force and joint torque experienced by each connecting rod in the sensor coordinate system $\left\{\mathrm{S}\right\}$, assuming no external force, within the force compensation algorithm. Among them, the generalized compensating resultant force is the sum of the three directional components of the generalized inertial force and the resultant force of the connecting rod’s own gravity, expressed as

$${\mathit{F}}_{jR}^{\ast }=F_{jx}^{\ast }\mathit{i}+F_{jy}^{\ast }\mathit{j}+F_{jz}^{\ast }\mathit{k}$$

(19)

$${\mathit{G}}_i={\displaystyle \sum _{i=1}^n{m}_i}\mathit{g}$$

(20)

$${\mathit{F}}_i^{\text{'}}={\mathit{F}}_{jR}^{\ast }+{\mathit{G}}_i$$

(21)

In the equation, i is the unit vector in the positive x-axis direction, j is the unit vector in the positive y-axis direction, k is the unit vector in the positive z-axis direction, ${\mathit{F}}_{jR}^{\ast }$ is the resultant force of the three directional components of the generalized inertial force, ${\mathit{G}}_i$ is the gravitational force of the connecting rod itself, and ${\mathit{F}}_i^{\text{'}}$ is the generalized compensating resultant force.

The inertial force analysis of robot linkages must be based on the center of mass, as the center of mass is the natural reference point for rigid-body motion. The direction vector w of the generalized compensating resultant force is derived based on the position vector of the centroid ${\mathit{C}}_i$, expressed as follows

$${\mathit{C}}_i={\left[\begin{array}{ccc}{\mathit{C}}_{ix}& {\mathit{C}}_{iy}& {\mathit{C}}_{iz}\end{array}\right]}^{\mathrm{T}}$$

(22)

$$\mathit{w}=\left(\cos \alpha ,\cos \beta ,\cos \gamma \right)$$

(23)

$$\left\{\begin{array}{c}\cos \alpha ={\displaystyle \frac{C_{ix}}{\sqrt{C_{ix}^2+C_{iy}^2}}}\\ \cos \beta ={\displaystyle \frac{C_{iy}}{\sqrt{C_{ix}^2+C_{iy}^2}}}\\ \cos \gamma ={\displaystyle \frac{C_{iz}}{\sqrt{C_{iy}^2+C_{iz}^2}}}\end{array}\right.$$

(24)

Then, the components of the generalized compensating force in three directions can be obtained, allowing the generalized compensating force ${\mathit{F}}_i$ to be uniformly represented as

$$\left\{\begin{array}{c}{F}_{ix}^{\prime }={\mathit{F}}_i^{\prime }\cos \alpha \\ F_{iy}^{\prime }={\mathit{F}}_i^{\prime }\cos \beta \\ F_{iz}^{\prime }={\mathit{F}}_i^{\prime }\cos \gamma \end{array}\right.$$

(25)

$${\mathit{F}}_i={\left[\begin{array}{ccc}{F}_{ix}^{\text{'}}& F_{iy}^{\text{'}}& F_{iz}^{\text{'}}\end{array}\right]}^{\mathrm{T}}$$

(26)

From Equations (19)–(26), it can be concluded that the generalized force/torque vector that needs to be compensated on connecting rod i is

$${}^i\mathcal{F}=\left[\begin{array}{c}{\mathit{F}}_i\\ {\mathit{M}}_i\end{array}\right]$$

(27)

According to the Cartesian coordinate transformation, it is represented in the coordinate system $\left\{S\right\}$, as follows

$${}^{S_i}\mathcal{F}={}_i{}^S\mathit{T}_f{}^i\mathcal{F}$$

(28)

In Equation (28), the transformation matrix ${}_i{}^S\mathit{T}_f$ is

$${}_i{}^S\mathit{T}_f=\left[\begin{array}{cc}{}_i{}^S\mathit{R}& \mathbf{0}\\ \mathit{S}({}^i\mathit{P}_S){}_i{}^S\mathit{R}& {}_i{}^S\mathit{R}\end{array}\right]$$

(29)

In Equation (29), ${}_i{}^S\mathit{R}$ is the rotation matrix from coordinate system $\left\{i\right\}$ to coordinate system $\left\{\mathrm{S}\right\}$, and $\mathit{S}({}^i\mathit{P}_S)$ represents the origin of the coordinate system $\left\{i\right\}$ based on the position vector matrix operator of the origin of the coordinate system $\left\{\mathrm{S}\right\}$, expressed as

$$\mathit{S}({}^i\mathit{P}_S)=\left[\begin{array}{ccc}0& -P_z& P_y\\ P_z& 0& -P_x\\ -P_y& P_x& 0\end{array}\right]$$

(30)

Then, the generalized force/torque vectors of each connecting rod can be obtained in the form of a summary in the coordinate system $\left\{\mathrm{S}\right\}$, as follows

$${}^S\mathcal{F}={\displaystyle \sum _{i=1}^n{}^{S_i}\mathcal{F}}$$

(31)

The final expression for the force compensation of the six-dimensional force sensor at the base can be obtained, namely ${}^S\mathit{F}$ and ${}^S\mathit{M}$.

When the robot is in a certain pose, the detection results of the six-dimensional force sensor on the base for force/torque are ${}^D\mathit{F}$ and ${}^D\mathit{M}$, respectively, expressed as ${}^D\mathcal{F}$. Therefore, the force/torque information $\mathcal{F}$ after force compensation is

$$\mathcal{F}=\left[\begin{array}{c}{}^D\mathit{F}-{}^S\mathit{F}\\ {}^D\mathit{M}-{}^S\mathit{M}\end{array}\right]=\mathbf{0}$$

(32)

The detection result of the robot’s six-dimensional force sensor remains zero during motion in the absence of external force due to force compensation derivation, thus achieving the detection of accidental collisions.

2.3. Collision Detection Algorithm

When discussing the existence of collision points for robot connecting rod i, Cartesian transformation is required to represent the generalized force vector and torque vector represented in the sensor coordinate system within the coordinate system $\left\{i\right\}$, as follows

$${}^i\mathcal{F}={}_S{}^i\mathit{T}_f{}^S\mathcal{F}$$

(33)

Furthermore, the representation of the spatial force vector equation on the robot connecting rod i in the coordinate system $\left\{i\right\}$ can be obtained, expressed as

$${\displaystyle \frac{x-x_i}{\cos {\alpha }_i}}={\displaystyle \frac{y-y_i}{\cos {\beta }_i}}={\displaystyle \frac{z-z_i}{\cos {\gamma }_i}}$$

(34)

By converting Equation (34) into a parametric equation, the following can be derived

$$\left\{\begin{array}{c}x=x_i+h\cos {\alpha }_i\\ y=y_i+h\cos {\beta }_i\\ z=z_i+h\cos {\gamma }_i\end{array}\right.$$

(35)

In Equation (35), $\left(x,y,z\right)$ is the generalized coordinate of the collision point position, $\left(x_i,y_i,z_i\right)$ represents a point on the coordinate system $\left\{i\right\}$ through which the spatial force vector passes, and h denotes the distance between possible collision points and $\left(x_i,y_i,z_i\right)$.

By combining Equation (35) with the external surface equation of the known robot connecting rod i, a quadratic equation based on the unknown variable h can be formulated for both equations. Considering the specificity of the equations for the outer surface of each connecting rod, this thesis discusses the relationship between $\Delta$ and 0 using the Delta root finding formula.

$$\Delta =b^2-4ac$$

(36)

$$h={\displaystyle \frac{-b\pm \sqrt{\Delta }}{2a}}$$

(37)

In the equation, a is the coefficient of the quadratic term; b is the coefficient of the first-order term; and c is a constant term.

By substituting the detection results into the equation, if $\Delta \ge 0$, the force vector equation intersects with the robot connecting rod i at ${}^i\mathit{p}={(x_i{y}_i{z}_i)}^{\mathrm{T}}$, where ${}^i\mathit{p}$ is the position vector of the collision point existing in the coordinate system $\left\{i\right\}$. The specific situation of the collision point can be discussed and solved in 9 different ways. If $\Delta <0$, meaning no collision point exists on connecting rod i, the same method should be applied to continue discussing the robot connecting rod $i+1(i=1,2\cdots )$. After obtaining ${}^i\mathit{p}$, it needs to be converted to the base coordinate system, where the resulting position vector is the final collision point ${}^0\mathit{p}={(x_i^{\text{'}}{y}_i^{\text{'}}{z}_i^{\text{'}})}^{\mathrm{T}}$, expressed as follows

$$\left[\begin{array}{c}{}^0\mathit{p}\\ 1\end{array}\right]={}_i{}^0\mathit{T}\left[\begin{array}{c}{}^i\mathit{p}\\ 1\end{array}\right]$$

(38)

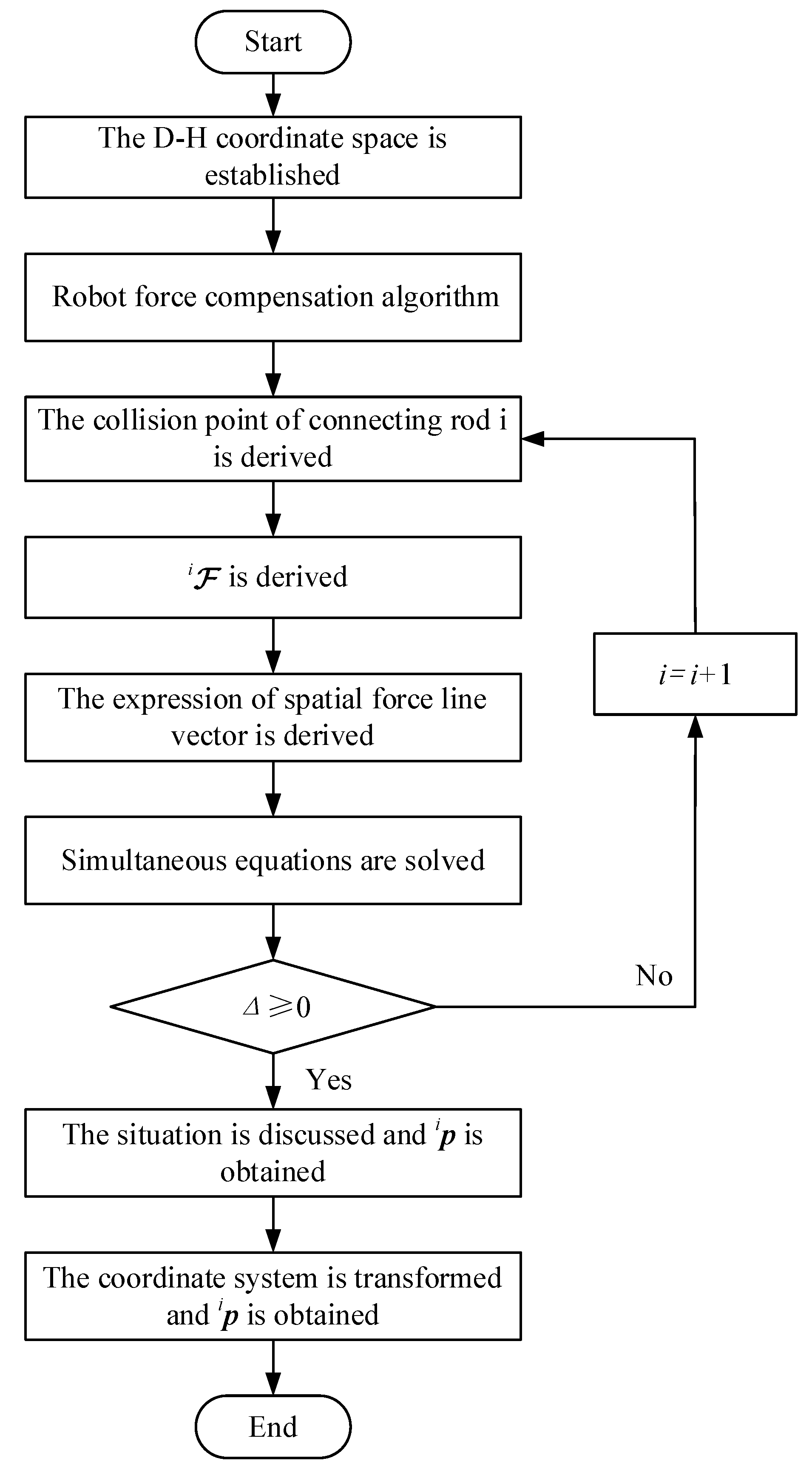
Figure 4 shows the flowchart of the solution process for the collision point.

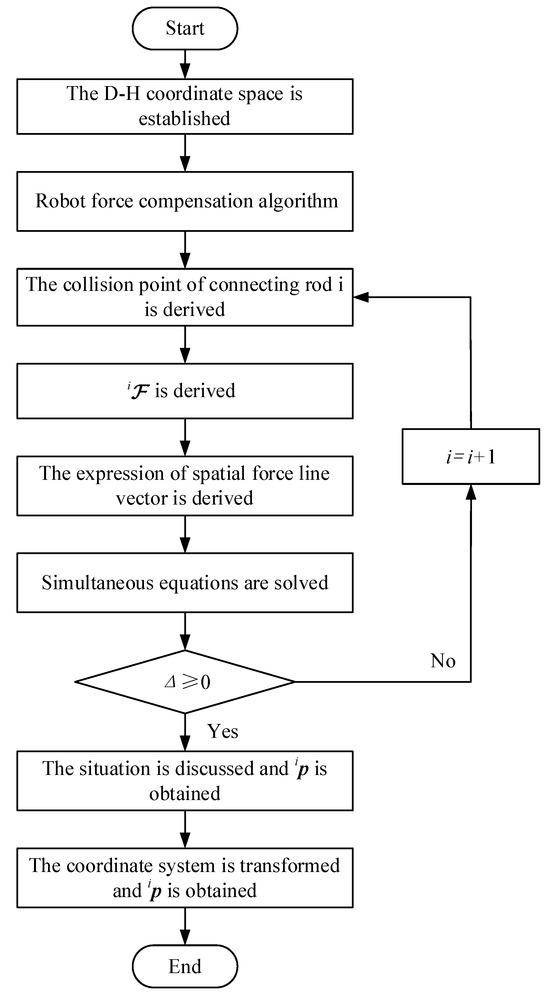
Figure 4. Flow chart for solving collision points.

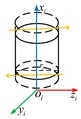
2.4. Solving Examples

Taking a joint robot with a cylindrical outer surface as an example, numerical verification is performed. By using Equations (33)–(35), the representation of the spatial force vector on connecting rod i can be obtained.

The cylindrical surface equation of the robot connecting rod i is given as follows

$$\left\{\begin{array}{c}{y}^2+z^2=r_i^2\\ L_{i1}\le x\le L_{i2}\\ L_i=L_{i2}-L_{i1}\end{array}\right.$$

(39)

In Equation (39), $r_i$ is the radius of connecting rod i; $L_i$ is the length of connecting rod i; $L_{i1}$ is the distance from the bottom of the circle to the origin of the coordinate system; and $L_{i2}$ is the distance from the top of the circle to the origin of the coordinate system.

By combining Equations (35) and (39), we obtain

$$({\cos }^2{\beta }_i+{\cos }^2{\gamma }_i)h^2+2(y_i\cos {\beta }_i+z_i\cos {\gamma }_i)h+y_i^2+z_i^2-r_i^2=0$$

(40)

The algebraic formula for $\Delta$ can be obtained from Equation (36) as follows

$$\Delta =4[{(y_i\cos {\beta }_i+z_i\cos {\gamma }_i)}^2-({\cos }^2{\beta }_i+{\cos }^2{\gamma }_i)(y_i^2+z_i^2-r_i^2)]$$

(41)

By discussing the value of $\Delta$, we can obtain the algebraic expressions of intersection points in three different situations.

• The situation of $\Delta >0$

When $\Delta >0$, the intersection point may appear on the cylindrical surface or the bottom/top circular surface.

(1) Appears on a cylindrical surface

According to Equation (37), it can be concluded that

$$h={\displaystyle \frac{-2(y_i\cos {\beta }_i+z_i\cos {\gamma }_i)\pm \sqrt{\Delta }}{2({\cos }^2{\beta }_i+{\cos }^2{\gamma }_i)}}$$

(42)

When $h_1={\displaystyle \frac{-2\left(y_i\cos {\beta }_i+z_i\cos {\gamma }_i\right)-\sqrt{\Delta }}{2\left({\cos }^2{\beta }_i+{\cos }^2{\gamma }_i\right)}}$, substituting $h_1$ into the force vector parameter equation in Equation (35) provides the following:

$$\left\{\begin{array}{c}{x}_1=x_i-{\displaystyle \frac{(y_i\cos {\alpha }_i\mathrm{c}\mathrm{o}\mathrm{s}{\beta }_i+z_i\cos {\alpha }_i\cos {\gamma }_i)+\cos {\alpha }_i\sqrt{\Delta }}{{\cos }^2{\beta }_i+{\cos }^2{\gamma }_i}}\\ y_1=y_i-{\displaystyle \frac{{(y}_i{\cos }^2{\beta }_i+z_i\cos {\beta }_i\cos {\gamma }_i)+\cos {\beta }_i\sqrt{\Delta }}{{\cos }^2{\beta }_i+{\cos }^2{\gamma }_i}}\\ z_1=z_i-{\displaystyle \frac{{(y}_i\cos {\beta }_i\cos {\gamma }_i+z_i{\cos }^2{\gamma }_i)+\cos {\gamma }_i\sqrt{\Delta }}{{\cos }^2{\beta }_i+{\cos }^2{\gamma }_i}}\end{array}\right.$$

(43)

Similarly, when $h_2={\displaystyle \frac{-2\left(y_i\cos {\beta }_i+z_i\cos {\gamma }_i\right)+\sqrt{\Delta }}{2\left({\cos }^2{\beta }_i+{\cos }^2{\gamma }_i\right)}}$, the following is obtained:

$$\left\{\begin{array}{c}{x}_2=x_i-{\displaystyle \frac{(y_i\cos {\alpha }_i\mathrm{c}\mathrm{o}\mathrm{s}{\beta }_i+z_i\cos {\alpha }_i\cos {\gamma }_i)-\cos {\alpha }_i\sqrt{\Delta }}{{\cos }^2{\beta }_i+{\cos }^2{\gamma }_i}}\\ y_2=y_i-{\displaystyle \frac{{(y}_i{\cos }^2{\beta }_i+z_i\cos {\beta }_i\cos {\gamma }_i)-\cos {\beta }_i\sqrt{\Delta }}{{\cos }^2{\beta }_i+{\cos }^2{\gamma }_i}}\\ z_2=z_i-{\displaystyle \frac{{(y}_i\cos {\beta }_i\cos {\gamma }_i+z_i{\cos }^2{\gamma }_i)-\cos {\gamma }_i\sqrt{\Delta }}{{\cos }^2{\beta }_i+{\cos }^2{\gamma }_i}}\end{array}\right.$$

(44)

(2) Appears on the bottom/top circular surface

When the intersection point appears on the bottom circle, substituting $x=L_{i1}$ into the force vector parameter equation yields

$$h_1={\displaystyle \frac{L_{i1}-x_i}{\cos {\alpha }_i}}$$

(45)

Substituting $h_1$ again and solving for y, z, the following is obtained:

$$\left\{\begin{array}{c}{y}_3=y_i+{\displaystyle \frac{\left(L_{i1}-x_i\right)\cos {\beta }_i}{\cos {\alpha }_i}}\\ z_3=z_i+{\displaystyle \frac{\left(L_{i1}-x_i\right)\cos {\gamma }_i}{\cos {\alpha }_i}}\end{array}\right.$$

(46)

When the intersection point appears on the top circle, substituting $x=L_{i2}$ into the force vector parameter equation yields

$$h_2={\displaystyle \frac{L_{i2}-x_i}{\cos {\alpha }_i}}$$

(47)

Substituting $h_2$ again and solving for y, z, the following is obtained:

$$\left\{\begin{array}{c}{y}_4=y_i+{\displaystyle \frac{\left(L_{i2}-x_i\right)\cos {\beta }_i}{\cos {\alpha }_i}}\\ z_4=z_i+{\displaystyle \frac{\left(L_{i2}-x_i\right)\cos {\gamma }_i}{\cos {\alpha }_i}}\end{array}\right.$$

(48)

2.

The situation of $\Delta =0$

When $\Delta =0$, there is a unique solution for h, given by

$$h=-{\displaystyle \frac{b}{2a}}=-{\displaystyle \frac{y_i\cos {\beta }_i+z_i\cos {\gamma }_i}{{\cos }^2{\beta }_i+{\cos }^2{\gamma }_i}}$$

(49)

By substituting h into the parameter equation of the force line vector, the result can be obtained, as follows

$$\left\{\begin{array}{c}{x}_5=x_i-{\displaystyle \frac{y_i\cos {\alpha }_i\cos {\beta }_i+z_i\cos {\alpha }_i\cos {\gamma }_i}{{\cos }^2{\beta }_i+{\cos }^2{\gamma }_i}}\\ y_5=y_i-{\displaystyle \frac{y_i{\cos }^2{\beta }_i+z_i\cos {\beta }_i\cos {\gamma }_i}{{\cos }^2{\beta }_i+{\cos }^2{\gamma }_i}}\\ z_5=z_i-{\displaystyle \frac{y_i\cos {\beta }_i\cos {\gamma }_i+z_i{\cos }^2{\gamma }_i}{{\mathrm{co}s}^2{\beta }_i+{\cos }^2{\gamma }_i}}\end{array}\right.$$

(50)

3.

The situation of $\Delta <0$

When $\Delta <0$, h does not exist, indicating that the collision point is not on the robot connecting rod in that segment.

According to the range of values for $\Delta$ and x, collisions are classified into 9 possible scenarios. Using Equations (42)–(50), the coordinates of the collision point are calculated for each possible scenario. According to Equation (38), the obtained collision point is represented in the base coordinate system, as shown in Table 2. Among them, the yellow vector represents the spatial force line vector, and the dashed cylinder represents the non-body connecting rod outside the length range of the robot connecting rod in the x-axis direction.

Table 2. Collision situation for connecting rods.

Number	$\mathit{\Delta }$ Value Situation	The Range of Values for x	Number of Collision Points	Collision Point Coordinates	Sketch Map
1	$\Delta <0$	none	0	none
2	$\Delta =0$	$x_5<L_{i1}$$\mathrm{or}{x}_5>L_{i2}$	0	none
3	$\Delta =0$	$L_{i1}\le x_5\le L_{i2}$	1	$\mathit{p}\left(x_5^{\text{'}},y_5^{\text{'}},z_5^{\text{'}}\right)$
4	$\Delta >0$	$x_1<L_{i1},$ $x_2<L_{i1}$ or $x_1>L_{i2},$ $x_2>L_{i2}$	0	none
5	$\Delta >0$	$x_1=L_{i1},$ $x_2<L_{i1}$ or $x_1=L_{i2},$ $x_2>L_{i2}$	1	$\mathit{p}\left(L_{i1},y_1^{\text{'}},z_1^{\text{'}}\right)$$\mathrm{or}\mathit{p}\left(L_{i2},y_1^{\text{'}},z_1^{\text{'}}\right)$
6	$\Delta >0$	$L_{i1}\le x_1\le L_{i2},$ $x_2<L_{i1}$ or $x_2>L_{i2}$	2	${\mathit{p}}_1\left(x_1^{\text{'}},y_1^{\text{'}},z_1^{\text{'}}\right)$ ${\mathit{p}}_2\left(L_{i1},y_3^{\text{'}},z_3^{\text{'}}\right)$ or ${\mathit{p}}_1\left(x_1^{\text{'}},y_1^{\text{'}},z_1^{\text{'}}\right)$ ${\mathit{p}}_2\left(L_{i2},y_4^{\text{'}},z_4^{\text{'}}\right)$
7	$\Delta >0$	$L_{i1}\le x_1\le L_{i2},$ $L_{i1}\le x_2\le L_{i2}$	2	${\mathit{p}}_1\left(x_1^{\text{'}},y_1^{\text{'}},z_1^{\text{'}}\right)$ ${\mathit{p}}_2\left(x_2^{\text{'}},y_2^{\text{'}},z_2^{\text{'}}\right)$
8	$\Delta >0$	$x_1<L_{i1},$ $x_2>L_{i2}$	2	${\mathit{p}}_1\left(L_{i1},y_3^{\text{'}},z_3^{\text{'}}\right)$ ${\mathit{p}}_2\left(L_{i2},y_4^{\text{'}},z_4^{\text{'}}\right)$
9	$\Delta >0$	$x_1=L_{i1},$ $x_2=L_{i2}$	2	${\mathit{p}}_1\left(L_{i1},y_1^{\text{'}},z_1^{\text{'}}\right)$ ${\mathit{p}}_2\left(L_{i2},y_2^{\text{'}},z_2^{\text{'}}\right)$

3. Algorithm Verification

3.1. Verification of Force Compensation Algorithm

3.1.1. Simulation Verification

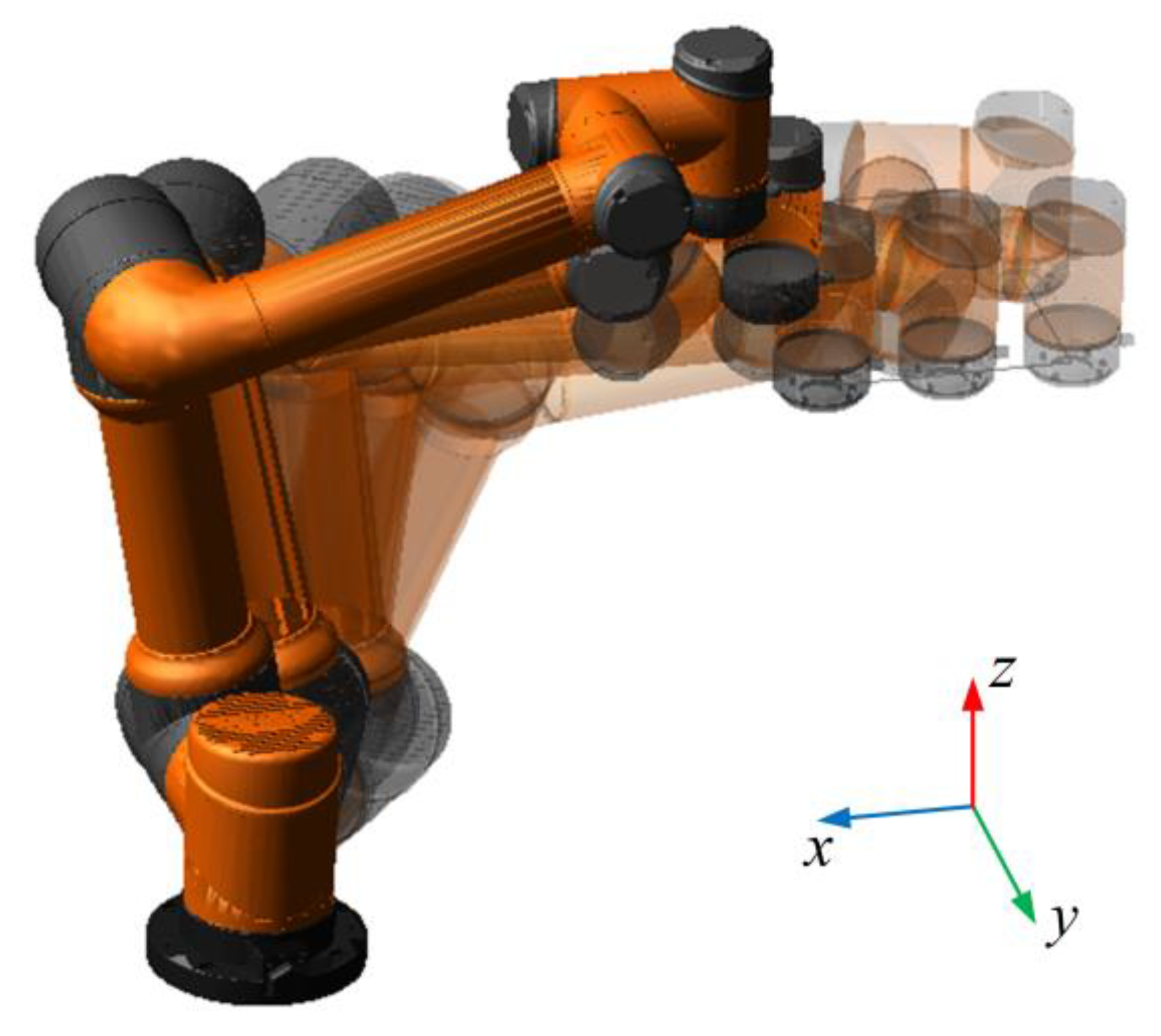
To verify the correctness and feasibility of the Kane’s dynamics-based robot compensation algorithm proposed in this thesis, the model of the AUBO-I5 articulated collaborative robot was imported into ADAMS (2020) for simulation verification. Motion pair conditions were added to each joint, and structural parameters such as the mass and inertia tension of each connecting rod of the robot were set. Point drives were also set at the end of the robot to run a simulated rectangular trajectory along the x-axis direction of 200 mm and the y-axis direction of 300 mm. In order to simulate the variable speed movements of robots, such as in an emergency stop and start, the robot will operate at three different speeds and accelerations: fast, medium, and slow. The simulation model is shown in Figure 5.

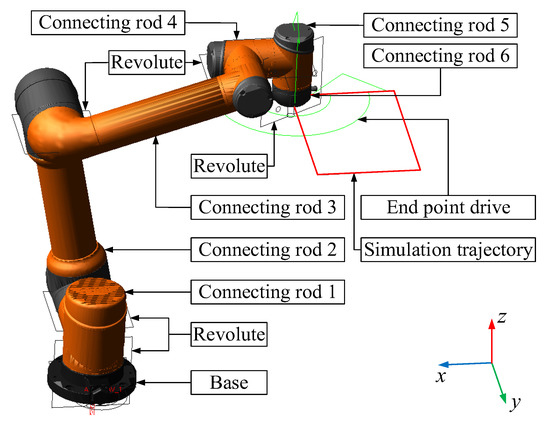
Figure 5. Simulation model of the AUBO-I5 robot.

The simulation motion has a termination time of 8.0 s and 400 steps. The residual image of the simulation motion is presented in Figure 6, while the point driving function at the end is provided in Table 3.

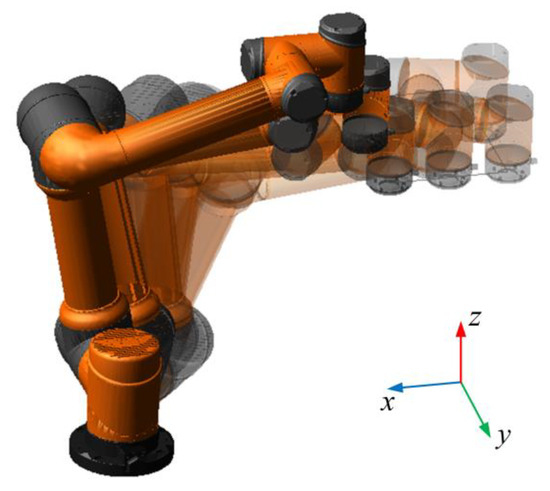
Figure 6. Simulated motion residual image.

Table 3. End point driving function.

Condition	Function
x-direction translation	Step (time, 0, 0, 1, −200) + step (time, 3, 0, 7, 200)
y-direction translation	Step (time, 1, 0, 3, 300) + step (time, 7, 0, 8, −300)
z-direction translation	0 * time
Rotate around the x-axis direction	0 * time
Rotate around the y-axis direction	0 * time
Rotate around the z-axis direction	0 * time

Set the sampling frequency to 1000 Hz, and during simulation motion, real-time statistics of the three directions of force and torque acting on the robot base can be obtained to obtain simulation motion results.

3.1.2. Experimental Verification

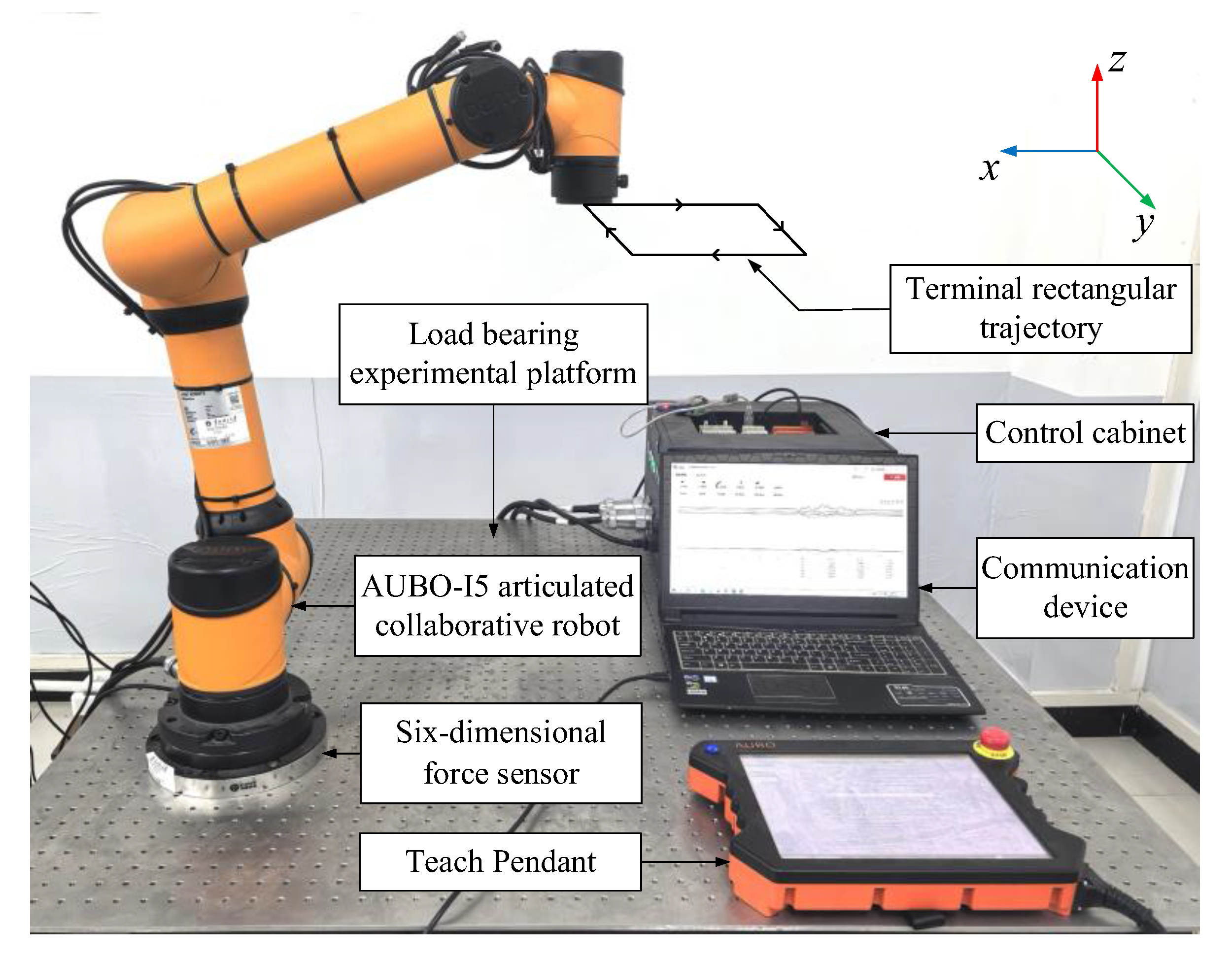
To verify the correctness of the force compensation algorithm and compare it with the simulation experiment results, the AUBO-I5 articulated collaborative robot (Aobo Intelligent Technology Co., Ltd., Beijing, China) was used for force compensation experiments. The robot has 6 degrees of freedom, a maximum working radius of 886.5 mm, a mass of 24 kg, and a repeat positioning accuracy of $\pm$0.02 mm. A KWR200X six-dimensional force sensor (Changzhou Kunwei Sensing Technology Co., Ltd., Beijing, China) was installed on the robot base and connected to communication equipment to facilitate interaction between the robot and the external environment. The sensor is made of alloy steel, with a diameter of 200 mm, a height of 25.5 mm, a resolution of 0.03% F.S., and an accuracy of 0.5% F.S.; the sampling frequency is 1000 Hz.

For comparative experiments, the robot was programmed to run the same rectangular trajectory as in the simulation experiment using a teaching pendant, and the three directions of force and torque acting on the base of the robot during operation were monitored in real time through the six-dimensional force sensor. The experiment is shown in Figure 7.

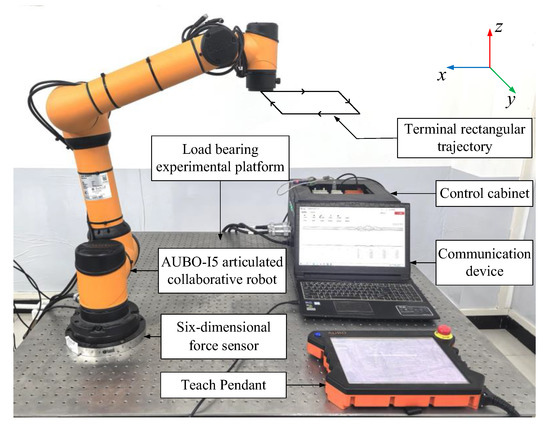
Figure 7. Experimental diagram of the AUBO-I5 robot force compensation.

When the robot runs along the planned path, it monitors the forces and torques acting on the base in real time through sensor data acquisition software, and the experimental motion results can be obtained from this.

3.1.3. Comparative Verification

According to Equations (14)–(17) and (19)–(32), the theoretical results for robot force compensation can be obtained. The velocity and acceleration during each time period can be obtained from the simulated velocity curve. Based on Equations (14)–(17), the velocity and acceleration at the end can be iterated onto each connecting rod, and the force and torque experienced by each connecting rod can be represented on the sensor coordinate system as theoretical values, expressed as $F_{tx}$, $F_{ty}$, $F_{tz}$, $M_{tx}$, $M_{ty}$, and $M_{tz}$. Similarly, the data obtained through simulation can be represented as $F_{sx}$, $F_{sy}$, $F_{sz}$, $M_{sx}$, $M_{sy}$, and $M_{sz}$. The data obtained through experiments can be represented as $F_{ex}$, $F_{ey}$, $F_{ez}$, $M_{ex}$, $M_{ey}$, and $M_{ez}$.

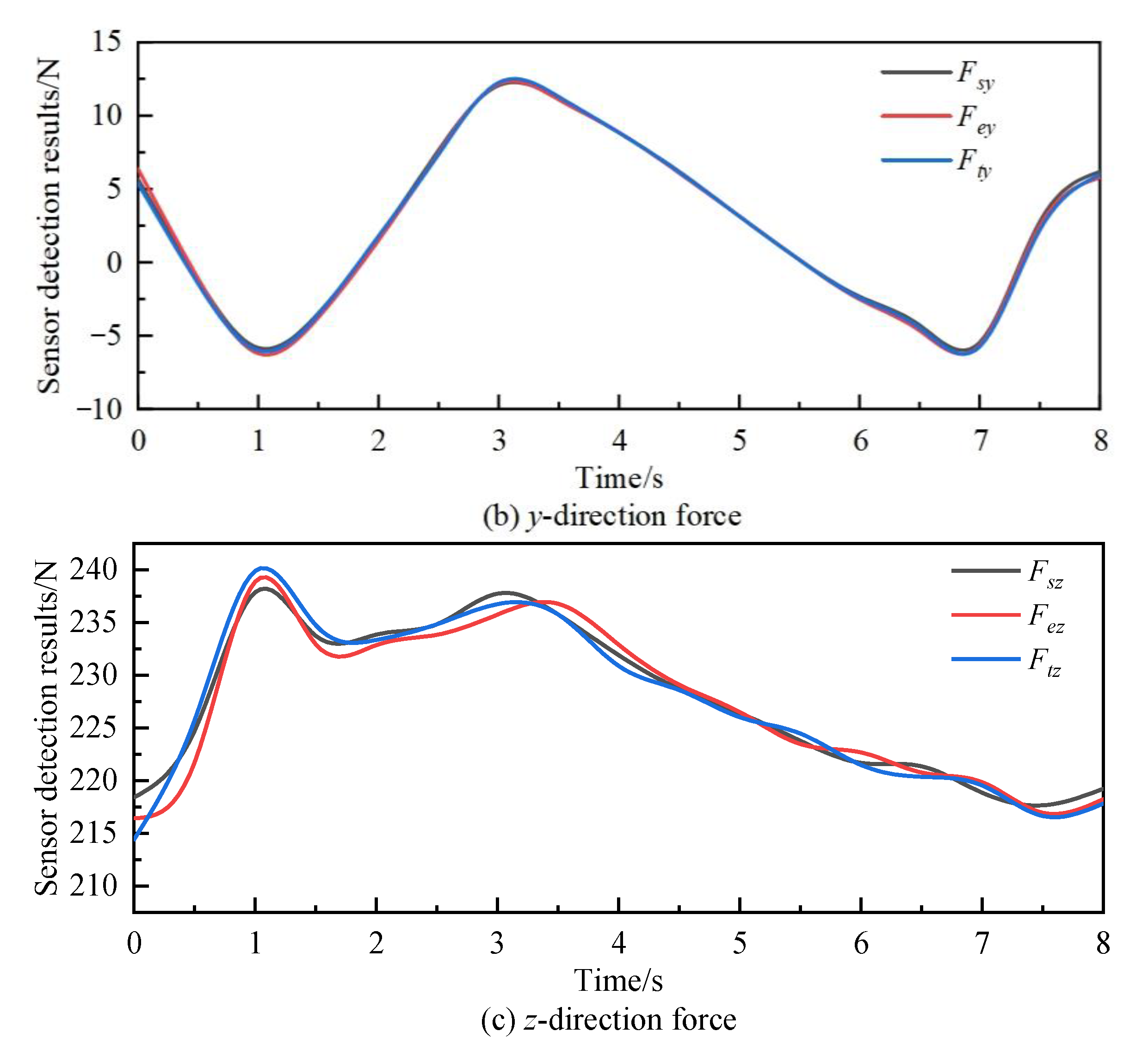
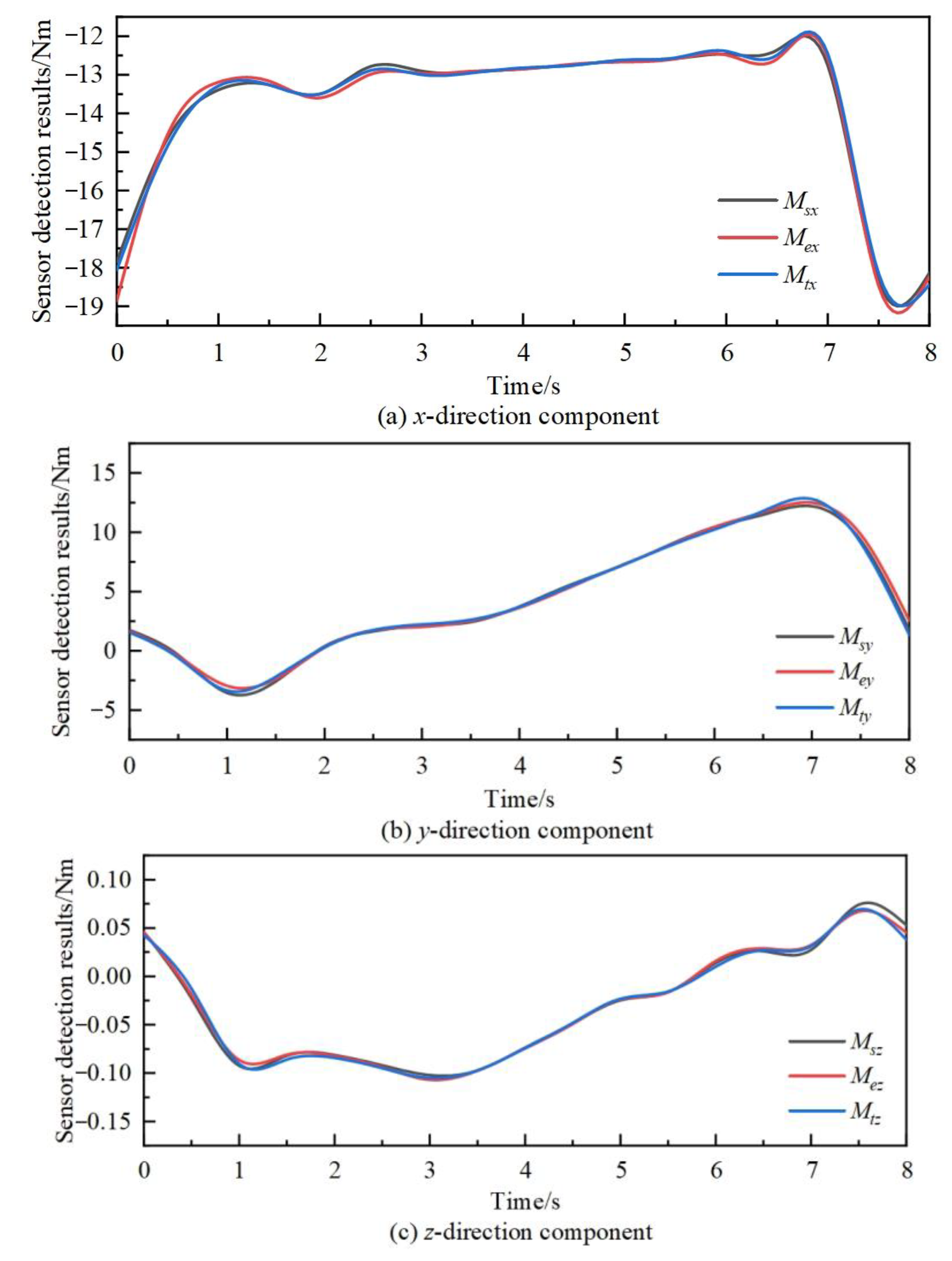
We compare the theoretical results, simulation results, and experimental results obtained from the calculation to verify the correctness of the theoretical analysis. The comparison of the component forces in three directions and the component moments in three directions is shown in Figure 8 and Figure 9.

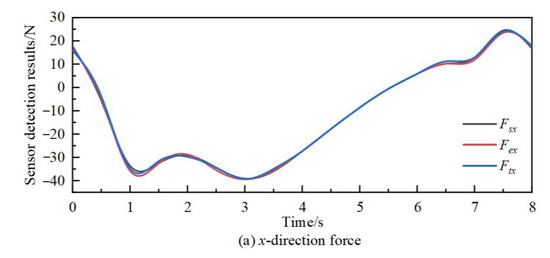
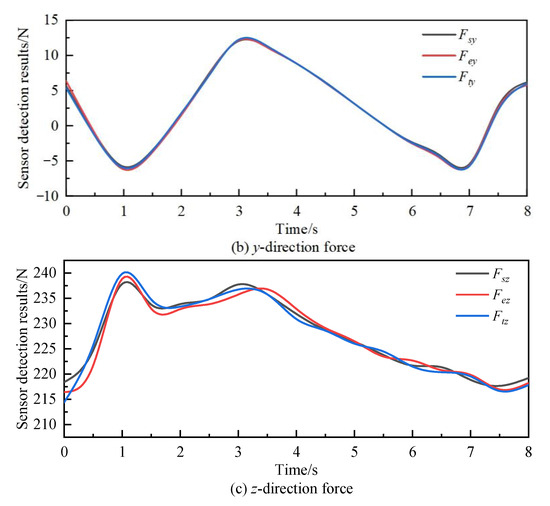
Figure 8. Force comparison chart.

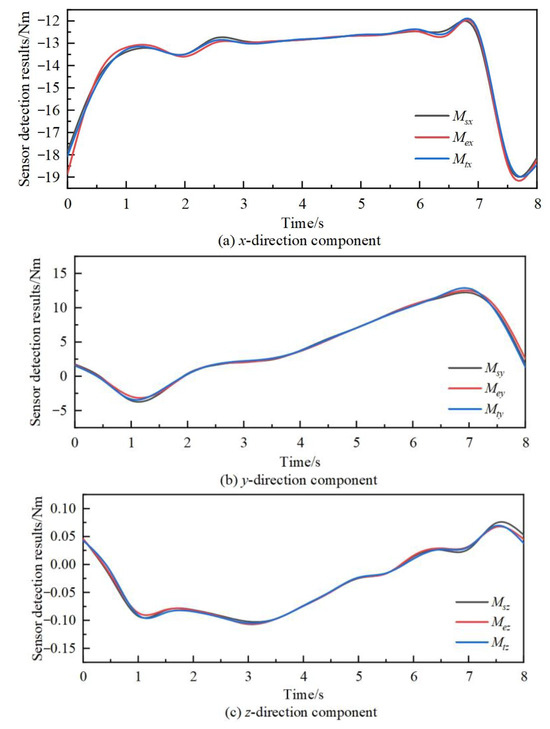
Figure 9. Torque comparison chart.

In Figure 8 and Figure 9, the curves represent the simulation results, experimental results, and theoretical results of forces and moments in the x, y, and z directions.

To further verify the accuracy of the force compensation algorithm, an error analysis was performed using theoretical results, simulation results, and experimental results. The relative error calculation formula for the three directional forces is given as follows

$$\delta F_{rm}={\displaystyle \frac{\Delta F_{stm}+\Delta F_{etm}}{\sqrt{F_{sm}^2+F_{em}^2}}}\times 100\%\hspace{1em}(r=1,2,3,\cdots ,17)$$

(51)

The meaning of the relative error constructed is to standardize the total deviation between the simulation and experimental results and the theoretical value using the joint magnitude of the two, avoiding the dominant error caused by a single result magnitude being too large, and playing a normalization role.

$$\Delta F_{stm}=\left|F_{sm}-F_{tm}\right|\hspace{1em}(m=x,y,z)$$

(52)

$$\Delta F_{etm}=\left|F_{em}-F_{tm}\right|\hspace{1em}(m=x,y,z)$$

(53)

In the equation, $F_{sm}$ is the force data in the simulation results, $F_{em}$ is the force data in the experimental results, and $F_{tm}$ is the force data in the theoretical results; $\Delta F_{stm}$ is the absolute error between simulation force and theoretical force, and $\Delta F_{etm}$ is the absolute error between experiment force and theoretical force.

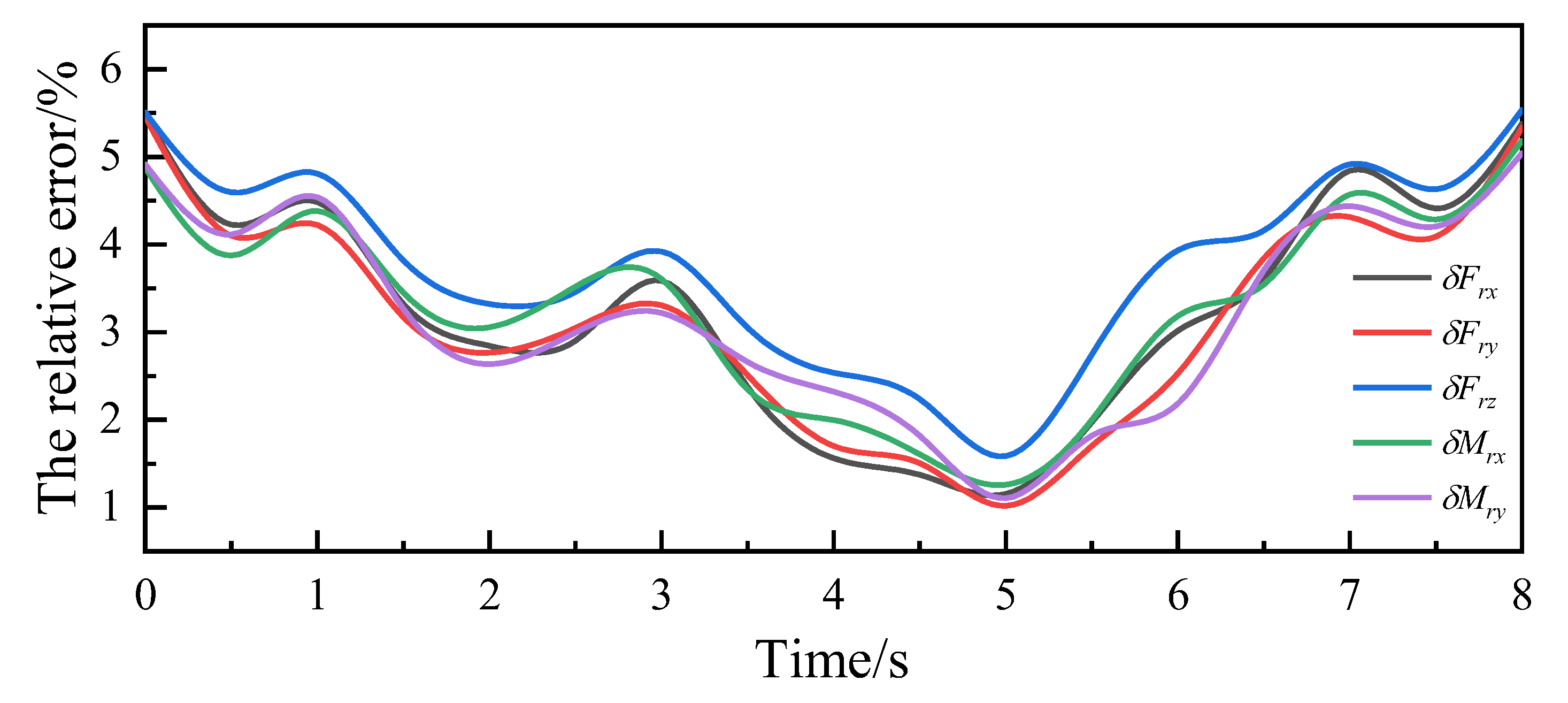
Similarly, the relative error $\delta M_{rm}$ of the torque in three directions is considered, where $\Delta M_{stm}$ is the absolute error between simulation torque and theoretical torque, and the absolute error $\Delta M_{etm}$ is the absolute error between experiment torque and theoretical torque, thus conducting error analysis on the torque in the three directions. Due to the small base of the moment $M_{rm}$ in the z-direction, a significant calculation error occurs, and its reference value is low, therefore, it is ignored. The relative error of the force/torque of the robot in theory, simulation, and experiment is shown in Figure 10, and the maximum value of the relative error is shown in Table 4.

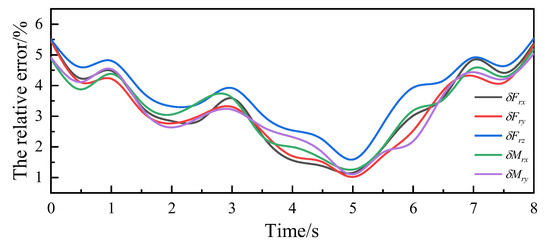
Figure 10. Relative error of force/torque.

Table 4. The maximum value of relative error.

Relative Error	$\mathit{\delta }{\mathit{F}}_{\mathit{r}\mathit{x}}$/%	$\mathit{\delta }{\mathit{F}}_{\mathit{r}\mathit{y}}$/%	$\mathit{\delta }{\mathit{F}}_{\mathit{r}\mathit{z}}$/%	$\mathit{\delta }{\mathit{M}}_{\mathit{r}\mathit{x}}$/%	$\mathit{\delta }{\mathit{M}}_{\mathit{r}\mathit{y}}$/%
Value	5.4824	5.4602	5.5359	5.1854	5.0423

From Figure 8, Figure 9 and Figure 10 and Table 4, it can be observed that the comparison curves of force/torque in the three directions remain consistent, with the maximum relative error occurring in the z-direction component. Due to the significant gravity and dynamic force exerted by the robot itself in this direction, the overall error during comparison verification is relatively high. However, the relative error does not exceed 5.6%, confirming the correctness of the theoretical analysis of the force compensation algorithm. When the robot runs for 4 s to 6 s, the relative error of the three directions of force/torque is minimized. During this period, the end of the robot moves in the x-positive direction, and the acceleration of the robot linkage motion is minimized. From this, it can be concluded that during the working process of the robot, a smaller rotation amplitude of each joint led to smoother movements and more stable changes in force/torque, resulting in more accurate force/torque compensation values. This force compensation algorithm demonstrates higher accuracy and stronger practicality, effectively compensating for the zero position value of the sensor of the robot in real time without external force.

3.2. Verification of Collision Detection Algorithm

To verify the effectiveness and accuracy of the collision point detection algorithm proposed in this thesis, collision point detection experiments were conducted using the AUBO-I5 robot. The robot’s pose during work is simulated by controlling its behavior through the control cabinet and teaching pendant.

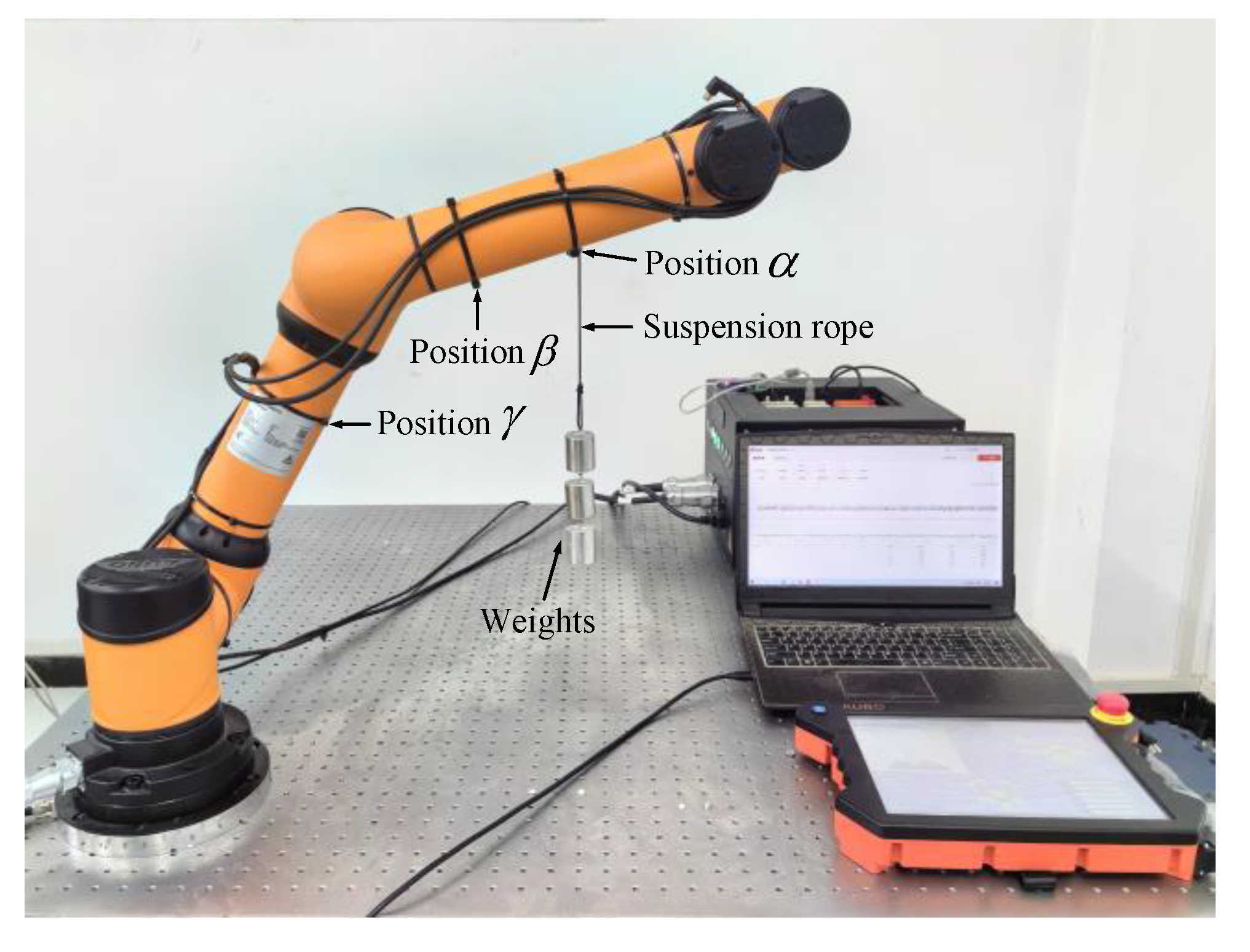
To simulate collision forces of known magnitude and direction, weights are suspended on the robot connecting rod and the suspension rope is cut to simulate the collision force. The position of the simulated collision force is known, and the experimental result is based on the sensor coordinate system.

The pose of the simulated robot in operation was set as follows: ${\theta }_1=50\text{°},{\theta }_2=30\text{°},{\theta }_3=-45\text{°},{\theta }_4={\theta }_5={\theta }_6=0$. Weights were hung at different positions (position α, position β, and position γ) on various connecting rods of the robot for collision testing. The specific coordinates of the collision location are shown in Table 5.

Table 5. Collision position coordinates.

Collision Position	x-Direction Vector/mm	y-Direction Vector/mm	z-Direction Vector/mm
α	−14.10	−35.54	51.36
β	−13.93	−25.61	48.17
γ	−8.45	−16.52	33.15

The detection results recorded by the data collection software at the moment of cutting were input into the proposed collision point detection algorithm. The experiment is shown in Figure 11.

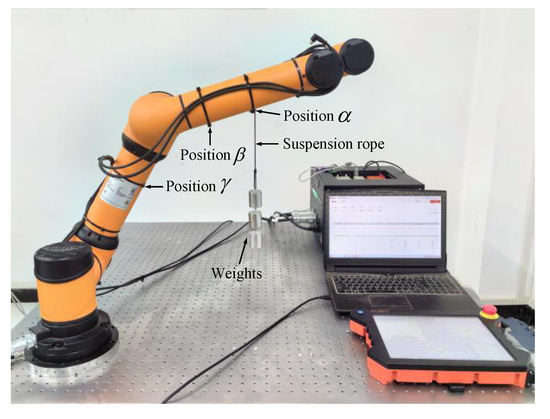
Figure 11. Experimental diagram of robot collision point detection.

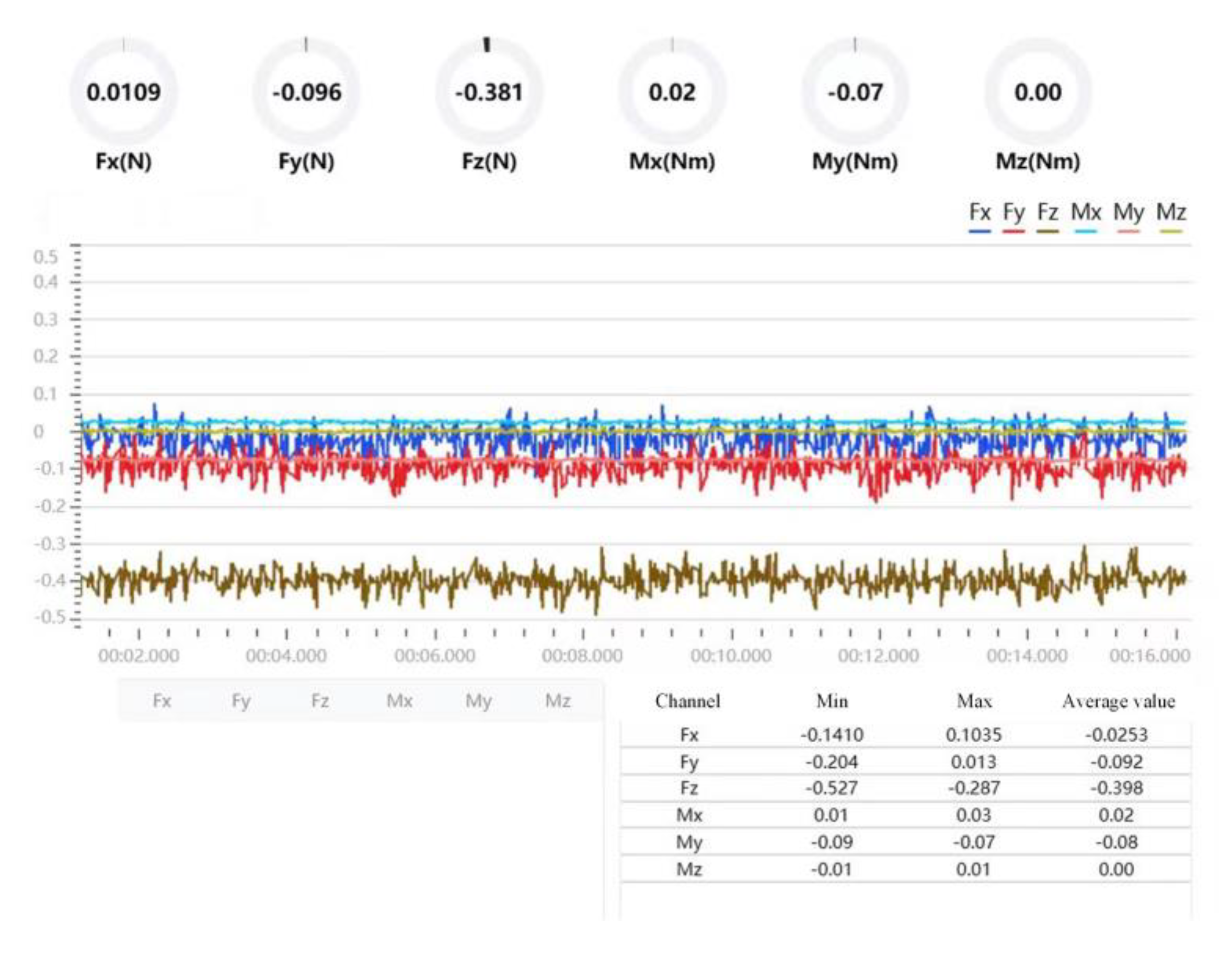
The display interface of the sensor data acquisition software is shown in Figure 12.

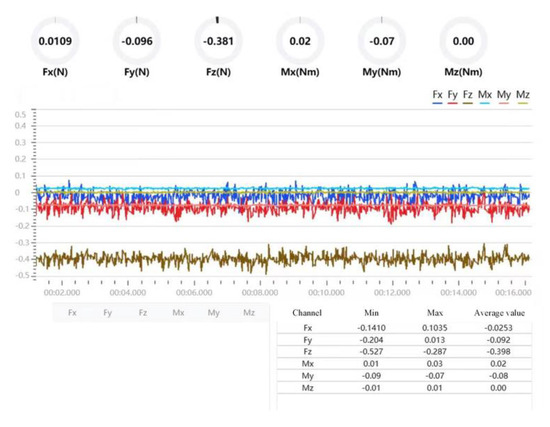
Figure 12. Display interface of sensor data acquisition software.

To verify the accuracy of the proposed algorithm, an error analysis was conducted on the experimental results.

The relative error calculation equation for each direction of a position is

$${\mathsf{\delta }\mathit{P}}_{\mathit{n}}={\displaystyle \frac{∆{\mathit{p}}_{\mathit{x}}+∆{\mathit{p}}_{\mathit{y}}+∆{\mathit{p}}_{\mathit{z}}}{\sqrt{{\mathit{p}}_{\mathit{Cx}}^2+{\mathit{p}}_{\mathit{Cy}}^2+{\mathit{p}}_{\mathit{Cz}}^2}}}\times 100\%\left(\mathit{n}=\mathrm{1,2},3,\cdots ,12\right)$$

(54)

$$∆{\mathit{p}}_{\mathit{n}}=\left|{\mathit{p}}_{\mathit{Jn}}-{\mathit{p}}_{\mathit{Cn}}\right|\left(\mathit{n}=\mathit{x},\mathit{y},\mathit{z}\right)$$

(55)

In the equation, $∆{\mathit{p}}_{\mathit{x}},∆{\mathit{p}}_{\mathit{y}},∆{\mathit{p}}_{\mathit{z}}$ represent the absolute errors in calculating the position; ${\mathit{p}}_{\mathit{Jx}},{\mathit{p}}_{\mathit{Jy}},{\mathit{p}}_{\mathit{Jz}}$ denote the calculated collision position coordinates; and the coordinates of the actual collision position are represented by ${\mathit{p}}_{\mathit{Cx}},{\mathit{p}}_{\mathit{Cy}},{\mathit{p}}_{\mathit{Cz}}$.

The experimental results of position α are shown in Table 6.

Table 6. Experimental results of collision detection at position α.

Number	Collision Force/N	Three Directional Force Vectors/N	Three Directional Torque Vectors/(N·mm)	Calculate Position/mm	Absolute Position Error/mm	Relative Positional Error/%
1	5.88	−0.2529	−0.0027	−12.5749	1.5251	5.7923
		−0.1854	0.0931	−34.0196	1.5204
		0.5435	−0.0287	50.6327	0.7273
2	7.84	−0.2688	−0.0900	−12.6538	1.4462	5.0752
		−0.1807	0.2432	−34.5375	1.0025
		0.7253	−0.0247	50.5591	0.8009
3	9.80	−0.2195	−0.0127	−15.1268	1.0268	3.8751
		−0.0523	0.0969	−36.2093	0.6693
		0.8790	−0.0256	50.5749	0.7851
4	11.76	−0.3560	−0.0045	−13.4817	0.6183	2.5957
		−0.2608	0.1274	−35.0753	0.4647
		1.0016	−0.0479	50.7810	0.5790

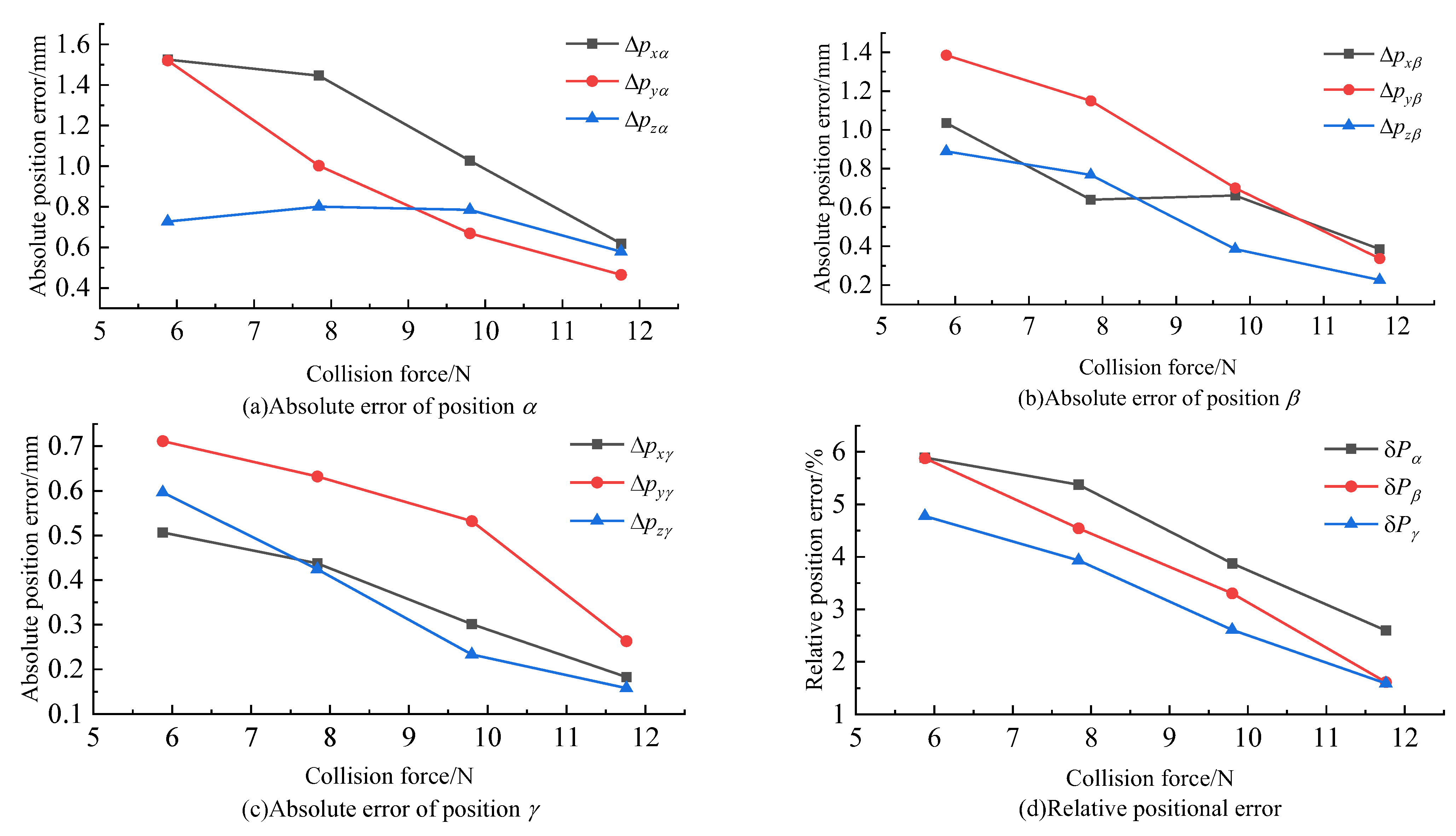
When the robot is subjected to different collision forces at different positions, its absolute and relative position errors are shown in Figure 13.

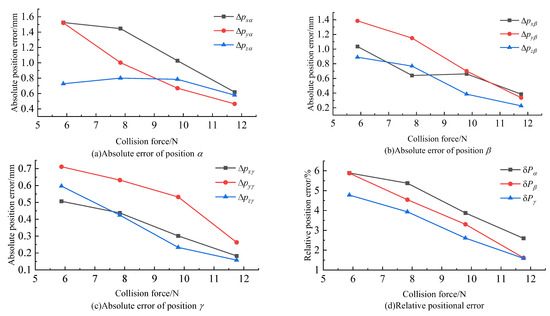
Figure 13. Experimental results.

From Figure 12, it can be observed that the relative error of the collision point position obtained through this algorithm decreases as the given external force increases, with the relative error remaining below 5.8%. Since position γ is closer to the base sensor than positions α and β, the absolute and relative position errors obtained in all directions at position γ are generally smaller compared to those at positions α and β. It can be inferred that the accuracy of the detected collision point position improves as the collision distance to the sensor decreases. This collision detection algorithm demonstrates smaller errors and effectively identifies the specific location coordinates of collision points.

4. Conclusions

Collision detection plays a crucial role in safety research on collaborative robots, providing a solid foundation for the smooth execution of human–robot collaboration and the continuous advancement of intelligent automation processes. Among these, force compensation calibrates the robot’s own force perception system, enabling the robot to avoid interference from gravity and inertial forces, thus accurately sensing the external collision force acting on it, laying the foundation for robot collision detection. To address the limitations of traditional collision detection algorithms for robots using six-dimensional force sensors, a force compensation algorithm based on Kane’s dynamics and a collision detection algorithm that combines the six-dimensional force sensor’s detection results with the robot’s outer surface equations to derive the collision point coordinates of the robot body are proposed. Force compensation and collision detection experiments were carried out on the AUBO-I5 joint-type collaborative robot. In the force compensation experiment, a comparison and error analysis were conducted for simulation, experimental, and theoretical results, obtaining force compensation comparison curves and error analysis results during the robot’s motion. The results showed that the comparison curves for forces/torques in three directions were consistent, with relative errors below 5.6%. In the collision detection experiment, the detection results for the base’s six-dimensional force sensor were recorded and input into the proposed collision point detection algorithm. The experimental results were consistent with the actual collision position, and the relative position error was below 5.8%. Both sets of experiments validated the correctness and feasibility of the theoretical analysis of the force compensation and collision detection algorithms.

The force compensation and collision detection algorithms proposed in this paper have the following future outlook: Due to the fact that a small number of robots may have complex shapes, solving the external surface equations of robots using this algorithm may result in complex equations, which may reduce the efficiency of solving the coordinates of collision points. In the future, we will continue to optimize collision detection algorithms, improve their universality, and attempt to develop a complete system that can detect whether a collision has occurred in real-time and, after a collision, detect the specific coordinates of the robot’s outer surface collision point in real-time and display them within the system. Through this system, when a collision occurs, the robot can be controlled in real-time to ensure safe operation during its work.