Deep Reinforcement Learning-Based Active Disturbance Rejection Control for Trajectory Tracking of Autonomous Ground Electric Vehicles
Abstract
1. Introduction
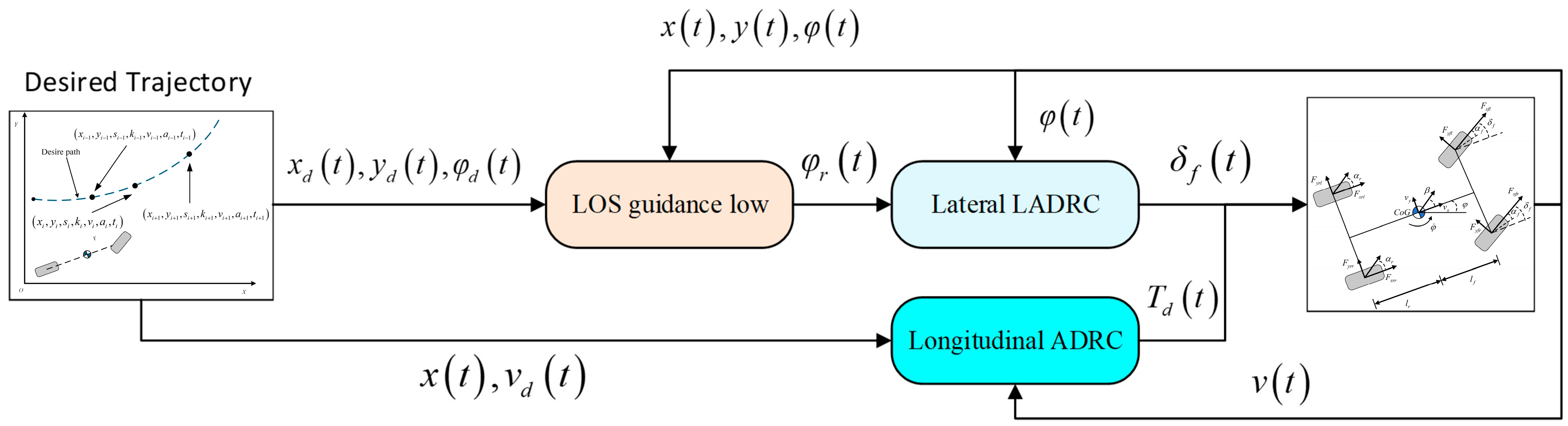
2. Design of Trajectory Tracking Control System
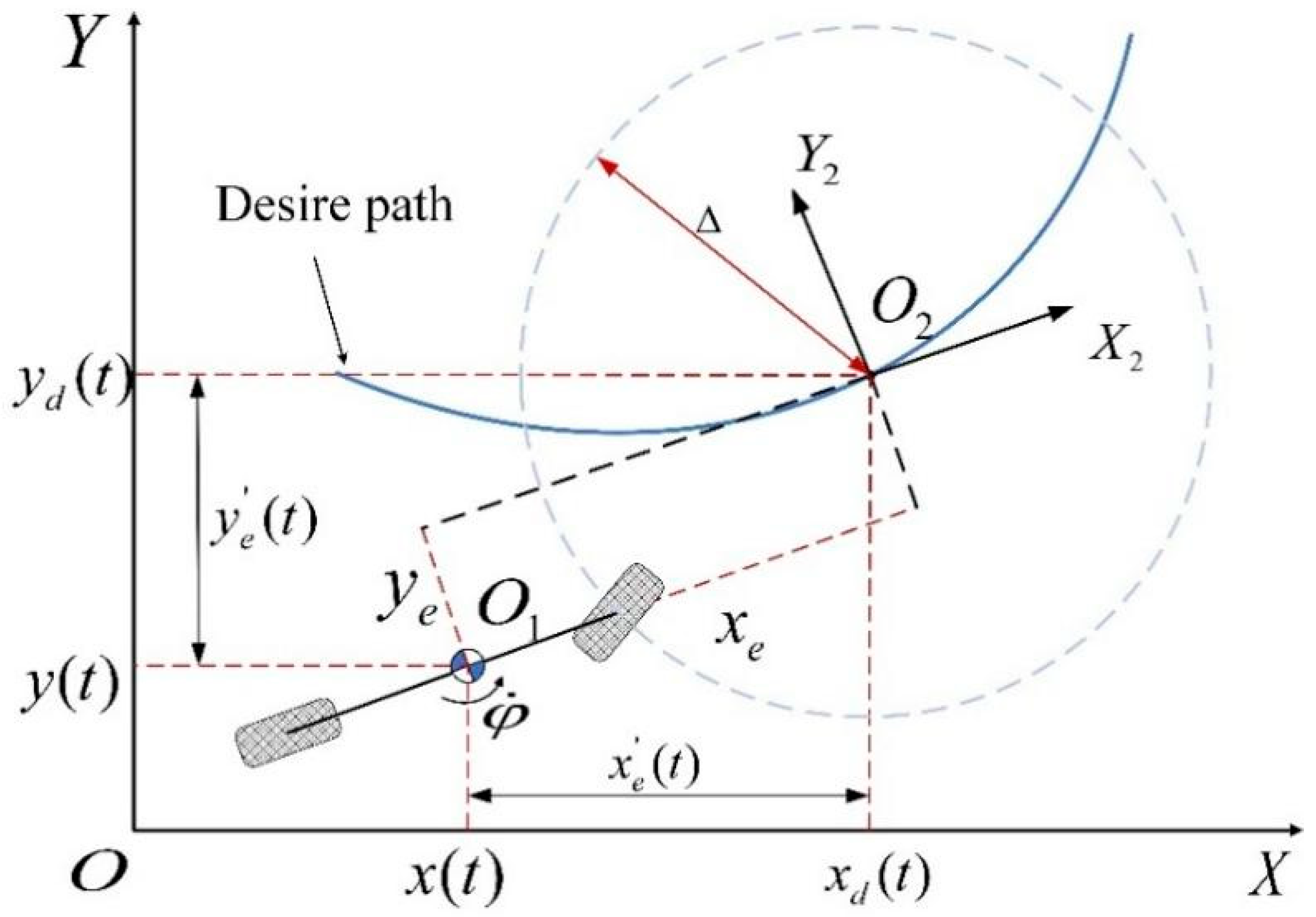
2.1. Design of Trajectory Tracking Guidance Law
2.2. Yaw Angle Controller Design
3. DRL-Based ADRC Strategy Design
3.1. Fundamental Concepts of Reinforcement Learning
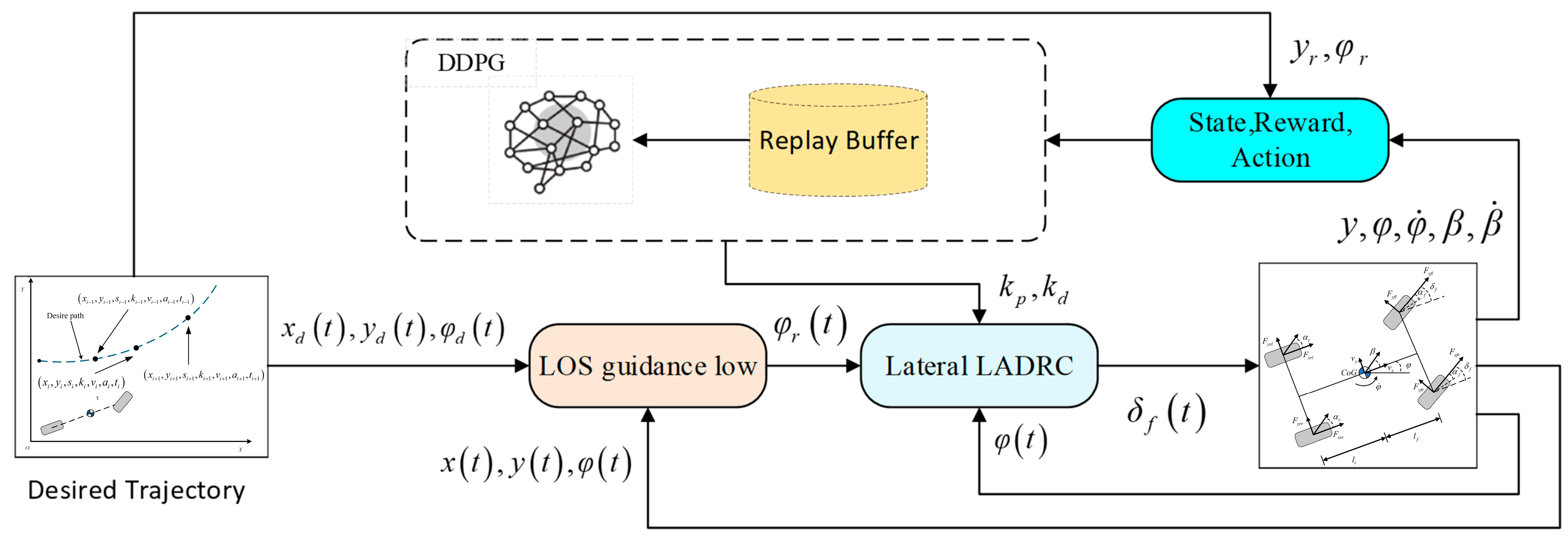
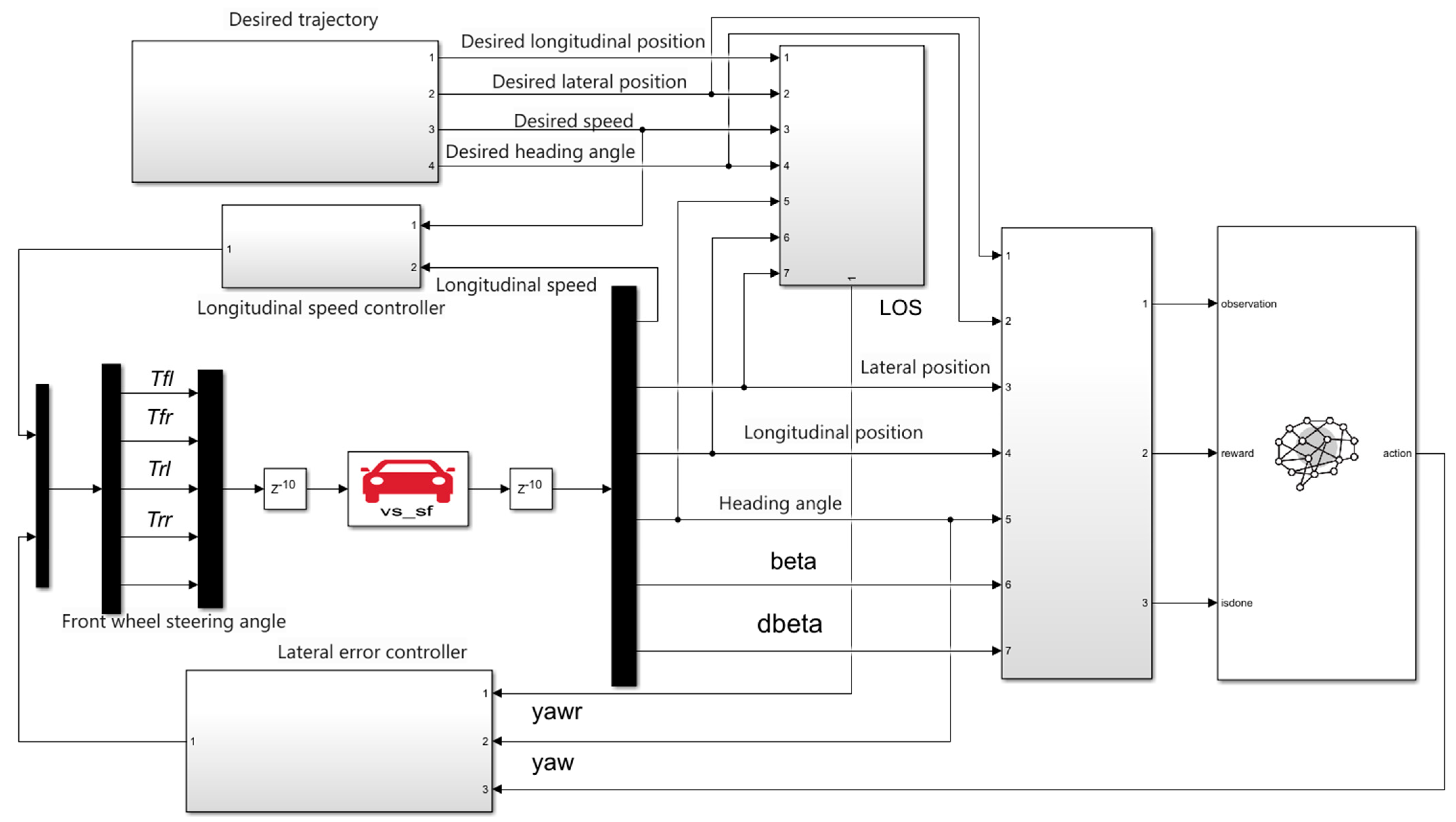
3.2. DRL-Based ADRC Trajectory Tracking System
| Algorithm 1: DDPG |
 |
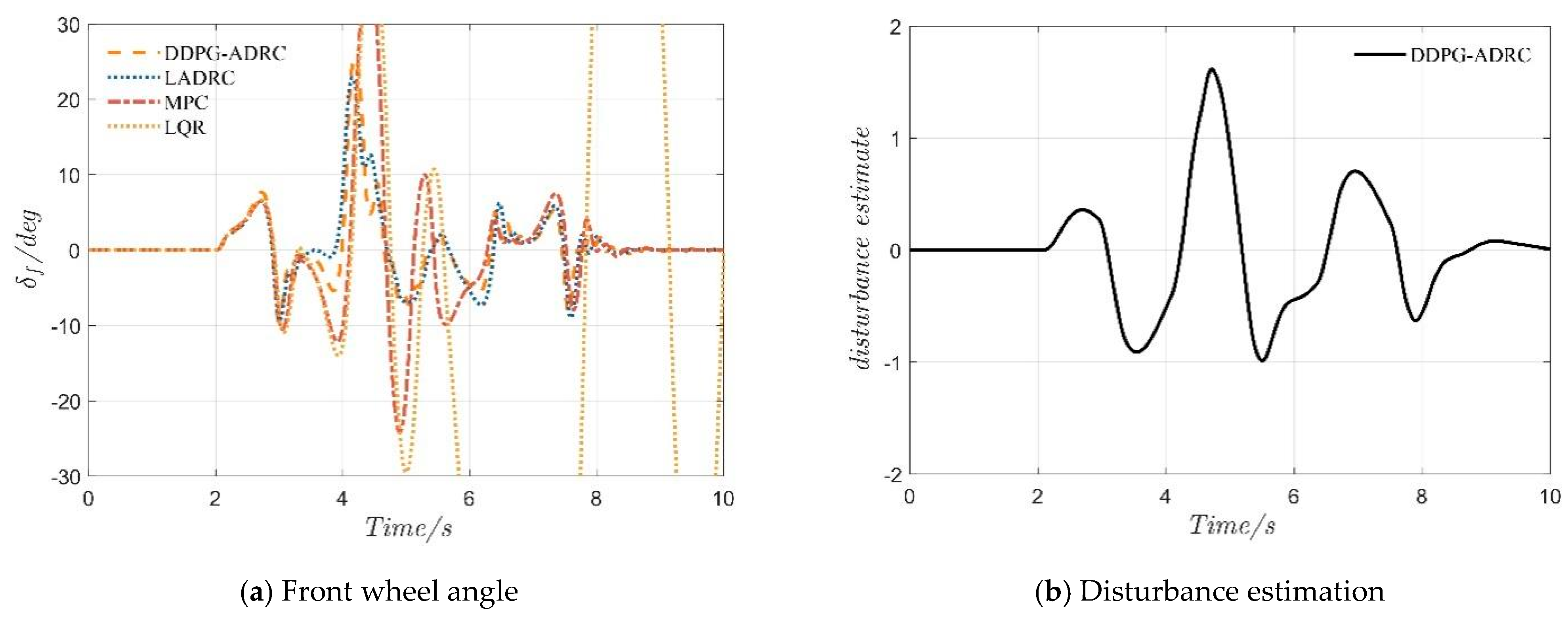
4. Simulation and Analysis
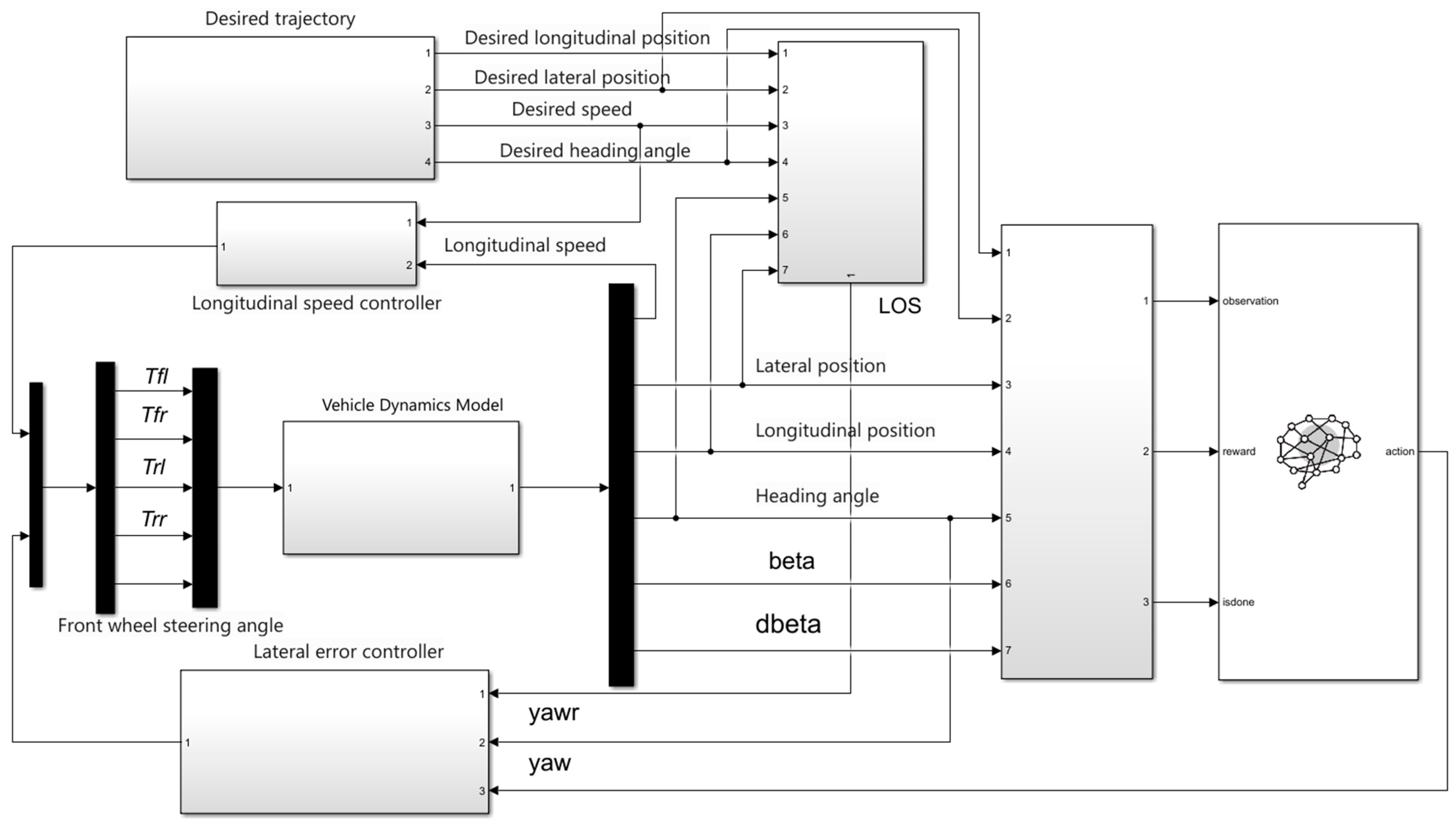
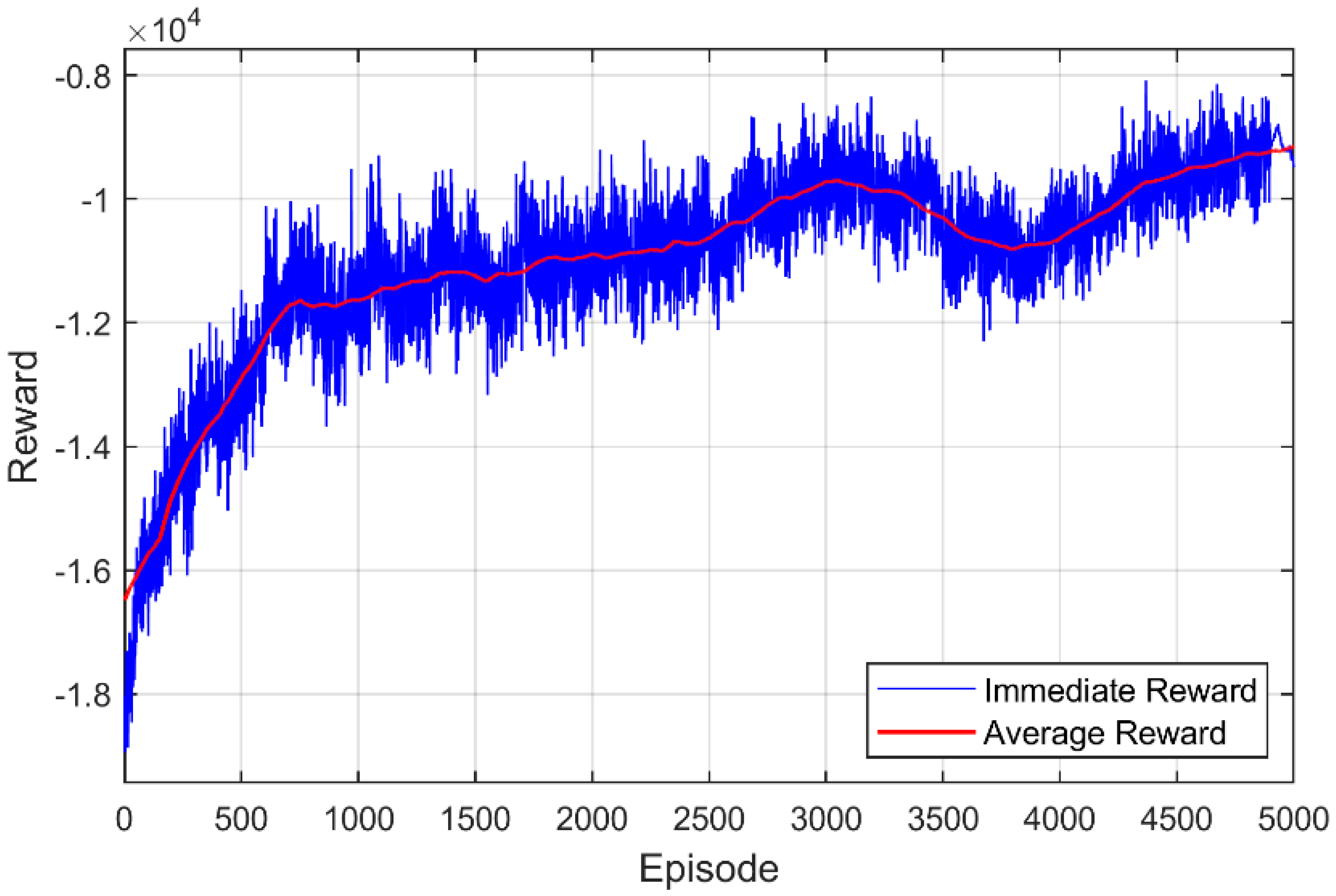
4.1. Simulation and Training Environment
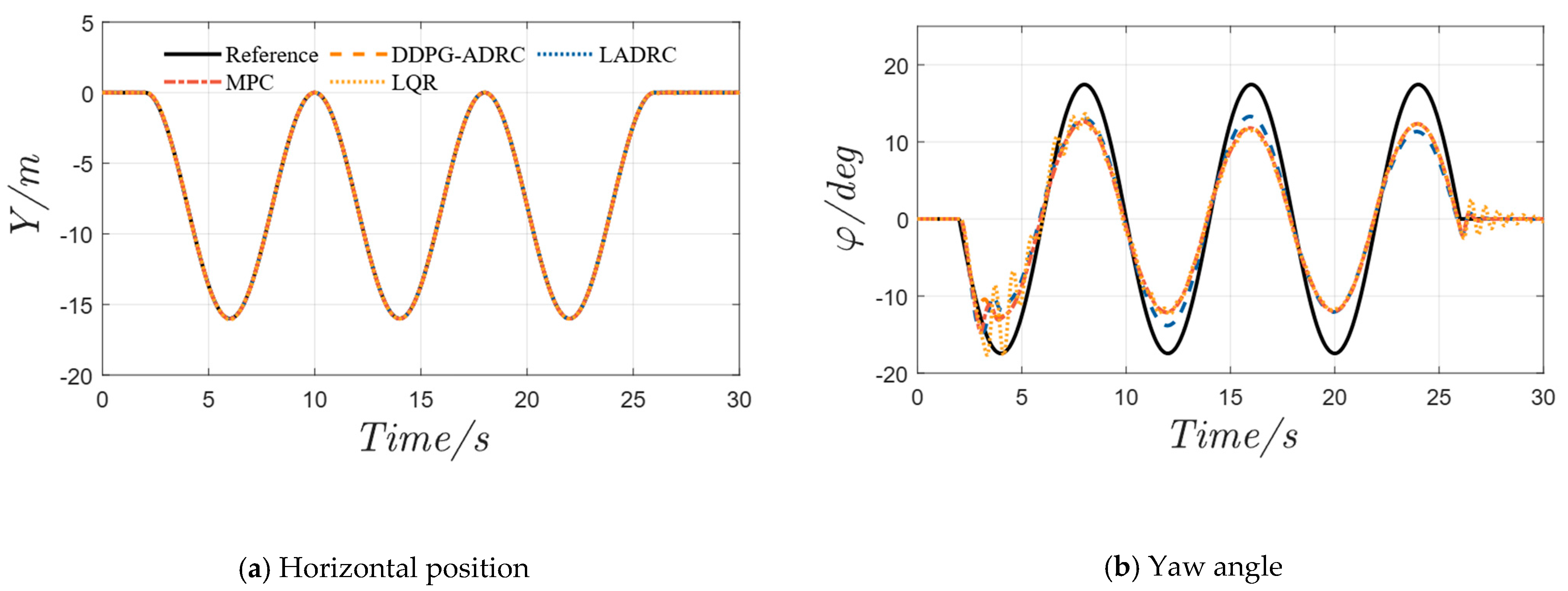
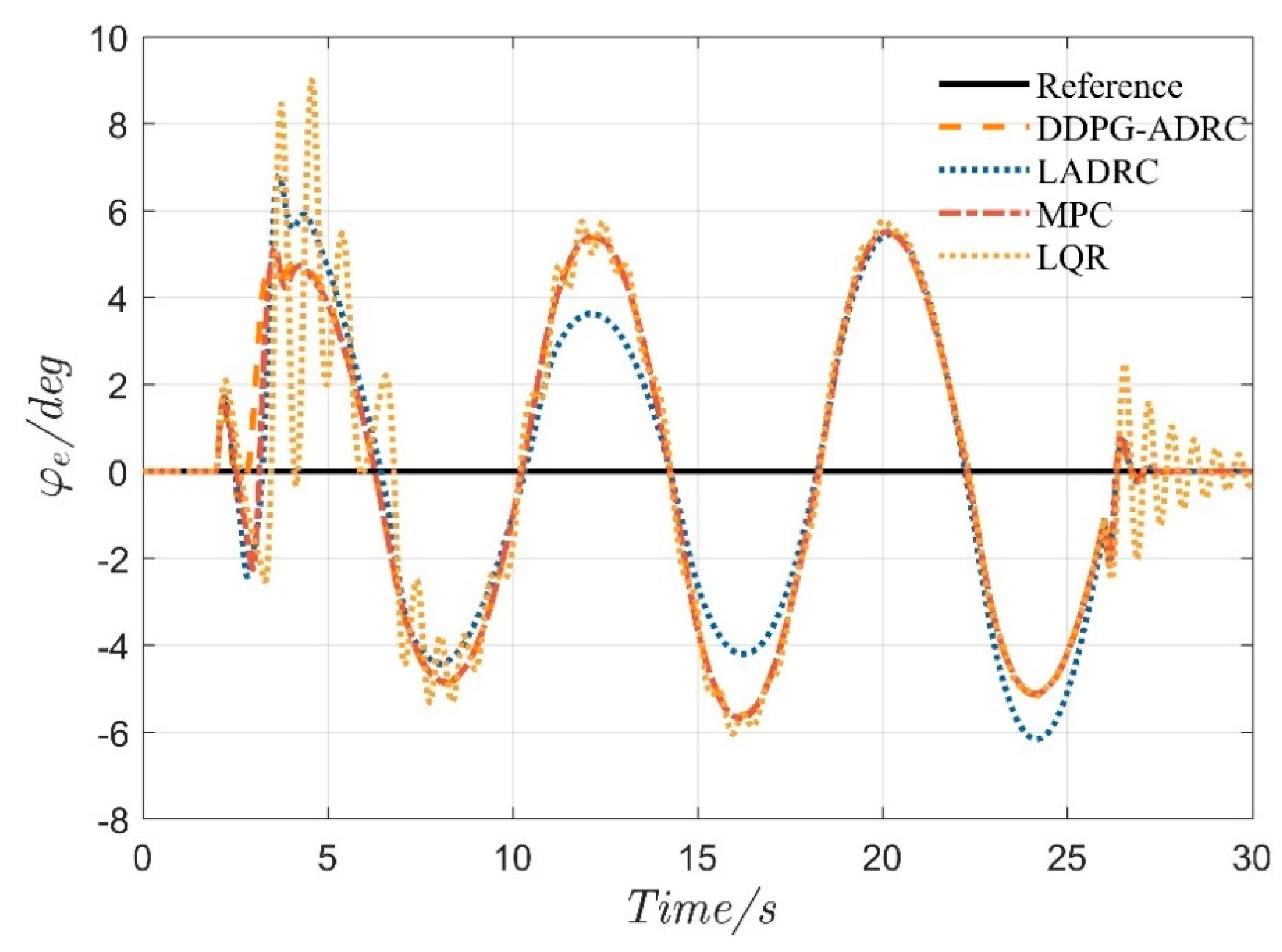
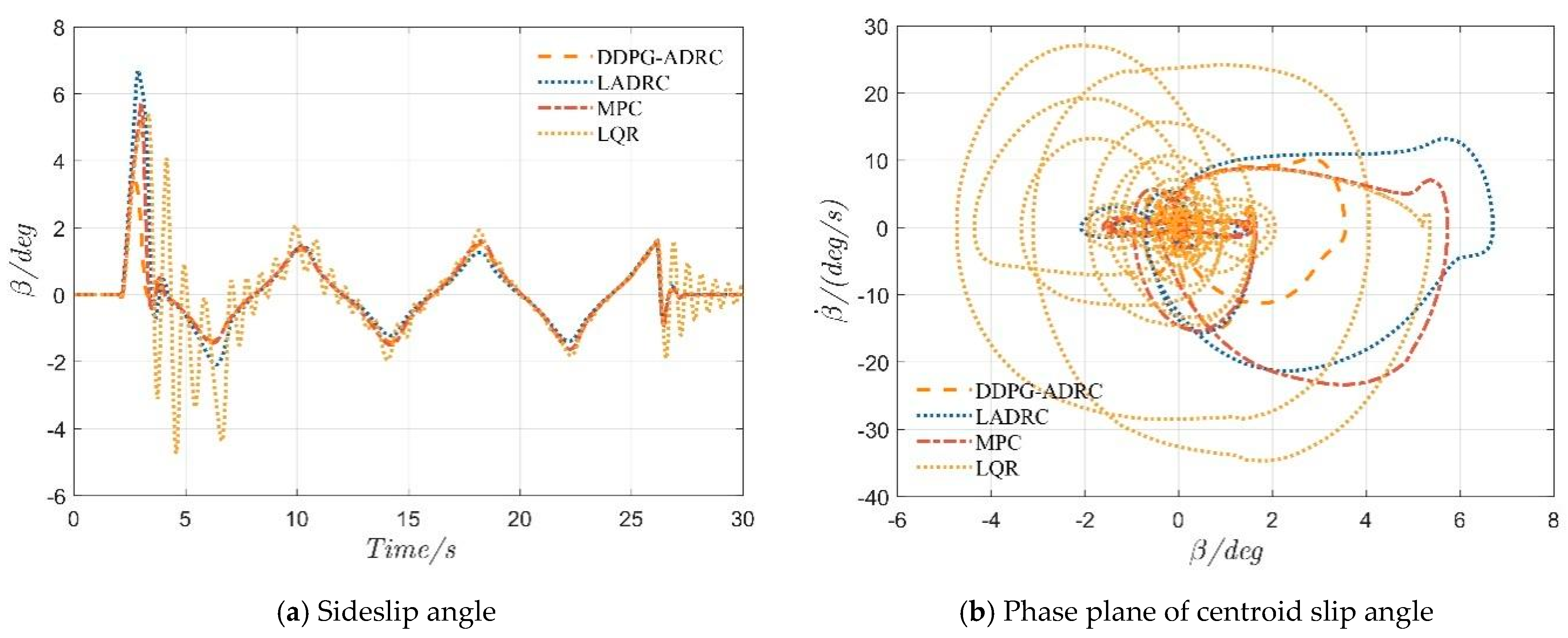
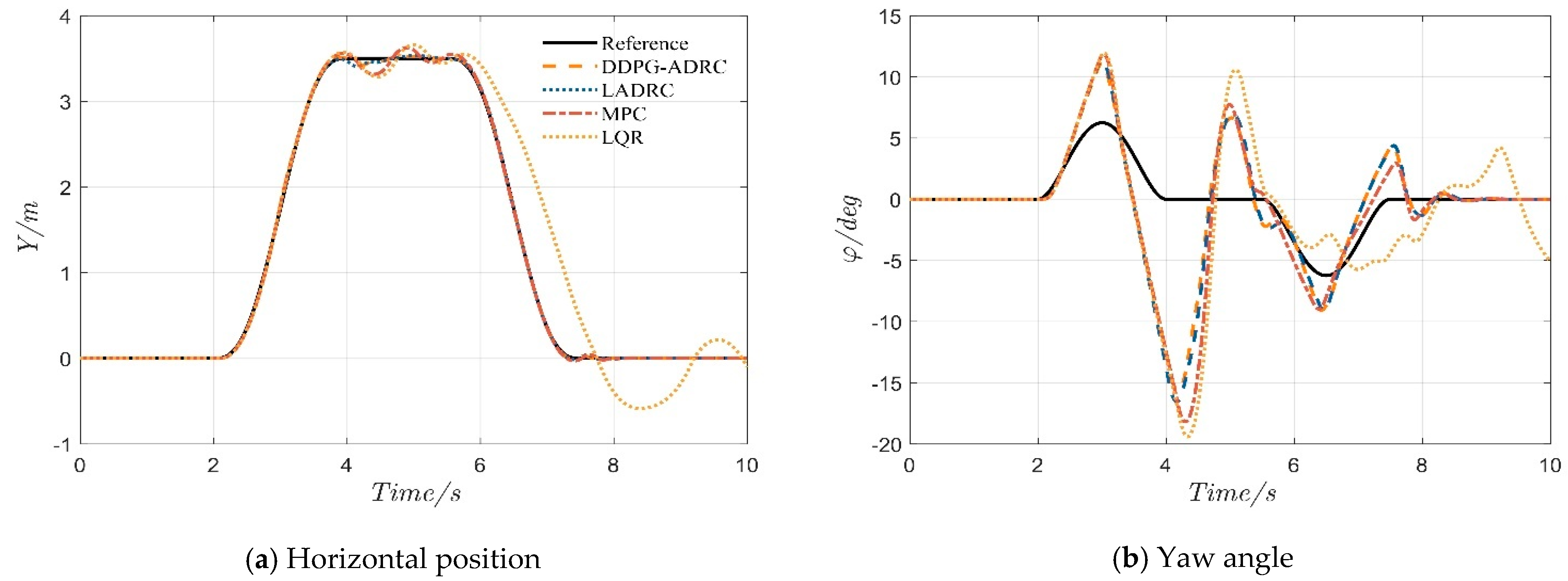
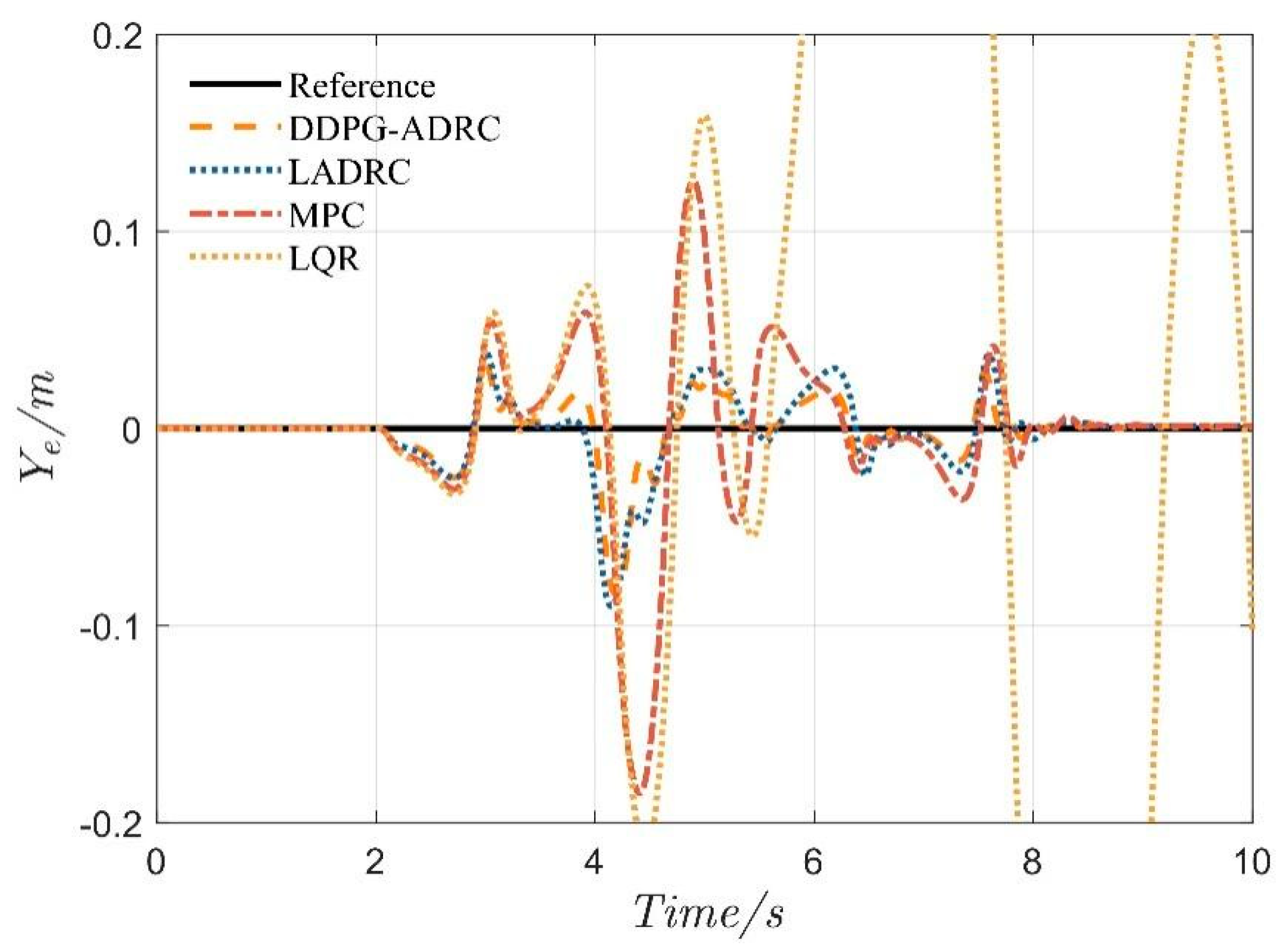
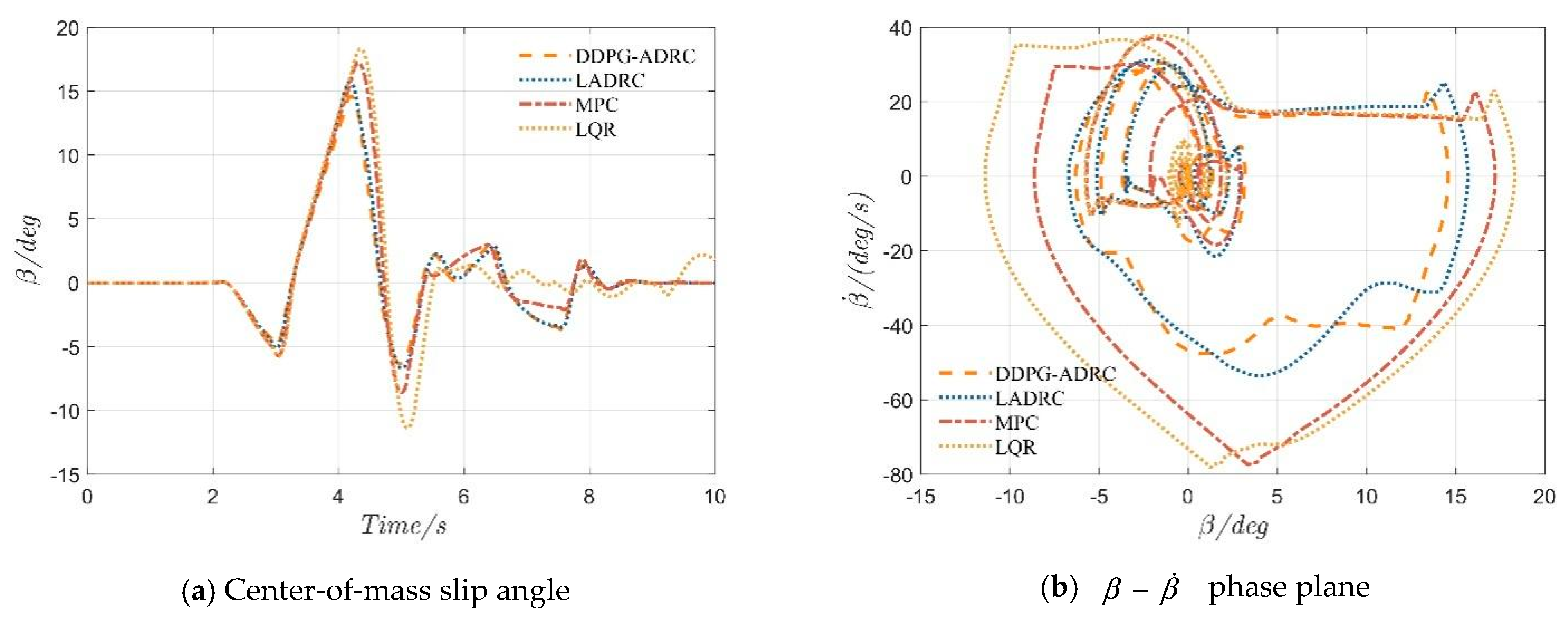
4.2. Serpentine Maneuver
4.3. Double-Lane-Change Maneuver
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Skačkauskas, P.; Karpenko, M.; Prentkovskis, O. Design and Implementation of a Hybrid Path Planning Approach for Autonomous Lane Change Manoeuvre. Int. J. Automot. Technol. 2024, 25, 83–95. [Google Scholar] [CrossRef]
- Coppola, A.; Lui, D.G.; Petrillo, A.; Santini, S. Eco-Driving Control Architecture for Platoons of Uncertain Heterogeneous Nonlinear Connected Autonomous Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 24220–24234. [Google Scholar] [CrossRef]
- Wang, F.; Shen, T.; Zhao, M.; Ren, Y.; Lu, Y.; Feng, B. Lane-Change Trajectory Planning and Control Based on Stability Region for Distributed Drive Electric Vehicle. IEEE Trans. Veh. Technol. 2024, 73, 504–521. [Google Scholar] [CrossRef]
- Liu, C.; Liu, H.; Han, L.; Wang, W.; Guo, C. Multi-Level Coordinated Yaw Stability Control Based on Sliding Mode Predictive Control for Distributed Drive Electric Vehicles Under Extreme Conditions. IEEE Trans. Veh. Technol. 2023, 72, 280–296. [Google Scholar] [CrossRef]
- Jin, X.; Wang, Q.; Yan, Z.; Yang, H.; Yin, G. Integrated robust control of path following and lateral stability for autonomous in-wheel-motor-driven electric vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2025, 239, 12696–12706. [Google Scholar] [CrossRef]
- Li, M.; Li, Z.; Cao, Z. Enhancing Car-Following Performance in Traffic Oscillations Using Expert Demonstration Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2024, 25, 7751–7766. [Google Scholar] [CrossRef]
- Acquarone, M.; Miretti, F.; Misul, D.; Sassara, L. Cooperative Adaptive Cruise Control Based on Reinforcement Learning for Heavy-Duty BEVs. IEEE Access 2023, 11, 127145–127156. [Google Scholar] [CrossRef]
- Selvaraj, D.C.; Hegde, S.; Amati, N.; Deflorio, F.; Chiasserini, C.F. An ML-Aided Reinforcement Learning Approach for Challenging Vehicle Maneuvers. IEEE Trans. Intell. Veh. 2023, 8, 1686–1698. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, Y.; Chu, H.; Yu, Q.; Gao, B.; Chen, H. Safety-Critical Control of 4WDEV Trajectory Tracking via Adaptive Control Barrier Function. IEEE Trans. Transp. Electrif. 2024, 10, 10361–10373. [Google Scholar] [CrossRef]
- Luo, Y.; Tang, F.; Zhang, H.; Yang, D. Synchronous Position-Attitude Loop Regulation-Based Distributed Optimal Trajectory Tracking Control for Multi-UAVs Formation With External Disturbances. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 7445–7456. [Google Scholar] [CrossRef]
- Pan, Z.; Sun, Z.; Deng, H.; Li, D. A Multilayer Graph for Multiagent Formation and Trajectory Tracking Control Based on MPC Algorithm. IEEE Trans. Cybern. 2022, 52, 13586–13597. [Google Scholar] [CrossRef] [PubMed]
- Najafqolian, M.A.; Alipour, K.; Mousavifard, R.; Tarvirdizadeh, B. Control of Aerial Robots Using Convex QP LMPC and Learning-Based Explicit-MPC. IEEE Trans. Ind. Inf. 2024, 20, 10883–10891. [Google Scholar] [CrossRef]
- Wang, P.; Bi, Y.; Gao, F.; Song, T.; Zhang, Y. An Improved Deadbeat Control Method for Single-Phase PWM Rectifiers in Charging System for EVs. IEEE Trans. Veh. Technol. 2019, 68, 9672–9681. [Google Scholar] [CrossRef]
- Dong, Q.; Liu, Y.; Zhang, Y.; Gao, S.; Chen, T. Improved ADRC With ILC Control of a CCD-Based Tracking Loop for Fast Steering Mirror System. IEEE Photonics J. 2018, 10, 1–14. [Google Scholar] [CrossRef]
- Aliamooei Lakeh, H.; Aliamooei Lakeh, S.; Toulabi, M.; Amraee, T. Enhancement in Robust Performance of Boost Converter-Based Distributed Generations Utilizing Active Disturbance Rejection Controller. IEEE Trans. Autom. Sci. Eng. 2024, 21, 6094–6108. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, Q.; Ren, B. Wind Turbine Crack Inspection Using a Quadrotor With Image Motion Blur Avoided. IEEE Rob. Autom. Lett. 2023, 8, 1069–1076. [Google Scholar] [CrossRef]
- Bilal, H.; Aslam, M.S.; Tian, Y.; Yahya, A.; Abu Izneid, B. Enhancing Trajectory Tracking and Vibration Control of Flexible Robots With Hybrid Fuzzy ADRC and Input Shaping. IEEE Access 2024, 12, 150574–150591. [Google Scholar] [CrossRef]
- Castañeda, L.A.; Luviano Juárez, A.; Chairez, I. Robust Trajectory Tracking of a Delta Robot Through Adaptive Active Disturbance Rejection Control. IEEE Trans. Control Syst. Technol. 2015, 23, 1387–1398. [Google Scholar] [CrossRef]
- Ramírez Neria, M.; Sira Ramírez, H.; Garrido Moctezuma, R.; Luviano Juárez, A.; Gao, Z. Active Disturbance Rejection Control for Reference Trajectory Tracking Tasks in the Pendubot System. IEEE Access 2021, 9, 102663–102670. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Dong, Y.; Ren, B. Bounded UDE-Based Control for a SLAM Equipped Quadrotor with Input Constraints. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 3117–3122. [Google Scholar]
- Kurunathan, H.; Li, K.; Tovar, E.; Mario Jorge, A.; Ni, W.; Jamalipour, A. DRL-KeyAgree: An Intelligent Combinatorial Deep Reinforcement Learning-Based Vehicular Platooning Secret Key Generation. IEEE Trans. Intell. Transp. Syst. 2024, 25, 16354–16369. [Google Scholar] [CrossRef]
- Ali, H.; Pham, D.T.; Alam, S. Toward Greener and Sustainable Airside Operations: A Deep Reinforcement Learning Approach to Pushback Rate Control for Mixed-Mode Runways. IEEE Trans. Intell. Transp. Syst. 2024, 25, 18354–18367. [Google Scholar] [CrossRef]
- Raju, M.R.; Mothku, S.K.; Somesula, M.K. DMITS: Dependency and Mobility-Aware Intelligent Task Scheduling in Socially-Enabled VFC Based on Federated DRL Approach. IEEE Trans. Intell. Transp. Syst. 2024, 25, 17007–17022. [Google Scholar] [CrossRef]
- Shalaby, A.A.; Abdeltawab, H.; Mohamed, Y.A.R.I. Model-Free Dynamic Operations Management for EV Battery Swapping Stations: A Deep Reinforcement Learning Approach. IEEE Trans. Intell. Transp. Syst. 2023, 24, 8371–8385. [Google Scholar] [CrossRef]
- Raja, G.; Begum, M.; Gurumoorthy, S.; Rajendran, D.S.; Srividya, P.; Dev, K. AI-Empowered Trajectory Anomaly Detection and Classification in 6G-V2X. IEEE Trans. Intell. Transp. Syst. 2023, 24, 4599–4607. [Google Scholar] [CrossRef]
- Saba, I.; Ullah, M.; Tariq, M. Advancing Electric Vehicle Battery Analysis With Digital Twins in Intelligent Transportation Systems. IEEE Trans. Intell. Transp. Syst. 2024, 25, 12141–12150. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, S.; Hu, J. Active Disturbance Rejection Control Based on Deep Reinforcement Learning of PMSM for More Electric Aircraft. IEEE Trans. Power Electron. 2023, 38, 406–416. [Google Scholar] [CrossRef]
- Gheisarnejad, M.; Khooban, M.H. IoT-Based DC/DC Deep Learning Power Converter Control: Real-Time Implementation. IEEE Trans. Power Electron. 2020, 35, 13621–13630. [Google Scholar] [CrossRef]
- Liu, X.; Yuan, Z.; Gao, Z.; Zhang, W. Reinforcement Learning-Based Fault-Tolerant Control for Quadrotor UAVs Under Actuator Fault. IEEE Trans. Ind. Inf. 2024, 20, 13926–13935. [Google Scholar] [CrossRef]
- You, S.; Byeon, K.; Seo, J.; Kim, W.; Tomizuka, M. Policy-Iteration-Based Active Disturbance Rejection Control for Uncertain Nonlinear Systems With Unknown Relative Degree. IEEE Trans. Cybern. 2025, 55, 1347–1358. [Google Scholar] [CrossRef]
- Ning, B.; Han, Q.; Zuo, Z.; Ding, L. Accelerated secondary frequency regulation and active power sharing for islanded microgrids with external disturbances: A fully distributed approach. Automatica 2025, 174, 112146. [Google Scholar] [CrossRef]




| State Symbol | Description | Unit | Agent Parameter | Value |
|---|---|---|---|---|
| y | Actual lateral position | m | Sampling time | 0.02 s |
| yr | Desired lateral position | m | Discount factor γ | 0.99 |
| φ | Actual yaw angle | deg | Actor learning rate | 0.003 |
| φr | Desired yaw angle | deg | Critic learning rate | 0.003 |
| Yaw rate | deg/s | τ | 0.001 | |
| β | Sideslip angle | deg | N | 64 |
| Sideslip rate | deg/s |
| Parameter | Description | Value | Unit |
|---|---|---|---|
| Upper bound of lateral acceleration | 6 | m/s2 | |
| Lower bound of lateral acceleration | 5 | m/s2 | |
| vx | Longitudinal velocity | 35 | m/s |
| ax | Longitudinal acceleration | 0 | m/s2 |
| κh | Upper bound of curvature | 2.0 | m−1 |
| κl | Lower bound of curvature | 0.5 | m−1 |
| Upper bound of front wheel steering angle | 30 | deg | |
| Lower bound of front wheel steering angle | −30 | deg | |
| T | Trajectory duration | 50 | s |
| Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|
| m | 1270 | kg | Iz | 1537 | kg·m2 |
| r | 0.325 | m | T | 0.02 | s |
| g | 9.81 | m/s2 | μ | 0.5, 0.6 | - |
| lf | 0.015 | m | lr | 1.895 | m |
| Nαf | 130728 | N/rad | Nαr | 70021 | N/rad |
| Wf | 1.675 | m | Wr | 1.675 | m |
| [10, 40] | - | [0.01, 0.5] | - |
| Parameter | Index | ADRC | LADRC | MPC | LQR | PA () | PB () | PC () |
|---|---|---|---|---|---|---|---|---|
| MAE | 2.7 | 4.6 | 6.1 | 20.6 | 40.99% | 55.87% | 86.83% | |
| RMSE | 3.6 | 6.9 | 9.8 | 32.1 | 46.71% | 62.51% | 88.54% | |
| MSE | 0.014 | 0.048 | 0.097 | 1.034 | 71.60% | 85.94% | 98.69% | |
| MAE | 2.74 | 3.01 | 2.74 | 2.88 | 8.97% | 0.06% | 4.64% | |
| RMSE | 3.37 | 3.61 | 3.38 | 3.52 | 6.65% | 0.29% | 4.26% | |
| MSE | 11.47 | 11.67 | 11.44 | 12.42 | 1.71% | 0.27% | 7.62% |
| Parameter | Index | ADRC | LADRC | MPC | LQR | PA () | PB () | PC () |
|---|---|---|---|---|---|---|---|---|
| MAE | 8.59 | 10.65 | 22.39 | 241.07 | 19.36% | 61.64% | 96.44% | |
| RMSE | 15.73 | 18.94 | 42.21 | 423.71 | 16.93% | 62.72% | 96.295 | |
| MSE | 0.25 | 0.36 | 1.78 | 179.53 | 30.99% | 86.10% | 99.86% | |
| MAE | 2.26 | 2.40 | 2.47 | 3.32 | 5.62% | 8.49% | 31.88% | |
| RMSE | 4.11 | 4.40 | 4.75 | 5.50 | 6.61% | 13.50% | 25.20% | |
| MSE | 16.90 | 19.38 | 22.59 | 30.21 | 12.79% | 25.17% | 44.06% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, X.; Lv, H.; Tao, Y.; Lu, J.; Lv, J.; Opinat Ikiela, N.V. Deep Reinforcement Learning-Based Active Disturbance Rejection Control for Trajectory Tracking of Autonomous Ground Electric Vehicles. Machines 2025, 13, 523. https://doi.org/10.3390/machines13060523
Jin X, Lv H, Tao Y, Lu J, Lv J, Opinat Ikiela NV. Deep Reinforcement Learning-Based Active Disturbance Rejection Control for Trajectory Tracking of Autonomous Ground Electric Vehicles. Machines. 2025; 13(6):523. https://doi.org/10.3390/machines13060523
Chicago/Turabian StyleJin, Xianjian, Huaizhen Lv, Yinchen Tao, Jianning Lu, Jianbo Lv, and Nonsly Valerienne Opinat Ikiela. 2025. "Deep Reinforcement Learning-Based Active Disturbance Rejection Control for Trajectory Tracking of Autonomous Ground Electric Vehicles" Machines 13, no. 6: 523. https://doi.org/10.3390/machines13060523
APA StyleJin, X., Lv, H., Tao, Y., Lu, J., Lv, J., & Opinat Ikiela, N. V. (2025). Deep Reinforcement Learning-Based Active Disturbance Rejection Control for Trajectory Tracking of Autonomous Ground Electric Vehicles. Machines, 13(6), 523. https://doi.org/10.3390/machines13060523






