Study on Steam Excitation Forces Induced by Tip Seal Leakage Flow in Steam Turbines
Abstract
1. Introduction
2. Computational Model and Numerical Methods
2.1. Physical Model and Computational Grid
2.2. Boundary Conditions
2.3. Numerical Methods
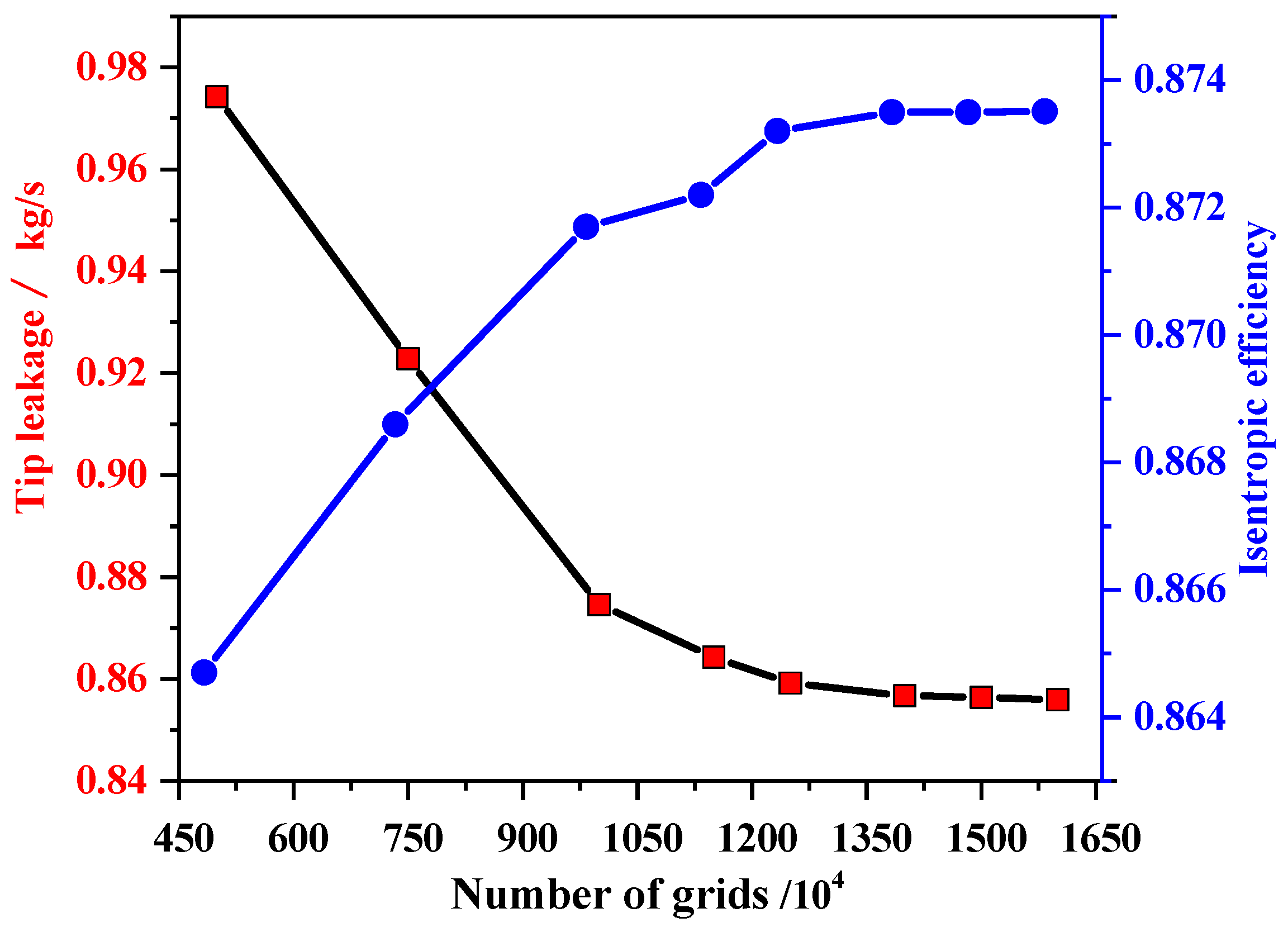
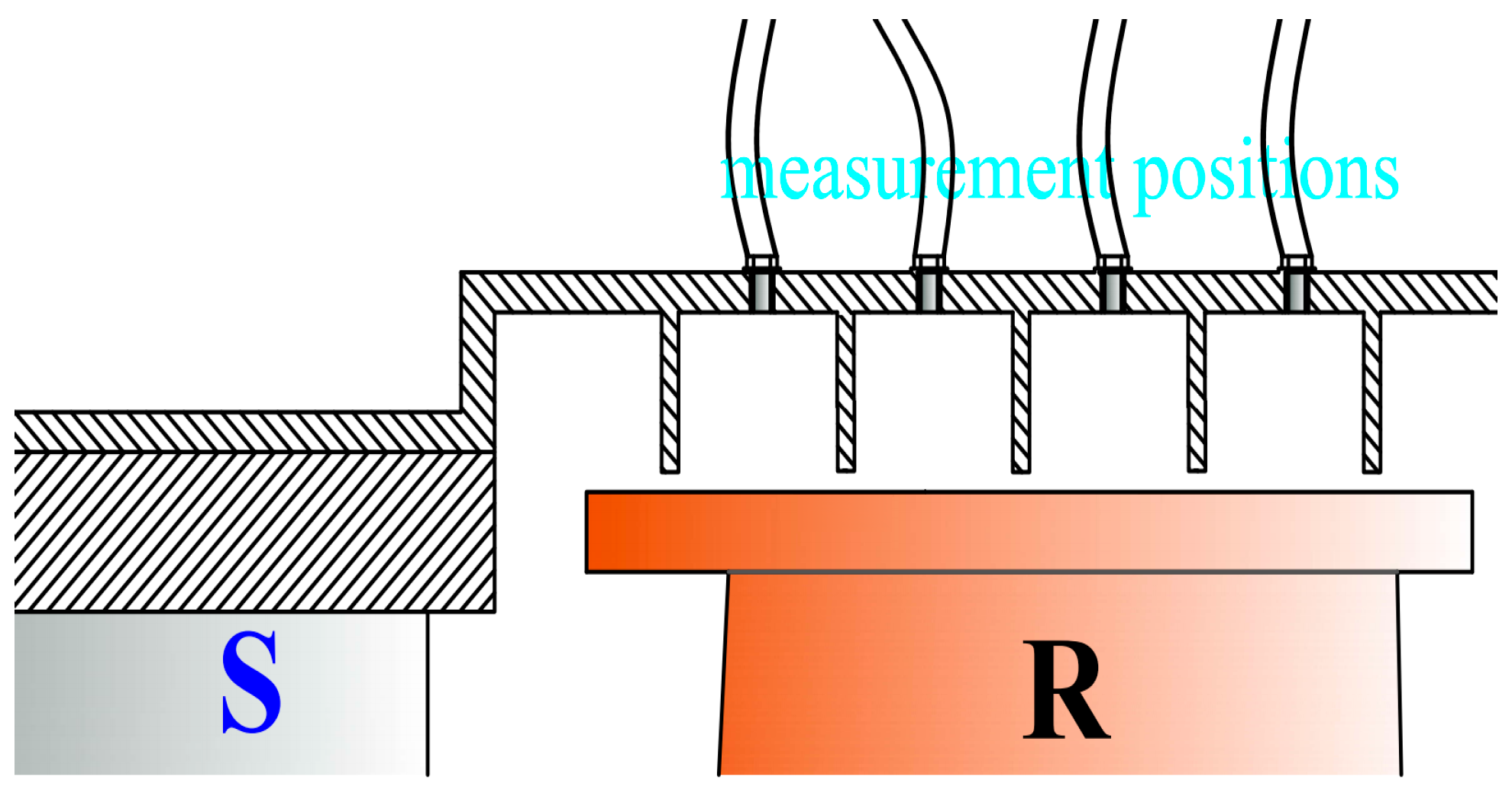
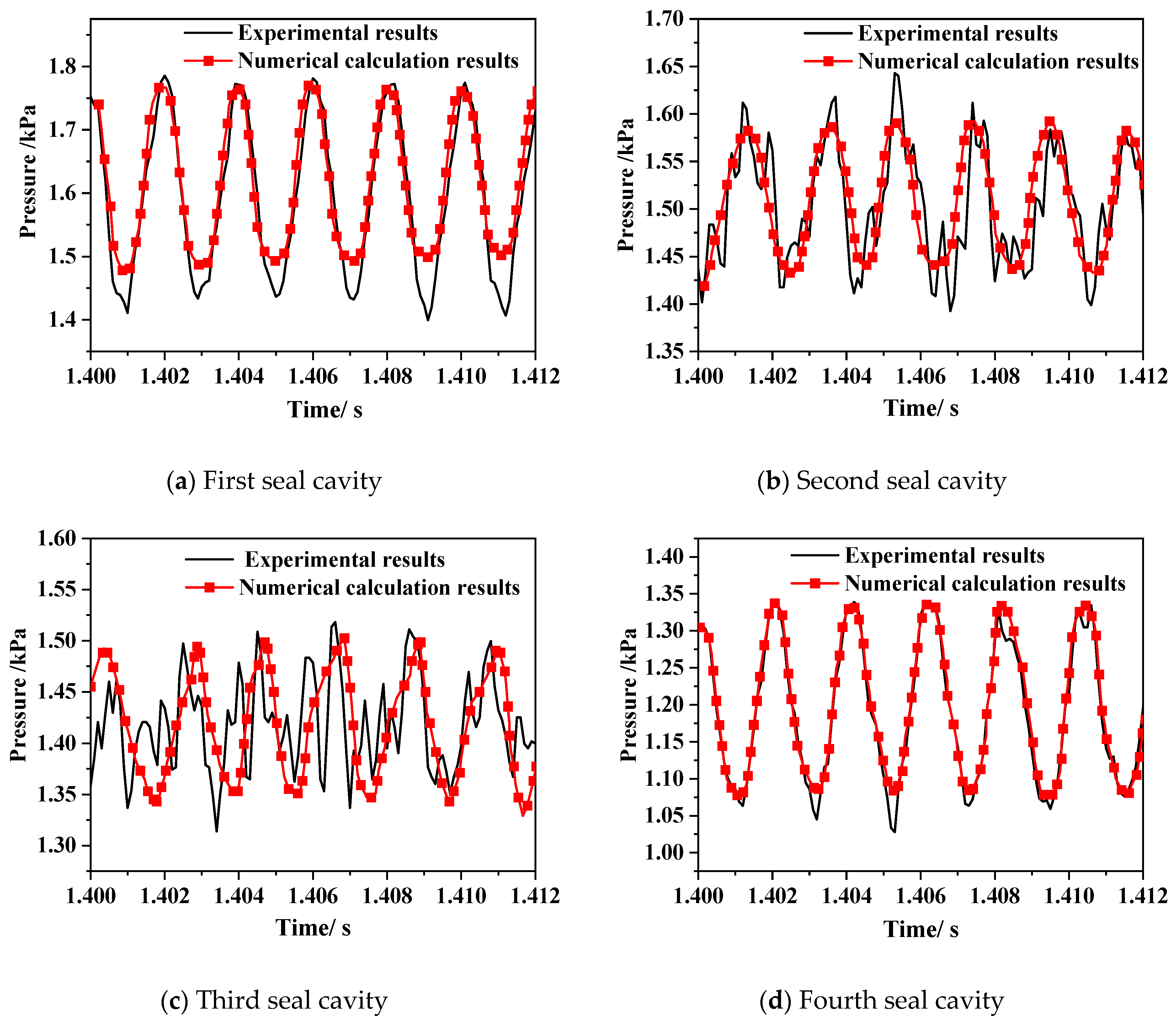
2.4. Validation of Results
3. Result Analysis
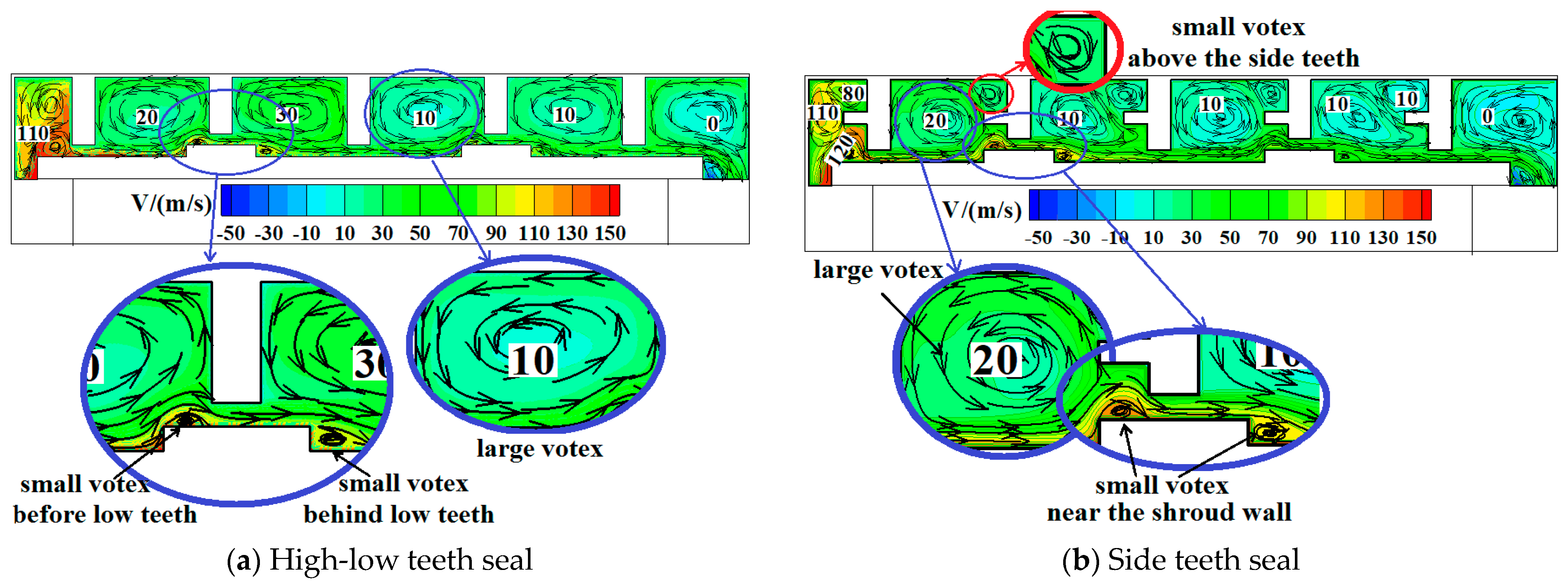
3.1. Flow Field Analysis
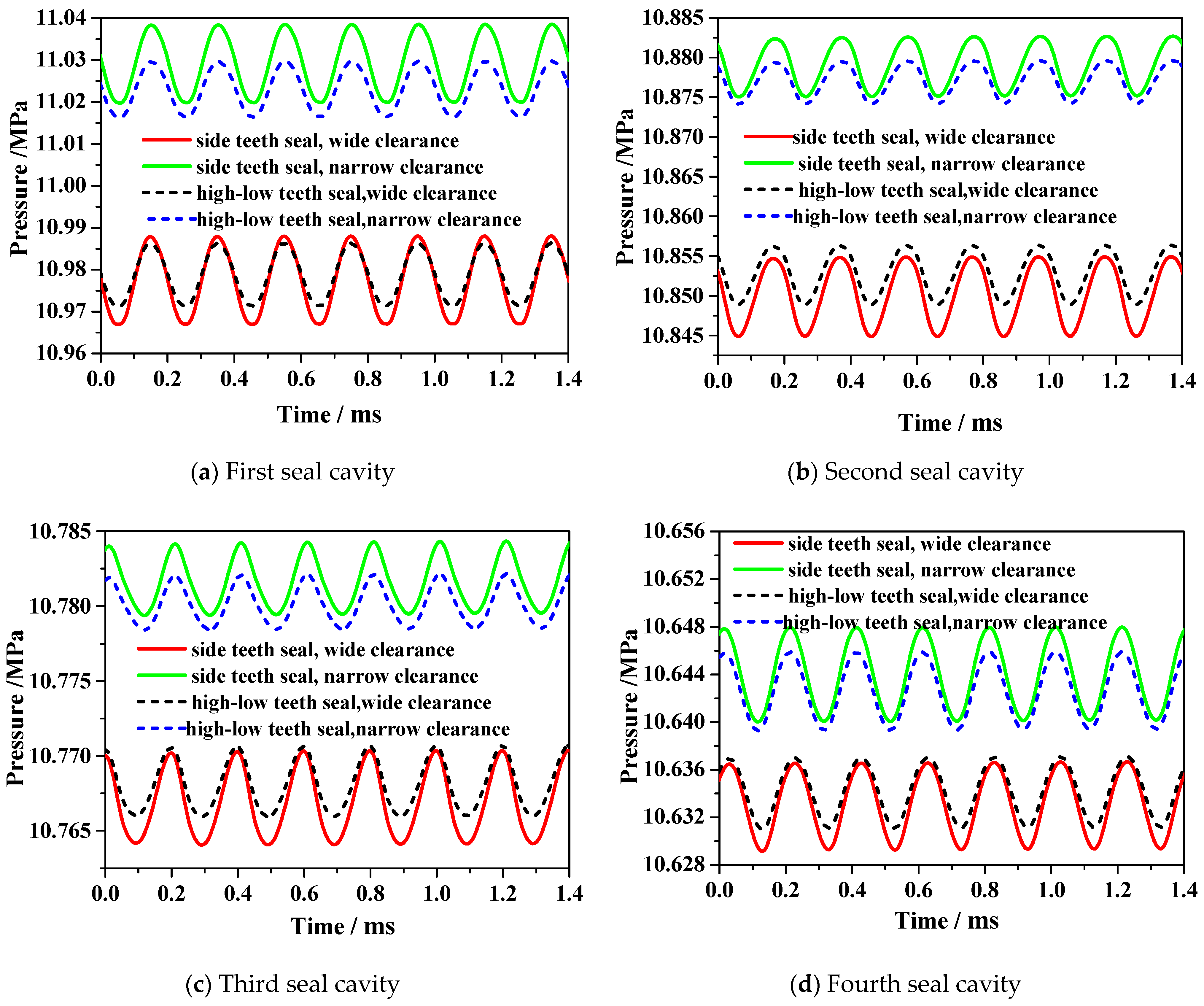
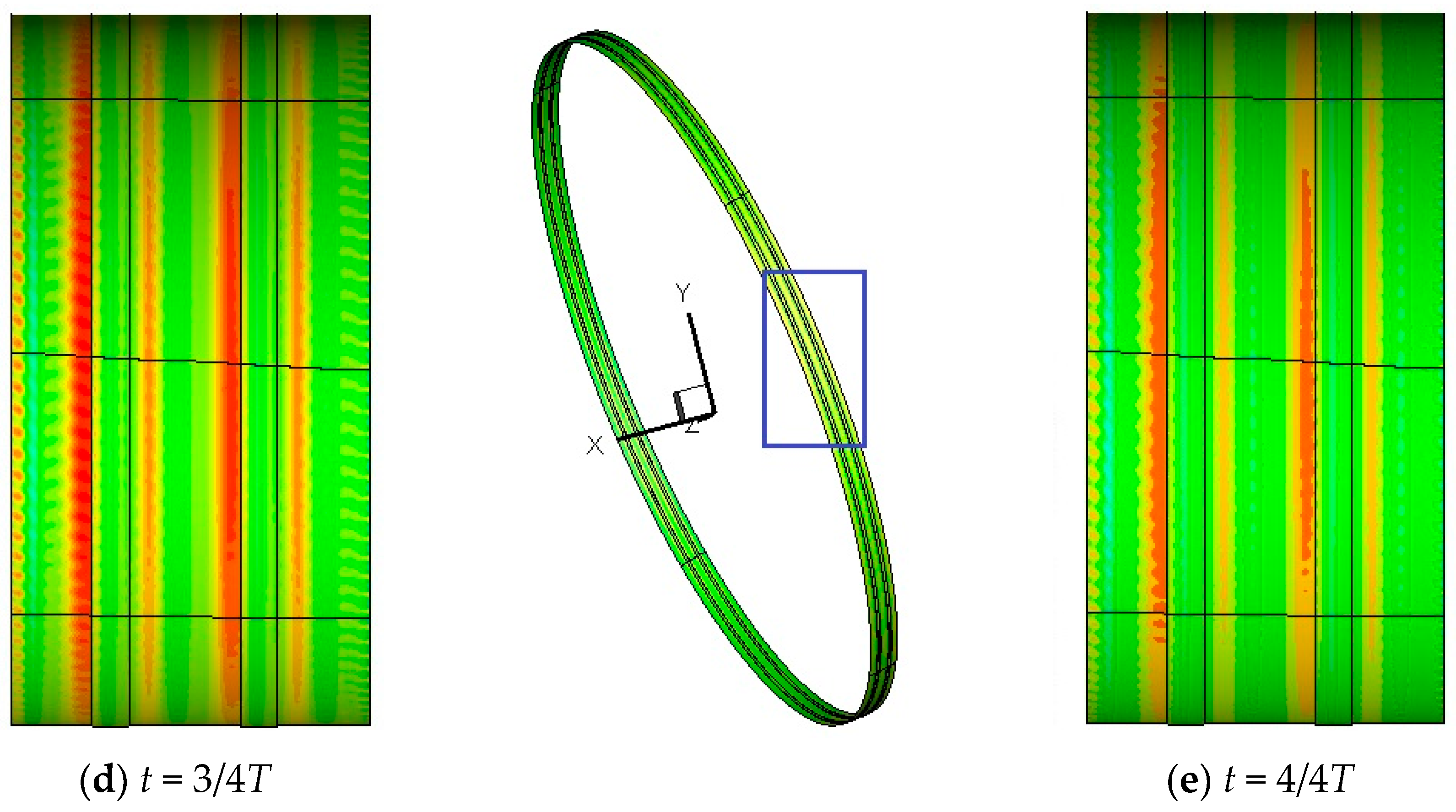
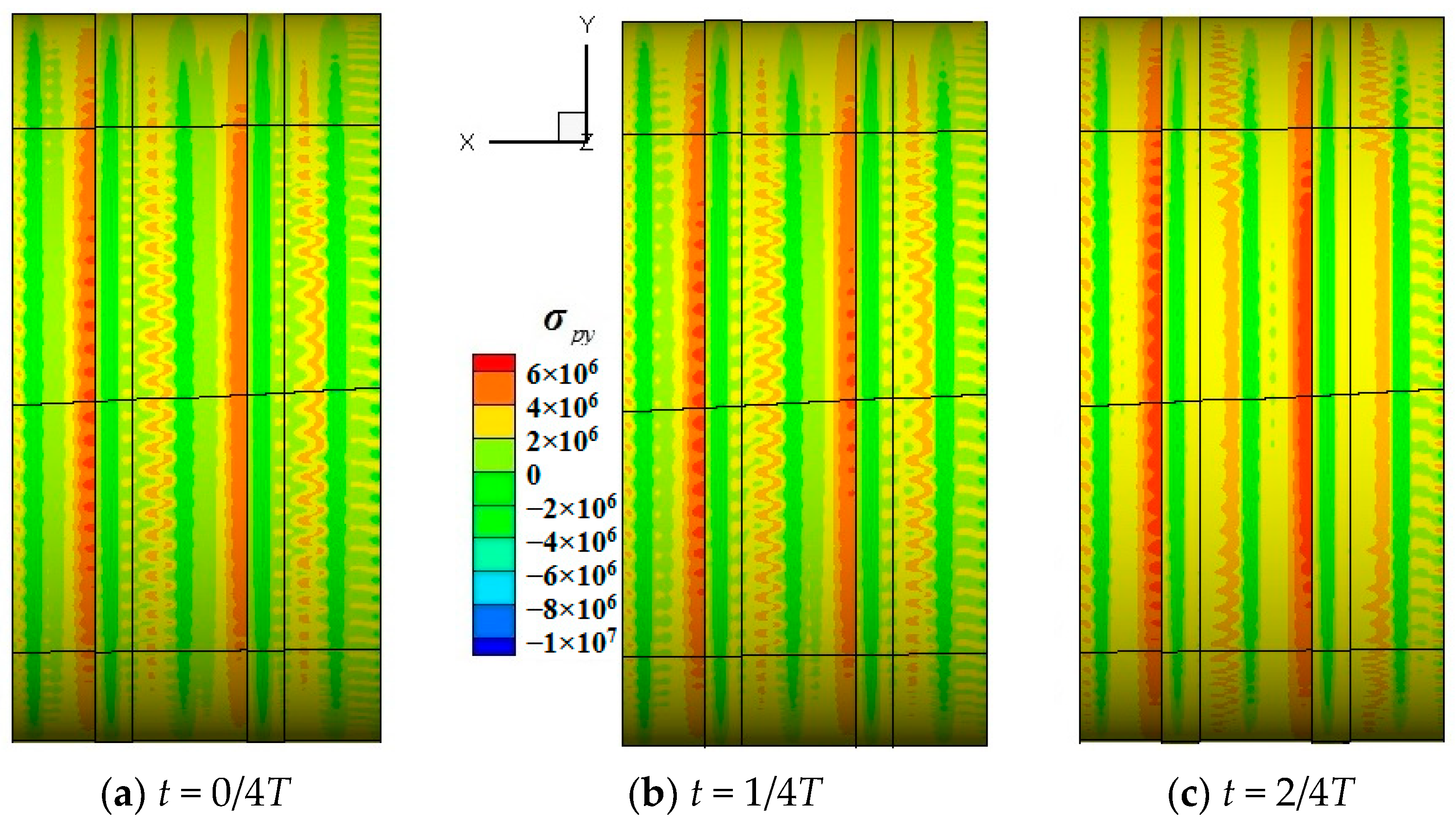
3.2. Analysis of Unsteady Variation in Shroud BVF
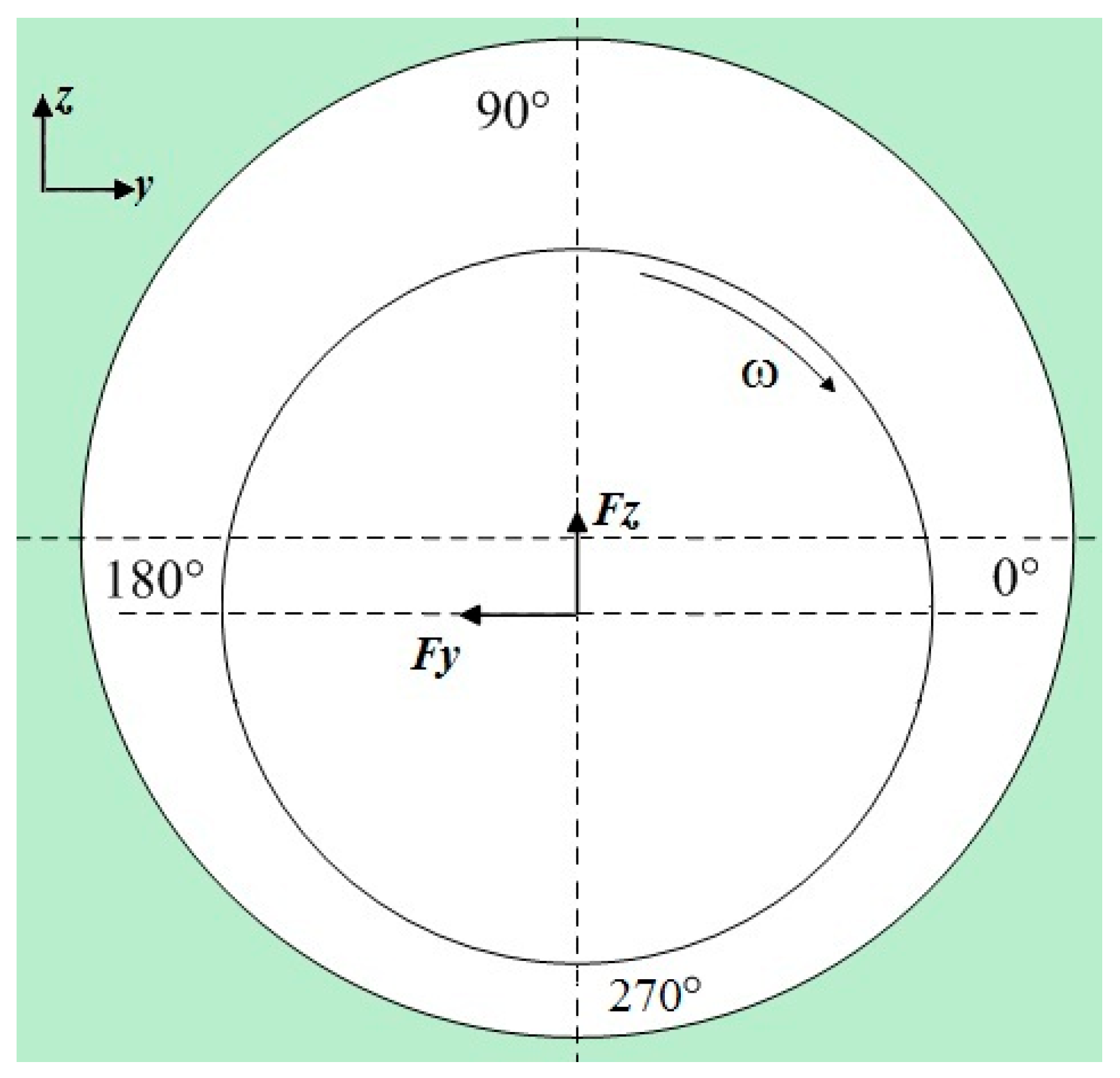
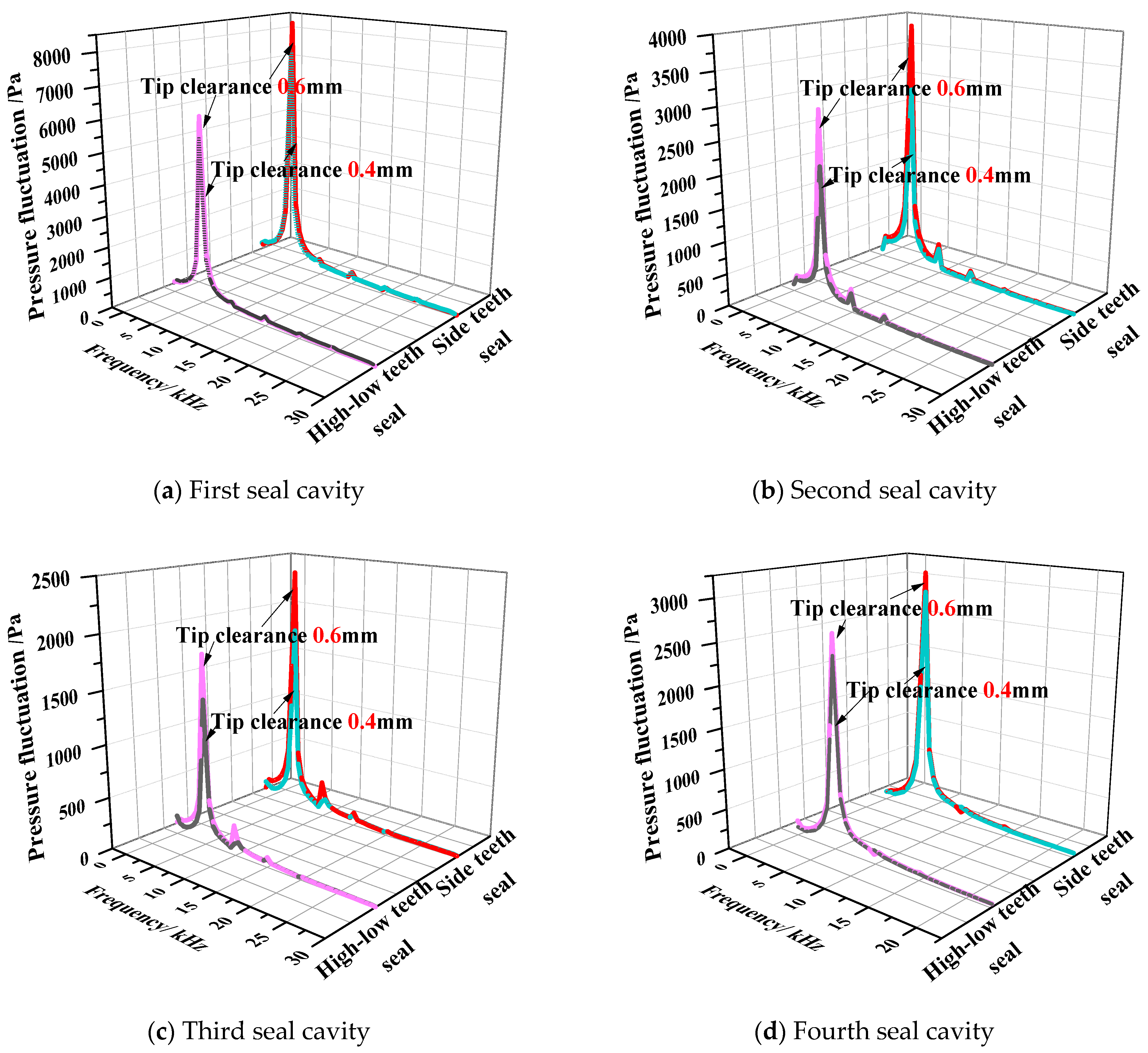
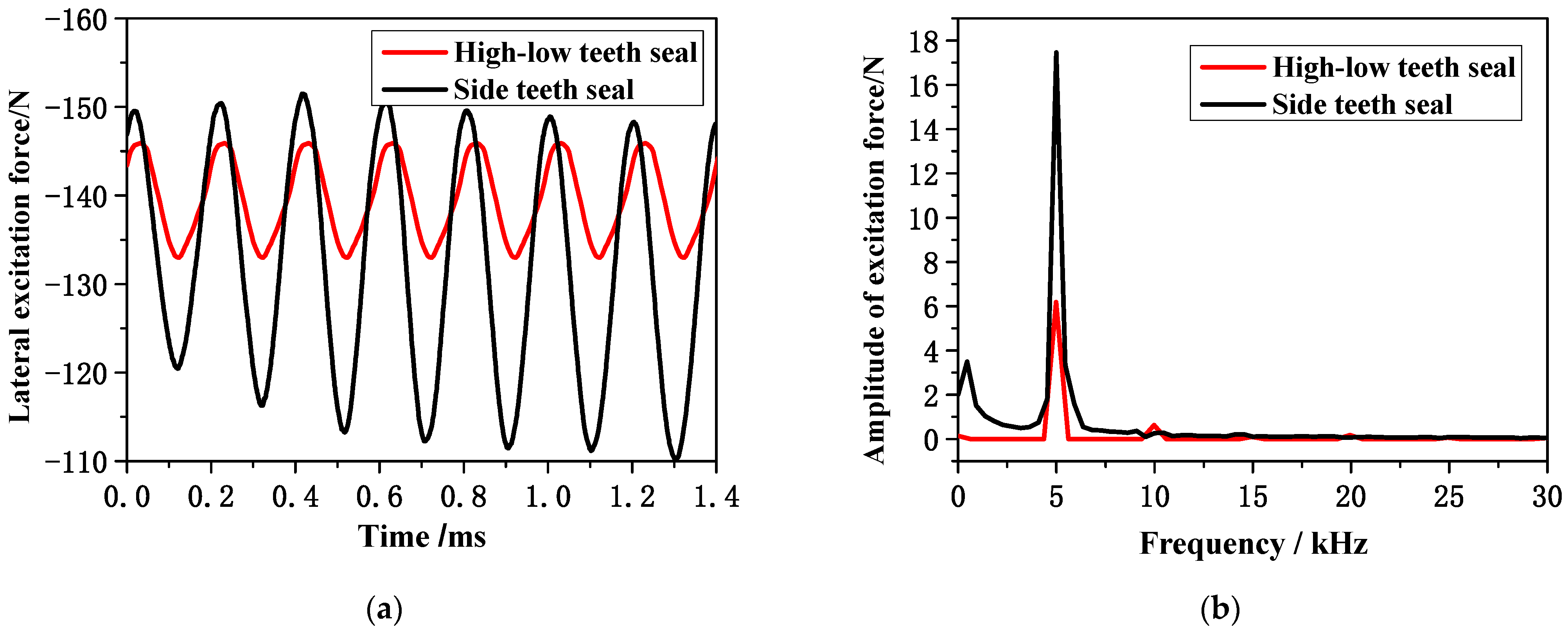
3.3. Analysis of Blade Tip Seal Steam Flow Excitation Force Fluctuation Patterns
4. Conclusions
- (1)
- The vortex system within the seal primarily consists of large vortices in the cavity and smaller vortices near the shroud wall. The shroud wall vortices exhibit periodic sinusoidal fluctuations, with a period corresponding to the time it takes for a rotor blade to pass through a stator blade passage. Compared to high-low teeth seals, side teeth seals exhibit a greater amplitude of shroud wall vortex pressure fluctuations, indicating that an increase in vortex structures within the seal cavity intensifies pressure fluctuations.
- (2)
- By introducing BVF, a relationship is established between the flow field in the blade tip seal clearance and the forces on the shroud surface. The effect of the leakage flow field on the lateral excitation force in the blade tip seal can be characterized by the distribution of BVF along the shroud surface. The periodic changes in BVF align with the fluctuation patterns of both the shroud wall vortices within the seal flow field and the lateral excitation force.
- (3)
- The instability of the leakage flow in the blade tip clearance induces fluctuations in the steam excitation force. The vortex motion in the shroud wall leads to periodic changes in BVF on the shroud surface, which are the primary cause of fluctuations in the lateral excitation force within the blade tip seal. Additionally, the unsteady circumferential pressure differential within the blade tip seal clearance ultimately results in fluctuations in the radial excitation force.
- (4)
- An increase in vortices within the tip seal cavity intensifies vortex–vortex interactions, leading to greater pressure fluctuation amplitudes and consequently larger induced steam excitation force variations. This phenomenon adversely affects rotor operational stability. By elucidating the mechanism of vortex-induced steam excitation force fluctuations in the tip seal cavity, this study provides theoretical foundations and references for enhancing steam turbine operational safety.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Roman letters | |
| p | Pressure [Pa] |
| T | Temperature [K] |
| y+ | Dimensionless wall distance [-] |
| k | Turbulent kinetic energy [m2s−2] |
| e | Eccentricity [m] |
| rb | Rotor radius [m] |
| n(n1, n2, n3) | Unit normal vector and its components in the Cartesian coordinate system |
| V(u, v, w) | Velocity vector and its components in the Cartesian coordinate system [m s−1] |
| a | Acceleration [m s−2] |
| f | Body force [N m−3] |
| Greek letters | |
| ω | Vorticity [s−1] |
| ω | Specific dissipation rate [m2s−3] |
| η | Isentropic efficiency [-] |
| γ | Adiabatic index [-] |
| τ | Shear stress [-] |
| ρ | Density [kg m−3] |
| ν | Kinematic viscosity [m2s−1] |
| Boundary Vorticity Flux [-] | |
| Radial BVF [-] | |
| Abbreviations | |
| CFD | Computational fluid dynamics |
| BVF | Boundary Vorticity Flux |
| LES | Large Eddy Simulation |
| SST | Shear Stress Transport |
References
- Gao, J.; Zheng, Q.; Zhang, H.; Chen, H. Comparative investigation of tip leakage flow and its effect on stage performance in shrouded and unshrouded turbines. J. Aerosp. Power 2016, 227, 1265–1276. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, M.; Peng, N. Study of heat transfer and leakage characteristics of brush seals based on local temperature non-equilibrium model. Machines 2022, 10, 823. [Google Scholar] [CrossRef]
- Biassoni, D.; Barsi, D.; Lengani, D. Effect of purge on secondary flows in turbine due to interaction between cavity flow and main channel. Machines 2025, 13, 77. [Google Scholar] [CrossRef]
- Molale, T.; Ahmed, N.; Bhamjee, M. Numerical analysis of flow induced vibrations of a low-pressure steam turbine rotating blade. JPCS 2019, 1378, 32–43. [Google Scholar] [CrossRef]
- Cao, L.H.; Wang, J.X.; Li, P.; Yun, A.X. Analysis on structure and high loss zone of tip leakage flow in steam turbine. Proc. CSEE 2018, 38, 2055–2062+2220. [Google Scholar]
- Sun, D.; Xiao, Z.H.; Zheng, T.S.; Wang, X.J. Study on influence factors of tangential fluid-induced force and radial fluid-induced force in seals. Lubr. Eng. 2013, 9, 33–36. [Google Scholar]
- Xue, C.; Cao, L.H.; Si, H.Y. Anisotropic Vibration Characteristics Analysis of Steam Turbine Rotor Influenced by Steam Flow Excited Force Coupling Thermal and Dynamic Loads. J. Energy Resour. Technol. 2023, 145, 071703. [Google Scholar] [CrossRef]
- Sun, T.; Liu, Y.Z.; Ma, Z.L. Numerical simulation of the relationship between steam flow excitation characteristics and coverage on the governing stage of marine steam turbine. Ocean. Eng. 2024, 314, 119526. [Google Scholar] [CrossRef]
- Chen, Y.X.; Li, Z.G.; Li, J. Fluid excited rotor dynamic characteristics of labyrinth seal during non-uniform inlet flowing. J. Xi’an Jiaotong Univ. 2017, 51, 145–152. [Google Scholar]
- Si, H.Y.; Cao, L.H.; Li, P. Effect of seal structure on rotor dynamic characteristics of steam turbine. Proc. CSEE 2020, 40, 165–175+384. [Google Scholar]
- Wang, H.; Wu, Y.D.; Ouyang, H.; Du, Z.H. Circumferential propagating characteristics of tip leakage flow oscillation and its induced rotating pressure wave. Proc. Inst. Mech. Eng. Part A J. Power Energy 2016, 230, 374–387. [Google Scholar]
- Towne, A.; Schmidt, O.T.; Colonius, T. Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 2018, 847, 821–867. [Google Scholar] [CrossRef]
- Jeffrey, M.J. Three-dimensional CFD rotordynamic analysis of gas labyrinth seals. J. Vib. Acoust. 2003, 125, 427–433. [Google Scholar]
- Zou, D.L.; Xue, L.; Yang, Y.Z.; Dong, X.G.; Ta, N.; Rao, Z.S. Research on the excitation force and vortex dynamics characteristics of pump-jet propulsor induced by shafting whirling vibration: Non-uniform blade tip clearance. Phys. Fluids 2024, 36, 065104. [Google Scholar] [CrossRef]
- Gu, Q.L.; Yang, J.G.; Zhang, W.F.; Zhang, M.J. On the rotordynamic performance of an annular gas seal with self-adaptive jet slots: Comparisons to the swirl brake and shunt injection. Tribol. Int. 2022, 176, 107898. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, W.F.; Gu, Q.L. Research on suppression method for circumferential flow and fluid-induced vibration of blade tip seal. J. Vib. Shock 2020, 39, 228–233. [Google Scholar]
- Sun, D.; Su, G.Z.; Zhao, H. Dynamic characteristics of labyrinth seal and rotor stability considering swirl brakes. J. Aerospace. Eng. 2023, 36, 04023057. [Google Scholar] [CrossRef]
- Lang, J.; Yang, J.G.; Cao, H. Calculation and experimental comparison of fluid induced force between the titling pad seal and the fixed pad seal. J. Mech. Eng. 2013, 49, 101–105. [Google Scholar] [CrossRef]
- Rzadkowski, R.; Rokicki, E.; Piechowski, L.; Szczepanik, R. Analysis of middle bearing failure in rotor jet engine using tip-timing and tip-clearance techniques. Mech. Syst. Signal. Pract. 2014, 76, 213–227. [Google Scholar] [CrossRef]
- Liu, B.; Hou, W.M.; Ma, C.Y.; Wang, Y.G. Measurement and analysis of tip clearance unsteady flow spectrum in axial-flow fan rotor. Front. Energy 2008, 2, 448–452. [Google Scholar] [CrossRef]
- Donghyun, Y.; Meng, W.; Parviz, M.; Rajat, M. Vortex dynamics and low-pressure fluctuations in the tip-clearance flow. J. Fluids Eng. 2007, 129, 1002–1014. [Google Scholar]
- Li, P.; Cao, L.H.; Si, H.Y. Investigation on the unsteady pressure fluctuation characteristic in the blade tip seal of steam turbine based on spectrum. Therm. Sci. 2020, 24, 3823–3834. [Google Scholar] [CrossRef]
- Wang, H.; Wu, Y.D.; Ouyang, H. Aerodynamic rotating instability and fluctuated characteristics of tip clearance flow in low speed axial flow compressor. J. Aerosp. Power 2016, 31, 2239–2250. [Google Scholar]
- Wu, J.Z.; Wu, J.M. Interaction between a solid surface and a viscous compressible flow field. J. Fluid Mech. 1993, 254, 183–211. [Google Scholar] [CrossRef]
- Ahmed, N.A.; Yen, J. Synthetic Jets as a Boundary Vorticity Flux Control Tool. AIAA J. 2013, 51, 510–513. [Google Scholar]
- Liu, H.; Jiang, B.Y.; Wang, W.; Yang, X.P.; Wang, J. Redesign of Axial Fan Using Viscous Inverse Design Method Based on Boundary Vorticity Flux Diagnosis. J. Turbomach. 2021, 143, 051006. [Google Scholar] [CrossRef]
- Zeng, Y.; Wang, H.B.; Xiong, D.P.; Yang, Y.X.; Sun, M.B.; Liu, W.D. A multi-physics correction of the shear-stress transport turbulence model for supersonic flows. Phys. Fluids 2024, 36, 125–139. [Google Scholar] [CrossRef]
- Cravero, C.; Marelli, S.; Marsano, D.; Usai, V. Fluid dynamic analysis and design strategies for a deswirler device for the direct measurement of radial turbine isentropic efficiency in experimental test rig. J. Heat Fluid Flow 2024, 106, 109270. [Google Scholar] [CrossRef]
- Li, P.; Cao, L.H. Effect of rotor-stator axial gap on the tip seal leakage flow of a steam turbine. J. Therm. Sci. 2021, 30, 973–982. [Google Scholar] [CrossRef]
- Tong, B.G.; Yin, X.Y.; Zhu, K.Q. The Theory of Vortex Motion, 3rd ed.; University of Science and Technology of China Press: Beijing, China, 2019; pp. 66–73. [Google Scholar]

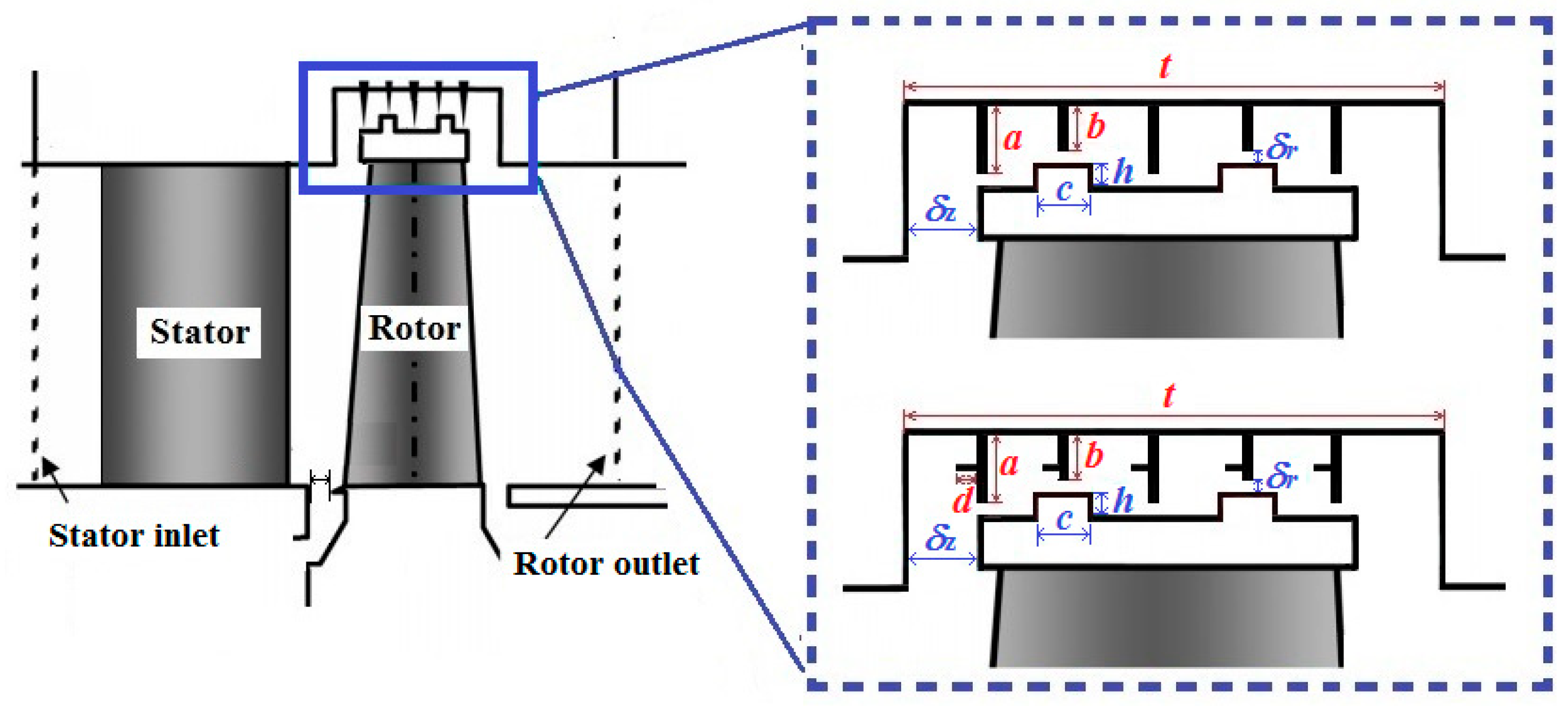
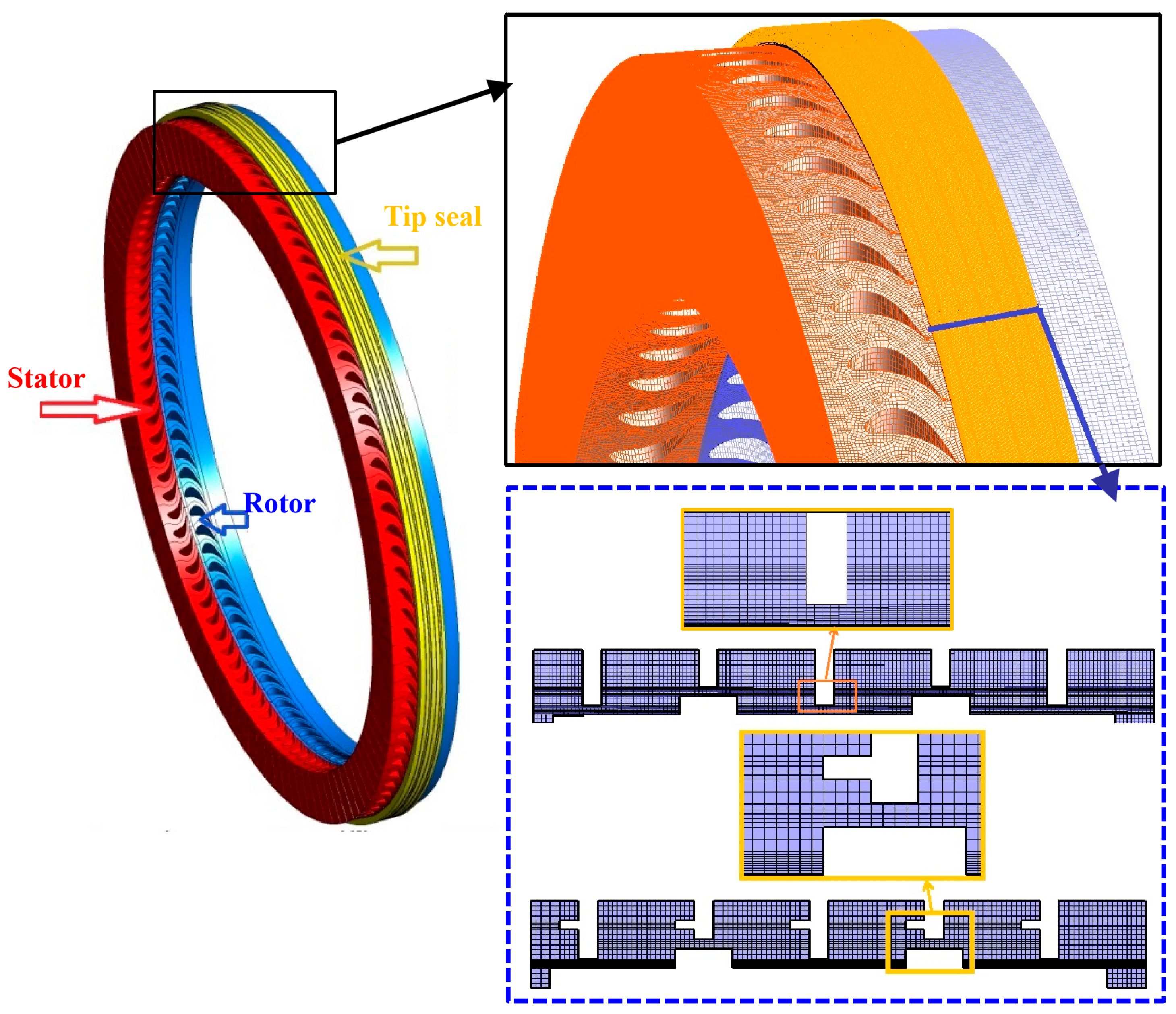





| Parameter/Name | Unit | Value |
|---|---|---|
| Hub radius | mm | 413.3 |
| Blade height | mm | 72.1 |
| Blade chord length | mm | 33.03 |
| Number of blades | 98 | |
| Blade installation angle | ° | 50.54 |
| Rotational speed | r/min | 3000 |
| Seal high tooth length/a | mm | 4 |
| Seal low tooth length/b | mm | 3 |
| Pedestal length/c | mm | 3 |
| Pedestal height/h | mm | 1 |
| Side tooth length/d | mm | 1 |
| Total length of blade tip seal/t | mm | 38.2 |
| Radial clearance of blade tip seal/ | mm | 0.5 |
| Axial gap of tip seal/ | mm | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Wang, H.; Peng, H.; Si, H.; Jiang, T. Study on Steam Excitation Forces Induced by Tip Seal Leakage Flow in Steam Turbines. Machines 2025, 13, 518. https://doi.org/10.3390/machines13060518
Li P, Wang H, Peng H, Si H, Jiang T. Study on Steam Excitation Forces Induced by Tip Seal Leakage Flow in Steam Turbines. Machines. 2025; 13(6):518. https://doi.org/10.3390/machines13060518
Chicago/Turabian StyleLi, Pan, Huan Wang, Haichao Peng, Heyong Si, and Tieliu Jiang. 2025. "Study on Steam Excitation Forces Induced by Tip Seal Leakage Flow in Steam Turbines" Machines 13, no. 6: 518. https://doi.org/10.3390/machines13060518
APA StyleLi, P., Wang, H., Peng, H., Si, H., & Jiang, T. (2025). Study on Steam Excitation Forces Induced by Tip Seal Leakage Flow in Steam Turbines. Machines, 13(6), 518. https://doi.org/10.3390/machines13060518





