Research on Online Non-Contact Test Device and Test Method for Bearing Stiffness of Electric Spindle
Abstract
1. Introduction
2. Research on Non-Contact Electric Spindle Stiffness Testing Device
2.1. Radial Magnetic Excitation Loading Principle
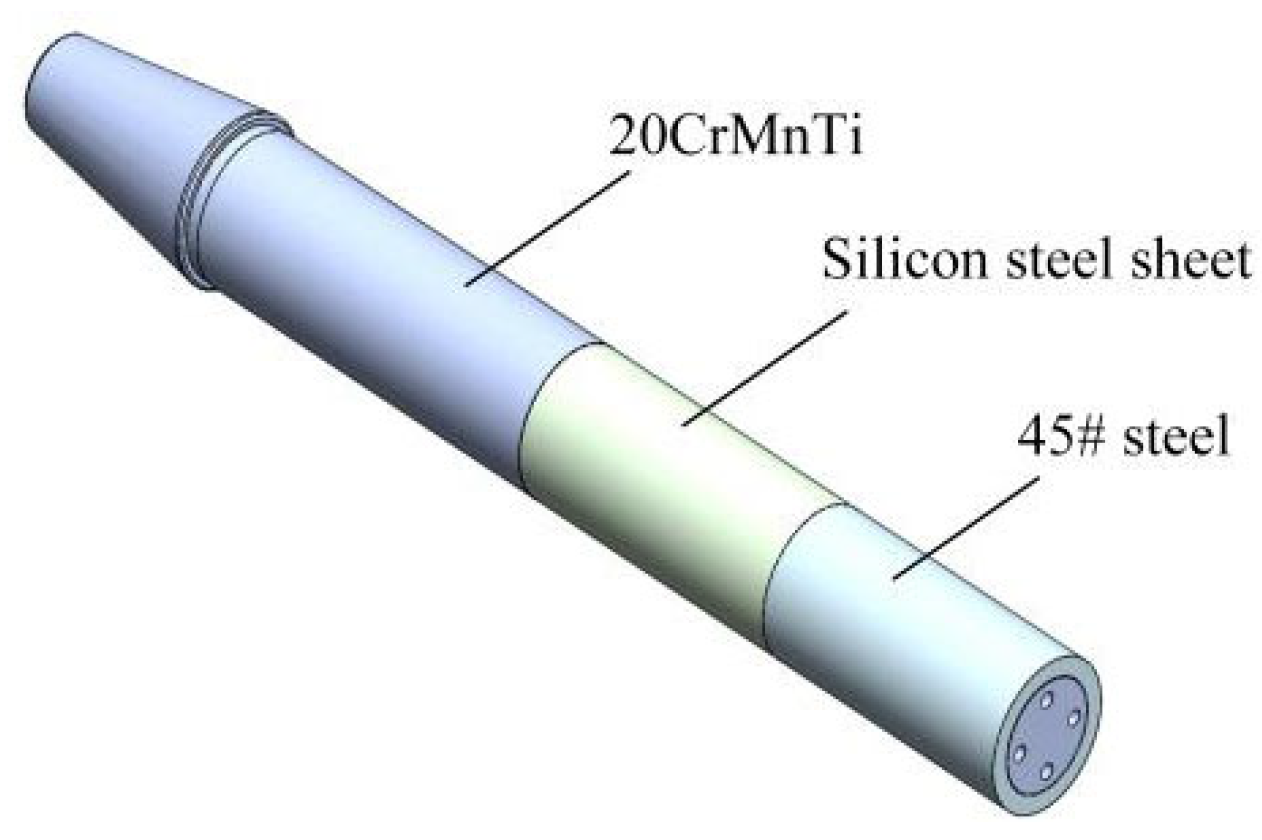
2.2. Radial Magnetic Excitation Structure
2.3. Axial Magnetic Excitation Structure
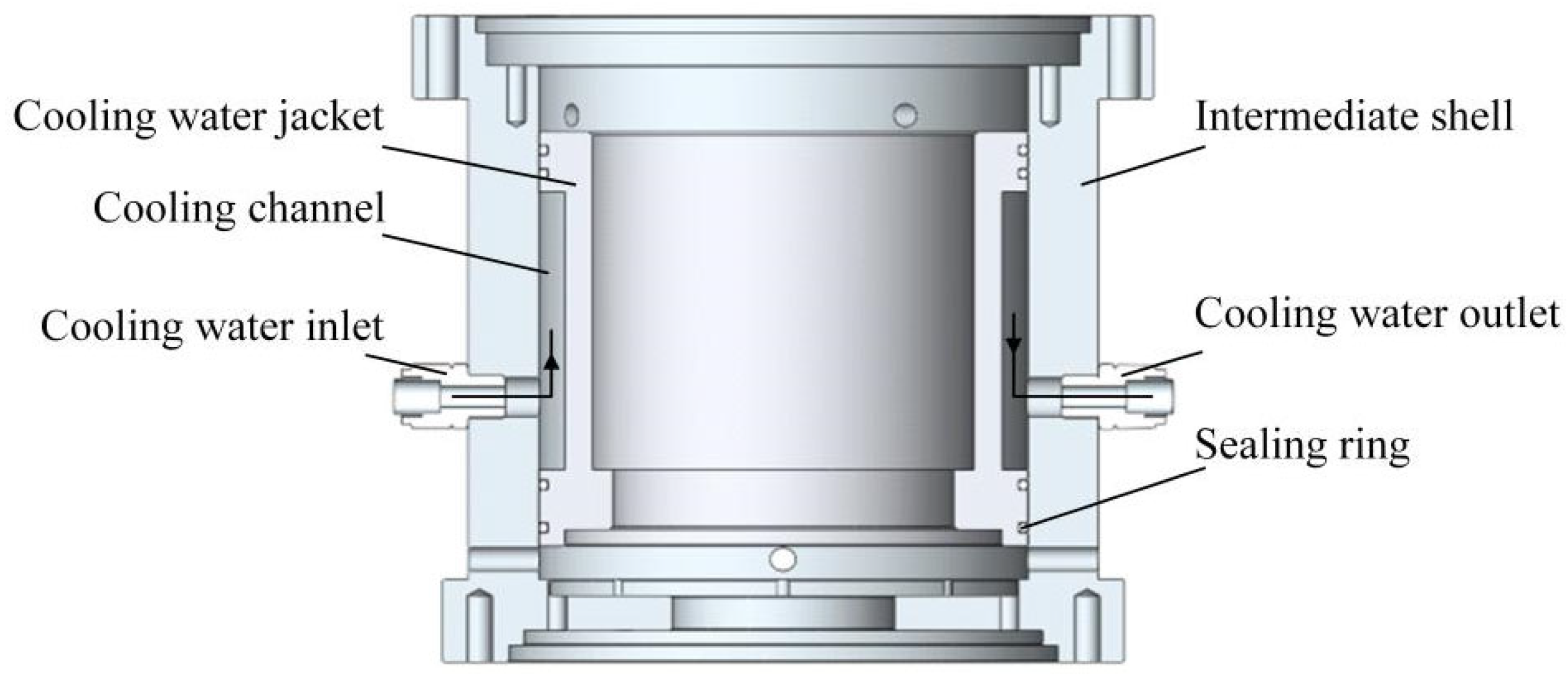
2.4. Cooling Structure Design
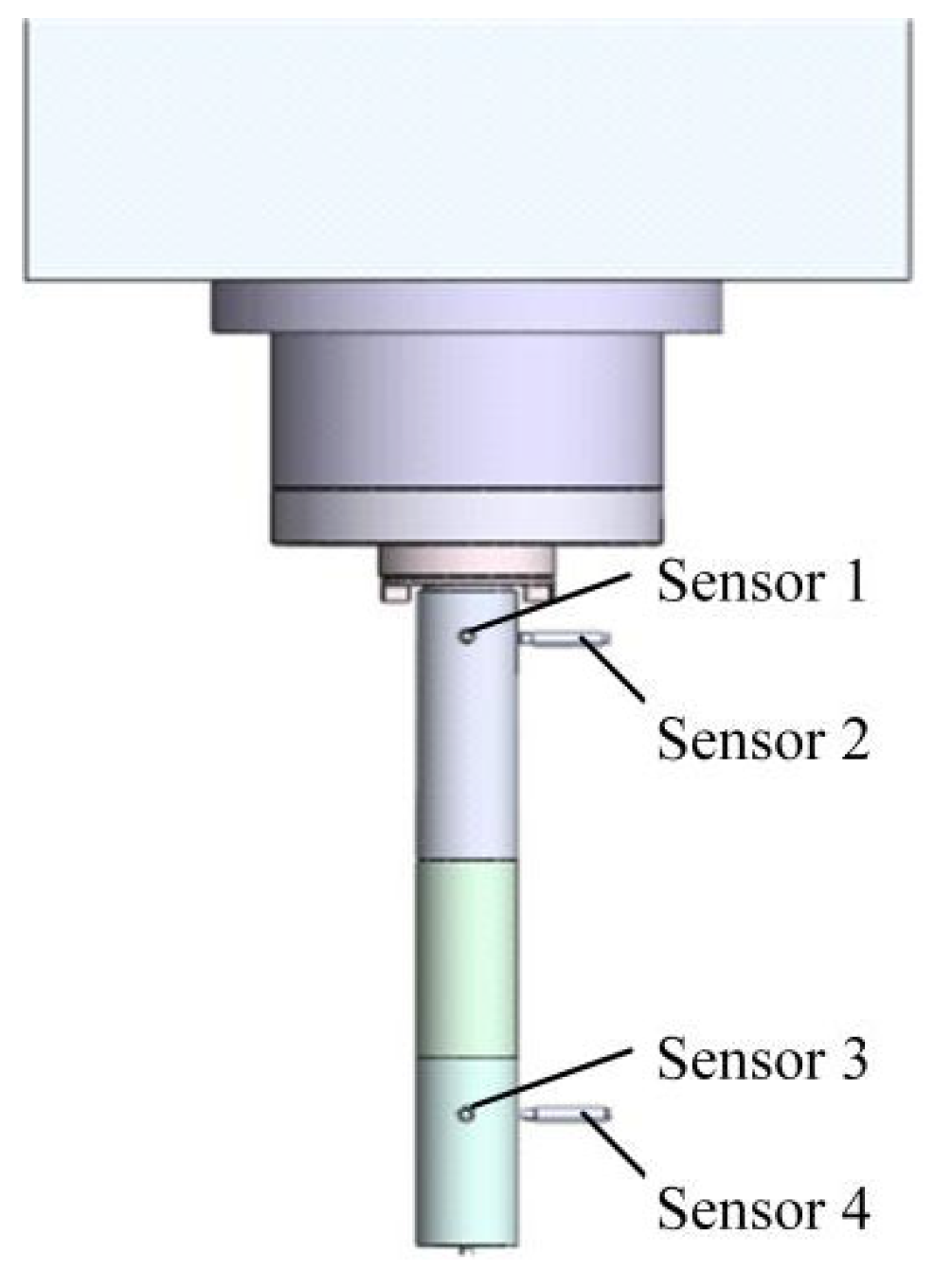
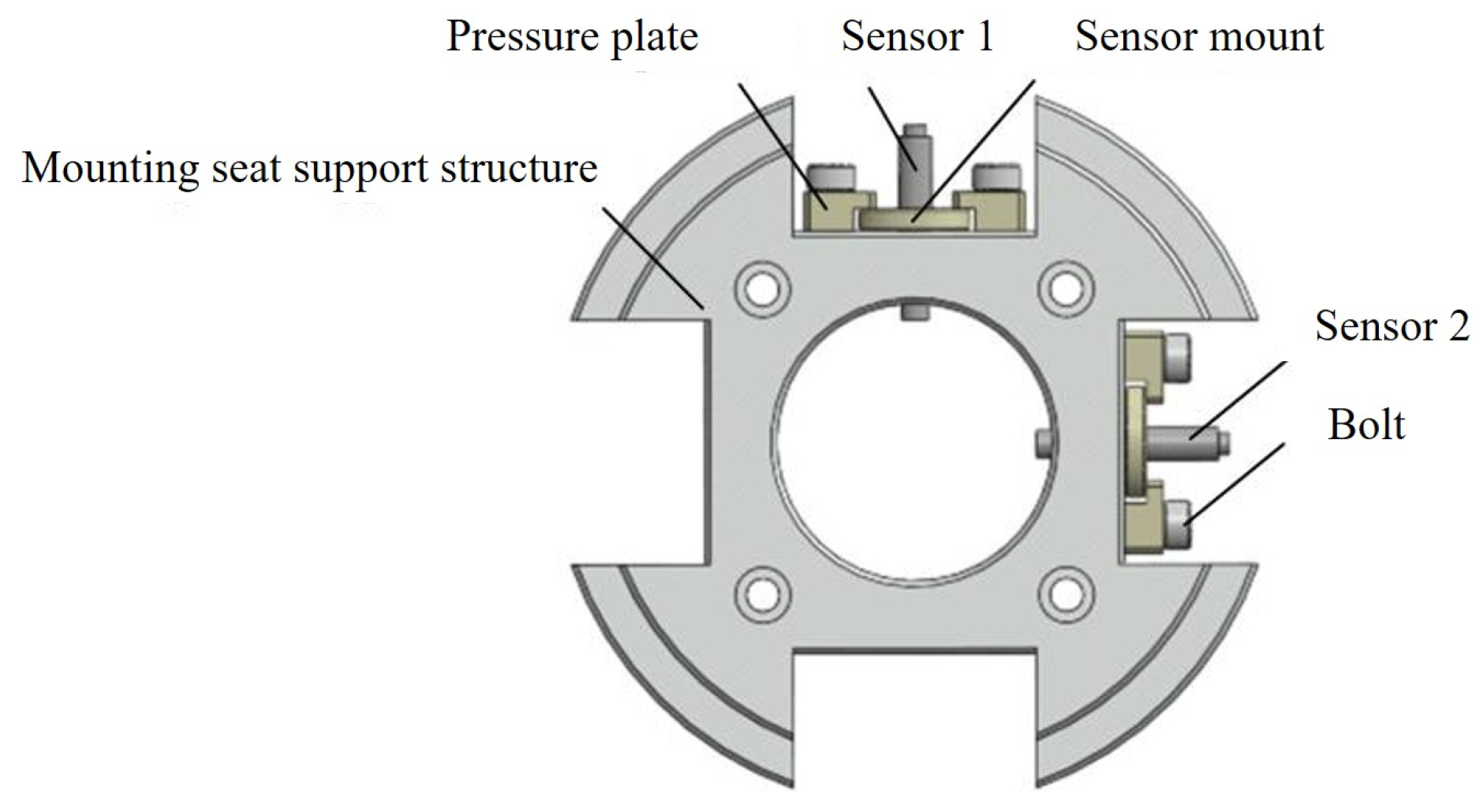
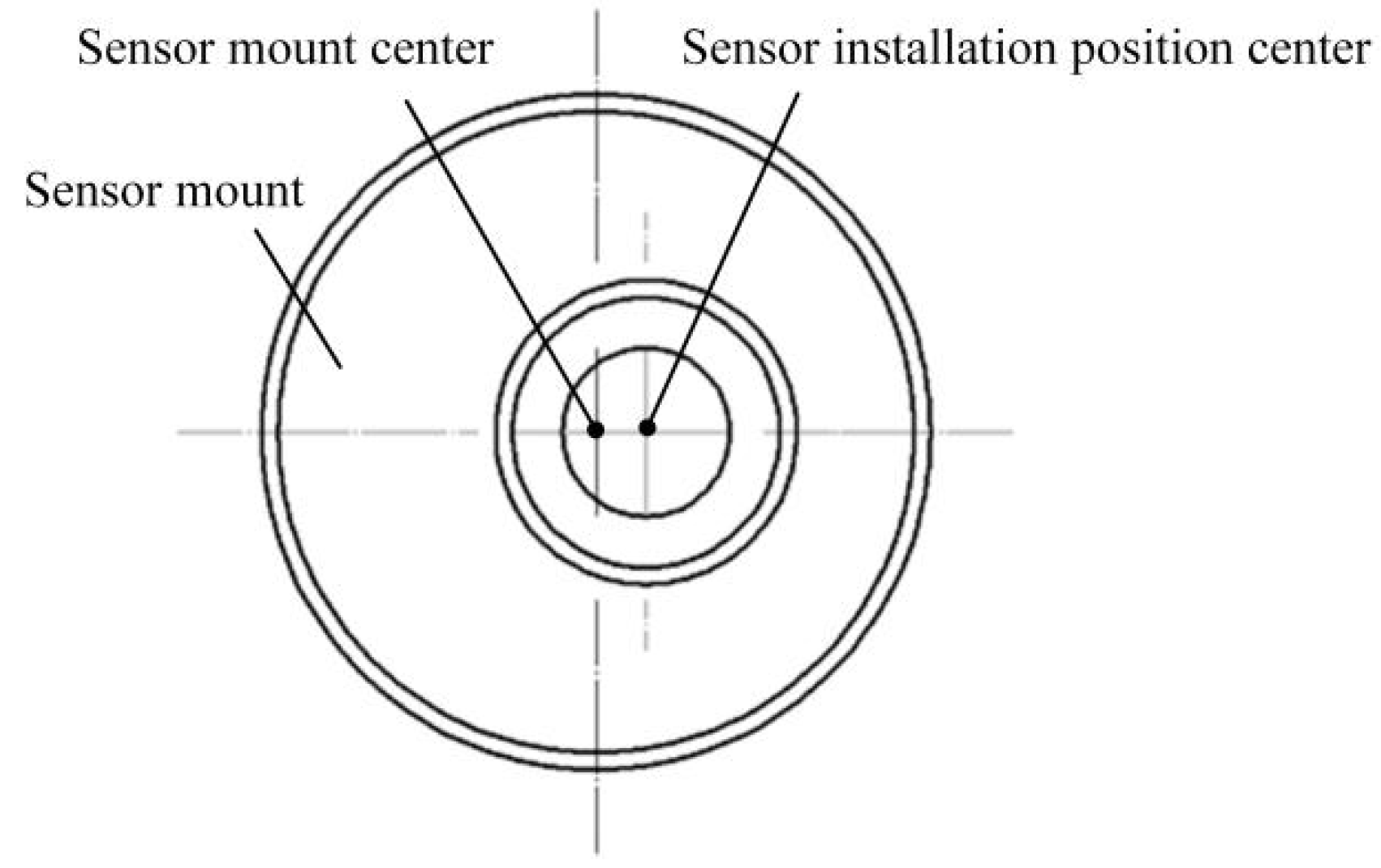
2.5. Sensor Position Layout and Support Structure Design
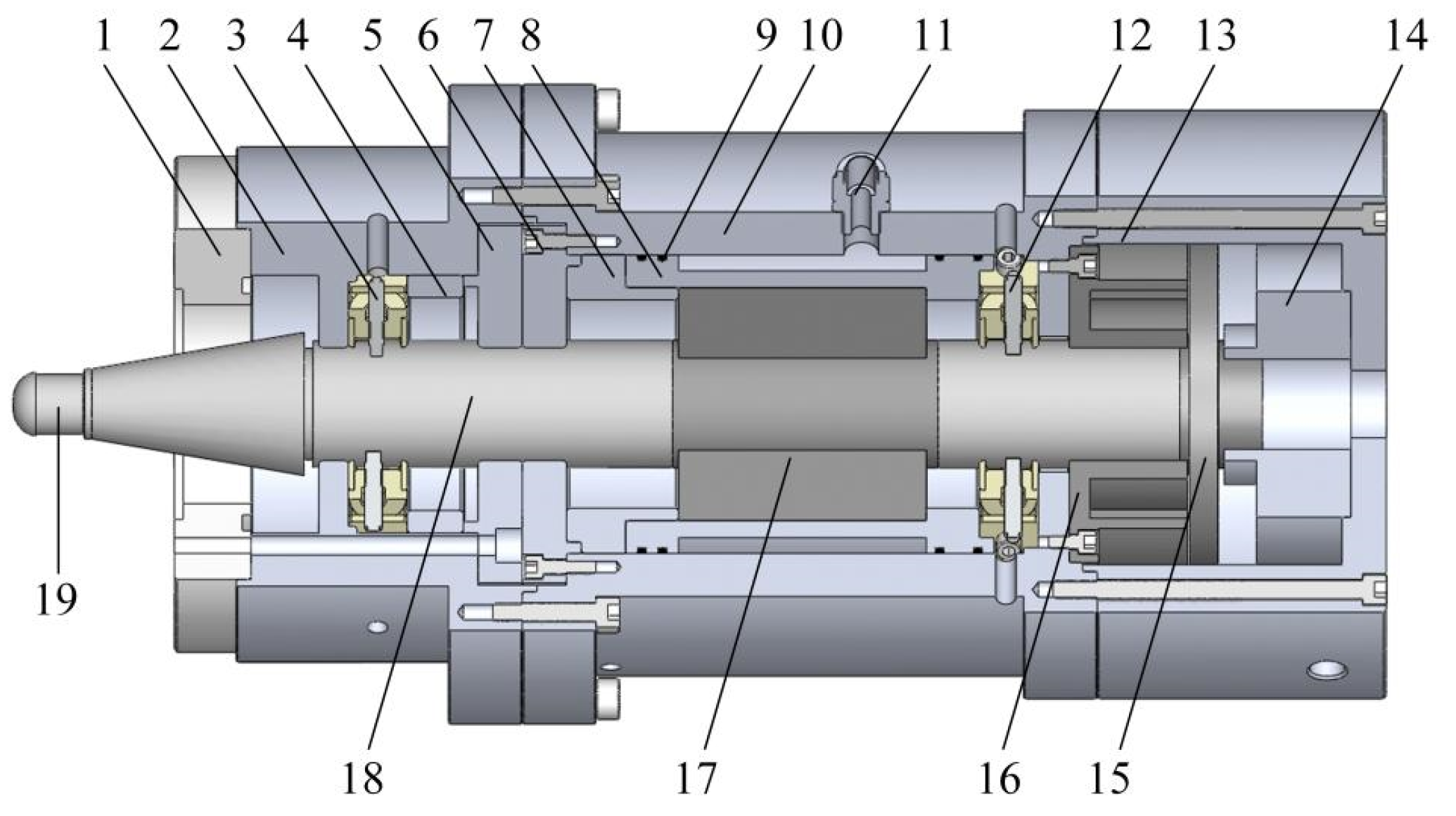
2.6. Overall Structural Design of Test Device
3. Stiffness Test and Test Data Analysis of Electric Spindle
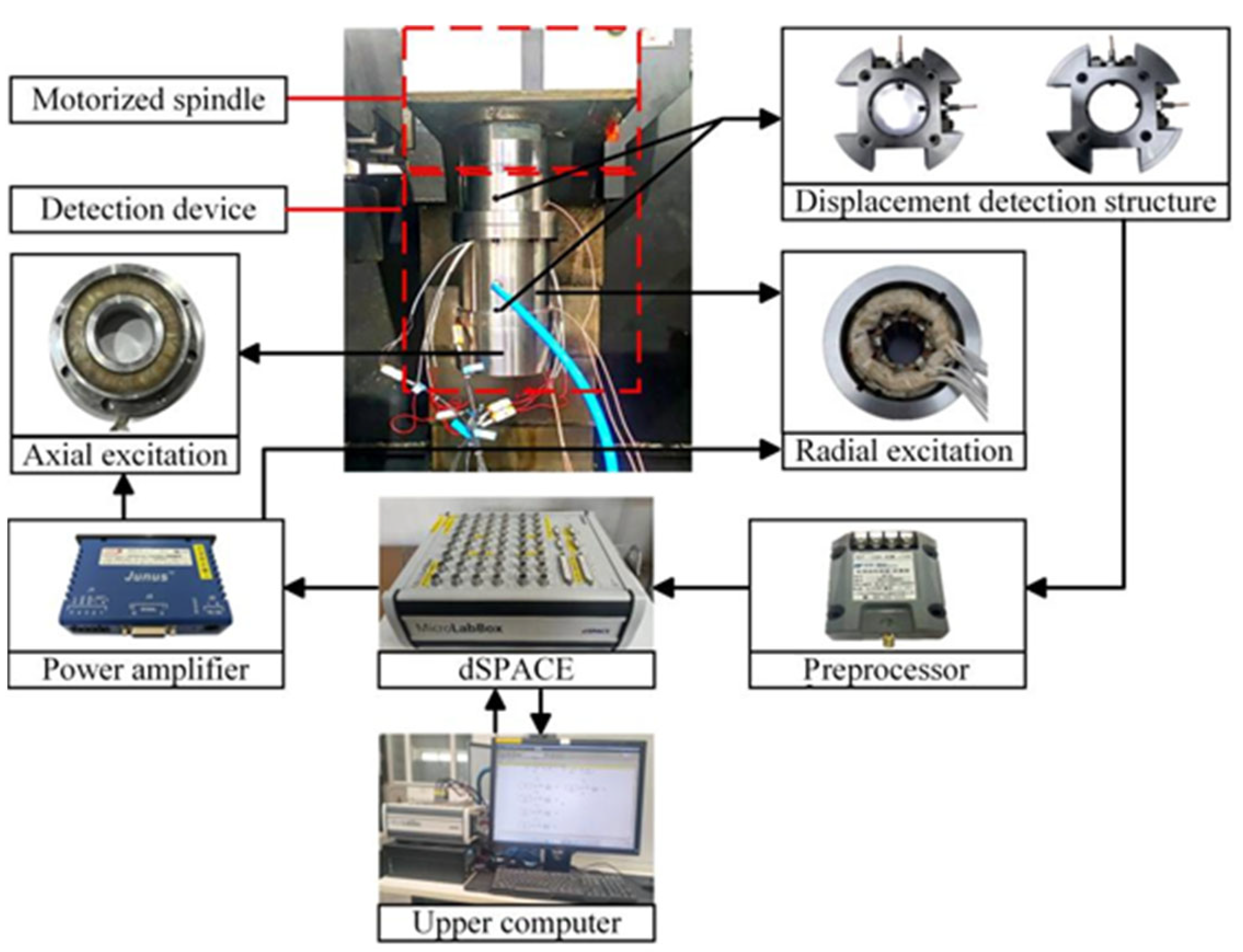
3.1. Electric Spindle Stiffness Test System Platform Construction
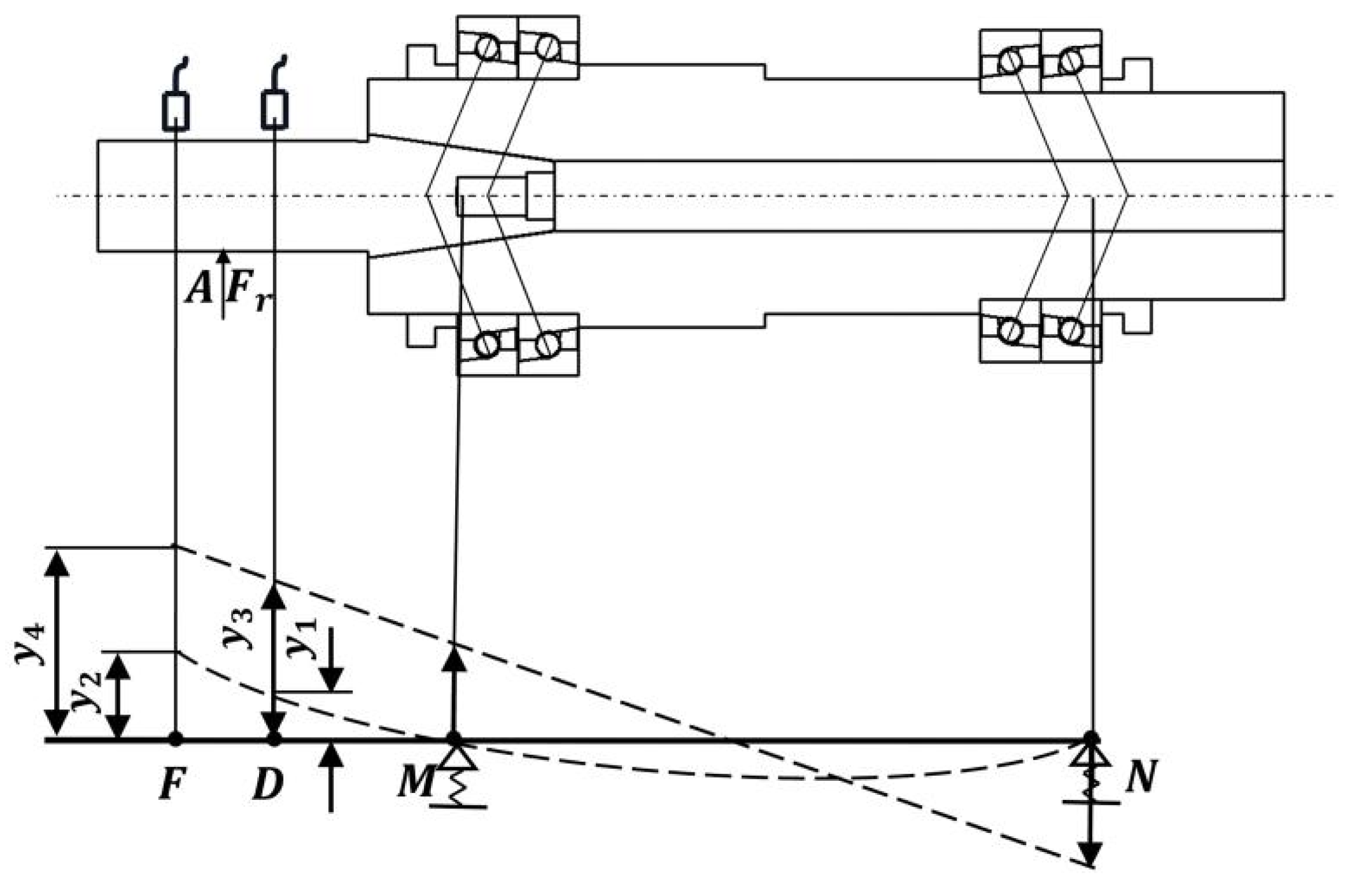
3.2. Test and Calculation Method of Support Stiffness of Electric Spindle Bearing
4. Discussion
5. Conclusions
- (1)
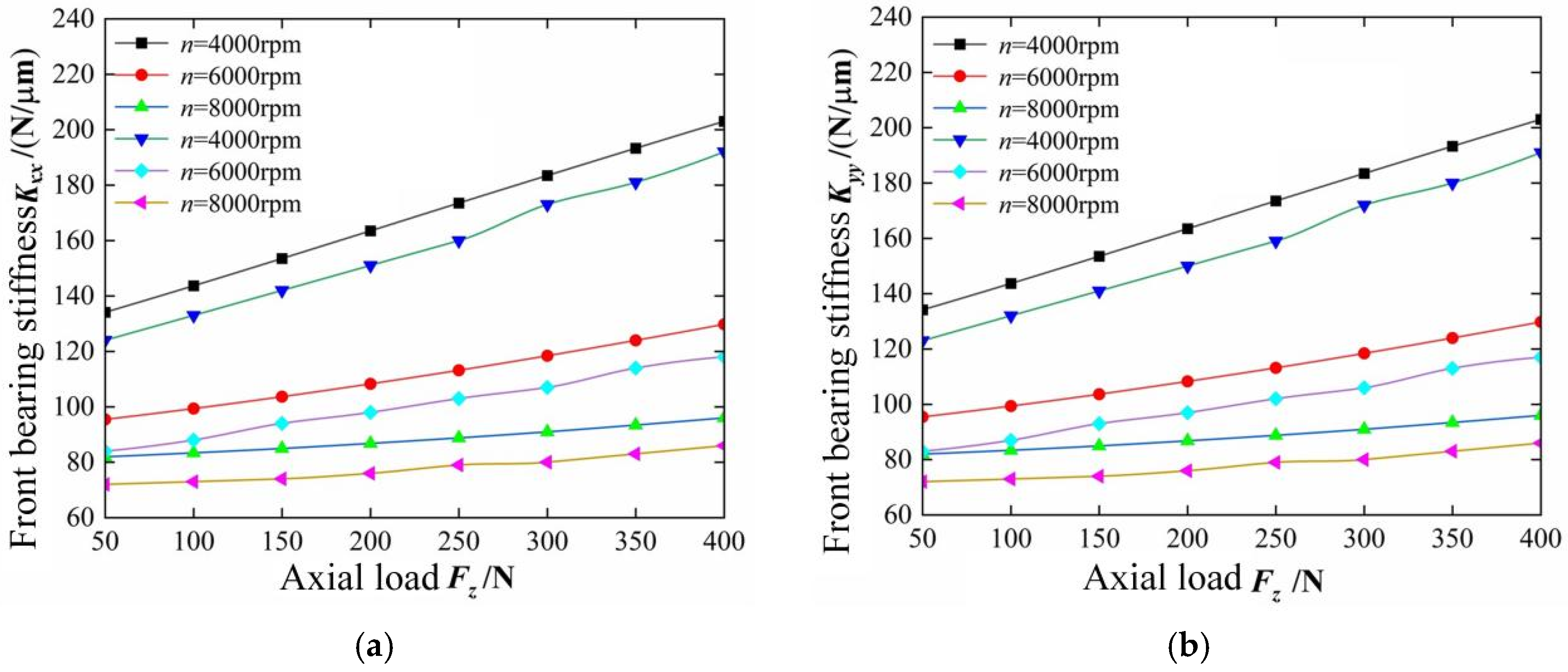
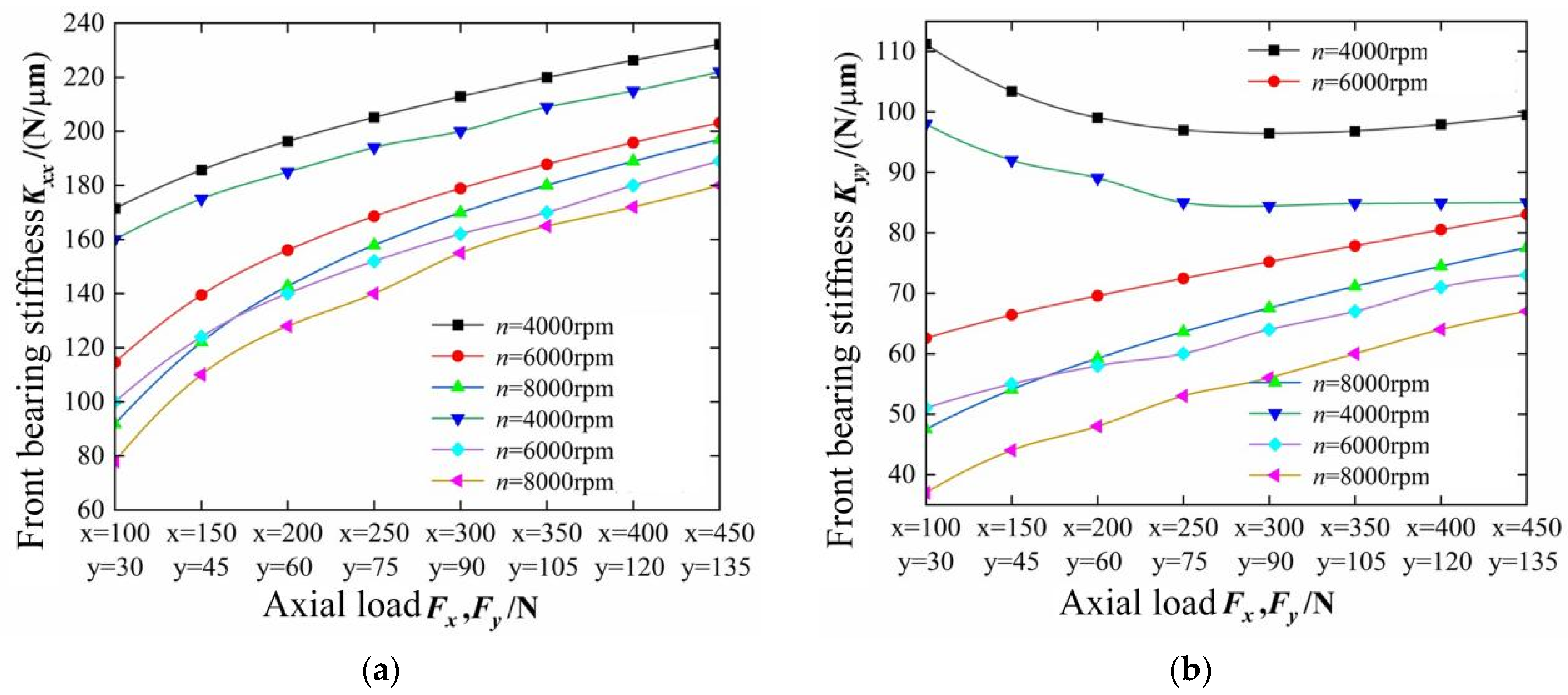
- The support stiffness of the front and rear bearings of the electric spindle increases with the increase in radial load, and the phenomenon of dynamic support stiffness “softening” caused by increasing rotational speed can be suppressed to some extent.
- (2)
- As the rotational speed of the electric spindle increases, the support stiffness of the front and rear bearings exhibits a reduction in stiffness. Under the influence of centrifugal force and inner ring expansion, the increase in rotational speed nonlinearly enlarges the contact angle and contact load between the rolling elements and the inner/outer raceways. However, the axial component of the contact load can partially counteract the stiffness “weakening” phenomenon caused by the increase in rotational speed.
- (3)
- An increase in axial load raises the preload on the front and rear bearings, enlarging the contact area between the rolling elements and the micro-convexities of the inner/outer raceways. Consequently, the dynamic support stiffness of the combined bearings improves, significantly mitigating the “softening” effect of the electric spindle’s dynamic support stiffness as rotational speed increases.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, T.; Luo, G.; Su, W.; Che, C.; Shi, J. Test method for Dynamic Characteristics of Rolling Bearing. Vib. Test Diagn. 1996, 16, 33–39. [Google Scholar] [CrossRef]
- Yun, X.; Mei, X.; Jiang, G.; Li, Y.; Yuan, S. Dynamic Stiffness Analysis and Test Method of Angular Contact Ball Bearing for High Speed spindle. Vib. Test Diagn. 2019, 39, 892–897+912. [Google Scholar] [CrossRef]
- Jia, Q.; Ouyang, W.; Zhang, X.; Yuan, X. Research on Magnetic Force Loading Excitation Technology for Stiffness Testing of Water-lubricated Bearing. Mach. Des. Manuf. 2014, 99–101. [Google Scholar] [CrossRef]
- Jin, X.; Li, B. Calculation and Measurement Method of Dynamic Stiffness of High Speed electric spindle. Mod. Manuf. Eng. 2016, 40–45+68. [Google Scholar] [CrossRef]
- Fan, C.C.; Pan, M.C. Experimental study on the whip elimination of rotor-bearing systems with electromagnetic exciters. Mech. Mach. Theory 2011, 46, 290–304. [Google Scholar] [CrossRef]
- Garrick, I.E.; Watkins, C.E. A Theoretical Study of the Effect of Forward Speed on the Free-Space Sound-Pressure Field Around Propellors; NACA Report 1198; NASA: Washington, DC, USA, 1954. [Google Scholar]
- Zhang, X.; Han, Q.; Peng, Z.; Chu, F. A comprehensive dynamic model to investigate the stability problems of the rotor–bearing system due to multiple excitations. Mech. Syst. Signal Process 2016, 70–71, 1171–1192. [Google Scholar] [CrossRef]
- Meng, J.; Chen, X.; Kang, H.; Chen, F. Study on Loading test of high-speed electric spindle. J. Mech. Strength 2009, 31, 689–692. [Google Scholar] [CrossRef]
- Aggarwal, S.; Nešić, N.; Xirouchakis, P. Cutting torque and tangential cutting force coefficient identification from spindle motor current. Int. J. Adv. Manuf. Technol. 2013, 65, 81–95. [Google Scholar] [CrossRef]
- Feng, M.; Zhao, Y.; Yang, W.; Chen, F. Development of Non-contact gas Film loading Stiffness Test bench for High Speed spindle. Mach. Des. Manuf. 2013, 102–105. [Google Scholar] [CrossRef]
- Matsubara, A.; Yamazaki, T.; Ikenaga, S. Non-contact measurement of spindle stiffness by using magnetic loading device. Int. J. Mach. Tools Manuf. 2013, 71, 20–25. [Google Scholar] [CrossRef]
- Ma, R. Research on Stiffness Characteristics and Test Methods of Machine Tool Under Spindle Rotation; Tsinghua University: Beijing, China, 2018. [Google Scholar] [CrossRef]
- Yu, Y.; Karimi, H.R.; Gelman, L.; Liu, X. A novel digital twin-enabled three-stage feature imputation framework for non-contact intelligent fault diagnosis. Adv. Eng. Inform. 2025, 66, 103434. [Google Scholar] [CrossRef]
- Tuninetti, V.; Alzugaray, R.; González, J.; Valenzuela, M.; Jaramillo, A.; Diez, E. Root cause and vibration analysis to increase veneer manufacturing process efficiency: A case study on an industrial peeling lathe. Eur. J. Wood Wood Prod. 2021, 79, 951–966. [Google Scholar] [CrossRef]
- He, P.P.; Gao, F.; Li, Y.; Wu, W.W.; Zhang, D.Y. Study on thermo-mechanical coupling characteristics of angle contact ball bearing with fix-position preload. Ind. Lubr. Tribol. 2019, 71, 795–802. [Google Scholar] [CrossRef]






| Bearing Parameters | Numerical Value |
|---|---|
| Inner raceway curvature radius ri | 6.2315 mm |
| Outer raceway curvature radius ro | 6.3525 mm |
| Initial contact angle α0 | 15° |
| The number of rolling elements z | 20 |
| Rolling element diameter D | 12.1 mm |
| The diameter of pitch circle Dm | 90 mm |
| Bearing Parameters | Numerical Value |
|---|---|
| Inner raceway curvature radius ri | 6.2315 mm |
| Outer raceway curvature radius ro | 6.3525 mm |
| Initial contact angle α0 | 15° |
| The number of rolling elements z | 20 |
| Rolling element diameter D | 12.1 mm |
| The diameter of pitch circle Dm | 76 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Zhang, L.; Hua, C.; Liu, Z.; Meng, Q.; Shi, J. Research on Online Non-Contact Test Device and Test Method for Bearing Stiffness of Electric Spindle. Machines 2025, 13, 516. https://doi.org/10.3390/machines13060516
Chen C, Zhang L, Hua C, Liu Z, Meng Q, Shi J. Research on Online Non-Contact Test Device and Test Method for Bearing Stiffness of Electric Spindle. Machines. 2025; 13(6):516. https://doi.org/10.3390/machines13060516
Chicago/Turabian StyleChen, Chuanhai, Liang Zhang, Chunlei Hua, Zhifeng Liu, Qingyu Meng, and Junze Shi. 2025. "Research on Online Non-Contact Test Device and Test Method for Bearing Stiffness of Electric Spindle" Machines 13, no. 6: 516. https://doi.org/10.3390/machines13060516
APA StyleChen, C., Zhang, L., Hua, C., Liu, Z., Meng, Q., & Shi, J. (2025). Research on Online Non-Contact Test Device and Test Method for Bearing Stiffness of Electric Spindle. Machines, 13(6), 516. https://doi.org/10.3390/machines13060516





