Non-Singular Fast Terminal Composite Sliding Mode Control of Marine Permanent Magnet Synchronous Propulsion Motors
Abstract
1. Introduction
- (1)
- Proposal of the NFTCSMC for PMSM in ship propulsion systems;
- (2)
- Design of a non-singular fast terminal sliding mode disturbance observer to enhance anti-disturbance capability;
- (3)
- Experimental validation showing that the NFTCSMC outperforms traditional control methods in dynamic response, anti-disturbance performance, and system stability.
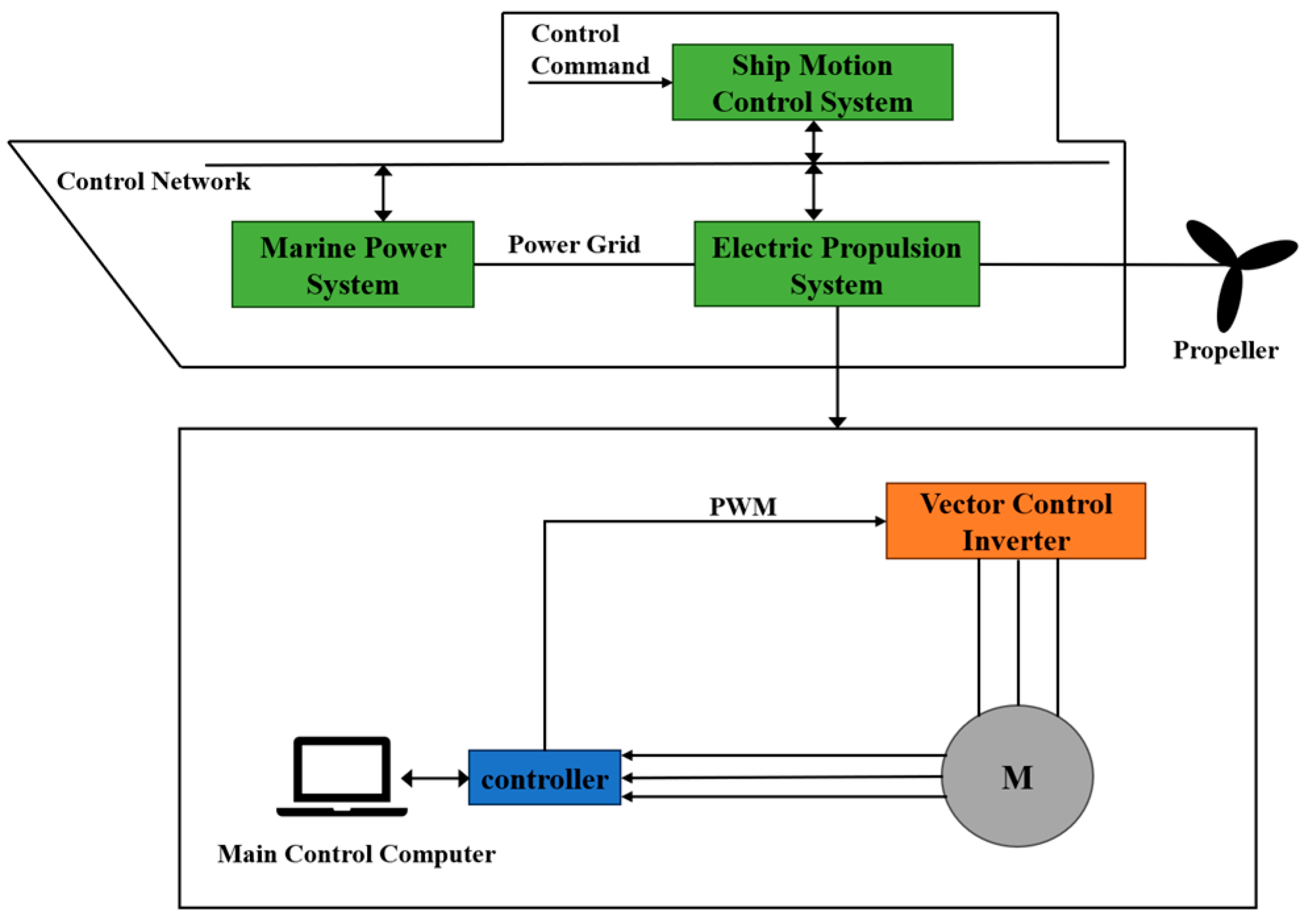
2. Mathematical Modeling of the Three-Phase PMSM for Ship Propulsion System
- (1)
- The saturation of the motor core is neglected, as well as the eddy current and hysteresis losses within the motor that are disregarded;
- (2)
- It is assumed that the stator windings are three-phase symmetric, and the magnetic field produced by the rotor’s permanent magnets exhibits a sinusoidal distribution in the air gap;
- (3)
- It is assumed that the conductivity of the permanent magnets is zero, and their magnetic permeability is considered to be the same as that of air;
- (4)
- No damping windings are present on the rotor.
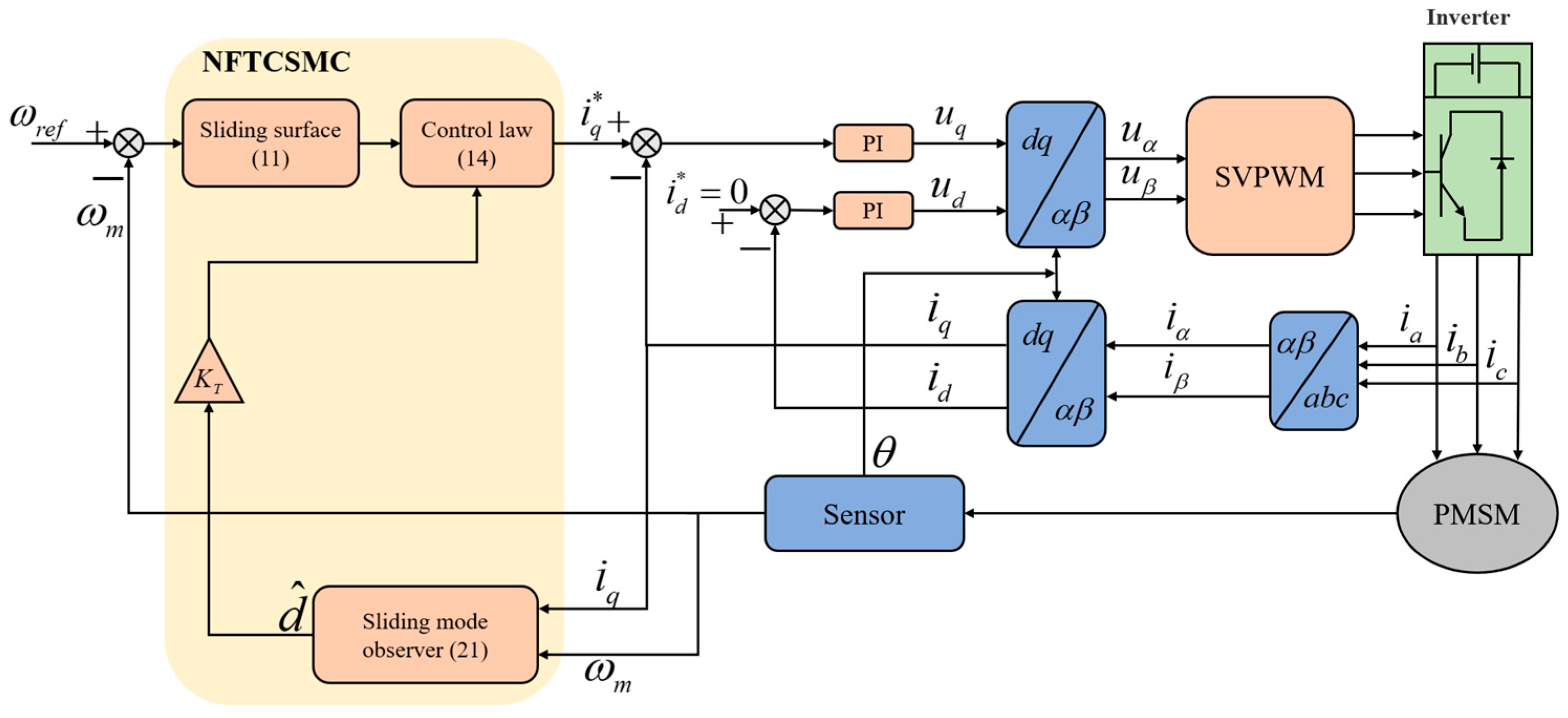
3. Control Strategy of Permanent Magnet Synchronous Propulsion Motor for Ships
3.1. Design of IERL
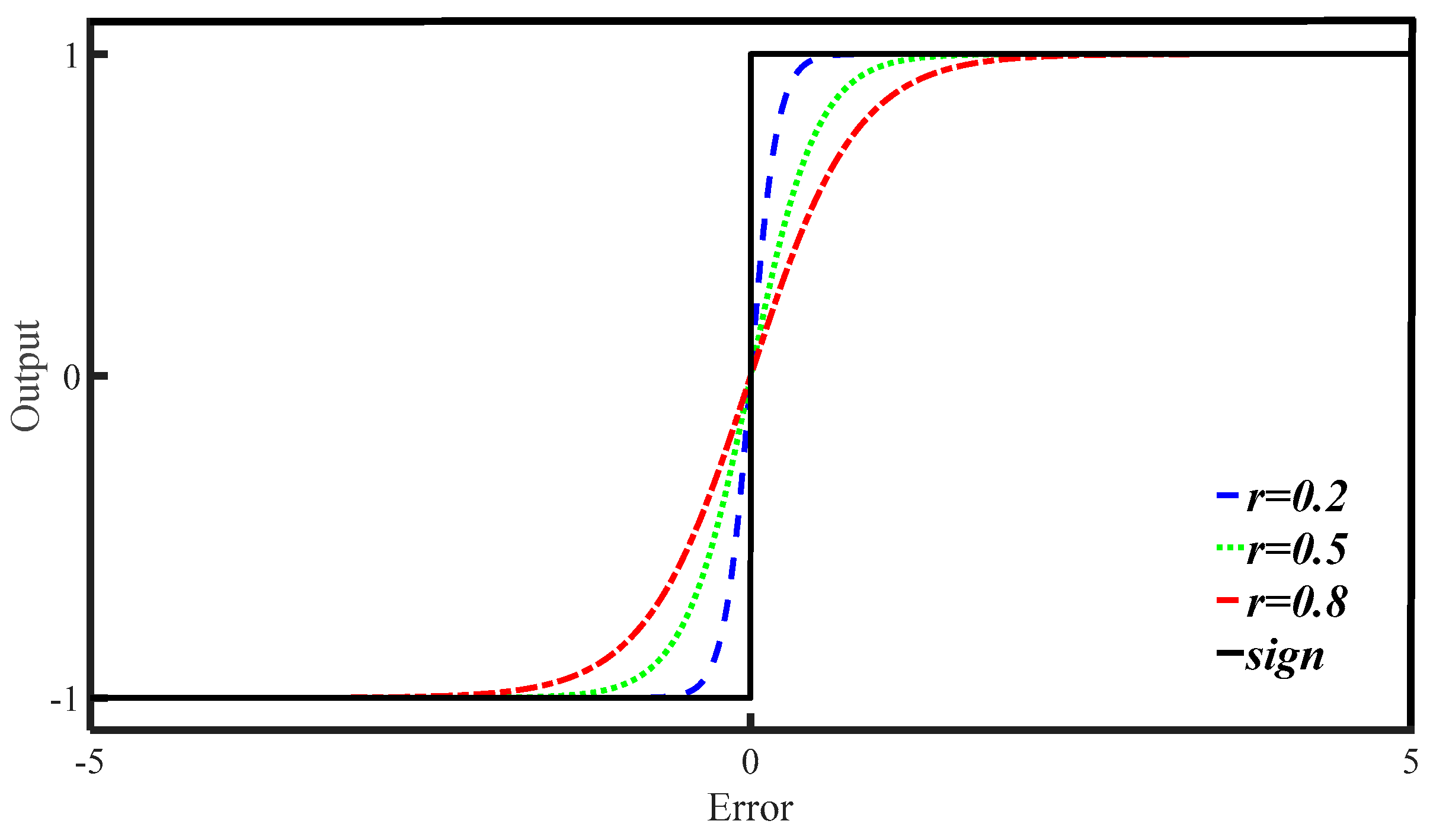
3.2. Design of NFTSMC
3.3. Design of SMDO
4. Experimental Verification and Analysis
4.1. Experimental Setup
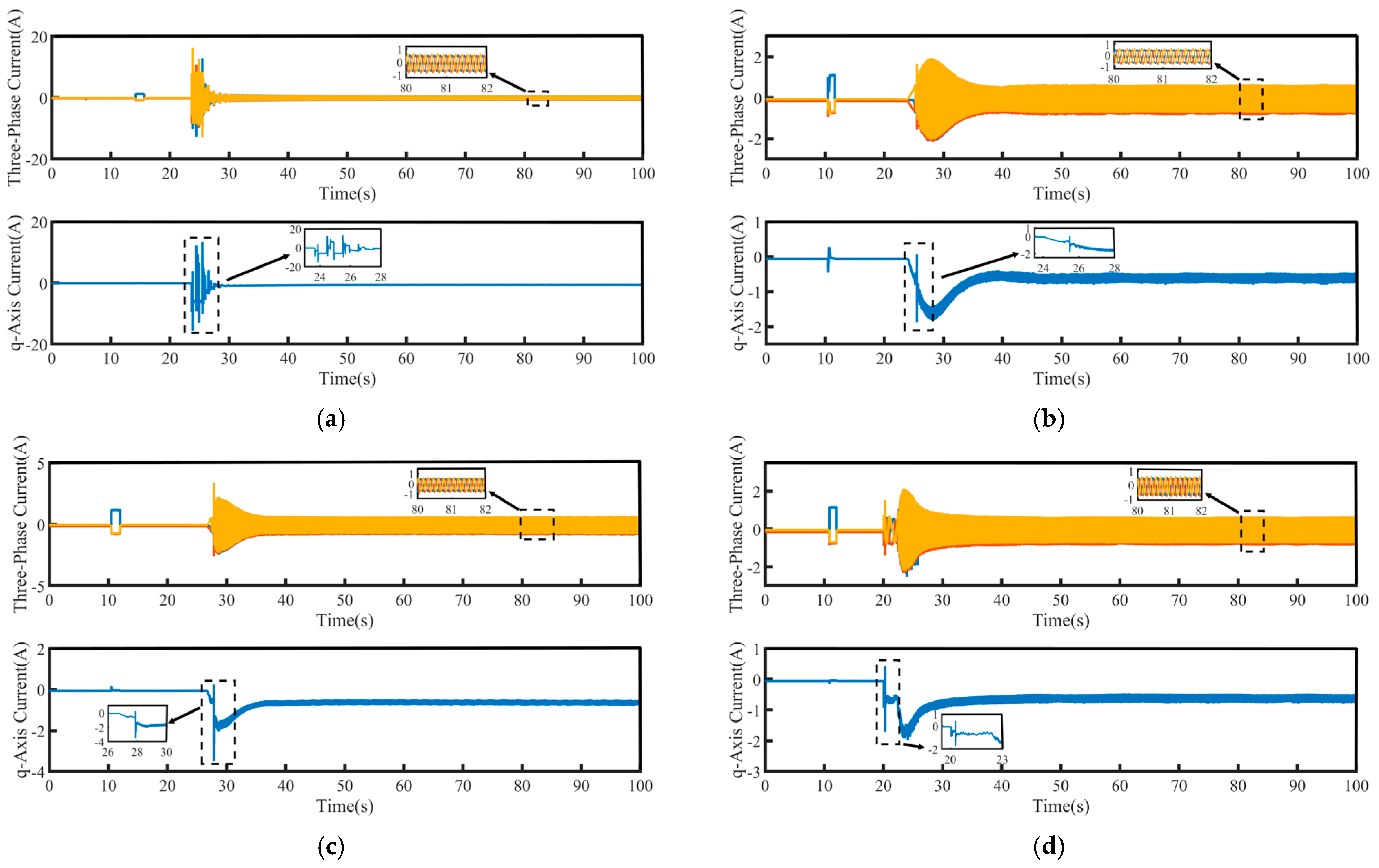
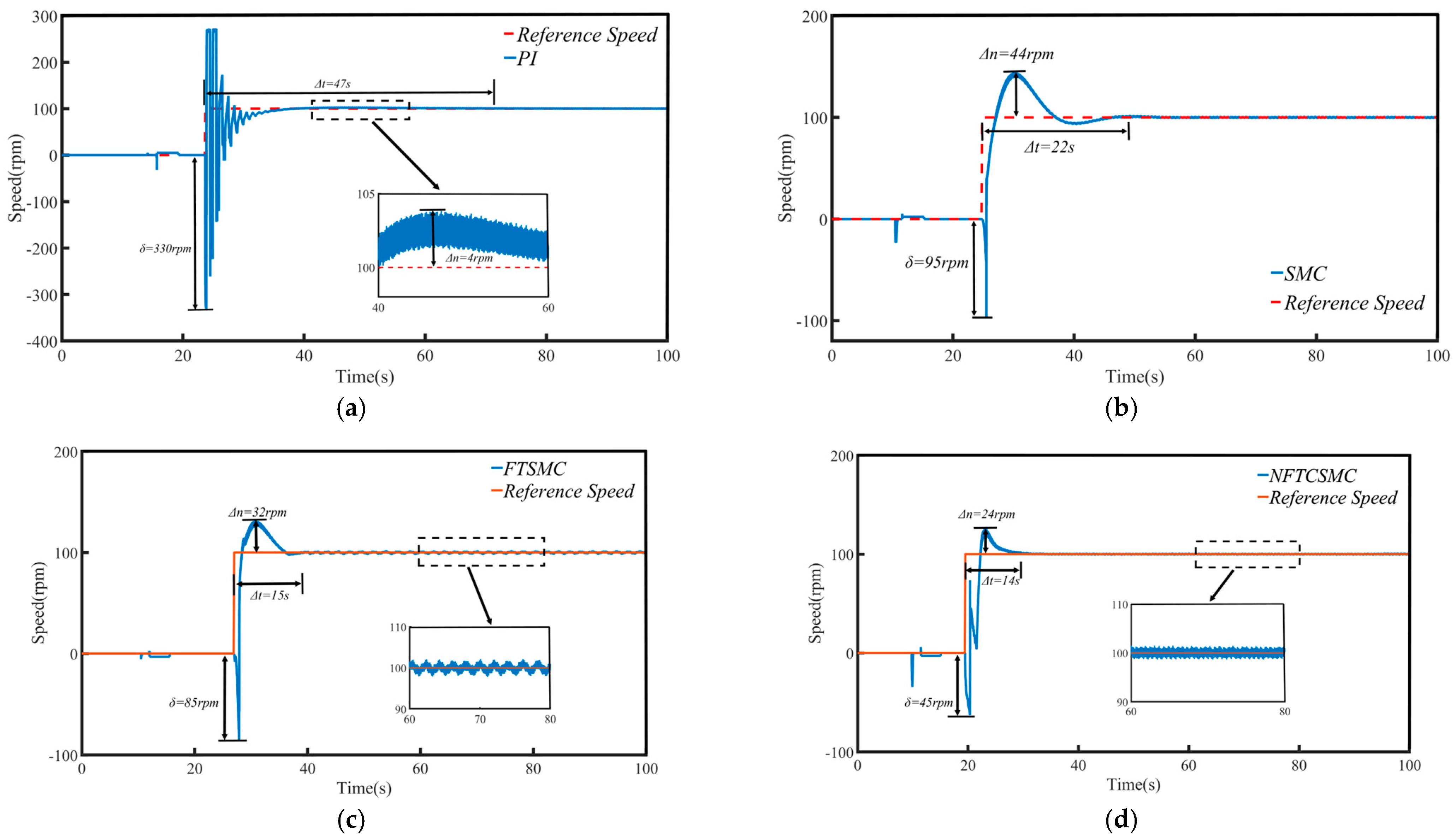
4.2. Start-Up Performance
4.3. Speed Command Tracking
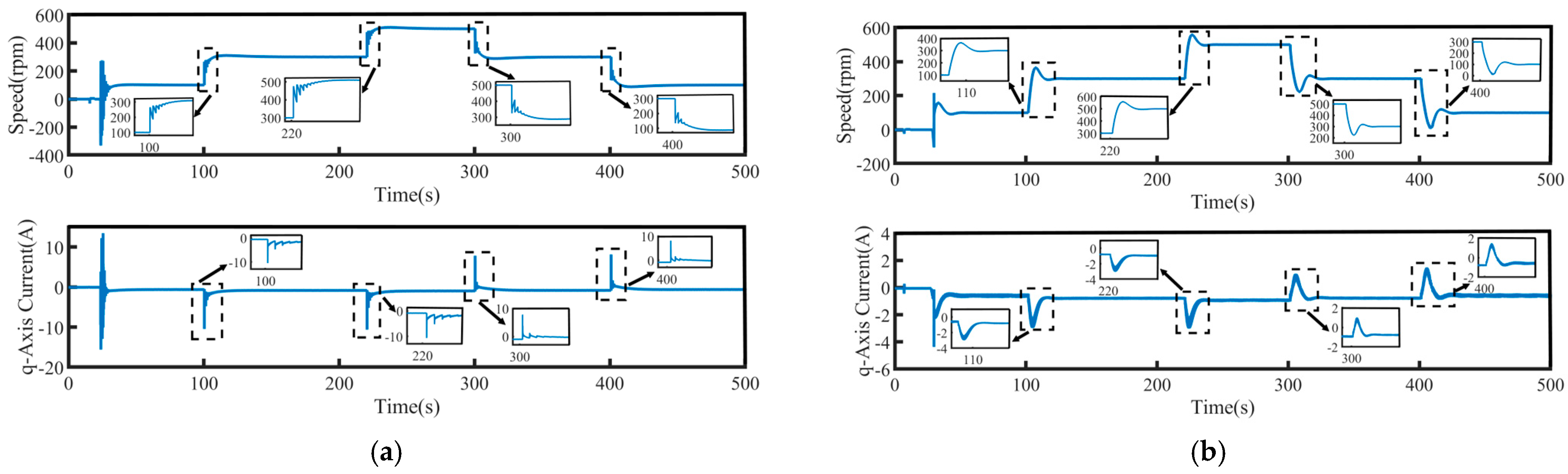
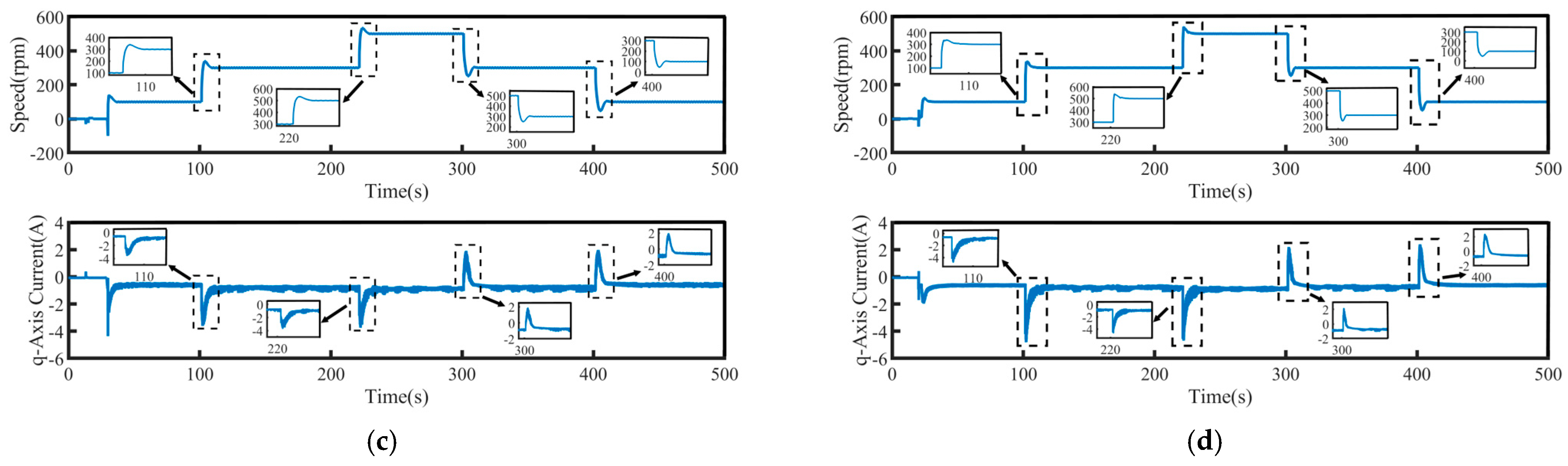
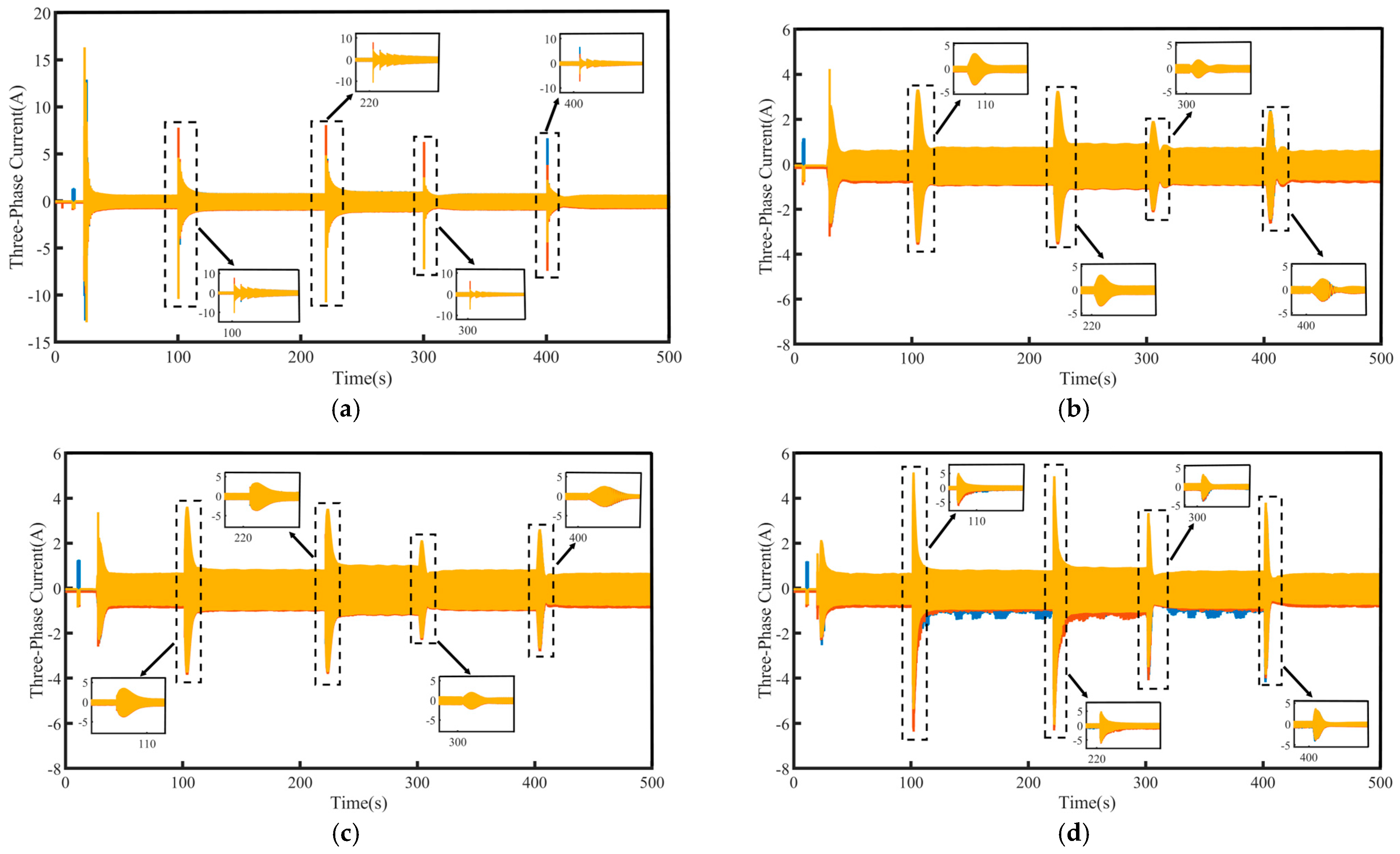
4.4. Load Torque Regulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Z.; Guo, H.; Liu, Y.; Zhang, Q.; Zhu, P.; Iqbal, R. An Improved Sensorless Control Strategy of Ship IPMSM at Full Speed Range. IEEE Access 2019, 7, 178652–178661. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Ding, J.; Wang, D. Adaptive type-2 fuzzy output feedback control using nonlinear observers for permanent magnet synchronous motor servo systems. Eng. Appl. Artif. Intell. 2024, 131, 107833. [Google Scholar] [CrossRef]
- Cheng, S.; Yu, J.; Zhao, L.; Ma, Y. Adaptive fuzzy control for permanent magnet synchronous motors considering input saturation in electric vehicle stochastic drive systems. J. Frankl. Inst. 2020, 357, 8473–8490. [Google Scholar] [CrossRef]
- Li, B.; Zhao, B. Neural Network-Based Adaptive Sliding Mode Control for T-S Fuzzy Fractional Order Systems. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 4549–4553. [Google Scholar] [CrossRef]
- Brosch, A.; Wallscheid, O.; Böcker, J. Time-Optimal Model Predictive Control of Permanent Magnet Synchronous Motors in the Whole Spe-ed and Modulation Range Considering Current and Torque Limits. IEEE Open J. Ind. Electron. Soc. 2023, 4, 643–658. [Google Scholar] [CrossRef]
- Li, T.; Sun, X.; Yao, M.; Guo, D.; Sun, Y. Improved Finite Control Set Model Predictive Current Control for Permanent Magnet Synchronous Motor with Sliding Mode Observer. IEEE Trans. Transp. Electrif. 2024, 10, 699–710. [Google Scholar] [CrossRef]
- He, L.; Wang, F.; Ke, D. FPGA-Based Sliding-Mode Predictive Control for PMSM Speed Regulation System Using an Adaptive Ultralocal Model. IEEE Trans. Power Electron. 2021, 36, 5784–5793. [Google Scholar] [CrossRef]
- Xu, Y.; Yan, Z.; Zhang, Y.; Song, R. Model Predictive Current Control of Permanent Magnet Synchronous Motor Based on Sliding Mode Observer with Enhanced Current and Speed Tracking Ability Under Disturbance. IEEE Trans. Energy Convers. 2023, 38, 948–958. [Google Scholar] [CrossRef]
- Zhang, Y.; Yin, Z.; Li, W.; Liu, J.; Zhang, Y. Adaptive Sliding-Mode-Based Speed Control in Finite Control Set Model Predictive Torque Control for Induction Motors. IEEE Trans. Power Electron. 2021, 36, 8076–8087. [Google Scholar] [CrossRef]
- Junejo, A.K.; Xu, W.; Mu, C.; Ismail, M.M.; Liu, Y. Adaptive Speed Control of PMSM Drive System Based a New Sliding-Mode Reaching Law. IEEE Trans. Power Electron. 2020, 35, 12110–12121. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, Z.; Bin, H.; Gong, L. Current Harmonics Suppression Strategy for PMSM with Nonsinusoidal Back-EMF Based on Adaptive Linear Neuron Method. IEEE Trans. Ind. Electron. 2020, 67, 9164–9173. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Nguyen, T.T.; Nguyen, V.Q.; Le, K.M.; Tran, H.N.; Jeon, J.W. An Adaptive Sliding-Mode Controller with a Modified Reduced-Order Proportional Integral Observer for Speed Regulation of a Permanent Magnet Synchronous Motor. IEEE Trans. Ind. Electron. 2022, 69, 7181–7191. [Google Scholar] [CrossRef]
- Yeam, T.-I.; Lee, D.-C. Design of Sliding-Mode Speed Controller with Active Damping Control for Single-Inverter Dual-PMSM Drive Systems. IEEE Trans. Power Electron. 2021, 36, 5794–5801. [Google Scholar] [CrossRef]
- Guo, X.; Huang, S.; Lu, K.; Peng, Y.; Wang, H.; Yang, J. A Fast Sliding Mode Speed Controller for PMSM Based on New Compound Reaching Law with Improved Sliding Mode Observer. IEEE Trans. Transp. Electrif. 2023, 9, 2955–2968. [Google Scholar] [CrossRef]
- Chen, S.; Chiang, H.; Liu, T.; Chang, C. Precision Motion Control of Permanent Magnet Linear Synchronous Motors Using Adaptive Fuzzy Fractional-Order Sliding-Mode Control. IEEE/ASME Trans. Mechatron. 2019, 24, 741–752. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, X.; Wang, W.; Chen, K.; Cheung, N.; Pan, J. Enhanced Sliding Mode Control for PMSM Speed Drive Systems Using a Novel Adaptive Sliding Mode Reaching Law Based on Exponential Function. IEEE Trans. Ind. Electron. 2024, 71, 11978–11988. [Google Scholar] [CrossRef]
- Sun, X.; Cao, J.; Lei, G.; Guo, Y.; Zhu, J. A Composite Sliding Mode Control for SPMSM Drives Based on a New Hybrid Reaching Law with Disturbance Compensation. IEEE Trans. Transp. Electrif. 2021, 7, 1427–1436. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, Y.; Zhang, X.; Liang, J. A New Reaching Law for Antidisturbance Sliding-Mode Control of PMSM Speed Regulation System. IEEE Trans. Power Electron. 2020, 35, 4117–4126. [Google Scholar] [CrossRef]
- Xu, W.; Junejo, A.K.; Liu, Y.; Hussien, M.G.; Zhu, J. An Efficient Antidisturbance Sliding-Mode Speed Control Method for PMSM Drive Systems. IEEE Trans. Power Electron. 2021, 36, 6879–6891. [Google Scholar] [CrossRef]
- Ma, Y.; Li, D.; Li, Y.; Yang, L. A Novel Discrete Compound Integral Terminal Sliding Mode Control with Disturbance Compensation for PMSM Speed System. IEEE/ASME Trans. Mechatron. 2022, 27, 549–560. [Google Scholar] [CrossRef]
- Hou, H.; Yu, X.; Xu, L.; Rsetam, K.; Cao, Z. Finite-Time Continuous Terminal Sliding Mode Control of Servo Motor Systems. IEEE Trans. Ind. Electron. 2020, 67, 5647–5656. [Google Scholar] [CrossRef]
- Zou, Q.; Chang, S. A new fixed-time terminal sliding mode control for second-order nonlinear systems. J. Frankl. Inst. 2024, 361, 1255–1267. [Google Scholar] [CrossRef]
- Cruz-Ortiz, D.; Chairez, I.; Poznyak, A. Non-singular terminal sliding-mode control for a manipulator robot using a barrier Lyapunov function. ISA Trans. 2022, 121, 268–283. [Google Scholar] [CrossRef] [PubMed]
- Hagh, Y.S.; Fekih, A.; Handroos, H. Robust PI-Based Non-Singular Terminal Synergetic Control for Nonlinear Systems via Hybrid Nonlinear Disturbance Observer. IEEE Access 2021, 9, 97401–97414. [Google Scholar] [CrossRef]
- Fu, D.; Zhao, X.; Zhu, J. A Novel Robust Super-Twisting Nonsingular Terminal Sliding Mode Controller for Permanent Magnet Linear Synchronous Motors. IEEE Trans. Power Electron. 2022, 37, 2936–2945. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, L.; Ji, W. Improved Non-Singular Fast Terminal Sliding Mode Control with Disturbance Observer for PMSM Drives. IEEE Trans. Transp. Electrif. 2021, 7, 2753–2762. [Google Scholar] [CrossRef]
- Hagras, A.A.; Azab, A.; Zaid, S. Model-Free Nonsingular Fast Terminal Sliding Mode Control of a Permanent Magnet Synchronous Motor. Acta Polytech. Hung. 2024, 21, 283–305. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, H.; Zhang, M.; Chen, B.; Jia, R.; Mao, J. Non-singular fast terminal sliding mode control of PMSMs with disturbance compensation. J. Power Electron. 2024, 1–11. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, L.; Vazquez, S.; Xu, R.; Dong, Z.; Liu, J.; Leon, J.I.; Wu, L.; Franquelo, L.G. Disturbance and Uncertainty Attenuation for Speed Regulation of PMSM Servo System Using Adaptive Optimal Control Strategy. IEEE Trans. Transp. Electrif. 2023, 9, 3410–3420. [Google Scholar] [CrossRef]
- Lin, X.; Wu, C.; Yao, W.; Liu, Z.; Shen, X.; Xu, R.; Sun, G.; Liu, J. Observer-Based Fixed-Time Control for Permanent-Magnet Synchronous Motors with Parameter Uncertainties. IEEE Trans. Power Electron. 2023, 38, 4335–4344. [Google Scholar] [CrossRef]
- Qu, L.; Qiao, W.; Qu, L. Active-Disturbance-Rejection-Based Sliding-Mode Current Control for Permanent-Magnet Synchronous Motors. IEEE Trans. Power Electron. 2021, 36, 751–760. [Google Scholar] [CrossRef]
- Lin, X.; Huang, W.; Jiang, W.; Zhao, Y.; Zhu, S. A Stator Flux Observer with Phase Self-Tuning for Direct Torque Control of Permanent Magnet Synchronous Motor. IEEE Trans. Power Electron. 2020, 35, 6140–6152. [Google Scholar] [CrossRef]
- Ke, D.; Wang, F.; He, L.; Li, Z. Predictive Current Control for PMSM Systems Using Extended Sliding Mode Observer with Hurwitz-Based Power Reaching Law. IEEE Trans. Power Electron. 2021, 36, 7223–7232. [Google Scholar] [CrossRef]
- Chen, L.; Jin, Z.; Shao, K.; Wang, H.; Wang, G.; Lu, H.; Fernando, T. Sensorless Fixed-Time Sliding Mode Control of PMSM Based on Barrier Function Adaptive Super-Twisting Observer. IEEE Trans. Power Electron. 2024, 39, 3037–3051. [Google Scholar] [CrossRef]
- Zhang, L.; Tao, R.; Zhang, Z.; Chien, Y.; Bai, J. PMSM non-singular fast terminal sliding mode control with disturbance compensation, Information Sciences. Inf. Sci. 2023, 642, 119040. [Google Scholar] [CrossRef]
- Gil, J.; You, S.; Lee, Y.; Kim, W. Nonlinear sliding mode controller using disturbance observer for permanent magnet synchronous motors under disturbance. Expert Syst. Appl. 2023, 214, 119085. [Google Scholar] [CrossRef]
- Liu, Y.C. Disturbance-Observer-Based Sliding-Mode Speed Control for Synchronous Reluctance Motor Drives via Generalized Super-Twisting Algorithm. Actuators 2024, 13, 233. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, C.; Chen, S.; Zhang, L. Research on Speed Control of Switched Reluctance Motors Based on Improved Super-Twisting Sliding Mode and Linear Active Disturbance Rejection Control. Electronics 2025, 14, 1065. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, J.; Yao, Z. PMSM Sliding Mode Control Based on Disturbance Observer and New Non-Singular Fast Terminal. Modul. Mach. Tool Autom. Manuf. Tech. 2022, 3, 84–87. (In Chinese) [Google Scholar]
- Qu, Y.; Zhang, B.; Chu, H.; Shen, H.; Zhang, J.; Yang, X. Sliding-mode anti-disturbance speed control of permanent magnet synchronous motor based on an advanced reaching law. ISA Trans. 2023, 139, 436–447. [Google Scholar] [CrossRef]


| Item | Main Parameters |
|---|---|
| Stator Resistance Rs | 1.29 Ω |
| Rated Speed ωN | 1500 rpm |
| d-axis Inductance Ld | 2.53 mH |
| q-axis Inductance Lq | 2.53 mH |
| Number of pole pairs Pn | 4 |
| Moment of Inertia J | 0.00194 kg·m2 |
| Permanent Magnet Flux Linkage φf | 0.2 Wb |
| Rated power | 1.5 Kw |
| Rated current | 6 A |
| Rated torque | 10 Nm |
| Control Strategy | Controller Parameters |
|---|---|
| PI | P = 0.08, I = 0.05 |
| SMC | c = 10, ε = 10, q = 20 |
| FTSMC | p = 9, q = 1, α = 3.5, β = 7, k = 5, ε = 12 |
| NFTCSMC | p = 3.5, q = 3.5, λ = 0.5, k = 5, ε = 3, r = 1.5, b = 0.5, δ = 0.4, γ = 1.1, pω = 5, qω = 5, kω = 20, εω = 5 |
| Three Control Strategies | PI | SMC | FTSMC | NFTCSMC |
|---|---|---|---|---|
| Δn (rpm) | 4 | 44 | 32 | 24 |
| Δt (s) | 47 | 22 | 15 | 14 |
| δ (rpm) | 330 | 95 | 85 | 45 |
| Three Control Strategies | PI | SMC | FTSMC | NFTCSMC | |
|---|---|---|---|---|---|
| Sudden loading | Δn (rpm) | 35 | 50 | 40 | 38 |
| Δt (s) | 90 | 50 | 25 | 20 | |
| Sudden unloading | Δn (rpm) | 34 | 50 | 40 | 38 |
| Δt (s) | 80 | 40 | 25 | 10 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Wang, X.; Zhou, P.; An, L.; Zhao, Z.; Jia, B.; Xu, Y. Non-Singular Fast Terminal Composite Sliding Mode Control of Marine Permanent Magnet Synchronous Propulsion Motors. Machines 2025, 13, 470. https://doi.org/10.3390/machines13060470
Liu Z, Wang X, Zhou P, An L, Zhao Z, Jia B, Xu Y. Non-Singular Fast Terminal Composite Sliding Mode Control of Marine Permanent Magnet Synchronous Propulsion Motors. Machines. 2025; 13(6):470. https://doi.org/10.3390/machines13060470
Chicago/Turabian StyleLiu, Zhaoting, Xi Wang, Peng Zhou, Liantong An, Zhengwei Zhao, Baozhu Jia, and Yuanyuan Xu. 2025. "Non-Singular Fast Terminal Composite Sliding Mode Control of Marine Permanent Magnet Synchronous Propulsion Motors" Machines 13, no. 6: 470. https://doi.org/10.3390/machines13060470
APA StyleLiu, Z., Wang, X., Zhou, P., An, L., Zhao, Z., Jia, B., & Xu, Y. (2025). Non-Singular Fast Terminal Composite Sliding Mode Control of Marine Permanent Magnet Synchronous Propulsion Motors. Machines, 13(6), 470. https://doi.org/10.3390/machines13060470






