A Review of Magnetostatic Field Derivation Techniques in Reluctance Motors and Possible Extensions to Segmented Design
Abstract
1. Introduction
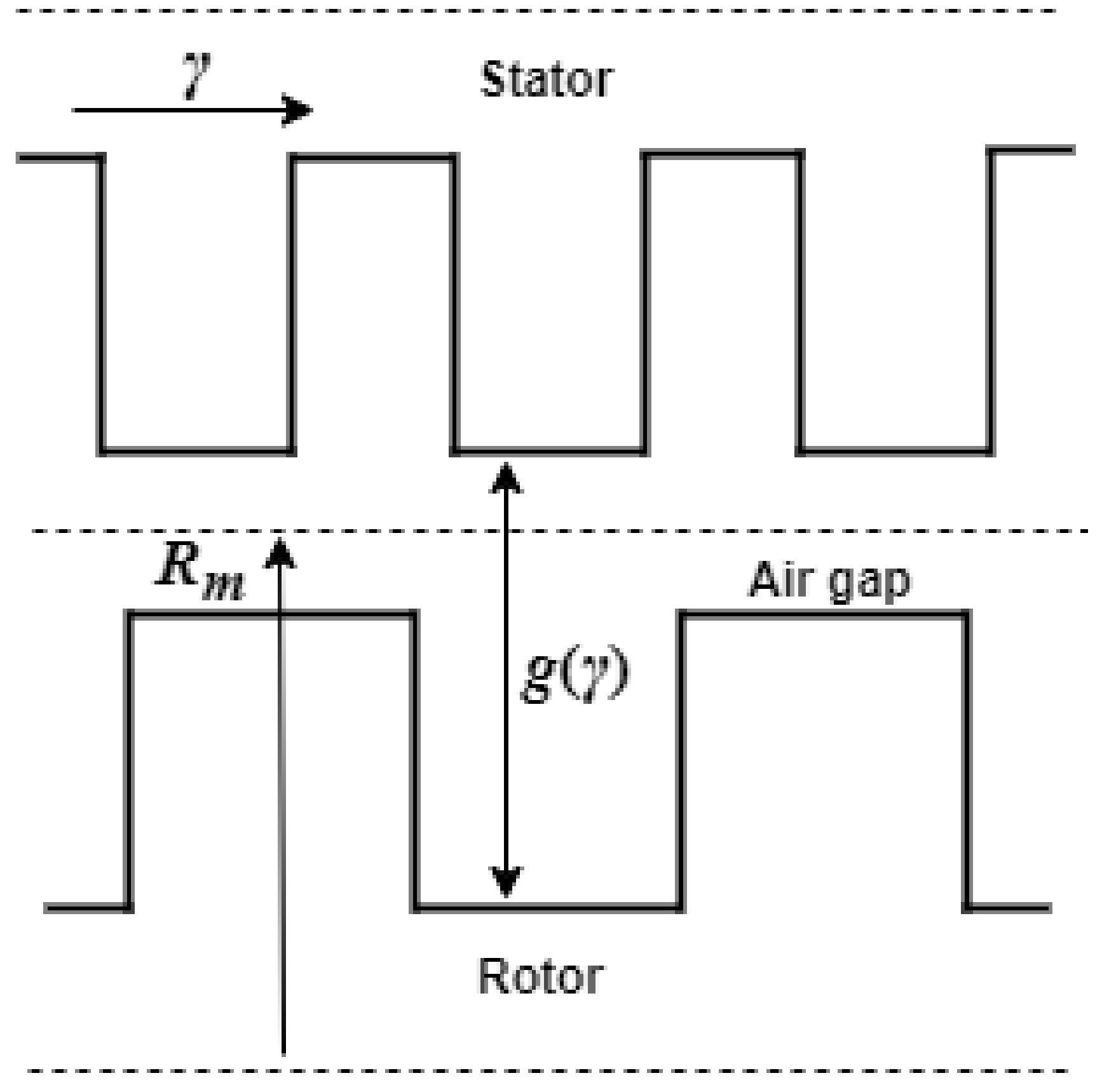
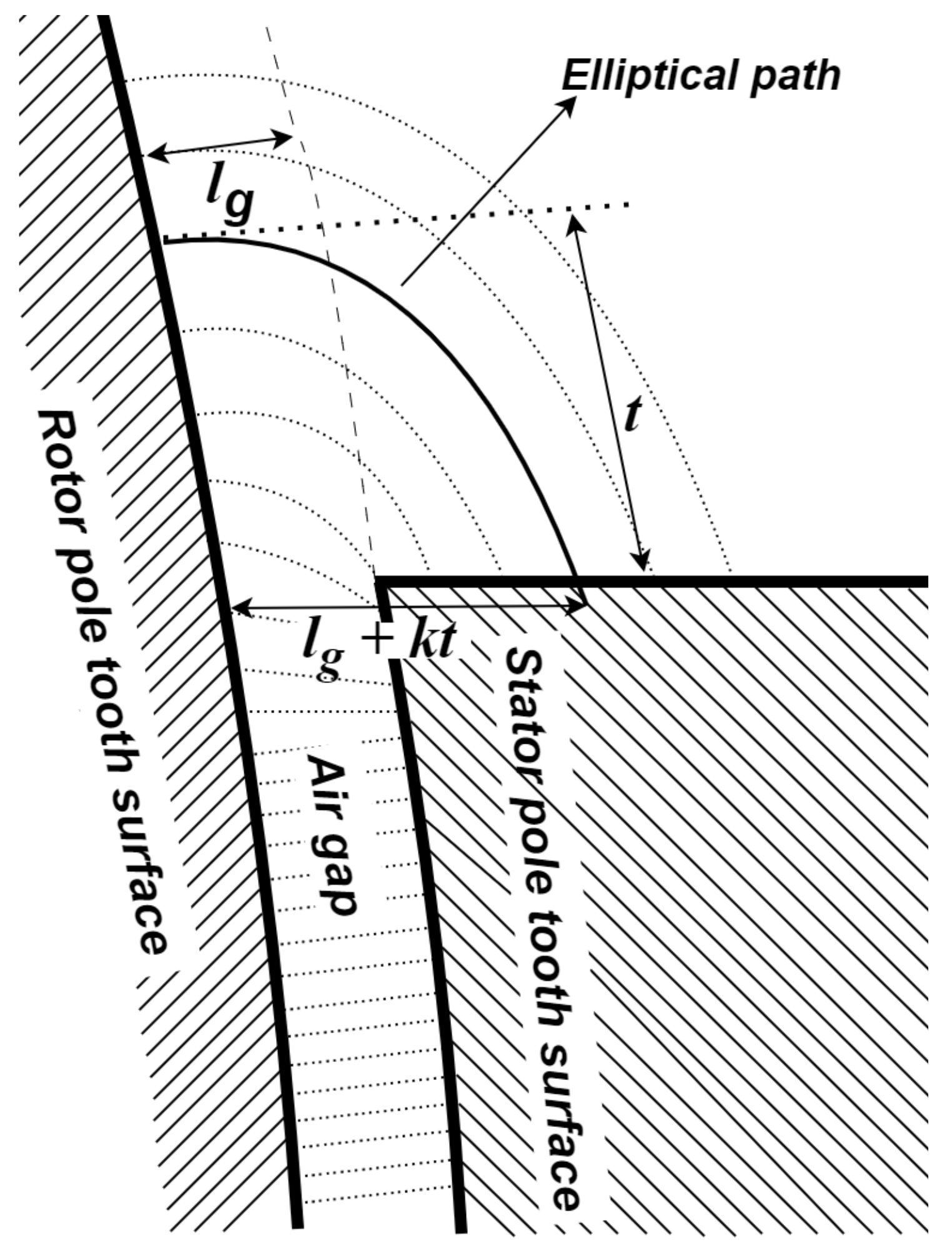
2. Air Gap Permeance
2.1. Theoretical Background
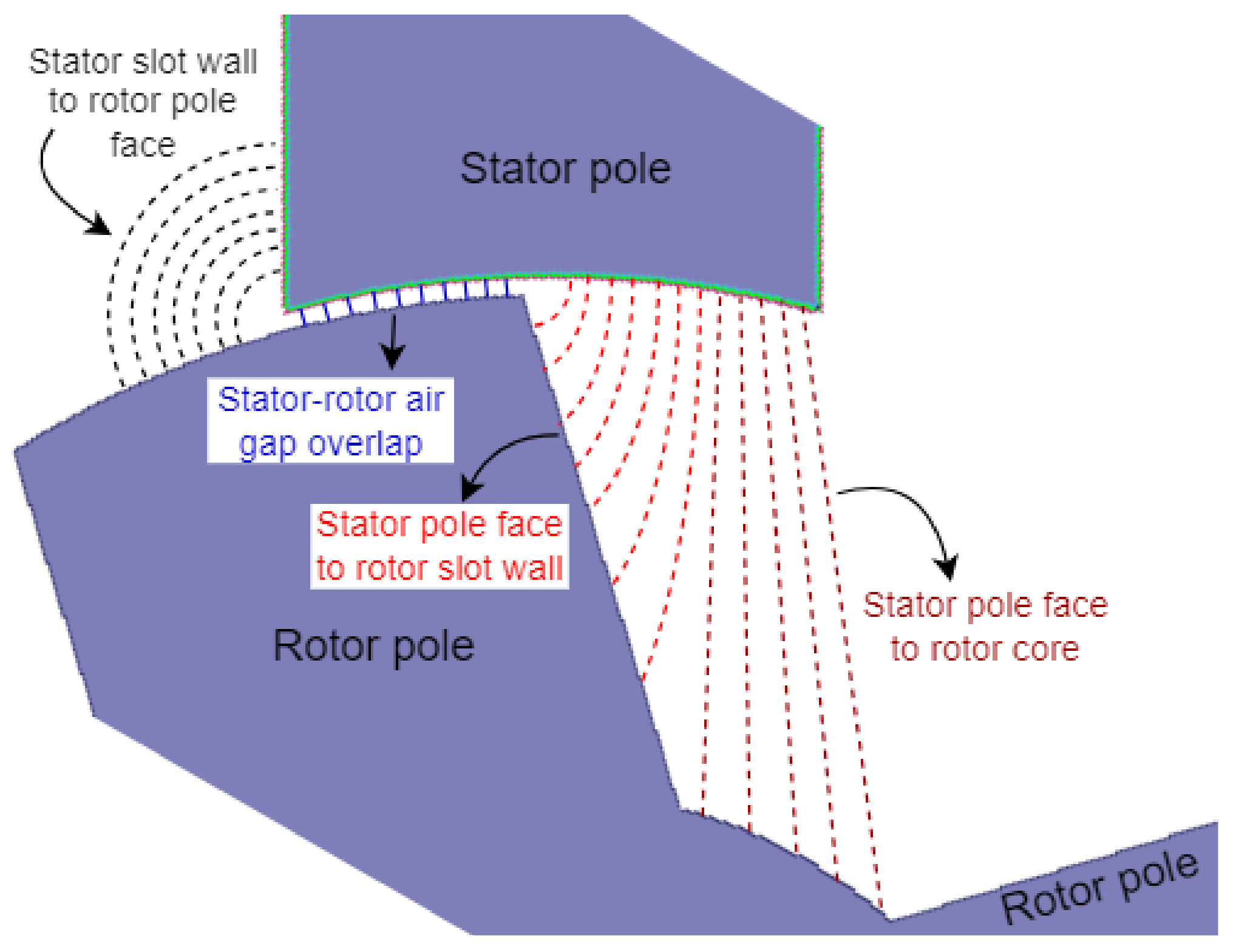
2.2. Using Air Gap Permeance for Reluctance Machine Analysis
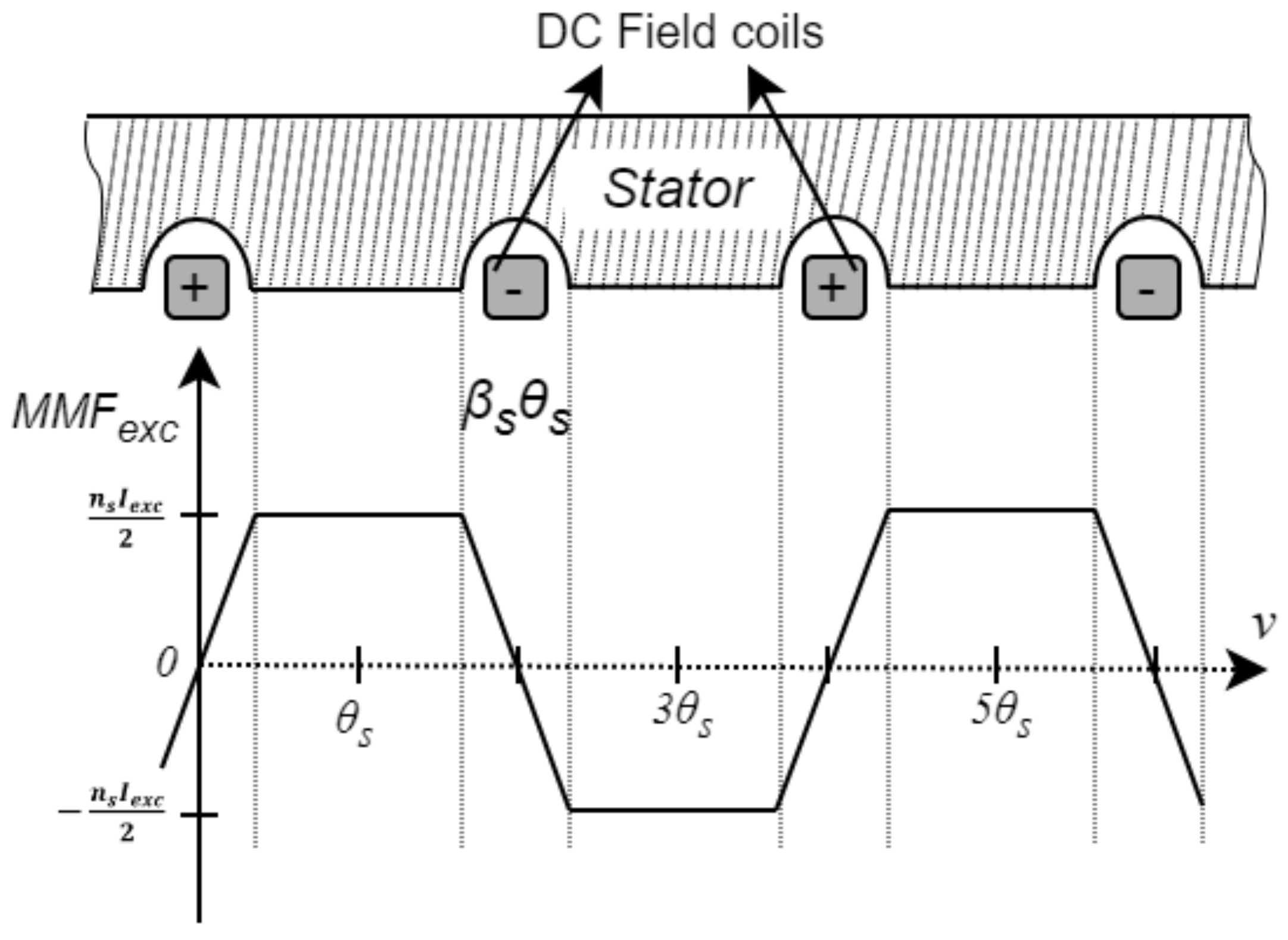
3. Magnetic Potentials
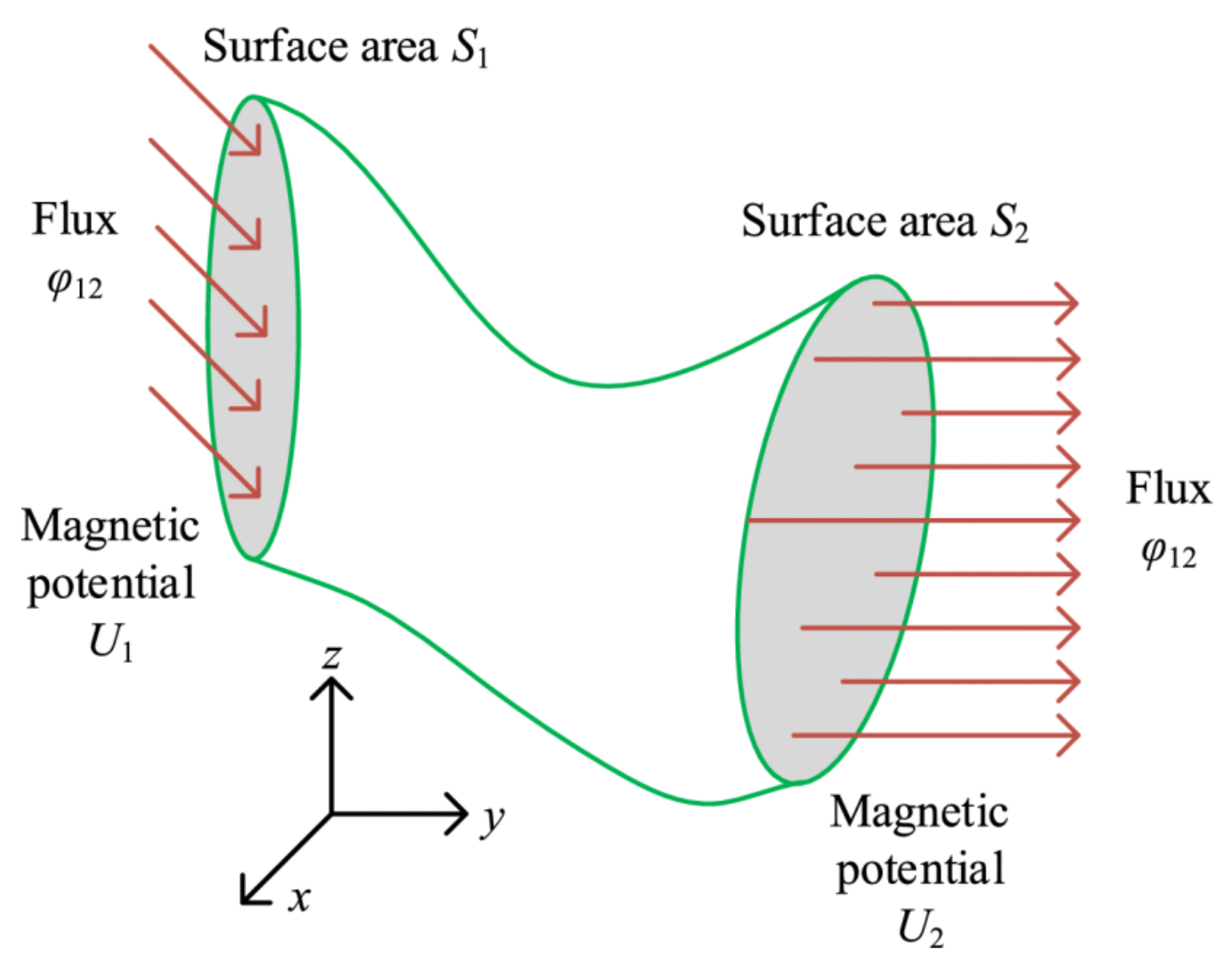
3.1. Theoretical Background of Magnetic Potentials
3.2. Applying Magnetic Potentials to Reluctance Motors
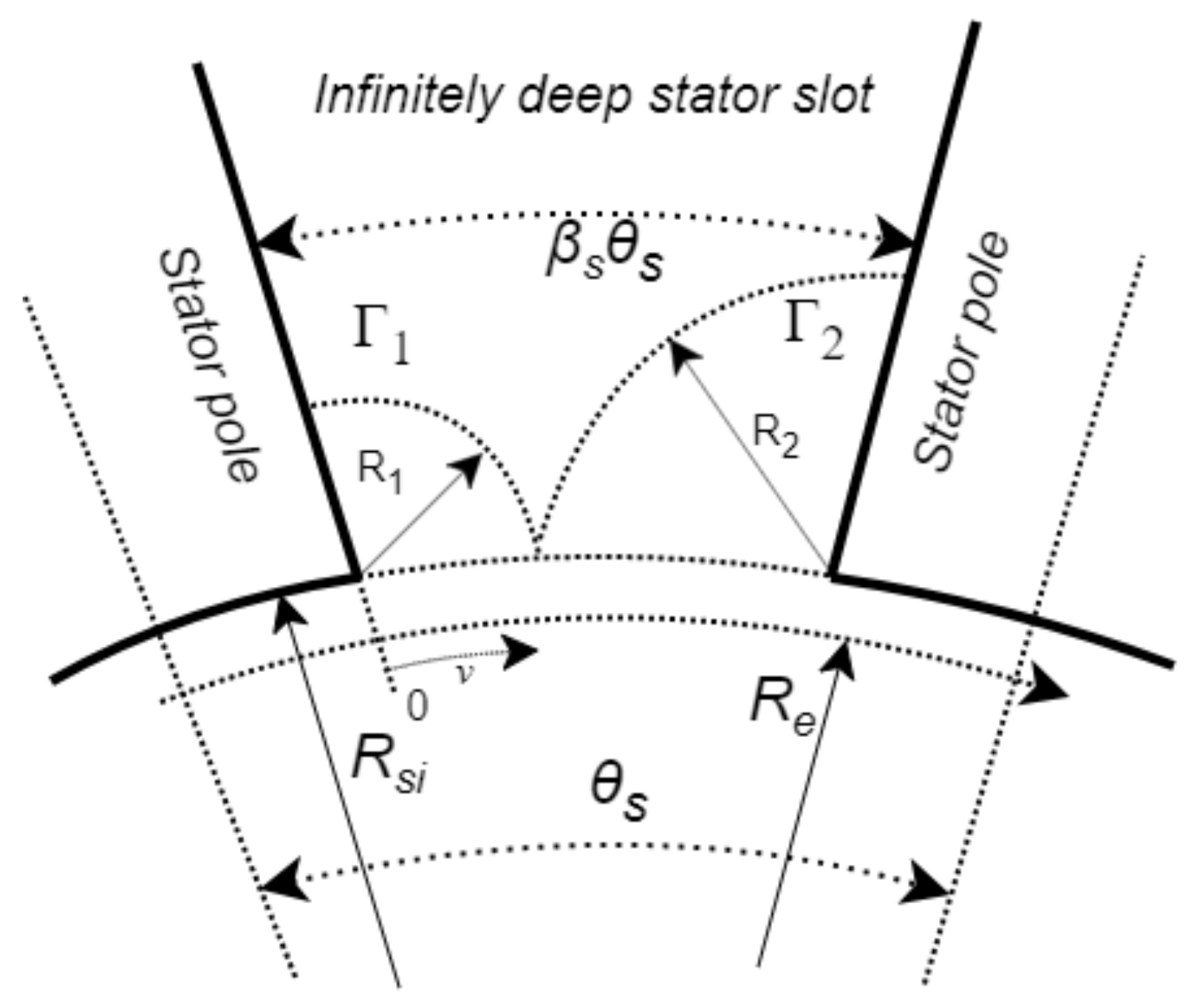
4. Conformal Mapping
4.1. Theoretical Background of Conformal Mapping
4.2. Conformal Mapping in Reluctance Motor Analysis
5. Summary of Major Techniques
6. Other Techniques Used in Reluctance Motor Research
6.1. Magnetic Equivalent Circuits
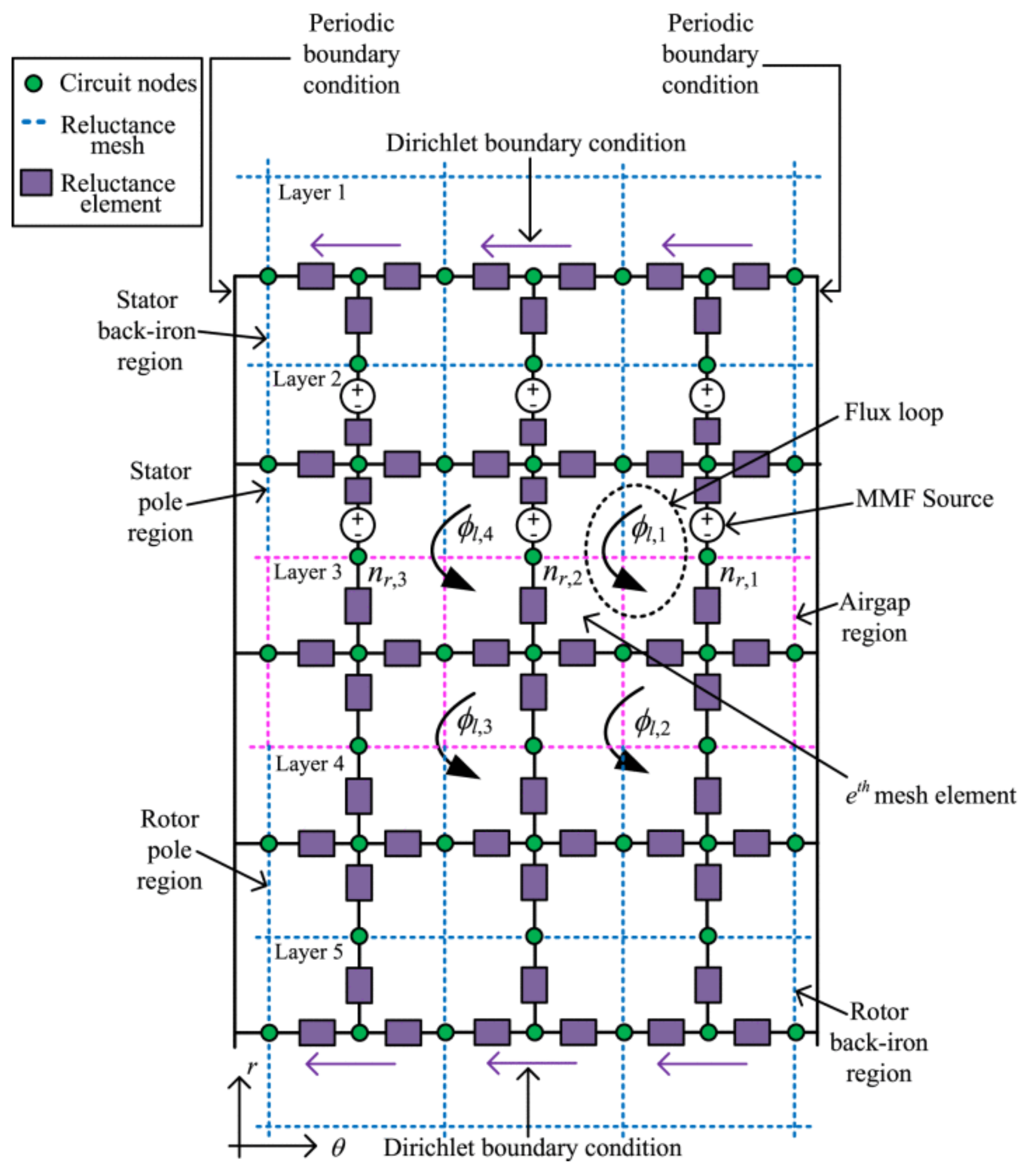
6.2. Reluctance Mesh and Flux Tubes
6.3. Maxwell Stress Tensor
7. Potential Applications to Segmented Reluctance Motor Design
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BEA | Boundary element analysis |
| CSSR | Conventional stator, segmented rotor |
| FEA | Finite element analysis |
| MEC | Magnetic equivalent circuit |
| MMF | Magnetomotive force |
| MST | Maxwell stress tensor |
| SRM | Switched reluctance motor |
| SC | Schwarz–Christoffel (transform) |
| SSSR | Segmented stator, segmented rotor |
References
- Diao, K.; Sun, X.; Lei, G.; Bramerdorfer, G.; Guo, Y.; Zhu, J. Robust Design Optimization of Switched Reluctance Motor Drive Systems Based on System-Level Sequential Taguchi Method. IEEE Trans. Energy Convers. 2021, 36, 3199–3207. [Google Scholar] [CrossRef]
- Li, S.; Zhang, S.; Habetler, T.G.; Harley, R.G. Modeling, Design Optimization, and Applications of Switched Reluctance Machines—A Review. IEEE Trans. Ind. Appl. 2019, 55, 2660–2681. [Google Scholar] [CrossRef]
- Diao, K.; Sun, X.; Bramerdorfer, G.; Cai, Y.; Lei, G.; Chen, L. Design optimization of switched reluctance machines for performance and reliability enhancements: A review. Renew. Sustain. Energy Rev. 2022, 168, 112785. [Google Scholar] [CrossRef]
- Omar, M.; Sayed, E.; Abdalmagid, M.; Bilgin, B.; Bakr, M.H.; Emadi, A. Review of Machine Learning Applications to the Modeling and Design Optimization of Switched Reluctance Motors. IEEE Access 2022, 10, 130444–130468. [Google Scholar] [CrossRef]
- Shao, H.; Zhong, C.; Habetler, T.G.; Li, S. Multi-Objective Design Optimization of Synchronous Reluctance Machines Based on the Analytical Model and the Evolutionary Algorithms. In Proceedings of the 2019 North American Power Symposium (NAPS), Wichita, KS, USA, 13–15 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Mecrow, B.; Finch, J.; El-Kharashi, E.; Jack, A. Switched reluctance motors with segmental rotors. IEE Proc.-Electr. Power Appl. 2002, 149, 245–254. [Google Scholar] [CrossRef]
- Ding, W.; Yang, S.; Hu, Y. Development and Investigation on Segmented-Stator Hybrid-Excitation Switched Reluctance Machines With Different Rotor Pole Numbers. IEEE Trans. Ind. Electron. 2017, 65, 3784–3794. [Google Scholar] [CrossRef]
- Widmer, J.; Mecrow, B. Optimised Segmental Rotor Switched Reluctance Machines with a greater number of rotor segments than stator slots. In Proceedings of the 2011 IEEE International Electric Machines & Drives Conference (IEMDC), Niagara Falls, ON, Canada, 15–18 May 2011; pp. 1183–1188. [Google Scholar] [CrossRef]
- Rallabandi, V.; Wu, J.; Zhou, P.; Dorrell, D.G.; Ionel, D.M. Optimal Design of a Switched Reluctance Motor With Magnetically Disconnected Rotor Modules Using a Design of Experiments Differential Evolution FEA-Based Method. IEEE Trans. Magn. 2018, 54, 8205705. [Google Scholar] [CrossRef]
- Ma, C.; Qu, L. Multiobjective Optimization of Switched Reluctance Motors Based on Design of Experiments and Particle Swarm Optimization. IEEE Trans. Energy Convers. 2015, 30, 1144–1153. [Google Scholar] [CrossRef]
- Watthewaduge, G.; Sayed, E.; Emadi, A.; Bilgin, B. Electromagnetic Modeling Techniques for Switched Reluctance Machines: State-of-the-Art Review. IEEE Open J. Ind. Electron. Soc. 2020, 1, 218–234. [Google Scholar] [CrossRef]
- Rocca, R.; De Donato, G.; Bolognesi, P.; Boccaletti, C.; Capponi, F.G. Improved Design-Oriented Analytical Modelling of Switched Reluctance Machines Based on Fröhlich-Kennelly Equations. IEEE Trans. Energy Convers. 2023, 39, 734–746. [Google Scholar] [CrossRef]
- Shi, M.; Wang, Q.; Li, G.; Xu, J.; Han, Q.; Ye, Q. A New Adaptive Analytical Model for the Spherical Reluctance Motor Based on Hybrid Trigonometric Function–Power Function. IEEE Trans. Ind. Electron. 2022, 70, 6099–6109. [Google Scholar] [CrossRef]
- Santos, R.F.L.; Tria, L.A.R. A Response Surface Method Approach to Modular Stator, Segmented Rotor Switched Reluctance Motor Design. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November–2 December 2020; pp. 484–489. [Google Scholar] [CrossRef]
- Hesse, M.H. Air gap permeance in doubly-slotted asynchronous machines. IEEE Trans. Energy Convers. 1992, 7, 491–499. [Google Scholar] [CrossRef]
- Krishnan, R. Switched Reluctance Motor Drives: Modeling, Simulation, Analysis, Design, and Applications; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Gaussens, B.; Hoang, E.; de la Barriere, O.; Saint-Michel, J.; Lecrivain, M.; Gabsi, M. Analytical Approach for Air-Gap Modeling of Field-Excited Flux-Switching Machine: No-Load Operation. IEEE Trans. Magn. 2012, 48, 2505–2517. [Google Scholar] [CrossRef]
- Fitzgerald, A.E.; Umans, S.D. Fitzgerald & Kingsley’s Electric Machinery, 7th ed.; McGraw-Hill: New York, NY, USA, 2014. [Google Scholar]
- Chapman, S.J. Electric Machinery Fundamentals, 5th ed.; McGraw-Hill: New York, NY, USA, 2012. [Google Scholar]
- Li, S.; Zhang, S.; Gong, C.; Habetler, T.G.; Harley, R.G. An Enhanced Analytical Calculation of the Phase Inductance of Switched Reluctance Machines. IEEE Trans. Ind. Appl. 2018, 55, 1392–1407. [Google Scholar] [CrossRef]
- Hua, H.; Hua, W. Analytical Prediction of Torque of Switched Reluctance Machines Considering Nonlinear Characteristics. IEEE Trans. Ind. Electron. 2021, 69, 190–201. [Google Scholar] [CrossRef]
- Lipo, T.A. Analysis of Synchronous Machines, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Zhu, Z.Q.; Howe, D. Instantaneous magnetic field distribution in brushless permanent magnet DC motors. III. Effect of stator slotting. IEEE Trans. Magn. 1993, 29, 143–151. [Google Scholar] [CrossRef]
- Wu, Z.; Fan, Y.; Chen, H.; Wang, X.; Lee, C.H.T. Electromagnetic Force and Vibration Study of Dual-Stator Consequent-Pole Hybrid Excitation Motor for Electric Vehicles. IEEE Trans. Veh. Technol. 2021, 70, 4377–4388. [Google Scholar] [CrossRef]
- Huang, L.R.; Feng, J.H.; Guo, S.Y.; Shi, J.X.; Chu, W.Q.; Zhu, Z.Q. Analysis of Torque Production in Variable Flux Reluctance Machines. IEEE Trans. Energy Convers. 2017, 32, 1297–1308. [Google Scholar] [CrossRef]
- Takemoto, M.; Suzuki, H.; Chiba, A.; Fukao, T.; Rahman, M. Improved analysis of a bearingless switched reluctance motor. IEEE Trans. Ind. Appl. 2001, 37, 26–34. [Google Scholar] [CrossRef]
- Carter, F.W. The magnetic field of the dynamo-electric machine. J. Inst. Electr. Eng. 1926, 64, 1115–1138. [Google Scholar] [CrossRef]
- Viorel, A.C.; Viorel, I.-A.; Strete, L. On the calculation of the Carter factor in the slotted electric machines. In Proceedings of the 2014 International Conference and Exposition on Electrical and Power Engineering (EPE), Iasi, Romania, 16–18 October 2014; pp. 332–336. [Google Scholar] [CrossRef]
- Parasiliti, F.; Villani, M. Magnetic analysis of flux barriers Synchronous Reluctance Motors. In Proceedings of the 2008 18th International Conference on Electrical Machines, Vilamoura, Portugal, 6–9 September 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Cheng, M.; Han, P.; Hua, W. General Airgap Field Modulation Theory for Electrical Machines. IEEE Trans. Ind. Electron. 2017, 64, 6063–6074. [Google Scholar] [CrossRef]
- Hannon, B.; Sergeant, P.; Dupré, L.; Pfister, P.-D. Two-Dimensional Fourier-Based Modeling of Electric Machines—An Overview. IEEE Trans. Magn. 2019, 55, 8107217. [Google Scholar] [CrossRef]
- Vanderlinde, J. Classical Electromagnetic Theory, 2nd ed.; Springer Science + Business Media, Inc.: Greer, SC, USA, 2005. [Google Scholar]
- Bacco, G.; Bianchi, N. Design Criteria of Flux-Barriers in Synchronous Reluctance Machines. IEEE Trans. Ind. Appl. 2018, 55, 2490–2498. [Google Scholar] [CrossRef]
- Helrich, C.S. The Classical Theory of Fields: Electromagnetism; Graduate Texts in Physics; Springer: Greer, SC, USA, 2012. [Google Scholar]
- Li, S.; Zhang, S.; Dang, J.; Habetler, T.G.; Harley, R.G. Calculating the unsaturated inductance of 4/2 switched reluctance motors at arbitrary rotor positions based on partial differential equations of magnetic potentials. In Proceedings of the 2015 North American Power Symposium (NAPS), Charlotte, NC, USA, 4–6 October 2015. [Google Scholar] [CrossRef]
- Gibbs, W.J. Conformal Transformations in Electrical Engineering; The British Thomson-Houston Co., Ltd.: Rugby, UK, 1958. [Google Scholar]
- Driscoll, T.A.; Trefethen, L.N. Schwarz-Christoffel Mapping; Cambridge University Press: Melbourne, Australia, 2002. [Google Scholar]
- Zarko, D.; Ban, D.; Lipo, T.A. Analytical calculation of magnetic field distribution in the slotted air gap of a surface permanent-magnet motor using complex relative air-gap permeance. IEEE Trans. Magn. 2006, 42, 1828–1837. [Google Scholar] [CrossRef]
- Costamagna, E.; Barba, P.D.; Savini, A. An effective application of Schwarz–Christoffel transformations to the shape design of permanent magnet motors. Int. J. Appl. Electromagn. Mech. 2005, 21, 21–37. [Google Scholar] [CrossRef]
- Krop, D.C.J.; Lomonova, E.A.; Vandenput, A.J.A. Application of Schwarz-Christoffel Mapping to Permanent-Magnet Linear Motor Analysis. IEEE Trans. Magn. 2008, 44, 352–359. [Google Scholar] [CrossRef]
- Ilhan, E.; Motoasca, E.T.; Paulides, J.; Lomonova, E. Conformal mapping: Schwarz-Christoffel method for flux-switching PM machines. Math. Sci. 2012, 6, 37. [Google Scholar] [CrossRef]
- Lim, D.-K.; Yi, K.-P.; Woo, D.-K.; Yeo, H.-K.; Ro, J.-S.; Lee, C.-G.; Jung, H.-K. Analysis and Design of a Multi-Layered and Multi-Segmented Interior Permanent Magnet Motor by Using an Analytic Method. IEEE Trans. Magn. 2014, 50, 8201308. [Google Scholar] [CrossRef]
- Tessarolo, A. Modeling and Analysis of Synchronous Reluctance Machines With Circular Flux Barriers Through Conformal Mapping. IEEE Trans. Magn. 2014, 51, 8104411. [Google Scholar] [CrossRef]
- Shao, H.; Li, S.; Habetler, T.G. Analytical Calculation of the Air-gap Flux Density and Magnetizing Inductance of Synchronous Reluctance Machines. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 5408–5413. [Google Scholar] [CrossRef]
- Masoumi, M.; Kondelaji, M.A.J.; Mirsalim, M.; Moghani, J.S. Analytical modelling and experimental verification of E-type reluctance motors. IET Electr. Power Appl. 2018, 13, 110–118. [Google Scholar] [CrossRef]
- Farahani, E.F.; Kondelaji, M.A.J.; Mirsalim, M. An Innovative Hybrid-Excited Multi-Tooth Switched Reluctance Motor for Torque Enhancement. IEEE Trans. Ind. Electron. 2020, 68, 982–992. [Google Scholar] [CrossRef]
- Sun, X.; Diao, K.; Lei, G.; Guo, Y.; Zhu, J. Real-Time HIL Emulation for a Segmented-Rotor Switched Reluctance Motor Using a New Magnetic Equivalent Circuit. IEEE Trans. Power Electron. 2019, 35, 3841–3849. [Google Scholar] [CrossRef]
- Hassan, M.H.; Krebs, G.; Marchand, C. A simplified time stepping nonlinear mesh based reluctance network for machine design. In Proceedings of the 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013; pp. 879–884. [Google Scholar] [CrossRef]
- Watthewaduge, G.; Bilgin, B. Reluctance Mesh-Based Magnetic Equivalent Circuit Modeling of Switched Reluctance Motors for Static and Dynamic Analysis. IEEE Trans. Transp. Electrification 2021, 8, 2164–2176. [Google Scholar] [CrossRef]
- Watthewaduge, G.; Bilgin, B. Radial Force Density Calculation of Switched Reluctance Machines Using Reluctance Mesh-Based Magnetic Equivalent Circuit. IEEE Open J. Ind. Electron. Soc. 2021, 3, 37–49. [Google Scholar] [CrossRef]
- Yavuz, S.; Parspour, N.; Ma, L. Analytical modelling of a parametrized switched reluctance motor with adapting flux tube method. In Proceedings of the 2018 IEEE International Conference on Industrial Technology (ICIT), Lyon, France, 20–22 February 2018; pp. 335–340. [Google Scholar] [CrossRef]
- Hameyer, K.; Belmans, R. Numerical Modelling and Design of Electric Machines and Devices; WIT Press: Southampton, UK, 1999. [Google Scholar]
- Popescu, M. Prediction of the electromagnetic torque in synchronous machines through Maxwell stress harmonic filter (HFT) method. Electr. Eng. 2005, 89, 117–125. [Google Scholar] [CrossRef]
- Ida, N.; Bastos, J.P.A. Electromagnetics and Calculation of Fields, 2nd ed.; Springer: New York, NY, USA, 1997. [Google Scholar]
- Xu, Z.; Huang, C.; Yu, S.; Wang, H.; Yi, T.; Zhang, Z. Mathematical Model of 12/14 Hybrid Stator Pole Type Bearingless Switched Reluctance Motor Based on Maxwell Stress Tensor Method. In Proceedings of the 2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nangjing, China, 27–29 May 2022; pp. 2452–2457. [Google Scholar] [CrossRef]
- Kim, Y.S. Electromagnetic Force Calculation Method in Finite Element Analysis for Programmers. Univers. J. Electr. Electron. Eng. 2019, 6, 62–67. [Google Scholar] [CrossRef]
- Niguchi, N.; Hirata, K.; Suzuki, H. Vibration Investigation of a 24/20 Switched Reluctance Motor Focusing on the Driving Methods. In Proceedings of the 2019 19th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering (ISEF), Nancy, France, 29–31 August 2019; pp. 1–2. [Google Scholar] [CrossRef]
- Xue, X.D.; Cheng, K.W.E.; Ng, T.W.; Cheung, N.C. Multi-Objective Optimization Design of In-Wheel Switched Reluctance Motors in Electric Vehicles. IEEE Trans. Ind. Electron. 2010, 57, 2980–2987. [Google Scholar] [CrossRef]
- Mecrow, B.C.; El-Kharashi, E.A.; Finch, J.W.; Jack, A.G. Performance evaluation of switched reluctance motors with segmental rotors. In Proceedings of the IEEE International Electric Machines and Drives Conference, 2003. IEMDC’03, Madison, WI, USA, 1–4 June 2003; Volume 1, pp. 568–574. [Google Scholar] [CrossRef]
- Eskandari, H.; Mirsalim, M. An Improved 9/12 Two-Phase E-Core Switched Reluctance Machine. IEEE Trans. Energy Convers. 2013, 28, 951–958. [Google Scholar] [CrossRef]
- Kondelaji, M.A.J.; Mirsalim, M. Segmented-Rotor Modular Switched Reluctance Motor With High Torque and Low Torque Ripple. IEEE Trans. Transp. Electrification 2020, 6, 62–72. [Google Scholar] [CrossRef]
- Ruba, M.; Szabo, L. Segmental Switched Reluctance Machine for Safety-Critical Applications. IEEE Trans. Ind. Appl. 2012, 48, 2223–2229. [Google Scholar] [CrossRef]
- Santos, R.F.; Sermeno, B.; Tria, L.A. Modular Stator, Segmented Rotor Switched Reluctance Motor Prototype: Assembly and Characterization. In Proceedings of the 2022 25th International Conference on Electrical Machines and Systems (ICEMS), Chiang Mai, Thailand, 29 November–2 December 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Wu, J.; Sun, X.; Zhu, J. Accurate torque modeling with PSO-based recursive robust LSSVR for a segmented-rotor switched reluctance motor. CES Trans. Electr. Mach. Syst. 2020, 4, 96–104. [Google Scholar] [CrossRef]
- Abdulah, N.; Shukor, F.A.A.; Othman, R.; Ahmad, S.; Nasir, N. Modelling methods and structure topology of the switched reluctance synchronous motor type machine: A review. Drive Syst. (IJPEDS) 2023, 14, 111–122. [Google Scholar] [CrossRef]
- Xu, Z.; Li, T.; Zhang, F.; Zhang, Y.; Lee, D.; Ahn, J. A Review on Segmented Switched Reluctance Motors. Energies 2022, 15, 9212. [Google Scholar] [CrossRef]


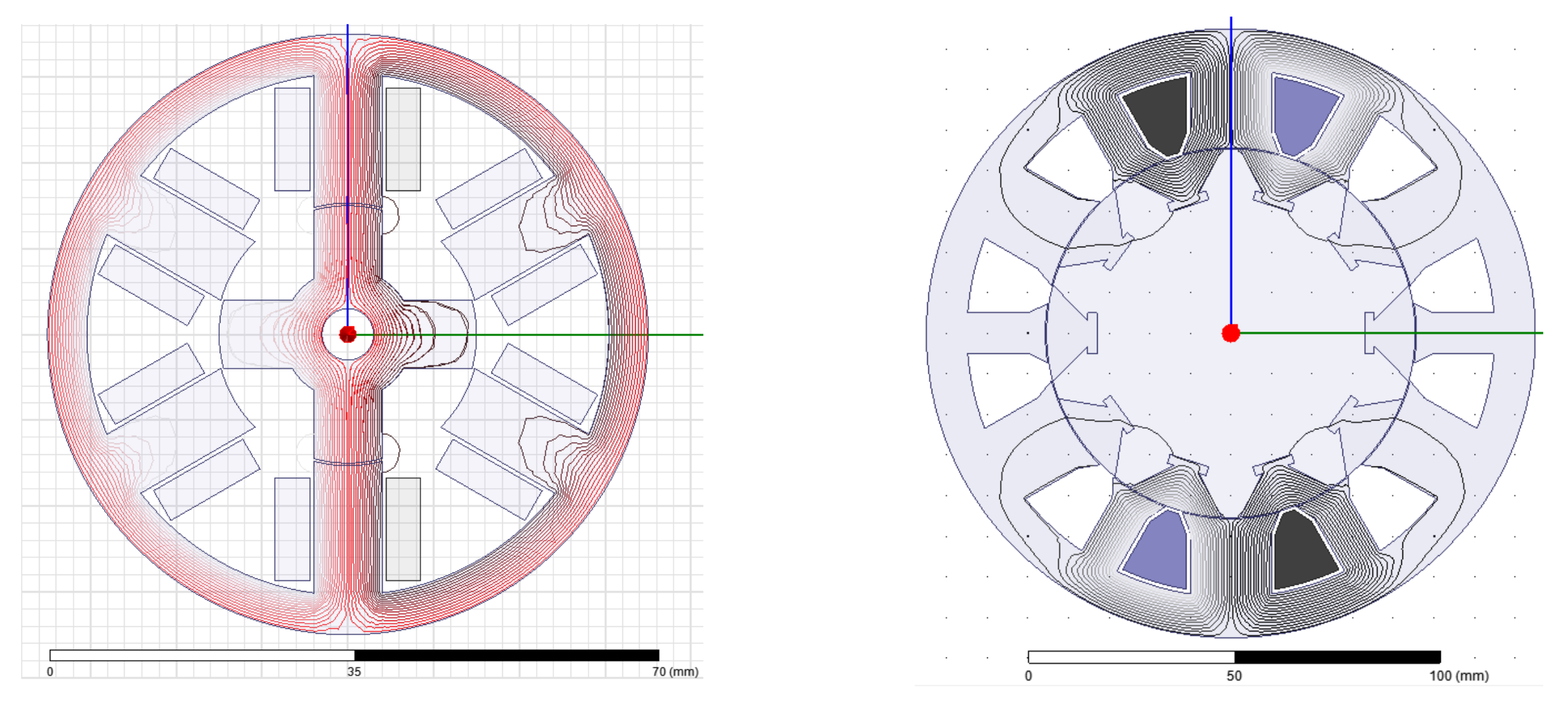


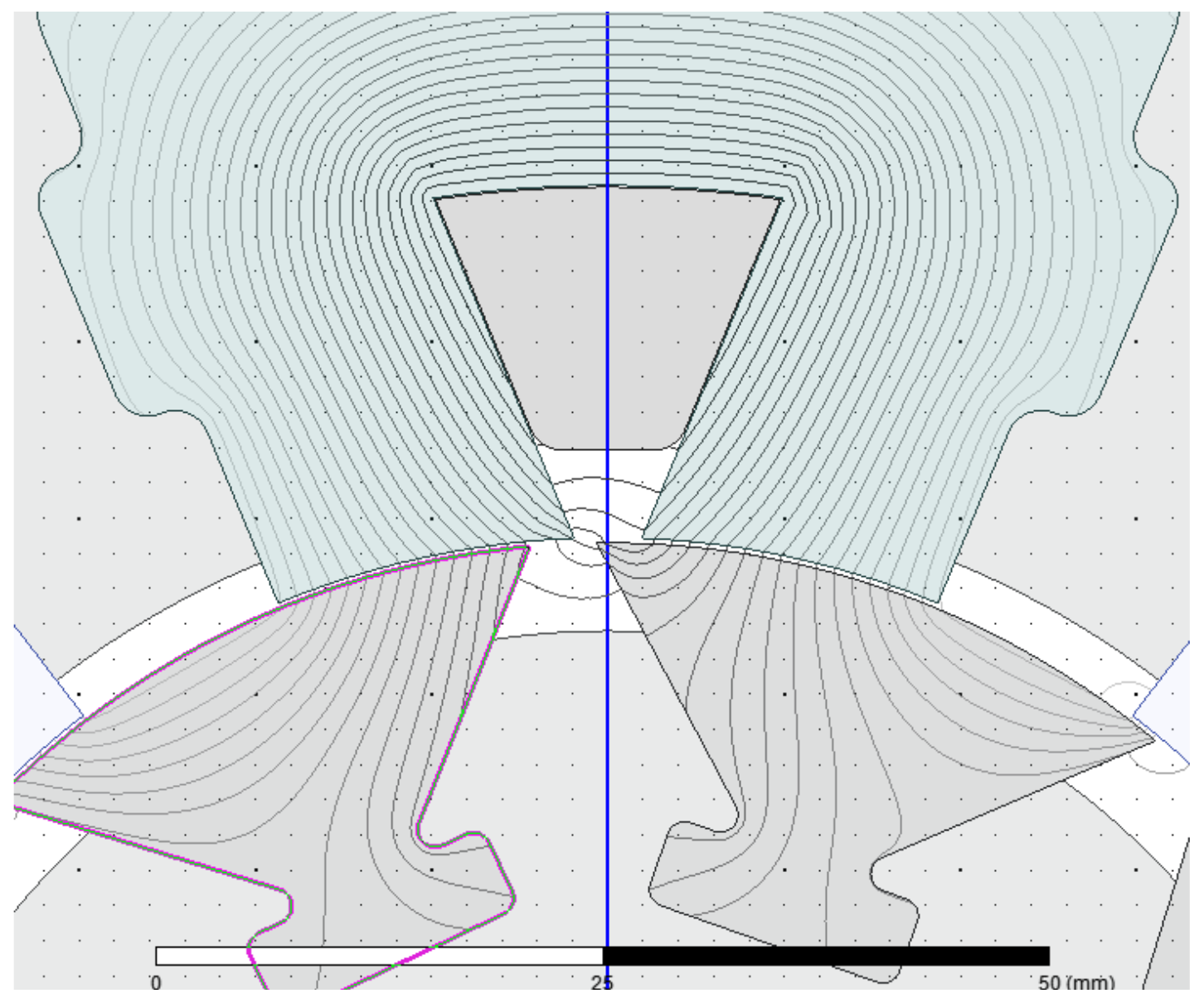
| Technique | Advantages | Disadvantages |
|---|---|---|
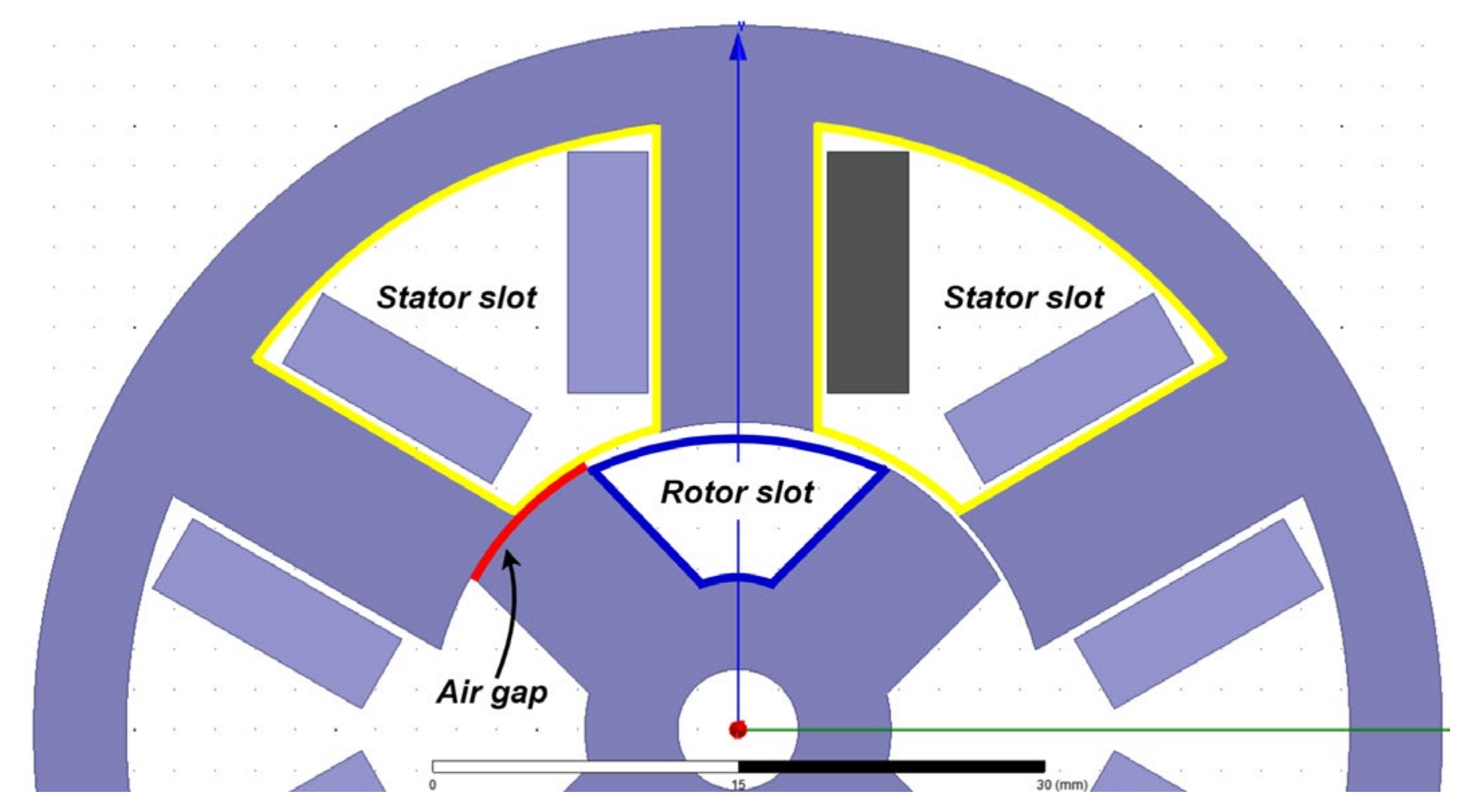
| Air gap permeance | Originates from a simplified expression for B around an air gap (see (1)). Assumed flux path shapes still predict simulated outputs well. | Relies on assumed circular flux paths that may only be true at small rotor angles from aligned positions. Different authors use different mathematical definitions of permeance. Assumed air gap paths and lengths sensitive to the geometry of the motor. |
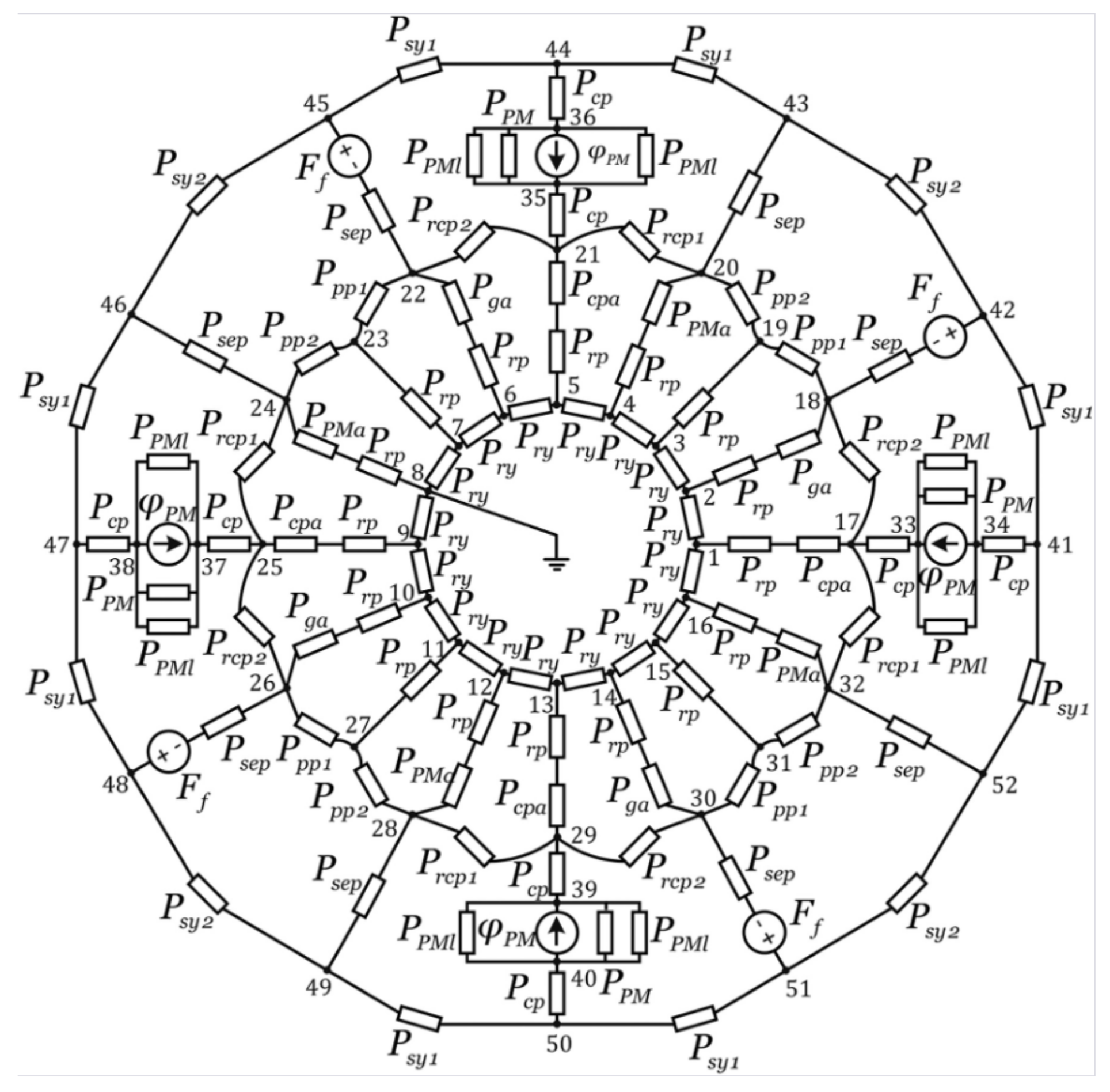
| Magnetic potentials | Directly derives from Maxwell’s equations. Resulting magnetic field distribution dependent on imposed boundary conditions only. | Boundary conditions for the scalar and vector potentials must be strongly defined. Form of solutions sensitive to the geometry of the motor and may require distortions to ease derivation. |
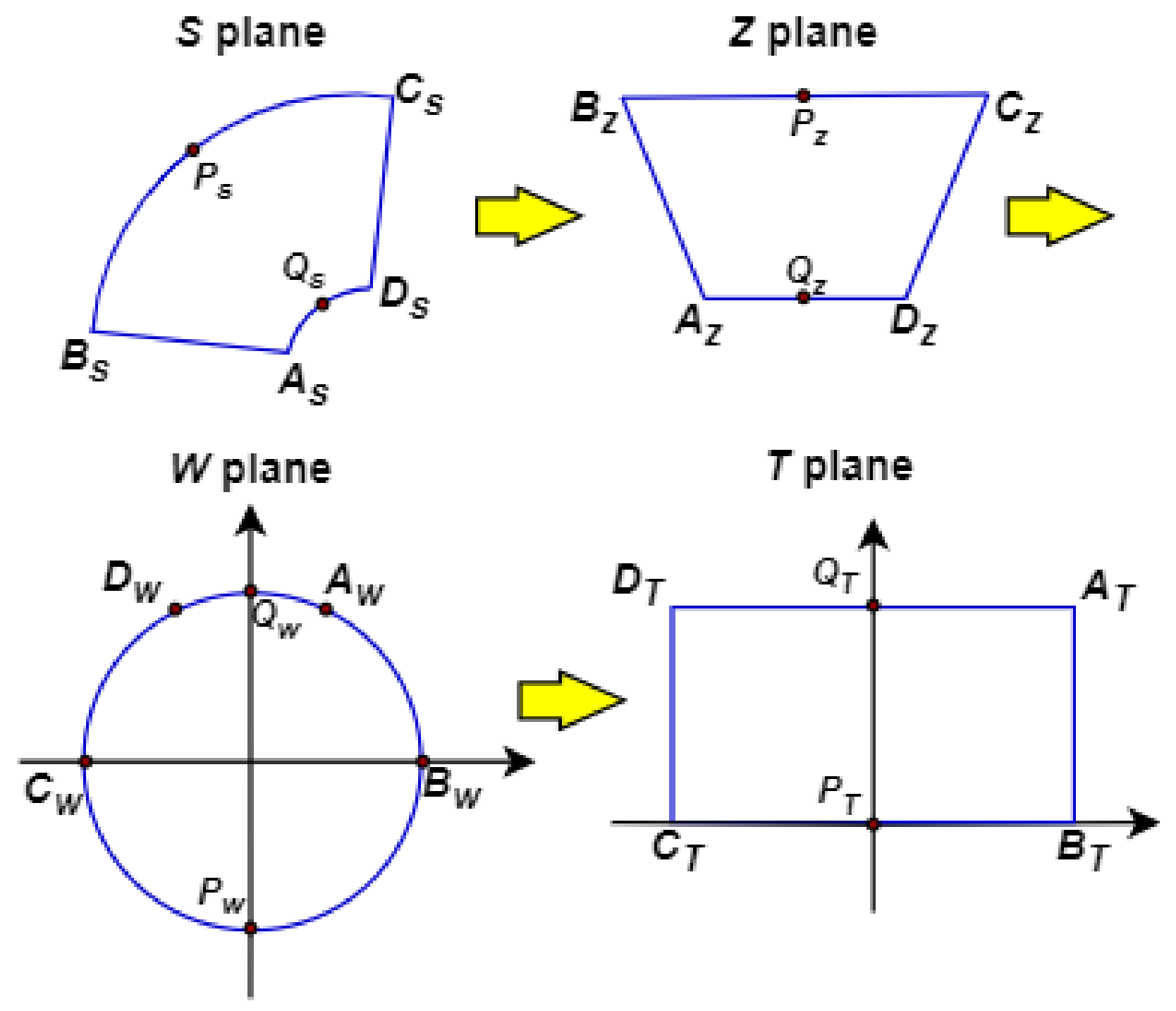
| Conformal transformation | Can be used to extend to other techniques since obtained potential values are invariant. With the correct transformations, the solutions can take the motor geometry as is without distortions. | Complex plane transformations used must correctly account for the actual geometry. Resulting integrals may require numerical solutions if not chosen appropriately. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, R.F.; Tria, L.A. A Review of Magnetostatic Field Derivation Techniques in Reluctance Motors and Possible Extensions to Segmented Design. Machines 2025, 13, 449. https://doi.org/10.3390/machines13060449
Santos RF, Tria LA. A Review of Magnetostatic Field Derivation Techniques in Reluctance Motors and Possible Extensions to Segmented Design. Machines. 2025; 13(6):449. https://doi.org/10.3390/machines13060449
Chicago/Turabian StyleSantos, Ramon Florentino, and Lew Andrew Tria. 2025. "A Review of Magnetostatic Field Derivation Techniques in Reluctance Motors and Possible Extensions to Segmented Design" Machines 13, no. 6: 449. https://doi.org/10.3390/machines13060449
APA StyleSantos, R. F., & Tria, L. A. (2025). A Review of Magnetostatic Field Derivation Techniques in Reluctance Motors and Possible Extensions to Segmented Design. Machines, 13(6), 449. https://doi.org/10.3390/machines13060449






