A 3-D Defect Profile Inversion Method Based on the Continuity Correction Strategy
Abstract
1. Introduction
- The continuity correction strategy is proposed to adjust the implausible depth values and help the inversion process shift away from local optima. This strategy enhances the accuracy of 3-D inversion, particularly in estimating the values at deeper points.
- The differential evolution strategy and perturbation strategy enhanced the search capability and fitting ability of SBOA, improving the accuracy of inverted profiles.
2. Forward Modeling
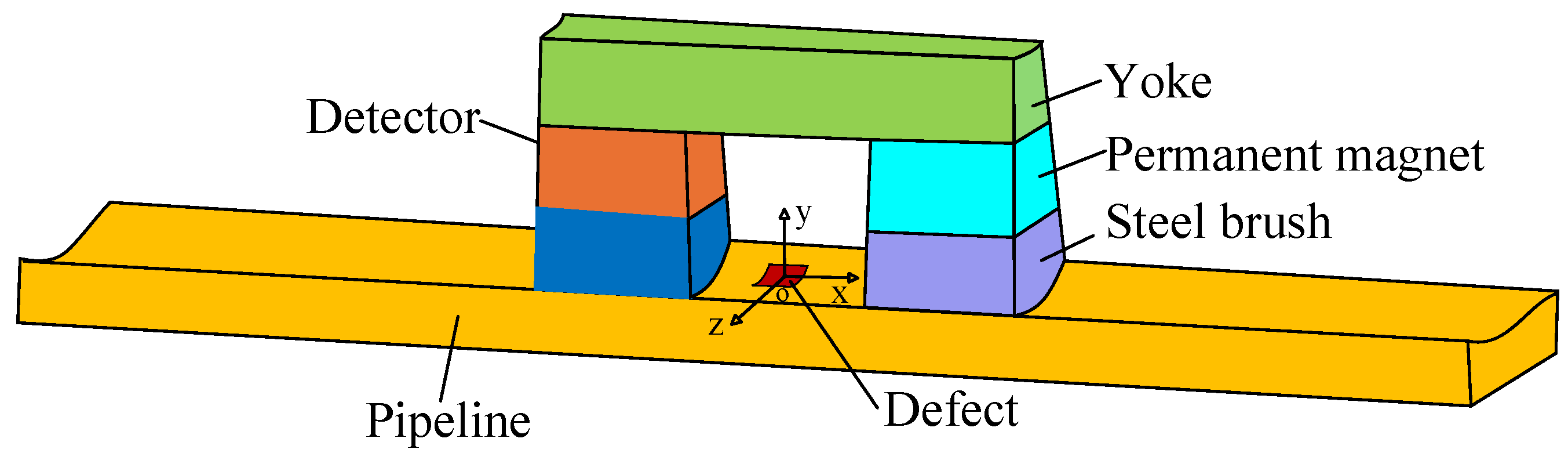
2.1. Measurement of MFL Signals in Pipelines
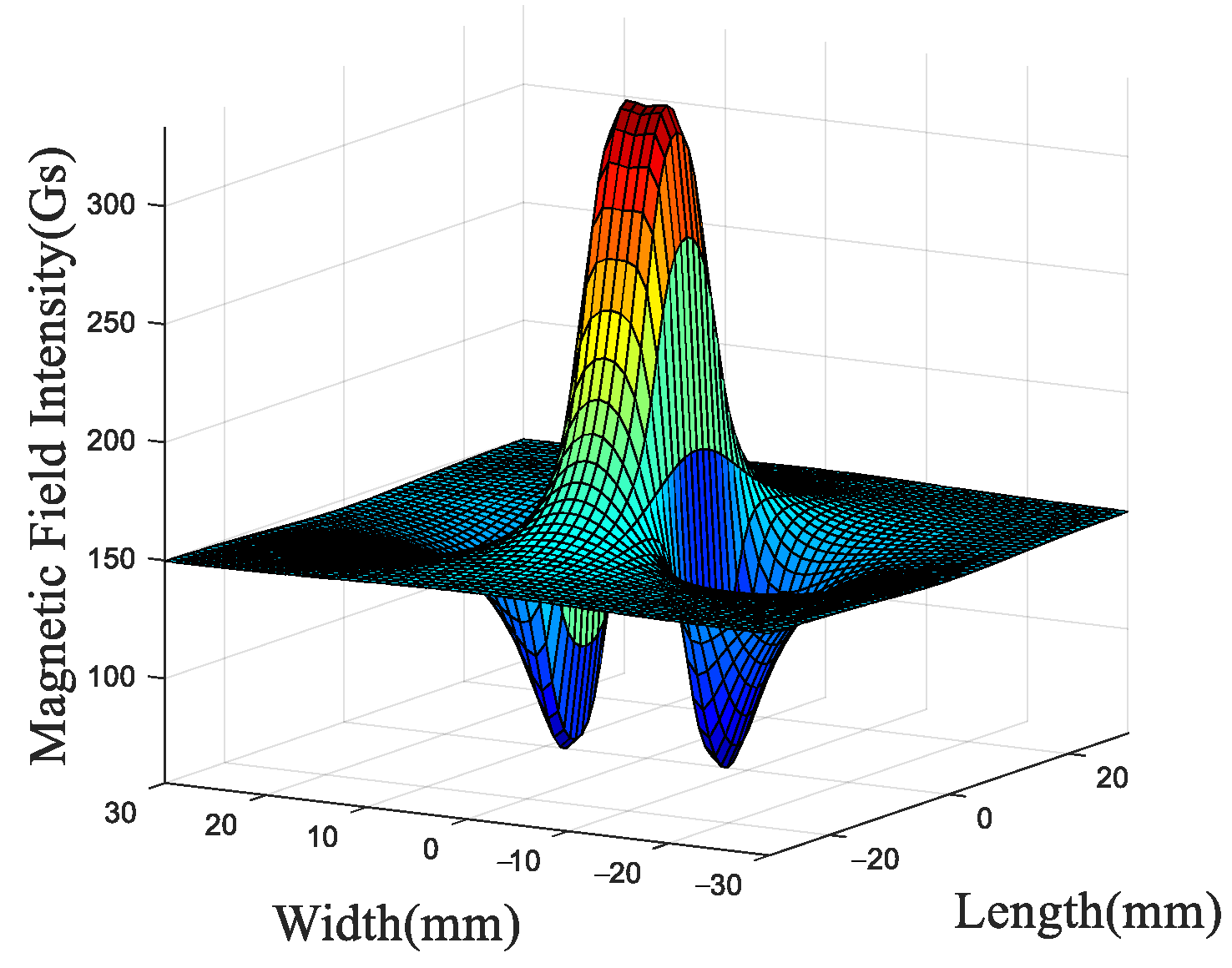
2.2. MFL Signal of the Defect
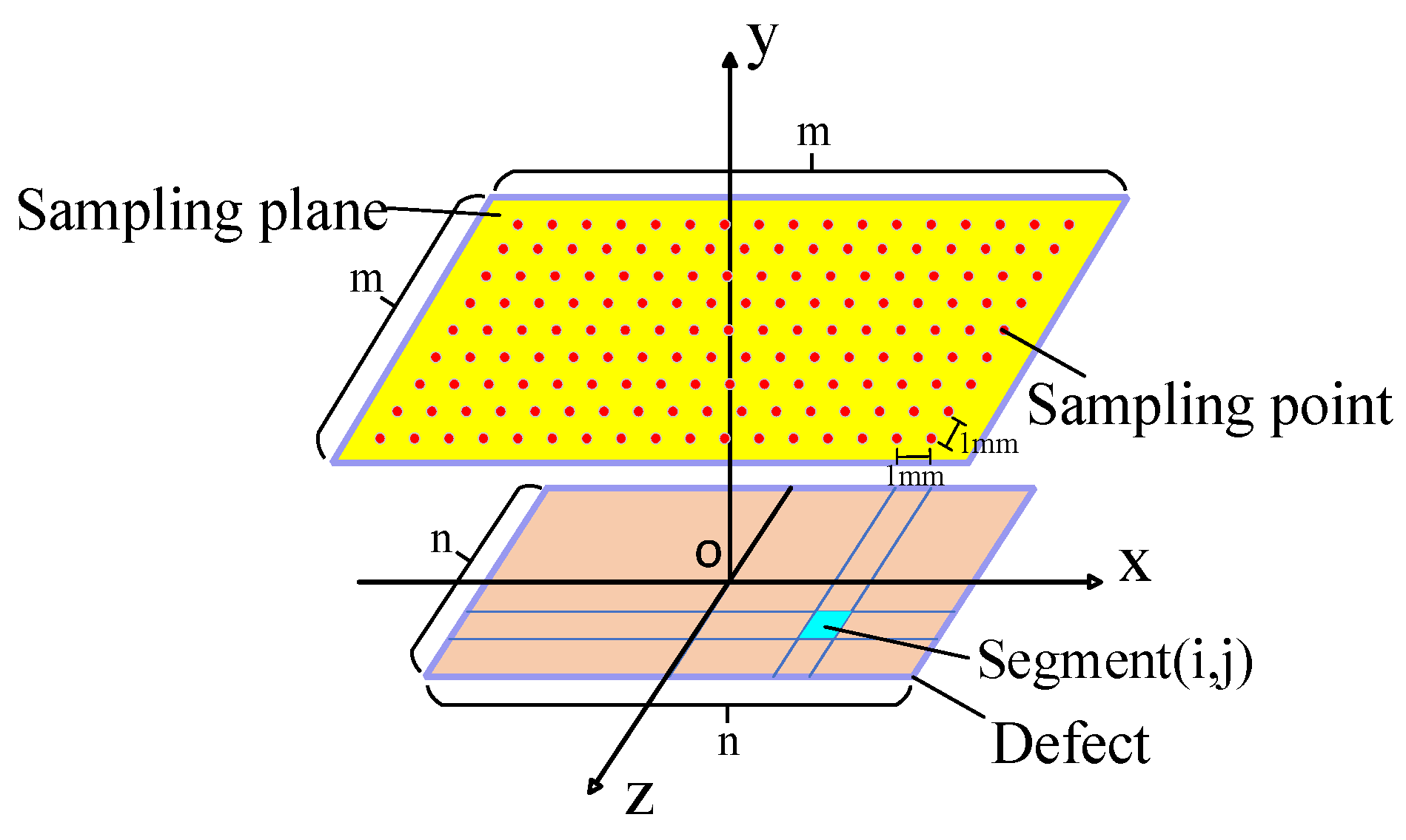
2.3. Forward Modeling and Profile Reconstruction
3. Inversion Algorithm
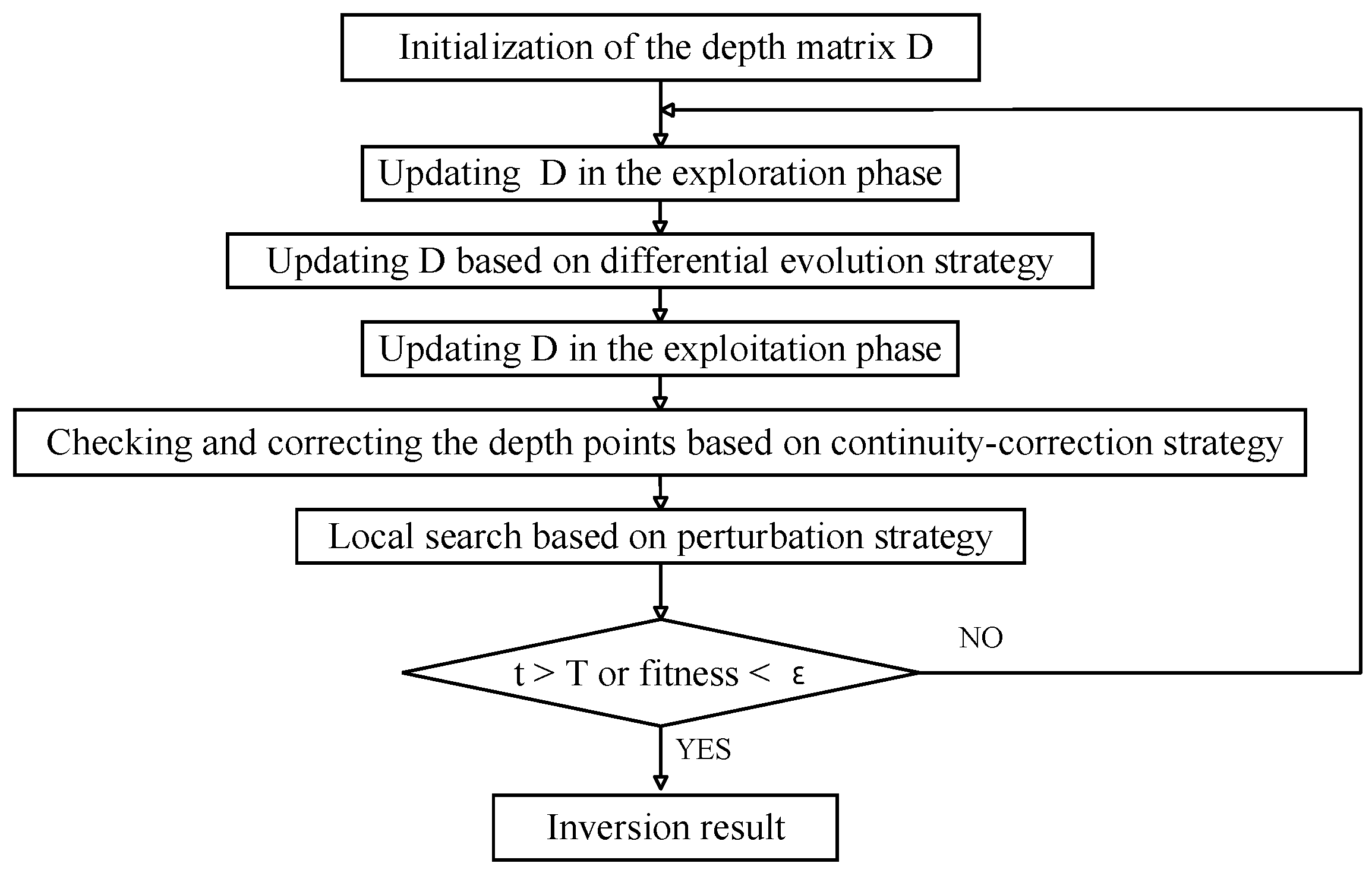
3.1. Inversion Based on CO-DE-SBOA
3.2. Continuity Correction (CO) Strategy
3.3. Secretary Bird Optimization Algorithm (SBOA)
3.4. Differential Evolution and Perturbation
3.5. Parameter Analysis
4. Experiment and Analysis
4.1. Experimental Conditions
4.2. Evaluation Metrics
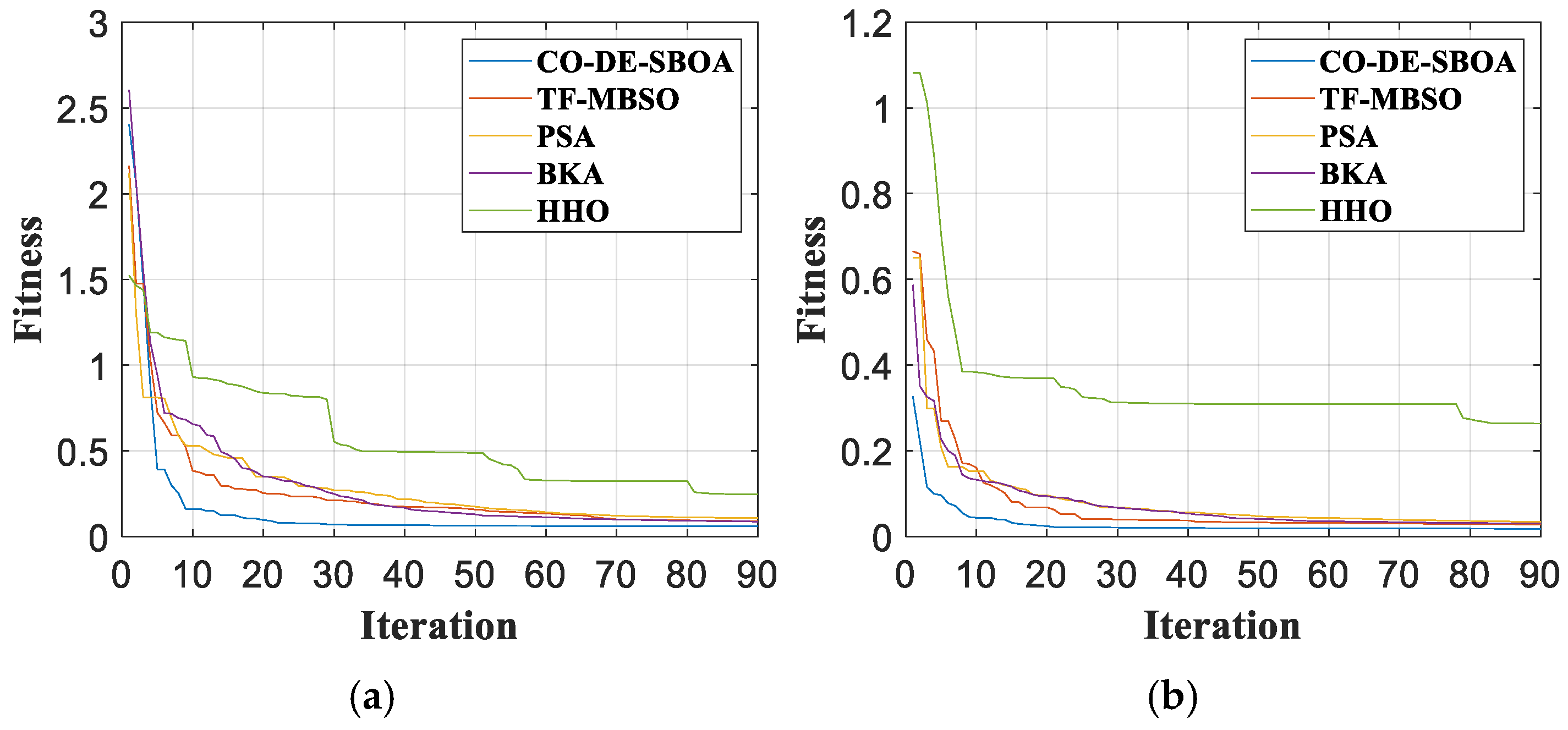
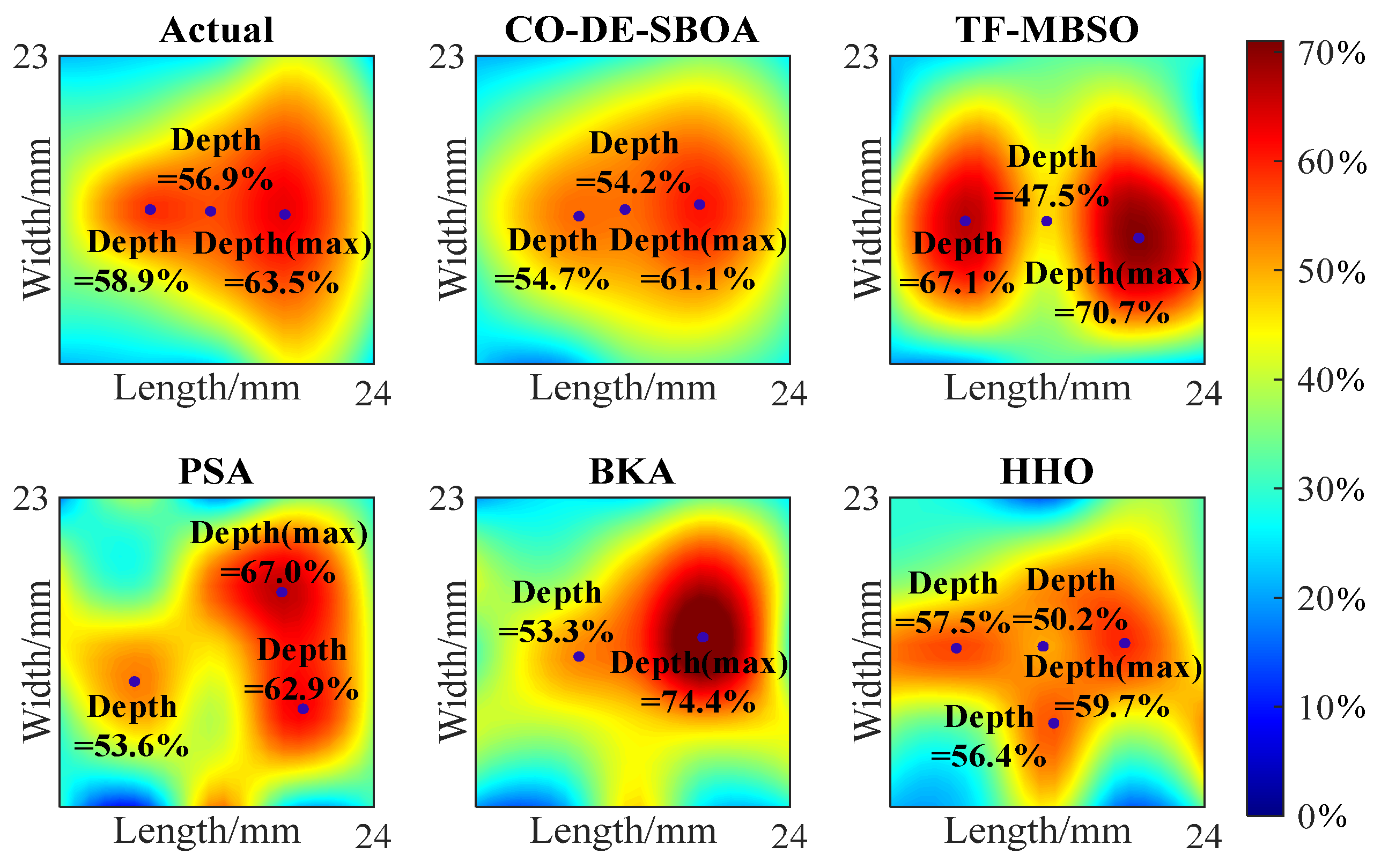
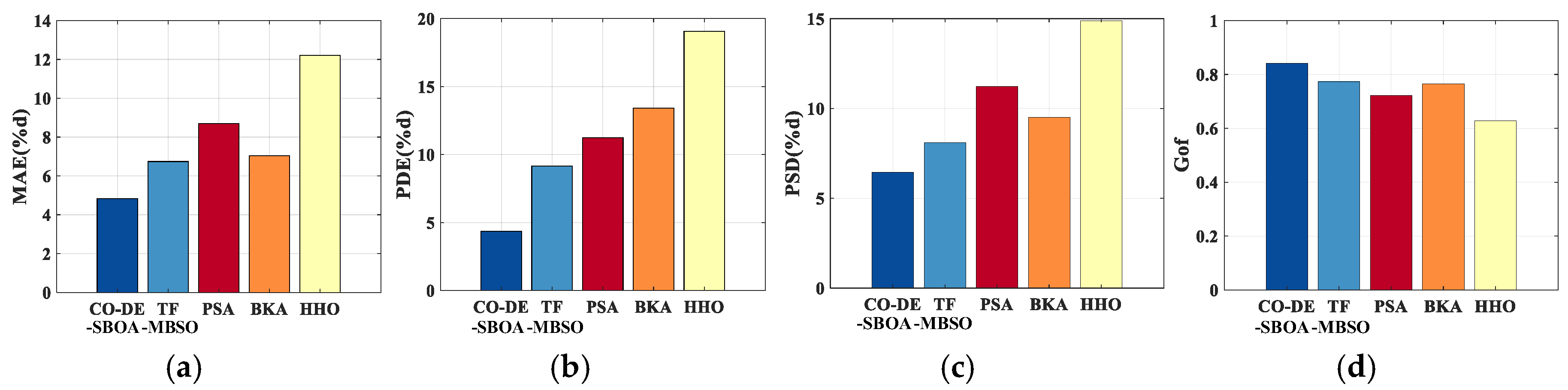
4.3. Accuracy Experiment
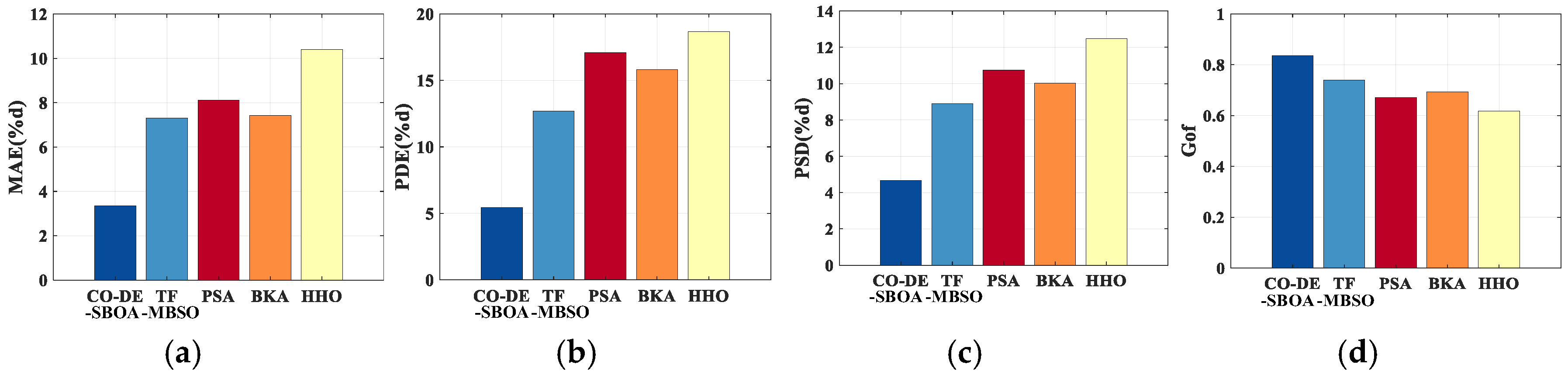
4.4. Robustness Experiment
4.5. Ablation Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Matrix of measured MFL signals | |
| Matrix of inverted MFL signals | |
| Depth value of depth point (i,j) | |
| Magnetic field distribution corresponding to depth point (i,j) | |
| Matrix of depth values | |
| n | Number of divisions per dimension of the defect |
| m | Number of sampling points along each dimension |
| Set of depth values of the depth points adjacent to depth point (i,j) | |
| Depth value of the depth point adjacent to depth point (i,j) | |
| Maximum allowable value of the continuity correction strategy | |
| Maximum variation in the continuity correction strategy | |
| Maximum number of iterations | |
| N | Number of secretary bird individuals |
| Upper bound of the initial solution | |
| Lower bound of the initial solution | |
| d | Thickness of the pipe wall |
| Dim | Dimension of the solution |
| s | Parameter related to Lévy flight |
| Parameter related to Lévy flight | |
| F | Adaptive mutant factor |
| Variation value of the dynamic mutation parameter | |
| Reference value of the dynamic mutation parameter | |
| Static mutation parameter | |
| Crossover rate | |
| p | Perturbation rate |
| Iteration stopping threshold | |
| Number of depth points in each defect | |
| Number of inversion experiments conducted for each defect | |
| Each error metric | |
| Average value of the error metric |
References
- Lu, S.; Zhou, T.; Wang, C.; Lin, Z.; Yi, G. An internal detector positioning method in oil pipelines using vibration signal. IEEE Sens. J. 2023, 23, 13411–13421. [Google Scholar] [CrossRef]
- Ma, Q.; Tian, G.; Zeng, Y.; Li, R.; Song, H.; Wang, Z.; Gao, B.; Zeng, K. Pipeline In-Line Inspection Method, Instrumentation and Data Management. Sensors 2021, 21, 3862. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Zhang, C.; Li, R.; Cai, M.; Jia, G. Theory and Application of Magnetic Flux Leakage Pipeline Detection. Sensors 2015, 15, 31036–31055. [Google Scholar] [CrossRef]
- Yu, G.; Liu, J.; Zhang, H.; Liu, C. An iterative stacking method for pipeline defect inversion with complex MFL signals. IEEE Trans. Instrum. Meas. 2019, 69, 3780–3788. [Google Scholar] [CrossRef]
- Wu, Z.; Deng, Y.; Liu, J.; Wang, L. A reinforcement learning-based reconstruction method for complex defect profiles in MFL inspection. IEEE Trans. Instrum. Meas. 2021, 70, 2506010. [Google Scholar] [CrossRef]
- Liu, J.; Shen, X.; Wang, J.; Jiang, L.; Zhang, H. An intelligent defect detection approach based on cascade attention network under complex magnetic flux leakage signals. IEEE Trans. Ind. Electron. 2022, 70, 7417–7427. [Google Scholar] [CrossRef]
- Yuksel, V.; Tetik, Y.E.; Basturk, M.O.; Recepoglu, O.; Gokce, K.; Cimen, M.A. A novel cascaded deep learning model for the detection and quantification of defects in pipelines via magnetic flux leakage signals. IEEE Trans. Instrum. Meas. 2023, 72, 2512709. [Google Scholar] [CrossRef]
- Khodayari-Rostamabad, A.; Reilly, J.P.; Nikolova, N.K.; Hare, J.R.; Pasha, S. Machine Learning Techniques for the Analysis of Magnetic Flux Leakage Images in Pipeline Inspection. IEEE Trans. Magn. 2009, 45, 3073–3084. [Google Scholar] [CrossRef]
- Pasadas, D.J.; Baskaran, P.; Ramos, H.G.; Ribeiro, A.L. Detection and Classification of Defects Using ECT and Multi-Level SVM Model. IEEE Sens. J. 2020, 20, 2329–2338. [Google Scholar] [CrossRef]
- Feng, B.; Wu, J.; Tu, H.; Tang, J.; Kang, Y. A Review of Magnetic Flux Leakage Nondestructive Testing. Materials 2022, 15, 7362. [Google Scholar] [CrossRef]
- Zhang, S.; Li, H.; Zhao, C. Magnetic-charge element method for magnetic flux leakage inspection. IEEE Trans. Instrum. Meas. 2022, 71, 6007910. [Google Scholar] [CrossRef]
- Gao, P.; Geng, H.; Yang, L.; Su, Y. Research on the Forward Solving Method of Defect Leakage Signal Based on the Non-Uniform Magnetic Charge Model. Sensors 2023, 23, 6221. [Google Scholar] [CrossRef]
- Liu, B.; Lian, Z.; Liu, T.; Wu, Z.; Ge, Q. Study of MFL signal identification in pipelines based on non-uniform magnetic charge distribution patterns. Meas. Sci. Technol. 2023, 34, 044003. [Google Scholar] [CrossRef]
- Amineh, R.K.; Koziel, S.; Nikolova, N.K.; Bandler, J.W.; Reilly, J.P. A Space Mapping Methodology for Defect Characterization From Magnetic Flux Leakage Measurements. IEEE Trans. Magn. 2008, 44, 2058–2065. [Google Scholar] [CrossRef]
- Priewald, R.H.; Magele, C.; Ledger, P.D.; Pearson, N.R.; Mason, J.S.D. Fast Magnetic Flux Leakage Signal Inversion for the Reconstruction of Arbitrary Defect Profiles in Steel Using Finite Elements. IEEE Trans. Magn. 2013, 49, 506–516. [Google Scholar] [CrossRef]
- Han, W.; Xu, J.; Zhou, M.; Tian, G.; Wang, P.; Shen, X.; Hou, E. Cuckoo search and particle filter-based inversing approach to estimating defects via magnetic flux leakage signals. IEEE Trans. Magn. 2015, 52, 6200511. [Google Scholar] [CrossRef]
- Lu, S.; Feng, J.; Li, F.; Liu, J. Precise inversion for the reconstruction of arbitrary defect profiles considering velocity effect in magnetic flux leakage testing. IEEE Trans. Magn. 2016, 53, 6201012. [Google Scholar] [CrossRef]
- Lu, S.; Liu, J.; Wu, J.; Fu, X. A Fast Globally Convergent Particle Swarm Optimization for Defect Profile Inversion Using MFL Detector. Machines 2022, 10, 1091. [Google Scholar] [CrossRef]
- Li, F.; Feng, J.; Zhang, H.; Liu, J.; Lu, S.; Ma, D. Quick reconstruction of arbitrary pipeline defect profiles from MFL measurements employing modified harmony search algorithm. IEEE Trans. Instrum. Meas. 2018, 67, 2200–2213. [Google Scholar] [CrossRef]
- Hou, D.; Lu, S.; Yi, G.; Qiu, J.; Liu, J. A Target-Focusing Optimization Method for 3D Profile Reconstruction of Defects using MFL Measurements. IEEE Trans. Instrum. Meas. 2023, 21, 2521911. [Google Scholar]
- Zhao, J.; Zhang, M.; Zhao, B.; Du, X.; Zhang, H.; Shang, L.; Wang, C. Integrated Reactive Power Optimisation for Power Grids Containing Large-Scale Wind Power Based on Improved HHO Algorithm. Sustainability 2023, 15, 12962. [Google Scholar] [CrossRef]
- Li, B.; Yang, J. A modified whale optimization algorithm for electromagnetic inverse problems. In Proceedings of the 2020 IEEE 1st China International Youth Conference on Electrical Engineering (CIYCEE), Wuhan, China, 1–4 November 2020; pp. 1–7. [Google Scholar]
- Gao, Y. PID-based search algorithm: A novel metaheuristic algorithm based on PID algorithm. Expert Syst. Appl. 2020, 232, 120886. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, D.; Chen, J.; He, L. Secretary bird optimization algorithm: A new metaheuristic for solving global optimization problems. Artif. Intell. Rev 2024, 57, 123. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.C.; Hu, X.X.; Qiu, L.; Zang, H.F. Black-winged kite algorithm: A nature-inspired meta-heuristic for solving benchmark functions and engineering problems. Artif. Intell. Rev. 2024, 57, 98. [Google Scholar] [CrossRef]
- Pipeline Operators Forum. POF 100: Specifications and Requirements for In-Line Inspection of Pipelines. 2021. Available online: https://pipelineoperators.org/documents (accessed on 18 May 2025).
- Banaszek, A.; Łosiewicz, Z.; Jurczak, W. Corrosion influence on safety of hydraulic pipelines installed on decks of contemporary product and chemical tankers. Pol. Marit. Res. 2018, 25, 71–77. [Google Scholar] [CrossRef]






| Name | Value | Name | Value | Name | Value | Name | Value |
|---|---|---|---|---|---|---|---|
| s | 0.01 | 1.5 | 0.5 | 0.5 | |||
| 0.1 | 0.9 | 0.1 | 0.5 | ||||
| 0.8 | p | 0.1 | 0.2 mm | d | 12.7 mm | ||
| N | 100 | T | 90 | 0.016 |
| Method | ||||
|---|---|---|---|---|
| CO-DE-SBOA | ||||
| TF-MBSO | ||||
| PSA | ||||
| BKA | ||||
| HHO |
| CO-DE-SBOA | TF-MBSO | PSA | BKA | |
|---|---|---|---|---|
| PDE < 10 (%d) | 95% | 84% | 76% | 73% |
| Noise | ||||
|---|---|---|---|---|
| 0% | ||||
| 5% | ||||
| 10% |
| SBOA | Continuity Correction | Differential Evolution | Perturbation | ||||
|---|---|---|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Tang, J.; Duan, Y.; Lu, S.; Wen, H. A 3-D Defect Profile Inversion Method Based on the Continuity Correction Strategy. Machines 2025, 13, 446. https://doi.org/10.3390/machines13060446
Wang C, Tang J, Duan Y, Lu S, Wen H. A 3-D Defect Profile Inversion Method Based on the Continuity Correction Strategy. Machines. 2025; 13(6):446. https://doi.org/10.3390/machines13060446
Chicago/Turabian StyleWang, Chenlin, Jianhua Tang, Yicheng Duan, Senxiang Lu, and Hao Wen. 2025. "A 3-D Defect Profile Inversion Method Based on the Continuity Correction Strategy" Machines 13, no. 6: 446. https://doi.org/10.3390/machines13060446
APA StyleWang, C., Tang, J., Duan, Y., Lu, S., & Wen, H. (2025). A 3-D Defect Profile Inversion Method Based on the Continuity Correction Strategy. Machines, 13(6), 446. https://doi.org/10.3390/machines13060446






