Multi-Scale Residual Convolutional Neural Network with Hybrid Attention for Bearing Fault Detection

Abstract

This paper proposes an advanced deep convolutional neural network model for motor bearing fault detection that was designed to overcome the limitations of traditional models in feature extraction, accuracy, and generalization under complex operating conditions. The model combines multi-scale residuals, hybrid attention mechanisms, and dual global pooling to enhance the performance. Convolutional layers efficiently extract features, while hybrid attention mechanisms strengthen the feature representation. The multi-scale residual network structure captures features at various scales, and fault classification is performed using global average and max pooling. The model was trained with the Adam optimizer and sparse categorical cross-entropy loss by incorporating a learning rate decay mechanism to refine the training process. Experiments on the University of Paderborn bearing dataset across four conditions showed that the model had superior performance, where it achieved a diagnostic accuracy of 99.7%, which surpassed traditional models, like AMCNN, LeNet5, and AlexNet. Comparative experiments on rolling bearing vibration and motor current datasets across four bearing conditions highlighted the model’s effectiveness and broad applicability in motor fault detection. Its robust feature extraction and classification capabilities make it a reliable solution for motor bearing fault diagnosis, with significant potential for real-world applications. This makes it a reliable solution for motor bearing fault diagnosis with significant potential for practical applications.

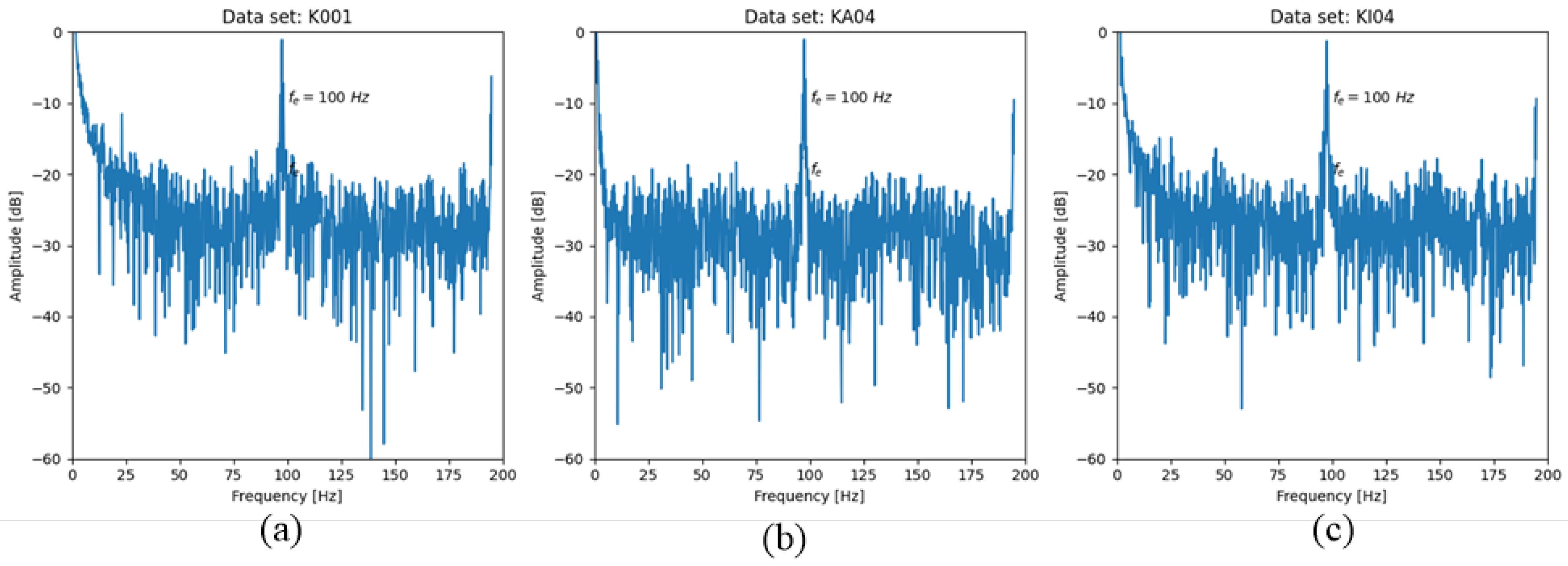
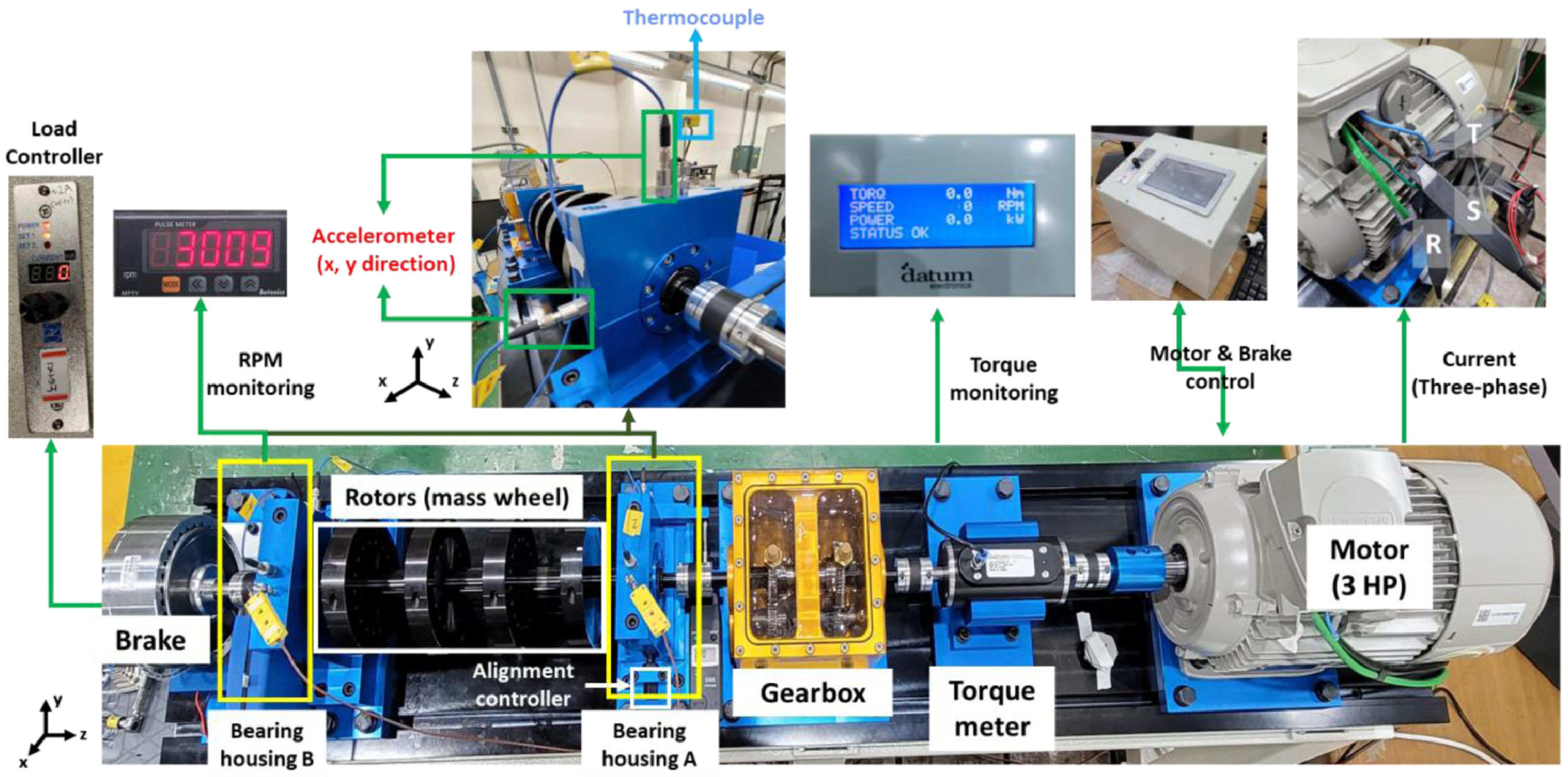
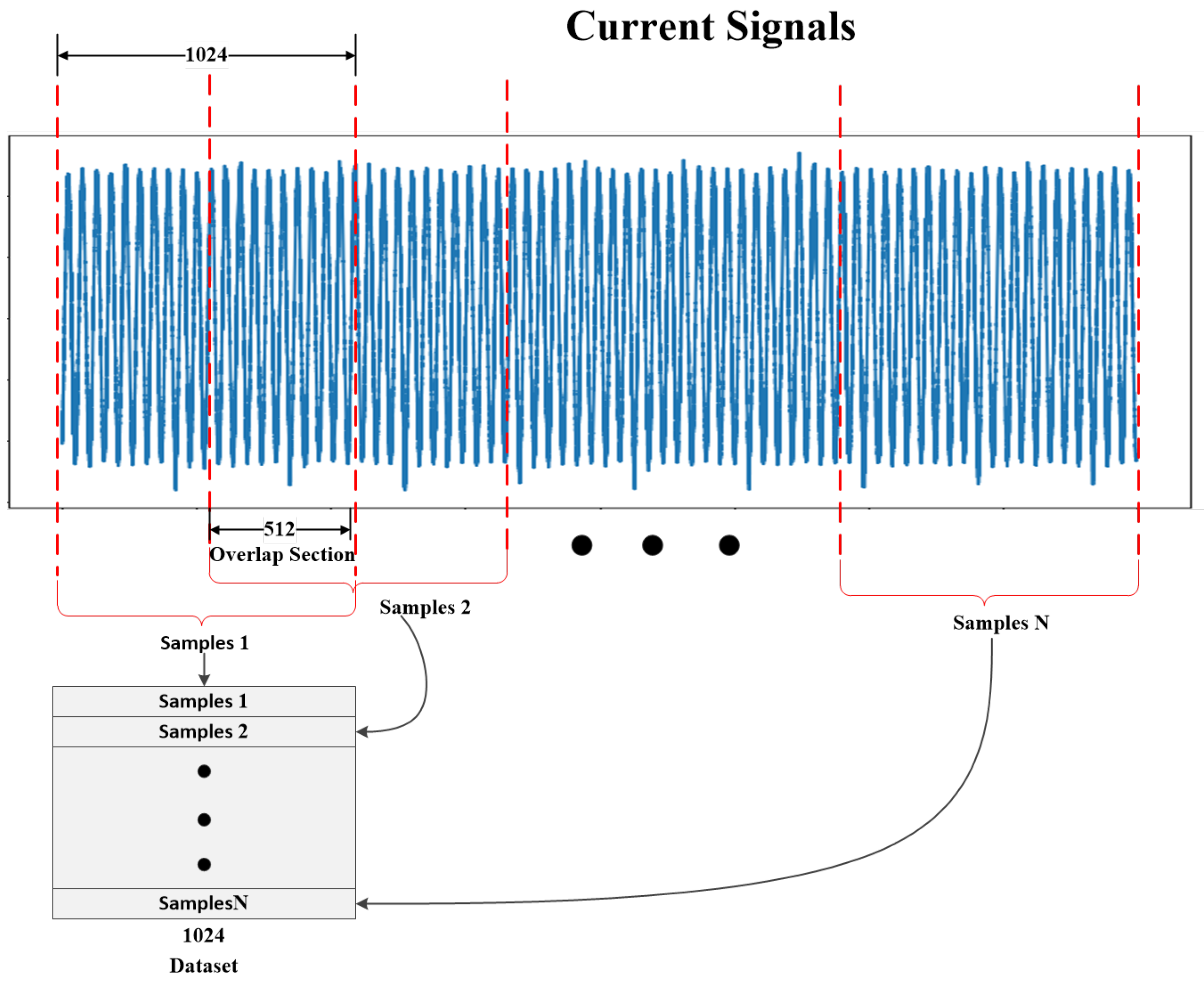
1. Introduction

As technology advances rapidly, motors have become indispensable in industrial production, serving as the backbone of modern industrial systems [1,2,3]. However, motors often operate in harsh environments and complex conditions, which can lead to issues such as fatigue damage, overheating, and insulation material degradation. These problems can cause equipment failure or even shutdowns, posing significant threats to the safe and stable operation of enterprises [4,5,6]. Therefore, implementing condition monitoring and precise fault diagnosis for motor bearings has emerged as a critical challenge in the industrial sector [7,8].

Traditional motor fault diagnosis techniques primarily rely on collecting signals, such as the current and vibration during motor operation, combined with advanced signal processing algorithms to detect faults [9]. To avoid the need for additional sensors and the installation space required by conventional vibration-signal-based methods, this study utilized current signals for feature extraction and fault diagnosis. Common current signal analysis methods include fast Fourier transform (FFT) [10], wavelet transform (WT) [11], empirical mode decomposition (EMD) [12], and variational mode decomposition (VMD) [13]. For instance, Merabet [14] employed the FFT for stator current spectral analysis, defining residual indicators to visualize changes in electrical and mechanical quantities, thereby enabling the real-time health monitoring and diagnosis of motor systems. Lu [15] proposed a gearbox fault diagnosis method based on motor current signature analysis, using variational mode decomposition and genetic algorithms to remove irrelevant information and wavelet transforms to extract fault features while suppressing noise, achieving effective gearbox fault diagnosis. Wu [16] introduced a bearing fault diagnosis method for induction motors, processing stator current signals with wavelet denoising and quasi-synchronous sampling to extract harmonic features, and mapping these features to fault labels using Random Vector Functional Link networks for an accurate distinction between healthy and faulty bearings. Jin [17], based on the dynamics and equivalent circuit model of a V-shaped ultrasonic motor (VSUM), investigated the relationship between real-time output characteristics and input signals by considering the nonlinear effects of preload variations, and established a current prediction model to simplify fault diagnosis. However, manually extracted fault features are often insufficient, with subtle fault characteristics easily overlooked or masked by noise.

With the development of artificial intelligence, intelligent fault diagnosis methods have gained significant attention, primarily categorized into machine learning [18] and deep learning approaches [19]. Machine learning-based methods rely on traditional signal-processing techniques for feature extraction, followed by classification using algorithms such as Support Vector Machines (SVMs), Random Forests, Principal Component Analysis (PCA), and Enhanced Principal Component Analysis (EPCA). For example, Santer [20] utilized current and vibration signals, proposing feature extraction methods based on envelope analysis and a wavelet packet transform, combined with a SVM for bearing fault detection in motors. Zhang [21] introduced a Harmonic Drive (HD) fault diagnosis method, eliminating speed effects through Equal Angular Displacement Signal Segmentation (EADSS) and optimizing weight matrices with an improved NAP method and cosine distance. Subsequently, PCA was used for feature extraction, followed by fault diagnosis with a Backpropagation Neural Network (BPNN). Liao [22] proposed a motor current signature analysis (MCSA) method based on Enhanced Principal Component Analysis (EPCA), employing power frequency filtering to reduce interference, enhance harmonic features, and extract fault characteristics for effective diagnosis. Nevertheless, machine learning-based methods are cumbersome and lack strong interdependencies between steps, limiting further improvements in diagnostic efficiency [23].

In contrast, deep learning methods can automatically learn features from raw data, significantly reducing the reliance on manual feature extraction and offering new opportunities for fault diagnosis technology. In recent years, CNNs have been increasingly applied to motor fault detection [24,25,26]. Some researchers have proposed models combining 1D CNN and Recurrent Neural Networks (RNNs) for induction motor fault detection, incorporating multi-head mechanisms to enhance the feature attention, simplifying the diagnostic process, and improving the accuracy [27]. Morales-Perez, Carlos [28] developed an ITSC fault diagnosis method based on current signal imaging and CNNs, highlighting fault spectrum features and converting them into images for CNN input, achieving high-precision fault identification with a test accuracy of 98.62%. Liu [29] introduced a fault diagnosis model combining CNN and Bidirectional Long Short-Term Memory (BiLSTM) networks. By extracting frequency-domain features from three-phase currents using CEEMD and leveraging CNN-BiLSTM, they addressed open-circuit fault detection and classification in permanent magnet synchronous motor inverters. Du [30] proposed a hybrid CNN model with multi-scale convolutional kernels for feature extraction and dynamic weighted layers for feature fusion. Experiments demonstrated its superiority over existing CNN models in bearing and gearbox fault diagnosis for motors.

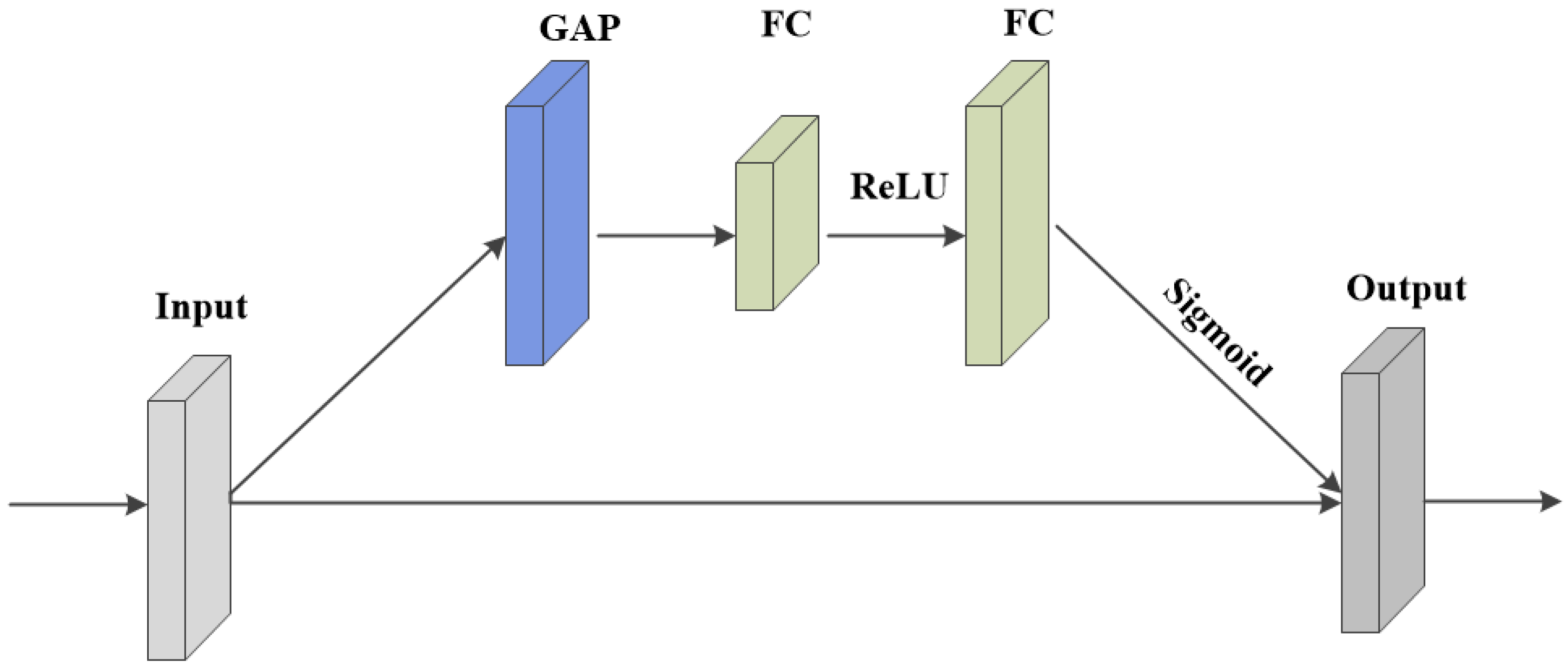
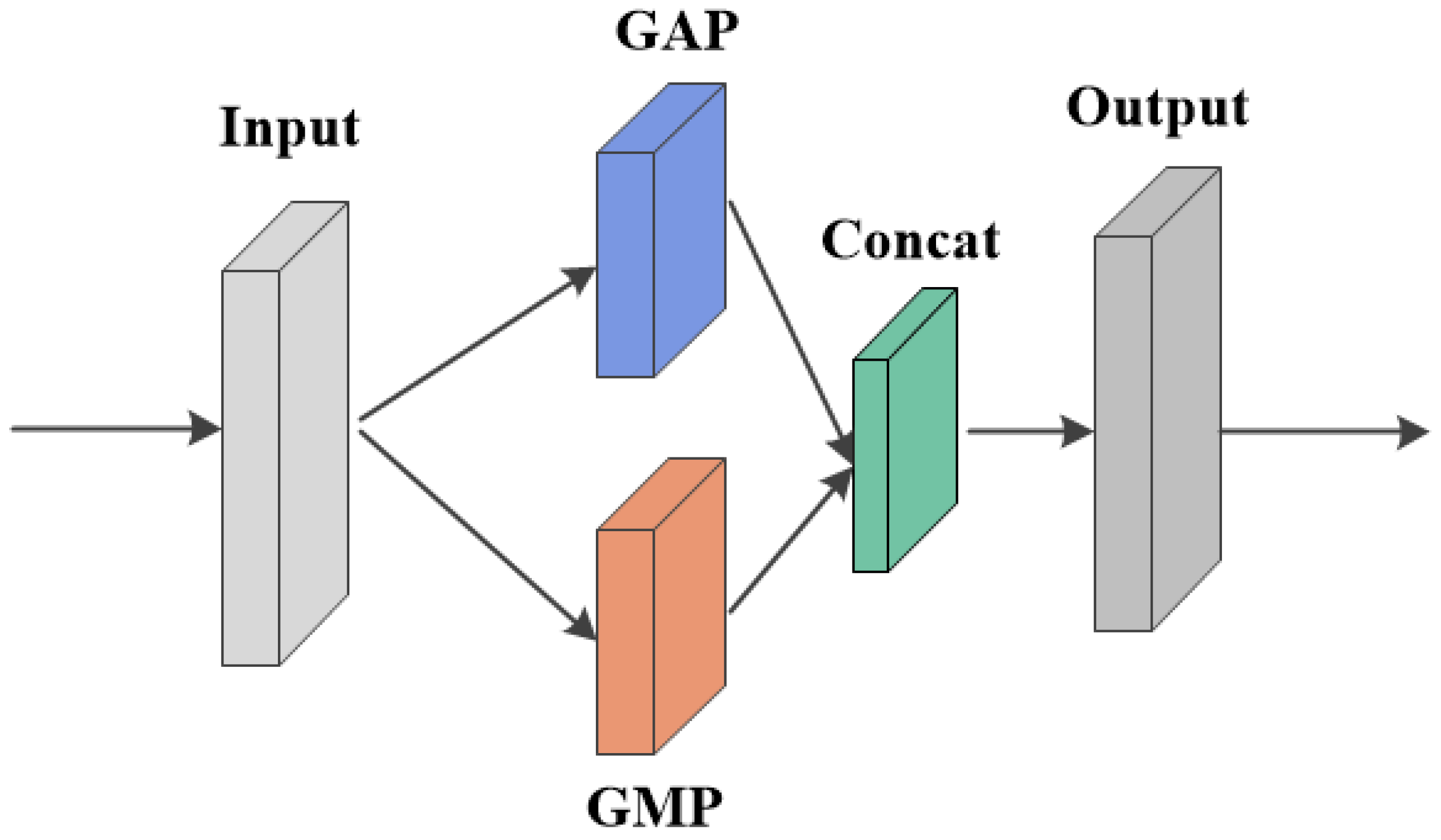
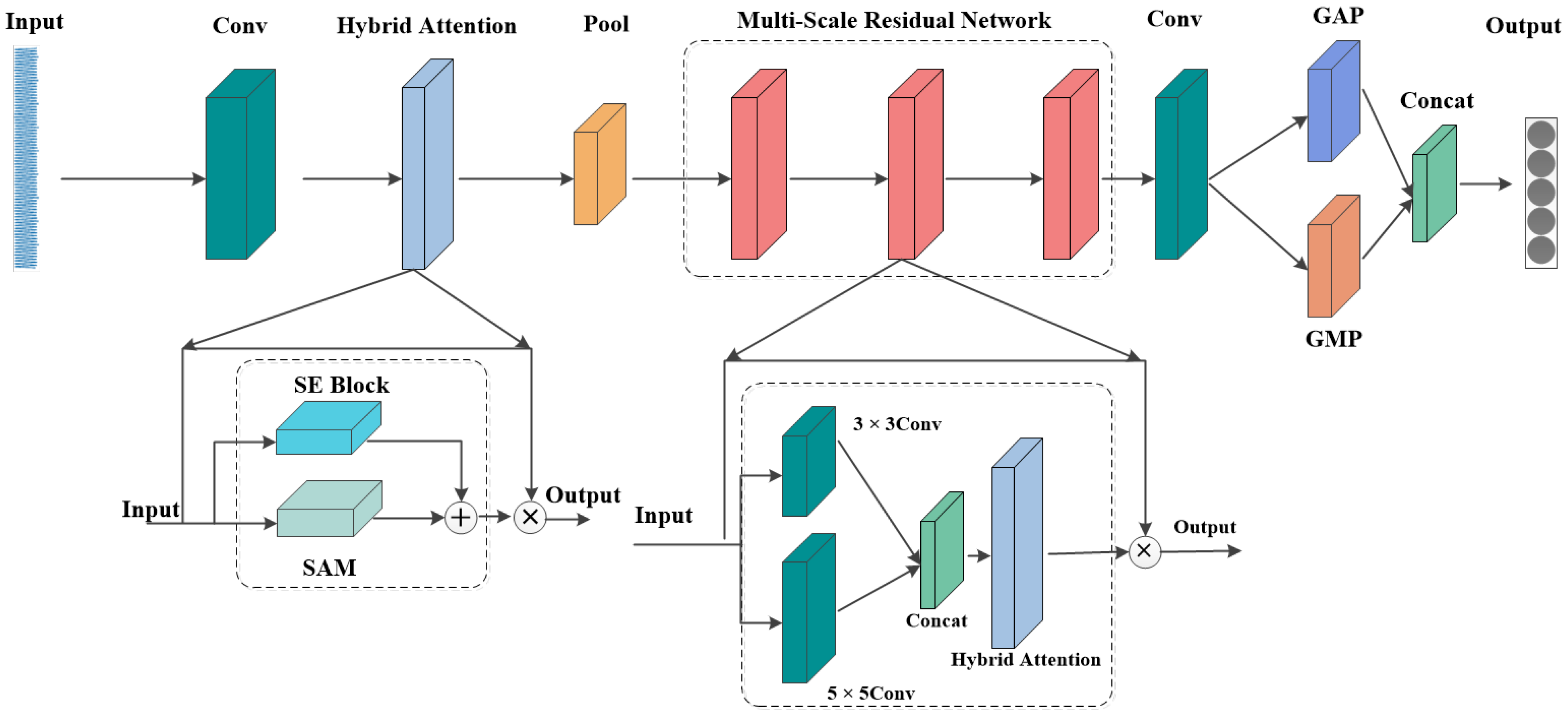
In summary, while CNNs are increasingly being utilized for motor bearing fault diagnosis, they frequently encounter challenges, such as limited feature extraction in complex conditions, insufficient diagnostic accuracy, and inadequate generalization capabilities. To address these limitations, this paper innovatively proposes a multi-scale residual CNN model specifically designed for motor bearing fault detection. The model integrates a hybrid attention mechanism that combines a squeeze and excitation (SE) block and spatial attention mechanism (SAM), thereby significantly enhancing the feature representation. By synergistically combining the hybrid attention mechanism with multi-scale residual modules, the model effectively captures and amplifies both local and global features. Additionally, the integration of dual global pooling further refines the feature extraction process. Empirical validation using publicly available datasets demonstrates that these enhancements enable the model to achieve a high diagnostic accuracy and robust generalization.

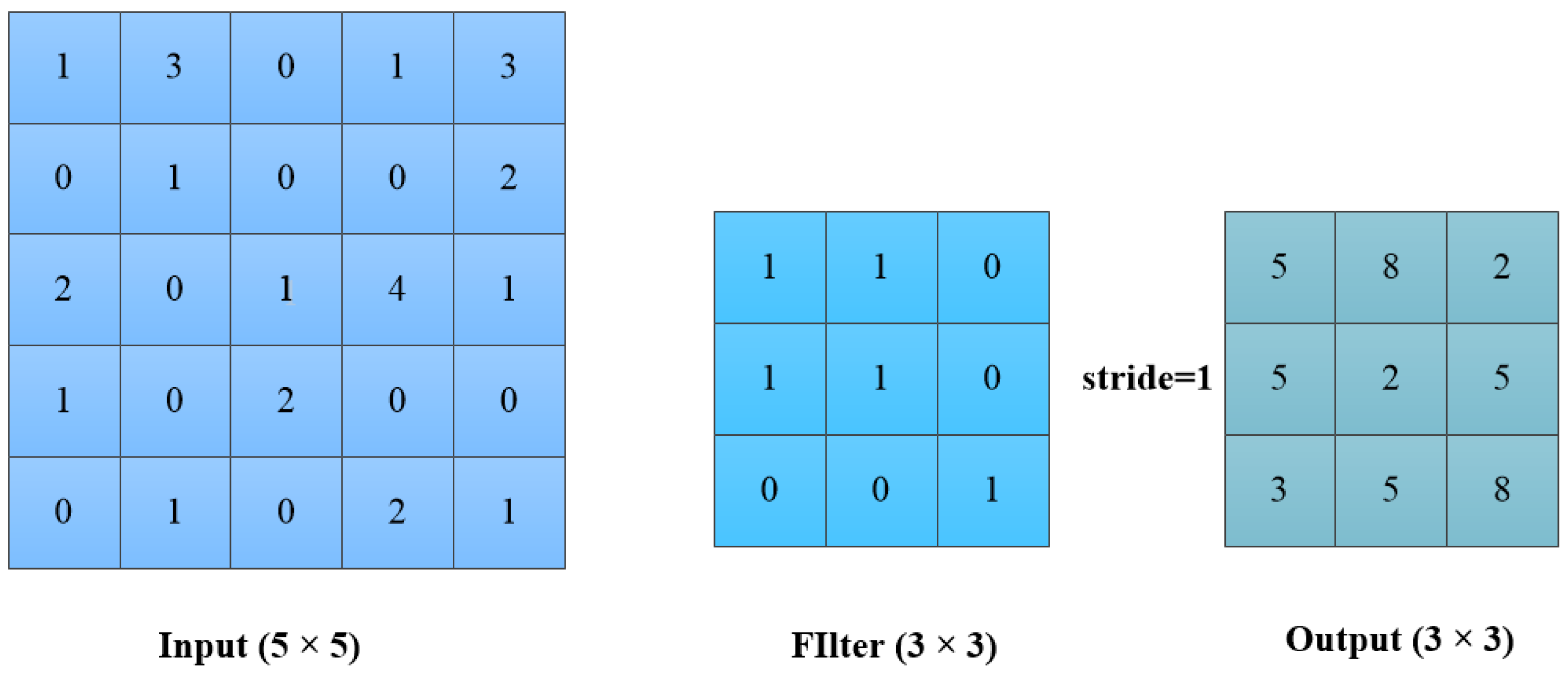
The rest of this article is organized as follows: Section 2 presents an overview of CNN and SE modules. Section 3 elaborates on the proposed hybrid attention mechanism, multi-scale residual network, and dual global pooling module. Section 4 introduces the experimental datasets, data preprocessing, and an analysis of how model parameters influenced the performance. Section 5 assesses the model’s performance through comparative and ablation experiments. Finally, Section 6 concludes this paper.

2. Materials

2.1. CNN

Convolutional layers serve as a cornerstone in deep neural networks for feature extraction, leveraging a parameter-sharing local connectivity mechanism. This architecture employs multiple trainable convolutional kernels to facilitate hierarchical feature learning. Each kernel, which is equipped with adjustable weights and bias parameters, functions as a specialized feature detector. During computation, the convolutional kernels traverse the input feature maps in a sliding window fashion, performing weighted summations within a defined receptive field, as shown in Figure 1.

2.2. SE Block

The SE Block [31] adaptively learns weights for each channel. This adaptive recalibration of feature channels enhances the discriminative power of the features and the expressive power of neural networks, thereby improving the model performance. The structure of the SE module is shown in Figure 2.

The module primarily consists of two parts: squeeze and excitation. In the squeeze part, global average pooling is employed to compress the feature map into a feature vector, as shown in Equation (1):

$$z=GAP\left(y\right)$$

(1)

In this equation, z denotes the feature vector obtained from the global average pooling, while y represents the input feature map. In the excitation part, a combination of two fully connected layers with nonlinear activation functions is used to learn the weight for each channel. Specifically, the first fully connected layer uses the ReLU function as the activation function, and the second fully connected layer employs the Sigmoid activation function, as shown in Equation (2):

$$s=\sigma \left(W_2\mathrm{ReLU}\left(W_{1}z\right)\right)$$

(2)

In this equation, s denotes the output after two fully connected layers, $W_1$ represents the weight parameters of the first fully connected layer, and $W_2$ represents the weight parameters of the second fully connected layer.

3. Method

3.1. Hybrid Attention

This paper proposes a hybrid attention mechanism based on SE–spatial dual-path processing. By parallelly processing the channel and spatial dimensions of the feature maps, this mechanism comprehensively extracts critical information. It optimizes both dimensions, enabling the model to focus on key features, enhancing the adaptability to various targets and scenarios, and improving the discriminability of low-salience small targets, thereby significantly boosting the overall model performance. The structure is shown in Figure 3.

The SE attention mechanism uses global average pooling to extract channel-wise statistics and generates channel weights through two fully connected layers, emphasizing important feature channels. By learning channel correlations via global average pooling and fully connected layers, it suppresses irrelevant features and enhances critical ones. The spatial attention mechanism employs a single-channel convolutional kernel to learn spatial correlations. By replicating across the channel dimension, it generates a spatial weight matrix. The mathematical formulation is expressed as shown in Equation (3):

$$SAM\left(x\right)=\mathrm{Repeat}(Con{v}_{1\times 7}\left(x\right),C)$$

(3)

The convolutional layer generates spatial attention weights, which emphasize important time steps in time-series data while suppressing noise and irrelevant information. Finally, by summing the channel and spatial attention weights and multiplying them with the input feature tensor, the model performs a weighted feature adjustment. This process highlights important features and suppresses less important ones.

3.2. Multi-Scale Residual Network

This paper proposes a method of using multi-scale residual block [32] connections with heterogeneous convolutional kernels to collaboratively extract multi-level features from time-series signals. The core design integrates multi-branch convolutions, dynamic feature fusion, and residual optimization. Specifically, parallel 3 × 3 and 5 × 5 convolutional kernels are used to capture local transient and global trend features of current signals, respectively. This multi-scale feature coverage enhances the model’s ability to represent complex fault patterns. Next, an SE–spatial hybrid attention mechanism is introduced to dynamically weight the concatenated heterogeneous features, emphasizing fault-sensitive frequency bands and critical time-domain segments. Finally, the method achieves the dimensionality-adaptive matching of residual paths, which not only addresses the vanishing gradient problem but also effectively prevents feature degradation during deep network training. The structure of the multi-scale residual module is shown in Figure 4.

3.3. Dual Global Pooling Architecture

This paper proposes extracting salient features from input tensors using global average pooling and global max pooling, followed by concatenation to form a multimodal feature representation. The dual global pooling structure is illustrated in Figure 5.

The global average pooling layer calculates the average value of each channel in the temporal dimension, thereby capturing the overall trend of the time-series data. In contrast, the global max pooling layer identifies the peak values of each channel, preserving critical peak information. The mathematical expressions are shown in Equation (4):

$$f_{\mathrm{fina}1}=\mathrm{Concat}(\mathrm{GAP}\left(x\right),\mathrm{GMP}\left(x\right))$$

(4)

Global average pooling reflects the overall feature distribution, while global max pooling captures the abnormal peaks. By concatenating the results of these two pooling operations, the generated feature map contains both the average and maximum feature information, creating a richer and more comprehensive feature description. This multi-level feature fusion strategy not only enhances the model’s ability to handle complex patterns but also improves its generalization ability.

3.4. Motor Bearing Fault Detection Model

In summary, this paper proposes a deep convolutional neural network for motor fault detection tasks. Starting from the input layer, the model incorporates a dynamic convolution block and a hybrid attention mechanism to extract local features and highlight important channels and time steps. It then employs multi-scale residual modules to capture features at different scales, alleviating the vanishing gradient problem. Finally, the model uses a dual global pooling module that combines global average pooling and global max pooling to aggregate features, followed by a classification head with a Softmax activation function to output fault classification results. The model was trained using the Adam optimizer and sparse categorical cross-entropy loss function, with a learning rate decay mechanism to update the learning rate in real time to enhance the model performance. The model architecture is shown in Figure 6.

4. Data Processing and Model Parameter Analysis

4.1. Data Processing

4.1.1. The University of Paderborn Bearing Fault Dataset

This study used two current signals from the bearing dataset [33] of Paderborn University to train the motor bearing fault detection model. As illustrated in Figure 7, the test platform employed an LEM CKSR 15-NP current transducer, which offered an accuracy of 0.8% relative to the IPN = 15 A current, to measure the motor phase currents. These signals were subsequently filtered through a 25 kHz low-pass filter and digitized at a 64 kHz sampling rate. Current transducers were chosen over the inverter’s internal ammeters to facilitate convenient external current measurements between the motor and inverter. During each measurement, the key operational parameters—rotational speed, radial force on the test bearing, and load torque—were maintained at constant levels.

Table 1. Different working conditions segmentation [33].

Condition Index	Rotational Speed (rpm)	Torque (Nm)	Radial Force (N)
1	1500	0.7	1000
2	900	0.7	1000
3	1500	0.1	1000
4	1500	0.7	400

details the fixed levels of these parameters. In the baseline configuration (Set no. 0), the test rig operated at n = 1500 rpm, M = 0.7 Nm, and F = 1000 N. Three additional configurations (Set nos. 1–3) individually reduced these parameters to n = 900 rpm, M = 0.1 Nm, and F = 400 N. For each configuration, 20 measurements that lasted 4 s each were recorded, with the temperature maintained at approximately 45–50 °C. Fault simulation experiments were conducted on 32 SKF6203 bearings across four operational conditions, including inner race faults, outer race faults, and healthy states, with each condition further divided into two severity levels. As depicted in Figure 8, the fast Fourier transform (FFT) of the motor current signals exhibited characteristic peaks at the fault frequency $f_e=100\mathrm{Hz}$ across different datasets, such as K001 (healthy bearing), KA04 (outer race fault), and KI04 (inner race fault). These spectral features were vital for distinguishing different fault types and their severity levels. This research evaluated the model’s performance using four naturally accelerated degraded bearings and one healthy bearing.

Table 2. Fault load information under different working conditions [33].

Dataset Index	Damage	Fault Type	Fault Severity	Label
K001	None	None	None	0
KA04	Fatigue pitting	Outer fault	1	1
KA16	Fatigue pitting	Outer fault	2	2
KI04	Fatigue pitting	Inner fault	1	3
KI16	Fatigue pitting	Inner fault	2	4

lists the fault load information under various working conditions. All bearings exhibited fatigue pitting as the damage formed, which covered two severity levels of outer and inner race faults. Consequently, each working condition comprised four fault categories and one healthy state.

4.1.2. Vibration and Motor Current Dataset of Rolling Element Bearing

To assess the model’s generalization capability in algorithm comparison experiments, this study utilized a dataset [34] comprising vibration and current signals of ball bearings with various fault types (inner ring, outer ring, and ball faults) across different motor speeds (680 rpm and 2460 rpm). As depicted in Figure 9, the experimental setup involved four PCB352C34 accelerometers positioned in the X- and Y-directions of bearing boxes A and B for the vibration data collection. Three-phase current data were acquired via three HIOKI CT6700 current transformers. The Siemens SCADA Mobile 5PM50 system sampled vibration signals at 25.6 kHz, while the NI9775 device sampled current signals at 100 kHz. The dataset includes 600 s of constant-speed data and 2100 s of variable-speed data. This study focused on current signals under variable-speed conditions for motor bearing fault detection.

Table 3. Description of the dataset containing vibration and current signals from ball bearings with different fault types [35].

Fault Types	Length (s)	Load (Nm)	Rotating Speed (rpm)	Sampling Rate (kHz)
Normal	2100	0	680–2460	100
Outer	2100	0	680–2460	100
Inner	2100	0	680–2460	100
Ball	2100	0	680–2460	100

details the datasets for different fault conditions, and the current signal frequency spectra are illustrated in Figure 10.

4.1.3. Data Preprocessing

To enhance the model accuracy and stability, each signal segment underwent standardization, as shown in Equation (5), to eliminate the dimensional differences between the features, placing them on the same scale:

$$\tilde{X}={\displaystyle \frac{x-\mu }{\sigma }}$$

(5)

The diagnosis of electric motor faults faces the typical challenge of data imbalance, where normal samples are overly predominant and fault samples are scarce. This distribution imbalance can easily lead to model overfitting to the majority class and make it difficult to effectively identify fault features. To address this, this section employs selective oversampling for data augmentation, as shown in Equation (6):

$$x_i\left[n\right]=x[n+i·(L-D)]$$

(6)

In this equation, $x_i\left[n\right]$ denotes the n-th sample of the i-th signal segment, where i is the segment index, L represents the length of each segment, and D is the number of overlapping samples. Overlapping sampling effectively increases the number of fault samples without additional data acquisition costs, balances the data distribution, and enhances the model’s generalization and detection accuracy.

In summary, the overall data-preprocessing procedure is illustrated in Figure 11. Initially, each signal segment underwent standardization to enhance the model stability. Subsequently, the continuous current signal was divided into multiple fixed-length frames, with each frame containing 1024 data points. Next, an overlapping window of 512 data points was employed for resampling each segment to increase the data diversity. Finally, the dataset was constructed using each frame of data after overlapping the sampling.

4.2. Model Parameter Analysis

4.2.1. Impact of the Number of Convolution Kernels in the First Layer

A CNN extracts multi-dimensional features from input data through multiple convolutional kernels. These kernels progressively capture patterns from simple to complex across layers, yielding richer feature information. In motor fault detection tasks, this architecture extracts fault-related features from motor current signals, serving as inputs to a classifier for accurate motor operation classification. This section examines the impacts of the number of convolutional kernels in the first layer (ranging from 1 to 12) on the fault detection accuracy and error rates (standard deviation) based on 10 repeated trials while keeping other parameters unchanged. The results are shown in Figure 12.

As shown in Figure 12, the number of convolutional kernels in the first layer significantly impacted the model’s performance for motor fault detection. The average accuracy initially rose rapidly and then stabilized as the number of kernels increased from 1 to 12. When the count increased from 1 to 5, the average accuracy increased from 82.37% to 97.07%, indicating an enhanced feature extraction. Beyond eight kernels, the accuracy stabilized near 99.75%, with marginal gains suggesting performance saturation. Increasing the kernels allowed the model to capture more feature dimensions, which improved the fault diagnosis. However, beyond a certain point, further increases yielded limited performance gains while adding computational complexity and resource use.

In summary, the optimal number of convolutional kernels in the first layer was 8, which achieved the highest average accuracy and lowest error. Deviating from this number reduced the accuracy and increased the error and resource consumption. Thus, this section used 8 kernels to construct the first convolutional layer for the motor fault detection.

4.2.2. Impact of the Size of Convolution Kernels in the First Layer

A CNN achieves hierarchical feature extraction through multi-scale convolutional kernel designs. Research indicates that selecting convolutional kernel sizes requires balancing the receptive field and computational efficiency. Larger kernels capture broader contextual information but increase the parameters and computational costs, while smaller kernels, though computationally efficient, may miss global features. This study systematically compared the impacts of the first-layer convolutional kernel sizes (1 × 1, 2 × 2, 3 × 3, 5 × 5, 7 × 7, and 11 × 11) on the fault detection performance for the motor fault diagnosis tasks. The experiments set the number of first-layer kernels to 8 and conducted 10 repeated trials with the other parameters unchanged. The influences of the first-layer kernel size on the model accuracy and error rate (standard deviation) are shown in Figure 13.

As shown in Figure 13, when the first-layer kernel size was set to 1, the model’s fault detection accuracy was only 95.06%, significantly lower than the other sizes. In contrast, a size 3 kernel achieved a markedly higher accuracy. Kernels of sizes 2, 5, and 7 yielded close accuracies (98.90%, 99.18%, 99.01%) and similar error rates. At size 9, the accuracy slightly dropped but the error rate reduced, which placed it second only to size 3. However, a size 11 kernel led to a significant accuracy drop and a higher error rate.

In summary, considering the accuracy, error rate, and the increased parameters and computations from larger kernels, this study selected a first-layer kernel size of 3 to construct the network model.

4.2.3. Impact of Batch Size

A CNN utilizes the backpropagation algorithm to update network weights. Different batch sizes impact the model performance in motor fault detection. Smaller batches, with higher gradient noise, can enhance the generalization and prevent overfitting. They allow the model to adapt to diverse data distributions, improving the detection of rare fault patterns. Conversely, larger batches offer more accurate gradient directions but may cause overfitting to training data, reducing the test performance.

This section explores how varying the batch sizes (from 4 to 64) affects the fault detection accuracy and error rates. The experiments used 8 first-layer convolutional kernels of size 3, with 10 repeated trials, while keeping the other parameters constant. The results are shown in Figure 14.

As shown in Figure 14, the model achieved the highest test accuracy of 99.65% with the smallest error when the batch size was 8. As the batch size increased from 16 to 48, the training accuracy decreased. Notably, when the batch size was 32, the error rate peaked significantly compared with the other batch sizes. Even though the model’s fault detection accuracy slightly recovered and the error reduced when the batch size was increased to 32, it still underperformed compared with smaller batch sizes in terms of the accuracy and error rate.

In summary, the training batch size had a significant impact on the model’s performance in the motor fault detection. A batch size of 8 was optimal, as it allowed the model to better adapt to different fault data types, which enhanced its ability to detect rare fault patterns. Therefore, this study selected a batch size of 8 for training the network model.

4.2.4. Impact of the Number of Multi-Scale Residual Networks

This section evaluates the impact of the number of multi-scale residual module layers on the model accuracy. Specifically, it assesses how varying the number of layers from 1 to 6 influenced the accuracy and error rates (standard deviation) based on 10 experimental trials. The first-layer convolutional kernel count and size were set to 8 and 3, respectively, with a batch size of 8, while the other parameters remained constant. The results, presented in Figure 15, revealed that the optimal balance between the accuracy and error rate was achieved with three layers of multi-scale residual modules. This configuration was thus selected for constructing the motor fault detection model.

As shown in Figure 15, the number of multi-scale residual module layers significantly impacted the fault detection model’s performance. When the number of layers increased from 1 to 2, the average accuracy rose from 90.65% to 98.56%. At 3 layers, the average accuracy peaked at 99.65% with the lowest error rate. However, at 4 layers, the model’s accuracy dropped markedly with a larger error. At 5 and 6 layers, the accuracies were 98.46% and 99.35%, respectively, with smaller errors, indicating a slight performance improvement and saturation. In summary, the model’s fault detection accuracy and error rate were optimal with three layers of multi-scale residual modules. Increasing the layers beyond this point led to a performance decline and higher computational demands. Thus, this study used 3-layer multi-scale residual modules for the motor fault detection model construction.

5. Experiments and Analysis

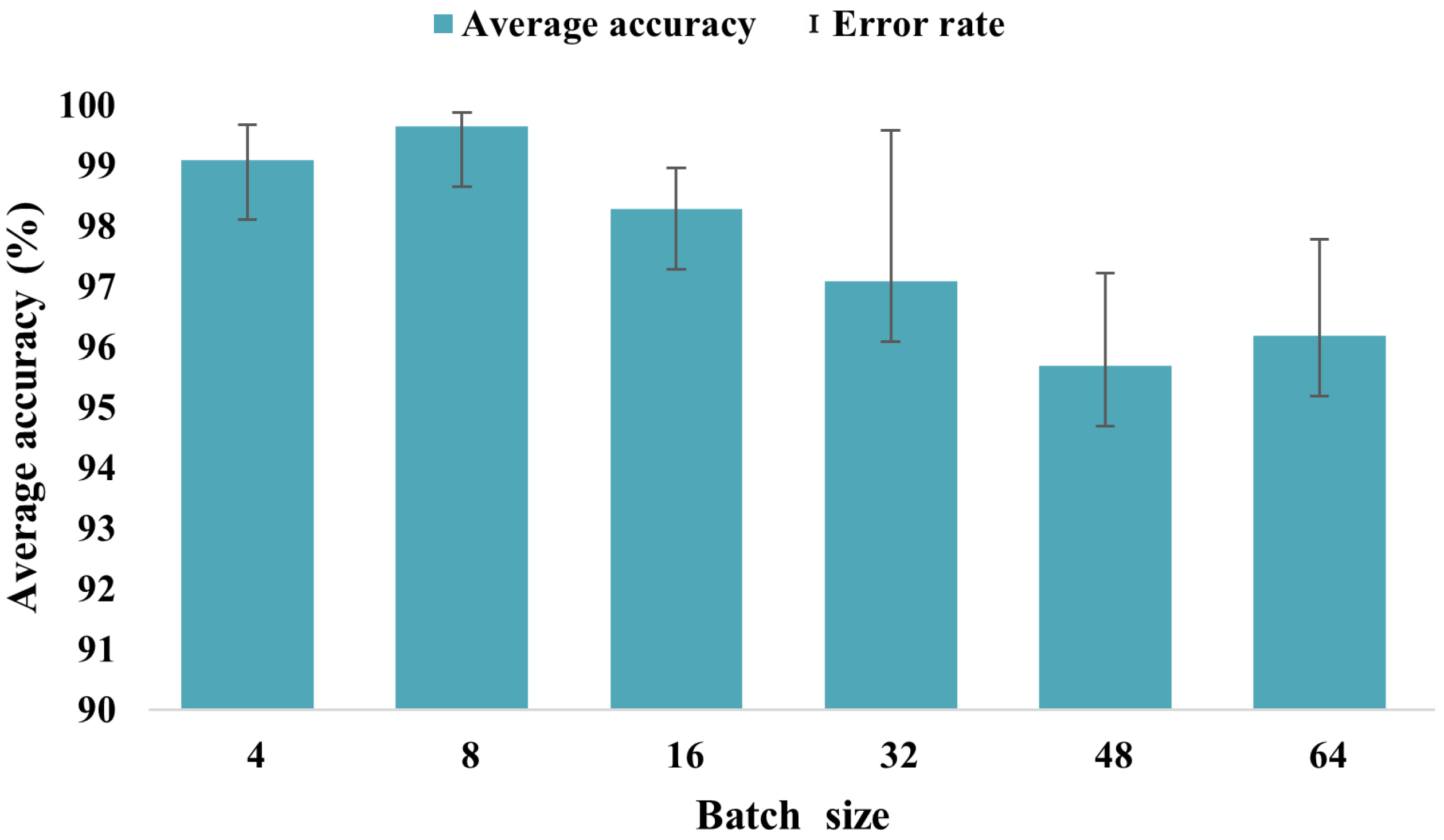
5.1. Model Parameter Settings

The model was trained using the Adam optimizer to update the weights, with a learning rate decay mechanism for dynamic adjustment. The batch size was set to 8, and the maximum number of iterations was 300. The dataset was split into training, validation, and testing sets in a 6:2:2 ratio. Detailed model parameters are provided in

Table 4. Model parameters.

Layer Structure	Output Dimensions	Number of Parameters	Activation Functions	Convolutional Kernel Size
Input	(None, 1024, 2)	0	None	None
Convolution	(None, 1024, 16)	176	ReLU	3 × 3
Hybrid attention	(None, 1024, 16)	261	Sigmoid, ReLU	None
Max pooling	(None, 512, 16)	39	ReLU	None
MSRB	(None, 256, 32)	3401	ReLU	3 × 3, 5 × 5
MSRB	(None, 256, 32)	3401	ReLU	3 × 3, 5 × 5
MRSB	(None, 256, 32)	3401	ReLU	3 × 3, 5 × 5
Convolution	(None, 256, 8)	1800	None	7 × 7
Hybrid attention	(None, 256, 8)	99	Sigmoid, ReLU	None
Dual global pooling	(None, 16)	0	None	None
Output	(None, 5)	85	None	None

. The experiments were conducted within the environment of TensorFlow 2.4.0 and Python 3.8, with the model initially trained on a PC equipped with an Intel i7-12700H processor (Intel, Santa Clara, CA, USA) operating at 4.7 GHz and featuring 16 GB of RAM.

5.2. Model Training

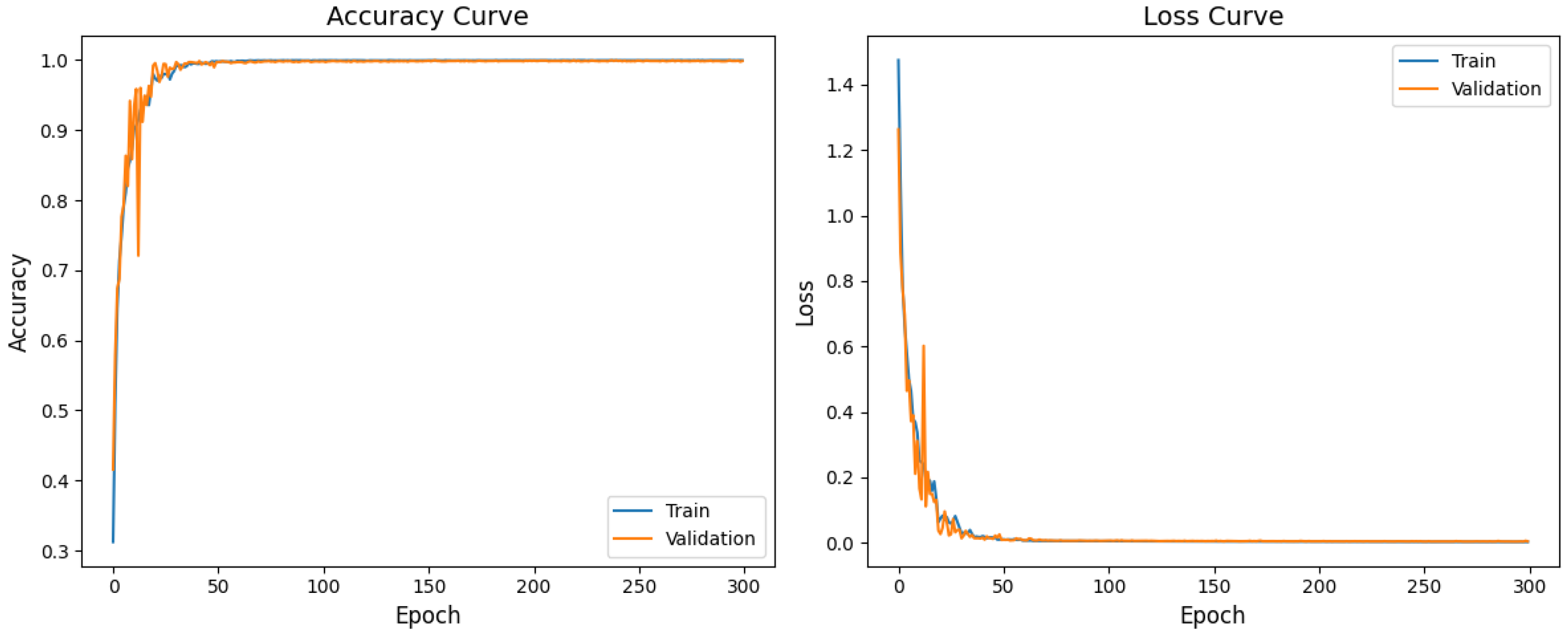
The model was trained 10 times, with 300 iterations each, where it achieved an average accuracy of 99.7%. As shown in Figure 16, the accuracy and loss rate curves indicate that the accuracy began to converge after 50 iterations and stabilized after 100. The loss gradually approached zero as the iterations increased, which reflected the model’s progressive learning of data features.

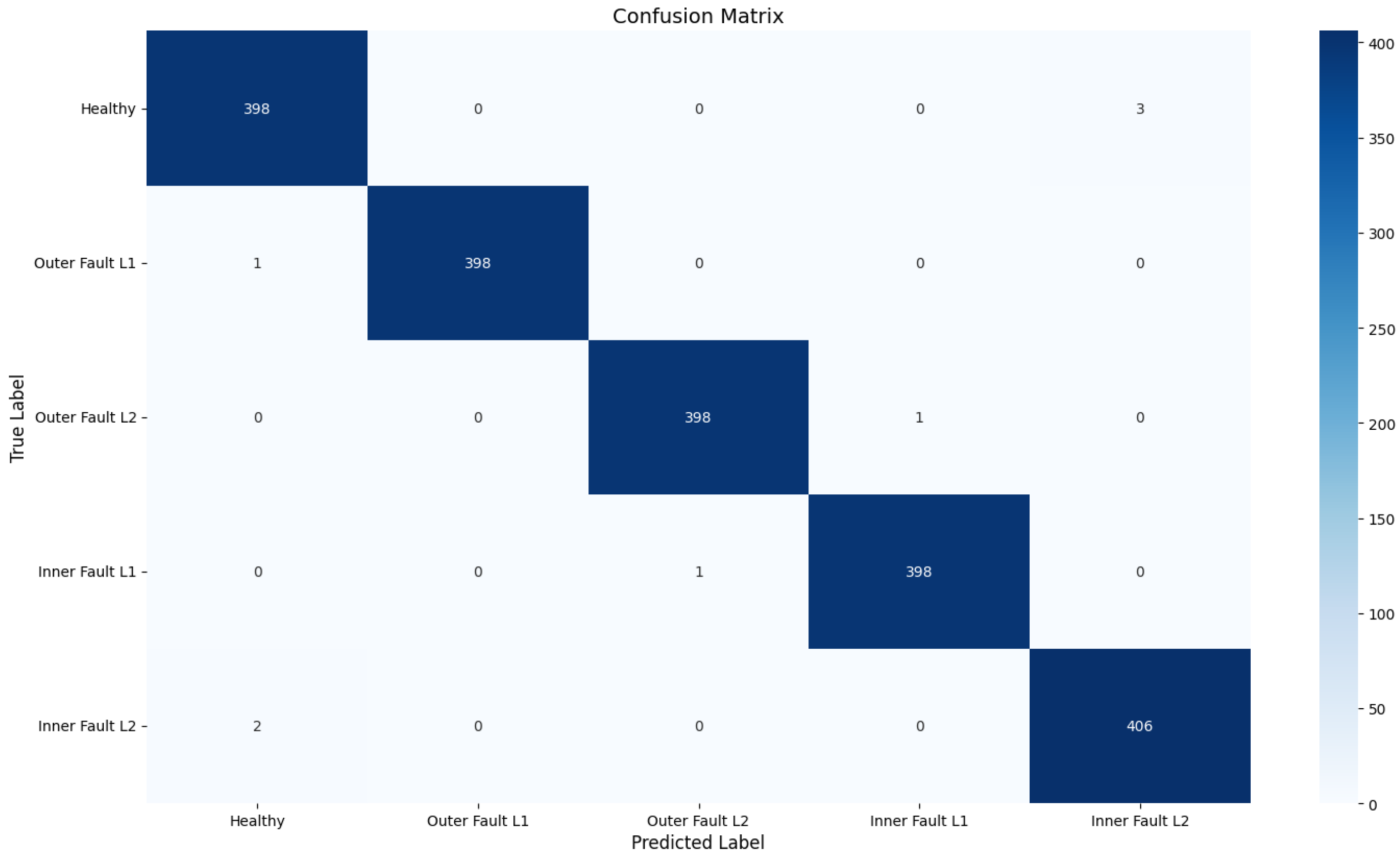
To verify the model’s cross-condition generalization in motor bearing fault detection, tests were conducted on four bearing faults. The confusion matrix in Figure 17 shows the model’s performance. The model underwent consecutive detections as follows: 401 for healthy bearings, 399 for outer fault L1, and 399 for outer fault L2, with misclassifications occurring 3, 1, and 1 times, respectively. Additionally, it performed 399 consecutive detections for both inner fault L1 and inner fault L2, misjudging them 1 and 2 times, respectively. These experimental results demonstrate that the model maintained a high level of detection accuracy, even in cross-condition motor bearing fault detection scenarios.

5.3. Comparison of Single-Phase and Dual-Phase Currents on Model Performance

The University of Paderborn bearing fault dataset comprises two current signals (U,V), namely, Current Signal 1 and Current Signal 2. To assess how these signals affected the model performance, this study compared the model’s performance when trained solely on each signal individually versus when trained on both signals concurrently. The findings of this comparison are summarized in

Table 5. Comparison of single-phase and dual-phase currents.

Data Type	Accuracy (%)	Recall (%)	F1 (%)
Current 1	97.33	96.90	97.11
Current 2	96.65	97.86	97.25
Dual-current	99.70	99.85	99.78

.

(1) Dual-phase vs. single-phase currents: The dual-phase current signals achieved an accuracy of 99.7%, recall of 99.85%, and F1 score of 99.78%, which all surpassed the single-phase currents. This indicates that the dual-phase currents provided richer feature information, which enhanced the model accuracy and robustness.

(2) Accuracy advantage: the higher accuracy of the dual-phase currents reduced the misclassification risks, which ensured more reliable fault detection.

(3) Recall advantage: The superior recall of the dual-phase currents ensured more comprehensive fault case identification, which minimized the risk of missed detections.

(4) F1 score improvement: The improved F1 score reflected a better balance between the precision and recall, which met the dual needs of accurate fault identification and comprehensive case coverage.

In summary, the dual-phase current signals offered significant advantages in motor fault detection by providing more accurate and robust performance. Thus, this study used dual-phase current signals as inputs for the motor fault detection model to better distinguish the various fault patterns.

5.4. Performance Comparison of Classic Fault Diagnosis Models

5.4.1. The University of Paderborn’s Bearing Dataset

This study employed a multi-dimensional evaluation method to compare the overall performances of four fault diagnosis models based on the University of Paderborn’s bearing dataset, with the experimental results presented in

Table 6. Comparison of different models.

Model	Accuracy (%)	Recall (%)	F1 (%)	Inference Time (s)
This paper	99.70	99.85	99.78	0.202
AMCNN	98.45	98.03	98.23	15.67
LeNet5	89.88	90.38	90.13	0.159
AlexNet	97.56	98.40	97.98	0.342
Transformer	98.77	98.56	98.66	1.322

.

As shown in Table 6, the AMCNN, LeNet5, AlexNet, and Transformer models achieved respective accuracies of 98.45%, 89.88%, 97.56%, and 98.77%. By contrast, the deep convolutional neural network model proposed in this study attained a superior accuracy of 99.7%, alongside higher recall and F1 scores. Although LeNet5 boasted a faster inference time than the model presented herein, the latter significantly outperformed the former across key evaluation metrics, including the accuracy, recall, and F1 score. In summary, the model introduced in this paper demonstrated exceptional accuracy and robustness in motor bearing fault detection tasks, highlighting its superior ability to effectively identify and classify motor bearing faults.

5.4.2. Vibration and Motor Current Dataset of Rolling Element Bearings

To evaluate the model’s generalization and universality, this study employed the vibration and motor current dataset of rolling element bearings [34], encompassing current data from four states: healthy, outer ring fault, inner ring fault, and ball fault. The comparative experimental results are presented in

Table 7. Comparative experiments of different algorithms.

Model	Accuracy (%)	Recall (%)	F1 (%)	Inference Time (s)
This paper	99.68	99.79	99.73	0.21
AMCNN	98.66	98.43	98.54	15.79
LeNet5	86.97	86.38	86.67	0.17
AlexNet	96.84	97.12	96.97	0.32
Transformer	98.89	99.15	99.02	1.245

.

The experimental results presented in this table demonstrate the superior performance of the model proposed in this paper compared with other established models. The model achieved remarkable accuracy, recall, and F1 scores of 99.68%, 99.79%, and 99.73%, respectively, which outperformed the AMCNN, LeNet5, AlexNet, and Transformer models. While LeNet5 showed the fastest inference time, this paper’s model also maintained a relatively low inference time of 0.21 s, thus balancing the efficiency and effectiveness. These results highlight the model’s potential for real-time and high-precision bearing fault detection applications.

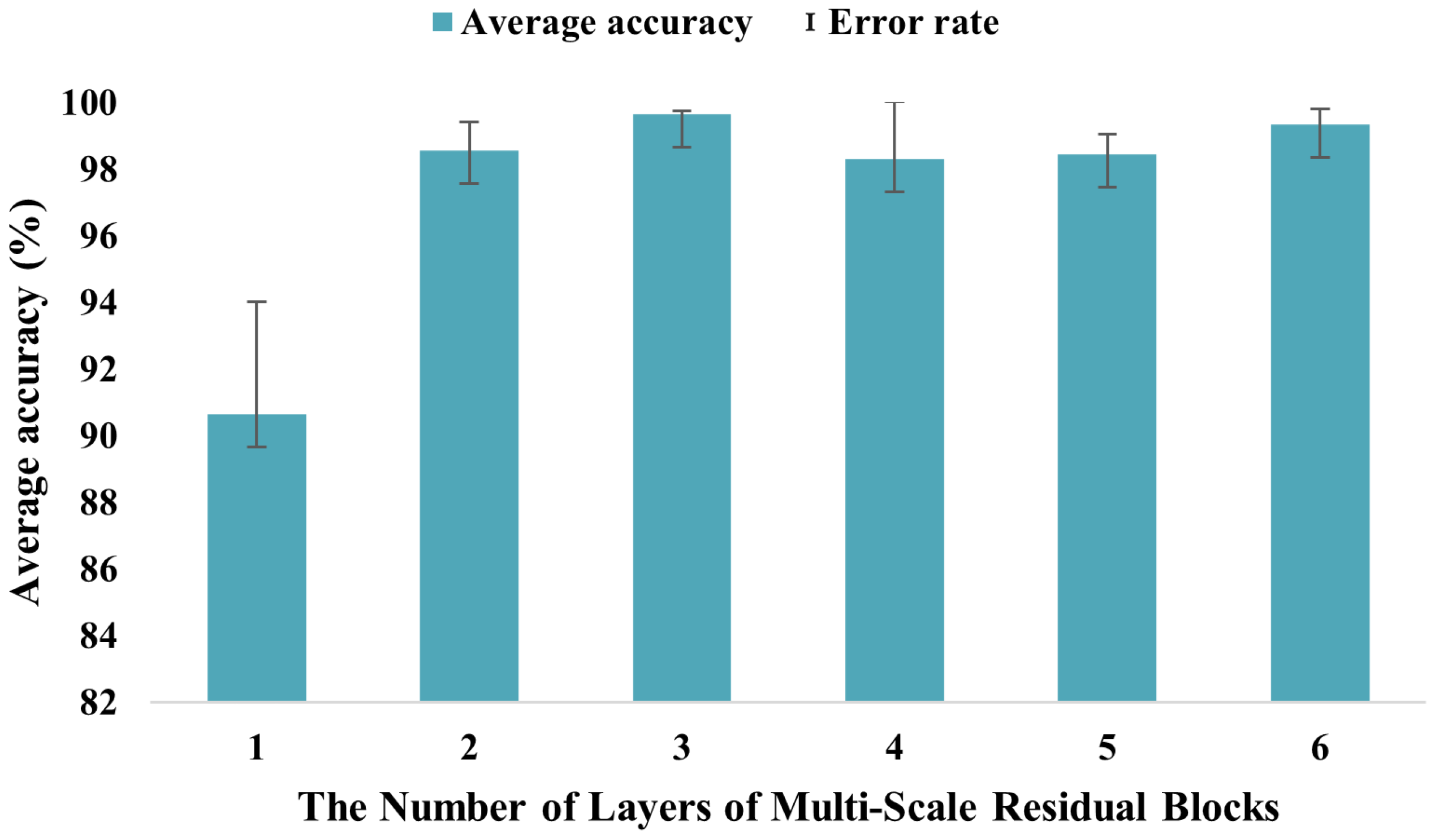
5.5. Ablation Experiment

To evaluate the model performance, an ablation study was conducted using the bearing dataset of the University of Paderborn in Germany to evaluate the effects of multi-scale residual modules, hybrid attention mechanisms, and dual global pooling, with the results shown in

Table 8. Ablation experiment.

Multi-Scale Residual	Hybrid Attention	Dual Global Pooling	Accuracy (%)	Recall (%)	F1 (%)
✓	✓	✓	90.41	91.22	90.81
✓	✓		95.61	95.23	95.42
✓		✓	97.48	97.33	97.40
✓	✓		98.47	98.66	98.56
✓		✓	97.85	97.01	97.42
✓	✓	✓	99.70	99.85	99.78

.

a. Multiscale residual modules and hybrid attention mechanism: Models using only global average or max pooling had accuracies of 98.47% and 97.85%, while omitting the dual global pooling reduced the accuracy to 95.61%. This highlights the dual global pooling’s importance in feature integration.

b. Multi-scale residual blocks and dual global pooling: Excluding the hybrid attention mechanism lowered the accuracy and recall to 97.48% and 97.33%, with an F1 score of 97.4%. This shows the hybrid attention mechanism enhanced the performance by integrating channel and spatial information.

c. Hybrid attention mechanism and dual global pooling: Omitting the multi-scale residual modules resulted in the lowest performance (97.48% accuracy, 97.33% recall, 97.4% F1 score). This indicates the multi-scale residual modules significantly boosted the performance by extracting features across scales and dimensions.

d. Full combination of all three techniques: when all three were used together, the model achieved the optimal performance, with a 99.7% accuracy, 99.85% recall, and 99.78% F1 score, showing that their synergy enhanced the model’s overall performance in motor fault detection.

In summary, the ablation studies demonstrated that multi-scale residual modules, hybrid attention mechanisms, and dual global pooling are all key to improving the model’s accuracy and reliability in motor fault detection. Their effective combination significantly boosted the performance.

6. Conclusions

A deep convolutional neural network model for motor fault detection is proposed in this paper. The model employs a spatial hybrid attention mechanism post-convolutional layer to extract channel and spatial information from the feature map. Subsequently, a three-layer multi-scale residual module acquires local and global features from the current signal following max pooling. Then, double global pooling is utilized to extract richer and more comprehensive feature information, thereby enhancing the model’s performance. Finally, the softmax function is used to output the classification results. The Adam optimizer and sparse categorical cross-entropy loss are employed to compile the model, with early stopping and learning rate decay applied to enhance the training effectiveness. While the experimental results indicate that the model could effectively detect bearing faults within the tested data range, it is important to note that the model’s effectiveness was assessed using motor bearing fault data collected by Padburn University under laboratory conditions, as well as rolling bearing vibration and motor current fault diagnosis datasets under variable-speed conditions. Compared with the single-phase current signals, this model demonstrated higher accuracy, recall, and F1 scores that outperformed the AMCNN, LeNet5, AlexNet, and Transformer models within the tested data range. However, the model has not yet been applied to engine fault detection, particularly under harsh industrial conditions. Future research will focus on validating the model’s performance in more complex and diverse industrial environments and across different types of motor faults.