Feasibility Assessment of Novel Multi-Mode Camshaft Design Through Modal Analysis
Abstract
1. Introduction
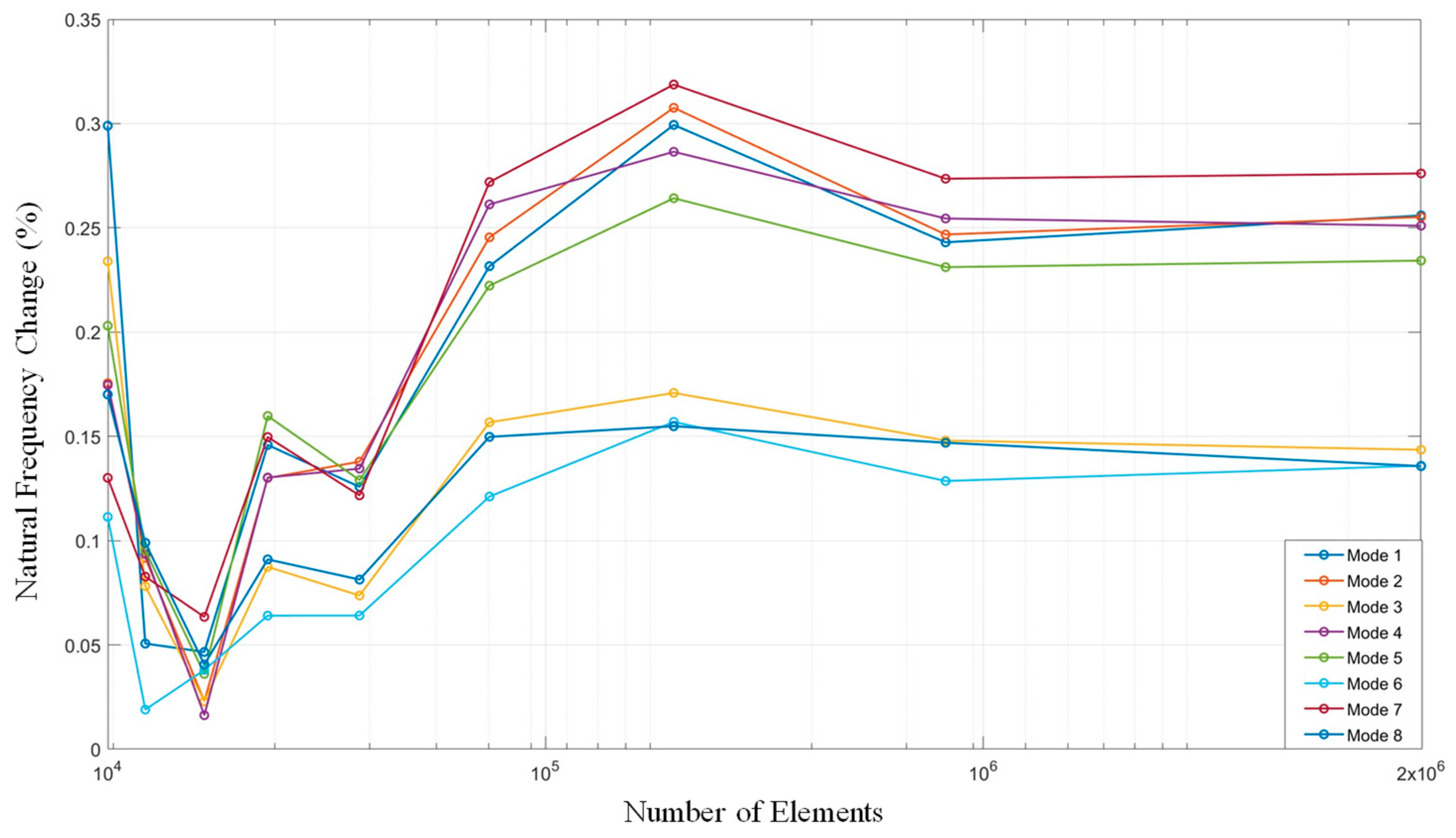
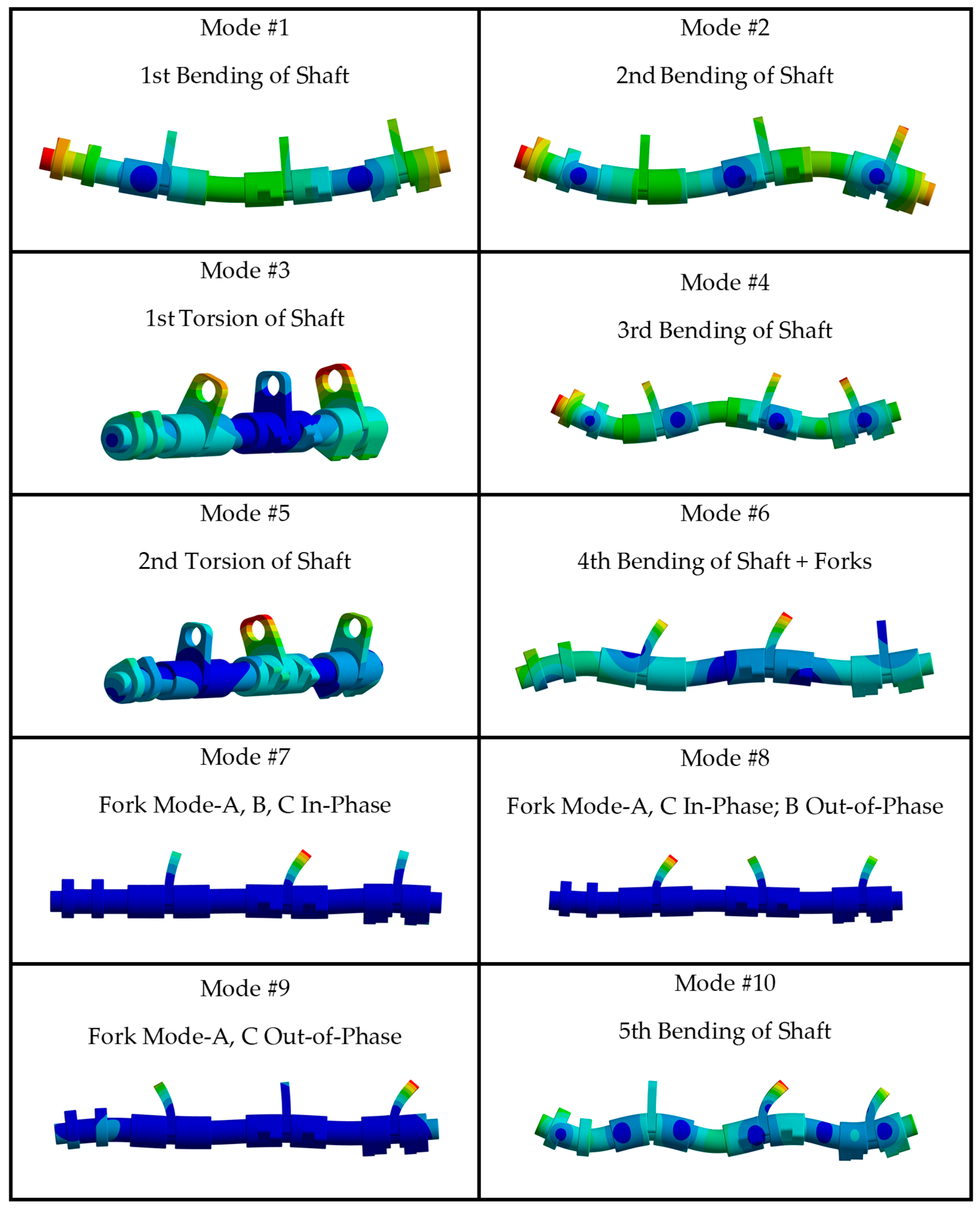
2. Computational Modal Analysis of Camshaft
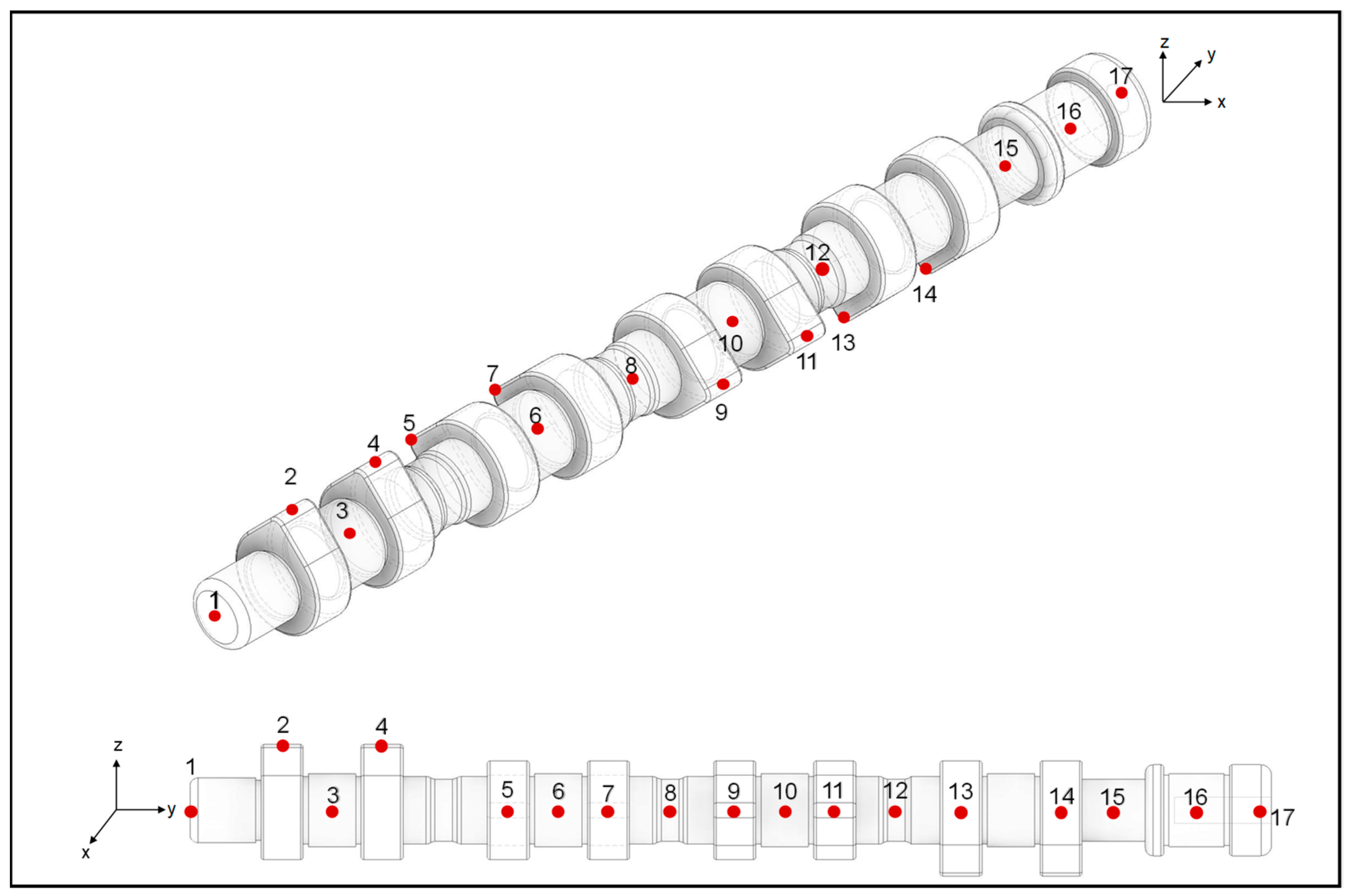
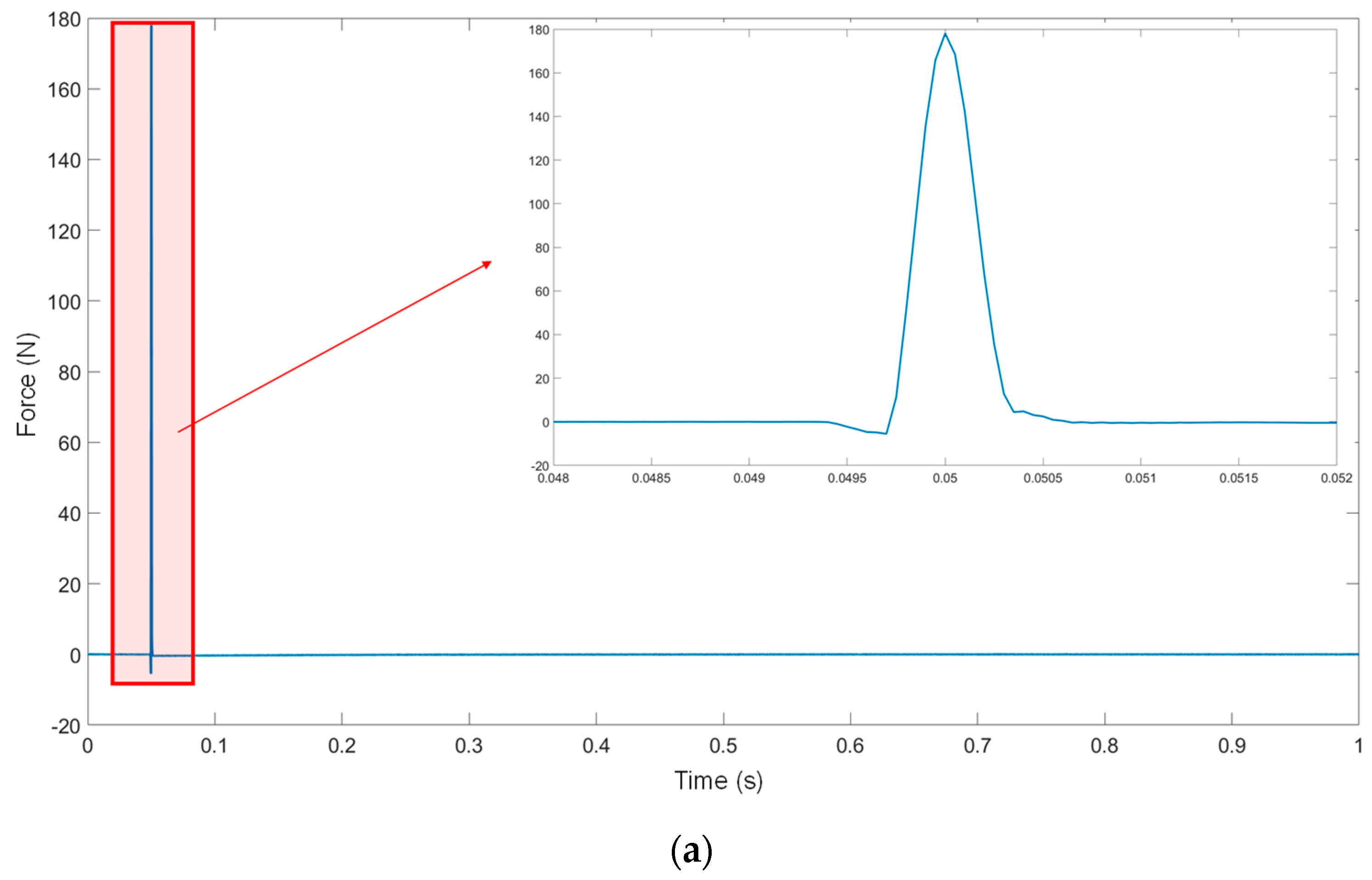
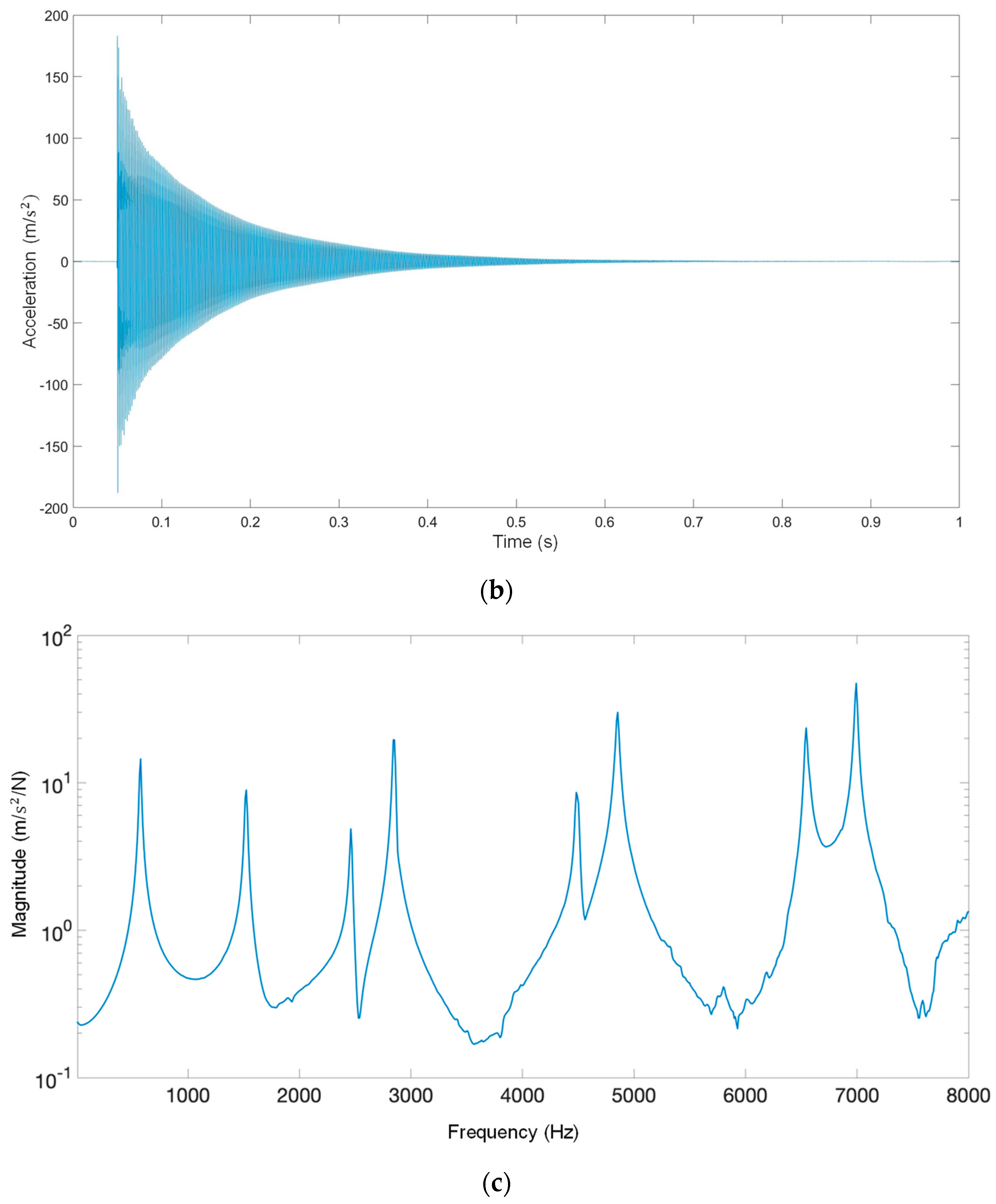
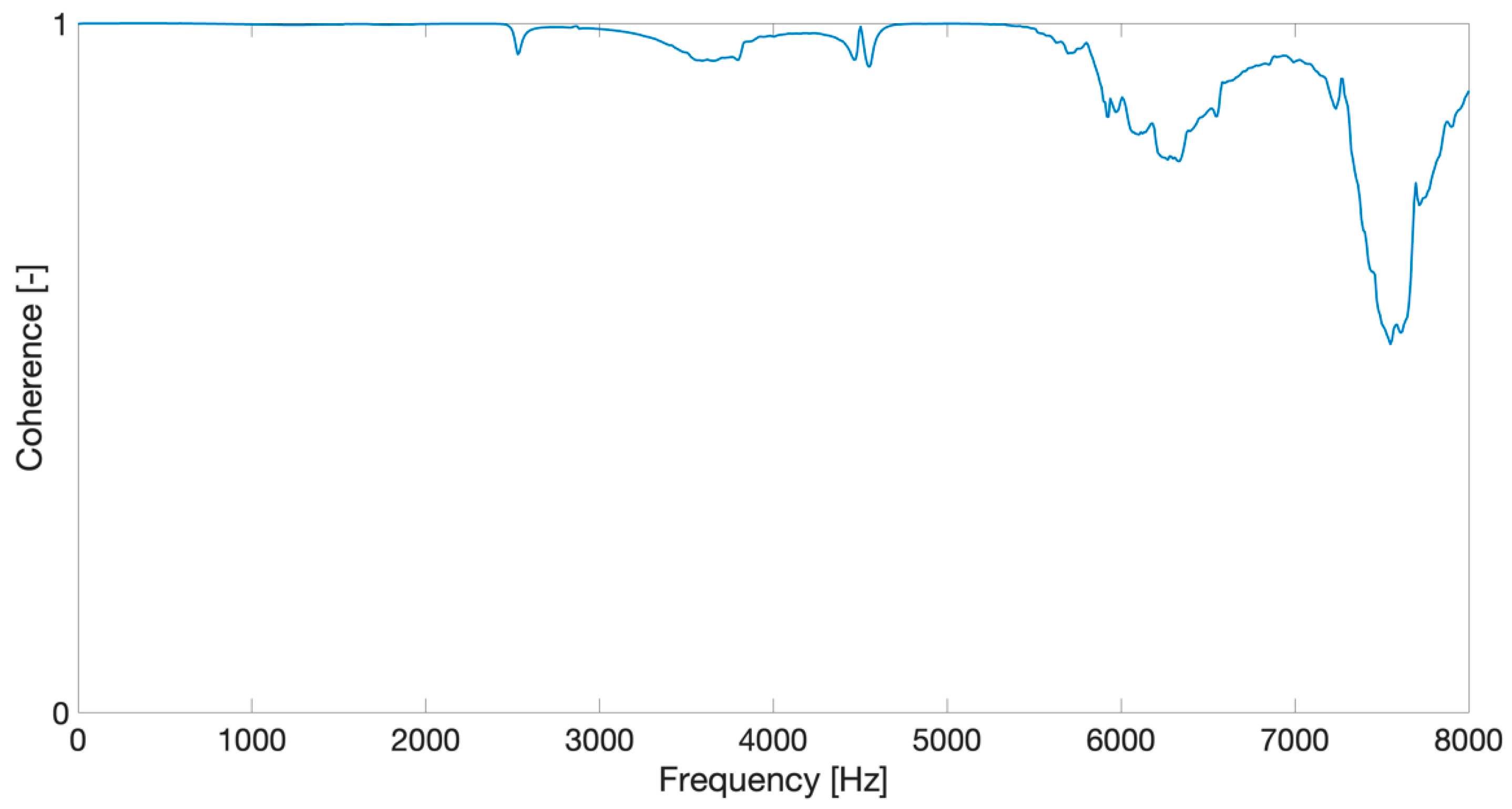
3. Experimental Modal Analysis of Camshaft
4. Model Updating and Validation of Computational Model
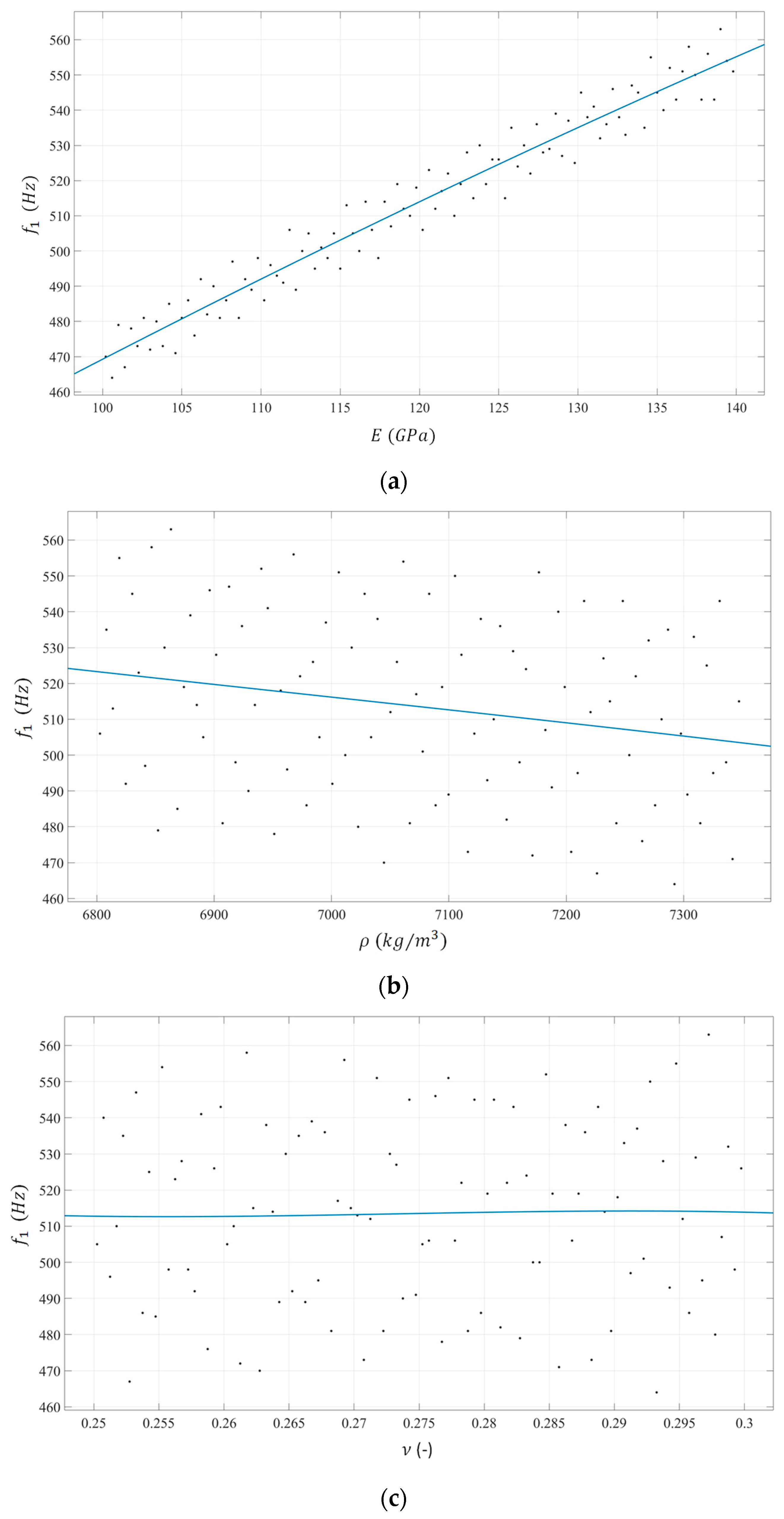
4.1. Sensitivity Analysis of Material Properties on Natural Frequencies
4.2. Optimization of Material Properties
4.2.1. Genetic Algorithm
4.2.2. Particle Swarm Optimization
4.2.3. Results of Optimization Process
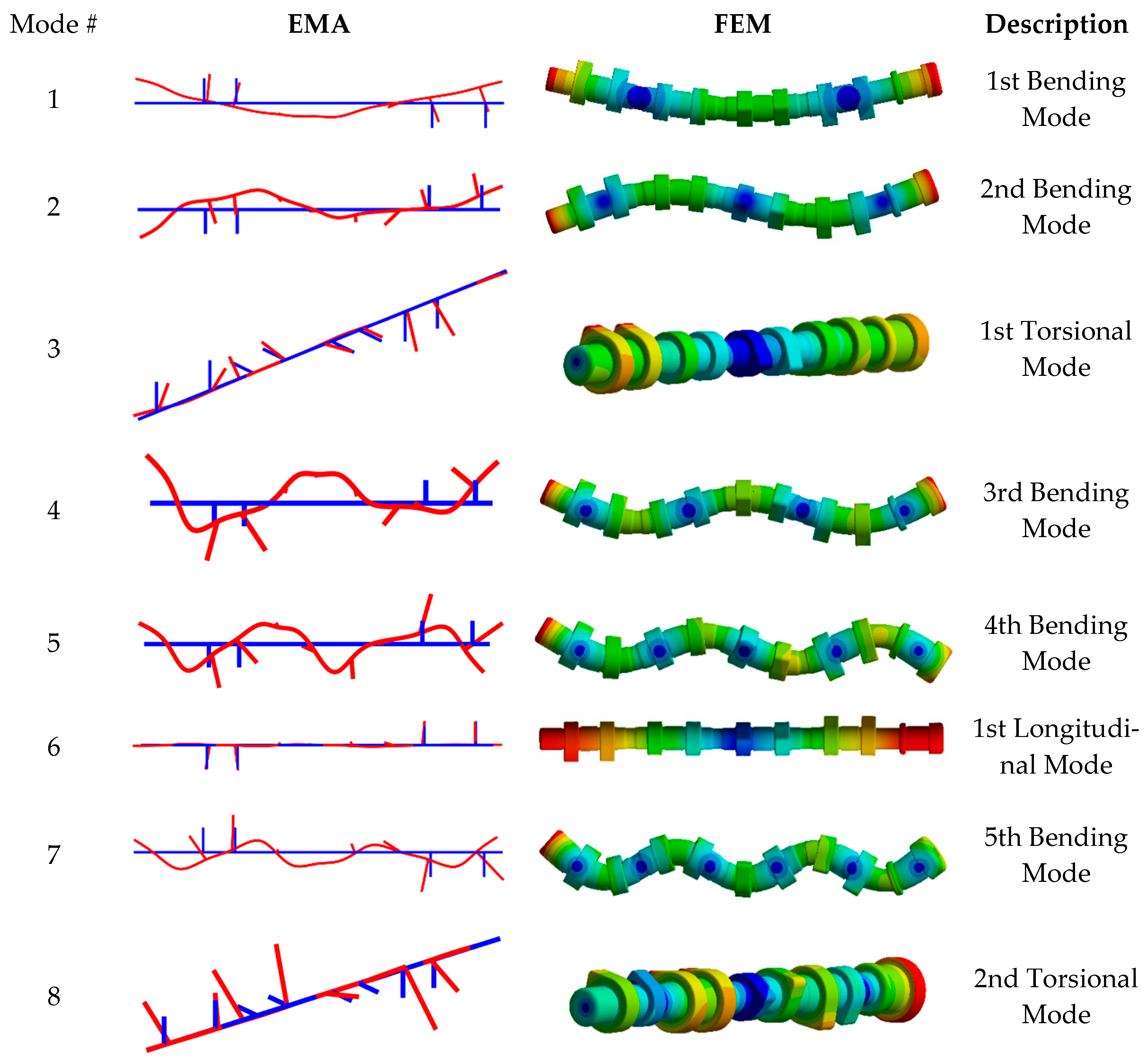
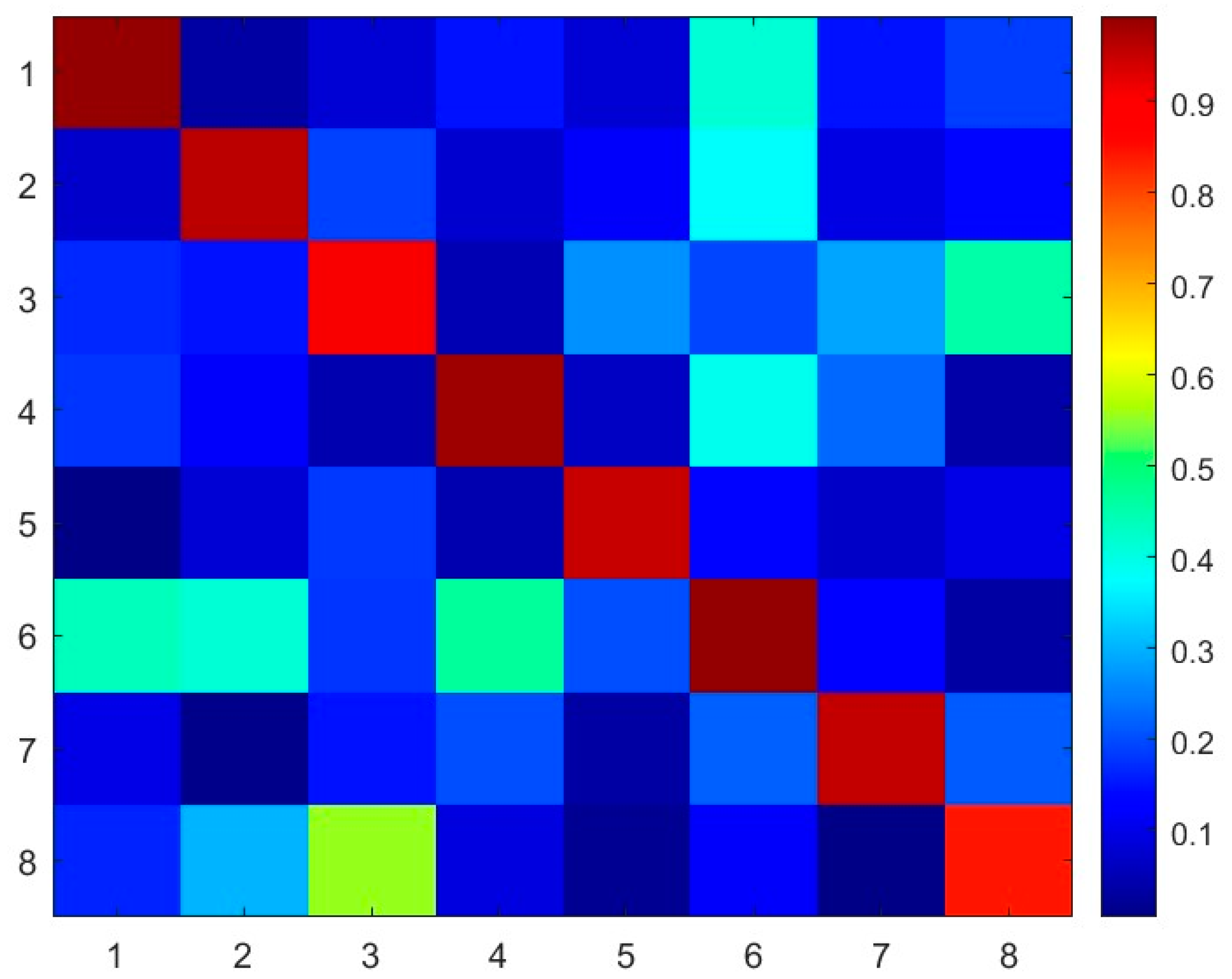
4.3. Comparison of Mode Shapes via Modal Assurance Criteria
5. Modified Camshaft Mechanism with Multiple Operating Modes
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Douglas, K.J.; Milovanovic, N.; Turner, J.; Blundell, D. Fuel Economy Improvement Using Combined CAI and Cylinder Deactivation (CDA)—An Initial Study; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2005; p. 2005-01-0110. [Google Scholar] [CrossRef]
- Rebbert, M.; Kreusen, G.; Lauer, S. A New Cylinder Deactivation by FEV and Mahle; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2008; p. 2008-01-1354. [Google Scholar] [CrossRef]
- Zhao, J.; Xi, Q.; Wang, S.; Wang, S. Improving the Partial-Load Fuel Economy of 4-Cylinder SI Engines by Combining Variable Valve Timing and Cylinder-Deactivation through Double Intake Manifolds. Appl. Therm. Eng. 2018, 141, 245–256. [Google Scholar] [CrossRef]
- Flierl, R.; Lauer, F.; Breuer, M.; Hannibal, W. Cylinder Deactivation with Mechanically Fully Variable Valve Train. SAE Int. J. Engines 2012, 5, 207–215. [Google Scholar] [CrossRef]
- Falkowski, A.; McElwee, M.; Bonne, M. Design and Development of the DaimlerChrysler 5.7L HEMI® Engine Multi-Displacement Cylinder Deactivation System; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2004; p. 2004-01-2106. [Google Scholar] [CrossRef]
- Hatano, K.; Iida, K.; Higashi, H.; Murata, S. Development of a New Multi-Mode Variable Valve Timing Engine. SAE Trans. 1993, 102, 930878. [Google Scholar] [CrossRef]
- Hosaka, T.; Hamazaki, M. Development of the Variable Valve Timing and Lift (VTEC) Engine for the Honda NSX; SAE Technical Paper; SAE International: Warrendale, PA, USA, 1991; p. 910008. [Google Scholar] [CrossRef]
- Huber, R.; Klumpp, P.; Ulbrich, H. Dynamic Analysis of the Audi Valvelift System. SAE Int. J. Engines 2010, 3, 839–849. [Google Scholar] [CrossRef]
- Millo, F.; Mirzaeian, M.; Luisi, S.; Doria, V.; Stroppiana, A. Engine Displacement Modularity for Enhancing Automotive s.i. Engines Efficiency at Part Load. Fuel 2016, 180, 645–652. [Google Scholar] [CrossRef]
- Fukui, T.; Nakagami, T.; Endo, H.; Katsumoto, T.; Danno, Y. Mitsubishi Orion-MD—A New Variable Displacement. SAE Trans. 1983, 92, 362–370. [Google Scholar]
- Maas, G.; Neukirchner, H.; Dingel, O.; Predelli, O. Potential of an Innovative, Fully Variable Valvetrain; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2004; p. 2004-01-1393. [Google Scholar] [CrossRef]
- Brüstle, C.; Schwarzenthal, D. VarioCam Plus—A Highlight of the Porsche 911 Turbo Engine; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2001; p. 2001-01-0245. [Google Scholar] [CrossRef]
- Azarniya, O.; Forooghi, A. Integrated Analysis of Free Vibrations in Hyperelastic Beams: Numerical Methods, Experimental Validation, and Neural Network Predictions. Multiscale Multidiscip. Model. Exp. Des. 2025, 8, 85. [Google Scholar] [CrossRef]
- Borgonovo, E.; Plischke, E. Sensitivity Analysis: A Review of Recent Advances. Eur. J. Oper. Res. 2016, 248, 869–887. [Google Scholar] [CrossRef]
- Bakir, P.G.; Reynders, E.; De Roeck, G. Sensitivity-Based Finite Element Model Updating Using Constrained Optimization with a Trust Region Algorithm. J. Sound Vib. 2007, 305, 211–225. [Google Scholar] [CrossRef]
- Bianconi, F.; Salachoris, G.P.; Clementi, F.; Lenci, S. A Genetic Algorithm Procedure for the Automatic Updating of FEM Based on Ambient Vibration Tests. Sensors 2020, 20, 3315. [Google Scholar] [CrossRef]
- Marwala, T. Finite-Element-Model Updating Using Computional Intelligence Techniques; Springer: London, UK, 2010. [Google Scholar] [CrossRef]
- Villa, M.; Ferreira, B.; Cruz, N. Genetic Algorithm to Solve Optimal Sensor Placement for Underwater Vehicle Localization with Range Dependent Noises. Sensors 2022, 22, 7205. [Google Scholar] [CrossRef] [PubMed]
- Boonlong, K. Vibration-Based Damage Detection in Beams by Cooperative Coevolutionary Genetic Algorithm. Adv. Mech. Eng. 2014, 6, 624949. [Google Scholar] [CrossRef]
- Tu, Z.; Lu, Y. FE Model Updating Using Artificial Boundary Conditions with Genetic Algorithms. Comput. Struct. 2008, 86, 714–727. [Google Scholar] [CrossRef]
- Girardi, M.; Padovani, C.; Pellegrini, D.; Robol, L. A Finite Element Model Updating Method Based on Global Optimization. Mech. Syst. Signal Process. 2021, 152, 107372. [Google Scholar] [CrossRef]
- Park, G.; Hong, K.-N.; Yoon, H. Vision-Based Structural FE Model Updating Using Genetic Algorithm. Appl. Sci. 2021, 11, 1622. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, Q.; Zordan, T.; Briseghella, B. Finite Element Model Updating of Canonica Bridge Using Experimental Modal Data and Genetic Algorithm. Struct. Eng. Int. 2016, 26, 27–36. [Google Scholar] [CrossRef]
- Alkayem, N.F.; Cao, M.; Zhang, Y.; Bayat, M.; Su, Z. Structural Damage Detection Using Finite Element Model Updating with Evolutionary Algorithms: A Survey. Neural Comput. Appl. 2018, 30, 389–411. [Google Scholar] [CrossRef]
- Mojtahedi, A.; Baybordi, S.; Fathi, A.; Yaghubzadeh, A. A Hybrid Particle Swarm Optimization and Genetic Algorithm for Model Updating of A Pier-Type Structure Using Experimental Modal Analysis. China Ocean. Eng. 2020, 34, 697–707. [Google Scholar] [CrossRef]
- Tran-Ngoc, H.; Khatir, S.; De Roeck, G.; Bui-Tien, T.; Nguyen-Ngoc, L.; Abdel Wahab, M. Model Updating for Nam O Bridge Using Particle Swarm Optimization Algorithm and Genetic Algorithm. Sensors 2018, 18, 4131. [Google Scholar] [CrossRef]
- Wang, S.; Xiang, B.; Wang, W.; Lian, P.; Zhao, Y.; Cui, H.; Lin, S.; Zhou, J. Finite Element Model Updating Method for Radio Telescope Antenna Based on Parameter Optimization with Surrogate Model. Appl. Sci. 2024, 14, 5620. [Google Scholar] [CrossRef]
- Shabbir, F.; Omenzetter, P. Model Updating Using Genetic Algorithms with Sequential Niche Technique. Eng. Struct. 2016, 120, 166–182. [Google Scholar] [CrossRef]
- Levin, R.I.; Lieven, N.A.J. Dynamic Finite Element Model Updating Using Simulated Annealing and Genetic Algorithms. Mech. Syst. Signal Process. 1998, 12, 91–120. [Google Scholar] [CrossRef]
- Allemang, R.J. The Modal Assurance Criterion—Twenty Years of Use and Abuse. Sound Vib. 2003, 37, 14–23. [Google Scholar]
- Pastor, M.; Binda, M.; Harčarik, T. Modal Assurance Criterion. Procedia Eng. 2012, 48, 543–548. [Google Scholar] [CrossRef]
- Jin, S.-S.; Cho, S.; Jung, H.-J.; Lee, J.-J.; Yun, C.-B. A New Multi-Objective Approach to Finite Element Model Updating. J. Sound Vib. 2014, 333, 2323–2338. [Google Scholar] [CrossRef]
- Zárate, B.A.; Caicedo, J.M. Finite Element Model Updating: Multiple Alternatives. Eng. Struct. 2008, 30, 3724–3730. [Google Scholar] [CrossRef]
- Zhou, X.; Kim, C.-W.; Zhang, F.-L.; Chang, K.-C. Vibration-Based Bayesian Model Updating of an Actual Steel Truss Bridge Subjected to Incremental Damage. Eng. Struct. 2022, 260, 114226. [Google Scholar] [CrossRef]
- Simoen, E.; De Roeck, G.; Lombaert, G. Dealing with Uncertainty in Model Updating for Damage Assessment: A Review. Mech. Syst. Signal Process. 2015, 56–57, 123–149. [Google Scholar] [CrossRef]
- Arora, V. Comparative Study of Finite Element Model Updating Methods. J. Vib. Control. 2011, 17, 2023–2039. [Google Scholar] [CrossRef]
- Jung, D.-S.; Kim, C.-Y. Finite Element Model Updating on Small-Scale Bridge Model Using the Hybrid Genetic Algorithm. Struct. Infrastruct. Eng. 2013, 9, 481–495. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, L.; Guo, Q.; Zhang, Y. Dynamic Finite Element Model Updating of Prestressed Concrete Continuous Box-Girder Bridge. Earthq. Eng. Eng. Vib. 2009, 8, 399–407. [Google Scholar] [CrossRef]
- Sehgal, S.; Kumar, H. Structural Dynamic Model Updating Techniques: A State of the Art Review. Arch. Comput. Methods Eng. 2016, 23, 515–533. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, J.; Di, L.; Zhao, C.; Guo, Q. Active Magnetic Bearing Rotor Model Updating Using Resonance and MAC Error. Shock. Vib. 2015, 2015, 263062. [Google Scholar] [CrossRef]
- Wu, Y.; Zhu, R.; Cao, Z.; Liu, Y.; Jiang, D. Model Updating Using Frequency Response Functions Based on Sherman–Morrison Formula. Appl. Sci. 2020, 10, 4985. [Google Scholar] [CrossRef]
- Hurtado, O.D.; Ortiz, A.R.; Gomez, D.; Astroza, R. Bayesian Model-Updating Implementation in a Five-Story Building. Buildings 2023, 13, 1568. [Google Scholar] [CrossRef]
- Dong, F.; Shi, Z.; Zhong, R.; Jin, N. FE Model Updating of Continuous Beam Bridge Based on Response Surface Method. Buildings 2024, 14, 960. [Google Scholar] [CrossRef]
- Hasani, H.; Freddi, F. Artificial Neural Network-Based Automated Finite Element Model Updating with an Integrated Graphical User Interface for Operational Modal Analysis of Structures. Buildings 2024, 14, 3093. [Google Scholar] [CrossRef]
- Mottershead, J.E.; Link, M.; Friswell, M.I. The Sensitivity Method in Finite Element Model Updating: A Tutorial. Mech. Syst. Signal Process. 2011, 25, 2275–2296. [Google Scholar] [CrossRef]
- Cuadrado, M.; Artero-Guerrero, J.A.; Pernas-Sánchez, J.; Varas, D. Model Updating of Uncertain Parameters of Carbon/Epoxy Composite Plates from Experimental Modal Data. J. Sound Vib. 2019, 455, 380–401. [Google Scholar] [CrossRef]
- Kumar, D.; Goyal, A.; Barmola, A.; Kushwaha, N.; Singha, S. Vibration Analysis of The Camshaft Using Finite Element Method. In Proceedings of the National Conference on Knowledge, Innovation in Technology and Engineering, Kerala, India, 10–11 April 2015; pp. 251–254. [Google Scholar]
- Patil, H.; Jeyakarthikeyan, P.V. Mesh Convergence Study and Estimation of Discretization Error of Hub in Clutch Disc with Integration of ANSYS. IOP Conf. Ser. Mater. Sci. Eng. 2018, 402, 012065. [Google Scholar] [CrossRef]
- Ibrahim, S.R.; MikuIcik, E.C. A method for the direct identification of vibration parameters from the free response. Shock Vib. Bull. 1997, 47, 183–196. [Google Scholar]
- Tran, M.Q.; Sousa, H.S.; Matos, J.; Fernandes, S.; Nguyen, Q.T.; Dang, S.N. Finite Element Model Updating for Composite Plate Structures Using Particle Swarm Optimization Algorithm. Appl. Sci. 2023, 13, 7719. [Google Scholar] [CrossRef]
- Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models; Reprinted; Saltelli, A., Ed.; Wiley: Chichester, UK; Weinheim, Germany, 2007. [Google Scholar]
- Lin, C.D.; Tang, B. Latin Hypercubes and Space-Filling Designs; Chapman and Hall/CRC: Boca Raton, FL, USA, 2015. [Google Scholar]
- Arora, J.S. Introduction to Optimum Design, 4th ed.; Elsevier: Amsterdam, The Netherlands; Academic Press: Boston, MA, USA, 2017. [Google Scholar]
- Mangla, C.; Ahmad, M.; Uddin, M. Optimization of Complex Nonlinear Systems Using Genetic Algorithm. Int. J. Inf. Tecnol. 2021, 13, 1913–1925. [Google Scholar] [CrossRef]
- John, H. Holland—Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; The MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Russotto, S.; Di Matteo, A.; Pirrotta, A. An Innovative Structural Dynamic Identification Procedure Combining Time Domain OMA Technique and GA. Buildings 2022, 12, 963. [Google Scholar] [CrossRef]
- Tang, K.S.; Man, K.F.; Kwong, S.; He, Q. Genetic Algorithms and Their Applications. IEEE Signal Process. Mag. 1996, 13, 22–37. [Google Scholar] [CrossRef]
- Guan, X.; Xie, S.; Chen, G.; Qu, M. Modal Parameter Identification by Adaptive Parameter Domain with Multiple Genetic Algorithms. J. Mech. Sci. Technol. 2020, 34, 4965–4980. [Google Scholar] [CrossRef]
- Jung, B.K.; Cho, J.R.; Jeong, W.B. Sensor Placement Optimization for Structural Modal Identification of Flexible Structures Using Genetic Algorithm. J. Mech. Sci. Technol. 2015, 29, 2775–2783. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; IEEE: Perth, WA, Australia, 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Gad, A.G. Particle Swarm Optimization Algorithm and Its Applications: A Systematic Review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle Swarm Optimization Algorithm: An Overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Mottershead, J.E.; Link, M.; Friswell, M.I.; Schedlinski, C. Model Updating. In Handbook of Experimental Structural Dynamics; Allemang, R., Avitabile, P., Eds.; Springer New York: New York, NY, USA, 2020; pp. 1–53. [Google Scholar] [CrossRef]
- Baykara, C.; Akin Kutlar, O.; Dogru, B.; Arslan, H. Skip Cycle Method with a Valve-Control Mechanism for Spark Ignition Engines. Energy Convers. Manag. 2017, 146, 134–146. [Google Scholar] [CrossRef]
- Kutlar, O.A.; Arslan, H.; Calik, A.T. Skip Cycle System for Spark Ignition Engines: An Experimental Investigation of a New Type Working Strategy. Energy Convers. Manag. 2007, 48, 370–379. [Google Scholar] [CrossRef]
- Fridrichová, K.; Drápal, L.; Vopařil, J.; Dlugoš, J. Overview of the Potential and Limitations of Cylinder Deactivation. Renew. Sustain. Energy Rev. 2021, 146, 111196. [Google Scholar] [CrossRef]
- Campos, C.H.F.; Hanriot, S.D.M.; Amorim, R.J.; Mazzaro, R.S. Cylinder Deactivation Strategy for Fuel Consumption Reduction. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 547. [Google Scholar] [CrossRef]
- Kuruppu, C.; Pesiridis, A.; Rajoo, S. Investigation of Cylinder Deactivation and Variable Valve Actuation on Gasoline Engine Performance; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2014; p. 2014-01-1170. [Google Scholar] [CrossRef]



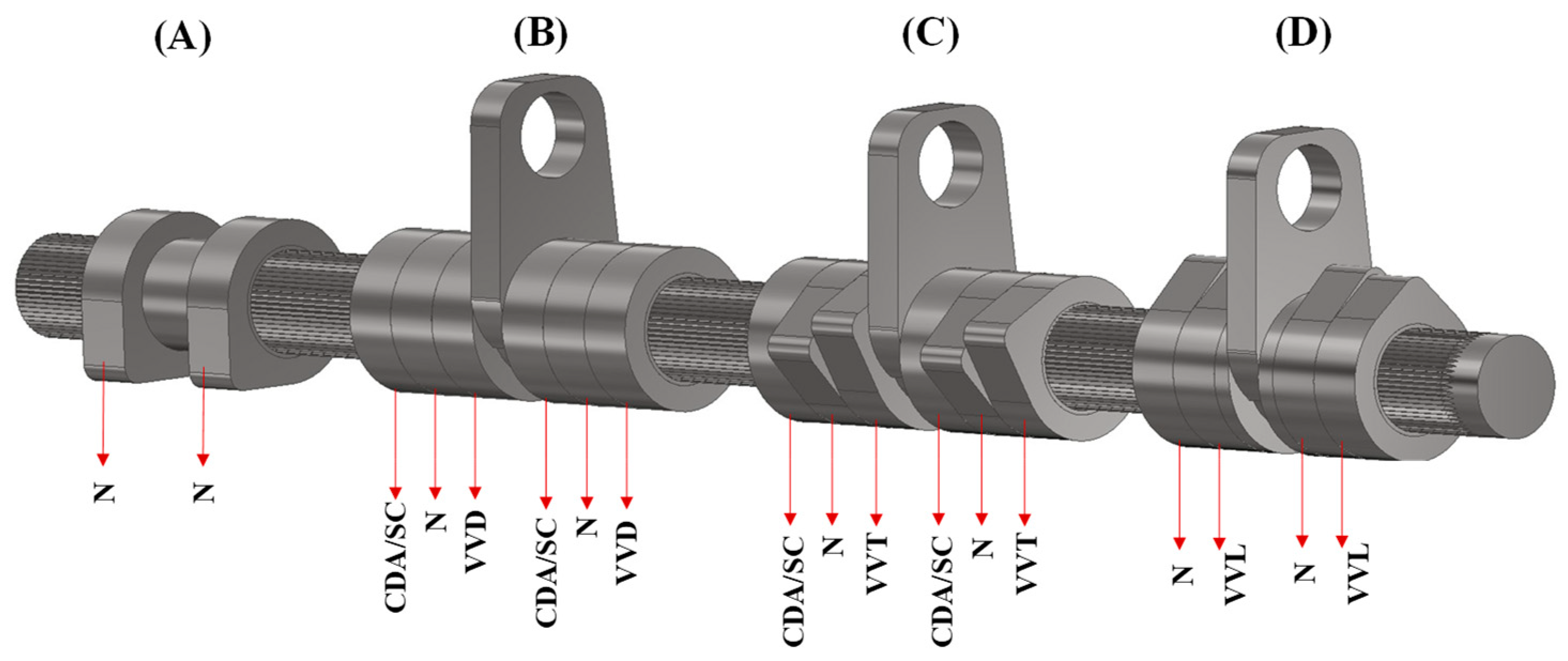
| Impact Location | Impact Direction |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 |
| Mode | [Hz] | [Hz] | |
|---|---|---|---|
| 1 | 488.4 | 576.1 | 17.96% |
| 2 | 1293.3 | 1523.4 | 17.79% |
| 3 | 2158.9 | 2460.9 | 13.99% |
| 4 | 2430.2 | 2851.5 | 17.34% |
| 5 | 3841.5 | 4482.4 | 16.68% |
| 6 | 4193.2 | 4853.5 | 15.75% |
| 7 | 5614.3 | 6542.9 | 16.54% |
| 8 | 6115.0 | 6992.2 | 14.35% |
| Material Property | Initial Value | Genetic Algorithm | Particle Swarm Optimization | ||
|---|---|---|---|---|---|
| Updated Value | Relative Change | Updated Value | Relative Change | ||
| ] | |||||
| ] | |||||
| ] | Genetic Algorithm | Particle Swarm Optimization | |||
|---|---|---|---|---|---|
| ] | ] | ] | ] | ||
| Module | Profile 1 | Profile 2 | Profile 3 |
|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Üngör, M.; Sen, O.T.; Yavuz, A.; Baykara, C. Feasibility Assessment of Novel Multi-Mode Camshaft Design Through Modal Analysis. Machines 2025, 13, 407. https://doi.org/10.3390/machines13050407
Üngör M, Sen OT, Yavuz A, Baykara C. Feasibility Assessment of Novel Multi-Mode Camshaft Design Through Modal Analysis. Machines. 2025; 13(5):407. https://doi.org/10.3390/machines13050407
Chicago/Turabian StyleÜngör, Merve, Osman Taha Sen, Akif Yavuz, and Cemal Baykara. 2025. "Feasibility Assessment of Novel Multi-Mode Camshaft Design Through Modal Analysis" Machines 13, no. 5: 407. https://doi.org/10.3390/machines13050407
APA StyleÜngör, M., Sen, O. T., Yavuz, A., & Baykara, C. (2025). Feasibility Assessment of Novel Multi-Mode Camshaft Design Through Modal Analysis. Machines, 13(5), 407. https://doi.org/10.3390/machines13050407






