Active Vibration Control of Cantilever Structures by Integrating the Closed Loop Control Action into Transient Solution of Finite Element Model and an Application to Aircraft Wing
Abstract
1. Introduction
2. Simulation of Active Vibration Control of Cantilever Beam with End Mass
2.1. Finite Element Model for Laplace Transform and Newmark Method Solution
2.2. Simulation by Laplace Transform Method
2.3. Simulation by Newmark Method
2.4. Simulation by ANSYS APDL
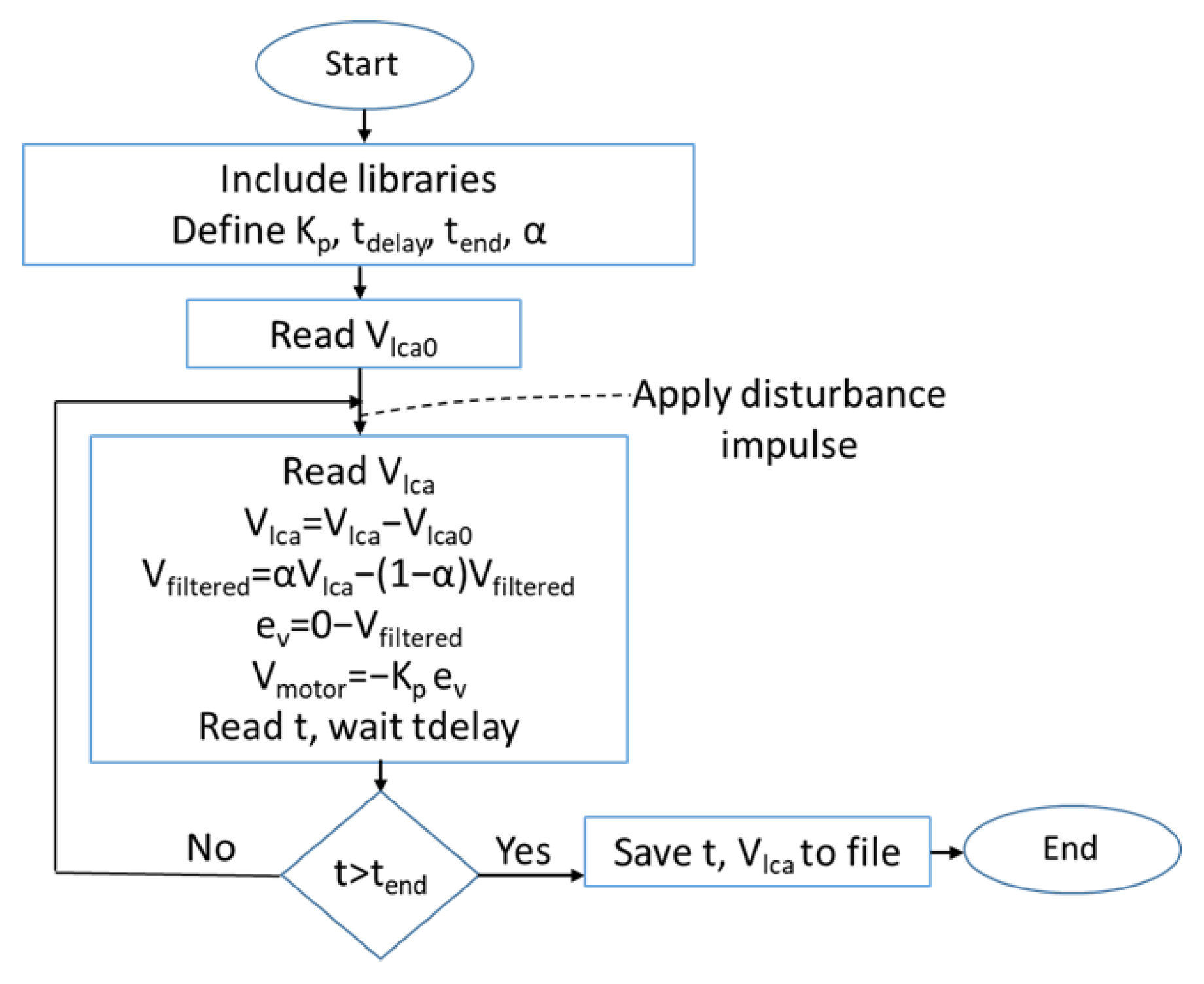
3. Experimental System of Active Vibration Control of Cantilever Beam
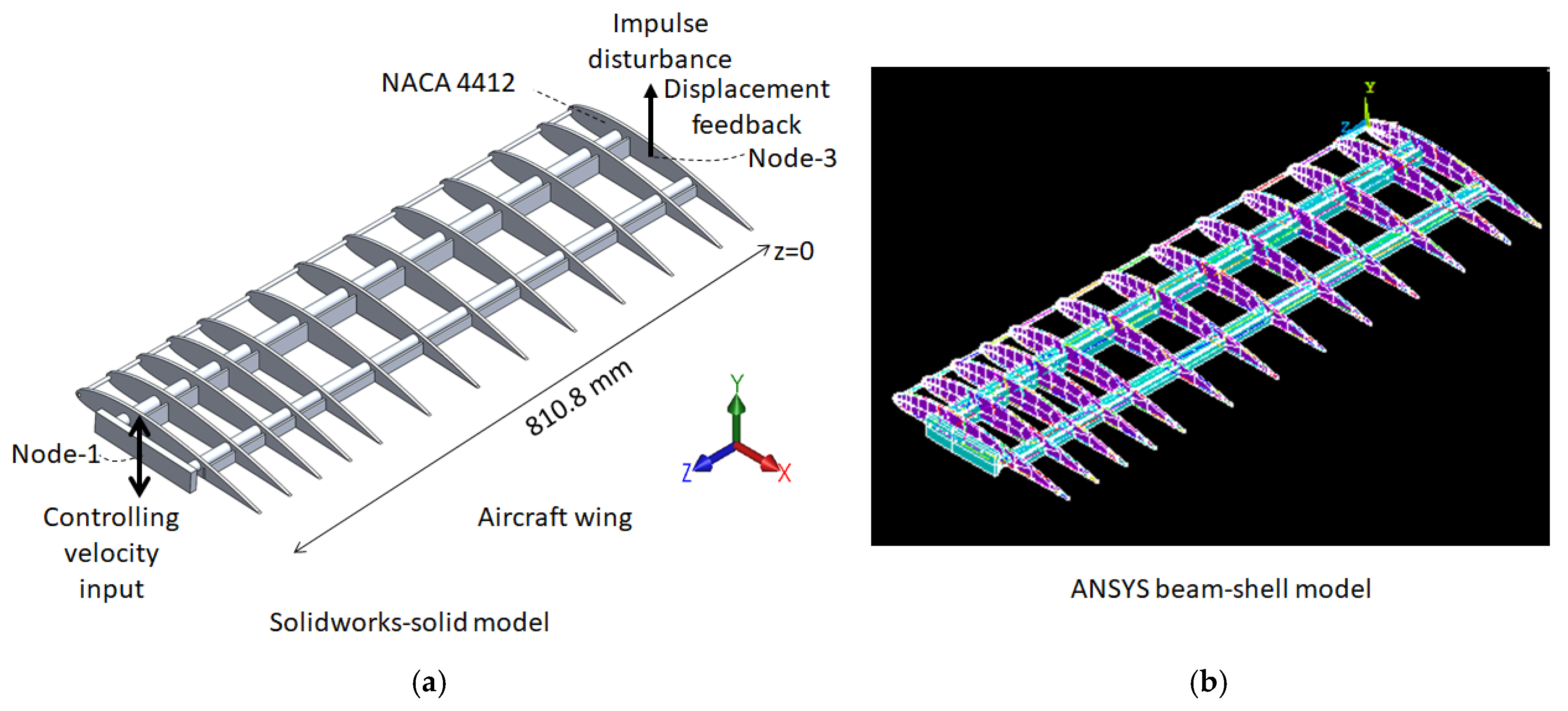
4. Simulation of Active Vibration Control of Aircraft Wing by ANSYS APDL
5. Results and Discussions
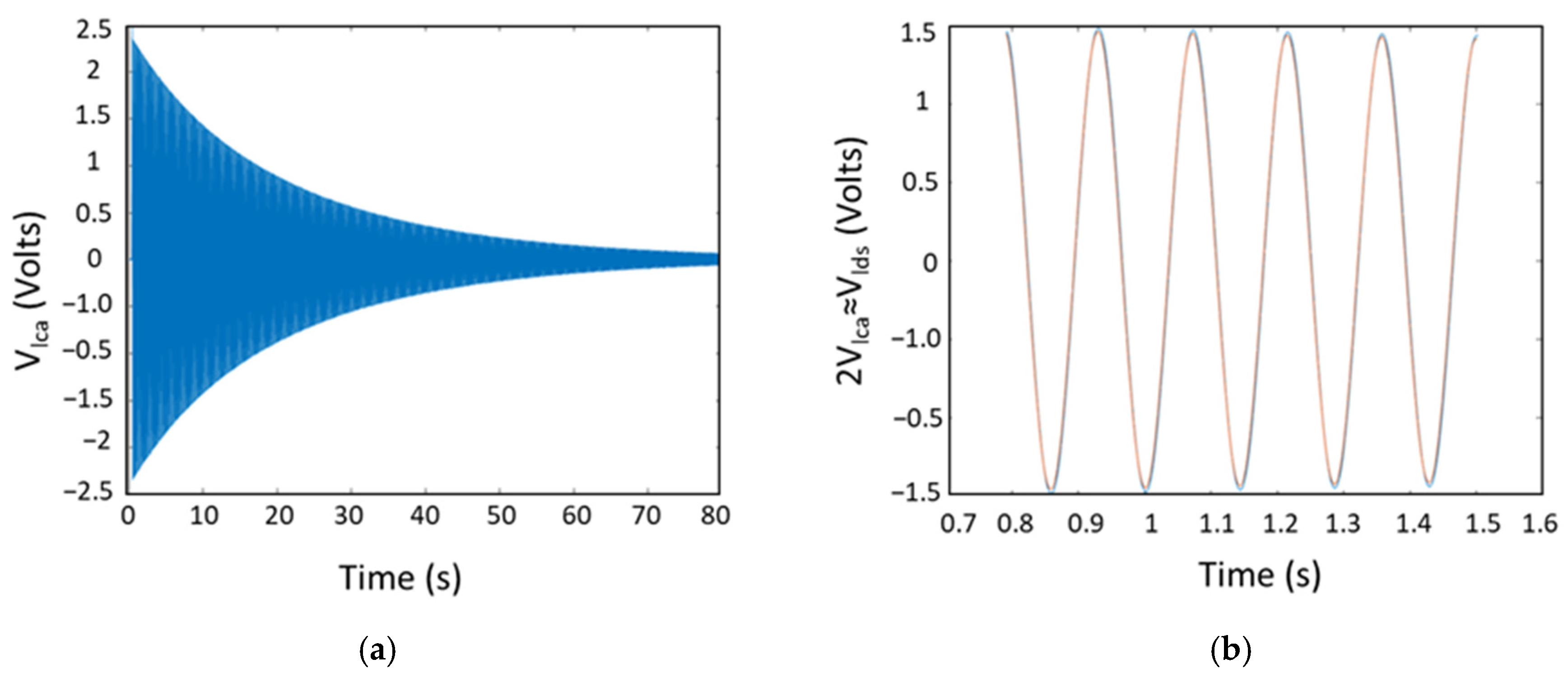
5.1. Comparison of Experimental Strain and Displacement Sensor Output Signals
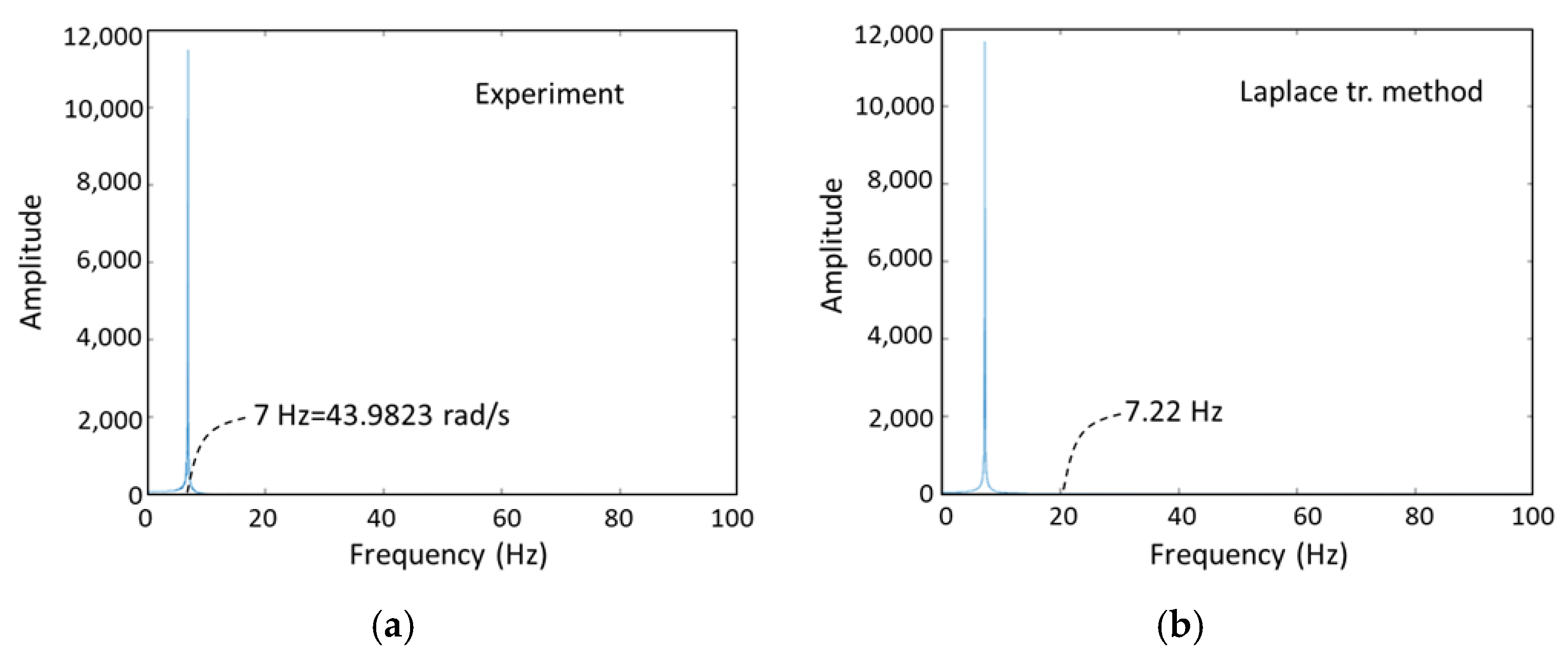
5.2. Determining Damping Constant Experimentally
5.3. AVC of Cantilever Beam Results Obtained by the Laplace Transform Method, Newmark Method, ANSYS, and Experiments
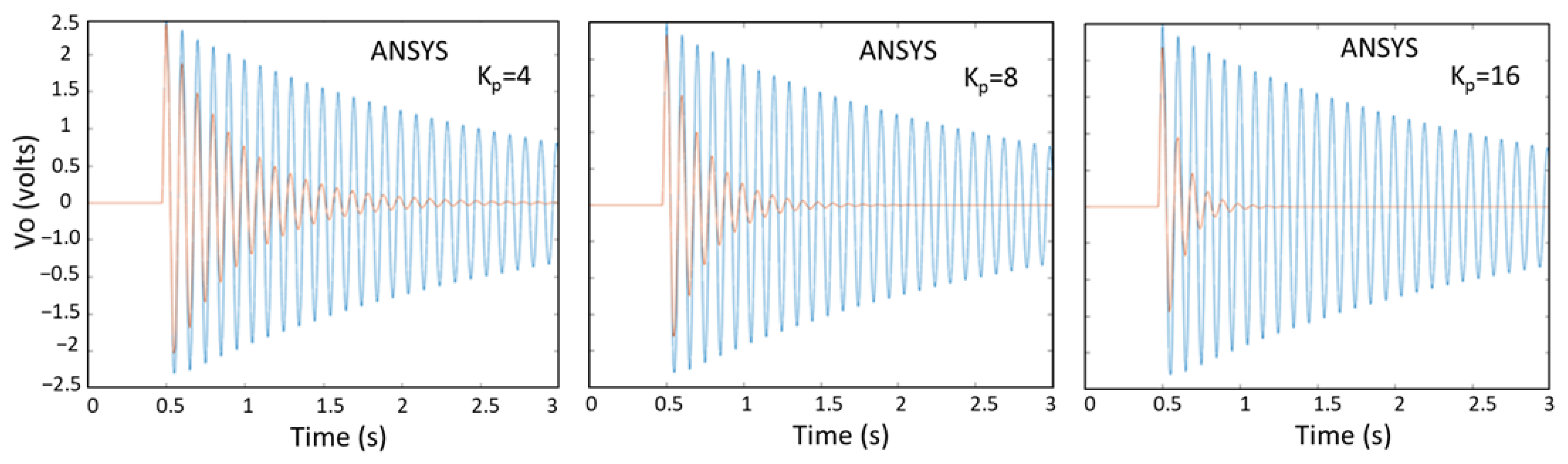
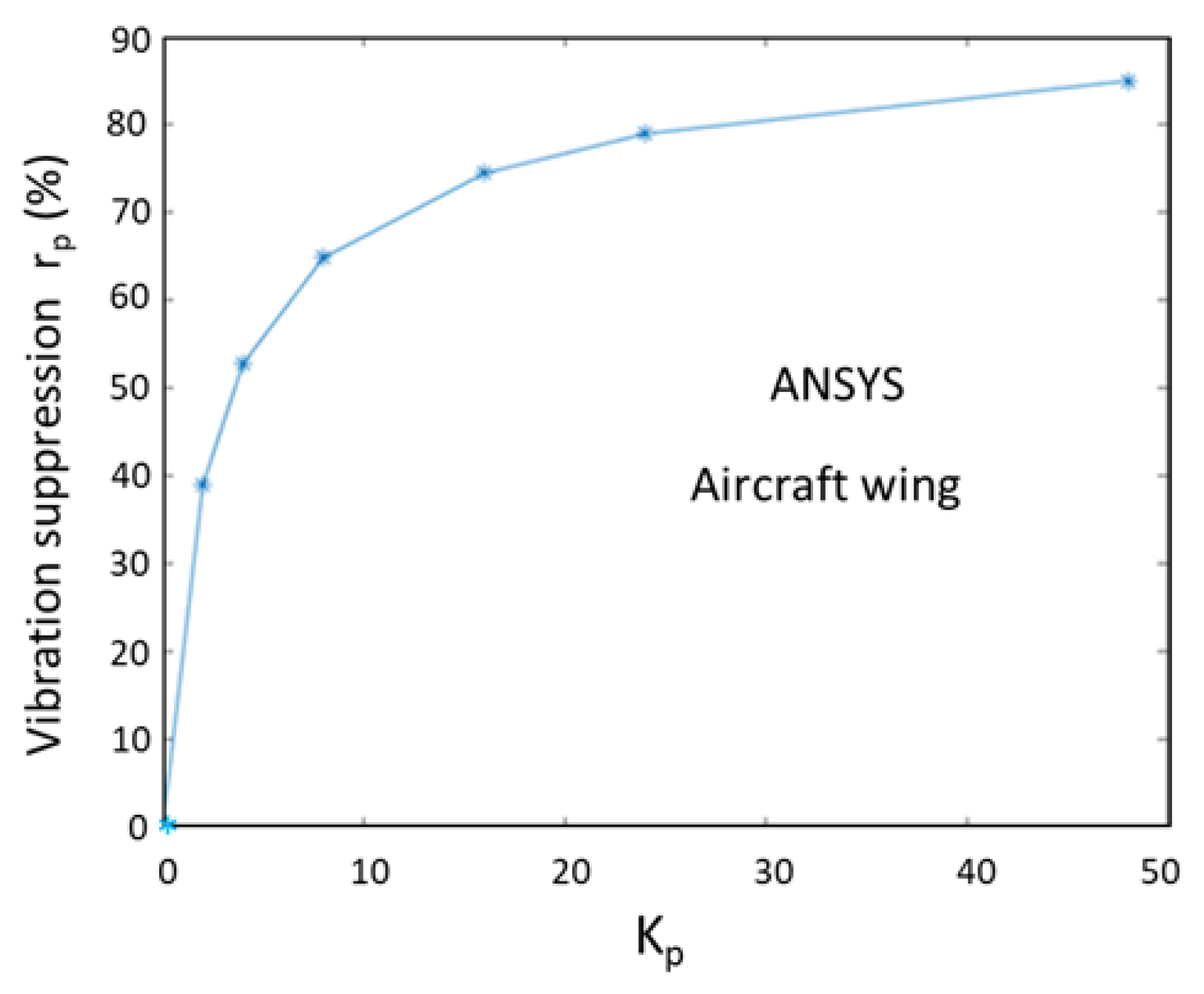
5.4. AVC of Aircraft Wing by ANSYS APDL
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. ANSYS APDL Code for AVC of Cantilever Beam
| finish /config,nres,10000 /clear,nostart !---------------- b=39.3e-3 h=2e-3 mend=171e-3 Iz=b*h**3/12 ymax=h/2 Kp=10 fl='va10' dt=0.005 tend=9 A=40 K1=0.0025 K2=250 !----- /prep7 mp,ex,1,200e9 mp,dens,1,7900 mp,nuxy,1,0.3 alphad,0 betad,7.8e-5 et,1,beam188 keyopt,1,2,1 keyopt,1,3,3 keyopt,1,4,1 keyopt,1,6,3 keyopt,1,7,1 keyopt,1,9,1 sectype,1,beam,rect,srect1,0 secdata,h,b,2,2 et,2,mass21 r,1,mend,0,0,0,0,0 n,1,0,0 n,2,0,349/1000 n,3,0,(6+265+46)/1000 n,4,0,6/1000 n,5,0,(6+265)/1000 e,1,4 e,4,5 e,5,3 e,3,2 type,2 real,1 e,3 /eshape,1,1 d,all,uy,0 d,all,uz,0 d,all,rotx,0 d,all,roty,0 d,1,all,0 gplot !-------------------- /solu keyw,pr_sgui,1 /output,null antype,trans,new outres,all,all kbc,0 deltim,dt *cfopen,fl,txt *vwrite,0,0 (E15.8,',',E15.8) ns=tend/dt+1 *do,n,2,ns,1 t=(n-1)*dt fd=0 *if,t,eq,dt,then fd=As *endif f,3,fx,fd time,t solve *get,dm,node,3,u,x *get,ds,node,1,u,x Vo=K2*(dm-ds) errv=0-Vo vs=-K1*Kp*errv d,1,velx,vs *vwrite,t,Vo (E15.8,',',E15.8) *enddo *cfclose finish /post26 nsol,2,2,u,x plvar,2 |
Appendix B. C Program for Experimental System
| #include <stdio.h> #include <stdlib.h> #include <math.h> #include <unistd.h> #include <string.h> #include "dask.h" #include <time.h> #include <conio.h> float alpha = 0.1; // 13.9728 Hz float Kp = 8; int tend = 10; float dt=1/790.1420; //dt=0.0011266 //------------------------ void pcon(float Kp, const char *flc, int tend) { long tdelay = 1000, trecord = tend * 1000000, tv = 0; U16 card_num = 0, Chai = 1, AdRange = AD_B_10_V, Value, Chao = 1; float Vfiltered = 0, *Vsens = NULL, *tval = NULL; Vsens = (float *)calloc(1000000, sizeof(float)); tval = (float *)calloc(1000000, sizeof(float)); FILE *fl; struct timespec t0, t; int n, ns = 0; I16 card, err; F64 Vsensor, Vsensor0, Vmotor; //--- card = Register_Card(PCI_9222, card_num); err = AO_VWriteChannel(card, Chao, 0); err = AI_ReadChannel(card, Chai, AdRange, &Value); AI_VoltScale(card, AdRange, Value, &Vsensor0); clock_gettime(CLOCK_MONOTONIC_RAW, &t0); printf("%f %f %s \n", Kp, alpha, flc); do { ns = ns + 1; err = AI_ReadChannel(card, Chai, AdRange, &Value); AI_VoltScale(card, AdRange, Value, &Vsensor); Vsensor = Vsensor - Vsensor0; if (ns == 0) Vfiltered = Vsensor; if (ns > 1) Vfiltered = alpha * Vsensor + (1 - alpha) * Vfiltered; Vsensor = Vfiltered; Vsens[ns] = Vsensor; float errv = 0-Vsensor; Vmotor = -Kp * errv; if (Vmotor > 10.0) Vmotor = 10.0; if (Vmotor < -10.0) Vmotor = -10.0; err = AO_VWriteChannel(card, Chao, Vmotor); clock_gettime(CLOCK_MONOTONIC_RAW, &t); tv = (t.tv_sec - t0.tv_sec) * 1000000L + (t.tv_nsec - t0.tv_nsec) / 1000; tval[ns] = tv / 1000000.0; usleep(tdelay); if (tv > trecord) break; } while (!kbhit()); err = AO_VWriteChannel(card, Chao, 0); Release_Card(card); fl = fopen(flc, "w"); for (n = 1; n < ns; n = n + 1) { fprintf(fl, "%f %f \n", tval[n], Vsens[n]); } fclose(fl); free(Vsens); free(tval); } //--------------------- void countdown(const char *message, int seconds) { for (int i = seconds; i > 0; i--) { printf("%s in %d seconds…\r", message, i); fflush(stdout); sleep(1); } printf("%s now starting…\n", message); } //--------------------------------------------------------- int main(int argc, char **argv) { countdown("Starting Control ON", 3); pcon(Kp, "vcon.txt",tend); FILE *gp = popen("gnuplot -persist", "w"); fprintf(gp,"plot '%s' with lines \n", "vcon.txt"); return 0; } |
References
- Wang, Y.; Wu, W.; Lou, X.; Görges, D. Adaptive vibration control for stabilisation of the Euler–Bernoulli beam with an unknown payload. Int. J. Control 2024, 1–12. [Google Scholar] [CrossRef]
- Lyu, Z.; Li, C.; Jia, T. Combined vibration control of flexible cantilever beam driven by MFC actuators and rotary motor. Acta Mech. 2024, 236, 305–320. [Google Scholar] [CrossRef]
- Li, W.; Yang, Z.; Li, K.; Wang, W. Hybrid feedback PID-FxLMS algorithm for active vibration control of cantilever beam with piezoelectric stack actuator. J. Sound Vib. 2021, 509, 116243. [Google Scholar] [CrossRef]
- Amer, Y.A.; EL-Sayed, A.T.; Abd EL-Salam, M.N. A suitable active control for suppression the vibrations of a cantilever beam. Sound Vib. 2022, 56, 89–104. [Google Scholar] [CrossRef]
- Saif, A.W.A.; Mohammed, A.A.; AlSunni, F.; El Ferik, S. Active Vibration Control of a Cantilever Beam Structure Using Pure Deep Learning and PID with Deep Learning-Based Tuning. Appl. Sci. 2024, 14, 11520. [Google Scholar] [CrossRef]
- Huang, Z.; Huang, F.; Wang, X.; Chu, F. Active vibration control of composite cantilever beams. Materials 2022, 16, 95. [Google Scholar] [CrossRef]
- Djokoto, S.S.; Dragašius, E.; Jūrėnas, V.; Agelin-Chaab, M. Controlling of vibrations in micro-cantilever beam using a layer of active electrorheological fluid support. IEEE Sens. J. 2019, 20, 4072–4079. [Google Scholar] [CrossRef]
- Cui, M.; Liu, H.; Jiang, H.; Zheng, Y.; Wang, X.; Liu, W. Active vibration optimal control of piezoelectric cantilever beam with uncertainties. Meas. Control 2022, 55, 359–369. [Google Scholar] [CrossRef]
- Umar, H.M.; Zhang, L.; Yu, R.; Gao, Z. Improved active vibration control of a cantilever beam using MFC actuators with Hammerstein model-based hysteresis modeling and VSS-FxLMS control algorithm. J. Low Freq. Noise Vib. Act. Control. 2024, 21, 14613484241295460. [Google Scholar] [CrossRef]
- Teoh, J.Q.; Tehrani, M.G.; Ferguson, N.S.; Elliott, S.J. Eigenvalue sensitivity minimisation for robust pole placement by the receptance method. Mech. Syst. Signal Process. 2022, 173, 108974. [Google Scholar] [CrossRef]
- Karagülle, H.; Malgaca, L.; Öktem, H.F. Analysis of active vibration control in smart structures by ANSYS. Smart Mater. Struct. 2004, 13, 661. [Google Scholar] [CrossRef]
- Ito, T.; Tagami, M.; Tagawa, Y. Active vibration control for high-rise buildings using displacement measurements by image processing. Struct. Control Health Monit. 2022, 29, e3136. [Google Scholar] [CrossRef]
- Ramírez-Neria, M.; Morales-Valdez, J.; Yu, W. Active vibration control of building structure using active disturbance rejection control. J. Vib. Control 2022, 28, 2171–2186. [Google Scholar] [CrossRef]
- Gheni, E.Z.; Al-Khafaji, H.M.; Alwan, H.M. A deep reinforcement learning framework to modify LQR for an active vibration control applied to 2D building models. Open Eng. 2024, 14, 20220496. [Google Scholar] [CrossRef]
- Zhang, Q.; Han, S.; El-Meligy, M.A.; Tlija, M. Active control vibrations of aircraft wings under dynamic loading: Introducing PSO-GWO algorithm to predict dynamical information. Aerosp. Sci. Technol. 2024, 153, 109430. [Google Scholar] [CrossRef]
- He, T.; Zhu, G.G.; Swei, S.S.M.; Su, W. Smooth-switching LPV control for vibration suppression of a flexible airplane wing. Aerosp. Sci. Technol. 2019, 84, 895–903. [Google Scholar] [CrossRef]
- Li, W.; Yang, Z.; Liu, K.; Wang, W. MIMO multi-frequency active vibration control for aircraft panel structure using piezoelectric actuators. Int. J. Struct. Stab. Dyn. 2023, 23, 2350157. [Google Scholar] [CrossRef]
- Dong, L.; Chen, Z.; Sun, M.; Sun, Q. Phase compensation active disturbance rejection control for shimmy vibration with magnetorheological damper of aircraft. Expert Syst. Appl. 2023, 213, 119126. [Google Scholar] [CrossRef]
- Sahin, M.; Karadal, F.M.; Yaman, Y.; Kircali, O.F.; Nalbantoglu, V.; Ulker, F.D.; Caliskan, T. Smart structures and their applications on active vibration control: Studies in the Department of Aerospace Engineering, METU. J. Electroceramics 2008, 20, 167–174. [Google Scholar] [CrossRef]
- Prakash, S.; Kumar, T.R.; Raja, S.; Dwarakanathan, D.; Subramani, H.; Karthikeyan, C. Active vibration control of a full scale aircraft wing using a reconfigurable controller. J. Sound Vib. 2016, 361, 32–49. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures, 2nd ed.; Prentice-Hall: Hoboken, NJ, USA, 2014. [Google Scholar]
- Rao, S.S. Mechanical Vibrations in SI Units, 6th ed.; Pearson Education Limited: Chennai, India, 2018; 1147p. [Google Scholar]
- Yavuz, Ş.; Akdağ, M.; Karagülle, H. A fast processing method to perform transient analysis for vibration control. Simul. Model. Pract. Theory 2020, 104, 102152. [Google Scholar] [CrossRef]
- Figliola, R.S.; Beasley, D.E. Theory and Design for Mechanical Measurements, 15th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Tan, L. Digital Signal Processing; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Available online: http://airfoiltools.com/airfoil/details?airfoil=naca4412-il (accessed on 3 January 2025).
- Brown, J.D.; Mustafa, M.; Moore, K.J. Vibration mitigation of a model aircraft with high-aspect-ratio wings using two-dimensional nonlinear vibration absorbers. Int. J. Non-Linear Mech. 2024, 167, 104878. [Google Scholar] [CrossRef]
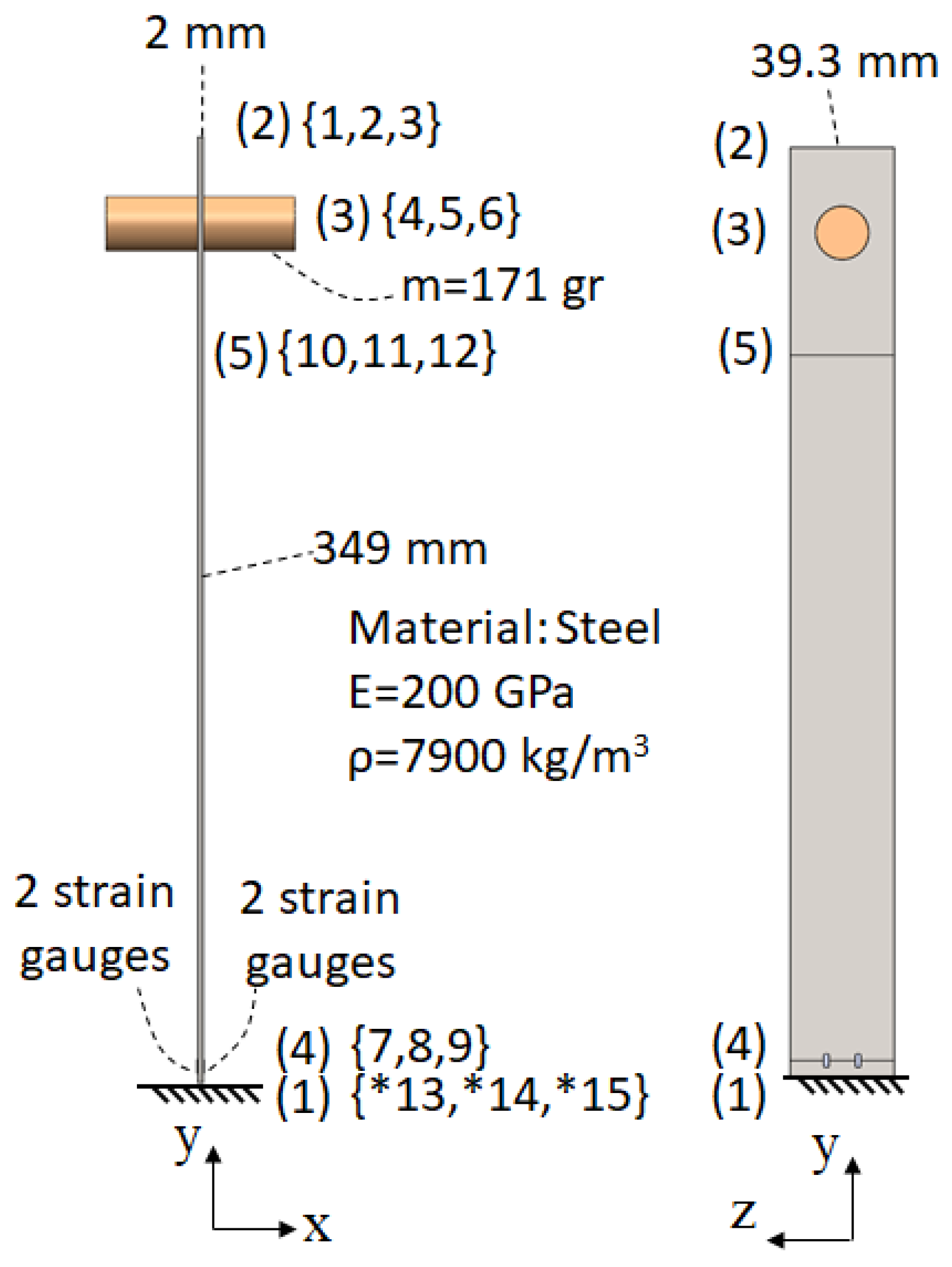
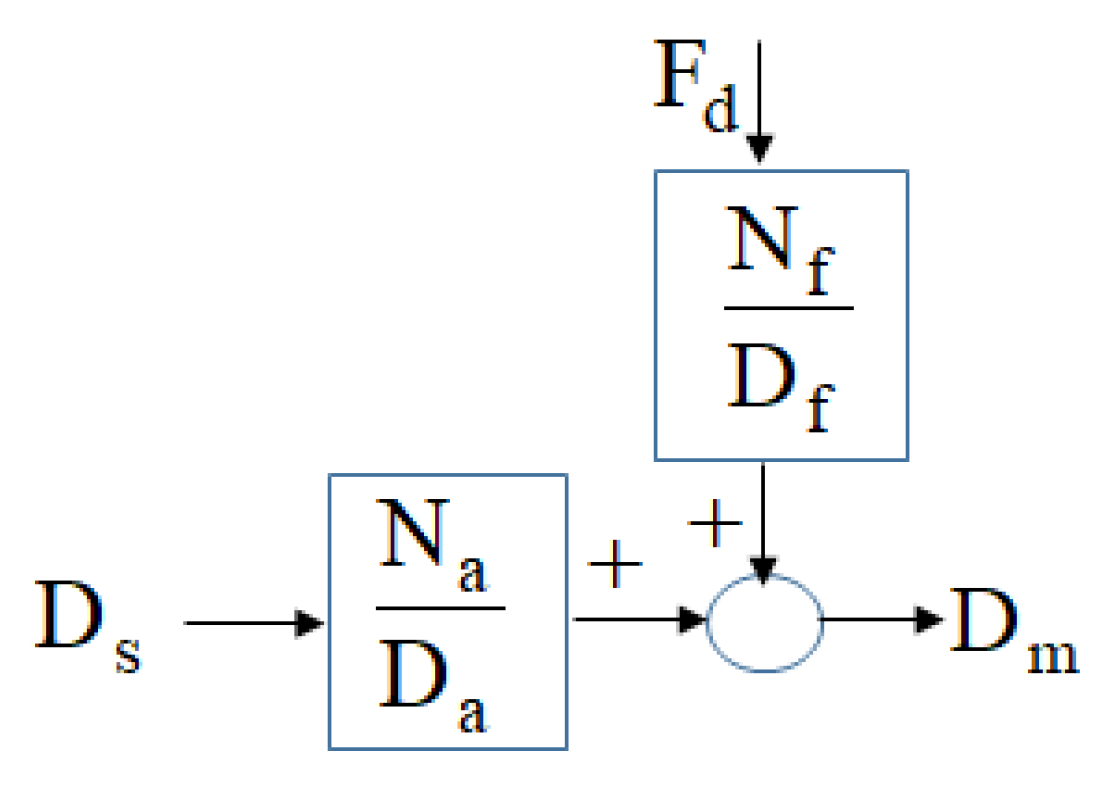
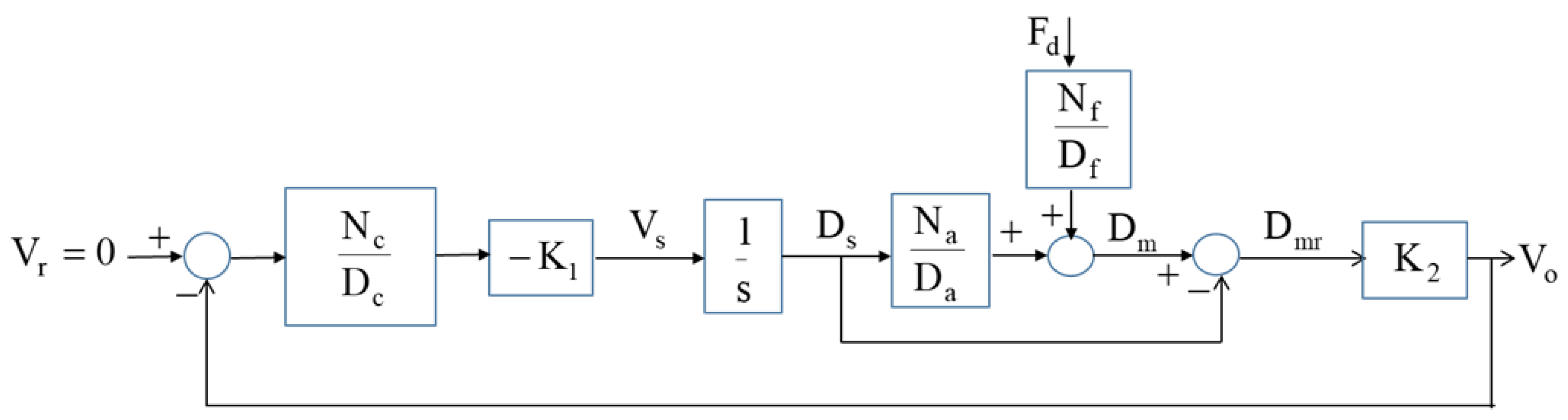
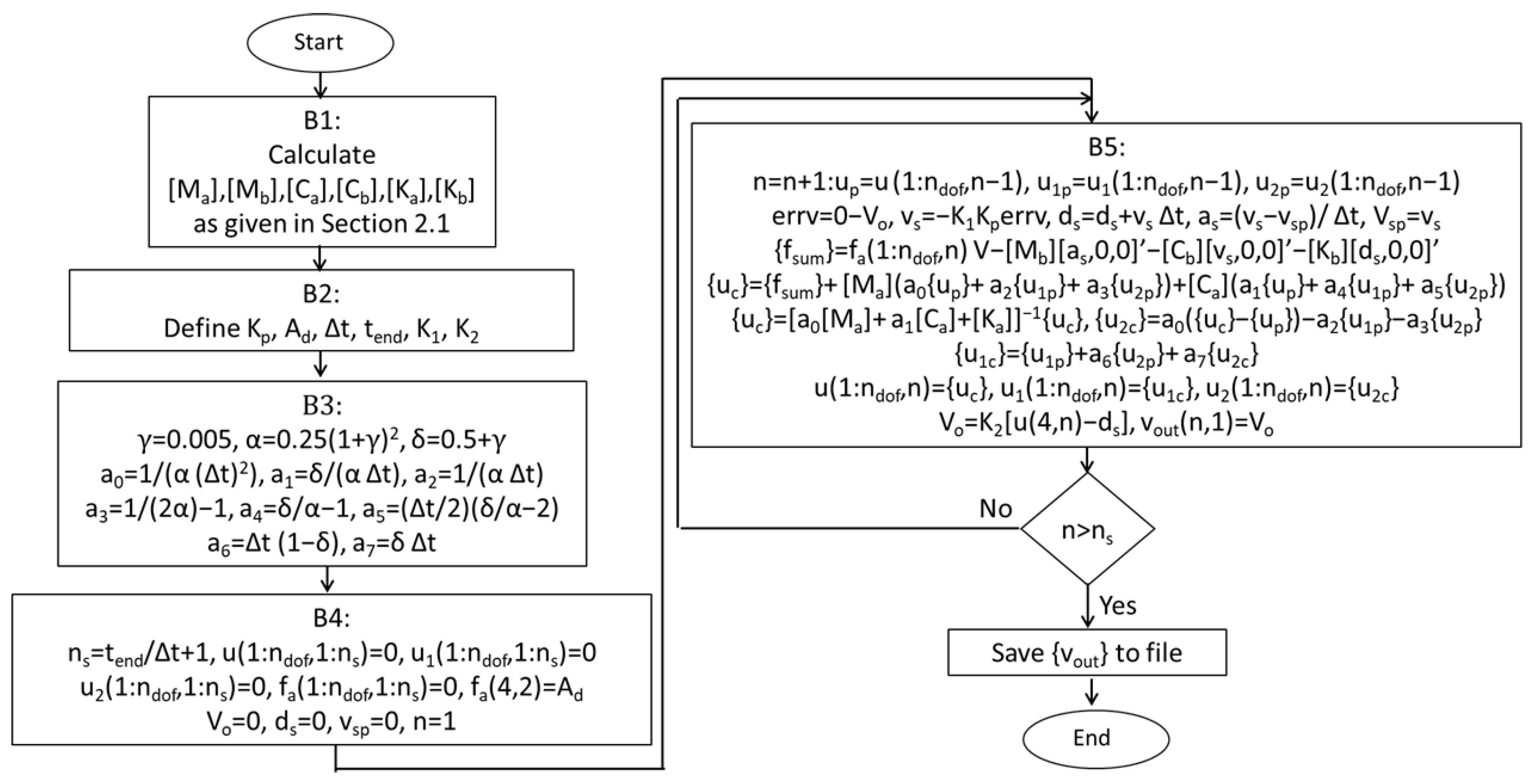

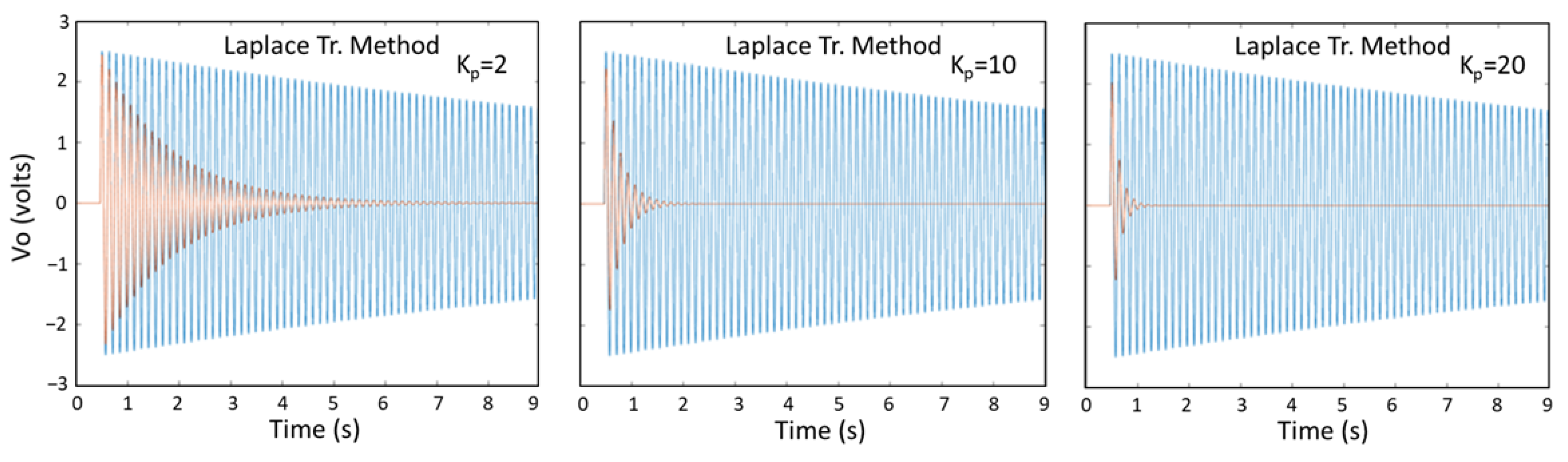

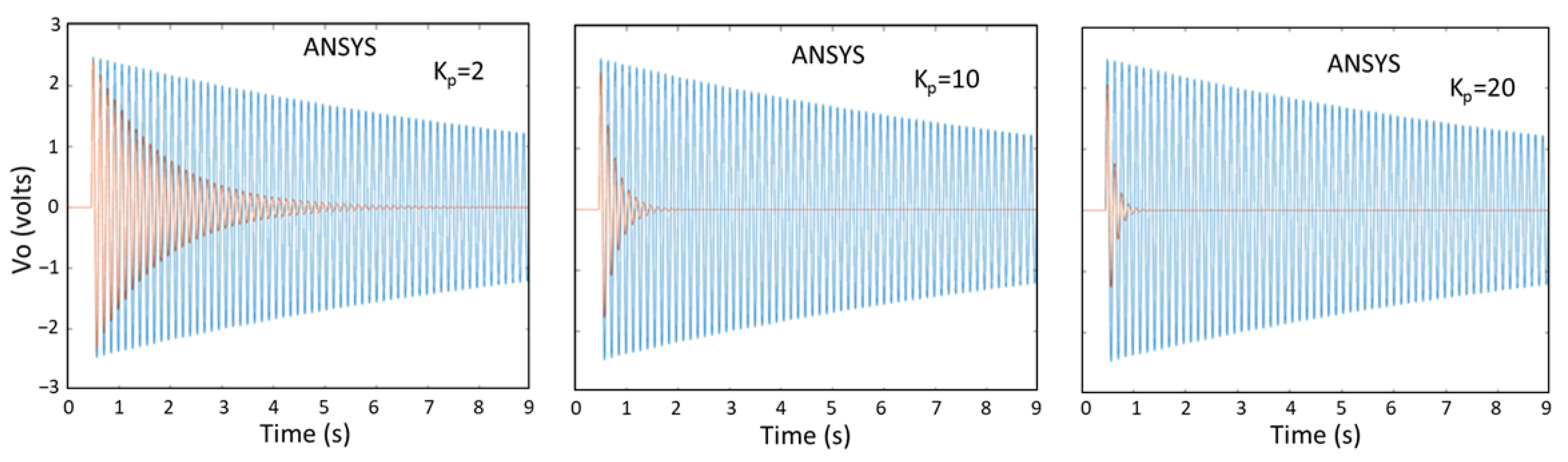
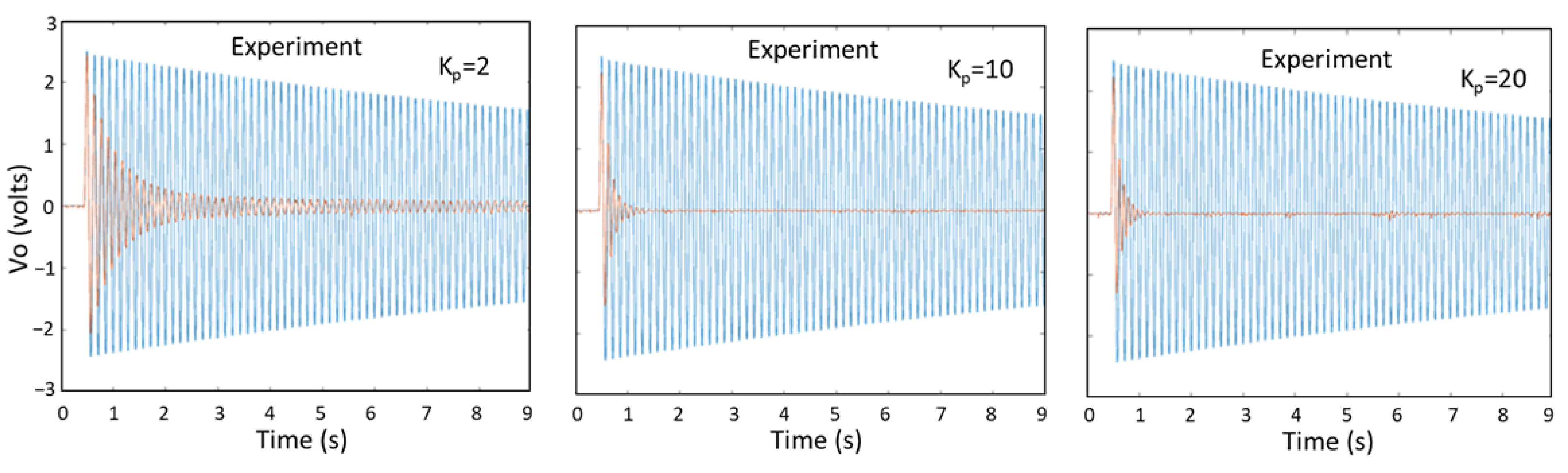
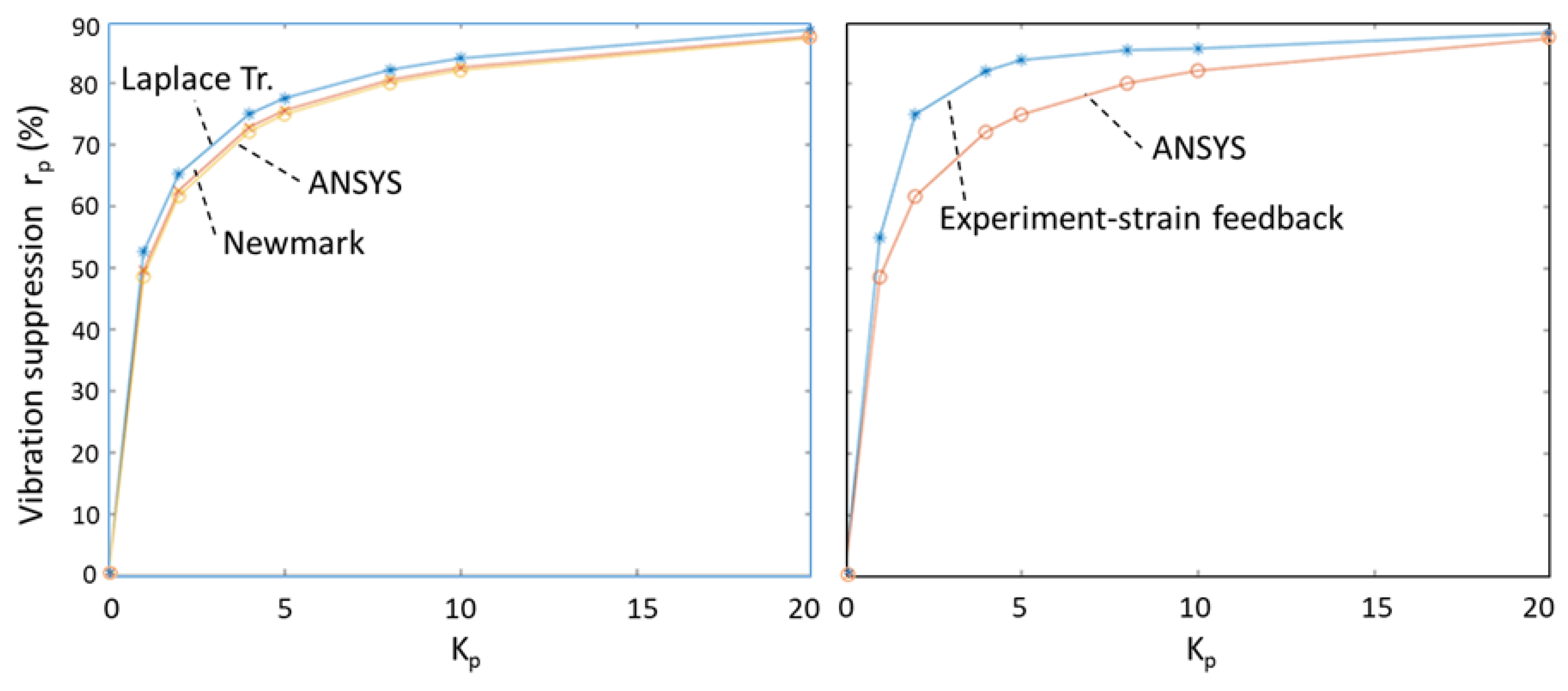
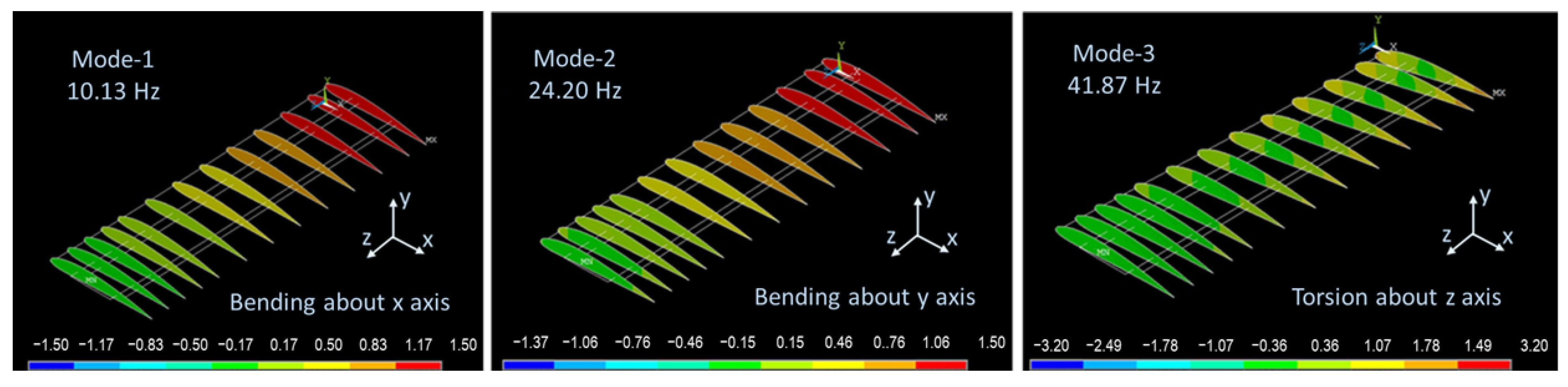
| FE | Nodes | H (mm) | (deg) | Assembly |
|---|---|---|---|---|
| 1 | (1)–(4) | 6 | 90 | *13, *14, *15, 7, 8, 9 |
| 2 | (4)–(5) | 265 | 90 | 7, 8, 9, 10, 11, 12 |
| 3 | (5)–(3) | 46 | 90 | 10, 11, 12, 4, 5, 6 |
| 4 | (3)–(2) | 32 | 90 | 4, 5, 6, 1, 2, 3 |
| Kp = 0 | Kp = 1 | Kp = 2 | Kp = 4 | Kp = 5 | Kp = 8 | Kp = 10 | Kp = 20 | |
|---|---|---|---|---|---|---|---|---|
| Experiment | 1.3190 | 0.5930 | 0.3307 | 0.2380 | 0.2146 | 0.1934 | 0.1900 | 0.1565 |
| Laplace Tr. | 1.3969 | 0.6627 | 0.4859 | 0.3501 | 0.3143 | 0.2499 | 0.2240 | 0.1590 |
| Newmark | 1.2667 | 0.6385 | 0.4746 | 0.3447 | 0.3101 | 0.2472 | 0.2217 | 0.1577 |
| ANSYS | 1.2484 | 0.6417 | 0.4787 | 0.3484 | 0.3125 | 0.2501 | 0.2244 | 0.1597 |
| Kp = 0 | Kp = 2 | Kp = 4 | Kp = 8 | Kp = 16 | Kp = 24 | Kp = 48 | |
|---|---|---|---|---|---|---|---|
| ANSYS 1 | 1.0047 | 0.6127 | 0.4747 | 0.3538 | 0.2575 | 0.2124 | 0.1520 |
| ANSYS 2 | 1.0372 | 0.6210 | 0.4790 | 0.3560 | 0.2588 | 0.2135 | 0.1533 |
| ANSYS 3 | 1.0051 | 0.6128 | 0.4747 | 0.3538 | 0.2575 | 0.2124 | 0.1520 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bülbül, İ.; Akdağ, M.; Karagülle, H. Active Vibration Control of Cantilever Structures by Integrating the Closed Loop Control Action into Transient Solution of Finite Element Model and an Application to Aircraft Wing. Machines 2025, 13, 379. https://doi.org/10.3390/machines13050379
Bülbül İ, Akdağ M, Karagülle H. Active Vibration Control of Cantilever Structures by Integrating the Closed Loop Control Action into Transient Solution of Finite Element Model and an Application to Aircraft Wing. Machines. 2025; 13(5):379. https://doi.org/10.3390/machines13050379
Chicago/Turabian StyleBülbül, İlker, Murat Akdağ, and Hira Karagülle. 2025. "Active Vibration Control of Cantilever Structures by Integrating the Closed Loop Control Action into Transient Solution of Finite Element Model and an Application to Aircraft Wing" Machines 13, no. 5: 379. https://doi.org/10.3390/machines13050379
APA StyleBülbül, İ., Akdağ, M., & Karagülle, H. (2025). Active Vibration Control of Cantilever Structures by Integrating the Closed Loop Control Action into Transient Solution of Finite Element Model and an Application to Aircraft Wing. Machines, 13(5), 379. https://doi.org/10.3390/machines13050379






