A Spatial Five-Bar Linkage as a Tilting Joint of the Breeding Blanket Transporter for the Remote Maintenance of EU DEMO

Abstract

The future fusion power plant EU DEMO will generate its own tritium fuel through the use of segmented breeding blankets (BBs), which must be replaced from time to time due to material damage caused by high-energy neutrons from the plasma. A vertical maintenance architecture has been proposed, using a robotic remote handling tool (transporter) to disengage the 180 $\mathrm{t}$ and 125 $\mathrm{t}$ outboard and inboard segments and manipulate them through an upper port. Safe disengagement without damaging the support structures requires the use of high-capacity tilting joints in the transporter. The trolley tilting mechanism (TTM) is proposed as a novel, compact, high-capacity robotic joint consisting of a five-bar spatial mechanism integrated in the BB transporter trolley link. A kinematic model of the TTM is established, and the analytical input–output relationships, including the position-dependent transmission ratio, are derived and used to guide the design and optimization of the mechanism. The model predictions are compared to an ADAMS multibody simulation and to the results of an experiment conducted on a down-scaled prototype, both of which validate the model accuracy.

1. Introduction

The development of fusion energy technology could lead to the deployment of high-output, carbon-free tokamak reactors in the future. 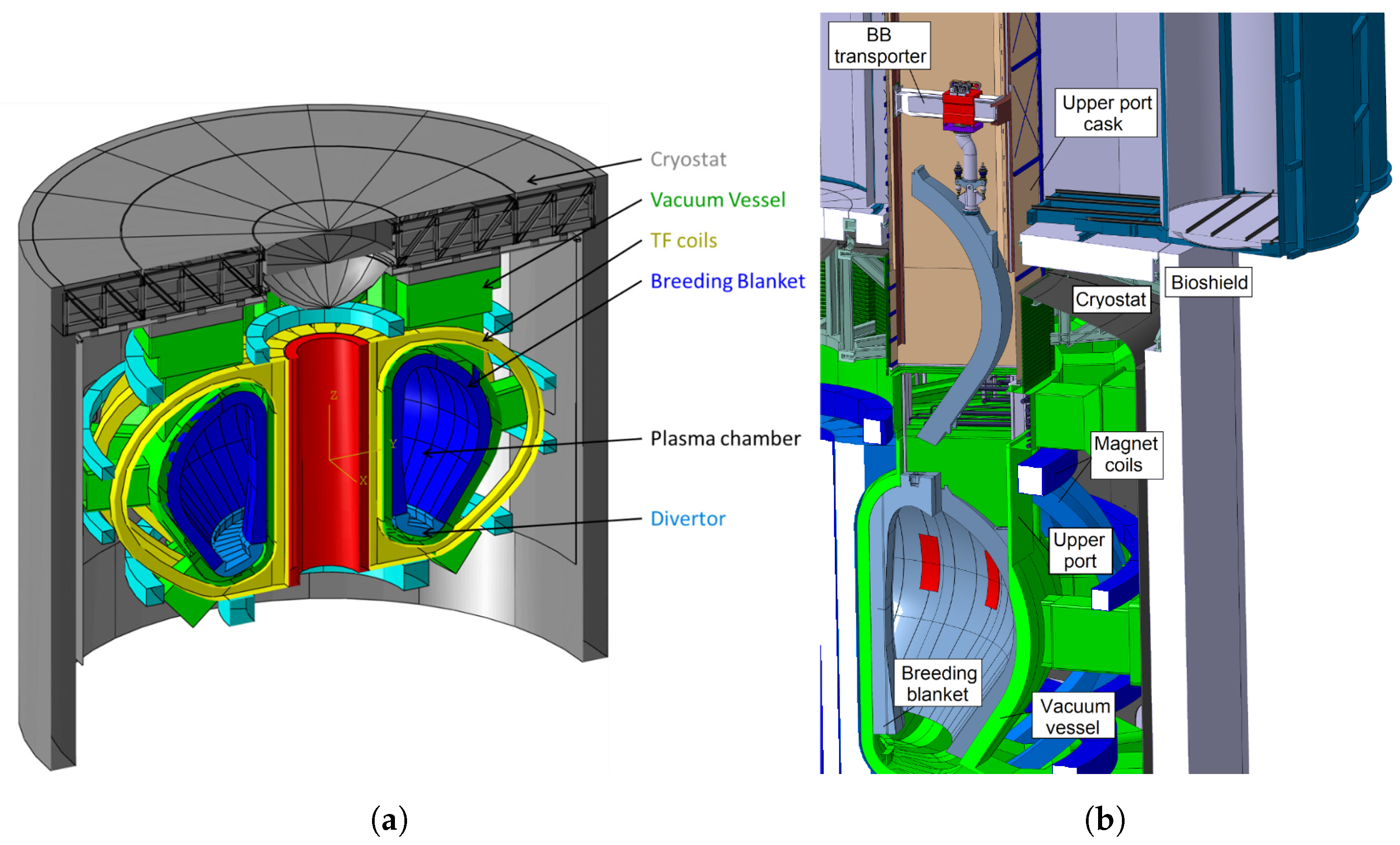ITER, the world’s largest experimental tokamak, is currently under construction, and the European successor, EU DEMO, is now being designed with the aim of demonstrating the technical and economic readiness of fusion energy while providing net electricity to the grid [1]. In addition to being larger and experiencing greater heat and mechanical loads than ITER, the DEMO tokamak (Figure 1a) will also integrate a self-sufficient tritium lifecycle based on breeding blankets (BBs) lining the inner vacuum vessel [2]. The BBs will be the largest and heaviest in-vessel components and will require occasioreplacement due to material degradation from neutron irradiation. It is a requirement that this remote maintenance task be carried out safely while minimizing the down-time of the plant [3].

Unlike ITER, European DEMO will use a vertical maintenance architecture for the BBs, which has also been considered for earlier tokamaks including INTOR [4]. This entails the maintenance of three 180 $\mathrm{t}$ outboard and two 125 $\mathrm{t}$ BB segments within each of the 16 tokamak sectors using a mobile cask that docks to a sector’s upper port and contains the necessary remote handling (RH) equipment to remove or replace a BB segment. This concept is illustrated in Figure 1b, depicting a robotic RH tool vertically transporting a BB segment within the confines of the vacuum vessel, upper port, and cask. This tool is the BB vertical transporter (BBVT), which was previously introduced in [5,6]. The idealized handling task requires the 3-D translation of each BB segment, plus rotation about the vertical and toroidal axes, in order to avoid collisions with the walls and neighboring BB segments during removal. Ignoring the trolley tilting joint, which is the subject of this work, the BBVT can be analyzed as a redundant serial robotic manipulator with six joints enabling this 5-degree-of-freedom task. A detailed kinematic model of the BBVT is derived in [7].

Figure 1. The DEMO tokamak and its vertical breeding blanket maintenance concept. (a) DEMO tokamak components; (b) BBVT handles a BB segment via the upper port. Reproduced from [6].

Figure 1. The DEMO tokamak and its vertical breeding blanket maintenance concept. (a) DEMO tokamak components; (b) BBVT handles a BB segment via the upper port. Reproduced from [6].

Attachment and support structures for the BB segments, seen in Figure 2a, were introduced in [8] and further developed in [9,10]. These include radial, vertical, and toroidal support structures which react against the different loading conditions of the BB segments during the operation of the tokamak. When the tokamak is powered down, as is the case during maintenance, each BB segment is vertically supported only at the bottom and can be lifted by a countersunk interface in the portion of the top surface exposed in the port [11]. A short vertical translation and toroidal tilt are required to free each BB segment from its lower supports.

Besides the vertical load, the BBVT is also subject to large moments [12]. This is due to the fact that the countersunk interface by which each BB segment is grasped is horizontally offset from the center of mass to be accessible by the BBVT inside the upper port. However, rather than being automatically reacted by the BBVT when initially loading a BB segment for lifting, these moments are primarily reacted by the radial and toroidal BB segment supports. This is a problem, as these loads could damage the supports as the contact surface areas shrink during disengagement. This is of particular concern for the toroidal shear keys. Thus, these horizontal moment components must be actively counteracted by the BBVT to avoid loading the supports during disengagement, as illustrated in Figure 2b.

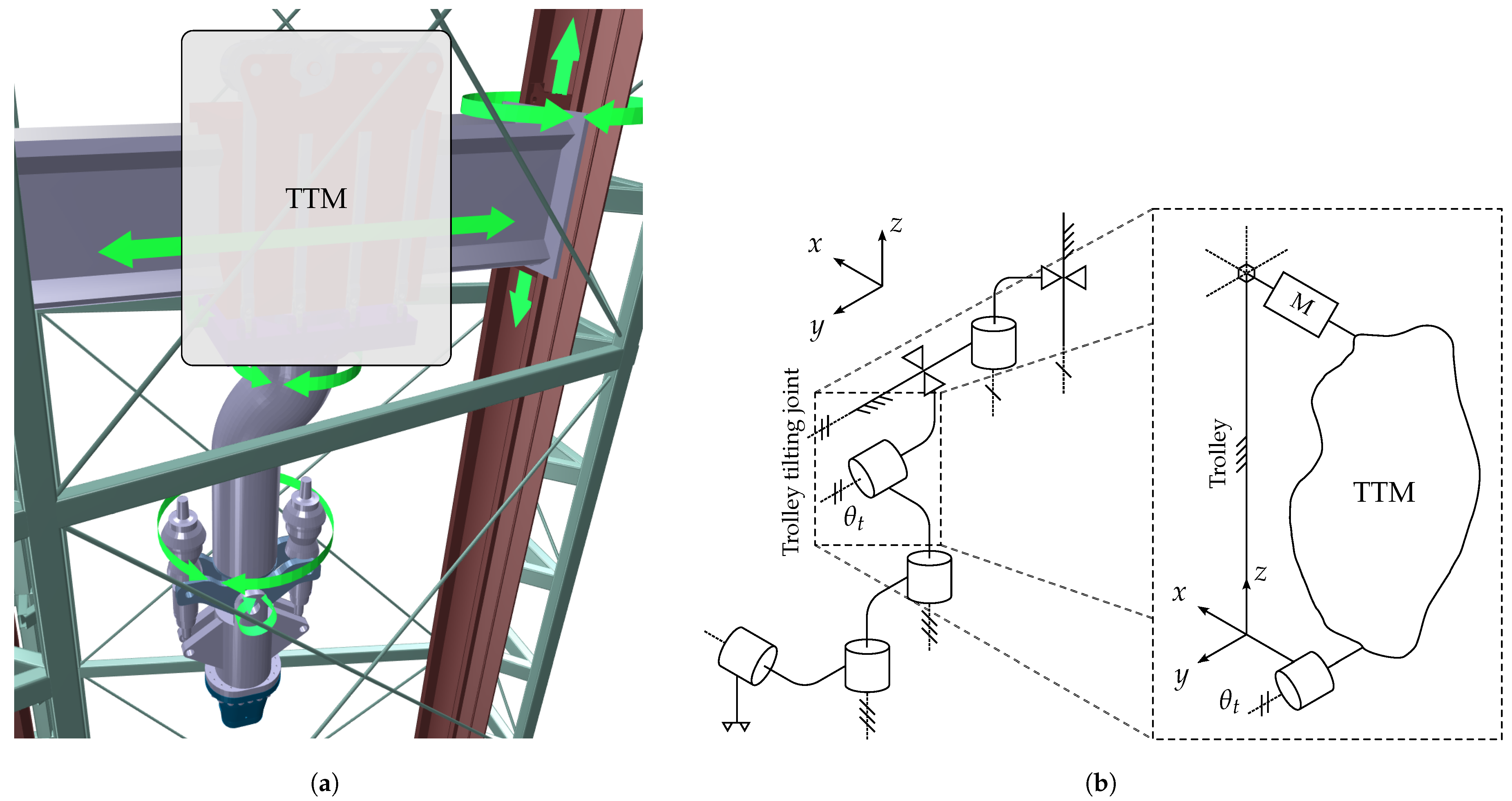
The need to counteract the BB segment support reactions during initial lifting motivates the incorporation of a radial tilting joint in addition to the toroidal tilting joint required for the kinematic BB segment removal task. Due to space constraints, the toroidal tilting joint is adjacent to the gripper and is referred to as the gripper tilting joint, while the radial tilting joint is incorporated in the central sliding trolley link and is referred to as the trolley tilting joint. Kinematically, this joint is also useful for adjusting the radial tilt by approximately 0.5° to 1.5° in order to ensure proper alignment to the interface during engagement in the non-ideal task. A major consideration for the design of the trolley tilting mechanism (TTM) is to minimize the trolley’s horizontal footprint, since this affects the workspace of the BBVT. Minimization of the required actuator size is also important in this regard, thus a mechanism with favorable mechanical advantage is sought. Figure 3 shows the location of the TTM as part of the BBVT both visually and schematically.

A five-bar RSRRR mechanism is proposed and designed in this work to address this unique set of challenges for the TTM. A kinematic model of the linkage is established and applied to analyze and optimize the design, and numerical simulations and experiments are performed to validate the design and the kinematic model.

Spatial linkages have been well studied. In 1983, ref. [13] derived generic but relatively complex (in terms of the number of coordinates and constraint equations) kinematic models of all single-loop spatial five-bar mechanisms, including the RSRRR, as combinations of different three-bar mechanisms with a crank. In 1996, ref. [14] analyzed the mobility of spatial four- and five-bar mechanisms with revolute and spherical joints. The bulk of recent research on applications of five-bar mechanisms appears to focus on spherical mechanisms, such as a spherical remote center of motion [15], a translational parallel manipulator based on two five-bar mechanisms [16], and a spherical adaptive gripper mechanism [17]. The mechanism proposed in this work is also closely related to the spatial four-bar RSSR linkage, the kinematics of which have been thoroughly analyzed [18,19] and which has found many applications, such as the recently designed steering mechanism of a gravity-powered vehicle [20]. Linkages with compliant members have also been studied extensively and applied widely, such as the use of a method for the analysis of flexible RSSR mechanisms using the pseudo-rigid-body model [21] and a mechanism for improved safety in robotic surgery [22].

The current work is divided into six sections. In Section 2, Mechanism Design, the design requirements and considerations for the TTM are detailed, and the current design is presented. In Section 3, Kinematics, the kinematic constraint equations for the TTM are derived and an analytical solution for the forward kinematics is presented, along with the configuration-dependent transmission ratio. In Section 4, Mechanical Design Optimization, the kinematic model is used as a basis to optimize two of the bar lengths with respect to range of motion and maximum static loads on the mechanism output and input during BB segment maintenance. In Section 5, Verification and Preliminary Down-Scaled Experiment, the kinematic model is verified by comparisons with a numerical simulation in ADAM and further validated by initial experiments on a down-scaled TTM prototype. Finally, in Section 6, Discussion and Conclusions, the results and contributions are discussed, and limitations and future work presented.

2. Mechanism Design

The main requirements for the TTM are to “preload” the 180 $\mathrm{t}$ outboard and 125 $\mathrm{t}$ inboard lateral BB segments with a radial moment to counter the formation of reactions within the support structures during lifting and to provide the ability to adjust the radial tilt of the gripper by a small angle (about 0.5° to 1.5°) in order to align it during engagement with the BB segment’s countersunk interface. Note that the latter requirement does not apply in the ideal case, where there should be no misalignments, gaps, or deformations which would require a radial gripper tilt. Thus, the idealized range of motion requirement is zero, while the realistic requirement depends on the rough estimation of these unknowns. This discourages the use of kinematic synthesis techniques based on the required output motion.

As indicated in Figure 3b, the TTM is placed as the fourth joint of the BBVT, between the links referred to as the trolley and the trunk. The reason for this is that the space adjacent to the gripper itself is taken by the gripper’s tilting joint, and the trolley is the next-closest link with available space. However, even here, the horizontal space is limited as the trolley (essentially a box) must fit within the constricted upper port while the BBVT is engaged with each of the 5 BB segments. As the trolley slides on a large radial rail, the radial faces are nearly inaccessible. Also, the lower vertical face is largely occupied by the trunk connection. Thus, the only practical location for the TTM actuator(s) is on the upper face, and the output radial motion must be applied to a tilting plate sitting between the trolley and trunk. The problem, then, is to connect the actuator(s) and tilting plate while affecting the toroidal and radial dimensions of the trolley assembly minimally. This combination of requirements and restrictions is difficult to solve compactly and reliably using only conventional transmission elements such as gearboxes, belts, chains, or screws.

Thus, a compact five-bar mechanism providing good mechanical advantage was designed, as shown in Figure 4a. It is a spatial linkage with structure RSRRR, where “R” denotes a revolute joint and “S” denotes a spherical joint, with the Grübler criterion equal to 1. The four mobile bars have been marked with their lengths a, b, c, and d. The first (a) is the eccentricity of a cam connected to the input shaft. This is connected via a radial bearing with spherical housing to the rod b. At its lower end, the rod attaches to a short connector c, which connects the rod and the tilting plate d using pins at right angles. The plate connects back to the trolley at the tilting hinge, which constitutes the TTM output.

The design of the mechanism is inspired by a planar four-bar mechanism, where a mechanical advantage is gained by the relative sizing of the bars connected to the input and output joints, while the connecting bars in between serve primarily to transfer the load. The mechanism wraps around the vertical and toroidal faces of the trolley, which is required in order to not interfere with the radial rail. However, a planar four-bar mechanism cannot carry this out while having good leverage and avoiding collision with the trolley. Instead, the input axis located above the trolley is made to be toroidal and perpendicular to the output axis. Then, a short extra bar (c) is added to connect the radial output and toroidal input. The main connecting bar (b) must then be able to tilt both toroidally and radially due to the interconnected motion of the input and output bars, necessitating the use of a spherical connection between a and b, in this case chosen as a radial bearing with spherical housing. This configuration also gives space radially along the top surface of the trolley to place multiple tilting mechanisms in parallel to reduce the load on the input actuator(s).

3. Kinematics

The optimization and control of the TTM require an accurate kinematic model, which will be derived in this section. Although kinematic models of five-bar RSRRR mechanisms exist, since the TTM is a special case, a model using only five relative rotation coordinates and 4 equations (compared with 15 equations in [13]) is derived based on the schematic diagram in Figure 4b. The coordinates are ${\theta }_1$, ${\theta }_2$, ${\theta }_3$, ${\theta }_4$, and ${\theta }_t$, where ${\theta }_1$ is the joint variable associated with the input of the mechanism and ${\theta }_t$ is associated with the output. The input shaft and output shaft angles are each defined as being zero when their respective bars (a and d) are horizontal. The following assumptions are made: the rotation axes of the joints $\left({\theta }_1,{\theta }_t\right)$ and $\left({\theta }_3,{\theta }_4\right)$ are pairwise perpendicular, and the rotation axes of the joints $\left({\theta }_2,{\theta }_4,{\theta }_t\right)$ are all parallel.

With reference to the schematic (Figure 4b), the following four independent equations constrain the kinematics:

$$\begin{array}{cc}\hfill acos{\theta }_1-bsin{\theta }_3& =p_y\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill dcos{\theta }_t-\left(c+bcos{\theta }_3\right)sin{\theta }_2& =p_x\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill -dsin{\theta }_t-\left(c+bcos{\theta }_3\right)cos{\theta }_2-asin{\theta }_1& =p_z\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\theta }_2+{\theta }_4& ={\theta }_t.\hfill \end{array}$$

(4)

where $(p_x,p_y,p_z)$ are the constant coordinates of the mechanism output point relative to the input point. For simplicity, and to ensure that ${\theta }_t=0$ when ${\theta }_1=0$, these will be assumed to take on the values $p_x=d$, $p_y=a$, and $p_z=-b-c$ when the equations are applied throughout this work, although it is not strictly necessary. For example, in the case of replacing the input cam with one of different size $a_n\ne a$ without also adjusting $b+c$ and d, this would not hold.

3.1. Forward Kinematic Solution

The forward kinematic solution presented here follows from the assumption that only ${\theta }_1$ is known, and it describes a procedure for calculating the remaining coordinates in the model. However, solutions are not substituted to be in terms of only ${\theta }_1$, since this quickly leads to complex nested expressions.

Treating the input angle ${\theta }_1$ as given, Equation (1) gives ${\theta }_3$ directly:

$$\begin{array}{cc}\hfill sin{\theta }_3& ={\displaystyle \frac{a}{b}}\left(cos{\theta }_1-{\displaystyle \frac{p_y}{a}}\right)\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill cos{\theta }_3& =\pm \sqrt{1-{sin}^2{\theta }_3}\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {\theta }_3& =atan2\left(sin{\theta }_3,cos{\theta }_3\right).\hfill \end{array}$$

(7)

By squaring and summing Equations (2) and (3) and utilizing Equation (4), ${\theta }_4$ can be found in terms of ${\theta }_1$ and ${\theta }_3$:

$$\begin{array}{cc}\hfill sin{\theta }_4& ={\displaystyle \frac{p_x^2-d^2+{\left(-p_z-asin{\theta }_1\right)}^2-{\left(c+bcos{\theta }_3\right)}^2}{2d(c+bcos{\theta }_3)}}\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill cos{\theta }_4& =\pm \sqrt{1-{sin}^2{\theta }_4}\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill {\theta }_4& =atan2\left(sin{\theta }_4,cos{\theta }_4\right).\hfill \end{array}$$

(10)

Physically valid and non-extraneous solutions are obtained by only taking the positive solutions for Equations (6) and (9).

Using Equation (4), ${\theta }_2$ can be eliminated from Equations (2) and (3). The system of equations can then be solved for ${\theta }_t$ in terms of known and derived angles (${\theta }_1$, ${\theta }_3$, and ${\theta }_4$) by taking advantage of the fact that a system of equations of the form

$$\begin{array}{cc}\hfill pcos{\theta }_t-qsin{\theta }_t& =r\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill psin{\theta }_t+qcos{\theta }_t& =s\hfill \end{array}$$

(12)

has the following solution:

$$\theta =atan2\left(ps-qr,pr+qs\right).$$

(13)

Thus,

$$\begin{array}{c}\hfill {\theta }_t=atan2\left(d+sin{\theta }_4\left(c+bcos{\theta }_3\right)\right)\left(-p_z-asin{\theta }_1\right)-p_{x}cos{\theta }_4\left(c+bcos{\theta }_3\right),\\ \hfill p_x\left(d+sin{\theta }_4\left(c+bcos{\theta }_3\right)\right)+cos{\theta }_4\left(c+bcos{\theta }_3\right)\left(-p_z-asin{\theta }_1\right).\end{array}$$

(14)

To find ${\theta }_2$, the solutions for ${\theta }_4$ and ${\theta }_t$ can be plugged into Equation (4). Alternatively, the same procedure used to find ${\theta }_t$ can be applied, but using Equation (4) to eliminate ${\theta }_t$ from Equations (2) and (3). Also, rather than relying on Equation (13), alternative forms of the solutions for ${\theta }_t$ and/or ${\theta }_2$ can be found using the tangent of the half-angle substitution method.

3.2. Transmission Ratio and Mechanical Advantage

The constraint Equations (1)–(3) can be differentiated with respect to time to give the following velocity constraints:

$${\mathbf{\Phi }}_{\mathbf{\Theta }}\dot{\mathbf{\Theta }}=\mathbf{0},$$

(15)

where $\dot{\mathbf{\Theta }}$ is the vector of time derivatives of the coordinates, and ${\mathbf{\Phi }}_{\mathbf{\Theta }}$ is the Jacobian matrix of the constraint equations:

$${\mathbf{\Phi }}_{\mathbf{\Theta }}=\left[\begin{array}{ccccc}asin\left({\theta }_1\right)& 0& bcos\left({\theta }_3\right)& 0& 0\\ 0& -cos\left({\theta }_2\right)c+bcos\left({\theta }_3\right)& bsin\left({\theta }_2\right)sin\left({\theta }_3\right)& 0& -dsin\left({\theta }_t\right)\\ acos\left({\theta }_1\right)& -sin\left({\theta }_2\right)c+bcos\left({\theta }_3\right)& -bcos\left({\theta }_2\right)sin\left({\theta }_3\right)& 0& dcos\left({\theta }_t\right)\\ 0& -1& 0& -1& 1\end{array}\right]$$

(16)

The system of four equations in Equation (15) can be solved to find the ratio of input and output speeds or transmission ratio $\eta$:

$$\eta ={\displaystyle \frac{{\dot{\theta }}_1}{{\dot{\theta }}_t}}=-{\displaystyle \frac{d}{a}}\left({\displaystyle \frac{cos{\theta }_{3}cos{\theta }_4}{cos{\theta }_{1}cos{\theta }_{2}cos{\theta }_3+sin{\theta }_{1}sin{\theta }_3}}\right)$$

(17)

By the conservation of energy and neglecting inertia and friction forces, the input power must equal the output power, leading to the assertion of the mechanical advantage provided by the mechanism:

$${\displaystyle \frac{{\tau }_1}{{\tau }_t}}={\left({\displaystyle \frac{{\dot{\theta }}_1}{{\dot{\theta }}_t}}\right)}^{-1}=-{\displaystyle \frac{a}{d}}\left({\displaystyle \frac{cos{\theta }_{1}cos{\theta }_{2}cos{\theta }_3+sin{\theta }_{1}sin{\theta }_3}{cos{\theta }_{3}cos{\theta }_4}}\right)=-{\displaystyle \frac{a}{d}}g,$$

(18)

where ${\tau }_1$ and ${\tau }_t$ are the torques at the input shaft and output hinge, respectively.

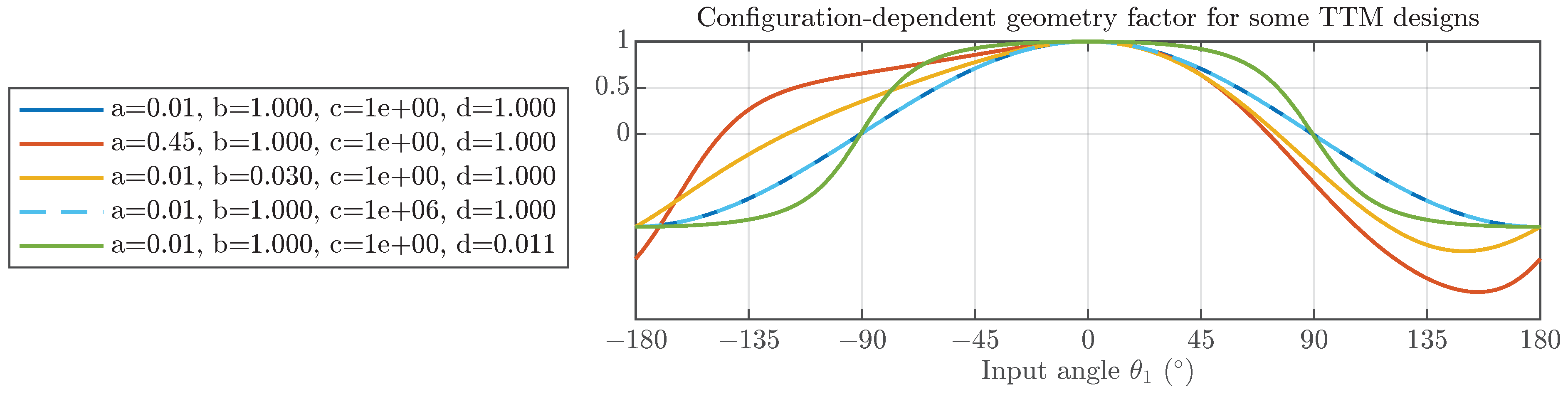
The factor in parentheses in Equation (18) depends on the configuration of the mechanism, as well as the chosen bar lengths. This is illustrated by Figure 5, where factor g is plotted as a function of the input angle for several TTM designs. As can be seen, g is sensitive to a, b, or d but does not depend strongly on c. When $g=0$, the mechanism is in a kinematic singularity where the output velocity goes to 0 regardless of the input velocity.

3.3. Inverse Kinematics

Although an analytical solution of the kinematic equations for ${\theta }_t$ exists when ${\theta }_1$ is known, as described in Section 3.1 above, the inverse is not true. Instead, the mechanism’s configuration can be found numerically using the Newton–Raphson method with the constraint Jacobian Equation (16), i.e., iteratively solving for ${\mathbf{\Theta }}_{i+1}$ with an equation of the following form:

$$\mathbf{\Phi }(\mathbf{\Theta },t)\approx \mathbf{\Phi }\left({\mathbf{\Theta }}_i\right)+{\mathbf{\Phi }}_{\mathit{q}}\left({\mathbf{\Theta }}_i\right)\left({\mathbf{\Theta }}_{i+1}-{\mathbf{\Theta }}_i\right)=0,$$

(19)

where $\mathbf{\Phi }\left({\mathbf{\Theta }}_i\right)$ is the vector of constraint Equations (1)–(4) evaluated at ${\mathbf{\Theta }}_i$.

4. Mechanical Design Optimization

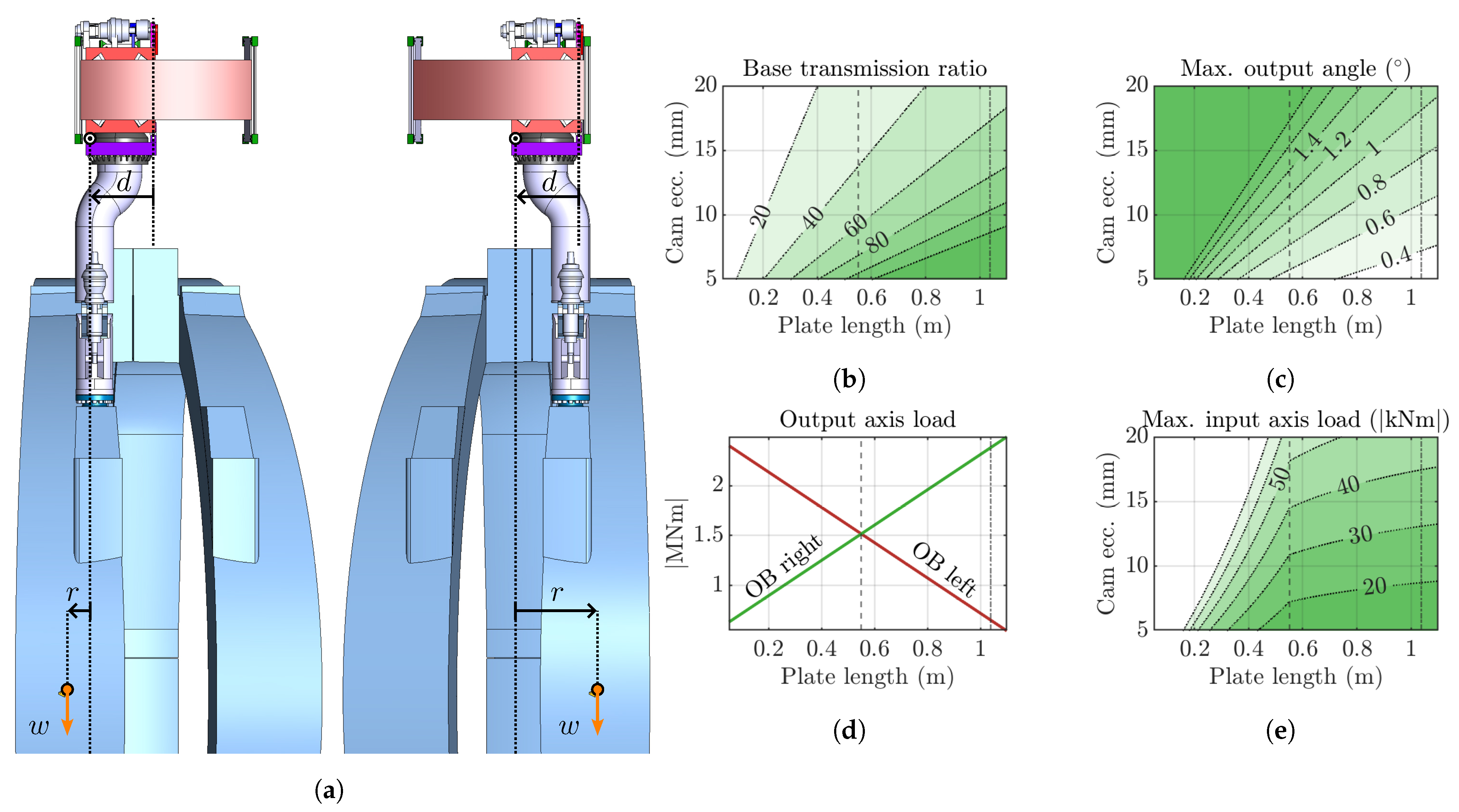
An initial sizing of the TTM based only on the space available and the geometry of the BBVT trolley gives $a=0.015\mathrm{m}$, $b=1.635\mathrm{m}$, $c=0.14\mathrm{m}$, and $d=1.038\mathrm{m}$. However, it is possible to optimize this using the kinematic model derived in Section 3. Two important properties of interest are the input load, which depends on the transmission ratio, and the output range of motion.

In the home position, the transmission ratio Equation (17) reduces to the simple ratio of the lengths of the output and input bars:

$${\eta }_{base}=-{\displaystyle \frac{d}{a}}.$$

(20)

We will refer Equation (20) as the base transmission ratio, as the true transmission ratio almost always increases in magnitude when the mechanism is not in home position due to the geometry factor generally obeying $\left|g\right|<1$ for designs where $a<<b$ and $a<<d$. In order to minimize the sizes of the required actuators and gearboxes, a base transmission ratio of about 50 to 100 is desired. Figure 6b plots expected values of $\left|{\eta }_{base}\right|$ for relevant ranges of a and d based on Equation (20), showing that smaller a and larger d values are desirable.

Another important property of the mechanism is the output range of motion. Since an exact expression for ${\theta }_{t,min}$ and ${\theta }_{t,max}$ is difficult to obtain, a simplification is used, namely that the rotating cam (a) connects directly to the trolley tilting plate (d). This is valid when $a<<b$ and $a<<d$ since the tilt angles ${\theta }_2$ and ${\theta }_3$ then remain small and contribute negligibly to the change in the height of the far end of the tilting plate. In that case, the maximum output angle corresponds to the input angle ${\theta }_1=\pm 90°$, and using Equation (3),

$$\begin{array}{cc}\hfill dsin{\theta }_{t,max}& \approx a\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill {\theta }_{t,max}& \approx {sin}^{-1}\left({\displaystyle \frac{a}{d}}\right)\approx {\displaystyle \frac{a}{d}}.\hfill \end{array}$$

(22)

Note that the simplification also leads to symmetrical extrema, ${\theta }_{t,min}=-{\theta }_{t,max}$, which is not true of the exact values. Figure 6c shows how the estimated ${\theta }_{t,max}$ varies for different bar lengths; specifically, smaller d and larger a values lead to an increased output range.

It should be noted that both the base transmission ratio and the approximate output range of motion depend exclusively on a and d. Thus, choosing appropriate lengths for the input and output bars is a major design consideration.

Another crucial value to consider is the load on the actuator gearbox connected to the TTM input. This depends not only on the transmission ratio and therefore the internal TTM geometry but also on the external problem geometry relating to the use case of lifting the BB segments. This is illustrated in Figure 6a, which shows the difference in the problem setup between the outboard’s (OB) left and right BB segments. These are the two which produce the greatest radial moments at the gripper interface due to their offset centers of mass. The radial moment load on the TTM output axis is different in each case due to the variable horizontal arm r, which depends on the chosen tilting plate length d. Figure 6d shows that a value of $d=0.55 \mathrm{m}$ gives equal loads on the output axis in the two cases, thus minimizing the overall largest load. By taking the larger of the two loads for a given value of d and dividing by the corresponding ${\eta }_{base}$, the maximum load on the TTM input is found (Figure 6e). This is not only useful for choosing a and d but also enables the optimal sizing of the input actuator(s) and gearbox(es).

The optimization problem can be stated as the minimization of the maximum input actuator load while respecting the required range of motion ${\theta }_{t,req}$ to overcome misalignments, gaps, and deflections during operation (as well as the maximum input actuator load rating ${\tau }_{1,max}$):

$$\begin{array}{cc}\hfill \underset{a,d}{min}& max\left(\left\{\left(a/d\right)\left(u_l-d\right)w,\left(a/d\right)\left(d-u_r\right)w\right\}\right)\hfill \\ \hfill \mathrm{subject}\mathrm{to}& a/d\ge {\theta }_{t,req}\hfill \\ \hfill & \left(a/d\right)\left(u_l-d\right)w\le {\tau }_{1,max}\hfill \\ \hfill & \left(a/d\right)\left(d-u_r\right)w\le {\tau }_{1,max},\hfill \end{array}$$

(23)

where w is the BB segment weight, and $u-d=r$ in Figure 6a. The value of u depends on whether the left or right outboard segment is considered (and on the chosen configuration of the redundant BB transporter mechanism during initial lifting), leading to the two actuator load expressions.

The analysis supports the idea of using a centered hinge, thus fixing d, one of the two main design variables. The centered hinge has the advantage of resulting in fully symmetric loading cases ($u_l-d=d-u_r$) assuming symmetric BBVT configurations. The optimization is then a simple matter of minimizing a (which minimizes the actuator load) subject to the constraints.

5. Verification and Preliminary Down-Scaled Experiment

5.1. Verification by Adams Model

The kinematic model is verified by comparison to a numerical simulation in MSC Adams. A TTM design with $a=15\mathrm{m}\mathrm{m}$, $b=50\mathrm{m}\mathrm{m}$, $c=5\mathrm{m}\mathrm{m}$, and $d=50\mathrm{m}\mathrm{m}$ is used for the verification. The input shaft is prescribed a constant speed of ${\dot{\theta }}_1=1^{\circ }{\mathrm{s}}^{-1}$, and the simulation is run for $t=\left[0\mathrm{s},359\mathrm{s}\right]$ with $\delta t=1\mathrm{s}$. Several configurations of the Adams model are pictured in Figure 7.

The results of the verification are given in Figure 8, where the coordinates ${\theta }_2$, ${\theta }_3$, and ${\theta }_t$, as well as the output shaft speed ${\theta }_t$, are plotted for a full revolution of the input shaft. The root mean square error of the position curves does not exceed 5 × 10⁻⁶ deg, and the RMSE the output shaft speed curve is just 8.5 × 10⁻⁸ deg/s.

5.2. Preliminary Down-Scaled Experiment

A down-scaled prototype of the TTM was manufactured and used to further validate the analytical model. Except the off-the-shelf spherical bearing and fasteners, the prototype parts are manufactured using fused filament fabrication in PLA materials using a Prusa MK4 3-D printer. The dimensions correspond to the full-scale TTM with $a=0.015\mathrm{m}$, $b=1.635\mathrm{m}$, $c=0.14\mathrm{m}$, and $d=0.55\mathrm{m}$, scaled by a factor $1/8.33$. The design of the prototype is shown in Figure 9a, and the setup of the experiment is shown in Figure 9b. The input shaft is driven by a MKS42C stepper motor, which has an internal absolute encoder with 1024 counts per revolution, and the output shaft is attached to a relative encoder with 14,400 counts per revolution. The motor is set to turn one revolution in 60 s with 4160 steps while the output shaft position measurements are collected via an Arduino microcontroller connected to a PC. No load is applied to the output shaft to avoid deformations and match the rigid-body assumption of the analytical model despite the plastic material.

To estimate the input and output shaft speeds, a linear fit was found for the input shaft position data, and a sine curve was fitted to the output shaft position data; the first derivatives of these curves were then taken as the experimental speeds, the ratio of which was used as the measured inverse transmission ratio to compare with the model (see Equation (17)). The numerical differentiation of the position data with a light Butterworth filter applied was also found as a reference for the shaft speeds.

The results of the experiment are given in Figure 10. There was a small error in the kinematic relationship between the input and output positions ${\theta }_1$ and ${\theta }_t$, with an RMSE of 6.6 × 10⁻² deg compared to an output range of motion of about $\pm 1.8deg$. A line with equation ${\theta }_1=6.029t-0.6628$ was fitted to the input position data, and a sine curve with equation ${\theta }_t=1.65sin\left(0.1052t-3.123\right)$ was fitted to the output position data. The derivatives of the fits were used to find the position-dependent (inverse) transmission ratio. The RMSE of the predicted and experimentally measured transmission ratio curves was 1.1 × 10⁻³ compared to a peak of about $\pm 0.3$.

6. Discussion and Conclusions

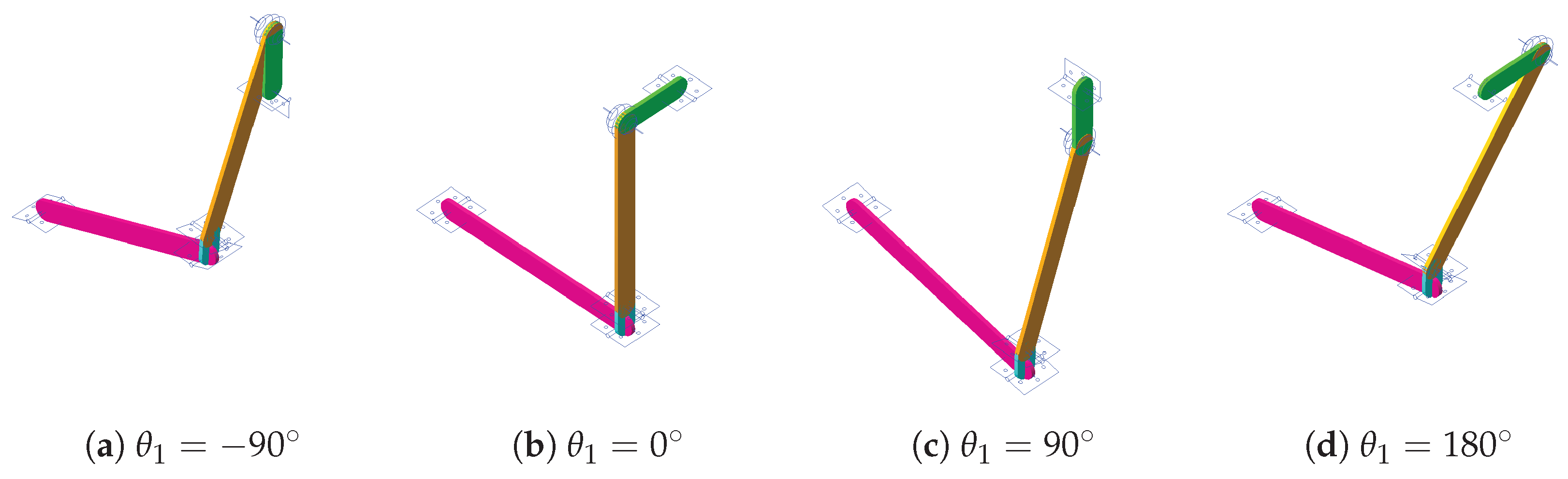
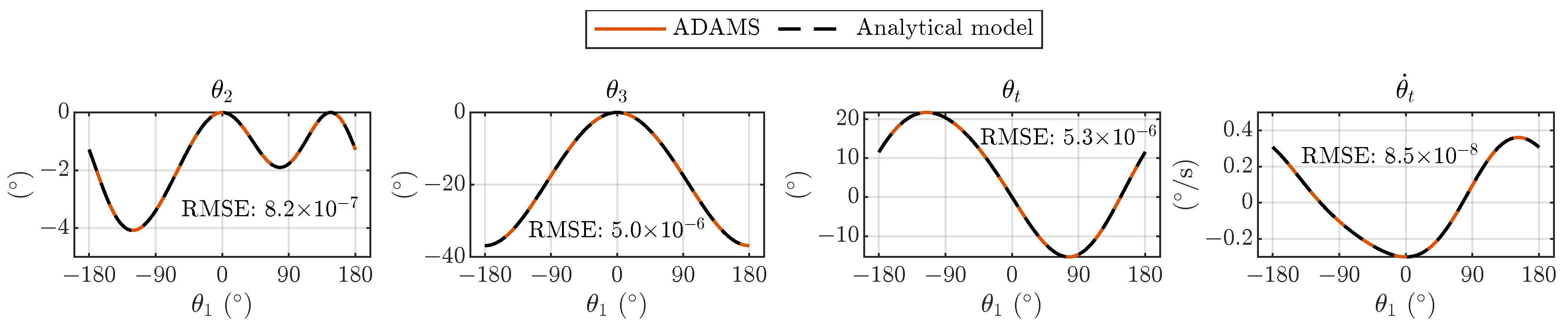
The predictions by the analytical model of the TTM joint positions and output shaft speed show great agreement with the numerical simulation in Adams, verifying the basic accuracy of the model. Although the experimental results show some small deviations compared with the predicted output shaft motions, the agreement is overall still good, and the discrepancies can be explained by geometrical uncertainties and material flexibility inherent in the plastic additive manufacturing of the down-scaled prototype.

A five-bar tilting mechanism was proposed and designed for the trolley tilting joint of the BBVT, and a detailed kinematic model was derived, verified by numerical simulations, and validated by experiment. Thus, the kinematic relationships between the mechanism’s input and output position, speed, and torque have been shown. In addition, the relationships of the base transmission ratio, output range of motion, output axis load, and input axis load to the cam eccentricity a and tilting plate length d have been detailed, allowing for the intelligent dimensioning of these parameters together with the joint gearbox(es) and actuator(s). The model has thus been applied in designing and optimizing the mechanism with respect to the very large static loads which it will experience during operation within the future DEMO power plant, supporting the feasibility of the TTM as a solution for safely lifting the BB segments.

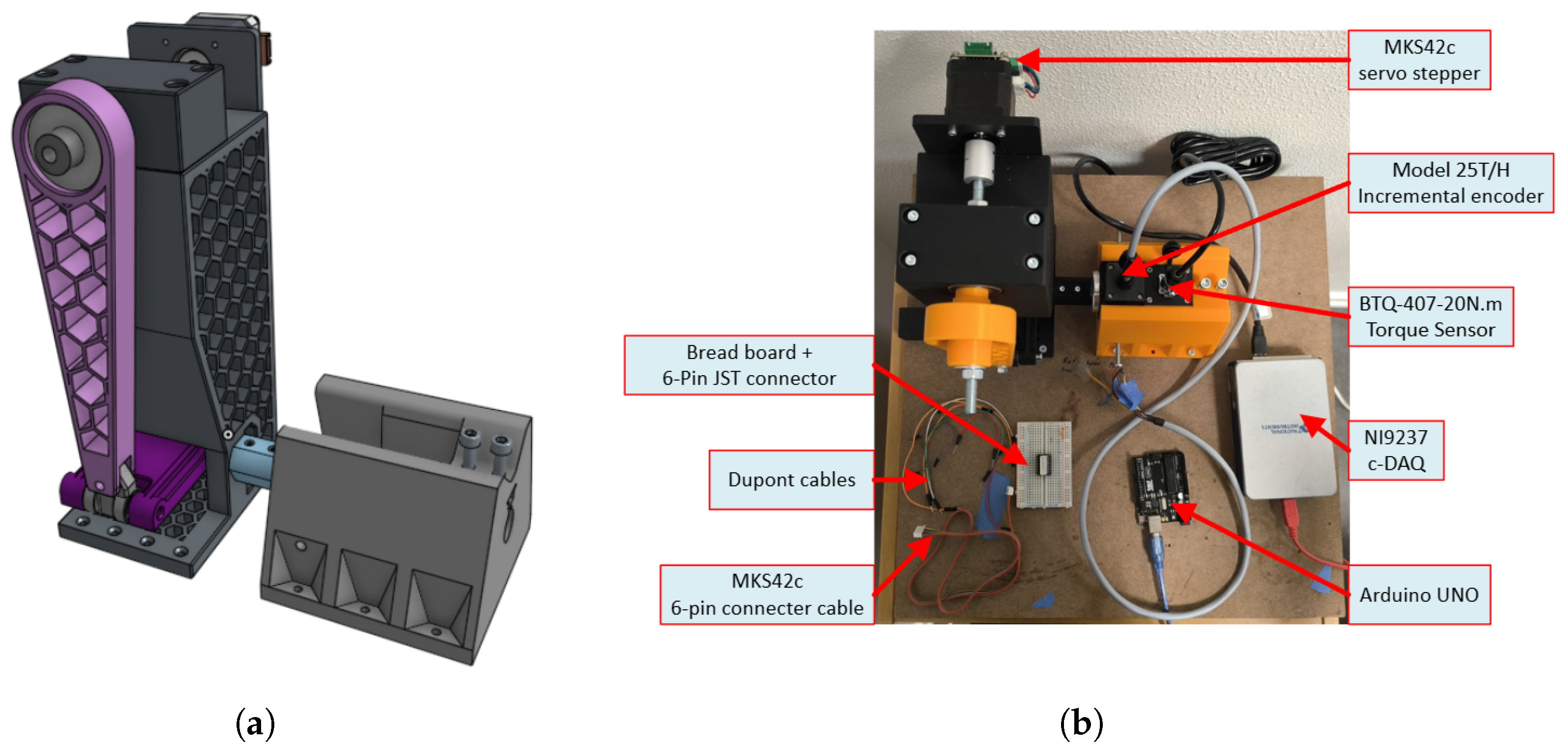
Due to the 3D printing process, the preliminary down-scaled TTM lacks the manufacturing precision and material stiffness required for a highly accurate validation of the kinematic model, especially under load. This also prevents carrying out experiments to validate the mechanical advantage predicted by the model. Thus, the construction of a high-precision down-scaled prototype using sturdier materials is considered essential future work in order to validate the force transmission.

Since the TTM is only foreseen to be used at low speeds, a multibody dynamics model of the mechanism is not considered necessary for now. However, the derived kinematic model can be used as a basis for future modelling, potentially including dynamic effects, as well as control solutions. Due to the high loads, a study of the compliance of the mechanism links and the development of a flexible model is considered for the future. More detailed design explorations guided by the model can also be carried out.