1. Introduction
With the rapid advancement of high-speed railway technology, the continuous increase in train operational speeds has imposed higher requirements on passive safety performance. In train collision accidents, how to effectively absorb impact energy, mitigate structural damage, and ensure passenger safety are among the core challenges in rail transit equipment development [
1]. As a critical component of train passive safety systems, anti-climbers primarily function by converting collision kinetic energy into thermal energy or plastic work through controlled plastic deformation and energy dissipation mechanisms, thereby suppressing impact force transmission pathways and preserving the integrity of the main car body structure and passenger compartments [
2]. Among these, planing-type anti-climbers have emerged as a research focus in high-speed train collision protection due to their advantages of high energy absorption efficiency, design repeatability, and structural compactness [
3]. However, the optimization of their cutting performance heavily relies on accurate predictions of dynamic cutting force characteristics [
4]. Inherent complexities, including material nonlinearity, thermomechanical coupling effects, and tool–workpiece interfacial friction during cutting processes, pose significant challenges to traditional design methodologies [
5]. Cutting force prediction is critical in the design of anti-climbers, as it serves as a key metric for evaluating energy absorption efficiency and structural dynamic stability. These factors directly influence the plastic deformation modes and energy dissipation pathways of anti-climbers. Prediction deviations may lead to insufficient energy absorption or localized stress concentrations, potentially triggering structural instability or even fracture, thereby jeopardizing passenger safety. Traditional methods relying on experimental calibration are costly and time-consuming, making them unsuitable for rapid iterations under complex working conditions. Consequently, developing high-precision cutting force prediction models with reduced experimental dependency is a technical prerequisite for enhancing passive safety performance and an urgent requirement for achieving intelligent design in rail transit equipment.
In recent years, domestic and international scholars have systematically investigated cutting force prediction models. Early empirical formula-based approaches simplified geometric relationships and mechanical equilibrium conditions to preliminarily reveal the influence of cutting parameters on cutting forces. However, their neglect of material dynamic response characteristics limited prediction accuracy [
6]. With the widespread adoption of finite element simulation technology, numerical simulation-based cutting analysis has gradually become mainstream [
7]. For instance, Yaich et al. (2020) employed a two-dimensional finite element model to elucidate the critical roles of mesh size and friction coefficients in thermomechanical coupling predictions for titanium alloy machining [
8]. Nevertheless, such methods require the precise calibration of material constitutive parameters, and the acquisition of traditional Johnson–Cook (JC) model parameters still relies on split-Hopkinson pressure bar (SHPB) experiments, which incur high costs and hinder rapid engineering iteration.
To overcome these limitations, recent studies have focused on developing high-precision prediction frameworks with reduced experimental dependency. Dou et al. (2025) conducted parametric numerical studies on orthogonal cutting processes using the smoothed particle hydrodynamics (SPH) method, achieving 92% prediction accuracy for aluminum alloy cutting forces through coupled thermomechanical effects and material dynamic responses [
9]. In complex material systems, Zan et al. (2024) compared the cutting performance of silicon carbide fiber-reinforced metal matrix composites, revealing that hardness variations in matrix materials could induce over 30% fluctuations in cutting forces, providing experimental foundations for multi-phase material cutting modeling [
10]. Additionally, Boldyrev (2018) proposed a free orthogonal cutting simulation method based on Smoothed Particle Galerkin (SPG), enhancing computational efficiency by 40% through simplified contact algorithms, though the model’s adaptability to extreme strain rates requires further validation [
11]. Fu et al. (2020) introduced crystal plasticity theory to establish an anisotropic aluminum alloy cutting model, offering theoretical support for nonlinear responses under complex loading conditions [
12].
The evolution of cutting force prediction theory has progressed through three stages: empirical formulas, analytical models, and numerical simulations. In the 1940s, Merchant established the orthogonal cutting model based on the minimum energy principle, laying the foundation for classical mechanics. However, its assumption of materials as ideal rigid-plastic bodies and neglect of strain hardening and temperature effects resulted in significant errors in high-strain-rate scenarios. With advancements in computational technology, data-driven methods have gained prominence. Marani et al. (2020) developed a neuro-fuzzy prediction model that integrates cutting parameters and material properties to achieve simultaneous predictions of surface roughness and cutting forces, though its generalization capability is constrained by training data diversity [
13]. In numerical algorithm optimization, Pantalé et al. (2022) proposed an improved Oxley analytical model-solving algorithm implemented via the Python 3.9.13 platform, enabling the efficient parametric analysis of orthogonal cutting processes and providing new tools for real-time predictions under complex working conditions [
14].
Current cutting force prediction models face multiple challenges. First, their heavy reliance on experimental calibration leads to computational inefficiency and cost issues. Finite element simulation models are overly complex and computationally intensive, failing to meet rapid engineering iteration demands [
15]. Second, early models inadequately addressed energy dissipation mechanisms under complex boundary conditions, resulting in insufficient adaptability to real-world scenarios [
16]. Furthermore, there exists a pronounced disconnect between theoretical developments and engineering applications, characterized by a lack of customized design tools and validation systems constrained by single-method verification rather than multi-dimensional closed-loop validation [
17].
To address these challenges, this study proposes a cutting force prediction model designed to eliminate dependence on experimental calibration and enable the efficient quantitative evaluation of planing-type anti-climber cutting performance.
The innovations of this research are threefold: (1) The introduction of mathematical modeling into cutting force prediction for planing-type anti-climbers, utilizing analytical methods to quantify the coupling effects between material dynamic responses and cutting parameters, thereby significantly reducing reliance on experimental data. (2) The development of a dual-loop validation strategy integrating simulation and physical experiments to balance computational efficiency with engineering accuracy, providing a reliable tool for anti-climber design under complex working conditions. (3) By revealing the impact patterns of cutting depth, tool rake angle, and speed on performance, this research offers specific design guidelines for creating planing-type anti-climbing devices that can efficiently absorb collision energy while maintaining structural stability. These contributions advance the intelligent upgrading of high-speed train passive safety technologies and demonstrate substantial academic value and engineering application prospects.
2. Cutting Force Prediction Model
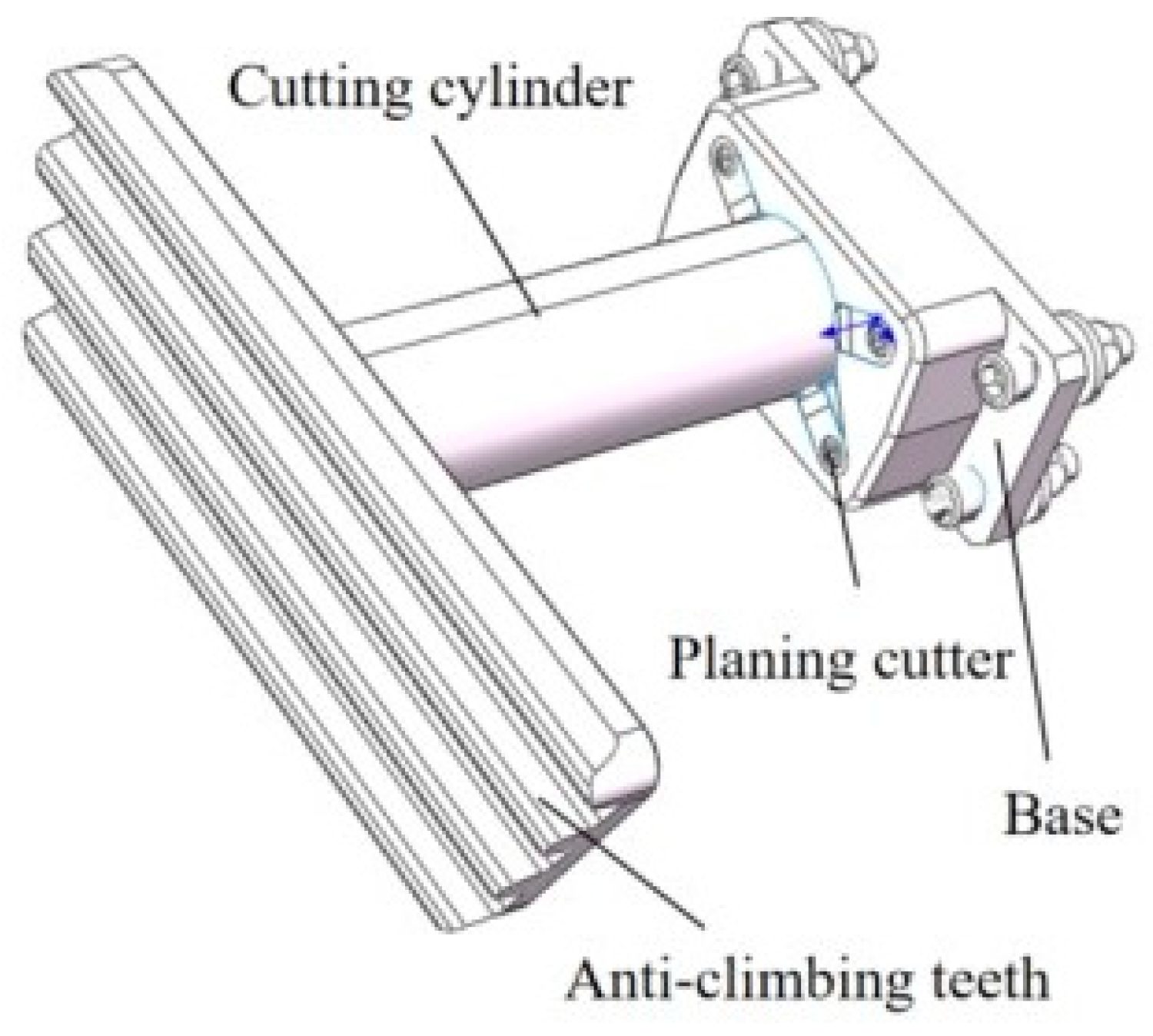
Having established the significance of planing-type anti-climbers and the limitations of existing research, this section focuses on the methodology for constructing a cutting force prediction model, which serves as the foundation for subsequent simulations and experimental validation. The planing-type anti-climber discussed in this study is primarily installed at the front and rear sections of trains. During collisions, the anti-climber absorbs substantial energy by inducing plastic deformation and the fracture of metallic materials through cutting, thereby effectively mitigating the transmission of impact forces to other vehicle components and safeguarding structural integrity and passenger safety.
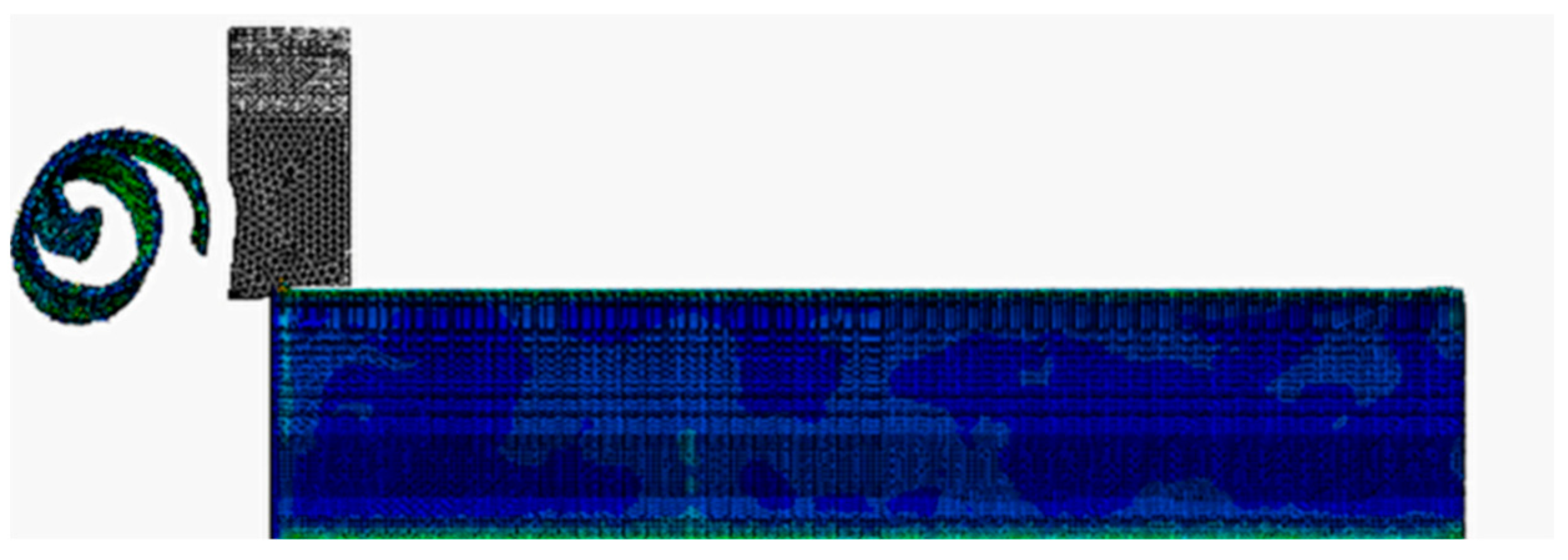
As illustrated in
Figure 1, which depicts the material cutting process by the anti-climber blade, the cutting mechanism can be identified as orthogonal cutting. Consequently, the cutting force prediction model for the planing-type anti-climber is formulated by simplifying the process to orthogonal cutting conditions.
The prediction of cutting forces
Fc primarily relies on deriving these forces from shear forces
Fs via geometric relationships. The governing equation is expressed as follows:
Here, denotes the tool rake angle. To solve Fc, additional parameters including the shear force Fs, friction angle , and shear angle must be determined.
Both
and
can be obtained experimentally or via empirical formulas. This study adopts empirical formulas [
18]:
The shear force
Fs is proportional to the shear stress
, governed by the shear area. Let
a represent the uncut chip thickness,
b the cutting width,
Ac the cross-sectional area of the undeformed chip, and
As the primary shear plane area. The shear force is expressed as follows [
19]:
To determine , a constitutive model is required.
Metal cutting mechanisms have been investigated for decades, with researchers striving to establish generalized theoretical models capable of precisely predicting process parameters, thereby reducing reliance on experimental validation [
20]. Despite inherent challenges—such as material fracture, thermomechanical coupling, and tool–chip interface friction—that introduce deviations in existing model predictions, these theoretical frameworks hold significant value in elucidating fundamental cutting principles and optimizing machining parameters [
21]. Consequently, they serve as a cornerstone for advancing manufacturing technology innovation [
22].
In this context, the Johnson–Cook (JC) constitutive model—a viscoplastic constitutive modeling approach with exceptional engineering applicability—has been widely adopted to characterize the dynamic mechanical response of metallic materials [
23]. The model correlates flow stress with the coupled effects of strain, strain rate, and temperature through five measurable parameters (A, B, C, n, m). Its mathematical simplicity and straightforward parameter calibration make it particularly suitable for dynamic loading scenarios, such as cutting force prediction [
24]. Although the JC model may exhibit limited accuracy in describing material softening behavior under high strain rates or extreme thermal conditions, its predictive capability has been continuously improved through parameter modifications and enhancements in multiphysics-coupled algorithms [
25]. To date, it remains the preferred tool for analyzing metal behavior under impact loading.
The constitutive equation is formulated as follows:
where
is the shear stress,
the shear strain,
the shear strain rate,
the reference shear strain rate,
T the instantaneous absolute temperature of the workpiece,
Tr the initial temperature of the workpiece, and
Tm the melting temperature of the workpiece. The parameters
A (yield strength, MPa),
B (hardening modulus, MPa),
C (strain rate sensitivity coefficient),
n (hardening exponent), and
m (thermal softening exponent) are material-specific constants that must be experimentally determined [
26].
The segmented power-law distribution method for shear strain rate is employed to derive the shear strain and shear strain rate at the initial shear line (
y = 0), primary shear plane (
y =
kh), and terminal shear line (
y =
h) by assigning specific values to
y. These quantities are expressed as follows:
In the equation above, represents the maximum shear strain rate, k denotes the unequal division coefficient, h is the shear band thickness (which can be determined from chip thickness and is taken as 0.25 in this study), V indicates velocity, and q serves as a velocity characterization coefficient with values of 3 for low-speed conditions and 7 for high-speed conditions (here adopted as 7). By solving this formulation, the shear strain and shear strain rate on the primary shear plane can be obtained, specifically the shear stress when y = kh.
Both the maximum shear strain rate and unequal division coefficient can be determined through the boundary conditions of tangential velocity components at the initial and final shear lines. These parameters are mathematically expressed as follows:
Based on the aforementioned equations and the intrinsic material properties, the shear stress distribution within the shear zone and the shear stress on the primary shear plane can be determined. Further substitution into the shear force calculation formula enables the prediction of cutting forces generated during orthogonal cutting.
After establishing the theoretical model, the subsequent analysis employs this model to investigate the influence patterns of various parameters on cutting forces under distinct machining conditions. The selected parameters for analysis include cutting speeds of 5.5 m/s and 6.94 m/s, depths of cut of 3 mm and 5 mm, and tool rake angles of 0 and 7, resulting in eight distinct combinations of machining conditions (as detailed in
Table 1). These datasets encompass diverse machining scenarios, allowing rigorous validation of the model’s predictive accuracy through comparative analyses with subsequent simulation results and experimental measurements.
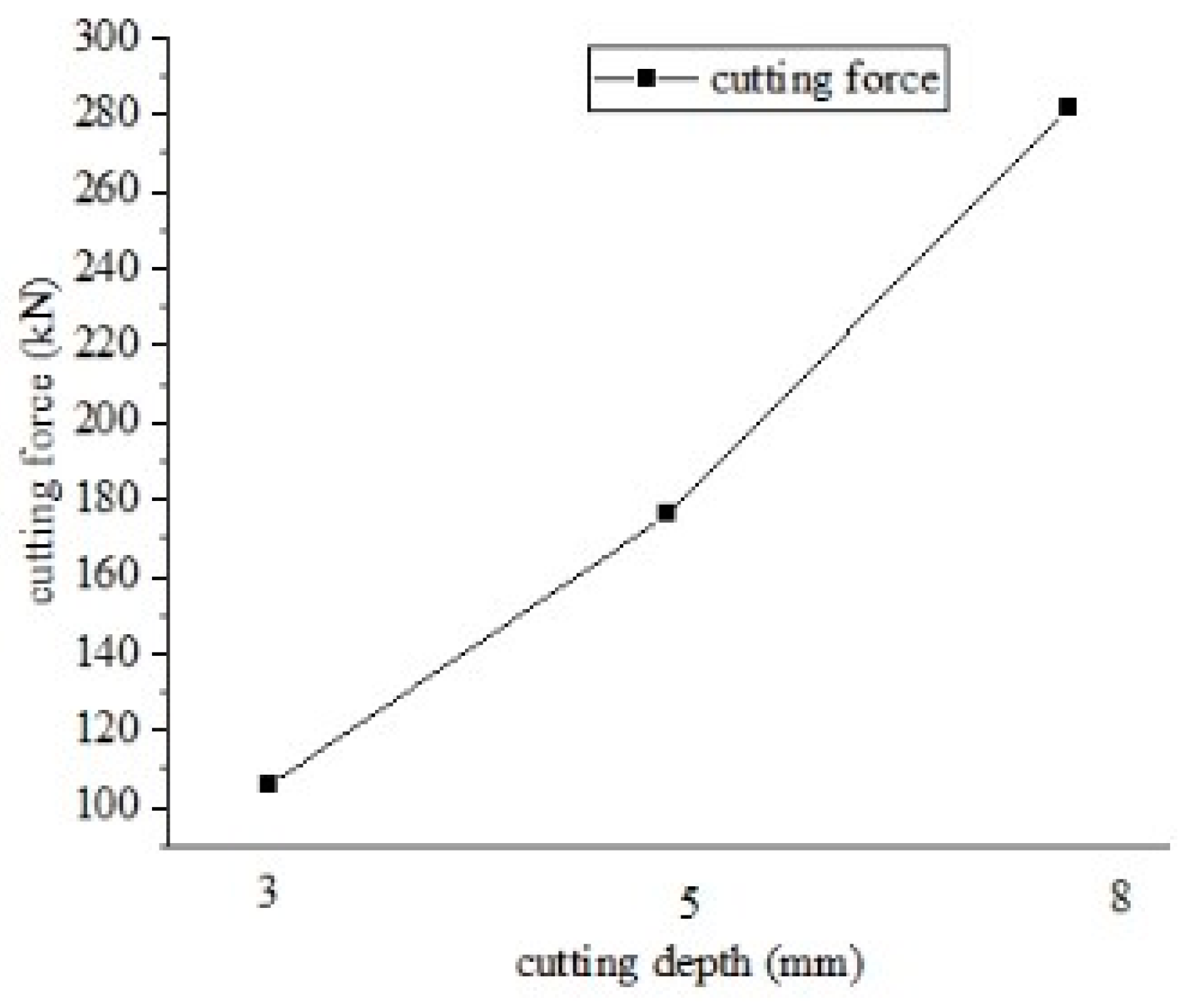
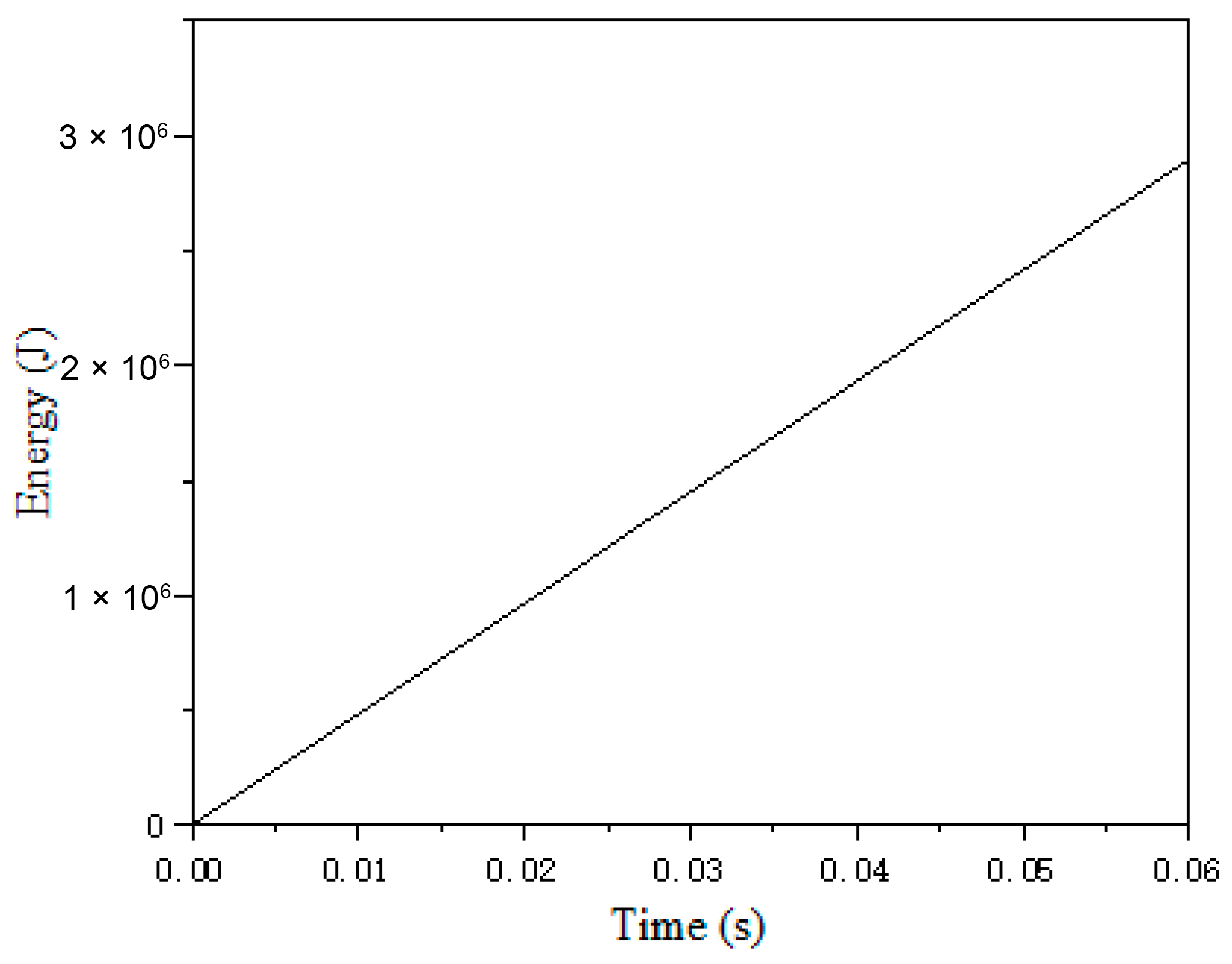
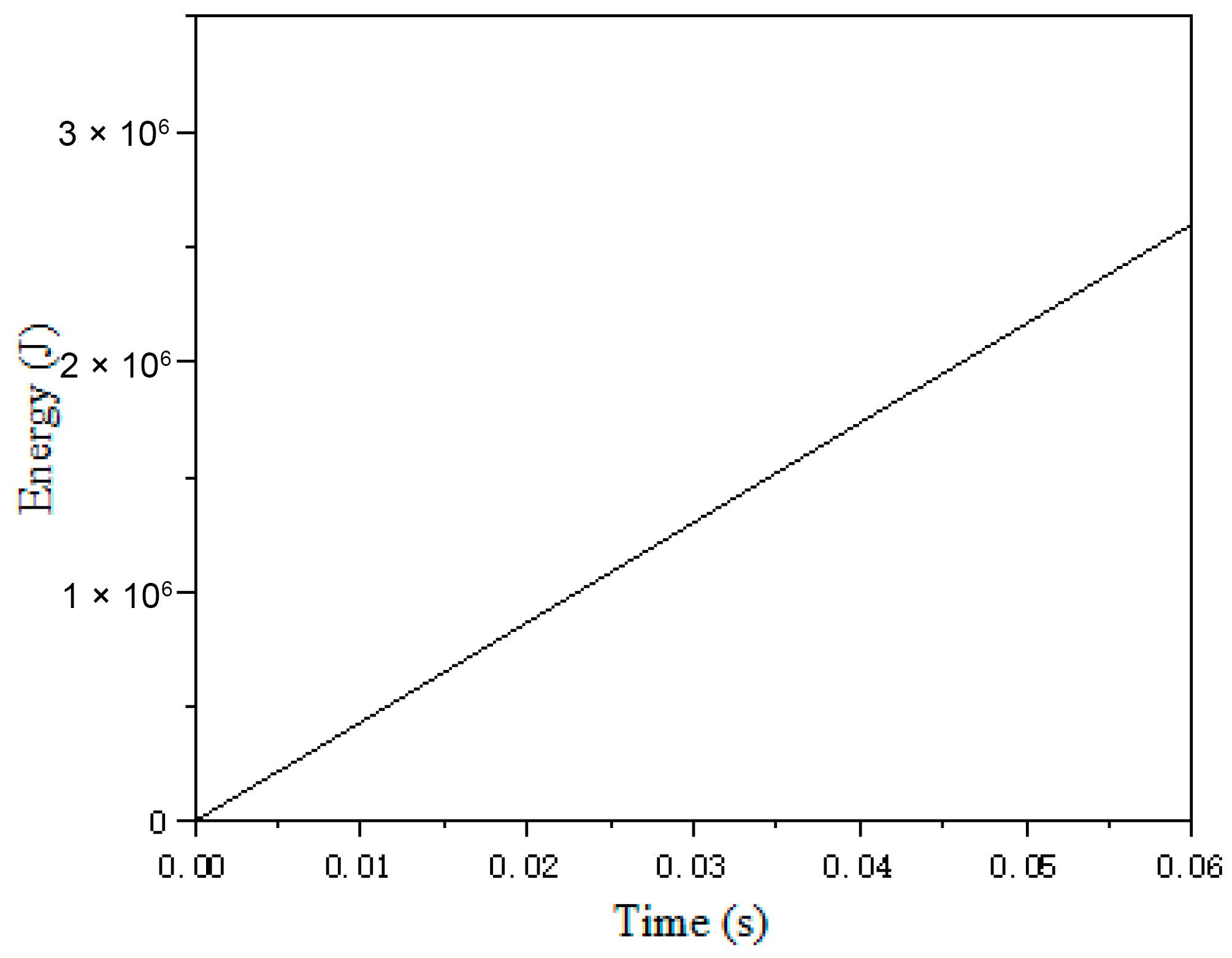
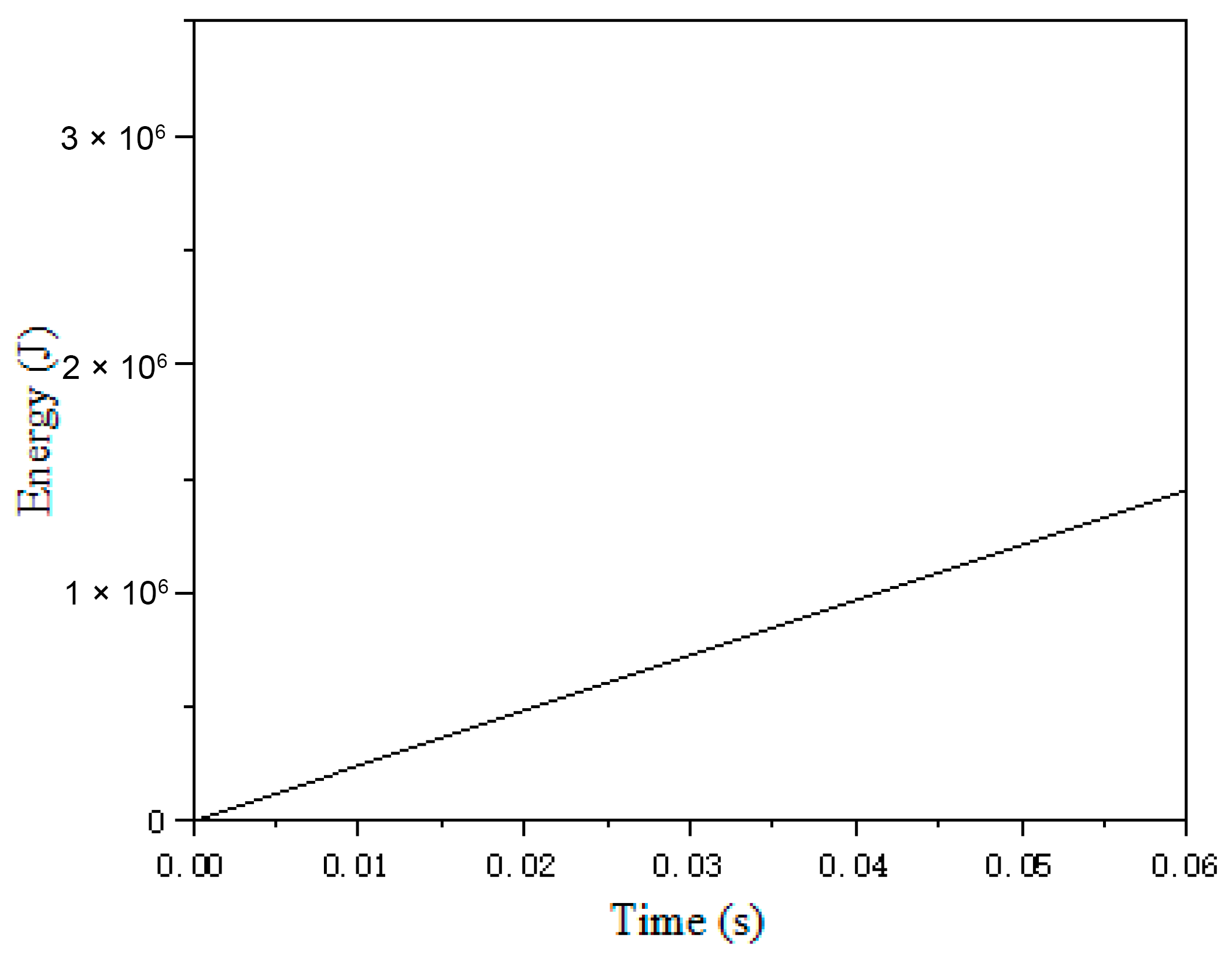
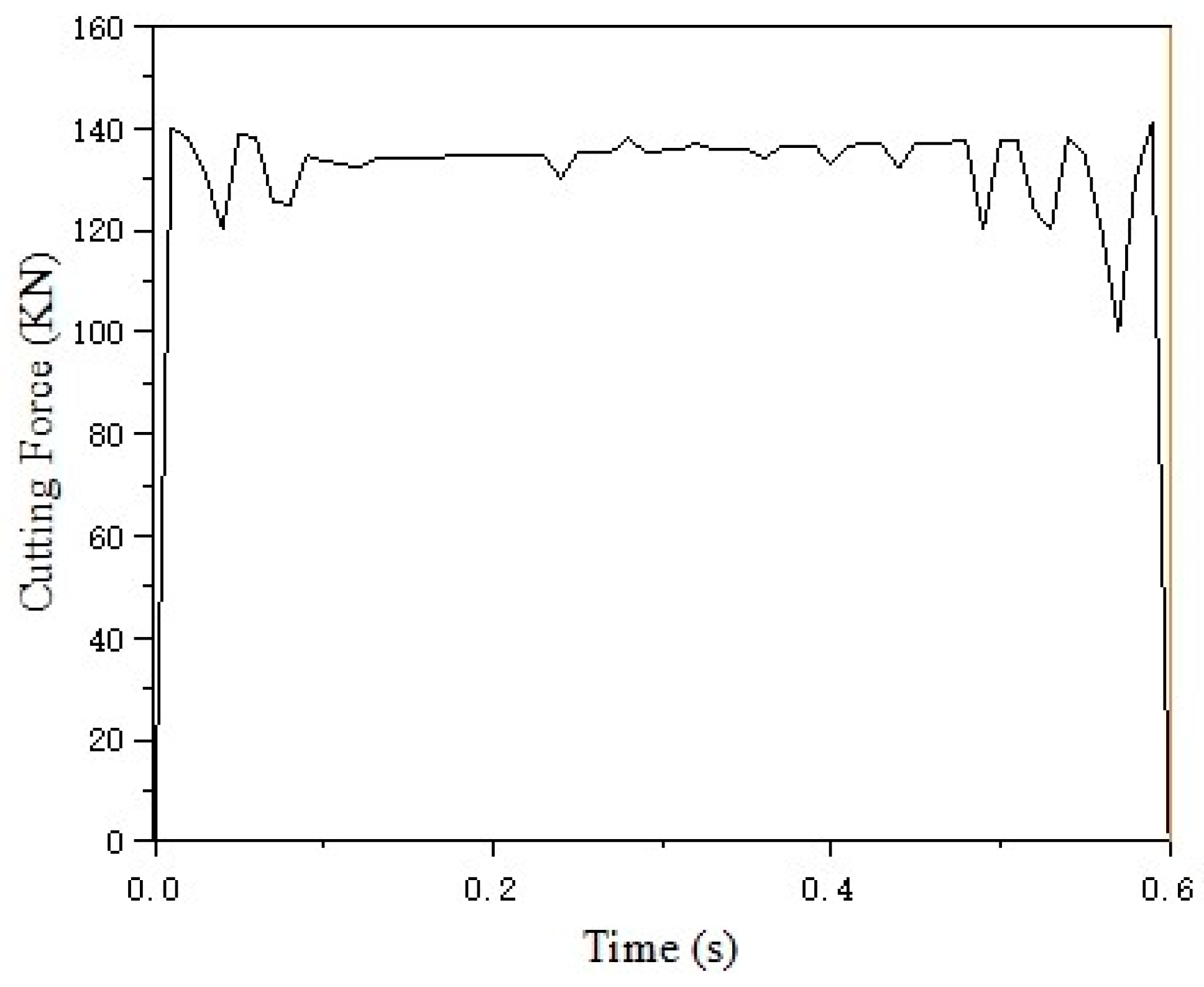
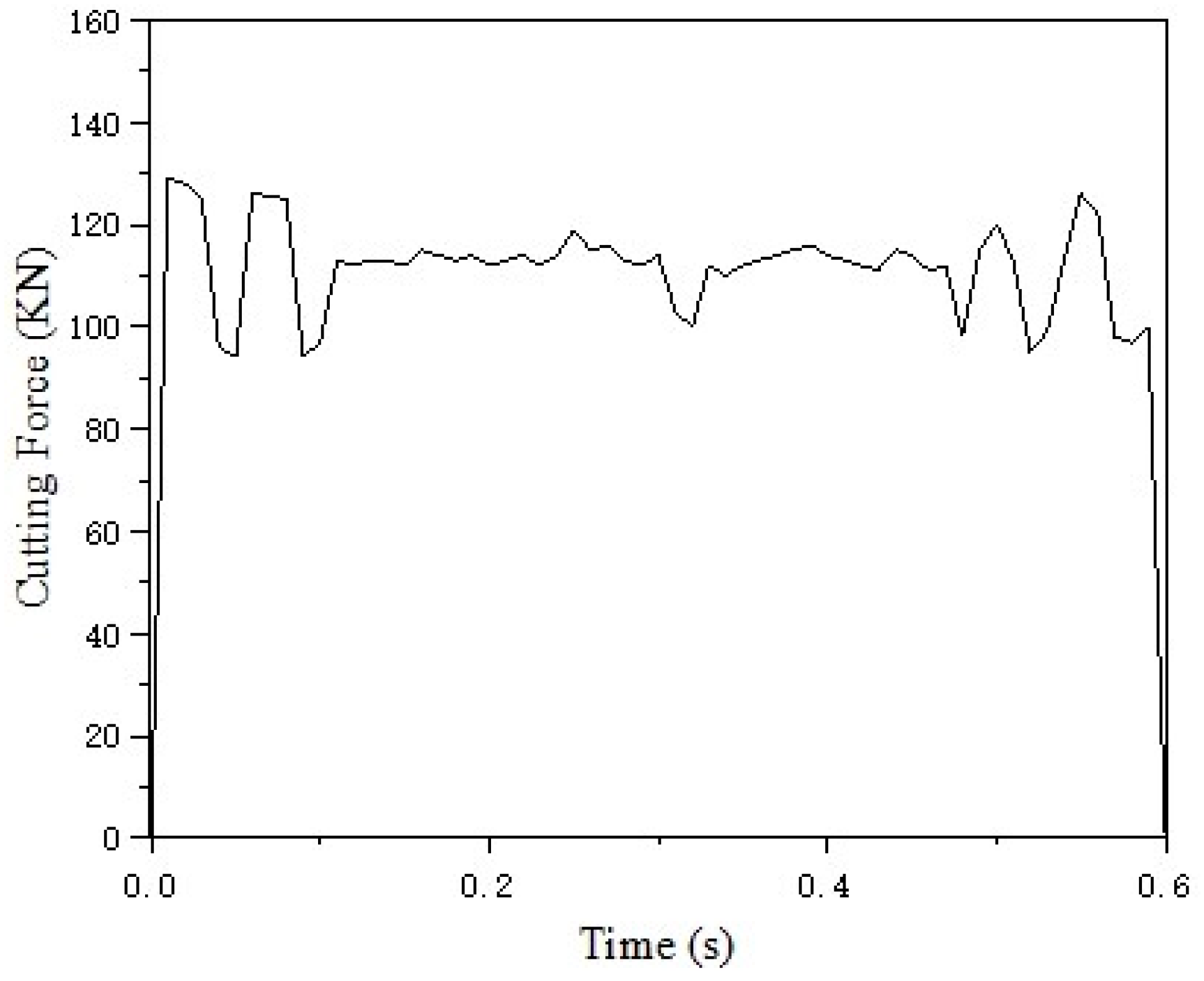
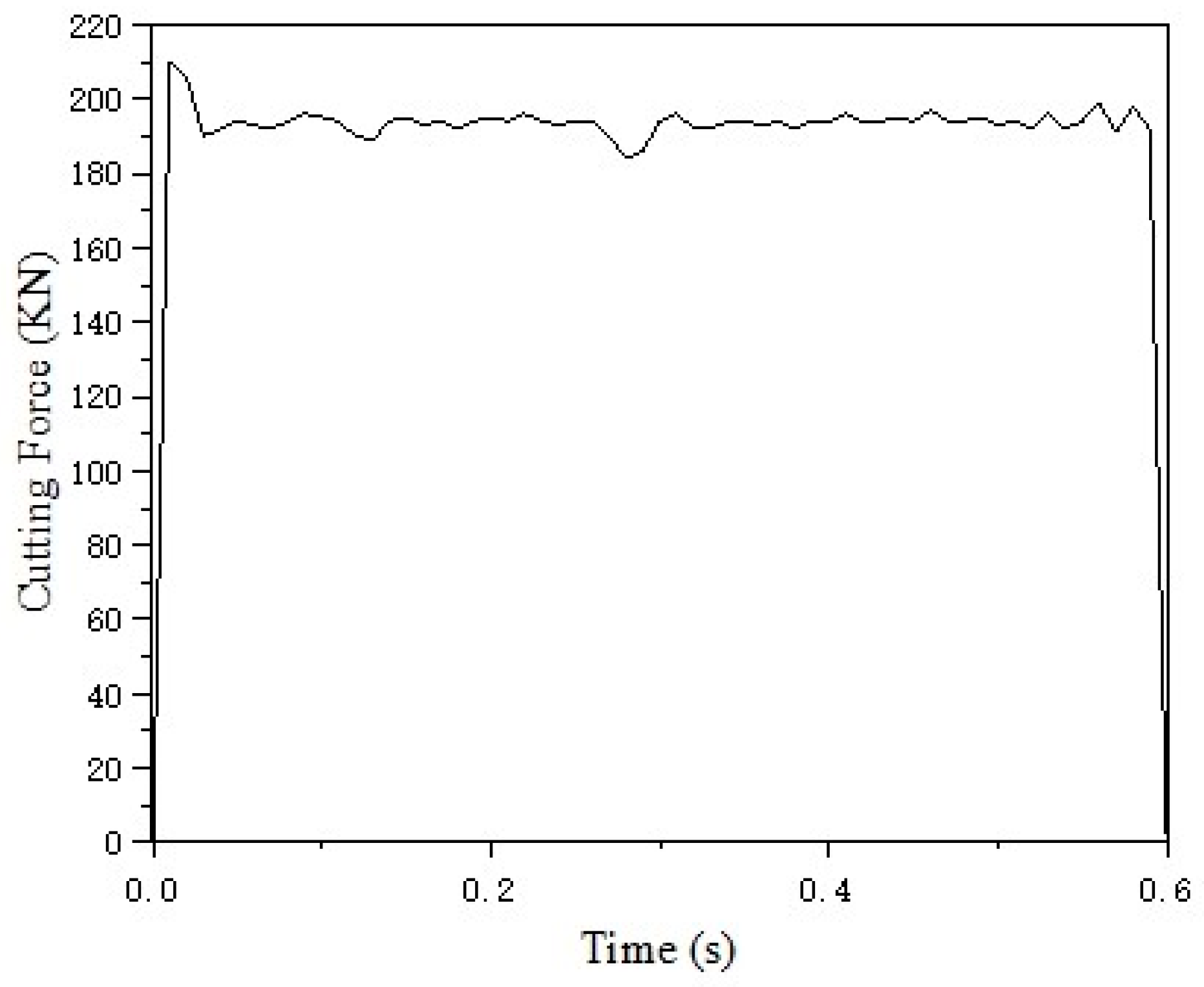
As indicated in the table, the cutting force exhibits a decreasing trend with an increase in tool rake angle. Similarly, a higher cutting speed correlates with a reduction in cutting force. To further analyze the effect of cutting depth, the model calculates cutting forces at depths of 3 mm, 5 mm, and 8 mm, yielding single-tool cutting forces of 105.62 kN, 176.03 kN, and 281.65 kN, respectively, as illustrated in
Figure 2. This demonstrates that, under constant machining conditions, the cutting force increases proportionally with cutting depth.
4. Experimental Verification
To verify the accuracy of the theoretical model and simulation analysis, experimental validation was conducted to provide robust evidence for the model’s reliability. Based on impact testing standards, this study established a validation framework for the cutting force prediction model, employing a dual-loop verification strategy integrating physical experiments and numerical simulations. The experimental platform incorporates a 13-ton counterweight sled, a high-speed hydraulic drive module, and a multi-dimensional sensor array, enabling the precise reproduction of train collision scenarios with a defined initial impact velocity against a rigid barrier. The core of the system is a modular cutting unit equipped with a tool angle adjustment mechanism and a closed-loop tool feed depth control system, achieving the precise parametric control of cutting depth and rake angle.
A high-speed NAC MEMRECAM HX-3 camera system at 4000 Hz was used to capture and analyze the structural deformation process. Six KISTLER piezoelectric load sensors were employed as the load-sensing elements. To eliminate boundary effects, the geometric parameters of the energy-absorbing tube strictly matched the simulation model: wall thickness of 6 mm and effective stroke of 220 mm. The tool assembly utilized YG20C cemented carbide, whose fine-grained microstructure ensures excellent resistance to thermal degradation, maintaining geometric integrity under complex stress states. The energy-absorbing tube was fabricated from a Q345B cold-drawn seamless steel tube. The experimental results are presented in
Figure 17.
Some results are as follows: At a cutting depth of 4 mm and speed of 4.86 m/s, the cutting force was 548 kN. At a cutting depth of 5 mm and speed of 4.15 m/s, it was 427 kN. At a cutting depth of 6 mm, the cutting force was 1100 kN at 2.81 m/s, and 930 kN at 5.6 m/s. At 5.8 m/s, the cutting force dropped from 1400 kN to 840 kN due to tool breakage. Two typical tests were chosen to compare the experimental and simulation data from the finite element analysis, as shown in
Table 4.
By inputting the measured boundary conditions into the cutting force prediction model established in this paper, the relative error between the model-predicted cutting forces and the experimentally measured values, as shown in
Table 5, is maintained below 5%, which is acceptable in engineering practice. This indicates that the cutting force model proposed in this paper is not only theoretically sound, but also effective and reliable in practical applications.
5. Conclusions
This study systematically investigates the energy dissipation mechanisms and performance optimization strategies of planing-type anti-climbing devices under dynamic collisions by establishing a cutting force prediction model. Grounded in orthogonal cutting theory and integrating material dynamic response characteristics with impact boundary conditions, an analytical model capable of directly predicting cutting forces without experimental calibration is proposed. The model’s reliability and engineering applicability are validated through theoretical calculations, finite element simulations, and dynamic impact tests. The relative errors between theoretical predictions and simulation results remain within 15%, while deviations from experimental measurements are below 5%, significantly reducing reliance on extensive empirical validation in traditional development processes. This provides an efficient quantitative tool for the customized design of high-speed train anti-climbing devices.
Based on the findings of this study, the following parameter optimization strategies are proposed:
Priority adjustment of cutting depth: Appropriately increasing the cutting depth under structural stability constraints significantly enhances energy absorption efficiency. However, excessive plastic deformation leading to structural failure must be avoided.
Selection of tool rake angle: Larger rake angles effectively reduce cutting forces, making them suitable for impact load-sensitive scenarios. This requires durability validation considering the strength of tool materials.
Velocity threshold management: Elevated cutting speeds induce a dynamic equilibrium between thermal softening effects and strain rate strengthening, resulting in reduced cutting forces. Under high-speed conditions, thermomechanical coupling analysis should balance these effects to prevent material property degradation caused by excessive temperatures.
However, the current model exhibits limitations in characterizing extreme thermal softening effects and multi-axis asymmetric loads. Future studies should optimize the predictive framework by coupling oblique cutting models or incorporating crystal plasticity theories. Additionally, the influence of anisotropic texture effects in cold-drawn steel tubes on cutting forces remains insufficiently explored. Further investigation into this mechanism is essential to provide comprehensive theoretical support for complex material dynamic responses.
By integrating theoretical modeling, simulation analysis, and experimental validation, this study elucidates the energy absorption mechanisms and performance modulation principles of planing-type anti-climbing devices. The proposed cutting force prediction model balances engineering applicability and computational efficiency, providing critical theoretical and practical foundations for passive safety design in high-speed trains. These advancements lay the groundwork for evolving rail transit equipment toward enhanced safety and intelligence, driving technological progress in the field.