Deep Transfer Learning-Based Performance Prediction Considering 3-D Flux in Outer Rotor Interior Permanent Magnet Synchronous Motors
Abstract
1. Introduction
2. Motor Performance Investigation According to Design Variables
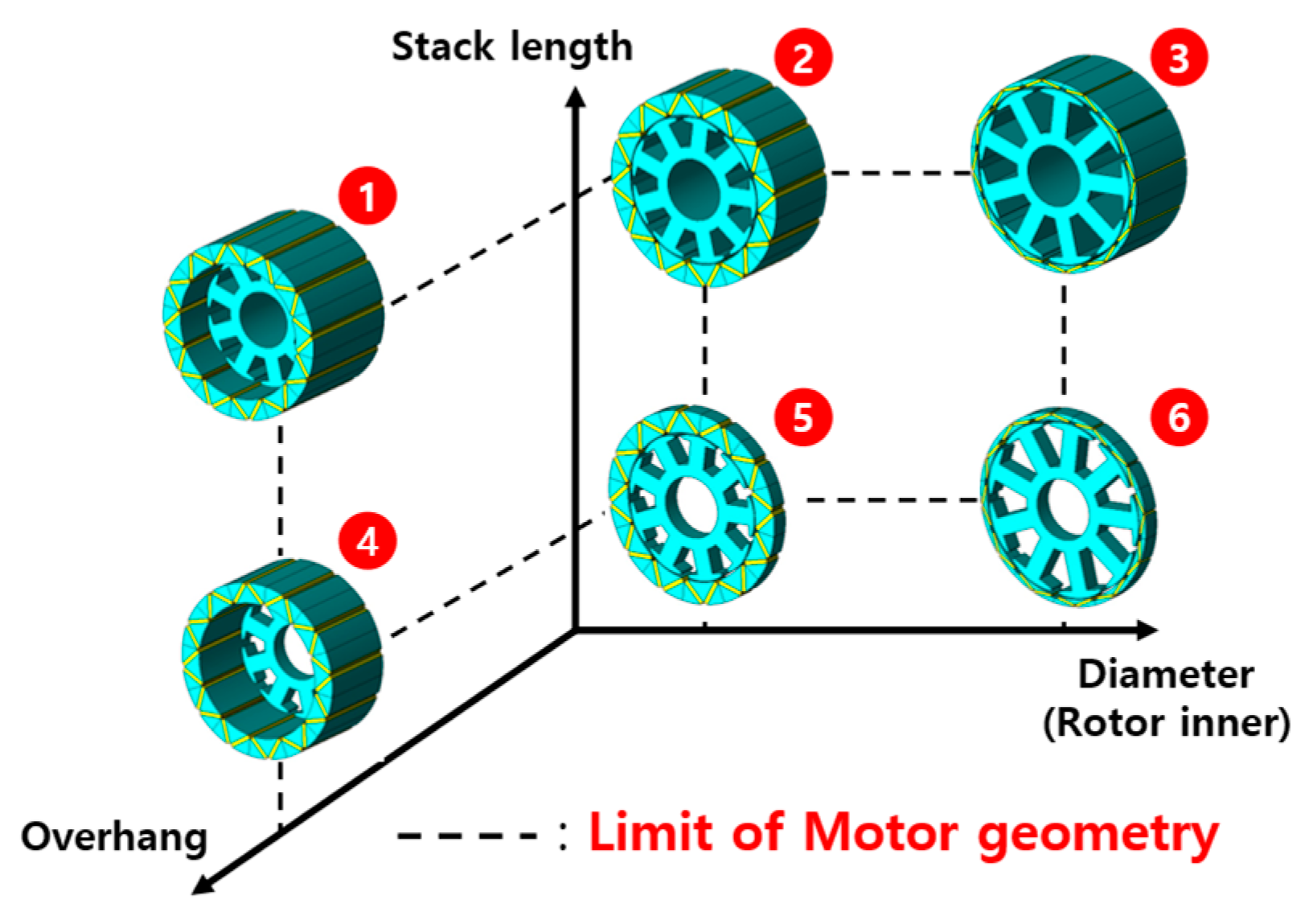
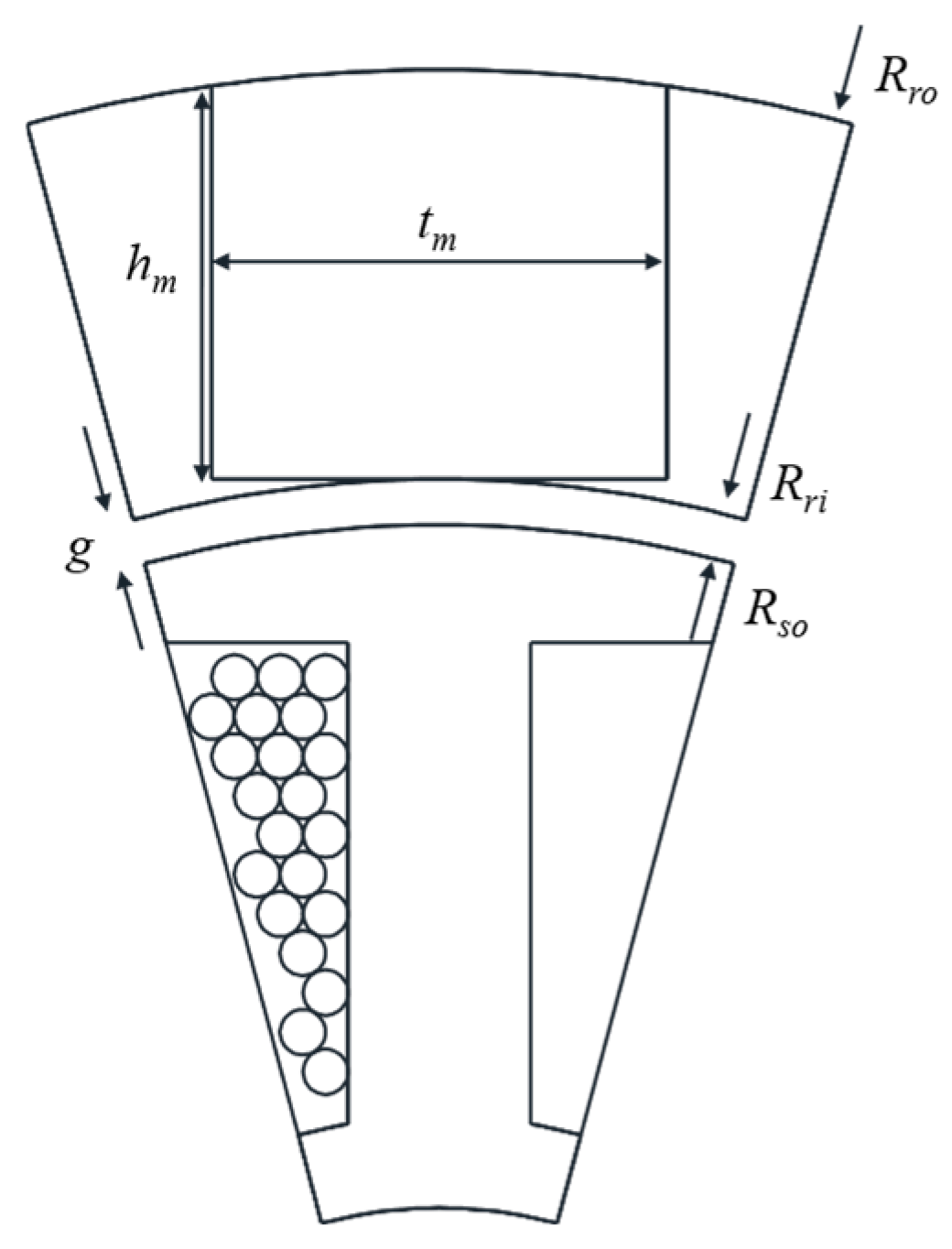
2.1. Motor Geometry According to Design Variables
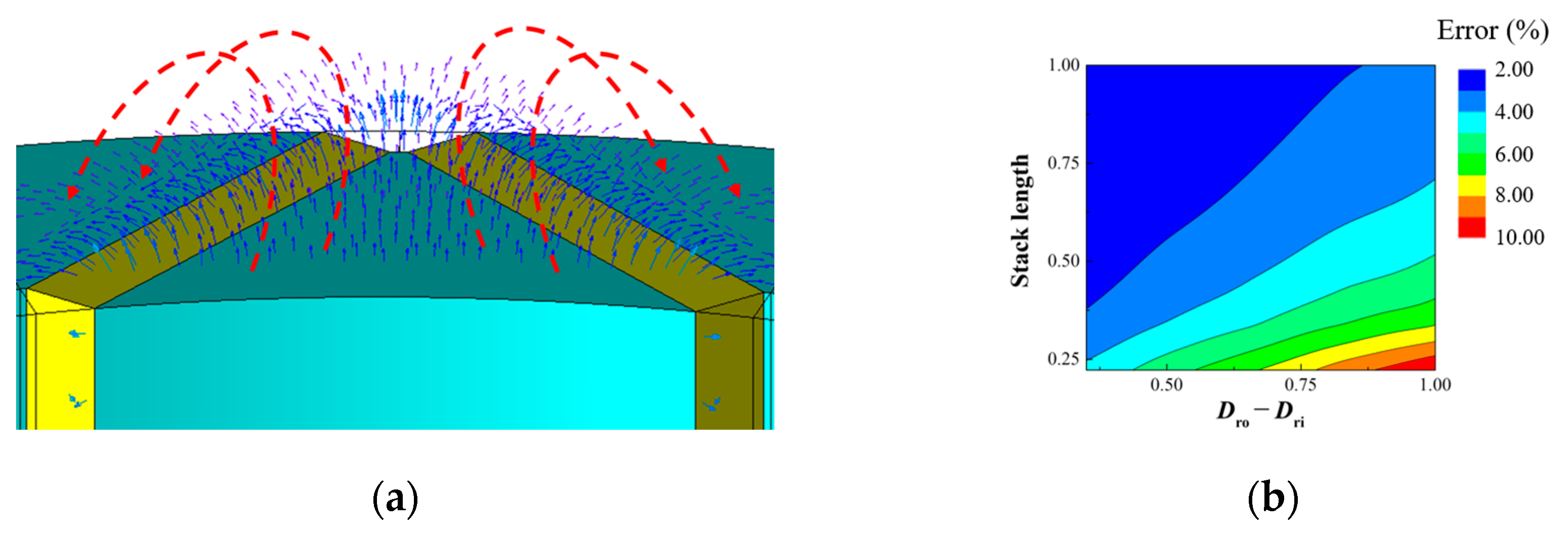
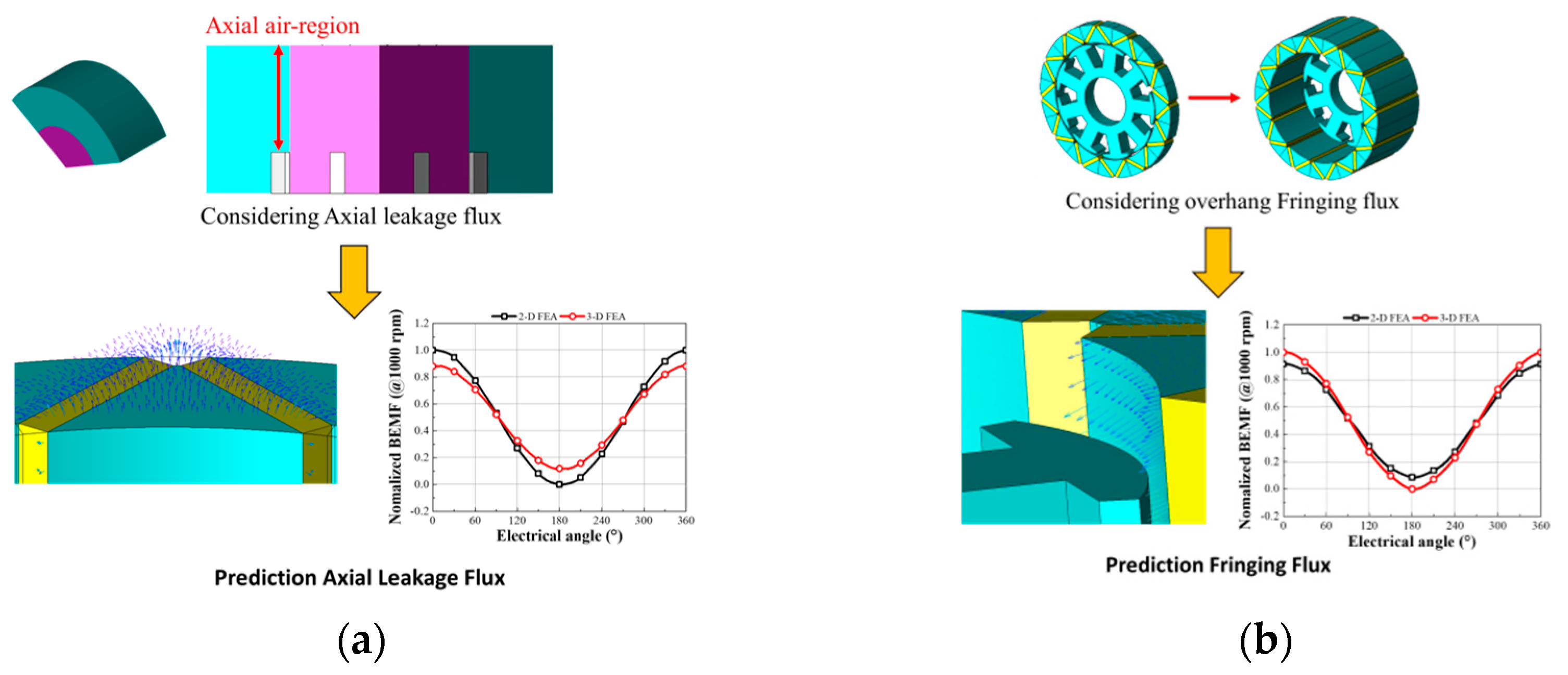
2.2. Axial Leakage Flux in Motor
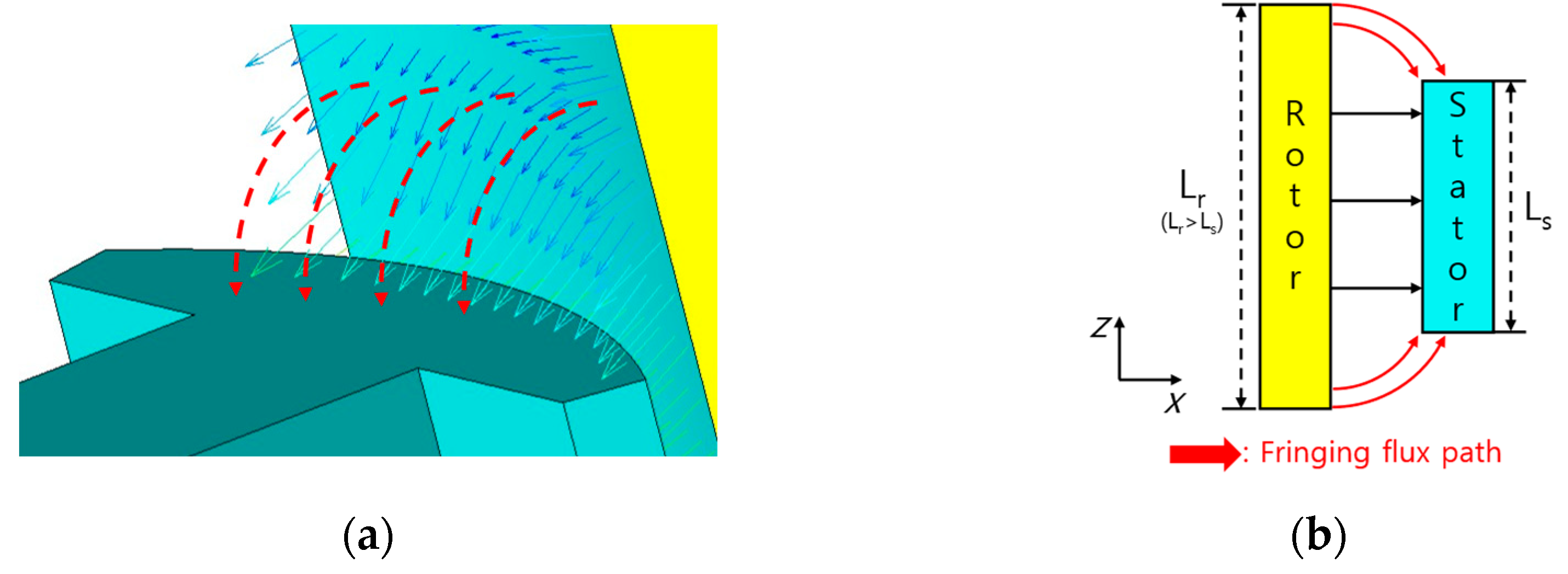
2.3. Fringing Flux Caused by Overhang
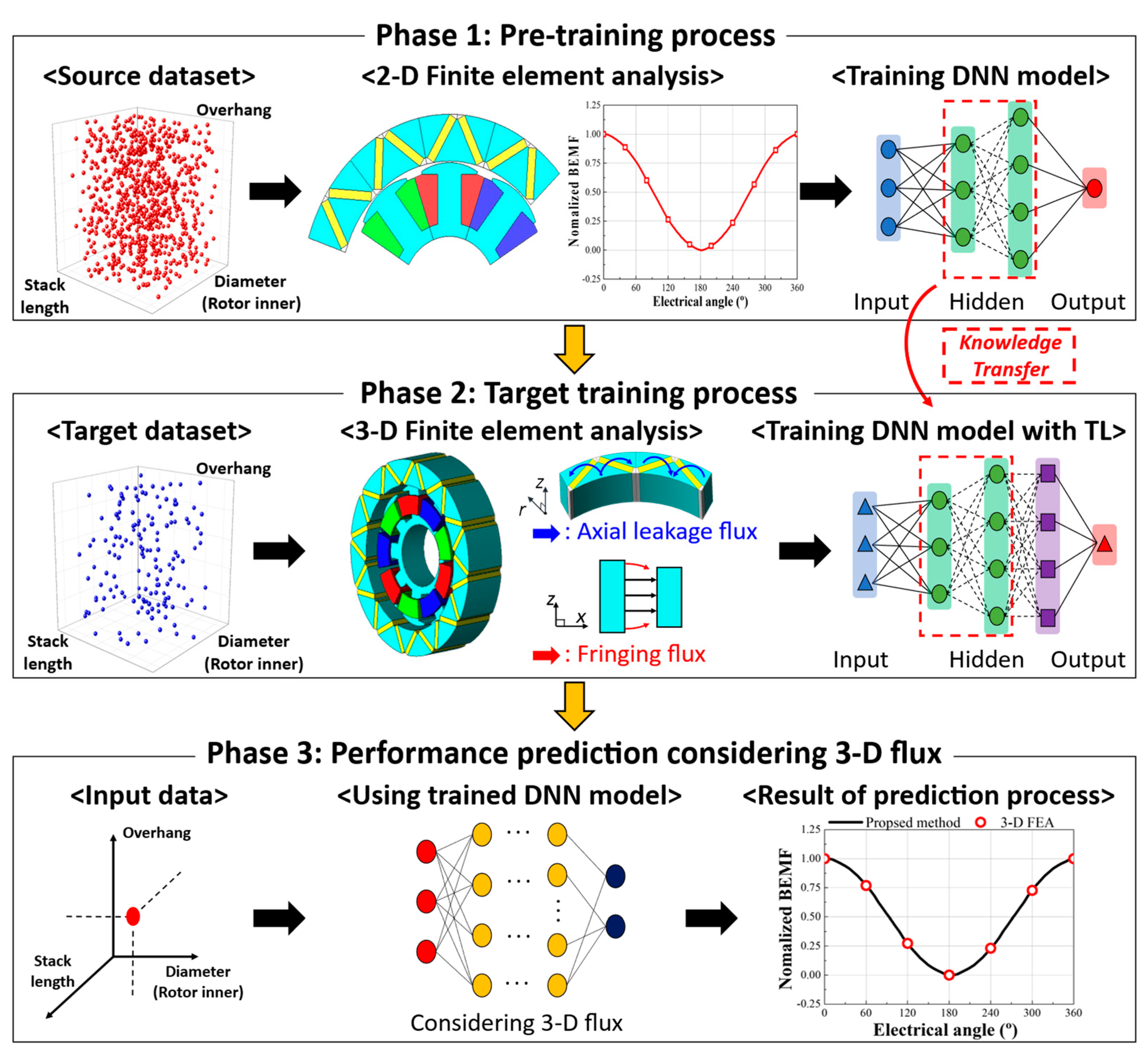
3. Deep Transfer Learning-Based Motor Performance Analysis
3.1. Deep Transfer Learning
3.2. Proposed Motor Performance Prediction Method
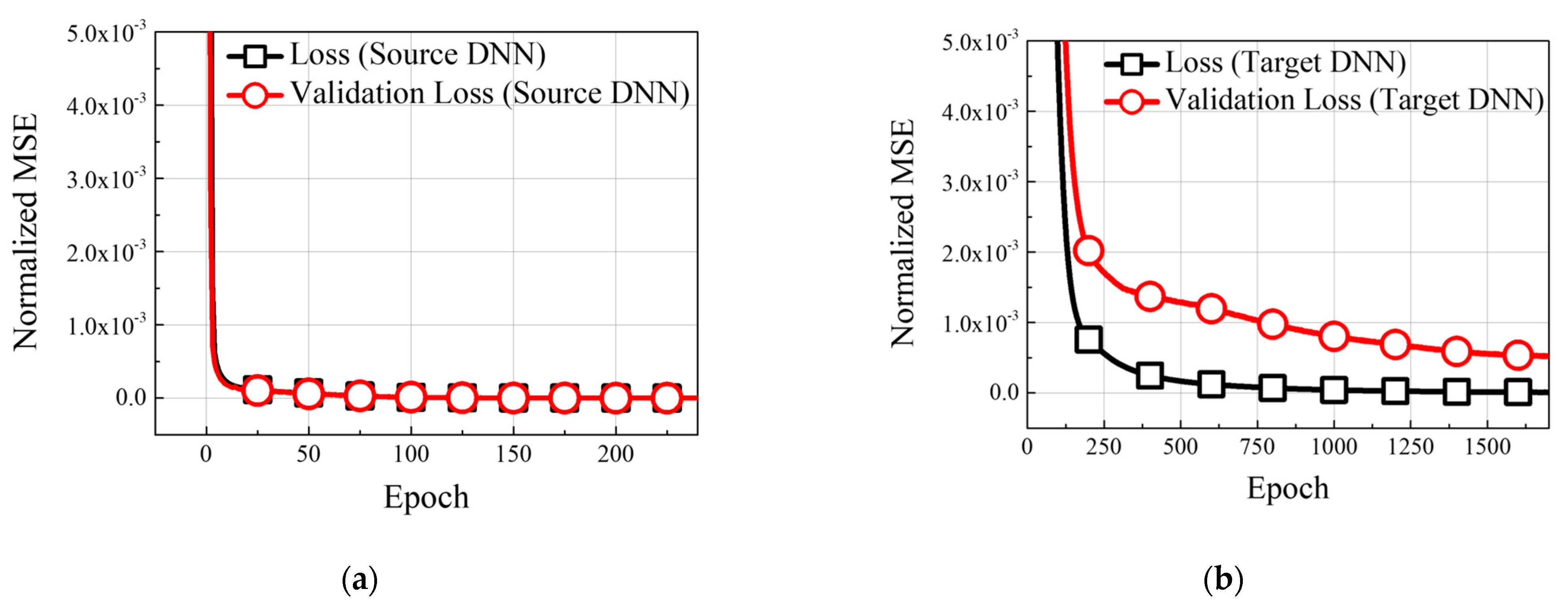
3.3. DTL Models: Validation and Performance Evaluation
4. Analysis of Irreversible Demagnetization Fault of Motor
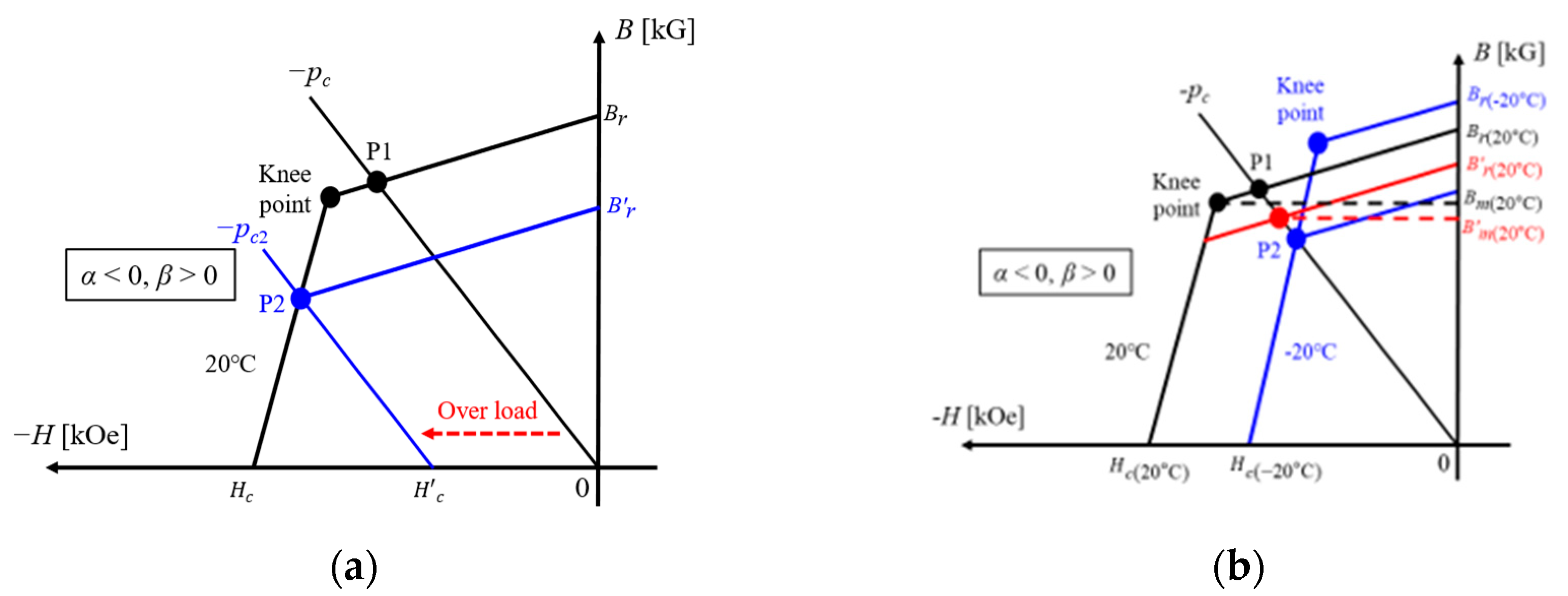
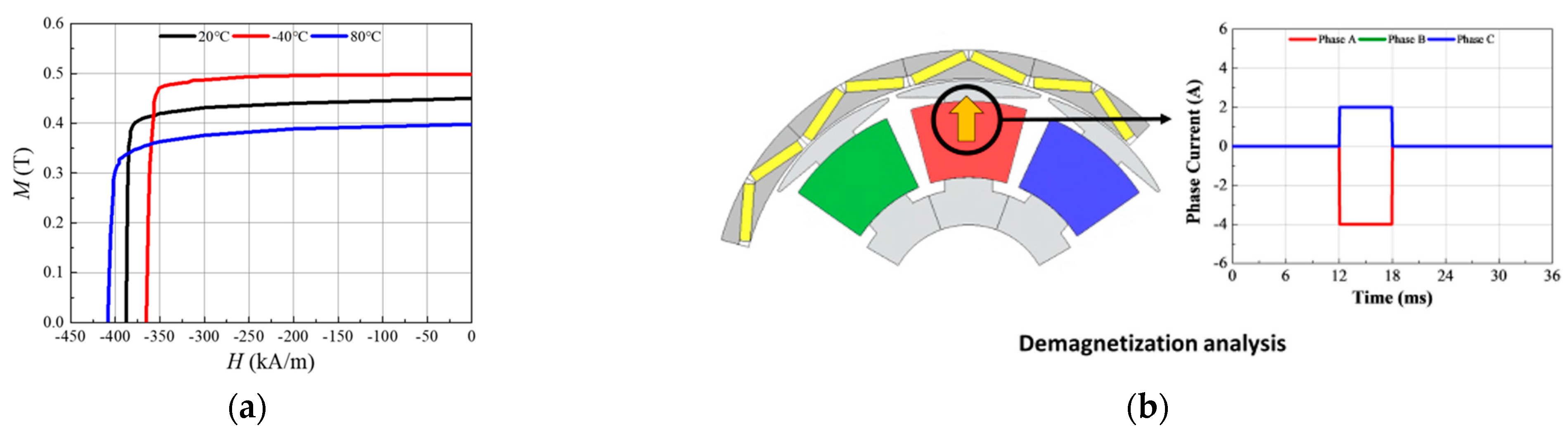
4.1. Irreversible Demagnetization Fault
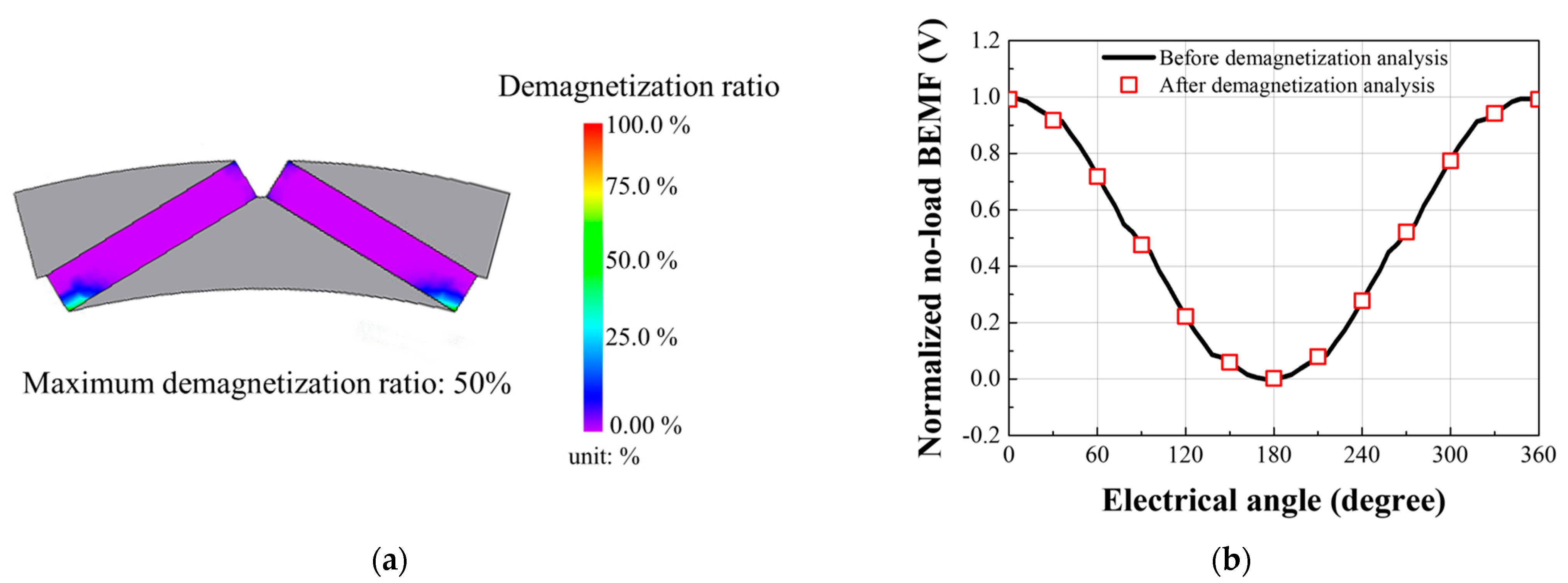
4.2. Demagnetization Analysis
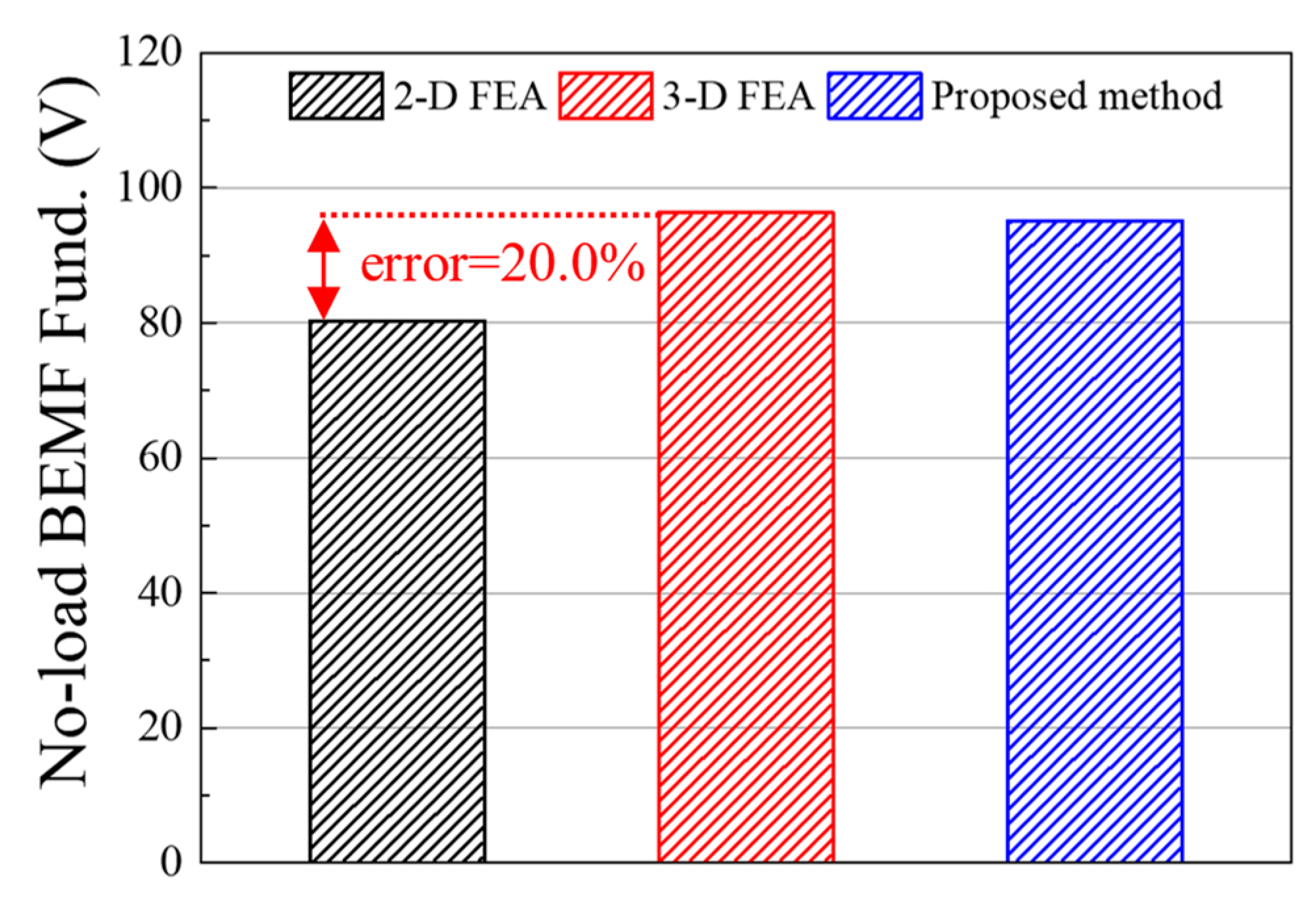
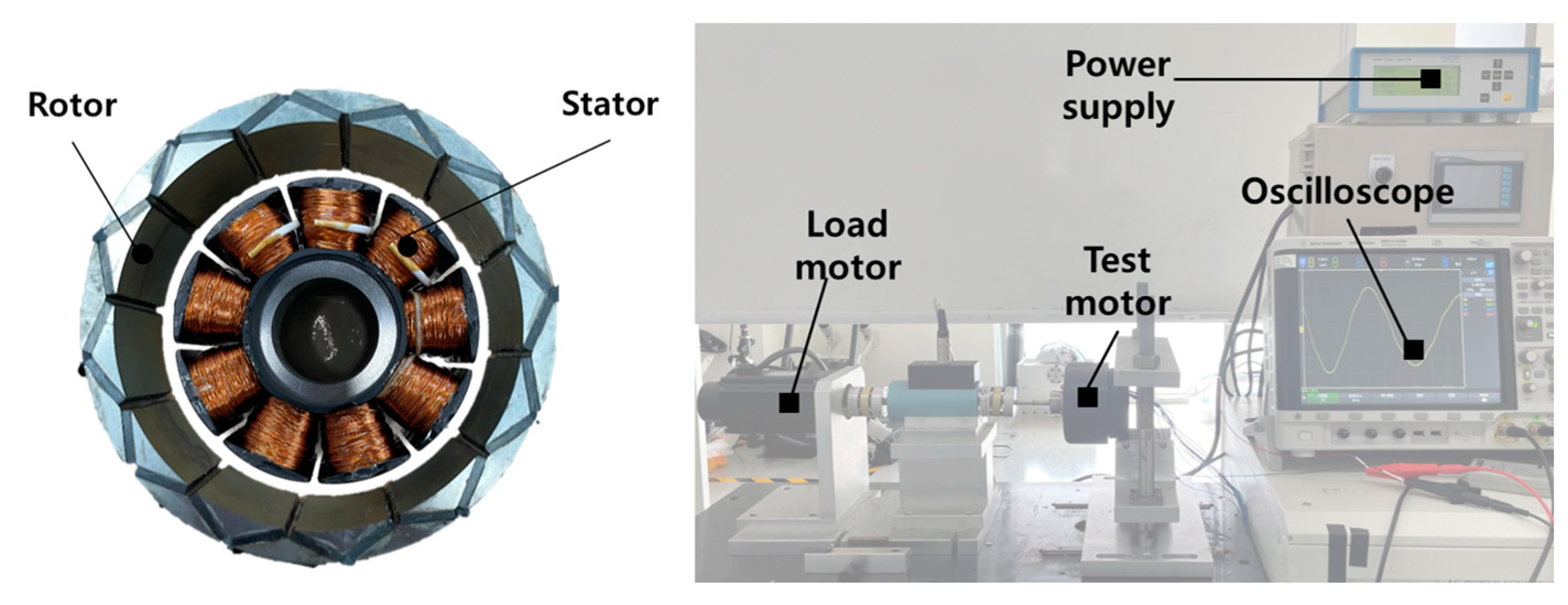
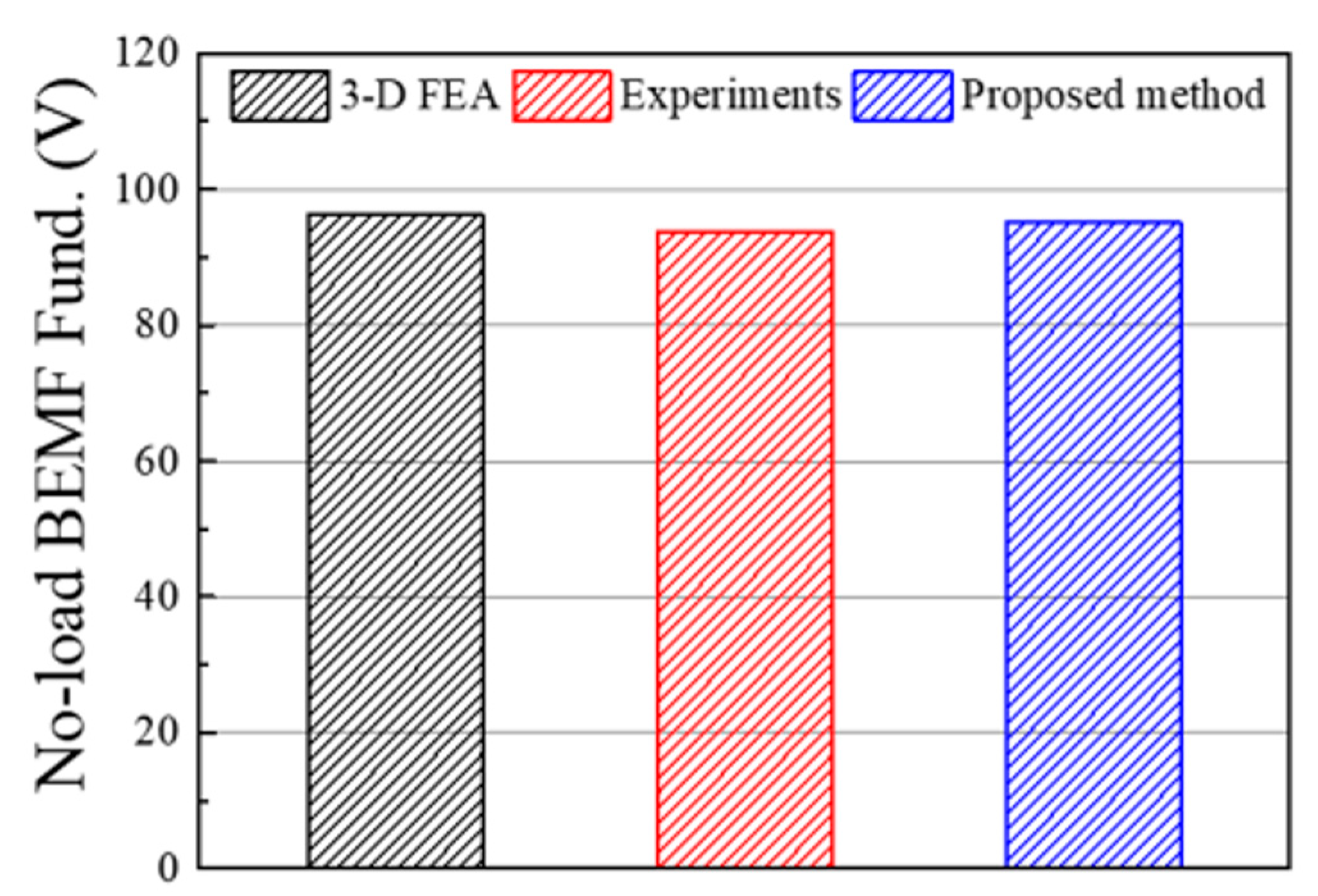
5. Simulation Result and Experimental Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jung, J.-W.; Jung, D.-H.; Lee, J. A Study on the Design Method for Improving the Efficiency of Spoke-Type PMSM. IEEE Trans. Magn. 2023, 59, 8200205. [Google Scholar] [CrossRef]
- Park, C.-S.; Kim, J.-H.; Park, S.-H.; Yoon, Y.-D.; Lim, M.-S. Multi-Physics Characteristics of PMSM for Compressor According to Driving Mode Considering PWM Frequency. IEEE Access 2022, 10, 114490–114500. [Google Scholar] [CrossRef]
- Li, L.; Zhang, J.; Zhang, C.; Yu, J. Research on Electromagnetic and Thermal Issue of High-Efficiency and High-Power-Density Outer-Rotor Motor. IEEE Trans. Appl. Supercond. 2016, 26, 5204805. [Google Scholar]
- Chen, H.; Demerdash, N.A.O.; El-Refaie, A.M.; Guo, Y.; Hua, W.; Lee, C.H.T. Investigation of a 3D-Magnetic Flux PMSM with High Torque Density for Electric Vehicles. IEEE Trans. Energy Convers. 2022, 37, 1442–1454. [Google Scholar]
- Lee, S.G.; Bae, J.; Kim, W.-H. Study on the Axial Leakage Magnetic Flux in a Spoke Type Permanent Magnet Synchronous Motor. IEEE Trans. Ind. Appl. 2019, 55, 5881–5887. [Google Scholar] [CrossRef]
- Jung, J.-W.; Park, H.-I.; Hong, J.-P.; Lee, B.-H. A Novel Approach for 2-D Electromagnetic Field Analysis of Surface Mounted Permanent Magnet Synchronous Motor Taking Into Account Axial End Leakage Flux. IEEE Trans. Magn. 2017, 53, 8208104. [Google Scholar]
- Jung, J.-W.; Jung, K.-T.; Lee, B.-H.; Hong, J.-P. Design and Analysis of Ferrite Magnet Flux Concentrated PMSM with Cross-Laminated Rotor Core Using Equivalent 2-D FEA. IEEE Trans. Energy Convers. 2019, 34, 1623–1631. [Google Scholar]
- Seok, C.-H.; Yoon, S.-Y.; Choi, H.-S.; Lee, H.-Y.; Seo, J. Analysis and Modeling of Axial Leakage for Spoke-Type Hybrid Permanent Magnet Machines. IEEE Access 2023, 11, 6385–6393. [Google Scholar]
- Lee, S.G.; Bae, J.-N.; Kim, M.; Kim, W.-H. Study on the Improvement of the Correction Coefficient Considering the 3-D Effect of Spoke-Type Permanent-Magnet Synchronous Motor. IEEE Trans. Mag. 2020, 56, 7513405. [Google Scholar]
- Xiao, C.; Han, A.; Xie, W.; He, M. Fast Design of Spoke-Type PM Motor with Auxiliary Notches Based on Lumped-Parameter Magnetic Equivalent Circuit Model and Hybrid Multiobjective Optimizer. IEEE Access 2022, 10, 99421–99434. [Google Scholar]
- Saneie, H.; Nasiri-Gheidari, Z. Performance Analysis of Outer-Rotor Single-Phase Induction Motor Based on Magnetic Equivalent Circuit. IEEE Trans. Ind. Electron. 2021, 68, 1046–1054. [Google Scholar] [CrossRef]
- Watthewaduge, G.; Bilgin, B. Reluctance Mesh-Based Magnetic Equivalent Circuit Modeling of Switched Reluctance Motors for Static and Dynamic Analysis. IEEE Trans. Transp. Electrif. 2022, 8, 2164–2176. [Google Scholar] [CrossRef]
- Won, Y.-J.; Kim, J.-H.; Park, S.-H.; Lee, J.-H.; An, S.-M.; Kim, D.-Y.; Lim, M.-S. Transfer Learning-Based Design Method for Cogging Torque Reduction in PMSM with Step-Skew Considering 3-D Leakage Flux. IEEE Trans. Magn. 2023, 59, 8204905. [Google Scholar] [CrossRef]
- Lee, J.H.; Park, S.H.; Kim, P.J.; Park, D.H.; Lim, M.S. Two-Dimensional FEA-Based Iron Loss Calculation Method for Linear Oscillating Actuator Considering the Circumferential Segmented Structure. IEEE Trans. Magn. 2023, 59, 1–5. [Google Scholar] [CrossRef]
- Bian, Y.; Wen, X.; Fan, T.; Li, H.; Liu, Z. Data-Driven-Model-Based Full-Region Optimal Mapping Method of Permanent Magnet Synchronous Motors in Wide Temperature Range. Machines 2023, 11, 324. [Google Scholar] [CrossRef]
- Bianchi, N.; Jahns, T.M. Design, Analysis, and Control of Interior PM Synchronous Machines. Presented at the IEEE Industry Applications Society Annual Meeting, Seatle, WA, USA, 3 October 2004; pp. 3–9. [Google Scholar]
- Khan, A.; Mohammadi, M.H.; Ghorbanian, V.; Lowther, D. Efficiency Map Prediction of Motor Drives Using Deep Learning. IEEE Trans. Mag. 2020, 56, 7511504. [Google Scholar] [CrossRef]
- Shao, S.; McAleer, S.; Yan, R.; Baldi, P. Highly Accurate Machine Fault Diagnosis Using Deep Transfer Learning. IEEE Trans. Ind. Inf. 2019, 15, 2446–2455. [Google Scholar] [CrossRef]
- Asanuma, J.; Doi, S.; Igarashi, H. Transfer Learning Through Deep Learning: Application to Topology Optimization of Electric Motor. IEEE Trans. Magn. 2020, 56, 7512404. [Google Scholar] [CrossRef]
- Park, S.-H.; Chin, J.-W.; Cha, K.-S.; Lim, M.-S. Deep Transfer Learning-Based Sizing Method of Permanent Magnet Synchronous Motors Considering Axial Leakage Flux. IEEE Trans. Mag. 2022, 58, 8206005. [Google Scholar] [CrossRef]
- Jeong, C.-L.; Hur, J. Optimization Design of PMSM with Hybrid-Type Permanent Magnet Considering Irreversible Demagnetization. IEEE Trans. Magn. 2017, 53, 8110904. [Google Scholar] [CrossRef]
- Hwang, K.-Y.; Yoon, K.-Y. Fault-Tolerant Design Process of Spoke-Type IPM Motor Considering Irreversible Demagnetization of PM in Integrated Electric Brake System. IEEE Trans. Mag. 2022, 58, 8206809. [Google Scholar] [CrossRef]
- Kang, Y.; Yao, L. Fault Diagnosis for Permanent Magnet Synchronous Motor with Demagnetization Fault and Sensor Fault. IEEE Trans. Instrum. Meas. 2024, 73, 3533311. [Google Scholar] [CrossRef]

| Item | Value | |
|---|---|---|
| Input components | Dri, stack length, rotor overhang | |
| Output components | No-load BEMF | |
| Number of datasets | 3000 (Source, 2-D FEA) | 100 (Target, 3-D FEA) |
| Loss function | Mean squared error (MSE) | |
| Number of hidden layers | 4 | |
| Activation function | ReLU | |
| Optimizer | Adam | |
| Analysis Method | Unit | Value |
|---|---|---|
| 2-D FEA | minute | 0.16 |
| 3-D FEA | 180 | |
| Proposed method | 5.0 |
| Item | Unit | Value |
|---|---|---|
| Motor type | - | Outer rotor IPMSM |
| Permanent magnet | - | Ferrite |
| Stator/rotor core | - | 35PN270 |
| Stator/rotor diameter ratio | % | 85.00 |
| Stator stack length | p.u. | 1.00 |
| Rotor stack length | p.u. | 1.44 |
| Phase per turn | - | 720 |
| Slot fill factor | % | 83.00 |
| Current density | Arms/mm2 | 4.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sung, M.-H.; Park, S.-H.; Cha, K.-S.; Sim, J.-H.; Lim, M.-S. Deep Transfer Learning-Based Performance Prediction Considering 3-D Flux in Outer Rotor Interior Permanent Magnet Synchronous Motors. Machines 2025, 13, 302. https://doi.org/10.3390/machines13040302
Sung M-H, Park S-H, Cha K-S, Sim J-H, Lim M-S. Deep Transfer Learning-Based Performance Prediction Considering 3-D Flux in Outer Rotor Interior Permanent Magnet Synchronous Motors. Machines. 2025; 13(4):302. https://doi.org/10.3390/machines13040302
Chicago/Turabian StyleSung, Moo-Hyun, Soo-Hwan Park, Kyoung-Soo Cha, Jae-Han Sim, and Myung-Seop Lim. 2025. "Deep Transfer Learning-Based Performance Prediction Considering 3-D Flux in Outer Rotor Interior Permanent Magnet Synchronous Motors" Machines 13, no. 4: 302. https://doi.org/10.3390/machines13040302
APA StyleSung, M.-H., Park, S.-H., Cha, K.-S., Sim, J.-H., & Lim, M.-S. (2025). Deep Transfer Learning-Based Performance Prediction Considering 3-D Flux in Outer Rotor Interior Permanent Magnet Synchronous Motors. Machines, 13(4), 302. https://doi.org/10.3390/machines13040302








