Study on Control Approaches for Servo Systems Exhibiting Uncertain Time Delays
Abstract
1. Introduction
2. Problem Description
3. Uncertain Time Delay Research
3.1. Establishment of Uncertain Time Delay Model
3.1.1. Discussion on Uncertain Delay Types
- ①
- The definition assumes that : The delay parameters of servo system follow normal distribution; The delay parameters follow the white noise distribution completely randomly. The delay parameter of is fixed constant and invariable.
- ②
- Prior probability: To facilitate the calculation of the posterior probability, set .
- ③
- Likelihood function:
- ④
- Bayesian analysis:
3.1.2. Time Delay Parameter Model Establishment
- (1)
- Estimation of expectation and variance under normal distribution
- (2)
- Specific iteration of MCMC
| Algorithm 1 MCMC Process | |
| 1 | iter = 0 |
| 2 | while (iter < 10000): |
| 3 | //tau_star <- candidate_example |
| 4 | //u <-random_number_ between_0_and_1 |
| 5 | calculate_prior_tau_star_value |
| 6 | calculate_prior_tau_current_value |
| 7 | calculate_likelihood_function_value_at_tau_star and tau_current |
| 8 | calculate_acceptance_probability(tau_current, tau_star) |
| 9 | if (u <= accept_prob): |
| 10 | tau_current = tau_star |
| 11 | tau_samples[iter] = tau_current |
| 12 | iter = iter + 1 |
| 13 | mu_p = calculate_average_of_tau_samples_array |
4. Delay Compensation System Design
4.1. Structure of Time Delay Compensation System
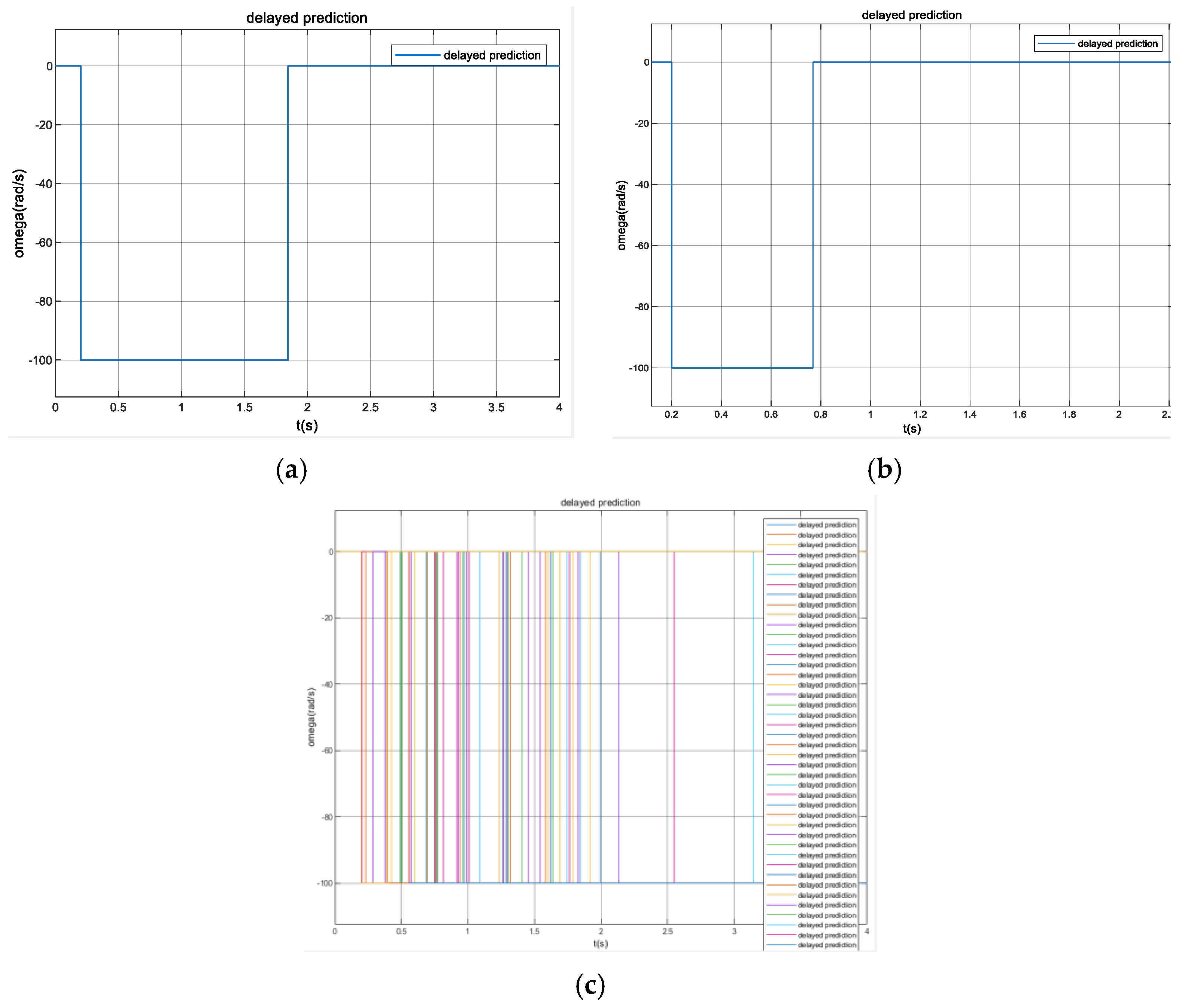
4.2. Delayed Prediction
| Algorithm 2 Delayed Prediction | |
| 1 | Function estimate_delay(x, d) |
| 2 | Input: |
| 3 | x: Input signal |
| 4 | d: Reference signal |
| 5 | Calculate the cross-correlation between input signal x and reference signal d |
| 6 | Find the maximum of the absolute value of the cross-correlation function |
| 7 | Estimate the delay |
| 8 | Obtain the cross-correlation peak value |
| 9 | correlation_peak |
| 10 | Return the result |
| 11 | End function |
4.3. Gain Optimization Feedback State Observer
| Algorithm 3 Gain Optimization | |
| 1 | Input: |
| 2 | Q: Status weight |
| 3 | R: Control weight |
| 4 | System matrix A, B, C |
| 5 | Function design_compensator(A, B, C, tau, Q, R): |
| 6 | set the matrix(A, B, C, Q, R, tau) |
| 7 | //Judge the observability and controllability of system |
| 8 | If the system (A, B, C) is not observable or not controllable then |
| 9 | Print “The system is either unobservable or uncontrollable”. |
| 10 | Return null |
| 11 | End If |
| 12 | Calculate V and D from A |
| 13 | Calculate the eigenvalues and eigenvectors of the system |
| 14 | Delayed manifestation: |
| 15 | //V is the eigenvalue of A, D is the eigenvector of A |
| 16 | Calculate the adjusted system matrix A_hat: |
| 17 | A_hat = V*diag(λ_i + τ*max(Re(λ_i)))*V^’ |
| 18 | //λ_i <- Diagonal elements of D |
| 19 | //Re(λ_i) <- Take the real part of λ_i |
| 20 | //max(Re(λ_i)) <- Find the maximum value of the real part of the diagonal element |
| 21 | //diag(W) <- Extract the diagonal elements of matrix W |
| 22 | //V^’ <- V transpose |
| 23 | Design observer gain matrix L0 |
| 24 | Design LQR controller |
| 25 | Construct the observation error system |
| 26 | Define the LMI variable |
| 27 | Construct Lyapunov-Krasovskii functional dependent LMI constraints |
| 28 | Solving LMI |
| 29 | Judge observer stability |
| 30 | return L,K |
5. Experimental Verification
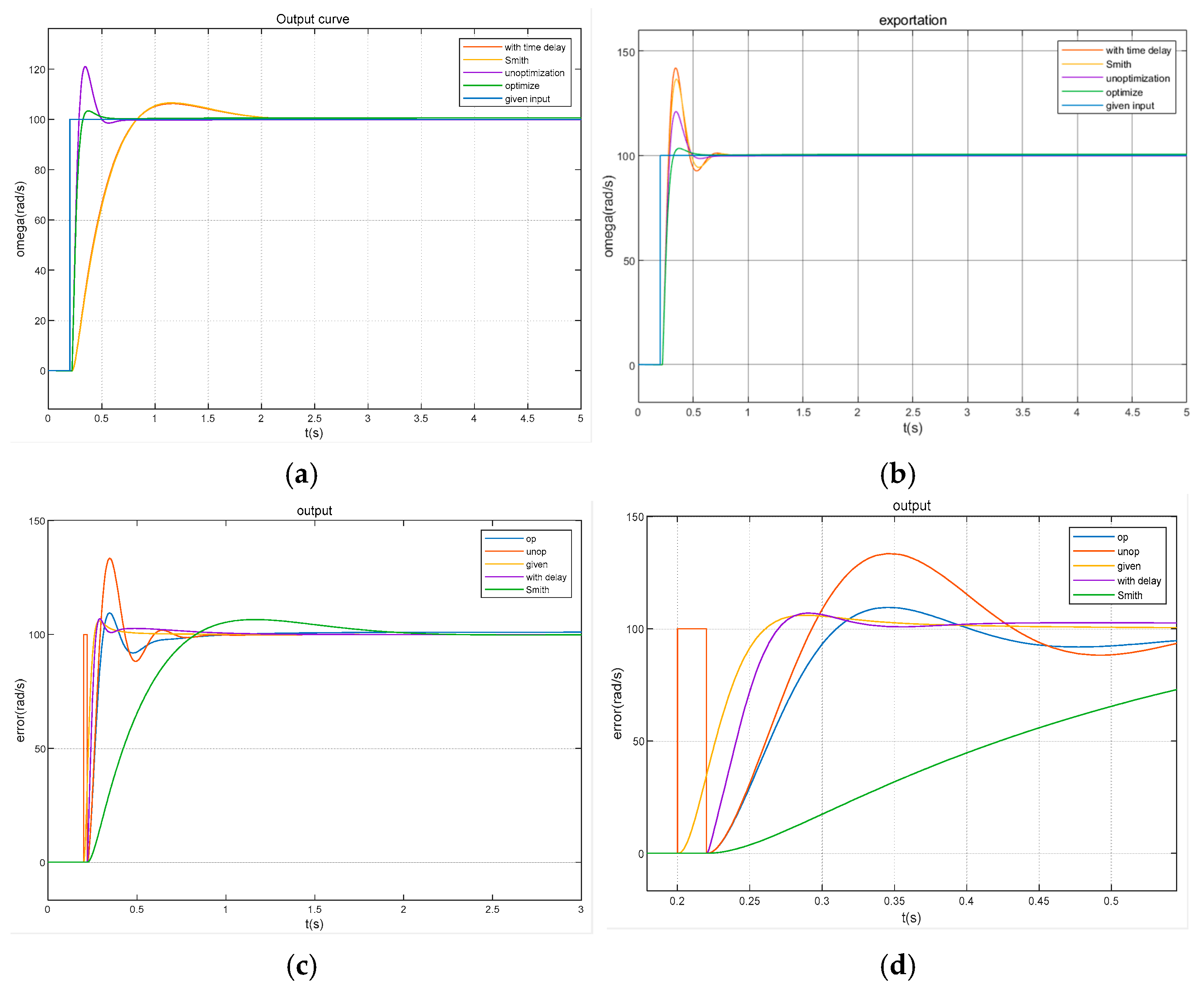
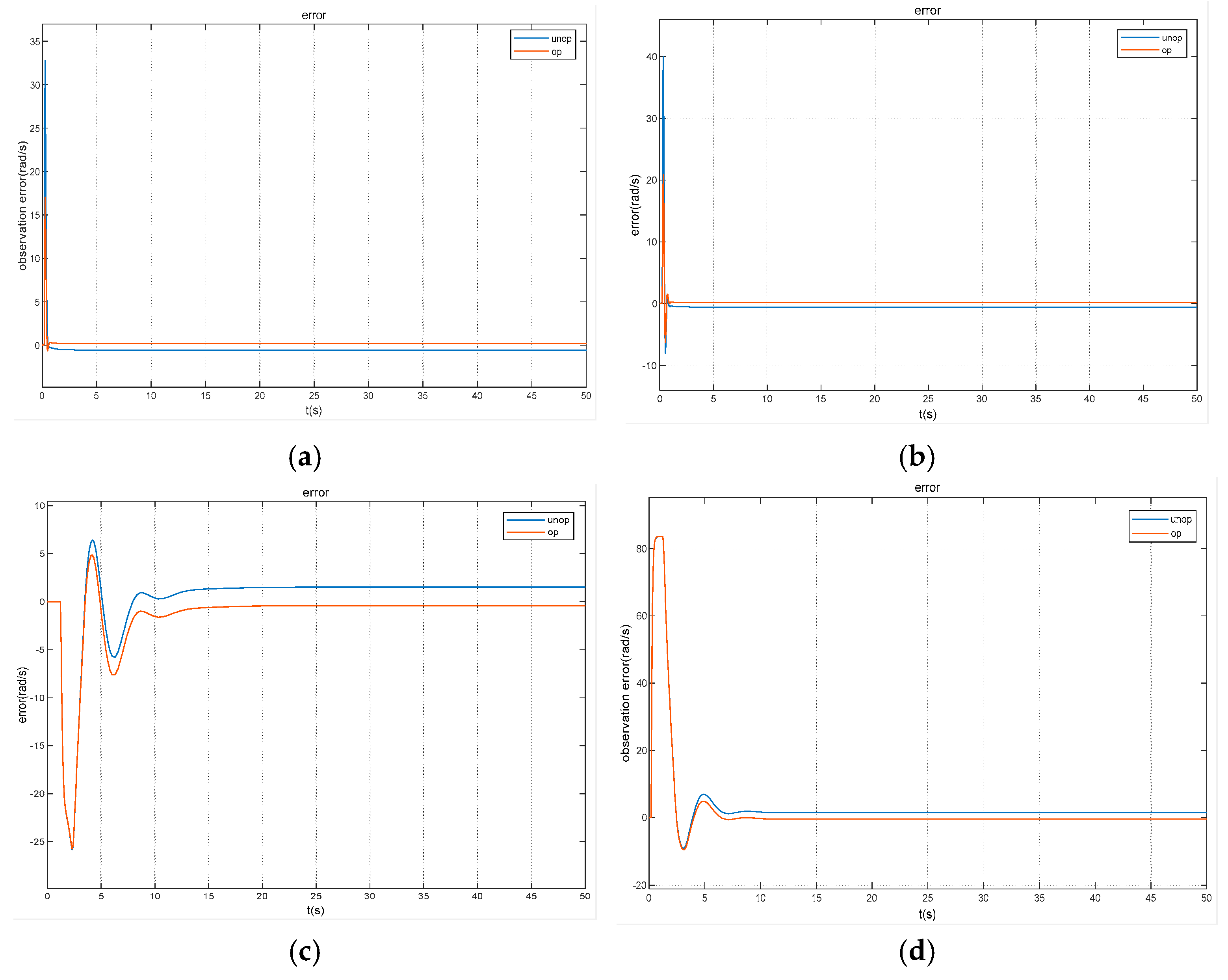
6. Analysis and Comparison of Experimental Results
6.1. Time Domain Analysis of System Response
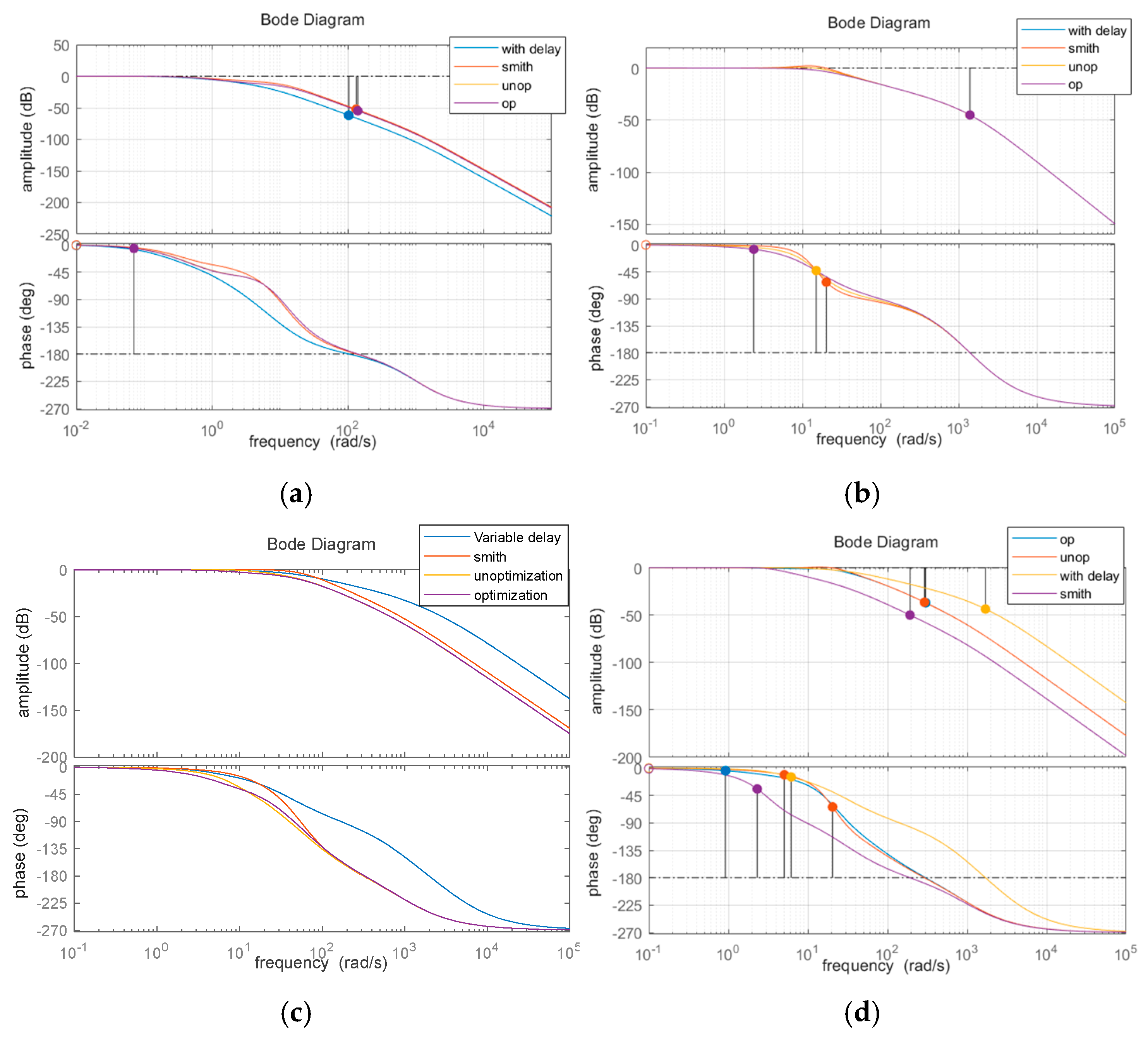
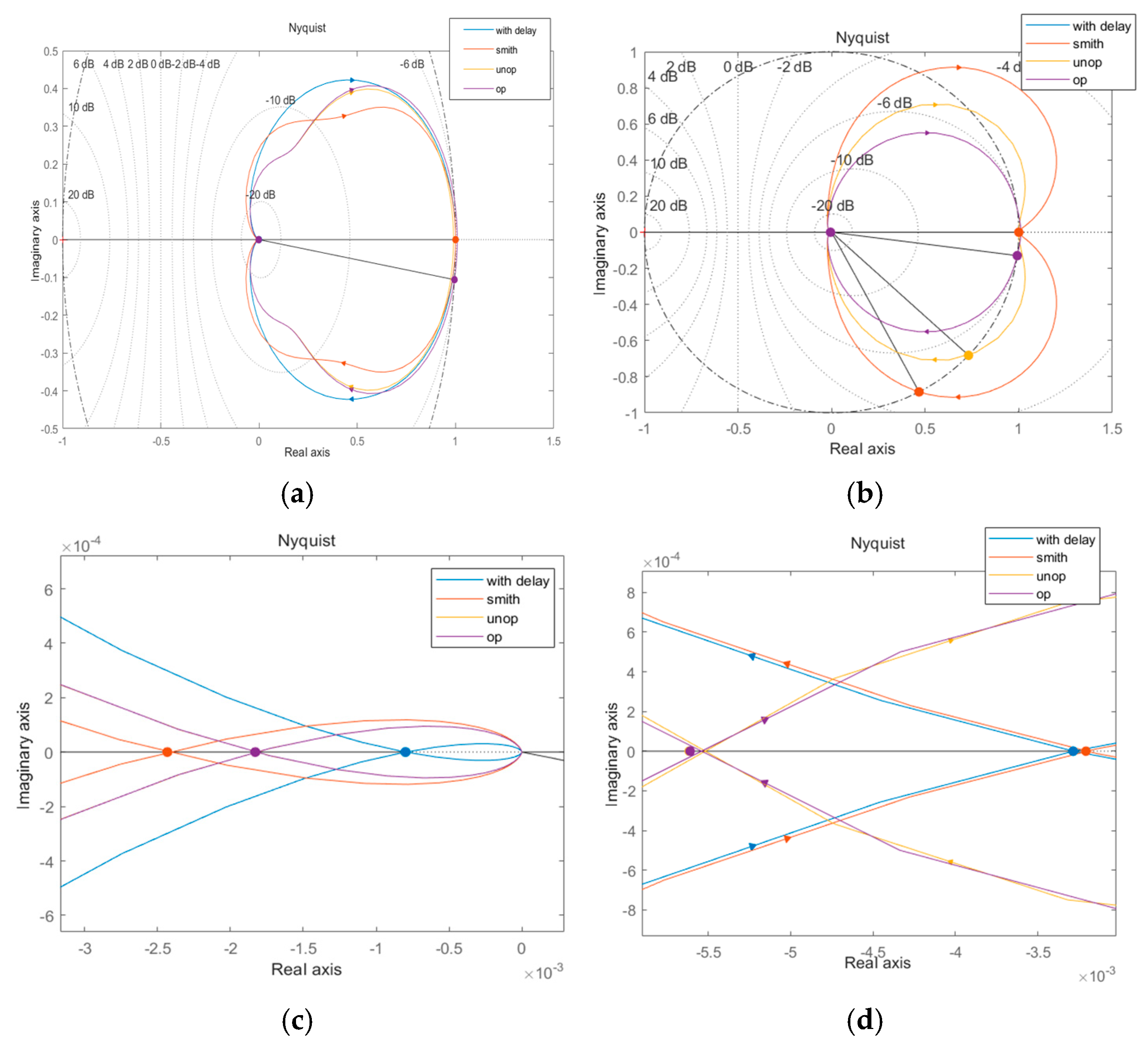
6.2. Frequency Domain Analysis of System Response
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, J.Q. Self-Tuning Anti-Disturbance Control for Time-Delay Objects. Control Eng. 2008, S2, 7–10+18. [Google Scholar]
- Tao, L.; Chen, S.; Fang, G.; Zu, G. Smith Predictor-Taylor Series-Based LQG Control for Time Delay Compensation of Vehicle Semiactive Suspension. Shock Vib. 2019, 2019, 1–12. [Google Scholar] [CrossRef]
- Nie, Y.; Zhang, P.; Cai, G.; Zhao, Y.; Xu, M. Unified Smith predictor compensation and optimal damping control for time-delay power system. Int. J. Electr. Power Energy Syst. 2020, 117, 105670. [Google Scholar] [CrossRef]
- Fan, Y.S.; Luo, E.Y.; Wang, G.F. Simulation of Position Control of Pneumatic System Based on Time-Delay Compensation. Sci. Technol. Eng. 2021, 21, 10680–10689. [Google Scholar]
- Ji, J.B.; Xu, J.C.; Wang, D.Y. Research on Sub-Structure Test Method of Vibration Table Based on Improved Smith Predictor. Mach. Tool Hydraul. 2024, 52, 14–21. [Google Scholar]
- Chen, L. Probability Prediction of Daily Water Consumption Based on Bayesian Theory. Syst. Eng. Theory Pract. 2017, 37, 761–767. [Google Scholar]
- Song, J.W.; Zhang, S.; Li, K.X. Adaptive Bayesian Model Updating Method with Variable Observation Domain. J. Beihang Univ. 2025, 1–13. [Google Scholar] [CrossRef]
- Shang, T.; Guo, M.Y.; Tang, B.M.; Xu, Y.T. Driving Risk Assessment of Underground Roads Based on Dynamic Bayesian Network. Transp. Syst. Eng. Inf. 2025, 1–22. [Google Scholar]
- Wang, C.X.; Wang, R.Q. Short-Term Trend Prediction Model of Stock Market Based on Pattern Recognition and Bayesian Decision-Making. Stat. Decis. 2024, 40, 154–158. [Google Scholar] [CrossRef]
- Yuan, X.Y.; Zhao, Y.D. Prediction of Water Supply Temperature in Heat—Exchange Station Based on Grey Markov Chain Prediction Model. Electron. Meas. Technol. 2015, 38, 32–34. [Google Scholar] [CrossRef]
- Zhu, C.X.; Zhang, Y.; Yan, Z.; Zhu, J.; Zhao, T. Modeling of Wind Power Sequence Using Improved Markov Chain Monte Carlo Method. Trans. China Electrotech. Soc. 2020, 35, 577–589. [Google Scholar] [CrossRef]
- Wang, Q.Q.; Yao, L.Z.; Xu, J.; Cheng, F.; Mao, B.; Wen, Z.; Chen, R. Probabilistic Assessment of Equivalent Inertia of High—Proportion Renewable Energy Power Systems Based on Slice Sampling—Markov Chain Monte Carlo Simulation. Power Syst. Technol. 2024, 48, 140–152. [Google Scholar] [CrossRef]
- Ye, L.; Jiang, H.K.; Zou, Y.Q.; Chen, H.P.; Wang, L.P. Bayesian Finite Element Model Updating Based on Markov Chain Population Competition. J. Mech. Strength 2025, 85–93. [Google Scholar]
- Miao, H.; Guo, W.L.; Liu, Z.Y.; Wang, R.J. Ultraviolet LED Lifetime Prediction Based on Bayesian MCMC and Other Models. Acta Opt. Sin. 2024, 44, 170–177. [Google Scholar]
- Padilla, G.J.L.; Azevedo, C.L.; Lachos, V.H. Parameter recovery of skew multidimensional multiple-group item response models (MGM-MIRT): A comparison of MCMC algorithms and assessment of effects of interest. J. Stat. Comput. Simul. 2025, 95, 467–489. [Google Scholar] [CrossRef]
- Chen, H.G.; Xu, L.L.; Tang, X.Q. Implicit Markov HDP Non-Parametric Bayesian Video Anomaly Detection. Control Eng. 2019, 26, 1763–1769. [Google Scholar] [CrossRef]
- de Oliveira, J.T.; de Carvalho Costa, L.R.; Estumano, D.C.; Féris, L.A. Applying Bayesian statistics and MCMC to ozone reaction kinetics: Implications for water treatment models. Chemosphere 2025, 373, 144164. [Google Scholar]
- Miao, J.; Duan, L.; Liu, J.M.; Lin, S.W.; Zhao, J.C. Structural Simulation Model Updating Based on Improved MCMC Method and Surrogate Model. J. Shanghai Jiao Tong Univ. Sci. 2025, 67, 1–17. [Google Scholar] [CrossRef]
- Arabpour, A.; Moghadam, H.R.; Niri, E.M. Geophysical bayesian inverse problem solving with tuning-free adaptive MCMC sampler. Earth Sci. Inform. 2025, 18, 186. [Google Scholar]
- Wang, L.Y.; Xi, C. An Improved MCMC Algorithm for Inverting Source Parameters Using GPS Data in Bayesian Framework. Chin. J. Geophys. 2024, 67, 3367–3385. [Google Scholar]
- Hu, J.M.; Liu, W.; Yan, F.; Hu, Y.J. Robust Optimal Reinsurance and Investment Strategies with Time-Delay under the Mean-Variance Premium Principle. Chin. J. Eng. Math. 2024, 41, 1–16. [Google Scholar]
- Chang, X.H.; Pan, T.T.; Xiong, J. A New Method for the Analysis and Design of State Observers. J. Jilin Norm. Univ. Nat. Sci. Ed. 2024, 45, 53–61. [Google Scholar]


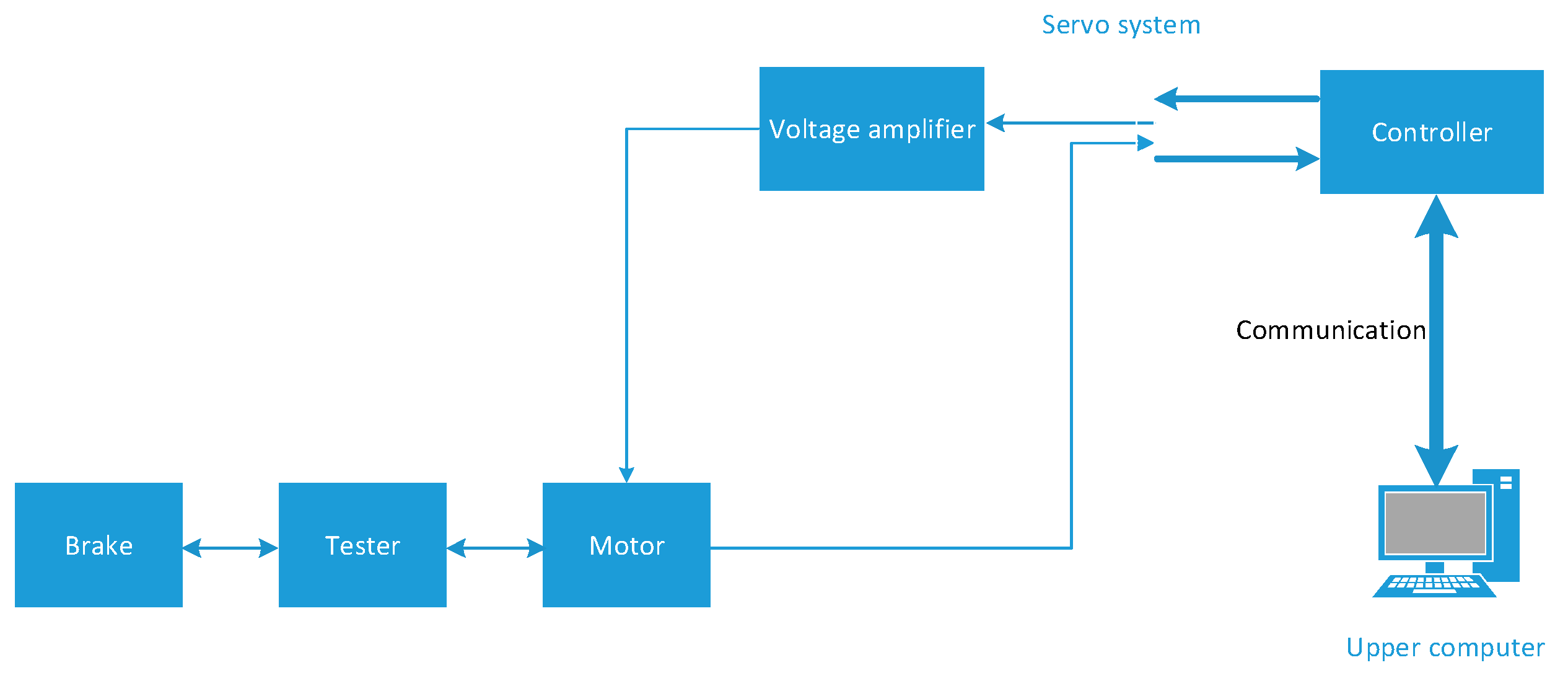


| Motor Parameter | Value |
|---|---|
| Rated voltage | 24 V |
| Rated current | 11.2 A |
| Rated speed | 3000 rpm |
| Rated power | 200 W |
| Number of poles | 4 |
| State | Gain Margin/dB | Phase Margin/deg | Delay Margin/s |
|---|---|---|---|
| Before compensation | 29.4 | 140 | 0.1 |
| Smith | 29.4 | 140 | 0.1 |
| Compensation—gain not optimized | 35.7 | 153 | 0.328 |
| Compensation-gain optimization | 36.1 | 173 | 2.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, M.; Yao, S.; Ma, W. Study on Control Approaches for Servo Systems Exhibiting Uncertain Time Delays. Machines 2025, 13, 264. https://doi.org/10.3390/machines13040264
Ma M, Yao S, Ma W. Study on Control Approaches for Servo Systems Exhibiting Uncertain Time Delays. Machines. 2025; 13(4):264. https://doi.org/10.3390/machines13040264
Chicago/Turabian StyleMa, Minyu, Shuncai Yao, and Weijie Ma. 2025. "Study on Control Approaches for Servo Systems Exhibiting Uncertain Time Delays" Machines 13, no. 4: 264. https://doi.org/10.3390/machines13040264
APA StyleMa, M., Yao, S., & Ma, W. (2025). Study on Control Approaches for Servo Systems Exhibiting Uncertain Time Delays. Machines, 13(4), 264. https://doi.org/10.3390/machines13040264





