Estimation of Vibration-Induced Fatigue Damage in a Tracked Vehicle Suspension Arm at Critical Locations Under Real-Time Random Excitations ^†

Abstract

Probabilistic random vibration can speed up wear and tear on several components of the tracked vehicle, including the track system, drivetrain, and suspension. Extended exposure to high levels of vibration can cause structural damage to the vehicle frame and other critical components. Assessing random vibration in track vehicles requires a comprehensive approach that considers both the root causes and potential consequences of the vibrations. This random vibration significantly influences the structural performance of suspension arm which is key component of tracked vehicle. Damage due to fatigue is conventionally computed using time domain loaded signals with stress or strain data. This approach generally holds good when loading is periodic in nature but not be a good choice when dynamic resonance is in process. In this case an alternative frequency domain fatigue life analysis is used where the random loads and responses are characterized using a concept called Power spectral density (PSD). The current research article investigates the fatigue damage characteristics of a tracked vehicle suspension arm considering the dynamic loads induced by traversing on smooth and rough terrain. The analysis focusses on assessing the damage and stress response Power spectral density (PSD) ground-based excitation which is termed PSD-G acceleration. Quasi Static Finite Element Method based approach is used to simulate the operational conditions experienced by the suspension arm. Through comprehensive numerical simulations, the fatigue damage accumulation patterns are examined, providing insights into the structure integrity and performance durability of the suspension arm under varying operational scenarios. The obtained stress response PSD data and fatigue damage showed that the rough terrain response exhibits higher stresses in suspension arm. The accumulated stresses in case of rough terrain may prompt to brittle failure at specific critical locations. This research contributes to the advancement to the design and optimization strategies for tracked vehicle components enhancing their reliability and longevity in demanding operational environments.

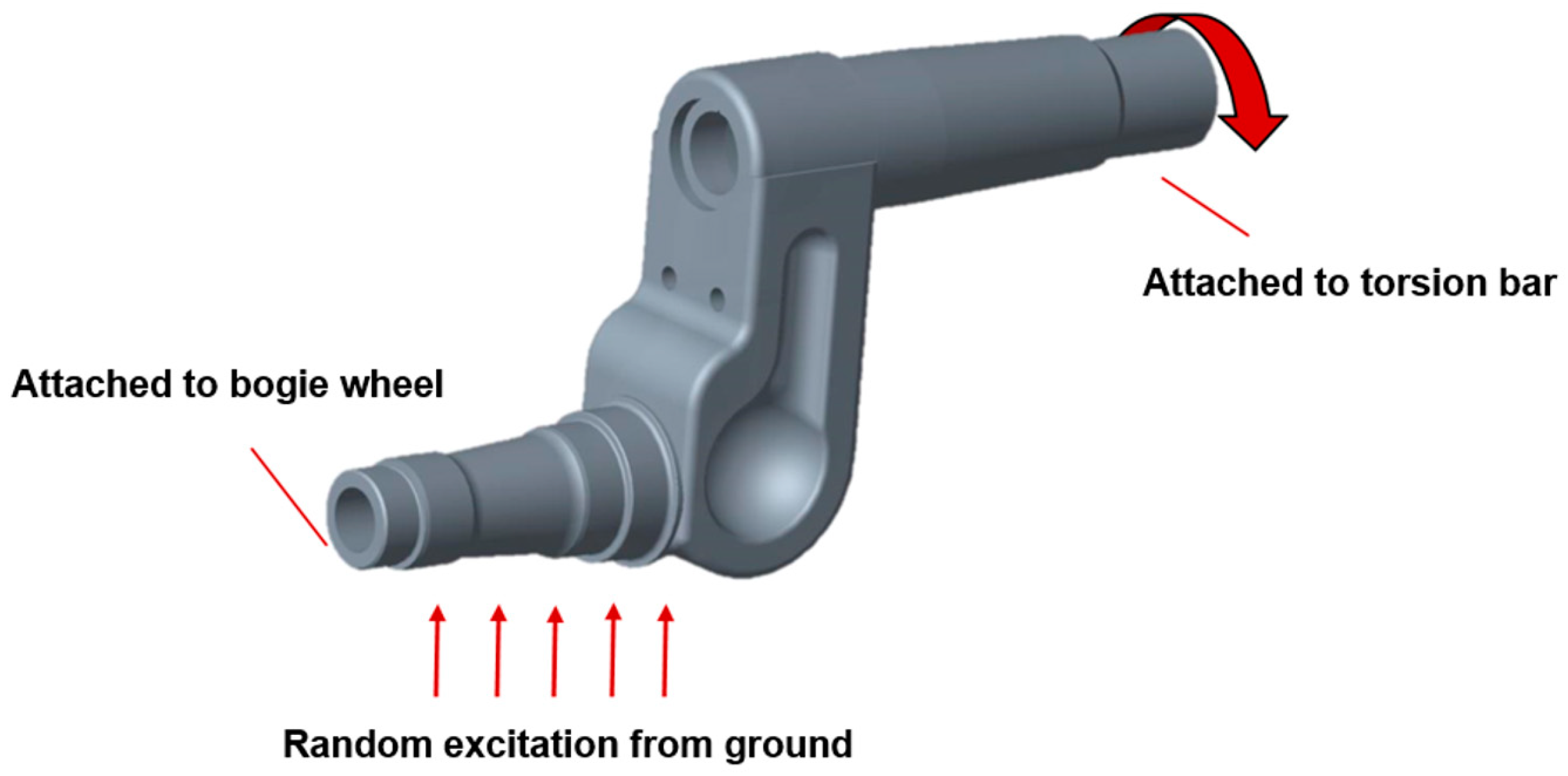
1. Introduction

Tracked suspension vehicles are vehicles equipped with continuous tracks (also known as caterpillar tracks) instead of wheels. These tracks provide better traction and weight distribution, allowing the vehicles to move efficiently over challenging terrains, such as mud, sand, snow, and rough ground. High-mobility tracked vehicles are designed to move over difficult off-road terrain, which subjects them to severe excitations. Their performance is normally limited by the operator’s ability to withstand transmitted shocks and vibrations and to retain control. The maximum allowable speed depends upon the roughness of the terrain and is primarily determined by the design characteristics of the suspension system [1].

In view of detrimental effects of ride vibration on health and safety of vehicle drivers and on vehicle mobility, the ride quality of wheeled vehicles has drawn considerable attention. However, the present trend is towards the use of hydro gas and passive suspension configurations (suspension arm) to maximize the ride limiting speeds [2,3]. These high-mobility tracked vehicles are usually fitted with passive suspension systems that include torsion bars with shock absorbers to dampen terrain-induced shocks and vibrations [4]. A suspension arm is a structural element of the tracked suspension system connecting the road wheels to the chassis of the vehicle [5,6,7].

The suspension arm, a crucial suspension part in tracked vehicles, plays a critical role in enhancing vehicle performance by absorbing shocks, supporting its weight, and maintaining proper track alignment over rough terrain. Similar to other suspension systems, the suspension arm is crucial for stabilizing the tracked vehicle and enhancing the ride comfort of the crew. The suspension arm acts as an essential link between the vehicle’s body and its undercarriage, in combination with torsion bars to absorb the forces generated by irregular and random road excitations [5]. By minimizing vibrations and shocks transmitted to the vehicle’s structure, the suspension arm helps maintain both vehicle durability and operational efficiency in undulating terrains. This component, designed to endure heavy stresses, is typically made from high-strength materials like steel or alloy, ensuring it remains sturdy and robust under the pressures of rough terrains. With its ability to undertake both torsional and bending loads, the suspension arm effectively mitigates the impact of rough terrains, contributing effectively to the overall stability and performance of tracked vehicles. The suspension arms help to equalize the weight of the vehicle on the tracks, therefore providing better grip and stability in changing surfaces and adaptability on uneven terrain. Under such uniform pressure on the track, the suspension arm works to help the vehicle overcome rough ground with greater ease and allows movement with more comfort by absorbing shock and vibration.

The reduction of vibrations using a suspension arm is essential for two practical reasons. Although one reason is to increase the occupants’ comfort level, another more important aspect is to reduce the probability of fatigue failure of structural components; which results in lower costs and reduces the possibility of a serious accident occurring. Thus, a suspension system that absorbs vibrations in the vertically accelerated direction is needed. The suspension system is a mechanical device with the primary function of minimizing vertical accelerations and displacements [8,9]. The random vibration fatigue experienced by structural components of the tracked vehicle can be detrimental and cause a significant reduction in fatigue life. Numerous studies have been carried out in the past about fatigue life estimation under the influence of random vibrations.

The life prediction can be done using two techniques, namely frequency-domain and time-domain analysis. Frequency domain fatigue approximation methods are based on stationary Gaussian processes, such as wide band and narrow band stress cycle distributions. The mathematical models are empirical and include Zhao and Baker [10], Tovo and Benasciutti [11], and Dirlik [12] in the case of wideband stress cycle distributions. In parallel, the distribution of cycles is found directly for narrow band stress cycle distributions, as presented in [13]. In frequency domain methods, power spectral density (PSD) of time history is computed. The power spectral density plot is represented as a frequency domain plot [14]. A PSD plot is a normalized density plot depicting the mean square amplitude of each sinusoidal wave with reference to its frequency. The area under the PSD curve over the desired frequency range can be used to determine mean square amplitude of a constituent sinusoidal wave. To regenerate a time-signal from the frequency domain, Inverse Fourier Transform on the complex vector of frequency domain results can be carried out. The next step is to calculate the essential spectral moments required by using the selected frequency domain fatigue estimation methods [15,16]. As per the selected method, related coefficients of the mathematical model are computed by means of the spectral moments. Next, total fatigue damage is computed by using the calculated coefficients, the S-N curve of the material, and spectral moments.

The time domain approach usually employs a counting method for damage estimation [14,17]. Some counting methods include rainflow counting, range-pair methods and range-mean stress. Along with the counting method, a damage accumulation rule like the Palmgren–Miner rule [18] is widely utilized for predicting damage due to fatigue. Rainflow cycle counting converts random time history data (usually in the form of stress) into equivalent stress cycles (usually in form of histogram) bearing mean stress and a constant range. The next step after cycle counting includes finding the damage accumulation using Miner’s rule. This rule is calculated by adding the contribution of each stress cycle to compute the total damage. Although there are many methods, rainflow cycle counting along with Miner’s rule are often used in fatigue damage prediction because of their accuracy [19]. Although time domain can provide more accurate damage estimation, implementing the time domain approach is cumbersome. Moreover, estimation of fatigue damage in the frequency domain is quicker than the time domain, and fatigue damage estimation can be computed for multiple locations where stress response PSDs are required. Another disadvantage of the time domain is the cost associated with the transient dynamic analysis as compared to frequency domain [20].

Investigation of stresses and damage in the suspension arm is completed through computer simulation using an analytical vehicle model, which is commonly employed to predict and quantify the effects of the above-mentioned excitations in the suspension arm with various road surface profiles before final design and testing. The analytical predictions should be experimentally validated to gain confidence in the use of the computer model. Historically, the suspension dynamics of track laying vehicles have been investigated with the aid of mathematical models of variable complexities. Simulations are then used to determine the overall stress and damage in the suspension arm.

This study presents an integration of Quasi-Static Finite Element Method-based simulations and experimental testing to analyze fatigue damage in tracked vehicle suspension arms. To the best of the authors’ knowledge, the combined approach, incorporating stress response PSD data to identify terrain-induced brittle failure is a unique study, making this work a valuable contribution to the field of structural durability and optimization. This work aims to address the issue of failure in the suspension arm of an industrial tracked vehicle by computing the fatigue damage due to random vibrations using real time experimental data. The work presents a comprehensive experimental analysis and numerical analysis for ascertaining fatigue damage. Main research questions addressed and contributions of this research work are presented as follows:

• Carrying out nondestructive testing (NDT) using penetrant testing (PT) and magnetic particle testing (MPT) to find defects (cracks) and failure locations in the suspension arm. An important research question that is addressed is “What is the effect of multiple road terrains (smooth and rough terrain) on the suspension arm of a tracked vehicle under the influence of probabilistic loads”?
• The research provides a comprehensive overview of how to carry out random vibration FEA by applying real time random acceleration ground input and determining its structural response in the form of stress response PSD on multiple locations (Location 1 and Location 2) of the suspension arm structure. The numerical analysis simulated 1-Sigma, 2-Sigma, and 3-Sigma stress levels, accurately predicting the highest stress concentrations at the same locations where failures were observed in the experimental analysis.
• The fatigue damage has also been computed using three distinct approaches, including Steinberg, Wirsching, and Narrowband. The findings also offer insights on how to determine frequency domain vibration characteristics of real time accelerometer data, including discussion on signal filtering, Kurtosis, probability density function, power spectral density, and its response on critical locations. The FEA and experimental results depict that the overall PSD stress response and root mean square acceleration (GRMS) for Location 1 exhibits higher values compared to the response obtained for Location 2. The GRMS comparison shows that Loc1’s GRMS value is nearly 33% higher than that of Loc2. Overall, this can lead to crack development and early failure at Location 1.

2. Governing Equations

The power spectral density of the ground-based excitation can be used to describe the random vibration input [8,9]. For an acceleration time series $x\left(t\right)$, the PSD is given by:

$$S_x(f)={\displaystyle \frac{1}{T}}|X(f){|}^2$$

(1)

For the quasi-static FEM approach, the equilibrium equations are:

$$\mathrm{K}\cdot \mathrm{u}=\mathrm{F}$$

(2)

The response of the model to the random vibrations can be characterized using the frequency response function (FRF), which relates the input PSD to the output PSD:

$$S_y\left(f\right)=\left|H\right(f\left){|}^2{S}_x\right(f)$$

(3)

The stress spectrum in the model due to random vibrations can be obtained from the response PSD:

$${ S}_{\sigma }(f)={\displaystyle \frac{1}{\alpha }}|H(f){|}^2{S}_x(f)$$

(4)

For complex scenarios, multivariate random vibrations have to be considered which involve multiple correlated vibration sources. This can be represented by a cross-spectral density matrix $S_{xy}\left(f\right)$:

$$S_{xy}(f)={\displaystyle \frac{1}{T}}⟨X_x\left(f\right)\cdot X_y^{\mathrm{*}}\left(f\right)⟩$$

(5)

where $X_x\left(f\right)$ and $X_y\left(f\right)$ are the Fourier transforms of different vibration signals, and $⟨\cdot ⟩$ denotes the expected value. When stress PSDs are required at each node on the FEA model in order to determine the fatigue life of the component, the equation of motion for the structural component can be used as follows:

$$\left[M\right].\ddot{x}\left(t\right)+\left[C\right].\dot{x}\left(t\right)+\left[K\right].x\left(t\right)=f\left(t\right)$$

(6)

where [M] is the global mass matrix, [C] is the global damping matrix, [K] is the global stiffness matrix, x(t) is the vector of nodal displacements, and f(t) is the vector of nodal forces.

To perform fatigue analysis, a single PSD is necessary at each node for showing stress invariant like Von-Mises, absolute maximum principal stress, or Tresca. These are found by computing the eigenvalues of the stress tensor matrix as presented below:

$$\left[\begin{array}{c}{\sigma }_1\left(\omega \right)\\ {\sigma }_2\left(\omega \right)\\ {\sigma }_3\left(\omega \right)\end{array}\right]=eigen values\left\{\left[\begin{array}{ccc}{S}_{xx}\left(\omega \right)& S_{xy}\left(\omega \right)& S_{xz}\left(\omega \right)\\ S_{xy}\left(\omega \right)& S_{yy}\left(\omega \right)& S_{yz}\left(\omega \right)\\ S_{xz}\left(\omega \right)& S_{yz}\left(\omega \right)& S_{zz}\left(\omega \right)\end{array}\right]\right\}$$

(7)

To improve comprehension of the frequency range, the Fast Fourier Transform (FFT) method is employed to compute the power spectral density (PSD). The PSD is an essential factor in forecasting fatigue life under vibration and is readily obtained from a time history using the FFT technique [13,21]. More precisely, the moments of the PSD function about the zero frequency axis are the fundamental building blocks employed in fatigue calculations. These are present in almost all commonly used analyses. The equation for the nth instant can be expressed as follows, where the x-axis represents the frequency (f) and the y-axis represents G:

$${\int }_0^{\infty }{f}^n.G\left(f\right)df=\sum f_k^n.G_k\left(f\right).\delta f$$

(8)

Several cumulative damage models are utilized for predicting fatigue life, including the modified Steinberg vibration lifetime model [22], which assumes that the effects of vibration are accurate predictions. Dirlik’s method [23] is another approach that employs the stress amplitudes and coefficients functions of the PSD of the stress in the analysis, and it is based on the empirical closed-form expression of the probability density function (PDF) of the rainflow amplitude:

$$P_{RR}\left(s\right)={\displaystyle \frac{\frac{D_1}{Q}{e}^{\frac{-Z}{Q}}+\frac{D_{2}Z}{R^2} {e }^{\frac{{-Z}^2}{2R^2}}+D_{3}Z{e}^{\frac{{-Z}^2}{2}}}{{2\left(m_0\right)}^{1/2}}}$$

(9)

The normalized variable Z can be expressed as a function of m₀, m₁, m₂, and m₄, where D₁, D₂, D₃, Q, and R are all functions of these same variables.

$${\displaystyle \frac{S}{2{\left(m_0\right)}^{1/2}}}$$

(10)

Other fatigue damage models have been created and examined [24], but when it comes to figuring out how much damage has accumulated, the majority of them employ the linear damage formula. This relation is famously known as Miner’s linear damage accumulation rule and is depicted as below:

$$D=\sum {\displaystyle \frac{n_i}{N_1}}=1$$

(11)

The variable D represents the fatigue damage, n_i indicates the number of cycles of applied load at a specific stress level σ_i, and N₁ represents the number of cycles to failure at stress level σ.

Incorporating damage models into vibration-based analysis is an effective way to capture the actual loading conditions and predict damage accurately. Monitoring the vibration of structural systems is crucial to ensure optimal performance, product quality, safety, and durability. It enables health monitoring of structures and timely preventive maintenance to prevent any breakdowns. Therefore, routine monitoring of vibration profiles is necessary to prevent potential failures. Vibration measurements provide a gauge of how successfully the instrument or system has been manufactured and can give a head start on potential operating issues.

This research article focuses on the use of real time data obtained by mounting accelerometers beneath a tracked vehicle structure. The acquired data is then processed to reduce noise via band pass filters, after which, fast Fourier transform is applied to analyze a vibration signal. The vibrating source’s frequency spectrum discloses the vibration level. In this way, the dynamic analysis output will consist of PSD matrices of the stress tensor components [25,26,27], which are then used for the damage assessment in the frequency domain [28,29,30,31].

3. Materials and Methods

3.1. Description of the Physical Model

The 3d model of the suspension arm (also known as balance arm) is developed and used in this study to assess fatigue damage and structural integrity. The suspension arm of the tracked vehicle is analyzed under various dynamic loading conditions, with a focus on the effects of probabilistic random vibrations. The mounting locations of the suspension arm are shown in Figure 1.

This model includes key components, such as a torsion bar on one side and a bogie wheel on the other. It considers dynamic loads caused by random forces and terrain variations, ranging from smooth to rough surfaces. Power spectral density (PSD) data, specifically PSD-G acceleration, represents the ground-induced excitation forces acting on the suspension arm. The suspension arm properties were characterized through chemical and mechanical analysis, identifying 36CrNiMo4 as the best material match. The suspension arm used is the same as the one used in Ref [7]; therefore, the material properties can directly be adopted from the same Ref. [7]. These properties are presented in

Table 1. Engineering data of suspension arm material [7].

Modulus of Elasticity	Ultimate Tensile Strength	Yield Strength	Poisson’s Ratio	Hardness
210 GPa	939 MPa	715 MPa	0.29	270 HB

.

This study integrates vibration analysis and non-destructive testing (NDT) to assess structural damage in the suspension arm. The experimental setup comprised an enDAQ accelerometer for vibration measurement, along with penetrant testing (PT) and magnetic particle testing (MPT) to detect defects. A high-performance laptop was used for data acquisition and analysis. The experimental equipment utilized for real time dynamic testing and analysis is presented in

Table 2. Experimental Equipment.

Name	Range	Quantity	Sampling Rate	Bandwidth	Resolution
enDAQ Accelerometer Along with mounting	±16 g	2	3200 Hz	0 to 300 Hz	0.004 g
NDT using MPT (Magnaflux) and PT along with surface preparation chemicals/spray	2.0–11.0 in (leg span)	1	25%, max on time is 90 s (duty cycle)	4.8 lb/2.2 kg (battery pack)	8 lb/3.6 kg (Yoke only) 5.2 lb/2.4 kg (Battery)
Laptop for data acquisition and analysis	AMD Ryzen 5 4500U with Radeon Graphics 2.38 GHz and 8GB RAM

.

3.2. Experimental Analysis

The quasi-static FEM approach is employed to simulate the operational conditions that the suspension arm experiences. The data was collected over time for simulation input, and was treated as a multivariate time series to allow for analyzing the interdependencies and temporal patterns between the different load variables. This method allows for the accurate representation data of stress and damage responses under the defined loading conditions. The model calculates the stress response of the suspension arm under different terrain conditions, using PSD data to assess how vibrations impact stress distribution.

Figure 2 depicts a tracked vehicle traveling over a smooth terrain and rough terrain (smooth terrain only shown for illustration), where road excitations induce cyclic loading on the suspension components lead to fatigue damage over time. The main tracked vehicle body (A) rests on a series of road wheels and track links (B), which transmit vibrations to the suspension arm (C), a critical pivoting element of the suspension that endures repeated stresses. Close-up views reveal that non-destructive testing (E) identifies cracks in suspension arm components, while scanning electron microscopy (D) confirms the presence of fatigue striations characteristic of progressive crack growth. Collectively, the figure highlights how the tracked vehicle has cracks initiated in the critical parts after undergoing routine operation under cyclical loads.

Early detection of cracks through NDT is crucial for preventing catastrophic failures in tracked vehicle suspension systems. The proposed model assesses fatigue damage by analyzing damage accumulation patterns over time, enabling proactive maintenance strategies. To conduct vibration tests under various operational conditions, tri-axial accelerometer was mounted at strategic location on the tracked vehicle’s suspension system as presented in Figure 3. The problem was formulated based on cracks and damaged suspension arms found from the analogous tracked vehicles. It is pertinent to mention that the suspension arm used for fatigue damage assessment was structurally intact, in good health and designated as safe for operation. This approach allowed for the correlation between controlled experimental results and actual field-induced vibration loading. The accelerometer was placed at the position considered most susceptible to high accelerations and vibrations. The sampling frequency was set to 200 Hz, in accordance with the Nyquist criterion, ensuring accurate data collection without aliasing. The vehicle was tested on both smooth and rough terrain, with smooth terrain conditions closely resembling vibrations typical of Road Class A, with geometric mean road roughness of 1 × 10⁻⁶ m³ as defined by ISO 8608, and rough terrain simulating conditions closer to Road Class E, with geometric mean road roughness of 256 × 10⁻⁶ m³ [32]. In order to capture a real life scenario, the trained operator of tracked vehicle was directed to operate the vehicle in his natural operating style. The tracked vehicle operated from a stationary position, achieving a maximum speed of 46 km/h on smooth terrain, with an average speed of 30 km/hr. On rough terrain, the maximum speed reached was 39 km/h, while the average speed remained 21 km/h. Due to the increased resistance and instability of rough terrain, the vehicle’s operational speed was naturally lower compared to smooth terrain. The frequency bandwidth of 0 to 100 Hz was selected to capture the critical vibration response of the suspension system, ensuring the measurement of the most relevant dynamic behavior. The primary excitation was induced by operating the vehicle over both smooth and rough terrain. This testing approach enabled a detailed analysis of the suspension system’s response to terrain-induced vibrations, offering valuable insights into its performance and durability.

3.3. Finding Defects in Suspension Arm Using NDT Techniques

Two non-destructive testing (NDT) techniques were employed to evaluate the structural integrity of the suspension arm: penetrant testing (PT) and magnetic particle testing (MPT) using the Magnaflux system. Both methods revealed significant cracks, highlighting critical areas of concern for fatigue failure (shown in Figure 4).

A portable electromagnetic yoke, compliant with ASTM E1444/E1444M, with an adjustable leg span of 2.0 to 11.0 inches, was used for MPT. The yoke was tested for proper lifting force, ensuring reliable defect detection. To prevent overheating, the device operated at a maximum duty cycle of 25%, with an on-time limit of 90 s, following manufacturer recommendations. Inspections were conducted under the required lighting conditions to identify discontinuities, potential cracks, or defects in the suspension arm [33]. Further details on penetrant testing are provided in Figure S1 and the corresponding text in the Supplementary Material. Further details on non-destructive testing (NDT) can be found in references [34,35,36,37,38].

Based on these findings, vibration testing was conducted to further assess fatigue damage accumulation. Two critical points were selected to analyze the vibration response of the model. At both locations, random vibration data were collected on smooth and rough terrain using accelerometers, providing insights into the structural behavior under operational conditions. These two locations are presented and marked in Figure 5, respectively. The analysis accounts for high-stress scenarios and predicts the likelihood of brittle failure at critical locations. The random vibration simulation considers two operational scenarios to evaluate the impact of different terrains on the suspension arm’s performance. Specifically, it compares stress distribution and fatigue damage accumulation between smooth and rough terrain conditions. The simulation results were further utilized to evaluate the ground-based excitation (PSD-G) and its impact on the suspension arm. PSD helps in understanding how different frequency components contribute to the overall vibration response. This method simulates the operational conditions and stress responses experienced by the suspension arm. The general procedure followed during this analysis is summarized and presented in Figure 6.

FEM is essential for capturing detailed stress distributions and damage patterns. Comprehensive numerical simulations are employed to evaluate the fatigue damage accumulation in the suspension arm. These simulations account for dynamic loads and terrain interactions (both smooth and rough). The research focuses on how different operational scenarios affect the fatigue damage and structural performance of the suspension arm. The computational simulations clearly reveal that traversing rough terrain precipitates elevated stress amplitudes and diminished fatigue life in tracked vehicle components, attributable to the exacerbation of fatigue damage incurred due to the intense vibrations and dynamic loading associated with navigating uneven landscapes, thereby necessitating the incorporation of robust design and optimization strategies to enhance component reliability and durability, mitigating the damaging effects of terrain-induced vibrations on structural integrity and lifespan, and ultimately contributing to improved vehicle performance, reduced maintenance costs, and extended service lifetimes by elevating the cumulative damage inflicted by repeated loading cycles, stress concentrations, and material degradation, thus informing the development of more resilient and sustainable tracked vehicle systems.

4. Results & Discussion

This section presents results and a comprehensive discussion of the vibration response obtained on smooth and rough terrain. The vibration data is applied to the suspension arm model in the form of power spectral density. The response is obtained for two locations.

The stress response is utilized for analyzing both locations to understand the location which is more critical. The results also discuss which frequencies are expected to cause more damage both on the smooth and rough terrain. By understanding the fatigue life of critical components, maintenance schedules can be efficiently optimized. Knowing the expected life in cycles helps predict mean time between failure (MTBF), allowing proactive replacement or reinforcement. This lessens unexpected breakdowns in the field, where repairs can be challenging and costly. Although fatigue life and damage can be predicted in time domain utilizing rainflow cycle counting and the Miner’s rule, this study focuses on predicting fatigue damage in the frequency domain and utilizing PSD ground inputs obtained from actual accelerometer data. The primary step is obtaining g-time accelerometer data, refining them, and applying the pwelch technique to convert them into PSD data. The data is initially recorded as an acceleration-time history using enDAQ accelerometer and presented in Figure 7. The vibration data on the y-axis exhibits a maximum peak acceleration of 34.5664 g at a timescale of 7.90 s, demonstrating a transient event categorized by a substantial dynamic load transmission via the suspension system. Although the complete time domain data is random in nature, the occurrence of such an increased peak suggests an interaction event such as localized terrain irregularity or a sudden force impulse transmitted from the track-ground interface. To further characterize the dynamic behavior of the system, statistical parameters such as GRMS and standard deviation should be computed to quantify the overall vibrational energy content. This has been completed in the latter part of the study. The power spectral density (PSD) in Panel B of Figure 7 measures the distribution of vibrational energy over frequency components, with the dominant peak detected at 31.5430 Hz, reaching a maximum power of 3.4312 g²/Hz. This frequency relates to the primary excitation mode of the tracked vehicle’s suspension system under smooth terrain conditions. The occurrence of a distinct peak in the power spectral density indicates the dominance of a specific modal or structural response, likely associated with the interaction frequency between the track links in contact with the ground or the natural frequency of the suspension system. The relatively high power at this frequency indicates a resonant excitation, requiring further damping analysis to ensure structural integrity under cyclic loading conditions. Given that acceleration fluctuations in dynamic systems often follow a Gaussian distribution under steady-state conditions, the deviation from normality, quantified by kurtosis and skewness, can reveal the presence of extreme events. This deviation may suggest non-Gaussian stochastic excitation, influenced by terrain-induced shocks and structural resonances. The probability density function (PDF) of acceleration amplitudes provides insights into the stochastic nature of the vehicle’s response to vibration.

The probability density plot in Figure 8 shows a peak value of 0.0396 occurring at an acceleration amplitude of 0.5394 g, approximately at the center. This indicates that the majority of vibrational occurrences are concentrated around this amplitude. A unimodal distribution of the probability density function with a sharp peak suggests a consistent and stable vibratory response, whereas a broader distribution would imply more significant variations in the vibrational amplitude. The kurtosis function, which measures the peakedness of the data distribution, exhibits a maximum peak of 4.379916 at 7.460 s, indicating the presence of intermittent high-intensity shocks or transient events. Time varying kurtosis shown in Figure 8 is indicative of random transient vibrations; however, a kurtosis value exceeding 3 (Gaussian distribution threshold) suggests a leptokurtic behavior, indicative of occasional extreme accelerations rather than a purely random vibrational response. The high kurtosis peak in proximity to the maximum acceleration peak (7.90 s) reinforces the theory that a localized impulse excitation has significantly influenced the system dynamics.

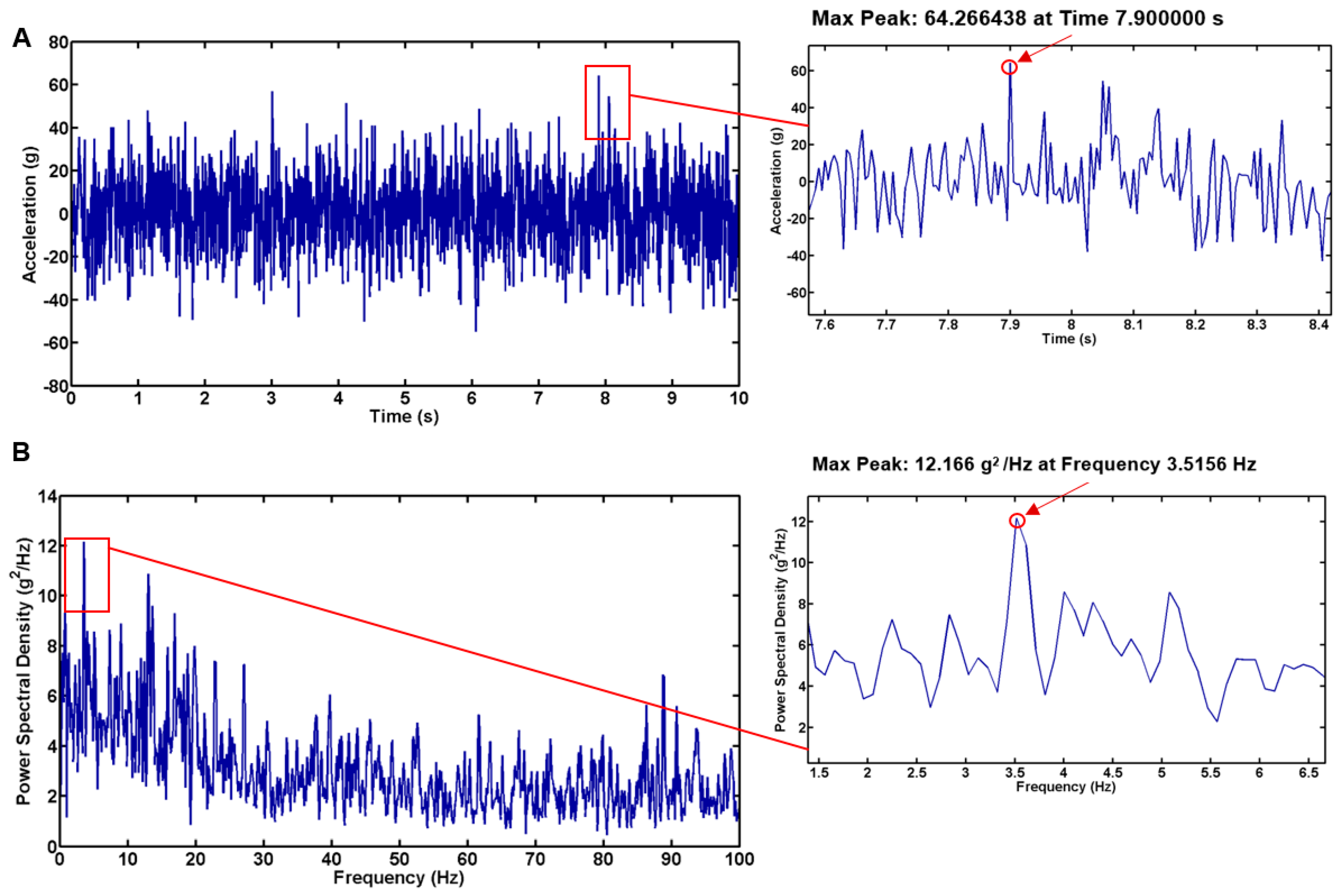
This could be ascribed to sudden terrain-induced excitation, track-segment interactions, or suspension nonlinearity under definite loading conditions. The next response was recorded on the rough terrain track. The rough terrain data presented in Figure 9 is a multi-layered dynamic response of the system. As per the trend, the analysis in the frequency domain, the Power Spectral Density (PSD) exhibits a peak of 12.166 g²/Hz at 3.5156 Hz. This dominant low-frequency excitation indicated that the system is greatly influenced by its natural suspension resonance and inherent structural dynamics.

The probability density function (PDF) shows a maximum peak of 0.0229 at an amplitude of 0.5228 g in Figure 10. This indicates that under normal conditions, most acceleration values are concentrated around 0.5228 g, suggesting a relatively stable and moderate vibrational energy distribution. However, as per the other statistical information, the kurtosis value of 5.2499 (well exceeding the Gaussian benchmark of 3) indicates a heavy-tailed distribution. This heavy-tail behavior depicts a higher likelihood of meeting extreme acceleration events than would be expected if the data were purely Gaussian. The recorded peak acceleration of 64.2664 g at 7.90 s (Figure 9A) stands out as a significant outlier from the overall trend. This extreme transient event is likely the result of a sudden, high-impact interaction, perhaps due to a sharp terrain irregularity or an abrupt force impulse from the track-ground interface. The simultaneous occurrence of elevated kurtosis around 7.455 s further corroborates that this transient event is not an isolated anomaly but part of a pattern where occasional extreme excitations punctuate the generally moderate vibrational behavior. Figure 11A presents the plot of the stress response PSD obtained for the suspension arm for smooth terrain for Location 1. The x-axis represents the vibration frequency (Hz), whereas the y-axis represents the stress response PSD is obtained after application of input PSD to the suspension arm. It is pertinent to mention here that the maximum stress response PSD is $1.57\times {10}^6 {\mathrm{P}\mathrm{a}}^2/\mathrm{H}\mathrm{z}$ at a frequency of $32.031 \mathrm{H}\mathrm{z}$. This indicates that under smooth terrain conditions, the system predominantly experiences vibrations or accelerations at this frequency.

Figure 11B presents the plot of the stress response PSD obtained for the suspension arm for rough terrain at Location 2. It can be observed that low frequencies are causing more excitations and developing higher stresses. The maximum stress response PSD is $5.54\times {10}^6 {\mathrm{P}\mathrm{a}}^2/\mathrm{H}\mathrm{z}$ at a frequency of $3.5156 \mathrm{H}\mathrm{z}$. The plot of the stress response PSD is also obtained for the suspension arm for the smooth terrain at Location 2. It is observed that the peak stress response PSD is $2.17\times {10}^4 {\mathrm{P}\mathrm{a}}^2/\mathrm{H}\mathrm{z}$ at a frequency of $31.543 \mathrm{H}\mathrm{z}$ is obtained on Location 2. Similarly, the plot exhibits the maximum stress response PSD at $7.68\times {10}^4 {\mathrm{P}\mathrm{a}}^2/\mathrm{H}\mathrm{z}$ at a frequency of $3.5156 \mathrm{H}\mathrm{z}$ for rough terrain. Considering that the stress response follows a Gaussian distribution, 1σ, 2σ, and 3σ stress levels along the X, Y, and Z axes are numerically simulated and presented in

Table 3. Experimental and actual failure point prediction.

Direction	1 Sigma (68.269%)	2 Sigma (95.45%)	3 Sigma (99.73%)	Numerical Failure Point Prediction	Actual Failure Observed Experimentally
X	191.76 MPa	383.52 MPa	575.28 MPa	Upper Part of the suspension arm	Slight surface cracks using Liquid penetrant testing observed
Y	417.57 MPa	835.14 MPa	1252.7 MPa	Lower part of the suspension arm (Location 1)	Fatigue failure observed (Location 1)
Z	133.74 MPa	267.49 MPa	401.23 MPa	Lower part at the back of the suspension arm	No cracks seen at this location

.

It is pertinent to mention here that, for the X and Z axes, the 3σ stresses of 575.28 MPa and 401.23 MPa, respectively, persist below the yield strength of the suspension arm (yield strength of 715 MPa), indicating that these directions principally operate within the elastic range under the influence of random vibration loads. However, the Y-axis exhibits a 3σ stress of 1252.7 MPa, significantly exceeding the yield strength.

Although about 68.3% of the stress cycles (represented by the 1 sigma level of 417.57 MPa) are within safe limits, the extreme stress events at the 3σ level, which occur occasionally (about 0.27% of the time), are likely to cause localized plastic deformation and accelerate fatigue damage accumulation. This has been observed experimentally as well in which suspension arms have been found broken along the Y-axis. Thus numerical results are validated by these experimental findings.

It is further important to note that that the experimental results and numerical results highlight the same area of high stresses and in turn the crack initiation points. The next step was carried out to assess and analyze damage in the suspension arm using fatigue analysis module. Figure 12 presents the 1 Sigma, 2 Sigma, and 3 Sigma plots along the X-, Y-, and Z-axes. It can be observed that the maximum damage is expected at the edge of the arm, which can be attributed to high stress concentration. The maximum damage is anticipated at the edge of the arm, but it is expected to spread to further areas as well.

Figure 13 presents a bar chart illustrating the mean response power spectral density (PSD) on a logarithmic scale along the Y-axis. The X-axis depicts both the input PSD and the corresponding stress response PSD at Location 1 and Location 2 for smooth and rough terrains. Location 1 is seen to exhibit higher mean values of stress response PSD as compared to Location 2. The rough terrain showcases response PSD of $6.14 \mathrm{P}{\mathrm{a}}^2/\mathrm{H}\mathrm{z}$ as compared to $5.66 {\mathrm{P}\mathrm{a}}^2/\mathrm{H}\mathrm{z}$ for smooth terrain at Location 1.

The next plot, in Figure 14, provides a comparison of GRMS values. GRMS is a statistical measure that represents the overall vibration level of a system or structure. It takes into account the frequency and amplitude content of the vibration signal, providing a unique value that characterizes the severity of vibration severity. GRMS is widely used in various setups, including manufacturing, aerospace & automotive industries. The following GRMS plot (Figure 14) compares the vibration severity of two locations (Loc1 and Loc2) under smooth and rough conditions. The GRMS shows that, at Location 1 (Loc1), the smooth terrain condition has a GRMS value of 9.88, which increases to 17.2 under rough conditions, representing a 73.5% rise in vibration severity. In contrast, at Location 2, the smooth terrain condition has a GRMS value of 9.3, increasing to 12.9 under rough conditions, indicating a 38.7% rise. Notably, both locations exhibit higher GRMS values under rough conditions, but the impact is more pronounced at Loc1. Despite this, both locations show similar GRMS values under smooth conditions, suggesting consistent vibration levels in these scenarios. Another important aspect is to predict fatigue damage based on the random vibration data. The same has been done using three distinct approaches namely Steinberg, Wirsching, and Narrow Band.

The fatigue damage has been predicted using three established methodologies—Steinberg, Wirsching, and Narrowband—based on acceleration data obtained through accelerometers and is presented in Figure 15. The results provide intuitions into how terrain roughness influences fatigue damage estimation. The detailed comparison is presented in Figure 15. Across all methods, rough terrain exhibits higher maximum fatigue damage than smooth terrain for all the three techniques. The subsequent plot shown in Figure 16 depicts percentage increase in fatigue damage based on the three approaches.

The Wirsching method shows the highest percentage increase (10.6%), suggesting that it is the most sensitive to rough terrain effects. The Narrowband method shows the least increase (3.5%), indicating a more stable prediction across terrain types. The Steinberg method provides an intermediate increase of 7.2%, balancing between Wirsching and Narrowband.

Steinberg is the most conservative for predicting maximum fatigue damage, but it underestimates minimum damage in rough terrain, making it less reliable in low-stress areas. Wirsching provides the largest increase in maximum fatigue damage (~10.6%), making it a more sensitive and potentially more conservative approach overall. Narrowband offers the most stable predictions, with minimal changes across terrain types, making it a balanced approach but slightly less conservative.

5. Conclusions

The analysis focusses on ascertaining the statistical vibration metrics, fatigue damage, GRMS, and stress response power spectral density (PSD) ground-based excitation using the actual vibration data obtained using accelerometer mounted on suspension arm. Random vibration FEA was used to simulate the operational conditions experienced by the suspension arm. Through comprehensive numerical simulations, the damage accumulation patterns and stress response PSDs were examined at two locations on the suspension arm. Location 1 was observed to be more critical under the influence of rough terrain conditions.

Experimental analysis was carried out using nondestructive testing techniques, specifically penetrant testing and magnetic particle testing. The NDT revealed significant cracks in the suspension arm at Location 1. The simulation results were validated with experimental results as crack initiation areas observed during experimental testing also revealed high stresses during numerical simulation. Current research conclusions made are as following:

• Rough terrain exhibits significantly severe dynamic loads where peak acceleration increases from 34.57 g at 7.90 s on smooth terrain to 64.27 g at 7.90 s on rough terrain—an approximate 86% increase. Moreover, the PSD peak shifts from 3.43 g²/Hz at 31.54 Hz (smooth) to 12.17 g²/Hz at 3.52 Hz (rough), demonstrating an extensive amplification of low-frequency excitation under rough conditions.
• The PDF analysis further shows that while smooth terrain clusters around 0.5394 g with a peak value of 0.0396, rough terrain shows a broader distribution with a lower maximum of 0.0229 at 0.5228 g, signifying more dispersed acceleration values and a higher probability of extreme events. Peak kurtosis rises from 4.38 on smooth terrain to 5.25 on rough terrain, underscoring a heavier-tailed distribution that confirms the increased occurrence of transient high-magnitude shocks in rough terrain.
• The X and Z axes exhibit 3σ stresses of 575.28 MPa and 401.23 MPa—both safely below the 715 MPa yield strength—indicating elastic behavior. In comparison, the Y-axis illustrates a 3σ stress of 1252.7 MPa, suggesting that although 68.3% of stress cycles are within safe limits, extreme events can induce plastic deformation and accelerate fatigue damage. This has been observed experimentally as well, in which the suspension arms have seen to fail along y-axis at Location 1 after the tracked vehicle has traversed under random road conditions.
• The mean vibration response in case of rough terrain for Location 1 is about 7.82 percent higher than for smooth terrain.
• The FEA results highlight that the overall PSD stress response for Location 1 exhibits higher values as compared to response obtained for Location 2. This can lead to crack development and early failure.
• The peak stress response PSD valued at $5.54\times {10}^6 {\mathrm{P}\mathrm{a}}^2/\mathrm{H}\mathrm{z}$ is obtained at Location 1 for rough terrain at a frequency of $3.5156 \mathrm{H}\mathrm{z}$.
• The elevated stress response PSD value suggests more powerful vibrations under rough terrain conditions, and the shift in frequency reflects a variate dynamic response of the system due to terrain irregularities.
• The GRMS comparison reveals that Loc1 experiences a more significant increase in vibration severity under rough conditions, with a GRMS value nearly 33% higher than Loc2.
• Wirsching method appears to be the most consistent method across both terrain types, ensuring a worst-case scenario approach for fatigue predictions.

Moreover, to mitigate or delay fatigue damage in suspension components, a combination of advanced material processing and design optimization strategies can be adopted. Surface hardening techniques, such as induction hardening and shot peening, play a crucial role in enhancing fatigue resistance by refining surface integrity and optimizing residual stress distribution. In addition, protective coatings, including thermal spray and nitriding treatments, can reduce surface degradation and enhance wear resistance. Optimizing material selection, applying stress-relief treatments, and implementing predictive maintenance strategies can further enhance the durability and reliability of these components under cyclic loading conditions.