Development of a Bicycle-like Magnetic-Wheeled Climbing Robot with Adaptive Plane-Transition Capabilities
Abstract
1. Introduction
- An innovative front wheel module was designed, whose unique tentacle mechanism passively rotates the ring magnet when passing through the concave corners, thereby achieving the switch of magnetic adhesion from one surface to another without any active control.
- A rear wheel module with an eccentric shaft-hole design was presented to facilitate smooth transition of magnetic adhesion between surfaces without active control.
- A bicycle-like climbing robot employing the front and the rear magnetic wheel designs was developed. The simulation analysis of magnetic adhesion force on both surfaces revealed the operational principle of the design during the transition process. Experiments demonstrated the robot’s excellent comprehensive capabilities in terms of plane-transition, ease of control, and load capacity.
2. System Development
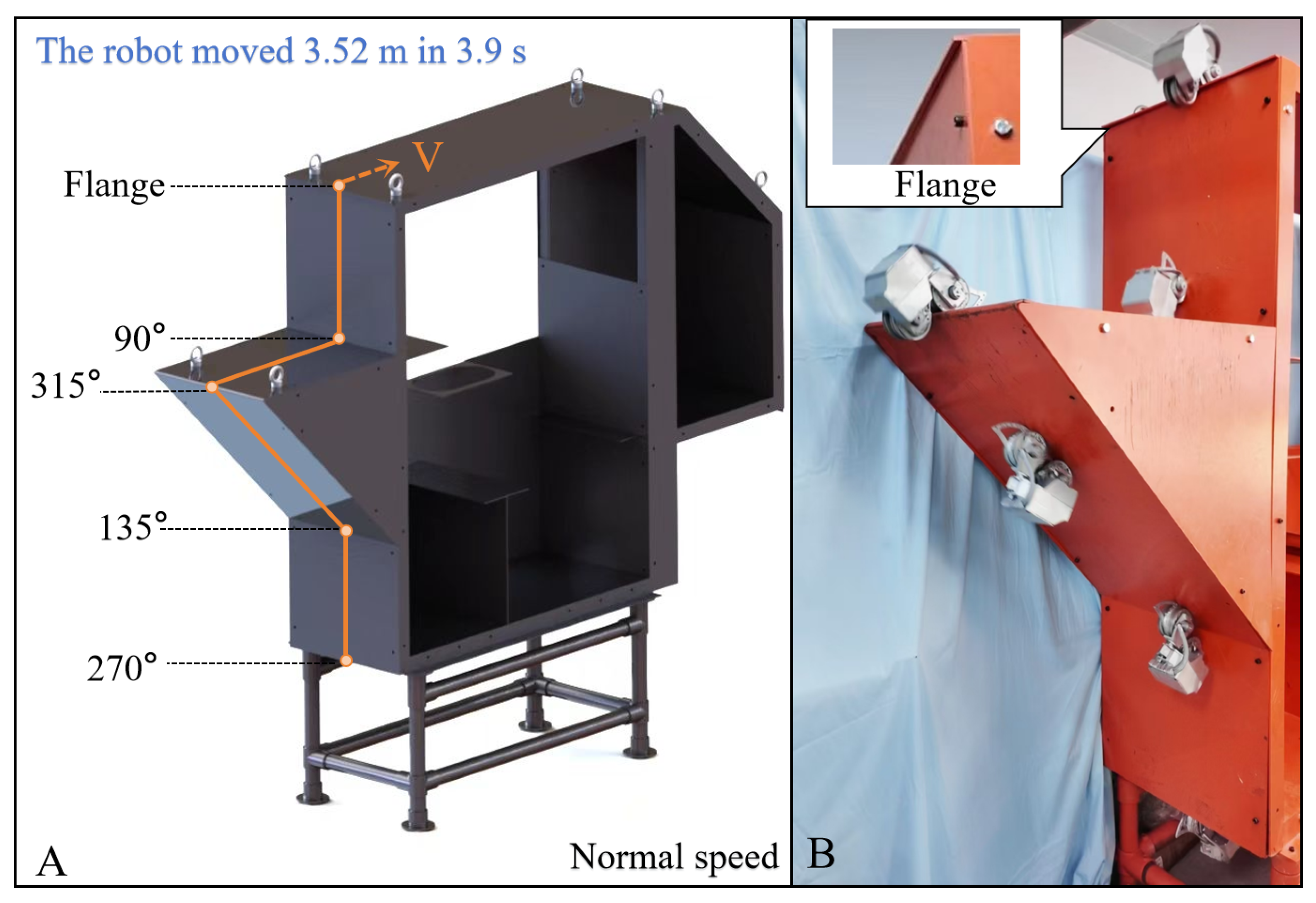
2.1. Robot System
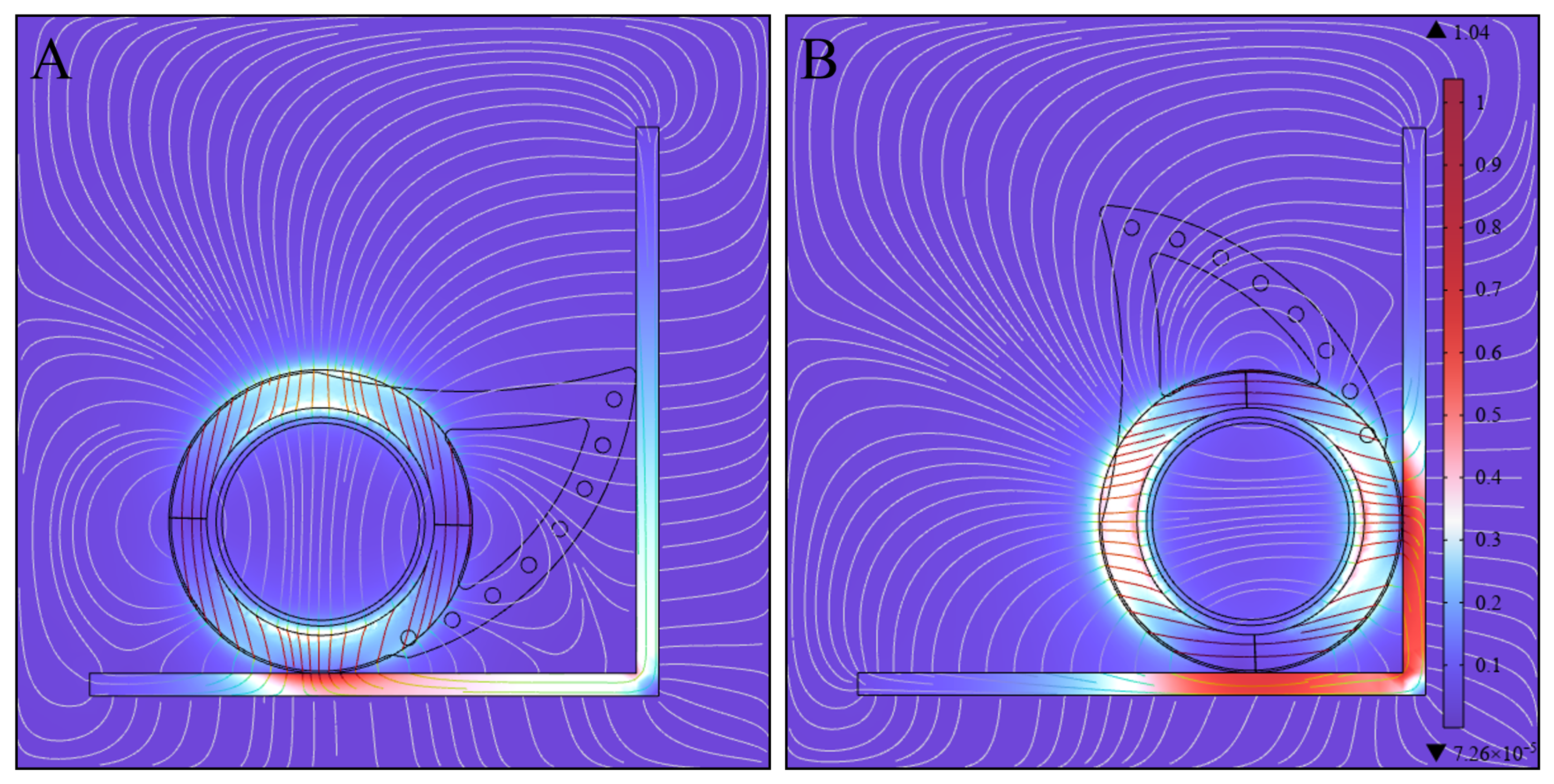
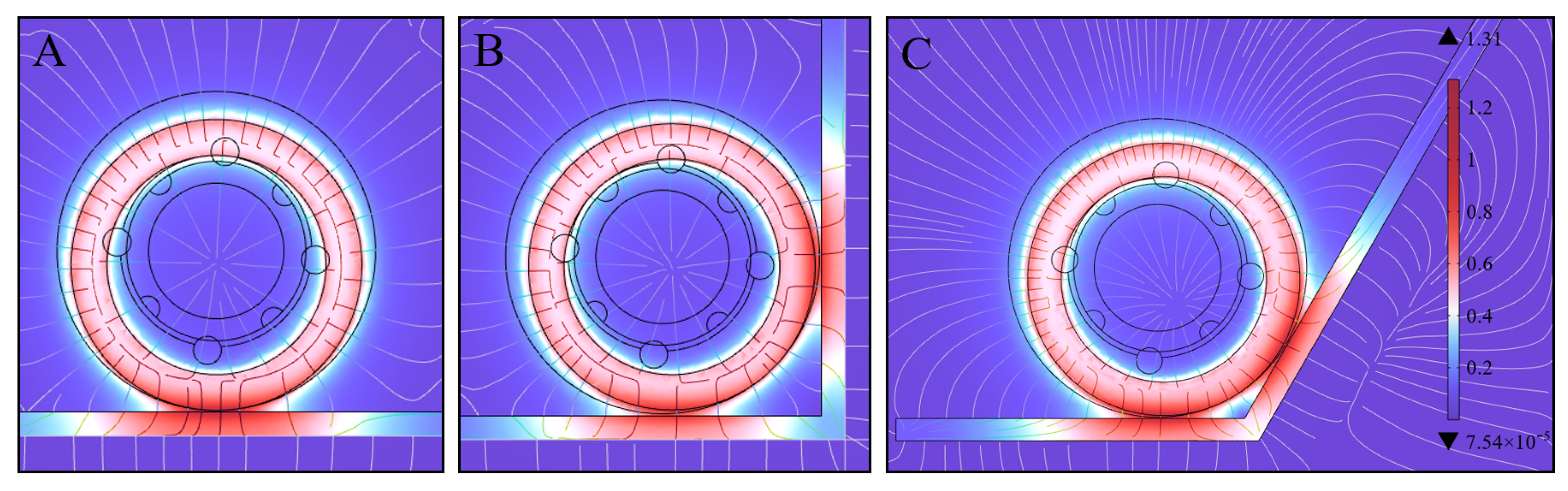
2.2. Magnetic Adhesion-Adaptive Front Wheel
2.3. Magnetic Adhesion-Adaptive Rear Wheel
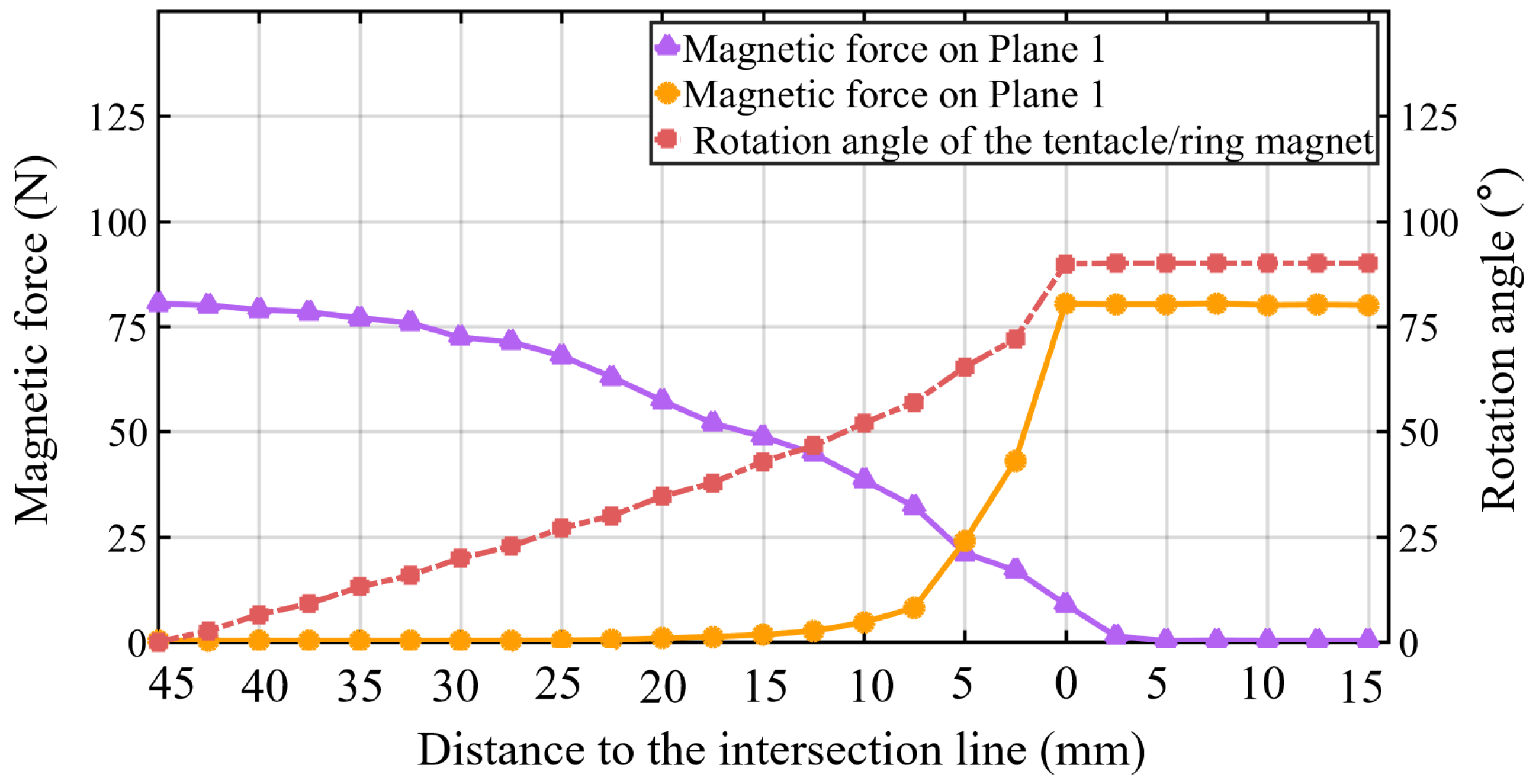
3. Simulations
4. Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Eich, M.; Bonnin-Pascual, F.; Garcia-Fidalgo, E.; Ortiz, A.; Bruzzone, G.; Koveos, Y.; Kirchner, F. A robot application for marine vessel inspection. J. Field Robot. 2014, 31, 319–341. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, M.; Jiao, S.; Zhang, X.; Li, M. Optimization Design and Parameter Analysis of a Wheel with Array Magnets. Symmetry 2023, 15, 962. [Google Scholar] [CrossRef]
- Wang, R.; Kawamura, Y. An automated sensing system for steel bridge inspection using GMR sensor array and magnetic wheels of climbing robot. J. Sens. 2016, 2016, 8121678. [Google Scholar] [CrossRef]
- Tavakoli, M.; Viegas, C.; Marques, L.; Pires, J.N.; de Almeida, A.T. Magnetic omnidirectional wheels for climbing robots. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 266–271. [Google Scholar]
- Song, Y.K.; Lee, C.M.; Koo, I.M.; Tran, D.T.; Moon, H.; Choi, H.R. Development of wall climbing robotic system for inspection purpose. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1990–1995. [Google Scholar]
- Han, S.C.; Kim, J.; Yi, H.C. A novel design of permanent magnet wheel with induction pin for mobile robot. Int. J. Precis. Eng. Manuf. 2009, 10, 143–146. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, J.; Yin, G.; Zhao, J.; Han, Q. A cross structured light sensor and stripe segmentation method for visual tracking of a wall climbing robot. Sensors 2015, 15, 13725–13751. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, S.T.; Nguyen, H.; Bui, S.T.; Ho, V.A.; La, H.M. Multi-directional bicycle robot for steel structure inspection. arXiv 2021, arXiv:2103.11522. [Google Scholar]
- Sirken, A.; Knizhnik, G.; McWilliams, J.; Bergbreiter, S. Bridge risk investigation diagnostic grouped exploratory (BRIDGE) bot. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 6526–6532. [Google Scholar]
- Tâche, F.; Fischer, W.; Caprari, G.; Siegwart, R.; Moser, R.; Mondada, F. Magnebike: A magnetic wheeled robot with high mobility for inspecting complex-shaped structures. J. Field Robot. 2009, 26, 453–476. [Google Scholar] [CrossRef]
- Eto, H.; Asada, H.H. Development of a wheeled wall-climbing robot with a shape-adaptive magnetic adhesion mechanism. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 9329–9335. [Google Scholar]
- Romao, J.C.; Tavakoli, M.; Viegas, C.; Neto, P.; de Almeida, A.T. InchwormClimber: A light-weight biped climbing robot with a switchable magnet adhesion unit. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 3320–3325. [Google Scholar]
- Hong, S.; Um, Y.; Park, J.; Park, H.W. Agile and versatile climbing on ferromagnetic surfaces with a quadrupedal robot. Sci. Robot. 2022, 7, eadd1017. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.; Hirai, M.; Hirose, S. Gunryu III: Reconfigurable magnetic wall-climbing robot for decommissioning of nuclear reactor. Adv. Robot. 2013, 27, 1099–1111. [Google Scholar] [CrossRef]
- Lin, T.H.; Putranto, A.; Chen, P.H.; Teng, Y.Z.; Chen, L. High-mobility inchworm climbing robot for steel bridge inspection. Autom. Constr. 2023, 152, 104905. [Google Scholar] [CrossRef]
- Tavakoli, M.; Lourenco, J.; Viegas, C.; Neto, P.; de Almeida, A.T. The hybrid OmniClimber robot: Wheel based climbing, arm based plane transition, and switchable magnet adhesion. Mechatronics 2016, 36, 136–146. [Google Scholar] [CrossRef]
- Ueno, S.; Nakajima, M.; Tanaka, M. Development of an articulated mobile robot moving on magnetic curved walls and passing over obstacles. Adv. Robot. 2022, 36, 1156–1171. [Google Scholar] [CrossRef]
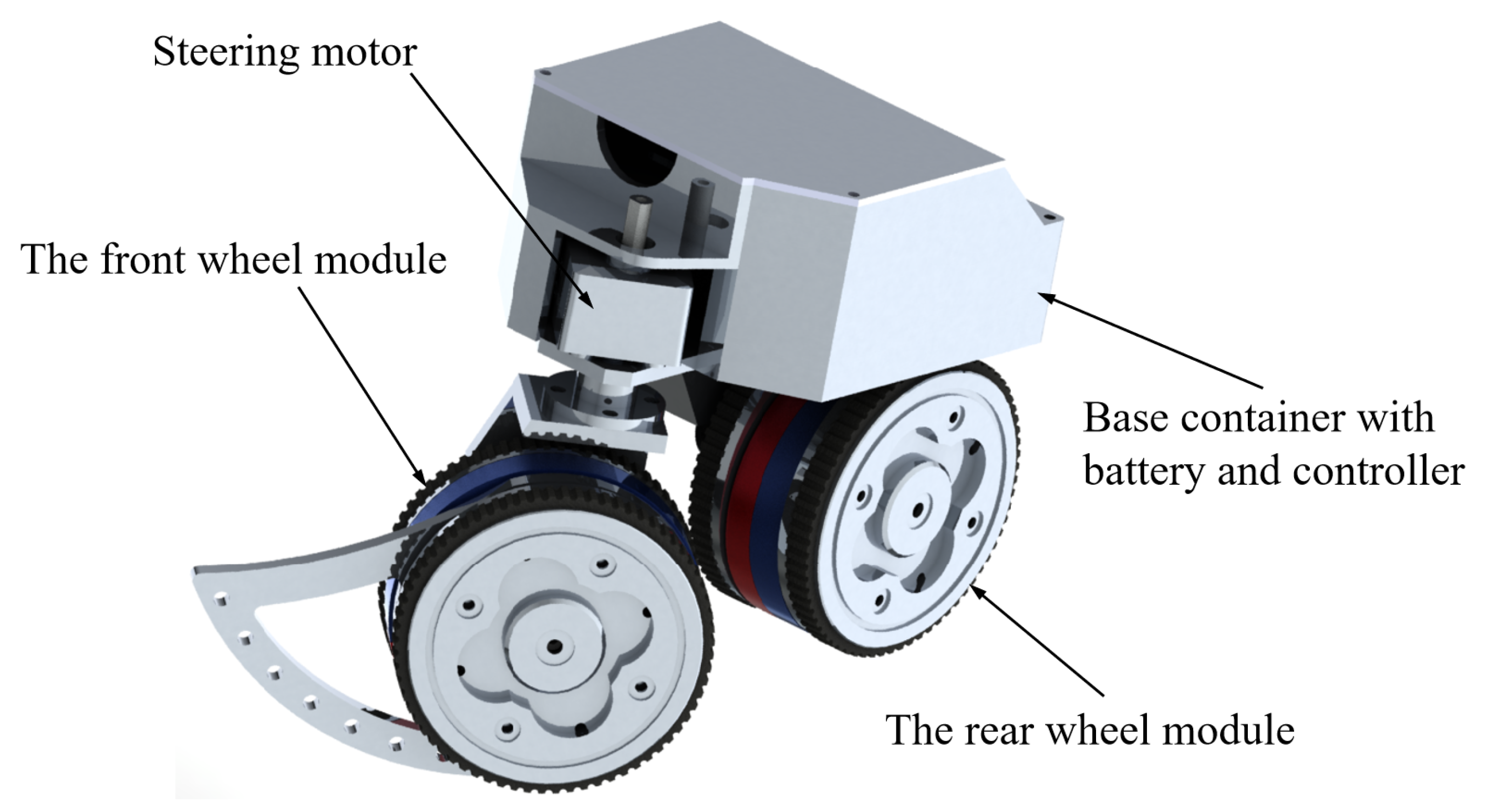
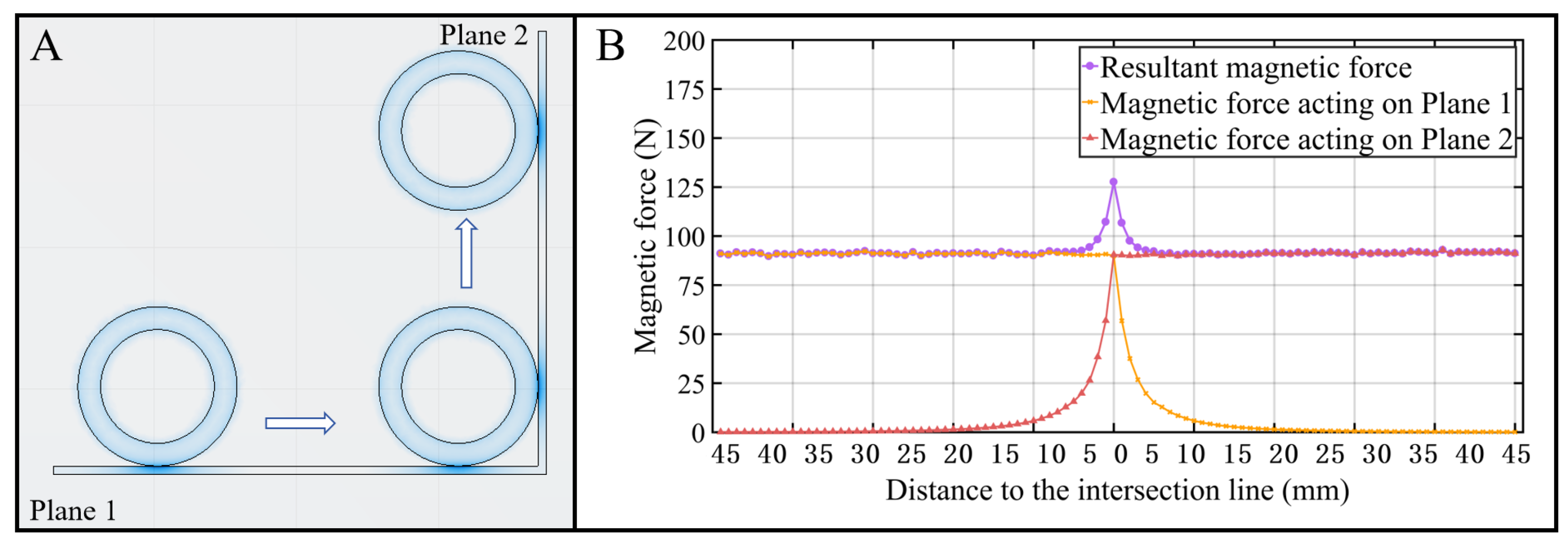


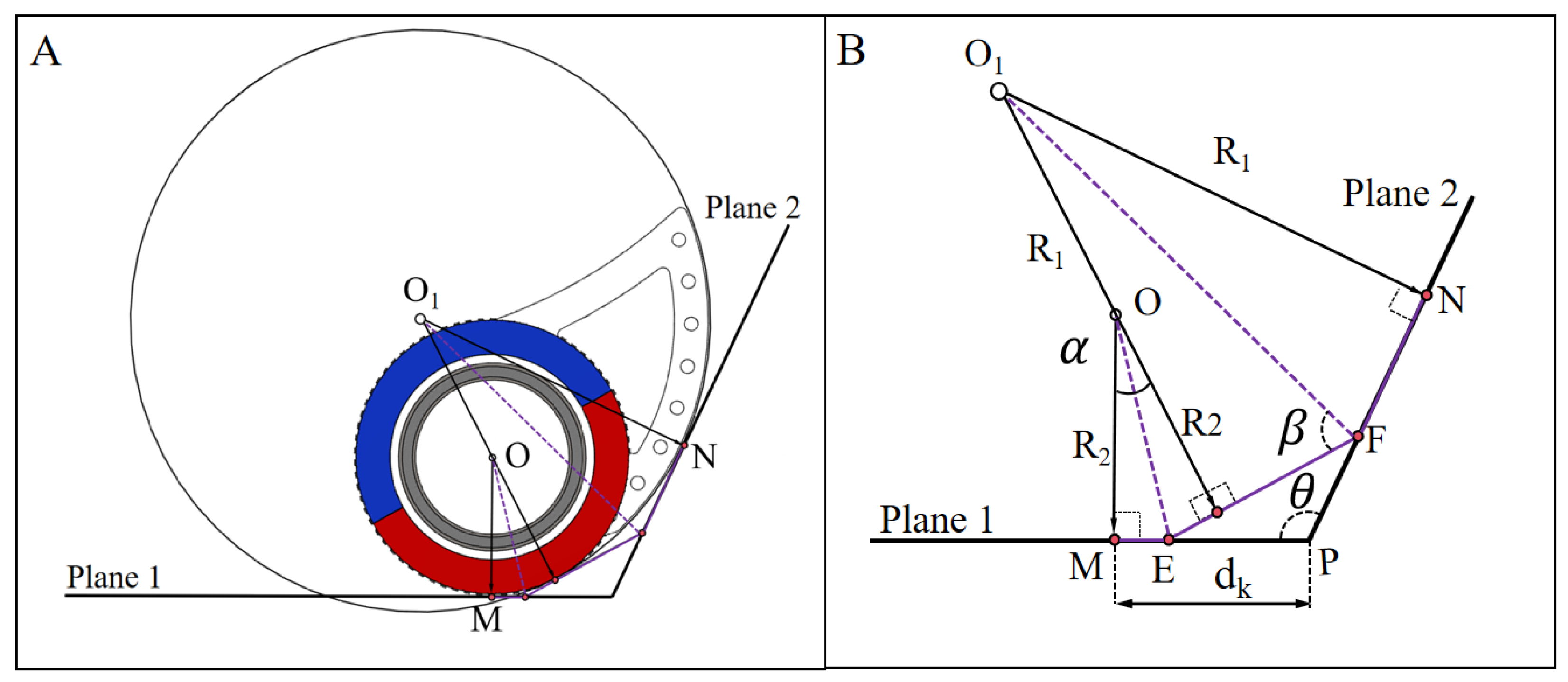

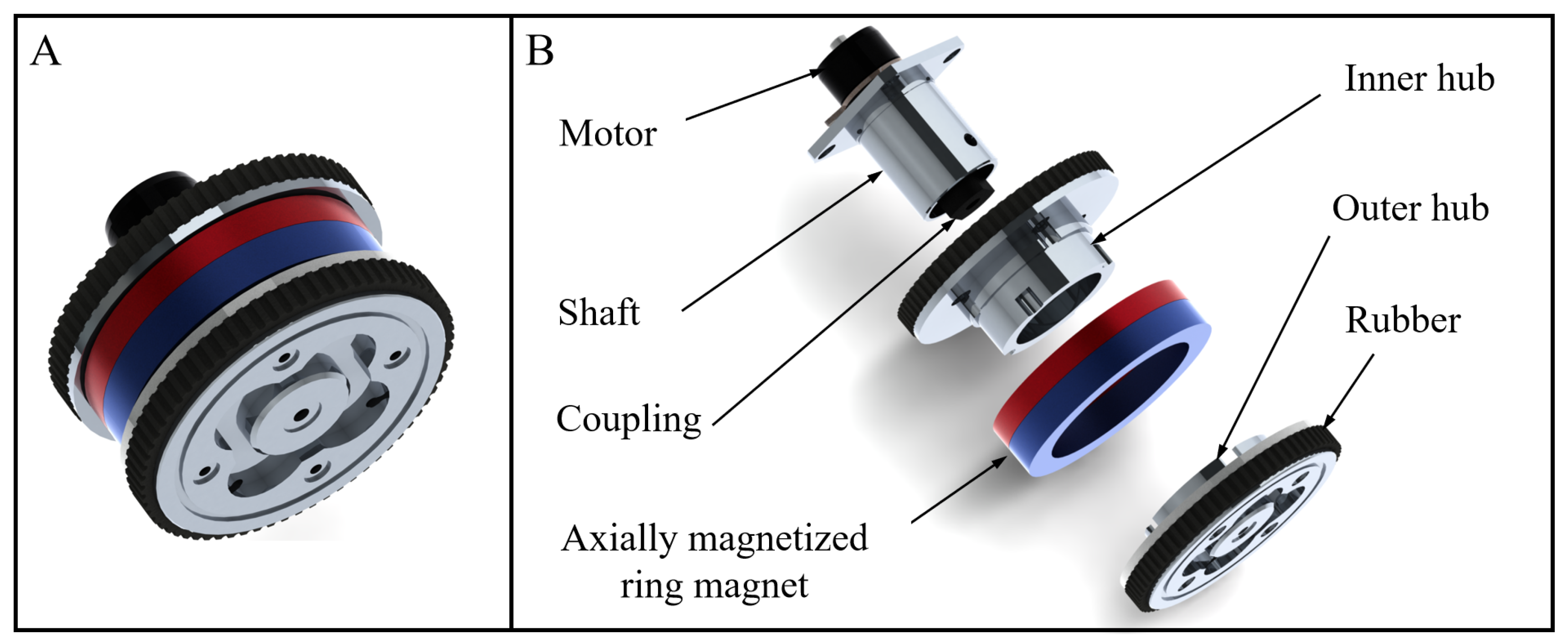



| Parameters | Value |
|---|---|
| Length × Width × Height (mm) | |
| Weight (Kg) | 1.6 |
| Climbing speed (m/s) | 0 to 0.9 |
| Minimum turning radius (mm) | 70 |
| Payload (Kg) | 2 |
| Endurance time (min) | 45 |
| Parameter | Value |
|---|---|
| Size of ring magnet (mm) | |
| Material of ring magnet | N42 |
| Magnetization direction | Radial |
| Outer diameter of rubber tire (mm) | |
| Radius of arc tentacle (mm) | 85 |
| Motor torque (Nm) | 1 |
| Weight of wheel module (Kg) | 0.7 |
| Parameter | Value |
|---|---|
| Size of ring magnet (mm) | |
| Material of ring magnet | N52 |
| Magnetization direction | Axial |
| Outer diameter of rubber tire (mm) | 81 |
| Motor torque (Nm) | 1 |
| Weight of wheel module (Kg) | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bu, Y.; Dun, L.; Deng, Y.; Jiang, B.; Jiang, A.; Zhu, H. Development of a Bicycle-like Magnetic-Wheeled Climbing Robot with Adaptive Plane-Transition Capabilities. Machines 2025, 13, 167. https://doi.org/10.3390/machines13020167
Bu Y, Dun L, Deng Y, Jiang B, Jiang A, Zhu H. Development of a Bicycle-like Magnetic-Wheeled Climbing Robot with Adaptive Plane-Transition Capabilities. Machines. 2025; 13(2):167. https://doi.org/10.3390/machines13020167
Chicago/Turabian StyleBu, Yongjian, Lide Dun, Yongtao Deng, Bingdong Jiang, Aihua Jiang, and Haifei Zhu. 2025. "Development of a Bicycle-like Magnetic-Wheeled Climbing Robot with Adaptive Plane-Transition Capabilities" Machines 13, no. 2: 167. https://doi.org/10.3390/machines13020167
APA StyleBu, Y., Dun, L., Deng, Y., Jiang, B., Jiang, A., & Zhu, H. (2025). Development of a Bicycle-like Magnetic-Wheeled Climbing Robot with Adaptive Plane-Transition Capabilities. Machines, 13(2), 167. https://doi.org/10.3390/machines13020167






