Method of Dynamic Modeling and Robust Optimization for Chain Transmission Mechanism with Time-Varying Load Uncertainty
Abstract
1. Introduction
- (1)
- A dynamic model of the chain transmission mechanism considering multiple clearances was established, and the accuracy of the simulation model was verified through experiments.
- (2)
- A robust optimization design method for the chain transmission mechanism based on K-L expansion and PCE was proposed. First, the K-L expansion method was used for the dimensionality reduction of the random driving loads. Then, based on the PCE method, a fast uncertainty propagation analysis of the chain transmission mechanism was conducted, and a robust optimization design model for the chain transmission mechanism was established.
- (3)
- The effectiveness of the proposed method was verified through engineering examples, providing theoretical reference for the robust optimization design of complex engineering chain transmission problems.
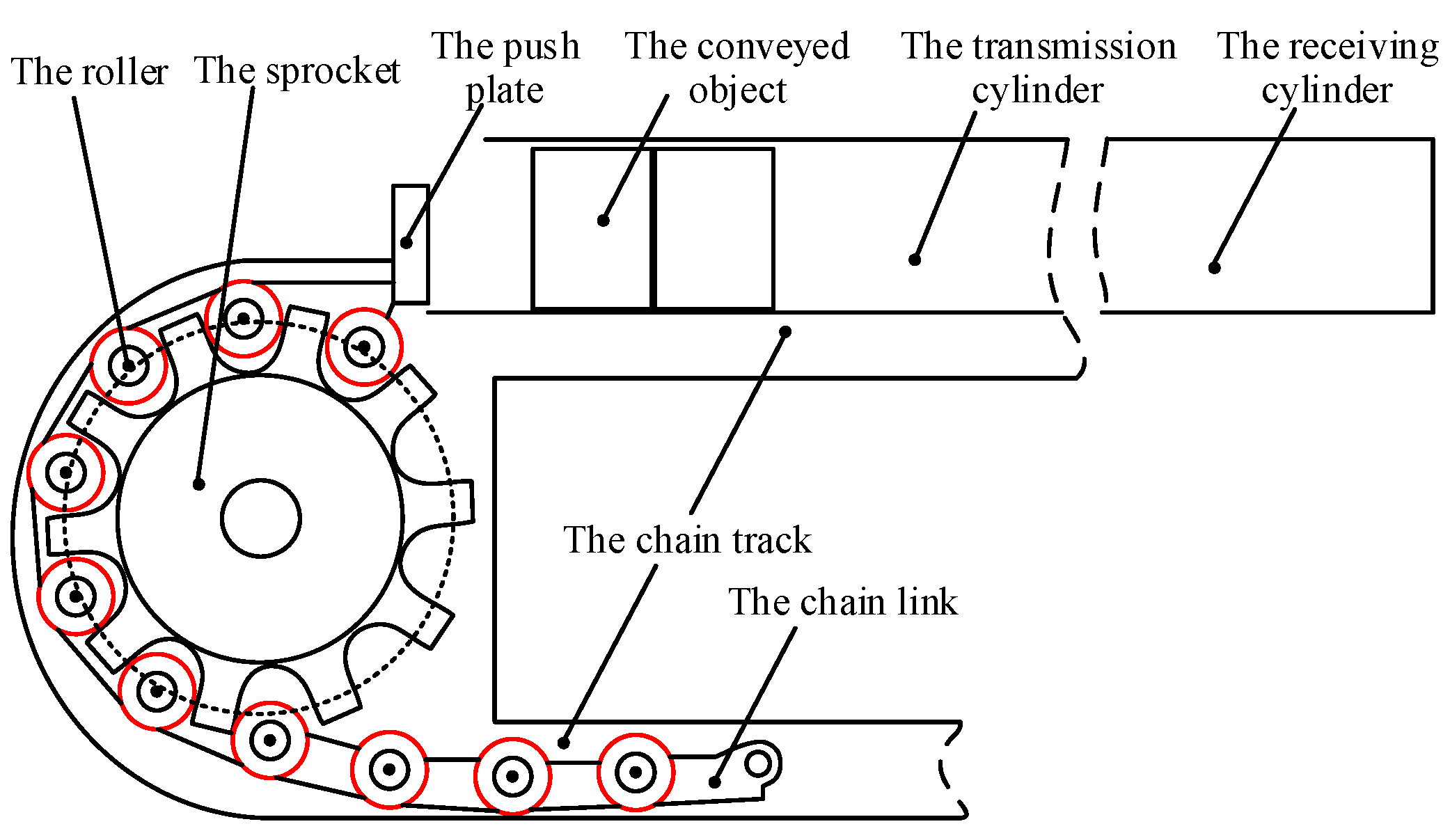
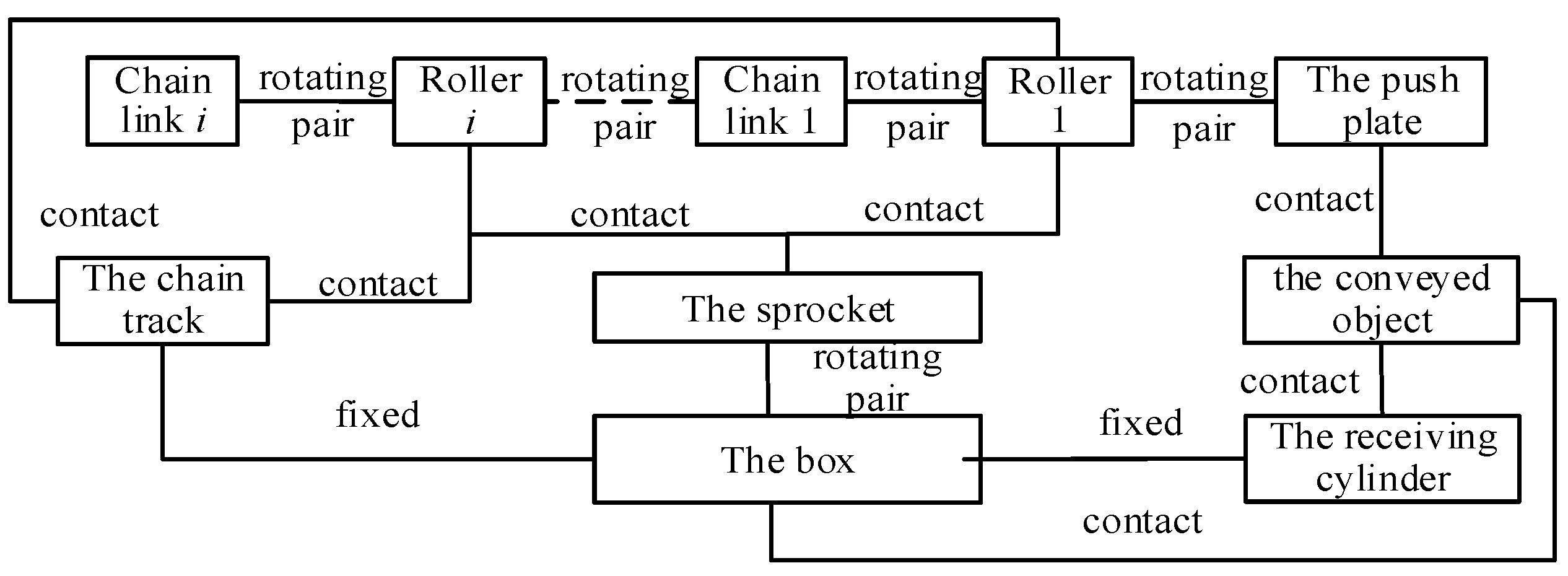
2. Dynamic Modeling of Chain Transmission Mechanism
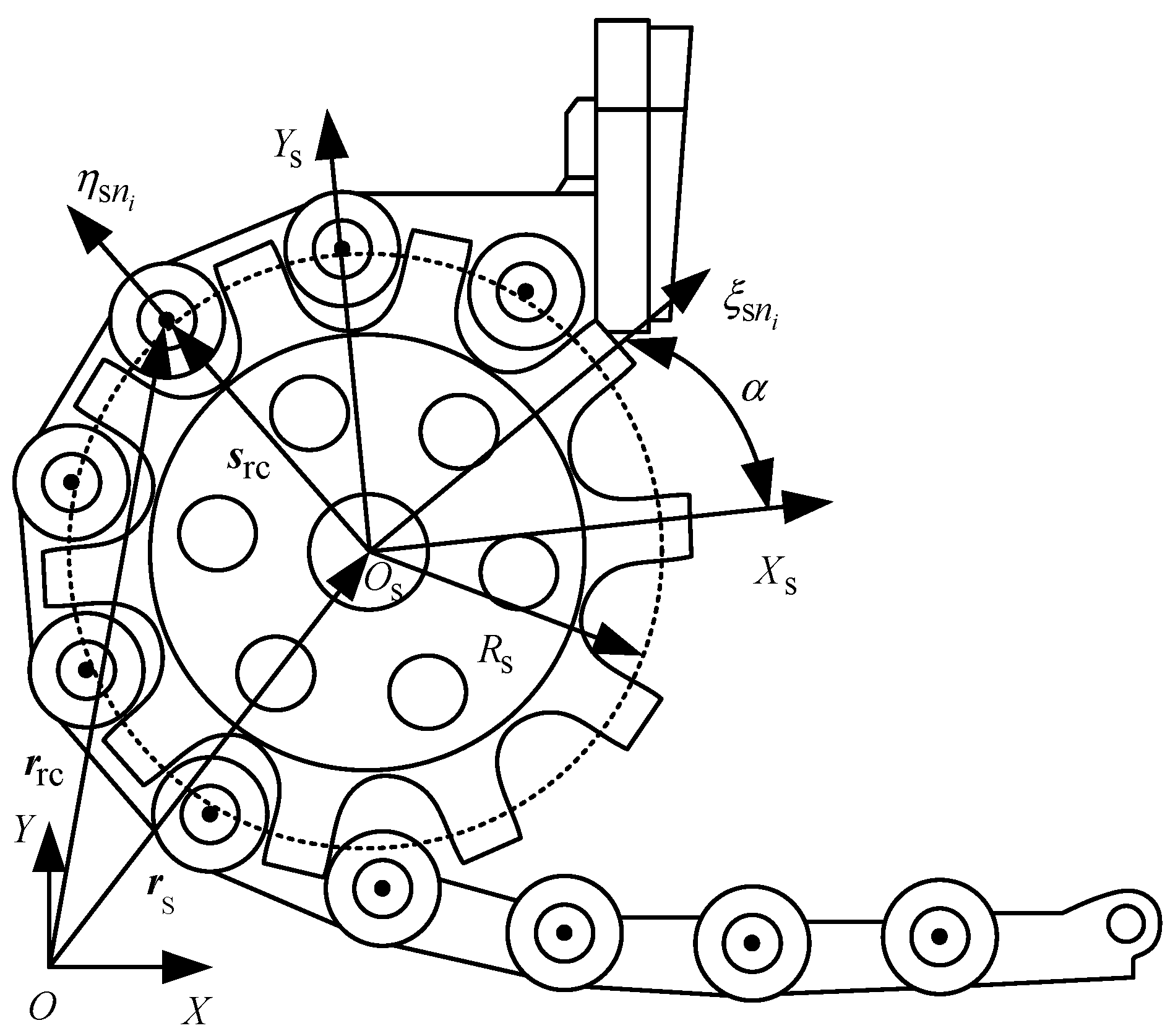
2.1. Model Description of Chain Transmission Mechanism
2.2. Basic Assumptions
- (1)
- The system operates under steady-state conditions, and external disturbances are assumed to be negligible;
- (2)
- The chain transmission system is treated as a rigid body system, with no deformation of components during operation;
- (3)
- The friction between chain links, sprockets, and rollers is assumed to be constant for simplification;
- (4)
- The relationship between the rotational motion of the sprocket and the translational motion of the chain is idealized, assuming no slipping or stretching of the chain;
- (5)
- The chain transmission mechanism is treated as a planar system, considering only the motion within the plane and rotation about its axis of rotation.
2.3. Motion and Contact Analysis of Open Chain System
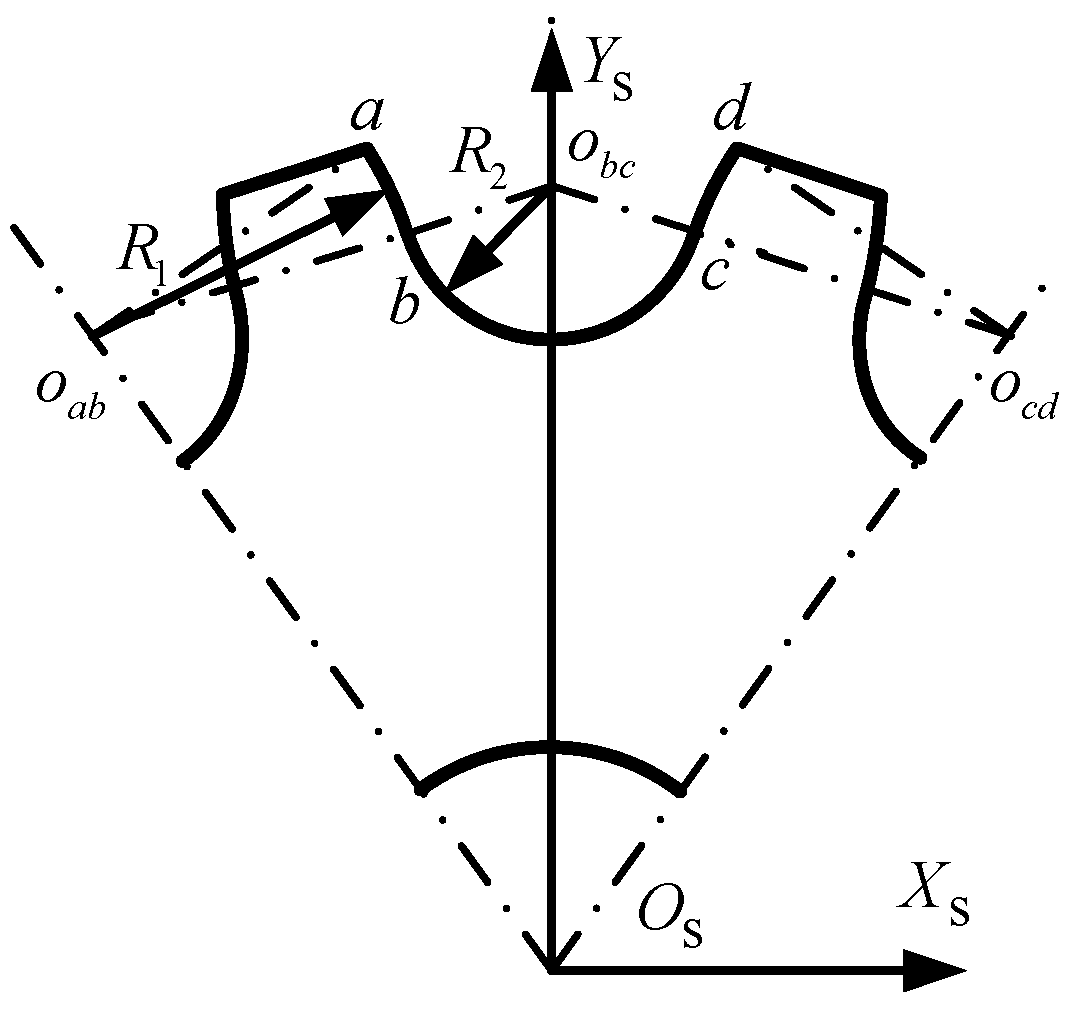
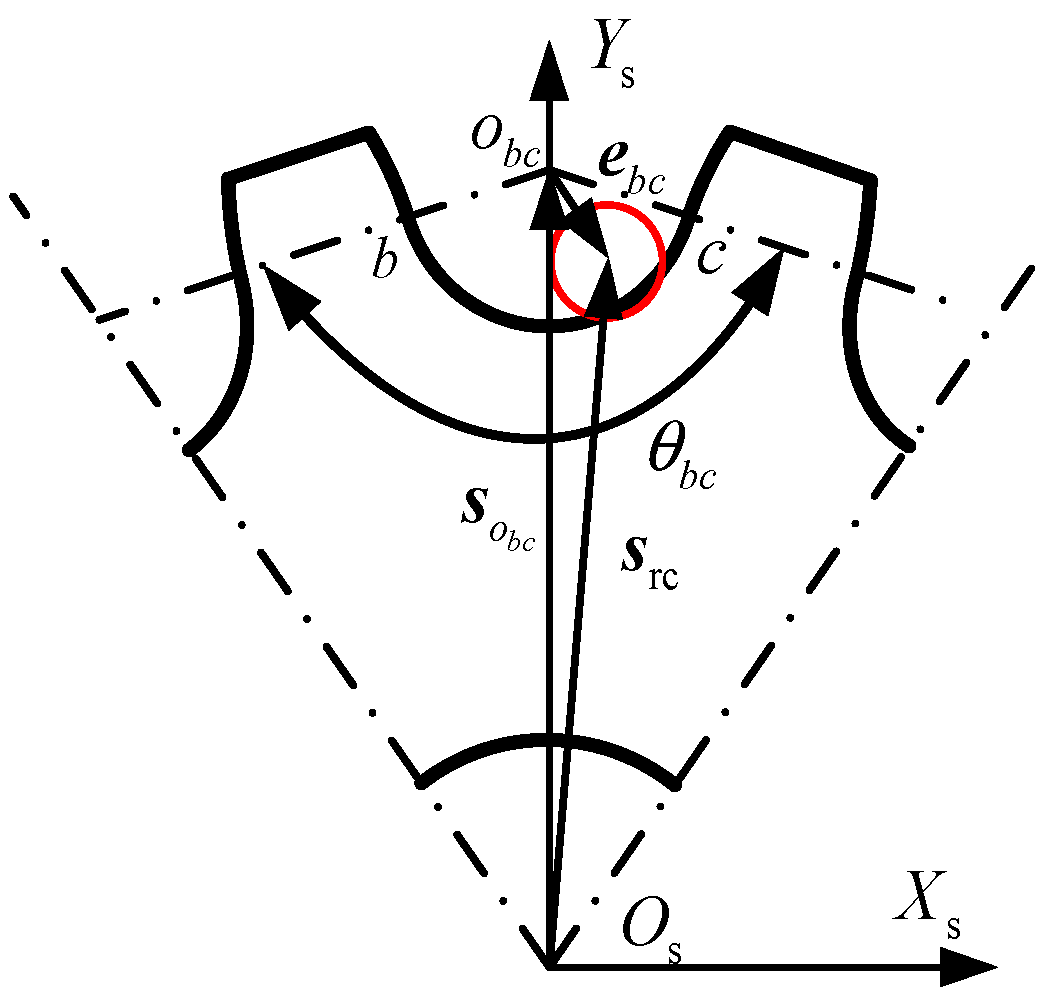
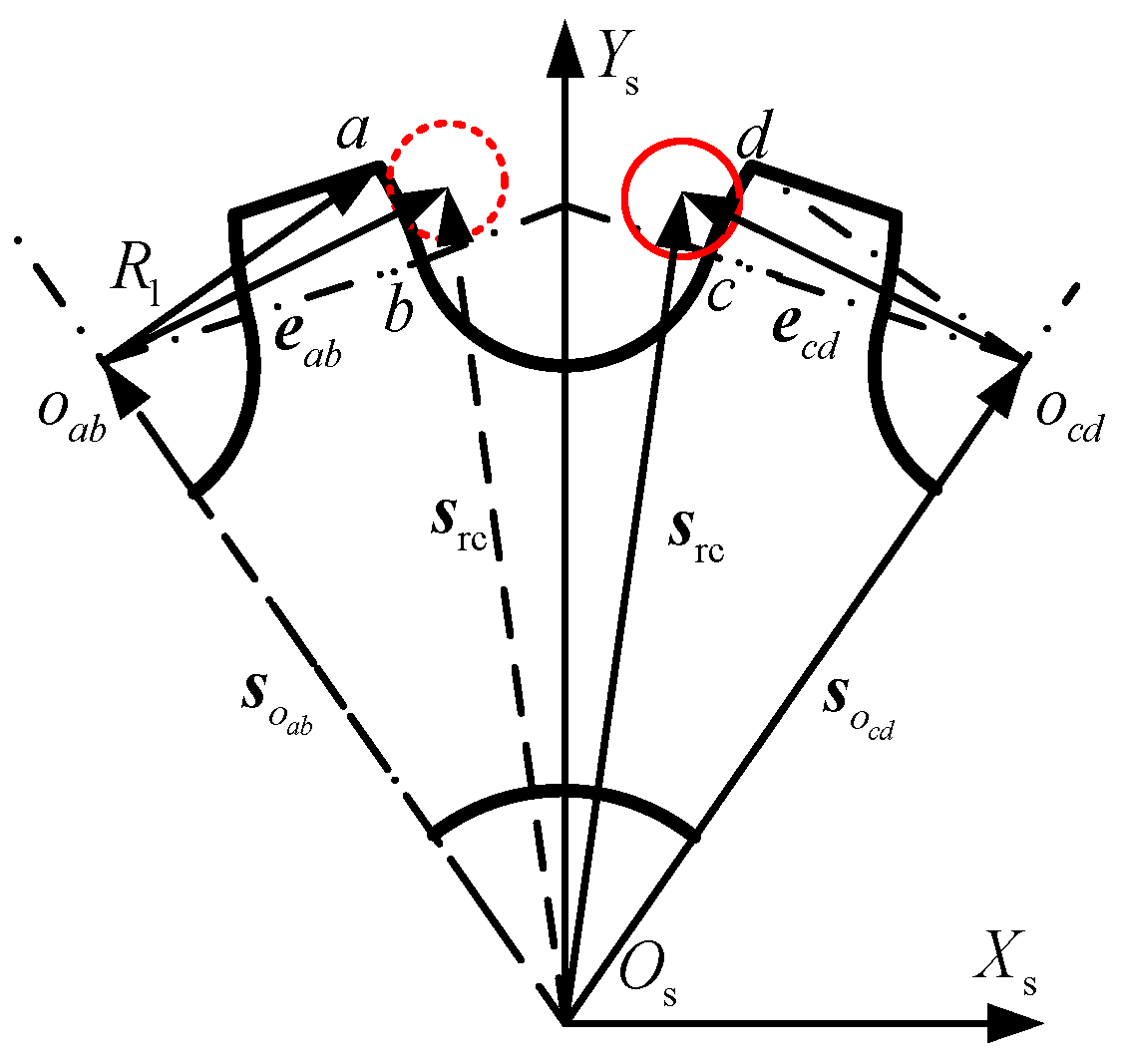
2.3.1. Geometric Relationship Between the Sprocket Tooth Groove and the Roller Contact
2.3.2. Contact Between Chain Links
2.4. Contact Force Model
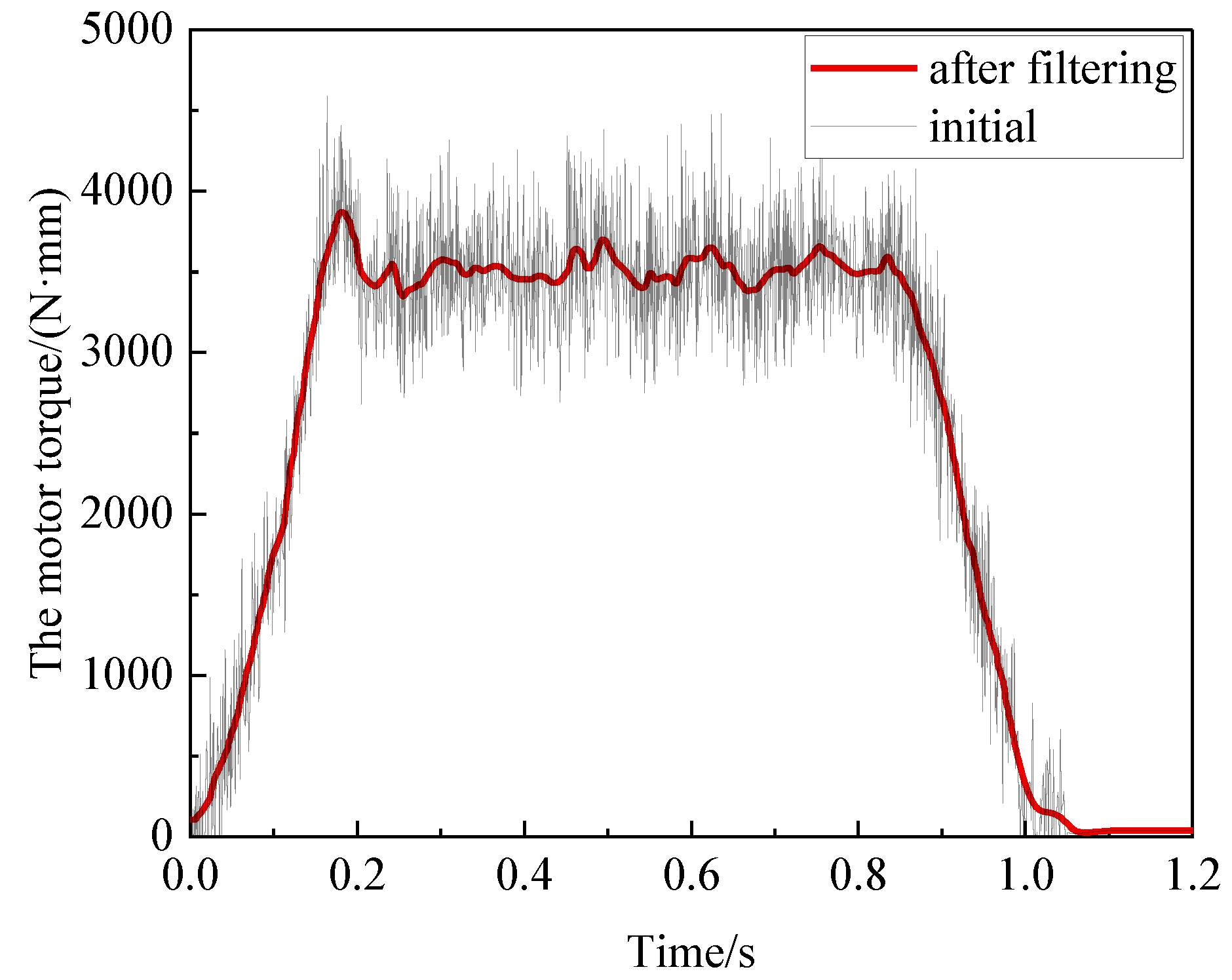
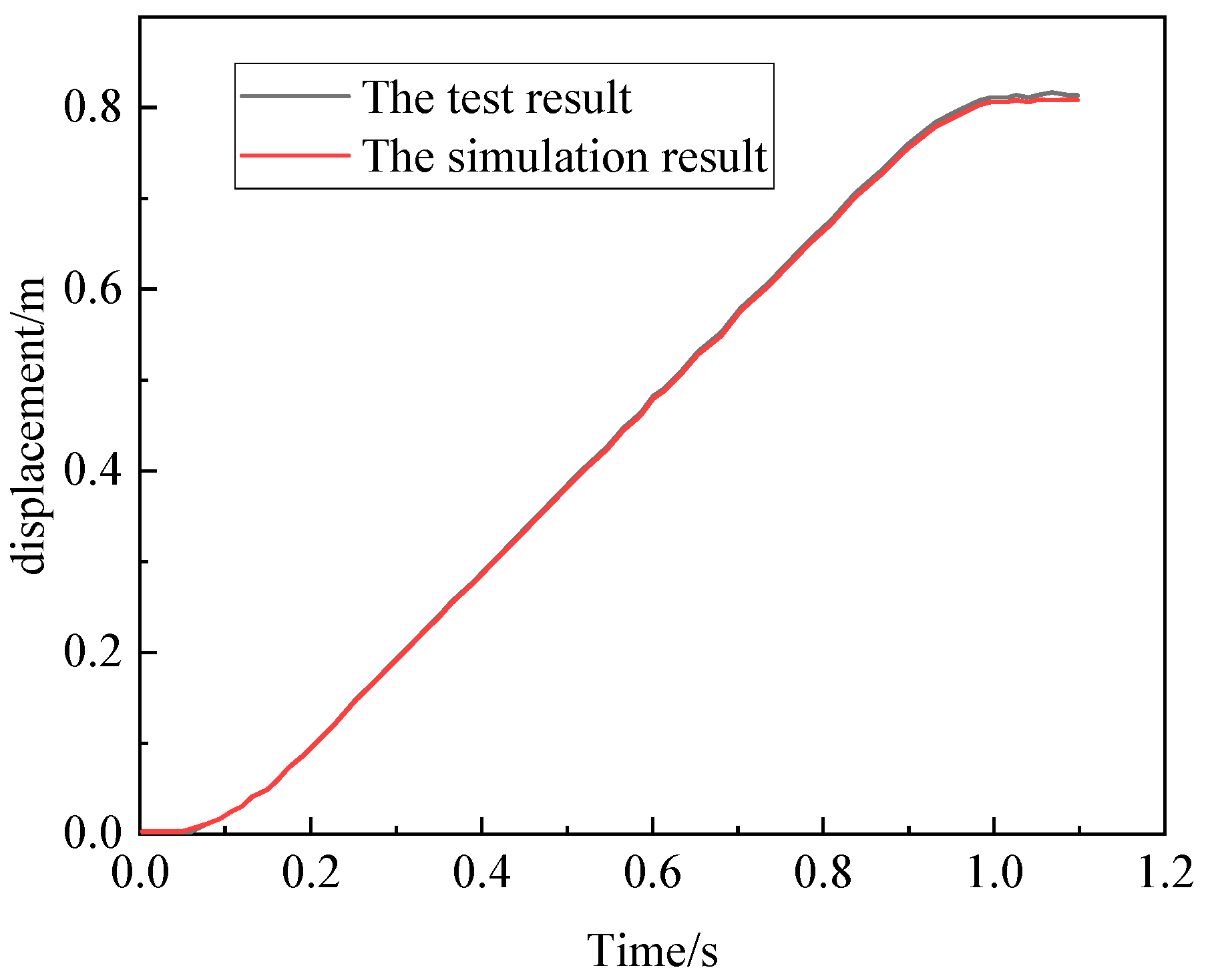
2.5. Dynamic Model and Experimental Validation of Chain Transmission Mechanism
- (1)
- According to the schematic diagram in Figure 8, arrange the experimental setup and connect the testing system. The data acquisition system is connected to the PLC control system to ensure the synchronization of the data signals. The displacement sensor is mounted at the rear of the chain transmission mechanism using a bracket. The sensor captures the laser signal of the moving conveyed object, and the displacement sensor is connected to the data acquisition system.
- (2)
- Power up the control system. Under the drive of the motor, the chain transmission mechanism moves the conveyed object forward. The PLC control system collects the current, while the data acquisition system collects the signals from the displacement sensor and the PLC’s synchronization signals.
- (3)
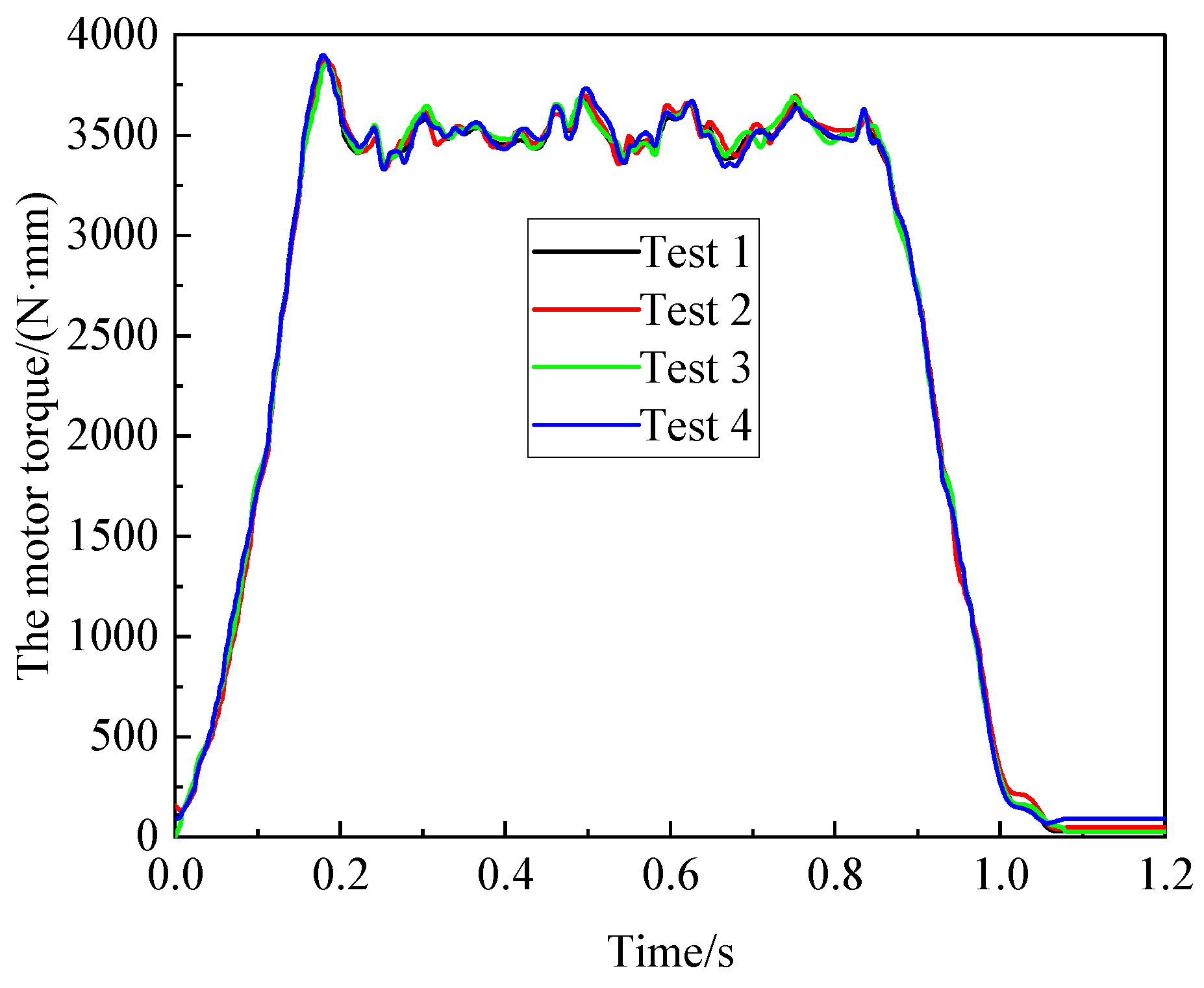
- To minimize the impact of external disturbances on parameter uncertainty, perform the test three times under the same conditions.
- (4)
- Data collection and processing: Export data from the PLC control system and data acquisition software (TranAX_3.4.1.1222, the USA). Extract valid data during the motion process of the conveyed object to conduct subsequent dynamic simulations and experimental comparisons. Then, take the average of the three data sets under the same operating conditions.
3. Robust Optimization Design Model for Chain Transmission Process Considering Random Loads
3.1. Random Parameters of the Chain Transmission Process
- (1)
- Structural dimension parameters: roller radius , sprocket tooth groove radius , sprocket transition arc radius , initial position of the transmitted object relative to the end face of the receiving cylinder , transmission cylinder radius , and the inner diameter of the receiving cylinder . To enhance the robustness of the chain transmission mechanism, the above structural dimension parameters are treated as design parameters, while considering the influence of parameter random fluctuations.
- (2)
- Physical property parameters: the coefficient of friction between the transmitted object and the transmission track and receiving cylinder , and the mass of the transmitted object . These parameters also have an influence on the positioning consistency of the transmitted object but are difficult to design. Therefore, they are not considered as design parameters, and only the effect of random fluctuations in these parameters is taken into account.
- (3)
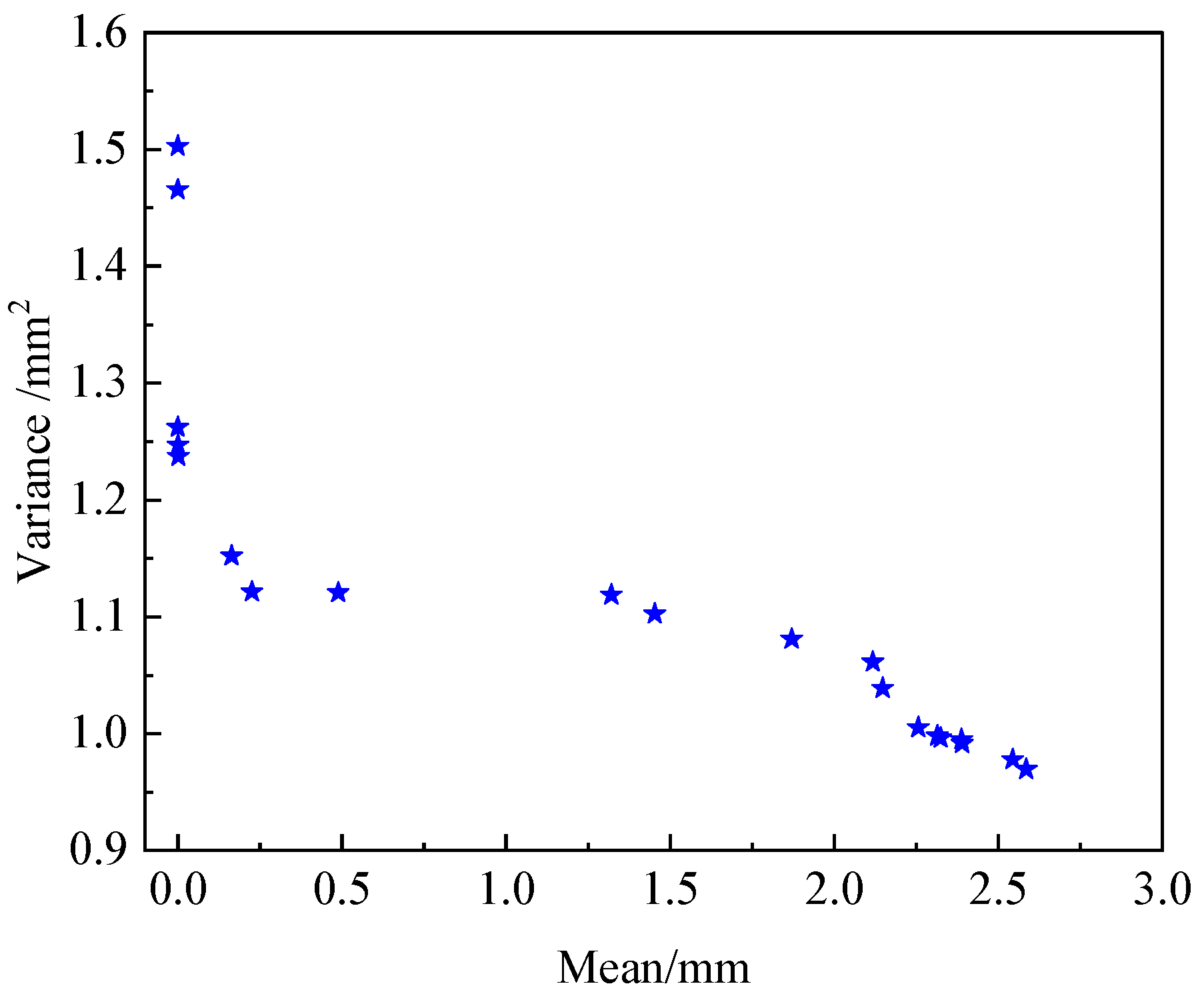
- Time-varying random loads: Based on the multiple torque curves after tests (Figure 11), it is observed that although the same motor speed is given, the driving load exhibits time-varying uncertainty. The fluctuations in the load have a significant effect on the positioning accuracy of the chain transmission mechanism. Therefore, the effect of time-varying random loads is considered.
3.2. Random Driving Load Analysis Based on Karhunen–Loeve Expansion
3.3. Chain Transmission Mechanism Surrogate Model Based on Polynomial Chaos Expansion
3.4. Robust Optimization Design Model for Chain Transmission Mechanism
- (1)
- Obtain multiple sets of dynamic driving loads through experiments and quantify the uncertainties, obtaining random dynamic load characteristics, such as mean, variance, autocorrelation function, and other stochastic features.
- (2)
- Solve the Fredholm integral equation using Equation (26) and arrange the obtained eigenvalues in descending order. Based on the given approximation degree, select the top M eigenvalues and their corresponding eigenfunctions.
- (3)
- For the reduced-dimensional random dynamic loads and uncertain input parameters, perform sampling and input them into the dynamic model to calculate the output response.
- (4)
- Use Equation (40) to establish the surrogate model of the chain transmission mechanism, relating the uncertain input parameters to the output response.
- (5)
- Combine Equation (41) and the surrogate model of the chain transmission mechanism to establish the robust optimization design model for the chain transmission mechanism.
- (6)
- Apply the MOPSO algorithm to solve the robust optimization design model of the chain transmission mechanism and obtain the optimal arrival displacement and its corresponding design parameters.
4. Case Study Analysis
5. Conclusions
- (1)
- The K-L expansion method can effectively reduce the dimensionality of time-varying random loads, solving the high-dimensional modeling difficulties by the PCE method.
- (2)
- A surrogate model for the chain transmission mechanism is established based on the PCE method, which greatly improves computational efficiency and saves computational costs while ensuring calculation accuracy.
- (3)
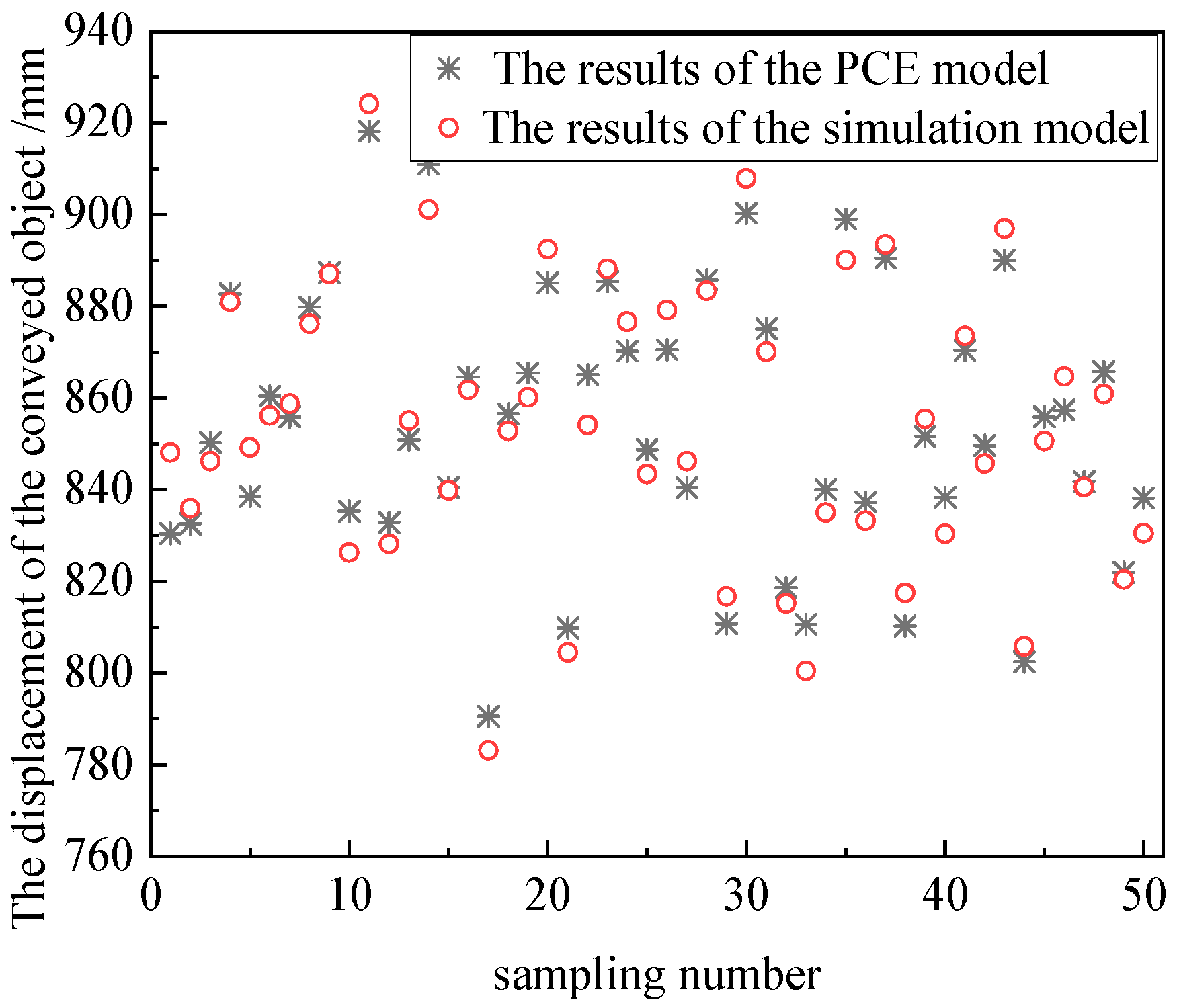
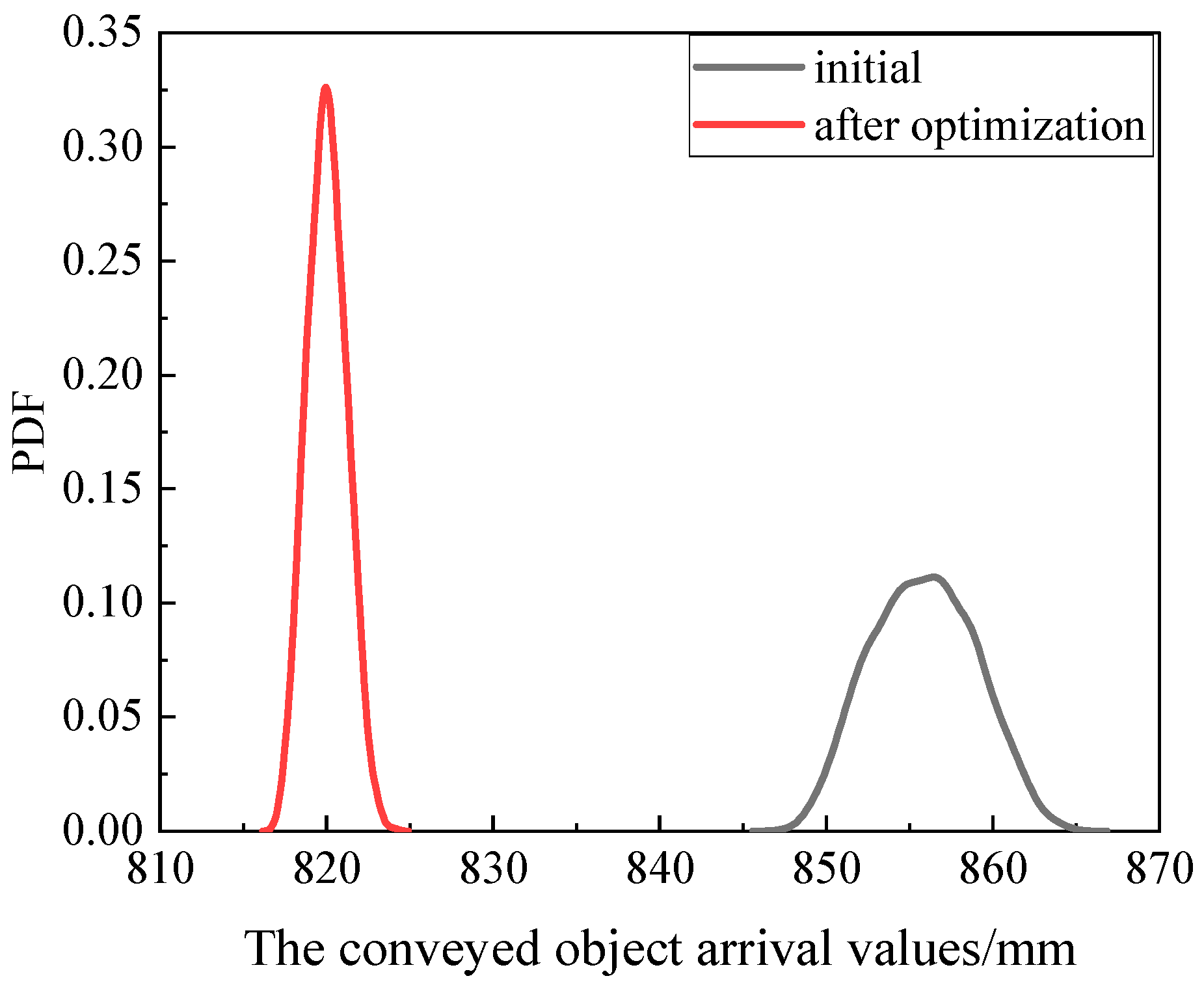
- The robust optimization design method can effectively improve the transmission accuracy of the chain transmission mechanism. Compared to the initial design, the variance of the transported object is reduced by 63.14%.
- (4)
- The optimized results prove the effectiveness of the proposed method in improving the consistency of the conveyed object positioning. This method and its results provide theoretical guidance for the design of chain transmission mechanisms.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| the teeth number of the sprocket | the original radius of the sprocket | ||
| the pitch angle of the sprocket | position vector of the sprocket’s center in the global coordinate system | ||
| the position vector of the roller in the global coordinate system | the vector from the sprocket center to the roller center | ||
| global coordinate system | sprocket coordinate system | ||
| local coordinate system of the tooth groove | the coordinate transformation matrix | ||
| the radius of the circular arcs in the respective segments ab and cd | the radius of the circular arcs in the respective segment bc | ||
| the radius of the roller | ,, | the eccentric vector between the center of the roller and the center of the bottom arc | |
| ,, | the vector from the center of the bottom arc to the center of the sprocket | ,, | angle of arc segment ab, bc, and cd |
| the angle between and | the angle between and | ||
| ,, | penetration between the roller and the sprocket tooth groove | , | the position vector from the origin of the global coordinate system to points Q and P |
| the position vector from point P to point Q | penetration between P and Q | ||
| the normal collision force | K | the stiffness coefficient of the two contacting bodies | |
| h | the penetration depth of the contact bodies | n | the contact index |
| C | the contact damping coefficient | the relative collision velocity at the contact point | |
| the equivalent stiffness of the planar contact | the tangential friction force | ||
| the coefficient of sliding friction | the dynamic correction factor | ||
| the relative tangential velocity | t | the motion time of the transmission process | |
| , , | the relative displacement, relative velocity, and relative acceleration of the rotational joints in the chain transmission mechanism | constraint equation of the chain transmission mechanism | |
| the derivative of with respect to | the Lagrange multiplier | ||
| the mass matrix of the chain transmission mechanism | the generalized damping matrix of the chain transmission mechanism | ||
| the external force acting on the chain transmission mechanism | the current of the chain transmission mechanism | ||
| the motor torque | the motor torque constant | ||
| k | transmission ratio |
Appendix A
Appendix A.1. Kinematics Equation of the Mechanism
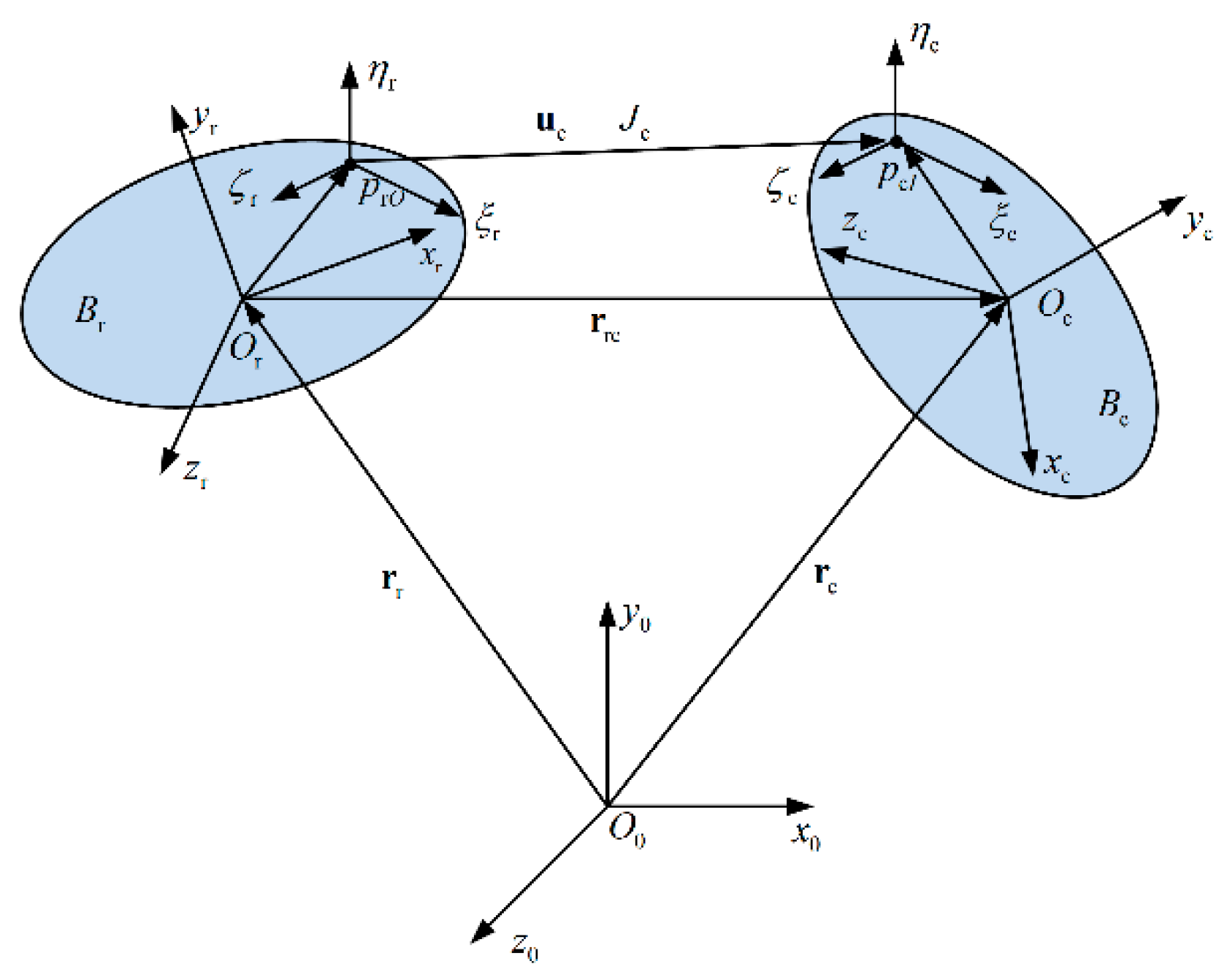
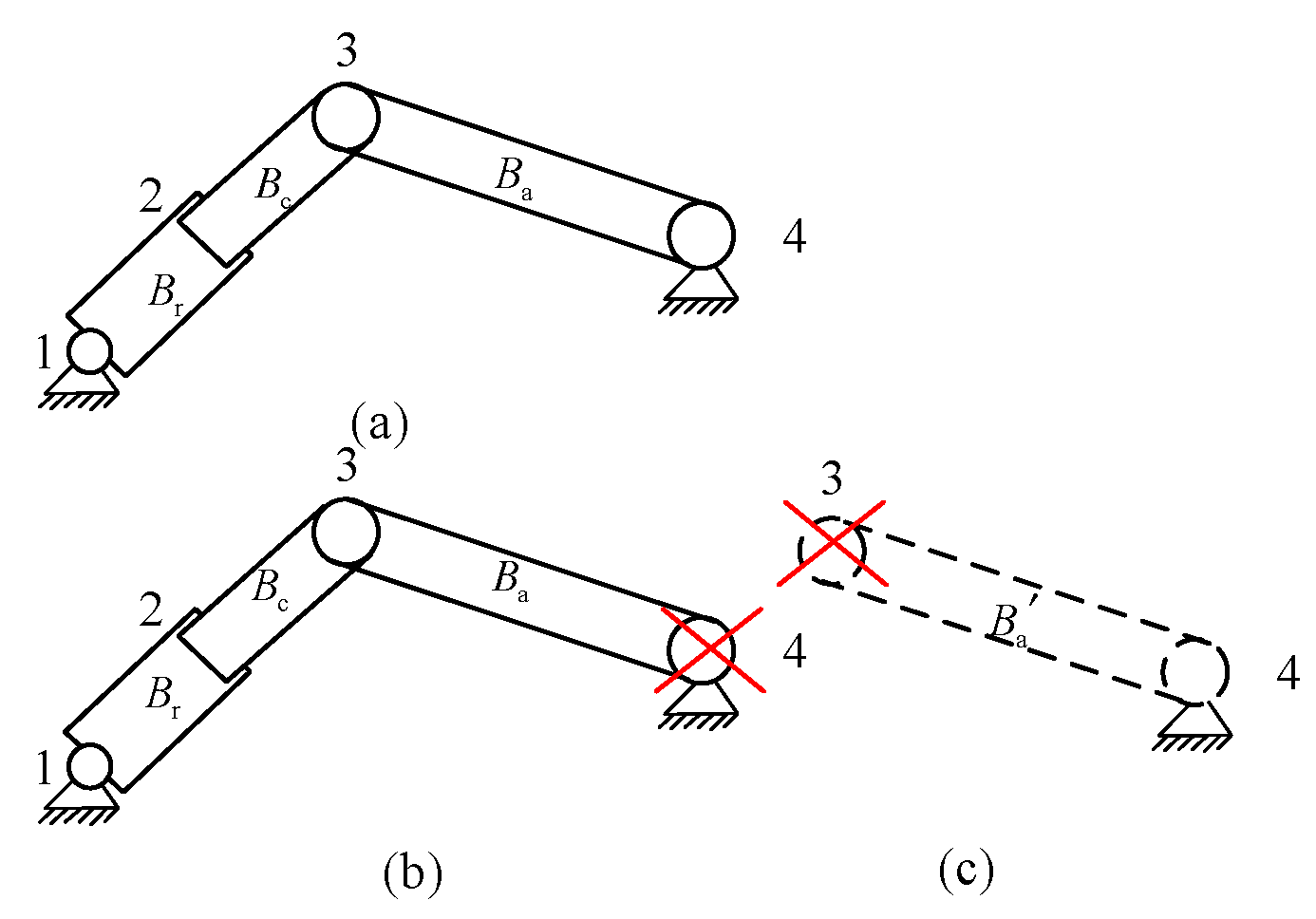
Appendix A.2. Dynamics Equation of the Mechanism
Appendix A.3. Dynamic Equations with Constraint Equations
References
- Li, Y.; Qian, L.; Chen, G.; Huang, W. Multiple clearance robustness optimization of a chain ramming machine based on a data-driven model. Nonlinear Dyn. 2023, 111, 13807–13828. [Google Scholar] [CrossRef]
- Zhuang, M.; Li, G.; Ding, K.; Xu, G. Optimized design of mechanical chain drive based on a wireless sensor network data algorithm. J. Sens. 2021, 2021, 2901624. [Google Scholar] [CrossRef]
- Chai, M.; Yuan, Y.; Zhao, W. An improved particle swarm optimization algorithm for dynamic analysis of chain drive based on multidisciplinary design optimization. Adv. Mech. Eng. 2019, 11, 1687814019829611. [Google Scholar] [CrossRef]
- Jiang, S.B.; Huang, S.; Zeng, Q.L.; Wang, C.L.; Gao, K.D.; Zhang, Y.Q. Dynamic properties of chain drive system considering multiple impact factors. Int. J. Simul. Model 2022, 21, 284–295. [Google Scholar] [CrossRef]
- Hong, L.; Li, X.J. Structural optimization of a chain transmission with constraints. Appl. Mech. Mater. 2014, 687, 523–526. [Google Scholar] [CrossRef]
- Da, L.; Ying, L.; Zheng, G.; Sun, M.; Liang, Z. Design of mechanical chain drive based on particle swarm optimization. In Proceedings of the 2022 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), Hengyang, China, 26–27 March 2022; IEEE: New York, NY, USA, 2022; pp. 97–101. [Google Scholar]
- Cheng, Y.; Guo, H.; Fu, Z.; Wan, N.; Li, L.; Wang, Y. Design and analysis of the Gemini chain system in dual clutch transmission of automobile. Chin. J. Mech. Eng. 2015, 28, 38–45. [Google Scholar] [CrossRef]
- Wang, Y.; Du, J.; Yang, T.; Zhou, J.; Wang, B.; Shi, Y.; Bai, J. Robust Optimization Design of a Blended Wing-Body Drone Considering Influence of Propulsion System. Aerosp. Sci. Technol. 2024, 156, 109751. [Google Scholar] [CrossRef]
- Zhang, W.; Qiang, W.; Fanzhi, Z.; Chao, Y. A novel robust aerodynamic optimization technique coupled with adjoint solvers and polynomial chaos expansion. Chin. J. Aeronaut. 2022, 35, 35–55. [Google Scholar] [CrossRef]
- Najlawi, B.; Nejlaoui, M.; Affi, Z.; Romdhane, L. Multi-objective robust design optimization of a sewing mechanism under uncertainties. J. Intell. Manuf. 2019, 30, 783–794. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, L.; Chen, G.; Liu, T. Data-Driven Modeling and Robust Optimization of the Ammunition Ramming Mechanism Based on Artificial Neural Network. In Proceedings of the International Conference on Mechanical System Dynamics, Beijing, China, 1–5 September 2023; Springer Nature: Singapore, 2023; pp. 691–705. [Google Scholar]
- Gao, H.; Sun, G.; Liu, Z.; Sun, C.; Li, N.; Ding, L.; Yu, H.; Deng, Z. Tension distribution algorithm based on graphics with high computational efficiency and robust optimization for two-redundant cable-driven parallel robots. Mech. Mach. Theory 2022, 172, 104739. [Google Scholar] [CrossRef]
- Guo, F.; Sun, Z.; Zhang, S.; Cao, R.; Li, H. Optimal design and reliability analysis of a compliant stroke amplification mechanism. Mech. Mach. Theory 2022, 171, 104748. [Google Scholar] [CrossRef]
- Wu, W.; Rao, S.S. Uncertainty analysis and allocation of joint tolerances in robot manipulators based on interval analysis. Reliab. Eng. Syst. Saf. 2007, 92, 54–64. [Google Scholar] [CrossRef]
- Du, X.; Venigella, P.K.; Liu, D. Robust mechanism synthesis with random and interval variables. Mech. Mach. Theory 2009, 44, 1321–1337. [Google Scholar] [CrossRef]
- Krüger, J.C.; Kranz, M.; Schmidt, T.; Seifried, R.; Kriegesmann, B. An efficient and non-intrusive approach for robust design optimization with the first-order second-moment method. Comput. Methods Appl. Mech. Eng. 2023, 414, 116136. [Google Scholar] [CrossRef]
- Meng, Z.; Wu, Y.; Wang, X.; Ren, S.; Yu, B. Robust topology optimization methodology for continuum structures under probabilistic and fuzzy uncertainties. Int. J. Numer. Methods Eng. 2021, 122, 2095–2111. [Google Scholar] [CrossRef]
- Kriegesmann, B.; Lüdeker, J.K. Robust compliance topology optimization using the first-order second-moment method. Struct. Multidiscip. Optim. 2019, 60, 269–286. [Google Scholar] [CrossRef]
- Cheng, J.; Lu, W.; Liu, Z.; Wu, D.; Gao, W.; Tan, J. Robust optimization of engineering structures involving hybrid probabilistic and interval uncertainties. Struct. Multidiscip. Optim. 2021, 63, 1327–1349. [Google Scholar] [CrossRef]
- Lee, S.H.; Chen, W.; Kwak, B.M. Robust design with arbitrary distributions using Gauss-type quadrature formula. Struct. Multidiscip. Optim. 2009, 39, 227–243. [Google Scholar] [CrossRef]
- Chatterjee, T.; Chowdhury, R.; Ramu, P. Decoupling uncertainty quantification from robust design optimization. Struct. Multidiscip. Optim. 2019, 59, 1969–1990. [Google Scholar] [CrossRef]
- Lee, D.; Rahman, S. Robust design optimization under dependent random variables by a generalized polynomial chaos expansion. Struct. Multidiscip. Optim. 2021, 63, 2425–2457. [Google Scholar] [CrossRef]
- Zafar, T.; Zhang, Y.; Wang, Z. An efficient Kriging based method for time-dependent reliability based robust design optimization via evolutionary algorithm. Comput. Methods Appl. Mech. Eng. 2020, 372, 113386. [Google Scholar] [CrossRef]
- Jiang, Z.; Wu, J.; Huang, F.; Lv, Y.; Wan, L. A novel adaptive Kriging method: Time-dependent reliability-based robust design optimization and case study. Comput. Ind. Eng. 2021, 162, 107692. [Google Scholar] [CrossRef]
- Cheng, J.; Wang, R.; Liu, Z.; Tan, J. Robust equilibrium optimization of structural dynamic characteristics considering different working conditions. Int. J. Mech. Sci. 2021, 210, 106741. [Google Scholar] [CrossRef]
- Pereira, C.; Ambrósio, J.; Ramalho, A. Dynamics of chain drives using a generalized revolute clearance joint formulation. Mech. Mach. Theory 2015, 92, 64–85. [Google Scholar] [CrossRef]
- Pedersen, S.L. Model of contact between rollers and sprockets in chain-drive systems. Arch. Appl. Mech. 2005, 74, 489–508. [Google Scholar] [CrossRef]
- Ma, J.; Bai, M.; Wang, J.; Dong, S.; Jie, H.; Hu, B.; Yin, L. A novel variable restitution coefficient model for sphere–substrate elastoplastic contact/impact process. Mech. Mach. Theory 2024, 202, 105773. [Google Scholar] [CrossRef]
- Ma, J.; Wang, J.; Peng, J.; Yin, L.; Dong, S.; Tang, J. Data-driven modeling for complex contacting phenomena via improved neural networks considering link switches. Mech. Mach. Theory 2024, 191, 105521. [Google Scholar] [CrossRef]
- Movahedi-Lankarani, H. Canonical Equations of Motion and Estimation of Parameters in the Analysis of Impact Problems. Ph.D. Thesis, University of Arizona, Tucson, AZ, USA, 1988. [Google Scholar]
- Liu, T.; Niu, Y.; Chen, G. A general methodology for simulation model validation and model updating of the coordination mechanism with uncertainty. J. Mech. Sci. Technol. 2023, 37, 6271–6286. [Google Scholar] [CrossRef]
- Bae, D.S.; Han, J.M.; Choi, J.H. An implementation method for constrained flexible multibody dynamics using a virtual body and joint. Multibody Syst. Dyn. 2000, 4, 297–315. [Google Scholar] [CrossRef]
- Tong, M.N.; Zhao, Y.G.; Zhao, Z. Simulating strongly non-Gaussian and non-stationary processes using Karhunen–Loève expansion and L-moments-based Hermite polynomial model. Mech. Syst. Signal Process. 2021, 160, 107953. [Google Scholar] [CrossRef]
- Blatman, G.; Sudret, B. Adaptive sparse polynomial chaos expansions based on Least Angle Regression. J. Comput. Phys. 2011, 230, 2345–2367. [Google Scholar] [CrossRef]
- Chen, G.S. The Study on the Dynamic of the Projectile-Barrel Coupled System and the Corresponding Key Parameters. Ph.D. Thesis, University of Science and Technology, Nanjing, China, 2016. [Google Scholar]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least Angle Regression. Annels Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef]


| Serial Number | Parameters | Nominal Value | Error Type | Error | Design Range |
|---|---|---|---|---|---|
| 1 | /kg | 3 | Normal | 0.03 | — |
| 2 | 0.2 | Uniform | [0.19, 0.21] | — | |
| 3 | 12.7 | Uniform | [0, 0.002] | [12.6, 12.8] | |
| 4 | 27.29 | Uniform | [0, 0.002] | [25, 30] | |
| 5 | 82 | Uniform | [0, 0.002] | [80, 84] | |
| 6 | 82 | Uniform | [0, 0.002] | [80, 84] | |
| 7 | 78 | — | — | — | |
| 8 | /mm | 12.5 | Uniform | [0, 0.002] | [12.4, 12.6] |
| 9 | /mm | 0 | Uniform | [0, 0.1] | [0, 5] |
| Methods | Correlation Coefficient |
|---|---|
| PCE | 0.1528 |
| KL-PCE | 0.9558 |
| KL-Kriging | 0.8547 |
| KL-RBF | 0.9234 |
| Serial Number | ||||||
|---|---|---|---|---|---|---|
| 1 | 12.6548 | 26.5823 | 83.0432 | 83.0384 | 12.4935 | 0.089 |
| 2 | 12.6544 | 26.5583 | 82.1473 | 82.1504 | 12.4933 | 0.043 |
| 3 | 12.6539 | 26.5476 | 83.0571 | 83.0413 | 12.4935 | 0.037 |
| 4 | 12.6489 | 26.5716 | 83.0147 | 83.0274 | 12.4945 | 0.049 |
| 5 | 12.6435 | 26.5804 | 82.7831 | 82.5731 | 12.4946 | 0.015 |
| 6 | 12.6601 | 26.5749 | 82.4397 | 82.3176 | 12.4945 | 0.085 |
| 7 | 12.6573 | 26.5614 | 83.0312 | 83.1047 | 12.4935 | 0.016 |
| 8 | 12.6683 | 26.5743 | 82.8734 | 82.7496 | 12.4935 | 0.0014 |
| 9 | 12.6415 | 26.5827 | 83.0187 | 83.0674 | 12.4945 | 0.0023 |
| 10 | 12.6573 | 26.5479 | 83.0243 | 83.0249 | 12.4934 | 0.0018 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, T.; Liu, Y.; Liu, P.; Du, X. Method of Dynamic Modeling and Robust Optimization for Chain Transmission Mechanism with Time-Varying Load Uncertainty. Machines 2025, 13, 166. https://doi.org/10.3390/machines13020166
Liu T, Liu Y, Liu P, Du X. Method of Dynamic Modeling and Robust Optimization for Chain Transmission Mechanism with Time-Varying Load Uncertainty. Machines. 2025; 13(2):166. https://doi.org/10.3390/machines13020166
Chicago/Turabian StyleLiu, Taisu, Yuan Liu, Peitong Liu, and Xiaofei Du. 2025. "Method of Dynamic Modeling and Robust Optimization for Chain Transmission Mechanism with Time-Varying Load Uncertainty" Machines 13, no. 2: 166. https://doi.org/10.3390/machines13020166
APA StyleLiu, T., Liu, Y., Liu, P., & Du, X. (2025). Method of Dynamic Modeling and Robust Optimization for Chain Transmission Mechanism with Time-Varying Load Uncertainty. Machines, 13(2), 166. https://doi.org/10.3390/machines13020166







