A Real-Time Demanded Current Observation-Based Sliding Mode Control of Permanent Magnet Synchronous Motors
Abstract
1. Introduction
- (1)
- Designed a SMC based on exponential reaching law.
- (2)
- A real-time demand current observer was designed to observe q-axis current disturbances and compensate for q-axis current, and combined with SMC, called SMC-ESO. This not only improves the performance of SMC but also demonstrates some of its characteristics.
- (3)
- Experiments have been conducted under various disturbance conditions, all of which indicate that SMC-ESO has better control performance.
2. Mathematical Modeling of PMSM
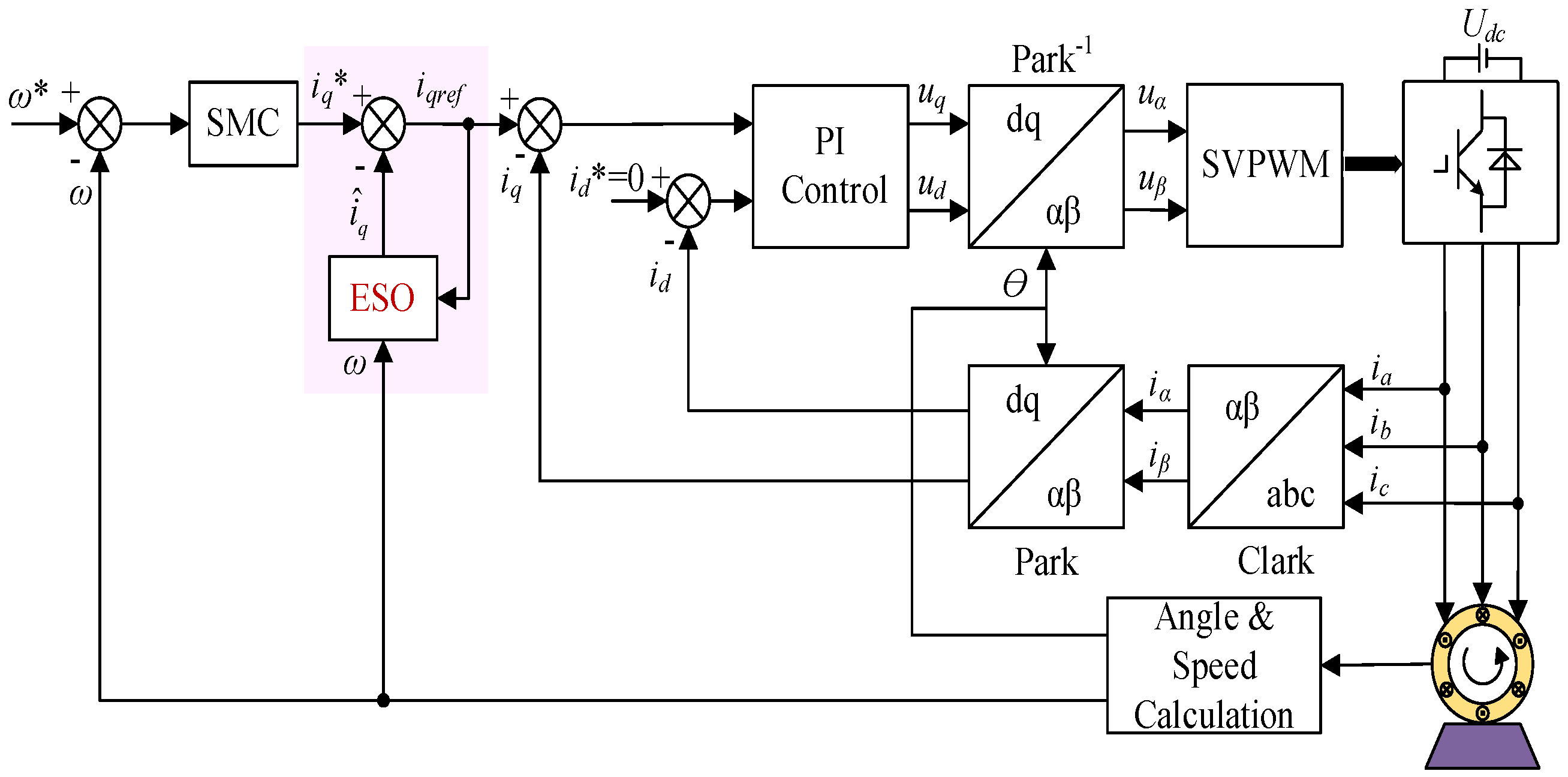
3. Design of Speed Controller
3.1. Design of Sliding Mode Controller
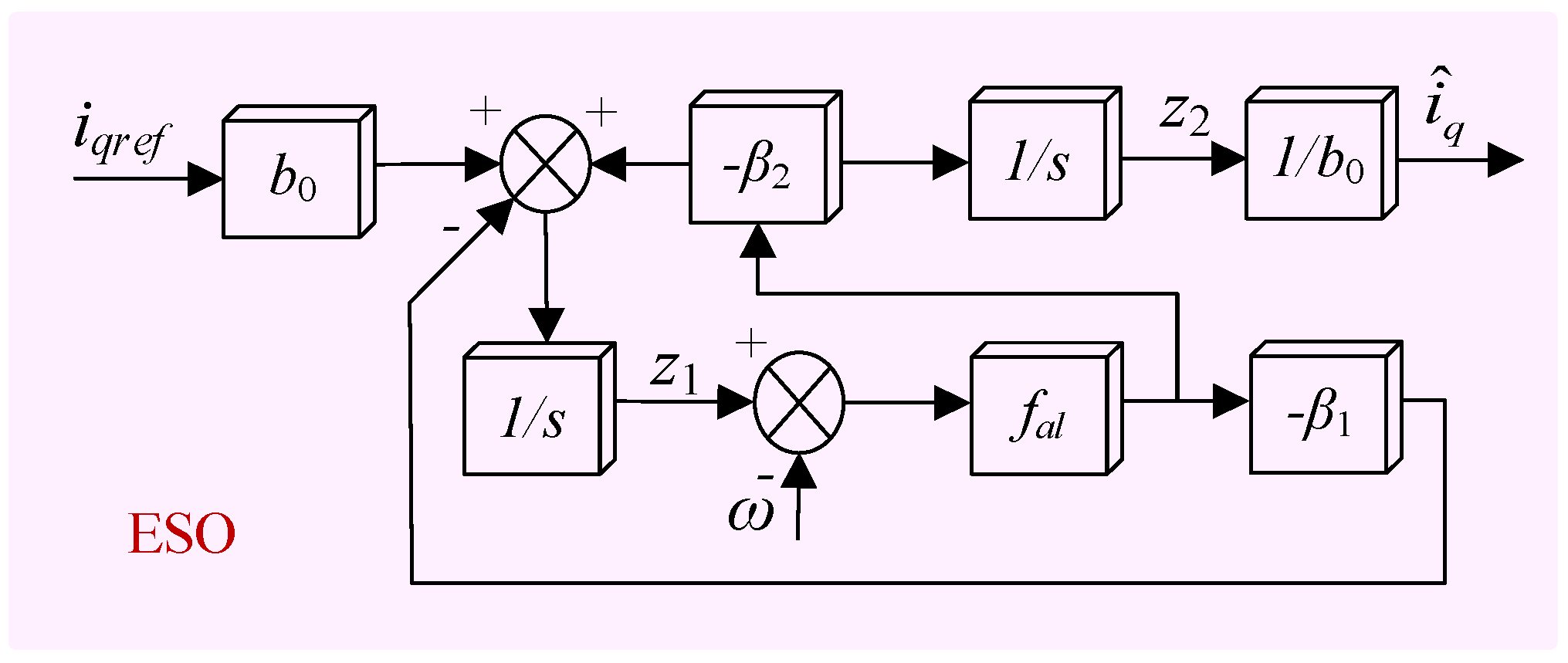
3.2. Design of Extended State Observer
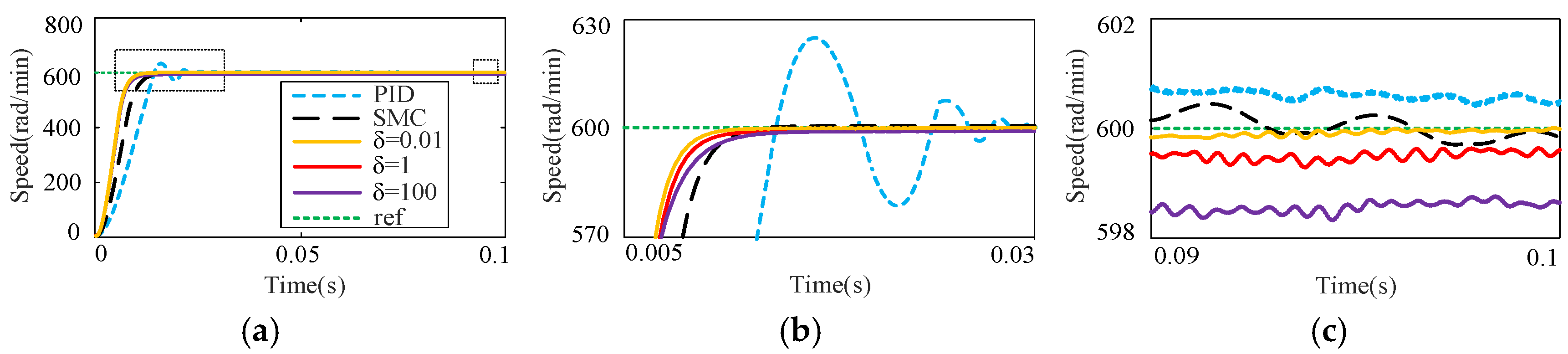
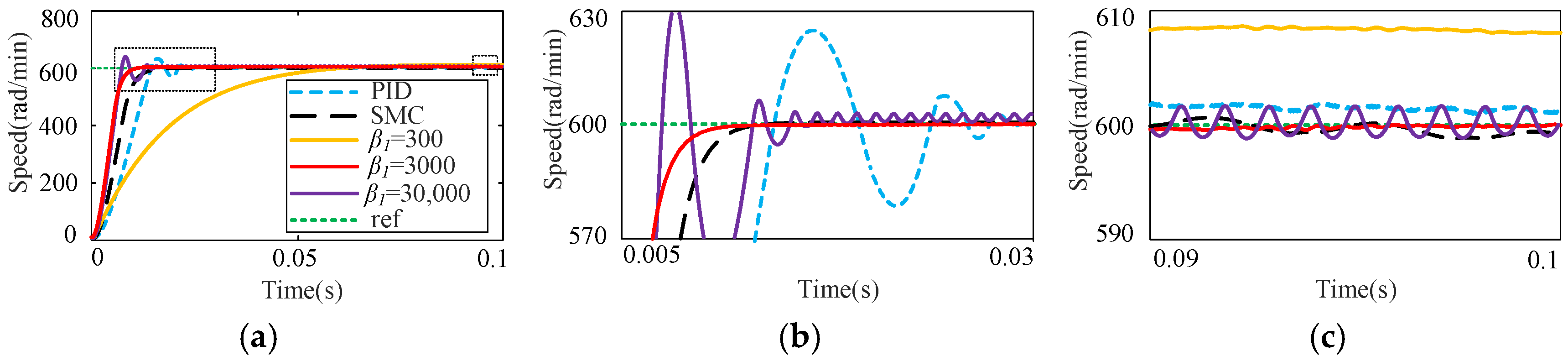
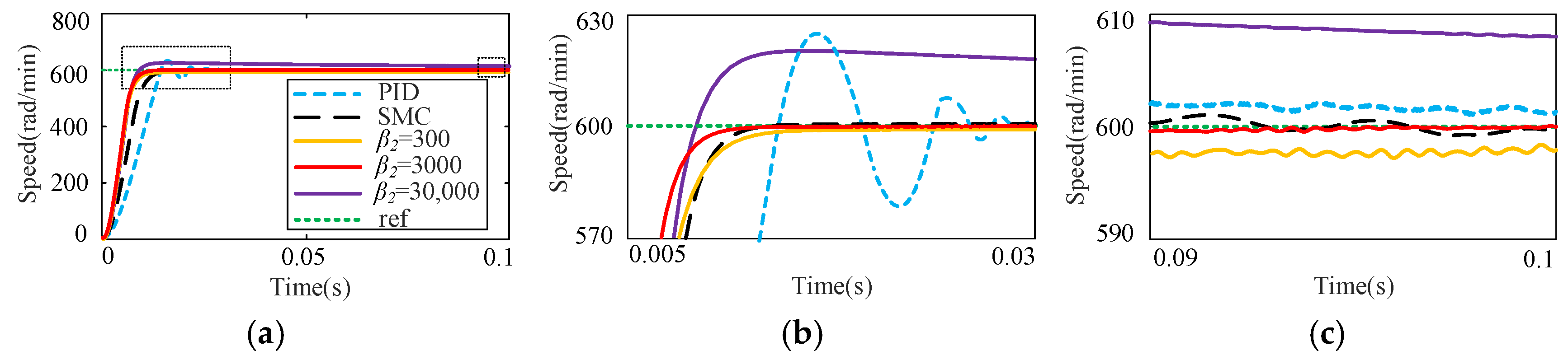
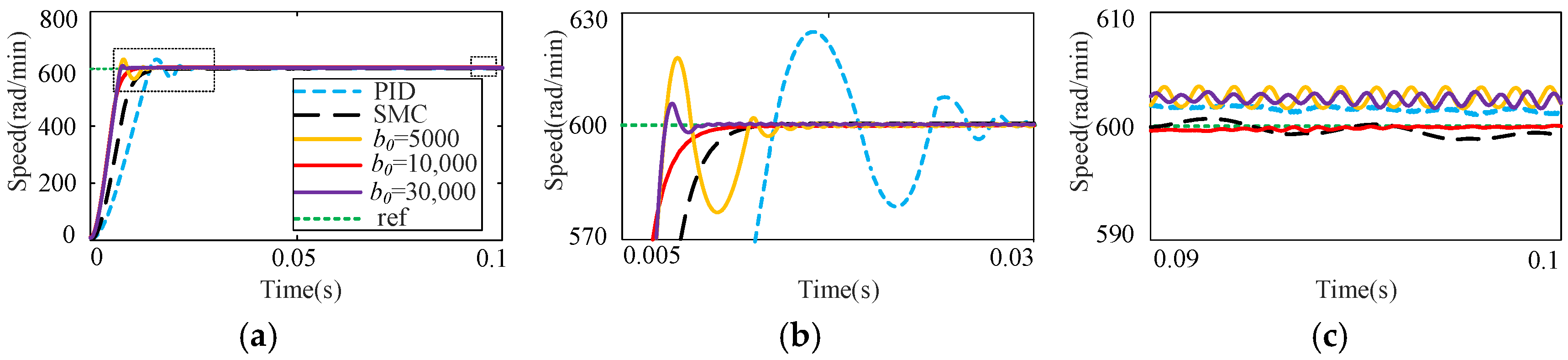
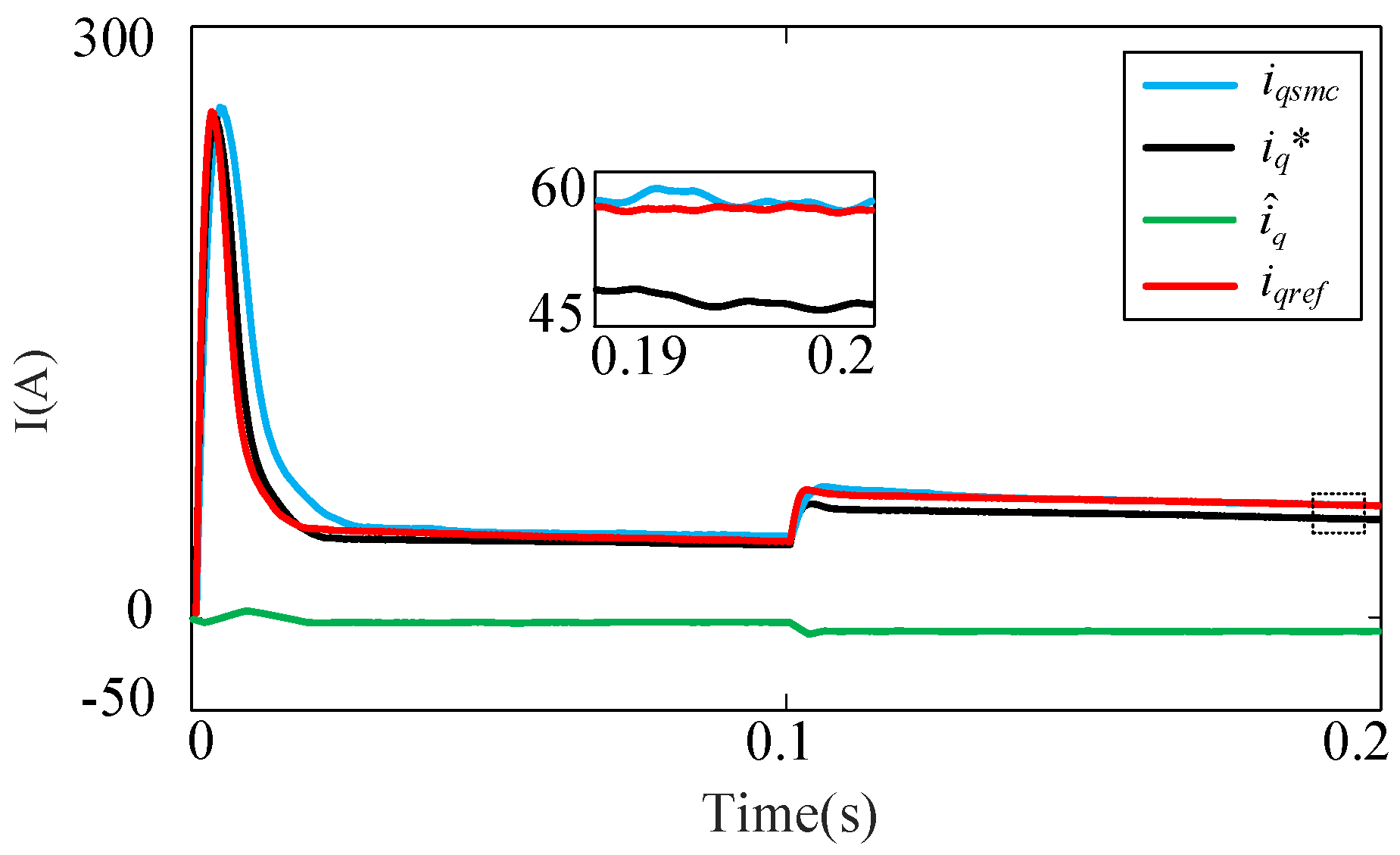
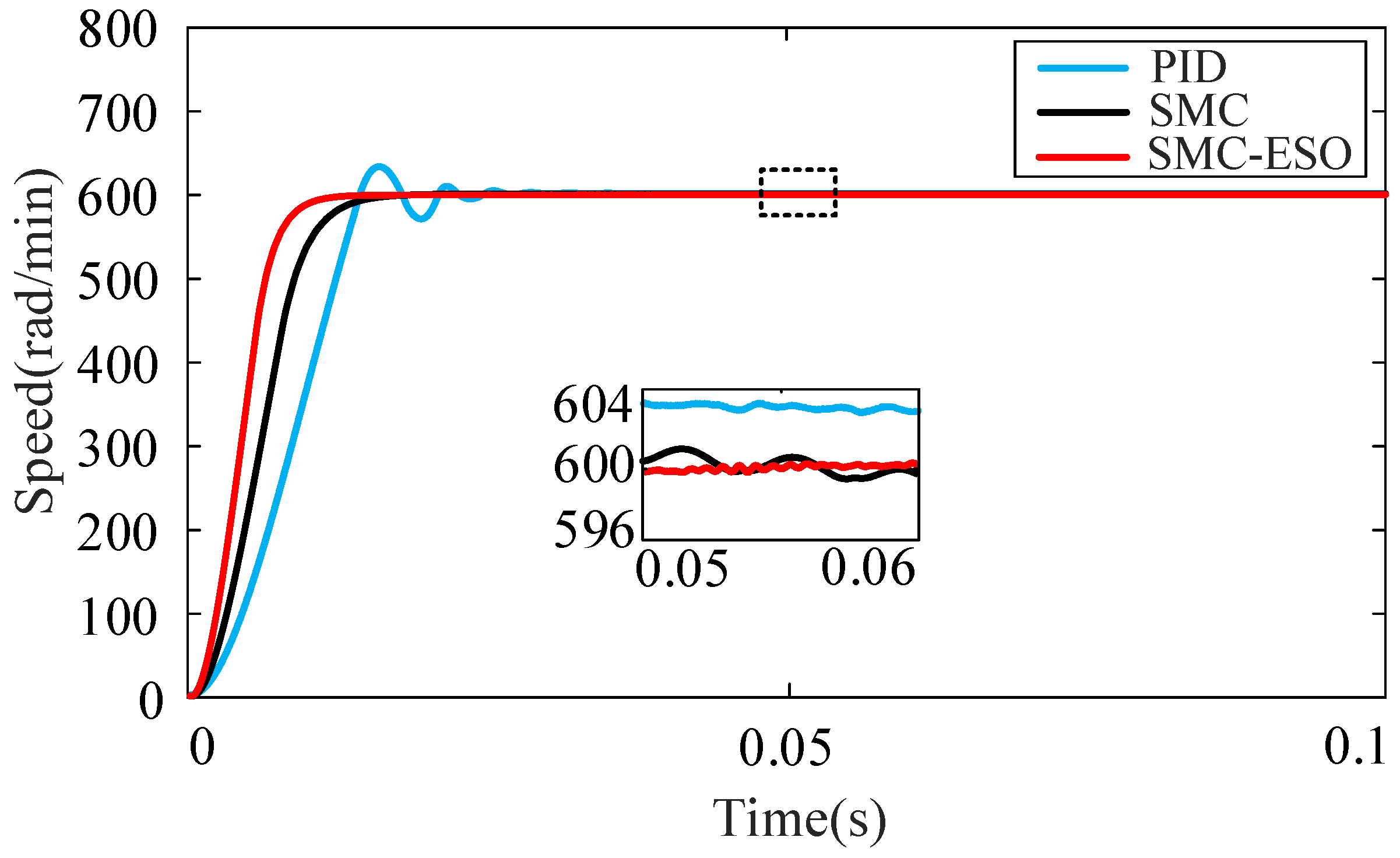
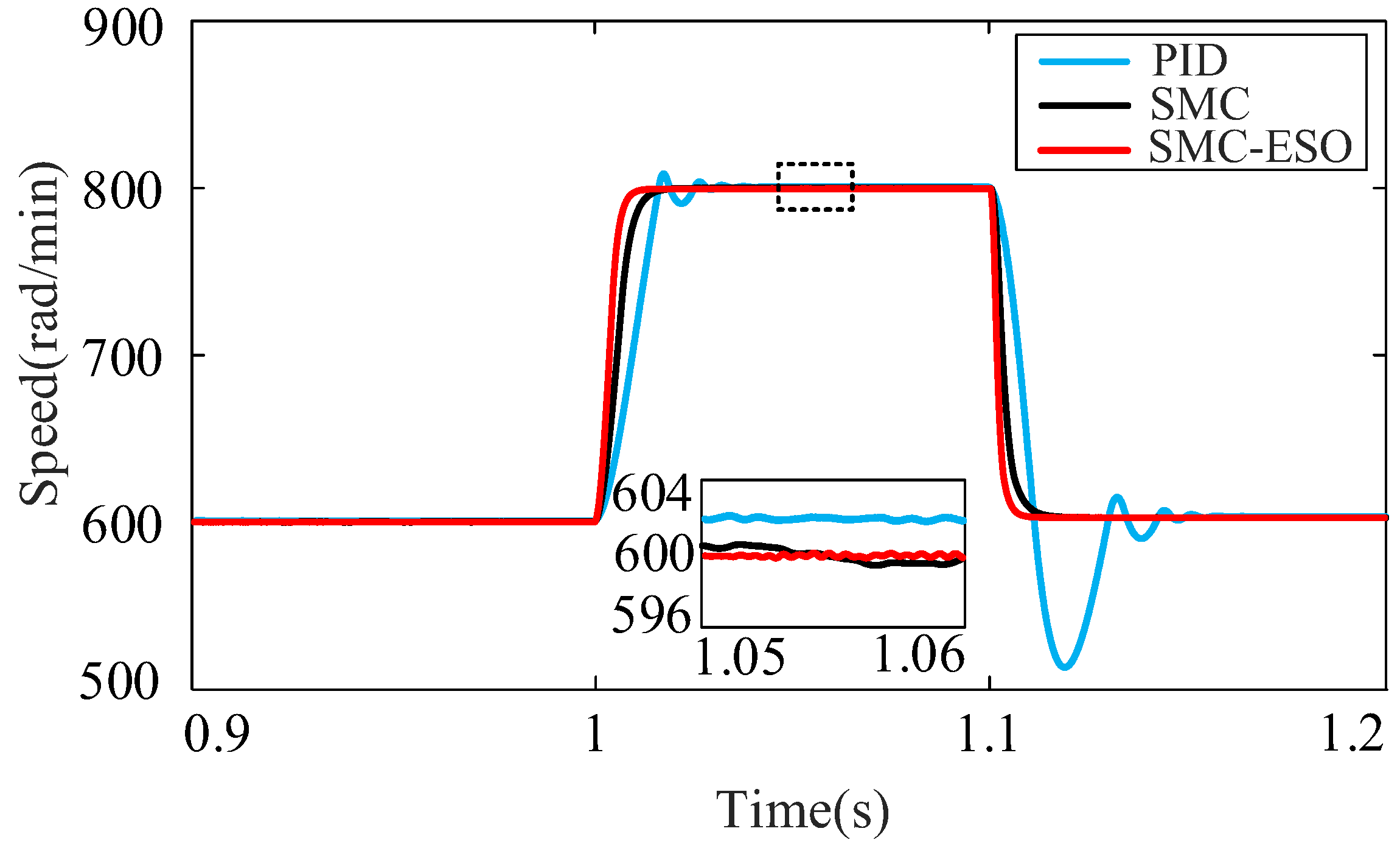
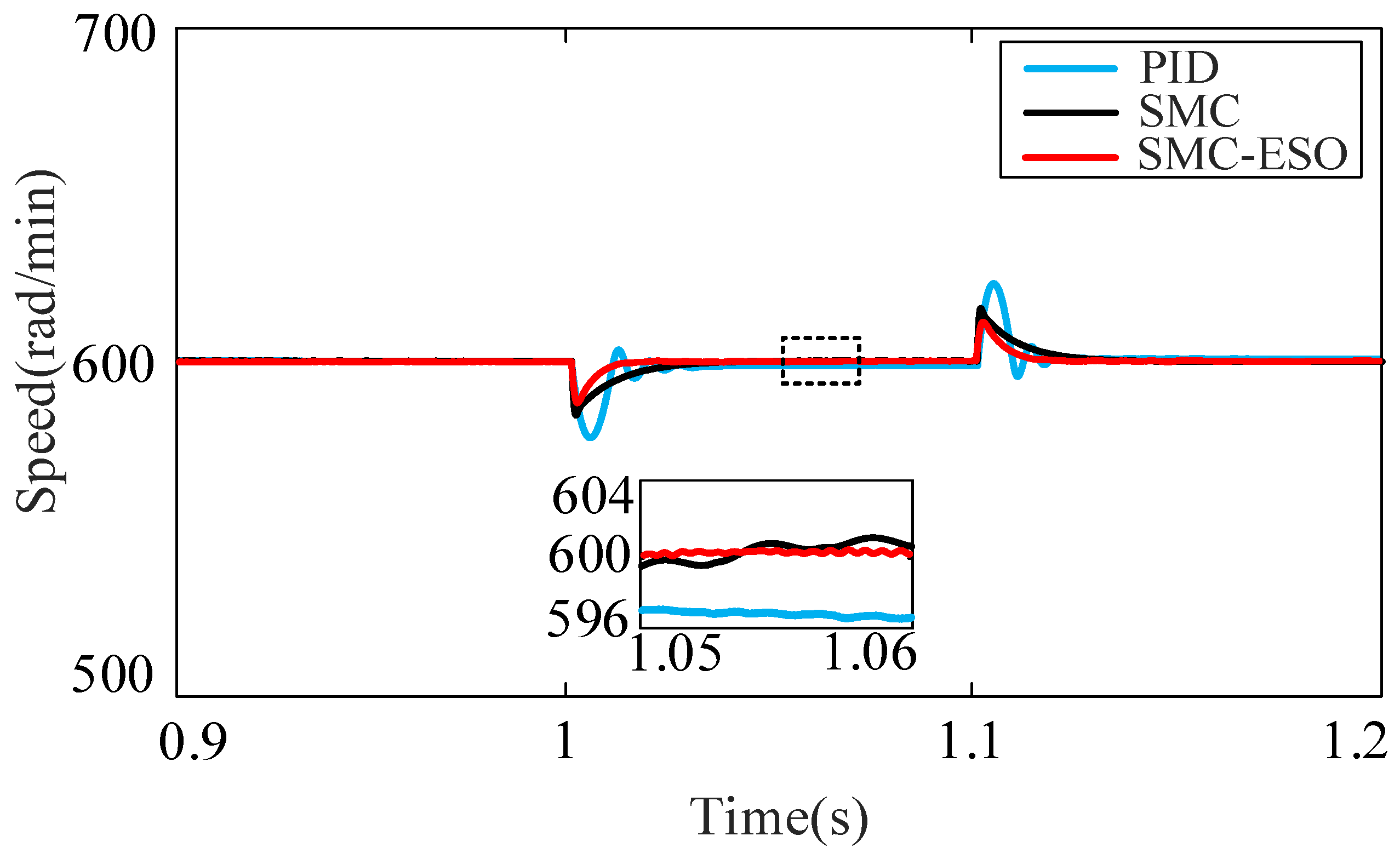
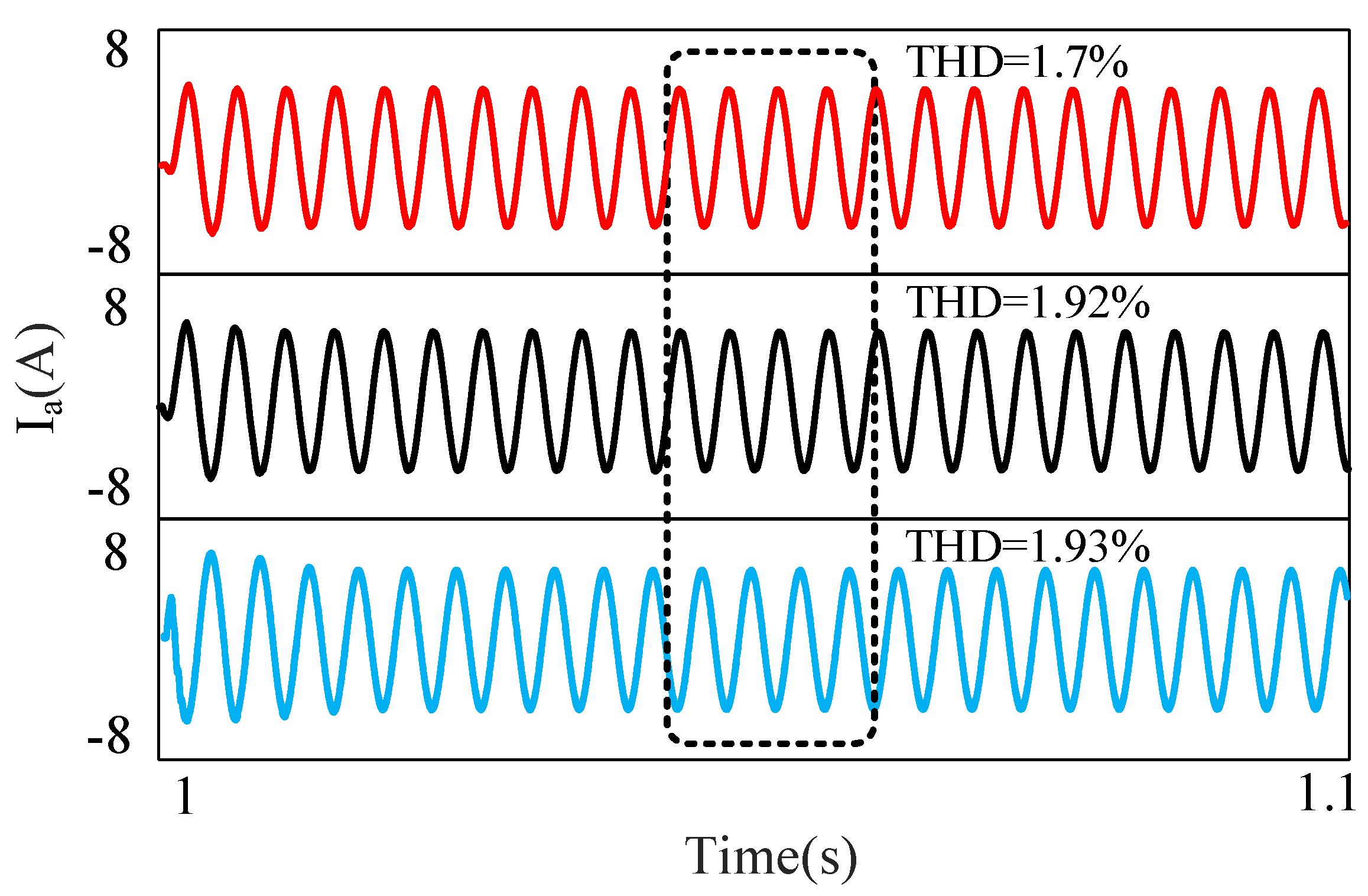
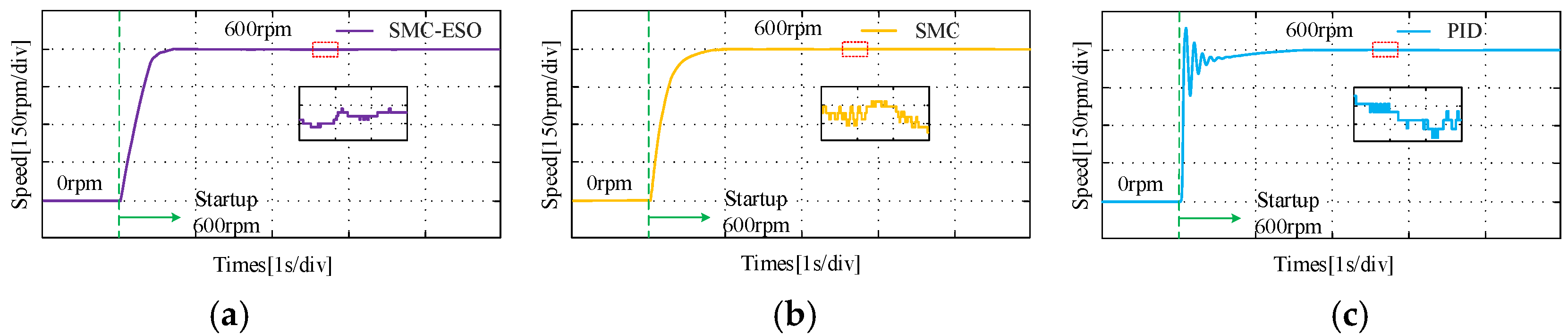
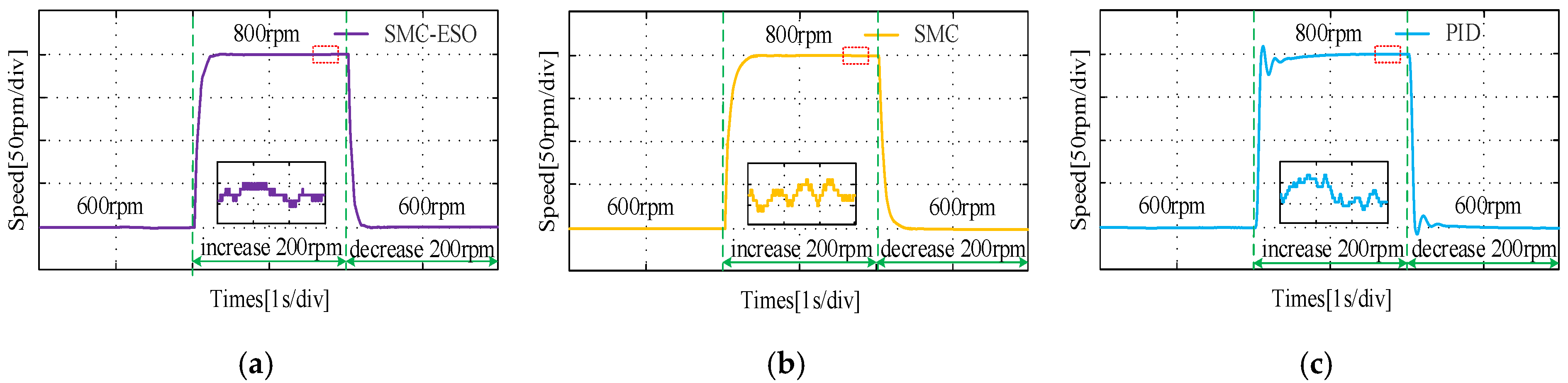
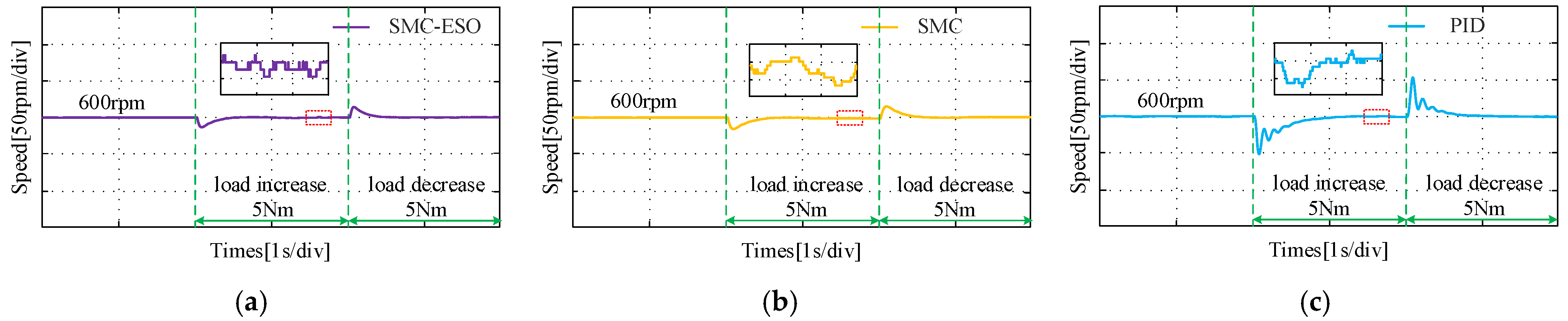
4. Simulation and Experimental Analysis
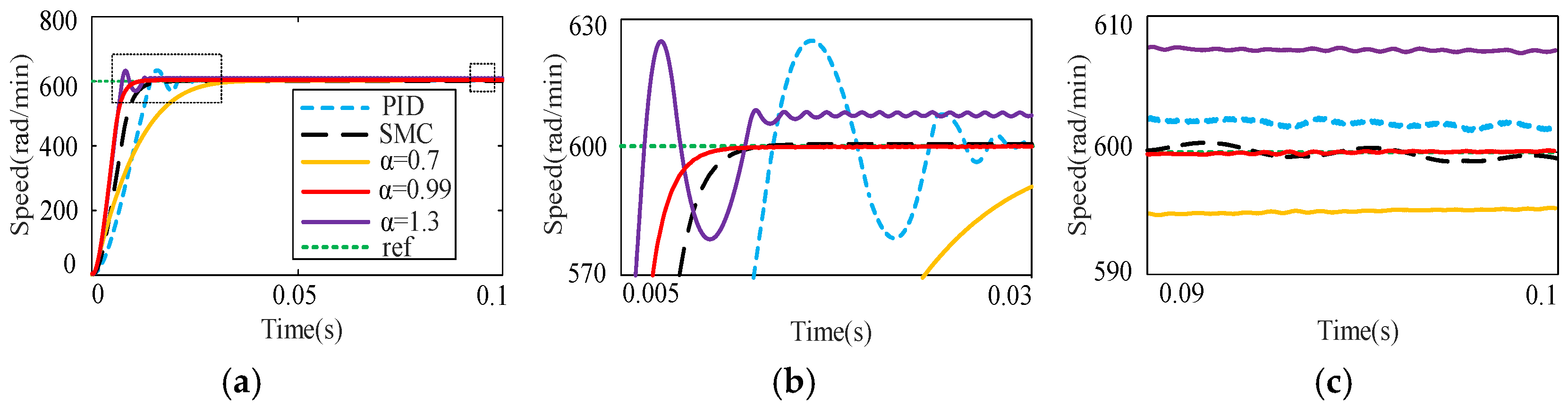
4.1. Analysis of Simulation
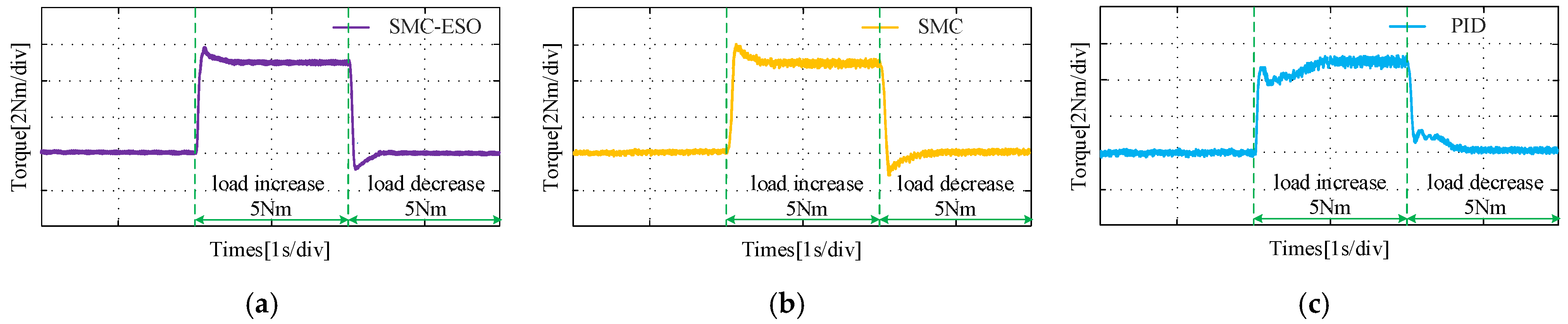
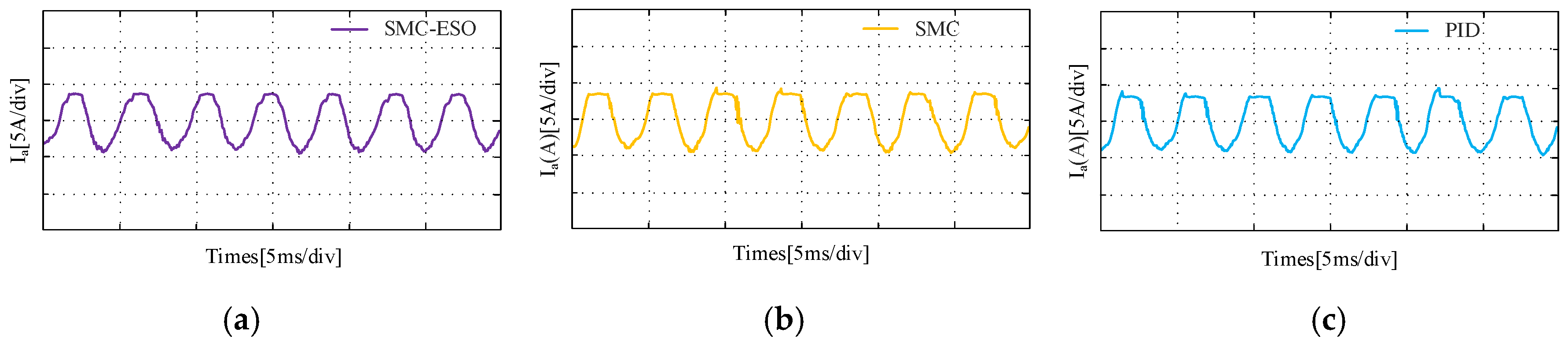
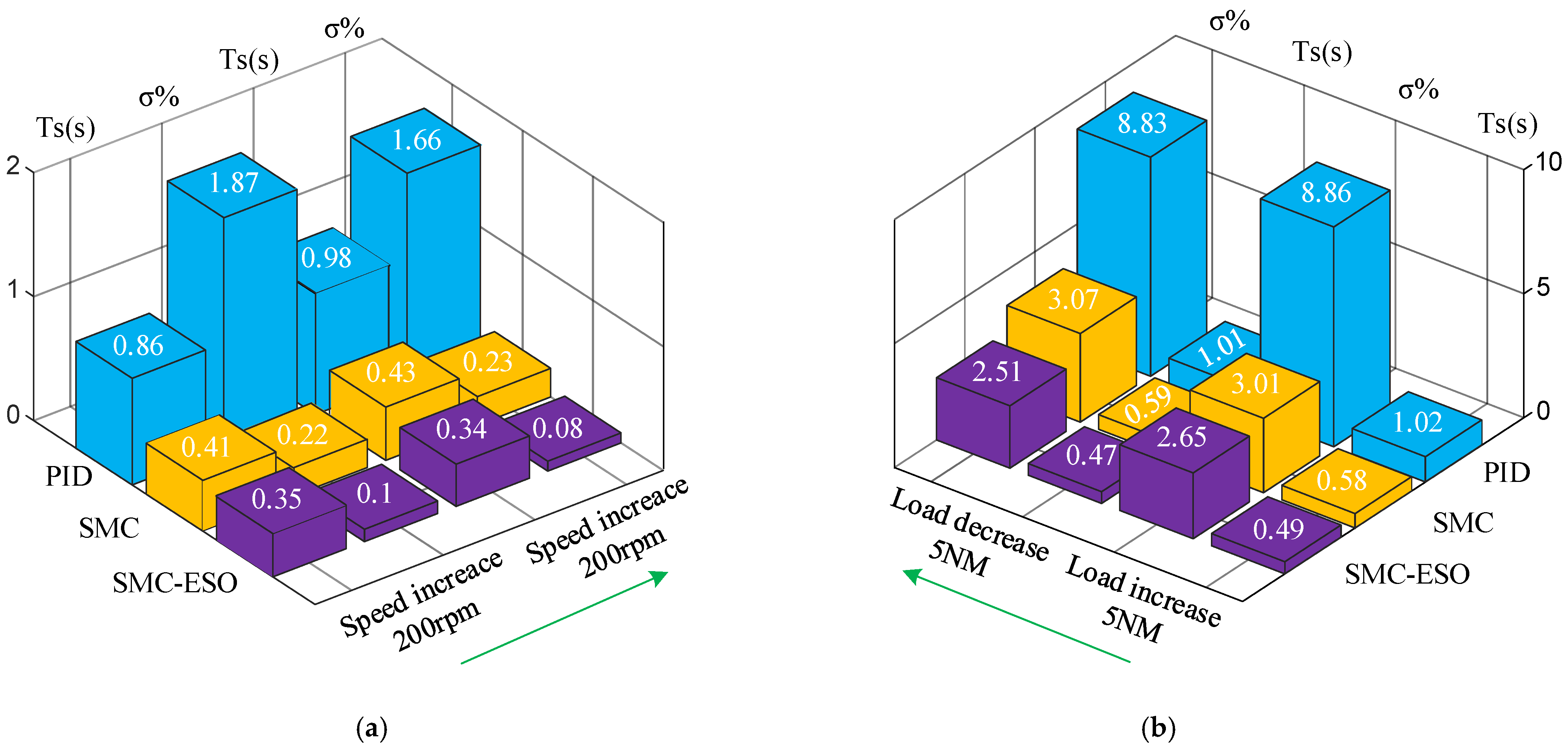
4.2. Results of Experimental
5. Conclusions
- (1)
- Due to the motion trajectory of sliding mode control moving back and forth on the sliding surface and eventually converging to a steady state, it is prone to jitter and vibration.
- (2)
- Real time observation and compensation of q-axis current by current observers can achieve stable control under interference and small jitter. Simulation and experimental results show that SMC-ESO improves dynamic and steady-state performance of PMSM.
- (3)
- Due to the current fluctuation observer, the motor can be used in more complex and high-precision operating environments, and this control method can be easily applied to practical industries without additional implementation costs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dong, H.; Yang, X.; Gao, H.; Yu, X. Practical Terminal Sliding-Mode Control and Its Applications in Servo Systems. IEEE Trans. Ind. Electron. 2023, 70, 752–761. [Google Scholar] [CrossRef]
- Wang, H.; Li, S.; Yang, J.; Zhou, X. Continuous Sliding Mode Control for Permanent Magnet Synchronous Motor Speed Regulation Systems Under Time-Varying Disturbances. J. Power Electron. 2016, 16, 1324–1335. [Google Scholar] [CrossRef]
- Apte, A.; Joshi, V.A.; Mehta, H.; Walambe, R. Disturbance-Observer-Based Sensorless Control of PMSM Using Integral State Feedback Controller. IEEE Trans. Power Electron. 2020, 35, 6082–6090. [Google Scholar] [CrossRef]
- Zhang, Y.; Yin, Z.; Zhang, Y.; Liu, J.; Tong, X. A Novel Sliding Mode Observer with Optimized Constant Rate Reaching Law for Sensorless Control of Induction Motor. IEEE Trans. Ind. Electron. 2020, 67, 5867–5878. [Google Scholar] [CrossRef]
- Tian, M.; Wang, B.; Yu, Y.; Dong, Q.; Xu, D. Discrete-Time Repetitive Control-Based ADRC for Current Loop Disturbances Suppression of PMSM Drives. IEEE Trans. Ind. Inform. 2022, 18, 3138–3149. [Google Scholar] [CrossRef]
- Abu-Ali, M.; Berkel, F.; Manderla, M.; Reimann, S.; Kennel, R.; Abdelrahem, M. Deep Learning-Based Long-Horizon MPC: Robust, High Performing, and Computationally Efficient Control for PMSM Drives. IEEE Trans. Power Electron. 2022, 37, 12486–12501. [Google Scholar] [CrossRef]
- Pang, S.; Zhang, Y.; Huangfu, Y.; Li, X.; Tan, B.; Li, P.; Tian, C.; Quan, S. A Virtual MPC-Based Artificial Neural Network Controller for PMSM Drives in Aircraft Electric Propulsion System. IEEE Trans. Ind. Appl. 2024, 60, 3603–3612. [Google Scholar] [CrossRef]
- Li, H.; Wang, S.; Xie, Y.; Zheng, S.; Shi, P. Virtual Reference-Based Fuzzy Noncascade Speed Control for PMSM Systems with Unmatched Disturbances and Current Constraints. IEEE Trans. Fuzzy Syst. 2023, 31, 4249–4261. [Google Scholar] [CrossRef]
- Chaoui, H.; Khayamy, M.; Aljarboua, A.A. Adaptive Interval Type-2 Fuzzy Logic Control for PMSM Drives with a Modified Reference Frame. IEEE Trans. Ind. Electron. 2017, 64, 3786–3797. [Google Scholar] [CrossRef]
- El-Sousy, F.F.M.; Amin, M.M.; Al-Durra, A. Adaptive Optimal Tracking Control Via Actor-Critic-Identifier Based Adaptive Dynamic Programming for Permanent-Magnet Synchronous Motor Drive System. IEEE Trans. Ind. Appl. 2021, 57, 6577–6591. [Google Scholar] [CrossRef]
- Zuo, Y.; Lai, C.; Galkina, A.; Grossbichler, M.; Iyer, L.V. Adaptive Current Observer Design for Single Current Sensor Control in PMSM Drives. IEEE Trans. Transport. Electrif. 2024, 10, 6928–6939. [Google Scholar] [CrossRef]
- Tang, P.; Zhao, Z.; Li, H. Short-Term Prediction Method of Transient Temperature Field Variation for PMSM in Electric Drive Gearbox Using Spatial-Temporal Relational Graph Convolutional Thermal Neural Network. IEEE Trans. Ind. Electron. 2024, 71, 7839–7852. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Nguyen, T.T.; Nguyen, V.Q.; Le, K.M.; Tran, H.N.; Jeon, J.W. An Adaptive Sliding-Mode Controller with a Modified Reduced-Order Proportional Integral Observer for Speed Regulation of a Permanent Magnet Synchronous Motor. IEEE Trans. Ind. Electron. 2022, 69, 7181–7191. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, L.; Ji, W. Improved Non-Singular Fast Terminal Sliding Mode Control with Disturbance Observer for PMSM Drives. IEEE Trans. Transport. Electrif. 2021, 7, 2753–2762. [Google Scholar] [CrossRef]
- Li, S.; Zhou, M.; Yu, X. Design and Implementation of Terminal Sliding Mode Control Method for PMSM Speed Regulation System. IEEE Trans. Ind. Inform. 2013, 9, 1879–1891. [Google Scholar] [CrossRef]
- Hu, Q.; Liu, L.; Yang, H. A sliding mode speed controller based on novel reaching law of permanent magnet synchronous motor system. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 954–958. [Google Scholar]
- Junejo, A.K.; Xu, W.; Mu, C.; Ismail, M.M.; Liu, Y. Adaptive Speed Control of PMSM Drive System Based a New Sliding-Mode Reaching Law. IEEE Trans. Power Electron. 2020, 35, 12110–12121. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, X.; Wang, W.; Chen, K.; Cheung, N.C.; Pan, J. Enhanced Sliding Mode Control for PMSM Speed Drive Systems Using a Novel Adaptive Sliding Mode Reaching Law Based on Exponential Function. IEEE Trans. Ind. Electron. 2024, 71, 11978–11988. [Google Scholar] [CrossRef]
- Guo, X.; Huang, S.; Lu, K.; Peng, Y.; Wang, H.; Yang, J. A Fast Sliding Mode Speed Controller for PMSM Based on New Compound Reaching Law With Improved Sliding Mode Observer. IEEE Trans. Transport. Electrif. 2023, 9, 2955–2968. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, Y.; Zhang, X.; Liang, J.; Cheng, X. New Reaching Law Control for Permanent Magnet Synchronous Motor with Extended Disturbance Observer. IEEE Access 2019, 7, 186296–186307. [Google Scholar] [CrossRef]
- Xu, W.; Qu, S.; Zhang, C. Fast Terminal Sliding Mode Current Control with Adaptive Extended State Disturbance Observer for PMSM System. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 418–431. [Google Scholar] [CrossRef]
- Long, K.; Zhang, X.; Xi, Z.; Li, N. Neural network sliding mode control based on improved fruit-fly optimization algorithm for permanent magnet synchronous motor systems. In Proceedings of the 2022 5th International Conference on Advanced Electronic Materials, Computers and Software Engineering (AEMCSE), Wuhan, China, 22–24 April 2022; pp. 488–491. [Google Scholar]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
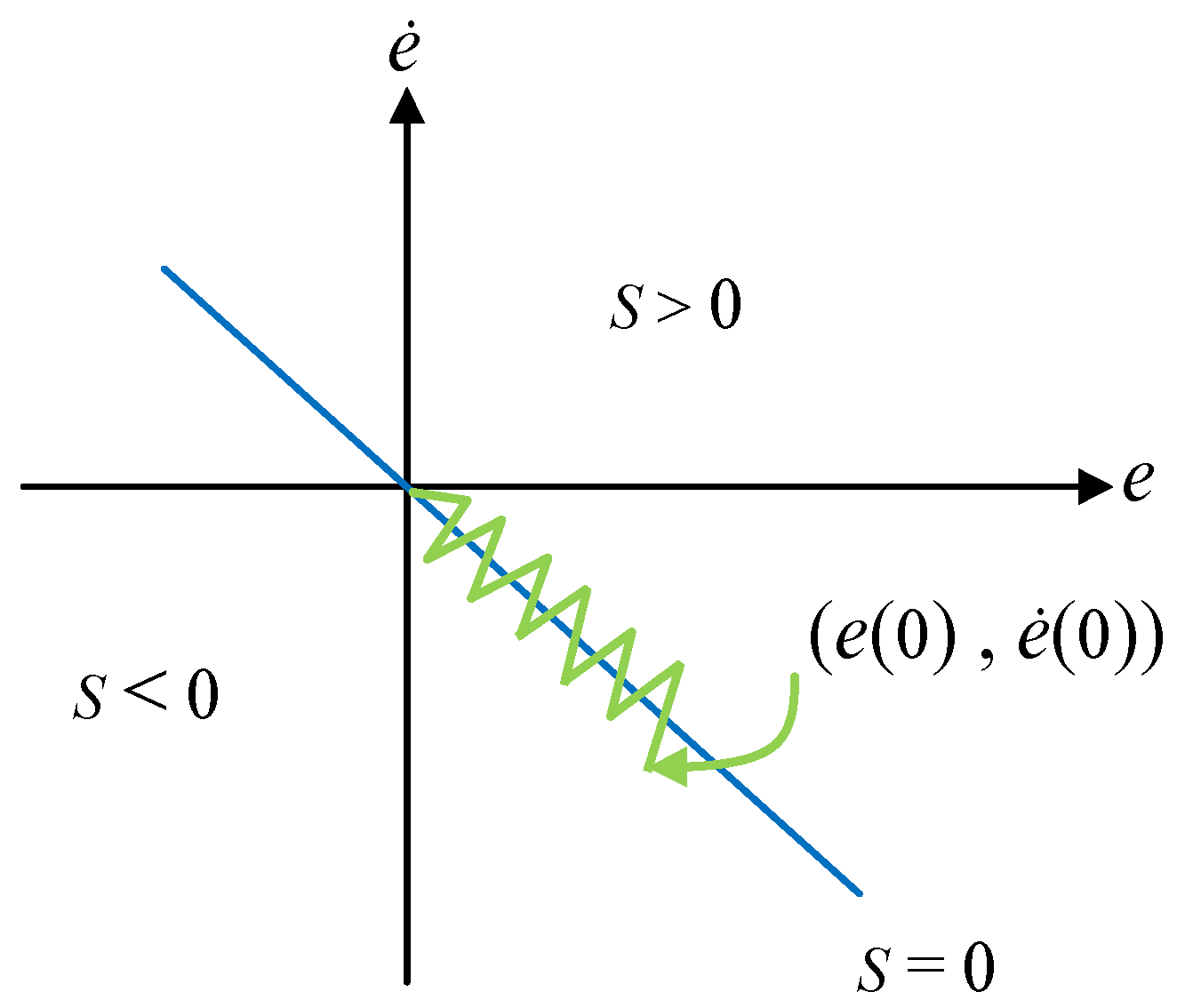

| Parameter | Value |
|---|---|
| Stator phase resistance (Rs) | 2.875 Ω |
| Inductance (Ld) | 8.5 × 10−3 H |
| Inductance (Lq) | 8.5 × 10−3 H |
| Flux linkage (Ψf) | 0.175 Wb |
| Inertia (J) | 1.6 × 10−3 kg·m2 |
| Pole pairs (p) | 4 |
| Viscous friction coefficient (B) | 3 × 10−4 N·m·s/rad |
| Control Structure | Control Parameters | |
|---|---|---|
| Speed Control | SMC | c = 50 k = 25 d = −1 ε = 30 A = 12,500 |
| ESO | α = 0.99 δ = 0.01 b0 = 12,500 β1 = 3000 β2 = 3000 | |
| Current Control | PI | Kpq = 2 Kiq = 1 Kpd = 2 Kid = 1 |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Rated Power | 6 KW | Rated Speed | 800 rpm |
| Rated Voltage | 144 V | Rated Torque | 35 Nm |
| Rated Current | 50 A | Number of pole pairs | 24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Zhong, G.; Hu, L.; Gong, P.; Li, G. A Real-Time Demanded Current Observation-Based Sliding Mode Control of Permanent Magnet Synchronous Motors. Machines 2025, 13, 146. https://doi.org/10.3390/machines13020146
Li G, Zhong G, Hu L, Gong P, Li G. A Real-Time Demanded Current Observation-Based Sliding Mode Control of Permanent Magnet Synchronous Motors. Machines. 2025; 13(2):146. https://doi.org/10.3390/machines13020146
Chicago/Turabian StyleLi, Guangping, Guolong Zhong, Likun Hu, Pingping Gong, and Gaoxiang Li. 2025. "A Real-Time Demanded Current Observation-Based Sliding Mode Control of Permanent Magnet Synchronous Motors" Machines 13, no. 2: 146. https://doi.org/10.3390/machines13020146
APA StyleLi, G., Zhong, G., Hu, L., Gong, P., & Li, G. (2025). A Real-Time Demanded Current Observation-Based Sliding Mode Control of Permanent Magnet Synchronous Motors. Machines, 13(2), 146. https://doi.org/10.3390/machines13020146






