The Secondary Lifting Performance of Crawler Crane Under Delay Coefficient Control Strategy
Abstract
1. Introduction
2. Crane Principle
2.1. Crane Working Mode
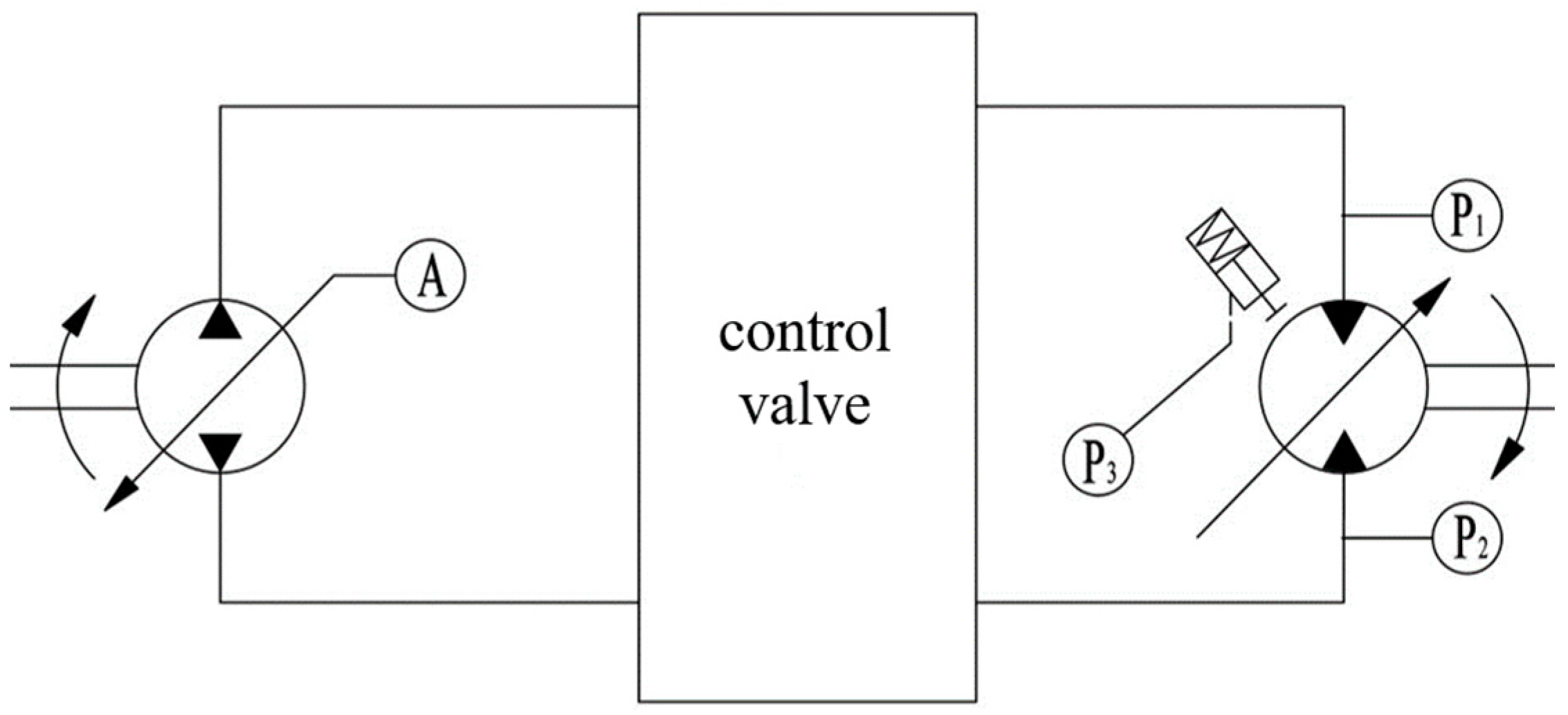
2.2. Mathematical Modeling of Secondary Lifting Systems
2.3. Analysis of Dynamic Characteristics of the Secondary Hoisting System
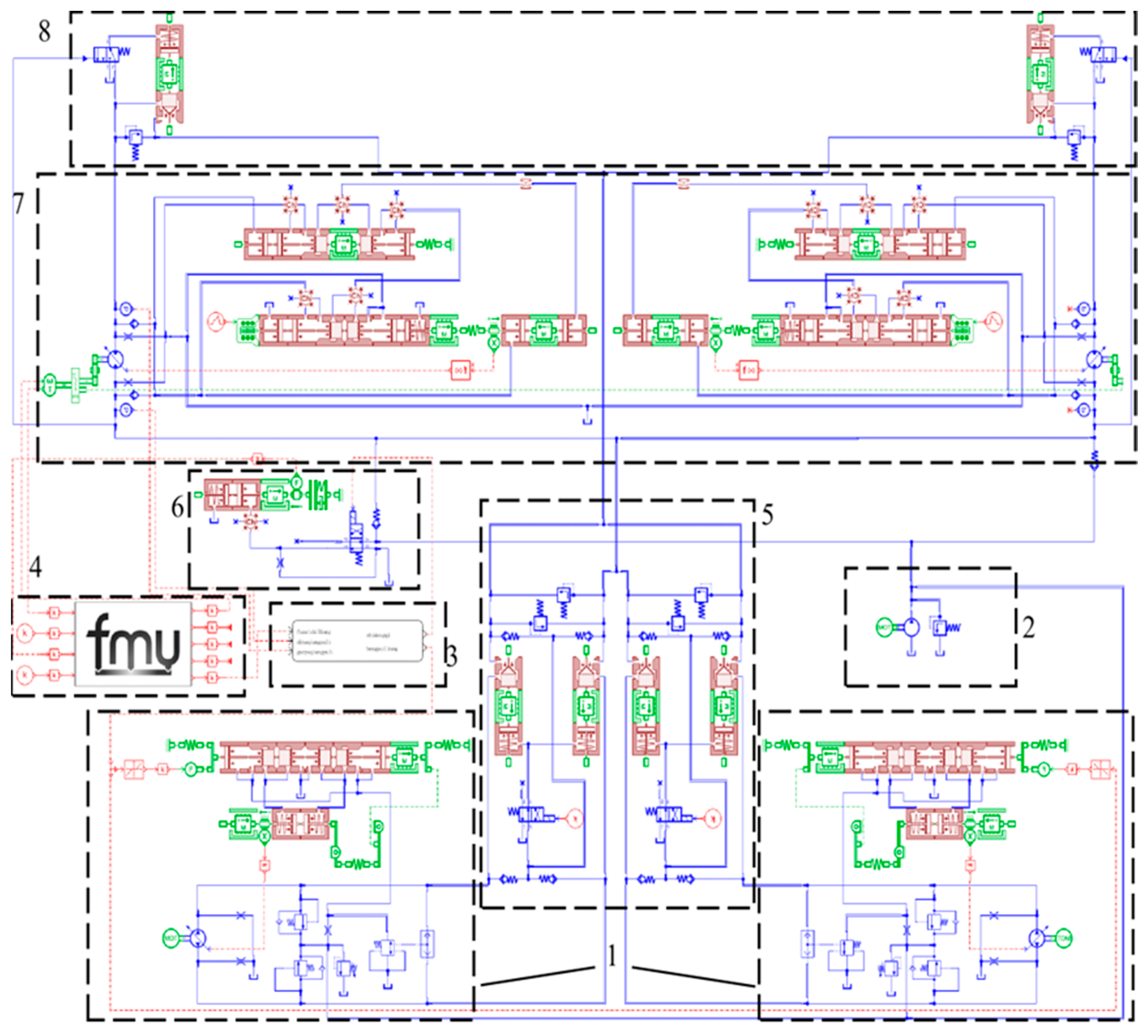
3. Electromechanical–Hydraulic Co-Simulation Modeling of Secondary Hoisting System
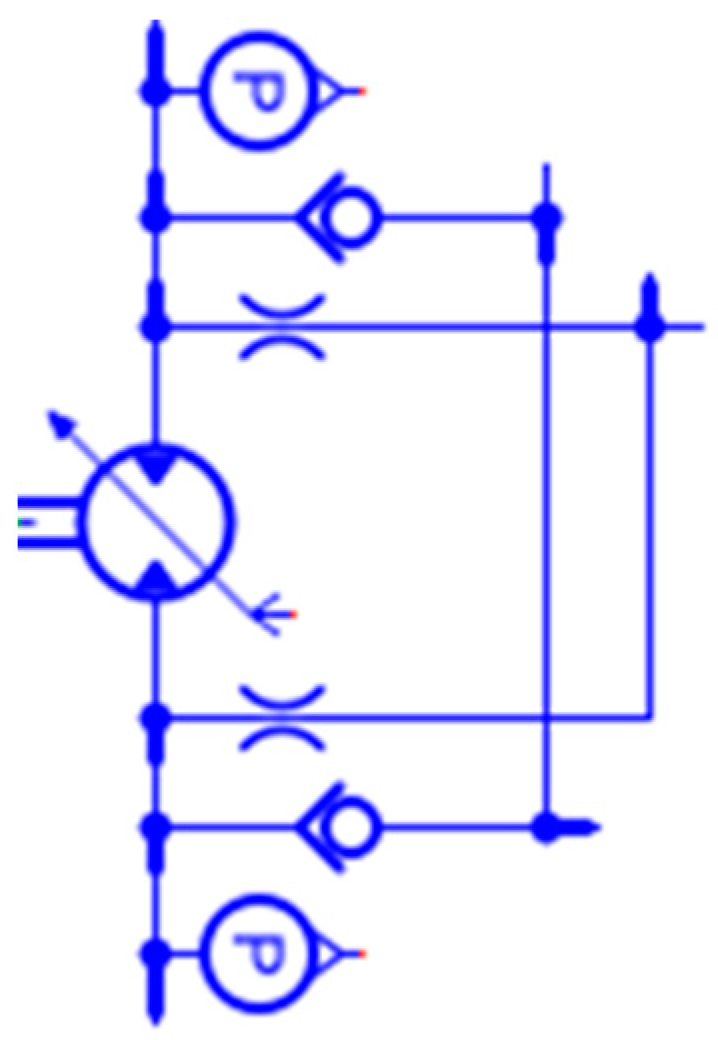
3.1. Simulation Model Establishment
3.1.1. Simulation Modeling of the Electric Control System of Lifting Mechanism
3.1.2. Mechanical Dynamics Simulation Modeling of Lifting Mechanism
3.1.3. Joint Simulation Model Establishment
3.2. Simulation Model Boundary Condition Setting
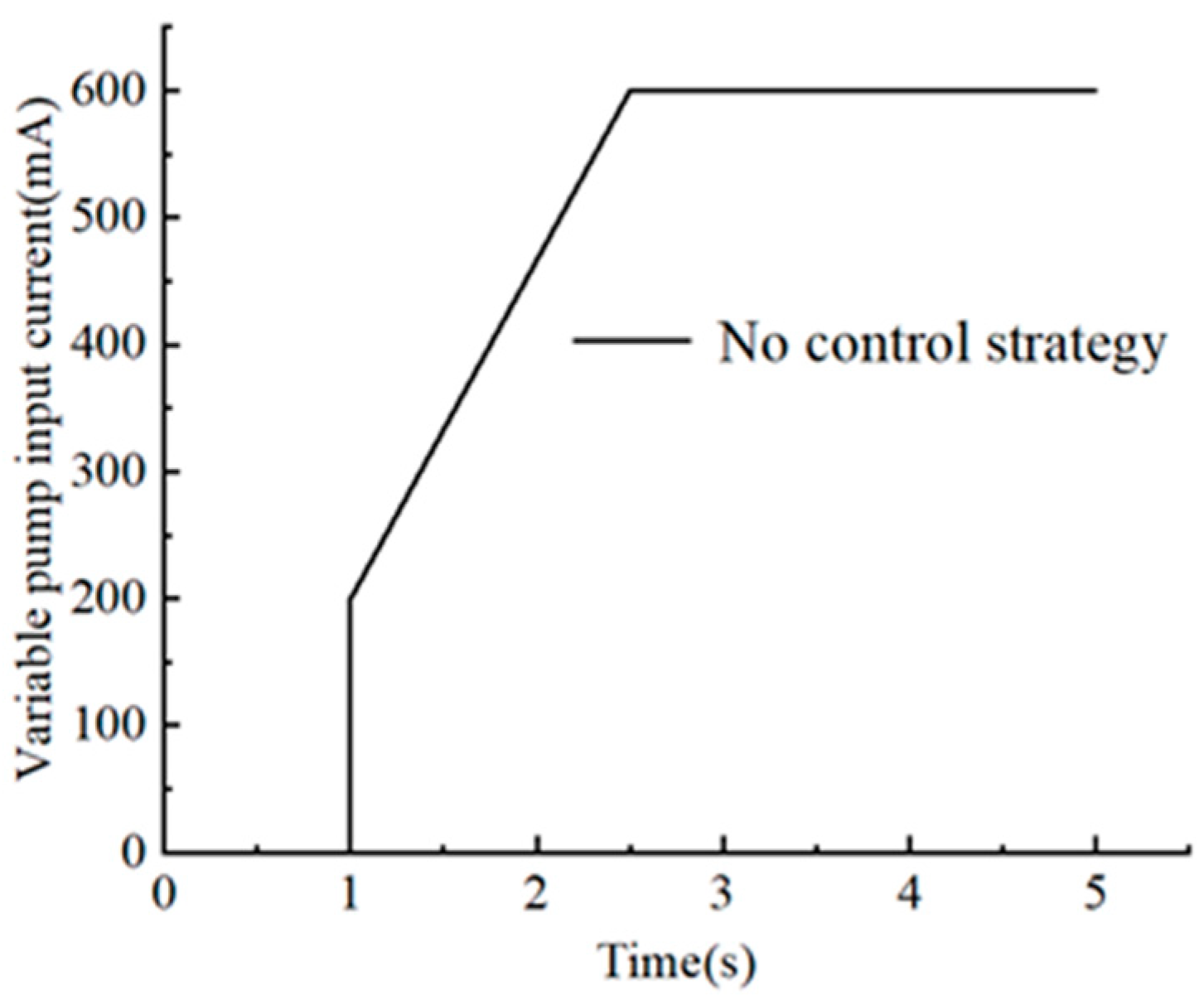
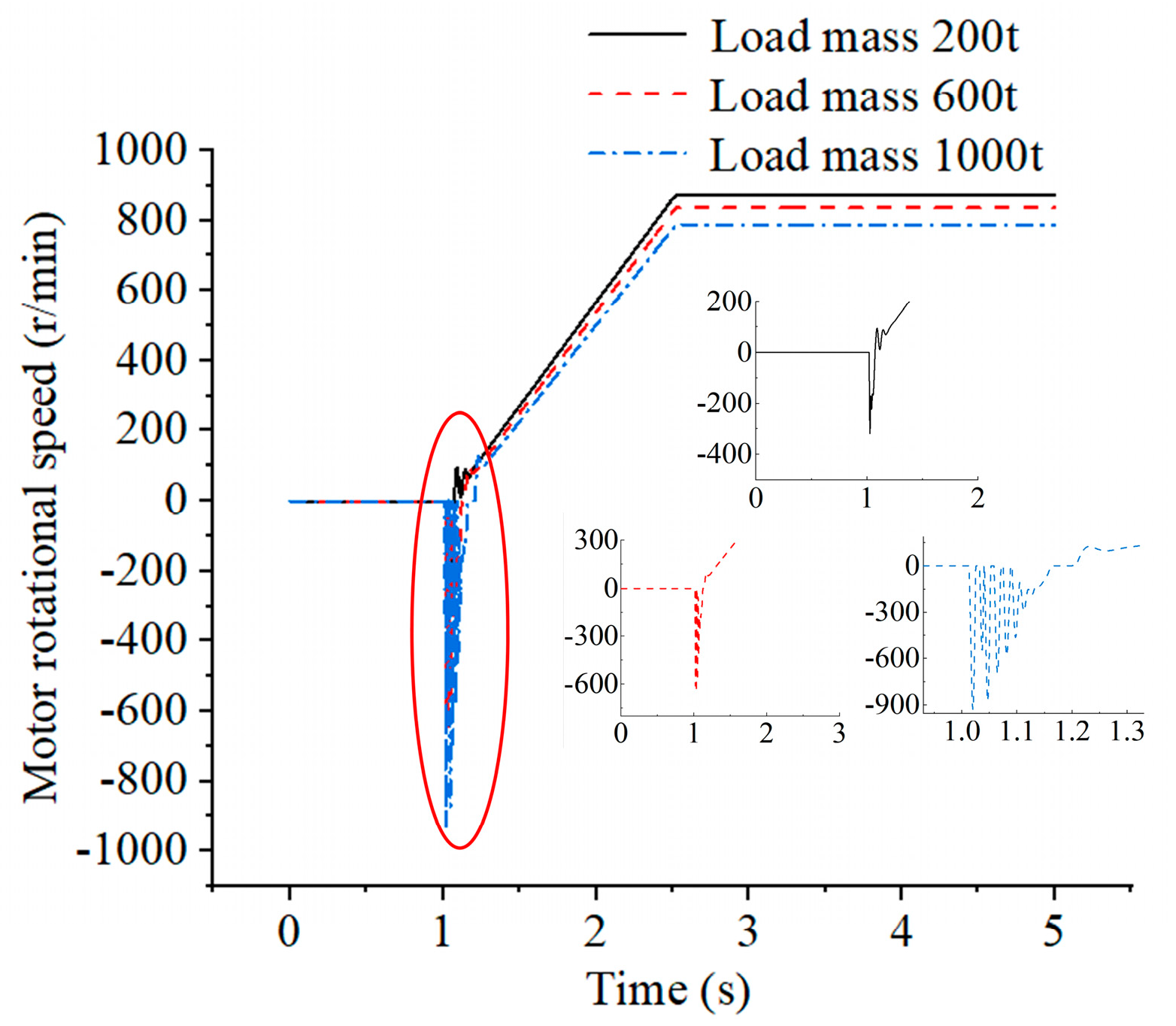
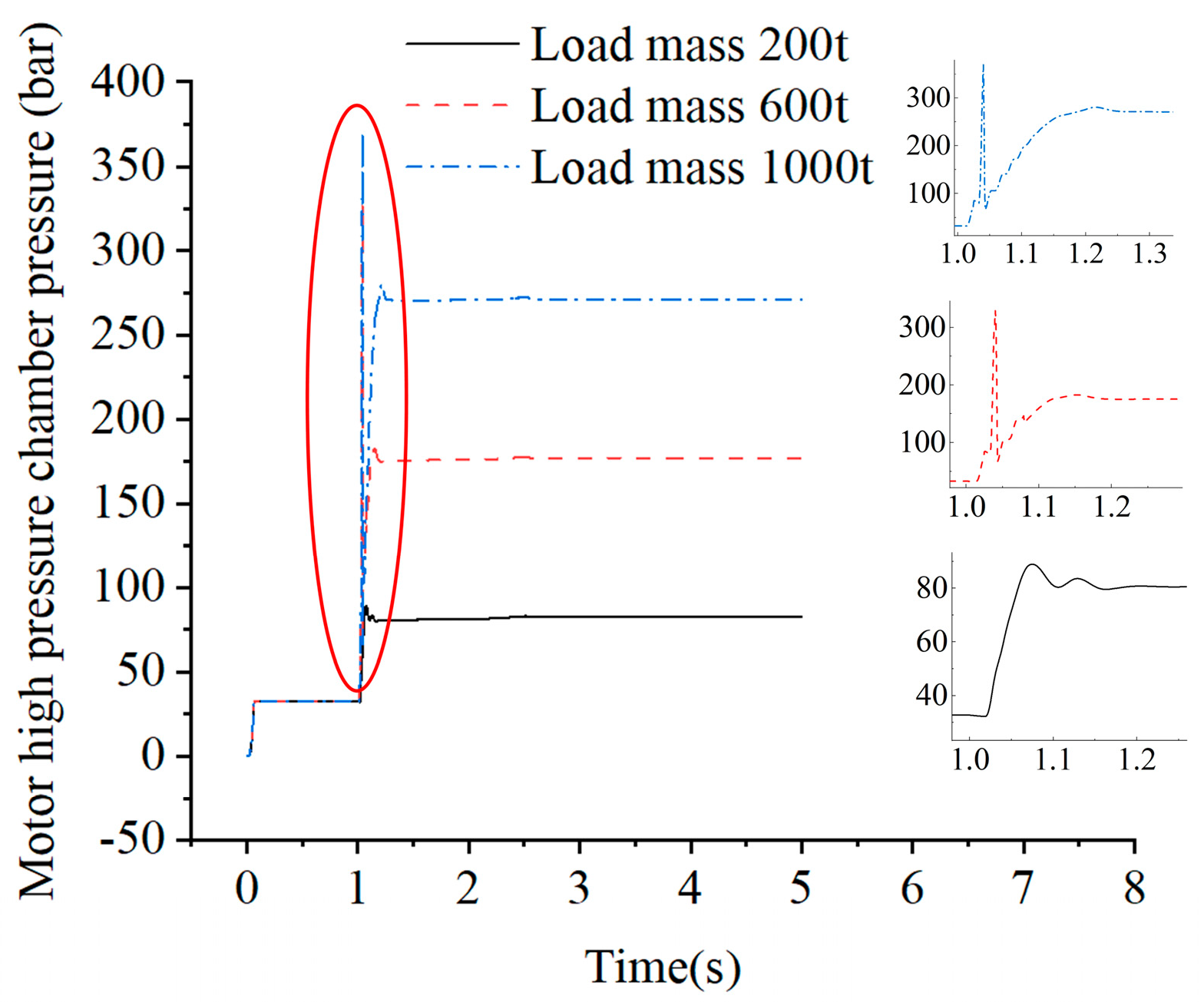
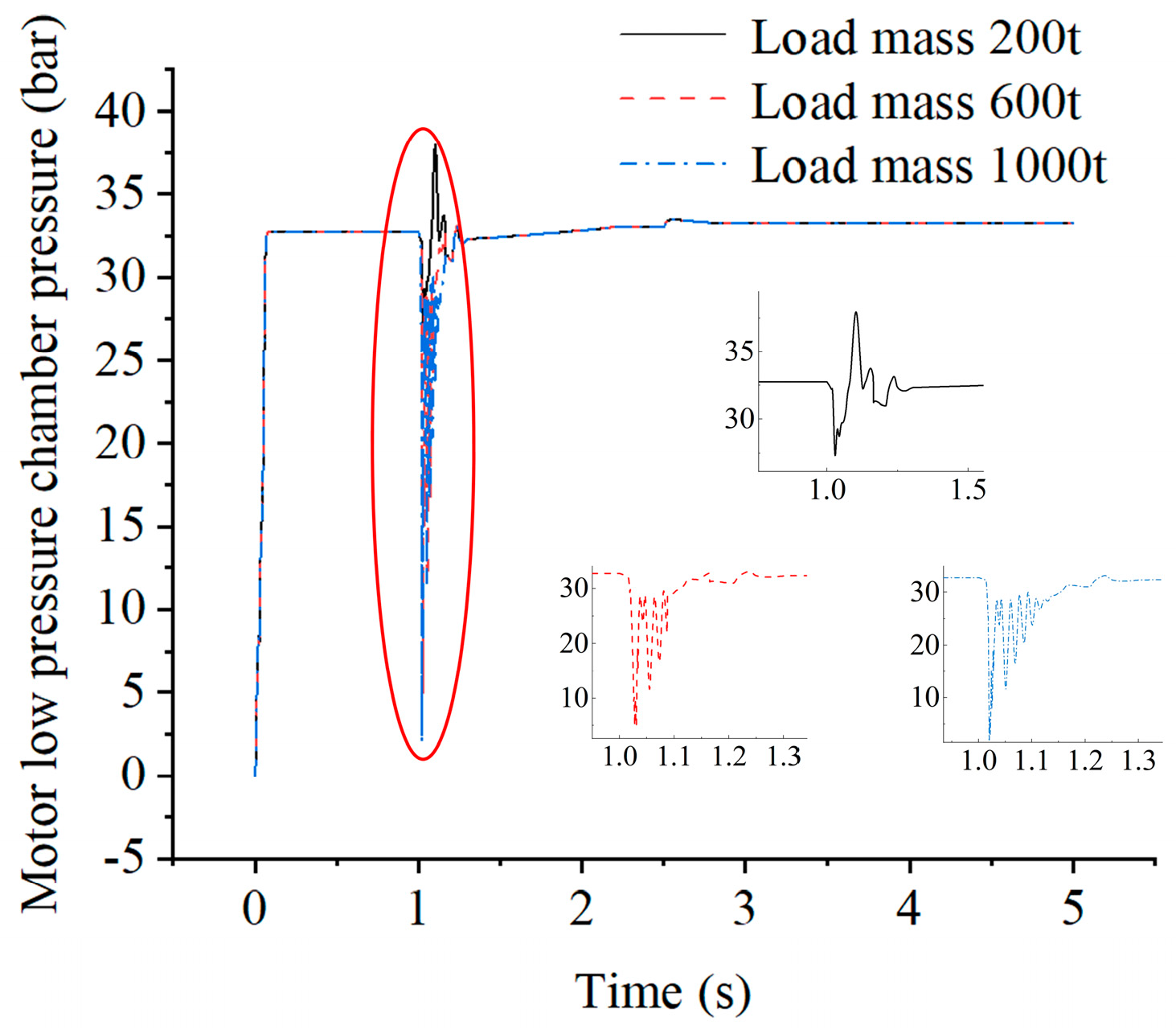
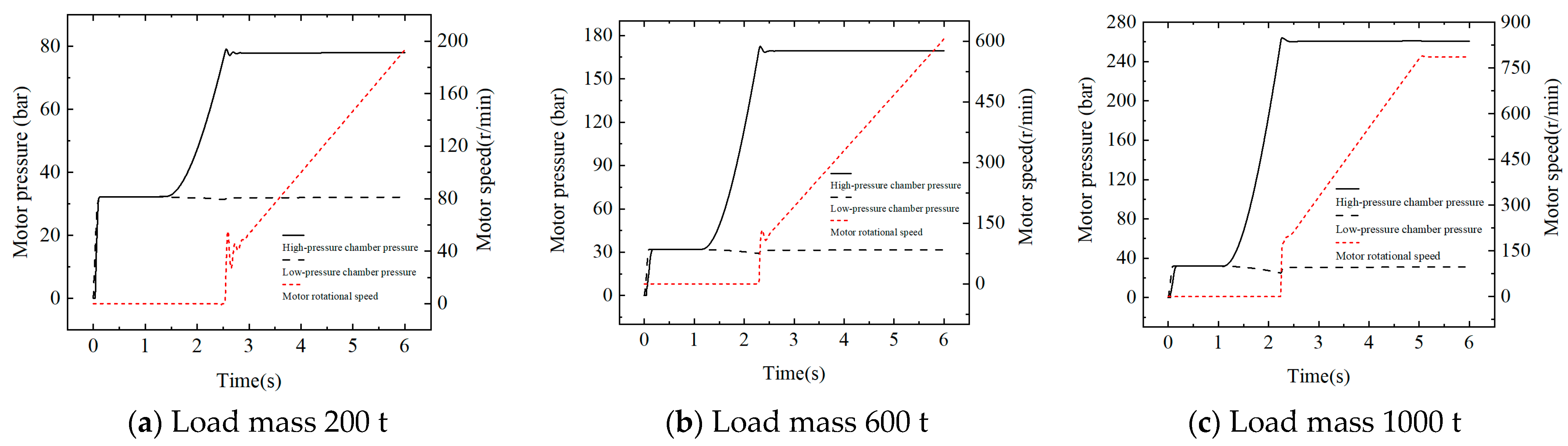
3.3. Simulation Without Control Strategy
4. Control Strategy Under the Influence of Delay Coefficient
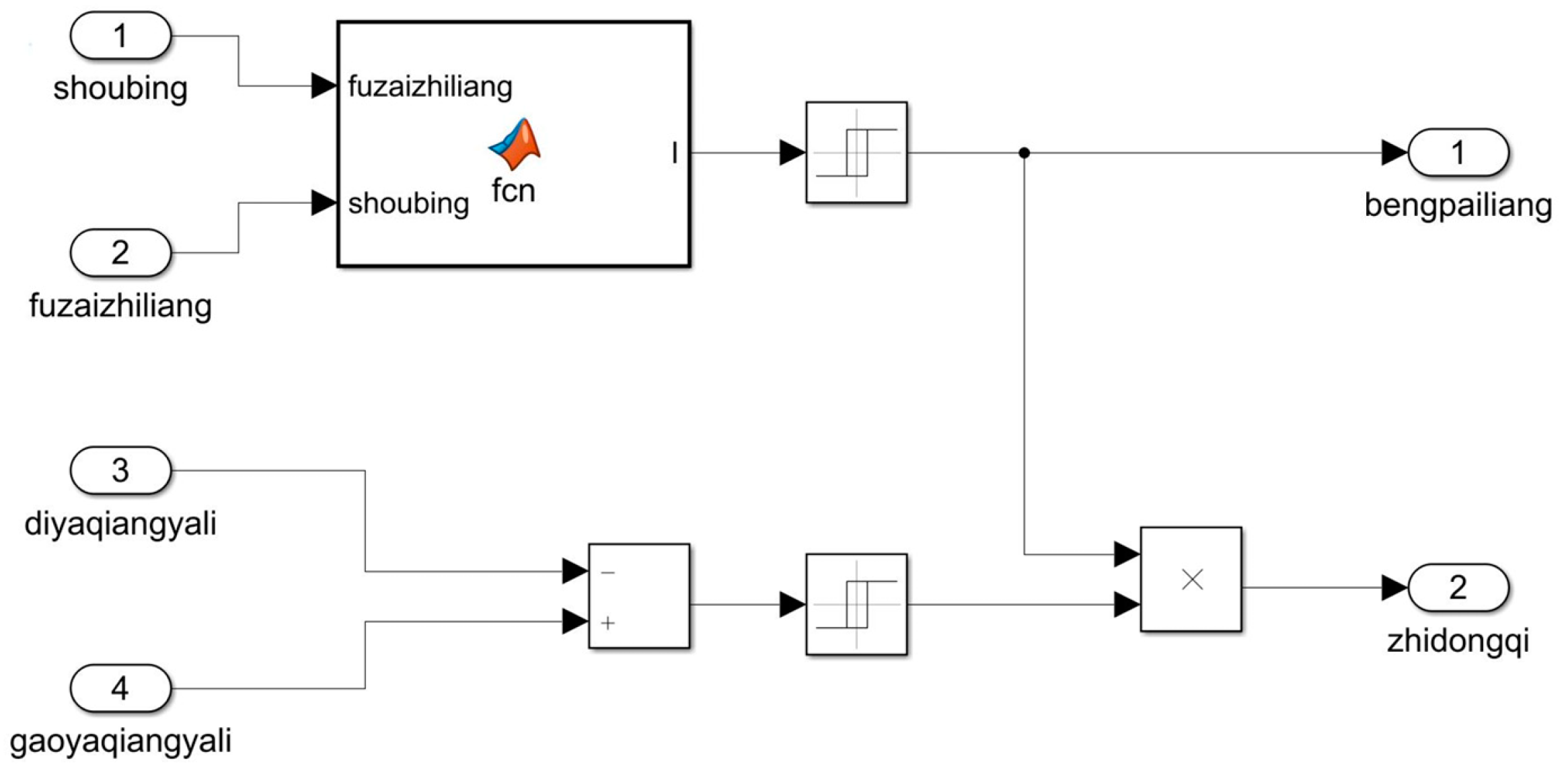
4.1. Control Strategy Design
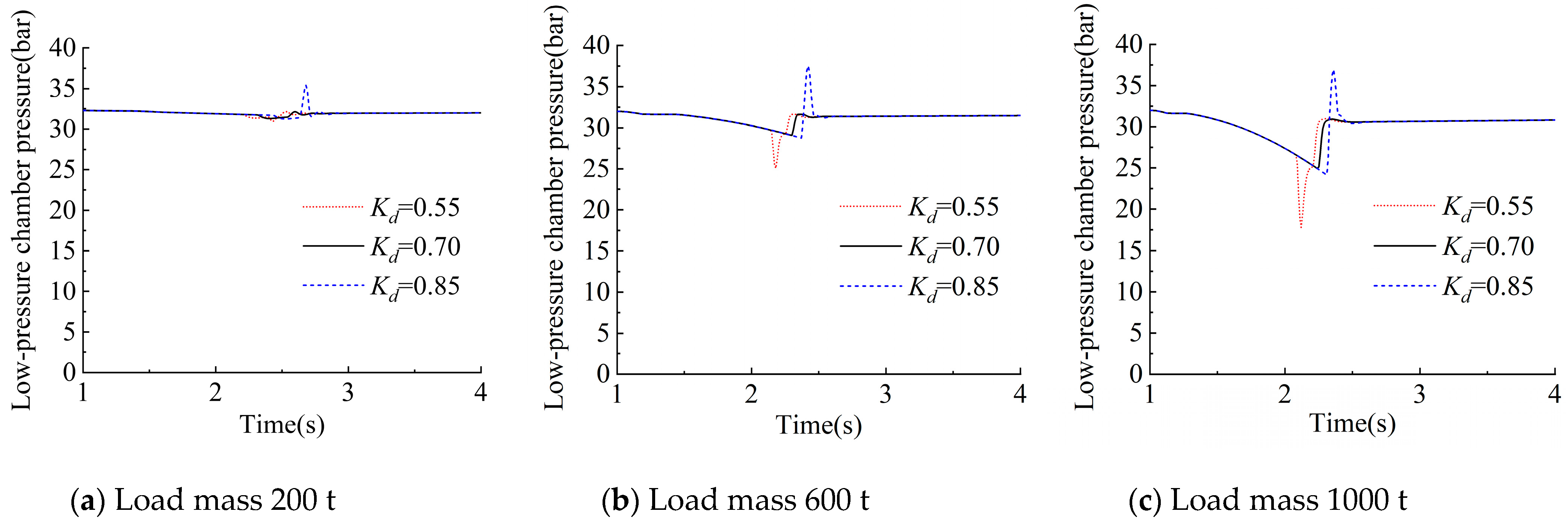
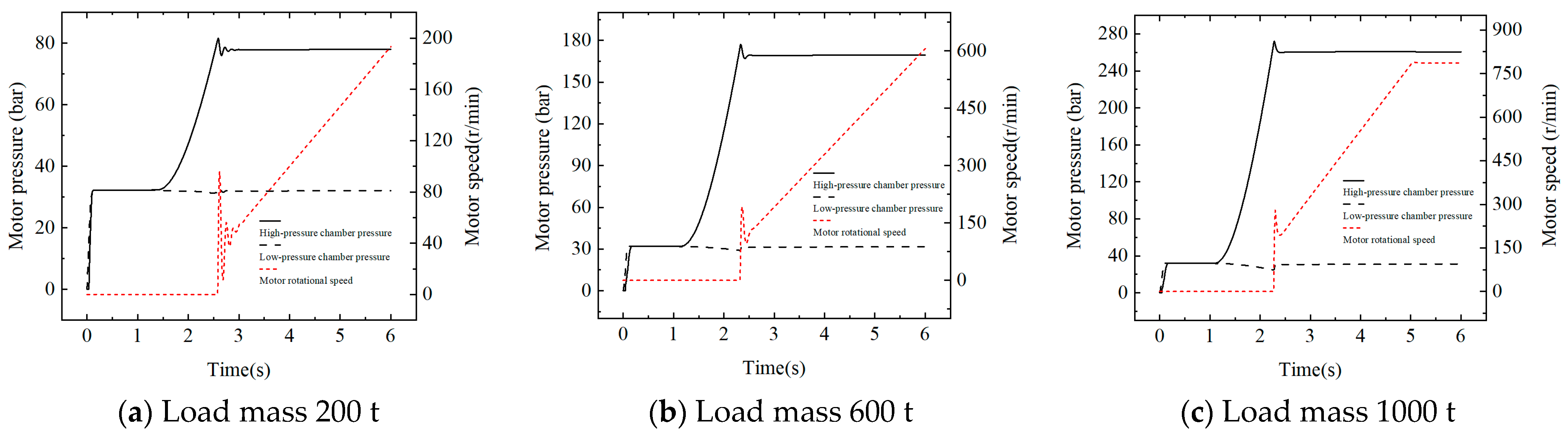
4.2. Simulation of Control Strategy
- (1)
- A simulation study on the influence of the dynamic performance of secondary lifting.
- (2)
- Simulation research on secondary lifting control strategy after adding interference.
5. Experimental Study of Secondary Lifting
5.1. Experimental Scheme
5.2. Experimental Test Results and Analysis of No Control Strategy
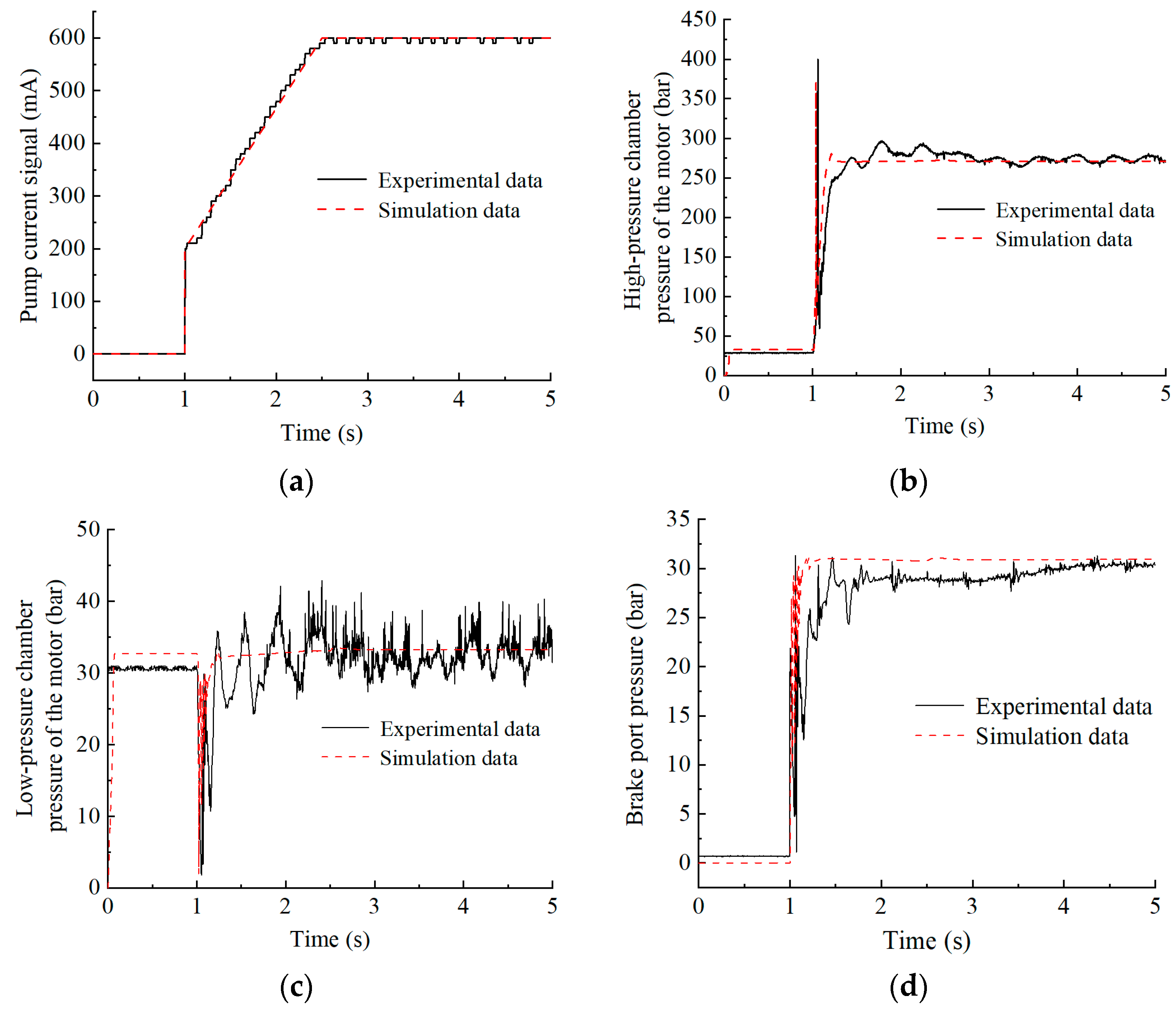
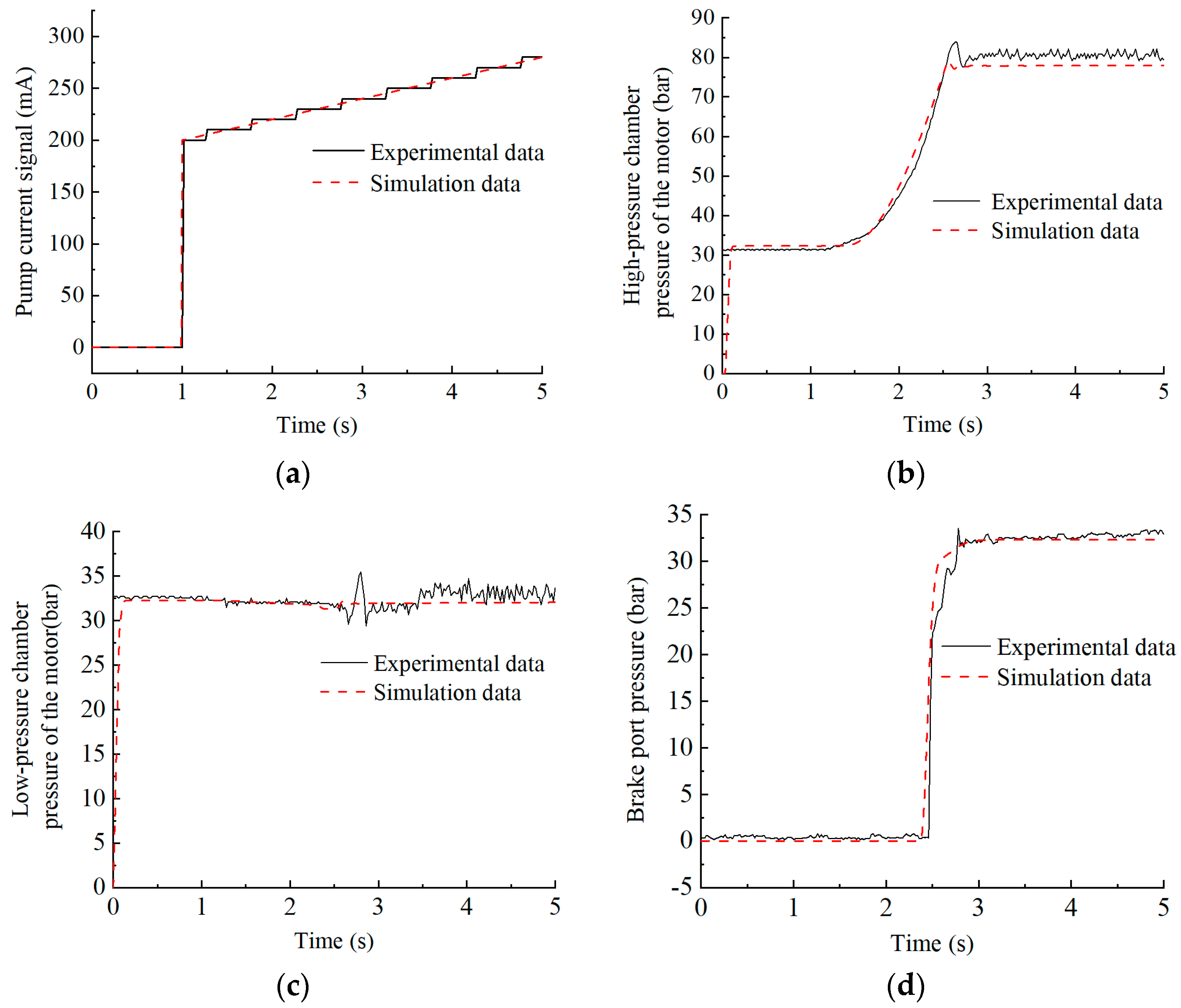
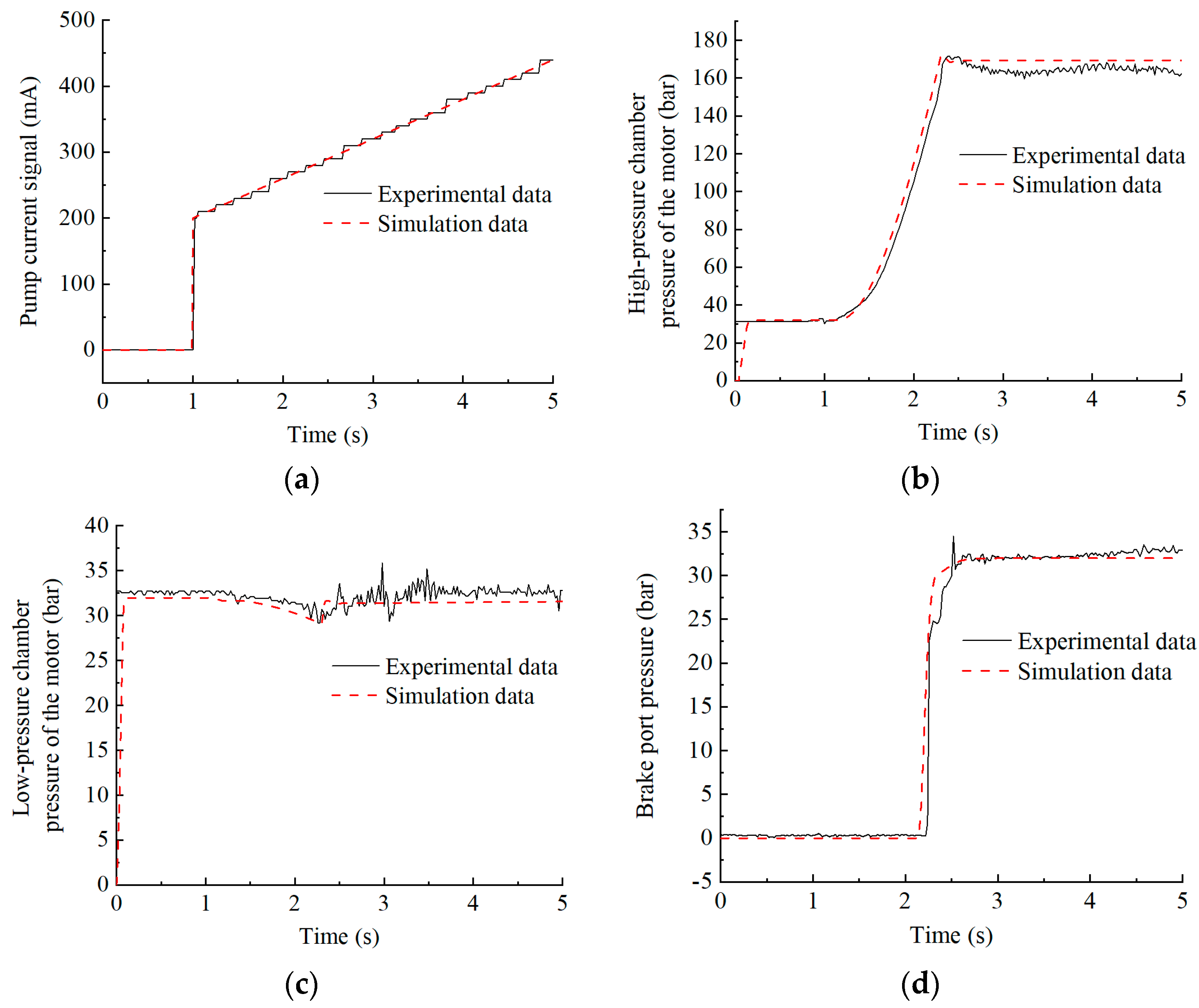
5.3. Experimental Test Analysis After Adding Control Strategy
6. Discussion
7. Conclusions
- (1)
- The secondary lifting performance of the crawler crane is analyzed using an electromechanical–hydraulic co-simulation platform, and the control strategy, which can adapt to different weights, is designed to solve the problem of secondary lifting and sliding.
- (2)
- Aiming at the problem of secondary lifting and sliding, a control strategy is designed and simulated. The anti-interference ability is analyzed by using a no-delay coefficient and considering the starting time of the motor. The secondary lifting experiment of the crawler crane is carried out. The experimental research is carried out without a control strategy and after adding a control strategy. The accuracy of the electromechanical–hydraulic co-simulation model is verified by comparing the experimental results with the simulation results.
- (3)
- The experimental data show that the proposed control strategy can effectively solve the problem of secondary lifting and sliding and has a good dynamic performance. Under different load conditions of 200–1000 t, the secondary lifting and sliding phenomenon did not appear in the control strategy. The average starting time of the motor was 1.32 s, and the average overshoot of the high-pressure chamber pressure of the motor was 1.75%. After adding interference, there was no secondary lifting and sliding phenomenon, and the over-shoot of the high-pressure chamber pressure did not exceed 5%. The optimal control strategy is obtained when the optimal delay coefficient is 0.70.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Singhose, W. Command shaping for flexible systems: A review of the first 50 years. Int. J. Precis. Eng. Manuf. 2009, 10, 153–168. [Google Scholar] [CrossRef]
- Li, Y.; Xi, X.; Xie, J.; Liu, C. Study and implementation of a cooperative hoisting for two crawler cranes. J. Intell. Robot. Syst. 2016, 83, 165–178. [Google Scholar] [CrossRef]
- Ramli, L.; Mohamed, Z.; Abdullahi, A.M.; Jaafar, H.; Lazim, I.M. Control strategies for crane systems: A comprehensive review. Mech. Syst. Signal Process. 2017, 95, 1–23. [Google Scholar] [CrossRef]
- Hu, S.; Fang, Y.; Bai, Y. Automation and optimization in crane lift planning: A critical review. Adv. Eng. Inform. 2021, 49, 101346. [Google Scholar] [CrossRef]
- Zhang, S.; Minav, T.; Pietola, M.; Kauranne, H.; Kajaste, J. The effects of control methods on energy efficiency and position tracking of an electro-hydraulic excavator equipped with zonal hydraulics. Autom. Constr. 2019, 100, 129–144. [Google Scholar] [CrossRef]
- Vaughan, J.; Singhose, W.; Kim, D. Analysis of unrestrained crawler-crane counterweights during tip-over accidents. Mech. Based Des. Struct. Mach. 2022, 50, 2006–2031. [Google Scholar] [CrossRef]
- Ai, X.; Zsaki, A.M. Stability assessment of homogeneous slopes loaded with mobile tracked cranes—An artificial neural network approach. Cogent Eng. 2017, 4, 1360236. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, Z.; Yang, T.; Xu, J.; Ma, Z.; Wang, C. Design of a novel modal space sliding mode controller for electro-hydraulic driven multi-dimensional force loading parallel mechanism. ISA Trans. 2020, 99, 374–386. [Google Scholar] [CrossRef] [PubMed]
- Hussain, M.; Ye, Z.; Chi, H.-L.; Hsu, S.-C. Predicting degraded lifting capacity of aging tower cranes: A digital twin-driven approach. Adv. Eng. Inform. 2024, 59, 102310. [Google Scholar] [CrossRef]
- Gu, J.; Qin, Y.; Xia, Y.; Wang, J.; Gao, H.; Jiao, Q. Failure analysis and prevention for tower crane as sudden unloading. J. Fail. Anal. Prev. 2021, 21, 1590–1595. [Google Scholar] [CrossRef]
- Fang, Y.; Wang, P.; Sun, N.; Zhang, Y. Dynamics analysis and nonlinear control of an offshore boom crane. IEEE Trans. Ind. Electron. 2013, 61, 414–427. [Google Scholar] [CrossRef]
- Schlott, P.; Rauscher, F.; Sawodny, O. Modelling the structural dynamics of a tower crane. In Proceedings of the2016 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Banff, AB, Canada, 12–15 July 2016; pp. 763–768. [Google Scholar]
- Zhao, Y.; Wu, X.; Li, F.; Zhang, Y. Positioning and swing elimination control of the overhead crane system with double-pendulum dynamics. J. Vib. Eng. Technol. 2024, 12, 971–978. [Google Scholar] [CrossRef]
- Johns, B.; Abdi, E.; Arashpour, M. Dynamical modelling of boom tower crane rigging systems: Model selection for construction. Arch. Civ. Mech. Eng. 2023, 23, 162. [Google Scholar] [CrossRef]
- Xin, Y.; Dong, R.; Lv, S. Dynamic Simulation Analysis of Truck Crane Based on ADAMS. Recent Pat. Mech. Eng. 2023, 16, 274–282. [Google Scholar] [CrossRef]
- Li, G.; Ma, X.; Li, Z.; Guo, P.; Li, Y. Kinematic coupling-based trajectory planning for rotary crane system with double-pendulum effects and output constraints. J. Field Robot. 2023, 40, 289–305. [Google Scholar] [CrossRef]
- Xia, M.; Wang, X.; Wu, Q. Modeling and anti-sway control method for vertical lift-up/lay-down process of slender-beam payload. ISA Trans. 2024, 149, 337–347. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Tan, N.; Zhou, C.; Zhang, C.; Zhi, Y. Anovel anti-swing positioning controller for two dimensional bridge crane via dynamic sliding mode variable structure. Procedia Comput. Sci. 2018, 131, 626–632. [Google Scholar] [CrossRef]
- Takahashi, H.; Farrage, A.; Terauchi, K.; Sasai, S.; Sakurai, H.; Okubo, M.; Uchiyama, N. Sensor-less and time-optimal control for load-sway and boom-twist suppression using boom horizontal motion of large cranes. Autom. Constr. 2022, 134, 104086. [Google Scholar] [CrossRef]
- Yang, C.; Du, C.; Liao, L. Design and implementation of finite time sliding mode controller for fuzzy overhead crane system. ISA Trans. 2022, 124, 374–385. [Google Scholar]
- Lee, S.G. Modeling and advanced sliding mode controls of crawler cranes considering wire rope elasticity and complicated operations. Mech. Syst. Signal Process. 2018, 103, 250–263. [Google Scholar]
- Rigatos, G. Nonlinear optimal control for the underactuated double-pendulum overhead crane. J. Vib. Eng. Technol. 2024, 12, 1203–1223. [Google Scholar] [CrossRef]
- Cai, P.; Cai, Y.; Chandrasekaran, I.; Zheng, J. Parallel genetic algorithm based automatic path planning for crane lifting in complex environments. Autom. Constr. 2016, 62, 133–147. [Google Scholar] [CrossRef]
- Cai, P.; Chandrasekaran, I.; Zheng, J.; Cai, Y. Automatic path planning for dual-crane lifting in complex environments using a prioritized multiobjective PGA. IEEE Trans. Ind. Inform. 2017, 14, 829–845. [Google Scholar] [CrossRef]
- Jin, X.; Xu, W. Neural network based adaptive robust synchronous control of double-lift overhead crane considering input saturation. J. Frankl. Inst. 2024, 361, 106922. [Google Scholar] [CrossRef]
- Chen, S.; Xie, P.; Liao, J. Cascade NMPC-PID control strategy of active heave compensation system for ship-mounted offshore crane. Ocean Eng. 2024, 302, 117648. [Google Scholar] [CrossRef]
- Chen, S.; Xie, P.; Liao, J.; Wu, S.; Su, Y. NMPC-PID control of secondary regulated active heave compensation system for offshore crane. Ocean Eng. 2023, 287, 115902. [Google Scholar] [CrossRef]
- Ranjan, P.; Wrat, G.; Bhola, M.; Mishra, S.K.; Das, J. A novel approach for the energy recovery and position control of a hybrid hydraulic excavator. ISA Trans. 2020, 99, 387–402. [Google Scholar] [CrossRef] [PubMed]










| System Parameter | Numerical Value |
|---|---|
| Engine parameter (r/min) | 1200 |
| Hydraulic oil density (kg/m3) | 850 |
| Viscosity of hydraulic oil (mm2/s) | 46 |
| The maximum displacement of the main pump (mL/r) | 125 |
| Maximum displacement of motor (mL/r) | 160 |
| Replenishment pump displacement (mL/r) | 52 |
| Compensating oil pressure (bar) | 30 |
| Maximum system pressure (bar) | 350 |
| Brake-opening pressure (bar) | 20 |
| Diameter of drum (m) | 0.7 |
| Speed ratio | 99 |
| Part line of pulley block | 62 |
| Diameter of wire rope (mm) | 32 |
| Payload mass (t) | 200–1200 |
| Load Mass (t) | Retardation Coefficient Kd | Motor Reverse Speed (r/min) | Pressure Overshoot of High-Pressure Chamber | Low-Pressure Chamber Minimum Pressure (bar) | Motor Delay Time (s) |
|---|---|---|---|---|---|
| 200 | 0.55 | 58.9 | 1.7% | 31 | 1.47 |
| 200 | 0.70 | 0 | 1.6% | 31.4 | 1.54 |
| 200 | 0.85 | 0 | 8.8% | 31.3 | 1.63 |
| 600 | 0.55 | 163.3 | 2.2% | 25.1 | 1.25 |
| 600 | 0.70 | 0 | 2% | 29 | 1.3 |
| 600 | 0.85 | 0 | 1.8% | 28.8 | 1.37 |
| 1000 | 0.55 | 248.1 | 1.8% | 17.8 | 1.2 |
| 1000 | 0.70 | 0 | 1.5% | 24.8 | 1.25 |
| 1000 | 0.85 | 0 | 9.1% | 24.1 | 1.31 |
| Load Mass (t) | Brake Interference Opening Time (ms) | Motor Reverse Speed (r/min) | Pressure Overshoot of High-Pressure Chamber |
|---|---|---|---|
| 200 | −70 | 0 | 1.6% |
| 600 | −70 | 0 | 2% |
| 1000 | −70 | 0 | 1.5% |
| 200 | +70 | 0 | 4.8% |
| 600 | +70 | 0 | 4.7% |
| 1000 | +70 | 0 | 4.5% |
| Control Strategy | Load Mass | Initial State | Handle Action | |
|---|---|---|---|---|
| 1 | no | 1000 t | The weight is 0.5 m off the ground. | The weight-lifting handle is slowly pushed to the bottom; keep; the handle slowly returns to the median |
| 2 | yes | 200 t | ||
| 3 | yes | 600 t |
| Contribution Area | Previous Works | Authors’ Proposal |
|---|---|---|
| Dynamic Control Strategies | Dynamic modeling and anti-sway control for vertical lifting of slender beam-shaped loads [18]; anti-sway positioning using sliding mode control [19]; time-optimal control for load sway suppression [20]. | Focuses on secondary lifting challenges, addressing load slipping caused by motor reversal during lifting transitions. |
| Intelligent Algorithms | Utilization of LQR, fuzzy control, and neural network control to optimize crane lifting processes [23,24,25]. | Incorporates a delay coefficient and pressure memory algorithm to achieve stability in secondary lifting operations. |
| Energy Recovery and Efficiency | Advanced energy recovery and position control strategies using neural networks and adaptive control [26,27,28]. | Ensures no load slipping and minimizes system shocks under varying load conditions (200 t, 600 t, 1000 t). |
| System Stability and Safety | Enhanced safety in off-shore crane operations with cascaded NMPC-PID control strategies [27]. | Provides theoretical guidance for stable and efficient operation of crawler crane secondary lifting systems. |
| Research Focus | Studies primarily address anti-sway control and dynamic modeling in cranes [12,13,14,15,16,17,18,19,20,21,22]. | Highlights unique challenges of secondary lifting in large-tonnage crawler cranes, focusing on hydraulic control. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Du, R.; Zhang, K.; Zhang, Y.; Li, Y.; Chen, X. The Secondary Lifting Performance of Crawler Crane Under Delay Coefficient Control Strategy. Machines 2025, 13, 106. https://doi.org/10.3390/machines13020106
Zhang J, Du R, Zhang K, Zhang Y, Li Y, Chen X. The Secondary Lifting Performance of Crawler Crane Under Delay Coefficient Control Strategy. Machines. 2025; 13(2):106. https://doi.org/10.3390/machines13020106
Chicago/Turabian StyleZhang, Jin, Ranheng Du, Kuo Zhang, Yin Zhang, Ying Li, and Xing Chen. 2025. "The Secondary Lifting Performance of Crawler Crane Under Delay Coefficient Control Strategy" Machines 13, no. 2: 106. https://doi.org/10.3390/machines13020106
APA StyleZhang, J., Du, R., Zhang, K., Zhang, Y., Li, Y., & Chen, X. (2025). The Secondary Lifting Performance of Crawler Crane Under Delay Coefficient Control Strategy. Machines, 13(2), 106. https://doi.org/10.3390/machines13020106






